苏州大学2017数学复试题目

合集下载

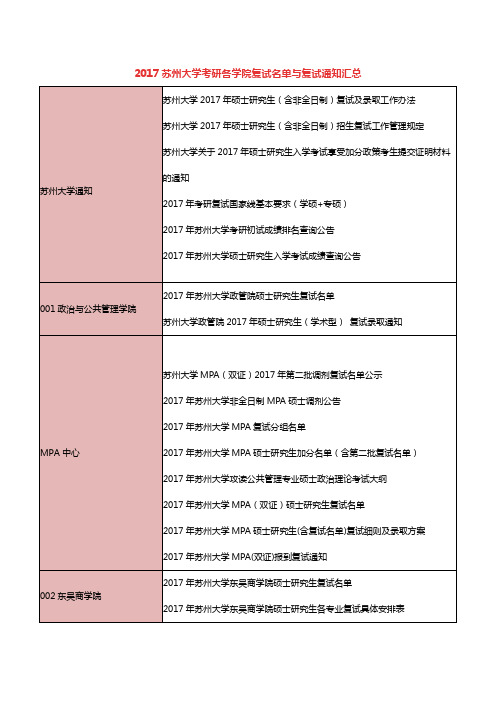
2017苏州大学考研各学院复试名单与复试通知汇总

苏州大学体育学院2017年硕士研究生（含非全日制）招生复试实施细则
2017年苏州大学体育学院硕士研究生入学复试具体安排表2（非全日制）
2017年苏州大学体育学院硕士研究生入学复试名单汇总表
2017年苏州大学体育学院调剂服务系统已开通
2017年苏州大学体育学院硕士研究生入学复试具体安排表
006文学院
2017年苏州大学文学院硕士研究生拟复试名单公示
025医学部附一院
2017年苏州大学附一院硕士研究生复试综合面试安排表
2017年苏州大学附属第一医院硕士研究生复试安排
2017年苏州大学附属第一医院硕士研究生拟复试名单
026医学部附二院
2017年度苏州大学附属第二医院硕士研究生拟复试名单
027护理学院
2017年苏州大学护理学院拟进入复试名单
2017年苏州大学学术学位型护理学硕士研究生入学考试复试方案
2017年苏州大学MPA复试分组名单
2017年苏州大学MPA硕士研究生加分名单（含第二批复试名单）
2017年苏州大学攻读公共管理专业硕士政治理论考试大纲
2017年苏州大学MPA（双证）硕士研究生复试名单
2017年苏州大学MPA硕士研究生(含复试名单)复试细则及录取方案
2017年苏州大学MPA(双证)报到复试通知
关于苏州大学2017年工商管理硕士专业学位(MBA)考生复试的通知
2017年苏州大学工商管理硕士专业学位(MBA)复试环节政治理论笔试大纲
003王健法学院
2017年苏州大学王健法学院硕士研究生复试笔试科目暨考场安排表
2017年苏州大学王健法学院硕士研究生各专业复试具体安排表
2017年苏大法学院硕士研究生拟复试总名单（含调剂复试考生名单）

苏州大学数学考研复试真题答案经验

苏州大学数学考研复试真题答案经验第一天:4月13号中午11.20出发,从温州到苏州汽车车程六个小时。

还是相当快的。

虽然一个人出发,但是一路上基本跟同考数学的几位战友发信息。

彼此照应。

并肩作战。

也不觉得孤单。

到达苏州,。

通过公交车窗。

看到一些很古典的建筑。

发现苏州的楼房多半比较低矮。

通常两三层的样子。

楼房都比较仿古。

尖瓦顶。

木格花窗。

晚上总是挂了很多小灯。

很别致。

街上人行道的围栏也是比较古朴的风格。

还有公交站牌。

网上找来一张图片。

就发上来看看。

这个算是比较典型的了吧。

很多站牌都挂了很多字画。

特别儒雅。

充满了人文气息。

很养眼吧哈。

苏州的确也有很多小石桥。

架在一些小河上。

河水有些绿。

跟温州的比算是很干净了。

伴着很多绿树。

我不禁感慨。

作为一个经济发达的现代城市。

可以保持这样的“小桥流水人家。

”真的相当不容易啊。

如考研论坛里一个朋友所说:像梦一样的国度。

下了站便有一位在考研论坛认识的研三学姐来接我。

领我去了她先订好的旅馆,在观前街醋坊桥这边。

去学校走路也不过十几分钟,离步行街(观前街)又近。

非常方便,学姐很照顾我。

替我提了开水。

看了地形,看到很多民工在。

她说我就一个女孩子在。

很不放心。

跟老板商讨。

还好我不怕哈。

不过第一天晚上睡觉时竟然还吧钥匙落在门上。

还好经学姐提醒。

睡前把门里面的插销插好了,然后学姐带我去逛了下学校。

学姐总是很怕我不认识路的样子。

总是提醒我要这么走。

真的很细心。

临近学校时。

学姐说:”看见苏大,别失望啊。

“我说不会的吧。

呵呵。

晚上灯光比较暗。

我也真的倒没看清楚。

不过可以朦胧中看到很多参天的大树。

还有一些很古朴的建筑。

感觉已经相当满足了。

沉醉其中~~。

走了一会。

研一的学姐发来信息。

说在图书馆。

我们一起过去。

两个学姐聊得挺投机的哈。

研一的学姐给我找来了苏大本科用的抽象代数,还有07年笔试过的一张试卷。

真的很感谢。

这些东西还帮我不少忙。

可以遇上这两位学姐。

实在庆幸至极晚上九点多回到住处。

梳洗整理下。

苏州大学考研复试历年上机题目及答案

if (is_prime(i) &&num-i>1) {printf("%d ", i);split(num-i);return;}}}int main(void){int i;while (scanf("%d", &i)){split(i);printf("\n");}getchar();}要求：统计篇文章中各英文字母的个数，并排序.程序：#include <stdio.h>#include <stdlib.h>typedef struct{char c;int n;} Letter;void swap(Letter*a, Letter*b){Letter temp=*a;*a=*b;*b=temp;}int compare(Letter*a, Letter*b){if (a->n<b->n)return-1;else if (a->n>b->n)return1;elsereturn0;void selection_sort(Letter*ptr, int count){for (int i=0; i<count; i++)for (int j=i+1; j<count; j++)if (compare(&ptr[i], &ptr[j]) >0)swap(&ptr[i], &ptr[j]);}bool is_upper(char c) { return c>='A'&&c<='Z'; } bool is_lower(char c) { return c>='a'&&c<='z'; }int main(void){FILE*fp=fopen("address.txt", "r");Letter letter[26];char c;if(!fp){printf("File opening failed");return EXIT_FAILURE;}for (int i=0; i<26; i++){letter[i].c=i+'a';letter[i].n=0;}while ((c=fgetc(fp)) !=EOF){if (is_upper(c))letter[c-'A'].n++;else if (is_lower(c))letter[c-'a'].n++;}selection_sort(letter, 26);for (int i=0; i<26; i++)printf("%c: %d\n", letter[i].c, letter[i].n);fclose(fp);}2006年复试上机题要求：找出100到1000内的不含9的素数，存到result文件中.程序：#include <stdio.h>bool is_prime(int num){if (num<2)return false;for (int i=2; i*i<=num; i++)if (num%i==0)return false;return true;}bool has9(int num){if (num<0)return false;while (num>0){if (num%10==9)return true;num/=10;}return false;}int main(){FILE*fp=fopen("result.txt", "w");for (int i=100; i<1000; i++)if (is_prime(i) &&!has9(i))fprintf(fp, "%d\n", i);fclose(fp);}2007年复试上机题要求：把10到1000之间满足以下两个条件的数，存到result.txt文件中.是素数.它的反数也是素数，如：123的反数是321.程序：#include <stdio.h>bool is_prime(int num){if (num<2)return false;for (int i=2; i*i<=num; i++)if (num%i==0)return true;}int reverse(int num){int rev=0;while (num>0){rev=rev*10+num%10;num/=10;}return rev;}int main(){FILE*fp=fopen("result.txt", "w");for (int i=100; i<1000; i++)if (is_prime(i) &&is_prime(reverse(i)))fprintf(fp, "%d %d\n", i, reverse(i));fclose(fp);}2008年复试上机题要求：用IE 从FTP 上下载org.dat ，并保存在D盘的根目录中.此文件中按文本方式存放了一段其他文章，其中有若干长度小于15的英文单词，单词之间用空格分开，无其他符号.顺序读取这段文章的不同的单词(大小写敏感)，同时在读取的过程中排除所有的单词THE以及变形，即这些单词不能出现在读取的结果中.将读取的所有单词的首字母转大写后，输出D 根目录下new.txt，每个单词一行.程序：#include <stdio.h>#include <stdlib.h>#include <string.h>bool is_the(char word[15]){char the[] ="the";if (strlen(word) !=strlen(the))return false;for (int i=0; i<strlen(word); i++)word[i] |=0x20;return strcmp(word, the) ==0;}int main(){FILE*fporg=fopen("org.dat", "r");FILE*fpnew=fopen("new.txt", "w");char word[15];if(!fporg||!fpnew){printf("File opening failed");return EXIT_FAILURE;}printf("org.dat:\n");while (fscanf(fporg, "%s", word) !=EOF){printf("%s ", word);if (!is_the(word)){word[0] = (word[0] |0x20) -0x20;fprintf(fpnew, "%s\n", word);}}printf("\n");fclose(fporg);fclose(fpnew);fpnew=fopen("new.txt", "r");printf("new.txt:\n");while (fscanf(fporg, "%s", word) !=EOF)printf("%s ", word);printf("\n");fclose(fpnew);return0;}输出：org.dat:The constructor is used to initialize the object The destructor is used to delete the Object the calling seqence of constructor is opposite to the calling sequence of destructornew.txt:Constructor Is Used To Initialize Object Destructor Is Used To Delete Object Calling Seqence Of Constructor Is Opposite To Calling Sequence Of Destructor2009年复试上机题要求：用IE 浏览器从FTP 上下载org.dat ，并保存在D盘的根目录下.此文件中按文本方式存放了一段其他文章，其中有若干长度小于15的十进制或八进制数字，数字之间用,分开，数字内部存在且仅存在空格.顺序读取这些数字将他们转变为十进制数后按从大到小的顺序排序后，输出到D盘根目录下new.txt，每个数字一行.eg：_235_,34__2,_043_1_,1_3，分别是：十进制235，十进制342，八进制431，十进制13，_代表空格.程序：#include <stdio.h>#include <stdlib.h>#include <string.h>void swap(int*a, int*b){int temp=*a;*a=*b;*b=temp;}int compare(int*a, int*b){if (a<b)return-1;else if (a>b)return1;elsereturn0;}void selection_sort(int*ptr, int count){for (int i=0; i<count; i++)for (int count=i+1; count<count; count++)if (compare(&ptr[i], &ptr[count]) >0)swap(&ptr[i], &ptr[count]);}bool is_num(char c) { return c>='0'&&c<='9'; }bool valid(char c) { return is_num(c) ||c==' '; }int main(){FILE*fporg=fopen("org.dat", "r");FILE*fpnew=fopen("new.txt", "w");int i;int count=0;int arr[128];char c;char num[15];printf("org.dat:\n");{if (is_num(c)){i=0;num[i++] =c;while ((c=fgetc(fporg)) !=EOF&&valid(c))if (is_num(c)) num[i++] =c;num[i] ='\0';printf("%s\n", num);arr[count++] =num[0] =='0'?strtol(num, NULL, 8) :strtol(num, NULL, 10);}}selection_sort(arr, count);for (i=0; i<count; i++)fprintf(fpnew, "%d\n", arr[i]);fclose(fporg);fclose(fpnew);fpnew=fopen("new.txt", "r");printf("new.txt:\n");while (fgets(num, sizeof(num), fpnew))printf("%s", num);fclose(fpnew);}输出：org.dat:235342043113new.txt:235342281132010年复试上机题要求：从FTP 上下载make.exe 和org.dat ，运行make.exe 输入准考证后三位生成data.txt，文件为二进制编码.data.txt内存有2048个整数，其中前n个为非0数，后2048-n个数为0，将其读入数组，计算非零数的个数n.选出n个数中的最大数和最小数.选出n个数中最大素数.将n个数从大到小排序，并平均分成三段(若n非3的整数倍，则不考虑最后的1-2个数)，选出中间段的最大数和最小数.程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>bool is_prime(int num){if (num<2)return false;for (int i=2; i*i<=num; i++)if (num%i==0)return false;return true;}void swap(int*a, int*b){int temp=*a;*a=*b;*b=temp;}int compare(int*a, int*b){if (a<b)return-1;else if (a>b)return1;elsereturn0;}void selection_sort(int*ptr, int count){for (int i=0; i<count; i++)for (int count=i+1; count<count; count++)if (compare(&ptr[i], &ptr[count]) >0)swap(&ptr[i], &ptr[count]);}int main(void){FILE*fp;int num[2048];int min=RAND_MAX;int max_prime=0;int n, i;fp=fopen("data.txt", "wb");if(!fp){printf("File opening failed");return EXIT_FAILURE;}srand(time(NULL));for (i=0; i<1000; i++)num[i] =rand() %4096;for (; i<2048; i++)num[i] =0;fwrite(num, sizeof(int), 2048, fp);fclose(fp);fp=fopen("data.txt", "rb");if(!fp){printf("File opening failed");return EXIT_FAILURE;}fread(num, sizeof(int), 2048, fp);for (n=0; n<2048; n++)if (num[n] ==0)break;printf("n = %d\n", n);for (i=0; i<n; i++){if (min>num[i]) min=num[i];if (max<num[i]) max=num[i];if (is_prime(num[i]) &&num[i] >max_prime) max_prime=num[i];}printf("min = %d\nmax = %d\nmax_prime = %d\n", min, max, max_prime);selection_sort(num, n);printf("min in mid_seg = %d\nmax in mid_seg = %d\n", num[n/3*2-1], num[n/3]);fclose(fp);}输出：n = 1000min = 1max = 4095max_prime = 4093min in mid_seg = 3630max in mid_seg = 18632011年复试上机题要求：输出1000-9999中满足以下条件的所有数：该数是素数.十位数和个位数组成的数是素数，百位数和个位数组成的数是素数.个位数和百位数组成的数是素数，个位数和十位数组成的数是素数. 比如1991，个位和十位组成的数就是19.程序：#include <stdio.h>bool is_prime(int num){if (num<2)return false;for (int i=2; i*i<=num; i++)if (num%i==0)return false;return true;}int main(void){for (int i=1000; i<=9999; i++){int g=i%10;int s= (i/10) %10;int b= (i/100) %10;if (is_prime(i) &&is_prime(i%100) &&is_prime(g*10+b) &&is_prime(g*10+s) &&is_prime(b*10+g))printf("%d ", i);}}输出：1117 1171 1997 2111 2113 2131 2137 2311 2371 2711 2713 2731 2917 3137 3331 3371 3779 3917 4111 4337 4397 4937 5113 5171 5197 5711 5779 6113 6131 6173 6197 6311 6317 6337 6397 6779 6917 6997 7331 7937 8111 8117 8171 8311 8317 8713 8731 8779 9137 9173 9311 9337 9371 93972012年复试上机题要求：从服务器上下载数据文件org.dat文件以二进制方式存放一系列整数，每个整数占4个字节. 从第一个整数规定处于第一象限的坐标点为有效点，请问数据文件中所有点的个数n为多少？有效点的个数k为多少？每个有效点与坐标原点构成一个的矩形，请问k个有效点与坐标原点构成的k个矩形的最小公共区域面积为多少？寻找有效点钟符合下列条件的点：以该点为坐标原点，其它有效点仍然是有效点即处于第一象限(不包括坐标轴上的点). 输出这些点.对所有有效点进行分组，每个有效点有且只有属于一个分组，分组内的点符合下列规则：若对组内所有点的x 坐标进行排序，点p1(x1, y1)在点p2(x2, y2)后面，即x1>x2那么y1>y2，请输出所有的分组.程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>typedef struct{int x;int y;} Coordinate;void swap(Coordinate*a, Coordinate*b){Coordinate temp=*a;*a=*b;*b=temp;}int compare(const Coordinate*lhs, const Coordinate*rhs){if (lhs->x<rhs->x)return-1;if (lhs->x>rhs->x)return1;elsereturn0;}void selection_sort(Coordinate*ptr, int begin, int end){for (int i=begin; i<end; i++)for (int j=i+1; j<end; j++)if (compare(&ptr[i], &ptr[j]) >0)swap(&ptr[i], &ptr[j]);}void display(Coordinate*ptr, int count){for (int i=0; i<count; i++)printf("\n");}int main(void){FILE*fp;Coordinate*xy;int*num;int n, count;fp=fopen("org.dat", "wb");num= (int*) malloc(sizeof(int) *128);srand(time(NULL));for (int i=0; i<128; i++)num[i] =rand() %128-64;fwrite(num, sizeof(int), 128, fp);free(num);fclose(fp);fp=fopen("org.dat", "rb");fseek(fp, 0, SEEK_END);count=ftell(fp) /sizeof(int);n=count/2;num= (int*) malloc(sizeof(int) *count);xy= (Coordinate*) malloc(sizeof(Coordinate) *n);rewind(fp);fread(num, sizeof(int), count, fp);fclose(fp);int k=0;int minx=RAND_MAX;int miny=RAND_MAX;for (int i=0; i<count; i+=2){if (num[i] >0&&num[i+1] >0){xy[k].x=num[i];xy[k].y=num[i+1];if (minx>xy[k].x)minx=xy[k].x;if (miny>xy[k].y)miny=xy[k].y;k++;}}selection_sort(xy, 0, k);printf("valid points:\n");display(xy, k);printf("n = %d k = %d\n", n, k);printf("min area = %d\n", minx*miny);int sorted=0;{selection_sort(xy, sorted, k);printf("points grouped by (%2d, %2d): ", xy[sorted].x, xy[sorted].y);miny=xy[sorted++].y;for (int i=sorted; i<k; i++){if (xy[i].y>=miny){miny=xy[i].y;printf("(%d, %d) ", xy[i].x, xy[i].y);swap(&xy[i], &xy[sorted++]);}}printf("\n");}}输出：valid points:( 3, 8) (10, 62) (11, 40) (20, 6) (26, 7) (26, 20) (29, 31) (33, 10) (34, 37) (37, 33) (50,55) (52, 59) (53, 49) (53, 8) (57, 16) (58, 20)n = 64 k = 16min area = 18points grouped by ( 3, 8): (10, 62)points grouped by (11, 40): (50, 55) (52, 59)points grouped by (20, 6): (26, 20) (29, 31) (34, 37) (53, 49)points grouped by (26, 7): (33, 10) (37, 33)points grouped by (53, 8): (57, 16) (58, 20)2013年复试上机题要求：IntroductionThe project will read ﬂight data from an input ﬁle and ﬂight path requests from another input ﬁle and output the required information.Your TaskYour program should determine if a particular destination airport can be reached from a particular originating airport within a particular number of hops. A hop (leg of a ﬂight) is a ﬂight from oneairport to another on the path between an originating and destination airports. For example, the ﬂight plan from PVG to PEK might be PVG -> CAN -> PEK. So PVG -> CAN would be a hop and CAN -> PEK would be a hop.Input Data FilesPath Input File(PathInput.txt)This input ﬁle will consist of a number of single origination/destination airport pairs (direct ﬂights).The ﬁrst line of the ﬁle will contain an integer representing the total number of pairs in the rest of the ﬁle.6[PVG, CAN][CAN, PEK][PVG, CTU][CTU, DLC][DLC, HAK][HAK, LXA]Path Request File(PathRequest.txt)This input ﬁle will contain a sequence of pairs of origination/destination airports and a max number of hops. The ﬁrst line of the ﬁle will contain an integer representing the number of pairs in the ﬁle.2[PVG, DLC, 2][PVG, LXA, 2]Output File(Output.txt )For each pair in the Path Request File, your program should output the pair followed by YES or NO indicating that it is possible to get from the origination to destination airports within the max number of hops or it is not possible, respectively.[PVG, DLC, YES][PVG, LXA, NO]Assumptions you can make:You may make the following simplifying assumptions in your project:C/C++ is allowed to be used.All airport codes will be 3 letters and will be in all capsOrigination/destination pairs are unidirectional. To indicate that both directions of ﬂight arepossible, two entries would appear in the ﬁle. For example, [PVG, PEK] and [PEK, PVG] wouldhave to be present in the ﬁle to indicate that one could ﬂy from Shanghai to Beijing and fromBeijing to Shanghai.程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>typedef struct Edge{int index;char city[4];struct Edge*next;typedef struct{char city[4];Edge*first;} Vertex;typedef struct{int size;int capacity;Vertex*vertices;} Graph;int find(Vertex*vertices, int count, char src[4]){int i;for (i=0; i<count; i++)if (strcmp(src, vertices[i].city) ==0)break;return i;}void add_edge(Graph*g, char src[4], char dst[4]){int i, j;Edge*e;i=find(g->vertices, g->size, src);if (i==g->size){strcpy(g->vertices[g->size].city, src);g->vertices[g->size].first=NULL;g->size++;}j=find(g->vertices, g->size, dst);if (j==g->size){strcpy(g->vertices[g->size].city, dst);g->vertices[g->size].first=NULL;g->size++;}for (e=g->vertices[i].first; e!=NULL; e=e->next) if (strcmp(e->city, dst) ==0)break;if (e==NULL){e= (Edge*) malloc(sizeof(Edge));strcpy(e->city, dst);e->index=j;e->next=g->vertices[i].first;g->vertices[i].first=e;}bool is_possible(Graph*g, bool*visited, char src[], char dst[], int step){int current;Edge*e;current=find(g->vertices, g->size, src);if (step==0||visited[current])return false;else{visited[current] =true;for (e=g->vertices[current].first; e!=NULL; e=e->next){if (strcmp(e->city, dst) ==0&&step==1)return true;else if (is_possible(g, visited, e->city, dst, step-1))return true;}visited[current] =false;}return false;}void destruct(Graph*g){for (int i=0; i<g->size; i++){while (g->vertices[i].first!=NULL){Edge*e=g->vertices[i].first->next;free(g->vertices[i].first);g->vertices[i].first=e;}}free(g->vertices);}void display(Graph*g){printf("adjacency list:\n");for (int i=0; i<g->size; i++){printf("%s: ", g->vertices[i].city);for (Edge*edge=g->vertices[i].first; edge!=NULL; edge=edge->next) printf("%s ", edge->city);printf("\n");}printf("\n");}int main(void)FILE*fpi=fopen("PathInput.txt", "r");FILE*fpr=fopen("PathRequest.txt", "r");FILE*fpo=fopen("Output.txt", "w");char line[16];char src[4];char dst[4];bool*visited;int step;int num;Graph g;if (!fpi||!fpr||!fpo){printf("failed to open files.\n");exit(-1);}memset(line, 0, sizeof(line));if (fgets(line, sizeof(line), fpi) !=NULL){g.size=0;g.capacity=atoi(line) *2;g.vertices= (Vertex*) malloc(g.capacity*sizeof(Vertex));memset(g.vertices, 0, g.capacity);}while (fgets(line, sizeof(line), fpi) !=NULL){memcpy(src, line+1, 3);src[3] ='\0';memcpy(dst, line+6, 3);dst[3] ='\0';add_edge(&g, src, dst);}display(&g);printf("flight info:\n");visited= (bool*) malloc(g.size);if (fgets(line, sizeof(line), fpr) !=NULL)num=atoi(line);while (fgets(line, sizeof(line), fpr) !=NULL){memcpy(src, line+1, 3);src[3] ='\0';memcpy(dst, line+6, 3);dst[3] ='\0';step=line[11] -'0';memset(visited, false, g.size);if (is_possible(&g, visited, src, dst, step)){printf("[%s, %s, %d, YES]\n", src, dst, step);fprintf(fpo, "[%s, %s, YES]\n", src, dst);}elseprintf("[%s, %s, %d, NO]\n", src, dst, step);fprintf(fpo, "[%s, %s, NO]\n", src, dst);}}destruct(&g);free(visited);fclose(fpi);fclose(fpr);fclose(fpo);}输出：adjacency list:PVG: CTU CANCAN: PEKPEK:CTU: DLCDLC: HAKHAK: LXALXA:flight info:[PVG, DLC, 2, YES][PVG, LXA, 2, NO]2014年复试上机题要求：从网页上下载input.dat 文件，里面是用二进制编写的，里面放了一堆int 型的数，每个数占4个字节，每次读取两个，这两个数构成一个坐标.规定处于第一象限的数是有效点(即x>0, y>0的坐标)，问这么多点中有效点有多少个？现在用户从键盘输入一个坐标和一个数字k，设计算法输出k个离该坐标距离最近的点的坐标和每个坐标到该点的距离，写入到output.txt文件中.程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>typedef struct{int x;int y;} Coordinate;Coordinate point;double distance(const Coordinate*a, const Coordinate*b) {int val= (a->x-b->x) * (a->x-b->x) +(a->y-b->y) * (a->y-b->y);return sqrt((double) val);}void swap(Coordinate*a, Coordinate*b){Coordinate temp=*a;*a=*b;*b=temp;}int compare(const Coordinate*a, const Coordinate*b){double dista=distance(a, &point);double distb=distance(b, &point);if (dista<distb)return-1;if (dista>distb)return1;elsereturn0;}void selection_sort(Coordinate*ptr, int begin, int end) {for (int i=begin; i<end; i++)for (int j=i+1; j<end; j++)if (compare(&ptr[i], &ptr[j]) >0)swap(&ptr[i], &ptr[j]);}void display(Coordinate*ptr, int count){for (int i=0; i<count; i++)printf("(%2d, %2d) ", ptr[i].x, ptr[i].y);printf("\n");}int main(void){FILE*fp;Coordinate*xy;int*num;int count, coord_count;num= (int*) malloc(sizeof(int) *128);srand(time(NULL));for (int i=0; i<128; i++)num[i] =rand() %128-64;fwrite(num, sizeof(int), 128, fp);free(num);fclose(fp);fp=fopen("org.dat", "rb");fseek(fp, 0, SEEK_END);count=ftell(fp) /sizeof(int);coord_count=count/2;num= (int*) malloc(sizeof(int) *count);xy= (Coordinate*) malloc(sizeof(Coordinate) *coord_count);rewind(fp);fread(num, sizeof(int), count, fp);fclose(fp);int valid=0;fp=fopen("output.txt", "w");for (int i=0; i<count; i+=2){if (num[i] >0&&num[i+1] >0){xy[valid].x=num[i];xy[valid].y=num[i+1];valid++;}}printf("valid points:\n");display(xy, valid);printf("total: %d\n", valid);int k;printf("coordinate: ");scanf("%d %d", &point.x, &point.y);printf("k = ");scanf("%d", &k);selection_sort(xy, 0, valid);printf("the nearest %d points to (%d, %d) are:\n", k, point.x, point.y);for (int i=0; i<k; i++){printf("(%2d, %2d) %7.2f\n", xy[i].x, xy[i].y, distance(&xy[i], &point));fprintf(fp, "(%2d, %2d) %7.2f\n", xy[i].x, xy[i].y, distance(&xy[i], &point));}fclose(fp);}输出：valid points:(49, 38) (59, 45) (53, 19) (34, 55) (23, 62) ( 2, 11) (14, 14) (55, 52) (62, 37) (46, 29) (19,57) (12, 18) ( 4, 7)total: 13coordinate: 0 0k = 5the nearest 5 points to (0, 0) are:( 4, 7) 8.06( 2, 11) 11.18(14, 14) 19.80(12, 18) 21.63(46, 29) 54.382015年复试上机题要求：从网页上下载input.dat 文件，里面是用二进制编写的，里面放了一堆int 型的数，每个数占4个字节，每次读取两个，这两个数构成一个坐标.规定处于第一象限的数是有效点(即x>0, y>0的坐标)，问这么多点中有效点有多少个？从键盘上输入k 和n ，从第一问中的有效点中找出距离小于n ，距离小于n 的点的个数要大于k，将它们以文本格式输出到文件中.程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>typedef struct{int x;int y;} Coordinate;Coordinate point;double distance(const Coordinate*a, const Coordinate*b){int val= (a->x-b->x) * (a->x-b->x) +(a->y-b->y) * (a->y-b->y);return sqrt((double) val);}void swap(Coordinate*a, Coordinate*b){Coordinate temp=*a;*a=*b;*b=temp;}int compare(const Coordinate*a, const Coordinate*b){double dista=distance(a, &point);double distb=distance(b, &point);if (dista<distb)return-1;if (dista>distb)return1;elsereturn0;}void selection_sort(Coordinate*ptr, int begin, int end){for (int i=begin; i<end; i++)for (int j=i+1; j<end; j++)if (compare(&ptr[i], &ptr[j]) >0)swap(&ptr[i], &ptr[j]);}void display(Coordinate*ptr, int count){for (int i=0; i<count; i++)printf("(%2d, %2d) ", ptr[i].x, ptr[i].y);printf("\n");}int main(void){FILE*fp;Coordinate*xy;int*num;int count, coord_count;fp=fopen("org.dat", "wb");num= (int*) malloc(sizeof(int) *128);srand(time(NULL));for (int i=0; i<128; i++)num[i] =rand() %128-64;fwrite(num, sizeof(int), 128, fp);free(num);fclose(fp);fp=fopen("org.dat", "rb");fseek(fp, 0, SEEK_END);count=ftell(fp) /sizeof(int);coord_count=count/2;num= (int*) malloc(sizeof(int) *count);xy= (Coordinate*) malloc(sizeof(Coordinate) *coord_count);输出：rewind(fp);fread(num, sizeof(int), count, fp); fclose(fp);int valid=0;fp=fopen("output.txt", "w");for (int i=0; i<count; i+=2){if (num[i] >0&&num[i+1] >0){xy[valid].x=num[i];xy[valid].y=num[i+1];valid++;}}printf("valid points:\n");display(xy, valid);printf("total: %d\n", valid);int k, n, pivot;printf("k = ");scanf("%d", &k);printf("n = ");scanf("%d", &n);pivot=0;while (pivot<valid){point.x=xy[pivot].x;point.y=xy[pivot].y;pivot++;selection_sort(xy, pivot, valid);printf("the points with a distance of less than %d to (%2d, %2d) are:\n", n, point.x, point.y);if (distance(&xy[pivot+k], &point) < (double)n){while (pivot<valid&&distance(&xy[pivot], &point) < (double)n){printf("(%2d, %2d) %7.2f\n", xy[pivot].x, xy[pivot].y, distance(&xy[pivot],&point));fprintf(fp, "(%2d, %2d) %7.2f\n", xy[pivot].x, xy[pivot].y, distance(&xy[pivot], &point));pivot++;}}}fclose(fp);}valid points:2016年复试上机题要求：文本文件input.txt 由若干英文单词和分隔符(空格，回车，换行)构成. 根据如下说明编写程序统计不同单词出现的次数(频度). 将统计结果按出现频度从高到低排序，并将出现频度大于5的单词及其频度输出到文件output.txt 中. 文件格式如图所示多个连续的分隔符被视为一个分隔符.大小写敏感. 每个单词的长度不超过20个字符.单词的数量未知. 如使用定义静态大数组的方式来统计，将被扣除5分.(11, 2) (26, 6) (24, 19) ( 8, 50) ( 2, 18) (60, 32) ( 4, 7) (50, 21) (21, 6) (34, 37) (30,40) ( 5, 16) (31, 59) (60, 34) (18, 32)total: 15k = 3n = 30the points with a distance of less than 30 to (11, 2) are:( 4, 7) 8.60(21, 6) 10.77( 5, 16) 15.23(26, 6) 15.52( 2, 18) 18.36(24, 19) 21.40the points with a distance of less than 30 to (18, 32) are:(30, 40) 14.42(34, 37) 16.76( 8, 50) 20.59(31, 59) 29.97the points with a distance of less than 30 to (50, 21) are:the points with a distance of less than 30 to (60, 32) are:the points with a distance of less than 30 to (60, 34) are:程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>typedef struct Word{int freq;char str[20];} Word;int compare(const Word*lhs, const Word*rhs){if (lhs->freq>rhs->freq) return-1;else if (lhs->freq<rhs->freq) return1;else return0;}void swap(Word*e1, Word*e2){Word tmp=*e1;*e1=*e2;*e2=tmp;}void insertion_sort(Word*ptr, int count){for (int i=1; i<count; i++){int j=i;Word ref=ptr[i];while (j>0&&compare(&ptr[j-1], &ref) >0) {ptr[j] =ptr[j-1];j--;}ptr[j] =ref;}}int find(Word*words, int count, char*str){int i;for (i=0; i<count; i++)if (strcmp(words[i].str, str) ==0)break;return i;}int main(void){FILE*fpr=fopen("input.txt", "r");FILE*fpw=fopen("output.txt", "w");Word*words;char buf[20];int count=0;while (fscanf(fpr, "%s", buf) !=EOF)count++;words= (Word*) malloc(sizeof(Word)*count);rewind(fpr);count=0;while (fscanf(fpr, "%s", buf) !=EOF){int i=find(words, count, buf);if (i==count){strcpy(words[count].str, buf);words[count].freq=0;count++;}words[i].freq++;}insertion_sort(words, count);for (int i=0; i<count&&words[i].freq>5; i++) {fprintf(fpw, "%s %d\n", words[i].str, words[i].freq);printf("%s %d\n", words[i].str, words[i].freq);}free(words);fclose(fpr);fclose(fpw);}输出：that 13The 11It 9to 8we 8here 8a 7and 62017年复试上机题要求：已知：二进制数据文件data.bin中存放了若干个整数，请编写程序完成如下功能：编写程序读取所有数据.以每相邻两个整数为一对按顺序构成二维平面上的坐标点. 例如：有数据12，34，53，25，61，28，78等，则构成六个坐标点如下：(12, 34)、(34, 53)，(53, 25), (25, 61), (61, 28), (28,78)；以每个坐标点为圆心，以该点与其后面第一个点的欧氏距离为半径r. 计算每个圆包含的坐标点数. 计算最后一个点时以其和第一个点的欧氏距离为半径.例如：坐标点(12, 34)的圆半径$r=\sqrt{(12-34)^2+(34-53)^2}$是坐标点(12, 34)与(34, 53)的欧式距离.坐标点(28, 78)的圆半径$r=\sqrt{(28-12)^2+(78-34)^2}$是坐标点(28, 78)与(12, 34)的欧式距离.计算所有圆的点密度值，然后输出点密度值最大的5个坐标点以及相应圆中包含的点数和点密度值. 输出格式要求：坐标点包含点数点密度(x坐标，y坐标)(占5列，右对齐)(占7列，右对齐，保留2位小数)上述文字部分不需要显示.其中：圆的点密度为圆包含的点数除以圆面积，如果点在圆上，则也算圆包含该点，在计算点密度时，圆心也算一个点. 计算圆面积时$\pi=3.14$. 例如：坐标点(2, 1)，则该坐标点也属该坐标点的圆内的一个点.程序：#include <math.h>#include <stdio.h>#include <stdlib.h>#include <string.h>#include <time.h>#define PI 3.14typedef struct{int x;int y;} Coordinate;typedef struct{double r;Coordinate point;int points_num;double density;} Circle;static int compare(const Circle*a, const Circle*b){if (a->density>b->density) return-1;else if (a->density<b->density) return1;else return0;。

2017苏州大学考研复试常见问题

2017苏州大学考研复试常见问题2017年考研复试时间:3月复试据了解，3月份，34所自主划线院校将陆续公布初试成绩基本要求，组织复试。

同时教育部将公布全国初试成绩基本要求，非自主划线院校复试、网上调剂也将开始。

4月份将确认复试时间及调剂。

6月份录取通知书将陆续下达给考生。

2017年考研复试什么时候考？34所自主划线院校会根据各院校的情况自行安排考试时间，除去34所院校，大部分院校都会在国家分数线出来后，大概两周到一个月左右的时间安排考试，所以考生一定要提前做好复试准备。

2016年考研复试国家线2015年考研复试国家线（专硕类）2015年考研复试国家线（学硕类）2014年全国硕士研究生招生考试考生进入复试的初试成绩基本要求2017年考研复试都考什么？复试时一般包括笔试和面试，大多数院校都考综合面试、专业课、英语，MPAcc专业还考政治，其他院校专业也会根据情况有所不同。

2017年考研复试注意事项？首先要带齐报考院校规定的资料，其次复试之前要特别注意吃饭、睡眠等生活问题，目的是为了保障考生有充沛的精神面貌应对考试，最后考生要注意整体形象，这就需要从着装到举止再到表达都要格外重视。

2017年考研复试分数线什么时间公布34所自主划线院校将在3月陆续公布初试成绩基本要求。

之后，自主划线院校开始复试，考生可提前了解招生单位及招生学院发布的复试时间、地点及具体安排，提前为复式做好准备。

3月，教育部也将公布全国初试成绩基本要求。

之后，非自主划线院校复试、网上调剂开始。

2016年苏州大学各学院考研分数线汇总2015年苏州大学考研复试名单各学院汇总2014苏州大学硕士研究生各专业录取分数线汇总2014年苏州大学考研复试分数线2013年苏州大学考研复试分数线2017年考研复试面试的形式？一般院校的复试都会采取结构化面试或是小组面试的形式：结构化面试：是传统的面试形式，大多数高校都采用此类型的复试面试，面试形式是多对一的，大部分是3对1、5对1和7对1，可能还有记录员。

苏州大学复试题及答案

苏州大学复试题及答案一、单项选择题（每题2分，共20分）1. 苏州大学位于哪个省份？A. 浙江省B. 江苏省C. 广东省D. 上海市答案：B2. 苏州大学成立于哪一年？A. 1900年B. 1910年C. 1921年D. 1931年答案：C3. 苏州大学的校训是什么？A. 厚德、博学、求是、创新B. 求是、创新、厚德、博学C. 厚德、博学、笃行、创新D. 笃行、厚德、博学、求是答案：A4. 苏州大学的主要校区位于哪个城市？A. 南京B. 苏州C. 无锡D. 扬州答案：B5. 苏州大学是否属于“211工程”高校？A. 是B. 否答案：A6. 苏州大学是否属于“985工程”高校？A. 是B. 否答案：B7. 苏州大学是否设有研究生院？A. 是B. 否答案：A8. 苏州大学的图书馆藏书量大约是多少？A. 100万册B. 200万册C. 300万册D. 400万册答案：C9. 苏州大学有多少个学院？A. 20个B. 30个C. 40个D. 50个答案：C10. 苏州大学的校徽颜色是什么？A. 蓝色B. 红色C. 绿色D. 黄色答案：A二、多项选择题（每题3分，共15分）1. 苏州大学的优势学科包括哪些？（）A. 工程学B. 材料科学C. 化学D. 计算机科学答案：A B C2. 苏州大学提供的学位类型包括哪些？（）A. 学士B. 硕士C. 博士D. 博士后答案：A B C3. 苏州大学的校园文化活动包括哪些？（）A. 学术讲座B. 文艺演出C. 体育比赛D. 社团活动答案：A B C D4. 苏州大学在哪些领域有国际合作项目？（）A. 教育B. 科研C. 经济D. 文化答案：A B5. 苏州大学的校园设施包括哪些？（）A. 图书馆B. 实验室C. 体育馆D. 学生宿舍答案：A B C D三、简答题（每题5分，共20分）1. 请简述苏州大学的历史沿革。

2. 苏州大学在国内外的学术影响力如何？3. 苏州大学的教育特色是什么？4. 苏州大学为学生提供了哪些就业指导服务？四、论述题（每题10分，共20分）1. 论述苏州大学在推动地方经济发展中的作用。

苏州大学考研真题—苏州大学

苏州大学政治与公共管理学院哲学概论2007公共管理基础理论2007（A卷），2007（B卷）公共部门管理（行政管理）2007（A卷）公共部门管理（社会医学与卫生事业理论）2007管理学（行政管理专业）2000，2001，2002，2003（A卷），2003（B卷），管理学原理（行政管理专业）2004（A卷）行政法学与管理学原理2006管理学与行政法学2005行政管理学1998，2000，2001，2002，2003（A卷），2003（B卷），2004（B卷），2005，2006管理学原理（行政管理学专业）2000——2004行政管理学2003年复试试卷（含行政法学、政治学原理）教育学专业基础综合（全国统考试卷）2007教育学2000——2005马克思主义基本原理2007马克思主义哲学原著2005——2006马克思主义哲学经典著作2002马克思主义哲学原理2002马克思主义哲学1999——2000西方哲学史1999——2000，2002，2004——2006现代西方哲学2006西方现代美学与哲学2005中国哲学原著解读2006伦理学原理1999——2000辩证唯物主义原理1999——2000历史唯物主义原理1999——2000政治学原理1998，2000，2004——2007西方政治思想史1998，2000，2004，2006中西政治思想史2007思想政治教育学2004，2006——2007邓小平理论2000法学院专业基础课（法学各专业）2007（A卷），2007（B卷）基础课（法学）2000——2001基础课(国际法专业)2002基础课（国际法专业）（含法理学、民法学、经济法）2004——2005基础课（诉讼法学专业）（含法理学、民法学、刑法学）2003——2006基础课二（法理学、民法学、经济法）2006（A卷）专业课（国际法学专业）2007（A卷），2007（B卷）专业课B（法律史专业）2007（A卷），2007（B卷）专业课C（宪法学与行政法学专业）2007（A卷），2007（B卷）专业课D（刑法学专业）2007（A卷）专业课E（民商法学专业）2007（A卷）中国法律史2006（A卷）西方法律思想史2006（B卷）行政法学（含行政诉讼法学）2006（A卷）经济法学专业（经济法学）2007（A卷），2007（B卷）中国刑法学2002国际法学与国际私法学2005（B卷），2006（B卷）国际公法和国际私法2000——2002法理学1999——2002，2004——2006国际经济法学2000——2002民法学2000——2002，2004——2006民商法学2002民事诉讼法学2002刑事诉讼法学与民事诉讼法学2003——2006法理学与经济犯罪学2004——2006（A卷）刑法总论与刑法分则2004——2006（A卷）行政法学与行政诉讼法学2005行政法学（含行政诉讼法学）2006（A卷）法理学与宪法学2006（A卷）中国刑事诉讼法2002宪法学2000——2002行政法学2000，2002综合卷（法学、法学理论专业）1999——2001综合卷（理论法学）2002综合卷(行政法专业)2002综合课(民事诉讼法专业)2002法学综合（国经方向）2002综合法学2000，2002体育学院体育学专业基础综合2007（A卷），2007（B卷）运动生理学2002——2005人体生理学2005运动训练学2002，2004——2005运动解剖学2005体育概论2003——2005体育社会学2005教育学院教育学专业基础综合（全国统考试卷）2007——2008教育学2000——2005教学论2000——2001中外教育史2000——2005高等教育2000——2001教育心理学2000——2002，2004教育心理学（课程与教学论专业）2005教育心理学（含发展心理学）（发展与教育心理学专业）2005——2006心理学研究方法2007（A卷），2008（A卷）普通心理学（含实验心理学）2000——2007心理统计与测量2003——2004心理统计2002管理心理学2000——2002公共管理基础理论2007（A卷），2007（B卷）教育经济学2005教育管理学2000——2002，2005文学院文学基础综合2007（A卷），2007（B卷），2008（A卷）评论写作（1）（美学、文艺学、中国古代文学、中国现当代文学、比较文学与世界文学、戏剧戏曲学专业）2007（A卷），2008（A卷）评论写作（戏剧戏曲专业）2004评论写作（中国古代文学专业）2003评论写作（2）（中国现当代文学专业）2000，2002评论写作（2）（新闻学、传播学专业）2007（A卷），2007（B卷）评论写作（3）（文艺学专业）2002评论写作（5）（新闻学、传播学专业）1999——2002新闻传播基础2007（B卷）新闻传播理论2004——2006新闻学基础1999——2006大众传播理论1999——2006古代汉语2001——2008现代汉语2002——2008语言学概论2002，2005（复试）中外文学与比较文学综合考试2005中外文学综合知识2002中国现当代文学史2000，2003——2004，2006中国现代文学史2002文学理论2003——2006文学概论2002中国古代文学2001——2006中国文论2003——2006中国文学史2002外国文学史2002——2006文艺理论2000，2002，2003比较文学原理2002——2006美学原理2004——2005中西美学史2004——2005，2007戏剧理论基础2005，2007中国戏剧2005中国戏剧（古典戏曲或现代戏剧）2006中国现代戏剧史2004语文教学论2004——2005教学论2000——2001教育学专业基础综合（全国统考试卷）2007——2008教育学2000——2005社会学院社会学原理2002——2005，2006（A卷），2007（A卷），2007（B卷）社会研究方法2002——2005，2006（A卷），2007（A卷），2007（B卷）社会调查方法2002中国历史文选2004——2005中国通史2004历史学专业基础（全国统考试卷）2007公共管理基础理论2007（A卷），2007（B卷）公共部门管理（社会保障学）2007（A卷），2007（B卷）管理学原理（旅游管理）2007管理学原理A（社会保障专业）2004（A卷），2004（B卷），2005（A卷），2006（B卷）西方经济学（社会保障专业）2004（A卷），2004（B卷），2005（A卷），2006（A卷）信息检索2007（A卷），2007（B卷）信息资源管理2007（A卷），2007（B卷）档案管理学2004——2005档案学原理2004——2005外国语学院二外法语2001——2002，2004——2008二外日语2000，2002——2008二外俄语2005——2006基础英语1997，1999——2008（1997有答案）翻译与写作1997，2003——2008（1997有答案）英汉双语翻译1999——2002英文写作1999——2002英美文学1997（1997有答案）英语语言学1997（1997有答案）二外英语2005——2007基础俄语2004——2007现代俄语2004——2005综合俄语2006——2007日语写作与翻译2008日语翻译与写作2007综合日语2007——2008教育学专业基础综合（全国统考试卷）2007——2008教育学2000——2005数学科学学院高等代数2000——2002，2004——2007数学分析2000——2002，2004——2007（2004——2005有答案）数学分析与高等代数2003（A卷），2003（B卷）教育学专业基础综合（全国统考试卷）2007教育学2000——2005物理科学与技术学院信号系统与数字逻辑2003——2007数字电子技术基础1999——2002信号与线性系统1997——2002自动控制原理2004——2007（其中2005试卷共3页，缺P3）高等数学2003——2007普通物理2004——2007教育学专业基础综合（全国统考试卷）2007教育学2000——2005信息光学工程、现代光学技术研究所信号系统与数字逻辑2003——2007数字电子技术基础1999——2002信号与线性系统1997——2002自动控制原理2004——2007（其中2005试卷共3页，缺P3）普通物理2004——2007化学化工学院有机化学和仪器分析2007（A卷）有机化学1999，2001，2003，2004，2005（第1种，代码为456），2005（第2种，代码为360），2006有机化学(1)2001——2002化学原理2007（A卷）化学（2）2004——2005化学（3）2003——2006化学四（含无机、分析）2005分析化学2003分析化学（含定量分析、仪器分析）2005无机化学(1)2001——2002无机化学2003——2005物理化学2000——2002，2004——2005高分子化学1999，2003——2007教育学专业基础综合（全国统考试卷）2007教育学2000——2005计算机科学与技术学院数据结构与操作系统2003——2007数据结构与编译原理2005操作系统原理1998——2002数据结构及程序设计1998——2002数据库2003年复试电子信息学院半导体物理与集成电路设计原理2006——2007半导体物理2004信号系统与数字逻辑2003——2007数字电子技术基础1999——2002信号与线性系统1997——2002自动控制原理2004——2007（其中2005试卷共3页，缺P3）机电工程学院理论力学2000——2001，2004——2007自动控制原理2004——2007（其中2005试卷共3页，缺P3）电子技术基础2007材料工程学院材料结构与性能（含高分子物理、无机非金属材料概论，两者任选一门考）2007 专业课程考试（高分子物理或无机非金属材料概论）2005纺织材料学1999，2004——2007纺织工艺学1999服装材料学2004——2005高分子材料成形工艺学1999有机化学和仪器分析2007（A卷）化学原理2007（A卷）有机化学1999，2001，2003，2004，2005（第1种，代码为456），2005（第2种，代码为360），2006有机化学(1)2001——2002高分子化学1999，2003——2005化学（2）2004——2005化学（3）2003——2006化学四（含无机、分析）2005自动控制原理2004——2007（其中2005试卷共3页，缺P3）商学院管理学（企业管理专业）2004——2006管理学（会计学、企业管理、农业经济管理专业）2007（A卷），2007（B卷）管理学原理（企业管理专业）2002——2003微观与宏观经济学2007（A卷），2007（B卷）经济学原理2004——2005经济学（含西方经济学）2002经济学A2002世界经济1998（B卷），1999（A卷），1999（B卷），2000 世界经济理论2003——2005国际经济合作1999——2000财政学2002——2005金融学联考2002——2007（2002——2005有答案）会计学（含财务管理）2002——2005区域经济学2005企业管理专业复试试题2003艺术学院绘画基础（色彩画）2007绘画基础（美术学专业）2003——2006（设计系）色彩2003——2005艺术史2007设计艺术史2005美术史2003——2005医学院基础医学系病理学1994——2005流行病学2005儿科学2002妇产科学2001内科学2002生理B2002生理学2003——2008生物化学2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005药理学2002药学综合2002，2007肿瘤学2002生命科学学院生物化学2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005细胞生物学2004——2007遗传学2005动物生理学2007教育学专业基础综合（全国统考试卷）2007——2008 教育学2000——2005放射医学与公共卫生病理学1994——2005预防综合2007流行病学2005儿科学2002妇产科学2001内科学2002生理B2002生理学2003——2008生物化学2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005药理学2002药学综合2002，2007肿瘤学2002普通物理2004——2007医学院临床医学儿科系病理学1994——2005流行病学2005儿科学2002妇产科学2001内科学2002生理B2002生理学2003——2008生物化学2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005药理学2002药学综合2002，2007肿瘤学2002医学院临床医学系病理学1994——2005流行病学2005儿科学2002妇产科学2001内科学2002生理B2002生理学2003——2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005药理学2002药学综合2002，2007肿瘤学2002药学院药学综合2002，2007药理学2002生物化学2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005化学（2）2004——2005化学（3）2003——2006化学四（含无机、分析）2005有机化学和仪器分析2007（A卷）化学原理2007（A卷）有机化学1999，2001，2003，2004，2005（第1种，代码为456），2005（第2种，代码为360），2006有机化学(1)2001——2002城市科学学院生物化学2008生物化学（生）2003——2007生物化学B 2001——2002，2004——2005。

历年苏州大学考研真题试卷与答案汇总-苏州大学考研真题试卷-苏大考研真题答案-苏大考研真题哪里找？

历年苏州大学考研真题试卷与答案汇总-苏大考研真题哪里找？东吴苏大考研网（苏州大学考研在线咨询入口）汇集了苏州大学各专业历年考研真题试卷（原版），同时与苏州大学专业课成绩前三名的各专业硕士研究生合作编写了配套的真题答案解析，答案部分包括了（解题思路、答案详解）两方面内容。

首先对每一道真题的解答思路进行引导，分析真题的结构、考察方向、考察目的，向考生传授解答过程中宏观的思维方式；其次对真题的答案进行详细解答，方便考生检查自身的掌握情况及不足之处，并借此巩固记忆加深理解，培养应试技巧与解题能力。

具体请点击进入【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大考研817国际法学考试解读与真题答案详解[东吴苏大考研网] 苏州大学347心理学专业综合考研真题试卷（2011-2018）[东吴苏大考研网] 苏州大学333教育综合历年考研真题试卷（2007-2018年）[东吴苏大考研网] 2015年苏州大学335出版综合素质与能力考研真题与答案[东吴苏大考研网] 苏州大学889英语教学论考研真题（2017-2018年，回忆版）[东吴苏大考研网] 苏州大学808管理学考研真题试卷（2000-2015）[东吴苏大考研网] 苏州大学884高分子材料化学考研真题与答案（2015-2018年）[东吴苏大考研网] 苏州大学823艺术史考研真题试卷(2004-2015年)[东吴苏大考研网] 苏州大学822新闻传播专业基础考研真题试卷（2000-2018）[东吴苏大考研网] 苏州大学633教育学专业基础综合真题答案（2007-2018）[东吴苏大考研网] 苏州大学832普通物理考研真题与答案（2003-2015年）[东吴苏大考研网] 苏州大学807微观与宏观经济学考研真题试卷（1999-2017，不含06）[东吴苏大考研网] 苏大637药学基础综合（1）考研真题试卷（09-17）[东吴苏大考研网] 苏大872数据结构与操作系统考研真题答案（真题99-17，答案05-17）[东吴苏大考研网] 2019苏州大学考研889英语教学论复习全析（含真题，共三册）[东吴苏大考研网] 2013-2015年苏州大学612绘画基础（素描命题画）考研真题试卷[东吴苏大考研网] 2019苏大考研398法硕联考专业基础课（非法学）强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研498法硕联考综合课（非法学）强化冲刺题库（共三册）[东吴苏大考研网] 2019苏大878电磁学考研强化冲刺题库[东吴苏大考研网] 2019苏大842自动控制原理考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大电子技术基础考研强化冲刺题库（共两册）【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大理论力学考研强化冲刺题库[东吴苏大考研网] 2019苏大837信号系统与数字逻辑考研强化冲刺题库（共三册）[东吴苏大考研网] 2019苏大考研856物理化学（F）冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研629无机化学（F）强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研628有机化学（F）强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大602高等数学（F）考研强化冲刺题库【共两册】[东吴苏大考研网] 2019苏大考研861高分子化学强化冲刺题库[东吴苏大考研网] 2019苏大考研853物理化学强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研884高分子材料化学强化冲刺题库[东吴苏大考研网] 2019苏大考研835有机化学B强化冲刺题库[东吴苏大考研网] 2019苏大考研834分析化学强化冲刺题库[东吴苏大考研网] 2019苏大考研620无机化学强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研635有机化学A强化冲刺题库[东吴苏大考研网] 2019苏大考研862材料科学基础强化冲刺题库[东吴苏大考研网] 2019苏大838信号与线性系统考研强化冲刺题库[东吴苏大考研网] 2019苏大832普通物理考研强化冲刺题库【共两册】[东吴苏大考研网] 2019苏大601高等数学考研强化冲刺题库【共两册】[东吴苏大考研网] 2019苏大831高等代数考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大618数学分析考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大432统计学考研强化冲刺题库[东吴苏大考研网] 2019苏州大学基础日语考研强化冲刺题库[东吴苏大考研网] 2019苏大448汉语写作与百科知识考研强化冲刺题库[东吴苏大考研网] 2019苏大357英语翻译基础考研强化冲刺题库[东吴苏大考研网] 2019苏大211翻译硕士英语考研强化冲刺题库[东吴苏大考研网] 2019苏大历史学基础考研强化冲刺题库[东吴苏大考研网] 2019苏大826社会保障学考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大658公共管理学考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研660世界史专业基础综合强化冲刺题库（共六册）[东吴苏大考研网] 2019苏大考研659中国史专业基础综合强化冲刺题库（共五册）[东吴苏大考研网] 2019苏大考研824社会研究方法强化冲刺题库[东吴苏大考研网] 2019苏大考研613社会学原理强化冲刺题库[东吴苏大考研网] 2019苏大戏剧与影视学考研核心考点与名校真题详解（共两册）[东吴苏大考研网] 2019苏州大学出版专硕考研强化冲刺题库【共4册】[东吴苏大考研网] 2019苏大822新闻传播专业基础考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大334新闻与传播专业综合能力考研强化冲刺题库[东吴苏大考研网] 2019苏大440新闻与传播专业基础考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大820评论写作（1）考研强化冲刺题库[东吴苏大考研网] 2019苏大625汉语言文字基础考研冲刺题库【共5册】[东吴苏大考研网] 2019苏大445汉语国际教育基础考研强化冲刺题库[东吴苏大考研网] 2019苏大354汉语基础考研强化冲刺题库[东吴苏大考研网] 2019苏州大学心理学考研强化冲刺题库（共七册）【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大802中西政治思想史考研强化冲刺题库[东吴苏大考研网] 2019苏大801中西哲学史考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大654公共管理基础理论考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大652政治学原理考研强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大651哲学概论考研强化冲刺题库[东吴苏大考研网] 2019苏大633教育学专业基础综合考研冲刺题库【共六册】[东吴苏大考研网] 2019苏大665中外音乐史考研复习全析（含历年真题）[东吴苏大考研网] 2019苏州大学666生物化学（农）考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大842自动控制原理考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大841电子技术基础（机电）考研复习全析（含历年真题）【共两册】[东吴苏大考研网] 2019苏大839管理信息系统与数据结构考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大850高等数学基础考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大627生物化学考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大862材料科学基础考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大858材料学（F）考研复习全析（共两册，含历年真题）[东吴苏大考研网] 2019苏大857细胞生物学（F）考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大631生物化学（F）考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大856物理化学（F）考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大629无机化学（F）考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大628有机化学（F）考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大602高等数学（F）考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大838信号与线性系统考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大601高等数学考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大625汉语言文字基础考研复习全析（含历年真题，共六册）[东吴苏大考研网] 2019苏大847金融学概论考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏州大学432统计学考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大831高等代数考研复习全析（含真题答案，共三册）[东吴苏大考研网] 2019苏大618数学分析考研复习全析（含真题答案，共四册）[东吴苏大考研网] 2019苏大616基础俄语考研复习全析（含真题答案，共五册）[东吴苏大考研网] 2019苏大考研243日语强化冲刺题库[东吴苏大考研网] 2019苏大考研241英语强化冲刺题库[东吴苏大考研网] 2019苏大考研245德语强化冲刺题库[东吴苏大考研网] 2019苏大241英语考研复习全析（含历年真题，共五册）[东吴苏大考研网] 2019苏大826社会保障学考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大658公共管理学考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大660世界史专业基础综合考研复习全析（含历年真题，共六册）【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大824社会研究方法考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大613社会学原理考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大437社会工作实务考研复习全析（含历年真题，共四册）[东吴苏大考研网] 2019苏大331社会工作原理考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大337设计基础考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大875设计艺术史考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大346体育综合考研强化冲刺题库（共三册）[东吴苏大考研网] 2019苏大考研《经济法》强化冲刺题库[东吴苏大考研网] 2019苏大817国际法学考研复习全析（含真题答案，共四册）[东吴苏大考研网] 2019苏大816环境与资源保护法学考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大815经济法学考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大813民商法学考研复习全析（含历年真题，共三册）[东吴苏大考研网] 苏大《行政法与行政诉讼法》考试重难点与历年考研真题[东吴苏大考研网] 2019苏大809法学理论考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大852土地资源管理考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大805行政管理学考研复习全析（含真题答案，共三册）[东吴苏大考研网] 2019苏大804管理学基础考研复习全析（含历年真题，共两册）[东吴苏大考研网] 2019苏大802中西政治思想史考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大654公共管理基础理论考研复习全析（共两册，含真题答案）[东吴苏大考研网] 2019苏州大学652政治学原理考研复习全析（含真题，共两册）[东吴苏大考研网] 2019苏州大学333教育综合考研强化冲刺题库[东吴苏大考研网] 2019苏州大学333教育综合考研复习全析（含真题答案，共八册）[东吴苏大考研网] 2019苏大637药学基础综合（1）考研复习全析[东吴苏大考研网] 2019苏大623生物综合考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大854电子技术基础（城市轨道）考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大818理论力学（城市轨道）考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大832普通物理考研复习全析（含历年真题答案，共三册）[东吴苏大考研网] 2019苏大659中国史专业基础综合考研复习全析（含历年真题答案）[东吴苏大考研网] 2019苏大872数据结构与操作系统考研复习全析（含历年真题答案，共三册）[东吴苏大考研网] 2019苏大837信号系统与数字逻辑考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大848植物生理与生物化学考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大840理论力学（机电）考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大346体育综合考研复习全析（含历年真题答案，共五册）[东吴苏大考研网] 2019苏大656体育学专业基础综合考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏州大学867化工原理考研复习全析（含历年真题）【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大835有机化学B考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大884高分子材料化学考研复习全析（含真题答案，共三册）[东吴苏大考研网] 2019苏大843材料科学基础考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大861高分子化学考研复习全析（含历年真题答案，共两册）[东吴苏大考研网] 2019苏大853物理化学考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大834分析化学考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大635有机化学A考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大620无机化学考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大307中医综合考研复习全析（共五册）[东吴苏大考研网] 2019苏大645西医医学综合考研复习全析（共五册）[东吴苏大考研网] 2019苏大653马克思主义基本原理概论考研复习全析（含历年真题）[东吴苏大考研网] 2019苏大803思想政治教育学考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大634心理学专业基础综合考研复习全析（含真题，共10册）[东吴苏大考研网] 2019苏大347心理学专业综合考研复习全析（含真题答案）（共12册）[东吴苏大考研网] 2019苏大考研397法硕联考专业基础（法学）强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研497法硕联考综合课（法学）强化冲刺题库（共三册）[东吴苏大考研网] 2019苏大中国法制史考研强化冲刺题库（张晋藩版）[东吴苏大考研网] 2019苏大考研《刑法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《民法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《行政法与行政诉讼法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《宪法》强化冲刺题库[东吴苏大考研网] 2019苏大考研《法理学》强化冲刺题库[东吴苏大考研网] 2019苏大考研808管理学强化冲刺题库[东吴苏大考研网] 2019苏州大学微观经济学考研强化冲刺题库[东吴苏大考研网] 2019苏州大学宏观经济学考研强化冲刺题库[东吴苏大考研网] 2019苏大801中西哲学史考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏州大学651哲学概论考研复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大433税务专业基础考研复习全析（含真题与答案）[东吴苏大考研网] 2019苏州大学431金融学综合考研复习全析（含历年真题答案，共六册）[东吴苏大考研网] 2019苏大398法硕联考基础课(非法学)考研复习全析（含真题答案，共三册）[东吴苏大考研网] 2019苏大397法硕联考专业基础课(法学)考研复习全析【含真题答案，共三册】东吴苏大考研网（苏州大学考研在线咨询入口）【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2019苏大497法硕联考综合课(法学)考研复习全析（含真题答案，共四册）[东吴苏大考研网] 2019苏大498法硕联考综合课(非法学)考研复习全析（含真题答案，共四册）[东吴苏大考研网] 2019苏大考研《文体与翻译》复习全析（刘宓庆，含历年真题答案）[东吴苏大考研网] 2019苏大考研661教育经济学强化冲刺题库[东吴苏大考研网] 2019苏大考研819教育管理学强化冲刺题库（共两册）[东吴苏大考研网] 2019苏大考研819教育管理学复习全析（含历年真题）[东吴苏大考研网] 2019苏大考研661教育经济学复习全析（含历年真题）[东吴苏大考研网] 2019苏大考研845细胞生物学强化冲刺题库[东吴苏大考研网] 2019苏大考研845细胞生物学复习全析（含历年真题）[东吴苏大考研网] 2019苏大考研621生物化学复习全析（含历年真题，共三册）[东吴苏大考研网] 2019苏大857细胞生物学（F）考研冲刺题库[东吴苏大考研网] 2019苏大生物化学考研强化冲刺题库【共两册】[东吴苏大考研网] 2012-2015年苏州大学880和声写作与分析考研真题[东吴苏大考研网] 2012-2015年苏州大学665中外音乐史考研真题[东吴苏大考研网] 2019苏州大学考研308护理综合考试解读与真题答案[东吴苏大考研网] 2011-2013年苏州大学850普通物理（生物医学工程）考研真题[东吴苏大考研网] 2011-2015年苏州大学859普通动物学考研真题[东吴苏大考研网] 2005、2013-2015年苏州大学882遗传学考研真题[东吴苏大考研网] 2011-2015年苏州大学879普通动物学与普通生态学考研真题[东吴苏大考研网] 2009-2010、2014-2015年苏州大学878电磁学考研真题[东吴苏大考研网] 2011-2015年苏州大学874药剂学考研真题[东吴苏大考研网] 2011-2015年苏州大学868生物教学论考研真题[东吴苏大考研网] 2013-2015年苏州大学860水产养殖学考研真题[东吴苏大考研网] 2009-2015年苏州大学851社会医学考研真题[东吴苏大考研网] 2004-2015年苏州大学845细胞生物学考研真题[东吴苏大考研网] 2013-2015年苏州大学666生物化学（农）考研真题[东吴苏大考研网] 2013-2015年苏州大学664动物生物化学与鱼类生理考研真题[东吴苏大考研网] 2006/2009-2016年苏州大学632卫生事业管理学考研真题[东吴苏大考研网] 2005-2015年苏州大学626预防综合考研真题[东吴苏大考研网] 2001-2015年苏州大学621生物化学考研真题[东吴苏大考研网] 2010-2015年苏州大学353卫生综合考研真题[东吴苏大考研网] 2011-2015年苏州大学349药学综合考研真题[东吴苏大考研网] 2011-2015年苏州大学340农业知识综合二考研真题[东吴苏大考研网] 2011-2013年苏州大学627园林设计基础考研真题[东吴苏大考研网] 2011-2013年苏州大学846中外建筑史考研真题[东吴苏大考研网] 2011、2013年苏州大学622建筑设计基础考研真题[东吴苏大考研网] 2014-2015年苏州大学846设计理论考研真题【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2014-2015年苏州大学622快题设计与表现考研真题[东吴苏大考研网] 2009-2015年苏州大学848植物生理与生物化学考研真题[东吴苏大考研网] 2009-2015年苏州大学662植物学考研真题[东吴苏大考研网] 2013年苏州大学663普通昆虫学考研真题[东吴苏大考研网] 2014-2015年苏州大学877土力学考研真题[东吴苏大考研网] 2012-2015年苏州大学873交通工程学考研真题[东吴苏大考研网] 2009-2015年854苏州大学电子技术基础(城市轨道)考研真题[东吴苏大考研网] 2011-2014年苏州大学818理论力学(城市轨道)考研真题[东吴苏大考研网] 2014-2015年苏州大学870生产计划与控制考研真题[东吴苏大考研网] 2004-2015年苏州大学842自动控制原理考研真题[东吴苏大考研网] 2008-2015年苏州大学841电子技术基础考研真题[东吴苏大考研网] 2000-2015年苏州大学840理论力学（机电）考研真题[东吴苏大考研网] 2014-2015年苏州大学833钢铁冶金学考研真题[东吴苏大考研网] 1999-2017年苏州大学872数据结构与操作系统考研真题[东吴苏大考研网] 2009-2015年苏州大学839管理信息系统与数据结构考研真题[东吴苏大考研网] 2010-2013年苏州大学871数字电路考研真题[东吴苏大考研网] 2014-2015年苏州大学850专业综合（2）考研真题【高等数学基础+生物信息学基础】[东吴苏大考研网] 2004-2015年苏州大学836半导体物理考研真题（换05、08）[东吴苏大考研网] 2014-2015年苏州大学627专业综合（1）考研真题（线性代数+生物化学）[东吴苏大考研网] 2010-2015年苏州大学858材料学（F）考研真题（不含11年）[东吴苏大考研网] 2011-2015年苏州大学857细胞生物学（F）考研真题[东吴苏大考研网] 苏州大学856物理化学（F）考研真题（2001-2006、2010-2015年）[东吴苏大考研网] 2010-2015年苏州大学855普通物理（F）考研真题[东吴苏大考研网] 2010-2015年苏州大学631生物化学（F）考研真题[东吴苏大考研网] 2010-2015年苏州大学629无机化学（F）考研真题[东吴苏大考研网] 2012-2015年苏州大学628有机化学（F）考研真题[东吴苏大考研网] 2010-2015年苏州大学602高等数学（F）考研真题[东吴苏大考研网] 2010-2011年苏州大学867化学教学论考研真题[东吴苏大考研网] 2009-2011年苏州大学834化学原理考研真题[东吴苏大考研网] 2001-2006、2010-2015年苏州大学853物理化学考研真题[东吴苏大考研网] 2013-2015年苏州大学867化工原理考研真题[东吴苏大考研网] 2001-2015年苏州大学835有机化学B考研真题[东吴苏大考研网] 2004-2006、2013-2015年苏州大学834分析化学考研真题[东吴苏大考研网] 2001-2015年苏州大学635有机化学A考研真题[东吴苏大考研网] 1999-2018年苏州大学861高分子化学考研真题[东吴苏大考研网] 2005-2015年苏州大学843材料结构基础考研真题[东吴苏大考研网] 2011-2015年苏州大学838普通物理（光学工程）考研真题[东吴苏大考研网] 2003-2015年苏州大学832普通物理考研真题[东吴苏大考研网] 2009-2015年苏州大学838信号与线性系统考研真题【历年苏州大学考研真题答案下载】[东吴苏大考研网] 2014-2015年苏州大学821材料物理化学考研真题[东吴苏大考研网] 2010-2015年苏州大学866中学物理教学法考研真题[东吴苏大考研网] 2014-2015年苏州大学化学综合考研真题[东吴苏大考研网] 2003-2015年苏州大学601高等数学考研真题[东吴苏大考研网] 2012年苏州大学632艺术理论考研真题[东吴苏大考研网] 2012-2013年苏州大学619戏剧戏曲艺术学考研真题[东吴苏大考研网] 2009-2015年苏州大学245德语考研真题（不含13）[东吴苏大考研网] 2001-2015年苏州大学244法语考研真题（不含03、13）[东吴苏大考研网] 2003-2015年苏州大学243日语考研真题（不含13）[东吴苏大考研网] 2005-2015年苏州大学242俄语考研真题与答案【不含07、08、13】[东吴苏大考研网] 2005-2015年苏州大学241英语考研真题（不含08、13）[东吴苏大考研网] 2010-2015年苏州大学211翻译硕士英语考研真题答案[东吴苏大考研网] 2002-2004、2011年苏州大学会计学考研真题[东吴苏大考研网] 2013-2015年苏州大学661教育学原理考研真题[东吴苏大考研网] 2002-2015年苏州大学634心理学专业基础综合（自命题）考研真题[东吴苏大考研网] 2012-2015年苏州大学881知识产权法学考研真题（无13）[东吴苏大考研网] 2011-2015年苏州大学434国际商务专业基础考研真题与答案[东吴苏大考研网] 1999、2007、2009-2015年苏州大学844纺织材料学考研真题[东吴苏大考研网] 2002-2017年苏州大学431金融学综合考研真题与答案解析[东吴苏大考研网] 2019苏州大学考研新闻与传播专业硕士复习全析（含真题与答案，共六册）[东吴苏大考研网] 2003-2015年苏州大学612绘画基础（色彩命题画）考研真题试卷[东吴苏大考研网] 2019苏大考研633教育学专业基础综合复习全析【含真题答案，共八册】[东吴苏大考研网] 2019苏大考研汉语国际教育硕士复习全析（共四册，含真题答案）[东吴苏大考研网] 2013-2015年苏州大学847金融学概论考研真题[东吴苏大考研网] 2007-2015年苏州大学617综合日语考研真题[东吴苏大考研网] 1998-2015年苏州大学658公共管理学考研真题（不含1999）[东吴苏大考研网] 2000、2004、2013-2016年苏州大学660世界史专业基础综合（自命题）考研真题[东吴苏大考研网] 2000-2017年苏州大学659中国史专业基础综合（自命题）考研真题与答案[东吴苏大考研网] 2002、2006-2015年苏州大学624药学基础综合（2）考研真题[东吴苏大考研网] 2006、2009-2017年苏州大学623生物综合考研真题[东吴苏大考研网] 2012-2015年苏州大学865影视评论写作考研真题[东吴苏大考研网] 2011-2015年苏州大学611影视艺术学考研真题[东吴苏大考研网] 2000-2015年苏州大学819教育管理学考研真题（不含03、04、07、08、09、11年）[东吴苏大考研网] 苏州大学311教育学专业基础综合真题与答案（2007-2017年）[东吴苏大考研网] 2000-2006，2010-2015年苏州大学856物理化学（F）考研真题。

考研复试数学面试题目(3篇)

第1篇一、数学分析1. 请解释实数的完备性及其意义。

2. 证明：若数列{an}单调有界，则{an}收敛。

3. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

4. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

5. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

6. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

7. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

8. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

9. 设函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≠0，证明：存在一点ξ∈(a, b)，使得f'(ξ)=f(b)-f(a)/(b-a)。

10. 证明：若函数f(x)在[a, b]上连续，在(a, b)内可导，且f'(x)≤0，则f(x)在[a, b]上单调递减。

二、高等代数1. 请解释行列式的定义及其性质。

2. 证明：若矩阵A可逆，则|A|≠0。

3. 设矩阵A为n阶方阵，求证：A的行列式|A|等于其特征值的乘积。

4. 证明：若矩阵A为n阶方阵，且|A|=0，则A不可逆。

5. 设矩阵A为n阶方阵，求证：A的行列式|A|等于其特征值的乘积。

数学专业复试题及答案大全

数学专业复试题及答案大全一、选择题1. 极限的定义是：A. 函数在某一点处的值B. 函数在某一点处的导数C. 函数在某一点处的无穷小D. 函数在某一点处的无穷小的比值答案：D2. 微分方程dy/dx = x^2 + y^2的解是：A. y = x^3 + CB. y = x^2 + CC. y = x^2 + CxD. y = Cx^2 + x答案：A3. 矩阵的秩是指：A. 矩阵的行数B. 矩阵的列数C. 矩阵中线性无关的行或列的最大数目D. 矩阵中元素的个数答案：C4. 欧拉公式e^(ix) = cos(x) + i*sin(x)中的i是：A. 虚数单位B. 复数单位C. 矩阵单位D. 向量单位答案：A5. 以下哪个命题是真命题？A. 所有实数都可以表示为有理数B. 所有实数都可以表示为无理数C. 存在无理数不能表示为有理数D. 所有实数都可以表示为整数答案：C二、填空题6. 函数f(x) = x^2 - 4在x = ______ 时取得极小值。

答案：27. 一个圆的半径为r，其面积S可以表示为 S = ______。

答案：πr^28. 集合{1, 2, 3}和{2, 3, 4}的交集是 ______。

答案：{2, 3}9. 若函数f(x)在区间(a, b)内单调递增，则f(x)在该区间的导数______。

答案：恒大于等于010. 欧拉恒等式e^(iπ) + 1 = 0中，π是 ______。

答案：圆周率三、解答题11. 证明：对于任意正整数n，n^5 - n 能被30整除。

证明：首先考虑n的奇偶性。

当n为奇数时，n^5 - n = n(n^4 - 1) = n(n^2 + 1)(n^2 - 1)= n(n^2 + 1)(n + 1)(n - 1)，其中n、n+1、n-1均为连续整数，根据连续整数的性质，至少有一个是5的倍数，另外两个是2的倍数，所以n^5 - n能被30整除。

当n为偶数时，n^5 - n = n(n^4 - 1) = 2n(n^2 + 1)(n^2 - 1) = 2n(n^2 + 1)(n + 1)(n - 1)，同理，其中至少有一个是5的倍数，另外两个是2的倍数，所以n^5 - n也能被30整除。

苏大研究生考试数学专业考研试题数分答案

05数分答案2证明:反证法,假设()f x 在[]0,1上有无穷多个零点,不妨设{}n x ⊂[]0,1,()0,1,2,n f x n ==,则存在一个{}n x 的子列{}kn x 使得0()k n x x k →→+∞,且()0k n f x =,000'0000()()()()()limlim 0k n x x x x f x f x f x f x f x x x x x →→--===--与题设条件矛盾,故()f x 在[]0,1上只有有限个零点.3证明:1).由条件2)()()f x f y L x y -≤-则∀0,,,x y R x y Lεεδδ>∃=∀∈-<有()().f x f y L x y L Lεε-≤-≤=故()f x 在R 上一致连续当然在R 上连续.2).令[]200,2()max (),()0M x f x f x f x dx ππ∈==⎰,由于积分中值定理得存在[]22000010,2,()()2()()02x f x dx f x f x f x dx πππππ∈=∴==⎰⎰讨论a)当0M x x =时,0()()0M f x f x ==当然有[]0,2max ()0x f x L ππ∈=≤b)当0M x x >,由()f x 的周期,得000002()()()()(2)()()(2)2M M M M M f x f x f x f x f x f x L x x L x x Lπππ-=-++-≤-++-=c)0M x x <时由周期性000002()()()()(2)()()(2)2M M M M f x f x f x f x f x f x L x x L x x Lπππ-=-++-≤-++-=综合a)b)c)结论可得.4解:作极坐标变换cos ,sin ,cos sin u u x u y u u x r y r r x r y r x yθθθθ∂∂∂∂∂∂∂===+=+∂∂∂∂∂∂∂ ① (sin )cos u u x u y u ur r x y x yθθθθθ∂∂∂∂∂∂∂=+=-+∂∂∂∂∂∂∂ ② 由① ②可得?,?u u x y ∂∂==∂∂,然后代入就得0uθ∂=∂5证明：1）（i ）当L=0时1()nn n f x a x∞==∑在（-1，1）上有定义（ii ）L ≠0时11lim 1n n nn n a x x a x ++→∞=<(1,1)x ∴∈-，即()f x 的定义域（-1，1） 2）11111lim(1)()lim(()())lim()n n n n x x x n x f x f x xf x a x a x ---∞+→→→=-=-=-∑=111111111111101111lim()lim()lim(())n n n n n n n n n n x x x n n n n n a x a xa x a x xa x a a x ---∞∞∞∞∞++++++++→→→=====-=+-=+-=∑∑∑∑∑11111()lim()n n n n n a a a a a L ∞++→∞=+-=-=∑6解：本题需要讨论，答案省略。

江苏省苏州大学2017届高三数学考前指导试题(含解析)

2017年江苏省苏州大学高考数学考前指导试卷一、填空题：（本大题共14小题，每小题5分，共70分）1．已知集合A={﹣1，0，2}，B={2，a2}，若B⊆A，则实数a的值为．2．已知（2﹣i）（m+2i）=10，i是虚数单位，则实数m的值为．3．一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本．已知B层中每个个体被抽到的概率都为，则总体中的个体数为．4．已知双曲线的离心率为，则b= ．5．如图是一个算法流程图，则输出的k值是6．若a，b∈{0，1，2}，则函数f（x）=ax2+2x+b有零点的概率为．7．设变量x，y满足约束条件，则目标函数z=2x+y的最小值为．8．《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺寸，容纳谷2000斛（1丈=10尺，1尺=10寸，斛为容积单位，1斛≈1.62立方尺，π≈3），则圆柱底面周长约为丈．9．等比数列{a n}的前n项和为S n，公比q≠1，若，则q的值为．10．已知圆C：（x﹣1）2+（y﹣a）2=16，若直线ax+y﹣2=0与圆C相交于AB两点，且CA⊥CB，则实数a的值是．11．设点A（1，2），非零向量，若对于直线3x+y﹣4=0上任意一点P，恒为定值，则= ．12．若a＞0，b＞0，且，则a+2b的最小值为．13．已知函数，若f（x1）=f（x2）=f（x3）（x1＜x2＜x3），则的取值范围为．14．在△ABC中，若3sinC=2sinB，点E，F分别是AC，AB的中点，则的取值范围为．二、解答题：本大题共6小题，共90分.解答应写出必要的文字说明或推理、验算过程.15．已知函数f（x）=（1+tanx）cos2x．（Ⅰ）求函数f（x）的定义域和最小正周期；（Ⅱ）当x∈（0，）时，求函数f（x）的值域．16．如图，在四棱锥S﹣ABCD中，四边形ABCD为矩形，E为SA的中点，SB=2，BC=3，．（Ⅰ）求证：SC∥平面BDE；（Ⅱ）求证：平面ABCD⊥平面SAB．17．在平面直角坐标系xoy中，已知点P（2，1）在椭圆C：上且离心率为．（1）求椭圆C的方程；（2）不经过坐标原点O的直线l与椭圆C交于A，B两点（不与点P重合），且线段AB的中为D，直线OD的斜率为1，记直线PA，PB的斜率分别为k1，k2，求证：k1•k2为定值．18．如图，某地区有一块长方形植物园ABCD，AB=8（百米），BC=4（百米），植物园西侧有一块荒地，现计划利用该荒地扩大植物园面积，使得新的植物园为HBCEFG满足下列要求：E在CD的延长线上，H在BA的延长线上，DE=0.5（百米），AH=4（百米），N为AH的中点，FN⊥AH，EF为曲线段，它上面的任意一点到AD与AH的距离乘积为定值，FG，GH均为线段，GH⊥HA，GH=0.5（百米）．（1）求四边形FGHN的面积；（2）已知音乐广场M在AB上，AM=2（百米），若计划在EFG的某一处P开一个植物园大门，在原植物园ABCD内选一点Q，为中心建一个休息区，使得QM=PM，且∠QMP=90°，问点P在何处，AQ最小．19．已知函数f（x）=，且方程f（x）﹣m=0有两个相异实数根x1，x2（x1＞x2）．（1）求函数f（x）的单调递增区间；（2）求实数m的取值范围；（3）证明：x12x2+x1x22＞2．20．已知数列{c n}的前n项和为S n，满足2S n=n（c n+2）．（1）求c1的值，并证明数列{c n}是等差数列；（2）若，且数列{a n}的最大项为．①求数列{a n}的通项公式；②若存在正整数x，使a m，a n，xa k成等差数列（m＜n＜k，m，n，k∈N*），则当T（x）=a m+a n+xa k 取得最大值时，求x的最小值．2017年江苏省苏州大学高考数学考前指导试卷参考答案与试题解析一、填空题：（本大题共14小题，每小题5分，共70分）1．已知集合A={﹣1，0，2}，B={2，a2}，若B⊆A，则实数a的值为0 ．【考点】18：集合的包含关系判断及应用．【分析】由B⊆A，可得a2=0，解得a．【解答】解：∵B⊆A，∴a2=0，解得a=0．故答案为：0．2．已知（2﹣i）（m+2i）=10，i是虚数单位，则实数m的值为 4 ．【考点】A5：复数代数形式的乘除运算．【分析】利用复数的运算法则、复数相等即可得出．【解答】解：（2﹣i）（m+2i）=10，化为：2m﹣8+（4﹣m）i=0，∴2m﹣8=4﹣m=0，解得m=4．故答案为：4．3．一个总体分为A，B两层，用分层抽样方法从总体中抽取一个容量为10的样本．已知B层中每个个体被抽到的概率都为，则总体中的个体数为120 ．【考点】B3：分层抽样方法；C7：等可能事件的概率．【分析】本题考查分层抽样，抽样过程中每个个体被抽到的可能性相同，这是解决一部分抽样问题的依据，样本容量、总体个数、每个个体被抽到的概率，这三者可以知二求一．【解答】解：∵B层中每个个体被抽到的概率都为，∴总体中每个个体被抽到的概率是，∴由分层抽样是等概率抽样得总体中的个体数为10÷=120故答案为：120．4．已知双曲线的离心率为，则b= ．【考点】KC：双曲线的简单性质．【分析】利用双曲线的离心率列出关系式求解即可．【解答】解：双曲线，可得a=1，e=，可得c=，则b==．故答案为：．5．如图是一个算法流程图，则输出的k值是11【考点】EF：程序框图．【分析】先判断程序框图的结构为直到型循环结构，然后按照程序框图进行循环，直到满足条件时输出k的值即可．【解答】解：根据程序框图分析，本框图为直到型循环结构第1次循环：k=2 S=4﹣5=﹣1 k=﹣1第2次循环：S=1﹣5=﹣4 k=﹣4第3次循环：S=16﹣5=11 k=11第3次循环：S=121﹣5=106 满足条件S＞100，跳出循环输出k的值为11．故答案为：11．6．若a，b∈{0，1，2}，则函数f（x）=ax2+2x+b有零点的概率为．【考点】CB：古典概型及其概率计算公式．【分析】当函数f（x）=ax2+2x+b没有零点时，a≠0，且△=4﹣4ab＜0，即ab＞1，由此利用对立事件概率计算公式能求出函数f（x）=ax2+2x+b有零点的概率．【解答】解：a，b∈{0，1，2}，当函数f（x）=ax2+2x+b没有零点时，a≠0，且△=4﹣4ab＜0，即ab＞1，∴（a，b）有三种情况：（1，2），（2，1），（2，2），基本事件总数n=3×3=9，∴函数f（x）=ax2+2x+b有零点的概率为p=1﹣．故答案为：．7．设变量x，y满足约束条件，则目标函数z=2x+y的最小值为 3 ．【考点】7C：简单线性规划．【分析】先根据条件画出可行域，设z=2x+y，再利用几何意义求最值，将最小值转化为y轴上的截距，只需求出直线z=2x+y，过可行域内的点B（1，1）时的最小值，从而得到z最小值即可．【解答】解：设变量x、y满足约束条件，在坐标系中画出可行域△ABC，A（2，0），B（1，1），C（3，3），则目标函数z=2x+y的最小值为3．故答案为：3．8．《九章算术》商功章有题：一圆柱形谷仓，高1丈3尺寸，容纳谷2000斛（1丈=10尺，1尺=10寸，斛为容积单位，1斛≈1.62立方尺，π≈3），则圆柱底面周长约为 5.4 丈．【考点】L2：棱柱的结构特征．【分析】根据圆柱的体积和高计算出圆柱的底面半径，从而求出圆周的底面周长．【解答】解：由题意得，圆柱形谷仓底面半径为r尺，谷仓高h=尺．于是谷仓的体积V==2000×1.62．解得r≈9．∴圆柱圆的周面周长为2πr≈54尺．故答案为：5.4．9．等比数列{a n}的前n项和为S n，公比q≠1，若，则q的值为﹣．【考点】89：等比数列的前n项和．【分析】根据等比数列的前n项和公式，列方程求解即可．【解答】解：等比数列{a n}中，其前n项和为S n，公比q≠1，由得=，整理得2q2﹣q﹣1=0，即（q﹣1）（2q+1）=0，解得q=﹣或q=1（不合题意，舍去），所以q的值为﹣．故答案为：﹣．10．已知圆C：（x﹣1）2+（y﹣a）2=16，若直线ax+y﹣2=0与圆C相交于AB两点，且CA⊥CB，则实数a的值是﹣1 ．【考点】J9：直线与圆的位置关系．【分析】求出圆C的圆心C（1，a），半径r=4，由直线ax+y﹣2=0与圆C相交于AB两点，且CA⊥CB，得到AB=4，由此利用圆心C（1，a）到直线AB的距离d==，能求出a．【解答】解：圆C：（x﹣1）2+（y﹣a）2=16的圆心C（1，a），半径r=4，∵直线ax+y﹣2=0与圆C相交于AB两点，且CA⊥CB，∴AB==4，∴圆心C（1，a）到直线AB的距离：d==，解得a=﹣1．故答案为：﹣1．11．设点A（1，2），非零向量，若对于直线3x+y﹣4=0上任意一点P，恒为定值，则= 3 ．【考点】9R：平面向量数量积的运算．【分析】设点P（x，y），由点P为直线上的任意一点，表示出向量，由•恒为定值，求出m、n的关系，再计算．【解答】解：设点P（x，y），∵点P为直线3x+y﹣4=0上的任意一点，∴y=4﹣3x，∴=（x﹣1，2﹣3x）；又非零向量=（m，n），∴•=m（x﹣1）+n（2﹣3x）=（m﹣3n）x+（2n﹣m），且恒为定值，∴m﹣3n=0，即m=3n；∴==3．故答案为：3．12．若a＞0，b＞0，且，则a+2b的最小值为．【考点】7F：基本不等式．【分析】把a+2b变形为a+2b=，再利用已知可得a+2b=，利用基本不等式即可得出．【解答】解：∵a＞0，b＞0，且，∴a+2b===﹣==．当且仅当，a＞0，b＞0，且，即，a=时取等号．∴a+2b的最小值为．故答案为．13．已知函数，若f（x1）=f（x2）=f（x3）（x1＜x2＜x3），则的取值范围为（﹣1，0）．【考点】5B：分段函数的应用．【分析】利用导数法，分析函数的单调性及极值，可得f（x1）=f（x2）=f（x3）∈（0，），即有﹣＜x1＜﹣，可得==1+，计算即可得到所求范围．【解答】解：函数，∴函数f′（x）=，故当x＜0时，函数为增函数，且f（x）＜，当0≤x＜1时，函数为增函数，且0≤f（x）＜，当x≥1时，函数为减函数，且0＜f（x）≤，若f（x1）=f（x2）=f（x3）（x1＜x2＜x3），则f（x1）=f（x2）=f（x3）∈（0，），即﹣＜x1＜﹣，故==1+∈（﹣1，0），故答案为：（﹣1，0）．14．在△ABC中，若3sinC=2sinB，点E，F分别是AC，AB的中点，则的取值范围为．【考点】HP：正弦定理．【分析】由已知及正弦定理得AC=AB，AE=AC，AF=，由余弦定理可求BE2=AB2﹣AB2cosA，CF2=AB2﹣AB2cosA，从而化简可得=，结合范围cosA∈（﹣1，1），可求的取值范围．【解答】解：∵3sinC=2sinB，可得：3AB=2AC，即：AC=AB，又∵点E，F分别是AC，AB的中点，∴AE=AC，AF=，∴在△ABE中，由余弦定理可得：BE2=AB2+AE2﹣2AB•AEco sA=AB2+（AB）2﹣2AB•AB•cosA=AB2﹣AB2cosA，在△ACF中，由余弦定理可得：CF2=AF2+AC2﹣2AF•ACcosA=（AB）2+（AB）2﹣2•AB•AB•cosA=AB2﹣AB2cosA，∴==，∵A∈（0，π），∴cosA∈（﹣1，1），可得：∈（，），∴可得： =∈．故答案为：．二、解答题：本大题共6小题，共90分.解答应写出必要的文字说明或推理、验算过程.15．已知函数f（x）=（1+tanx）cos2x．（Ⅰ）求函数f（x）的定义域和最小正周期；（Ⅱ）当x∈（0，）时，求函数f（x）的值域．【考点】GL：三角函数中的恒等变换应用；H1：三角函数的周期性及其求法．【分析】（1）由二倍角公式和两角和的正弦公式对函数化简，利用周期公式求得函数的最小正周期．（2）根据x的范围确定2x+的范围，进而利用正弦函数的性质求得函数的值域．【解答】解：（Ⅰ）函数f（x）的定义域为{x|x≠+kπ，k∈Z}，∵f（x）=（1+tanx）cos2x=cos2x+sinxcosx，=cos2x+sin2x+=sin（2x+）+，∴f（x）的最小正周期为T=π．（Ⅱ）∵x∈（0，），∴＜2x+＜，∴sin（2x+）∈（﹣，1]，∴f（x）∈（0，]，即当x∈（0，）时，求函数f（x）的值域为（0，]．16．如图，在四棱锥S﹣ABCD中，四边形ABCD为矩形，E为SA的中点，SB=2，BC=3，．（Ⅰ）求证：SC∥平面BDE；（Ⅱ）求证：平面ABCD⊥平面SAB．【考点】LY：平面与平面垂直的判定；LS：直线与平面平行的判定．【分析】（Ⅰ）连接AC交BD于F，则F为AC中点，连接EF，可得EF∥SC，即SC∥平面BDE．（Ⅱ）由SB2+BC2=SC2，得BC⊥SB，又四边形ABCD为矩形，即BC⊥平面SAB，可证平面ABCD ⊥平面SAB．【解答】证明：（Ⅰ）连接AC交BD于F，则F为AC中点，连接EF，∵E为SA的中点，F为AC中点，∴EF∥SC，又EF⊂面BDE，SC⊄面BDE，∴SC∥平面BDE．（Ⅱ）∵SB=2，BC=3，，∴SB2+BC2=SC2，∴BC⊥SB，又四边形ABCD为矩形，∴BC⊥AB，又AB、SB在平面SAB内且相交，∴BC⊥平面SAB，又BC⊂平面ABCD，∴平面ABCD⊥平面SAB．17．在平面直角坐标系xoy中，已知点P（2，1）在椭圆C：上且离心率为．（1）求椭圆C的方程；（2）不经过坐标原点O的直线l与椭圆C交于A，B两点（不与点P重合），且线段AB的中为D，直线OD的斜率为1，记直线PA，PB的斜率分别为k1，k2，求证：k1•k2为定值．【考点】KH：直线与圆锥曲线的综合问题；K4：椭圆的简单性质；KL：直线与椭圆的位置关系．【分析】（1）根据椭圆的离心率公式，将P代入椭圆方程，即可求得a和b的值，求得椭圆方程；（2）根据中点坐标公式及直线斜率公式，求得x1+x2=y1+y2，利用点差法求得直线l的斜率，将直线方程代入椭圆方程，利用韦达定理及直线的斜率公式，即可求得k1•k2为定值．【解答】解：（1）由椭圆的离心率e===，则a2=2b2，由P（2，1）在椭圆上，则，解得：b2=3，则a2=6，∴椭圆的标准方程：；（2）证明：设A（x1，y1），B（x2，y2），则D（，），由直线的斜率为1，则x1+x2=y1+y2，由点A，B在椭圆上，则，，两式相减整理得：，x1﹣x2+2（y1﹣y2）=0，则=﹣，设直线l的方程y=﹣x+t，，整理得：3x2﹣4tx+4t2﹣12=0，则x1+x2=，x1x2=，则k1•k2==，===，∴k1•k2为定值．18．如图，某地区有一块长方形植物园ABCD，AB=8（百米），BC=4（百米），植物园西侧有一块荒地，现计划利用该荒地扩大植物园面积，使得新的植物园为HBCEFG满足下列要求：E在CD的延长线上，H在BA的延长线上，DE=0.5（百米），AH=4（百米），N为AH的中点，FN⊥AH，EF为曲线段，它上面的任意一点到AD与AH的距离乘积为定值，FG，GH均为线段，GH⊥HA，GH=0.5（百米）．（1）求四边形FGHN的面积；（2）已知音乐广场M在AB上，AM=2（百米），若计划在EFG的某一处P开一个植物园大门，在原植物园ABCD内选一点Q，为中心建一个休息区，使得QM=PM，且∠QMP=90°，问点P在何处，AQ最小．【考点】5C：根据实际问题选择函数类型．【分析】（1）建立坐标系，根据E点坐标得出曲线EF的方程，从而得出F点坐标，代入梯形的面积公式即可；（2）设P（x，y），用x，y表示出，，根据Q点位置求出x的范围得出P在曲线EF上，利用距离公式和基本不等式的性质得出AQ最小时的x的值即可得出P点位置．【解答】解：（1）以A为原点，以AB，AD所在直线为坐标轴建立平面直角坐标系xOy，如图所示：则E（﹣，4），∴曲线EF的方程为y=﹣，∴F（﹣2，1），N（﹣2，0），H（﹣4，0），G（﹣4，），∴FN=1，GH=，HN=2，∴四边形FGHN的面积为S==（平方百米）．（2）设P（x，y），则=（x﹣2，y），=（y，2﹣x），=（2+y，2﹣x），∴，解得﹣2≤x≤2，∴P点在曲线EF上，﹣2≤x≤﹣，∴y=﹣，∴|AQ|=====﹣x﹣+2≥2+2，当且仅当﹣x=即x=﹣时取等号．∴当P为（﹣，﹣）时，|AQ|最小．19．已知函数f（x）=，且方程f（x）﹣m=0有两个相异实数根x1，x2（x1＞x2）．（1）求函数f（x）的单调递增区间；（2）求实数m的取值范围；（3）证明：x12x2+x1x22＞2．【考点】6B：利用导数研究函数的单调性；6K：导数在最大值、最小值问题中的应用．【分析】（1）求出函数的导数，解关于导函数的不等式，求出函数的递增区间即可；（2）根据函数的单调性求出f（x）的最大值，通过讨论m的范围，结合函数的单调性判断出方程f（x）﹣m=0有两个相异实数根的m的范围即可；（3）由f（x1）=f（x2），得=，令x1=x2t，∵x1＞x2，∴t＞1，问题转化为证明lnt﹣1＞0，即证lnt﹣＞0，（*），令g（t）=lnt﹣，根据函数的单调性证明即可．【解答】解：（1）函数f（x）的定义域是（0，+∞），f′（x）=，令f′（x）＞0，解得：0＜x＜1，故f（x）在（0，1）递增；（2）由（1），令f′（x）＜0，解得：x＞1，故f（x）在（0，1）递增，在（1，+∞）递减，故f（x）max=f（1）=1，①m＞1时，f（x）=m无解，②m=1时，f（x）=1有1个解，③m≤0，x∈（1，+∞）时，f（x）＞0，f（x）=m无解，x∈（0，1）时，f（x）递增，f（x）=m至多1个解，故x∈（0，+∞）时，f（x）=m至多1个解，④0＜m＜1时，x∈（0，1）时，f（x）递增，f（）=0，f（1）=1，f（x）的图象不间断，f（）＜m＜f（1），f（x）=m在（，1）内有1个解，即在（0，1）内有1个解，x∈（1，+∞）时，f（x）是减函数，先证明lnx≤x，令g（x）=lnx﹣x，则g′（x）=，令g′（x）＞0，解得：0＜x＜e，令g′（x）＜0，解得：x＞e，故g（x）在（0，e）递增，在（e，+∞）递减，故g（x）max=g（e）=0，故lnx≤x，x∈（1，+∞）时，f（x）=≤＜＜=，令=m，即x=时，f（）＜m，又m＜f（1），f（x）在（1，+∞）递减，故f（x）=m在（1，）内有1解，即在（1，+∞）内有1解，综上，当且仅当0＜m＜1时，f（x）=m在（0，+∞）内有2解，实数m的范围是（0，1）；（3）由f（x1）=f（x2），得=，令x1=x2t，∵x1＞x2，∴t＞1，=1+2lnx2，则lnx2=lnt﹣，下面证明x1x2＞1，∵lnx1+lnx2=2lnx2+lnt=lnt﹣1，故只需证明lnt﹣1＞0，即证lnt﹣＞0，（*），令g（t）=lnt﹣，∵g′（t）=＞0，∴g（t）在（1，+∞）递增，g（t）在（0，+∞）上的图象不间断，则g（t）＞g（1）=0，（*）成立，故x1x2＞1，由基本不等式得x1+x2＞2＞2，故x12x2+x1x22＞2．20．已知数列{c n}的前n项和为S n，满足2S n=n（c n+2）．（1）求c1的值，并证明数列{c n}是等差数列；（2）若，且数列{a n}的最大项为．①求数列{a n}的通项公式；②若存在正整数x，使a m，a n，xa k成等差数列（m＜n＜k，m，n，k∈N*），则当T（x）=a m+a n+xa k 取得最大值时，求x的最小值．【考点】8H：数列递推式；8E：数列的求和．【分析】（1）2S n=n（c n+2），2S1=2c1=c1+2，解得c1=2，n≥2时，2c n=2S n﹣2S n﹣1．化为：（n﹣2）c n﹣（n﹣1）c n﹣1+2=0．可得（n﹣1）c n+1﹣nc n+2=0，相减可得：2c n=c n+1+c n﹣1．即可证明．（2）①设数列{c n}的公差为d，则a n=．对d分类讨论，d≤0时舍去，d＞0，a n+1﹣a n=＜0，在n≥2时恒成立，可得a2为最大值．由a2==，解得d．可得a n．②存在正整数x，使a m，a n，xa k成等差数列（m＜n＜k，m，n，k∈N*），可得2a n=a m+xa k，T（x）=a m+a n+xa k=3a n，由①可知：a2最大，首先考察a2．此时xa k=2a2﹣a1．即=，解得x=（k≥3）．利用其单调性即可得出．【解答】解：（1）∵2S n=n（c n+2），∴2S1=2c1=c1+2，解得c1=2，n≥2时，2c n=2S n﹣2S n﹣1=n（c n+2）﹣（n﹣1）（c n﹣1+2）．化为：（n﹣2）c n﹣（n﹣1）c n﹣1+2=0．∴（n﹣1）c n+1﹣nc n+2=0，相减可得：2c n=c n+1+c n﹣1．经典资料经典资料一 ∴数列{c n }是等差数列，首项为2．（2）①设数列{c n }的公差为d ，则a n=．若d ≤0，则a n=≤a 1=1，与已知数列{a n }的最大项为矛盾．若d ＞0，a n+1﹣a n=﹣=＜0，在n ≥2时恒成立，可得a 2为最大值．由a 2==，解得d=3．∴a n=．②∵存在正整数x ，使a m ，a n ，xa k 成等差数列（m ＜n ＜k ，m ，n ，k ∈N *），∴2a n =a m +xa k ，T （x ）=a m +a n +xa k =3a n ，由①可知：a 2最大，首先考察a 2．此时xa k =2a 2﹣a 1=﹣1=．即=，解得x=（k ≥3）．考察3k ﹣1=8，11，14，17，…．当k=11时，x 取得最小值，x==96∈N *．∴当T （x ）=a m +a n +xa k 取得最大值时，x 的最小值为96．。

苏州大学历年考研各学科复试真题与经验合集

历年苏州大学考研复试真题与经验合集2016年2016年苏州大学计算机技术专硕考研复试经验2016年苏州大学设计类考研复试经验2016年苏州大学431金融学考研复试总结与分析2016年苏州大学会计专硕考研复试真题+心得分享2016年苏州大学翻译硕士MTI考研复试真题与经验总结2016年苏州大学汉语国际教育考研复试真题2016年苏州大学区域经济学考研复试真题2016年苏州大学计算机技术专硕考研复试经验2015年2015年苏州大学考研法理学复试全程回顾2015年苏州大学艺术设计考研复试必知2015苏大外院MTI英语口译考研复试回顾2015年苏州大学汉硕考研复试真题2015年苏州大学法律硕士（法学）考研复试真题2015年苏州大学高等教育学考研复试真题回顾2015年苏州大学产业经济学考研复试真题2015年苏州大学现当代文学考研复试真题2015年苏州大学古代文学复试真题2015年苏州大学计算机考研复试经验与总结2015苏州大学英语语言文学考研复试真题与经验回顾2015年苏大考研翻译硕士复试经验心得2014年2014年苏州大学社会学考研复试经历总结2014年苏州大学外院英语笔译MTI考研复试经验分享2014年苏州大学翻译硕士mti考研复试经验东吴苏大考研网：苏州大学王健法学院考研复试指南2014苏州大学艺术学院设计学环艺方向考研复试经验2014年苏州大学世界史考研复试真题2014年苏州大学英语语言文学考研复试真题2014年苏州大学古代汉语考研初试+复试看书经验2014年苏州大学文学院考研复试真题苏州大学中国现当代文学考研复试经验分享2013年2013年苏州大学英语笔译考研复试经验2013年苏州大学王建法学院考研复试经验回顾2013年苏州大学分析化学考研复试真题2013年苏州大学mpacc会计专硕考研复试经验分享2013苏州大学法学专业考研复试情况2013年苏州大学计算机考研指南及复试特色2012年2012年苏州大学文学院考研复试真题2012年苏州大学民商法考研复试真题2012年苏州大学会计硕士考研复试真题2012年苏州大学行政管理考研复试真题2012年苏州大学行政法考研复试真题2012年苏州大学分析化学考研复试真题2012年苏州大学骨外科考研复试真题2012年苏州大学翻译硕士（MTI）考研复试经历2012届苏大电子信息学院信息与通信工程专业复试经验分享2012届苏大电子信息学院、信息与通信工程专业的复试情况2011年2011年苏州大学普外科考研复试真题2011年苏州大学汉语教学考研复试真题2011年苏州大学分析化学考研复试真题2011年苏州大学金融学硕考研复试经验2011年苏州大学应用心理学考研复试真题与经验2011年苏州大学发展与教育考研复试经验2010年2010年苏州大学基础数学&应用数学考研复试真题2010年苏州大学计算机学院考研复试经验2010年苏州大学普外考研复试真题2010年苏州大学分析化学考研复试真题（笔试）2009年2009年苏州大学基础数学&应用数学考研复试真题2009年苏州大学现当代文学考研复试真题2009年苏州大学文学史考研复试真题苏州大学数学学院考研复试要点总结2009年苏州大学数学考研复试经验2008年2008年苏州大学法学院考研复试经验2008年苏州大学民商法考研复试经验2008年苏州大学现当代文学考研复试经验2008年苏州大学现当代文学考研复试真题08年苏大企业管理专业复试经验2007年2007年苏州大学基础数学&应用数学考研复试真题2007年苏州大学宪法学与行政法考研复试真题2007年苏州大学刑法学考研复试真题（刑事政策学）2007年苏州大学政管院考研复试真题（政治学）2007年苏州大学诉讼法考研复试经验回顾2007年苏州大学法学理论考研复试真题2007年苏州大学法律史考研复试真题2007年苏州大学国际法学考研复试真题2007年苏州大学环境与资源保护法考研复试真题2007年苏州大学行政法考研复试真题2007年苏州大学经济法学考研复试真题2007年苏州大学民商法考研复试真题各高校往年考生谈考研复试经验2002年苏州大学传媒学院评论写作考研复试真题本文摘自东吴苏大考研网。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2017年苏州大学数学学院数学专业复试题目
《实变函数》
1. 叙述Lebesgue 可积的准确定义。

2. A 是无限集，B 是有限集，证明A 与A B 的势相等（或基数相等）。

3. 求Lebesgue 积分10()f x dx ∫，函数1,()0,c x Q f x x Q
∈ = ∈ 。

4.
求70lim n xdx →∞∫的值。

《常微分方程》
1. 求解微分方程组()211()()212()()112()x t x t y t y t z t z t ′−   ′=−−−   ′− 。

（好像是这个矩阵，具体数字可能有点出入，但如果我没做错的话，计算结果是一样的。

）
2. 证明()()sin x t x t t ′+=有唯一的2π周期解，并求它的2π周期解。

3. 已知,a b 是()()()0x t ax t bx t ′′′++=的参数，
方程的解满足x →∞时，()x y o e −=，求,a b 的取值。

《近世代数》
1. a 是正整数，p 是素数，证明11(mod )p a p −≡。

2. G 是一个n 阶循环群，存在正整数k 使k n ，证明：G 有且仅有一个k 阶子群。

3. R 是一个含幺交换环，M 是一个理想，证明：M 是一个极大理想当且仅当对
任意的r R M ∈−，存在x R ∈，使得1rx M −∈。

《复变函数》
1. 写出函数解析的充要条件（除定义外至少三种）。

2. 计算105()(1)(3)
C dz z i z z +−−∫ ，其中C 表示2z =的周线。

3. 有调和函数(,)y x y x µϕ =
，求它的共轭调和函数(,)x y υ使得()(,)(,)f z x y i x y µυ=+是解析函数。