Matlab粒子群算法工具箱使用方法及实例演示
matlab遗传算法结合粒子群算法

matlab遗传算法结合粒子群算法Matlab中可以将遗传算法和粒子群算法结合起来进行优化问题的求解。
遗传算法是一种模拟生物进化过程的优化算法,通过模拟自然选择、交叉和变异等操作来搜索最优解。
而粒子群算法则是通过模拟鸟群或鱼群等生物体的行为方式来进行搜索。
将遗传算法和粒子群算法结合的方法通常被称为遗传粒子群算法,也被广泛应用于各种实际问题的求解。
下面是一种常见的遗传粒子群算法的步骤:1. 初始化种群:根据问题的特点和要求,初始化一定数量的个体(粒子),每个个体包含染色体和速度信息。
2. 评估适应度:根据问题的适应度函数,对每个个体进行评估,得到其适应度值。
3. 群体最优更新:根据适应度值,更新全局最优个体的位置和适应度值。
4. 个体最优更新:根据个体历史最优位置和群体最优位置,更新每个个体的速度和位置。
5. 选择操作:根据个体适应度值,使用选择算子选择新一代个体。
6. 交叉和变异操作:使用交叉和变异算子对选择后的个体进行操作,生成新的个体。
7. 终止条件判断:判断是否满足终止条件,如达到最大迭代次数或找到满意的解。
8. 返回最优解:返回得到的最优解。
在Matlab中,可以使用遗传算法工具箱(Genetic Algorithm Toolbox)和粒子群算法工具箱(Particle Swarm Optimization Toolbox)来实现遗传粒子群算法。
这两个工具箱提供了相应的函数和工具来方便地进行算法的实现和求解。
需要注意的是,遗传粒子群算法的性能和效果往往与参数的选择有关,因此需要根据具体问题进行调参和优化,以获得更好的结果。
另外,也可以根据具体需求对算法进行改进和扩展,以适应不同类型的问题求解。
给Matlab添加工具箱Toolbox的方法(有截图详细讲解)

给Matlab添加⼯具箱Toolbox的⽅法(有截图详细讲解)
测试环境:Matlab R2012b, Windows 7.
虽然庞⼤的Matlab已经有了很多⼯具箱,但是这些Toolbox可能仍不能满⾜你的要求,常常需要⾃⼰添加Toolbox。
下⾯以添加卡尔曼滤波器⼯具箱为例,讲诉给Matlab添加⼯具箱的⽅法。
Step1:将下载的Kalman.zip解压得到KalmanAll⽂件夹,然后将该⽂件夹拷贝⾄Matlab的Toolbox⽬录,例如:D:\Program
Files\MATLAB\R2010b\toolbox。
Step2:打开Matlab,点击“File->Set Path->Add Folder”,添加刚才拷贝进⼊的KalmanAll⽂件夹。
切记如果你要添加的⽂件夹⾥⾯还有⼦⽂件夹,⼀定要点击“Add with Subfolders”,选择KalmanAll⽂件夹,添加该⽂件夹的所有⼦⽂件夹。
Step3:然后在“File->Preferences->General”⾥⾯,update Toolbox Path Cache就可以了。
最后可以测试⼀下,有没有添加成功。
在Matlab⾥⾯输⼊:which kalman_filter.m,如果可以显⽰正确的路径就OK了。
然后可以输⼊testKalman运⾏⼀个⼩例⼦。
matlab调用粒子群算法

matlab调用粒子群算法
在MATLAB中调用粒子群算法可以通过以下步骤实现:
1. 导入数据,首先,你需要准备好你的数据,包括目标函数、约束条件等。
这些数据将作为粒子群算法的输入。
2. 编写目标函数,在MATLAB中,你需要编写你的目标函数,这是粒子群算法的核心。
目标函数的设计应该能够评估给定参数下的解的质量。
3. 设置粒子群算法参数,在MATLAB中,你需要设置粒子群算法的参数,包括种群大小、迭代次数、惯性权重等。
这些参数的选择会影响算法的性能和收敛速度。
4. 调用粒子群算法函数,MATLAB提供了内置的粒子群算法函数,如“particleswarm”。
你可以直接调用这些函数,并将目标函数和参数传递给它们。
5. 运行算法并获取结果,一旦调用了粒子群算法函数,你就可以运行算法并获取优化后的结果。
你可以分析结果,比较不同参数
设置下的性能,以及对算法进行调优。
总的来说,在MATLAB中调用粒子群算法涉及到准备数据、编写目标函数、设置参数、调用算法函数以及分析结果等步骤。
通过这些步骤,你可以利用MATLAB中的粒子群算法来解决优化问题。
希望这些信息能够帮助到你。
matlab中调用量子粒子群优化算法__理论说明

matlab中调用量子粒子群优化算法理论说明1. 引言1.1 概述本文将介绍在MATLAB中调用量子粒子群优化算法的理论说明。
量子粒子群优化算法是一种启发式搜索算法,利用了经典的粒子群优化算法和量子力学概念,能够有效地解决许多实际问题。
本文将从算法原理、算法流程、参数调节方法等方面对量子粒子群优化算法进行介绍,并重点探讨如何在MATLAB中调用和使用这一算法。
1.2 文章结构本文共分为5个部分,除了引言,还包括量子粒子群优化算法的介绍、MATLAB 中的实现、实验结果与讨论以及结论与未来展望。
首先,我们将详细介绍量子粒子群优化算法的原理和流程,并讨论其相关参数的调节方法。
接下来,我们会简要介绍MATLAB中的优化工具箱,并指导读者如何调用和使用其中的量子粒子群优化函数。
随后,我们将通过案例分析展示该算法在解决实际问题上的应用效果,并进行结果对比分析和讨论。
最后,我们将总结主要研究成果并提出改进方向建议,并探讨未来研究方向和展望。
1.3 目的本文的目的是帮助读者了解量子粒子群优化算法以及如何在MATLAB中调用和使用该算法。
通过本文的阅读,读者将能够掌握量子粒子群优化算法的原理和流程,并具备使用MATLAB工具箱进行实际问题求解的能力。
此外,我们还将通过案例分析和结果讨论,展示该算法在实际问题中的有效性和可行性,并为其改进提出建议。
最后,在结论部分,我们将总结文章内容并提出未来研究方向供读者参考。
2. 量子粒子群优化算法介绍:2.1 量子粒子群优化算法原理量子粒子群优化算法(Quantum Particle Swarm Optimization,简称QPSO)是一种基于群体智能的全局优化算法。
该算法的原理基于典型的粒子群优化算法(Particle Swarm Optimization,简称PSO),同时引入了量子力学中的概念和思想。
在传统的PSO中,每个粒子代表一个搜索解,并通过不断更新自己的位置和速度来寻找全局最优解。
改进粒子群算法matlab代码

改进粒子群算法matlab代码粒子群算法是一种基于群体智能的优化算法,其主要思想是将优化问题转化为粒子在搜索空间中寻找最优解的过程。
粒子群算法的运作方式是通过定义一群随机粒子,并根据它们在搜索空间中的位置和速度,来引导粒子向着更好的解决方案进行搜索。
以下是改进版粒子群算法的MATLAB代码:%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 粒子群算法-改进版%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 初始化参数和粒子群function [gbest_x, gbest_y] = PSO(num_particles,max_iterations, f, lower_bound, upper_bound)% 定义粒子群基本参数w = 0.7; % 惯性权重c1 = 1.4; % 学习因子1c2 = 1.4; % 学习因子2% 初始化粒子位置和速度particles_position = unifrnd(lower_bound, upper_bound, [num_particles, 2]);particles_velocity = zeros(num_particles, 2);% 初始化个体最优解和全局最优解pbest_position = particles_position;pbest_value = zeros(num_particles, 1);for i = 1:num_particlespbest_value(i) = f(particles_position(i,:));end[global_min_value, global_min_index] = min(pbest_value); gbest_position = particles_position(global_min_index, :);gbest_value = global_min_value;% 迭代优化for iter = 1:max_iterationsfor i = 1:num_particles% 更新粒子速度particles_velocity(i,:) = w *particles_velocity(i,:) ...+ c1 * rand() * (pbest_position(i,:) -particles_position(i,:)) ...+ c2 * rand() * (gbest_position -particles_position(i,:));% 限制粒子速度范围particles_velocity(i,1) = max(particles_velocity(i,1), lower_bound);particles_velocity(i,1) = min(particles_velocity(i,1), upper_bound);particles_velocity(i,2) = max(particles_velocity(i,2), lower_bound);particles_velocity(i,2) = min(particles_velocity(i,2), upper_bound);% 更新粒子位置particles_position(i,:) = particles_position(i,:) + particles_velocity(i,:);% 限制粒子位置范围particles_position(i,1) = max(particles_position(i,1), lower_bound);particles_position(i,1) = min(particles_position(i,1),upper_bound);particles_position(i,2) = max(particles_position(i,2), lower_bound);particles_position(i,2) = min(particles_position(i,2), upper_bound);% 更新个体最优解temp_value = f(particles_position(i,:));if temp_value < pbest_value(i)pbest_value(i) = temp_value;pbest_position(i,:) = particles_position(i,:);endend% 更新全局最优解[temp_min_value, temp_min_index] = min(pbest_value);if temp_min_value < gbest_valuegbest_value = temp_min_value;gbest_position = pbest_position(temp_min_index,:);endend% 返回全局最优解gbest_x = gbest_position(1);gbest_y = gbest_position(2);end其中,num_particles为粒子数目,max_iterations为最大迭代次数,f为目标函数句柄,lower_bound和upper_bound为搜索空间的下界和上界。
matlab粒子群算法默认种群规模

【主题】matlab粒子裙算法默认种裙规模【内容】一、介绍matlab粒子裙算法matlab粒子裙算法(Particle Swarm Optimization,简称PSO)是一种启发式优化算法,源自于鸟裙觅食的行为。
PSO算法通过迭代搜索空间中的潜在解,寻找最优解。
其基本思想是模拟鸟裙觅食的行为,在搜索空间中不断调整潜在解的位置,直至找到最优解。
二、 PSO算法的种裙规模在matlab中,PSO算法的种裙规模即为裙体中粒子的数量,它决定了搜索空间的范围和算法的性能。
PSO算法的默认种裙规模为50。
种裙规模的设定直接影响算法的搜索速度和全局最优解的找寻能力。
三、种裙规模的设置原则1. 确定问题的复杂度:种裙规模应根据待解决问题的复杂度来设定。
对于复杂、高维度的问题,适当增加种裙规模有助于提高搜索效率。
2. 计算资源的限制:种裙规模的增加会带来更高的计算开销,因此在资源有限的情况下,需要平衡种裙规模和计算性能。
3. 经验设定:在实际应用中,也可根据经验和实验结果来调整种裙规模,找到最适合问题的设置。
四、调整种裙规模的方法1. 网格搜索法:通过在一定范围内以一定步长遍历种裙规模,评估不同规模下算法的性能和收敛速度,找到最佳的种裙规模。
2. 实验验证法:在实际问题中,通过对不同种裙规模下算法的性能进行实验验证,找到最适合问题的种裙规模。
3. 算法迭代法:根据算法的迭代次数和搜索效果来动态调整种裙规模,逐步优化算法的性能。
五、结语种裙规模是PSO算法中一个重要的参数,它直接关系到算法的搜索效率和性能。
在使用matlab的PSO算法时,合理设置种裙规模对于解决实际问题非常重要。
需要根据问题本身的特点、计算资源的限制以及实际应用情况来进行合理的选择和调整。
希望本文对于matlab粒子裙算法默认种裙规模的设置能够提供一些参考和帮助。
六、种裙规模与算法性能的关系种裙规模是PSO算法中最为关键的参数之一,其大小直接影响算法的搜索效率和全局最优解的寻找能力。
Matlab粒子群算法工具箱使用方法及实例演示

粒子群算法是一种优化算法,本演示将介绍Matlab粒子群算法工具箱的使用 方法,并给出实例演示。
了解粒子群算法
优点
全局搜索能力强
缺点
易受局部最优解影响
应用领域
函数优化、机器学习、图 像处理、模式识别等
Matlab粒子群算法工具箱介绍
1 功能
提供了丰富的粒子群算 法相关函数
判断算法是否达到收敛
优化函数
定义待优化的问题
粒子群算法案例实现
1
训练数据集创建
2
准备训练数据集,用于优化问题求解
3
构建优化函数
定义优化问题,如函数最小化或参数 寻优
粒子初始化
随机生成粒子群初始状态
粒子群算法参数调节方法
惯性权重
控制粒子搜索速度和全局局 部权衡
加速度因子
影响粒子个体与全局经验信 息的权重
2 使用
方便易学,适用于不同 应用场景
3 扩展性
支持自定义函数和参数 设置
工具箱的下载和安装
1
下载
从MathWorks官网或File Exchange下载工具箱
2
安装
运行安装程序并按照提示进行安装
3
添加路径
将工具箱文件夹添加到Matlab的路径中
工具箱的主要函数
初始化函数
用于生成初始粒子群状态
收敛性判断函数
收敛因子
控制算法收敛速度和精确度
粒子群算法在函数优化中的应用
1 目标函束优化
有约束条件下的函数优化问题
2 参数寻优
机器学习算法参数调优
粒子群算法在机器学习中的应用
神经网络训练
优化神经网络的权重和偏置
matlab粒子群算法实例

matlab粒子群算法实例
粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,常用于解决寻优问题。
在Matlab中,你可以使用以下示例来实现粒子群算法:
matlab.
% 首先,定义适应度函数。
fitnessFunction = @(x) x(1)^2 + x(2)^2; % 这里以一个简单的二元函数 x^2 + y^2 为例。
% 然后,设置粒子群算法的参数。
options =
optimoptions('particleswarm','SwarmSize',100,'HybridFcn',@f mincon);
% 接着,运行粒子群算法。
[x,fval] = particleswarm(fitnessFunction,2,[-10,-
10],[10,10],options);
% 最后,输出结果。
disp('最优解,');
disp(x);
disp('最优值,');
disp(fval);
在这个示例中,首先定义了一个简单的二元适应度函数,然后
使用`optimoptions`函数设置了粒子群算法的参数,包括群体大小
和混合函数。
接着调用`particleswarm`函数来运行粒子群算法,最
后输出最优解和最优值。
当然,这只是一个简单的示例,实际应用中你可能需要根据具
体问题对适应度函数和算法参数进行调整。
希望这个示例能帮到你。
matlab自带粒子群算法

matlab自带粒子群算法中括号在MATLAB中具有重要的功能和应用,其中之一就是在自带的粒子群算法中。
粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,广泛应用于解决优化问题。
而MATLAB则提供了丰富的工具箱,包括自带的粒子群算法函数,方便用户直接使用这一高效优化算法来解决复杂的问题。
本文将详细介绍MATLAB中自带的粒子群算法的基本概念、工作原理、使用方法,以及一些注意事项和优化技巧。
一、粒子群算法的基本概念和原理粒子群算法是一种启发式算法,模拟了鸟群或鱼群等群体的行为进行问题求解。
算法的基本思想是将可能的解空间看作是粒子的搜寻范围,每个粒子代表一种解,通过迭代的方式不断更新粒子的位置和速度,以找到最优解。
1.1 粒子的位置和速度粒子的位置是解的表示,而速度则是解的搜索方向和速率。
在粒子群算法中,可以将解空间看作是一个多维空间,每个粒子都有一个位置向量,表示该粒子对应的解。
而速度向量则表示了该粒子在搜索过程中的移动方向和速率。
1.2 适应度函数适应度函数用于评价每个粒子的解的质量,也称为目标函数。
在优化问题中,我们希望通过粒子群算法求解的是目标函数的最小(或最大)值。
因此,适应度函数的选择在粒子群算法中尤为重要,它直接影响到算法的性能和效果。
1.3 群体的协作群体的协作是粒子群算法的核心思想之一。
每个粒子通过与其他粒子之间的信息交流来调整自己的搜索方向和速率,从而达到更好的解。
这种信息交流一般通过粒子之间的位置和速度更新公式来实现。
二、MATLAB中自带的粒子群算法函数MATLAB提供了自带的粒子群算法函数,可以直接调用并应用于问题求解。
下面将介绍一些常用的粒子群算法函数及其使用方法。
2.1 PSO函数在MATLAB中,可以使用pso函数来进行粒子群算法的优化。
该函数的基本形式如下:[x,fval,exitFlag,output] = pso(problem)其中,problem是一个结构体,用于存储问题的相关信息,包括目标函数、约束条件等。
(完整word版)用MATLAB编写PSO算法及实例

用MATLAB 编写PSO 算法及实例1.1 粒子群算法PSO 从这种模型中得到启示并用于解决优化问题。
PSO 中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为粒子。
所有的粒子都有一个由被优化的函数决定的适值( fitness value) ,每个粒子还有一个速度决定它们飞翔的方向和距离。
然后粒子们就追随当前的最优粒子在解空间中搜索。
PSO 初始化为一群随机粒子(随机解),然后通过迭代找到最优解。
在每一次迭代中,粒子通过跟踪两个极值来更新自己;第一个就是粒子本身所找到的最优解,这个解称为个体极值;另一个极值是整个种群目前找到的最优解,这个极值是全局极值。
另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。
假设在一个维的目标搜索空间中,有个粒子组成一个群落,其中第个粒子表示为一个维的向量,。
第个粒子的“飞行 ”速度也是一个维的向量,记为,。
第个粒子迄今为止搜索到的最优位置称为个体极值,记为,。
整个粒子群迄今为止搜索到的最优位置为全局极值,记为在找到这两个最优值时,粒子根据如下的公式(1.1)和( 1.2)来更新自己的速度和位置:(1.1) (1. 2)其中:和为学习因子,也称加速常数(acceleration constant),和为[0,1]范围内的均匀随机数。
式(1.1)右边由三部分组成,第一部分为“惯性(inertia)”或“动量(momentum)”部分,反映了粒子的运动“习惯(habit)”,代表粒子有维持自己D N i D ),,,(21iD i i i x x x X N i ,,2,1 i D ),,21i iD i i v v v V ,( 3,2,1 i i ),,,(21iD i i best p p p p N i ,,2,1 ),,,(21gD g g best p p p g )(2211id gd id id id id x p r c x p r c v w v id id id v x x 1c 2c 1r 2r先前速度的趋势;第二部分为“认知(cognition)”部分,反映了粒子对自身历史经验的记忆(memory)或回忆(remembrance),代表粒子有向自身历史最佳位置逼近的趋势;第三部分为“社会(social)”部分,反映了粒子间协同合作与知识共享的群体历史经验。
粒子群算法解决VRP代码(matlab)

粒子群算法解决VRP代码(matlab)particle_swarm_optimization.m文件:function PSOforTSP%初始化Alpha=0.25; %个体经验保留概率Beta=0.25; %全局经验保留概率NC_max=100; %最大迭代次数m=80; %微粒数CityNum=14; %问题的规模(城市个数)[dislist,Clist]=tsp(CityNum);NC=1;%迭代计数器R_best=zeros(NC_max,CityNum); %各代最佳路线L_best=inf.*ones(NC_max,1);%各代最佳路线的长度L_ave=zeros(NC_max,1);%各代路线的平均长度%产生微粒的初始位置for i=1:mx(i,:)=randperm(CityNum);L(i)=CalDist(dislist,x(i,:));endp=x; %p为个体最好解pL=L;[L_best(1,1) n_best]=min(L);R_best(1,:)=x(n_best,:);L_ave(1,1)=mean(L);%初始交换序v=ones(CityNum-1,2,m)*(round(rand*(CityNum-1))+1);figure(1);while NC<=NC_max %停止条件之一:达到最大迭代次数for i=1:mxnew(i,:)=changeFun(x(i,:),v(:,:,i));A=changeNum(x(i,:),p(i,:));Arand=randFun(A,Alpha);xnew(i,:)=changeFun(xnew(i,:),Arand);B=changeNum(x(i,:),R_best(NC,:));Brand=randFun(B,Beta);xnew(i,:)=changeFun(xnew(i,:),Brand);v(:,:,i)=changeNum(x(i,:),xnew(i,:));L(i)=CalDist(dislist,xnew(i,:));if L(i)<pl(i)< p="">p(i,:)=xnew(i,:);pL(i)=L(i);endend[L_bestnew n_best]=min(L);R_bestnew=xnew(n_best,:);L_ave(NC+1,1)=mean(L);if L_bestnew<l_best(nc,1)< p="">L_best(NC+1,1)=L_bestnew;R_best(NC+1,:)=R_bestnew;elseL_best(NC+1,1)=L_best(NC,1);R_best(NC+1,:)=R_best(NC,:);endx=xnew;drawTSP10(Clist,R_best(NC,:),L_best(NC,1),NC,0); %pause;NC=NC+1;end%输出结果Pos=find(L_best==min(L_best));Shortest_Route=R_best(Pos(1),:);Shortest_Length=L_best(Pos(1)); figure(2);plot([L_best L_ave]);legend('最短距离','平均距离'); endfunction xnew=changeFun(x,C); changeLen=size(C,1);xnew=x;for i=1:changeLena=xnew(C(i,1));xnew(C(i,1))=xnew(C(i,2));xnew(C(i,2))=a;endendfunction C=changeNum(x,y); CityNum=size(x,2);C=ones(CityNum-1,2);for i=1:CityNum-1pos=find(x==y(i));C(i,:)=[i pos];x=changeFun(x,C(i,:));endendfunction v=randFun(v,w);randLen=size(v,1);for i=1:randLenif rand>wv(i,2)=v(i,1);endendendfunction F=CalDist(dislist,s)%计算回路路径距离DistanV=0;n=size(s,2);for i=1:(n-1)DistanV=DistanV+dislist(s(i),s(i+1));endDistanV=DistanV+dislist(s(n),s(1));F=DistanV;endfunction [DLn,cityn]=tsp(n)city14=[0 0;0.3 0.334;0.08 0.433;0.166 0.456;0.5 0.4439;0.2439 0.1463;0.1207 0.2293;0.2293 0.761;0.6171 0.9414;0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];for i=1:14for j=1:14DL14(i,j)=((city14(i,1)-city14(j,1))^2+(city14(i,2)-city14(j,2))^2)^0.5;endendDLn=DL14;cityn=city14;enddrawTSP10.m文件:function m=drawTSP(Clist,BSF,bsf,p,f)CityNum=size(Clist,1);for i=1:CityNum-1plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(BSF(i +1),2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');hold on;endaxis([0,1,0,1]);plot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNu m),2),Clist(BSF(1), 2)],'ms-','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g');title([num2str(CityNum),'城市TSP']);if f==0text(0.1,0.1,['第',int2str(p),' 步',' 最短距离为',num2str(bsf)]);elsetext(0.1,0.1,['最终搜索结果:最短距离',num2str(bsf)]);endhold off;pause(0.05);</l_best(nc,1)<></pl(i)<>。
gpu粒子群算法 matlab

gpu粒子群算法 matlabGPU(图形处理器单元)粒子群算法在MATLAB中的应用是一个相对复杂的问题,需要从多个角度来进行讨论。
首先,让我们来谈谈GPU加速。
在MATLAB中,可以使用Parallel Computing Toolbox来利用GPU加速算法。
粒子群算法作为一种基于迭代的优化算法,可以通过并行化加速来提高计算性能。
在MATLAB中,可以使用GPUArray来将数据传输到GPU上进行并行计算,从而加速粒子群算法的执行。
这种方法可以显著提高算法的运行速度,特别是在处理大规模数据时。
其次,需要考虑粒子群算法在GPU上的实现。
在MATLAB中,可以使用内置的粒子群优化函数(如particleswarm)来实现粒子群算法。
通过将数据和计算迁移到GPU上,可以利用并行计算的优势来加速粒子群算法的执行。
需要注意的是,对于一些特定的问题,需要对粒子群算法进行适当的调整和优化,以便在GPU上获得更好的性能表现。
此外,还需要考虑到GPU编程的复杂性。
虽然使用GPU加速可以提高算法的性能,但是GPU编程相对复杂,需要考虑到数据传输、内存管理以及并行计算等方面的问题。
在使用GPU加速粒子群算法时,需要仔细考虑算法的并行化实现,以及如何最大限度地利用GPU资源来提高算法的性能。
总的来说,GPU粒子群算法在MATLAB中的应用涉及到GPU加速、算法实现以及并行计算等多个方面。
通过合理地利用GPU资源,可以显著提高粒子群算法的执行效率,特别是在处理大规模数据和复杂优化问题时。
然而,需要注意到GPU编程的复杂性,以及对算法进行适当的调整和优化,才能充分发挥GPU加速的优势。
有约束多目标粒子群算法matlab程序

有约束多目标粒子群算法matlab程序约束多目标粒子群算法(Constrained Multi-Objective Particle Swarm Optimization,CMOPSO)是一种用于处理多目标优化问题的进化算法。
以下是一个简单的MATLAB 示例程序,演示了如何实现CMOPSO。
请注意,这只是一个基本的框架,你可能需要根据你的具体问题进行适当的修改。
```matlabfunction [paretoFront, paretoSet] = cmopso(objectiveFunction, constraintFunction, nParticles, nIterations, nObjectives)% 参数设置nVariables = 2; % 例子中假设有两个变量w = 0.5; % 权重因子c1 = 2; % 学习因子1c2 = 2; % 学习因子2vMax = 0.2; % 最大速度nConstraints = 2; % 约束数量% 初始化粒子群particles.position = rand(nParticles, nVariables);particles.velocity = rand(nParticles, nVariables);particles.bestPosition = particles.position;particles.bestValue = inf(nParticles, nObjectives);% 迭代优化for iteration = 1:nIterations% 更新粒子位置和速度for i = 1:nParticles% 计算适应值fitness = objectiveFunction(particles.position(i, :));% 计算约束违反度constraintViolation = constraintFunction(particles.position(i, :));% 更新粒子最优解if all(constraintViolation <= 0) && dominates(fitness, particles.bestValue(i, :))particles.bestPosition(i, :) = particles.position(i, :);particles.bestValue(i, :) = fitness;end% 更新全局最优解if all(constraintViolation <= 0) && dominates(fitness, globalBestValue)globalBestPosition = particles.position(i, :);globalBestValue = fitness;end% 更新粒子速度和位置r1 = rand(1, nVariables);r2 = rand(1, nVariables);particles.velocity(i, :) = w * particles.velocity(i, :) + ...c1 * r1 .* (particles.bestPosition(i, :) - particles.position(i, :)) + ...c2 * r2 .* (globalBestPosition - particles.position(i, :));% 速度限制particles.velocity(i, :) = min(max(particles.velocity(i, :), -vMax), vMax);% 更新粒子位置particles.position(i, :) = particles.position(i, :) + particles.velocity(i, :);endend% 获取Pareto 前沿和Pareto 集paretoFront = [];paretoSet = [];for i = 1:nParticlesif all(constraintFunction(particles.position(i, :)) <= 0)isDominated = false;for j = 1:size(paretoFront, 1)if dominates(particles.bestValue(i, :), paretoFront(j, :))isDominated = true;break;elseif dominates(paretoFront(j, :), particles.bestValue(i, :))paretoFront(j, :) = [];break;endendif ~isDominatedparetoFront = [paretoFront; particles.bestValue(i, :)];paretoSet = [paretoSet; particles.bestPosition(i, :)];endendendendfunction result = dominates(a, b)% 判断a 是否支配bresult = all(a <= b) && any(a < b);end```请注意,这只是一个简单的示例,具体问题的约束函数和目标函数需要根据你的应用进行修改。
多变量粒子群算法matlab

多变量粒子群算法matlab多变量粒子群算法是一种基于群体智能的优化算法,通过模拟鸟群觅食过程中的群体行为,寻找最优解。
本文将介绍如何使用Matlab实现多变量粒子群算法,并通过实例说明其应用场景和优势。
一、粒子群优化算法概述粒子群优化算法是一种基于群体智能的优化算法,通过不断迭代寻找最优解。
该算法模拟鸟群觅食过程,每个粒子代表一个解,粒子的速度和位置反映了当前解的质量。
在搜索过程中,粒子会根据自身经验和群体经验不断调整速度和位置,最终找到最优解。
二、多变量粒子群算法特点多变量粒子群算法是在单变量粒子群算法的基础上,通过引入多个自变量进行优化的一种算法。
它能够处理多变量系统中的复杂问题,通过调整粒子的速度和位置,优化自变量和因变量之间的关系,从而达到优化目标。
相较于单变量粒子群算法,多变量粒子群算法更加灵活,适用于处理更复杂的问题。
三、Matlab实现多变量粒子群算法1. 初始化粒子群首先需要初始化粒子的速度和位置,以及粒子的最佳位置。
每个粒子代表一个解,粒子的最佳位置反映了当前解的质量。
在Matlab中,可以使用随机数生成器生成粒子的初始位置和速度。
2. 评估粒子的适应度根据问题定义,对每个粒子进行评估,计算其适应度值。
在多变量粒子群算法中,适应度函数需要考虑多个自变量的影响,通过调整自变量的取值,找到最优解。
3. 更新粒子的速度和位置根据粒子的适应度值和最佳位置的更新规则,更新粒子的速度和位置。
在Matlab中,可以使用加速度法等算法来更新粒子的速度和位置。
4. 终止条件当满足终止条件时(如达到最大迭代次数或找到最优解),算法停止运行。
在Matlab中,可以使用循环结构来实现算法的迭代。
四、应用场景和优势多变量粒子群算法适用于处理多变量系统中的优化问题,如控制系统、电力电子等领域。
相较于传统优化方法,多变量粒子群算法具有以下优势:1. 适用于处理复杂问题:多变量粒子群算法能够处理多个自变量的优化问题,适用于处理更复杂的问题。
粒子群算法matlab代码

一、粒子群主程序psize=20; %粒子个数的设置pd=12; %粒子的维数lz=zeros(psize,pd);for i=1:psize %随机生成粒子群,psize行pd列,pd维。
suiji=rand(1,pd);for j=1:pd/2if suiji(j)<0.5lz(i,j)=fix(unifrnd(0,100))*100;elselz(i,j)=fix(unifrnd(0,100)+1)*100;endendfor j=pd/2+1:1:pdif suiji(j)<0.5lz(i,j)=fix(unifrnd(0,45))/100;elselz(i,j)=fix(unifrnd(0,45)+1)/100;endendlz(i,1:pd/2)=sort(lz(i,1:pd/2));lz(i,pd/2+1:pd)=sort(lz(i,pd/2+1:pd));endlv=lz;goodvalue=lz; %每个粒子自己历史最好值初始化,psize行pd列。
vmax=20; %速度上限c1=2;c2=2; %学习因子w=0.729; %随机因子和惯性因子bestvalue=zeros(1,pd); %全局最好值初始化,1行pd列for j=1:pdbestvalue(1,j)=goodvalue(1,j);endfnew=zeros(1,psize);for j=1:psizefnew(j)=fpso(lz(1,:));endfold=fnew;flagstop=0; %终止标志k=0; %迭代次数记录f0=fpso(bestvalue); %适应值初始化while flagstop==0for i=1:psize %适应值比较,更新各自历史最好值(位置)fnew(i)=fpso(lz(i,:)); %记录每次每个粒子的适应值,便于以后设置终止条件if fnew(i)<fold(i)fold(i)=fnew(i); %fold记录每个粒子的最好历史值goodvalue(i,j)=lz(i,j);endendendfor i=1:psize%每个粒子历史最好值比较,更新全局最好值f1=fold(i);if f1<f0f0=f1;for j=1:pdbestvalue(1,j)=goodvalue(i,j);endendend%*********粒子趋一点终止条件*********%flagstop0=max(abs(fold)); %比较当次的所有粒子的适应值,flagstop1=min(abs(fold)); %若它们之间差别较小,则可以停止。
粒子群算法详解-附matlab代码说明
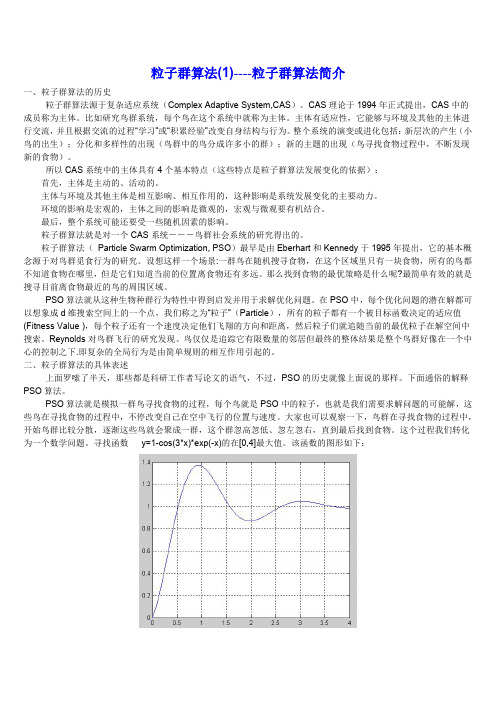
位置更新公式
该算法在文献中讨论了系数 n 取各种不同情况的情况,并且运行来了 20000 次来分析各种系数的结果。
(2)粒子群算法的混合
这个分支主要是将粒子群算法与各种算法相混合,有人将它与模拟退火算法相混合,有些人将它与单纯形方法相
混合。但是最多的是将它与遗传算法的混合。根据遗传算法的三种不同算子可以生成 3 中不同的混合算法。
这两个点就是粒子群算法中的粒子。 该函数的最大值就是鸟群中的食物 计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。 更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。 下面演示一下这个算法运行一次的大概过程: 第一次初始化
第一次更新位置
第二次更新位置
第 21 次更新 最后的结果(30 次迭代) 最后所有的点都集中在最大值的地方。
粒子群算法与选择算子的结合,这里相混合的思想是:在原来的粒子群算法中,我们选择粒子群群体的最优值
作为 pg,但是相结合的版本是根据所有粒子的适应度的大小给每个粒子赋予一个被选中的概率,然后依据概率对这些 粒子进行选择,被选中的粒子作为 pg,其它的情况都不变。这样的算法可以在算法运行过程中保持粒子群的多样性, 但是致命的缺点是收敛速度缓慢。
上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO 的历史就像上面说的那样。下面通俗的解释 PSO 算法。
PSO 算法就是模拟一群鸟寻找食物的过程,每个鸟就是 PSO 中的粒子,也就是我们需要求解问题的可能解,这 些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。大家也可以观察一下,鸟群在寻找食物的过程中, 开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。这个过程我们转化 为一个数学问题。寻找函数 y=1-cos(3*x)*exp(-x)的在[0,4]最大值。该函数的图形如下:
matlab粒子群算法解决指派问题

一、概述我们来介绍一下Matlab的粒子裙算法及指派问题的背景,粒子裙算法是一种基于裙体智能的优化算法,模拟了鸟裙或鱼裙寻找食物的行为,在解决各种优化问题中具有较好的效果。
指派问题是一类组合优化问题,解决的是将N个任务分配给N个执行者,使得总成本最小的问题。
二、Matlab粒子裙算法Matlab提供了丰富的工具箱,其中就包括了粒子裙算法工具箱。
通过Matlab的粒子裙算法工具箱,用户可以方便地进行粒子裙算法的实现和优化。
该工具箱提供了丰富的函数和命令,能够满足不同问题的求解需求。
三、指派问题指派问题是一类常见的优化问题,其应用广泛,如作业调度、资源分配等。
指派问题的目标是找到一种最优的分配方案,使得总成本或总收益最大化。
在实际应用中,指派问题的规模可能很大,需要借助优化算法进行求解。
四、粒子裙算法解决指派问题1. 问题建模首先需要将指派问题进行数学建模,将任务和执行者的关系用矩阵表示,定义适应度函数,指派问题的目标是最小化总成本,即适应度函数的最小化。
2. 算法实现利用Matlab提供的粒子裙算法工具箱,可以方便地实现指派问题的求解。
通过编写相应的Matlab脚本,调用粒子裙算法进行优化求解。
3. 求解结果分析求解出最优的分配方案之后,需要对结果进行分析和验证,确保所得的分配方案满足问题的要求,并对算法的性能进行评估。
五、实例分析为了验证粒子裙算法在解决指派问题中的有效性,我们选取了几个典型的指派问题实例进行分析和比较,通过Matlab实现粒子裙算法进行求解,与其他优化算法进行对比,验证了粒子裙算法在求解指派问题中的有效性和效率。
六、总结与展望通过本文对Matlab粒子裙算法解决指派问题的分析与研究,我们证明了粒子裙算法在解决指派问题中的有效性,同时也发现了其中的一些不足之处。
我们希望在未来的研究中,针对粒子裙算法在解决指派问题中的不足之处进行改进,提高算法的效率和稳定性,推动其在实际应用中的更广泛使用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工具箱应用实例
求非线性函数极大值
f(x, y)
sin x y
2
2
x y
2
2
e
cos 2 x cos 2 y 2
2.71289
工具箱应用实例
工具箱应用实例
(1)编写待优化函数程序 function z = test_func(in) nn=size(in); %输入的是矩阵 ,即算法中随机产生一组x和 y ,按[x(nn, 1), y(nn, 1)]排列 x=in(:,1); y=in(:,2); nx=nn(1); for i=1:nx temp=sin(sqrt(x(i)^2+y(i)^2))/sqrt(x(i)^2+y(i)^2)+exp((cos( 2*pi*x(i))+cos(2*pi*y(i)))/2)-2.71289; z(i,:)=temp; end
3。抽象
PSO初始化为一群随机粒子 (随机解、一群鸟),然后通
过迭代找到最优解。在每一次迭代中,粒子(鸟)通过跟
踪两个“极值”来更新自己的位置。一个就是粒子本身所找 到的最优解,这个解叫做个体极值 pBest ,另一个极值是 整个种群目前找到的最优解,这个极值是全局极值 gBest 。(gBest是pBest中最好值)
Vmax: 最大速度,决定粒子在一个循环中最大的移动距 离, 通常设定为粒子的范围宽度,例如,粒子 (x1, x2, x3) , x1 属于 [-10, 10], 那么 Vmax 的大小就是 20。 学习因子: 使粒子具有自我总结和向群体中优秀个体学习 的能力,从而向群体内或邻域内最优点靠近,c1 和 c2 通常 等于2,并且范围在 0 和 4 之间。 中止条件: 最大循环数以及最小错误要求。 惯性权重w :决定了对粒子当前速度继承多少,合适的选 择可以使粒子具有均衡的探索能力和开发能力,惯性权 重的取法有常数法、线性递减法、自适应法等。
粒子群优化算法Matlab工具箱简介
Matlab粒子群工具箱(PSOt)提供了非常先进的粒子群
优化算法 ,可指定惯性因子的起始值和中止值 ,可约定各 维变量的取值范围 、粒子在遇到边界时是否反弹等各种参 数 。除此以外 ,粒子群工具箱既可以在用户约定的范围内 自动随机生成指定群体规模的初始粒子群 ,也可人工输入 小于群体规模的任意数目的初始粒子 ,具备非常强的灵活 性。
3。算法介绍
• 在找到这两个最优值时,粒子根据如下的公式来更新自己 的速度和位置:
其中 ,V 是粒子的速度,Present 是粒子的当前位置 ,pB est 与 gBest见前面定义。rand ( )是(0 ,1)之间的随机数 ,c1和c 2被称作学习因子。通常 ,c1 = c2 = 2。w 是加权系数(惯性 权重),取值在 0. 1到0. 9之间。粒子通过不断学习更新 , 最终飞至解空间中最优解所在的位置 ,搜索过程结束。最后 输出的 gBest 就是全局最优解。在更新过程中 ,粒子每一维的 最大速率限被限制为 Vmax ,如果某一维更新后的速度超过设 定的Vmax,那么这一维的速度就被限定为Vmax。
粒子群优化算法Matlab工具箱简介
粒子群优化算法Matlab工具箱简介
PSOt具有非常强的灵活性,在实际计算中,用户只要根据 需求编写好目标函数,并设置好函数自变量的取值范围和 每步迭代允许的最大变化量,PSOt即可自动进行优化计算 。 该工具箱的使用方法主要分为一下几个步骤:
(1)在MATLAB的命令窗口中点击“File”,“Set Path
”,设置工具箱的路径。
(2)编写待优化的函数(test_func),保存为同名m文件
粒子群优化算法Matlab工具箱简介
(3)调用粒子群算法的核心模块:pso_Trelea_vectorized
.m,其调用格式为:
pso_Trelea_vectorized(functname, D, mv, VarRange , minmax, PSOparams, plotfcn, PSOseedValue)
2。算法思想
• PSO模拟鸟群的捕食行为。 设想这样一个场景:一群鸟在随机搜索食物,在这个区域里 只有一块食物,所有的鸟都不知道食物在那里,但是它们 知道当前的位置离食物还有多远,那么找到食物的最优策 略是什么呢? 最简单有效的就是搜寻目前离食物最近的鸟的周围区域。 都向这片区域靠拢。
3。抽象
PSO中,将问题的搜索空间类比于鸟类的飞行空间,将 每只鸟抽象为一个无质量无体积的微粒,用以表征优化问题 的一个候选解,我们称之为“粒子”,优化所需要寻找的最 优解则等同于要寻找的食物。 所有的粒子都有一个由被优化的函数决定的适应值(fitness value),每个粒子还有一个速度决定他们飞翔的方向和距离 ,然后粒子们就追随当前的最优粒子在解空间中搜索。
粒子群算法工具箱应用 简介
1。引言
• 粒子群算法(PSO算法) • 定义:粒子群算法,又称粒子群优化算法(Partical Swarm Optimization),缩写为 PSO, 是近年来发 展起来的一种新的进化算法(Evolutionary Algorith m - EA),由Eberhart 博士和kennedy 博士于1995 年提出,其源于对鸟群捕食的行为研究。
工具箱应用实例
(2)编写调用函数 x_range=[-2,2]; y_range=[-2,2]; range=[x_range; y_range]; Max_V=0.2* (range(:,2) - range(:,1)); %最大速度取范围 的 10%~ 20% n=2; %粒子维数 PSOparams=[10 300 20 2 2 0.9 0.4 1500 1e-25 250 NaN 0 0] %个体数目 20 ,进化次数 300 PSO_Trelea_vectorized('test_func', n, Max_V, range, 1, PSOparams)
3。算法介绍
• 例:对于问题 f(x) = x1^2 + x2^2+x3^2 求解,粒 子可以直接编码为 (x1, x2, x3),而适应度函数就 是f(x),接着我们就可以利用前面的过程去寻优 ,寻优过程是一个迭代过程, 中止条件一般为设 置为达到最大循环数或者最小错误要求。
3。算法介绍
• PSO框架图
3。算法介绍
将粒子延伸到N维空间,粒子i在N维空间里的位置表示为 一个矢量,每个粒子的飞行速度也表示为一个矢量。
ห้องสมุดไป่ตู้
粒子数(鸟的个数): 一般取 1~40. 其实对于大部分的 问题10个粒子已经足够可以取得好的结果; 粒子的长度(维度): 这是由优化问题决定, 就是问题解 的长度(决策变量个数); 粒子的范围: 由优化问题决定,每一维可以设定不同的 范围;
pso_Trelea_vectorized(functname, D, mv, VarRange, minmax, PSOparams, plotfcn, PSOseedValue) Functname:目标函数名 D:待优化问题的维数; mv:粒子飞行的最大速度; VarRange:参数变化范围矩阵; Minmax:寻优类型,取0代表求目标函数最小值,取1代表求目 标函数最大值); PSOparams:参数矩阵,包括最大迭代次数、粒子群规模、惯 性因子、学习因子、终止迭代条件等; Plotfcn:寻优过程中用于展示寻优过程的画图函数; PSOseedValue:可允许用户输入任意多组初始粒子。
