大地测量控制点坐标转换技术规范
工程测量坐标换算方法

工程测量坐标换算方法引言在工程测量中,常常需要使用不同的坐标系统进行测量和计算。
不同的坐标系统可能采用不同的原点、坐标轴方向、单位等。
在实际应用中,我们经常需要将一个坐标点在不同坐标系统下进行换算和转换。
本文将介绍工程测量中常用的坐标换算方法,旨在帮助读者理解和应用这些方法。
1. 直角坐标系直角坐标系是工程测量中最常用的坐标系统之一。
在直角坐标系中,一个点的位置可以用两个坐标值表示,分别表示点在水平和垂直方向的投影距离。
水平方向的坐标称为X坐标,垂直方向的坐标称为Y坐标。
1.1 原点位置直角坐标系的原点一般位于被测量对象的某个特定位置。
在实际测量中,我们可根据需要将原点设置在合适的位置。
1.2 坐标轴方向直角坐标系的坐标轴一般选择水平和垂直两个方向。
水平方向通常用来表示东西方向,以正东方向为正轴向。
垂直方向通常用来表示南北方向,以正北方向为正轴向。
1.3 坐标的表示在直角坐标系中,一个点的位置可以用一个有序对表示,格式为(X, Y)。
其中,X表示点在水平方向的坐标,Y表示点在垂直方向的坐标。
2. 大地坐标系大地坐标系是工程测量中常用的另一种坐标系统。
大地坐标系以地球的形状和地球表面上的某个参考点为基础,通过经纬度来确定一个点的位置。
2.1 经纬度表示在大地坐标系中,经度是指一个点位于地球上的东西方向位置。
经度的表示方法是以0°经线(即本初子午线)为基准,以东经为正,西经为负,范围为-180°到+180°。
纬度是指一个点位于地球上的南北方向位置。
纬度的表示方法是以赤道为基准,以南纬为负,北纬为正,范围为-90°到+90°。
2.2 坐标换算方法在工程测量中,经常需要将大地坐标系中的经纬度换算为直角坐标系中的X、Y坐标,或者将直角坐标系中的X、Y坐标换算为大地坐标系中的经纬度。
常用的大地坐标与直角坐标的换算方法有以下几种:•大地坐标系(经纬度)到直角坐标系的换算方法,称为大地坐标系的正算方法。
云南省2000国家大地坐标系坐标转换部分
相同历元不同框架坐标比较
相同历元不同框架点位坐标差异,下表以昆明站为例
IGS坐标
X(m)
Y(m)
Z(m) ΔX(m) ΔY(m) ΔZ(m)
ITRF2000
-1281255.473
5640746.079
2682880.117
-0.0318,-0.0024,-0.0203
ITRF2005
ITRF2000 ITRF2005
-1281255.565
5640746.060
2682880.057
IGS站坐标和速度场的解算精度
σ X(mm)
10
σY(mm) 22
σZ(mm) 12
1.0
1.0
1.0
-0.0317, 0.0035.-0.0147
σX1(mm) σY1(mm) σZ1(mm)
3.7 8.3 4.3 0.2 0.4 0.2
顾及全部7参数和椭球大小变化的转化公式又称为广义大地坐 标微分公式或广义变换椭球微分公式。
dB
- sinBcosL M+H
dL
=
-
(N
sinL + H)cosB
dH
cosBcosL
- sinBsinL M+H cosL
(N + H)cosB cosBsinL
cosB
M+H 0
sinB
T (t) T (tk ) T (t tk )
GPS C级网转换到CGCS2000 坐标系
从ITRF2000转换到以前框架的转换参数与速率(历元1997. 0)
转换参数
T1(cm) T2(cm) T3(cm)
Dppb
R1.001" R2.001" R3.001"
CGCS2000坐标系转换问题分析及处理措施

CGCS2000坐标系转换问题分析及处理措施CGCS2000坐标系是中国大地测量系统2000年大地基准系的简称,是中国大地测量工作中常用的大地坐标系。
随着国家自然资源部的《国家基准点、基准站、基准线、基准面和基准桩设置管理办法》的颁布实施以及全国基准点、基准站等基本测量资料的更新换代,CGCS2000坐标系的转换问题也逐渐凸显出来。
在实际测量、地理信息处理以及工程测量中,CGCS2000坐标系的转换问题至关重要,影响着测量数据的准确性和工程成果的质量。
对于CGCS2000坐标系转换问题的分析和处理措施至关重要。
一、CGCS2000坐标系转换问题分析1. 坐标系转换的必要性随着测量技术的不断发展和应用领域的不断拓展,原有的坐标系可能无法满足现有的测量需求。
中国的东部城市可能采用的是1954年北京坐标系,而西部城市可能采用的是1980年西安坐标系,这就需要进行坐标系的转换,以满足不同坐标系之间的数据传递和应用需求。
2. CGCS2000坐标系转换存在的问题CGCS2000坐标系转换存在一些问题,主要包括以下几个方面:(1) 坐标系参数不一致:不同坐标系的参数不一致,比如椭球体参数、基准面参数等,这会导致坐标转换的误差增大。
(2) 转换算法误差:现有的坐标系转换算法存在一定的误差,特别是在边界地区和高原地区,误差更加明显。
(3) 数据量较大:随着大地测量数据的积累和更新换代,CGCS2000坐标系转换的数据量将逐渐增大,需要更高效的转换方法和工具。
二、CGCS2000坐标系转换问题的处理措施针对CGCS2000坐标系转换的问题,我们应该采取相应的处理措施,以确保测量数据的准确性和工程成果的质量。
1. 加强坐标系转换算法研究对于CGCS2000坐标系转换算法的研究,需要加强对椭球面参数、基准面参数等关键参数的精准性研究,提高转换算法的精确度和稳定性。
对于不同地区的转换误差情况,需要进一步研究和改进相应的算法,提高转换的精度。
大地测量控制点坐标转换技术规程

近似表示地球的形状和大小,并且其表面为等位面的旋 转椭球。 3.3 参考椭球 reference ellipsoid 最符合一定区域的大地水准面,具有一定大小和定位参 数的旋转地球椭球。 3.4 国 际 地 球 参 考 系 统 Reference System,ITRS 由国际地球自转服务(IERS)给出的地球 International Terrestrial Reference Frame,ITRF 国际地球参考系统(ITRS)的实现。由国际地球自转服 务局(IERS)根据空间大地测量技术,包括甚长基线干涉测 量(VLBI) 、卫星激光测距(SLR) 、多里斯系统(DORIS) 、 全球定位系统(GPS)等,所确定的地面点的坐标所构成的 集合。 3.6 大地坐标系 geodetic coordinate system 以地球椭球中心为原点、起始子午面和赤道面为基准面 的地球坐标系。 3.7 1954 年 北 京 坐 标 系 Beijing Geodetic Coordinate System 1954 将我国大地控制网与苏联 1942 普尔科沃大地坐标系联 结后建立的我国过渡性大地坐标系。 International Terrestrial
大地测量控制点坐标转换技术规程
1 范围
本规程规定了各种坐标系控制点坐标转换到 2000 国家 大地坐标系时控制点选取、坐标转换模型、转换方法、精度 评价等方面应遵循的原则、适用范围和精度要求。 本规程适用于大地测量控制点坐标转换过程中的重合 点选取、模型选择和转换方法。 2 规范性引用文件 下列文件对于本文件的应用是必不可少的。凡是注日期 的引用文件,仅注日期的版本适用于本文件。凡是不注日期 的引用文件,其最新版本(包括所有的修改单)适用于本文 件。 GB/T 17159-2009 GB/T 18314-2009 GB/T 19391-2003 GB/T 22021-2008 GB/T 28588 - 2012 站网技术规范 CH/T 1004-2005 2010(第三版) 3 术语和定义 下列术语和定义适用于本文件。 3.1 控制点 control point 以一定精度测定其位置为其他测绘工作提供依据的固 定点。 3.2 地球椭球 earth ellipsoid 测绘技术设计规定 测绘学名词 大地测量术语 全球定位系统(GPS)测量规范 全球定位系统(GPS)术语及定义 国家大地测量基本技术规定 全球导航卫星系统连续运行基准
2000国家大地坐标系转换指南

2000国家大地坐标系转换指南2000国家大地坐标系(以下简称2000大地坐标系)是中国用于地理测量和地图制图的坐标参考系统之一、它是根据2000国家大地坐标基准系统建立的,具有高精度和较低的误差,广泛应用于各种地理空间分析和测量项目中。
在实际应用中,由于不同地区和不同应用领域的需求,需要将2000大地坐标系转换成其他坐标系,以便进行更准确的测量和分析。
本文将介绍2000大地坐标系的转换指南,包括转换的目的、方法和常见问题。
一、转换的目的2000大地坐标系的转换目的主要有两个:1.建立多种不同坐标系之间的转换关系,以便在不同系统之间进行数据交换和共享。
这对于地理信息系统(GIS)和地图制图尤为重要,因为不同的应用和软件可能使用不同的坐标系统,为了数据的一致性和准确性,需进行坐标系的转换。
2.提供更准确的测量和分析结果。
2000大地坐标系是根据国家大地基准系统建立的,具有较高的精度和较低的误差。
然而,在实际测量和分析中,可能需要使用其他坐标系统,如经纬度坐标系或投影坐标系,以便满足具体的测量和分析需求。
二、转换的方法2000大地坐标系的转换方法可以分为两类:地理坐标系转换和投影坐标系转换。
1.地理坐标系转换:地理坐标系通常使用经纬度来表示地球上的位置。
2000大地坐标系的地理坐标系是基于国家大地基准系统的,与其他一些常用地理坐标系存在差异。
转换地理坐标系的方法主要有以下几种:-大地坐标系转经纬度坐标系:这是最常见的坐标系转换方法之一,可以通过利用大地基准系统的参数和转换公式将大地坐标系转换为经纬度坐标系。
-经纬度坐标系转大地坐标系:与上述方法相反,通过使用转换公式和参数,可以将经纬度坐标系转换为大地坐标系。
-大地坐标系转换:在不同大地坐标系之间进行转换时,可以利用大地基准系统的参数和转换公式进行转换。
2.投影坐标系转换:投影坐标系主要用于地图制图和测量,可以将地球表面上的经纬度坐标投影到平面上。
2000大地坐标系的投影坐标系采用高斯克吕格投影或墨卡托投影等常用的投影方法。
建筑坐标与测量坐标如何进行换算

建筑坐标与测量坐标如何进行换算建筑坐标和测量坐标在建筑行业和土地测量领域起着重要的作用。
在建筑设计、施工和测量中,经常需要进行建筑坐标与测量坐标之间的换算。
这个过程涉及到各种数学计算和坐标系统的使用。
本文将介绍建筑坐标和测量坐标的概念,并讨论如何准确地进行换算。
建筑坐标建筑坐标是建筑物在建筑设计和施工中使用的一种坐标系统。
它常用于确定建筑物内外的各个构件的位置和尺寸。
建筑坐标通常采用笛卡尔坐标系,即以建筑物的某一参考点为原点,通过水平和垂直方向的坐标轴来确定各个点的位置。
建筑坐标的单位通常是米或者毫米。
测量坐标测量坐标是土地测量中使用的一种坐标系统。
它常用于确定地表特征,如地界、地形以及地物的位置和尺寸。
测量坐标通常采用大地坐标系,即以地球椭球体为基准,通过经纬度来确定各个点的位置。
测量坐标的单位通常是度、分、秒或者十进制度。
建筑坐标与测量坐标的换算在实际工作中,建筑坐标和测量坐标之间需要相互转换。
这种换算涉及到旋转、平移和尺度变换等数学计算。
下面介绍一种常用的方法来进行建筑坐标与测量坐标的换算。
坐标转换首先,需要确定建筑坐标和测量坐标之间的对应关系。
可以通过在建筑物和地面上设置控制点来实现。
测量员在地面上测量这些控制点的坐标,并记录下来。
然后,建筑师在建筑物上测量控制点的建筑坐标,并记录下来。
通过比较这些坐标,可以确定建筑坐标和测量坐标之间的换算关系。
建筑坐标到测量坐标的转换将建筑坐标转换为测量坐标的方法如下:1.将建筑坐标原点与测量坐标原点对齐。
可以通过平移建筑坐标系的原点,使其与测量坐标系的原点重合。
2.确定建筑坐标系与测量坐标系之间的旋转角度。
可以通过在建筑物上放置一个参考物体,并在地面上以该物体为中心进行测量,然后在建筑物上测量该物体在建筑坐标系中的位置。
通过比较这两个位置,可以确定建筑坐标系与测量坐标系之间的旋转角度。
3.进行尺度变换。
由于建筑坐标和测量坐标通常采用不同的单位,需要进行尺度变换,将建筑坐标的单位转换为测量坐标的单位。
大地测量中常用的坐标转换方法

大地测量中常用的坐标转换方法大地测量是地理信息技术的重要组成部分,它用于测量地球表面的形态和地球参照系统。
在大地测量中,常常需要进行坐标转换,以便对不同坐标系统的地理数据进行有效管理和应用。
本文将介绍一些常用的坐标转换方法。
一、大地测量简介大地测量是研究地球形态和地球参照系统的科学与技术。
地球的形态非常复杂,不同地区的地形和地壳运动都会导致地球表面坐标的差异。
为了实现地球表面数据的一致性和互操作性,需要进行坐标转换。
二、地球参照系统地球参照系统是用于描述和定位地球表面上的物体的方法。
常见的地球参照系统有地理坐标系统(经纬度)、投影坐标系统(平面坐标)和高程坐标系统。
不同的地理信息系统常使用不同的地球参照系统,因此需要进行坐标转换以实现数据的兼容和交互。
三、大地水准面大地水准面是描述地球海平面的数学模型。
世界上各地的大地水准面存在差异,因此在进行海拔高度计算时需要进行水准面的转换。
常用的水准面模型有地球椭球体、高斯-克吕格地球模型等。
四、大地空间大地基准面大地基准面是用于确定地球表面上点的位置的参考面。
不同的地区可能使用不同的大地基准面,如WGS84、PZ-90等。
为了将数据在不同的大地基准面下进行比较和分析,需要进行大地基准面的转换。
五、坐标转换方法1. 大地测量中最常用的坐标转换方法是地理坐标与投影坐标之间的转换。
地理坐标使用经度和纬度表示,而投影坐标使用平面坐标系表示。
常见的投影坐标系统有UTM坐标系统、高斯投影坐标系统等。
通过合适的坐标转换公式,可以将地理坐标转换为投影坐标,或者反之。
2. 在进行海拔高度计算时,需要进行水准面的转换。
常见的水准面转换方法有正高转换和高程异常转换。
正高转换是将某地的高程值从一个水准面转换到另一个水准面,高程异常转换则是将某点的高程值转换为相对于某个水准面的高程异常值。
3. 大地基准面转换常用的方法是七参数法。
七参数法通过平移、旋转和尺度变换等操作,将一个大地基准面上的点的坐标转换到另一个大地基准面上。
作为测绘人,还不懂CGCS2000坐标系?

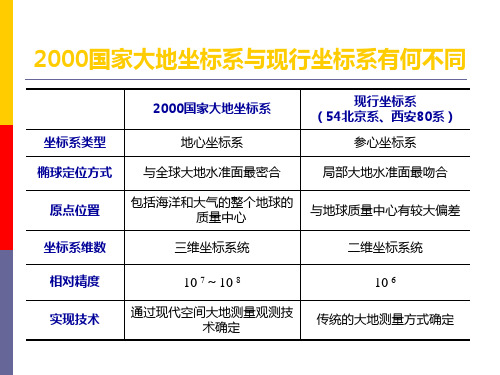
作为测绘人,还不懂CGCS2000坐标系?2000国家大地坐标系,是我国当前最新的国家大地坐标系,英文名称为China Geodetic Coordinate System 2000,英文缩写为CGCS2000。
CGCS2000是2000国家大地坐标系,属于地心大地坐标系统,该系统以ITRF97参考框架为基准,参考框架历元为2000.0。
1坐标参数2000国家大地坐标系定义原点:包括海洋和大气的整个地球的质量中心;Z轴:由原点指向历元2000.0的地球参考极的方向;X轴:由原点指向格林尼治参考子午线与赤道面(历元2000.0)的交点;Y轴:与Z轴、X轴构成右手正交坐标系;2000国家大地坐标系采用椭球简称CGCS2000椭球。
CGCS2000椭球参数长半轴α=6378137m扁率ƒ=1/298.257222101地心引力常数 GM=3.986004418x1014m3s-2地球自转角速度ω=7.292115x10-5rads-1CGCS2000参考椭球a)CGCS2000参考椭球是一旋转椭球,其几何中心与CGCS2000的原点重合,旋转轴与CGCS2000的Z轴一致,其表面代表地球的数学表面。
b)CGCS2000参考椭球又是其表面为正常重力场的等位面的正常椭球。
c)CGCS2000参考椭球由四个常数(a,GM,J2,ω)定义。
一般规定a)“2000中国大地坐标系”,又称“2000 国家大地坐标系”;英译为 China Geodetic Coordinate System 2000,缩写为CGCS2000;b)CGCS2000由原点、尺度、坐标轴的定向及其时间演变定义,由地面点集合的坐标和速度实现;c) 采用CGCS2000参考椭球参数进行三维坐标变换;d) 大地经纬度变换为地图平面坐标,采用高斯-克吕格投影或墨卡托投影。
2坐标意义(1)原点位于地球质量中心的三维国家大地坐标系;(2)遥感卫星资料可基于地心坐标系;(3)应用现代空间技术进行地形图测绘和定位,可以大幅度提高点位表达的准确性,并且可以快速获取精确的三维地心坐标;陆态网CORS站分布图3坐标背景为了我国经济的持续发展,为信息化社会发展提供一个地理平台作为基础,为了可以更科学的动态的描述地球,特别是随着各种空间大地测量技术的不断发展和完善,世界各国都在更新和完善各自的大地坐标系统和它相应的坐标框架。
测绘技术坐标转换方法详解

测绘技术坐标转换方法详解测绘技术是一门研究地球表面地理和空间分布的科学,其主要目的是获取和处理与地球表面相关的各种数据。
在测绘技术中,坐标转换方法是至关重要的,它可以理解为将一个地点或物体在不同坐标系统下的表达方式进行转换的过程。
本文将详细讨论测绘技术中常用的坐标转换方法。
首先,介绍最常用的坐标转换方法之一——大地坐标转换。
大地坐标是用经纬度来表示地球上某个点的位置,它是表达地理坐标的最基本方式。
然而,在实际应用中,我们往往需要将大地坐标转换为其他坐标系统,比如平面坐标系统。
大地坐标转换方法主要包括正反算法和解析算法。
正算法是将大地坐标转换为平面坐标的过程。
其中,最常见的正算法是大地坐标转高斯平面坐标。
高斯投影是将地球表面经纬度网格投射到平面上的方法,这是非常常用的坐标转换方法之一。
其主要思想是将地球表面的曲线地带分为若干等宽度的带带,然后再将经纬度坐标转换为与该带带相关的高斯平面坐标。
通过这种方式,我们可以将地球上的任何一点的经纬度坐标转换为该带带内的平面坐标。
反算法是将平面坐标转换为大地坐标的过程。
在大地测量中,我们常常需要根据已知的平面坐标来计算对应的大地坐标。
这就需要用到反算法,比如高斯平面坐标转大地坐标。
该过程是正算的逆过程,通过已知的平面坐标和带号,可以反推出对应的大地坐标。
这在工程测量和地图制图中非常常见,能够提高数据的精度和准确性。
除了大地坐标转换,还有其他坐标转换方法也非常重要。
例如,UTM(通用横轴墨卡托投影)坐标转换。
UTM投影是一种将地球表面划分为若干个6°的带带,并将这些带带投影到平面上的方法,它是世界上最为广泛使用的坐标系统之一。
通过UTM坐标转换,我们可以将经纬度坐标转换为与UTM相关的平面坐标,从而实现不同坐标系统之间的转换。
此外,还有一种常见的坐标转换是大地水准面高程转换。
大地水准面是一种近似于地心引力势场的曲面,在地理测量和工程测量中非常重要。
然而,大地水准面高程与常见的高程系统(例如正高程和平高程)存在差异。
测绘技术中坐标转换的常见问题

测绘技术中坐标转换的常见问题在测绘领域中,坐标转换是一个非常重要的环节。
坐标转换的目的是将不同坐标系统下的地理位置相互转换,以实现数据的无缝对接和共享。
然而,由于不同坐标系统的定义和测量方法不同,坐标转换中常常会遇到一些问题。
本文将介绍测绘技术中常见的坐标转换问题,以及解决这些问题的方法。
首先,一个常见的问题是坐标系统不匹配。
不同地区和测绘机构使用的坐标系统可能存在差异。
例如,某个地区使用的是经纬度坐标系统,而另一个地区使用的是投影坐标系统。
这种情况下,需要进行坐标转换,将一种坐标系统转换为另一种坐标系统。
这通常需要利用地理坐标参照系参数来进行计算。
对于这种问题,可以通过调整坐标系参数或者使用数学模型来完成坐标转换。
其次,坐标转换时可能会出现精度损失的问题。
由于不同坐标系统的精度范围不同,进行坐标转换会导致精度损失。
尤其是在进行多次坐标转换的情况下,精度损失会累积。
为了解决这个问题,可以采用精度较高的坐标系统或者使用更精确的计算方法进行坐标转换。
此外,还可以通过选择合适的投影方式和区域来最大程度减小精度损失。
另外一个常见的问题是坐标转换时存在的误差积累。
由于测量仪器的误差、地球形状的不规则性等因素的影响,进行坐标转换时不可避免地会引入一定的误差。
这种误差会随着坐标转换次数的增加而积累。
为了解决这个问题,可以采用差分坐标转换方法,即利用已知控制点的坐标信息,通过差值计算来消除坐标转换误差。
此外,还可以利用平差理论和数学模型来对误差进行修正,提高坐标转换的精度。
此外,坐标转换还会面临一些特殊情况下的问题。
例如,当进行大尺度的坐标转换时,由于地球表面存在高程变化、地壳运动等因素,需要考虑地球形状和形变的影响。
此时,需要引入大地测量学的知识,利用大地水准面和椭球面参数来进行坐标转换。
此外,当进行跨国或跨地区的坐标转换时,还需要考虑不同地区的大地基准面和椭球参数差异,进行合适的参数转换。
综上所述,测绘技术中的坐标转换是一个复杂而关键的环节。
2000大地坐标系转换技术指南

2000大地坐标系转换技术指南引言:2000大地坐标系(GCS)是一个常用的地理参考系统,广泛用于测量、地图制作和地理信息系统(GIS)领域。
它采用经度、纬度和高程来描述地球上任何一个点的位置。
在一些情况下,需要将2000GCS转换成其他坐标系统,例如平面坐标系或其他地理参考系统。
本指南将介绍2000GCS转换的基本原理和常用的技术方法。
一、2000大地坐标系基本概念1.1经度和纬度:经度是指地球表面上其中一点相对于本初子午线的角度,通常用度来表示;纬度是指地球表面上其中一点相对于赤道的角度,也通常用度来表示。
1.2高程:高程是指地球表面上其中一点相对于平均海平面的高度。
1.3大地水准面:大地水准面是地球表面上所有点在高程上的理论参照面。
在2000GCS中,大地水准面被定义为WGS84椭球体的平均海平面。
二、2000GCS转换的基本原理2.1坐标转换:2000GCS到其他坐标系统的转换通常包括经纬度到平面坐标的转换,以及经纬度到其他地理参考系统的转换。
2.2平面坐标转换:将经纬度转换为平面坐标的方法包括正算和反算。
正算是根据给定的经纬度计算出相应的平面坐标;反算是根据给定的平面坐标计算出相应的经纬度。
2.3空间大地参照系统转换:2000GCS可以通过转换参数从一个大地参照系统转换到另一个大地参照系统。
常见的大地参照系统包括WGS84、北京54和西安80。
三、2000GCS转换的技术方法3.1基于数学模型的转换方法:基于数学模型的转换方法是通过建立数学模型来实现经纬度和平面坐标之间的转换。
常见的模型包括经纬度和UTM坐标之间的转换。
3.2基于地理坐标转换工具的方法:现在有很多地理信息系统软件和工具可以实现2000GCS转换。
这些工具通常提供了快速、准确的转换结果,但需要使用者具备一定的专业知识。
3.3基于在线转换服务的方法:现在有很多在线地理数据转换服务可以实现2000GCS转换。
用户可以通过上传数据或使用API接口来实现转换,具有便捷和实时性的特点。
如何进行测绘数据的全球定位与坐标转换

如何进行测绘数据的全球定位与坐标转换全球定位系统(GPS)是现代测绘领域中极为重要的技术手段之一,几乎所有的测绘工作都需要使用GPS来获取地理位置信息。
然而,在进行测绘数据的全球定位与坐标转换时,会面临一些挑战。
本文将讨论如何有效地进行测绘数据的全球定位与坐标转换,以提高测绘工作的准确性和效率。
引言全球定位系统(GPS)已经成为现代测绘工作中不可或缺的工具。
通过使用GPS接收器收集的卫星信号,我们可以确定任何一个点的精确地理位置,并将其转化为坐标数据。
但是,由于地球形状复杂、测量条件多变等原因,测绘数据的全球定位与坐标转换并非易事。
然而,只要我们掌握了一些关键概念和方法,就可以轻松应对这些挑战。
一、选择合适的地球参考椭球体和大地水准面在进行测绘数据的全球定位与坐标转换之前,我们首先需要选择合适的地球参考椭球体和大地水准面。
目前常用的地球参考椭球体有WGS84、CGCS2000等,而大地水准面则有EGM96、CGVD2013等。
根据不同的测绘需求,我们要选择适合的参考椭球体和大地水准面,以确保测绘结果的准确性和一致性。
二、选择合适的坐标系统和投影方式测绘数据的坐标转换包括从地理坐标系到投影坐标系的转换。
地理坐标系是以地球为基准的三维坐标系统,而投影坐标系则是将地球表面上的点投影到二维平面上的坐标系统。
在选择坐标系统和投影方式时,我们要考虑测绘区域的形状、尺度和精度要求等因素。
常见的投影方式有等距圆柱投影、墨卡托投影等,每种投影方式都有其适用的测绘任务。
三、进行坐标转换和大地测量计算进行测绘数据的全球定位与坐标转换时,我们需要使用一些数学方法和计算工具。
其中,坐标转换是指将一个坐标系中的点的坐标转换到另一个坐标系中。
常见的坐标转换方法有参数法、七参数法等。
大地测量计算是指根据已知的测量数据,计算出测量区域内各点的坐标、距离、方位角等参数。
这些计算可以通过计算机软件或编程语言来实现。
四、进行坐标纠正和差值处理由于各种误差的存在,测绘数据中的坐标可能会存在一定的偏差。
测绘技术中的大地坐标与平面坐标转换

测绘技术中的大地坐标与平面坐标转换测绘技术是现代化建设和国土资源管理的重要基础,而大地坐标与平面坐标转换则是测绘工作中的一项关键技术。
本文将探讨大地坐标与平面坐标转换的原理、方法以及应用。
一、概述测绘工作中,通常需要将地球表面上的点的经纬度坐标(大地坐标)转换为二维平面上的坐标(平面坐标),以便进行地图制图、空间数据分析等工作。
这是因为地球是一个近似于椭球形的三维曲面,而制图需要二维平面的坐标系统。
二、大地坐标与平面坐标的基本概念大地坐标是使用经度和纬度表示的地球上点的坐标系统。
经度表示东经和西经的角度,纬度表示北纬和南纬的角度。
平面坐标则是指在地球表面上引入某种平面坐标系后,将点的坐标表示为相应的二维平面坐标。
三、大地坐标与平面坐标转换的原理大地坐标与平面坐标转换所依据的原理主要有大地测量学和大地基准。
1. 大地测量学原理大地测量学是研究地球形状和尺寸的科学,它包括测定地球形状的精确度量、大地基准的建立、大地测量的方法等内容。
大地测量学提供了将大地坐标转换为平面坐标的基本理论。
2. 大地基准原理大地基准是指为了进行大地测量和地图制图,建立起的确定地球点的三维坐标和国家、地区或全球间的统一坐标系统。
大地基准是进行大地坐标与平面坐标转换的重要基础。
四、大地坐标与平面坐标转换的方法大地坐标与平面坐标转换的方法有多种,下面介绍其中的几种常用方法。
1. 投影变换法投影变换法是将地球表面上的点坐标投影到平面上的坐标系中。
常见的投影坐标系有墨卡托投影、高斯投影、正轴等角圆锥投影等。
通过选择不同的投影方式和参数,可以将大地坐标转换为平面坐标。
2. 大地坐标系统转换法大地坐标系统转换法是指通过对大地坐标系的转换,将大地坐标转换为平面坐标。
常用的大地坐标系包括经纬度坐标系、通用横轴墨卡托坐标系、高斯平面直角坐标系等。
3. 数据拟合法数据拟合法是一种基于统计学原理的大地坐标与平面坐标转换方法。
通过测量一定数量的场地控制点和控制网的观测数据,利用最小二乘拟合或参数估计的方法,建立数学模型,实现大地坐标与平面坐标之间的转换。
测绘技术中的坐标变换方法介绍

测绘技术中的坐标变换方法介绍测绘技术作为一门专业学科,它不单纯是以地理学、地图学为基础知识,还融合了各种测量和数学方法。
其中,坐标变换是测绘技术中的一个重要概念和方法。
在测绘工作中,坐标变换可以帮助我们实现不同坐标系之间的转换,为地理信息系统、地图制图等提供了极大的便利。
本文将介绍测绘技术中的常见坐标变换方法。
一、平面坐标与大地坐标的转换方法在测绘工作中,我们通常会遇到不同坐标系之间的转换。
最常见的就是平面坐标与大地坐标之间的转换。
平面坐标是利用平面坐标系来表示地理位置的坐标值,而大地坐标则是使用经纬度等来表示地理位置的坐标值。
为了实现平面坐标与大地坐标的转换,我们可以利用以下方法:1. 大地坐标系统的参数化转换方法大地坐标系是地球表面上各个点的经纬度坐标表示。
要将大地坐标转换为平面坐标,我们可以采用参数化转换方法。
该方法通过定义一系列参数,以实现大地坐标到平面坐标的转换。
具体的参数化转换方法有著名的高斯投影、横轴墨卡托等。
2. 七参数变换法七参数变换法是常用的坐标变换方法,它适用于平面坐标与大地坐标之间的转换。
它通过七个参数的定义,分别对应平移、旋转和尺度变换等,从而将平面坐标与大地坐标之间进行转化。
二、不同大地坐标系之间的转换方法除了平面坐标与大地坐标之间的转换外,不同大地坐标系之间的转换也是测绘技术中常见的任务之一。
这是因为不同地区采用的大地坐标系可能具有不同的参数,因此需要进行转换以实现一致性。
以下是常见的大地坐标系转换方法:1. 布尔莎参数法布尔莎参数法是一种常用的大地坐标系转换方法。
它通过定义一系列参数,如椭球参数和基准点坐标等,以实现不同大地坐标系之间的转换。
2. 七参数变换法七参数变换法同样适用于不同大地坐标系之间的转换。
通过定义不同的七参数值,我们可以将一个大地坐标系转换为另一个大地坐标系,以满足具体测绘需求。
三、测量数据的坐标变换方法在测绘工作中,我们还需要对测量数据进行坐标变换,以将测量结果与已知的地理坐标体系相匹配。
大地测量控制点坐标转换技术规范

大地测量控制点坐标转换技术规范目录前言 (3)1. 范围 (4)2. 术语、定义和缩略语 (4)2.1. 术语和定义 (4)2.2. 缩略语 (5)3. 控制点类型 (6)3.1. 控制点分类 (6)3.2. 控制点精度 (6)3.3. 控制点使用原则 (7)4. 控制点坐标转换模型及适用范围 (7)5.1. 坐标系 (7)5.2. 坐标转换模型 (8)5.3. 模型选用和适用范围 (14)5. 控制点坐标转换 (15)5.1. 省、地市级卫星导航定位基准站坐标归算 (15)5.2. 省、地市级卫星大地控制网点坐标归算 (20)5.3. WGS-84控制点坐标归算 (21)5.4. 其他控制点坐标转换 (21)6. 精度要求 (22)6.1. 省级卫星导航定位基准站点坐标归算精度要求 (22)6.2. 地市级卫星大地控制网点坐标转换精度要求 (22)6.3. 坐标转换精度评定方法 (22)参考文献 (24)前言本标准的起草规则依据GB/T 1.1-2009。
本标准由国家测绘地理信息局提出并归口。
本标准起草单位:中国测绘科学研究院、国家测绘产品质量检验测试中心、广州市城市规划勘测设计研究院。
本标准主要起草人:程鹏飞、成英燕、秘金钟、王华、欧海平、文汉江、徐彥田。
1.范围本标准规定了大地测量控制点坐标转换到2000国家大地坐标系的技术要求,包括重合点选取、标转换模型、转换方法、精度评价等。
本标准适用于地方独立坐标系、1954北京坐标系、1980西安坐标系、WGS-84坐标系,以及ITRF框架下的大地测量控制点向2000国家大地坐标系的坐标转换。
2.术语、定义和缩略语2.1.术语和定义下列术语、定义适用于本文件。
2.1.1.坐标转换coordinate transformation采用适用的转换模型和转换参数,将大地测量控制点坐标从某一坐标系转换到另一坐标系。
2.1.2.坐标归算coordinate reduction根据板块运动速度计算测站的速度,并依据计算速度将站点坐标从某-.历元归算到另一历元。
测绘技术中的大地测量与大地坐标系转换

测绘技术中的大地测量与大地坐标系转换引言测绘技术是地理信息系统(GIS)和地理空间数据不可或缺的基础。
其中,大地测量和大地坐标系转换作为测绘技术中的重要环节,为实现地理数据的精确定位和空间分析提供了基础。
一、大地测量大地测量是通过测量地球上的点之间的空间相对位置来推导出地球的真实形状的一门学科。
大地测量的核心理论是通过测量经纬度和高程等参数来描述地球的形状和尺寸。
1. 球面三角学测量地球表面的点之间的距离和方向需要球面三角学的理论支持。
球面三角学是将平面三角学的基本概念和方法应用于球面上的点之间的测量,通过建立球面上各点之间的距离、方向和角度的关系来实现大地测量。
2. 大地测角大地测角是大地测量中的重要技术手段之一。
通过使用全站仪、经纬仪等测量仪器,在测量站点上测量天体、地平线等天体的仰角和方位角,从而确定测站的绝对和相对位置。
3. 大地测距大地测距是测量地球表面两点之间的水平距离的方法。
几何水平距离是测量从测量站点到目标点的空间直线距离;大地线距离则通过考虑地球几何形状如椭球体和椭球仪等因素来测量两点之间的距离。
二、大地坐标系转换在实际的测绘工作中,需要将地球上的点的大地坐标转换为平面坐标或投影坐标,以实现地理数据的精确定位和分析。
1. 大地坐标系大地坐标系是描述地球上点的位置的一种坐标系统。
根据国际上通用的大地测量理论和方法,常用的大地坐标系有经纬度坐标系统和空间直角坐标系统。
2. 大地坐标转换大地坐标转换是将大地测量获得的经纬度和高程等参数转换为平面坐标或投影坐标的过程。
常用的大地坐标转换方法包括投影转换、大地坐标系转换和空间坐标转换等。
3. 坐标转换精度在进行大地坐标转换时,需要考虑转换精度。
由于大地测量的不可避免误差,以及大地坐标系转换本身的理论和计算误差,坐标转换结果通常存在一定的误差。
结论大地测量与大地坐标系转换是测绘技术中的重要内容,为地理信息系统和地理空间数据提供了基本支持。
通过对地球形状和尺寸的测量,以及大地测量数据的转换和计算,可以实现地理数据的精确定位和空间分析。
CGCS2000坐标系转换问题分析及处理措施

CGCS2000坐标系转换问题分析及处理措施1. 引言1.1 CGCS2000坐标系转换问题分析及处理措施:CGCS2000坐标系是我国现阶段主要采用的大地坐标系,它的应用范围涵盖了测绘、导航、遥感等多个领域。
在实际应用中,CGCS2000坐标系转换问题是一个不容忽视的议题,因为误差的累积可能导致严重的后果。
本文将围绕CGCS2000坐标系转换问题展开分析,并提出一些处理措施,以期为广大从事相关工作的专业人士提供一些参考与帮助。
在CGCS2000坐标系转换中,误差的来源主要包括数据采集、数据处理、参数设置等多个方面。
数据采集精度不高会导致原始数据误差的积累;在数据处理过程中,所选取的坐标系转换方法和算法也会对结果产生影响;参数设置不当或者标准不一致也是造成误差的关键因素之一。
综合分析这些问题,我们可以制定相应的处理措施,例如加强对原始数据的质量控制、优化坐标系转换算法、规范参数设置等。
在接下来的正文中,我们将对CGCS2000坐标系转换引起的误差进行深入分析,探讨常见问题并提出解决方法,以及介绍精度提升技巧和软件应用指南。
通过这些内容的讨论,我们希望能够全面了解CGCS2000坐标系转换问题,并找到更有效的解决方案。
2. 正文2.1 CGCS2000坐标系转换引起的误差分析1. 大地测量参数误差:由于大地测量参数的不确定性以及测量方法的误差,会导致CGCS2000坐标系转换时出现误差。
例如椭球体参数的不确定性、大地水准面的高程误差等都会对坐标系转换结果产生影响。
2. 原始数据质量问题:在进行坐标系转换时,如果原始数据的质量不高,比如存在较大的粗差、系统误差等,也会导致转换结果存在误差。
在进行坐标系转换之前,首先需要对原始数据进行严格的质量控制。
3. 转换参数误差:在进行坐标系转换时,通常需要采用一定的转换参数,比如七参数、十四参数等。
如果这些参数的确定有误,或者参数的取值不准确,也会导致转换结果存在误差。
测绘技术中的坐标系转换方法及精度评估

测绘技术中的坐标系转换方法及精度评估引言:测绘技术是一门关于地球形状测量、地球表面及其上各种对象的测量、计算、制图、刻度、记录、存储与再现的学科。
坐标系转换是测绘技术中的一个重要环节,它将不同坐标系下的数据进行转换以满足不同需求。
本文将介绍测绘技术中常用的坐标系转换方法,并探讨如何评估其精度。
一、坐标系转换方法1.1 大地水准面转换大地水准面转换是将地球椭球体上的高程数据转换为平面坐标数据的方法。
常用的转换方法有正算和反算两种。
正算是通过已知的椭球体参数、基准点的经纬度和高程,计算出对应的平面坐标。
反算则相反,通过已知的平面坐标计算出对应的经纬度和高程。
1.2 平面坐标转换平面坐标转换通常指的是将地球表面上的经纬度坐标转换为平面坐标。
这种转换方法常用于地图制图和地理信息系统等领域。
常见的转换方法有高斯投影法、墨卡托投影法等。
1.3 高程数据转换高程数据转换是将不同高程数据间进行转换的方法。
常见的高程数据包括正常高、大地高、椭球高等。
转换方法主要有高程差法、高程变换法等。
二、精度评估精度评估是对坐标系转换结果进行准确性和可靠性的评估。
常见的评估方法有以下几种。
2.1 残差分析法残差分析法是通过对已知控制点进行观测,得到转换后的坐标与实际坐标之间的差异,从而评估坐标系转换的精度。
该方法适用于小范围的转换评估。
2.2 精度评定法精度评定法是通过对已知控制点进行观测,计算出转换前后坐标之间的差异,从而评估转换的精度。
这种方法需要较多的控制点,并且对控制点的选择有一定要求。
2.3 网形控制法网形控制法是通过建立一定数量的控制网,测量控制网上的点在转换前后的坐标差异,并根据这些差异来评估转换的精度。
这种方法适用于大范围的转换评估。
2.4 统计分析法统计分析法是通过对转换前后坐标差异的统计分析来评估转换的精度。
常用的统计分析方法包括平均误差分析、方差分析等。
结论:在测绘技术中,坐标系转换是一个重要的环节,它可以将不同坐标系下的数据进行转换以满足不同需求。
2000国家大地坐标系转换指南

2000国家大地坐标系转换指南【引言】2000年版国家大地坐标系转换指南是指导国内测绘及相关领域在使用新的2000国家大地坐标系进行自由测量和实际应用时,进行大地坐标转换的技术规范和方法指南。
本指南旨在规范和统一各类坐标数据的转换,提高数据的精度和一致性,保证地理信息数据的正确性和可靠性,以满足工程和科学研究的需要。
【概述】2000国家大地坐标系是中国测绘界在2000年采用的新的地理坐标系统,该系统基于国家2000大地坐标参考系统和2000年国家大地坐标转换参数模型,用于计算和表示地球上任意点的坐标。
此次转换指南主要介绍了2000国家大地坐标系在测绘领域内的应用和坐标转换方法。
【主要内容】一、坐标系的基本知识1.1坐标系的概念和作用1.2空间直角坐标系和大地坐标系的区别1.32000国家大地坐标系的基本特点二、基准的确定和转换2.12000地理坐标基准的建立2.2基准面的参数模型和计算方法2.3基准转换的技术方法三、坐标转换的基本原理和方法3.1大地坐标的表示方法3.2大地坐标转换的数学原理3.3坐标转换的常用方法和相关参数四、坐标转换的实际应用4.1坐标转换的数据准备和处理4.2坐标转换的精度分析与控制4.3基于坐标转换的实际案例分析五、坐标转换的软件和工具5.1坐标转换的软件介绍和功能5.2坐标转换工具的使用方法5.3坐标转换的自动化处理六、坐标转换的注意事项和问题解决6.1常见问题的解答和说明6.2坐标转换中的注意事项和技巧【结论】本指南详细介绍了2000国家大地坐标系的基本知识、基准确定和转换、坐标转换的原理和方法、实际应用、软件和工具、注意事项和问题解决等内容。
通过本指南的学习和实践,可以帮助测绘人员和相关领域的专业人员准确、高效地进行2000国家大地坐标系的转换工作,提高数据质量,推动地理信息领域的发展。
同时,也为今后国内大地坐标系转换工作的规范和方法提供了参考和借鉴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大地测量控制点坐标转换技术规范目录前言 (3)1. 范围 (4)2. 术语、定义和缩略语 (4)2.1. 术语和定义 (4)2.2. 缩略语 (5)3. 控制点类型 (6)3.1. 控制点分类 (6)3.2. 控制点精度 (6)3.3. 控制点使用原则 (7)4. 控制点坐标转换模型及适用范围 (7)5.1. 坐标系 (7)5.2. 坐标转换模型 (8)5.3. 模型选用和适用范围 (14)5. 控制点坐标转换 (15)5.1. 省、地市级卫星导航定位基准站坐标归算 (15)5.2. 省、地市级卫星大地控制网点坐标归算 (20)5.3. WGS-84 控制点坐标归算 (21)5.4. 其他控制点坐标转换 (21)6. 精度要求 (22)6.1. 省级卫星导航定位基准站点坐标归算精度要求 (22)6.2. 地市级卫星大地控制网点坐标转换精度要求 (22)6.3. 坐标转换精度评定方法 (22)参考文献 (24)前言本标准的起草规则依据GB/T 1.1-2009 。
本标准由国家测绘地理信息局提出并归口。
本标准起草单位: 中国测绘科学研究院、国家测绘产品质量检验测试中心、广州市城市规划勘测设计研究院。
本标准主要起草人: 程鹏飞、成英燕、秘金钟、王华、欧海平、文汉江、徐彥田。
1. 范围本标准规定了大地测量控制点坐标转换到2000 国家大地坐标系的技术要求, 包括重合点选取、标转换模型、转换方法、精度评价等。
本标准适用于地方独立坐标系、1954 北京坐标系、1980西安坐标系、WGS-84 坐标系,以及ITRF 框架下的大地测量控制点向2000国家大地坐标系的坐标转换。
2. 术语、定义和缩略语2.1. 术语和定义下列术语、定义适用于本文件。
2.1.1. 坐标转换coordinate transformation 采用适用的转换模型和转换参数,将大地测量控制点坐标从某一坐标系转换到另一坐标系。
2.1.2. 坐标归算coordinate reduction 根据板块运动速度计算测站的速度, 并依据计算速度将站点坐标从某-. 历元归算到另一历元。
2.1.3. 归算误差reduction error 测站速度精度与当前历元到归算历元以小数年表示的时间间隔的乘积。
2.1.4. 重合点coincident point 同时具有不同坐标系坐标的大地测量控制点, 可用于计算转换参数。
2.1.5. 平移参数translation parameters 两坐标系转换时,新坐标系原点在原坐标系中的坐标分量。
2.1.6. 旋转参数rotation parameters 两坐标系转换时, 把原坐标系中的各坐标轴左旋转到与新坐标系相应的坐标轴重合或平行时,坐标系各轴依次转过的角度。
2.1.7. 尺度参数scale parameter 两坐标系转换时引人的两坐标系的长度变化参数。
2.1.8. 参考历元reference epochGNSS观测或数据处理中所选用的起算时刻2.1.9. 观测历元epoch of observation GNSS观测数据对应的时刻或观测时段中选用的某一时刻。
2.1.10. 板块运动plate movement 地球岩石圈一个板块对于另一个板块的相对运动。
2.1.11. 2000国家GPS大地控制网National GPS GeodeticControlNetwork 2000在国家测绘地理信息局GPSA 、B级网, 中国人民解放军总参测绘导航局GPS-、二级网, 中国地震局“中国地壳运动观测网络工程” 三个大规模GPS网的基础上,进行统一. 平差后得到的以三维地心坐标为特征的高精度国家级大地控制网。
2.2. 缩略语下列缩略语适用于本文件。
CORS连续运行基准站(continuously operating reference station)CPM-CGCS20002000 国家大地坐标系板块模型(China Plate Model- CGCS2000合) 额IGS国际GNSS服务组织(International GNSS Servce)ITRF 国际地球参考框架(international terrestrial reference frame)GNSS全球导航卫星系统(global navigation satellite system)WGS-8 41984 世界大地坐标系( World Geodetic System 1984)3. 控制点类型3.1. 控制点分类3.1.1. 控制点分类如下:a) 国家级卫星导航定位基准站点;b) 2000 国家GPS大地控制网点;c) 国家一、二、三、四等天文大地点;d) 省、地市级卫星导航定位基准站点;e) 省、地市级卫星大地控制网C级点、D级点;f) 其他1954北京坐标系、1980西安坐标系及相对独立的平面坐标系下的控制点3.1.2.3.1.1 a)、b)、c) 三类控制点已有2000国家大地坐标系坐标,d) 、e) 两类控制点应归算到2000 国家大地坐标系,f) 类控制点应转换到2000国家大地坐标系。
3.2. 控制点精度2000 国家大地坐标系控制点实现精度及省、地市级卫星大地控制网C级点、D级点转换后的精度要求见表1。
3.3. 控制点使用原则高精度控制点可用于低精度控制网的外部控制。
控制点使用原则为:a) 国家级卫星导航定位基准站点: 可作为省级及以下卫星导航定位基准站网建立时的控制点。
b) 省、地市级卫星导航定位基准站点: 点位坐标归算到2000 国家大地坐标系后,可作为C级控制点、D级控制点及相对独立的平面坐标系建立时的控制点。
c) 2000 国家GPS大地控制网点: 可作为天文大地点控制点及相对独立的平面坐标系建立时的控制点。
d) 省、地市级卫星大地控制网C级点、D级点:点位坐标归算到2000 国家大地坐标系后,可作为相对独立的平面坐标系建立时的控制点。
4. 控制点坐标转换模型及适用范围4.1. 坐标系在控制点坐标转换过程中,涉及的坐标系有1954北京坐标系、1980 西安坐标系、2000国家大地坐标系、WGS-84坐标系、相对独立的平面坐标系。
其中1954 北京坐标系、1980西安坐标系、2000 国家大地坐标系、WGS-84的常用参考椭球基本参数见附录A。
4.2. 坐标转换模型4.2.1. 坐标转换模型包括以下6种形式:a)空间直角坐标转换模型: 包括布尔莎模型和莫洛坚斯基模型, 用于不同参考椭球间的空间直角坐标转换, 重合点坐标为X、Y和Z;共7 个转换参数, 即 3 个平移参数、 3 个旋转参数和 1 个尺度参数。
b) 三维七参数大地坐标转换模型: 用于不同参考椭球间的大地坐标转换, 重合点坐标为B、L 和H;共7个转换参数, 即3个平移参数、3个旋转参数和1个尺度参数。
c) 二维七参数大地坐标转换模型: 用于不同参考椭球间的椭球面上大地坐标转换,重合点坐标为B和L; 共7 个转换参数, 即 3 个平移参数、3个旋转参数和 1 个尺度参数。
d) 三维四参数空间直角坐标转换模型: 用于不同参考椭球间的空间直角坐标系间的坐标转换,重合点坐标为X、Y和Z;共 4 个转换参数,即 3 个平移参数和1 个旋转参数。
e) 二维四参数平面坐标转换模型: 用于不同高斯投影平面坐标转换,重合点坐标为x 和y; 共4个转换参数, 即2个平移参数、1个旋转参数和1个尺度参数。
f) 多项式拟合模型: 有椭球面和平面两种形式。
4.2.2. 坐标转换模型详见附录B。
坐标輕换模翌实质h⅛ t 用τ,.τr ,T t 3个唯标平轉■和I r 整制鸡水平定Aa⅛Wft B ⅛CH/T 2014—2016Q总V- si∏βc——(1—<,βin ,B)L a式中I r ——第一HS 心率的平方"Xfil^r i =2/-∕*i M—JtJtitft⅛ T≠Wl ∣ħ≠√}∕( 1-√ιιn ,B)τ tN——球卯削圈曲李半•径,单位为米(m>t N-a . <l-√5iπ3B)hB f L.H―点拉纬度、绘度.大地術+经舛康单怕为弧度Wad 八大地高单位为*<m> +ΛB.∆L>∆H 点怕在两个唱拆系下的缔度希,蝉度程■九她离叢・證纬度幷IH 单位为角榕1巾・ X⅛Λ⅛ffi 单也为i ∣UEh P ―痢屢与呱度ItiI 转換Id.单览穷用秒L)屮B18OX3 6∞∕ιIt α*4≈ ——桶球获半辖和氏半轴基.单ti⅛* <m)1of 严吗斗τ;' r⅛in^J)⅛in r β「&] ∣'⅛a i a B B I S∙ s i S F⅜∙*L Δ∕J(E.3)——Iffi 球京率和.β≠⅛:,无匾炯; T^T.,T r ——平秽倉数*单f⅞为JIUmn R j .R,.K h ——茨祥•敕,单也为帮秒W D —尺廈參戡,无■堀* B 4二僅七•■大地生标炜换張显 ^iriL NCOtB P ninBco⅛L n PCQgLNcosB P FiinBsinL [nnBcos∕, IanBsiii/- —MnLCQSLC⅛sH 0Nt -βinBcf ∣ + H∕∣ —~~芒学 Hy 打CLBBt 耳』L^/.tB. 4)式中I∖ f.N子Fwi 和卯胃崗的側乖半和,申位为號Wlnβ,L,∆fi.∆L 点位州度.矩庫・矗其在两牛士标幕下的tfar^b jSM⅛,fif1JtΨ{i⅛⅛f t <rsd].K½⅛ 单 1⅛⅛ft⅛(*)∣P -fl⅛Jl 与St 慢间转嶽址-单■位为超秒心申=iMX3 60⅛ π; Sg——Iffil H⅞半轴和泾半轴基*单<i¾*tm)∣Λ∆∕R. .R r ^R. D——Iffi 球扁窄和⅛-T^.¾it⅛H: ——平样書数.单位为Jttfm 卄⅛H⅛tt^⅛⅛JftW'Γ)r 应廈⅛tl⅛ +无It 纲*B 5三Nt 四•撻空WSm 标讀換揍型Xr/T/ZrCMlEltALr L L 4 -Y t ⅛h ∣B. Y t . - Yc+Z J cosJJ.. coaL p ÷ X I ^LnB oZ.Z :T 3-_Y L CO≡P E CnSf... — X I rUSiJ l SlnL I .式中IXSH 2000国宣大地半标系F 的W 斷華位为米{m 八 Bn 丄.区域中心I f .⅛⅛¾大Jtii "坤摩,单位脚弧度“詔)FX C T Y , Z. ——丸地土仙杲(1954北京屮怖系或ISKy 府安坐标最)坐栋.单也为米(mJ ; T 1,T,.T,——坐标 ff⅝⅛i ≠f⅞⅛⅛t(m>i α——雄转荡锻.WJ 区械中心P ,虫祛t£为庭转轴的揑制网水平定向嶙转ft<JWfil9≡4北尬世阪层或刊安坐杯乐平rtf*fc⅛lħ ,⅛i⅛ft 定问与200€国家丸地覺标系的建 ⅛^IJ j lft⅛⅛标愛化.单位为弧MUN l M.B 6二煩国∙*fc 平面坐标转揍顿型式中,4-∣ ,Ji ——膿坐标霍下平面S⅛*标.单位为5Mm 卄肝——EOUfl 国家大地聖标廉T 的平面∣⅛ft ⅛∣⅞ •单t⅛⅛*fm); ∆J.4y —平移參 t⅛,⅛⅛ 位为 *f∏⅛)j・—⅛H⅛tt^{i⅛⅞CΛtCrdd)I 用——尺厦拱Ifc,无*姻.8 7事项爺拟舍Hl 型 B-7. 1橘瑶■上拟合公式为JH — σ.l +∏ B ÷ t ∣ L ■ LlIBL4 濟杆 +(«; L I dJ. = ⅛, ■ ⅛. L~*-b ; B —b t H∕-4-∕*1 L j 4-⅛τ⅛l i J式中1fl.L 养贋.険痕+单位为英度IndhmΛm<t⅞ttv⅛ii ■小二砸求解"B 7 2平面Itt 合公式为±t ≡-Jι + iJ I j⅛ = y ∣ +∆> f如欧平 ⅛⅛fl⅛±tei新平Ifi 白.角坠拯B 卡拯转换改1F.hi.Il 算处式为ior»ii.t +a L x + djy+uu r +<j μjy÷α: I y J -+u ∣x 1 ÷U J j ,>+α∣jr>l 十α*y' + ■“ Δjr=Λ> ÷Λh X ÷ ⅛⅛y +^Jr f +⅛4Λ-> +⅛ j t +i⅛J l ÷⅛J ,j*+⅛J∙y+⅛⅛jf i + ■*■ 其申M 上 j⅛Ml⅞f^o,L.2- >,⅛ii<小二離求解.CHrr 2014—2Ole[co⅛fSina—NlnaTOlSl][;:卜(B. 6)(H,8)CH/T 2014- 20164.3. 模型选用和适用范围各种坐标转换模型及适用范围见表25. 控制点坐标转换5.1. 省、地市级卫星导航定位基准站坐标归算5.1.1. 一般规定省、地市级卫星导航定位基准站坐标向2000 国家大地坐标系的归算,每年应定期归算1次,使用连续观测时间不少于 1 个月的观测数据。
