简单几何体表面积体积
8.3简单几何体的表面积与体积-【新教材】人教A版(2019)高中数学必修第二册同步讲义

如图所示:
设外接球和内切球的半径分别为R,r,由于正四面体是中心对称图形,
所以外心和内心重合,球心O在高线上,底面中心为 ,
因为正四面体棱长为2,
所以 ,
在 中, ,即 ,
解得 ,
因为正四面体的体积为 ,
所以 ,
解得
9、在直三棱柱 中, , , , .
(1)求三棱锥 的表面积;
(2)求 到面 的距离.
故选:
题型七表面积、体积与函数
例7 底面半径为2,高为 的圆锥有一个内接的正四棱柱(底面是正方形,侧棱与底面垂直的四棱柱).
(1)设正四棱柱的底面边长为 ,试将棱柱的高 表示成 的函数.
(2)当 取何值时,此正四棱柱的表面积最大,并求出最大值.
【答案】(1) ;(2) , .
【分析】
(1)根据轴截面的三角形的比例关系,列式求函数;(2)根据 ,列出正四棱柱的表面积,并利用二次函数求最大值.
下底面面积:S下底=πr2
侧面积:S侧=πl(r+r′)
表面积:S=π(r′2+r2+r′l+rl)
2、体积公式
(1)柱体:柱体的底面面积为S,高为h,则V=Sh.
(2)锥体:锥体的底面面积为S,高为h,则V= Sh.
(3)台体:台体的上,下底面面积分别为S′,S,高为h,则V= (S′+ +S)h.
【详解】
(1)过圆锥及其内接圆柱的轴作截面,如图所示,
因为 ,所以 .从而 .
(2)由(1) ,因为 ,
所以当 时, 最大,
即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.
1、已知正方体外接球的体积是 ,那么该正方体的内切球的表面积为_____________.
【答案】
常见几何体的表面积体积公式

常见几何体的表面积体积公式1、长方体V:体积s:面积a:长b:宽h:高(1)表面积(长×宽+长×高+宽×高)×2 {S=2(ab+ah+bh)(2)体积=长×宽×高(V=abh)2、圆柱体v:体积h:高s;底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径3、圆锥体v:体积h:高s;底面积r:底面半径体积=底面积×高÷34、正方体V:体积s:面积a:边长体积:边长×边长×边长扩展资料周长:1、正方形C周长S面积a边长周长=边长×4(C=4a)面积=边长×边长(S=a×a)2、长方形C周长S面积a边长周长=(长+宽)×2(C=2(a+b))面积=长×宽(S=ab)3、三角形s面积a底h高面积=底×高÷2(s=ah÷2)三角形高=面积×2÷底三角形底=面积×2÷高4、平行四边形s面积a底h高面积=底×高(s=ah)5、梯形s面积a上底b下底h高面积=(上底+下底)×高÷2(s=(a+b)×h÷2)6、圆形S面积C周长πd=直径r=半径(1)周长=直径×π=2×π×半径(C=πd=2πr)(2)面积=半径×半径×π。
8.3简单几何体的表面积和体积说课稿2023-2024学年高一下学期数学人教A版(2019)必修二

《简单几何体的表面积与体积》说课稿各位老师,大家好:今天我说课的内容是《简单几何体的表面积与体积》。
本节位于必修课程主题三几何与代数对应立体几何初步这一单元。
本节之前从形的角度认识了空间几何体,接下来将从度量的角度进一步认识空间几何体。
下面我将从教材分析、学情分析、教学目标、教学重难点、教学分析、教学评价等六方面加以分析和说明。
一、说教材分析。
1. 内容结构:2.内容分析:本节主要内容是简单几何体的表面积和体积的计算方法,是在前面学习了基本立体图形的分类、概念、结构特征、平面表示的基础上,从度量的角度进一步认识简单几何体.也是研究生产、生活中更复杂形状的物体的表面积和体积的基础。
本节内容包括棱柱、棱锥、棱台的表面积与体积;圆柱、圆锥、圆台、球的表面积与体积.3.育人价值:在实际教学过程中,在对简单几何体的表面积与体积公式的了解与使用公式解决简单的实际问题过程中,提高学生逻辑推理、数学运算、直观想象等素养和空间想象等能力,让学生体会数学来源于生活,激发学习激情。
二、说学情分析。
1.学生在小学、初中阶段已经学习了正方体、长方体、圆柱的表面积和体积以及圆锥体积的计算方法.2.通过之前的学习,学生已经熟悉一些平面图形和空间几何体的互化的思想,尤其是空间几何问题向平面问题的转化。
3.学习圆的面积公式时“分割、近似替代、求和、取极限”这种思想已有体现,现在需要学生进一步体会这种重要思想方法。
三、说教学目标。
目标:1).掌握简单几何体的表面积和体积公式,并能利用这些公式解决简单的实际问题; 简单几何体的表面积和体积 柱体、椎体、台体的表面积和体积 球的表面积和体积(第三课时) 圆柱、圆锥、圆台的表面积和体积(第二课时) 棱柱、棱锥、棱台的表面积和体积(第一课时) 球的体积球的表面积2).柱体、锥体、台体、球的体积公式的推导过程,掌握探究过程中的类比、一般化与特殊化、极限等数学思想方法,并尝试使用这些数学思想方法进行数学学习.目标分析:(1)学生能结合基本立体图形的结构特征掌握简单几何体的表面积和体积公式;能从联系的角度认识柱体、锥体、台体的体积公式的联系。
常见几何体面积体积公式

常见几何体面积体积公式咱们从小学到高中,数学里那常见的几何体面积体积公式可真是重要得很呐!就拿我曾经遇到的一件小事儿来说吧。
有一次我去朋友家做客,他家孩子正为数学作业发愁呢,作业里就有不少关于几何体面积体积计算的题目。
那孩子一脸苦相,抓耳挠腮的,我就凑过去瞧了瞧。
嘿,这不就是咱们熟悉的那些几何体嘛!先来说说正方体。
正方体的表面积公式那就是 6a²,其中 a 是正方体的棱长;体积公式则是 a³。
想象一下,一个边长为 5 厘米的正方体盒子,它的表面积就是 6×5×5 = 150 平方厘米,能装的东西的体积就是5×5×5 = 125 立方厘米。
这就好像是在做一个精致的小盒子,你得清楚它的外表能占多大地方,里面又能装多少宝贝。
再说说长方体。
长方体表面积是 2(ab + ah + bh),体积是 abh 。
假设一个长方体,长 8 厘米,宽 6 厘米,高 4 厘米。
那它的表面积就是2×(8×6 + 8×4 + 6×4) = 208 平方厘米,体积就是 8×6×4 = 192 立方厘米。
这就好比是在给一个大柜子量尺寸,算能占多少空间。
圆柱也常见得很。
圆柱的表面积由侧面积和两个底面积组成,公式是2πr² + 2πrh ,体积是πr²h 。
比如说有个底面半径是 3 厘米,高是 10厘米的圆柱,表面积算下来大约是 244.92 平方厘米,体积大约是 282.6 立方厘米。
这就像在算一个大水桶能装多少水,外面的铁皮又得用多少。
圆锥呢,表面积的计算相对复杂点,咱重点说体积,公式是1/3πr²h 。
想象一下,一个圆锥形的冰淇淋甜筒,底面半径 2 厘米,高6 厘米,体积大约就是 25.12 立方厘米。
球就更有趣啦,表面积是4πr²,体积是4/3πr³ 。
就好像是个足球,知道半径就能算出它的大小和外表面积。
空间几何体的表面积及体积计算公式

空间几何体的表面积及体积计算公式空间几何体是指在三维坐标系中存在的几何图形,包括立方体、圆锥体、圆柱体、球体等等。
对于这些几何体来说,求其表面积和体积是我们在学习空间几何时需要掌握的核心内容。
下面我们将详细介绍各种空间几何体的表面积及体积的计算公式。
一、立方体立方体是一种六个面都是正方形的几何体,其表面积和体积计算公式如下:表面积 = 6 × a²体积 = a³其中,a为立方体的边长。
二、正方体正方体是一种所有面都是正方形的几何体,其表面积和体积计算公式如下:表面积 = 6 × a²体积 = a³其中,a为正方体的边长。
三、圆锥体圆锥体是一种由一个圆锥顶点和一个底面为圆形的仿射锥面构成的几何体,其表面积和体积计算公式如下:表面积= πr²+πrl体积= 1/3πr²h其中,r为底面圆半径,l为母线长度,h为圆锥体的高。
四、圆柱体圆柱体是一种由平行于固定轴的两个相等且共面的圆面和它们之间的圆柱面所围成的几何体,其表面积和体积计算公式如下:表面积= 2πrh+2πr²体积= πr²h其中,r为底面圆半径,h为圆柱体的高。
五、球体球体是一种由所有到球心的距离等于固定半径的点所组成的几何体,其表面积和体积计算公式如下:表面积= 4πr²体积= 4/3πr³其中,r为球体的半径。
以上就是五种常见空间几何体的表面积及体积计算公式,希望能够对大家在学习空间几何时有所帮助。
同时,我们也需要关注其实际应用,在工程建设和生活中经常会涉及到这些几何体的计算,因此深化这些知识点的学习,将对我们未来的发展产生积极的影响。
空间几何体的表面积及体积公式大全

空间⼏何体的表⾯积及体积公式⼤全空间⼏何体的表⾯积与体积公式⼤全⼀、全(表)⾯积(含侧⾯积) 1、柱体①棱柱②圆柱 2、锥体①棱锥:h c S ‘底棱锥侧21=②圆锥:l c S 底圆锥侧213、台体①棱台:h c c S )(21‘下底上底棱台侧+=②圆台:l c c S )(21下底上底棱台侧+=4、球体①球:r S 24π=球②球冠:略③球缺:略⼆、体积 1、柱体①棱柱②圆柱 2、①棱锥②圆锥3、①棱台②圆台 4、球体①球:rV 334π=球②球冠:略③球缺:略说明:棱锥、棱台计算侧⾯积时使⽤侧⾯的斜⾼h '计算;⽽圆锥、圆台的侧⾯积计算时使⽤母线l 计算。
三、拓展提⾼ 1、祖暅原理:(祖暅:祖冲之的⼉⼦)夹在两个平⾏平⾯间的两个⼏何体,如果它们在任意⾼度上的平⾏截⾯⾯积都相等,那么这两个⼏何体的体积相等。
最早推导出球体体积的祖冲之⽗⼦便是运⽤这个原理实现的。
2、阿基⽶德原理:(圆柱容球)圆柱容球原理:在⼀个⾼和底⾯直径都是r 2的圆柱形容器内装⼀个最⼤的球体,则该球体的全⾯积等于圆柱的侧⾯积,体积等于圆柱体积的32。
分析:圆柱体积:r r h S V r 3222)(ππ=?==圆柱圆柱侧⾯积:r h cS r r 242)2(ππ=?==圆柱侧因此:球体体积:r r V 3334232ππ=?=球球体表⾯积:r S 24π=球通过上述分析,我们可以得到⼀个很重要的关系(如图)+ =即底⾯直径和⾼相等的圆柱体积等于与它等底等⾼的圆锥与同直径的球体积之和 3、台体体积公式公式: )(31S SS S h V 下下上上台++=证明:如图过台体的上下两底⾯中⼼连线的纵切⾯为梯形ABCD 。
延长两侧棱相交于⼀点P 。
设台体上底⾯积为S 上,下底⾯积为S 下⾼为h 。
易知:PDC ?∽PAB ?,设h PE 1=,则h h PF +=1由相似三⾓形的性质得:PFPEAB CD =即:hh hSS +=11下上(相似⽐等于⾯积⽐的算术平⽅根)整理得:SS h S h 上下上-=1⼜因为台体的体积=⼤锥体体积—⼩锥体体积∴h S S S h h S h h S V 下上下上下台)(31)(313131111+-=-+=代⼊:SS h S h 上下上-=1得:h S S S SS h S V 下上下上下上台31)(31+--=即:)(3131)(31S SS S h h S S S hS V 下下上上下上下上台++=++=∴)(3S S h V 下下上上台++=4、球体体积公式推导分析:将半球平⾏分成相同⾼度的若⼲层(层n ),n 越⼤,每⼀层越近似于圆柱,+∞→n 时,每⼀层都可以看作是⼀个圆柱。
最新人教A版高一数学必修二课件:8.3 简单几何体的表面积与体积-第1课时

| 自学导引 |
| 课堂互动 |
| 素养达成 |
| 课后提能训练 |
数学 必修第二册 配人版A版
第六章第八平章面向立量体及几其何应初用步
方向 3 补形法 如图,一个底面半径为 2 的圆柱被一平面所截,截得的几
何体的最短和最长母线长分别为 2 和 3,则该几何体的体积为________.
素养点睛:本题考查了直观想象的核心素养.
| 自学导引 |
| 课堂互动 |
| 素养达成 |
| 课后提能训练 |
数学 必修第二册 配人版A版
第六章第八平章面向立量体及几其何应初用步
柱体、锥体与台体的体积公式
几何体
体积
说明
柱体 锥体 台体
V 柱体=Sh
S 为柱体的_底__面__积___,h 为柱体的 _高___
V 锥体=13Sh
S 为锥体的_底__面__积___,h 为锥体的 _高___
AH=A1A·cos 60°=4(cm). 设 O1A1=r1,OA=r2,则 r2-r1=AH=4.①
| 自学导引 |
| 课堂互动 |
| 素养达成 |
| 课后提能训练 |
数学 必修第二册 配人版A版
第六章第八平章面向立量体及几其何应初用步
设 A1B 与 AB1 的交点为 M,则 A1M=B1M. 又∵A1B⊥AB1,∴∠A1MO1=∠B1MO1=45°. ∴O1M=O1A1=r1. 同理 OM=OA=r2. ∴O1O=O1M+OM=r1+r2=4 3,② 由①②可得 r1=2( 3-1),r2=2( 3+1). ∴S 表=πr21+πr22+π(r1+r2)l=32(1+ 3)π(cm2).
【答案】6+2 2 【解析】V 台体=13(2+4+ 2×4)×3=31×3×(6+2 2)=6+2 2.
8.2 - 简单几何体的表面积与体积

§8.2简单几何体的表面积与体积2014高考会这样考 1.与三视图相结合,考查几何体的表面积、体积;2.作为解答题中的某一问,与空间线面关系相结合考查几何体体积的计算.复习备考要这样做 1.熟记公式,理解公式的意义;2.结合几何体的结构特征,运用公式解决一些计算问题.2.几何体的表面积(1)棱柱、棱锥、棱台的表面积就是各面面积之和.(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和.[难点正本疑点清源]1.几何体的侧面积和全面积几何体的侧面积是指(各个)侧面面积之和,而全面积是侧面积与所有底面积之和.对侧面积公式的记忆,最好结合几何体的侧面展开图来进行.要特别留意根据几何体侧面展开图的平面图形的特点来求解相关问题.如直棱柱(圆柱)侧面展开图是一矩形,则可用矩形面积公式求解.再如圆锥侧面展开图为扇形,此扇形的特点是半径为圆锥的母线长,圆弧长等于底面的周长,利用这一点可以求出展开图扇形的圆心角的大小.2.等积法等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高,这一方法回避了具体通过作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.1.圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是________. 2.设某几何体的三视图如下(尺寸的长度单位为m).则该几何体的体积为________m 3.3.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 4.一个球与一个正方体的各个面均相切,正方体的边长为a ,则球的表面积为________.5.如图所示,在棱长为4的正方体ABCD —A 1B 1C 1D 1中,P 是A 1B 1上一点,且PB 1=14A 1B 1,则多面体P —BB 1C 1C 的体积为________.题型一 简单几何体的表面积例1 一个空间几何体的三视图如图所示,则该几何体的表面积为( )A .48B .32+817C .48+817D .80一个几何体的三视图(单位:cm)如图所示,则该几何体的表面积是________cm 2.题型二简单几何体的体积例2如图所示,已知E、F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1—B1EDF的体积.(2012·课标全国)已知三棱锥S-ABC的所有顶点都在球O的球面上,△ABC 是边长为1的正三角形,SC为球O的直径,且SC=2,则此棱锥的体积为()A.26 B.36 C.23 D.22题型三几何体的展开与折叠问题例3(1)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、B、C、D、O为顶点的四面体的体积为________.(2)有一根长为3π cm,底面直径为2 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为________ cm.如图,已知一个多面体的平面展开图由一边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是_______.转化思想在立体几何计算中的应用典例:(12分)如图,在直棱柱ABC—A′B′C′中,底面是边长为3的等边三角形,AA′=4,M为AA′的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC′到M的最短路线长为29,设这条最短路线与CC′的交点为N,求:(1)该三棱柱的侧面展开图的对角线长;(2)PC与NC的长;(3)三棱锥C—MNP的体积.方法与技巧1.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决.2.要注意将空间问题转化为平面问题.3.求几何体的体积,要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解.4.一些几何体表面上的最短距离问题,常常利用几何体的展开图解决.失误与防范1.几何体展开、折叠问题,要抓住前后两个图形间的联系,找出其中的量的关系.2.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.A 组 专项基础训练 (时间:35分钟,满分:57分)一、选择题(每小题5分,共20分)1.(2012·课标全国)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .182 . 已知高为3的直棱柱ABC —A ′B ′C ′的底面是边长为1的正三角形(如右图所示),则三棱锥B ′—ABC 的体积为( )A.14B.12C.36D.34 3.正六棱柱的高为6,底面边长为4,则它的全面积为( )A .48(3+3)B .48(3+23)C .24(6+2)D .1444.(2012·北京)某三棱锥的三视图如图所示,该三棱锥的表面积是 ( )A .28+6 5B .30+6 5C .56+12 5D .60+12 5二、填空题(每小题5分,共15分)5.(2012·山东)如图,正方体ABCD -A 1B 1C 1D 1的棱长为1,E ,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为________.6.(2011·天津)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.7.已知三棱锥A—BCD的所有棱长都为2,则该三棱锥的外接球的表面积为________.三、解答题(共22分)8.(10分)如图所示,在边长为5+2的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.9.(12分)有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.B 组 专项能力提升 (时间:25分钟,满分:43分)一、选择题(每小题5分,共15分)1.某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为( )A.32π B .π+3C.32π+ 3D.52π+ 3 2.在四棱锥E —ABCD 中,底面ABCD 为梯形,AB ∥CD,2AB =3CD ,M 为AE 的中点,设E —ABCD 的体积为V ,那么三棱锥M —EBC 的体积为( )A.25VB.13VC.23VD.310V 3.(2011·辽宁)已知球的直径SC =4,A 、B 是该球球面上的两点,AB =3,∠ASC =∠BSC=30°,则棱锥S -ABC 的体积为( )A .3 3B .2 3C. 3D .1二、填空题(每小题5分,共15分)4.如图,已知正三棱柱ABC —A 1B 1C 1的底面边长为2 cm ,高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线 的长为______ cm.5.已知一个几何体是由上、下两部分构成的组合体,其三视图如图所示,若图中圆的半径为1,等腰三角形的腰长为5,则该几何体的体积是________.6.(2012·上海)如图,AD 与BC 是四面体ABCD 中互相垂直的棱,BC =2.若AD =2c ,且AB +BD =AC +CD =2a ,其中a 、c 为常数,则四面体ABCD 的体积的最大值是________.三、解答题7.(13分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D—ABC,如图2所示.图1图2(1)求证:BC⊥平面ACD;(2)求几何体D—ABC的体积.。
简单几何体的表面积和体积

基础知识梳理
(3)锥体 圆锥和棱锥 的体积 锥体(圆锥和棱锥 锥体 圆锥和棱锥)的体积
1 V锥体= Sh. 3
1 其中V圆锥= 3 πr2h ,r为底面半径. 其中 为底面半径. 为底面半径
基础知识梳理
(4)台体的体积公式 台体的体积公式 V台=h(S++ . ++S′). ++ 为台体的高, 和 分别为上下 注:h为台体的高,S′和S分别为上下 为台体的高 两个底面的面积. 两个底面的面积. 1 + 其中V 其中 圆台= 3 πh(r2+rr′+r′2) . 为台体的高, 、 分别为上 分别为上、 注:h为台体的高,r′、r分别为上、 为台体的高 下两底的半径. 下两底的半径. (5)球的体积 球的体积 4 3 V球= 3 πR .
课堂互动讲练
跟踪训练
(2)由(1)知 AB⊥BD.∵CD∥AB, 由 知 ⊥ ∵ ∥ , ∴CD⊥BD,从而 DE⊥BD. ⊥ , ⊥ 在 Rt△DBE 中,∵DB=2 3, △ = , DE=DC=AB=2, = = = , 1 ∴S△DBE=2DBDE=2 3. = 又∵AB⊥平面 EBD,BE平面 ⊥ , EBD,∴AB⊥BE. , ⊥ ∵BE=BC=AD=4,∴S△ABE= = = = , 1 ABBE=4. = 2
高中数学必修二 (教案)简单几何体的表面积与体积

简单几何体的表面积与体积【第一课时】【教学目标】1.了解柱体、锥体、台体的侧面展开图,掌握柱体、柱、锥、台的体积2.能利用柱体、锥体、台体的体积公式求体积,理解柱体、锥体、台体的体积之间的关系【教学重难点】1.柱、锥、台的表面积2.锥体、台体的表面积的求法【教学过程】一、问题导入预习教材内容,思考以下问题:1.棱柱、棱锥、棱台的表面积如何计算?2.圆柱、圆锥、圆台的侧面展开图分别是什么?3.圆柱、圆锥、圆台的侧面积公式是什么?4.柱体、锥体、台体的体积公式分别是什么?5.圆柱、圆锥、圆台的侧面积公式、体积公式之间分别有怎样的关系?二、新知探究柱、锥、台的表面积例1:(1)若圆锥的正视图是正三角形,则它的侧面积是底面积的()A.2倍B.3 倍C.2 倍D.5 倍(2)已知正方体的8 个顶点中,有 4 个为侧面是等边三角形的三棱锥的顶点,则这个三棱锥与正方体的表面积之比为()A.1∶ 2B.1∶3C.2∶ 2D.3∶6(3)已知某圆台的一个底面周长是另一个底面周长的 3 倍,母线长为 3 ,圆台的侧面积为84π,则该圆台较小底面的半径为()A.7B.6C.5D.3【解析】(1)设圆锥的底面半径为r,母线长为l,则由题意可知,l=2r,于是S侧=πr·2r=2πr2,S底=πr2,可知选 C.(2)棱锥B′ACD′为适合条件的棱锥,四个面为全等的等边三角形,设正方体的棱长为1,则B′C=2,S△B′AC=3 2.三棱锥的表面积S锥=4×32=23,又正方体的表面积S正=6.因此S锥∶S正=23∶6=1∶ 3.(3)设圆台较小底面的半径为r,则另一底面的半径为3r.由S侧=3π(r+3r)=84π,解得r=7.【答案】(1)C(2)B(3)A[规律方法]空间几何体表面积的求法技巧(1)多面体的表面积是各个面的面积之和.(2)组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形计算,而表面积是侧面积与底面圆的面积之和.柱、锥、台的体积例2:如图所示,正方体ABCDA1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥.(1)求剩余部分的体积;(2)求三棱锥AA1BD的体积及高.【解】(1)V三棱锥A1ABD=13S△ABD·A1A=13×1 2·AB·AD·A1A=16a3.故剩余部分的体积V=V正方体-V三棱锥A1ABD=a3-16a3=56a3.(2)V三棱锥AA1BD=V三棱锥A1ABD=1 6a 3.设三棱锥AA1BD的高为h,则V三棱锥AA1BD=13·S△A1BD·h=13×12×32(2a)2h=36a2h,故36a2h=16a3,解得h=3 3a.[规律方法]求几何体体积的常用方法(1)公式法:直接代入公式求解.(2)等积法:例如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可.(3)补体法:将几何体补成易求解的几何体,如棱锥补成棱柱,棱台补成棱锥等.(4)分割法:将几何体分割成易求解的几部分,分别求体积.[提醒]求几何体的体积时,要注意利用好几何体的轴截面(尤其为圆柱、圆锥时),准确求出几何体的高和底面积.组合体的表面积和体积例3:如图在底面半径为2,母线长为 4 的圆锥中内接一个高为3的圆柱,求圆柱的表面积.【解】设圆锥的底面半径为 R ,圆柱的底面半径为 r ,表面积为 S . 则 R =OC =2,AC =4, AO =42-22=2 3. 如图所示,易知△AEB ∽△AOC ,所以AE AO =EB OC ,即323=r 2,所以 r =1,S 底=2πr 2=2π,S 侧=2πr ·h =23π. 所以 S =S 底+S 侧=2π+23π =(2+23)π.1.[变问法]本例中的条件不变,求圆柱的体积与圆锥的体积之比. 解:由例题解析可知:圆柱的底面半径为 r =1,高 h =3,所以圆柱的体积 V 1=πr 2h =π×12×3=3π.圆锥的体积 V 2=13π×22×23=833π.所以圆柱与圆锥的体积比为 3∶8.2.[变问法]本例中的条件不变,求图中圆台的表面积与体积.解:由例题解析可知:圆台的上底面半径 r =1,下底面半径 R =2,高 h =3,母线 l =2,所以圆台的表面积 S =π(r 2+R 2+r ·l +Rl )=π(12+22+1×2+2×2)=11π.圆台的体积 V =13π(r 2+rR +R 2)h =13π(12+2+22)×3=733π. 3.[变条件、变问法]本例中的“高为3”改为“高为 h ”,试求圆柱侧面积的最大值.解:设圆锥的底面半径为 R ,圆柱的底面半径为 r ,则R=OC=2,AC=4,AO=42-22=2 3.如图所示易知△AEB∽△AOC,所以AEAO =EBOC,即23-h23=r2,所以h=23-3r,S圆柱侧=2πrh=2πr(23-3r)=-23πr2+43πr,所以当r=1,h=3时,圆柱的侧面积最大,其最大值为23π.[规律方法]求组合体的表面积与体积的步骤(1)分析结构特征:弄清组合体的组成形式,找准有关简单几何体的关键量.(2)设计计算方法:根据组成形式,设计计算方法,特别要注意“拼接面”面积的处理,利用“切割”“补形”的方法求体积.(3)计算求值:根据设计的计算方法求值.【课堂总结】1.棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和.2.棱柱、棱锥、棱台的体积(1)V棱柱=Sh;(2)V棱锥=13Sh;V棱台=13h(S′+SS′+S),其中S′,S分别是棱台的上、下底面面积,h为棱台的高.3.圆柱、圆锥、圆台的表面积和体积名称图形公式圆柱底面积:S底=πr2侧面积:S侧=2πrl表面积:S=2πrl+2πr2体积:V=πr2l[名师点拨]1.柱体、锥体、台体的体积(1)柱体:柱体的底面面积为S ,高为h ,则V =Sh .(2)锥体:锥体的底面面积为S ,高为h ,则V =13Sh . (3)台体:台体的上、下底面面积分别为S ′、S ,高为h ,则V =13()S ′+SS ′+S h .2.圆柱、圆锥、圆台的侧面积公式之间的关系S 圆柱侧=2πrl ――→r ′=r S 圆台侧=π(r ′+r )l ――→r ′=0S 圆锥侧=πrl . 3.柱体、锥体、台体的体积公式之间的关系V 柱体=Sh ――→S ′=S V 台体=13(S ′+S ′S +S )h ――→S ′=0V 锥体=13Sh .【课堂检测】1.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为( )A .22B .20C .10D .11解析:选A.所求长方体的表面积S =2×(1×2)+2×(1×3)+2×(2×3)=22.2.正三棱锥的高为3,侧棱长为23,则这个正三棱锥的体积为( )A.274B.94C.2734D.934解析:选D.由题意可得底面正三角形的边长为3,所以V =13×34×32×3=934.故选D.3.已知圆台的上、下底面的面积之比为9∶25,那么它的中截面截得的上、下两台体的侧面积之比是________.解析:圆台的上、下底面半径之比为3∶5,设上、下底面半径为3x ,5x ,则中截面半径为4x ,设上台体的母线长为l ,则下台体的母线长也为l ,上台体侧面积S 1=π(3x +4x )l =7πxl ,下台体侧面积S 2=π(4x +5x )l =9πxl ,所以S 1∶S 2=7∶9.答案:7∶9 4.如图,三棱台ABC A 1B 1C 1中,AB ∶A 1B 1=1∶2,求三棱锥A 1ABC ,三棱锥B A 1B 1C ,三棱锥CA 1B 1C 1的体积之比.解:设棱台的高为h ,S △ABC =S ,则S △A 1B 1C 1=4S .所以VA 1ABC =13S △ABC ·h =13Sh ,VC A 1B 1C 1=13S △A 1B 1C 1·h =43Sh .又V 台=13h (S +4S +2S )=73Sh , 所以VB A 1B 1C =V 台-VA 1ABC -VCA 1B 1C 1=73Sh -Sh 3-4Sh 3=23Sh , 所以体积比为1∶2∶4.【第二课时】 【教学目标】1.记准球的表面积和体积公式,会计算球的表面积和体积 2.能解决与球有关的组合体的计算问题【教学重难点】1.球的表面积与体积 2.与球有关的组合体【教学过程】一、问题导入预习教材内容,思考以下问题:1.球的表面积公式是什么?2.球的体积公式什么?二、新知探究球的表面积与体积例1:(1)已知球的体积是32π3,则此球的表面积是()A.12πB.16πC.16π3 D.64π3(2)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的体积是28π3,则它的表面积是()A.17π B.18πC.20π D.28π【解析】(1)设球的半径为R,则由已知得V=43πR3=32π3,解得R=2.所以球的表面积S=4πR2=16π.(2)由三视图可得此几何体为一个球切割掉18后剩下的几何体,设球的半径为r,故78×43πr3=283π,所以r=2,表面积S=78×4πr2+34πr2=17π,选A.【答案】(1)B(2)A[归纳反思]球的体积与表面积的求法及注意事项(1)要求球的体积或表面积,必须知道半径R或者通过条件能求出半径R,然后代入体积或表面积公式求解.(2)半径和球心是球的最关键要素,把握住了这两点,计算球的表面积或体积的相关题目也就易如反掌了.球的截面问题例2:如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器厚度,则球的体积为()A.500π3cm3 B.866π3cm3C.1 372π3cm3 D.2 048π3cm3【解析】如图,作出球的一个截面,则MC=8-6=2(cm),BM=12AB=12×8=4(cm).设球的半径为R cm,则R2=OM2+MB2=(R-2)2+42,所以R=5,所以V球=43π×53=5003π (cm3).【答案】A[规律方法]球的截面问题的解题技巧(1)有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题.(2)解题时要注意借助球半径R,截面圆半径r,球心到截面的距离d构成的直角三角形,即R2=d2+r2.与球有关的切、接问题角度一球的外切正方体问题例3:将棱长为 2 的正方体木块削成一个体积最大的球,则该球的体积为()A.4π3B.2π3C.3π2D.π6【解析】由题意知,此球是正方体的内切球,根据其几何特征知,此球的直径与正方体的棱长是相等的,故可得球的直径为 2,故半径为 1,其体积是43×π×13=4π3.【答案】A角度二球的内接长方体问题例4:一个长方体的各个顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 1,2,3,则此球的表面积为________.【解析】长方体外接球直径长等于长方体体对角线长,即 2R =12+22+32=14,所以球的表面积 S =4πR 2=14π. 【答案】14π角度三球的内接正四面体问题例5:若棱长为 a 的正四面体的各个顶点都在半径为 R 的球面上,求球的表面积.【解】把正四面体放在正方体中,设正方体棱长为 x ,则 a =2x ,由题意2R =3x =3×2a 2=62a ,所以 S 球=4πR 2=32πa 2.角度四球的内接圆锥问题例6:球的一个内接圆锥满足:球心到该圆锥底面的距离是球半径的一半,则该圆锥的体积和此球体积的比值为________.【解析】①当圆锥顶点与底面在球心两侧时,如图所示,设球半径为 r ,则球心到该圆锥底面的距离是r 2,于是圆锥的底面半径为 r 2-⎝ ⎛⎭⎪⎫r 22=3r 2,高为3r 2.该圆锥的体积为 13 ×π×⎝ ⎛⎭⎪⎫3r 22 ×3r 2=38πr 3,球体积为43 πr 3,所以11 / 13该圆锥的体积和此球体积的比值为38πr 343πr 3=932. ②同理,当圆锥顶点与底面在球心同侧时,该圆锥的体积和此球体积的比值为332.【答案】932或332角度五球的内接直棱柱问题例7:设三棱柱的侧棱垂直于底面,所有棱的长都为 a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2B.73πa 2C.113πa 2 D .5πa 2【解析】由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为 a .如图,P 为三棱柱上底面的中心,O 为球心,易知 AP=23×32a =33a ,OP =12a ,所以球的半径 R = OA 满足R 2=⎝ ⎛⎭⎪⎫33a 2+⎝ ⎛⎭⎪⎫12a 2=712a 2,故 S 球=4πR 2=73πa 2. 【答案】B[规律方法](1)正方体的内切球球与正方体的六个面都相切,称球为正方体的内切球,此时球的半径为 r 1=a 2,过在一个平面上的四个切点作截面如图(1). (2)长方体的外接球长方体的八个顶点都在球面上,称球为长方体的外接球,根据球的定义可知,长方体的体对角线是球的直径,若长方体过同一顶点的三条棱长为 a ,b ,c ,过球心作长方体的对角线,则球的半径为 r 2=12 a 2+b 2+c 2,如图(2).12 / 13(3)正四面体的外接球正四面体的棱长 a 与外接球半径 R 的关系为:2R =62a .【课堂总结】1.球的表面积设球的半径为R ,则球的表面积S =4πR 2.2.球的体积设球的半径为R ,则球的体积V =43πR 3.[名师点拨]对球的体积和表面积的几点认识(1)从公式看,球的表面积和体积的大小,只与球的半径相关,给定R 都有唯一确定的S 和V 与之对应,故表面积和体积是关于R 的函数.(2)由于球的表面不能展开成平面,所以,球的表面积公式的推导与前面所学的多面体与旋转体的表面积公式的推导方法是不一样的.(3)球的表面积恰好是球的大圆(过球心的平面截球面所得的圆)面积的4倍.【课堂检测】1.直径为 6 的球的表面积和体积分别是( )A .36π,144πB .36π,36πC .144π,36πD .144π,144π解析:选 B .球的半径为 3,表面积 S =4π·32=36π,体积 V =43π·33=36π.2.一个正方体的表面积与一个球的表面积相等,那么它们的体积比是( ) A.6π6 B.π2C.2π2D.3π2π解析:选 A .设正方体棱长为 a ,球半径为 R ,由 6a 2=4πR 2 得a R =2π3,所以V 1V 2=a 343πR 3=34π⎝ ⎛⎭⎪⎫2π33=6π6. 3.若两球的体积之和是 12π,经过两球球心的截面圆周长之和为 6π,则两球的半径之差为( )A .1B .213 / 13C .3D .4解析:选 A .设两球的半径分别为 R ,r (R >r ),则由题意得⎩⎪⎨⎪⎧4π3R 3+4π3r 3=12π,2πR +2πr =6π,解得⎩⎨⎧R =2,r =1.故 R -r =1. 4.已知棱长为 2 的正方体的体积与球 O 的体积相等,则球 O 的半径为________.解析:设球 O 的半径为 r ,则43πr 3=23,解得 r =36π. 答案:36π5.已知过球面上 A ,B ,C 三点的截面和球心的距离为球半径的一半,且 AB =BC =CA =2,求球的表面积.解:设截面圆心为O ′,球心为 O ,连接 O ′A ,OA ,OO ′,设球的半径为 R .因为O ′A =23×32×2=233.在 Rt △O ′OA 中,OA 2=O ′A 2+O ′O 2,所以 R 2=⎝ ⎛⎭⎪⎫2332+14R 2, 所以 R =43,所以 S 球=4πR 2=649π.。
第二节 简单几何体的表面积和体积(知识梳理)
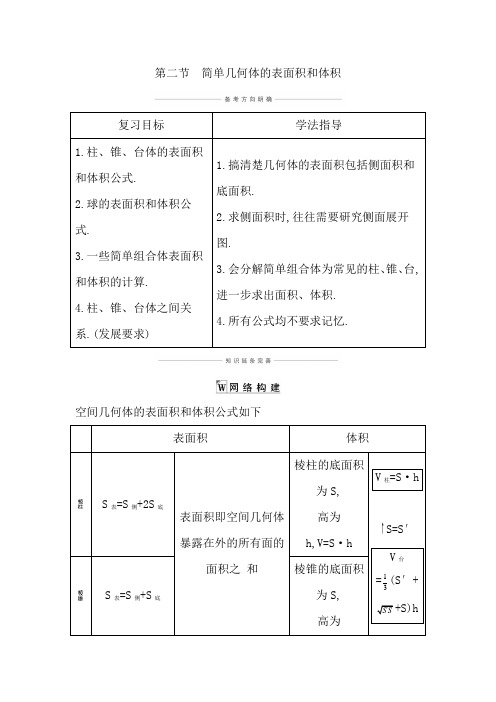
第二节简单几何体的表面积和体积复习目标学法指导1.柱、锥、台体的表面积和体积公式.2.球的表面积和体积公式.3.一些简单组合体表面积和体积的计算.4.柱、锥、台体之间关系.(发展要求)1.搞清楚几何体的表面积包括侧面积和底面积.2.求侧面积时,往往需要研究侧面展开图.3.会分解简单组合体为常见的柱、锥、台,进一步求出面积、体积.4.所有公式均不要求记忆.空间几何体的表面积和体积公式如下表面积体积S表=S侧+2S底表面积即空间几何体暴露在外的所有面的面积之和棱柱的底面积为S,高为h,V=S·hV柱=S·hS=S′V台=13(S′+S S +S)h S表=S侧+S底棱锥的底面积为S,高为h,V=13S ·h S ′=0 V 锥=13S ·hS 表=S 侧+ S 上底+S 下底棱台的上、下底面 面积分别为S ′,S,高为h, V=13(S ′+ S S+S)h圆柱的底面半径和母线长分别为r,lS 表=2πr 2+2πrl 圆柱的高为h,V=πr 2h圆锥的底面半径和母线长分别为r,l S 表=πr 2+πrl 圆锥的高为h,V=13πr 2h圆台的上、下底面半 径和母线长分圆台的高为h,V=13π(r ′2+别为r,r′,l,S表=π(r′2+r2+r′l+rl)r′r+r2)h球球半径为R,S球=4πR2V球=43πR31.概念理解(1)表面积应为侧面积和底面积的和,要注意组合体中哪些部分暴露或遮挡.(2)求空间几何体体积的常用方法①公式法:直接根据相关的体积公式计算.②等积法:根据体积计算公式,通过转换空间几何体的底面和高使得体积计算更容易,或是求出一些体积比等.③割补法:把不能直接计算体积的空间几何体进行适当的分割或补形,转化为可计算体积的几何体.2.求面积或体积中相关联的结论几个与球有关的切、接常用结论(1)正方体的棱长为a,球的半径为R,①正方体的外接球,则3②正方体的内切球,则2R=a;③球与正方体的各棱相切,则2(2)长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=222a b c ++.(3)正四面体的外接球与内切球的半径之比为3∶1.1.圆柱的底面积为S,侧面展开图是一个正方形,那么圆柱的侧面积是( A )(A)4πS (B)2πS (C)πS (D)23πS 解析:由πr 2=S 得圆柱的底面半径是πS , 故侧面展开图的边长为2π·πS =2πS,所以圆柱的侧面积是4πS.故选A.2.正三棱柱ABC-A 1B 1C 1的底面边长为2,侧棱长为3,D为BC 的中点,则三棱锥A-B 1DC 1的体积为 . 解析:如图,在正三棱柱ABC-A 1B 1C 1中, 因为AD ⊥BC,AD ⊥BB 1, BB 1∩BC=B,所以AD ⊥平面B 1DC 1. 所以11A B DC V-=1113B DC S ∆·AD=13×12×233=1. 答案:13.某几何体的三视图如图所示(单位:cm),则该几何体的体积为 cm 3,表面积为 cm 2.解析:由三视图可得该几何体为二分之一圆锥, 圆锥的底面半径为1,高为2,所以可得该几何体的体积为12×13×π×12×2=π3, 该几何体的表面积为12×π×12+12π×114++12×2×2=)51π2+2.答案: π3)51π2+24.已知正四棱锥O-ABCD 32,3,则以O 为球心,OA 为半径的球的表面积是 . 解析:设O 到底面的距离为h,则13×3×32,解得32()()2233+62262h ⎛⎫+ ⎪ ⎪⎝⎭6故球的表面积为4π×62=24π.答案:24π5.(2019·浙江宁波模拟)已知一个三棱锥的三视图如图所示,其中俯视图是顶角为120°的等腰三角形,侧视图为直角三角形,则该三棱锥的表面积为,该三棱锥的外接球体积为.解析:由三视图得几何体的直观图如图.所以S表=2×12×2×2+12×3512×3 1153如图,作DE⊥DB,以D为原点,DB所在直线为x轴,DE所在直线为y 轴,DA所在直线为z轴,建立空间直角坐标系,则3设球心坐标为(x,y,z),因为(x-2)2+y2+z2=x2+y2+z2,①x2+y2+(z-2)2=x2+y2+z2,②(x+1)23)2+z2=x2+y2+z2,③所以x=1,y=3,z=1,所以球心的坐标是(1,3,1), 所以球的半径是()222131++=5.所以球的体积是43π×(5)3=2053π.答案:4+15+32053π考点一几何体的表面积[例1] (1)(2018·金丽衢十二校联考)某四面体的三视图如图所示,正视图、侧视图都是腰长为2的等腰直角三角形,俯视图是边长为2的正方形,则此四面体的最大面的面积是( )(A)2 23(D)4(2)(2019·湖州模拟)某几何体的三视图如图所示,其中侧视图的下半部分曲线为半圆弧,则该几何体的表面积为( )(A)4π3(B)5π3(C)4π3(D)5π3(3)若圆锥的侧面积与过轴的截面面积之比为2π,则其母线与轴的夹角的大小为;(4)四棱锥S-ABCD中,底面ABCD是边长为2的正方形,侧面SAD是以SD为斜边的等腰直角三角形,若四棱锥S-ABCD的体积取值范围为4383],则该四棱锥外接球表面积的取值范围是.解析:(1)因为几何体为一个四面体,六条棱长分别为2223所以四面体的四个面的面积分别为12×2×2=2,12×2×2212×2×221 2×22sin π33因此四面体的最大面的面积是3.故选C.(2)由三视图可知该几何体是一个正三棱柱和一个半圆柱的组合体,三棱柱的两个侧面面积之和为2×4×2=16,两个底面面积之和为2×12×2×3=23;半圆柱的侧面积为π×4=4π,两个底面面积之和为2×12×π×12=π,所以几何体的表面积为5π+16+23,故选D.(3)设圆锥底面半径为r,母线长为l,母线与轴夹角为θ, 则=22π122rl r l r⋅-2π,r l=3,即sin θ=3,θ=π3. 解析:(4)四棱锥S-ABCD 中,可得AD ⊥SA,AD ⊥AB ⇒AD ⊥平面SAB ⇒平面SAB ⊥平面ABCD,过S 作SO ⊥AB 于O,则SO ⊥平面ABCD, 设∠SAB=θ, 故S ABCDV-=13S 四边形ABCD ·SO=83sin θ, 所以sin θ∈[3,1]⇒θ∈[π3,2π3]⇒-12≤cos θ≤12, 在△SAB 中,SA=AB=2, 则有SB=221cos θ-,所以△SAB 的外接圆半径r=2sin SBθ=21cos θ-,将该四棱锥补成一个以SAB 为一个底面的直三棱柱,得外接球的半径R=21r +⇒S=4πR2=4π(21cos θ++1), 所以S ∈[28π3,20π]. 答案:(1)C (2)D (3)π3答案:(4)[28π3,20π] (1)已知几何体的三视图求其表面积,一般是先根据三视图判断空间几何体的形状,再根据题目所给数据与几何体的表面积公式,求其表面积.(2)多面体的表面积是各个面的面积之和,组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开成平面图形计算,而表面积是侧面积与底面圆的面积之和.1.(2019·浙江十校联盟)如图所示,已知某几何体的三视图及其尺寸(单位:cm),则该几何体的表面积为( C )(A)15π cm2(B)21π cm2(C)24π cm2(D)33π cm2解析:由三视图可知,则该几何体是一个圆锥,圆锥的底面半径为3,母线长为5,故该几何体的表面积为S表=πr2+πrl=π×32+π×3×5=24π(cm2).故选C.2.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( A )(A)81π4(B)16π(C)9π(D)27π4解析:易知球心在正四棱锥的高上,设球的半径为R,则(4-R)2+(2)2=R2, 解得R=94,所以球的表面积为4π×(94)2=814π.故选A.考点二几何体的体积[例2] (1)已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( )(A)12cm3(B)1 cm3(C)16 cm3 (D)13cm3(2)(2018·天津卷)已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD 外,该正方体其余各面的中心分别为点E,F,G,H, M(如图),则四棱锥M-EFGH的体积为.解析:(1)由题意,根据给定的三视图可知,该几何体表示一个底面为腰长为1的等腰直角三角形,高为1的三棱锥, 如图所示,所以该三棱锥的体积为V=13×12×1×1×1=16(cm 3),故选C.解析:(2)依题意,易知四棱锥M-EFGH 是一个正四棱锥,且底面边长为2,高为12. 故M EFGHV=13×(2)2×12=112. 答案:(1)C 答案:(2)112(1)若所给定的几何体是柱体、锥体或台体等规则几何体,则可直接利用公式进行求解,其中,等积转换法多用来求三棱锥的体积.(2)若所给定的几何体是不规则几何体,则将不规则的几何体通过分割或补形转化为规则几何体,再利用公式求解.(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.某三棱锥的三视图如图所示,则该三棱锥的体积为( D )(A)60 (B)30 (C)20 (D)10解析:如图,把三棱锥A-BCD 放到长方体中,长方体的长、宽、高分别为5,3,4,△BCD 为直角三角形,直角边分别为5和3,三棱锥A-BCD 的高为4,故该三棱锥的体积V=13×12×5×3×4=10.故选D.考点三 与面积、体积相关的综合问题[例3] (1)若一个正四面体的表面积为S 1,其内切球的表面积为S 2,则12S S = ;(2)将边长为a 的正方形ABCD 沿对角线AC 折起,点A,B,C,D 折叠后对应点为A ′,B ′,C ′,D ′,使B ′D ′=a,则三棱锥D ′-A ′B ′C ′的体积为 .解析:(1)设正四面体棱长为a,则正四面体的表面积为 S 1=43a 23a2,正四面体的高2233a a ⎛⎫- ⎪ ⎪⎝⎭6a,由13r ·S 1=1332·h 知r=146a. 因此内切球的表面积为S 2=4πr 2=2π6a,则12S S 2236a a 63.解析:(2)如图所示,正方形ABCD 及折叠后的直观图.易知在直观图中,A ′B ′=B ′C ′=C ′D ′=D ′A ′=a, 且A ′D ′⊥D ′C ′,A ′B ′⊥B ′C ′, 取A ′C ′的中点E,连接D ′E,B ′E, 则D ′E ⊥A ′C ′,D ′E=EB ′=2a,所以D ′E ⊥EB ′,所以D ′E ⊥平面A ′B ′C ′. D ′E 即为三棱锥D ′-A ′B ′C ′的高. 故D A B C V''''-=13S △A ′B ′C ′·D ′E =13×12×a ×a ×2a=2a 3.答案:(1)63 答案:(2)2a 3(1)①解决与球有关问题的关键是球心及球的半径,在球中球心与截面圆圆心的连线、截面圆圆心与截面圆周上一点、该点与球心的连线构成一个直角三角形.②解决多面体(或旋转体)的外接球、内切球问题的关键是确定球心在多面体(或旋转体)中的位置,找到球半径(或直径)与几何体相关元素之间的关系.有时将多面体补形为正(长)方体再求解.(2)求几何体表面上两点间的最短距离的常用方法是选择恰当的母线或棱将几何体展开,转化为求平面上两点间的最短距离.1.已知直三棱柱ABC-A 1B 1C 1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB ⊥AC,AA 1=12,则球O 的半径为( C ) (A)3172 (B)210(C)132(D)310解析:如图,由球心作平面ABC 的垂线, 则垂足为BC 的中点M.又AM=12BC=52,OM=12AA 1=6, 所以球O 的半径 R=OA=22562⎛⎫+ ⎪⎝⎭=132. 故选C.2.已知某几何体的三视图如图所示,则该几何体的表面积是 ,体积是 .解析:本题考查空间几何体的三视图、体积和表面积的计算.由三视图得该几何体为底面是以上底为1,下底为3,高为3的直角梯形,高为3的直四棱柱,则其表面积为2×3×1+32+3×3+1×3+3×3+3×13=33+313,体积为3×3×1+32=18.答案:33+31318考点四易错辨析[例4] (2019·浙江绍兴模拟)如图是由半球和圆柱组合而成的几何体的三视图,则该几何体的体积为( )(A)5π3 (B)8π3(C)10π3(D)12+2π3解析:由题得,几何体是水平放置的一个圆柱和半个球,所以该几何体的体积为V=43π×13×12+π×12×2=83π,故选B.正确解决此类问题应注意确认几何体的形状时,要紧扣三视图,不能凭感觉去确定.已知直三棱柱ABC-A1B1C1的侧棱长为4,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ 为直角三角形,则该直角三角形斜边长的最小值为( C ) 2(B)3 3(D)4解析:如图,不妨设N在B处,AM=h,CQ=m,则有MB2=h2+4,BQ2=m2+4,MQ2=(h-m)2+4,由MB2=BQ2+MQ2,得m2-hm+2=0.则Δ=h2-8≥0,即h2≥8,所以该直角三角形的斜边MB≥23.故选C.类型一几何体的表面积1.如图是一个封闭几何体的三视图,则该几何体的表面积为( C )(A)7π cm2(B)8π cm2(C)9π cm2(D)11π cm2解析:依题意,题中的几何体是从一个圆柱中挖去一个半球后所剩余的部分,其中圆柱的底面半径是1 cm、高是 3 cm,球的半径是1 cm,因此该几何体表面积等于12×(4π×12)+π×12+2π×1×3=9π(cm2).故选C.2.某三棱锥的三视图如图所示,该三棱锥的表面积是( B )(A)28+65(B)30+65(C)56+125(D)60+125解析:根据三棱锥的三视图可还原此几何体的直观图如图,此几何体为一个底面为直角三角形,高为4的三棱锥,因此表面积为S=12×(2+3)×4+12×4×5+12×4×(2+3)+12×5415 5故选B.类型二几何体的体积3.某几何体的三视图如图所示,它的体积为( C )(A)72π(B)48π(C)30π(D)24π解析:由三视图知该几何体是由一个半球和一个圆锥构成的组合体,所以其体积为V=12×43π×33+13π×32×4=30π.故选C.4.某几何体的三视图如图所示,则该几何体的体积为( D )(A)π2(B)1+π2(C)1+π(D)2+π解析:由三视图可得,该几何体是一个长方体和半个圆柱的组合体,则该几何体的体积为V=12×2+12×π×12×2=2+π,故选D.5.(2018·全国Ⅲ卷)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为3则三棱锥D-ABC体积的最大值为( B )3333解析:由等边△ABC的面积为3323,所以AB=6,所以等边△ABC的外接圆的半径为r=33AB=23.设球的半径为R,球心到等边△ABC的外接圆圆心的距离为d,则d=22R r-=1612-=2.所以三棱锥D-ABC高的最大值为2+4=6,所以三棱锥D-ABC体积的最大值为13×93×6=183.故选B.6.(2019·名校协作体模拟)某几何体的三视图(单位:mm)如图所示,则它的体积是cm3,表面积是cm2.解析:由三视图得该几何体底面是一个以上底为2,下底为4,高为3的直角梯形,高为33的四棱锥,则其体积为13×33×2+42×3=93(cm3),表面积为1 2×3×33+2+42×3+12×3×2+12×3×4+12×5×33=(18+63)(cm2).答案:93(18+63)7.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.解析:由题意知所给的几何体是棱长均为2的八面体,它是由两个有公共底面的正四棱锥组合而成的,正四棱锥的高为1,所以这个八面体的体积为2V 正四棱锥=2×13×(2)2×1=43.答案:43类型三 面积、体积综合问题8.(2018·浙江绍兴质量调测)已知一个几何体的三视图如图所示,则该几何体的体积是( A )(A)83 (B)8 (C)203(D)6 解析:如图所示,在棱长为2的正方体中,题中的三视图对应的几何体为四棱锥P-ADC 1B 1,其中P 为棱A 1D 1的中点,则该几何体的体积11P ADC B V -=211P DB C V -=211D PB C V-=2×13×11PB C S∆×DD 1=83. 故选A.9.已知球的直径SC=4,A,B是该球球面上的两点,AB=3,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( C )(A)33(B)23(C)3 (D)1解析:由题意知,如图所示,在棱锥S-ABC中,△SAC,△SBC都是有一个角为30°的直角三角形,且3,SC=4,所以3作BD⊥3×3)2×3. SC于D点,连接AD,易证SC⊥平面ABD,因此V=13故选C.。
2023高考数学基础知识综合复习第18讲简单几何体的表面积与体积 课件(共24张PPT)

(2)旋转体的形成
几何体
旋转图形
圆柱
矩形
旋转轴
矩形一边所在的直线
圆锥
直角三角形
一直角边所在的直线
圆台
直角梯形或等腰梯形
球
半圆或圆
直角腰所在的直线或等腰梯形
上下底中点连线所在的直线
直径所在的直线
2.空间几何体的直观图
空间几何体的直观图常用斜二测画法来画,其画法步骤为:
①画轴:在平面图形上取互相垂直的x轴和y轴,作出与之对应的x'轴
3
4
3 = .故选 D.
考点一
考点二
考点三
本题考查四面体的体积的最大值的求法,涉及空间中线线、线面、
面面间的位置关系等基础知识,考查运算求解能力,属于难题.处理
此类问题时,往往先去找到不变的量,再根据题中的所给条件的变
化规律找到最值,从而得到体积的最值.
和y'轴,使得它们正方向的夹角为45°(或135°);
②画线(取长度):平面图形中与x轴平行(或重合)的线段画出与x'轴
平行(或重合)的线段,且长度不变,平面图形中与y轴平行(或重合)的
线段画出与y'轴平行(或重合)的线段,且长度为原来长度的一半;
③连线(去辅助线):连接有关线段,擦去作图过程中的辅助线.
径,从而进一步求解.
考点一
考点二
考点三
◆角度3.体积最值问题
例5(1)(2019年1月浙江学考)如图,线段AB是圆的直径,圆内一条动
弦CD与AB交于点M,且MB=2AM=2,现将半圆沿直径AB翻折,则三
棱锥C-ABD体积的最大值是(
)
2
3
1
3
A.
高中数学的几何体表面积和体积公式是哪些

高中数学的几何体表面积和体积公式是哪些高中数学的几何体表面积和体积公式1、圆柱体:表面积:2πRr+2πRh体积:πR2h(R为圆柱体上下底圆半径,h为圆柱体高)2、圆锥体:表面积:πR2+πR[(h2+R2)的平方根]体积:πR2h/3(r为圆锥体低圆半径,h为其高)3、正方体:表面积:S=6a2,体积:V=a3(a-边长)4、长方体:表面积:S=2(ab+ac+bc)体积:V=abc(a-长,b-宽,c-高)5、棱柱:体积:V=Sh(S-底面积,h-高)6、棱锥:体积:V=Sh/3(S-底面积,h-高)7、棱台:V=h[S1+S2+(S1S2)^1/2]/3(S1上底面积,S2下底面积,h-高)8、拟柱体:V=h(S1+S2+4S0)/6(S1-上底面积,S2-下底面积,S0-中截面积,h-高)9、圆柱:S底=πr2,S侧=Ch,S表=Ch+2S底,V=S底h=πr2h(r-底半径,h-高,C—底面周长,S底—底面积,S侧—侧面积,S表—表面积)10、空心圆柱:V=πh(R^2-r^2)(R-外圆半径,r-内圆半径,h-高)11、直圆锥:V=πr^2h/3(r-底半径,h-高)12、圆台:V=πh(R2+Rr+r2)/3(r-上底半径,R-下底半径,h-高)13、球:V=4/3πr^3=πd^3/6(r-半径,d-直径)14、球缺:V=πh(3a2+h2)/6=πh2(3r-h)/3(h-球缺高,r-球半径,a-球缺底半径)15、球台:V=πh[3(r12+r22)+h2]/6(r1球台上底半径,r2-球台下底半径,h-高)16、圆环体:V=2π2Rr2=π2Dd2/4(R-环体半径,D-环体直径,r-环体截面半径,d-环体截面直径)数学基础差的学生如何提高数学成绩基础薄弱的同学提高数学成绩的方法数学基础打牢,是个非常重要的事,很多及格成绩不到的同学,基本是连计算和公式都不是很过关。
对于这一类学生有以下几点建议。
几何体的表面积和体积公式

几何体的表面积和体积公式一、柱体。
1. 棱柱。
- 表面积公式:- 直棱柱的表面积S = 2S_底+S_侧,其中S_底为底面多边形的面积,S_侧为侧面积。
若直棱柱底面多边形的边长为a,边数为n,棱柱的高为h,则S_侧=nah。
- 体积公式:V = S_底h,h为棱柱的高。
2. 圆柱。
- 表面积公式:S = 2π r^2+2π rh,其中r为底面半径,h为圆柱的高。
- 体积公式:V=π r^2h。
二、锥体。
1. 棱锥。
- 表面积公式:S = S_底+S_侧,棱锥的侧面积S_侧等于各个侧面三角形面积之和。
若棱锥底面多边形的边长为a,边数为n,斜高(侧面三角形底边上的高)为h',则S_侧=(1)/(2)nah'。
- 体积公式:V=(1)/(3)S_底h,h为棱锥的高。
2. 圆锥。
- 表面积公式:S=π r^2+π rl,其中r为底面半径,l为母线长。
- 体积公式:V = (1)/(3)π r^2h,h为圆锥的高。
三、台体。
1. 棱台。
- 表面积公式:S = S_上底+S_下底+S_侧,棱台的侧面积S_侧=(1)/(2)(n(a + b)h'),其中n为底面边数,a为上底面多边形的边长,b为下底面多边形的边长,h'为斜高。
- 体积公式:V=(1)/(3)h(S_上底+S_下底+√(S_上底)S_{下底}),h为棱台的高。
2. 圆台。
- 表面积公式:S=π r^2+π R^2+π l(R + r),其中r为上底面半径,R为下底面半径,l为母线长。
- 体积公式:V=(1)/(3)π h(r^2+R^2+rR),h为圆台的高。
四、球体。
- 表面积公式:S = 4π R^2,其中R为球的半径。
- 体积公式:V=(4)/(3)π R^3。
简单几何体的表面积和体积 (教师版)

简单几何体的表面积和体积1 柱体①棱柱体积:V=sℎ(其中ℎ是棱柱的高)②圆柱(1) 侧面积:S=2πrℎ(2) 全面积:S=2πrℎ+2πr2(3) 体积:V=Sℎ=πr2ℎ(其中r为底圆的半径,ℎ为圆柱的高)2 锥体①棱锥棱锥体积:V=13Sℎ(其中ℎ为圆柱的高);②圆锥(1) 圆锥侧面积:S=πrl(2) 圆锥全面积:S=πr(r+l)(其中r为底圆的半径,l为圆锥母线)(3) 圆锥体积:V=13Sℎ=13πr2ℎ(其中r为底圆的半径,ℎ为圆柱的高)3台体①圆台表面积S=π (r′2+r′2+r′l+rl)其中r′是上底面圆的半径,r是下底面圆的半径,l是母线的长度.②台体体积V=13(S′+√SS′ +S) ℎ其中S , S′分别为上,下底面面积,ℎ为圆台的高.4 球体面积S=4πR2,体积V=43πR3(其中R为球的半径)【题型一】几何体的表面积【典题1】已知正四棱柱ABCD-A1B1C1D1中AB=2,AA1=3,O为上底面中心.设正四棱柱ABCD-A1B1C1D1与正四棱锥O-A1B1C1D1的侧面积分别为S1,S2,则S2S1=.【解析】如图,正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=3,则正四棱柱ABCD-A1B1C1D1的侧面积分别为S1=4×2×3=24;正四棱锥O-A1B1C1D1的斜高为√12+32=√10.∴正四棱锥O-A1B1C1D1的侧面积S2=4×12×2×√10=4√10.∴S2S1=4√1024=√106.【点拨】注意侧面积和全面积的区别.【典题2】一个底面半径为2,高为4的圆锥中有一个内接圆柱,该圆柱侧面积的最大值为()A.2π B.3πC.4πD.5π【解析】圆锥的底面半径为2,高为4,∴内接圆柱的底面半径为x时,它的上底面截圆锥得小圆锥的高为2x因此,内接圆柱的高 ℎ=4−2x;∴圆柱的侧面积为:S=2πx(4−2x)=4 π(2x−x2)(0<x<2)令t=2x−x2,当x=1时t max=1;所以当x=1时,S max=4π.即圆柱的底面半径为1时,圆柱的侧面积最大,最大值为4π.故选:C .【点拨】① 圆柱的侧面积S =2πrℎ,则需要知道圆柱的高ℎ与底圆半径r ;② 在处理圆锥、圆柱问题时,要清楚母线、高、底圆的半径之间的关系,则要看轴截面(如下图),此时由相似三角形的性质可以得到每个量的关系.【典题3】 一个圆台上、下底面半径分别为r 、R ,高为ℎ,若其侧面积等于两底面面积之和,则下列关系正确的是( )A .2ℎ=1R +1rB .1ℎ=1R +1rC .1r =1R +1ℎD .2R =1r +1ℎ 【解析】设圆台的母线长为l ,根据题意可得圆台的上底面面积为S 上=πr 2,圆台的下底面面积为S 下=πR 2,∵圆台的侧面面积等于两底面面积之和,∴侧面积S 侧=π(r 2+R 2)=π(r +R)l ,解之得l =r 2+R 2r+R ∵l =√ℎ2+(R −r)2∴r 2+R 2r+R =√ℎ2+(R −r)2,∴(r 2+R 2r +R )2=ℎ2+(R -r)2 ∴2ℎ=1R +1r .故选 A . 【点拨】在处理圆台问题时,要清楚母线、上底圆半径、下底圆半径、高之间的关系,则要看轴截面(如下图),有 l =√ℎ2+(R −r)2.【题型二】几何体的体积【典题1】正方形ABCD被对角线BD和以A为圆心,AB为半径的圆弧DB̂分成三部分,绕AD旋转,所得旋转体的体积V1、V2、V3之比是()A.2: 1: 1B.1∶2: 1C.1∶1∶1D.2∶2: 1【解析】设正方形ABCD的边长为1,可得图1旋转所得旋转体为以AD为轴的圆锥体,高AD=1且底面半径r=1∴该圆锥的体积为V1=13π×AB2×AD=13π;图2旋转所得旋转体,是以AD为半径的一个半球,减去图1旋转所得圆锥体而形成,∴该圆锥的体积为V2=V半球−V1=12×43π×AD2-V1=13π;图3旋转所得旋转体,是以AD为轴的圆柱体,减去图2旋转所得半球而形成,∴该圆锥的体积为V3=π×AB2×AD-V半球=π-23π=13π综上所述V1=V2=V3=13π,由此可得图中1、2、3三部分旋转所得旋转体的体积之比为1∶1∶1.故选 C.【点拨】①圆锥是由直角三角形以某一直角边为轴旋转得到;圆柱是由矩形以某一边为轴旋转得到;球是由半圆以直径为轴旋转得到;②求解不规则图形可用“割补法”.【典题2】如图,圆锥形容器的高为ℎ,圆锥内水面的高为ℎ1,且ℎ1=13ℎ,若将圆锥的倒置,水面高为ℎ2,则ℎ2等于()A.23ℎB.1927ℎC.√633ℎD.√1933ℎ【解析】方法一设圆锥形容器的底面积为S,则未倒置前液面的面积为49S.∴水的体积V =13Sℎ-13×49S ×(ℎ−ℎ1)=1981Sℎ. 设倒置后液面面积为S′,则S′S =(ℎ2ℎ)2,∴S′=Sℎ22ℎ2.∴水的体积V =13S′ℎ2=Sℎ233ℎ2. ∴1981Sℎ=Sℎ233ℎ2,解得ℎ2=√193ℎ3. 故选 D .方法二 设容器为圆锥1,高为ℎ,体积为V ;倒置前液面上的锥体为圆锥2,高为ℎ′=ℎ−ℎ1,体积为V 1;倒置后液面以下的锥体为圆锥3,高为ℎ2,体积为V 2.∵ℎ1ℎ=13 ∴ℎ′ℎ=23 ∴V−V 水V =(23)3=827⇒V 水V =1927, 在倒置后,又有V 水V =(ℎ2ℎ)3 ∴(ℎ2ℎ)3=1927⇒ℎ2=√193ℎ3【点拨】 ① 涉及圆台的表面积和体积,可把圆台补全为圆锥;② 两个相似几何体,若相似比为a ,则对应线段比为a ,对应的平面面积比为a 2,对应的几何体体积比是a 3.【典题3】 已知球的直径SC =4,A ,B 是该球球面上的两点,AB =2,∠ASC =∠BSC =45°,则棱锥S −ABC 的体积V = .【解析】由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,如图所示,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥SABD 和CABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DBC =∠DAC =45°,所以在△BDC 中,BD =4-x ,所以x =4-x ,解得x =2,所以AD =BD =2,所以 ABD 为正三角形,所以V =13S △ABD ×4=4√33.【点拨】① 圆内直径所对的圆周角为90°;② 若垂直于三棱锥的某棱长的截面面积为S ,棱长长ℎ,则三棱锥的体积为13Sℎ.【题型三】与球有关的切、接问题【典题1】 已知三棱锥D −ABC 的四个顶点在球O 的球面上,若AB =AC =BC =DB =DC =1,当三棱锥D -ABC 的体积取到最大值时,球O 的表面积为( )A. 5π3B. 2 πC. 5 πD. 20π3【解析】 如图,当三棱锥D −ABC 的体积取到最大值时,则平面ABC ⊥平面DBC ,取BC 的中点G ,连接AG ,DG ,则AG ⊥BC ,DG ⊥BC ,分别取△ABC 与△DBC 的外心E ,F ,分别过E ,F 作平面ABC 与平面DBC 的垂线,相交于O ,则O 为四面体ABCD 的球心,由AB =AC =BC =DB =DC =1,得正方形OEGF 的边长为√36,则OG =√66∴四面体A −BCD 的外接球的半径R =√OG 2+B G 2=√(√66)2+(12)2=√512 ∴球O 的表面积为=4 π×(√512)2=5π3,故选:A .【典题2】 如图,在一个底面边长为2,侧棱长为√10的正四棱锥P -ABCD 中,大球O 1内切于该四棱锥,小球O 2与大球O 1及四棱锥的四个侧面相切,则小球O 2的体积为 .【解析】设O为正方形ABCD的中心,AB的中点为M,连接PM,OM,PO,则OM=1,PM=√PA2−AM2=√10−1=3,PO=√9−1=2√2,如图,在截面PMO中,设N为球O1与平面PAB的切点,则N在PM上,且O1N⊥PM,设球O1的半径为R,则O1N=R,因为sin∠MPO=OMPM =13,所以NO1PO1=13,则PO1=3R,PO=PO1+OO1=4R=2√2,所以R=√22,设球O1与球O2相切与点Q,则PQ=PO-2R=2R,设球O2的半径为r,同理可得PQ=4r,所以r=R2=√24,故小球O2的体积V=43πr3=√224π,故答案为√224π.巩固练习1(★)如图1所示,一只封闭的圆柱形水桶内盛了半桶水(桶的厚度忽略不计),圆柱形水桶的底面直径与母线长相等,现将该水桶水平放置后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S1、S2,则S1与S2的大小关系是()A.S1≤S2B.S1<S2C.S1>S2D.S1≥S2【答案】B【解析】设圆柱的底面半径为r,图1水的表面积为 S1=2πr2+2πr•r=4πr2.对于图2,上面的矩形的面积的长是2r,宽是2r.则面积是4r2.曲面展开后的矩形长是πr,宽是2r.则面积是2πr2.上下底面的面积的和是π×r2.图2水的表面积S2=(4+3π)r2.显然S1<S2.故选B.2(★) 若一个圆锥的母线长为4,且其侧面积为其轴截面面积的4倍,则该圆锥的高为()A.πB.3π2C.2π3D.π2【答案】A【解析】设圆锥的底面圆半径为r,高为ℎ;由圆锥的母线长为4,所以圆锥的侧面积为πr•4=4πr;又圆锥的轴截面面积为12•2r•ℎ=rℎ,所以4πr=4rℎ,解得ℎ=π;所以该圆锥的高为π.故选:A.3(★★) 某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得到的(如图).则该几何体共有个面;如果被截正方体的棱长是50cm,那么石凳的表面积是cm2.【答案】14,10000【解析】由题意知,截去的八个四面体是全等的正三棱锥,8个底面三角形,再加上6个小正方形,所以该几何体共有14个面;如果被截正方体的棱长是50cm,那么石凳的表面积是S表面积=8×12×25√2×25√2×sin60°+6×25√2×25√2=10000(cm2).故答案为:14,10000.4(★★) 直角梯形的上、下底和不垂直于底的腰的长度之比为12√3,那么以垂直于底的腰所在的直线为轴,将梯形旋转一周,所得的圆台上、下底面积和侧面面积之比是.【答案】1: 4: 3√3【解析】由题意可设直角梯形上底、下底和不垂直于底的腰为x,2x,√3x;则圆台的上、下底半径和母线长分别为x,2x,√3x,如图所示;所以上底面的面积为S上底=π•x2;下底面的面积为S下底=π•(2x)2=4πx2;侧面积为S侧面=π(x+2x)•√3x=3√3πx2;所以圆台的上底、下底面积和侧面面积之比是πx2∶4πx2: 3√3πx2=1: 4: 3√3.5(★★) 如图,四面体各个面都是边长为1的正三角形,其三个顶点在一个圆柱的下底面圆周上,另一个顶点是上底面圆心,圆柱的侧面积是.【答案】2√2π3【解析】如图所示,过点P 作PE ⊥平面ABC ,E 为垂足,点E 为的等边三角形ABC 的中心.AE =23AD ,AD =√32. ∴AE =23×√32=√33.∴PE =√PA 2−AE 2=√63.设圆柱底面半径为R ,则2R =1sin60°=2√3, ∴圆柱的侧面积=2πR •PE =√3π×√63=2√2π3,6(★★) 一竖立在地面上的圆锥形物体的母线长为4m ,侧面展开图的圆心角为2π3,则这个圆锥的体积等于 . 【答案】128√281πm 3【解析】设圆锥的底面半径为r ,圆锥形物体的母线长l =4m ,侧面展开图的圆心角为2π3,故2πr =2π3,解得 r =43m , 故圆锥的高ℎ=√l 2−r 2=83√2m ,故圆锥的体积V =13πr 2ℎ=128√281πm 3.7(★★) 如图①,一个圆锥形容器的高为a ,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为a2(如图②),则图①中的水面高度为 .【答案】(1−√732)a【解析】 令圆锥倒置时水的体积为V ′,圆锥体积为V ,则v′v =(a 2)3÷a 3=18,∴V 空V 锥=78,倒置后 V 水=18V , 设此时水高为ℎ,则ℎ3 a 3=78,∴ℎ=(1−√732)a . 故原来水面的高度为(1−√732)a .8(★★★) 半径为2的球O 内有一个内接正三棱柱,则正三棱柱的侧面积的最大值为 .【答案】12√3【解析】如图所示,设正三棱柱上下底面的中心分别为O 1,O 2,底面边长与高分别为x ,ℎ,则O 2A =√33x ,在Rt △OAO 2中,ℎ24+x 23=4, 化为ℎ2=16−43x 2,∵S 侧=3xℎ,∴S 侧2=9x 2ℎ2=12x 2(12−x 2)≤12(x 2+12−x 22)2=432.当且仅当x 2=12-x 2,即x =√6时取等号,此时S 侧=12√3.9(★★★) 如图所示,在边长为5+√2的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M 、N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥底面,围成一个圆锥,则圆锥的全面积与体积分别是 与 .【答案】10π,2√303π【解析】设圆锥的母线长为l ,底面半径为r ,高为ℎ,由已知条件可得{l+r+√2r=(5+√2)×√22πrl=π2,解得r=√2,l=4√2,∴S=πrl+πr2=10π,又∵h=√l2−r2=√30,∴V=13πr2ℎ=2√303π.故答案为10π,2√303π10(★★★) 已知四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,现将四面体ABCD放入一个主视图为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,则圆锥侧面积的最小值为.【答案】27π4【解析】因为四面体ABCD的棱长满足AB=AC=BD=CD=2,BC=AD=1,所以可以把其放到长宽高分别为a,b,c的长方体中,四面体的棱长是长方体的面对角线,∴a2+b2=22,①;b2+c2=22,②;c2+a2=12,③故四面体的外接球半径R满足:8R2=22+22+12=9;∴R2=98.∵四面体ABCD放入一个主视图为等边三角形的圆锥中,使得四面体ABCD可以在圆锥中任意转动,要想圆锥的侧面积最小;故需满足四面体的外接球恰好是圆锥的内切球;作圆锥的轴截面,如图:设BE=r,则AB=2r,AE=√3r;可得:OB2=OE2+EB2;∴R2=(√3r-R)2+r2⇒r=√3R;故圆锥侧面积的最小值为:πrl=2πr2=2π•3R2=27π4.故答案为:27π4.11(★★★) 在直三棱柱ABC-A1B1C1中,平面ABC是下底面.M是BB1上的点,AB=3,BC=4,AC=5,CC1=7,过三点A、M、C1作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为.【答案】1110【解析】由AB=3,BC=4,AC=5,得AB2+BC2=AC2,∴AB⊥BC.将平面ABB1A1与平面BCC1B1放在一个平面内,连接AC1,与BB1的交点即为M,此时BM=3,设四棱锥A-BCC1M的体积为V1,则V1=13×12×(3+7)×4×3=20,三棱柱ABC-A1B1C1的体积V=12×4×3×7=42.∴当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为V−V1V1=1110.12(★★★) 如图,在直三棱柱ABC-A1B1C1中,AB=1,BC=2,BB1=3,∠ABC=90°,点D为侧棱BB1上的动点,当AD+DC1最小时,三棱锥D-ABC1的体积为.【答案】13【解析】将直三棱柱ABC-A1B1C1展开成矩形ACC1A1,如图,连结AC1,交BB1于D,此时AD+DC1最小,∵AB =1,BC =2,BB 1=3,∠ABC =90°,点D 为侧棱BB 1上的动点,∴当AD +DC 1最小时,BD =1,此时三棱锥D -ABC 1的体积V D−ABC 1=V C 1−ABD =13×S △ABD ×B 1C 1=13×12×AB ×BD ×B 1C 1=13×12×1×1×2=13.13(★★★) 已知△SAB 是边长为2的等边三角形,∠ACB =45°,当三棱锥S -ABC 体积最大时,其外接球的表面积为 .【答案】28π3【解析】由题可知,平面CAB ⊥平面SAB ,且CA =CB 时,三棱锥S -ABC 体积达到最大,如右图所示, 则点D ,点E 分别为△ASB ,△ACB 的外心,并过两个三角形的外心作所在三角形面的垂线,两垂直交于点O .∴点O 是此三棱锥外接球的球心,AO 即为球的半径.在△ACB 中,AB =2,∠ACB =45°⇒∠AEB =90°,由正弦定理可知,AB sin∠ACB =2AE ,∴AE =EB =EC =√2,延长CE 交AB 于点F ,延长SD 交AB 于点F ,∴四边形EFDO 是矩形,且OE ⊥平面ACB ,则有OE ⊥AE ,又∵OE =DF =13SF =13×√32AB =√33, ∴OA =√OE 2+AE 2=√73.∴S 球表面积=4πR 2=4π×( √73)2=28π3.14(★★★)如图,在△ABC 中,AB =BC =2,∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD =DA ,PB =BA ,则四面体PBCD 的体积的最大值是 .【答案】12【解析】如图,M是AC的中点.①当AD=t <AM=√3时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AE,DM=√3-t,由△ADE∽△BDM,可得ℎ1=√(√3−t)2+1,∴ℎ=√(√3−t)2+1,V=13⋅12⋅(2√3−t)⋅1⋅√(√3−t)2+1=16√3−t)2√(√3−t)2+1,t∈(0,√3)②当AD=t>AM=√3时,如图,此时高为P到BD的距离,也就是A到BD的距离,即图中AH,DM=t-√3,由等面积,可得12⋅AD⋅BM=12⋅BD⋅AH,∴1 2⋅t⋅1=12√(t−√3)2+1,∴ℎ=√(√3−t)2+1,∴V=13⋅12⋅(2√3−t)⋅1√(√3−t)2+1=16⋅√3−t)2√(√3−t)2+1,t∈(√3,2√3)综上所述,V=16√3−t)2√(√3−t)2+1,t∈(0,2√3)令m=√(√3−t)2+1∈[1,2),则V=16⋅4−m2m,∴m=1时,V max=12.故答案为12.。
8.3简单几何体的表面积与体积(1)PPT课件(人教版)

问题4:扇环的面积公式是怎样的?
•O
解: 设OA m,则有 l1 l2 , ∴m l1l .
m lm
l2 l1
∴S扇环 =S扇形OAB
S扇形OAB
=
1 2
l2 (l
m)
1 2
l1m
m
A′
l
l1
=
1 2
l2l
1 2
m(l2
l1
)
1 2
l2l
1 2
l1l
1 2
l (l2
l1 ).
A
S扇环
1 2
(l1
1 (r2 rr r2 )h
3
r •O
V圆台
=
1 3
(S
SS S)h
3 圆柱、圆锥、圆台的体积
圆柱、圆锥、圆台的体积公式之间有什么关系?你能用圆柱、圆 锥、圆台的结构特征来解释这种关系吗?
• O'
h
l
r •O
V圆柱 r 2h
上底面扩大到 与下底面全等
r' •O' hl
r •O
上底面缩小 为一个点
故圆锥的体积 V 圆锥=13πr2h=634π.
3 圆柱、圆锥、圆台的体积
例2(3) 已知圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的体积
为_2_2_4_π__.
解析 设上底面半径为r,则下底面半径为4r,高为4r,如图. ∵母线长为10,∴102=(4r)2+(4r-r)2,解得r=2. ∴下底面半径R=8,高h=8,
r •O
V柱体 Sh
S′=S
V台体
=
1 3
(S
SS S)h
S′=0
简单几何体的表面积与体积_课件

总结
旋转体的面积和体积公 式
名称
圆柱
圆锥
圆台
球
V
表中l、h分别表示母线、高,r表示圆柱、圆锥与球冠的底半径,x、x分别表示圆台上、 下底面半径,R表示半径
棱柱体积
长方体体积: 正方体体积:
底面积 高
棱柱体积
(其中S为底面面积,h为柱体的高 )
棱锥体积 (底面积S,高h)
注意:三棱锥的顶点和底面可以根据需要变换,四面体的 每一个面都可以作为底面,可以用来求点到面的距离。
棱锥体积 (底面积S,高h)
棱锥的体积公式 :
(其中S为底面面积,h为高 )
类比利用圆周长求圆面积的方法,我们可以利用球的表面积求球的体积。如 图把球O的表而分成n个小网格,连接球心O和每个小网格的顶点,整个球体 就被分割成n个“小锥体”。 当n越大,每个小网格越小时,每个“小锥体”的底面 就越平,“小锥体”就越近似于棱锥,其高越近似于球 半径R.设 O-ABCD是其中一个“小锥体”,它的体积是
圆台的侧面展开图是扇 环
圆柱、圆锥、圆台三者的表面积公式之间有什么关系 ?
r’ =r
上底扩大
r’ =0
上底缩小
圆柱、圆锥和圆台的表面 积
理解并掌握圆柱、圆锥和圆台的表面积公 式 能够根据公式进行求 值
圆柱体积
h
圆锥体积
h
(其中S为底面面积,h为高 )
圆台体积
上下底面积分别是s',s,高是h, 则
某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样 的四面体得到的,如果被酸正方体的棱长是50cm,那么石凳的体积是多 少?
求证:直三棱柱的任意两个侧面的面积和大于第三个侧面的面
积. 提示:侧面均为矩
简单几何体的表面积和体积 课时1(课件)高一数学(人教A版2019必修第二册)

情境设置
合作探究·提素养
问题1:你能计算出小明搭的帐篷的侧面积吗?
[答案] 侧面三角形的高为 ,所以侧面积为 .
问题2:棱柱、棱锥、棱台的侧面展开图是什么?
[答案] 棱柱的侧面展开图是平行四边形,一边是棱柱的侧棱,另一边等于棱柱的底面周长,如图①所示;棱锥的侧面展开图是由若干个三角形拼成的,如图②所示;棱台的侧面展开图是由若干个梯形拼接而成的,如图③所示.
4.已知正三棱柱的底面边长为1,侧棱长为2,则它的侧面积为___,表面积为_ ______.
6
[解析] 正三棱柱的底面为正三角形,侧面为三个全等的矩形,所以侧面积为 , 又 ,所以它的表面积为 .
探究1 棱柱、棱锥、棱台的表面积
小明在自家花园为他家小狗搭了个外形为正三棱锥的小帐篷,帐篷的底面边长为 ,侧棱长为 ,如图所示.
求多面体的表面积方法:(1)对于简单几何体,我们可利用公式,直接求出其表面积,而在求不规则几何体的表面积时,通常将所给几何体分割或补全成基本的柱、锥、台体,先求出这些基本的柱、锥、台体的表面积,再通过求和或作差,求出几何体的表面积.
(2)求解棱锥的表面积时,注意棱锥的四个基本量:底面边长、高、斜高、侧棱.并注意它们组成的直角三角形的应用.
√
自学检测
2.若长方体的长、宽、高分别为 , , ,则长方体的体积为( ).
A. B. C. D.
B
[解析] .
3.已知正四棱锥的底面边长为2,高为3,则它的体积为( ).
A. B. C. D.
B
[解析] 正四棱锥的底面积为 ,则其体积为 .
[解析] .故选B.
随堂检测·精评价
2.棱长都是1的三棱锥的侧面积为( ).
A. B. C. D.
第九章 立体几何9-2简单几何体的表面积和体积

(文)圆柱的侧面展开图是长 12cm,宽 8cm 的矩形, 则这个圆柱的体积为( 288 3 A. cm π 288 3 192 3 C. π cm 或 π cm ) 192 3 B. cm π D.192πcm3
解析:分两种情况 6 (1)若 12 为底面圆周长,则 2πr=12,∴r=π,
6 288 2 · ∴V=π· π 8= π (cm3).
(2)连接 AE, AC, EC, E 作 EG∥PA 交 AB 于点 G, 过 1 则 EG⊥平面 ABCD,且 EG=2PA. 在△PAB 中,AP=AB,∠PAB=90° ,BP=2, 2 ∴AP=AB= 2,EG= , 2 1 1 ∴S△ABC=2AB· BC=2× 2×2= 2, 1 1 2 1 ∴VE—ABC=3S△ABC· EG=3× 2× 2 =3.
答案:C 点评:(1)等底面积与高的柱体(锥体)体积相 等,且柱体体积是锥体体积的3倍,在求体 积和等积变换中是经常用到的结论. (2)求棱锥的体积,关键找(求)出棱锥的高.
(理)如图,已知在多面体ABC-DEFG中, AB、AC、AD两两互相垂直,平面ABC∥平 面DEFG,平面BEF∥平面ADGC,AB= AD=DG=2,AC=EF=1,则该多面体的 体积为( ) A.2 B.4 C.6 D.8
分析:(1)由E、F为中点易想到中位线获
证.
(2)求三棱锥E-ABC的体积,由于△ABC面
积易求,需看E到平面ABC的距离是否可求,
注意到E为PB中点,PA⊥平面ABCD,因此
只需取AB中点G,则EG为高,或由E为PB
中点知,E到平面ABC的距离等于P到平面 ABC的距离的一半.而P到平面ABC的距离 为PA,也可获解.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单几何体的表面积与体积1.柱、锥、台和球的侧面积和体积面积 体积圆柱 S 侧=2πrh V =Sh =πr 2h 圆锥S 侧=πrlV =13Sh =13πr 2h =13πr 2l 2-r 2圆台 S 侧=π(r 1+r 2)l V =13(S 上+S 下+S 上S 下)h=13π(r 21+r 22+r 1r 2)h 直棱柱 S 侧=Ch V =Sh 正棱锥 S 侧=12Ch ′V =13Sh正棱台 S 侧=12(C +C ′)h ′V =13(S 上+S 下+S 上S 下)h球S 球面=4πR 2V =43πR 32.几何体的表面积(1)棱柱、棱锥、棱台的表面积就是各面面积之和.(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形;它们的表面积等于侧面积与底面面积之和. [难点正本 疑点清源] 1.几何体的侧面积和全面积几何体的侧面积是指(各个)侧面面积之和,而全面积是侧面积与所有底面积之和.对侧面积公式的记忆,最好结合几何体的侧面展开图来进行.要特别留意根据几何体侧面展开图的平面图形的特点来求解相关问题.如直棱柱(圆柱)侧面展开图是一矩形,则可用矩形面积公式求解.再如圆锥侧面展开图为扇形,此扇形的特点是半径为圆锥的母线长,圆弧长等于底面的周长,利用这一点可以求出展开图扇形的圆心角的大小. 2.等积法等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高,这一方法回避了具体通过作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.1.圆柱的一个底面积为S ,侧面展开图是一个正方形,那么这个圆柱的侧面积是________.2.设某几何体的三视图如下(尺寸的长度单位为m).则该几何体的体积为________m 3.3.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________.4.一个球与一个正方体的各个面均相切,正方体的边长为a ,则球的表面积为________.5.如图所示,在棱长为4的正方体ABCD —A 1B 1C 1D 1中,P 是A 1B 1上一点,且PB 1=14A 1B 1,则多面体P —BB 1C 1C 的体积为________.题型一 简单几何体的表面积例1 一个空间几何体的三视图如图所示,则该几何体的表面积为( )A .48B .32+817C .48+817D .80探究提高(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.一个几何体的三视图(单位:cm)如图所示,则该几何体的表面积是________cm2.题型二简单几何体的体积例2如图所示,已知E、F分别是棱长为a的正方体ABCD—A1B1C1D1的棱A1A、CC1的中点,求四棱锥C1—B1EDF的体积.思维启迪:思路一:先求出四棱锥C1—B1EDF的高及其底面积,再利用棱锥的体积公式求出其体积;思路二:先将四棱锥C1—B1EDF化为两个三棱锥B1—C1EF与D—C1EF,再求四棱锥C1—B1EDF的体积.解 方法一 连接A 1C 1,B 1D 1交于点O 1,连接B 1D ,EF ,过O 1作O 1H ⊥B 1D 于H .∵EF ∥A 1C 1,且A 1C 1 平面B 1EDF ,∴A 1C 1∥平面B 1EDF .∴C 1到平面B 1EDF 的距离就是A 1C 1到平面B 1EDF 的距离. ∵平面B 1D 1D ⊥平面B 1EDF , 平面B 1D 1D ∩平面B 1EDF =B 1D ,∴O 1H ⊥平面B 1EDF ,即O 1H 为棱锥的高. ∵△B 1O 1H ∽△B 1DD 1,∴O 1H =B 1O 1·DD 1B 1D =66a .∴VC 1—B 1EDF =13S 四边形B 1EDF ·O 1H=13·12·EF ·B 1D ·O 1H =13·12·2a ·3a ·66a =16a 3. 方法二 连接EF ,B 1D .设B 1到平面C 1EF 的距离为h 1,D 到平面C 1EF 的距离为h 2,则h 1+h 2=B 1D 1=2a . 由题意得,VC 1—B 1EDF =VB 1—C 1EF +VD —C 1EF =13·S △C 1EF ·(h 1+h 2)=16a 3. 探究提高 在求解一些不规则的几何体的体积以及两个几何体的体积之比时,常常需要用到分割法.在求一个几何体被分成两部分的体积之比时,若有一部分为不规则几何体,则可用整个几何体的体积减去规则几何体的体积求出其体积.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2,则此棱锥的体积为( ) A.26 B.36 C.23D.22题型三几何体的展开与折叠问题例3(1)如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、B、C、D、O为顶点的四面体的体积为________.(2)有一根长为3π cm,底面直径为2 cm的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为________ cm.思维启迪:(1)考虑折叠后所得几何体的形状及数量关系;(2)可利用圆柱的侧面展开图.(2)研究几何体表面上两点的最短距离问题,常选择恰当的母线或棱展开,转化为平面上两点间的最短距离问题.如图,已知一个多面体的平面展开图由一边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是_______..方法与技巧1.对于基本概念和能用公式直接求出棱柱、棱锥、棱台与球的表面积的问题,要结合它们的结构特点与平面几何知识来解决.2.要注意将空间问题转化为平面问题.3.求几何体的体积,要注意分割与补形.将不规则的几何体通过分割或补形将其转化为规则的几何体求解.4.一些几何体表面上的最短距离问题,常常利用几何体的展开图解决.A 组 专项基础训练 (时间:35分钟,满分:57分)一、选择题(每小题5分,共20分)1.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A .6B .9C .12D .182 . 已知高为3的直棱柱ABC —A ′B ′C ′的底面是边长为1的正三角形(如右图所示),则三棱锥B ′—ABC 的体积为( )A.14B.12C.36D.343.正六棱柱的高为6,底面边长为4,则它的全面积为( )A .48(3+3)B .48(3+23)C .24(6+2)D .1444.某三棱锥的三视图如图所示,该三棱锥的表面积是 ( )A.28+6 5 B.30+6 5C.56+12 5 D.60+12 5二、填空题(每小题5分,共15分)5.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.6.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.7.已知三棱锥A—BCD的所有棱长都为2,则该三棱锥的外接球的表面积为________.三、解答题(共22分)8.(10分)如图所示,在边长为5+2的正方形ABCD中,以A为圆心画一个扇形,以O为圆心画一个圆,M,N,K 为切点,以扇形为圆锥的侧面,以圆O为圆锥底面,围成一个圆锥,求圆锥的全面积与体积.9.(12分)有一个倒圆锥形容器,它的轴截面是一个正三角形,在容器内放一个半径为r的铁球,并注入水,使水面与球正好相切,然后将球取出,求这时容器中水的深度.B 组 专项能力提升 (时间:25分钟,满分:43分)一、选择题(每小题5分,共15分)1.某几何体的三视图如图所示,其中俯视图是个半圆,则该几何体的表面积为( )A.32π B .π+3C.32π+ 3D.52π+ 3 2.在四棱锥E —ABCD 中,底面ABCD 为梯形,AB ∥CD,2AB =3CD ,M 为AE 的中点,设E —ABCD 的体积为V ,那么三棱锥M —EBC 的体积为( ) A.25V B.13VC.23VD.310V 3.已知球的直径SC =4,A 、B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S -ABC 的体积为( ) A .3 3B .2 3C. 3D .1二、填空题(每小题5分,共15分)4.如图,已知正三棱柱ABC —A 1B 1C 1的底面边长为2 cm ,高为5 cm ,则 一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线 的长为______ cm.5.已知一个几何体是由上、下两部分构成的组合体,其三视图如图所示,若图中圆的半径为1,等腰三角形的腰长为5,则该几何体的体积是________.6.如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2.若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是________.三、解答题7.(13分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D—ABC,如图2所示.图1图2(1)求证:BC⊥平面ACD;(2)求几何体D—ABC的体积.。
