粒子群算法优化模糊pid

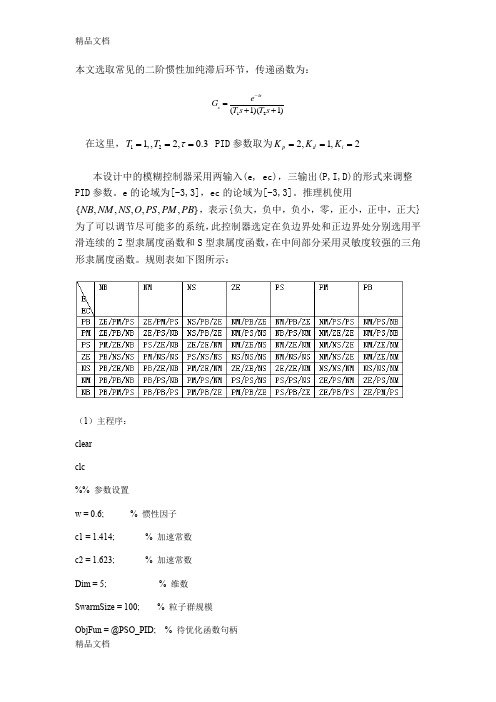
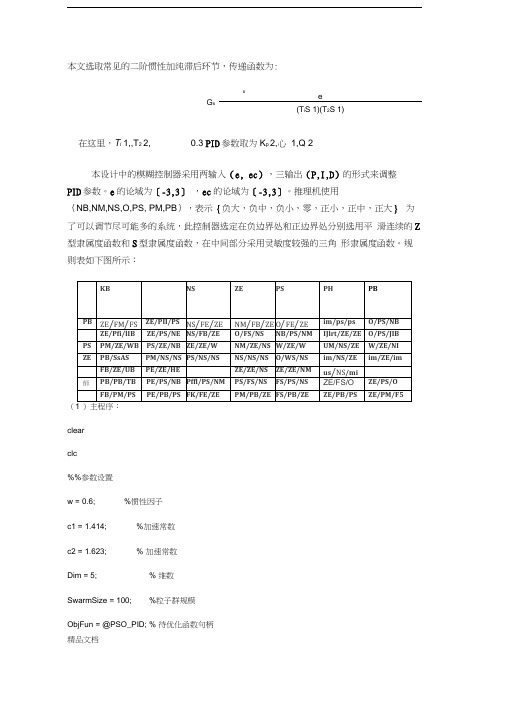
本文选取常见的二阶惯性加纯滞后环节,传递函数为: )1)(1(21++=-s T s T e G s
s τ
在这里,3.0,2,,121===τT T PID 参数取为2,1,2===i d p K K K
本设计中的模糊控制器采用两输入(e, ec),三输出(P,I,D)的形式来调整PID 参数。

e 的论域为[-3,3],ec 的论域为[-3,3]。

推理机使用
{,,,,,,}NB NM NS O PS PM PB ,表示{负大,负中,负小,零,正小,正中,正大}为了可以调节尽可能多的系统,此控制器选定在负边界处与正边界处分别选用平滑连续的Z 型隶属度函数与S 型隶属度函数,在中间部分采用灵敏度较强的三角形隶属度函数。

规则表如下图所示:
(1)主程序:
clear
clc
%% 参数设置
w = 0、6; % 惯性因子
c1 = 1、414; % 加速常数
c2 = 1、623; % 加速常数
Dim = 5; % 维数
SwarmSize = 100; % 粒子群规模
ObjFun = @PSO_PID; % 待优化函数句柄
MaxIter = 100; % 最大迭代次数
MinFit = 0、01; % 最小适应值
Vmax = 2;
Vmin =-2;
Ub = [20 50 1 1 1];
Lb = [0 0 0 0 0];
%% 粒子群初始化
Range = ones(SwarmSize,1)*(Ub-Lb);
Swarm = rand(SwarmSize,Dim)、*Range + ones(SwarmSize,1)*Lb; % 初始化粒子群
VStep = rand(SwarmSize,Dim)*(Vmax-Vmin) + Vmin; % 初始化速度
fSwarm = zeros(SwarmSize,1);
for i=1:SwarmSize
fSwarm(i,:) = feval(ObjFun,Swarm(i,:)); % 粒子群的适应值
end
%% 个体极值与群体极值
[bestf,bestindex]=min(fSwarm);
zbest=Swarm(bestindex,:); % 全局最佳
gbest=Swarm; % 个体最佳
fgbest=fSwarm; % 个体最佳适应值
fzbest=bestf; % 全局最佳适应值
%% 迭代寻优
iter = 0;
y_fitness = zeros(1,MaxIter); % 预先产生4个空矩阵
K_p = zeros(1,MaxIter);
K_i = zeros(1,MaxIter);
K_d = zeros(1,MaxIter);
e= zeros(1,MaxIter);
ec = zeros(1,MaxIter);
while( (iter < MaxIter) && (fzbest > MinFit) )
for j=1:SwarmSize
% 速度更新
VStep(j,:) = w*VStep(j,:) + c1*rand*(gbest(j,:) - Swarm(j,:)) + c2*rand*(zbest - Swarm(j,:));
if VStep(j,:)>Vmax, VStep(j,:)=Vmax; end
if VStep(j,:)<Vmin, VStep(j,:)=Vmin; end
% 位置更新
Swarm(j,:)=Swarm(j,:)+VStep(j,:);
for k=1:Dim
if Swarm(j,k)>Ub(k), Swarm(j,k)=Ub(k); end
if Swarm(j,k)<Lb(k), Swarm(j,k)=Lb(k); end
end
% 适应值
fSwarm(j,:) = feval(ObjFun,Swarm(j,:));
% 个体最优更新
if fSwarm(j) < fgbest(j)
gbest(j,:) = Swarm(j,:);
fgbest(j) = fSwarm(j);
end
% 群体最优更新
if fSwarm(j) < fzbest
zbest = Swarm(j,:);
fzbest = fSwarm(j);
end
end
iter = iter+1; % 迭代次数更新y_fitness(1,iter) = fzbest; % 为绘图做准备
K_p(1,iter) = zbest(1);
K_i(1,iter) = zbest(2);
K_d(1,iter) = zbest(3);
e(1,iter) = zbest(4);
ec(1,iter) = zbest(5);
end
%% 绘图输出
figure(1) % 绘制性能指标ITAE的变化曲线
plot(y_fitness,'LineWidth',2)
title('最优个体适应值', 'fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('适应值','fontsize',18); set(gca,'Fontsize',18);
figure(2) % 绘制PID控制器参数变化曲线
plot(K_p)
hold on
plot(K_i,'k','LineWidth',3)
title('Kp、Ki优化曲线','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('参数值','fontsize',18);
set(gca,'Fontsize',18);
legend('Kp','Ki',1);
figure(3) % 绘制PID控制器参数变化曲线
plot(e)
hold on
plot(ec,'k','LineWidth',3)
title('e、ec 优化曲线','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('参数值','fontsize',18); set(gca,'Fontsize',18);
legend('e','ec',1);
figure(4) % 绘制PID控制器参数变化曲线
plot(K_d)
hold on
title('Kd 优化曲线','fontsize',18);
xlabel('迭代次数','fontsize',18);ylabel('参数值','fontsize',18); set(gca,'Fontsize',18);
legend('Kd',1);
clear
clc
(2)simulnik与算法结合程序
function z=PSO_PID(x)
assignin('base','Kp',x(1));
assignin('base','Ki',x(2));
assignin('base','Kd',x(3));
assignin('base','e',x(4));
assignin('base','ec',x(5));
[t_time,x_state,y_out]=sim('pca',[0,20]);
z=y_out(end,1);
(3)Simulink 仿真图:
实验结果:8446.8,1,20,15====ITAE K K K d i p ,波形如下图所示。

实验结论:本次设计使用的就是pid,粒子群算法模糊pid,粒子群算法模糊smith pid 相结合,仿真波形如下图所示。

黄色的就是pid 波形,红色的就是粒子群算法模糊pid,蓝色的就是粒子群算法模糊smith pid 。

从图中明显的可以瞧出加入粒子群算法模糊控制后波形超调量减少,调节时间缩短;在加入smith 后波形有了明显的改善。