matlab布朗运动完整答案

(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a（1（2）用（3）用（42.矩阵的运算（1）利用矩阵除法解线性方程组。

⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ，计算X=A\B 。

（2）利用矩阵的基本运算求解矩阵方程。

已知矩阵A 和B 满足关系式A -1BA=6A+BA ，计算矩阵B 。

其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ，Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a（3）计算矩阵的特征值和特征向量。

已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ，计算其特征值和特征向量。

（4）Page:322利用数学函数进行矩阵运算。

已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01，10]，按对数均匀分布。

3.多项式的运算（1）多项式的运算。

已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式，并计算当x 在[0，20]内变化时G(x)的值，计算出G(x)=0的根。

Page 324（2）多项式的拟合与插值。

将多项式G(x)=x 4-5x 3-17x 2+129x-180，当x 在[0，20]多项式的值上下加上随机数的偏差构成y1，对y1进行拟合。

对G(x)和y1分别进行插值，计算在5.5处的值。

Page 325 四、思考练习题1.使用logspace 函数创建0～4π的行向量，有20个元素，查看其元素分布情况。

Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1）f(x)=2x 2+3x+5x+8用向量表示该多项式，并计算f(10)值. 2）根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。

matlab课后习题答案（附图）

matlab课后习题答案（附图）习题2.1画出下列常见曲线的图形y （1）⽴⽅抛物线3x命令：syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令：clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令：>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令：>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令：>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令：>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令：clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令：cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令：>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值（1）nnn n3→命令：>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3（2）)121(lim n n n n ++-+∞→命令：>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0（3）x x x 2cot lim 0→命令：syms x ；>> limit(x*cot(2*x),x,0) ans = 1/2 （4）)(coslimcm xx ∞→命令：syms x m ； limit((cos(m/x))^x,x,inf) ans = 1（5）)111(lim 1--→exx x命令：syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) （6）)(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分，并⽤diff 验证：（1）+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1）dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2）xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552（4）>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752（5） >> clear >> syms x1判断下列级数的收敛性，若收敛，求出其收敛值。

使用Matlab对布朗运动的模拟

使用Matlab对布朗运动的模拟作者：王富帅陈正昊孙琦来源：《科技风》2019年第29期摘要：根据朗之万方程，通过对朗之万方程的数值推导，得到单个布朗粒子布朗运动下的位移方程，位移方程可以反推至爱因斯坦平均差位移方程。

本文利用位移方程写出数值模拟下的布朗运动的轨迹。

通过Matlab软件编程，得到了布朗运动随机轨迹三维图。

关键词：布朗运动;朗之万方程;Matlab模拟仿真2.2 软件模拟为了便于模拟我们不妨令步长Δt=1，无单位，仅仅是作为数学处理的单位。

ψ（0，）是平均值为0，方差为的正态分布，若仅仅考虑单个粒子，可以考虑为符合正态分布一组数据中的一个。

我们可以使用Matlab軟件中的normrnd函数来产生一个随机正态分布数组。

由于所取得的正态分布数为随机数，因此使用Matlab软件得到的轨迹每次都不一样，这也正好反映了布朗运动的随机性。

2.3 主程序以迭代1000次的程序为例：a=500;n=1.003;T=300;k=1.380649e-23;r=6*pi*a*n;D=k*T/r;d=sqrt（2.*D）;a=normrnd（0，d，[1 1000]）;b=normrnd（0，d，[1 1000]）;c=normrnd（0，d，[1 1000]）;x=[];y=[];z=[];o=0;p=0;q=0;for i=1：1000{o=o+a（1，i）;p=p+b（1，i）;q=q+c（1，i）;x（1，i）=o;y（1，i）=p;z（1，i）=q;}endplot3（x，y，z）3 结论通过对朗之万函数的数值化处理，我们得到了具有统计学规律的位移函数，导出了位移关系式，并且，经过推导可以得到爱因斯坦的平均矢量位移关系式，并且得出布朗粒子布朗运动的轨迹是一个具有一定统计学规律的随机方程。

然后利用Matlab软件进行编译，通过已推导出的关系式，模拟布朗运动的轨迹，将其轨迹画出。

参考文献：[1]Einstein A.Investigations on the Theory of the Brownian Movement[M].New York：Dover Pulieation Inc，1956.[2]Smoluchowski M von.Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen[J].Annalen der Physik，1906，326（14）：756-780.[3]Langevin P.Sur la théorie du mouvement brownien[J].CR Acad Sci Paris，1908，146：530-533.。

利用Matlab模拟布朗运动测量实验

与纯布朗运动的情况相比较
在显微镜下的粒子跟踪实验中，由于样品池内溶液的挥发或者热对流等等原因经常会导致粒子产生某一方向的定向运动，粒子本身的布朗与运动耦合在一起，实验误差增大。拟程序稍加使模改写也可模拟这种运动。４模拟了在ｚ，向图Ｙ方上耦合有０１０２．，．ａ幅度定向运动的＜＞一ｔ
方法再生成一组随机分布向量。
上Ｕ
其中Ａ一２４４× １一，一２７８Ｃ一．１０Ｂ４．，
１０Ｔ是开尔文温度。过该式求得室温２８Ｋ４，通９下水的粘度系数为８３５ａＳ通常胶体粒子直９．Ｐ．ｏ径都在ｍ量级，文模拟选取直径为２ｇ大小本ｍ
１。ＯＪ・
十分吻合。
本模拟结果也可为显微镜下通过粒子跟踪方法测量粒子运动轨迹所需要平均的粒子个数提供
即通过对多个这样的布朗运动轨迹计算位移均方
差然后进行统计平均得到。图２依次显示了通过
对１，０，００１０１００和１００００个粒子的轨迹跟踪测
据越来越接近线性趋势，合误差也相应减小。拟当模拟的粒子个数高达１０个以上时，拟数０００模据已几乎与理论预测完全一致了。图３显示了多次测量下四种不同个数粒子情况下所得到的扩散
小误差。而计算机模拟可只用一个循环过程便可

（完整版）MATLAB）课后实验答案[1]

（完整版）MATLAB）课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值，然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。

(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建⽴⼀个字符串向量，删除其中的⼤写字母。

解：(1) 结果：(2). 建⽴⼀个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵，试通过数值计算验证2 2E R RS A O S +??=。

解: M ⽂件如下；5. 下⾯是⼀个线性⽅程组：1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。

(2) 将⽅程右边向量元素b 3改为0.53再求解，并⽐较b 3的变化和解的相对变化。

(3) 计算系数矩阵A 的条件数并分析结论。

解： M ⽂件如下：123d4e56g9实验三选择结构程序设计1. 求分段函数的值。

2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

解：M ⽂件如下：2. 输⼊⼀个百分制成绩，要求输出成绩等级A、B、C、D、E。

matlab怎么表达布朗运动的积分

matlab怎么表达布朗运动的积分表达布朗运动的积分1. 什么是布朗运动布朗运动（Brownian motion）是指微观颗粒在液体或气体中由于碰撞而进行的无规则运动。

它是一种随机过程，被广泛应用于物理、数学和金融等领域。

2. 布朗运动的数学描述布朗运动可以通过随机变量来描述，常用的数学模型是随机游走（random walk）。

在连续时间下，布朗运动可以使用随机积分来表示。

3. 随机积分随机积分（stochastic integration）是对随机过程进行积分的一种数学方法。

在数学中，常用的随机积分方法是伊藤积分（Itô integral）。

4. MATLAB 中表达布朗运动的积分在 MATLAB 中，我们可以使用符号运算工具箱（Symbolic Math Toolbox）来处理随机积分。

首先，我们需要引入符号运算工具箱和随机过程工具箱。

可以使用以下命令将它们引入 MATLAB：syms t; % 定义符号变量 tsyms B(t) W(t); % 定义布朗运动符号变量 B(t) 和标准布朗过程符号变量 W(t)然后，我们可以使用随机过程工具箱中的int函数来进行积分操作。

例如，要计算从时刻0到时刻T的布朗运动的积分，可以使用以下命令：integral_B = int(B(t), t, 0, T);其中，B(t)表示布朗运动，t表示时间变量，0和T分别表示积分的起始时间和结束时间。

5. 示例下面通过一个简单的示例来说明如何在 MATLAB 中表达布朗运动的积分。

假设我们要计算从时刻0到时刻T的布朗运动的积分。

首先，我们需要定义布朗运动符号变量和时间变量：syms t;syms B(t);然后，我们可以使用int函数来进行积分计算：T = 1; % 结束时间integral_B = int(B(t), t, 0, T);最后，我们可以使用subs函数将特定时间点的值代入积分结果中来验证计算结果：subs(integral_B, t, T) % 输出从时刻 0 到时刻 T 的布朗运动的积分值6. 总结通过引入符号运算工具箱和随机过程工具箱，我们可以在 MATLAB 中方便地表达布朗运动的积分。

Matlab实验报告

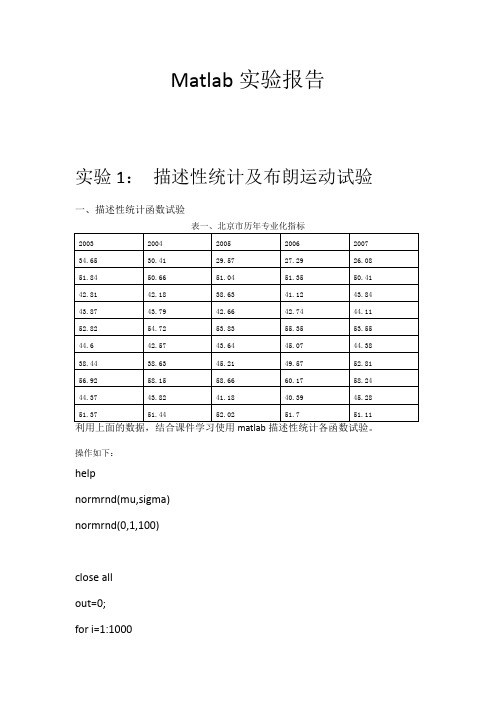
Matlab实验报告实验1：描述性统计及布朗运动试验一、描述性统计函数试验操作如下：helpnormrnd(mu,sigma)normrnd(0,1,100)close allout=0;for i=1:1000out(i+1)=out(i)+normrnd(0,1);endplot(out);close allout=zeros(1001,10);for j=1:10for i=1:1000out(i+1,j)=out(i,j)+normrnd(0,1);end;end;plot(out);b=normrnd(0,1,100,4);kurtosis(b)二、编制布朗运动程序布朗运动是整个金融工程的基石，而标准布朗运动则被称为维纳过程原理，初始时刻设为原点，下一时刻即时刻1数值为前一点数值基础上加上一个以0为均值，1为方差的标准正态的随机扰动量，得到1时候的数值，然后把这一点打印出来，再下一时刻即2时刻，其数值则是在1时刻的数值基础上再加上一个0为均值，1为方差的标准正态的随机扰动量，得到2时候的数值，然后把这一点打印出来；依次类推…,直到1000点。

Clc;Close all;A=0;For i=1:100 A(i)=A(i+1)+normrnd(0,1) Plot(A); 运行图像如下：clc close allout=zeros(10,1000); for j=1:10for i=1:1000 out(i+1,j)=out(i,j)+normrnd(0,1); end020040060080010001200-20-15-10-551015end plot(out)运行图像如下：实验2：2010年欧盟各国风能发电情况。

1、根据上述表对欧洲风电产能以及所占比率进行96%置信水平作一区间估计，2、假定中国风力产能年100000兆瓦，所占发电总量1.5%，试编程实现对中国、欧洲与北欧、整个欧洲是否存在差异，3、直接应用matlab 函数实现对2的假设检验操作如下：x=[27214 20676 5797 5660 5204 3898 3752 2237 2163 1428 6242]; xbar=mean(x); s=sqrt(var(x)); n1=sqrt(11); t=tinv(0.02,11);20040060080010001200-80-60-40-20204060mu1=xbar+s/n1*t;mu2=xbar-s/n1*t;fprintf('[mu1, mu2]=[%.0f, %.0f], ',mu1,mu2);[mu1, mu2]=[1808, 13514], >>>> y=[0.31 0.25 0.07 0.07 0.06 0.05 0.04 0.03 0.03 0.03 0.02 0.07];ybar=mean(y);sy=sqrt(var(y));mu3=ybar+sy/n1*t;mu4=ybar-sy/n1*t;fprintf('[mu3, mu4]=[%.2f, %.2f], ',mu3,mu4);[mu3, mu4]=[0.02, 0.15], >>>> x=[27214 20676 5797 5660 5204 3898 3752 2237 2163 1428 6242]; sx=sqrt(var(x));xbar=mean(x);y=[0.31 0.25 0.07 0.07 0.06 0.05 0.04 0.03 0.03 0.03 0.02 0.07];sy=sqrt(var(y));ybar=mean(y);n1=11;n2=31;Sw=sqrt(((n1-1)*sx^2+(n2-1)*sy^2)/(n1+n2-2));T=(xbar-ybar)/(Sw*sqrt(1 /n1+1/n2));if (abs(T)>tinv(0.025,n1+n2-2))|(abs(T)==tinv(0.025,n1+n2-2));H=1;elseH=0;end>> clear alla(1)=0;b(1)=0;c(1)=0;nalpha=norminv(0.05); for i=2:10000a(i)=normrnd(0,1)+a(i-1); b(i)=a(i)+nalpha;c(i)=a(i)-nalpha;endplot(a);hold onplot(b,'b');hold onplot(c,'y');实验3：一、使用matlab 函数对下面数据进行试验：已知x1-x5与y 之间取的样本如下1、试用回归方法2、多项式回归3、非线性回归模型4、 Stepwise操作如下：010002000300040005000600070008000900010000-5050100150200250300X=[ones(10,1) (1:10)']X =1 11 21 31 41 51 61 71 81 91 10y=X*[10;1]+normrnd(0,0.1,10,1) y =10.956711.833413.012514.028814.885416.119117.118917.996219.032720.0175b,bint]=regress(y,X,0.05)b =10.06120.9931bint =9.9179 10.20450.9700 1.0162[b,bint,r,rint]=regress(y,X,0.05)b =10.06120.9931bint =9.9179 10.20450.9700 1.0162r =-0.07290.0253-0.09920.1848-0.0402-0.00820.09400.0001-0.0084-0.0752rint =-0.2429 0.0970-0.1679 0.2184-0.2835 0.08510.0509 0.3188-0.2497 0.1693-0.2205 0.2040-0.0989 0.2868-0.2035 0.2037-0.2027 0.1858-0.2444 0.0940>> rcoplot(r,rint)[p,S]=polyfit(1:10,[1:10]+normrnd(0,1,1,10),1) p =0.9434 0.3367S =R: [2x2 double]df: 8normr: 3.5323Y=polyval(p,0.9)Y =1.1857赋值x=0.9>> [Y,DELTA]=polyval(p,0.9,S)Y =1.1857DELTA =1.4545不赋值x[Y,DELTA]=polyval(p,X,S)Y =1.2801 1.28011.28012.22341.2801 3.16681.2801 4.11021.2801 5.05361.2801 5.99701.2801 6.94041.2801 7.88371.2801 8.82711.2801 9.7705DELTA =1.4486 1.44861.4486 1.39541.4486 1.35421.4486 1.32601.4486 1.31161.4486 1.31161.4486 1.32601.4486 1.35421.4486 1.39541.4486 1.4486X=[23,25,21,14,15,20,17,11,26,21,16,19,13,16,24,20,21,18,27,24; 28,30,19,17,22,26,24,21,25,26,19,18,19,20,25,26,26,28,29,23; 18,15,23,18,10,21,25,12,12,22,19,23,22,14,13,22,13,12,22,19]; P=anova2(X',5) 0.0005 0.2311 0.7229 12345678910-0.2-0.10.10.20.3Residual Case Order PlotR e s i d u a l s Case Number。

使用Matlab对布朗运动的模拟

科技风2019年10月电子信息DOI：10.19392/ki.1671-7341.201929086使用Matlab对布朗运动的模拟王富帅陈正昊孙琦沈阳航空航天大学辽宁沈阳110136摘要:根据朗之万方程，通过对朗之万方程的数值推导,得到单个布朗粒子布朗运动下的位移方程，位移方程可以反推至爱因斯坦平均差位移方程。

本文利用位移方程写出数值模拟下的布朗运动的轨迹。

通过Matlab软件编程，得到了布朗运动随机轨迹三维图。

关键词：布朗运动；朗之万方程；Matlab模拟仿真布朗运动是指微小粒子在溶剂中表现出的无规则运动。

自1827年英国的科学家布朗发现了花粉颗粒在水溶液中做永不停顿的无规则运动以来，人们关于布朗运动的研究层出不穷。

至1905年，由爱因斯坦根据统计理论和流体力学方法，给出了在t时间里，微粒在某一方向上位移的统计平均值,即方均根值此同时，斯莫卢霍夫斯基也独立得提岀自己的一套理论来解释布朗运动,并给出了相似的结果#)2*1908年，朗之万为单个粒子写岀在随机力作用下的“牛顿方程”，即著名的朗之万方程)3*2-'~ET=Mi~dt^(1(其中3为布朗颗粒的质量，兀为位移矢量，%：为布朗粒子受到的其他颗粒或外场的作用力之和/(2为布朗粒子周围液体分子的作用力,'字为粒子受到的粘滞阻力，其中'd是粒子的阻力系数，对于半径为a的球形粒子,按照斯托克斯公式计算阻力系数为：'=6«z)(2)其中)是液体在一定温度下的黏度。

朗之万方程是历史上以一个随机微分方程。

至此关于布朗运动的理论研究已经趋于完善。

通过前人的研究我们可以得知，粒子在溶液中所做的布朗运动是一种无规则轨迹运动，但又具备相应的统计学规律。

借助与现代计算机技术，我们可以对粒子做布朗运动做模拟与仿真。

Matlab软件是一款在数值计算和模拟分析领域非常出色的软件，通过语言编程，我们就可以轻松实现对单个粒子布朗运动的仿真模拟。

matlab中标准布朗运动

matlab中标准布朗运动
在MATLAB中，标准布朗运动（Standard Brownian Motion）是一个随机过程，表示为一个连续时间、连续状态的随机变量。

它在金融、物理和统计学等领域有广泛的应用。

在MATLAB中，可以使用以下代码生成标准布朗运动：
```MATLAB
生成一个初始值为0的标准布朗运动序列
Brownian_ Motion = randn(1, 100);
计算序列的均值和方差
mean_value = mean(Brownian_Motion);
variance = var(Brownian_Motion);
计算序列的标准差
std_dev = sqrt(variance);
打印结果
disp('均值：');
disp(mean_value);
disp('方差：');
disp(variance);
disp('标准差：');
disp(std_dev);
```
上述代码首先生成了一个1x100的随机矩阵，表示100个时间点的标准布朗运动。

然后计算了该序列的均值、方差和标准差。

最后打印出这些统计量。

需要注意的是，这里生成的标准布朗运动序列是基于随机数生成的，每次运行结果可能不同。

你可以调整生成的序列长度来观察不同长度下的统计特性。

分数布朗运动 matlab程序

分数布朗运动 matlab程序英文回答：Fractional Brownian motion (fBm) is a type of Gaussian process that is characterized by its self-similarity and long-range dependence. It is often used to model phenomena that exhibit these properties, such as financial time series, turbulence, and the growth of biological systems.fBm is defined by its Hurst exponent, H, which determines the degree of self-similarity and long-range dependence. For H = 0.5, fBm is equivalent to standard Brownian motion, which is a continuous-time random walk. For H < 0.5, fBm has a negative Hurst exponent and is said to be anti-persistent, meaning that its values tend to alternate between positive and negative. For H > 0.5, fBm has a positive Hurst exponent and is said to be persistent, meaning that its values tend to stay in the same direction over long periods of time.There are a number of different ways to generate fBm in MATLAB. One common method is to use the `fracdiff` function from the Fractal Brownian Motion toolbox. This function takes a vector of data and a Hurst exponent as input, and returns a vector of fBm values.Another method for generating fBm is to use the `fBm` function from the Wavelab toolbox. This function takes a vector of data and a Hurst exponent as input, and returns a fractional Brownian motion process.Once you have generated a vector of fBm values, you can plot it to see the characteristic self-similarity and long-range dependence. You can also use the `hurst` function from the Fractal Brownian Motion toolbox to estimate the Hurst exponent of the data.Here is an example of how to generate and plot fBm in MATLAB:matlab.% Generate fBm with Hurst exponent H = 0.5。

（完整版）MATLAB作业2参考答案

（完整版）MATLAB作业2参考答案MATLAB 作业⼆参考答案1、试求出如下极限。

【求解】极限问题可以由下⾯语句直接求解。

>> syms x; f=(x+2)A(x+2)*(x+3)A(x+3)/(x+5F(2*x+5); limit(f,x,i nf) ans = exp(-5) >> syms x yfa=(x A 2*y+x*y A 3)/(x+y)A 3; limit(limit(fa,x,-1),y,2) ans = -6>> fc=(1-cos(xA2+yA2))*exp(xA2+yA2)/(xA2+yA2); limit(limit(fc,x,O),y,O) ans = 02、试求出下⾯函数的导数。

(1) y(x) . xsinx 、1e x , (2) atan yIn(x 2 y 2)x【求解】由求导函数diff() 可以直接得出如下结果，其中 (2)为隐函数，故需要⽤隐函数求导公式得出导数。

>> syms x;f=sqrt(x*si n( x)*sqrt(1-exp(x))); simple(diff(f)) ans =1/2/(x*s in (x)*(1-exp(x))A(1/2))A(1/2)*(si n(x)*(1-exp(x))A(1/2)+ x*cos(x)*(1-exp(x))A(1/2)-1/2*x*sin (x)/(1-exp(x))A(1/2)*exp(x)) >> syms x,y; f=ata n(y /x)_log(xA2+yA2); f1=simple(-diff(f,x)/diff(f,y)) f1 =(y+2*x)/(x-2*y)2 23、假设U cos 1 J *，试验证⼀———。

\y x y y x【求解】证明⼆者相等亦可以由⼆者之差为零来证明，故由下⾯的语句直接证明。

>> syms x y; u=acos(x/y); diff(diff(u,x),y)-diff(diff(u,y),x) ans =(1) limx (x 2)x 2(x 3)x3(x 5)2x 52..x y lim y 21(x xy 3y)3H xy2Xos2Xe2o o2xyt 2x2f2f2f4、假设 f (x, y) e dt ，试求 22 2y x x yy【求解】由下⾯的命令可以得出所需结果。

matlab课后答案完整版

matlab课后答案完整版ones表⽰1矩阵zeros表⽰0矩阵ones(4)表⽰4x4的1矩阵zeros(4)表⽰4x4的0矩阵zeros(4,5)表⽰4x5的矩阵eye(10,10)表⽰10x10的单位矩阵rand(4,5)表⽰4x5的伴随矩阵det(a)表⽰计算a的⾏列式inv(a)表⽰计算a的逆矩阵Jordan(a)表⽰求a矩阵的约当标准块rank(a)表⽰求矩阵a的秩[v,d]=eig(a)对⾓矩阵b=a’表⽰求a矩阵的转置矩阵sqrt表⽰求平⽅根exp表⽰⾃然指数函数log⾃然对数函数abs绝对值第⼀章⼀、5（1）b=[97 67 34 10;-78 75 65 5;32 5 -23 -59]; >> c=[97 67;-78 75;32 5;0 -12]; >> d=[65 5;-23 -59;54 7];>> e=b*ce =5271 11574-11336 6641978 3112（2）a=50:1:100⼆、1 、x=-74;y=-27;z=(sin(x.^2+y.^2))/(sqrt(tan(abs(x+y)))+pi) z =-0.09012、a=-3.0:0.1:3.0;>> b=exp(-0.3*a).*sin(a+0.3)y =0.7218 1.0474-0.2180 1.15624、a*b表⽰a矩阵和b矩阵相乘a.*b表⽰a矩阵和b矩阵单个元素相乘A(m,n)表⽰取a矩阵第m⾏，第n列A(m,:)表⽰取a矩阵第m⾏的全部元素A(:,n)表⽰取a矩阵的第n列全部元素A./B表⽰a矩阵除以b矩阵的对应元素，B.\A等价于A./BA.^B表⽰两个矩阵对应元素进⾏乘⽅运算A.^2表⽰a中的每个元素的平⽅A^2表⽰A*A例：x=[1,2,3];y=[4,5,6];z=x.^yz=1 32 729指数可以是标量（如y=2）.底数也可以是标量（如x=2）5、a=1+2i;>> b=3+4i;>> c=exp((pi*i)/6)c =0.8660 + 0.5000id=c+a*b/(a+b)d =1.6353 + 1.8462i第⼆章⼆、4、（1）y=0;k=0;>> while y<3k=k+1;>> display([k-1,y-1/(2*k-1)])ans =56.0000 2.9944第三章⼆1（1） x=0:pi/10:2*pi; >> y=x-x.^3/6; >> plot(x,y)1234567-40-35-30-25-20-15-10-505（2）x=0:pi/10:2*pi; y=(exp(-x.^2/2))/2*pi;plot(x,y)012345670.20.40.60.811.21.41.6（3）x=-8:0.01:8; y=sqrt((64-x.^2)/2);plot(x,y)-8-6-4-2024680123456（4）t=0:0.1:8*pi; >> x=t.*sin(t); >> y=t.*cos(t);-25-20-15-10-50510152025-30-20-10102030例3.4x=0:pi/100:2*pi; y1=exp(-0.5*x);y2=exp(-0.5*x).*sin(2*x); plot(x,y1,x,y2)>> title('x from 0 to 2{\pi} '); >> xlabel('variable x'); >> ylabel('variable y'); >> text(1.5,0.5,'曲线y1=e^(-0.5x)'); >> text(3,0.1,'曲线y2=cos(4{\pi}x)e^{-0.5x}'); >> legend('y1','y2')1234567-0.4-0.20.20.40.60.81x from 0 to 2πvariable xv a r i a b l e y曲线y1=e (-0.5x)曲线y2=cos(4πx)e -0.5xy1y22、(1)y1=2*x-0.5;t=linspace(0,pi,100); x=sin(3*t).*cos(t); y=sin(3*t).*sin(t);>> k=find(abs(y-x)<1e-2); >> t1=t(k) t1 =0 0.7933 1.04722.0944>> z=sin(3.*(t1)).*cos(t1) z =0 0.4841 0.0000 0.0000 -0.0000>> plot(t,x,t,y,'k:',t1,z,'bp');0.511.522.533.5-1-0.8-0.6-0.4-0.200.20.40.60.81（2）subplot(1,2,1); >> scatter(x1,y1,10)； >> title('y=2x-0.5')； >> subplot(1,2,2); >> scatter(x,y,10)-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.63、subplot(1,2,1); x=0:0.01:pi; y=sin(1./x); plot(x,y)subplot(1,2,2);fplot('sin(1./x)',[1,100])1234-1-0.8-0.6-0.4-0.200.20.40.60.81204060801000.10.20.30.44、t=0:pi:2*pi; y=1./(1+exp(-t));subplot(2,2,1);%图形窗⼝的分割bar(t,'group'); %绘制柱形图（分组） subplot(2,2,2);barh(t,'stack');%绘制柱形图（堆积） subplot(2,2,3);loglog(t,y); %函数使⽤全对数坐标，x,y 均采⽤常⽤对数刻度 subplot(2,2,4); semilogy(t,y); %函数使⽤半对数坐标，y 轴为常⽤对数刻度，x 轴仍为线性刻度1230246802468123100.5100.710-0.01810-0.0010246810-0.310-0.210-0.15、（1）theta=linspace(-pi,pi,100); ro=5.*cos(theta)+4; polar(theta,ro); （2）x=linspace(0,2*pi,100);a=1>> r=a.*(1+cos(x)); polar(x,r);3021060240902701203001503301806、（1）t=0:pi/10:2*pi;>> x=exp((-t)/20).*cos(t); >> y=exp((-t)/20).*sin(t); >> z=t; >> plot3(x,y,z);-1-0.50.51-1-0.50.5102468（2）t=0:0.01:1; x=t;>> y=t.^2; >> z=t.^3;>> plot3(x,y,z);0.20.40.60.800.20.40.60.817、x=-30:0.1:0; >> y=0:0.1:30;>> [x,y]=meshgrid(x,y); >>z=10.*sin(sqrt(x.^2+y.^2))./sqrt(1+x.^2+y.^2);>> meshc(x,y,z);绘制曲⾯图和等⾼线-30-20-10102030-4-202468、x=linspace(-3,3,100); >> y=linspace(-3,3,100); >> [x y]=meshgrid(x,y); %可以将向量转化为矩阵 >> fxy=-5./(1+x.^2+y.^2); >> i=find(abs(x)<=0.8 & abs(y)<=0.5); >> fxy(i)=NaN; >>surf(x,y,fxy) %绘制三维曲⾯图-4-224-4-224-4-3-2-19、u=linspace(1,10,100); v=linspace(-pi,pi,100);[u v]=meshgrid(u,v); x=3.*u.*sin(v); y=2.*u.*cos(v); z=4*u.^2; surf(x,y,z); shading interp;-40-20-1010200100200300400第五章⼆1、a=rand(1,30000);mean(a) %求平均数 ans =0.5010 >>b=std(a) %求标准差 b =0.2882 >> c=max(a) c =0.9999 >> d=min(a) d =3.5706e-005size(find(a>0.5))/size(a) %求⼤于0.5的随机数个数占总数的百分⽐ans =0.50322、h=[466,715,950,1422,1635]; >> w=[7.04,4.28,3.40,2.52,2.13]; >> hh=[500,900,1500]; >> ww=interp1(h,w,hh,'spline')ww =6.4903 3.5226 2.3845 3、x=linspace(1,10,50); y=log(x);f=polyfit(x,y,5); %求曲线的拟合 >> yy=polyval(f,x); >> plot(x,y,'r-',x,yy,'g.') 123456789100.511.522.55、（1）、（2） p1=[1,2,0,7]; p2=[1,-2]; p3=[1,0,5,1]; p12=conv(p1,p2); >>p=p12+[zeros(1,size(p12,2)-size(p3,2)),p3]; >> roots(p) ans =-3.4656 0.6128 + 1.6278i 0.6128 - 1.6278i 1.2400-29 291 95 19 -3 697 -13 697 1427 >>y2=polyvalm(p,a)%以矩阵a 为⾃变量 y2 =391 2084 3273 502 2693 4207 720 3775 5892 6、（1）z=fzero('3*x-sin(x)+1',0) %求x=0时附近的根 z =-0.4903 第⼋章⼆、2t=0:pi/20:2*pi; x=sin(t); y=cos(t); x1=sin(7*t); y1=cos(7*t);h=plot(x,y,x1,y1);set(h,'marker','x','linewidth',2); set(gca,'xtick',-1:0.1:1); title('篮筐')-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3-0.2-0.100.10.20.30.40.50.60.70.80.91 -1-0.8-0.6-0.4-0.200.20.40.60.81篮筐3、x=0:pi/10:5*pi;y=exp(-0.2*x).*cos(x)+2; h=plot(x,y);set(gca,'color','red','linestyle','-','linewidth',3);text(5,2.4,'y=exp(-0.2*x).*cos(x)+2');02468101214161.41.61.822.22.42.62.83y=exp(-0.2*x).*cos(x)+24、t=-pi:pi/100:pi; x=cos(t); y=sin(t); z=t;h=plot(t,x,t,y,t,z);set(h,'linestyle','-','linewidth',3);-4-3-2-101234-4-3-2-101234字符串例ch='Welcome to Beijing';subch=ch(12:18) 选12~18个字符串（空格也算）ans =WELCOME TO BEIJING >> length(k)统计⼩写字母的个数ans = 14 例：已知y=1-1/2+1/3-1/4.........-1/100求y 的值y=0; >> n=100; >> for i=1:100; y=y+(-1)^(i-1)/i; end>> disp(y)0.6882绘制⼆维曲线图x=0:pi/100:2*pi; >> y1=0.2*exp(-0.5*x).*cos(4*pi*x); >> y2=1.5*exp(-0.5*x).*cos(pi*x); >> plotyy(x,y1,x,y2); 7-0.20.20123456-202绘制三维图像例：x=sint+tcost y=cost-tsint z=tt=0:pi/10:10*pi; x=sin(t)+t.*cos(t); y=cos(t)-t.*sin(t); z=t; plot3(x,y,z); axis([-30 30 -30 30 0 35]); 坐标轴的最⼤值与最⼩值title('line in 3-D space'); 图形的题⽬ >> xlabel('x');ylabel('y');zlabel('z'); 标注坐标>> grid on; 加⽹格线 -30-20-10102030-20205101520253035xline in 3-D spaceyz三维例]2/,0[],,0[,cos sin 22ππ∈∈+=y x y x z [x,y]=meshgrid(0:pi/100:pi,0:pi/100:pi/2);>> z=sin(x.^2)+cos(y.^2);>> mesh(x,y,z);>> axis([0 4 0 1.8 -1.5 1.5]); 012340.511.5-1.5-1-0.500.511.5例3.16t=0:pi/20:2*pi; subplot(1,2,1);[x,y,z]=cylinder(sin(t),30);surf(x,y,z); 绘制三维曲⾯图subplot(1,2,2);>> [x,y,z]=peaks(100);>> mesh(x,y,z); 绘制三维⽹格图-11-10100.20.40.60.81-55-505-10-5510多项式求导例：f(x)=1/x^2+5 p=[1];>> q=[1,0,5];>> [p,q]=polyder(p,q)注：c=conv(a,b) 表⽰a 多项式与b 多项式乘积[p,r]=deconv(a,b) 表⽰a 多项式与b 多项式相除其中p 为商向量 r 为余数向量p=polyder(p) 表⽰求p 的导数 p=poleder(p,q) 表⽰求p 乘以q 的导数[p,q]=poleder(p,q) 表⽰p 除以q 的导数多项式求根例：f(x)=2x^4-12x^3+3x^2+5 p=[2,-12,3,0,5]; >> x=roots(p); >> p=[2,-12,3,0,5]; x=roots(p) 求⽅程f(x)=0的根 x =5.7246 0.8997 -0.3122 + 0.6229i -0.3122 - 0.6229i>> g=poly(x) 已知多项式的根求多项式 g =1.0000 -6.0000 1.5000 -0.00002.5000符号求导例7.3x=a(t-tsint)y=b(1-cost) 求y 对x 的⼀阶导数 syms x y a b t;>> f21=a*(t-sin(t)); >> f22=b*(1-cos(t));>> diff(f22)/diff(f21) 求y 对x 的⼀阶导数ans =b*sin(t)/a/(1-cos(t))注：diff(f1,x,2) 表⽰f1对x 的⼆阶导数diff （f3,x ）表⽰z 对x 的偏导 diff （f3,y ）表⽰z 对y 的偏导求不定积分int(f) 求f 的不定积分 f1=int(f,a,b) 求f 在a ，b 之间的定积分eval （f1）计算积分值符号求极限例7.2 syms x h>> f=(sin(x+h)-sin(x))/h;>> limit(f,h,0) h 趋向于0ans =cos(x)例2f=sym('(1+t/x)^x');limit(f,inf) f趋向于⽆穷ans =exp(t)例3f=sym('x*(sqrt(x^2+1)-x)');limit(f,sym('x'),inf,'left') x 趋向于正⽆穷ans =1/2⼤⼩写ch='Welcome to Beijing';subch=ch(12:18)subch =Beijing>> k=find(ch>='A'&ch<='Z'); ch(k)=ch(k)-('A'-'a');>> char(ch)ans =welcome to beijing>> length(k)ans =2。

MATLAB全部实验及答案

MATLAB全部实验及答案MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤4、有关向量、矩阵或数组的一些运算（1）设A=15；B=20；求C=A+B与c=a+b？（2）设A=[1 2 3;4 5 6;7 8 9]，B=[9 8 7;6 5 4;3 2 1]；求A*B 与A.*B？A*B就是线代里面的矩阵相乘A.*B是对应位置的元素相乘（3）设a=10，b=20；求i=a/b=0.5与j=a\b=2？（4）设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序，分别找出小于0的矩阵元素及其位置（单下标、全下标的形式），并将其单下标转换成全下标。

clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc（5）在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8]；看结果如何？如果改成运行A=[1,2;3,4]+i[5,6;7,8]，结果又如何？前面那个是虚数矩阵，后面那个出错（6）请写出完成下列计算的指令：a=[1 2 3;3 4 2;5 2 3]，求a^2=？,a.^2=？a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9（7）有一段指令如下，请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量（8）使用三元组方法，创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一：clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二：不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a（9）写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B5、已知+?=-334sin 234πt e y t 若需要计算t ∈[-1,1]，取间隔为0.01，试计算出相对应的y 值。

使用Matlab对布朗运动的模拟

使用Matlab对布朗运动的模拟1. 引言1.1 介绍布朗运动布朗运动是指微观粒子在液体或气体中由于受到周围分子的碰撞而表现出的无规则运动。

这种运动是由英国植物学家罗伯特·布朗于1828年首次观察到并描述的，因此得名。

布朗运动的存在证实了分子动力学理论，并为原子理论的确立提供了实验依据。

在布朗运动中，微粒子随机地在液体或气体中运动，其运动路径呈现出无规则、不可预测的特征。

这种运动是由于液体或气体中的分子热运动引起的，其中微粒受到来自周围分子的不断碰撞和推动。

布朗运动在自然界和科学研究中具有重要的意义。

在物理学中，布朗运动是研究分子尺度上的运动和扩散现象的重要实验现象。

在生物学中，布朗运动也被用来解释细胞内分子在胞质中的扩散和运输过程。

布朗运动还被应用于金融市场的波动性建模和股票价格的预测等领域。

布朗运动是一个广泛存在且具有重要意义的现象，其模拟和研究对于理解微观世界和提升科学技术水平具有重要意义。

1.2 布朗运动的重要性布朗运动在生物学研究中也扮演着重要的角色。

生物体内的许多基本生命过程，如细胞内的物质运输、细胞分裂等，都与布朗运动密切相关。

通过观察和分析细胞内物质的布朗运动，科学家们可以更好地理解生物体内的生命活动机制，推动生物学研究的深入发展。

布朗运动的研究还对纳米技术、材料科学等领域具有重要意义。

在纳米尺度下，物质的性质和行为往往受到布朗运动的影响，了解和控制布朗运动对于设计和制备纳米材料具有重要意义。

通过对布朗运动的研究，人们可以更好地设计新型材料，提高材料的性能和应用价值。

布朗运动的重要性不仅体现在基础科学研究中，同时也对未来的技术创新和应用发展具有重要的推动作用。

2. 正文2.1 布朗运动的数学模型布朗运动的数学模型是描述微观粒子在液体或气体中做无规则运动的数学模型。

布朗运动最早由苏格兰生物学家罗伯特·布朗观察到，他发现在显微镜下观察一颗花粉粒子，发现花粉粒子在水中呈现出不规则的运动轨迹，这种现象后来被称为布朗运动。

matlab布朗函数命令

matlab布朗函数命令
在MATLAB中，可以使用`brownian`函数来生成布朗运动的路径。

`brownian`函数的语法如下：
matlab.
brownian(n, 'Type', type, 'N', N, 'T', T, 'Y0', Y0)。

其中，参数含义如下：
`n`，生成布朗运动路径的离散点数量。

`'Type'`，布朗运动类型，可以是`'Arithmetic'`（等差布朗
运动）或者`'Geometric'`（等比布朗运动）。

`'N'`，布朗运动的离散步数。

`'T'`，总的时间长度。

`'Y0'`，起始值。

例如，要生成一个等差布朗运动的路径，可以使用以下代码： matlab.
n = 1000;
type = 'Arithmetic';
N = 1000;
T = 1;
Y0 = 0;
brownian(n, 'Type', type, 'N', N, 'T', T, 'Y0', Y0);
这将生成一个包含1000个离散点的等差布朗运动路径。

除了`brownian`函数外，MATLAB还提供了其他用于生成布朗运动的函数，例如`geometric_brownian_motion`和
`arithmetic_brownian_motion`等，具体使用取决于你的需求和版本。

希望这些信息能够帮助到你。

(完整版)MATLAB)课后实验答案[1]

实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。

(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

解：(1) 结果：(2). 建立一个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。

解: M 文件如下；5. 下面是一个线性方程组：1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。

(2) 将方程右边向量元素b 3改为0.53再求解，并比较b 3的变化和解的相对变化。

(3) 计算系数矩阵A 的条件数并分析结论。

解： M 文件如下： 123d4e56g9实验三选择结构程序设计1. 求分段函数的值。

2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

matlab课后习题参考答案

Matlab课后习题部分参考答案习题二2．student=struct('name',{'zhang','wang','li'},'age',{18,21,[] },'email',{['zh ang@','zhang@'],'',''})5、a=[1 0 0;1 1 0;0 0 1];b=[2 3 4;5 6 7;8 9 10];c=[a b]d=[a;b]c =1 0 023 41 1 0 5 6 70 0 1 8 9 10d =1 0 01 1 00 0 12 3 45 6 78 9 1010、reshape(c,2,9)1 0 1 0 1 5 3 9 71 0 0 02 8 6 4 10 reshape(d,2,9)ans =1 0 5 0 0 6 0 1 71 2 8 1 3 9 0 4 10 (注意：重新排列矩阵，是将原来的矩阵按列排序)11、a.’12、a+b a.*ba\b (即inv(a)*b，考试时，要求能自己手算出a的逆)ans =2 3 43 3 38 9 1013、c=4*ones(3);a>=cb>=c14．strcat('The picture is ','very good')a=['The picture is ','very good']18．double('very good')1．norm（A），det（A），rank（A）2．b=[1 1 1 1 1];c=b';a=[17,24,1,8,50;23,5,7,14,49;4,6,13,20,43;10,12,19,21,62;11,18,25,2,56]; x=a\c习题四1、a=14*rand(1,10)-5;for i=1:9max=i;for j=i+1:10if a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;enda将上述脚本保存为script41.m2、function y=function42(n)3*randn(1,n)+3;for i=1:n-1max=i;for j=i+1:nif a(j)>a(max)max=j;endendtemp=a(i);a(i)=a(max);a(max)=temp;endy=a;将上述函数保存为function42.m 3、r=input(‘please input 1/2: ’);if r= =1script41;elsen=input(‘please input the length: ’);y=funtion42(n);end4．function f=function1(x,y)if y==1f=sin(x);elseif y==2f=cos(x);elsef=sin(x).*cos(x);end在命令窗口调用函数f=function1(1,3) 5．function result=function3(x,n)result=0;for i=1:nresult=result+sin(x.*i)+(-1).^i.*cos(i.*x); endfunction result=function4(n,t)result=0;A=[1 2 3;0 1 2;0 0 1];for i=1:nresult=result+A*i.*exp(A*i.*t);end习题五3．x1=-2:0.01:2;x2=-2:0.01:2;y1=x1.*sin(x2);y2=x2.*cos(x1);plot3(x1,x2,y 1,'-d',x1,x2,y2,'-d')14、x=8*rand(1,100)-2;y=reshape(x,10,10);save mydata.mat yclearclcload mydatak=y>ones(10);totel=0;for i=1:100if k(i)==1totel=totel+1;endend15、x=rand(5); %生成5*5均匀分布的随机矩阵（该处只作举例，未按题目要求）fid=fopen(‘text.txt’,’w’);count=fwrite(fid,x,’int32’); closestatus=fclose(fid);清除内存，关闭所有窗口fid=fopen(‘text.txt’,’r’);x=fread(fid,[5,5],’int32’); closestatus=fclose(fid); inv(x)16．随便生成一个矩阵，x1=-1:0.2:0.8;x2=-1:0.2:0.8;y1=x1.*sin(x2)；y2=x2.*cos(x1)；a=reshape([y1;y2],10,10)；fid=fopen('table.txt','w'); fprintf (fid,‘%f’，a); fclose(fid) ;清除内存，关闭所有窗口a=fscanf('table.txt','%f') ; exp(a) ;fclose(fid) ;习题六1.c=ploy2str(A)；B=[2,0,0,1,3,5]；2.x=1:10;B=ployval(A，x)；。