MATLABSimulink北航第二次课2
MATLABSIMULINK的操作指导
MATLAB/SIMULINK的操作指导一SIMULINK简介Simulink是MATLAB下的一个软件包,是一个结合了框图界面和交互仿真能力的系统级设计和仿真工具。
它以MATLAB的核心数学、图形和语言为基础,可以让用户毫不费力地完成从算法开发、仿真或者模型验证的全过程,而不需要传递数据、重写代码或改变软件环境。
Simulink是基于MATLAB的图形化仿真环境。
它使用图形化的系统模块对动态系统进行描述,并在此基础上进行动态系统的求解。
利用Simulink对动态系统进行仿真的核心在于,MATLAB计算引擎对系统微分方程核差分方程求解。
Simulink与MATLAB时高度集成在一起的,因此,Simulink与MATLAB之间可以灵活的交互操作。
1 Simulink的窗体介绍由于Simulink是基于MATLAB环境之上的高性能的系统及仿真平台。
因此,启动Simulink 之前必须首先运行MATLAB,然后,才能启动Simulink并建立系统的仿真模型。
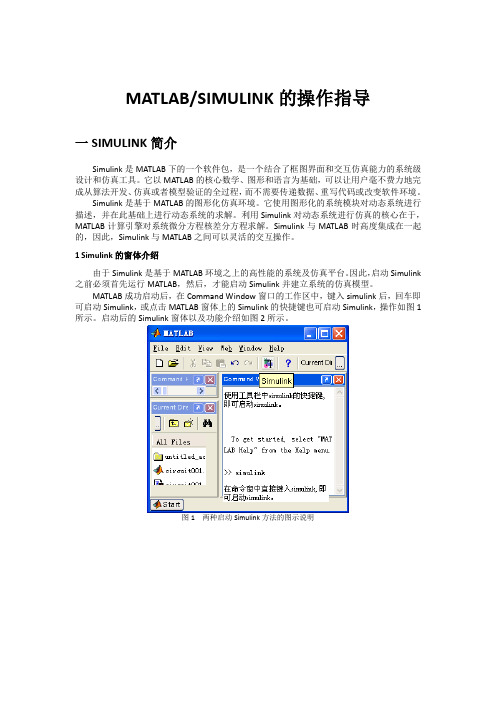
MATLAB成功启动后,在Command Window窗口的工作区中,键入simulink后,回车即可启动Simulink,或点击MATLAB窗体上的Simulink的快捷键也可启动Simulink,操作如图1所示。
启动后的Simulink窗体以及功能介绍如图2所示。
图1 两种启动Simulink方法的图示说明图.2 Simulink库浏览器窗口2 一个MATLAB/Simulink库自代的演示实例MATLAB/Simulink自代了大量的演示实例,为读者创建模型提供许多有益的帮助,读者可借鉴这些实例。
浏览演示实例可在Command Window窗的工作区键入demo回车即可,或点击MATLAB窗体的左下角的Start按钮也可浏览,选择出所需的模型。
线性电路的暂态分析模型如图3所示,其运行结果如图.4所示。
图 3 线性电路暂态分析的演示仿真模型图.4 线性电路暂态分析的演示仿真模型的运行结果3 创建一个MATLAB实例对Simulink库有了初步了解后,创建一个简单电路的仿真模型并运行。
(MATLAB与工程应用)第8章(simulink2)

Simulink建模与仿真 入门
8.1 绪论 8.2 动态系统模型及Simulink表示 8.3 创建Simulink模型 8.4 Simulink与MATLAB的接口设计 8.5 使用Simulink进行简单的仿真
8.3 创建Simlink模型
8.3.1 Simulink的启动 8.3.2 Simulink的模块库介绍 8.3.3 构建Simulink框图
连续模块(Continuous) continuous.mdl
Integrator:输入信号积分 Derivative:输入信号微分 State-Space:线性状态空间系统模型 Transfer-Fcn:线性传递函数模型 Zero-Pole:以零极点表示的传递函数模型 Memory:存储上一时刻的状态值 Transport Delay:输入信号延时一个固定时 间再输出 Variable Transport Delay:输入信号延时一 个可变时间再输出
Logical Operator:逻辑运算 Relational Operator:关系运算 Complex to Magnitude-Angle:由复数输入转为幅值 和相角输出 Magnitude-Angle to Complex:由幅值和相角输入合 成复数输出 Complex to Real-Imag:由复数输入转为实部和虚部 输出 Real-Imag to Complex:由实部和虚部输入合成复数 输出
Constant:常数信号。 Clock:时钟信号。 From Workspace:来自MATLAB的工作空间。 From File(.mat):来自数据文件。 Pulse Generator:脉冲发生器。 Repeating Sequence:重复信号。 Signal Generator:信号发生器,可以产生正弦、方 波、锯齿波及随意波。 Sine Wave:正弦波信号。 Step:阶跃波信号。
MATLAB最重要的组件Simulink仿真入门教程优秀PPT课件

解决方案
使用技巧
多模块复制粘贴:在Simulink模型中,可以通过复制和粘贴操作实现多个相同模块的快速添加和参数设置。
模块连接自动对齐:在Simulink模型中,可以通过右键菜单中的“自动对齐”选项实现模块连接的自动对齐。
模块快速拖拽:在Simulink模型中,可以通过按住Ctrl键并拖动模块,实现模块的快速移动。
通信工程
Simulink可以用于通信工程的仿真和优化,支持多种通信协议和信号处理算法,可以对通信系统的性能进行评估和优化。
嵌入式系统
Simulink可以与嵌入式系统紧密结合,对嵌入式系统的硬件和软件进行仿真和测试,从而加速嵌入式系统的开发和调试。
信号处理
Simulink提供了信号处理模块库,支持信号的采集、处理、分析和可视化等功能,可以方便地进行信号处理领域的各种研究和开发。
详细描述
模型建立不正确解决方案:采用MATLAB提供的帮助文档和Simulink GUI界面提示
运行效率低解决方案:采用MATLAB提供的性能分析工具对模型进行优化,例如通过减少模块计算量和增加缓存等措施提高运行效率
结果可视化不美观解决方案:采用MATLAB提供的图形界面工具对结果进行美化,例如调整图表颜色、样式和标注等。
复杂系统仿真
实际应用仿真
案例九 电液伺服系统的仿真
案例十二 机器人控制系统的仿真
案例十 车辆动力系统的仿真
案例十一 工业过程控制系统的仿真
THANKS
感谢观看
《matlab最重要的组件simulink仿真入门教程优秀ppt课件》
xx年xx月xx日
Simulink软件介绍Simulink基本操作Simulink高级操作Simulink常见问题及解决方案Simulink案例教程
matlab中simulink使用技巧

matlab中simulink使用技巧参加数学建模已经很多年了,算来其中所学多源于网络上各位前辈的无私奉献。
饮水当思源,承志以后继。
故而添加此分类,用于交流我这些年的心得。
心得分为软件和算法两类,软件可能会包括matlab/simulink,maple,mathematica,spss(被收购成了pasw),ansys,ansoft/maxwell,comsol,pscad,tc,算法可能有GA,NNs。
当然,受到专业研究所限,很多时候无法得心应手,献丑于此,只为提醒自己要做到更好。
恰巧,我在自己学校的bbs上申请了相关版面的版主职位,也希望自己能整理出些基础教学,以备后生晚辈们入门。
暂时的想法是,先说些simulink的相关知识,因为工科学生最常用的就是这个仿真环境,而其他软件又恰好对他保留了接口,可以说这个软件成为了算法的中心。
以后将陆续说些simulink不能完成的任务,并推荐能完成这些任务的工具。
开始吧——simulink可以视作matlab下的工具库,matlab版本不断更新,simulink也不断更新,当前版本为matlab2011b。
首先要明确,simulink的作用为求解常微分方程(组)!且这是他唯一的作用!也就是说偏微分方程在simulink中是无法求解的,需要其他工具或软件作为接口,或者你够牛的,就直接写个有限元的程序。
当然,常微分方程是不够的,为适应数字控制电路等离散系统,simulink可以求解离散的常微分方程,也就是差分方程,略微麻烦,不做重点介绍。
然后来看看simulink求解常微分方程(组)的方法,首先要把方程写成如下形式:y1'=f1(y1,y2,...yn,t)y2'=f2(y1,y2...yn,t)...yn'=fn(y1,y2...yn,t)至于如何写成这种形式,就是降阶了,线性代数里说的很多了,比如y1=y;y2=y1'=y';y3=y2'=y''...需要注意的是,等号右侧不能有导数项,如果等号右边出现了导数项,则说明这个方程需要积分一次。
Matlab_高级讲义_第五章_SIMULINK仿真基础

3、 Function&Tables(函数和平台模块) function.mdl
Fcn:用自定义的函数(表达式)进行运算 MATLAB Fcn:利用matlab的现有函数进行运算 S-Function:调用自编的S函数的程序进行运算 Look-Up Table:建立输入信号的查询表(线性峰值匹配) Look-Up Table(2-D):建立两个输入信号的查询表(线性峰值匹配)
Logical Operator:逻辑运算 Relational Operator:关系运算 Complex to Magnitude-Angle:由复数输入转为幅值和相角输出 Magnitude-Angle to Complex:由幅值和相角输入合成复数输出 Complex to Real-Imag:由复数输入转为实部和虚部输出 Real-Imag to Complex:由实部和虚部输入合成复数输出
线的折弯:按住Shift键,再用鼠标在要折弯的线处单击一下,就会出现 圆圈,表示折点,利用折点就可以改变线的形状。
1) 移动:选中模块,按住鼠标左键将其拖曳到所需的位置即可。若要 脱离线而移动,可按住shift键,再进行拖曳。
2) 复制:选中模块,然后按住鼠标右键进行拖曳即可复制同样的一个 功能模块。
3) 删除:选中模块,按Delete键即可。若要删除多个模块,可以同时 按住Shift键,再用鼠标选中多个模块,按Delete键即可。也可以用鼠 标选取某区域,再按Delete键就可以把该区域中的所有模块和线等 全部删除。
SIMULINK的最新版本是SIMULINK4.0(包含在MATLAB6.0 里),MATLAB5.3里的版本为3.0版,它们的变化不大。
二、SIMULINK的启动
1、在MATLAB命令窗口中输入simulink
第2部分创建Simulink模型

(6) Stateflow(驱动过程):对使用状态图 所表达的有限状态机模型进行建模仿真和代码生 成。有限状态机用来描述基于事件的控制逻辑, 也可用于描述响应型系统。
哈尔滨商业大学 计算机与信息工程学院 苏晓东
模块功能说明: 求取信号的绝对值 输出强制系统输入为零的代数状态 按位逻辑运算 逻辑真值查找 输出输入复数的幅值与相位 输出系统输入的实部或虚部 点乘运算 信号增益 信号逻辑运算 幅值与相位转化为复数形式 特定的一些数学函数 矩阵增益 求取输入的最小或最大值 乘法或除法器 从输入实部与虚部构造复数 关系运算器 求整运算器 符号运算 渐变增益 对输入求和或差 三角与双曲函数
此外还可以进行以下操作: (1) 使用鼠标左键选择并拖动系统模块,并 将其拷贝到系统模型中。 (2) 在模块搜索栏中搜索所需的系统模块。
哈尔滨商业大学 计算机与信息工程学院 苏晓东
2.2.3 模块选择
从2.2.3到2.2.5作为一个小应用,请同学们自己动手完成
哈尔滨商业大学 计算机与信息工程学院 苏晓东
9.Simulink子 系统模块库及 其功能
ห้องสมุดไป่ตู้
哈尔滨商业大学 计算机与信息工程学院 苏晓东
Simulink 公共模块库中提供了大量内置的系 统模块,这些系统模块的用途非常广泛,一般的 动态系统模型都可以使用公共模块库中的模块来 构建。
除了公共模块库之外,Simulink 中还集成了 许多面向不同专业领域的专业模块库。在此,对 Simulink 专业模块库的部分功能做简单的概述。 详细内容,可以在 Simulink 的模块描述栏了解 其主要功能。
北航Matlab教程(R2016a)习题2解答 2-推荐下载

习题21.说出以下四条指令产生的结果各属于哪种数据类型,是“双精度”对象,还是“符号”对象?3/7+0.1, sym(3/7+0.1), vpa(sym(3/7+0.1))a=class(3/7+0.1)%双精度b=class(sym(3/7+0.1))%符号c=class(vpa(sym(3/7+0.1),4))%符号d=class(vpa(sym(3/7+0.1)))%符号2.在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是独立自由变量。
sym('sin(w*t)') , sym('a*exp(-X)' ) , sym('z*exp(j*th)')a=sym('sin(w*t)');symvar(a)b=sym('a*exp(-X)');symvar(b)c=sym('z*exp(j*th)');symvar(c)3.求以下两个方程的解:(提示:关于符号变量的假设要注意)(1)试写出求三阶方程05.443=-x 正实根的程序。
注意:只要正实根,不要出现其他根。
x=sym('x','positive');f=x^3-44.5;x=solve(f,x)(2)试求二阶方程在时的根。
022=+-a ax x 0>a a=sym('a','positive');syms x;f=x^2-a*x+a^a;x=solve(f,x)4.观察一个数(在此用@记述)在以下四条不同指令作用下的异同:a = @ ,b = sym( @ ),c = sym( @ ,'d ' ), d = sym( '@ ' )在此,@ 分别代表具体数值 7/3 , pi/3 , pi*3^(1/3) ;而异同通过vpa(abs(a-d)) , vpa(abs(b-d)) , vpa(abs(c-d))等来观察。
92598-MATLABSimulink——北航——第二次课2

第二章MATLAB在数值分析中的应用董素君新主楼C-503dsj@思考题进行下列计算,给出不使用for 和while 等循环语句的计算方法; 1 .2.求出y=x*sin(x) 在0<x<100的每个峰值,并绘制曲线∑==632i ik >> sum(2.^[0:63]) a ns =1.8447e+019>> x=0.01*pi:0.01*pi:32*pi;>> y=x.*sin(x);>> plot(x,y)>> hold on >> grid max sort主要内容1.1 MATLAB环境1.2 基本程序元素1.3 数据类型及常用函数1.4 矩阵1.5 字符串数组1.6 程序设计1.7 图形可视化1.8 MATLAB在数值分析中的应用 1.9 图形用户界面GUI开发多项式使用降幂系数的行向量表示,如多项式表示为:p=[1 -12 0 25 116]roots :求多项式等于0的根,根用列向量表示 poly :已知多项式的根,构建相应多项式 polyval(p,n):求多项式函数值polyder(p):求多项式的微分多项式11625012234+++−x x x x 》p=[1 -12 0 25 116]》r=roots(p)r =11.7473 2.7028 -1.2251 + 1.4672i -1.2251 -1.4672i 》p=poly(r)p =1 -12 -0 25 116》a=[1 2 3] ; 》polyval(a,2)ans =11》polyder(a)ans =2 2多项式使用降幂系数的行向量表示,如多项式表示为:p=[1 -12 0 25 116] roots :求多项式等于0的根,根用列向量表示 poly :已知多项式的根,构建相应多项式 polyval(p,n):求多项式函数值polyder(p):求多项式的微分多项式11625012234+++−x x x x 求极值:>> p=[1,-12,0,25,116];x=[0:1:10];y=polyval(p,x);plot(x,y)hold ongrid pp=polyder(p)xx=roots(pp)yy=polyval(p,xx)plot(xx,yy,'ro')多项式多项式的运算[例14]:相乘conv》a=[1 2 3] ;》b=[1 2];》c=conv(a,b)c =1 4 7 6conv指令可以嵌套使用,如:》conv(conv(a,b),c)ans=1 8 30 68 97 84 36例15]:相除deconv》[q,r]=deconv(c,b)q =1 2 3r =0 0 0 0q 为商多项式,r为余多项式插值一维插值interp1()例exp2_16.m yi=interp1(x,y,xi)yi=interp1(x,y,xi,’method’)yi=interp1(x,y,xi,’method’,’extrap’)‘method’用于指定插值算法,其值可以是:‘nearest’——最近插值(执行速度最快,输出结果为直角转折)‘linear’——线性插值(默认值,在样本点上斜率变化很大)‘spline’——分段三次样条插值(最花时间,输出结果最平滑)‘cubic’, ‘pchip’——分段三次Hermite插值(最占内存,输出结果与spline差不多)二维插值zi=interp2(x,y,z,xi,yi,’method’)三维插值vi=interp3(x,y,z,v,xi,yi,zi,’method’)三次样条插值pp=spline(x,y),返回三次样条插值的分段多项式形式的向量,以进行插值计算:yi=ppval(pp,xi)例2:多项式插值》ys=[0 0.9 0.6 1 0 0.1 -0.3 -0.7 -0.9 -0.2]; %已有的样本点ys 》xs=0:length(ys)-1; %已有的样本点xs》x=0:0.1:length(ys)-1;%新的样本点x》y1=interp1(xs,ys,x,'nearest'); %插值产生新的样本点y1 》y2=interp1(xs,ys,x,'linear'); %插值产生新的样本点y2》y3=interp1(xs,ys,x,'spline'); %插值产生新的样本点y3 》y4=interp1(xs,ys,x,'cubic'); %插值产生新的样本点y4 》plot(xs,ys,'+k',x,y1,':r',x,y2,'-m',x,y3,'--c',x,y4,'--b') %分别绘制不同方法产生的曲线》legend('sampled point','nearest','linear','spline','cubic')exm19.m拟合最小二乘法多项式拟合函数p=ployfit(x,y,n) 或[p,s]=ployfit(x,y,n)(x,y)为已知数据,n为多项式阶数;输出参数p为拟合生成的多项式的系数向量(长度为n+1),s为结构参数通过调用y=polyval(p,x)可以获得x处估计相应的多项式函数值y样条拟合函数>>help splines可快速查看函数列表使用这些函数拟合得到曲线函数sp以后,可利用fnval()计算任意自变量下的函数值[例18]:多项式的拟合》clc》clear》x=0:0.1:2*pi; %生成样本点x》y=sin(x)+0.5*rand(size(x)); %生成样本点y,通过随机矩阵 》p=polyfit(x,y,3) %拟合出多项式(3阶)》y1=polyval(p,x); %求多项式的值》plot(x,y,'+',x,y1,'-r') %绘制多项式曲线,以验证结果程序运行结果如图3-1所示:图3-1多项式拟合示例程序运行结果图微/积分y=exp(-0.5*t).*sin(t+pi/6) 已知函数y=f(x),在区间[a,b]内y对x的积分为梯形法数值积分:z=trapz(y):单位步长计算y的积分,否则需乘以步长 自适应simpson法数值积分:quad()q=quad(@fun,a,b)q=quad(@fun,a,b,tol)q=quad(@fun,a,b,tol,trace,p1,p2,…)输入:fun为被积函数,表达式必须使用点运算符(.*、./ 和.^)以支持向量;a,b即积分上下限;tol绝对误差限(默认1.e-6);p1,p2…直接传递给函数fun的已知参数输出:q积分结果自适应Lobatto法数值积分:quadl()使用方法同上[例42] 对进行数值积分。
MATLAB Simulink用法
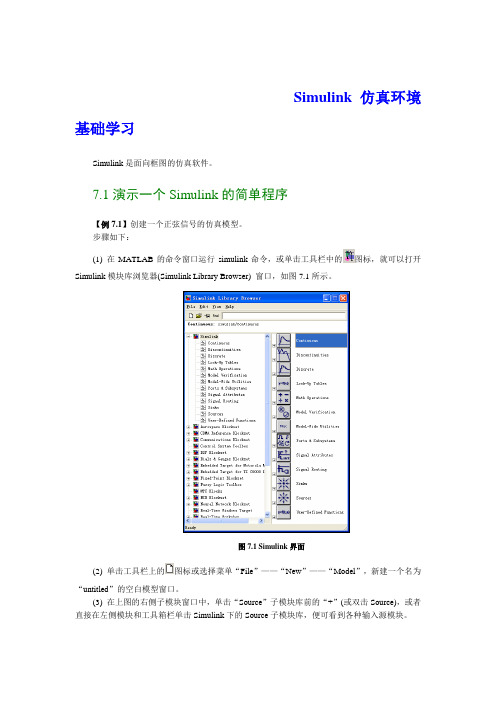
Simulink仿真环境基础学习Simulink是面向框图的仿真软件。
7.1演示一个Simulink的简单程序【例7.1】创建一个正弦信号的仿真模型。
步骤如下:(1) 在MATLAB的命令窗口运行simulink 命令,或单击工具栏中的图标,就可以打开Simulink模块库浏览器(Simulink Library Browser) 窗口,如图7.1所示。
图7.1 Simulink界面(2) 单击工具栏上的图标或选择菜单“File”——“New”——“Model”,新建一个名为“untitled”的空白模型窗口。
(3) 在上图的右侧子模块窗口中,单击“Source”子模块库前的“+”(或双击Source),或者直接在左侧模块和工具箱栏单击Simulink下的Source子模块库,便可看到各种输入源模块。
(4) 用鼠标单击所需要的输入信号源模块“Sine Wave”(正弦信号),将其拖放到的空白模型窗口“untitled”,则“Sine Wave”模块就被添加到untitled窗口;也可以用鼠标选中“Sine Wave”模块,单击鼠标右键,在快捷菜单中选择“add to 'untitled'”命令,就可以将“Sine Wave”模块添加到untitled窗口,如图7.2所示。
(5) 用同样的方法打开接收模块库“Sinks”,选择其中的“Scope”模块(示波器)拖放到“untitled”窗口中。
(6) 在“untitled”窗口中,用鼠标指向“Sine Wave”右侧的输出端,当光标变为十字符时,按住鼠标拖向“Scope”模块的输入端,松开鼠标按键,就完成了两个模块间的信号线连接,一个简单模型已经建成。
如图7.3所示。
(7) 开始仿真,单击“untitled”模型窗口中“开始仿真”图标,或者选择菜单“Simulink”——“Start”,则仿真开始。
双击“Scope”模块出现示波器显示屏,可以看到黄色的正弦波形。
simulink matlab教程

第7章Simulink仿真环境Simulink是面向框图的仿真软件。
7.1演示一个Simulink的简单程序【例7.1】创建一个正弦信号的仿真模型。
步骤如下:(1) 在MATLAB的命令窗口运行simulink命令,或单击工具栏中的图标,就可以打开Simulink模块库浏览器(Simulink Library Browser) 窗口,如图7.1所示。
图7.1 Simulink界面(2) 单击工具栏上的图标或选择菜单“File”——“New”——“Model”,新建一个名为“untitled”的空白模型窗口。
(3) 在上图的右侧子模块窗口中,单击“Source”子模块库前的“+”(或双击Source),或者直接在左侧模块和工具箱栏单击Simulink下的Source子模块库,便可看到各种输入源模块。
(4) 用鼠标单击所需要的输入信号源模块“Sine Wave”(正弦信号),将其拖放到的空白模型窗口“untitled”,则“Sine Wave”模块就被添加到untitled窗口;也可以用鼠标选中“Sine Wave”模块,单击鼠标右键,在快捷菜单中选择“add to 'untitled'”命令,就可以将“Sine Wave”模块添加到untitled窗口,如图7.2所示。
图7.2 Simulink界面(5) 用同样的方法打开接收模块库“Sinks”,选择其中的“Scope”模块(示波器)拖放到“untitled”窗口中。
(6) 在“untitled”窗口中,用鼠标指向“Sine Wave”右侧的输出端,当光标变为十字符时,按住鼠标拖向“Scope”模块的输入端,松开鼠标按键,就完成了两个模块间的信号线连接,一个简单模型已经建成。
如图7.3所示。
(7) 开始仿真,单击“untitled”模型窗口中“开始仿真”图标,或者选择菜单“Simulink”——“Start”,则仿真开始。
双击“Scope”模块出现示波器显示屏,可以看到黄色的正弦波形。
Simulink与控制系统仿真第二版课程设计 (2)

MATLAB/Simulink与控制系统仿真第二版课程设计1. 简介本文档旨在介绍MATLAB/Simulink与控制系统仿真第二版课程的设计方案和实现过程。
该课程旨在通过对MATLAB/Simulink软件的学习,并运用其进行控制系统仿真,增强学生对控制系统的理解和应用能力。
2. 课程设计目标•掌握MATLAB/Simulink软件的基本操作•学习控制系统的基础理论•能够设计和实现控制系统模型•运用仿真工具进行控制系统的仿真•分析仿真结果,评估控制系统性能3. 课程内容3.1 MATLAB/Simulink基础操作•MATLAB/Simulink软件介绍•基础命令和语法•变量、向量和矩阵的操作•函数和脚本编写•Simulink模型的创建和仿真3.2 控制系统基础理论•控制系统基本原理•系统建模方法•传递函数和状态空间模型•比例、积分、微分控制器•反馈控制系统的设计3.3 控制系统仿真•Simulink模型中添加控制器•控制器实现方法的比较,如PID控制器和LQR控制器•仿真分析和结果展示4. 课程设计方案4.1 课程形式该课程采用理论讲解、实例演示和实验练习相结合的方式进行。
4.2 课程设置•第一周:MATLAB/Simulink软件介绍及基础操作•第二周:控制系统基础理论讲解•第三周:传递函数和状态空间模型的建立•第四周:控制器实现方法的比较•第五周:控制系统仿真实验•第六周:实验结果分析和总结4.3 实验设置使用Simulink对以下两个控制系统进行建模并进行仿真实验。
•倒立摆控制系统:实现倒立摆稳定控制•直流电机控制系统:实现转速控制和位置控制4.4 实验步骤实验1:倒立摆控制系统1.建立倒立摆的系统模型2.设计控制器,实现倒立摆的稳定控制3.仿真运行,记录并分析仿真结果实验2:直流电机控制系统1.建立直流电机的系统模型2.设计转速控制器,实现直流电机的转速控制3.设计位置控制器,实现直流电机的位置控制4.仿真运行,记录并分析仿真结果5. 结论通过本次课程设计,学生能掌握MATLAB/Simulink软件的基本操作,以及控制系统的基础理论,学习如何建立控制器,如何运用Simulink进行控制系统仿真,了解仿真结果的分析和评估,提高了学生的控制系统理论知识和工程应用能力。
最新MATLAB-SIMULINK讲解完整版教学讲义PPT

第3章 SIMULINK应用基础
具体到电力系统仿真而言,原来的MATLAB编程仿真 是在文本命令窗口中进行的,编制的程序是一行行的命令和 MATLAB函数,不直观也难以与实际电力模型建立形象的 联系。在SIMULINK环境中,电力系统元器件的模型都用框 图来表达,框图之间的连线表示了信号流动的方向。对用户 而言,只要熟悉了SIMULINK仿真平台的使用方法以及模型 库的内容,就可以使用鼠标和键盘绘制和组织系统模型,并 实现系统的仿真,完全不必从头设计模型函数或死记那些复 杂的函数。
MATLAB-SIMULINK讲解完整 版
第3章 SIMULINK应用基础
3.1 SIMULINK仿真环境
SIMULINK是MATLAB的一个分支产品,主要用来实现 对工程问题的模型化及动态仿真。SIMULINK体现了模块化 设计和系统级仿真的思想,采用模块组合的方法使用户能够 快速、准确地创建动态系统的计算机模型,使得建模仿真如 同搭积木一样简单。SIMULINK现已成为仿真领域首选的计 算机环境。
适的位置,松开鼠标按键; 方法 2:选中模块,使用[Edit>Copy]及[Edit>Paste]命令
第3章 SIMULINK应用基础
单击模块,拖曳模块到合适的位置,松开鼠标按键
方法 1:选中模块,选择菜单命令[Format>Rotate Block], 模块顺时针旋转 90°;选择菜单命令[Format>Flip Block],
模块顺时针旋转 180°; 方法 2:右键单击目标模块,在弹出的快捷菜单中进行与
方法 1 同样的菜单项选择 方法 1:先按住“Ctrl”键,再单击模块,拖曳模块到合
SIMULINK 仿真平台窗
口中 可对多个模块同时进
matlab2021asimulink飞机纵向飞行示例讲解

matlab2021asimulink飞机纵向飞行示例讲解摘要:一、Matlab 2021a 简介二、Simulink 简介三、飞机纵向飞行模型搭建四、模型参数设置与仿真五、结果分析与讨论六、总结与展望正文:Matlab 2021a 是一款数学计算软件,功能强大,广泛应用于科学计算、工程仿真等领域。
在本篇文章中,我们将重点介绍如何使用Matlab 2021a 及其Simulink 工具箱搭建一个飞机纵向飞行模型,并进行仿真分析。
首先,我们对Matlab 2021a 和Simulink 进行简要介绍。
Matlab 2021a 提供了丰富的内置函数和工具箱,可以方便地进行数学计算、数据处理和算法设计。
Simulink 是一款基于图形的仿真工具,可以用于模拟和分析动态系统。
通过Simulink,用户可以轻松构建复杂的系统模型,并进行参数调整和性能分析。
接下来,我们构建一个飞机纵向飞行模型。
飞机纵向飞行模型主要包括动力学部分、气动部分和控制部分。
动力学部分主要包括质量、速度、加速度等变量;气动部分主要包括升力、阻力等;控制部分主要包括舵面控制等。
在Simulink 中,我们可以使用相应的模块来表示这些部分,然后用线连接起来,形成一个完整的飞机纵向飞行模型。
在模型搭建完成后,我们需要对模型参数进行设置。
这些参数包括飞机的质量、翼展、飞行速度等。
设置好参数后,我们可以使用Simulink 的仿真功能对模型进行仿真。
仿真过程中,我们可以观察飞机的纵向飞行状态,如速度、高度等,以便分析飞机的性能。
仿真完成后,我们需要对结果进行分析与讨论。
首先,我们可以观察仿真曲线,分析飞机在不同条件下的飞行性能。
其次,我们可以利用Matlab 2021a 的数据分析功能,对仿真结果进行进一步的处理,如求均值、标准差等。
最后,根据分析结果,我们可以对飞机纵向飞行模型进行优化和改进,以提高飞机的性能。
在总结与展望部分,我们可以总结本次飞机纵向飞行模型搭建与仿真的过程和成果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
董素君
新主楼 C-503
dsj@
思考题
进行下列计算,给出不使用for和while等循环语句的计算方法;
1.
k 2
i 0
63
i
>> sum(2.^[0:63]) ans = 1.8447e+019
2.求出y=x*sin(x) 在0<x<100的每个峰值,并绘制曲线
1.8 MATLAB在数值分析中的应用
多项式
使用降幂系数的行向量表示,如
4 3 2
》 p=[1 -12 0 25 116]
》 r=roots(p) x 12x 0 x 25x 116 r = 11.7473 多项式表示为:p=[1 -12 0 25 116] 2.7028 roots:求多项式等于0的根,根用列向量表示 -1.2251 + 1.4672i poly:已知多项式的根,构建相应多项式 -1.2251 - 1.4672i polyval(p,n):求多项式函数值 》p=poly(r) p= polyder(p):求多项式的微分多项式 1 -12 -0 25 116 >>polyval(p,5) ans = -634 >> pp=polyder(p) pp = 4 -36 0 25
x 12x 0 x 25x 116
4 3 2
1.8 MATLAB在数值分析中的应用
多项式
多项式的运算 [例14]:相乘conv 》a=[1 2 3] ; 》b=[1 2]; 》c=conv(a,b) c= 1 4 7 6 conv指令可以嵌套使用,如: 》conv(conv(a,b),c) ans = 1 8 30 68 97 84 36
输入:fun为被积函数,表达式必须使用点运算符(.*、./ 和.^)以 支持向量;a,b即积分上下限;tol绝对误差限(默认1.e-6); p1,p2…直接传递给函数fun的已知参数 输出:q积分结果 使用方法同上
自适应Lobatto法数值积分:quadl()
1.8 MATLAB在数值分析中的应用
1.8 MATLAB在数值分析中的应用
[例18]:多项式的拟合
》clc 》clear
》x=0:0.1:2*pi; %生成样本点x
》y=sin(x)+0.5*rand(size(x)); %生成样本点y,通过随机矩阵 》p=polyfit(x,y,3) %拟合出多项式(3阶) 》y1=polyval(p,x); %求多项式的值 》plot(x,y,'+',x,y1,'-r') %绘制多项式曲线,以验证结果 程序运行结果如图3-1所示: 图3-1多项式拟合示例程序运行结果图
设置对象属性值: set(h,’PropertyName’,’PropertyValue’),set(h), set(h,’PropertyName’)
获取当前的图形、坐标轴和对象 gcf:获取当前图形窗口句柄值
roots:求多项式等于0的根,根用列向量表示 poly:已知多项式的根,构建相应多项式 polyval(p,n):求多项式函数值 polyder(p):求多项式的微分多项式
》a=[1 2 3] ; 》polyval(a,2) ans = 11 》polyder(a) ans = 2 2
[例42] 对进行数值积分。
用梯形求积函数trapz()、自适应Simpson求积(低阶)函数quad()和 自适应Lobatto求积(高阶)函数quad了()进行计算。
注:被积函数func()的表达式必须是向量形式:
y=exp(-0.5*t).*sin(t+pi/6),式中t和y为向量,所以用到点乘符号“.*”。
get(figure), get(h,’PropertyName’)
>> get(0,'ScreenSize') ans = 1 1 1280 800 >> set(0,'Units','norm'); >> get(0,'ScreenSize') ans = 0 0 1 1 >> figure(‘Units’,‘norm’,… 'position',[0 0 1 1])
例15]:相除deconv 》[q,r]=deconv(c,b) q= 1 2 3 r= 0 0 0 0 q 为商多项式,r为余多项式
1.8 MATLAB在数值分析中的应用
插值
一维插值interp1()
yi=interp1(x,y,xi)
例exp2_16.m
yi=interp1(x,y,xi,’method’)
1.8 MATLAB在数值分析中的应用
多项式
使用降幂系数的行向量表示,如
x 12x 0 x 25x 116
4 3 2
Hale Waihona Puke 多项式表示为:p=[1 -12 0 25 116] 》 p=[1 -12 0 25 116] 》 r=roots(p) r= 11.7473 2.7028 -1.2251 + 1.4672i -1.2251 - 1.4672i 》p=poly(r) p= 1 -12 -0 25 116
1.8 MATLAB在数值分析中的应用
多项式
使用降幂系数的行向量表示,如
求极值: >> p=[1,-12,0,25,116]; 多项式表示为:p=[1 -12 0 25 116] x=[0:1:10]; roots:求多项式等于0的根,根用列向量表示 y=polyval(p,x); poly:已知多项式的根,构建相应多项式 plot(x,y) polyval(p,n):求多项式函数值 hold on polyder(p):求多项式的微分多项式 grid pp=polyder(p) xx=roots(pp) yy=polyval(p,xx) plot(xx,yy,'ro')
制不同方法产生的曲线
》legend('sampled point','nearest','linear','spline','cubic')
exm19.m
1.8 MATLAB在数值分析中的应用
1.8 MATLAB在数值分析中的应用
拟合
最小二乘法多项式拟合函数
p=ployfit(x,y,n) 或 [p,s]=ployfit(x,y,n)
1.8 MATLAB在数值分析中的应用
梯形法数值积分: z=trapz(y)
自适应simpson法数值积分:quad() q=quad(@fun,a,b)
q=quad(@fun,a,b,tol)
q=quad(@fun,a,b,tol,trace,p1,p2,…)
y=exp(-0.5*t).*sin(t+pi/6)
二维插值zi=interp2(x,y,z,xi,yi,’method’) 三维插值vi=interp3(x,y,z,v,xi,yi,zi,’method’) 三次样条插值pp=spline(x,y),返回三次样条插值的分段多项式形式的向 量,以进行插值计算:yi=ppval(pp,xi)
1.8 MATLAB在数值分析中的应用
(x,y)为已知数据,n为多项式阶数;输出参数p为拟合生成 的多项式的系数向量(长度为n+1),s为结构参数
通过调用y=polyval(p,x)可以获得x处估计相应的多项式函数值y
样条拟合函数
>>help splines可快速查看函数列表 使用这些函数拟合得到曲线函数sp以后,可利用fnval()计算任意自 变量下的函数值
function xIntegration clear all clc % the interval: [a, b], the step: d a = 0; % 积分下限 b = 3*pi; % 积分上限 d = pi/1000; % 积分步长 t = a:d:b; y = func(t);
format long % 梯形数值积分 y_trapz = trapz(y) * d % 自适应Simpson法 y_quad = quad(@func,a,b) y_quadl = quadl(@func,a,b) disp('Results:') disp(' Trapz Qquad Quadl') disp([y_trapz,y_quad,y_quadl]) function y = func(t) y = exp(-0.5*t) .* sin(t+pi/6);
a = 0; % 积分下限 b = 3*pi; % 积分上限 d = pi/1000; % 积分步长
1.9 句柄图形系统
句柄图形对象
层次结构
创建:
Root,figure,axed,uicontrol,uimenu,uicontextmenu,uitoolbar,uibuttongroup ,uipanel
yi=interp1(x,y,xi,’method’,’extrap’) ‘method’用于指定插值算法,其值可以是: ‘nearest’——最近插值(执行速度最快,输出结果为直角转折) ‘linear’——线性插值(默认值,在样本点上斜率变化很大) ‘spline’——分段三次样条插值(最花时间,输出结果最平滑) ‘cubic’, ‘pchip’——分段三次Hermite插值(最占内存,输出结 果与spline差不多)
