使用ABAQUS计算应力强度因子
ABAQUS在反复加载卸载应力应变计算说明

ABAQUS 反复加载卸载应力应变计算说明1、 塑性模型采用Armstrong and Frederick model (AF 模型)[1] (1) 屈服准则(Mises 屈服)屈服函数为2)~~(:)~~(23Y s s F ---=αα 式中:s ~为应力偏量,α~为总背应力,Y 为屈服极限 (2) 流动准则(the associated flow rule )σλε~~∂∂=Fp 式中:pε~为塑性应变对时间的微分,λ 为待定量[2],σ~为应力张量 (3) 硬化准则<1> p h i i p i i )()()()(~~32~αζεα-= 式中:)(~i α为背应力分量对时间的微分;)(i h ,)(i ζ为材料常数为已知量,p 为等效塑性应变对时间的微分。
<2> )1()(1)(0pMi i i e r Y Y ζ-=-+=∑式中:Y 为对应于等效塑性应变p 的屈服极限,0Y 为初始屈服极限为已知量,)(i r 为材料常数为已知量。
2、 反复加载卸载应力应变计算过程说明假设在受载前,物体的初始应力、应变以及背应力均为零2.1加载过程计算<1> 外力不足以使得物体中的任何一点的Mises 应力值大于屈服极限此时:塑性应变、背应力均保持为零,屈服极限保持不变。
应力由e e D εσ~:~~~=计算,总应变值等于弹性应变。
<2> 外力使得物体中的任何一点的Mises 应力值大于屈服极限为了说明ABAQUS 是如何确定应变增量1~+∆n ε,有必要对ABAQUS 求解材料非线性问题进行简单介绍[3]。
ABAQUS 首先将载荷分为若干个微小增量,如图1所示。
当结构收到一个微小增量P ∆时,ABAQUS 用与初始结构位移相对应的初始刚度矩阵K 和载荷增量P ∆计算出结构在这一增量后的位移修正a c 、修正后的位移值a u 和相应的新的刚度矩阵a K 。
使用ABAQUS计算应力强度因子

使用ABAQUS计算应力强度因子应力强度因子(Stress Intensity Factor,简称SIF)是应力场的一种特征参数,用于描述应力状态下混合模式断裂的倾向性。
它在断裂力学和疲劳断裂力学中起着非常重要的作用。
在ABAQUS软件中,可以通过线性弹性断裂力学方法来计算应力强度因子。
ABAQUS中计算SIF的方法通常分为两步:1.求解应力场2.计算SIF在求解应力场时,可以采用以下几种途径:1.固定边界条件:如果边界条件已知并且不会发生变化,则可以直接固定边界条件来求解应力场。
这种方法适用于简单的几何形状和加载情况。
2.施加约束:对于复杂几何形状和加载情况,可以施加约束来求解应力场。
例如,可以在加载边界上施加位移或力,并在其他边界上施加自由边界条件。
ABAQUS软件将通过求解线性弹性方程来获得应力场。
3.等效边界法:对于无法通过上述两种方法求解应力场的情况,可以采用等效边界法。
该方法将复杂几何体简化为等效的几何体,通过在等效边界上施加约束来求解应力场。
然后,可以使用所得的应力场计算SIF。
在计算SIF时,可以采用两种方法:1.J积分方法:这是一种基于应变能的方法,通过计算闭合路径上的应力和应变来计算SIF。
ABAQUS提供了J积分的计算方法,可以直接计算SIF。
2.基于位移法:这是一种基于位移的方法,通过计算表面位移场的奇异性来计算SIF。
ABAQUS也提供了这种方法的计算选项。
计算SIF的步骤一般如下:1.定义几何模型和输入材料参数。
2.设置边界条件和加载条件。
3.运行ABAQUS求解应力场。
4.运行相应的计算器(如J计算器或位移计算器)以计算SIF。
5.根据得到的SIF结果进行进一步的断裂力学分析。
需要注意的是,计算SIF是一个相对复杂的过程,需要对模型几何形状、边界条件、加载条件和材料参数等进行仔细考虑和设置。
此外,模型的网格划分和数值求解的精度也会对计算结果产生影响,因此需要进行适当的验证和后处理分析。
abaqus 应力强度因子

应力强度因子是断裂力学中表征裂纹尖端应力应变场强度的一个极为重要的参数,用应力强度因子表达的脆断准则为KI=KIC,其中,KIC为材料的断裂韧度,KI是构件裂纹尖端的应力强度因子,由材料的尺寸、形状和所受的载荷形式确定。
在ABAQUS中,可以通过解析法、数值解法和实验标定法等求取应力强度因子。
其中,解析法主要适用于裂纹尺寸较小的情况,数值解法适用于裂纹尺寸较大的情况,实验标定法则需要实际的试验数据。
在ABAQUS中,可以使用多种方法计算应力强度因子。
一种常见的方法是通过设置裂纹尖端的网格密度和形状来控制应力强度因子的求解精度。
另外,还可以通过扩展有限元方法(XFEM)来模拟裂纹的扩展过程,并计算应力强度因子。
此外,也可以通过定义损伤起始的判据、损伤演化规律、损伤稳定性控制等相关参数来实现裂纹扩展,并计算应力强度因子。
总之,ABAQUS是一个强大的有限元分析软件,可以通过多种方法计算应力强度因子,为断裂力学的分析和研究提供了有力的支持。
含圆孔和裂纹板应力强度因子分析

《断裂力学》大作业题目:含圆孔和裂纹板应力强度因子分析姓名:学号:专业:授课教师:一、问题描述含多裂纹矩形板受垂直方向拉伸载荷作用,如图 1 所示,计算中心裂纹尖端的应力强度因子KⅠ和KⅡ,并讨论其随即和参数L、h、a、D、 等的变化规律,写一篇分析报告。
图1. 含三条裂纹矩形板受垂直拉伸载荷作用要求(1)报告中计算所用到的分析方法和模型应阐述清楚,并写出必要的计算公式。
(2)绘制应力强度因子随几何参数的变化曲线。
(3)列出必要的参考文献二、理论分析在线弹性断裂力学中,I型裂纹尖端的应力场为:(1sin sin)222(1sin sin)222cos cos222333xyxyσστθθθθθθθθθ⎧=-⎪⎪⎪=+⎨⎪⎪=⎪⎩I型裂纹尖端的位移场为:1)cos(1cos)221)sin sin2233uvκκθθθθ⎧=--⎪⎪⎨⎪=+⎪⎩其中:3431νκνν-⎧⎪=⎨-⎪+⎩平面应变平面应力同理,对II型裂纹尖端的应力场:(2cos cos)222cos sin cos222(1sin sin)222333xyxyσστθθθθθθθθθ⎧=+⎪⎪⎪=⎨⎪⎪=-⎪⎩显然,位移场和应力场均可以表示成应力强度因子的形式。
通过对裂纹尖端的应力应变场分析来求解对应的应力强度因子,便是传统有限元求解应力强度因子的原理。
而对于I、II复合型裂纹尖端的应力强度因子,可通过它们的叠加获得。
确定应力强度因子的方法有3大类:解析法、数值解法和实验方法。
解析法只能计算简单问题,大多数问题需要采用数值解法,当前工程中广泛采用的数值解法是有限单元法。
随着有限元法的发展,有限元在断裂力学中的应用越来越普及。
近年来,计算机技术得到了迅猛发展,许多功能强大的有限元软件也相继问世,大型通用有限元程序abaqus就是当前工程中应用最广泛的有限元软件之一。
采用abaqus软件计算裂纹尖端的应力强度因子,通过阅读abaqus 的帮助文件,得到abaqus基于有限元方法在线弹性范围内计算应力强度因子的原理。
Abaqus 齿轮力和应力计算

Ken Youssefi
Mechanical Engineering Dept.
14
Surface Strength Analysis
The basic surface deterioration Scoring
If the surface asperity welding and tearing cause a transfer of metal from one surface to the other, the resulting surface damage is called scoring. If the local welding of asperities becomes so extensive that the surfaces no longer slide on each other, the resulting failure is called seizure. Initial scoring on 4340 steel helical gear Moderate scoring on a 3310 steel spur gear.
Wt
F
Substituting for x and introducing p (circular pitch),
The form factor y is called Lewis form factor. Substituting P = / p and Y = y
Lewis’ equation, where
Ken Youssefi Mechanical Engineering Dept.
6
Modification of Lewis’ Equation
Assumptions made in deriving Lewis’ equation
ABAQUS中应力、应变详解

ABAQUS中应力、应变详解
真实应力、名义应力、真实应变、名义应变的关系
名义应变,又称相对应变或工程应变、适用于小应变分析。
名义应变又可分线应变和切应变。
真实应变,又称对数应变;假设物体内两质点相距为L0, 经变形后距离为 Ln, 则相对线应变为
ε = (Ln-L0)/L0 ,这种相对线应变一般用于小应变情况。
而在实际变形过程中,长度L0系经过无穷多个中间的数值变成L, 如L0,L1,L2,L3 …… Ln-1,Ln, 其中相邻两长度相差均极微小,由 L0-Ln 的总的变形程度,可以近似地看作是各个阶段相对应变之和,
大多数实验数据常常是用名义应力和名义应变值给出的,所以我们应将其转换为真实应力和真实应变。
其转换公式如下:
塑性分析中的注意问题:对于大应变,真实应变和名义应变之间的差值就会很大,所以在给abaqus提供应力-应变数据时,一定要注意正确的给予赋值,在小应变的情况下,真实应变和名义应变之间的差别很小,不是很重要。
几何非线性开关打开时,ABAQUS中可输出LE(真实应变)、EE (弹性应变)、NE(名义应变)等
几何非线性开关关闭时,ABAQUS中可输出E(真实应变)、EE (弹性应变)等。
Ⅰ-Ⅱ复合型裂缝应力强度因子和应变能释放率的关系

Ⅰ-Ⅱ复合型裂缝应力强度因子和应变能释放率的关系刘梦和;王向东;邵兵【摘要】为了探究复合型裂缝的应力强度因子K和应变能释放率G的关系,基于最大应力准则,采用能量法对Ⅰ-Ⅱ复合型裂缝的扩展进行理论分析.根据单一型裂缝应力强度因子和应变能释放率的关系,推导出Ⅰ-Ⅱ复合型裂缝K与G的关系公式,利用Abaqus软件建立Ⅰ-Ⅱ复合型裂缝的有限元模型,计算Ⅰ-Ⅱ复合型裂缝的应力强度因子和应变能释放率,与推导公式的计算结果进行对比,二者误差仅为2.5%,验证了推导公式的合理性.%In order to study the relationship between stress intensity factor and strain energy release rate of mixed mode cracks, the growth of I-II mixed mode cracks is theoretically analyzed by means of the energy method based on the maximum stress criterion. A formula for the relationship between the stress intensity factor and the strain energy release rate of the I-II mixed mode cracks is deduced according to the available relationship between the stress intensity factor and the strain energy release rate of single mode crack. A FEM model for the I-II mixed mode cracks is established by use of the software ABAQUS. It is employed to calculate the stress intensity factor and strain energy release rate of the I-II mixed mode cracks. The model results are compared with those calculated by the deduced formula. The error is only 2. 5% , and the rationality of the proposed formula is validated.【期刊名称】《水利水电科技进展》【年(卷),期】2012(032)006【总页数】3页(P31-33)【关键词】Ⅰ-Ⅱ复合型裂缝;最大应力准则;应力强度因子;应变能释放率【作者】刘梦和;王向东;邵兵【作者单位】河海大学力学与材料学院,江苏南京210098;河海大学力学与材料学院,江苏南京210098;河海大学力学与材料学院,江苏南京210098【正文语种】中文【中图分类】TV313断裂力学是以含裂缝构件为研究对象,分析在各种外界因素(荷载、腐蚀和温变等)作用下裂缝稳定扩展或失稳扩展的规律,研究含裂缝构件安全性的学科[1]。
如何使用ABAQUS计算应力强度因子

如何使用ABAQUS计算应力强度因子ABAQUS是一种广泛使用的有限元分析软件,可用于计算应力强度因子。
应力强度因子用于评估材料中的裂纹扩展性能,是断裂力学中的重要参数。
以下是使用ABAQUS计算应力强度因子的一般步骤:1.准备模型:在使用ABAQUS计算应力强度因子之前,需要先准备好模型。
模型应包含有裂纹的几何形状,以及材料的属性。
2.确定边界条件:要使用ABAQUS计算应力强度因子,必须指定适当的边界条件。
这些条件可以是约束的位移或力。
3.定义材料特性:为了计算应力强度因子,需要定义材料的特性,如弹性模量和泊松比。
这些特性通常可以从实验数据中获取。
4.创建网格:在使用ABAQUS计算应力强度因子之前,需要对模型进行离散化处理,将其划分为有限个单元。
这可以通过使用ABAQUS提供的网格生成工具来完成。
5.应用载荷:定义适当的载荷类型和大小,以便在模型上施加负载。
这可以是施加在边界上的力或位移。
6.定义裂纹:使用ABAQUS的初始裂纹命令或裂纹离散化工具来创建裂纹几何。
裂纹可以是直线裂纹,也可以是不规则或曲线裂纹。
7.定义断裂准则:使用ABAQUS的断裂准则定义工具,指定在何种条件下认为破坏发生。
常用的断裂准则包括应力强度因子法和能量释放率法。
8.运行ABAQUS求解器:在定义了模型、边界条件、材料特性、网格和载荷之后,可以运行ABAQUS求解器。
根据模型的复杂程度,可能需要较长的计算时间。
9.后处理结果:一旦ABAQUS求解器完成计算,可以使用ABAQUS提供的后处理工具来分析结果。
这些工具可以用于计算应力强度因子及其分布。
10.计算应力强度因子:通过使用ABAQUS的应力强度因子计算工具,可以计算裂纹尖端处的应力强度因子。
这些结果可以用来预测裂纹的扩展和破坏行为。
应力强度因子的数值计算方法

应力强度因子的数值计算方法一、引言数值计算方法通过将裂纹尖端的应力场分布模拟为一个虚拟的数学模型,利用计算机进行数值求解来得到应力强度因子的数值。
数值计算方法通常分为两种类型:直接方法和间接方法。
1.直接方法直接方法是指直接通过有限元分析软件求解裂纹尖端的应力场分布,并通过一些后处理技术来计算应力强度因子。
其中最常用的方法是J积分法和节点法。
(1)J积分法:J积分法是一种常用的裂纹应力强度因子计算方法,它通过在裂纹尖端附近引入一个虚拟断裂面,将裂纹尖端附近的应力场分布(由有限元分析得到)转化为裂纹尖端处的应力强度因子。
具体计算方法较为复杂,一般需要通过数值积分的方法求解。
(2)节点法:节点法是一种基于有限元网格节点的方法,其基本思想是通过增加节点对裂纹尖端附近的应力场进行离散,利用节点处的应力场计算应力强度因子。
节点法相对于J积分法计算简单,但适用条件较为有限。
2.间接方法间接方法是指通过已知应力场的变化率来计算应力强度因子的方法。
常用的间接方法有格里菲斯准则法、欠奇性法和EOS法。
(1)格里菲斯准则法:格里菲斯准则法是最早提出的计算裂纹扩展的方法之一,基于弹性力学理论和线弹性断裂力学基本假设,通过对裂纹尖端周围应力场的分析,得到应力强度因子与裂纹尖端形状和尺寸以及应力场的关系。
(2)欠奇性法:欠奇性法是一种基于能量原理的裂纹尖端应力强度因子计算方法,通过构造合适的应变能表达式和裂纹尖端应力强度因子的定义,利用应变能的分式展开求解裂纹尖端处的应力强度因子。
(3)EOS法:EOS法是一种在裂纹尖端周围选取合适的控制体,通过求解控制体内外表面的应力分布,建立应力强度因子与表面应力之间的关系,从而计算裂纹尖端处的应力强度因子。
三、应用场景1.断裂力学:数值计算方法可以用于预测和分析裂纹扩展行为,在断裂力学领域中有着重要的应用。
通过计算裂纹尖端的应力强度因子,可以评估材料的断裂韧性和脆性。
2.疲劳分析:3.材料破坏:数值计算方法可以用于分析材料的破坏机理和破坏行为。
基于ABAQUS的两种应力强度因子计算方法对比

21
50.363 2
5
282.285 291 2
25
1 411.426 456
22
49.705
5.25
285.476 037 7
27.562 5
1 498.749 198
23
49.082 3
5.5
288.533 458 1
30.25
1 586.934 019
24
48.524 8
5.75
291.667 209 7
5.062 5
740.943 363 2
11
74.684 7
2.5
295.999 907 7
6.25
739.999 769 2
12
65.193 5
2.75
270.994 561 2
7.562 5
745.235 043 2
13
59.114 6
3
256.652 390 1
9
769.957 170 4
14
,则其截距
2 ABAQUS中两种SIF计算方法的实 现[5-=]
2.1 ABAQUS内置方法计算SIF
ABAQUS 中建立半宽,=100 ??,半高-=200 mm,
厚度1 mm的平板模型( 2),该平板中心预制有一
条裂纹,其半裂纹长度 20 mm; 弹性模量 2!
105MPa,泊松 0.25的“弹性各向异性”固体材料;
31
K FACTOR ESTIMATES
CRACK CRACKFRONT
CONTOURS
(平均:75%)
NAME
NODE SET
+1.054e+03
应力强度因子的数值计算方法

应力强度因子的数值计算方法应力强度因子是用来描述裂纹尖端应力场的重要参数,它在研究裂纹扩展、断裂行为等问题中具有重要的应用价值。
本文将介绍应力强度因子的数值计算方法,包括解析方法和数值方法。
一、解析方法解析方法是指通过求解弹性力学方程,得到应力场的解析表达式,进而计算应力强度因子。
常见的解析方法有:1. 爱尔兰函数法:该方法适用于轴对称问题,通过引入爱尔兰函数,将弹性力学方程转化为常微分方程,进而得到应力强度因子的解析表达式。
2. 奇异积分法:该方法适用于不规则裂纹形状或复杂载荷情况。
通过奇异积分的性质,将应力场分解为奇异和非奇异两部分,进而得到应力强度因子的解析表达式。
3. 线性弹性断裂力学方法:该方法通过建立合适的应力强度因子与裂纹尺寸之间的关系,利用裂纹尖端应力场的奇异性,通过分析弹性力学方程的边界条件,得到应力强度因子的解析表达式。
二、数值方法数值方法是指通过数值计算的方式,求解弹性力学方程,得到应力场的数值解,从而计算应力强度因子。
常见的数值方法有:1. 有限元法:有限元法是一种广泛应用的数值方法,通过将结构离散为有限个单元,建立节点间的关系,利用数值方法求解离散方程组,得到应力场的数值解,进而计算应力强度因子。
2. 边界元法:边界元法是一种基于边界积分方程的数值方法,通过将边界上的应力场表示为边界积分方程的形式,利用数值方法对积分方程进行离散求解,得到应力场的数值解,进而计算应力强度因子。
3. 区域积分法:区域积分法是一种基于区域积分方程的数值方法,通过将应力场表示为积分方程的形式,利用数值方法对积分方程进行离散求解,得到应力场的数值解,进而计算应力强度因子。
以上介绍了应力强度因子的数值计算方法,包括解析方法和数值方法。
解析方法适用于问题简单、载荷条件规则的情况,可以得到解析表达式并具有较高的精度;数值方法适用于问题复杂、载荷条件不规则的情况,通过数值计算可以得到应力场的数值解,并利用数值解计算应力强度因子。
ABAQUS计算J积分细节
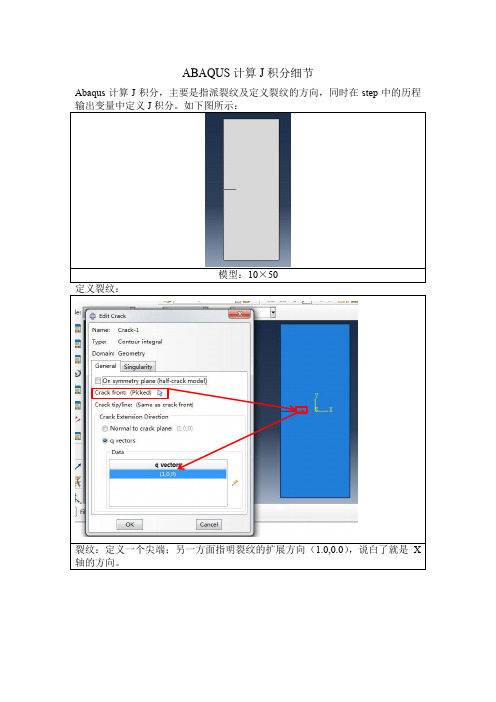
ABAQUS计算J积分细节Abaqus计算J积分,主要是指派裂纹及定义裂纹的方向,同时在step中的历程模型:10×50裂纹:定义一个尖端;另一方面指明裂纹的扩展方向(1.0,0.0),说白了就是X积分数值,图中输入10,则输出10个J积分值计算包含裂纹尖端的包络区域的面积即为J积分避开裂纹尖端塑形区域的不可计算的特性。
同时J积分的计算数值与积分路径无从以上图例可以看出J积分数值区域稳定。
疑问:为何计算多个积分点,是否最后的稳定数值就是需要计算的J积分数值?J积分应该是数值,而不是多个不同的数值。
我个人觉得最后的稳定数值应该是需要计算的积分数值。
从dat文件到inp文件,找到积分区域。
pickseted12以及pickseted13都是节点4,坐标如图所示,在cad模型中的位置如箭头指向,即裂纹尖端。
详细的需要看一下abaqus帮助文档,关于J积分的计算细节。
积分点的个数的意义我还没有搞清楚。
对于应力强度因子K,表征裂纹尖端受力的一个参量,在裂纹尖端的应力场的一定范围内,不同的节点计算数值大体是相同的。
计算应力强度因子:可以利用abaqus直接输出,也可以利用公式计算应力强度因子,以下为利用有限元法计算应力强度因子:计算应力强度因子:从上图可以看出,计算应力强度应力的点与计算J积分的点是一致的。
Abaqus计算的应力强度因子为裂尖处的应力强度因子。
下面我们利用有限元法计算y=0处的应力强度因子,最后外推到裂尖处的应力强度因子。
选取不同的半Abaqus计算J积分注意事项:(1)一、Interaction模块1.1 预制裂纹(步骤:菜单/special/crack/assign seam)注意:并不是作裂纹分析都要定义seam,如果你的裂纹不是一条缝,而是一个缺口,则不需要assign seam,直接走下一步(定义裂纹)就行。
1.2 创建裂纹(步骤:菜单/special/crack/create,type:contour integral)—crack front:crack front是用来定义第一围线积分的区域,2D下我们可以选择包围裂尖点的面,3D则选择包围裂尖线的面;另外还有一种定义crack front的方法,就是直接选择裂尖点(2D)或裂尖线3D),用这个方法定义crack front不需要再定义下一步的crack tip/line,比较简便,两种方法算出的结果没有明显的差别,其实只是影响积分路线的问题,但是J积分值是路径无关的,看个人喜好吧—crack tip/line:这个比较好理解就是裂尖点(2D)或线(3D),如果我们在上一步中用方法二定义crack front,这一步就直接跳过了—crack extension direction(定义裂纹扩展方向):这里定义的其实是一个虚拟的裂纹扩展方向,定义了这个参考方向后,我们才能通过输出的角度判断裂纹扩展方向,可以通过两种方法:(1)q vector:输入一个方向,用来作为计算裂纹的扩展方向的参考方向;(2)normal to crack plane:crack plane表示裂纹的对称面(当裂纹在一个平面内时,可能需要分开定义多个裂纹),这种方法下我们只需定义裂纹面的法线方向,通过(t表示裂纹尖端的切线), 会在每个节点得出一个q方向;(3)注意:q的方向对输出的应力强度因子,J积分等都会有影响,一般情况下,q最好在裂纹平面内,且垂直于裂尖线的切线,否则算出的应力强度因子,J积分值等等在不同围线积分中会差别较大。
使用ABAQUS计算应力强度因子

------------------------------------------------------------------------------------------------------- 如何使用ABAQUS计算应力强度因子Simwefanhj(fanhjhj@)2011.9.9------------------------------------------------------------------------------------------------------- 问题描述:以无限大平板含有一贯穿裂纹为例,裂纹长度为10mm(2a),在远场受双向均布拉应力σ=100N/mm2。
按解析解,此I型裂纹计算出的应力=396.23(N.mm-3/2)强度因子πσaK=I以下为使用ABAQUS6.10的计算该问题的过程。
第一步:进入part模块①建立平板part(2D Planar;Deformation;shell),平板的尺寸相对于裂纹足够大,本例的尺寸为100×50(mm)。
②使用Partation Face:sketch工具,将part分隔成如图1形式。
图1第二步:进入property模块①建立弹性材料;②截面选择平面问题的solid,homogeneous;③赋予截面。
第三步:进入Assembly模块不详述。
需注意的是:实体的类型(instance type)选择independent。
第四步:进入mesh模块除小圈内使用CPS6单元外,其它位置使用CPS8单元离散(图2)。
裂纹尖端的奇异在interaction模块中(图4)考虑。
图2第五步:进入interaction模块①指定裂纹special/creak/assign seam,选中示意图3中的黄色线,done!②生成裂纹crack 1,special/crack/create,name:crack 1,type: contour integral.当提示选择裂纹前端时,选则示意图的红圈区域,当提示裂纹尖端区域时选择红圈的圆心,用向量q表示裂纹扩展方向(示意图3绿色箭头)。
ABAQUS计算J积分细节
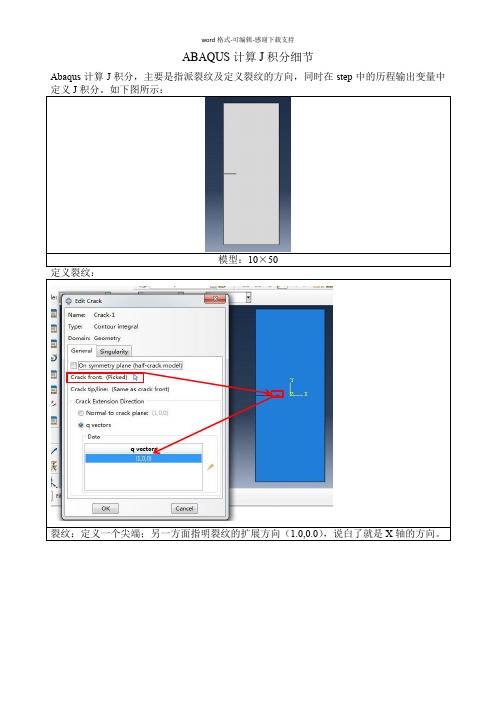
ABAQUS计算J积分细节Abaqus计算J积分,主要是指派裂纹及定义裂纹的方向,同时在step中的历程输出变量中定义J积分。
如下图所示:模型:10×50定义裂纹:裂纹:定义一个尖端;另一方面指明裂纹的扩展方向(1.0,0.0),说白了就是X轴的方向。
Step中输出裂纹参量:积分数值,图中输入10,则输出10个J积分值J积分的理解:计算包含裂纹尖端的包络区域的面积即为J积分尖端塑形区域的不可计算的特性。
同时J积分的计算数值与积分路径无关。
以下为六个计算从以上图例可以看出J积分数值区域稳定。
疑问:为何计算多个积分点,是否最后的稳定数值就是需要计算的J积分数值?J积分应该是数值,而不是多个不同的数值。
我个人觉得最后的稳定数值应该是需要计算的积分数值。
从dat文件到inp文件,找到积分区域。
pickseted12以及pickseted13都是节点4,坐标如图所示,在cad模型中的位置如箭头指向,即裂纹尖端。
详细的需要看一下abaqus帮助文档,关于J积分的计算细节。
积分点的个数的意义我还没有搞清楚。
对于应力强度因子K,表征裂纹尖端受力的一个参量,在裂纹尖端的应力场的一定范围内,不同的节点计算数值大体是相同的。
计算应力强度因子:可以利用abaqus直接输出,也可以利用公式计算应力强度因子,以下为利用有限元法计算应力强度因子:计算应力强度因子:从上图可以看出,计算应力强度应力的点与计算J积分的点是一致的。
Abaqus计算的应力强度因子为裂尖处的应力强度因子。
下面我们利用有限元法计算y=0处的应力强度因子,最后外推到裂尖处的应力强度因子。
选取不同的半径r值计算得到的应力Abaqus计算J积分注意事项:(1)一、Interaction模块(2) 1.1 预制裂纹(步骤:菜单/special/crack/assign seam)(3)注意:并不是作裂纹分析都要定义seam,如果你的裂纹不是一条缝,而是一个缺口,则不需要assign seam,直接走下一步(定义裂纹)就行。
ABAQUS中分析裂纹问题常用方法概述

ABAQUS中分析裂纹问题常用方法概述
1、用定义seam的方法来预设裂纹扩展路径,随着载荷的施加,裂纹会沿seam扩展。
这种方法可以模拟裂纹尖端的奇异性(通过在ABAQUS中设置实现),能很方便的计算出应力强度因子、J积分等断裂参量。
2、用debond命令实现裂纹开裂,为了观察开裂需要在指定的路径上定义一个集合,这种方法简单,但实际应用范围相当有限。
3、用cohesive单元,通过设置damage initiation和evolution 准则等相关参数实现裂纹问题的模拟,同时,ABAQUS提供了多种准则可供选择,后处理时通过dispaly group可以观察裂纹扩展。
此功能用途较广,而且通过在ABAQUS平台上开发实现多裂纹扩展的模拟。
4、在ABAQUS 6.9中推出的新功能XFEM(扩展有限元),利用XFEM能够很好的模拟裂纹的扩展,而无需用户提前定义扩展路径。
通过设置损伤起始的判据,损伤演化规律,损伤稳定性控制等相关参数实现裂纹扩展。
5、除此之外,对于裂纹问题,还可以通过二次开发、模型对称性、边界条件随分析步的改变等方式实现。
总之,ABAQUS处理裂纹问题的手段很多,功能也十分强大,若能获得较准确的相关材料数据,数值模拟的结果是很有参考价值的。
基于ABAQUS的复杂裂纹应力强度因子的研究

基于ABAQUS的复杂裂纹应力强度因子的研究摘要:在实际工程领域,裂纹问题一直都是一个影响结构安全性的难题。
本文从现实工程角度出发,针对复杂裂纹的断裂破坏机理,采用基于ABAQUS的数值模拟技术,进行了深入的研究。
为了证明采用数值模拟技术研究复杂裂纹的可靠性,本文首先利用ABAQUS对其他学者做出的理论值进行了验证,结果表明理论和数值具有高度的吻合性。
然后进行了复杂裂纹在不同情况下的裂尖应力强度因子进行了研究。
从而为现实工程建设中一些不便于实验研究的复杂情况,提出了研究的可行性方法,具有较强的实践意义。
关键词:裂纹;应力强度因子;ABAQUS;数值模拟0 引言断裂力学是研究带裂纹体的强度和裂纹扩展规律的一门学科。
断裂力学的最早理论可以追溯到1920年,为了研究玻璃、陶瓷等脆性材料的实际强度比理论强度低的原因,Griffith[1-2]提出了在材料中存在裂纹的设想,而Irwin[3-4]在1957年提出了应力强度因子以及其后形成的断裂韧度的概念后,断裂力学理论出现了重大的突破,奠定了线弹性断裂力学的基础。
当前国内外许多学者[5-8]已将多裂纹问题作为主攻方向,但是受到诸多条件的制约,目前并未取得明显的成果。
1复杂裂纹研究的现实依据图(a)是位于四川的几大主要断裂带的分布图,在宏观上形成了V型的断层结构。
汶川Ms8.0级地震,就是龙门山断裂带在构造应力场长期作用下,积累的应变能突然释放的结果。
图(b)是2002年11月3日,阿拉斯加中部迪纳利断层发生了一次M w7.9级地震。
从图(b)可以看出三条主断裂层形成了典型的的分支结构,究断层的性质对于预知、了解地质作用,估计可能发生的破坏具有重要参考价值。
图1 现实V型、Y型裂纹存在模型2 Y型裂纹的应力强度因子研究2.1有限元建模中间带有裂纹的双轴压缩试件,如图2所示,在相关断裂力学的试验分析中被广泛应用。
故此,本文以此典型试件作为研究对象,进行数值模拟计算。
abaqus模型单位为mm,算出来的应力单位

[序号1] 为了更好地研究材料的力学性能以及进行工程设计,工程师和科研人员常常借助计算机辅助设计软件来进行有限元分析,其中abaqus是一款常用的有限元分析软件之一。
在使用abaqus进行模型建立和应力分析时,我们需要特别注意其单位的设置以及最终计算出来的应力的单位。
[序号2] abaqus模型的单位一般设定为毫米(mm),这是因为有限元分析常常涉及到微观结构和小尺度的力学问题,使用毫米作为单位能更好地刻画材料的微观特性,也更符合实际工程中常见的尺度。
[序号3] 在abaqus中进行应力分析时,最终计算出来的应力单位一般也是以标准国际单位制中的帕斯卡(Pa)来表示。
帕斯卡是国际单位制中力的单位牛顿(N)除以面积的单位平方米(m^2)所得到的。
在有限元分析中,我们常常关注材料的应力分布情况,通过计算得到的应力分布图和数据能够帮助我们更直观地了解材料在受力状态下的性能表现。
[序号4] 当进行单位转换时,我们需要牢记一些基本的单位换算关系。
在abaqus中,如果我们在模型建立时设置了毫米为长度单位,那么在后续的应力分析中计算得到的应力值就是以帕斯卡为单位的,即1N/mm^2等于1MPa。
在解读abaqus计算结果时,需要将数值转换成常见的力学应力单位,如兆帕(MPa)、千帕(kPa)等,以便更好地与实际工程需求和材料规格相对应。
[序号5] 正确设置模型单位并准确理解计算得到的应力单位,能够有效提高有限元分析的准确性和实用性。
在工程设计和科研工作中,abaqus作为一款强大的有限元分析软件,为我们提供了丰富的功能和工具,但只有在正确使用和理解的前提下才能发挥出最大的作用。
[结尾] abaqus模型单位为mm,计算出来的应力单位为帕斯卡,正确设置和理解模型的单位,将有助于我们准确分析材料力学性能,为工程设计和科研工作提供更可靠的依据。
希望本文能够为大家在使用abaqus进行有限元分析时提供一些帮助和启发。
基于ABAQUS的裂纹形状对应力强度因子的影响

基于ABAQUS的裂纹形状对应力强度因子的影响作者:李宗揆来源:《中国科技博览》2015年第12期[摘要]工程实际应用中的构件几乎全部是带裂缝工作,介绍了ABAQUS软件断裂力学计算模块,采用ABAQUS分析软件对三点弯曲试验进行裂纹分析,讨论在不同开裂方向对于裂纹尖端应力强度因子的影响,并得出相关结论。
[关键词]J积分;应力强度因子;ABAQUS中图分类号:O346.11 文献标识码:A 文章编号:1009-914X(2015)12-0100-011 前言实际工程中构件通常都是带裂缝工作,此时传统的屈服判据失效,不能再去判断结构发生断裂的时机,为此,我们应当借助断裂力学得到新的断裂判据。
断裂的发生源于裂纹的扩展,而裂纹的失稳扩展通常由裂纹端点开始。
裂纹端点区应力应变场强度的大小是裂纹能否扩展的决定因素,因此需要找到一个能够表征裂纹端点区应力应变场强度的参量。
断裂力学中使用应力强度因子的概念去衡量裂纹尖端的应力场强度,当裂纹尖端区应力场的形式恒定,其强度完全由应力强度因子的大小来确定。
本文通过有限元分析,讨论三点弯曲试验中,处于同样荷载状况下,不同的开裂角度对于梁体裂纹尖端区应力强度因子的影响,以期得到一个合理的变化规律。
2 计算分析2.1 断裂力学的能量方法及应力强度因子在断裂的过程中,裂纹尖端处要释放出一定的能量。
因此,必须结合能量释放率寻求裂纹尖端附近应力—应变场的解答。
在二维Ⅰ型裂纹问题中,考虑一个离裂纹端很近、位置在极坐标(r,θ)的平面问题的应力单元,由Westergaard应力函数法给出裂纹尖端区域应力场的解析解为当r→0时,应力分量都会趋于无穷大。
裂纹问题的关键是计算裂纹尖端处的应力场,为保证计算精度,裂纹尖端单元应设计为奇异性单元,并在此周围区域局部加密。
是由裂纹下表面某点逆时针绕行到裂纹上表面某点的简单的积分围道,表示收缩到裂纹尖端;q是虚拟裂纹扩展方向的单位向量;n是的外法线方向;H的定义为,其中弹性材料W是弹性应力能量。
abaqus 屈服压应力比 -回复

abaqus 屈服压应力比-回复abaqus是一种广泛应用于工程领域的有限元分析软件,它的强大功能使其成为许多工程师和研究人员进行结构、材料和流体的数值模拟的首选工具。
其中一个重要的功能是求解材料的屈服压应力比,这个参数在工程设计和材料优化中起着重要的作用。
接下来,我将详细介绍abaqus在求解屈服压应力比方面的步骤。
首先,我们需要理解什么是屈服压应力比。
屈服压应力比是材料屈服时抗压强度与抗拉强度之比,它是衡量材料在受到压力作用时抗压能力相对于抗拉能力的一个重要参数。
通过求解屈服压应力比,可以更好地了解材料的力学特性,并选择适合特定工程应用的材料。
在abaqus中,我们可以通过以下步骤来计算屈服压应力比。
第一步是建立模型。
首先,我们需要确定模型的几何形状和尺寸。
例如,如果我们想研究一个圆柱形的材料试件,我们需要定义其半径和高度。
然后,我们需要选择合适的材料模型来描述材料的本构行为。
在abaqus中,常用的模型包括线性弹性模型、von Mises屈服准则、Drucker-Prager 准则等。
第二步是设置加载条件。
我们需要确定模型的加载方式。
在计算屈服压应力比时,我们可以施加一个恒定的压力或沿着材料的轴向施加一个拉伸载荷。
第三步是设定材料属性。
我们需要为模型指定材料的力学性质。
这些性质可以根据实验数据或文献中的材料特性来确定。
在abaqus中,我们可以指定材料的弹性模量、泊松比、屈服强度、塑性硬化参数等。
第四步是求解模型。
在设置好加载条件和材料属性后,我们可以使用abaqus的求解器来解决模型。
求解过程中,abaqus会根据指定的加载条件和材料模型,计算模型在给定加载状态下的应力和应变分布。
第五步是分析结果。
在模型求解完成后,我们可以通过abaqus提供的后处理工具来分析结果。
其中,关注屈服压应力的结果特别重要。
abaqus 可以输出每个单元的应力和应变数据,并提供各种图形和数据分析工具来展示和解读结果。
