不完整非对称性曲线线型优化及其坐标计算
平面直角坐标系与图形的对称

对称中心
对于中心对称图形,存在一个固定点,使得图形关于这个点 对称。这个点被称为对称中心。
对称变换基本性质
对称变换不改变图形的形状和大小, 只改变图形的方向或位置。
对于轴对称图形,对称轴两侧的图形 完全重合;对于中心对称图形,关于 对称中心的任意两点连线都被对称中 心平分。
对称变换具有可逆性,即如果图形A 经过对称变换得到图形B,那么图形B 也可以经过相应的对称变换得到图形 A。
03
对于某些具有旋转对称性的图形,通过旋转坐标系可以使得对
称性的描述更加直观。
坐标系变换下图形对称性变化规律
平移变换
平移变换不改变图形的对称性,但会改变对称轴或对称中心的位 置。
旋转变换
旋转变换可以改变图形的对称性,如将轴对称图形转变为中心对称 图形或将非对称图形转变为对称图形。
缩放变换
缩放变换不改变图形的对称性类型,但会改变对称轴或对称中心的 位置以及对称点的坐标。
。
02
图形对称性质简介
对称图形定义及分类
定义
如果一个图形经过一次变换后,与另 一个图形重合,则称这两个图形关于 这次变换对称。
分类
根据对称变换的不同,对称图形可以 分为轴对称图形和中心对称图形。
对称轴和对称中心概念
对称轴
对于轴对称图形,存在一条直线,使得图形关于这条直线对 称。这条直线被称为对称轴。
定义
平面直角坐标系由两条互相垂直、原点重合的数轴组成,通常水平方向的数轴 称为x轴,竖直方向的数轴称为y轴。
性质
在平面直角坐标系中,任意一点都可以用一对有序实数来表示,即点的坐标。 坐标原点用(0,0)表示,x轴上的点纵坐标为0,y轴上的点横坐标为0。
坐标轴上点表示方法
非对称缓和曲线的绳正法整正计算

测点 n 1 2 3 4 5 6 7 8 9 10
表 3 计划正矢计算
纵距率 γ
计划正矢Πmm 说明
算式 得数 取整
测点 纵距率
n
γ
计划正矢Πmm 算式 得数 取整
010732 017623
0155 1 γΔ1
5175 6
13128 13
11
( n - XZHΔ1 ) 73164 74
12 013132
1 曲中点位置公式推导
非对称缓和曲线的设计正矢如表 1 。
表 1 非对称缓和曲线的设计正矢 测点 设计正矢 测点 设计正矢 测点 设计正矢
1 ( ZH) fcΠ(6 n)
n + 1 ( HY)
fc[1 (6 n) - 1 ]
k + 2 ( m - 1) fcΠm
2
f cΠn
n+2
3
2 fcΠn
…
Xz = ( ∑∑f + S修 ) Π∑f
2 算例
某非对称缓和曲线及测点布置如图 1 。 fc = 83 mm , n = 11 , m = 4 ,实测正矢如表 2 。 211 曲线主点位置计算 由表 2 可 知 , ∑f = 945 mm , ∑ ∑f = 11 384 mm , S修 = ( n2 - m2 ) f cΠ24 = 363. 1 mm。 曲中 点 位 置 XZ = ( ∑ ∑f + S修 ) Π∑f = 12. 43 (段) 原圆曲线长 ly = ∑fΠfc = 11. 39 (段) 原圆曲线头位置 Xt = Xz - lyΠ2 = 6174 (段) 原 圆 曲 线 尾 位 置 Xw = Xz + lyΠ2 =
累计之和 S对 为 : S对 = [3 ( n + 1) ( n + 2) + 3 ( n + 1) 2 +
18讲 非完整缓和曲线坐标计算

交接控制桩
直线转点 曲线交点 副交点 水准基点
技 立 业
曲线要素表
水准基点表
曲线五大桩
延伸控制桩 延伸水准基点
二、 线路施工复测
2、线路施工复测:为了确保线路施工测量精度,施工前,
德 修 身
施工单位应全面恢复定测桩点,同时检查移交桩点的可靠性, 这项工作称为线路施工复测。
复测提交资料
技 立 业
(1)复测说明 (2)复测线路示意图 (3)控制桩复测角度与设计角度比较表 (4)复测曲线偏角与设计曲线偏角比较表 (5)控制桩复测距离与设计距离比较表 (6)水准点复测高差与设计高差比较表 (7)复测控制点桩点表 (9)测量仪器检定证书复印件
2
( R1 * R2 )* l f ( R1 R2 )
pz p 180 p
2 p p 2 3 3A
2 lp
p p
L2 180 p 2 RL0
工程测量教研室
工程测量Ⅱ
三、计算施工坐标系下点的坐标
当转向角为有右时:
X i xi cos yi sin X ZH Yi yi cos xi sin YZH
当转向角为左时:
X i xi cos yi sin X ZH Yi yi cos xi sin YZH
工程测量教研室
二、 线路施工复测
1、交(接)桩:设计单位交付图纸资料的同时,在现场将控
制点实地位置移交给施工单位,这项工作成为交(接)桩。
德 修 身
图纸资料
工程测量Ⅱ
第6章 全站仪坐标法中线测量
—非完整缓和曲线坐标计算
不完整非对称性曲线线型优化及其坐标计算20页PPT

谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起而 读书。 ——周 恩来
不完整非对称性曲线线型优化及其坐
标计算
21、没有人陪你走一辈子,所以你要 适应孤 独,没 有人会 帮你一 辈子, 所以你 要奋斗 一生。 22、当眼泪流尽的时候,留下的应该 是坚强 。 23、要改变命运,首先改变自己。
24、勇气很有理由被当作人类 的德性 。--温 斯顿. 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ,它只 是让人 们的脚 放上一 段时间 ,以便 让别一 只脚能 够再往 上登。
非对称非完整缓和曲线推算公式

RL R L R R R L R R y p R L L R L R L R R L L R x m R L L x R L R L y L R L L R L y L R L L R L dLdy R L L L x R L L dL dx RL L R L RL dL L R dL d L R L R R L R L s s s hy ss ss s hy shy ss hy s xs x s xs x s xx s xxs sxx s xx x x x xs x s x x *24))*81((*6)cos (*2402)*482(**40sin **40*336*6**336**6)**48*2(sin *sin **40)**4*21(cos *cos *2**2****22220233323s 023s 3423373336222522402=---=--=-=---=-=-=-=-=-≈=-=-≈=======βββββββββ缓和曲线综合要素则缓圆点独立坐标标缓和曲线上任意一点坐缓和曲线性质:1121112213111221'12'11'11'1'11'12122211'212123221221111'*2轴正方向建立坐标系X 为JD 为原点ZH 以'*sin 1cot '*''*6'*40'*2*)(*轴X 为JD'为原点ZH'以)cos (sin 1tan tan sin cos cos sin sin cos cos cos )cos(cos cos cos cos *240)(2*24)(tan *)(R L Y E HH Y X E ZH R L Y R L L X R L RR L R L L L R L R p R p R p R p R p R p R R L L L L m RL L p m p R T HH HH HH xHH xx HH x x x x x x x ==∙-=∙=-==-=∴+=-++=∴+=+=-==+++=+∴=+=+-+=+=++=ββββααθθααθθαθαθθαθθθθαθθβθθ 正方向建立坐标系非对称非完整缓和曲线JDA A ZH T AF JD A E HH EF A HH AF E JD EF E ZH JD ZH E JD R L L Y A HH Y X A ZH R L Y R L L X x HHHH HH HH HH∙+∙=∴=∙∙-+∙=∙=∙-∙=∙--=-=-=-=-=∴+==∙-=∙=-=3664'''236354112155212212121311sin sin *中F -JD -A 在三角形sin sin *'||||'中F -JD'-E 在三角形*2*sin 1cot **6*40ββββββπβαπββαβββββββββ 改正数切线标高设计标高改正值:里程差为任一点与起点或终点)(变坡点标高切线标高设计标高变坡点高程又变坡点竖曲线起点±==-±=-==∴-==∴===-=Rx y x i x T TK E R E R E R L T R T E i i *2*K *88*2*2*2竖曲线222221ωωωω。
不对称缓和曲线要数的计算方法

精心整理不对称缓和曲线要数的计算方法????????? 发布日期:2012-02-12??浏览次数:52圆曲线两端缓和曲线不等长的测设方法,圆曲线起始端缓和曲线的长度为L1终端的缓和曲线长度为L2圆曲线半径为R,所测转角为a切线角切线增量内移值切线长曲线长或者外矢距Goto 1 ↙(注:↙表示按EXE键即可)2. XLZBZB使用说明:K? 正算时所求点的里程:L(-Z+Y) 正算时所求点距该里程中线的边距(左侧取负值,右侧取正值,在中线上取零(即数字0))3. 正算子程序程序名:SUB14→DimZ ↙(注:↙表示按EXE键即可)↙(注:↙表示按EXE键即可)I+J(Acos(G+QCJ(1÷P+CJD)×180÷π)+Bcos(G+QEJ(1÷P+EJD)×180÷π)+Z[4]cos(G+QZ[1]J(1÷P+Z[1]JD)×180÷π)+Bcos(G+Q(1-E)J(1÷P+(1-E)JD)×180÷π)+A cos(G+Q(1-C)J(1÷P+(1-C)JD) ×180÷π)) →X ↙段线元起点切线方位角→G: 二段线元终点里程→H: 二段线元起点曲率半径→P:二段线元终点曲率半径→R:二段线元左右偏标志→Q:…………………(注:如有多个曲线元要素,还要继续添加到数据库DAT中)I= 线元起点的X坐标:S= 线元起点的Y坐标: O= 线元起点里程:G= 线元起点切线方位角: H= 线元终点里程P= 线元起点曲率半径R= 线元终点曲率半径Q= 线元左右偏标志(注:左偏为-1,右偏为+1 )(注:如有多个曲线元要素,还要继续添加到数据库DAT中,曲率半径直径输入半径值)5. 坐标反算程序名:ZBFS“U=”:S÷666.667→U ▲ 亩Goto 1(注:0表示数字零)说明:点位必须按顺序输入成封闭形图型!A B C D 为第一,二两点坐标(常量),X Y……为第三,四,五,六点坐标(变量)。
一种小线段的非对称S曲线速度规划与前瞻算法

一种小线段的非对称S曲线速度规划与前瞻算法陈光胜;梅雪松【摘要】针对基于小线段高速、高精度数控加工路径,提出并实现了一种具有速度前瞻功能的非对称S曲线加减速规划策略.首先对已知线段总长的加工路径实现非对称S曲线加减速算法进行了阐述,然后基于小线段间的转折角提出了适用于小线段加工的实用前瞻模型.利用模型通过计算小线段间的转折角来对转折处加工速度进行预规划,在实现轨迹精度的前提下使加工速度达到最高,从而实现小线段数控加工时在高速度和高精度之间达到协调.实验结果证明了该算法的有效性和实用性.【期刊名称】《机械设计与制造》【年(卷),期】2010(000)008【总页数】3页(P47-49)【关键词】数控加工;小线段;速度规划;前瞻算法【作者】陈光胜;梅雪松【作者单位】西安交通大学机械工程学院,西安,710049;西安交通大学机械工程学院,西安,710049;西安交通大学机械制造系统工程国家重点实验室,西安,710049【正文语种】中文【中图分类】TH16;TP2731 引言在高速数控加工中,为有效避免各进给轴产生冲击、失步、超程和振荡,保证运动部件的平稳和准确定位,必须进行加减速控制,以使进给速度平滑过渡。
而S 型加减速位移曲线的一次及二次导数都是连续的,将可能的冲击减小到最小,进给过程中速度变化较为平稳,具有良好的柔性,所以,适用于高速高精度运动控制系统[1]。
在传统的控制器,S 加减速控制用于高精度位置控制,不具有前瞻功能,若保证小线段转角处精度,必须以每一条代码段为控制范围,实现对称的曲线速度控制,即每一段曲线,电机都有一个从0 加速到最大,再从最大速度下降到0 的过程,起停频繁,影响加工效率。
或是以若干小线段作为控制范围,忽略小线段转角时产生的加速度,从面造成转角处的轮廓超差[2]。
为改善这种情况,提出一种基于线段转折角前瞻功能的非对称S 曲线加减速规划策略。
该策略的实现将使机床进给在高速度和高精度之间达到协调。
非对称缓和曲线坐标计算程序

非对称缓和曲线坐标计算程序CASIO fx-4800P QXZB曲线坐标计算CASIO4800 QXZB可计算不等缓和曲线、圆曲线上的任意中、边桩坐标:该程序适用于计算器 CASIO fx-4800P,可计算与线路中心成任意夹角的缓和曲线、圆曲线中、边桩坐标及待测点方位角和距离。
1、DK(JD)?输入交点桩号2、X(JD)?输入交点坐标X3、Y(JD)?输入交点坐标Y4、T1?输入第一切线长(如果只有一条切线两者都输入一致)5、T2?输入第二切线长(如果只有一条切线两者都输入一致)6、FWJ?输入直线方位角(ZH→JD)7、A?输入转角:左转为负,右转为正8、R?输入圆曲线半径9、LS1?输入第一缓和曲线长(如果只有一条缓和曲线两者都输入一致)10、LY?输入圆曲线长(L-LS1-LS2)11、LS2?输入第二缓和曲线长(如果只有一条缓和曲线两者都输入一致)12、X(ZJD)?输入置镜点坐标X13、Y(ZJD)?输入置镜点坐标Y14、JSDK?输入前视点里程15、PL?输入偏距16、PA?输入偏角程序下载地址:/blog/post/QXZB-4800.html评价答案好:18不好:1原创:18非原创:0菲メ帆ぅ回答采纳率:52.8% 2010-06-02 17:37满意答案好评率:57%(for Casio-fx4850)扩展变量操作(15个):Defm 15←┚ ( O为字母、0为数字)J-PQX (平面数据输入,自行切换到J-JSMS)Defm 15←┚A“JD” B“JDX” C“JDY” F“FWJ” O“A0:Z-,Y+” RE“LS1” K“LS2”:E<1=>E=1E-9⊿K<1=>K=1E-9⊿Z[1]=EE÷24R-E∧4÷2688RRR:Z[2]=E÷2-EEE÷240RR:X=(EE-KK)÷24R÷sin Abs O :“T1=”:Z[3]=(R+Z[1])tan(Abs O÷2)+Z[2]-X◢“T2=”:Z[4]=(R+KK÷24R-K∧4÷2688RRR)tan(Abs O ÷2)+K÷2-KKK÷240RR+X◢“L=”:L=Abs OπR÷180+(E+K)÷2◢J=tan-1((R+Z[1])÷(Z[3]-Z[2]):“E=”:X=(R+Z[1])÷sin J-R◢X=A-Z[3]:Y=X+E:E<1=>“ZY=”:X◢≠=> “ZH=”:X◢“HY=”:Y◢⊿ “QZ=”:Y =X+(L-K-E)÷2+E◢Y=X+L-K:X=X+L:K<1=> “YZ=”:X◢≠=> “YH=”:Y◢“HZ=”:X◢⊿Prog“J-JSMS” ←┚J-JSMS(放样模式主程序)“1-ZS, FY,3-FS”: Lb1 0:{Z}: Z“MS”≤2=>Goto 1: ≠=> Z≤4=> Goto2⊿⊿←┚Lb1 1 :Q“X-YIQI”S“Y-YIQI”T“X-HOUSI”U“Y-HOUSI”:{PDW}:P“F=”D“BZ=”W“BJ=”: Prog“JP”: Prog“FY”: Goto 1←┚Lb1 2 :{XYW}:XYW“BJ”: Prog“JF”: “P=”: P◢“BZ=”: D◢JP(平曲线正算子程序)Fixm←┚Lb1 1 :J=F:X= B-Z[3]cos F :Y= C-Z[3]sin F :G=E←┚P≤A-Z[3]=>I=A-Z[3]-P:M=-I:N=0:H=F+W:Goto 5←┚≠=>P≤A-Z[3]+E=>I=P-A+Z[3]:H=90II÷REπ:O<0=>H=-H⊿H=H+W+F:Goto 3←┚≠=>P≤A-Z[3]+L-K=>I=P-A+Z[3]-E:Goto 4: ≠=>Goto 2⊿⊿←┚Lb1 2 :X= B+Z[4]cos(F+O :Y= C+Z[4]sin(F+O :J=F+O+180:G=K←┚P≤A-Z[3]+L=>I=A-Z[3]+L-P:H=90II÷RKπ:O>0=>H=-H⊿H=H+J+W+180:Goto 3 ←┚≠=>I=P-A+Z[3]-L:M=-I:N=0:H=J+W+180:Goto 5 ←┚Lb1 3 :M=I-I∧5÷40RRGG:N=III÷6GR-I∧7÷336RRRGGG:Goto 5 ←┚Lb1 4 :H=(E+2I)×90÷πR:M=R sin H+Z[2]:N=R(1-cos H)+Z[1]:O<0=>H=-H⊿H=J+H+W: Goto 5←┚Lb1 5 :P≤A-Z[3]+L-K=> O<0=>N=-N⊿≠=>O>0=>N=-N⊿⊿Goto 6←┚Lb1 6 :X =X+M cos J-N sin J+D cos H:Y =Y+M sin J+N cos J+D sin H“X=”: X ◢“Y=”: Y ◢JF(平曲线反算子程序)Fixm←┚U=X:V=Y:D=0:J=F-W:P=A+(Y-C)cos J-(X-B)sin J←┚Lb1 1:Prog“JP”:J=H-180:I=(V-Y)cos J-(U-X)sin J:Abs I<1E-4=>Goto 2:≠=>P=P+I:Goto 1⊿←┚Lb2: D=(V-Y)÷sinHFY(放样计算子程序)Pol(T-Q,U-S):“HOUSI D=”:I◢J<0=>J=J+360⊿J>360=>J=J-360⊿“HOUSI J=”:J→DMS◢Pol(X-Q,Y-S):“I=”:I◢J<0=>J=J+360⊿J>360=>J=J-360⊿“J=”:J→DMS◢一、程序简介本套程序是共有2个主程序,3个子程序。
牛顿-拉夫逊算法(极坐标)潮流计算算例

极坐标系下的潮流计算
潮流计算
在电力系统中,潮流计算是一种常用的计算方法,用于确定在给定网络结构和参数下,各节点的电压 、电流和功率分布。在极坐标系下进行潮流计算,可以更好地描述和分析电力系统的电磁场分布和变 化。
极坐标系下的潮流计算特点
在极坐标系下进行潮流计算,可以更直观地描述电力线路的走向和角度变化,更好地反映电力系统的 复杂性和实际情况。此外,极坐标系下的潮流计算还可以方便地处理电力系统的非对称性和不对称故 障等问题。
03
CATALOGUE
极坐标系下的牛顿-拉夫逊算法
极坐标系简介
极坐标系
一种二维坐标系统,由一个原点(称为极点)和一条从极点出发的射线(称为 极轴)组成。在极坐标系中,点P的位置由一个角度θ和一个距离r确定。
极坐标系的应用
极坐标系广泛应用于物理学、工程学、经济学等领域,特别是在电力系统和通 信网络中,用于描述电场、磁场、电流和电压等物理量的分布和变化。
极坐标形式
将电力系统的节点和支路参数以极坐 标形式表示,将实数问题转化为复数 问题,简化计算过程并提高计算效率 。
02
CATALOGUE
牛顿-拉夫逊算法原理
算法概述
牛顿-拉夫逊算法是一种迭代算法,用于求解非线性方程组。在电力系统中,它 被广泛应用于潮流计算,以求解电力网络中的电压、电流和功率等参数。
准确的结果。
通过极坐标系的处理,算法 能够更好地处理电力系统的 复杂结构和不对称性,提高 了计算的准确性和适应性。
算例分析表明,该算法在处理 大规模电力系统时仍具有较好 的性能,能够满足实际应用的
需求。
展望
进一步研究牛顿-拉夫逊算法在极坐标 系下的收敛性分析,探讨收敛速度与电 力系统规模、结构和参数之间的关系, 为算法的优后的电压、电流和功 率等参数。
非完整缓和曲线计算实例
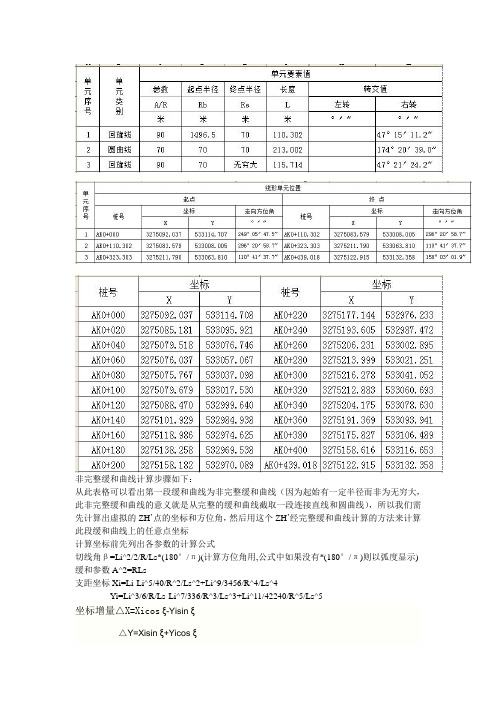
非完整缓和曲线计算步骤如下:从此表格可以看出第一段缓和曲线为非完整缓和曲线(因为起始有一定半径而非为无穷大,此非完整缓和曲线的意义就是从完整的缓和曲线截取一段连接直线和圆曲线),所以我们需先计算出虚拟的ZH’点的坐标和方位角,然后用这个ZH’经完整缓和曲线计算的方法来计算此段缓和曲线上的任意点坐标计算坐标前先列出各参数的计算公式切线角β=Li^2/2/R/Ls*(180°/π)(计算方位角用,公式中如果没有*(180°/π)则以弧度显示) 缓和参数A^2=RLs支距坐标Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5坐标增量△X=Xicosξ-Yisin ξ△Y=Xisin ξ+Yicos ξ在第一缓和曲线时,ξ为ZH到JD的方位角,曲线左转时Yi为负号带入,右转时以正号代入在第二缓和曲线时,ξ为HZ到JD的方位角,曲线左转时Yi为正号带入,右转时以负号代入备注:Li:所求点弧长(此点至ZH‘的里程距离)R:曲线半径(以接圆曲线的半径为准)Ls:缓和曲线长(此为非完整缓和曲线,以计算出的完整缓和曲线长为准,而不是截取的缓和曲线长)开始计算:1. 先计算出虚拟的ZH’点桩号,因为根据缓和参数公式A^2=RLs,表格中已知缓和参数为90,半径为70所以求得缓和曲线长Ls=A^2/R=90^2/70=115.714,而根据表格知道实际缓和曲线长为110.302,则在起点里程AK0+000之前还有115.714-110.302=5.412M,所以此段缓和曲线的起点里程应为AK -5.4122. 计算切线角根据公式β=Li^2/2/R/Ls*(180°/π)=5.412^2/2/70/115.714*(180°/π)=0°6′12.93″3. 计算虚拟起点ZH‘方位角α,因为此线路为右转,从起点计算曲线任意点方位角时应为加,现在倒过来计算方位角所以为减,由已知条件得知AK0+000方位角为249°5′47.5″,所以虚拟ZH‘的方位角ξ为249°5′47.5″-0°6′12.93″=248°59′34.57″4. 计算虚拟起点ZH‘坐标,Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=5.412-5.412^5/40/70^2/115.714^2+5.412^9/3456/70^4/115.714^4=5.412Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=5.412^3/6/70 /115.714-5.412^11/42240/70^5/115.714^5=0.0033线路右转,在第一缓和曲线上,则Yi以正号代入△X=Xicosξ-Yisin ξ=5.412*cos(248°59′34.57″)-0.0033*sin(248°59′34.57″)=-1.937△Y=Xisin ξ+Yicosξ=5.412*sin(248°59′34.57″)+0.0033*cos(248°59′34.57″)=-5.0535虚拟起点ZH‘的坐标为(由于虚拟点在线元起点的前面(如果是在第二缓和曲线时虚拟点再线元终点的后面,则还是正常计算,为加上坐标增量)所以计算时应倒过来计算,所以为减去坐标增量)XZH‘=XZH-△X=3275092.037-(-1.937)=3275093.974YZH‘=YZH-△Y=533114.707-(-5.0535)=533119.7615. 现在可以开始由于虚拟点ZH‘来计算此段缓和曲线上的任意点,这里先计算缓和曲线终点HY点的坐标(HY点里程为ZH‘+115.714=AK0+110.302)Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=115.714-115.714^5/40/70^ 2/115.714^2+115.714^9/3456/70^4/115.714^4=108.059Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=115.714^3/6/ 70/115.714-115.714^7/336/70^3/115.714^3+115.714^11/42240/70^5/115.714 ^5=30.359线路右转,在第一缓和曲线上,则Yi以正号代入△X=Xicosξ-Yisin ξ=108.059*cos(248°59′34.57″)-30.359*sin(248°59′34.57″)=-10.396△Y=Xisin ξ+Yicosξ=108.059*sin(248°59′34.57″)+30.359*cos(248°59′34.57″)=-111.760XHY=XZH‘+△X=3275093.974+(-10.396)=3275083.578YHY=YZH‘+△Y=533119.761 +(-111.760)=533008.001切线角β= Li^2/2/R/Ls*(180°/π)=115.714^2/2/70/115.714*(180°/π)=47°21′23.76″所以HY点方位角为虚拟点ZH’加上(因为线路右转)47°21′23.76″=248°59′34.57″+47°21′23.76″=296°20′58.33″6.接着计算曲线上任意点坐标,方法同上,比如计算AK0+020的坐标(这里的AK0+020实际为AK0+025.412)曲线长Li为25.412,半径R为70,计算如下:Xi=Li-Li^5/40/R^2/Ls^2+Li^9/3456/R^4/Ls^4=25.412-25.412^5/40/70^2/ 115.714^2+25.412^9/3456/70^4/115.714^4=25.408Yi=Li^3/6/R/Ls-Li^7/336/R^3/Ls^3+Li^11/42240/R^5/Ls^5=25.412^3/6/7 0/115.714-25.412^7/336/70^3/115.714^3+25.412^11/42240/70^5/115.714^5= 0.3376线路右转,在第一缓和曲线上,则Yi以正号代入△X=Xicosξ-Yisin ξ=25.408*cos(248°59′34.57″)-0.3376*sin(248°59′34.57″)=-8.7932△Y=Xisin ξ+Yicosξ=25.408*sin(248°59′34.57″)+0.3376*cos(248°59′34.57″)=-23.840X=XZH‘+△X=3275093.974+(-8.7932)=3275085.181Y=YZH‘+△Y=533119.761 +(-23.840)=533095.921切线角β= Li^2/2/R/Ls*(180°/π)=25.412^2/2/70/115.714*(180°/π)=2°17′2.22″所以HY点方位角为虚拟点ZH’加上(因为线路右转)2°17′2.22″=248°59′34.57″+2°17′2.22″=251°16′36.79″。
浅谈不完整非对称性曲线在高速公路线型控制中的优化应用

浅谈不完整非对称性曲线在高速公路线型控制中的优化应用摘要:针对目前山区高速公路设计中出现的不完整非对称性线型的控制难点,结合现有的工程测量曲线计算理论和在工程实例中的应用,提出一种经过分析处理和优化设计改进后的方法,最终将不完整非对称性的线型计算补强后变得简单易操作,进而为施工现场提供了一种简捷易懂的计算方法。
关键词:不完整非对称性;补强;线型控制0引言在平面线型优化设计中,曲线组合类型比较多,所占线路总长的比例也是很大的。
近年来在山区高速公路曲线设计过程中,传统的曲线设计已经远远不能满足地形复杂的山区公路的选线设计要求,设置不完整非对称曲线来优化保证线路设计参数,进一步满足行车设计需要。
但这种线型的设计给现场施工的线路平面测设进度和质量的控制方面带来较大难度,本文结合现有的工程测量曲线计算理论和在工程实例中的应用,提出一种经过分析处理和优化设计后的改进方法,最终将不完整非对称性的线型计算补强后变得简单易操作。
1山区路段线型选择的技术规定为满足山区公路困难地段线型选择和设计的技术指标的均衡性与连续性,需要满足以下几点:(1)长直线尽头尽量不要接以小半径曲线,特别是在长下坡段尽头。
若由于地形所限小半径曲线难免时,中间应插入中等曲率的过渡性曲线。
使纵坡不应过大。
(2)高、低标准之间要有过渡。
而在高速公路线型设计基本要素中主要由直线、圆曲线、缓和曲线三个要素构成。
《规范》规定,基本型也可以使用非对称性的缓和曲线或者具有不完整性质的曲线特性,以适应周围的地形地物,也即是圆心位置不变而通过调整缓和曲线参数A或者截取一段距离的缓和曲线的方法来实现不完整非对称缓和曲线的设计。
对高速公路线路上不完整非对称性缓和曲线的线型控制,过去常采用的方法是用CAXIO-fx5800计算软件或计算机辅助技术将此段曲线分解为多段(至少3段)进行分别计算,且所需的计算要素繁多,输入要素不断变换。
下面通过对该线型通过一定的方法将该特点进行优化设计,并通过实例对优化设计思路进行透析,从而避免了变换曲线要素所带来的烦琐。
非完整缓和曲线坐标计算

非完整缓和曲线坐标计算公路、铁路主干线一般线形采用曲线基本型,而在公路匝道部分常采用线形单元组合形式,组合线形的坐标计算只能按线形单元分段计算。
通常设计文件中提供各特征点的桩号、坐标、切线方位角。
圆曲线计算较为简单,这里主要讨论非完整缓和曲线的桩点的坐标计算。
一、计算ZH(HZ)点的坐标已知数据:如图4.9.1所示,起点p的半径Rp ,桩号Lp坐标Xp、Yp,切线方位角αp,缓和曲线参数A。
式中各项计算如下:图4.9.1 非完整缓和曲线αpZ的计算:其中Δp——右偏用“-”,左偏用“+”。
ZH切线坐标方位角:其中βp——左偏用“+”,右偏用“-”(ZH换成HZ时,左偏用“-”,右偏用“+”)。
二、计算缓和曲线切线坐标系各点坐标计算出缓和曲线起点坐标后即可按式4.8.2计算各中线点坐标。
三、计算施工坐标系坐标切线坐标系转换为施工坐标系需要进行坐标平移和转轴计算,当转向角为右时按式(4.9.7)、(4.9.8)计算;当转向角为左时按式(4.9.9)、(4.9.10)计算。
(1)当转向角为右时:(2)当转向角为左时:式中 Xi ,Yi——路线统一坐标系坐标;x i ,yi——切线坐标;α——转向点之间的切线方位角。
【例4.9.1】如图4.9.2所示,起点P处半径RP =9 579.228 m,桩号lP=0+889.975,XP =19 698.065,YP=28 469.399,起点的切线方位角αP=82°34′06″,缓和曲线参数A=60。
与缓和曲线相接的圆曲线半径R=55 m,公切点的桩号lGQ=K0+824.896试计算K0+860的坐标。
图4.9.2 非完整缓和曲线【解】(1)计算ZH的桩号和XZH ,YZH:(左偏)用“+”:(2)计算αZH切线方位角:(3)计算K0+860坐标:+860点切线坐标系坐标:x=30.30 m,y=1.293 m(计算过程略)+860点施工坐标系坐标:。
非对称鞍点问题的修正非线性Uzawa算法

< , <
1 ( 一 +1 )
‘
此 时,如 下两个 不等式 成立
(+g ( A 。, ) ( 。 p ((+£ ( As , ) ( s , ) 1 ) ( ) e +( e e 2 1 ) ( ) 。 +( e e ) Q ) Y ) 。 Q ee X ) 3
(3 1) .
基金项目:国家 自然科学基金 (0 2 1 0 6 9 3 1 ) 1 9 6 9 , 0 7 0 5 和国防重点实验室基金 ( 10 6 0 0 0 0 )资助 94 C 923 96
N. o1
李建 磊等 :非对 称鞍 点问题 的修正 非 线性 U a a算 法 zw
21 5
对正 常数 Q 1 立 .我 们将 用到如 下 引理 . 成
(.) 21
引理 2 [ . 1 ]若 A正定,则 (一) A 也正定且满足
( 一) ,) ( ) WW ( WW ( 一 ,)
( 一) ,) W∈ ( W, R.
(2 2) .
Y 1 i (x 1 y一 ) i =Y+ B i 一C i 9, + +
(.) 21 3 (. ) 21 4 (. ) 21 5
=西 1 B (+ — i + 一Q l Y . )
定理 234 假设 式 (. )(.2 成立 ,则 算法 3收 敛 ,如 果 .f J 21 一 21 ) 0
X l i Q ( 一 x — Ti i :z + . A i B Y , + , ) Y 1 ( l C i ) 一Y+ B 。 — y一9. + +
其 中 QA满 足 ( " f ( )fu,V ∈R .) ( J ) QA , j
和
(.) 28
非对称基本型曲线坐标计算

非对称 基本型 曲线要素计算
非对称基本型平曲线如图 l 所示 ,图
2
、
嘉 一 , 譬 譬 一
=
l 为第一缓和曲线上任意点至 Z H点的 曲线长 。 ( )圆曲线 ( YH)任意点坐 2 HY 标 :
co
中P, 、P 分别为左右 两侧 曲线 的内移值 , q 、q , 分 别为左右两 侧曲线的切线增值 。 通 过 圆心 0 作 与 J D的 连 线 OC,将 四边 形 OACB分成两个直角三角形 ,通过 圆心 0 作 左 右 两侧 切 线 的平 行 线 分 别 交 AC、BC
( £ s +8一 )秽 { 曲线 长. 置 ) k 0 + 】 一∞ o
式中 :l 为圆曲线上任意点至 HY点的 ( )第二缓和 曲线 ( 3 HZ—YH)任
÷ +)sl s一9 ) , ( E∞k ̄ o , 】 宾 0 1 ・ 0
最 m x c c岛 越 删 t 鲁
( )第一缓和 曲线 ( 1 ZH—HY)任 意 点坐 标 :
半 径 圆曲线时 ,会突然 产生 离心 力 的变 化 ,使 行 车安 全感 和 舒 适 受 到 影 响 。 为 了 抵 消 突 然 产生 离心 力变 化 的 作 用 ,需 要 在 直线与圆曲线 间加设一段半径 由无穷大逐 渐变化到圆曲线半径 ( 或反之 )的缓和曲 线 。 在 路 线 设 计 中 , 对 于 圆 曲 线 , 使 用 时两端的缓和 曲线长度取相等值 ,该组合 两端 切线长 相等 ,称之 为对 称基 本型 曲 线 ;相反 ,如果 圆曲线两端 的缓 和曲线长 度取 值不相 等 ,该组 合两 端 切线长 不相 等 ,称之为非对称基本型曲线 。本文针对 非对称基本型 曲线的问题 ,利用非对称基 本型 曲线交点大地坐标 ,计 算出圆曲线 圆 心点大地坐标 ,从而推导 出非对称基本型 曲线 上任 意点坐 标 。
非完整缓和曲线计算方法

第一章TOPCON GTS-312 全站仪的使用一、仪器外观和功能说明1、仪器外观图 1 :GTS-312 全站仪外观及各部件名称2、面板上按键功能——进入坐标测量模式键。
◢——进入距离测量模式键。
ANG ——进入角度测量模式键。
MENU ——进入主菜单测量模式键。
ESC ——用于中断正在进行的操作,退回到上一级菜单。
POWER ——电源开关键◢◣——光标左右移动键▲ ▼ ——光标上下移动、翻屏键F1 、F2 、F3 、F4 ——软功能键,分别对应显示屏上相应位置显示的命令。
3、显示屏上显示符号的含义V ——竖盘读数;HR ——水平读盘读数(右向计数);HL ——水平读盘读数(左向计数);HD ——水平距离;VD ——仪器望远镜至棱镜间高差;SD ——斜距;* ——正在测距;N ——北坐标,相当于x ;E ——东坐标,相当于y ;Z ——天顶方向坐标,相当于高程H 。
二、角度测量模式功能:按ANG 键进入,可进行水平角、竖直角测量,倾斜改正开关设置。
三、距离测量模式功能:先按◢键进入,可进行水平角、竖直角、斜距、平距、高差测量及PSM 、PPM 、距离单位等设置第 1 页F1 MEAS :进行测量。
F2 MODE :设置测量模式,Fine/coarse/tragcking(精测/ 粗测/ 跟踪)。
F3 S/A :设置棱镜常数改正值(PSM )、大气改正值(PPM )。
F4 P1 ↓:进入第2 页。
第 2 页F1 OFSET :偏心测量方式。
F2 SO :距离放样测量方式。
F3 m /f/i :距离单位米/ 英尺/ 英寸的切换。
F4 P2 ↓:进入第1 页。
四、坐标测量模式功能:按进入,可进行坐标(N,E ,H)、水平角、竖直角、斜距测量及PSM 、PPM 、距离单位等设置。
第1 页F1 MEAS :进行测量。
F2 MODE :设置测量模式,Fine/Coarse/Tracking 。
F3 S/A :设置棱镜改正值(PSM ),大气改正值(PPM )常数。
非对称曲线桩点坐标计算的程序设计

非对称曲线桩点坐标计算的程序设计摘要:无论是铁路、公路还是轨道交通,由于受到地形、地物、地质及其它因素的限制,经常要改变线路的前进方向。
当线路的方向改变时,在转向处需要用曲线将两直线连接起来。
曲线按其线形可分为:圆曲线、对称型(基本型)缓和曲线、复曲线和竖曲线等,而在路线的平面线形设计中除了采用常见的圆曲线、复曲线和对称型(基本型)缓和曲线外,为了实际需要还必须采用非对称型缓和曲线。
关键词:道路曲线放样;非一般曲线任意桩点坐标;测量程序设计Abstract: Both the railway, highway and light rail or subway tunnel, due to the topography, surface features, geology and other factors, often to change the orientation of lines. When the line changed direction at the curve to the need for a straight line connecting the two. Its linear curve can be divided into: a round curve, symmetrical (basic) Curve, the complex curves and vertical curves, and the horizontal alignment of the road design in addition to the common circular curve, the complex curves and symmetrical (basic Type) Curve, to the actual needs must also ease the use of non-symmetrical curves.Key words: road curve layingout; non-general of arbitrary pile point coordinates; Surveying procedure designing.1引言本报告主要介绍了非对称曲线要素的计算方法和根据极坐标法测设曲线的计算原理(线路设计模型一体化)利用C++语言编写了非一般曲线任意桩点坐标的计算程序,并将程序计算结果与实例结果进行比较,验证了该方法的正确性2研究的思路和内容在实际工程中,由于地形条件的限制,路线线形常常采用增长或缩短切线长度的方法来满足规范中对于曲线间直线长度的要求。
基于非对称七段S型曲线的矿用电铲轨迹优化

5.2 仿真实验结果分析....................................21
5.3 实验结果对比与评估..................................22
6. 实际应用案例...........................................23
降低能耗:通过对电铲轨迹的优化,减少不必要的能量消耗,提高能源利用效率,降低运营成本。
提升作业安全性:通过精确控制电铲的作业轨迹,减少作业过程中的碰撞和事故风险,保障矿工的生命安全和设备的完好。
促进技术创新:研究基于非对称七段S型曲线的矿用电铲轨迹优化,有助于推动相关理论和技术的发展,为矿用电铲的智能化、自动化提供技术支持。
优化矿产资源开发:通过对矿用电铲轨迹的优化,提高矿产资源开发的综合效益,为我国矿产资源的可持续利用和经济发展做出贡献。
理论意义:丰富和发展矿用电铲轨迹优化理论,为相关领域的研究提供新的思路和方法。
实践意义:为矿用电铲的实际应用提供技术支持,提升矿业生产效率和经济效益。
社会意义:通过提高矿用电铲作业的智能化水平,促进我国矿业产业的转型升级,推动矿业生产的绿色、安全发展。
再者,非对称七段S型曲线在优化过程中具有较强的鲁棒性。当矿用电铲在实际作业中遇到突发状况时,如地面不平整、障碍物等,非对称七段S型曲线能够快速适应环境变化,保证轨迹的连续性和稳定性。
2.3 非对称七段S型曲线数学模型
在矿用电铲轨迹优化过程中,选择合适的曲线模型对于提高作业效率和降低能耗至关重要。非对称七段S型曲线因其具有良好的平滑性、较小的曲率变化以及易于参数调整等优点,被广泛应用于矿用电铲的轨迹规划中。本节将详细介绍非对称七段S型曲线的数学模型。
一道“非对称性”问题的解法优化与拓展

一道“非对称性”问题的解法优化与拓展
张倩;吴志勇
【期刊名称】《中学数学研究》
【年(卷),期】2024()1
【摘要】圆锥曲线中极点和极线的理论为我们求有关定点、定值部分问题提供了大的方向,而韦达定理的使用往往使方向的正确性得到了严谨的证明.但在实际的解题中我们经常会遇到仅仅套用韦达定理不能一次性解决的“非对称性”问题.本文以对一道试题解法进行优化处理为例,借此来谈谈对解决有关圆锥曲线中“非对称性”问题的想法.
【总页数】3页(P60-62)
【作者】张倩;吴志勇
【作者单位】安徽省合肥市合肥一六八中学
【正文语种】中文
【中图分类】G63
【相关文献】
1.立足学生选择视角优化解法提升能力——对一道最值问题不同视角、不同解法的优化
2.深挖导数考题,拓展优化解法——对一道高考导数压轴题的解法探究
3.探讨解析几何问题,开展思路解法优化——对一道解析几何问题的解法探究
4.突破问题解法,拓展探究结论——以一道高考解析几何定点问题为例
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
螺旋角β
R新 =
J0 W F
∞
ZH 31 新 +4 6 YK
6 .9
6
800 2 = R起
5911 . 7 3 3 1 R=
a
0
原ZH 96.605 5 YK6+
b
1 T0 计算 J W F
T1
HY .605 6 7 7 + 6 YK
c
JD0
图-2
R=1 337
PJ0
JD1
PJ右
e
11
.59
YH YK6 +
虽然设计中提供的参数不同,但是所涉及到的线 型是一样,我们所设计优化的过程是一样的。对 于此类曲线的优化设计中,曲线测设计算是影响 线路平面测设进度和质量的重要因素,而对不完 整非对称缓和曲线的设计更是增加了曲线测设坐 标计算的难度。 1 概念综述 对于不完整非对称性缓和曲线的坐标计算,过 去经常采用的方法是用CAXIO-fx5800计算程序 将此段曲线分解为多段(至少3段)进行分别计算, 且所需的坐标计算要素繁多,输入要素不断变换。
4.2.3 计算恢复完整后平曲线的起算方位角FWJ0及 线路偏角PJ0 FWJ0=FWJ计算-β0=132°6′32″- 1°41′4.19″=130°25′27.81″。 PJ0=PJ 右 +β0=16°37′45″+1°41′4.19″=18°18′49.19″。 4.2.4 计算恢复后平曲线切线长To1和To2 前后半曲线圆曲线内移值为:P01=L01*L01/(24R) -L014/(2688R³ )=3.700 P02=L02*L02/(24R) -L024/(2688R³ )=0.900
YJD -----交点的Y坐标 DKJD -----交点的计算里程 FWJ计算----不完整曲线的起算方位 A1 ------第一缓和曲线参数 A2 ------第二缓和曲线参数 4.2 计算步骤及过程 4.2.1 缓和曲线参数计算 第一段缓和曲线完整长度 Lo1=A1*A1/R=678.962/1337.5911=344.639> Lh1=180 第二段缓和曲线完整长度 Lo2=A2*A2/R=476.8502/1337.5911=169.997≈ Lh2=170
主要控制桩点里程ZH HY YH HZ
6+776.605 8+205.220 6+946.827 8+730.844 6+596.605 7+116.827 8+730.844
由上表可知:第一段平曲线为完整平曲线,第二 段平曲线为不完整平曲线,直接连接在第一段平曲线 的缓直(HZ)点上,第三段平曲线是完整的平曲线, 和第二段平曲线通过直线相连。第二段平曲线如图-2 所示:
946
HZ YK7 +
.82 7
f
116
.82
7
该段平曲线提供的曲线要素为: PJ (右)=16°37′45″, R起=2800, R=1337.5911,Lh1=180, Lh2=170, T1=241.312 ,T2=281.937,XJD=2937454.259, YJD=511401.03,DKJD=6+837.917, FWJ计算 =132°06′32″,A1=678.96,A2=476.850。 PJ右-----曲线偏角 R起 -----起点曲线半径 R -----圆曲线半径 Lh1 -----第一缓长 Lh2 -----第二缓长 T1 -----第一切线长 T2 -----第二切线长 XJD -----交点的X坐标
前后半曲线切线增长量为: Q01=
L01/2- L01³ /(240R² )=172.224 Q02= L02/2- L02³ /(240R² )=84.993 所以,第一段缓和曲线段切线长 T01=[R+P02(R+P01)CosPJ0]/SinPJ0+Q01=379.525 第二段缓和曲线段切线长 T02=[R+P01(R+P02)CosPJ0]/SinPJ0+Q02=309.045
JD1
c
d
a
b
图-1
e
JD2
f
g
该平曲线的特点是: 1)平面线由直线、圆曲线和缓和曲线三要素组 成。 直线:曲率为零(或半径为无限大); 圆曲线:曲率为常数(或半径为常数); 缓和曲线:曲率为变数(或半径为变数); 2)平曲线的组合不是固定的。可以是连续的圆 曲线或缓和曲线相连也可以是中间加入直线后相 连。 3)缓和曲线与直线或着圆曲线相连时可以是不 完整的,但必须满足以下两种关系: ①A*A=L*R;② A*A=(L*R1*R2)/( R1-R2);A为 缓和曲线参数。
出完整非对称性平曲线要素来进行计算。在高速 公路中对不完整缓和曲线进行了完整恢复后使用 取得非常好的计算效果,使得该段不完整缓和曲 线段坐标计算变得很简捷方便且精度很高!!
请各位提出批评并指正!
3 计算原理 3.1根据已知的设计曲线要素将不完整的缓和曲线 段补充完整; 3.2求出新的曲线直缓(ZH)点或缓直(HZ)点; 3.3进而求出待补充完整曲线新交点(JD)的位 置等相关曲线要素; 3.4利用补充完整后的曲线要素资料计算相应段内 的点位坐标。 4 算例 4.1基础数据 以衡(阳)-炎(陵)高速公路3合同段为例,该 合同段全长2.72KM,分为左右线,其中右线设 置3个平曲线,相关设计数据如下页:
5 计算时应注意的事项 5.1采用补充完整后的非对称性平曲线要素进行坐 标计算线路中桩坐标; 5.2计算里程:只能计算补充完整前曲线里程上的 中桩坐标,而被补充的一段曲线不能被计算,仅能 作为曲线计算方便的补充。 5.3原不完整平曲线的要素在计算线路坐标和线路 关系时无法使用,只能使用补充完整后的曲线要素。 6 结论 上述不完整平曲线段任意一点坐标计算不能直 接采用设计曲线的要素进行计算,通过对此类曲线 线型的优化而应将其恢复为完整的平曲线,并解算
桩 号
YK6+400.899 YK6+837.917 YK8+468.754
第一切线长T1 第二切线长T2 曲线长L
196.357 241.312 263.534 196.357 281.937 263.534 392.073 520.222 525.624 6+204.532 6+596.605 8+205.220
而通过一定的方法将不完整非对称平曲线补充并 转换成完整的平曲线,并将线型进行优化设计, 将曲线要素确定,利用特定曲线坐标程序连续计 算该补充完整后平曲线上(包括不完整非对称段) 任一点的坐标,从而避免了变换曲线要素所带来 的烦琐。 2 不完整非对称平曲线的优化设计思路及其特点
在不完整缓和曲线设计之初,首先确定该不完整 缓和曲线两端圆曲线半径和不完整缓和曲线的长 度。它的设计思路是将完整的缓和曲线切掉半径 无穷大方向的一段后,与前一段圆曲线相连,其 后连接一段圆曲线后,与一段完整或不完整缓和 曲线相连,构成一条不完整非对称性平曲线。如 图-1所示:其中a-b、d-e、f-g三段为缓和曲 线,b-c、c-d、e-f三段为圆曲线,且b-c、c -d两段为圆曲线直接相连。
Lo1即图-2中的a-c段,Lh1即图-2中的b-c段, Lo2即图-2中的e-f段。 以上计算得如下结论:第一段缓和曲线是不完整 的,a-c段是补充完整后的缓和曲线,第二段缓 和曲线是完整的。 4.2.2 不完整缓和曲线起点螺旋角β0计算: 由4.2.1结果中,第一段缓和曲线中被去掉的一段 长度Lf=Lo1- Lh1=344.639-180=164.639,所以 第一段缓和曲线上半径为R起=2800处的螺旋角 β0=Lf² /(2R*Lh1)=164.639² /(2×1337.5911×344. 639)=1°41′4.19″。
不完整非对称性曲线线型优化 及其坐标计算
王科 2013年8月
目的:通过对不完整非对称性平曲线补充完整
的优化过程,利用补充完整的平曲线要素计算设 计曲线上相应里程段内任意点的坐标,进而为工 程测量工作提供了一种简捷快速的坐标计算方法. 0 前言 在平面线型优化设计中,曲线组合类型比较多, 所占线路总长的比例也是很大的,近年来在高速 公路曲线设计过程中,往往会由于实际线型的需 要而设置了不完整非对称缓和曲线。在四处施工 的项目中有新河高速公路项目、衡炎高速公路项 目、雅泸高速公路项目、汶马二级公路项目、葫 白公路项目等。
4.3 由以上可以得到恢复完整后非对称性平曲线 要素如下: PJ0=18°18′49.19″, R0=1337.5911, L01= 344.639, L02=170, T01=344.639, T02=281.937, X0=2937477.9444,Y0=511386.6596, K0=6+811.491,FWJ0=130°25′27.81″ 得到上述曲线要素后,采用常用的曲线坐标 计算方法就可以很方便地计算线路上任意点的坐 标。
桩 号
坐标 (X Y)
半径R
曲线参数A1A2
678.96;476.85
第一缓长Lh1 第二缓长Lh2
0 180 0 170
YK6+400.899 ( 2937747.259,511401.039) 2800 YK6+837.917 (2937454.259,511401.039) 2800;1337.591 YK8+468.754 (2936057.627,512248.933) 2900
4.2.5计算恢复后平曲线交点JD0的坐标(X0,Y0) 及里程K0 由前四步计算可得到恢复后的平曲线交点的坐标: X0=X1+(T02-T2)Cos(FWJ0+PJ0180)=2937477.9444 Y0=Y1+(T02-T2)Sin(FWJ0+PJ0180)=511386.6596 由第2步可知:恢复完整后新的ZH点里程= 6596.605-Lf=6431.966 所以恢复后平曲线交点的里程 K0=6431.966+T01=6811.491
