近几全国物理竞赛复赛力学
2024年9月第41届全国中学生物理竞赛复赛试题参考解答

第41届全国中学生物理竞赛复赛试题参考解答(2024年9月21日9:00-12:00)一、(45分) (1)(1.1)记质量为M 的振子偏离平衡位置的位移为x (向左为正),单摆的偏转角为θ(向左为正),摆臂上的张力为T ,按牛顿第二定律,摆锤在水平方向上的运动方程为m ẍ+lθcos θ−lθ sin θ =−T sin θ ①在竖直方向上的运动方程为m −l sin θθ−lθ cos θ =m g −T cos θ ② 利用小幅度振动条件,保留到小量θ的领头阶,有sin cos 1 , ③将③式代入①②式,并保留到小量θ的领头阶,得T mg ④ ẍ+lθ+g θ=0⑤【注: 利用悬点不动的非惯性系也可更方便地得到上述结果。
在悬点不动的非惯性系中,摆锤额外受到横向的惯性力−mẍ,有角向运动方程mlθ=−m g sin θ−mẍcosθ ①′ 同时也有径向运动方程2θcosθsin ml mx g T m ②′进一步利用小摆幅条件,保留到小量θ的领头阶,即得⑤④式。
】质量为M 的振子在水平方向上做一维运动, 由牛顿第二定律得Mẍ=−kx +T sin θ+H cos ωt ⑥由③④⑥式得Mẍ+kx −m g θ=H cos ωt ⑦只考虑系统在强迫力下的稳定振动,稳定振动的圆频率为ω,设cos(x x A t ) ⑧ cos()l B t ⑨其中φ 、φ 是稳定振动与所受强迫力之间的位相差。
将⑧⑨式代入方程⑤⑦后,所得出的两个方程对任意时间 t 均成立,故有00x ,⑩进而有22M m k A m B H⑪ 22200A B⑫由⑪⑫式得2202222200()()()HA k M m⑬222222222000()()H B A k M m⑭其中(1.2)由⑬式可知,当没有阻尼器时(这时0m ),有2HA k M ⑮即当风的频率为⑯时,大楼受迫振动幅度最大。
当风的频率取⑮式所示的值、但有阻尼器时,由⑬式得k g H H kl Mg M l A g k gkm m l M⑰为了调节阻尼器的参数m 、l 使得A 最小,可取Mgl k, ⑱或m 尽可能大。
29届全国中学生物理竞赛复赛(高清试题图片Word答案)

1234567第29届全国中学生物理竞赛复赛试卷参考答案一、由于湖面足够宽阔而物块体积很小,所以湖面的绝对高度在物块运动过程中始终保持不变,因此,可选湖面为坐标原点并以竖直向下方向为正方向建立x坐标系,以下简称系. 设物块下底面的坐标为,在物块未完全浸没入湖水时,x其所受到的浮力为g式中为重力加速度.物块的重力为设物块的加速度为,根据牛顿第二定律有将(1)和(2)式代入(3)式得将系坐标原点向下移动而建立新坐标系,简称系. 新旧坐标的关系为把(5)式代入(4)式得式表示物块的运动是简谐振动. 若,则,对应于物块的平衡位置. 由式可知,当物块处于平衡位置时,物块下底面在系中的坐标为0物块运动方程在系中可写为利用参考圆可将其振动速度表示为式中为振动的圆频率在(8)和(9)式中和分别是振幅和初相位,由初始条件决定. 在物块刚被释放Ax=0时,即时刻有,由(5)式得由(8)至(12)式可求得(13) 将(10)、(13)和(14)式分别代人(8)和(9)式得由(15)式可知,物块再次返回到初始位置时恰好完成一个振动周期;但物块的运动始终由(15)表示是有条件的,那就是在运动过程中物块始终没有完全浸没在湖水中. 若物块从某时刻起全部浸没在湖水中,则湖水作用于物块的浮力变成恒力,物块此后的运动将不再是简谐振动,物块再次返回到初始位置所需的时间也就不再全由振动的周期决定. 为此,必须研究物块可能完全浸没在湖水中的情况. 显然,在系中看,物块下底面坐标为时,物块刚好被完全浸没;由(5)式x b 知在系中这一临界坐标值为(17) 即物块刚好完全浸没在湖水中时,其下底面在平衡位置以下处. 注意到在Xb振动过程中,物块下底面离平衡位置的最大距离等于振动的振蝠,下面分两种A情况讨论:I.. 由(13)和(17)两式得在这种情况下,物块在运动过程中至多刚好全部浸没在湖水中. 因而,物块从初始位置起,经一个振动周期,再次返回至初始位置. 由(10)式得振动周期物块从初始位置出发往返一次所需的时间II.. 由(13)和(17)两式得A X b (21) 在这种情况下,物块在运动过程中会从某时刻起全部浸没在湖水表面之下. 设从t初始位置起,经过时间物块刚好全部浸入湖水中,这时. 由(15)和(17)11b式得(22) cos11取合理值,有 (23) arccos11由上式和(16)式可求得这时物块的速度为2 (24) V(t)1-11此后,物块在液体内作匀减速运动,以表示加速度的大小,由牛顿定律a有 (25) 设物块从刚好完全浸入湖水到速度为零时所用的时间为,有t2(26) 12由(24)-(26)得2(27)112()物块从初始位置出发往返一次所需的时间为22(28) 2()2arccos111II12()评分标准:本题17分.(6)式2分,(10)(15)(16)(17)(18)式各1分,(20)式3分,(21)式1分,(23)式3分,(27)式2分,(28)式1分.10二、 1. i.通过计算卫星在脱离点的动能和万有引力势能可知,卫星的机械能为负值. 由开普勒第一定律可推知,此卫星的运动轨道为椭圆(或圆),地心为椭圆的一个焦点(或圆的圆心),如图所示.由于卫星在脱离点的速度垂直于地心和脱离点的连线,因此脱离点必为卫星椭圆轨道的远地点(或近地点);设近地点(或远地点)离地心的距离为,r R 0.80R 卫星在此点的速度为.由开普勒第v a 二定律可知2式中为地球自转的角速度e令表示卫星的质量,根据机械能守m恒定律有1G(2)由2r20.80R(1)和(2)式解得可见该点为近地点,而脱离处为远地点. 【(3)式结果亦可由关系式:直接求得】同步卫星的轨道半径满足2R由(3)和(4)式并代入数据得4可见近地点到地心的距离大于地球半径,因此卫星不会撞击地球. ii.由开普勒第二定律可知卫星的面积速度为常量,从远地点可求出该常量为s2设和分别为卫星椭圆轨道的半长轴和半短轴,由椭圆的几何关系有 ab 110.280.80R (7) 220.800.2822 (8) 2T卫星运动的周期为(9) s代人相关数值可求出(10)9.5h 卫星刚脱离太空电梯时恰好处于远地点,根据开普勒第二定律可知此时刻卫星具有最小角速度,其后的一周期内其角速度都应不比该值小,所以卫星始终不比太空电梯转动得慢;换言之,太空电梯不可能追上卫星.设想自卫星与太空电梯脱离后经过,卫星到达近地点,而此时太空电梯已转过此(约14小时)1.5T点,这说明在此前卫星尚未追上太空电梯.由此推断在卫星脱落后的0-12小时内二者不可能相遇;而在卫星脱落后12-24小时内卫星将完成两个多周期的运动,同时太空电梯完成一个运动周期,所以在12-24小时内二者必相遇,从而可以实现卫星回收. 2.根据题意,卫星轨道与地球赤道相切点和卫星在太空电梯上的脱离点分别为其轨道的近地点和远地点.在脱离处的总能量为1GMmGMm2(11)m(R)x2xxe此式可化为32GM xx(12) 123e e e这是关于的四次方程,用数值方法求解可得R x4(13)4.7 3.010kmxe表示卫星与赤道相切点v【亦可用开普勒第二定律和能量守恒定律求得.令R xe即近地点的速率,则有2eex和 121GMm1GMm22(R)ex2R2R ex由上两式联立可得到方程532GM2GM xxx02323eee其中除外其余各量均已知, 因此这是关于的五次方程. 同样可以用数值方法解得.】RRR xxx卫星从脱离太空电梯到与地球赤道相切经过了半个周期的时间,为了求出卫星运行的周期,设椭圆的半长轴为,半短轴为,有xe (14) 222ex (15)因为面积速度可表示为12(16) sx2所以卫星的运动周期为(17) s代入相关数值可得 h(18) 6.8卫星与地球赤道第一次相切时已在太空中运行了半个周期,在这段时间内,如果地球不转动,卫星沿地球自转方向运行180度,落到西经处与赤道相切. 但由于地球自转,在这(180110)期间地球同时转过了角度,地球自转角速度,因此卫星与地球赤道T/2360/24h15/h相切点位于赤道的经度为西经(19)1801101212即卫星着地点在赤道上约西经121度处. 评分标准:本题23分.第1问16分,第i小问8分,(1)、(2)式各2分,(4)式2分,(5)式和结论共2分.第ii小问8分,(9)、(10)式各2分,说出在0-12小时时间段内卫星不可能与太空电梯相遇并给出正确理由共2分,说出在12-24小时时间段内卫星必与太空电梯相遇并给出正确理由共2分.5%第2问7分,(11)式1分,(13)式2分,(18)式1分,(19)式3分. (数值结果允许有的相对误差)三、 13解法一如图1所示,建直角坐标,轴与挡板垂直,轴与挡板重合. 碰撞前体系质心的速xy Oxy,方向沿x轴正方向,以表示系统的质心,以和表示碰撞后质心的速度分量,vPvv度为Py0Px表示墙作用于小球的冲量的大小. 根据质心运动定理有 JC (1)(2)由(1)和(2)式得(3)Px3m (4)可在质心参考系中考察系统对质心的角动量. 在球 O C x 与挡板碰撞过程中,质心的坐标为(5)(6)l P3CP球碰挡板前,三小球相对于质心静止,对质心的角C C 动量为零;球碰挡板后,质心相对质心参考系仍是C静止的,三小球相对质心参考系的运动是绕质心的转动,若转动角速度为,则三小球对质心的角动量P图(7)式中、和分别是、和三球到质ABClllAPBPCP心的距离,由图1可知(8)cos sin(9)sin(10)CP9由(7)、(8)、(9)和(10)各式得(11)3在碰撞过程中,质心有加速度,质心参考系是非惯性参考系,在质心参考系中考察动力学问题时,必须引入惯性力. 但作用于质点系的惯性力的合力通过质心,对质心的力矩等于零,不影响质点系对质心的角动量,故在质心参考系中,相对质心角动量的变化仍取决于作用于球C的冲量的冲量矩,即有(12)3【也可以始终在惯性参考系中考察问题,即把桌面上与体系质心重合的那一点作为角动量的参考点,则对该参考点(12)式也成立】由(11)和(12)式得 14 sin球相对于质心参考系的速度分量分别为(参考图1)CP球相对固定参考系速度的x分量为 C (16)由(3)、(6)、(13)和(16)各式得 J (17)Cx02根据题意有 (18)由(17)和(18)式得 2 (19)由(13)和(19)式得(20) l 球若先于球与挡板发生碰撞,则在球与挡板碰撞后,整ABC 个系统至少应绕质心转过角,即杆至少转到沿y 方向,如图2所示. 系统绕质心转过所需时间(21) 在此时间内质心沿x 方向向右移动的距离 B (22)若 (23)则球先于球与挡板碰撞. 由(5)、(6)、(14)、(16)、(18)、BA (21)、(22)和(23)式得 图2 3 (24)即(25) 评分标准: 本题25分.(1)、(2)、(11)、(12)、(19)、(20)式各3分,(21)式1分,(22)、(23)式各2分.(24)或(25)式2分. 15解法二 如图1所示,建直角坐标系,轴与挡板垂直,x Oxy y v 、、、、和 分vvvvvv 以轴与挡板重合,vy AyByCyAxBxCxAyBy 别表示球与挡板刚碰撞后、和三球速度的分量,ABCC vv B A O 根据题意有 AxBxx (1) v Cy 以表示挡板作用于球的冲量的大小,其方向沿轴x J C 的负方向,根据质点组的动量定理有 C(2)(3)图1 AyByCy以坐标原点为参考点,根据质点组的角动量定理有(4)因为连结小球的杆都是刚性的,故小球沿连结杆的速度分量相等,故有(5)(6)(7)(7)式中为杆与连线的夹角. 由几何关系有(8)(9)解以上各式得(10)(11)(12)(13)16(14)0By(15)cosCy0按题意,自球与挡板碰撞结束到球(也可能球)碰撞挡板墙前,整个系统不受外力作用,ABC系统的质心作匀速直线运动. 若以质心为参考系,则相对质心参考系,质心是静止不动的,、A和三球构成的刚性系统相对质心的运动是绕质心的转动. 为了求出转动角速度,可考察球BCB相对质心的速度.由(11)到(15)各式,在球与挡板碰撞刚结束时系统质心的速度2(16) 2vv AxBxCx sin Px03m 3AyByCy (17) 0 Py3m 这时系统质心的坐标为(18) cosP1 (19)sin P3不难看出,此时质心正好在球的正下方,至球的距离为,而球相对质心的速度 y PBBBP 12(20) sin BPxBxPx03 (21) 0BPy 可见此时球的速度正好垂直,故整个系统对质心转动的角速度 B BP (22) ylP 若使球先于球与挡板发生碰撞,则在球与挡板ABC y 碰撞后,整个系统至少应绕质心转过角,即杆至少ABπ/2转到沿y 方向,如图2所示. 系统绕质心转过所需时间 π/2 A 1π 2 (23)x O 在此时间内质心沿x 方向向右移动的距离 P B(24)Px 若 C (25) PP 17 图2则球先于球与挡板碰撞. 由以上有关各式得(26)即(27) 评分标准: 本题25分. (2)、(3)、(4)、(5)、(6)、(7)式各2分,(10)、(22)式各3分,(23)式1分,(24)、(25)式各2分,(26)或(27)式2分. 四、 参考解答: 1.虚线小方框内2n 个平行板电容器每两个并联后再串联,其电路的等效C 电容满足下式 t11n (1) C2Ct1即 2C (2) t1n 式中 S(3)虚线大方框中无限网络的等效电容满足下式 C t2(4)即 C (5)t22整个电容网络的等效电容为 CC2Ct1t2 (6)等效电容器带的电量(即与电池正极连接的电容器极板上电量之和)(7)当电容器a两极板的距离变为2d后,2n个平行板电容器联成的网络的等效满足下式电容C t1(8)由此得(9)t1整个电容网络的等效电容为(10)整个电容网络的等效电容器带的电荷量为(11)在电容器a两极板的距离由d变为2d后,等效电容器所带电荷量的改变为(12)电容器储能变化为(13)在此过程中,电池所做的功为(14)(3外力所做的功为(15)设金属薄板插入到电容器a后,a的左极板所带电荷量为,金属薄板左侧带电荷量为,右侧带电荷量为,a的右极板带电荷量为,与并联的电容器左右两极板带电荷量分别为和.由于电容器a和与其并联的电容器两极板电压相同,所以有(16)SSC由(2)式和上式得(17)d上式表示电容器a左极板和与其并联的电容器左极板所带电荷量的总和,也是虚线大方框中无限网络的等效电容所带电荷量(即与电池正极连接的电容器的C t2极板上电荷量之和). 整个电容网络两端的电压等于电池的电动势,即 19(18)(1)c2CC t2将(2)、(5)和(17)式代入(18)式得电容器a左极板带电荷量(5)(2)(19)(313)2kd(313)d评分标准:本题21分. 第1问13分,(2)式1分,(5)式2分,(6)、(7)、(10)、(11)、(12)式各1分,(13)式2分,(14)式1分,(15)式2分. 第2问8分,(16)、(17)、(18)、(19)式各2分. 五、参考解答: c a 如图1所示,当长直金属杆在ab位置以速度水平v向右滑动到时,因切割磁力线,在金属杆中产生由b指向a的感应电动势的大小为ll 1 2 (1)式中为金属杆在ab位置时与大圆环两接触点间的长LII 1 2 度,由几何关系有2222R(2)111100在金属杆由ab位置滑动到cd位置过程中,金属杆与大 b d 圆环接触的两点之间的长度可视为不变,近似为.2RL1图 1 将(2)式代入(1)式得,在金属杆由ab滑动到cd过程中感应电动势大小始终为(3)1以、和分别表示金属杆、杆左和右圆弧中的电流,方向如图1所示,以表示a、b两IIIU21ab端的电压,由欧姆定律有(4)ab110 (5)ab220式中,和分别为金属杆左、右圆弧的弧长.根据提示,和中的电流在圆心处产生的磁感llll1212应强度的大小分别为Il11 (6)1m2R1Il22(7)2m2R1方向竖直向上,方向竖直向下.BB12由(4)、(5)、(6)和(7)式可知整个大圆环电流在圆心处产生的磁感应强度为 20(8)无论长直金属杆滑动到大圆环上何处,上述结论都成立,于是在圆心处只有金属杆的电流I所产生磁场. 在金属杆由ab滑动到cd的过程中,金属杆都处在圆心附近,故金属杆可近似视为无限长直导线,由提示,金属杆在ab位置时,杆中电流产生的磁感应强度大小为 2I (9)3mR1100方向竖直向下.对应图1的等效电路如图2,杆中的电流 a(10)IIIRR 1 2 右左右左左右其中为金属杆与大圆环两接触点间这段金属杆的电阻,R R R左ab 和分别为金属杆左右两侧圆弧的电阻,由于长直金属杆非R右常靠近圆心,故 b (11)图 2 ab111右左利用(3)、(9)、(10)和(11)式可得v800kBm (12)3由于小圆环半径,小圆环圆面上各点的磁场可近似视为均匀的,且都等于长直金属杆在圆心处产生的磁场. 当金属杆位于ab处时,穿过小圆环圆面的磁感应通量为(13)当长直金属杆滑到cd位置时,杆中电流产生的磁感应强度的大小仍由(13)式表示,但方向相反,故穿过小圆环圆面的磁感应通量为(14)在长直金属杆以速度从ab移动到cd的时间间隔内,穿过小圆环圆面的磁感应通量的v改变为(15)由法拉第电磁感应定律可得,在小圆环中产生的感应电动势为大小为(16)在长直金属杆从ab移动cd过程中,在小圆环导线中产生的感应电流为(17)于是,利用(12)和(17)式,在时间间隔内通过小环导线横截面的电荷量为(18)i评分标准:本题25分. (3)式3分,(4)、(5)式各1分,(8)、(10)式各3分,(12)式3分, (15)式4分,(16)、(17)式各2分,(18)式3分. 六、参考解答: nn设重新关闭阀门后容器A中气体的摩尔数为,B中气体的摩尔数为,12则气体总摩尔数为(1) 12把两容器中的气体作为整体考虑,设重新关闭阀门后容器A中气体温度为,B中气体温度为,重新关闭阀门之后与打开阀门之前气体内能的变化可表12示为(2)由于容器是刚性绝热的,按热力学第一定律有(3) pV令表示容器A的体积, 初始时A中气体的压强为,关闭阀门后A中气体压强为,由理想气体状态方程可知 1pV (4)(5)由以上各式可解得由于进入容器B中的气体与仍留在容器A中的气体之间没有热量交换,因而在阀门打开到重新关闭的过程中留在容器A中的那部分气体经历了一个绝热Vp过程,设这部分气体初始时体积为(压强为时),则有10(6) 11011 22利用状态方程可得(7)由(1)至(7)式得,阀门重新关闭后容器B中气体质量与气体总质量之比RC(8)Rn评分标准:本题15分. (1)式1分,(2)式3分,(3)式2分,(4)、(5)式各1分,(6)式3分,(7)式1分,(8)式3分. 七、答案与评分标准: 1. 19.2 (4分,填19.0至19.4的,都给4分) 10.2 (4分,填10.0至10.4的,都给4分) 2. 20.3 (4分,填20.1至20.5的,都给4分) 4.2 (4分,填4.0至4.4的,都给4分) 八、参考解答:在相对于正离子静止的参考系S中,导线中的正离子不动,导电电子以速向下匀速运动;在相对于导电电子静止的参考系中,导线中导电电子不动,v度0向上匀速运动.下面分四步进行分析. v正离子以速度第一步,在参考系中,考虑导线2对导线1中正离子施加电场力的大小和方向.若S系中一些正离子所占据的长度为,则在系中这些正离子所占据的长l,由相对论中的长度收缩公式有度变为(1),由于离子设在参考系S和中,每单位长度导线中正离子电荷量分别为和的电荷量与惯性参考系的选取无关,故(2)由(1)和(2)式得(3)设在S系中一些导电电子所占据的长度为,在系中这些导电电子所占据l,则由相对论中的长度收缩公式有的长度为(4)同理,由于电子电荷量的值与惯性参考系的选取无关,便有(5)分别为在参考系S和中单位长度导线中导电电子的电荷量. 式中,和在参照系中,导线2单位长度带的电荷量为(6)它在导线1处产生的电场强度的大小为(7)q电场强度方向水平向左.导线1中电荷量为的正离子受到的电场力的大小为(8)电场力方向水平向左第二步,在参考系中,考虑导线2对导线1中正离子施加磁场力的大小和向上运动的正离子形成的电流为 v方向.在参考系中,以速度(9)导线2中的电流在导线1处产生磁场的磁感应强度大小为(10)磁感应强度方向垂直纸面向外.导线1中电荷量为的正离子所受到的磁场力的大小为 2v(11)方向水平向右,与正离子所受到的电场力的方向相反. 第三步,在参考系S中,考虑导线2对导线1中正离子施加电场力和磁场力的大小和方向.由题设条件,导线2所带的正电荷与负电荷的和为零,即(12)因而,导线2对导线1中正离子施加电场力为零(13)注意到在S系中,导线1中正离子不动(14)导线2对导线1中正离子施加磁场力为零(15)式中,是在S系中导线2的电流在导线1处产生的磁感应强度的大小.于是,B在S系中,导线2对导线1中正离子施加电场力和磁场力的合力为零. 第四步,已说明在S系中导线2对导线1中正离子施加电场力和磁场力的合力为零,如果导线1中正离子还受到其他力的作用,所有其它力的合力必为零(因为正离子静止).在系中,导线2对导线1中正离子施加的电场力和磁场力的合力的大小为因为相对系,上述可能存在的其它力的合力仍应为零,而正离子仍处在勻速运动状态,所以(16)式应等于零,故(17)由(8)、(11)和(17)式得 k2e (18)km 评分标准:本题18分. (1)至(18)式各1分. 26。
全国中学生高中物理竞赛集锦(力学)答案
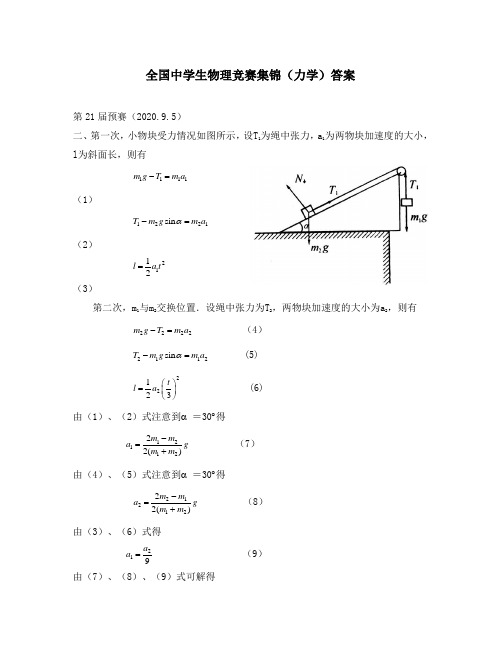
T0-mg=ma(15)
T0=2T(16)
由(14)、(15)和(16)式得
(17)
托盘的加速度向上,初速度v2向下,设经历时间t2,托盘速度变为零,有
v2=at2(18)
由(7)、(12)、(17)和(18)式,得
(19)
即砝码1自与弹簧分离到速度为零经历的时间与托盘自分离到速度为零经历的时间相等。由对称性可知,当砝码回到分离位置时,托盘亦回到分离位置,即再经历t1,砝码与弹簧相遇。题中要求的时间
(23)
评分标准:本题20分。
第一小问13分:求得式(15)、(16)各3分,式(17)2分,求得式(19)并说明“ ”取“+”的理由给5分。第二小问7分:式(20)2分,式(22)2分,式(23)3分。
第二十届复赛
三、参考解答
位于通道内、质量为 的物体距地心 为 时(见图复解20-3),它受到地球的引力可以表示为
(1)
(2)
因而
(3)
由能量守恒
(4)
由(3)、(4)两式及mB=2mA得
(5)
(6)
评分标准:
本题(15)分.(1)、(2)式各3分,(4)式5分,(5)、(6)两式各2分。
九、设从烧断线到砝码1与弹簧分离经历的时间为△t,在这段时间内,各砝码和砝码托盘的受力情况如图1所示:图中,F表示△t时间内任意时刻弹簧的弹力,T表示该时刻跨过滑轮组的轻绳中的张力,mg为重力,T0为悬挂托盘的绳的拉力。因D的质量忽略不计,有
要求作斜抛运动的摆球击中 点,则应满足下列关系式:
,(5)
(6)
利用式(5)和式(6)消去 ,得到
(7)
由式(3)、(7)得到
(8)
第37届全国中学生物理竞赛复赛试题解析,附试卷及答案

总评这套题作为复赛题的难度还是比较大的。
从这套题我们大概可以看出来,计算量增大、基础知识向大学普通物理靠拢(甚至直接用普通物理作为最底层的基础)、微积分作为最基本的数学工具、题目模型直接采用现实科研前沿模型已经成为物理竞赛的趋势。
这一套题从题型、模型新颖程度、计算量和阅读分析能力上来看逐渐向国际比赛的风格靠拢,是一套非常优秀的考题(虽然对于基础不扎实的考生来说并不友好)。
第一题热学题,采用了现实生活中的装置作为模型,比较考验抽象出模型的能力。
该题计算量较大,加上需要自己理解模型,对于未经过此类建模计算题目训练的同学难度较大。
较有区分度。
第二题这套卷子为数不多的较为常规的题目。
第一问考察刚体的动力学,第二题运动学分析。
考查基础知识,对刚体力学基础扎实的同学来说应该不难。
但要注意计算的仔细程度,第二问的运动学量矢量运算稍显复杂。
第三题考察交流电路系统。
需要对交流电路的微分方程有一个扎实的基础知识。
虽然这道题给出了解的形式降低了一部分难度,但是具体的计算量还是较大的。
对于理解谐振系统的解的物理意义的要求也很高。
同时交流电也是一个冷门考点,如果考生在备赛的时候忽略了这一部分知识的复习,那么这道题拿到高分的希望渺茫。
第四题基础的高能粒子物理题目。
回旋加速器应该是很常见的模型,具体原理应该要求考生掌握。
这套卷子中的常规送分题目,要把握好。
第五题相对论题目,内容比较基础,但涉及到繁杂的参照系变换。
对于在平时学习中弄不清参照系变换的考生有极大的考验。
并且由于过程繁杂,这道题对考生的细心程度和阅读理解能力造成了了不小的考验。
第六题光学题,并且和相对论结合。
这道题的模型和科研前沿结合较为紧密,并考察了光在介质中的传播的相对论变换。
计算量相对不大,但对于平时只练习常规题目的考生来说是个很大的挑战。
第七题引力波。
这直接用了近年来的科研最前沿的模型。
但冷静分析后在这道题里面引力波只是一个“能量损失的原因”,并不需要分析引力波的具体物理机制。
33届物理竞赛复赛试题

33届物理竞赛复赛试题全文共四篇示例,供读者参考第一篇示例:第33届物理竞赛复赛试题将会考察参赛者在物理知识和解题能力方面的实力。
本次考试难度适中,题目设计涵盖了力学、热学、光学、电磁学等各个领域的知识点。
以下是本次复赛试题的部分内容,希望可以帮助参赛者更好地备战。
一、力学部分1. 一辆质量为m的汽车以速度v行驶在水平路面上,其动能为多少?2. 一个质量为m的物体从高为h的斜面上滑下,当物体到达底部时,其速度为多少?3. 一个质点做直线运动,位置随时间t的变化满足公式x(t)=At^2+Bt+C,求该质点的加速度a(t)是多少?1. 一个理想气体的内能与温度之间的关系满足U = 3/2nRT,求该气体的热容比Cv / Cp是多少?2. 一个装满理想气体的容器,容器与外界热源完全绝缘,气体的体积变小了一半,气体的内能变化了多少?1. 一束光射入玻璃介质,入射角为30度,折射角为20度,求玻璃的折射率是多少?2. 一块凸透镜的焦距为10cm,物体放在焦距的前方10cm处,求成像的位置是多少?1. 一根长为L的直导线通以电流I,求该导线周围的磁感应强度是多少?2. 一个电容器的电容为C,电压为V,求电容器中储存的电荷量是多少?以上仅为部分试题内容,参赛者在考试时需要结合物理知识和解题技巧进行答题。
希望所有参赛者都能在本次竞赛中取得优异的成绩,加油!第二篇示例:第33届物理竞赛复赛试题欢迎参加第33届物理竞赛复赛!本次试题共分为三部分,包括选择题、填空题和解答题。
希望各位选手发扬科学精神,全力以赴,展现自己的物理才能。
祝你们取得优异的成绩!选择题:1. 下列哪个物理现象不是经典力学能够解释的?A. 光的干涉与衍射B. 行星的运动C. 惯性力的作用D. 弹性碰撞答案:A. 光的干涉与衍射2. 在真空中,光速的数值大小为多少?A. 300,000米/秒B. 200,000米/秒C. 400,000米/秒D. 500,000米/秒答案:A. 300,000米/秒3. 一个物体的质量是10kg,如果它处于地球表面,那么它的重力大小为多少?A. 98NB. 100NC. 105ND. 110N答案:A. 98N填空题:4. 一个在真空中的光波的波长为500nm,求它的频率。
全国高中物理竞赛复赛试题及答案

全国高中物理竞赛复赛试题及答案第二十届全国中学生物理竞赛复赛试卷一、(15分)给定一个半径为R的均匀带电球体a,球心为O。
已知球表面处的电势为U=1000V,取无限远处的电势为零。
一个动能为2000eV的质子b以与O O平行的方向射向a。
设b与O O线之间的垂直距离为l,求l的最大值,使得质子b能够与带电球体a的表面相碰。
再将质子换成电子,求l的最大值。
二、(15分)一个U形管包含两支管A、B和水平管C,它们都是由内径均匀的细玻璃管制成的。
三部分的截面积分别为SA=1.0×10^-2 cm^2,SB=3.0×10^-2 cm^2,SC=2.0×10^-2cm^2.在C管中有一段空气柱,两侧被水银封闭。
当温度为t1=27℃时,空气柱长为l=30cm,C中气柱两侧的水银柱长分别为a=2.0cm和b=3.0cm,A、B两支管都很长,其中的水银柱高均为h=12cm。
大气压强保持为p=76cmHg不变。
不考虑温度变化时管和水银的热膨胀。
试求气柱中空气温度缓慢升高到t=97℃时空气的体积。
三、(20分)有人提出了一种不用火箭发射人造地球卫星的设想。
其设想如下:沿地球的一条弦挖一通道,在通道的两个出口处A 和B,分别将质量为M的物体和质量为m的待发射卫星同时自由释放。
只要M比m足够大,碰撞后,质量为m的物体,即待发射的卫星就会从通道口B冲出通道。
设待发卫星上有一种装置,在待发卫星刚离开出口B时,立即把待发卫星的速度方向变为沿该处地球切线的方向,但不改变速度的大小。
这样待发卫星便有可能绕地心运动,成为一个人造卫星。
若人造卫星正好沿地球表面绕地心做圆周运动,则地心到该通道的距离为多少?已知M=20m,地球半径R=6400km。
假定地球是质量均匀分布的球体,通道是光滑的,两物体间的碰撞是弹性的。
四、(20分)一个半径为R、折射率为n的玻璃半球放在空气中,平表面中央半径为h的区域被涂黑。
2023年全国中学生物理竞赛复赛试题参考解答

全国中学生物理竞赛复赛试题参考解答、评分标准一、参考解答令 表达质子的质量, 和 分别表达质子的初速度和到达a 球球面处的速度, 表达元电荷, 由能量守恒可知2201122mv mv eU =+ (1)由于a 不动, 可取其球心 为原点, 由于质子所受的a 球对它的静电库仑力总是通过a 球的球心, 所以此力对原点的力矩始终为零, 质子对 点的角动量守恒。
所求 的最大值相应于质子到达a 球表面处时其速度方向刚好与该处球面相切(见复解20-1-1)。
以 表达 的最大值, 由角动量守恒有 max 0mv l mvR = (2)由式(1)、(2)可得20max 1/2eU l R mv =- (3) 代入数据, 可得max 22l R = (4) 若把质子换成电子, 则如图复解20-1-2所示, 此时式(1)中 改为 。
同理可求得 max 62l R =(5)评分标准: 本题15分。
式(1)、(2)各4分, 式(4)2分, 式(5)5分。
二、参考解答在温度为 时, 气柱中的空气的压强和体积分别为, (1)1C V lS = (2)当气柱中空气的温度升高时, 气柱两侧的水银将被缓慢压入A 管和B 管。
设温度升高届时 , 气柱右侧水银刚好所有压到B 管中, 使管中水银高度增大C BbS h S ∆= (3) 由此导致气柱中空气体积的增大量为C V bS '∆= (4)与此同时, 气柱左侧的水银也有一部分进入A 管, 进入A 管的水银使A 管中的水银高度也应增大 , 使两支管的压强平衡, 由此导致气柱空气体积增大量为A V hS ''∆=∆ (5)所以, 当温度为 时空气的体积和压强分别为21V V V V '''=+∆+∆ (6)21p p h =+∆ (7)由状态方程知112212p V p V T T = (8) 由以上各式, 代入数据可得2347.7T =K (9)此值小于题给的最终温度 K, 所以温度将继续升高。
物理竞赛1-35届真题分类02力学(无答案)

真题分类--力学(17初赛)二、(15分)一半径为 1.00m R =的水平光滑圆桌面,圆心为O ,有一竖直的立柱固定在桌面上的圆心附近,立柱与桌面的交线是一条凸的平滑的封闭曲线C ,如图预17-2所示。
一根不可伸长的柔软的细轻绳,一端固定在封闭曲线上的某一点,另一端系一质量为27.510kg m =⨯-的小物块。
将小物块放在桌面上并把绳拉直,再给小物块一个方向与绳垂直、大小为0 4.0m/s v =的初速度。
物块在桌面上运动时,绳将缠绕在立柱上。
已知当绳的张力为0 2.0NT =时,绳即断开,在绳断开前物块始终在桌面上运动.1.问绳刚要断开时,绳的伸直部分的长度为多少?2.若绳刚要断开时,桌面圆心O 到绳的伸直部分与封闭曲线的接触点的连线正好与绳的伸直部分垂直,问物块的落地点到桌面圆心O 的水平距离为多少?已知桌面高度0.80m H =.物块在桌面上运动时未与立柱相碰.取重力加速度大小为210m/s .(15届复赛)二、(25分)如图2所示,有两条位于同一坚直平面内的水平轨道,相距为h 。
轨道上有两个物体A 和B ,它们通过一根绕过定滑轮O 的不可伸长的轻绳相连接。
物体A 在下面的轨道上以匀速率v 运动。
在轨道间的绳子与轨道成300角的瞬间,绳子BO 段的中点处有一与绳相对静止的小水滴P 与绳子分离,设绳长BO 远大于滑轮直径,求:1、小水滴P 脱离绳子时速度的大小和方向。
2、小水滴P 离开绳子落到下面轨道所需要的时间。
(18届复赛)六、(27分)一玩具“火箭”由上下两部分和一短而硬(即劲度系数很大)的轻质弹簧构成.上部分1G 的质量为1m ,下部分2G 的质量为2m ,弹簧夹在1G 与2G 之间,与二者接触而不固连.让1G 、2G 压紧弹簧,并将它们锁定,此时弹簧的弹性势能为己知的定值0E .通过遥控可解除锁定,让弹簧恢复至原长并释放其弹性势能,设这—释放过程的时间极短.第一种方案是让玩具位于一枯井的井口处并处于静止状态时解除锁定,从而使上部分1G 升空.第二种方案是让玩具在井口处从静止开始自由下落,撞击井底(井足够深)后以原速率反弹,反弹后当玩具垂直向上运动到离井口深度为某值h 的时刻解除锁定.1.在第一种方案中,玩具的上部分1G 升空到达的最大高度(从井口算起)为多少?其能量是从何种形式的能量转化来的?2.在第二种方案中,玩具的上部分1G 升空可能达到的最大高度(亦从井口算起)为多少?并定量地讨论其能量可能是从何种形式的能量转化来的.(19届复赛)七、(26分)一根不可伸长的细轻绳,穿上一粒质量为m 的珠子(视为质点),绳的下端固定在A 点,上端系在轻质小环上,小环可沿固定的水平细杆滑动(小环的质量及与细杆摩擦皆可忽略不计)。
21---30届全国物理竞赛力学部分复赛试题

(第20届全国中学生物理竞赛复赛题)有人提出了一种不用火箭发射人造地球卫星的设想.其设想如下:沿地球的一条弦挖一通道,如图所示.在通道的两个出口处A和B,分别将质量为M的物体和质量为m的待发射卫星同时自由释放,只要M比m足够大,碰撞后,质量为m的物体,即待发射的卫星就会从通道口B冲出通道;设待发卫星上有一种装置,在待发卫星刚离开出口B时,立即把待发卫星的速度方向变为沿该处地球切线的方向,但不改变速度的大小.这样待发卫星便有可能绕地心运动,成为一个人造卫星.若人造卫星正好沿地球表面绕地心做圆周运动,则地心到该通道的距离为多少?己知M=20m,地球半径0R =6400 km.假定地球是质量均匀分布的球体,通道是光滑的,两物体间的碰撞是弹性的.(第20届全国中学生物理竞赛复赛题)有一半径为R的圆柱A,静止在水平地面上,并与竖直墙面相接触.现有另一质量与A相同,半径为r的较细圆柱B,用手扶着圆柱A,将B 放在A的上面,并使之与墙面相接触,如图所示,然后放手.己知圆柱A与地面的静摩擦系数为0.20,两圆柱之间的静摩擦系数为0.30.若放手后,两圆柱体能保持图示的平衡,问圆柱B与墙面间的静摩擦系数和圆柱B的半径r的值各应满足什么条件?(第20届全国中学生物理竞赛复赛题)如图所示,将一铁饼状小物块在离地面高为h 处沿水平方向以初速v 抛出.己知物块碰地弹起时沿竖直方向的分速度的大小与碰前沿竖直方向的分速度的大小之比为e (<1).又知沿水平方向物块与地面之间的滑动摩擦系数为μ(≠0):每次碰撞过程的时间都非常短,而且都是“饼面”着地.求物块沿水平方向运动的最远距离.(第21届全国中学生物理竞赛复赛题)二、(20分) 两颗人造卫星绕地球沿同一椭圆轨道同向运动,它们通过轨道上同一点的时间相差半个周期.已知轨道近地点离地心的距离是地球半径R 的2倍,卫星通过近地点时的速度RGM 43=v ,式中M 为地球质量,G 为引力常量.卫星上装有同样的角度测量仪,可测出卫星与任意两点的两条连线之间的夹角.试设计一种测量方案,利用这两个测量仪测定太空中某星体与地心在某时刻的距离.(最后结果要求用测得量和地球半径R 表示)(第21届全国中学生物理竞赛复赛题)如图所示,三个质量都是m 的刚性小球A 、B 、C 位于光滑的水平桌面上(图中纸面),A 、B 之间,B 、C 之间分别用刚性轻杆相连,杆与A 、B 、C 的各连接处皆为“铰链式”的(不能对小球产生垂直于杆方向的作用力).已知杆AB 与BC 的夹角为 ,< /2.DE 为固定在桌面上一块挡板,它与AB 连线方向垂直.现令A 、B 、C 一起以共同的速度v 沿平行于AB 连线方向向DE 运动,已知在C 与挡板碰撞过程中C 与挡板之间无摩擦力作用,求碰撞时当C 沿垂直于DE 方向的速度由v 变为0这一极短时间内挡板对C 的冲量的大小.(第22届全国中学生物理竞赛复赛题)图中的AOB 是游乐场中的滑道模型,它位于竖直平面内,由两个半径都是R 的1/4圆周连接而成,它们的圆心1O 、2O 与两圆弧的连接点O 在同一竖直线上.B O 2沿水池的水面.一小滑块可由弧AO 的任意点从静止开始下滑. 1.若小滑块从开始下滑到脱离滑道过程中,在两个圆弧上滑过的弧长相等,则小滑块开始下滑时应在圆弧AO 上的何处?(用该处到1O 的连线与竖直线的夹角表示).2.凡能在O 点脱离滑道的小滑块,其落水点到2O 的距离如何?O 1O 2O ABABCπ-αDE(第22届全国中学生物理竞赛复赛题) 如图所示,在一个劲度系数为 k 的轻质弹簧两端分别拴着一个质量为 m 的小球A 和质量为 2m 的小球B .A 用细线拴住悬挂起来,系统处于静止状态,此时弹簧长度为l .现将细线烧断,并以此时为计时零点,取一相对地面静止的、竖直向下为正方向的坐标轴Ox ,原点O 与此时A 球的位置重合如图.试求任意时刻两球的坐标.(第23届全国中学生物理竞赛复赛题)有一竖直放置、两端封闭的长玻璃管,管内为真空,管内有一小球自某处自由下落(初速度为零),落到玻璃管底部时与底部发生弹性碰撞.以后小球将在玻璃管内不停地上下跳动。
40届物理竞赛复赛试题

40届物理竞赛复赛试题正文:题目一:力学1. 一个作图题,给出了一个小球从竖直高度为H的斜面上滑下的过程,需要在图中标出速度的大小和方向。
2. 一枚小球质量为m,在光滑的水平面上的固定点O处,用一根长为L的线和一个质量为M的物块相连,物块贴在光滑的立直滑槽内。
物块和滑坡的间的磨擦系数为μ,求当小球质量为m大于多少时,保持平衡。
题目二:电磁学1. 一个小球质量m带电量Q被一个质量为M的平面吸引,在某一时刻,小球离平面的距离d取得最大值。
(1)求小球到平面的距离d的最大值;(2)当小球处于最大离平面距离时,求小球速度的大小;(3)当小球离平面距离为d时,求小球速度的大小;(4)求当小球发生碰撞时,小球的速度。
题目三:波动光学1. 一条平行两楔的波纹水槽中,波长为λ=0.5cm的平面波垂直入射。
设两周期相差Δφ=π/2。
问:(1)波纹的周期d为多少?(2)相邻两条波纹间的干涉纹比最暗处的光的强度要弱多少倍?题目四:热学1. 把一个质量为m的气体,温度为T1,压强为P1的气体,通过绝热不可逆过程,使气体膨胀到一个容器中,体积变为原来的V倍,气体对外做功W摩尔。
问:气体的温度和压强变化了多少?2. 一定质量的气体首先经过等体过程T1升到T2,然后经过等压过程T2降到T3,最后经过等容过程T3降到T1,求气体吸收或放出的热量。
题目五:现代物理1. 对于光子的双缝干涉实验,当干涉图样距离点光源A还远时,图样是变暗、亮纹变宽,且逐渐平摊至全光源的形态。
(1)解释为什么当干涉图样距离点光源A还远时图样是变暗、亮纹变宽,且逐渐平摊至全光源的形态?(2)对于A点光源,干涉图样是什么样的?(3)当A点光源与B、C两点光源距离相等时,干涉图样是什么样的?结语:以上就是40届物理竞赛复赛试题的题目及要求,不同题目涉及到力学、电磁学、波动光学、热学和现代物理等不同领域。
考生在回答这些问题时,需要熟练掌握各个物理学科的基本原理和公式,并能够运用所学知识解决实际问题。
第31届全国中学生物理竞赛复赛试题及答案

第31届全国中学生物理竞赛复赛试题及答案31届全国中学生物理竞赛复赛理论考试试题解答一、(12分)题目一:球形液滴的振动频率假设球形液滴振动频率与其半径r、密度ρ和表面张力系数σ之间的关系式为f=kρσr,其中k是常数。
根据单位分析法,可以得到单位等式[f]=[ρ][σ][r]。
力学的基本物理量包括质量m、长度l和时间t,分别对应的单位是千克(kg)、米(m)和秒(s)。
根据单位等式,[f]=[t]^-1,[r]=[l],[ρ]=[m][l]^-3,[σ]=[m][t]^-2.将这些单位代入单位等式,得到[t]^-1=[l]^-3[m]^[ρ][t]^-2[σ],即[t]^-1=[l]^[ρ][m]^[σ][t]^-2.由此可以得到三个未知量的关系式:α-3β=0,β+γ=0,2γ=1.解得α=-1,β=-1,γ=1/2.解法二:假设球形液滴振动频率与其半径r、密度ρ和表面张力系数σ之间的关系式为f=kρσr,其中k是常数。
根据单位分析法,可以得到单位等式[f]=[ρ][σ][r]。
在国际单位制中,振动频率的单位是赫兹(Hz),半径r的单位是米(m),密度ρ的单位是千克每立方米(kg/m^3),表面张力系数σ的单位是牛每米(N/m)=千克每秒平方(m/s^2)。
根据单位等式,[f]=s^-1,[r]=m,[ρ]=kg/m^3,[σ]=kg/s^-2.将这些单位代入单位等式,得到[s]^-1=[m][ρ][σ],即[s]^-1=[m][kg/m^3][kg/s^-2]。
将这个式子代入f=kρσr,得到k=f/ρσr。
1.(V。
T)。
(p。
V。
T)和(pf。
V。
T)分别表示气体在初态、中间态和末态的压强、体积和温度。
留在瓶内的气体先后满足绝热方程和等容过程方程:p1 * V1^γ = p2 * V2^γ (绝热方程)V1 = V2 * (p1/p2) (等容过程方程)联立以上两式可得:p1/T1 = p2/T2 = pf/Tf由此得到以下式子:p1/pf = (p1/pf)^(1/γ)ln(p1/pf) = ln(p1) - ln(pf) = (1/γ) * ln(p1/pf)pf = p1 / (e^(γ * ln(p1/pf)))2.根据力学平衡条件,有:pi = p + ρghipf = p + ρghf其中,p是瓶外大气压强,ρ是U型管中液体的密度,g 是重力加速度大小。
第十七届全国中学生物理竞赛复赛试题参考答案

第十七届全国中学生物理竞赛复赛试题参考答案一、解:设玻璃管内空气柱的长度为h,大气压强为p0,管内空气的压强为p,水银密度为ρ,重力加速度为g,由图4知p+(l-h)ρg=p0,①根据题给的数据,可知p0=lρg,得p=ρgh,②若玻璃管的横截面积为S,则管内空气的体积为V=Sh,③由②、③式,得p=(V/S)ρg,④即管内空气的压强与其体积成正比,由克拉珀龙方程pV=nRT,得ρg(V2/S)=nRT,⑤由⑤式可知,随着温度降低,管内空气的体积变小,根据④式可知管内空气的压强也变小,压强随体积的变化关系为p-V图上过原点的直线,如图5所示.在管内气体的温度由T1降到T2的过程中,气体的体积由V1变到V2,体积缩小,外界对气体做正功,功的数值可用图中划有斜线的梯形面积来表示,即有图4 图5W=(1/2)ρg((V1/S)+(V2/S))(V1-V2)=ρg(V12-V22)/2S,⑥管内空气内能的变化为ΔU=nCV(T2-T1),⑦设Q为外界传给气体的热量,则由热力学第一定律W+Q=ΔU,有Q=ΔU-W,⑧由⑤、⑥、⑦、⑧式代入得Q=n(T2-T1)(CV+(1/2)R),⑨代入有关数据得Q=-0.247J,Q<0,表示管内空气放出热量,故空气放出的热量为Q′=-Q=0.247J.(10)二、解:在由直线BC与小球球心O所确定的平面中,激光光束两次折射的光路BCDE如图6所示,图中入射光线BC与出射光线DE的延长线交于点G,按照光的折射定律有图6n0sinα=nsinβ,①式中α与β分别是相应的入射角与折射角,由几何关系还可知sinα=l/r.②激光光束经两次折射,频率ν保持不变,故在两次折射前后,光束中一个光子的动量的大小p与p′相等,即p=hν/c=p′,③式中c为真空中的光速,h为普朗克常量.因射入小球的光束中光子的动量p沿BC方向,射出小球的光束中光子的动量p′沿DE方向,光子动量的方向由于光束的折射而偏转了一个角度2θ,由图中几何关系可知2θ=2(α-β).④若取线段GN1的长度正比于光子动量p,GN2的长度正比于光子动量p′,则线段N1N2的长度正比于光子动量的改变量Δp,由几何关系得Δp=2psinθ=2(hν/c)sinθ,⑤△GN1N2为等腰三角形,其底边上的高GH与CD平行,故光子动量的改变量Δp的方向沿垂直CD的方向,且由G指向球心O.光子与小球作用的时间可认为是光束在小球内的传播时间,即Δt=2rcosβ/(cn0/n),⑥式中cn0/n是光在小球内的传播速率,按照牛顿第二定律,光子所受小球平均作用力的大小为f=Δp/Δt=n0hνsinθ/nrcosβ,⑦按照牛顿第三定律,光子对小球的平均作用力大小F=f,即F=n0hνsinθ/nrcosβ,⑧力的方向由点O指向点G.由①、②、④及⑧式,通过三角函数关系运算,最后可得F=(n0lhν/nr2)(1-).⑨三、解:1.相距为r的电量为Q1与Q2的两点电荷之间的库仑力FQ与电势能UQ公式为FQ=k(Q1Q2/r2),UQ=-k(Q1Q2/r),①现在已知正反顶夸克之间的强相互作用势能为U(r)=-k(4as/3r),根据直接类比可知,正反顶夸克之间的强相互作用力为F(r)=-k(4as/3r2),②设正反顶夸克绕其连线的中点做匀速圆周运动的速率为v,因二者相距r0,二者所受的向心力均为F(r0),二者的运动方程均为m1v2/(r0/2)=k(4as/3r02).③由题给的量子化条件,粒子处于基态时,取量子数n=1,得2m1v(r0/2)=h/2π.④由③与④两式,解得r0=3h2/8π2m1ask,⑤代入数据得r0=1.4×10-17m.⑥2.由③、④两式,可得v=(π/h)(k4as/3),⑦由v与r0可算出正反顶夸克做匀速圆周运动的周期T为T=2π(r0/2)/v=h3/2π2m1(k4as/3)2,⑧代入数值得T=1.8×10-24s,⑨由此可知τ/T=0.22.(10)因正反顶夸克的寿命只有它们构成的束缚系统的周期的1/5,故正反顶夸克的束缚态通常是不存在的.四、解:1.设太阳的质量为M0,飞行器的质量为m,飞行器绕太阳做圆周运动的轨道半径为R.根据所设计的方案,可知飞行器是从其原先的圆轨道上某处出发,沿着半个椭圆轨道到达小行星轨道上的,该椭圆既与飞行器原先的圆轨道相切,又与小行星的圆轨道相切.要使飞行器沿此椭圆轨道运动,应点燃发动机使飞行器的速度在极短的时间内,由v0变为某一值u0.设飞行器椭圆轨道达小行星轨道到时的速度为u,因大小为u0与u的这两个速度的方向都与椭圆的长轴垂直,由开普勒第二定律,得u0R=6uR,①由能量关系,有(1/2)mu02-G(M0m/R)=(1/2)mu2-G(M0m/6R),②由牛顿万有引力定律,有G(M0m/R2)=m(v02/R),或者v0=.③解①、②、③式,得u0=v0,④u=v0.⑤设小行星绕太阳运动的速度为v,小行星的质量M,由牛顿万有引力定律,有GM0M/(6R)2=Mv2/6R,得v=v0,⑥能够看出v>u.⑦由此可见,只要选择好飞行器在圆轨道上合适的位置离开圆轨道,使得它到达小行星轨道外时,小行星的前缘也正好运动到该处,则飞行器就能被小行星撞击.能够把小行星看做是相对静止的,飞行器以相对速度为v-u射向小行星,由于小行星的质量比飞行器的质量大得多,碰撞后,飞行器以同样的速率v-u弹离,即碰撞后,飞行器相对小行星的速度的大小为v-u,方向与小行星的速度的方向相同,故飞行器相对太阳的速度为u1=v+v-u=2v-u,或者将⑤、⑥式代入得u1=(v0.⑧假如飞行器能从小行星的轨道上直接飞出太阳系,它应具有的最小速度为u2,则有(1/2)mu22-G(M0m/6R)=0,得u2=v0,⑨能够看出u1=v0=u2.(10)飞行器被小行星撞击后具有的速度足以保证它能飞出太阳系.2.为使飞行器能进入椭圆轨道,发动机应使飞行器的速度由v0增加到u0,飞行器从发动机取得的能量E1=(1/2)mu02-(1/2)mv02=(1/2)m(12/7)v02-(1/2)mv02=(5/14)mv02.(11)若飞行器从其圆周轨道上直接飞出太阳系,飞行器应具有的最小速度为u3,则有(1/2)mu32-G(M0m/R)=0,由此得u3=v0.(12)飞行器的速度由v0增加到u3,应从发动机获取的能量为E2=(1/2)mu32-(1/2)mv02=(1/2)mv02,(13)因此E1/E2=(5/14)mv22/(1/2)mv22=0.71.(14)五、解法一:带电质点静止释放时,受重力作用做自由落体运动,当它到达坐标原点时,速度为v1==2.0m·s-1,①方向竖直向下.带电质点进入磁场后,除受重力作用外,还受到洛伦兹力作用,质点速度的大小与方向都将变化,洛伦兹力的大小与方向亦随之变化.我们能够设想,在带电质点到达原点时,给质点附加上沿x轴正方向与负方向两个大小都是v0的初速度,由于这两个方向相反的速度的合速度为零,因而不影响带电质点以后的运动.在t=0时刻,带电质点因具有沿x轴正方向的初速度v0而受洛伦兹力f1的作用,即f1=qv0B,②其方向与重力的方向相反.适当选择v0的大小,使f1等于重力,即qv0B=mg,③v0=g/(q/m)B=2.0m·s-1,④只要带电质点保持④式决定的v0沿x轴正方向运动,f1与重力的合力永远等于零.但如今,位于坐标原点的带电质点还具有竖直向下的速度v1与沿x轴负方向的速度v0,二者的合成速度大小为v==2.8m·s-1,⑤方向指向左下方,设它与x轴的负方向的夹角为α,如图7所示,则tgα=v1/v0=1,α=π/4,⑥图7因而带电质点从t=0时刻起的运动能够看做是速率为v0,沿x轴的正方向的匀速直线运动与在xOy平面内速率为v的匀速圆周运动的合成.圆周半径为R=mv/qB=0.56m.⑦带电质点进入磁场瞬间所对应的圆周运动的圆心O′位于垂直于质点如今速度v的直线上,由图7可知,其坐标为xO′=Rsinα=0.40m,⑧yO′=Rcosα=0.40m.圆周运动的角速度为ω=v/R=5.0rad·s-1.⑨由图7可知,在带电质点离开磁场区域前的任何时刻t,质点位置的坐标为x=v0t-[Rsin(ωt+α)-xO′],(10)y=yO′-Rcos(ωt+α),(11)式中v0、R、ω、α、xO′、yO′已分别由④、⑦、⑨、⑥、⑧各式给出.带电质点到达磁场区域下边界时,y=L=0.80m,代入(11)式,再代入有关数值,解得t=0.31s,(12)将(12)式代入(10)式,再代入有关数值,得x=0.63m,(13)因此带电质点离开磁场下边界时的位置的坐标为x=0.63m,y=0.80m,z=0.(14)带电质点在磁场内的运动可分解成一个速率为v的匀速圆周运动与一个速率为v0的沿x轴正方向的匀速直线运动,任何时刻t,带电质点的速度v′便是匀速圆周运动速度v与匀速直线运动的速度v0的合速度.若圆周运动的速度在x方向与y方向的分量为vx′、vy′,则质点合速度在x方向的分速度分别为vx′=vx+v0,(15)vy′=vy.(16)尽管=v,v由⑤式决定,其大小是恒定不变的,v0由④式决定,也是恒定不变的,但在质点运动过程中因v的方向不断变化,它在x方向与y方向的分量vx与vy都随时间变化,因此vx′与vy′也随时间变化,取决于所考察时刻质点做圆周运动速度的方向,由于圆周运动的圆心的y坐标恰为磁场区域宽度的一半,由对称性可知,带电质点离开磁场下边缘时,圆周运动的速度方向应指向右下方,与x轴正方向夹角α′=π/4,故代入数值得vx=vcosα′=2.0m·s-1,vy=vsinα′=2.0m·s-1,将以上两式及⑤式代入(15)、(16)式,便得带电质点刚离开磁场区域时的速度分量,它们分别为vx′=4.0m·s-1,(17)vy′=2.0m·s-1,(18)速度大小为v′==4.5m·s-1,(19)设v′的方向与x轴的夹角为β,如图8所示,则tgβ=vy′/vx′=1/2,得β=27°.(20)图8解法二:若以带电质点到达坐标原点O的时刻作为起始时刻(t=0),则质点的初速度为v1==2.0m·s-1,①方向沿y轴正方向.进入磁场区后,带电质点将受到洛伦兹力作用,洛伦兹力在x方向的分力取决于质点在y方向的分速度,因此质点动量在x方向的分量的增量为mΔvx=qvyBΔt=qΔyB,②Δy是带电质点在Δt时间内沿y方向的位移,质点在磁场中运动的整个过程中,此式对每一段Δt时间都成立,因此在t=0到t=t时间内x方向的分量的改变为mvx-mv0x=qB(y-y0),因初始时刻(t=0),带电质点在x轴方向的动量mv0x为零,其位置在原点,y0=0,因而得mvx=qyB,即vx=(qB/m)y.③当带电质点具有x方向的速度后,便立即受到沿y负方向的洛伦兹力的作用.根据牛顿第二定律,在y方向上有加速度ay,则may=mg-qvxB,④将③式代入④式,得may=-[(qB)2/m](y-(m2/q2B2)g),⑤令y′=y-D,⑥式中D=m2g/(qB)2=g/(q/m)2B2=0.40m,⑦即在y方向作用于带电质点的合力Fy=-ky′,其中k=q2B2/m,Fy是准弹性力,在Fy作用下,带电质点在y′方向的运动是简谐运动,其振动的圆频率为ω==5.0rad·s-1,⑧y′随时间变化的规律为y′=Acos(ωt+φ0),⑨或者y=Acos(ωt+φ0)+D,(10)图9A与φ0是待求的常量,质点的简谐运动能够用参考圆来描写,以所考察的简谐运动的振幅A为半径作一圆,过圆心O1作一直角坐标x′O1y′.若有质点M沿此圆周做匀速率圆周运动,运动的角速度等于所考察简谐运动的角频率ω,且按逆时针方向转动,在t=0时刻,点M的在圆周上的位置恰使连线O1M与y′轴的夹角等于⑨式中的常量φ0,则在任意时刻t,点O1与点M的连线与y′轴的夹角等于ωt+φ0,因此连线O1M在y′轴上的投影即为⑨式所示的简谐运动,将x′轴平行下移D=0.40m,连线O1M在y轴的投影即如(10)式所示(参看图9所示),点M做圆周运动的速度大小v=Aω,方向与O1M垂直,速度v的y分量就是带电质点沿y轴做简谐运动的速度,即vy=-Aωsin(ωt+φ0),(11)(10)与(11)两式中的A与φ0可由下面的方法求得:由于已知在t=0时,带电质点位于y=0处,速度vy=v1,把这个条件代入(10)式与(11)式,得Acosφ0+D=0,v1=-Aωsinφ0.解上面两式,结合①、⑧式,注意到振幅A总是正的,故得φ0=5π/4,(12)A=0.56m.(13)把(10)式代入③式,便得带电质点沿x轴运动的速度为vx=ωD+Aωcos(ωt+φ0),(14)(14)式表示带电质点在x方向上的速度是由两个速度合成的,即沿x方向的匀速运动速度ωD与x方向的简谐运动速度Aωcos(ωt+φ0)的合成,带电质点沿x方向的简谐运动匀速运动的位移为x′=ωDt.(15)由沿x方向的简谐振动速度Aωcos(ωt+φ0)可知,沿x方向振动位移的振幅等于速度的最大值与角频率的比值(参看图8),即等于A.由参考圆方法可知,沿x方向的振动的位移x″具有如下的形式,即Acos(ωt+φ0-(π/2))=Asin(ωt+φ0),它可能是x″=Asin(ωt+φ0),亦可能是x″-b=Asin(ωt+φ0).在本题中,t=0时刻,x应为零,故前一表示不符合题意.后一表示式中,b应取的值为b=-Asinφ0,故有x″=-Asinφ0+Asin(ωt+φ0).(16)带电质点在x方向的合位移x=x′+x″,由(15)、(16)式,得x=ωDt-Asinφ0+Asin(ωt+φ0).(17)(17)、(10)、(14)与(11)式分别给出了带电质点在离开磁场区域前任何时刻t的位置坐标与速度的x分量与y分量,式中常量ω、A、φ0、D已分别由⑧、(13)、(12)与⑦式给出.当带电质点达到磁场的下边界时,有y=L=0.80m,(18)将与(10)式有关的数据代入,可解得t=0.31s,(19)代入(17)式,得x≈0.63m,(20)将(19)式分别代入(14)、(11)式,得vx=4.0m·s-1,vy=2.0m·s-1,速度大小为v==4.5m·s-1,(21)速度方向为α=arctg(vy/vx)=27°.(22)图10六、1.由于光纤内所有光线都从轴上的点O出发,在光纤中传播的光线都与轴相交,位于通过轴的纵剖面内,图10为纵剖面内的光路图,设由点O发出的与轴的夹角为α的光线,射至A、B分界面的入射角为i,反射角也为i.该光线在光纤中多次反射时的入射角均为i,射至出射端面时的入射角为α.若该光线折射后的折射角为θ,则由几何关系与折射定律可得i+α=90°,①nAsinα=nFsinθ.②当i大于全反射临界角iC时将发生全反射,没有光能缺失,相应的光线将以不变的光强射向出射端面,而i<iC的光线则因在发生反射时有部分光线通过折射进入B,反射光强随着反射次数的增大而越来越弱,以致在未到达出射端面之前就已经衰减为零了.因而能射向出射端面的光线的i的数值一定大于或者等于iC,iC的值由下式决定,即nAsiniC=nB,③与iC对应的α值为αC=90°-iC,④当α0>αC时,即sinα0>sinαC=cosiC=时,或者nAsinα0>时,由点O发出的光束中,只有α≤αC的光线才满足i≥iC的条件,才能射向端面,如今出射端面处α的最大值为αmax=αC=90°-iC.⑤若α0<αC,即nAsinα0<时,则由点O发出的光线都能满足i>iC的条件,因而都能射向端面,如今出射端面处α的最大值为αmax=α0.⑥端面处入射角α最大时,折射角θ也达最大值,设为θmax,由②式可知nFsinθmax=nAsinαmax.⑦由⑥、⑦式可得,当α0<αC时,有nF=nAsinα0/sinθmax,⑧当α0≥αC时,由③至⑦式可得,nF=nAcosiC/sinθmax=/sinθmax,⑨θmax的数值可由图11上的几何关系求得sinθmax=((d2-d1)/2)/.(10)图11因此当α0<αC时,nF的表达式应为nF=nAsinα0(/((d2-d1)/2),(11)当α0≥αC时,有nF=(/((d2-d1)/2).(12)2.可将输出端介质改为空气,光源保持不变,按同样手续再做一次测量,可测得h1′、h2′、d1′、d2′,这里打撇的量与前面未打撇的量意义相同.已知空气的折射率等于1,故有当α0<αC时,有1=nAsinα0/((d2′-d1′)/2),(13)当α0≥αC时,有1=(/((d2′-d1′)/2),(14)将(11)、(12)两式分别与(13)、(14)式相除,均得nF=((d2′-d1′)/(d2-d1))(/).(15)此结果适用于α0为任何值的情况.。
2023高中物理竞赛复赛题

2023高中物理竞赛复赛题一、试卷整体结构这是一份2023高中物理竞赛复赛题的试卷哦。
试卷满分是100分呢。
二、具体题目1. 力学部分(共30分)第一题(5分):一个质量为m的小球,在光滑的斜面上,斜面倾角为θ,小球受到一个水平向右的恒力F的作用,求小球沿斜面向上运动的加速度。
第二题(8分):有一根轻质弹簧,劲度系数为k,一端固定在墙上,另一端连接一个质量为M的物体。
现在用一个力F拉动物体,使弹簧伸长了x,求此时物体的速度(假设物体从静止开始运动,忽略摩擦力)。
第三题(12分):一个行星绕着恒星做圆周运动,行星的质量为m,恒星的质量为M,行星与恒星之间的距离为r。
求行星的运动周期和行星受到的向心力。
第四题(5分):在一个光滑的水平面上,有两个质量分别为m1和m2的小球,它们以速度v1和v2相向运动,碰撞后粘在一起,求碰撞后的速度。
2. 电磁学部分(共35分)第五题(6分):一个平行板电容器,极板面积为S,极板间距为d,极板间充满相对介电常数为εr的电介质。
求电容器的电容。
第六题(8分):有一个半径为R的圆形导线,通有电流I,求圆心处的磁感应强度。
第七题(10分):一个带电粒子,电荷量为q,质量为m,以速度v进入一个匀强磁场,磁场方向垂直于粒子的速度方向,磁感应强度为B。
求粒子在磁场中的运动轨迹和运动周期。
第八题(6分):一个电阻为R的导体,两端的电压为U,求通过导体的电流和导体的电功率。
第九题(5分):一个电感为L的线圈,通有电流I,求线圈的自感电动势。
3. 热学部分(共20分)第十题(5分):一定质量的理想气体,初始状态的压强为p1,体积为V1,温度为T1。
经过等压变化后,体积变为V2,求此时的温度T2。
第十一题(8分):一个卡诺热机,高温热源的温度为T1,低温热源的温度为T2,求热机的效率。
第十二题(7分):有一个物体,质量为m,比热容为c,温度从T1升高到T2,求物体吸收的热量。
4. 近代物理部分(共15分)第十三题(5分):根据爱因斯坦的光电效应方程,解释光电效应的现象。
第十七届全国高中生物理竞赛复赛试题及答案#(精选.)

第十七届全国中学生物理比赛复赛试题题号一二三四五六总计全卷共六题,总分140 分一、( 20 分)在一大水银槽中竖直插有一根玻璃管,管上端封闭,下端张口.已知槽中水银液面以上的那部分玻璃管的长度l 76 cm ,管内封闭有n- 31.0 10 mol 的空气,保持水银槽与玻璃管都不动而想法使玻璃管内空气的温度迟缓地降低10℃,问在此过程中管内空气放出的热量为多少?已知管外大气的压强为76 cm 汞柱高,每摩尔空气的内能U C V T ,此中T为绝对温度,常量 C V 20.5 J (mol K) -1 ,普适气体常量R 8.31J (mol K) -1 。
二、( 20 分)如图复17-2 所示,在真空中有一个折射率为 n ( n n0, n0为真空的折射率)、半径为 r 的质地均匀的小球。
频次为的细激光束在真空中沿直线BC 流传,直线 BC 与小球球心 O 的距离为 l ( l r ),光束于小球体表面的点 C 点经折射进入小球(小球成为光流传的介质),并于小球表面的点 D 点又经折射进入真空.设激光束的频次在上述两次折射后保持不变.求在两次折射过程中激光束中一个光子对小球作用的均匀力的大小.三、( 25 分)1995年,美国费米国家实验室 CDF 实验组和 DO 实验组在质子反质子对撞机TEVATRON的实验中,察看到了顶夸克,测得它的静止质量 m111 2 -251.75 10 eV/c 3.1 10 kg ,寿命- 24s ,这是近十几年来粒子物理研究最重要的实验进展之一.0.4 101.正、反顶夸克之间的强互相作用势能可写为U (r ) 4a S,式中 r 是正、反顶夸克之k3r间的距离, a 0.12 是强互相作用耦合常数,k 是与单位制相关的常数,在国际单位制中Sk0.319 10-25 J m .为估量正、反顶夸克可否构成一个处在约束状态的系统,可把约束状态假想为正反顶夸克在相互间的吸引力作用下绕它们连线的中点做匀速圆周运动.如能构成约束态,试用玻尔理论确立系统处于基态中正、反顶夸克之间的距离r0.已知处于约束态的正、反夸克粒子知足量子化条件,即2mv r0 n hn 1, 2 , 3,2 2式中 mv r0为一个粒子的动量mv 与其轨道半径r0的乘积, n 为量子数, h 6.63 10-34 J s 2 2为普朗克常量.2.试求正、反顶夸克在上述假想的基态中做匀速圆周运动的周期T .你以为正、反顶夸克的这类约束态能存在吗 ?四、( 25 分)宇宙飞翔器和小行星都绕太阳在同一平面内做圆周运动,飞翔器的质量比小行星的质量小得好多,飞翔器的速率为v0,小行星的轨道半径为飞翔器轨道半径的 6 倍.有人企图借助飞翔器与小行星的碰撞使飞翔器飞出太阳系,于是他便设计了以下方案:Ⅰ.当飞翔器在其圆周轨道的适合地点时,忽然点燃飞翔器上的喷气发动机,经过极短时间后立刻封闭发动机,以使飞翔器获取所需的速度,沿圆周轨道的切线方向走开圆轨道;Ⅱ . 飞翔器抵达小行星的轨道时正好位于小行星的前缘,速度的方向和小行星在该处速度的方向相同,正好可被小行星碰撞;Ⅲ .小行星与飞翔器的碰撞是弹性正碰,不计焚烧的燃料质量.1.试经过计算证明按上述方案能使飞翔器飞出太阳系;2.设在上述方案中,飞翔器从发动机获得的能量为E1.假如不采纳上述方案而是令飞翔器在圆轨道上忽然点燃喷气发动机,经过极短时间后立刻封闭发动机,以使飞翔器获取足够的速度沿圆轨道切线方向走开圆轨道后能直接飞出太阳系.采纳这类方法时,飞翔器从发动机获得的能量的最小值用 E 表示,问E1为多少?2 E2五、( 25 分)在真空中成立一坐标系,以水平向右为x 轴正方向,竖直向下为 y 轴正方向,z轴垂直纸面向里(图复17-5).在0 y L 的地区内有匀强磁场,L 0.80 m ,磁场的磁感强度的方向沿 z 轴的正方向,其大小 B 0.10 T .今把一荷质比q / m 50 C kg-1的带正电质点在x 0 , y 0.20 m ,z 0 处静止开释,将带电质点过原点的时辰定为 t 0 时辰,求带电质点在磁场中任一时辰 t 的地点坐标.并求它刚走开磁场时的地点和速度.取重力加快度g10 m s-2。
第38届物理竞赛复赛试题

1、一物体在恒力作用下做直线运动,若突然将该恒力方向改变90度但大小不变,则物体之后的运动状态将是:A、继续做直线运动B、开始做曲线运动C、立即静止D、开始做匀速圆周运动(答案)B解析:物体原本在恒力作用下做直线运动,说明力与速度方向在同一直线上。
当力的方向突然改变90度后,力与速度方向不再同一直线上,物体将受到与速度方向不在同一直线上的力,因此开始做曲线运动。
2、关于光的折射,下列说法正确的是:A、光从光密介质进入光疏介质时,折射角总是大于入射角B、光从光疏介质进入光密介质时,折射角总是大于入射角C、光发生折射时,入射光线、折射光线和法线可能不在同一平面内D、光在两种介质的分界面上一定会发生折射(答案)A解析:根据折射定律,光从光密介质进入光疏介质时,折射角总是大于入射角,A项正确。
光从光疏介质进入光密介质时,折射角总是小于入射角,B项错误。
光发生折射时,入射光线、折射光线和法线一定在同一平面内,C项错误。
光在两种介质的分界面上若发生全反射,则不会发生折射,D项错误。
3、关于牛顿第三定律,下列说法正确的是:A、作用力和反作用力总是大小相等、方向相反、作用在不同物体上B、作用力和反作用力总是大小相等、方向相反、作用在同一物体上C、作用力和反作用力可以独立存在,不需要相互依存D、作用力消失后,反作用力仍会存在一段时间(答案)A解析:牛顿第三定律表明,作用力和反作用力总是大小相等、方向相反、作用在不同物体上,A项正确。
作用力和反作用力不能作用在同一物体上,否则物体将无法保持平衡,B 项错误。
作用力和反作用力是相互依存的,没有作用力就没有反作用力,C项错误。
作用力消失后,反作用力也会立即消失,D项错误。
4、关于电磁感应,下列说法正确的是:A、闭合电路的一部分导体在磁场中做切割磁感线运动时,导体中一定会产生感应电流B、闭合电路的全部导体在磁场中做切割磁感线运动时,导体中一定会产生感应电流C、感应电流的方向总是与导体切割磁感线的运动方向相同D、感应电流的产生需要闭合电路中的磁通量发生变化(答案)D解析:闭合电路的一部分导体在磁场中做切割磁感线运动时,并不一定会产生感应电流,需要满足磁通量发生变化的条件,A项错误。
40届物理竞赛复赛试卷

1、在静电场中,关于电场强度和电势的说法正确的是:A. 电场强度为零的地方,电势也一定为零B. 电场强度的方向处处与等势面垂直C. 由静止释放的正电荷,仅在电场力作用下的运动轨迹一定与电场线重合D. 电场中任一点的电场强度方向总是指向该点电势降落最快的方向(答案:B、D)解析:电场强度与电势无必然联系,电场强度为零的地方电势不一定为零;电场强度的方向处处与等势面垂直,且由高电势指向低电势;正电荷在电场中仅在电场力作用下,其运动轨迹不一定与电场线重合,除非电场线是直线且电荷初速度为零或初速度方向与电场线共线;电场中任一点的电场强度方向是电势降落最快的方向。
2、关于电磁波,下列说法正确的是:A. 电磁波在真空中的传播速度小于在介质中的传播速度B. 变化的电场一定能够产生变化的磁场C. 电磁波是由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动而产生的D. 电磁波的传播需要介质,无法在真空中传播(答案:C)解析:电磁波在真空中的传播速度最大,等于光速;均匀变化的电场产生恒定的磁场,非均匀变化的电场产生变化的磁场;电磁波是由同相振荡且互相垂直的电场与磁场在空间中以波的形式移动而产生的;电磁波的传播不需要介质,可以在真空中传播。
3、关于光的折射现象,下列说法正确的是:A. 光从光密介质进入光疏介质时,折射角大于入射角B. 光从光疏介质进入光密介质时,折射角大于入射角C. 光的折射现象中,入射角增大,折射角一定减小D. 光的折射现象中,入射光线、折射光线和法线一定在同一平面内(答案:A、D)解析:光从光密介质进入光疏介质时,折射角大于入射角;光从光疏介质进入光密介质时,折射角小于入射角;光的折射现象中,入射角增大,折射角也增大,但始终小于入射角(在光从光密介质进入光疏介质时);光的折射现象中,入射光线、折射光线和法线一定在同一平面内。
4、关于原子物理,下列说法正确的是:A. 原子核由质子和中子组成,质子和中子都是不可再分的粒子B. 原子核内部存在强相互作用力,使得核子紧密结合在一起C. 原子核发生衰变时,质量数和电荷数一定都守恒D. 原子核的裂变和聚变都是释放核能的过程,且裂变比聚变释放的能量更大(答案:B、C)解析:原子核由质子和中子组成,但质子和中子仍可分解为夸克等更小粒子;原子核内部存在强相互作用力,即核力,使得核子紧密结合在一起;原子核发生衰变时,遵循质量数和电荷数守恒定律;原子核的裂变和聚变都是释放核能的过程,但聚变反应释放的能量通常比裂变反应更大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)
以及对A点的力矩
即
(3)
式中 待求. 是过 的竖直线与过 的水平线的交点, 为 与 的交点.由几何关系有
(4)
取杆CD为研究对象,由平衡条件有
(5)
(6)
以及对 点的力矩
(7)
解以上各式可得
(8)
(9)
(10)
(11)
(12)
(13)
CD杆平衡的必要条件为
(14)
由(12)、(13)、(14)式得
3.解法一
取直角坐标系Oxy,原点O位于椭圆的中心,则哈雷彗星的椭圆轨道方程为
(1)
a、b分别为椭圆的半长轴和半短轴,太阳S位于椭圆的一个焦点处,如图1所示.
以 表示地球绕太阳运动的周期,则 ;以 表示地球到太阳的距离(认为地球绕太阳作圆周运动),则 ,根据开普勒第三定律,有
(2)
设c为椭圆中心到焦点的距离,由几何关系得
4、(20分)质量均匀分布的刚性杆AB、CD如图放置,A点与水平地面接触,与地面间的静摩擦因数为μA,B、D两点与光滑竖直墙面接触,杆AB和CD接触处的静摩擦因数为μC,两杆的质量均为m,长度均为l.
(1)已知系统平衡时AB杆与墙面夹角θ,求CD杆与墙面的夹角α应满足的条件(用α及已知量满足的方程式表示)。
(3)
(4)
由图1可知,P点的坐标
(5)
(6)
把(5)、(6)式代入(1)式化简得
(7)
根据求根公式可得
(8)
由(2)、(3)、(4)、(8)各式并代入有关数据得
(9)
可以证明,彗星绕太阳作椭圆运动的机械能为
(10)
式中m为彗星的质量.以 表示彗星在P点时速度的大小,根据机械能守恒定律有
(11)
得
(12)
1.若碰前滑块A的速度为 ,求碰撞过程中轴受到的作用力的冲量;
2.若碰后物块D、C和杆刚好做匀速转动,求碰前滑块A的速度 应满足的条件.(30届复赛)
6.(22分)如图,一质量均匀分布的刚性螺旋环质量为m,半径为R,螺距H =πR,可绕竖直的对称轴OO′,无摩擦地转动,连接螺旋环与转轴的两支撑杆的质量可忽略不计.一质量也为m的小球穿在螺旋环上并可沿螺旋环无摩擦地滑动,首先扶住小球使其静止于螺旋环上的某一点A,这时螺旋环也处于静止状态.然后放开小球,让小球沿螺旋环下滑,螺旋环便绕转轴OO′,转动.求当小球下滑到离其初始位置沿竖直方向的距离为h时,螺旋环转动的角速度和小球对螺旋环作用力的大小.(27届复赛)
代入有关数据得
(13)
设P点速度方向与 的夹角为 (见图2),根据开普勒第二定律
(14)
其中 为面积速度,并有
(15)
由(9)、(13)、(14)、(15)式并代入有关数据可得
(16)
4.二、参考解答:
1.建立如图所示坐标系Oxy.两杆的受力情况如图:
为地面作用于杆 的摩擦力, 为地面对杆 的支持力, 、 为杆 作用于杆 的摩擦力和支持力, 、 分别为墙对杆 和 的作用力, 为重力.取杆 和 构成的系统为研究对象,系统平衡时,由平衡条件有
.(1)
以A、B、C、D为系统,在碰撞过程中,系统相对于轴不受外力矩作用,其相对于轴的角动量守恒
.(2)
由于轴对系统的作用力不做功,系统内仅有弹力起作用,所以系统机械能守恒.又由于碰撞时间 很小,弹簧来不及伸缩碰撞已结束,所以不必考虑弹性势能的变化.故
.(3)
由(1)、(2)、(3)式解得
(4)
[代替(3)式,可利用弹性碰撞特点
.(3’)
同样可解,(5)
方向与 方向相反.于是,A对D的作用力为 的冲量为
(6)
方向与 方向相同.
以B、C、D为系统,设其质心离转轴的距离为 ,则
.(7)
质心在碰后瞬间的速度为
.(8)
轴与杆的作用时间也为 ,设轴对杆的作用力为 ,由质心运动定理有
(2)若μA=,μC=,θ=°,求系统平衡时α的取值范围(用数值计算求出)。(28届复赛)
5.(20分)一长为2l的轻质刚性细杆位于水平的光滑桌面上,杆的两端分别固定一质量为m的小物块D和一质量为 ( 为常数)的小物块B,杆可绕通过小物块B所在端的竖直固定转轴无摩擦地转动.一质量为m的小环C套在细杆上(C与杆密接),可沿杆滑动,环C与杆之间的摩擦可忽略.一轻质弹簧原长为l,劲度系数为k,两端分别与小环C和物块B相连.一质量为m的小滑块A在桌面上以垂直于杆的速度飞向物块D,并与之发生完全弹性正碰,碰撞时间极短.碰撞时滑块C恰好静止在距轴为 ( )处.
(29届复赛)
3.(20分)如图所示,哈雷彗星绕太阳S沿椭圆轨道逆时针方向运动,其周期T为年。1986年它过近日点P0时,与太阳S的距离r0=,AU是天文单位,它等于地球与太阳的平均距离。经过一段时间,彗星到达轨道上的P点,SP与SP0的夹角θP=°.已知:1AU=×1011m,引力常量G=×10-11m3?kg-1?s-2,太阳质量mS=×1030kg.试求P到太阳S的距离rP及彗星过P点时速度的大小及方向(用速度方向与SP0的夹角表示)。(28届复赛)
近几全国物理竞赛复赛力学
近几年全国物理竞赛复赛力学
1.(15分)一半径为 、内侧光滑的半球面固定在地面上,开口水平且朝上.一小滑块在半球面内侧最高点处获得沿球面的水平速度,其大小为 ( ).求滑块在整个运动过程中可能达到的最大速率.重力加速度大小为 .(30届复赛)
2.如图所示,两根刚性轻杆 和 在 段牢固粘接在一起, 延长线与 的夹角 为锐角,杆 长为 ,杆 长为 。在杆的 、 和 三点各固连一质量均为 的小球,构成一刚性系统。整个系统放在光滑水平桌面上,桌面上有一固定的光滑竖直挡板,杆 延长线与挡板垂直。现使该系统以大小为 、方向沿 的速度向挡板平动。在某时刻,小球 与挡板碰撞,碰撞结束时球 在垂直于挡板方向的分速度为零,且球 与挡板不粘连。若使球 碰撞后,球 先于球 与挡板相碰,求夹角 应满足的条件。
(15)
AB杆平衡的必要条件为
(16)
由(10)、(11)、(16)式得
(17)
因此,使系统平衡, 应满足的条件为(15)式和(17)式.
2.将题给的数据代入(15)式可得
(18)
将题给的数据代入(17)式,经数值计算可得
(19)
因此, 的取值范围为
(20)
5.由于碰撞时间 很小,弹簧来不及伸缩碰撞已结束.设碰后A、C、D的速度分别为 、 、 ,显然有
