第十六届华罗庚金杯少年数学邀请赛决赛试卷(七年级组A卷)含答案
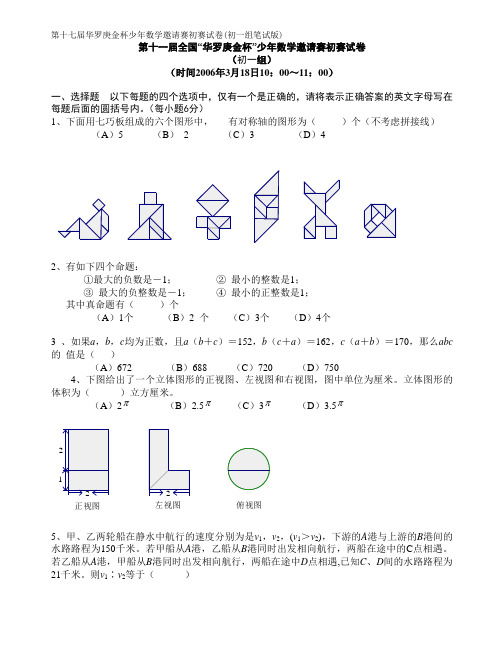
第十七届华杯赛决赛初一笔试A答案

第十七届华罗庚金杯少年数学邀请赛决赛笔试试题A 参考答案(初一组)一、填空(每题 10 分, 共80分)一、填空题(每小题 10分, 共80分)1. 计算:=-⨯-+⎪⎭⎫⎝⎛-⨯-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--÷---⨯-)]21(31[81221|10|)1()2(22334 . 原式=43210219122--⨯++=31226-⨯=4216-=-2. 一串有规律排列的数, 从第二项起每一项都等于1加前一项的倒数之和.当第五项是0时, 第一项是 .分析:设这列数从第一项起依次为12345,,,,a a a a a 根据题意4101a =+,可以得出41a =-。
倒推可以得到135a =-3. 如图, AB=BC=CA=AD , 则∠BDC= .解:设AC 与BD 的交点是E∵AB=BC=CA=AD∴△ABC 是正三角形,每个内角为600,△ABD 和△ACD 是等腰三角形。
∴∠ABD =∠ADB ,∠ACD =∠ADC∵∠ABE +∠BAE +∠BEA =∠EDC +∠DCE+∠CED 。
∵∠BEA=∠CED∴∠ABE +∠BAE =∠EDC +∠DCE 。
∵∠DCE=∠EDC+∠ADB∴∠ABE +∠BAE=∠EDC+∠EDC+∠ADB 。
∴∠BAE=∠EDC+∠EDC ,即600=2∠EDC ∴∠EDC =3004. 已知c b a 2+=, c b 3=, 207--=a b c , 那么b =_______. 解:∵c b a 2+=, c b 3=∴5a c =把a ,b 的值代入207--=a b c ,得21520c c c =--,得解方程得c =43把解方程得c =43带入c b 3=,得4b =分析:根据c b a 2+=, c b 3=,得到5a c =。
把a ,b 的值代入207--=a b c ,得到关于c 的一元一次方程。
21520c c c =--,解方程得c =43,4b =。
(完整版)第11-17届初一华杯赛试题及答案
由上式和b >α,b=13,α=1,d=l所以,K=12,m和n有唯一解m=13n =156.
答:m=13n =156.
7、已知 ,则小于S的最大的整数是(0)
8.如图2,数轴上标有2n+1个点,它们对应的整数是:
为了确保从这些点中可以取出2006个,其中任何两个点之间的距离都不等于4,则n的最小值是(2005)
二.解答下列各题,要求写出简要过程
9、如图3,ABCD是矩形,BC=6cm,AB =10cm,AC和
BD是对角线.图中的阴影部分以CD为轴旋转一周,则阴影
②直角边为1的三角形有36×2=72(个);斜边长是2的三角形,1-6行依次有4+4+4+3+1+4=20(个),1-6列依次3+3+3+2+3+3=17(个),共20+17=37(个);直角边长是2的1-2行8个,2-3行6个,3-4行2个,4-5行8个,5-6行6个,共8+6+2+8+6=30(个);直角边长是3的1-3行4个,3-5行2个,4-6行4个,共4+2+4=10(个);斜边长是4的1-4行1个,2-5行2个,4-5行1个,共1+2+1=4(个);直角边长是4的3-6行2个。共72+37+30+10+4+2=155(个)
第十一届全国"华罗庚金杯"少年数学邀请赛
决赛试卷(初一组)
(红色字为参考答案)
(时间2006年4月22日10:00~l l :30〉
一、.填空
1、计算: ( )
第十六届华罗庚金杯少年数学邀请赛初一决赛A试卷答案及其详细解析

解析:因为在1~22之间只有13、17、19没有相对应的倍数,所以三个 数中只有一个数和1组成一个整数分数;其余的数都可以成相对应的整 数分式,如:
7.下面两串单项式各有2011个单项式:, 其中为非负整数, 则这两串 单项式中共有 402 对同类项. 解析: 8.将能被3整除、被5除余2、被11除余4的所有这种正整数依照从小到 大的顺序排成一列, 记为. 如果, 则等于 13 . 解析: 二、解答下列各题(每题10分, 共40分, 要求写出简要过程) 9.将9个各不相同的正整数填在3×3表格的格子中, 一个格子填一个 数, 使得每个2×2子表格中四个数的和都恰好等于100. 求这9个正整 数总和的最小值. 解析:我们可以在每一个小格子里设字母
2011年第十六届华罗庚金杯少年数学ห้องสมุดไป่ตู้请赛决赛试题A (初中组)
一、填空题(每小题 10分, 共80分) 1.计算: =. 解析: 2.算式: 中的汉字代表0~9的数字, 相同的汉字代表相同的数字, 不 同的汉字代表不同的数字, 所代表的四位数是 8547 . 解析: 3.将12个小球放入编号为1至4的四个盒子中, 每个盒子中的小球数不 小于盒子编号数, 那么共有 10 种不同的放法. 解析: 4.有一列数, 第一个数是10, 第二个数是20, 从第三个数开始, 每个 数都是前面所有数的平均数, 那么第2011个数是 15 . 解析:第一个数和第二个数的平均数。则第三个数也是15.第四个数还 是15 、由此可知。后面的N个数都是15 ,则第2011个数还是15. 5.设是有理数, , 则P的最小值为 21 . 解析:去绝对值符号 得到函数 ;由函数图像可知,当x=3是取得最小 值,Pmin =21
华杯赛决赛第13~16届(初一组)试题及答案

y 的, 而当 y 1时, 由第一个等式得到 2x 1, 所以 x 1 .
2 评分参考: 1) (1)之前给 2 分; 2) (1)和(2)各给 4 分.
三、解答下列各题(每题 15 分,共 30 分,要求写出详细过程)
1 k
4k 2 9
4k
2
9
,
其中,
对于有理数
x,
x= x x.
所以有1 k2
,
9
1
1
k
4k 9
2
0.
当 k 取不同整数时, 1 k 4k 2 的情况如下表: 9
k
2
1
0
=1
=2
xy 0 . 因此, 三个相等的式子只有两种可能:
(1) x y xy x . 由后一等式得到, y 1或 y 1, 而 y 1是不可能的, 因为 y
此时由第一个等式得到 x 1 x , 矛盾. 当 y 1 时, 由第一个等式得到 x 1 x , 即 2x 1 , 所以 x 1 .
第十三届全国“华罗庚庚金杯”少年数学邀请赛决赛试卷(初一组)
第十三届“华罗庚金杯”少年数学邀请赛 决赛试卷(初一组)
(建议考试时间:2008 年 4 月 19 日 10:00~11:30)
一、填空(每题 10 分,共 80 分)
1. 某地区 2008 年 2 月 21 日至 28 日的平均气温为-1℃,2 月 22 日至 29 日的平
枚围棋
第十三届全国“华罗庚庚金杯”少年数学邀请赛决赛试卷(初一组)
第十届全国华罗庚金杯少年数学邀请赛初一组决赛试卷与解答

第十届全国”华罗庚金杯”少年数学邀请赛决赛试题:初一组一. 填空(每题10分,共80分)1.①计算: 22111134413(12)(0.5)(2)22412433⎡⎤-⨯-÷-÷⨯-⨯--=⎣⎦ . ②已知: 0abc ≠且0a b c ++=,则a b b c c a a b b c c a++= . 2.m 和n 均不为零, 233x y 和2235m nx y ++-是同类项,则322332233395369m m n mn n m m n mn n -++=+-+ . 3.由于浮力的作用,金放在水里秤量和它的重量比较,在水中的”重量”会减少119;银放在水里秤量和它的重量相比较,在水中的”重量”会减少110.某个只含有金银成分的古文物,重量是150克,在水中秤量,”重量”是141克,则古文物中金占 %.(精确到1%)4.图1是几何学中非常著名的美丽的轴对称的图形,它有 条对称轴.5.甲加工一种零件,乙加工另一种零件.甲用A 型机器需要6小时才能完成任务,用B 型机器效率降低60%;乙用B 型机器需要10小时才能完成任务,用A 型机器效率提高20%.如果甲用A 型机器,乙用B 型机器同时开始工作,中途某一时刻交换使用机器,甲和乙同时完成任务.则甲完成任务所用的时间是 小时.6.一个直角三角形三条边的长度是3,4,5.如果分别以各边为轴旋转一周,得到三个立体,那么三个立体中最大的体积和最小的体积的比是 .7.一列自然数0,1,2,3……,2005,……,2024.第一个数是0,从第二个数开始,每一个都比它前一个大1,最后一个是2004.现在将这列自然数排成以下数表:3 8 15 (1)2 7 14 (4)5 6 13 …… 9 10 11 12 ………… …… …… …… ……规定横排为行,竖排为列,则2005在数表中位于第 行和第 列。
8。
(31)635m x x -=-是关于x 的方程,为确保该方程的解是负整数,m 能取的最大 值 。
“华罗庚金杯”少年数学邀请赛(口试)试题1-10届

华罗庚金杯少年数学邀请赛口试试题第01届华罗庚金杯少年数学邀请赛口试试题1. 这是七巧板拼成的正方形,正方形边长20厘米,问七巧板中平行四边形的一块(如右图中阴影部分)的面积是多少?2.从所有分母小于10的真分数中,找出一个最接近0.618的分数。
3.有49个小孩子,每人胸前有一个号码,号码从1到49各不相同,请你挑选出若干个小孩,排成一个圆圈,使任何相邻两个小孩的号码数的乘积小于100,你最多能挑选出多少个小孩子?4.有一路公共汽车,包括起点和终点站共有15个车站,如果有一辆车,除终点到站外,每一站上车的乘客中,恰好各有一位乘客从这一站到以后的每一站,为了使每位乘客都有座位,问这辆公共汽车最少要有多少个座位?5.正方形的树林每边长1000米,里面有白杨树和榆树,小明从树林的西南角走入树林,碰见一株白杨树就往正北走,碰见一株榆树就往正东走,最后他走了东北角上,问:小明一共走了多少米的距离?6.自然数按从小到大的顺序排成螺旋形,在2处拐第一个弯,在3处拐第二个弯,在5处拐第三个弯……问拐第二十个弯的地方是哪一个数?第02届华罗庚金杯少年数学邀请赛口试试题1、如下图是一个对称的图形,黑色部分面积大还是阴影部分面积大?2、你能不能将自然数1到9分别填入右面的方格中,使得每个横格中的三个数之和都是偶数?3、司机开车按顺序到五个车站接学生到学校(如下图),每个站都有学生上车,第一站上了一批学生,以后每站上车的人数都是前一站上车人数的一半,车到学校时,车上最少有多少学生?4、如图中五个正方形的边长分别是1米、2米、3米、4米、5米。
问:白色部分面积与阴影部分面积之比是多少?5、用1、2、3、4、5这五个数两两相乘,可以得到10个不同的乘积,问乘积中是偶数多还是奇数多?6、7、将右边的硬纸片沿虚线折起来,便可作成一个正方体,问:这个正方体的2号面对面是几号面?(如下图)8、下面是一个11位数,它的每三个相邻数之和都是20,你知道打“?”的数字是几?9、有八张卡片,右图分别写着自然数1到8,从中取出三张,要使这三张卡片上的数字之和为9,问有多少种不同的取法?第03届华罗庚金杯少年数学邀请赛团体决赛口试1.一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道红条,如右图阴影所示部分,红条宽都是2厘米.问:这条手帕白色部分的面积是多少?2.伸出你的左手,从大拇指开始如图所示的那样数数字,1,2,3,……,问:数到1991时,你数在那个手指上?3.有3个工厂共订300份吉林日报,每个工厂订了至少99份,至多101份.问:一共有多少种不同的订法?4.图上有两条垂直相交的直线段AB、CD,交点为E(如下图).已知:DE=2CE,BE=3AE.在AB和CD上取3个点画一个三角形.问:怎样取这3个点,画出的三角形面积最大?5.如下图中有两个红色的圆,两个蓝色的圆,红色圆的直径分别是1992厘米和1949厘米,蓝色圆的直径分别是1990厘米和1951厘米.问:红色二圆面积大还是蓝色二圆面积大?6.在一张9行9列的方格纸上,把每个方格所在的行数和列数加起来(如下图),填在这个方格中,例如a=5+3=8.问:填入的81个数字中,奇数多还是偶数多?7.能不能在下式:1□2□3□4□5□6□7□8□9=10的每个方框中,分别填入加号或减号,使等式成立?8.把一个时钟改装成一个玩具钟(如右图),使得时针每转一圈,分针转16圈,秒针转36圈.开始时3针重合.问:在时针旋转一周的过程中,3针重合了几次?(不计起始和终止的位置).9.将1,2,3,4,5,6,7,8这8个数分成3组,分别计算各组数的和.已知这3个和互不相等,且最大的和是最小的和的2倍.问:最小的和是多少?10.这是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上.问:共有多少种不同的放法(如下图)?11.这是两个圆,它们的面积之和为1991平方厘米,小圆的周长是大圆周长的90%(如右图).问:大圆的面积是多少?12.有一根1米长的木条,第一次去掉它的,第二次去掉余下木条的;第三次又去掉第二次余下木条的,等等;这样一直下去,最后一次去掉上次余下木条的.问:这根木条最后还剩下多长?13.这是一个楼梯的截面图(如下图),高2.8米,每级台阶的宽和高都是20厘米.问:此楼梯截面的面积是多少?14.请找出6个不同的自然数,分别填入6个括号中,使这个等式成立.第04届华罗庚金杯少年数学邀请赛团体决赛口试1.2×3×5×7×11×13×17这个算式中有七个数连乘,请回答:最后得到的乘积中,所有数位上的数字和是多少?请讲一讲你是怎样算的?2.这是一个中国象棋盘(图中小方格都是相等的正方形,“界河”的宽等于小正方形边长),黑方有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12, 13,14中的两个位置.问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?3.将一根长为374厘米的合金铝管截成若干根36厘米和24厘米两种形状的短管(加工损耗忽略不计)问:剩余部分的管子最少是多少厘米?4.乙两人同时从A出发向B行进,甲速度始终不变,乙在走前面路程时,速度为甲的2倍,而走后面路程时,速度是甲的,问甲、乙二人谁选到B?请你说明理由。
第十六届华赛杯小学组决赛试题及答案

第十六届华罗庚金杯少年数学邀请赛决赛试题(深圳赛区小学组)(时间: 2011年4月16日)一、填空(每题 10 分, 共80分)1.11122181819 .2320320192020⎛⎫⎛⎫⎛⎫++++++++++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭2.甲车从A 出发驶向B,往返来回;乙车从B 同时出发驶向A,往返来回.两车第一次相遇后,甲车继续行驶4小时到达B ,乙车继续行驶1小时到达A. 若A,B 两地相距100千米,那么当甲车第一次到达B 时,乙车的位置距离A 千米。
3.每个铅字上刻有一个数码.如果印刷十二页书,所用的页码铅字要以下15个:1,2,3,4,5,6,7,8,9,1,0,1,1,1,2。
现要印刷一本新书,从库房领出页码铅字共2011个,排版完成后有剩余.那么,这本书最多有页.最少剩余 个铅字.4. 一列数:8,3,1,4,.….., 从第三个开始,每个数都是最靠近它前两个数的和的个位数.那么第2011个数是 .5.编号从1到50的50个球排成一行,现在按照如下方法涂色:1)涂2个球;2)被涂色的2个球的编号之差大于2.如果一种涂法被涂色的两个球与另一种涂法被涂色的两个球至少有一个是不同号的,这两种涂法就称为”不同的”.那么不同的涂色方法有种.6. A,B两地相距100千米。
甲车从A到B要走m个小时,乙车从A 到B要走n个小时,m ,n是整数.现在甲车从A,乙车从B同时出发,相向而行,经过5小时在途中C点相遇。
若甲车已经走过路程的一半,那么C到A路程是千米。
7. 自然数b与175的最大公约数记为d. 如果176(111)51⨯-⨯+=⨯+,b d d则b = .8. 如右图. ABCD为平行四边形.AE=2EB.若三角形CEF的面积=1.那么,平行四边形ABCD的面积= .二、解答下列各题(每题10 分, 共40分, 要求写出简要过程)9.三位数的十位数字与个位数字的和等于百位数字的数,称为”好数”.共有多少个好数?10.在下列2n 个数中,最多能选出多少个数,使得被选出的数中任意两个数的比都不是2或12?2345213, 32, 32, 32, 32, 32,, 32.n -⨯⨯⨯⨯⨯⨯11 .一个四位数abcd 和它的反序数dcba 都是65 的倍数.求这个数.12. 用写有+1和-1的长方块放在10n方格中,使得每一列和每一行的数的乘积都是正的,n的最小值是多少?三、解答下列各题(每题15 分, 共30分, 要求写出详细过程)13. 十五个盒子,每个盒子装一个白球或一个黑球.,且白球不多于 12个.你可以任选三个盒子来提问:“这三个盒子中的球是否有白球?”并得到真实的回答. 那么你最少要问多少次,就能找出一个或更多的白球?14. 求与2001互质,且小于2001的所有自然数的和。
(华杯)16届初一总决赛试题答案讲解版

第十六届华罗庚金杯少年数学邀请赛总决赛初一组一试试题解答一、填空题(共3题,每题10分)1. 计算)]5(31[)41(2)32(|231|)1()2(22343-⨯-+-⨯-⎥⎦⎤⎢⎣⎡--÷---⨯-= 解: 3432228594(2)(1)|123|()8122832781146472()[13(5)]4⎡⎤-⨯---÷---⨯-÷--⎢⎥⎣⎦==+-⨯-+-⨯- 6459431.4784--==-⨯ 2. 正方形ABCD 的面积等于625平方厘米.如图,DE 与CF 相交于G.已知125ADE CDG S S ∆∆==平方厘米.△BFG 的面积是 平方厘米.答:△BFG 的面积是50平方厘米.解:由于正方形ABCD 的面积等于625平方厘米.所以,边长25AB =厘米.由于125ADE S ∆=平方厘米,所以AE =10厘米.连接CE , 则1162531222CDE S ∆=⨯=(平方厘米). 而已知125CDG S ∆=(平方厘米), 则1252,312.55CDG CDE S DG DE S ∆∆===连接AG . 由221255055ADG ADE S S ∆∆==⨯=(平方厘米) 但16252ADGCBG S S ∆∆+=⨯,而16252BFG CBG S S ∆∆+=⨯,比较可得 50BFG ADG S S ∆∆==(平方厘米).3. 用长度分别为50,,2,1 的木条去摆三角形,每个三角形的三条边的长度分别为c b a ,,,c b a <<,问),,(c b a 最多有多少种不同的取法?答案:9500.解:利用三条边可以构成三角形的条件:任意的两个边的和大于第三边. 边长为1的木条不能与其它长度的木条构成三角形.三角形的最小边长为2时,边长为2的木条只能与差值为1的两个木条构成三角形,故有47对.三角形的最小边长为3时,边长为3的木条只能与差值为1,2的两个木条构成三角形,故有46+45对.三角形的最小边长为4时,边长为3的木条只能与差值为1,2,3的两个木条构成三角形,故有45+44+43对.......三角形的最小边长为k ()25≤k 时,边长k 为的木条只能与差值为1,2,3,⋯,1-k 的两个木条构成三角形,故有(49)(491)(4922)k k k -+--++-+ 对.三角形的最小边长为k ()25>k 时,边长k 为的木条只能与差值为1,2,3,⋯,1-k 的两个木条构成三角形,故有1)149()49(++--+- k k 对. 故总数为(47461)(45441)(43421)(212k k +++++++++++++-+-+++ (321)1++++ 47244523(21)53321k k =⨯+⨯++-⨯++⨯+⨯+()22224231(24231)9500.=+++-+++=二、解答题(共3题,每题10分,写出解答过程)4. 用)(n S 表示自然数n 的数字和,如1)1(=S ,6)123(=S ,10)1234(=S 等等,求自然数n ,使得2011)(=+n S n .答: 1991.解1: 2011)(=+n S n ,20111900<<∴n 则可设y x n ++=101900或y x n ++=102000,其中90,90≤≤≤≤y x ,且y x ,为整数.若y x n ++=101900,则201191101900=++++++y x y x ,即101211=+y x ⎩⎨⎧==∴19y x 1991=n 若y x n ++=102000,则20112102000=+++++y x y x ,即9211=+y x 没有符合条件的整数解.因此,n =1991.解2:因为()(mod9),n S n ≡要使2011)(=+n S n ,只须()2011(mod9),n S n +≡ 即220114(mod9)2(mod9).n n ≡≡⇒≡已知在2011n ≤时()S n 最大为38,所以19832011,n ≤≤其中被9除余2的有1991,2000,2009.其中只有1991满足1991+20=2011,所以1991.n =5. 两个21位自然数m 和n ,每个都由三个1、三个2、三个3、三个4、三个5、三个6和三个7组成,使得nm k =是自然数,问k 能取哪几个自然数?说明你的理由.答:1.解:显然777666555444333222111 1.777666555444333222111k == 假设存在这样的m 和n ,使得数m n 是一个大于1的自然数,则可设m k n=,故m kn =. 两边分别除以9,用数被9除的性质知m 和n 被9除的余数均等于3(1234567)⨯++++++被9除的余数,即84被9除的余数,为3. 因此3与3k 模9同余. 由7776665554443332221117111222333444555666777m k n =≤<, 及m 和n 不同(即1k ≠)推得4k =,即4m n =. 考虑数n 最低位的数字7,当把n 乘以4时,这个数字7的下一位(如果有)最多为6,因此乘以4最多进两位,这说明m 中对应位的数字为8(下面不进位,7×4=28)或9(下面进一位)或0(下面进两位),这与m 由三个1、三个2、三个3、三个4、三个5、三个6和三个7组成相矛盾!即不存在满足条件的m 和n .使得数m n是一个大于1的自然数. 所以,只有 1.k =6. 使得关于未知数x 的方程k x x =⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡32无解的自然数 k 由小到大排成一行,其前2011个k 的值之和等于多少?解. k0 1 2 3 x 1 2 3 4 23x x ⎡⎤⎡⎤+⎢⎥⎢⎥⎣⎦⎣⎦ 0 1 2 3 设5,0,1,2,3k m r r =+=;令6,x m p p =+待定. 325232323x x p p p p m m m ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=+++=++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦. 从上表可知,=,0,1,2,3,23p p r r ⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦是有解的. 因此,5,0,1,2,3,(1)k m r r =+=都有解.下面考虑 5 1.k m =-显然,665.23m m m ⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦而对于01,q <<66323121115 2.232323m q m q q q q q m m m m m --⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=-+-=-+-+-+-=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦上式对于任意01q <<的q 成立. 所以当51k m =-时,方程无正有理数解.因此,前2011个k 的值之和=20112012(511)(521)(520111)5201110113319.2⨯⨯-+⨯-++⨯-=⨯-=初一组二试试题解答图3 一、填空题(共3题,每题10分)1. 一水池有一进水口,若干同样大小的排水口.如果同时打开进水口和5个排水口,连续30个小时可以将水排尽;如果同时打开进水口和6个排水口,连续20小时可以将水排尽.如果同时打开进水口和15个排水口,几小时可以将水排尽?答:5小时.解:设一水池水为z 立方米,进水口每小时过水y 立方米,一个排水口每小时排水x 立方米.于是 3053020620x y z x y z ⨯=+⎧⎨⨯=+⎩由此此得 2305230232063203x y z xy z ⨯⨯=⨯+⎧⎨⨯⨯=⨯+⎩ 两式两边分别相减得 60x z = ∴ 160x z =;同样可得 120y z =. 设同时打开一进水口和15个排水口,t 小时可以将水排尽. 则1115,6020t z t z z ⨯=⨯+ 即 11 1.420t t =+ 所以 1155t t =⇒=(小时). 2. 图中,四边形ABCD 是一个长方形,EF //AB ,GH //AD , EF 和GH 相交于点O , 三角形OBD 的面积是m ,求长方形OFCH 的面积和长方形AGOE 的面积差.答:2.m解:从图中可见,1.2BODC BOD ABCD BODA BOD S S S S S ∆∆-==+ 即 22.BODC BODA BOD S S S m ∆-==即 ()()2O F C H B O F D O H A G O E B O G D O ES S S S S S m ∆∆∆∆++-++= 但 ,,BOF BOG DOH DOE S S S S ∆∆∆∆== 因此得2.OFCH AGOE S S m -=3. 自然数a ,b 互质,如果a a b =⎥⎦⎤⎢⎣⎡,n b a b 101⨯=⎭⎬⎫⎩⎨⎧,n 是10进制数b 的位数,则a b = .其中⎥⎦⎤⎢⎣⎡a b 表示不超过a b 的最大整数,⎭⎬⎫⎩⎨⎧a b 表示a b 的小数部分.答:.25 解:设符合题意的最简分数为b a ,a 、b 均为正整数且互质.可知b >a ,根据题意即,则110n b a b a+⨯=,整理成正整数方程为210()n b a -=ab . 从方程中可知2a a b ≤<.因为a 与b 互质,所以b - a 2与ab 也互质.因为若 b -a 2与ab 有公因子p ,那么p 能整除a (或能整除b ),也能整除b -a 2,从而p 也能整除b (或也能整除a ),这样,与题意最简分数(分子与分母互质的分数)矛盾.因此,互质的a 与b 的积只能是10n 与1的乘积或5n 与2n 的乘积两种可能.若10n b =,1a =,这时21b a -≠; 若ab =10n =)(52n⨯,b =5n ,2n a =, 这时b -a =1得25(2)1n n -=,即()2521n n -=. 因此,n 只能是1时才成立,即a =2,b =5. 最简分数为.25 二、解答题(共3题,每题10分,写出解答过程)4. 将正整数1,2,3,… ,8分别放置于正方体的8个顶点,每个顶点与相邻3个顶点上的数之和称为该顶点的“众数”.对每一种填法,都可以得到最大“众数”的与最小“众数”的差,那么这个差至少等于多少.答:2解:首先考虑这样的8个众数能否全相等,如果能,因为它们的和等于144,即 1444364)8_321(=⨯=⨯+++,所以每个都等于18,那么最大与最小的众数之差就是0.如果不能全相等,为了求得最小可能值,如果有一个是19,那么 相应地得有一个是17,(总和须等于144)所以这个最小的可能值就不能小于21719=-.这样我们只要先证明8个众数不能全相等,然后找出一种布法,其最大与最小众数之差等于2,就可以断定所求的这个最小值是2.设顶点的编号为1,2,3,4,5,6,7,8,如图,记在顶点i 的数为,18,i x i ≤≤.这样,顶点1的众数为1234x x x x +++;顶点5的众数为1568x x x x +++. 若此二顶点的众数相等,则864286515421x x x x x x x x x x x x +=+⇒+++=+++同样地,顶点2的众数为1236x x x x +++,顶点4的众数为1348x x x x +++,若此二顶点的众数相等,则846284316321x x x x x x x x x x x x +=+⇒+++=+++由上面得到的二式相加得 2822,x x =即 28,x x =这是不可能的. 这就证明了8个众数不能全相等.构造一个摆放方式的图例(见右图),最大数和最小数的差等于2,故最小差值等于2.5. 已知三角形边长都是整数,周长不超过28,三个边长两两之差的平方和等于14. 问这样的三角形共有多少个?(三条边长分别对应相等的三角形只算1个)答:12个.解:设三角形三条边长分别为a,b,c ,由已知等式可得:()()()22214a b b c a c -+-+-=. ①令a b m,b c n -=-=,则a c m n -=+,其中m,n 均为自然数.于是,等式①变为 227m n mn ++=. ② 由于m,n 均为自然数,判断易知,2()3737.m n mn mn -+=⇒≤因此,使得等式②成立的m ,n 只有两组:21m n =⎧⎨=⎩ 和 12m n =⎧⎨=⎩. (1)当m =2,n =1时,b =c +1,a =c +3.又a ,b ,c 为三角形的三边长,所以b c a +>,即13c c c ++>+,解得2c >.又因为三角形的周长不超过28,即3428a b c c ++=+≤,解得8c ≤.因此28c <≤,所以c 可以取值3,4,5,6,7,8,对应可得到6个符合条件的三角形.(2)当12m ,n ==时,23b c ,a c =+=+.a,b,c 又为三角形的三边长,所以b c a +>,即23c c c ++>+.解得1c >.又因为三角形的周长不超过28,即()()3228a b c c c c ++=++++≤,解得233c ≤,因此17c <≤,所以c 可以取值2,3,4,5,6,7,对应可得到6个符合条件的三角形,且和(1)中得到的三角形不同.综合可知:符合条件且周长不超过28的三角形的个数为6612+=个.6. 求最小自然数k , 使得对于任意正整数n , k 个奇数2n +1, 2n +3, ……, 2n +2k -1中至少有一个数, 不能被3, 5, 7, 11中的任何一个整除.解. 试验可知,我们有6个奇数: 115,117,119,121,123,125,它们中每一个都可以被3,5,7,11中的一个或几个数整除.所以,k>6.对于任意的正整数 n , 当 k >6时, 取前7 个数:2n +1, 2n +3, ….., 2n +13 (1)由于2个能被3整除的奇数之差,不小于6; 2个能被5整除的奇数之差,不小于10; 2个能被7整除的奇数之差,不小于14; 2个能被11整除的奇数之差,不小于22. 因此,(1)中能被3整除的数最多有3个,且只能是2n +1, 2n +7, 2n +13.(1)中能被5整除的数最多有2个,且只能是2n +1,2n +11或者2n +3,2n +13;(1)中能被7整除的数最多有1个;(1)中能被11整除的数最多有1个.下面证明(1)中能被3 或5 整除的数的个数不超过4.若能被3整除的数只有2个,显然能能被3 或5 整除的数的个数不超过4. 若能被3整除的数有3个,不管什么情况,能被3整除的数和能被5整除的数,必有一个重合. 能被3整除和能被5整除的数一共不能超过4个.除了能被3 或5 整除的数外,还余下3个.但能被7或11整除的数最多只有2个,因此,必有一个数不能含有质因子3,5,7,11.即这个数不能被3, 5, 7, 11中的任何一个整除.答.k的最小值是7。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、解答下列各题 (每题 10 分, 共 40 分, 要求写出解题过程)
9、一本书标有 2011 页, 从第一页开始每 11 页就在最后一页的页面加注一个红 圈, 直到末页. 然后从末页开始向前, 每 21 页也在最前一页加注一个红圈, 直到 第一页. 问一共有多少页加注了两个红圈, 并写出它们的页面号码. 10、 如图, M , N 分别为四边形 ABCD对角线 AC、BD 的中点 , 过 M、N 的直线分别交 CD、AB 于 E、F . 如果三角形 ABE 的面积为 45, 求三角形 CDF 的面积. 11、设 S1 | x1 |, S 2 | S1 x2 |, , S n | S n 1 xn | , 将1, 2, 3, , 2011这些数适当地分 配给 x1 , x2 , x3 , , x2011 , 使得 S 2011 尽量大, 那么 S 2011 最大是多少? 12、求所有正整数 x, y, 使得 x2+3y 与 y2+3x 都是完全平方数.
m 1 0 0 2k 3, 1
由
100 2k 3 1 2 0 11 k 0 。 8
所以,两圈重合的页面有 9 页。 10. 答案:45 解: 因为 M 是 AC 的中点, 所以 A与C到EF 的距离相等, 因此 S AEF S CEF 。 同理: S BEF S DEF 。 两式相加可得 S ABE S CDF 。
选手诚信协议:
在参加本次“华杯赛”活动期间,我确定没有就所涉及的问题或结论,与任何人、用 任何方式进行交流或讨论. 我确定本试卷的答案均为我个人独立完成的成果, 否则愿接受本 次成绩无效的处罚. 我同意遵守以上协议. 选手签名: .
一、填空题(每小题 10 分, 共 80 分)
1、公交车的线路号是由数字显示器显示的三位数, 其中每个数字是由横竖放置 的七支荧光管显示, 如下图所示.
初中七年级组 A 卷
-6-
初中七年级组 A 卷
-4-
三、解答下列各题 (每小题 15 分,共 30 分,要求写出详细过程)
13. 答案:|a-b| 解答: 分两种情况: (1)B 和 C 分别在 L 的两侧,如下图。
D' A
D
B E
C
三角形 ABD 绕 A 选择到 AD’C 的位置,由ABD+DAB=DAB+CAE=90o,知 ABD=CAE, BAD+CAE=ACE+CAE=90o, 知BAD=ACE, AB=AC, 所 以四边形 AECD’是长方形 , 那么 AD=AD’=CE, BD=CD’=AE=AD+DE=CE+DE.
2011个"|"
|| | 3 5 | 6 | 4 | | (4k 3) | (4k 5) | (4k 6) | (4k 3) |
| 2007 | 2009 | 2010 | 2008 | 2 | 1 | 2011 | 2010
综上所述 |||| x1 x2| x3| | x2011| 的最大值为 2010。
m 16 21k ' , k ' 0,1, 2, ,94
(2)
结合(1)和(2)于是得到
' m 1 1 1 k 1 6 2 k 1 ' 1 k1 ( k
) ' k1 0
1 5 'k
4
于是 m 16 21 4 100 是两圈重合的页面号码之最小者,注意到 11 和 21 的最大公约数 [11, 21] 231 ,因此,两圈重合的页面号码一般是
9. 答案:9 解:第一次从前向后加注红圈时,设加红圈的页面号码为 m,则
m 1 1 1 k , k 1, 2 , 3 , m 2 0 1 1(1)
由
1 1 k 1 2 0 1 1
2 01 1 1 1
, 182 1 k9 182
第二次从后向前加注红圈时,由 2011 21 95 16 ,可知这时加红圈的页面 号码 m 就是从第 16 页开始向后每隔 20 页加注红圈的页面号码,除了第 16 页和最末的一页(第 2011 页)是例外,于是第二次加注红圈的页面号码就是
7k a 7k 3 3,17,31
此时 20 号是星期三。 当 4 a 7 时, 7k a 不可能有三个奇数。 因此,本月的三个星期日是 1 号,15 号和 29 号。于是本月 20 号是星期五. 注:2011 年五月就是这种情况。七月有 31 天,3 号,17 号,31 号是星期日.
x1 x 2 x3 x 2011 1 2 2011 2011 1006 的奇偶性相同,为偶数。
所以它不能等于 2011,最大可能为 2010。 另一方面,对于任意四个连续的自然数 n, n 1, n 2, n 3 ,有
||| n - (n 2) | (n 3) | (n 1) | 0 ,故有
初中七年级组 A 卷 -3-
故三角形 CDF 的面积是 45。 11. 答案:2010 解答: 注意到任何非零正整数 x、 y、 z, 总有 | x y | 小于 x 并且小于 y , 即| x y | 小于 {x, y} 中最大值。 || x y | z | 小于 | x y | 并且小于 z ,而 | x-y| 小于 {x, y} 中最大值,故 || x y | z | 小于 {x, y, z} 中最大值。所以有小于 x1 , x 2 , x3 , , x 2011 中最大值。易知 S 2011 的奇偶性与和
2 1 时间开三个水管同时排水, 再用 时间只开一个水管排水, 把池中 3 3
水排尽. 这样排完一池水所化时间比前面注满一池水少用 2 个小时. 水池的容积 是 ▲ 立方米.
-1-
初中七年级组 A 卷
6、有
▲
个不同的整数 a, 使得来自a 2 4a 302 是正整数. a 17
7、用 [ x] 表示不大于 x 的最大整数, {x} x [ x] , 则
7k a(k是整数 , 7k a 31). 要求有三个奇数。
当 a=1 时,要使 7k+a 是奇数,k 为偶数,即 k 可取 0,2,4 三个值,此时,
7k a 7k 1 1,15,29
这时 20 号是星期五。
初中七年级组 A 卷 -5-
当 a=2 时,要使 7k+a 是奇数,k 为奇数,即 k 可取 1,3 两个值,7k+a 不可能有 三个奇数; 当 a=3 时,要使 7k+a 是奇数,k 为偶数,即 k 可取 0,2,4 三个值,此时
5 7 1 5 7 2 5 7 3 5 7 2010 2011 2011 2011 2011
的值等于
▲
.
8、在 3 3 的方格图内, 填上适当的整数, 就能使每一 行、每一列和每条对角线上三个数之和都相等, 此和记 作 s . 如果下列两个方格图中都要填上 2 , 0, 1 和 3 四个 数, 另外至少再加 ▲ 个不同的整数, 方能使得两个方格图的 s 不同.
4、如右图, 长方体中 J 为棱 EF 上一点, 三角形 EHJ 与三 角形 JFB 的面积都是 50 平方厘米, 四边形 BCGF 的周长 为 24 厘米, 长方体的体积是 ▲ 立方厘米.
5、一水池有三个流量相同的注排两用水管, 开一个水管一个小时注排水 50 立方 米. 假设先开一个进水管注满半池水, 再同时开三个进水管注满另一半池水;排 水时, 先用
2011个“|”
12. 答案:所有解为(1,1),(11,16),(16,11) 解:若 x=y∈N*,且 x2+3x 为完全平方数, 而 (x+1)2=x2+2x+1≤x2+2x+x=x2+3x<x2+4x+4=(x+2)2. ∴ 当且仅当 x=1 时等号成立, ∴ x=y=1; 若 x>y,则 x2<x2+3<x2+3y<x2+3x<(x+2)2. ∴ x2+3y=(x+1)2=x2+2x+1. ∴ 3y=2x+12x=3y-1=2y+y-1,从而 y-1=2k(k∈N*);此时有 x= 3k+1. y2+3x=(2k+1)2+9k+3=4k2+13k+4. ∵ (2k+2)2=4k2+8k+4<4k2+13k+4<(2k+4)2=4k2+16k+16. ∴ 只能有 4k2+13k+4=(2k+3)2=4k2+12k+9k=5. ∴ x=16,y=11. ∴ 所有解为(x,y)=(1,1),(11,16),(16,11).
江苏教育出版社《时代学习报》杯
第十六届华罗庚金杯少年数学邀请赛决赛试卷(七年级组 A 卷)
(时间: 2011 年 4 月 16 日 10:00~11:30)
注意事项: 1、请选手先填好答题纸密封线内的考生信息,并将本试卷的所有答案写在答题纸上; 2、不允许使用计算器、MP3、手机等具有记忆功能或计算功能的电子设备.
初中七年级组 A 卷 -2-
BD⊥L 于 D, CE⊥L
第十六届华罗庚金杯少年数学邀请赛
决赛试题参考答案(初中组) 一、 填空题 (每小题 10 分,共 80 分)
题号 答案 1 11 2 15.89 3 57 4 1200 5 420 6 6 7 1005 8 4
二、解答下列各题 (每题 10 分,共 40 分, 要求写出简要过程)
a =CE+ b ,∴CE= | a b |
(2)B 和 C 分别在 L 一侧,如下图
E
D
A
B
D'
C
类似于(1) ,可以得出:DE=DB+CE. b =CE+ a ,∴CE= | a b | 14. 答案: 3;5.
解答. 设这个月的第一个星期日是 a 日(1≤a≤7),则这个月内星期日的日期是
