大连理工大学矩阵与数值分析上机作业代码
大连理工线代上机实验

基本操作
四则运算、转置、求逆、求秩、求行列式、组合、 化为行最简形、求特征值
常见任务
① 矩阵的赋值和其加、减、乘、除(求逆)命令; ② 矩阵化为最简行阶梯型的计算命令;[U0,ip]=rref(A) ③ 多元线性方程组MATLAB求解的几种方法;x=inv(A)*b, U=rref(A) ④ 行列式的几种计算机求解方法; D=det(A),[L,U]=lu(A);D=prod(diag(L)) ⑤ n个m维向量组的相关性及其秩的计算方法和命令; r=rank(A),U=rref(A) ⑥ 求欠定线性方程组的基础解系及超定方程解的MATLAB 命令;xb=null(A) ⑦ 矩阵的特征方程、特征根和特征向量的计算命令; f=poly(A);[P,D]=eig(A) ⑧ 化二次型为标准型的MATLAB命令;yTDy=xTAx; 其中 y=P-1x,
• • • •
-66.5556 25.6667 -18.7778 26.5556
• >>
例三、求秩
• • • • • • • • • • • • >> A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; >> r=rank(A); >> r= % = 计算机不显示r的值 ??? r= | Error: Expression or statement is incomplete or incorrect. >> rank(A) ans = 4 >> r r= 4 %不打;则计算机将显示rank(A)的值
例1 用直接解法求解下列线性方程组. 命令如下: A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4]; b=[13,-9,6,0]'; x=A\b
Removed_大连理工大学工科数学分析上机作业

工科数学分析上机作业说明:以下两道题均是使用Matlab 语言,且在Matlab 7.0中运行通过。
1.(两个重要极限)计算下列函数的函数值并画出图形,观察两个重要极限值。
(1)y=f(x)=; (2)y=f(x)=.sin x x (1+x)1x 解:(1)求解过程如下:>> syms x>> y=limit(sin(x)/x)y =1>> ezplot(sin(x)/x,[-10*pi,10*pi])>> ezplot(sin(x)/x,[-1*pi,1*pi])其图形如下:(2)求解过程如下:>> syms x>> y=(1+x)^(1/x)y =(1+x)^(1/x)>> y=limit((1+x)^(1/x))y =exp(1)>> ezplot((1+x)^(1/x),[-1000,1000]) >> ezplot((1+x)^(1/x),[-10,10]) >> ezplot((1+x)^(1/x),[-1,1])其图像如下:分析如下:(1)当x 取值为[-30,30]时,由该题的第一个图像可以看到,函数值在不断震荡,一会为正数,一会为负数。
而当x 取值为[-3,3]时,函数值始终大于0。
当x 趋近于0时,由该题的第二个图像可以得到函数值为1。
另外,该结论也可以由夹逼法则证明,结果不变,当x 趋近于0时,函数值仍为1。
(2)由该题的三个图像可以知道,该函数在定义域内为单调递减函数。
且由该题的第一和二个图像知道,当x 在[0,10]区间内,函数递减趋势非常迅速。
由该题的第三个图像知道,当x 趋于0 时,函数值为自然对数的底数 e ,即约为2.71828.3.计算f(x)=,12+1√2π∫x 0e ‒t 2/2dt 1≪x ≪3的函数值{f (0.1k );k=1,2,…,30}.计算结果取7位有效数字。
矩阵与数值分析 误差分析

x
称为近似值a 的相对误差。 相对误差也可正可负。 实际计算中,如果真值 x 未知时, 通常取
作为a的相对误差, 条件是
xa xa x a
xa 较小。 x
相对误差的绝对值上界叫做相对误差界(限), 记为:
xa a
ea a
相对误差界(限)
例
有两个量 x=3.000, a=3.100, 则其绝对误差: x a 0.1 绝对误差 其相对误差为: x a 0.1 0.333 101 , x 3.00 又有两个量 x 300.0 , a 310.0, 则其绝对误差:
1.1验并列为三大科学方法。
我们所学习的内容属于一门新学科——科学计算。
即现代意义下的计算数学。 主要研究在计算机上可计算的有效算法及相关理论。
本课程主要研究用计算机求解各种数学问题
的数值计算方法及其理论与软件实现
主要内容包括: 数值代数
Ax b
到x的前几位近似值a, 例如
x π 3.14159265
a1 0.00159265 取5位: a2 3.1416, a2 0.00000735
取3位: a1 3.14, 那么,它们的误差界的取法应为:
1 π 3.14 10 2 , 2
近似的,因此在此过程中,误差无处不在。
计 算 机 科 学 计 算 的 流 程 图
实际问题 数学模型 数值计算方法
编程实现算法 计算机数值结果
模型误差
方法误差或称为 截断误差 观测误差
舍入误差
1.模型误差 由实际问题抽象出数学模型,要简化许多 条件,这就不可避免地要产生误差.实际问题的解与数学模 型的解之间的误差
大连理工大学-矩阵与数值分析第一章上

–对C的类型系统改进和扩充(更安全)
–支持面向对象
C++保持与C兼容(快速普及) C++不是纯粹的面向对象的语言
33
1.2 程序的编译过程
34
1.3 C++的词法记号
关键字 各种常量 操作符 标识符 分隔符
35
1.4 C++程序的结构
#include <iostream.h> int main() { cout<<”this is the start of something wonderful!”; cout<<endl; cout<<”And now we can say even more!”; return 0; }
Sub1
Sub2
….
Subn
各子流程实现----函数化 Func1 Func2 …. Funcn
根据系统的流程组建软件,通过函数的调用实现
17
面向对象思想
问题域 (Domain) 以问题域中的事物为中心思考问题 Object1 Object2
….
Objectn
对象归类----抽象化 Class1 Class2 …. Classn
返回类型
{ 函数体; }
50
函数名(形式参数1, 形式参数2,。。。,形式参数
3.2 参数的传递
值调用
#include <iostream.h> double Volume(double radius,double height); int main() { double v; v=Volume(3.0,3.0); cout<<"Volume="<<v<<endl; return 0; } double Volume(double radius,double height) { double result=3.14 * radius * radius * height; return result; }
大连理工大学线代上机

软1414 叶秀云201492015 上机报告上机作业一Trial>> A=round(5*rand(5))B=round(5*rand(5))C=round(5*rand(5))b=round(5*rand(5,1))A+BA-BA*B+B*Ainv(A)*binv(A)rank(A)det(B)inv(B)rank(B)inv(A*B)rank(A*B)(B')*(A')inv(A*B)inv(B)*inv(A)inv(A)*C*inv(B)A =4 0 1 1 35 1 5 2 01 3 5 5 45 5 2 4 53 545 3B =4 4 4 2 24 0 3 2 22 1 2 4 33 0 54 41 0 0 1 4C =1 2 4 5 43 5 1 3 13 2 3 1 41 3 3 1 11 1 4 1 5b =21132ans =8 4 5 3 59 1 8 4 23 4 7 9 78 5 7 8 94 5 4 6 7 ans =0 -4 -3 -1 11 12 0 -2-1 2 3 1 12 5 -3 0 12 5 4 4 -1 ans =80 53 79 69 7175 54 74 77 7589 51 85 97 102110 77 111 113 12379 41 79 80 80ans =0.4754-0.3197-0.59840.9672-0.0902ans =0.3197 -0.0164 -0.2541 -0.2049 0.3607-0.8443 0.2869 0.1967 0.8361 -0.8115 -0.7213 0.4344 0.4836 0.6803 -1.05741.4262 -0.6885 -0.6721 -1.60662.1475-0.3279 0.1066 0.4016 0.5820 -0.8443 ans =5ans =418.0000ans =-0.0144 0.4354 0.0574 -0.2727 0.01910.2321 -0.2057 0.0718 -0.0909 0.02390.0718 -0.1770 -0.2871 0.3636 -0.0957-0.1100 0.0048 0.4402 -0.0909 -0.18660.0311 -0.1100 -0.1244 0.0909 0.2919 ans =5ans =-0.8088 0.3399 0.3081 0.8553 -1.02110.0586 0.0335 0.0060 -0.0108 -0.04070.9295 -0.4372 -0.4747 -0.9979 1.3348-0.4252 0.2371 0.2279 0.3635 -0.54670.2265 -0.1176 -0.0336 -0.1592 0.1809 ans =5ans =24 40 45 61 5817 25 9 22 1623 43 48 59 6019 40 52 49 5527 35 59 62 60ans =-0.8088 0.3399 0.3081 0.8553 -1.02110.0586 0.0335 0.0060 -0.0108 -0.04070.9295 -0.4372 -0.4747 -0.9979 1.3348-0.4252 0.2371 0.2279 0.3635 -0.54670.2265 -0.1176 -0.0336 -0.1592 0.1809 ans =-0.8088 0.3399 0.3081 0.8553 -1.02110.0586 0.0335 0.0060 -0.0108 -0.04070.9295 -0.4372 -0.4747 -0.9979 1.3348-0.4252 0.2371 0.2279 0.3635 -0.54670.2265 -0.1176 -0.0336 -0.1592 0.1809 ans =-0.0497 -0.5353 -0.0060 0.6289 0.12910.3583 1.0632 0.4029 -1.7332 -0.66080.4518 1.2872 0.8731 -2.1207 -0.6844-0.7394 -2.4091 -1.6491 4.0507 1.62510.2658 0.7208 0.5187 -1.1788 -0.5129 Trial>>上机作业二Trial>> A=rand(4)B=rand(4)C=rand(4)D=rand(4)Z=[A,B;C,D]det(Z)det(A*D-C*B)A=diag([rand rand rand rand])C=diag([rand rand rand rand])Z=[A,B;C,D]det(Z)det(A*D-C*B)A =0.9027 0.3377 0.7803 0.09650.9448 0.9001 0.3897 0.13200.4909 0.3692 0.2417 0.94210.4893 0.1112 0.4039 0.9561B =0.5752 0.8212 0.6491 0.54700.0598 0.0154 0.7317 0.29630.2348 0.0430 0.6477 0.74470.3532 0.1690 0.4509 0.1890C =0.6868 0.7802 0.4868 0.50850.1835 0.0811 0.4359 0.51080.3685 0.9294 0.4468 0.81760.6256 0.7757 0.3063 0.7948D =0.6443 0.3507 0.6225 0.47090.3786 0.9390 0.5870 0.23050.8116 0.8759 0.2077 0.84430.5328 0.5502 0.3012 0.1948Z =0.9027 0.3377 0.7803 0.0965 0.5752 0.8212 0.6491 0.54700.9448 0.9001 0.3897 0.1320 0.0598 0.0154 0.7317 0.29630.4909 0.3692 0.2417 0.9421 0.2348 0.0430 0.6477 0.74470.4893 0.1112 0.4039 0.9561 0.3532 0.1690 0.4509 0.18900.6868 0.7802 0.4868 0.5085 0.6443 0.3507 0.6225 0.47090.1835 0.0811 0.4359 0.5108 0.3786 0.9390 0.5870 0.23050.3685 0.9294 0.4468 0.8176 0.8116 0.8759 0.2077 0.84430.6256 0.7757 0.3063 0.7948 0.5328 0.5502 0.3012 0.1948 ans =-0.0232ans =0.0161A =0.2259 0 0 00 0.1707 0 00 0 0.2277 00 0 0 0.4357C =0.3111 0 0 00 0.9234 0 00 0 0.4302 00 0 0 0.1848Z =0.2259 0 0 0 0.5752 0.8212 0.6491 0.54700 0.1707 0 0 0.0598 0.0154 0.7317 0.29630 0 0.2277 0 0.2348 0.0430 0.6477 0.74470 0 0 0.4357 0.3532 0.1690 0.4509 0.18900.3111 0 0 0 0.6443 0.3507 0.6225 0.47090 0.9234 0 0 0.3786 0.9390 0.5870 0.23050 0 0.4302 0 0.8116 0.8759 0.2077 0.84430 0 0 0.1848 0.5328 0.5502 0.3012 0.1948 ans =7.3868e-04ans =7.3868e-04Trial>>上机作业三N=201492015;a=15;b=49;c=01;d=41;e=21;f=95;g=45;Trial>> h=90;Trial>> A=[a,b,c,d,3,4;1,2,3,4,4,3;12,15,22,17,5,7;e,f,g,h,8,0]; Trial>> B=rref(A)B =1.0000 0 0 0 0.4130 0.95680 1.0000 0 0 -1.7984 -1.49040 0 1.0000 0 -0.3796 -0.37590 0 0 1.0000 2.0806 1.5380N=201492015;a=15;b=49;c=01;d=41;e=21;f=95;g=45;Trial>> h=90;Trial>> A=[a,b,c,d,3,4;1,2,3,4,4,3;12,15,22,17,5,7;e,f,g,h,8,0]; Trial>> B=rref(A)B =1.0000 0 0 0 0.4130 0.95680 1.0000 0 0 -1.7984 -1.49040 0 1.0000 0 -0.3796 -0.37590 0 0 1.0000 2.0806 1.5380上机作业四Trial>> b1=[1,1.9,f,c];Trial>> b2=[1,1.8,f,c];Trial>> A1=[a,b,c,d;0.5,1,1.5,2;12,15,22,17;e,f,g,h];Trial>> A2=[a,b,c,d;0.3,0.6,0.9,1.2;12,15,22,17;e,f,g,h];Trial>> A3=[a,b,c,d;0.1,0.2,0.3,0.4;12,15,22,17;e,f,g,h];Trial>> A4=[a,b,c,d;0.05,0.1,0.15,0.2;12,15,22,17;e,f,g,h];Trial>> x1=A1/b1 x1 =0.02700.01630.23780.5057 Trial>> x2=A2/b1 x2 =0.02700.00980.23780.5057 Trial>> x3=A4/b1 x3 =0.02700.00160.23780.5057 Trial>> x4=A4/b1 x4 =0.02700.00160.23780.5057 Trial>> x5=A1/b2 x5 =0.02650.01630.23760.5046Trial>> x6=A2/b2x6 =0.02650.00980.23760.5046Trial>> x7=A3/b2x7 =0.02650.00330.23760.5046Trial>> x8=A4/b2x8 =0.02650.00160.23760.5046Trial>>上机作业五a1=rand(5,1)a2=rand(5,1)a3=rand(5,1)a4=rand(5,1)a5=rand(5,1)A=[a1,a2,a3,a4,a5]orth(A)a1 =0.90490.97970.43890.11110.2581 a2 =0.40870.59490.26220.60280.7112 a3 =0.22170.11740.29670.31880.4242 a4 =0.50790.08550.26250.80100.0292 a5 =0.92890.73030.48860.57850.2373A =0.9049 0.4087 0.2217 0.5079 0.92890.9797 0.5949 0.1174 0.0855 0.73030.4389 0.2622 0.2967 0.2625 0.48860.1111 0.6028 0.3188 0.8010 0.57850.2581 0.7112 0.4242 0.0292 0.2373 ans =-0.5932 -0.1881 -0.4330 0.1909 -0.6235 -0.5319 -0.5286 0.1934 -0.5094 0.3752 -0.3288 0.0079 -0.0670 0.7395 0.5835 -0.4137 0.8042 -0.1828 -0.3450 0.1723 -0.2931 0.1960 0.8586 0.1953 -0.3167Trial>>上机作业六Trial>> A=rand(5)eig(A)[d,v]=eig(A)x=rand(5,1)eig(x*x')A =0.4588 0.4889 0.9880 0.0987 0.72120.9631 0.6241 0.0377 0.2619 0.10680.5468 0.6791 0.8852 0.3354 0.65380.5211 0.3955 0.9133 0.6797 0.49420.2316 0.3674 0.7962 0.1366 0.7791 ans =2.6238 + 0.0000i0.0391 + 0.2666i0.0391 - 0.2666i0.2420 + 0.0000i0.4829 + 0.0000id =-0.4582 + 0.0000i -0.4322 + 0.1366i -0.4322 - 0.1366i 0.1428 + 0.0000i 0.2020 + 0.0000i-0.3197 + 0.0000i 0.7401 + 0.0000i 0.7401 + 0.0000i -0.6192 + 0.0000i 0.3539 + 0.0000i-0.5143 + 0.0000i -0.0341 - 0.3116i -0.0341 + 0.3116i -0.2603 + 0.0000i -0.0520 + 0.0000i-0.5266 + 0.0000i 0.0473 + 0.2327i 0.0473 - 0.2327i 0.1237 + 0.0000i -0.9110 + 0.0000i-0.3821 + 0.0000i -0.2604 + 0.1558i -0.2604 - 0.1558i 0.7164 + 0.0000i -0.0373 + 0.0000iv =2.6238 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0391 + 0.2666i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0000 + 0.0000i 0.0391 - 0.2666i 0.0000 + 0.0000i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.2420 + 0.0000i 0.0000 + 0.0000i0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.4829 + 0.0000i上机作业七A=[1,3/2,0;3/2,-1,1;0,1,1]rref(A)eig(A)B=[1,0,2;0,-1,-2;2,-2,0]rref(B)eig(B)A =1.0000 1.5000 01.5000 -1.0000 1.00000 1.0000 1.0000ans =1 0 00 1 00 0 1ans =-2.06161.00002.0616B =1 0 20 -1 -22 -2 0ans =1 0 20 1 20 0 0ans =-3.0000-0.00003.0000Trial>>上机作业八Trial>> A=[0.7,0.2,0.1;0.2,0.7,0.1;0.1,0.1,0.8]P0=[15;9;6]A =0.7000 0.2000 0.10000.2000 0.7000 0.10000.1000 0.1000 0.8000 P0 =1596Trial>> A*P0ans =12.90009.90007.2000Trial>> A*A*P0ans =11.730010.23008.0400Trial>> A*A*A*A*A*P0ans =10.429910.24249.3277Trial>>。
大连理工大学矩阵与数值分析上机作业代码

T
方程组,并比较计算结果。
1.1 程序
(1)高斯消元法 n=10 时, >> [A,b]=CreateMatrix(10) A= 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6 8 0 0 0 0 0 0 0 0 1 6
1.3 M 文件
.m 1.3.1 CreateMatrix CreateMatrix.m function [A,b]=CreateMatrix(n) %用于存放习题1的题目信息,并建立构造题目中矩阵的函数 %对矩阵A赋值 A1=6*ones(1,n); A2=ones(1,n-1); A3=8*ones(1,n-1); A=diag(A1)+diag(A2,1)+diag(A3,-1); %对向量b赋值 b=15*ones(n,1); b(1)=7; b(n)=14;
10
,迭代次数上限取默认值
50,使用 Jacobi 法进行迭代。 >> test2 >> b=ones(20,1) >> x0=zeros(20,1) >> [x,n]=JacobiMethod(A,b,x0) x= 0.2766 0.2327 0.2159 0.2223 0.2227 0.2221 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2221 0.2227 0.2223 0.2159 0.2327 0.2766
大连理工矩阵上机作业

第一题Lagrange插值函数function y=lagrange(x0,y0,x);n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;endx0=[1:10];y0=[67.052,68.008,69.803,72.024,73.400,72.063,74.669,74.487,74.065,76 .777];lagrange(x0,y0,17)ans=-1.9516e+12x=[1:0.1:10];x=x';plot(x0,y0,'r');hold onplot(x,y,'k');legend('原函数','拟合函数')拟合图像如下拟合函数出现了龙格现象,运用多项式进行插值拟合时,效果并不好,高次多项式会因为误差的不断累积,导致龙格现象的发生。
第二题function fun =nihe(n)m=[67.052*10^6,68.008*10^6,69.803*10^6,72.024*10^6,73.400*10^6,72.063 *10^6,74.669*10^6,74.487*10^6,74.065*10^6,76.777*10^6];w=[1,2,3,4,5,6,7,8,9,10];d1=0;d2=0;d3=0;y1=polyfit(m,w,1);y2=polyfit(m,w,2);y3=polyfit(m,w,3);y2=poly2sym(s2);y3=poly2sym(s3);y4=poly2sym(s4);f1=subs(y1,17);f2=subs(y2,17);f3=subs(y3,17);for p=1:10;d1=d1+(subs(y1,w(p))-m(p))^2;d2=d2+(subs(y2,w(p))-m(p))^2;d3=d3+(subs(y3,w(p))-m(p))^2;endd1=sqrt(d1);d2=sqrt(d2);d3=sqrt(d3);fun=[f1 f2 f3;d2 d3 d4];return;结果三次函数的均方误差最小,拟合的最好。
大连理工大学矩阵与数值分析上机作业

end
case2%2-范数
fori=1:n
s=s+x(i)^2;
end
s=sqrt(s);
caseinf%无穷-范数
s=max(abs(x));
end
计算向量x,y的范数
Test1.m
clearall;
clc;
n1=10;n2=100;n3=1000;
x1=1./[1:n1]';x2=1./[1:n2]';x3=1./[1:n3]';
xlabel('x');ylabel('p(x)');
运行结果:
x=2的邻域:
x =
1.6000 1.8000 2.0000 2.2000 2.4000
相应多项式p值:
p =
1.0e-003 *
-0.2621 -0.0005 0 0.0005 0.2621
p(x)在 [1.95,20.5]上的图像
程序:
[L,U]=LUDe.(A);%LU分解
xLU=U\(L\b)
disp('利用PLU分解方程组的解:');
[P,L,U] =PLUDe.(A);%PLU分解
xPLU=U\(L\(P\b))
%求解A的逆矩阵
disp('A的准确逆矩阵:');
InvA=inv(A)
InvAL=zeros(n);%利用LU分解求A的逆矩阵
0 0 0.5000 -0.2500 -0.1250 -0.0625 -0.0625
0 0 0 0.5000 -0.2500 -0.1250 -0.1250
0 0 0 0 0.5000 -0.2500 -0.2500
大连理工大学矩阵分析matlab上机作业

x(i)=1/i; %按要求给向量 x 赋值,其值递减 end normx1=norm(x,1); %求解向量 x 的 1 范数 normx1 normx2=norm(x,2); %求解向量 x 的 2 范数 normx2 normxinf=norm(x,inf); %求解向量 x 的无穷范数 normxinf normy1=norm(y,1); %求解向量 y 的 1 范数 normy1 normy2=norm(y,2); %求解向量 y 的 2 范数 normy2 normyinf=norm(y,inf); %求解向量 y 的无穷范数 normyinf z1=[normx1,normx2,normxinf]; z2=[normy1,normy2,normyinf]; end
for i=2:n
for j=i:n U(i,j)=A(i,j)-L(i,1:i-1)*U(1:i-1,j);
式
%Doolittle 分解计算上三角矩阵的公
L(j,i)=(A(j,i)-L(j,1:i-1)*U(1:i-1,i))/U(i,i); %Doolittle 分解计算下三角矩 阵的公式
end
1 1 1 ������ x = (1, 2 , 3 , … , ������) ,
������ = (1,2, … , ������)������.
对n = 10,100,1000甚至更大的n计算其范数,你会发现什么结果?你能否修改
你的程序使得计算结果相对精确呢?
1.1 源代码
function [z1,z2]=norm_vector(n) %向量 z1 的值为向量 x 的是三种范数,向量 z2 的值为向量 y 的三 种范数,n 为输入参数
大连理工_2012矩阵与数值分析大作业

矩阵与数值分析学生:学号:任课老师:金光日教学班号:(2)班院系:电子信息与电气工程学部《矩阵与数值分析》课程数值实验题目1.给定n 阶方程组A x b =,其中6186186186A ⎛⎫ ⎪ ⎪⎪= ⎪ ⎪ ⎪⎝⎭,7151514b ⎛⎫ ⎪⎪ ⎪= ⎪ ⎪⎪⎝⎭则方程组有解(1,1,,1)T x = 。
对10n =和84n =,分别用Gauss 消去法和列主元消去法解方程组,并比较计算结果。
1答: 程序1. Gauss 消元法function x=DelGauss(A,b) % Gauss 消去法 [n,m]=size(A); det=1; %存储行列式值 x=zeros(n,1); for k=1:n-1 for i=k+1:n if A(k,k)==0 return endm=A(i,k)/A(k,k); for j=k+1:nA(i,j)=A(i,j)-m*A(k,j); endb(i)=b(i)-m*b(k); enddet=det*A(k,k); %计算行列式enddet=det*A(n,n);for k=n:-1:1 %回代求解for j=k+1:nb(k)=b(k)-A(k,j)*x(j);endx(k)=b(k)/A(k,k);end2. 列主元Gauss消去法:function x=detGauss(A,b)% Gauss列主元消去法[n,m]=size(A);nb=length(b);det=1; %存储行列式值x=zeros(n,1);for k=1:n-1amax=0; %选主元for i=k:nif abs(A(i,k))>amaxamax=abs(A(i,k));r=i;endendif amax<1e-10return;endif r>k %交换两行for j=k:nz=A(k,j);A(k,j)=A(r,j);A(r,j)=z;endz=b(k);b(k)=b(r);b(r)=z;det=-det;endfor i=k+1:n %进行消元m=A(i,k)/A(k,k);for j=k+1:nA(i,j)=A(i,j)-m*A(k,j);endb(i)=b(i)-m*b(k);enddet=det*A(k,k);enddet=det*A(n,n);for k=n:-1:1 %回代求解for j=k+1:nb(k)=b(k)-A(k,j)*x(j);endx(k)=b(k)/A(k,k);end矩阵A和b的构造clc;clear;n=10;%n=84;A=eye(n)*6+diag(ones(1,n-1)*8,-1)+diag(ones(1,n-1),1); b=[7,15*ones(1,n-2),14]';计算结果:(1)n=10时Gauss消元法>>x=DelGauss(A,b)x =1.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000列主元Gauss消去法>>x=detGauss(A,b)x =1111111111(2) n=84时Gauss消元法>>x=DelGauss(A,b) x =1.0e+008 *0.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.00000.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0001 0.0002 -0.0003 0.0007 -0.0013 0.0026 -0.0052 0.0105 -0.0209 0.0419 -0.0836 0.16650.6501-1.25822.3487-4.02635.3684列主元Gauss消去法>>x=detGauss(A,b) x =1.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.00001.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.00001.0000 1.0000 1.00001.00001.0000 1.0000结果分析由上述实验结果可知,对于n=10采用Gauss 消去法和Gauss 列主元消去法得到的实验结果是相同的,而对于n=84,Gauss 消去法所得到的结果是错误的,Gauss 列主元消去法得到的结果是正确的。
大连理工大学-2015年矩阵上机编程作业
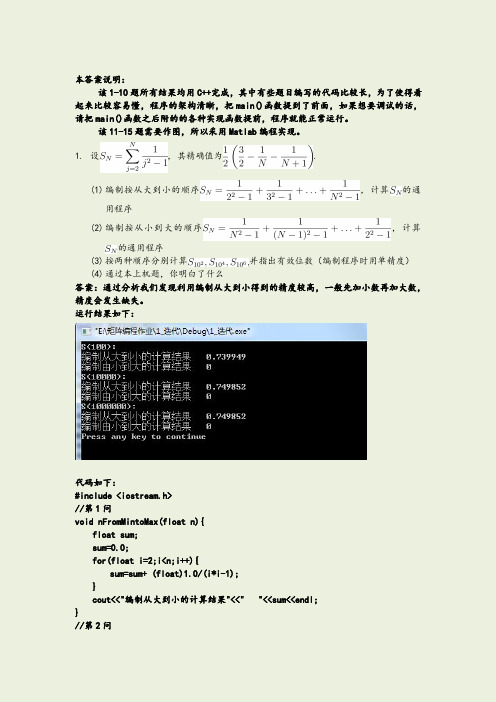
} //Ax=b 的解答,A 为上三角矩阵 void SolveOne(double a[9][10],int m,int n){
int j=n-2; double answer[9]; for (int s=m-1;s>=0;s--){
answer[j]=a[s][n-1]/a[s][j]; for(int i=0;i<=s-1;i++){
} } }
} // 发现绝对值最大的元素所在一行和当前的一行做交换 void change(double a[9][10],int m,int n,int nowi,int nowj){
int record=nowi;//记录该和哪一行做交换 bool flag=true; //标志是否需要做交换 double max=a[nowi][nowj]; for(int i=nowi+1;i<m-1;i++){
}
//Gauss 消元解法 //先转化为上三角矩阵 void Gauss(double a[9][10],int m,int n){
double r[9]; //r 为每次的倍数 int k=0; for (int nowi=0,nowj=0;nowi<m-1 && nowj<n-1;nowi++,nowj++){
1. 设
, 其精确值为
.
(1) 编制按从大到小的顺序
, 计算 的通
用程序 (2) 编制按从小到大的顺序
, 计算
的通用程序
(3) 按两种顺序分别计算
并指出有效位数(编制程序时用单精度)
大连理工大学矩阵与数值分析上机作业13388

大连理工大学矩阵与数值分析上机作业课程名称:矩阵与数值分析研究生姓名:交作业日时间:2016 年12 月20日1.1程序:Clear all;n=input('请输入向量的长度n:')for i=1:n;v(i)=1/i;endY1=norm(v,1)Y2=norm(v,2)Y3=norm(v,inf)1.2结果n=10 Y1 =2.9290Y2 =1.2449Y3 =1n=100 Y1 =5.1874Y2 =1.2787Y3 =1n=1000 Y1 =7.4855Y2 =1.2822Y3 =1N=10000 Y1 =9.7876Y2 =1.2825Y3 =11.3 分析一范数逐渐递增,随着n的增加,范数的增加速度减小;二范数随着n的增加,逐渐趋于定值,无群范数都是1.2.1程序clear all;x(1)=-10^-15;dx=10^-18;L=2*10^3;for i=1:Ly1(i)=log(1+x(i))/x(i); d=1+x(i);if d == 1y2(i)=1;elsey2(i)=log(d)/(d-1);endx(i+1)=x(i)+dx;endx=x(1:length(x)-1);plot(x,y1,'r');hold onplot(x,y2);2.2 结果2.3 分析红色的曲线代表未考虑题中算法时的情况,如果考虑题中的算法则数值大小始终为1,这主要是由于大数加小数的原因。
第3题3.1 程序clear all;A=[1 -18 144 -672 2016 -4032 5376 -4608 2304 -512];x=1.95:0.005:2.05;for i=1:length(x);y1(i)=f(A,x(i));y2(i)=(x(i)-2)^9;endfigure(3);plot(x,y1);hold on;plot(x,y2,'r');F.m文件function y=f(A,x) y=A(1);for i=2:length(A); y=x*y+A(i); end;3.2 结果第4题4.1 程序clear all;n=input('请输入向量的长度n:')A=2*eye(n)-tril(ones(n,n),0);for i=1:nA(i,n)=1;endn=length(A);U=A;e=eye(n);for i=1:n-1[max_data,max_index]=max(abs(U(i:n,i))); e0=eye(n);max_index=max_index+i-1;U=e0*U;e1=eye(n);for j=i+1:ne1(j,i)=-U(j,i)/U(i,i);endU=e1*U;P{i}=e0;%把变换矩阵存到P中L{i}=e1;e=e1*e0*e;endfor k=1:n-2Ldot{k}=L{k};for i=k+1:n-1Ldot{k}=P{i}*Ldot{k}*P{i};endendLdot{n-1}=L{n-1};LL=eye(n);PP=eye(n);for i=1:n-1PP=P{i}*PP;LL=Ldot{i}*LL;endb=ones(n,2);b=e*b; %解方程x=zeros(n,1);x(n)=b(n)/U(n,n);for i=n-1:-1:1x(i)=(b(i)-U(i,:)*x)/U(i,i);endX=U^-1*e^-1*eye(n);%计算逆矩阵AN=X';result2{n-4,1}=AN;result1{n-4,1}=x;fprintf('%d:\n',n)fprintf('%d ',AN);4.2 结果n=51.0625 -0.875 -0.75 -0.5 -0.06250.0625 1.125 -0.75 -0.5 -0.06250.0625 0.125 1.25 -0.5 -0.06250.0625 0.125 0.25 1.5 -0.0625-0.0625 -0.125 -0.25 -0.5 0.0625n=101.0625 -0.875 -0.75 -0.5 -0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 1.125 -0.75 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 1.25 -0.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 0.0625 0.125 0.25 1.5 -0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625 -0.0625 -0.125 -0.25 -0.5 0.0625同样的方法可以算出n=20,n=30时的结果,这里就不罗列了。
大连理工大学矩阵与数值分析MATLAB上机实验

二、解线性方程组 1.分别 Jacobi 迭代法和 Gauss-Seidel 迭代法求解线性方程组
3 1 0 0 x1 1 1 3 1 0 x2 0 , 0 1 2 1 x3 0 0 0 1 3 x4 0
Gauss 列主元消去法程序:
clc; clear; format long a=[2,4,3,1;8,2,0,0;5,0,4,0;9,0,0,5]; %系数矩阵 b=[12;6;23;16]; [n,m]=size(a); nb=length(b); det=1; for k=1:n-1 amax=0; for i=k:n if abs(a(i,k))>amax amax=abs(a(i,k)); r=i; end end if amax<1e-10 return; end if r>k for j=k:n z=a(k,j); a(k,j)=a(r,j); a(r,j)=z; end z=b(k);
从小到大求和程序计算结果:
N 100 10000 1000000 从小到大求和程序得 到的 SN 0.497512437810945 0.499975001249937 0.499999750000134 真实值������������ = ������ 2������ + 1 0.497512437810945 0.499975001249937 0.499999750000125 计算值有效位数 15 15 13
8
2
1 dx x
复化梯形公式程序
clc; clear; format long syms t m=int(1/t,2,8); %真实值 a=2; b=8; n=300; h=(b-a)/n; sum=0; f=inline('1/x'); for i=1:n-1 sum=sum+f(a+i.*h); end T=h/2*(f(a)+2*sum+f(b))
大连理工大学矩阵与数值分析上机作业13388

共享知识分享快乐大连理工大学矩阵与数值分析上机作业课程名称:矩阵与数值分析研究生姓名:12 交作业日时间:日20 月年2016卑微如蝼蚁、坚强似大象.共享知识分享快乐第1题1.1程序:Clear ;all n=input('请输入向量的长度n:') for i=1:n;v(i)=1/i;endY1=norm(v,1)Y2=norm(v,2)Y3=norm(v,inf)1.2结果n=10 Y1 =2.9290Y2 =1.2449Y3 =1n=100 Y1 =5.1874Y2 =1.2787Y3 =1n=1000 Y1 =7.4855Y2 =1.2822Y3 =1N=10000 Y1 =9.7876Y2 =1.2825Y3 =11.3 分析一范数逐渐递增,随着n的增加,范数的增加速度减小;二范数随着n的增加,逐渐趋于定值,无群范数都是1.卑微如蝼蚁、坚强似大象.共享知识分享快乐第2题2.1程序;clear all x(1)=-10^-15;dx=10^-18;L=2*10^3; i=1:L fory1(i)=log(1+x(i))/x(i); d=1+x(i); d == 1ify2(i)=1;elsey2(i)=log(d)/(d-1);endx(i+1)=x(i)+dx;end x=x(1:length(x)-1););'r'plot(x,y1,on holdplot(x,y2);卑微如蝼蚁、坚强似大象.共享知识分享快乐2.2 结果2.3 分析红色的曲线代表未考虑题中算法时的情况,如果考虑题中的算法则数值大小始终为1,这主要是由于大数加小数的原因。
第3题3.1 程序;clear all A=[1 -18 144 -672 2016 -4032 5376 -4608 2304 -512];x=1.95:0.005:2.05; i=1:length(x);for y1(i)=f(A,x(i)); y2(i)=(x(i)-2)^9;end figure(3);plot(x,y1);;on hold卑微如蝼蚁、坚强似大象.共享知识分享快乐);'r'plot(x,y2,F.m文件y=f(A,x)function y=A(1); i=2:length(A);for y=x*y+A(i);;end3.2 结果第4题卑微如蝼蚁、坚强似大象.共享知识分享快乐4.1 程序;clear all n=input('请输入向量的长度n:')A=2*eye(n)-tril(ones(n,n),0); i=1:n for A(i,n)=1;end n=length(A);U=A; e=eye(n);for i=1:n-1[max_data,max_index]=max(abs(U(i:n,i))); e0=eye(n);max_index=max_index+i-1; U=e0*U; e1=eye(n); j=i+1:n fore1(j,i)=-U(j,i)/U(i,i);endU=e1*U;中把变换矩阵存到P P{i}=e0;% L{i}=e1; e=e1*e0*e;endk=1:n-2for Ldot{k}=L{k}; i=k+1:n-1forLdot{k}=P{i}*Ldot{k}*P{i};endend Ldot{n-1}=L{n-1};LL=eye(n);PP=eye(n); i=1:n-1for PP=P{i}*PP;LL=Ldot{i}*LL;endb=ones(n,2);解方程 %b=e*b;x=zeros(n,1);x(n)=b(n)/U(n,n); i=n-1:-1:1for卑微如蝼蚁、坚强似大象.共享知识分享快乐x(i)=(b(i)-U(i,:)*x)/U(i,i);end计算逆矩阵%X=U^-1*e^-1*eye(n);AN=X'; result2{n-4,1}=AN;result1{n-4,1}=x;,n)'%d:\n'fprintf(fprintf('%d ',AN);4.2 结果n=51.0625 -0.875 -0.75 -0.5 -0.0625-0.0625 0.0625 -0.75 1.125 -0.5-0.0625 0.125 0.0625 1.25 -0.5-0.0625 0.1250.25 0.06251.50.0625-0.5-0.25-0.0625 -0.125n=101.0625 -0.875 -0.75 -0.5 -0.0625 1.0625 -0.875 -0.75 -0.5 -0.0625 -0.0625 1.125 0.0625 -0.75 -0.5 -0.5 0.0625 1.125 -0.75 -0.0625 -0.0625 0.0625 0.125 1.25 1.25 -0.0625 -0.5 0.0625 0.125 -0.5-0.0625 0.250.250.0625 0.1251.5 1.5 -0.0625 0.1250.06250.0625 -0.0625 -0.125 -0.25 0.0625 -0.5 -0.0625 -0.125 -0.25 -0.5 -0.0625 -0.75 1.0625 -0.5 -0.0625 -0.875 -0.5 -0.75 1.0625 -0.875 -0.0625 -0.5 0.0625 1.125 -0.5 0.0625 1.125 -0.75 -0.0625 -0.75 1.25 0.125 0.0625 -0.0625 -0.0625 -0.5 -0.5 0.0625 0.125 1.250.25-0.0625 -0.0625 1.50.1250.0625 0.0625 0.250.1251.5-0.0625 -0.125 -0.25 0.0625-0.5 0.0625 -0.0625 -0.125 -0.25-0.5同样的方法可以算出n=20,n=30时的结果,这里就不罗列了。
大连理工大学程名松矩阵与数值分析计算方法-第3章

1 (1 − ρ ( A ) ) > 0 一定存在 2 一种相容的矩阵范数 ⋅ ,使得 A ≤ ρ ( A) + ε 。
充分性 根据定理2.8,对于 ε =
又根据相容矩阵范数的性质, 再注意到上述关系式有 1 ρ ( A ) + ε = (1 + ρ ( A ) ) < 1 2 那么
A k ≤ A ≤ ( ρ ( A) + ε ) ≤ q k < 1
k→∞
k→∞
1⎞ lim ⎛ 1 + ⎟ k →∞ ⎜ ⎝ k⎠
k
lim sin k k →∞ k lim
lim
k →∞
k →∞
e− k
k
k
⎞ ⎛e 0 ⎞ ⎟ ⎜1 0 ⎟= A ⎟ =⎜ ⎟ ⎟ ⎜1 1 ⎟ ⎠ ⎠ ⎝
由矩阵序列极限的定义可以看出,矩阵序列收敛的性质和数 列收敛性质相似。 由定义可见,C m × n 中的矩阵序列的收敛相当于mn个数列同时 收敛。 因此可以用初等分析的方法来研究它。
∞ ∞
并且 则
lim Ak = A , k →∞
lim Bk = B
k →∞
lim A k B k = AB
k →∞
证 由
Ak Bk − AB = Ak Bk − Ak B + Ak B − AB
≤ B ⋅ Ak − A + Ak ⋅ Bk − B
由定理1和推论可知,结论成立。
性质3
n n lim Ak = A 并且 设 {Ak }k=1∈C × 中的矩阵序列,
∞
⎛ 0.1 0.7⎞ 。 由于 A ∞ = 0.9 < 1 ,故 计算 ∑ A ,其中 A = ⎜ ⎟ k =0 ⎝ 0.3 0.6⎠ ∞ k ρ ( A ) < 1,从而 ∑ A 收敛,且有
数值分析 上机作业

1.已知矩阵A=1078775658610975910⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,B=2345644567036780028900010⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,错误!未找到引用源。
=11/21/31/41/51/6 1/21/31/41/51/61/7 1/31/41/51/61/71/8 1/41/51/61/71/81/9 1/51/61/71/81/91/10 1/61/71/81/91/101/11⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦(1)用MATLAB函数“eig”求矩阵全部特征值。
(2)用基本QR算法求全部特征值(可用MA TLAB函数“qr”实现矩阵的QR分解)。
解:MATLAB程序如下:求矩阵A的特征值:clear;A=[10 7 8 7;7 5 6 5;8 6 10 9;7 5 9 10];E=eig(A)输出结果:求矩阵B的特征值:clear;B=[2 3 4 5 6;4 4 5 6 7;0 3 6 7 8;0 0 2 8 9;0 0 0 1 0];E=eig(B)输出结果:求矩阵错误!未找到引用源。
的特征值:clear;错误!未找到引用源。
=[1 1/2 1/3 1/4 1/5 1/6; 1/2 1/3 1/4 1/5 1/6 1/7; 1/3 1/4 1/5 1/6 1/7 1/8; 1/4 1/5 1/6 1/7 1/8 1/9;1/5 1/6 1/7 1/8 1/9 1/10; 1/6 1/7 1/8 1/9 1/10 1/11]; E=eig(错误!未找到引用源。
)输出结果:(2)A=1078775658610975910第一步:A0=hess(A);[Q0,R0]=qr(A0);A1=R0*Q0 返回得到:第二部:[Q1,R1]=qr(A1);A2=R1*Q1第三部:[Q2,R2]=qr(A2);A3=R2*Q2现在收缩,继续对A3的子矩阵错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n= 9 (3)取 x
(0)
= 0 , b =(1,0,1,0,……,1,0)T,迭代误差取默认值
10
−5
,迭代次数上限取默认
值 50,使用 Jacobi 法进行迭代。 >> test2 >> b=[1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0]' >> x0=zeros(20,1) >> [x,n]=JacobiMethod(A,b,x0) x= 0.3238 -0.0985 0.3116 -0.0881 0.3110
…… 1.0000 1.0000 1.0000 1.0000
1.2 计算结果分析
对于高斯消元法, 当 n=10 时, 得到的计算结果为 x= (1.0000, 1.0000, 1.0000, 1.0000, ……, T 1.0000) , 恰好为精确值; 但当 n=84 时, 得到的计算结果却为 x=(0.0000,0.0000,0.0000,……, -0.0001,0.0002, ……,2.3487,-4.0263,5.3684)T,完全偏离了精确值。 对于列主元消去法,当 n=10 时,得到的计算结果为 x= ( 1.0000 , 1.0000 , 1.0000 , T 1.0000, ……, 1.0000) , 恰好为精确值; 当 n=10 时, 得到的计算结果为 x= (1.0000, 1.0000, 1.0000,1.0000, ……,1.0000)T,恰好为精确值。 由于使用高斯消元法时可能会出现小主元作除数的情况,虽然在求解系数矩阵为 10 阶 的方程时,由于步数较少,尚能求得精确解,但在求解求解系数矩阵为 84 阶的巨型方程时, 由于求解步数太多,使得小主元作除数的情况累加,最终导致“大数除小数”的情况发生, 因而所得解严重偏离精确解。 而使用列主元消去法时, 由于有效地避免了这一不利情况, 因而无论是在求解系数矩阵 为 10 阶还是 84 阶的方程时,都能得到精确解。
-0.0889 0.3111 -0.0889 0.3111 -0.0889 0.3111 -0.0889 0.3111 -0.0889 0.3111 -0.0882 0.3105 -0.0957 0.3313 -0.0472
n= 16 (4)取 x
(0)
= 0 , b =(1,0,1,0,……,1,0)T,迭代误差取默认值
习题 2
设有方程组 Ax = b ,其中 A ∈ R
20× 20
,
−0.5 −0.25 ⎛ 3 ⎜ 3 −0.5 ⎜ −0.5 ⎜ −0.25 −0.5 ⋱ ⎜ A=⎜ ⋱ ⋱ ⎜ ⋱ ⎜ ⎜ ⎜ ⎝
(a) 选 取 不 同 的 初 始 向 量 x
(0)
⋱ ⋱ ⋱ ⋱ ⋱
⎞ ⎟ ⎟ ⎟ ⋱ ⎟ ⋱ ⎟ ⋱ −0.5 −0.25 ⎟ ⎟ −0.5 3 −0.5 ⎟ −0.25 −0.5 3 ⎟ ⎠
-0.0209 0.0419 -0.0836 0.1665 -0.3303 0.6501 -1.2582 2.3487 -4.0263 5.3684 (2)列主元消去法 n=10 时, >> [A,b]=CreateMatrix(10) >> x=MainElementMethod(A,b) x= 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 n=84 时, >> [A,b]=CreateMatrix(84) >> x=MainElementMethod(A,b) x= 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000
U=p{i}*U; for j=i+1:n l{i}(j,i)=-U(j,i)/Max; end U=l{i}*U; end %计算L L=eye(n); for i=1:n-2 for j=i+1:n-1 l{i}=p{j}*l{i}/p{j}; end L=l{i}*L; end L=inv(L*l{n-1}); %计算P P=eye(n); for i=1:n-1 P=p{i}*P; end %计算x x=U\(L\P*b);
1.3.2 GaussMethod.m function x=GaussMethod(A,b) %高斯消元法返回方程Ax=b的解
%x是方程的解 %A为方程的系数矩阵 %b为方程的常数矩阵 n=length(b); %定义单位下三角矩阵元胞数组,并将全部数组元素赋值为n阶单位阵 l=cell(1,n-1); l(:)={eye(n)}; U=A; for i=1:n-1 for j=i+1:n l{i}(j,i)=-U(j,i)/U(i,i); end U=l{i}*U; end %计算L和U L=inv(l{1}); for i=2:n-1 L=L/l{i}; end x=U\(L\b); .m 1.3.3 MainElementMethod MainElementMethod.m function x=MainElementMethod(A,b) %列主元消去法返回方程Ax=b的解 %x是方程的解 %A为方程的系数矩阵 %b为方程的常数矩阵 n=length(b); %定义单位下三角矩阵元胞数组,并将全部数组元素赋值为n阶单位阵 l=cell(1,n-1); l(:)={eye(n)}; p=cell(1,n-1); p(:)={eye(n)}; U=A; for i=1:n-1 %找出列主元所在行,并交换首行,得到Pi [Max,row]=max(U(i:n,i)); row=row+i-1; mid=p{i}(row,:); p{i}(row,:)=p{i}(i,:); p{i}(i,:)=mid;
1.3 M 文件
.m 1.3.1 CreateMatrix CreateMatrix.m function [A,b]=CreateMatrix(n) %用于存放习题1的题目信息,并建立构造题目中矩阵的函数 %对矩阵A赋值 A1=6*ones(1,n); A2=ones(1,n-1); A3=8*ones(1,n-1); A=diag(A1)+diag(A2,1)+diag(A3,-1); %对向量b赋值 b=15*ones(n,1); b(1)=7; b(n)=14;
0.3111 -0.0882 0.3104 -0.0957 0.3313 -0.0472 n= 9 (5)取 x
(0)
=(1,1, ……,1,1)T, b =(1,1, ……,1,1)T,迭代误差取默认值
10
−5
,迭代次
数上限取默认值 50,使用 Jacobi 法进行迭代。 >> test2 >> b=zeros(20,1) >> x0=zeros(20,1) >> [x,n]=JacobiMethod(A,b,x0) x= 0.2766 0.2327 0.2159 0.2223 0.2228 0.2221 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2221 0.2228 0.2223 0.2159 0.2327 0.2766 n= 19 (6)取 x
将 A 的主对角线元素成倍增长若干次,非主对角元素不变,每次用 Jacobi 法计算,要求迭 代误差满足 x ( k +1) − x ( k )
∞
< 10−6 ,比较收敛速度,分析现象并得出你的结论。
2.1 程序
(0) −5
(1)取 x
= 0 , b =(1,1, ……,1,1)T,迭代误差取默认值
10
−5
,迭代次数上限取默认
值 50,使用 Gauss-Seidel 法进行迭代。 >> test2 >> b=[1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0]' >> x0=zeros(20,1) >> [x,n]=Gauss_SeidelMethod(A,b,x0) x= 0.3238 -0.0985 0.3115 -0.0881 0.3110 -0.0889 0.3111 -0.0889 0.3111 -0.0889 0.3111 -0.0889 0.3111 -0.0889
n= 17 (2)取 x
(0)
= 0 , b =(1,1, ……,1,1)T,迭代误差取默认值
10
−5
,迭代次数上限取默认值
50,使用 Gauss-Seidel 法进行迭代。 >> test2
>> b=ones(20,1) >> x0=zeros(20,1) >> [x,n]=Gauss_SeidelMethod(A,b,x0) x= 0.2766 0.2327 0.2159 0.2223 0.2228 0.2221 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2221 0.2228 0.2223 0.2159 0.2327 0.2766
10
,迭代次数上限取默认值
50,使用 Jacobi 法进行迭代。 >> test2 >> b=ones(20,1) >> x0=zeros(20,1) >> [x,n]=JacobiMethod(A,b,x0) x= 0.2766 0.2327 0.2159 0.2223 0.2227 0.2221 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2222 0.2221 0.2227 0.2223 0.2159 0.2327 0.2766
