中考数学复习指导:例析追击和相遇问题的解题方法
第三讲:追击及相遇问题

经典例题及追击相遇问题(看情况是否具体)一、相遇和追击问题的实质研究的两物体能否在相同的时刻到达相同的空间位置的问题。
二、解相遇和追击问题的关键画出物体运动的情景图,理清三大关系 (1)时间关系:0t t t B A ±=(2)位移关系:0A B x x x =±(3)速度关系:两者速度相等。
它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
三、追击、相遇问题的分析方法:A. 画出两个物体运动示意图,根据两个物体的运动性质,选择同一参照物,列出两个物体的位移方程;B. 找出两个物体在运动时间上的关系C. 找出两个物体在运动位移上的数量关系D. 联立方程求解.说明:追击问题中常用的临界条件:⑴速度小者追速度大者,追上前两个物体速度相等时,有最大距离;⑵速度大者减速追赶速度小者,追上前在两个物体速度相等时,有最小距离.即必须在此之前追上,否则就不能追上.四、典型例题分析:(一).匀加速运动追匀速运动的情况(开始时v 1< v 2):v 1< v 2时,两者距离变大;v 1= v 2时, 两者距离最大;v 1>v 2时,两者距离变小,相遇时满足x 1= x 2+Δx ,全程只相遇(即追上)一次。
【例1】一小汽车从静止开始以3m/s 2的加速度行驶,恰有一自行车以6m/s 的速度从车边匀速驶过.求:(1)小汽车从开动到追上自行车之前经过多长时间两者相距最远?此时距离是多少? (2)小汽车什么时候追上自行车,此时小汽车的速度是多少? 法一 根据匀变速运动规律求解法二 利用相对运动求解法三 极值法法四 图象法(二).匀速运动追匀加速运动的情况(开始时v 1> v 2):v 1> v 2时,两者距离变小;v 1= v 2时,①若满足x 1< x 2+Δx ,则永远追不上,此时两者距离最近;②若满足x 1=x 2+Δx ,则恰能追上,全程只相遇一次;③若满足x1> x2+Δx,则后者撞上前者(或超越前者),此条件下理论上全程要相遇两次。
四种数学方法分析追及和相遇问题

四种数学方法分析追及和相遇问题例1 在水平道路上有两辆汽车A 和B 相距x ,A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动,而B 车同时做初速度为零、加速度为a 的匀加速直线运动,两车运动方向相同,如图1所示.要使两车不相撞,求A 车的初速度v 0满足什么条件.图1解析 解法一:解方程法A 、B 两车的运动过程如图所示.对A 车,有x A =v 0t -12×2at 2,v A =v 0-2at 对B 车,有x B =12at 2,v B =at . 两车恰好不相撞的条件是:当x =x A -x B 时,v A =v B ,联立以上各式解得v 0=6ax ,故要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤6ax . 解法二:判别式法设A 车经过时间t 恰好追上B 车,两车的位移关系为x A =x +x B ,即v 0t -12×2at 2=x +12at 2,整理得3at 2-2v 0t +2x =0,这是一个关于时间t 的一元二次方程,当判别式Δ=(-2v 0)2-4·3a ·2x ≤0时,t 无实数解或只有一个解,即两车不相撞,所以要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤6ax .解法三:图象法先作出A 、B 两车的v -t 图象,如图所示.设经过时间t 两车刚好不相撞,则:对A 车,有v A =v =v 0-2at ;对B 车,有v B =v =at ,解得t =v 03a. 两车相遇时的位移差等于x ,它可用图中的阴影面积表示,由图象可知x =12v 0t =v 026a,所以要使两车不相撞,A车的初速度v0≤6ax.解法四:相对运动法以B车为参考系,A车的初速度为v0,加速度为a′=-2a-a=-3a,A车追上B车且刚好不相撞的条件是v t=0,这一过程A车相对于B车的位移为x,由运动学公式得-v02=2×(-3a)x,所以v0=6ax,即要使两车不相撞,A车的初速度v0应满足的条件是v0≤6ax.答案v0≤6ax。
追及和相遇问题解题技巧
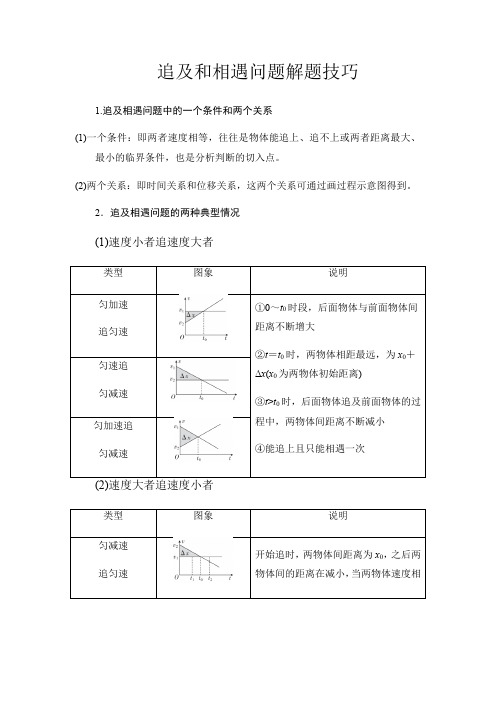
追及和相遇问题解题技巧1.追及相遇问题中的一个条件和两个关系(1)一个条件:即两者速度相等,往往是物体能追上、追不上或两者距离最大、最小的临界条件,也是分析判断的切入点。
(2)两个关系:即时间关系和位移关系,这两个关系可通过画过程示意图得到。
2.追及相遇问题的两种典型情况(1)速度小者追速度大者这一时刻一辆自行车以v=6 m/s的速度匀速驶来,从旁边超过汽车。
试求:自(1)汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?(2)什么时候汽车能追上自行车?此时汽车的速度是多少?(1)追上前汽车和自行车相距最远的条件是什么?提示:汽车和自行车速度相等。
(2)追上时汽车和自行车的位移关系是什么?提示:位移相等。
尝试解答(1)2_s__6_m__(2)4_s__12_m/s(1)解法一:(物理分析法)如图甲所示,汽车与自行车的速度相等时相距最远,设此时经过的时间为t1,汽车和自行车间的距离为Δx,则有v自=at1所以t1=v自a=2 sΔx=v自t1-12at21=6 m。
解法二:(相对运动法)以自行车为参考系,则从开始到相距最远的这段时间内,汽车相对这个参考系的各个物理量为初速度v0=v汽初-v自=0-6 m/s=-6 m/s末速度v t=v汽车-v自=0加速度a′=a-a自=3 m/s2-0=3 m/s2所以汽车和自行车相距最远时经历的时间为t1=v t-v0a′=2 s最大距离Δx=v2t-v202a′=-6 m负号表示汽车在后。
注意:利用相对运动的方法解题,要抓住三个关键:①选取哪个物体为研究对象;②选取哪个物体为参考系;③规定哪个方向为正方向。
解法三:(极值法)设汽车在追上自行车之前经过时间t1汽车和自行车相距为Δx,则Δx=v自t1-12at21代入已知数据得Δx=6t1-3 2t21由二次函数求极值的条件知:t1=2 s时,Δx有最大值6 m。
所以经过t1=2 s后,汽车和自行车相距最远,为Δx=6 m。
中考数学复习指导:例析追击和相遇问题的解题方法

例析追击和相遇问题的解题方法一、追击类问题例1 甲乙两人同时去B 地,甲骑自行车,乙骑摩托车中途摩托车出现故障改步行,下图是他们的路程随时间变化的图线。
(1)求出甲乙两人路程与时间的关系函数;(2)甲到达终点用了多长时间?(3)两人何时相距最远,最远距离是多少?解析 (1)对于第一问,欲求甲乙的路程 - 时间关系函数,利用图中给出的数据即可求出。
设甲路程随时间变化的关系式为1y k x =,由于甲图过点(1.5,15),解出10k =,代回上式可得甲的路程 - 时间关系函数为110y x =。
从图中可以看出乙的曲线呈现分段变化,设第一段时乙的关系函数为22y k x =,则当[0,1.5]x ∈时,将已知点(1.5,30)代入,得到乙的关系函数为220y x =。
在第二段中,当[1.5,7.5]x ∈时,设其关系函数表达式为33y k x b =+,将点(1.5,,30)、(7.5,60)代入得到表达式3522.5y x =+,综上可知乙的路程 - 时间关系函数为20 1.5522.5 1.57.5x x x x ≤≤⎧⎨+<≤⎩, 0, 。
(2)已知甲的路程 - 时间关系函数,将60y =代入,即可求出对应的时间6x =。
(3)从路程 - 时间关系图的几何意义出发,甲乙两人的距离即是两图线之间的纵向距离,观察图形,两人距离最值可能出现在 1.5x =及6x =处,代入计算可知,当 1.5x =时,两人距离最远,最远为15km 。
点拨 对于一次函数的追击类问题,只要围绕图形结合题设便可迅速求解。
值得注意的是必须看清图形坐标轴信息,理清图形语言的几何意义,为解题提供捷径。
二、相遇类问题例2 甲乙两地之间有一条笔直的公路,小明从甲地出发沿公路步行前往乙地,同时小亮从乙地出发沿公路骑自行车前往甲地,小亮到达甲地后停留一段时间,原路原速返回,追上小明后两人一起步行到乙地。
设小明与甲地的距离为1y ,小亮与甲地的距离为2y ,小明小亮之间的距离为s ,小明行走时间为x ,12y y 、与x 之间的函数图象如图1,s 与x 之间的部分图形如图2。
中考数学:例析追击和相遇问题的解题方法

例析追击和相遇问题的解题方法一、追击类问题例1甲乙两人同时去B 地,甲骑自行车,乙骑摩托车中途摩托车出现故障改步行,下图是他们的路程随时间变化的图线。
(1)求出甲乙两人路程与时间的关系函数;(2)甲到达终点用了多长时间?(3)两人何时相距最远,最远距离是多少?解析(1)对于第一问,欲求甲乙的路程-时间关系函数,利用图中给出的数据即可求出。
设甲路程随时间变化的关系式为1y k x =,由于甲图过点(1.5,15),解出10k =,代回上式可得甲的路程-时间关系函数为110y x =。
从图中可以看出乙的曲线呈现分段变化,设第一段时乙的关系函数为22y k x =,则当[0,1.5]x ∈时,将已知点(1.5,30)代入,得到乙的关系函数为220y x =。
在第二段中,当[1.5,7.5]x ∈时,设其关系函数表达式为33y k x b =+,将点(1.5,,30)、(7.5,60)代入得到表达式3522.5y x =+,综上可知乙的路程-时间关系函数为20 1.5522.5 1.57.5x x x x ≤≤⎧⎨+<≤⎩, 0, 。
(2)已知甲的路程-时间关系函数,将60y =代入,即可求出对应的时间6x =。
(3)从路程-时间关系图的几何意义出发,甲乙两人的距离即是两图线之间的纵向距离,观察图形,两人距离最值可能出现在 1.5x =及6x =处,代入计算可知,当 1.5x =时,两人距离最远,最远为15km 。
点拨对于一次函数的追击类问题,只要围绕图形结合题设便可迅速求解。
值得注意的是必须看清图形坐标轴信息,理清图形语言的几何意义,为解题提供捷径。
二、相遇类问题例2甲乙两地之间有一条笔直的公路,小明从甲地出发沿公路步行前往乙地,同时小亮从乙地出发沿公路骑自行车前往甲地,小亮到达甲地后停留一段时间,原路原速返回,追上小明后两人一起步行到乙地。
设小明与甲地的距离为1y ,小亮与甲地的距离为2y ,小明小亮之间的距离为s ,小明行走时间为x ,12y y 、与x 之间的函数图象如图1,s 与x 之间的部分图形如图2。
追及问题公式和相遇问题公式

追及问题公式和相遇问题公式
追击问题:路程=速度差×追击时间;相遇问题:路程=速度和×相遇时间。
相遇问题的关系式是:速度和×相遇时间=路程;路程÷速度和=相遇时间;路程÷相遇时间=速度和。
解题技巧
解答这类问题,要弄清题意,按照题意画出线段图,分析各数量之间的关系,选择解答方法。
相遇问题除了要弄清路程,速度与相遇时间外,在审题时还要注意一些重要的问题:是否是同时出发,如果题目中有谁先出发,就把先行的路程去掉,找到同时行的路程。
驶的方向,是相向,同向还是背向.不同的方向解题方法就不一样。
是否相遇.有的题目行驶的物体并没有相遇,要把相距的路程去掉;有的题目是两者错过,要把多行的路程加上,得到同时行驶的路程。
追及与相遇问题知识详解及典型例题

追及与相遇问题知识详解及典型例题(精品)知识要点追及和相遇问题主要涉及在同一直线上运动的两个物体的运动关系,所应用的规律是匀变速直线运动的相关规律。
追及、相遇问题常常涉及到临界问题,分析临界状态,找出临界条件是解决这类问题的关键。
速度相等是物体恰能追上或恰不相碰、或间距最大或最小的临界条件。
在两物体沿同一直线上的追及、相遇或避免碰撞问题中关键的条件是:两物体能否同时到达空间某位置。
因此应分别对两物体研究,列出位移方程,然后利用时间关系、速度关系、位移关系解出。
解答追及、相遇问题时要特别注意明确两物体的位移关系、时间关系、速度关系,这些关系是我们根据相关运动学公式列方程的依据。
1. 追及追和被追的两者的速度相等常是能追上、追不上、二者距离有极值的临界条件。
如匀减速运动的物体追从不同地点出发同向的匀速运动的物体时,若二者速度相等了,还没有追上,则永远追不上,此时二者间有最小距离。
若二者相遇时(追上了),追者速度等于被追者的速度,则恰能追上,也是二者避免碰撞的临界条件;若二者相遇时追者速度仍大于被追者的速度,则被追者还有一次追上追者的机会,其间速度相等时二者的距离有一个较大值。
再如初速度为零的匀加速运动的物体追从同一地点出发同向匀速运动的物体时,当二者速度相等时二者有最大距离,位移相等即追上。
“追上”的主要条件是两个物体在追赶过程中处在同一位置,常见的情形有三种:一是初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙时,一定能追上,在追上之前两者有最大距离的条件是两物体速度相等,即v甲=v乙;二是匀速运动的物体甲追赶同方向做匀加速运动的物体乙时,存在一个恰好追上或恰好追不上的临界条件:两物体速度相等,即v甲>v乙,此临界条件给出了一个判断此种追赶情形能否追上的方法,即可通过比较两物体处在同一位置时的速度大小来分析,具体方法是:假定在追赶过程中两者能处在同一位置,比较此时的速度大小,若v甲>v乙,则能追上去,若v甲<v乙,则追不上,如果始终追不上,当两物体速度相等时,两物体的间距最小;三是匀减速运动的物体追赶同方向的匀速运动的物体时,情形跟第二种相类似。
追击相遇问题专题讲解

追击与相遇专题讲解1.速度小者追速度大者:匀速追匀减速2.速度大者追速度小者:次相遇,说明: ①表中的Δx 是开始追及以后,后面物体因速度大而比前面物体多运动的位移; ②x 0是开始追及以前两物体之间的距离; ③t 2-t 0=t 0-t 1;④v 1是前面物体的速度,v 2是后面物体的速度.考点1 追击问题1、追及问题中两者速度大小与两者距离变化的关系。
甲物体追赶前方的乙物体,若甲的速度大于乙的速度,则两者之间的距离 。
若甲的速度小于乙的速度,则两者之间的距离 。
若开始甲的速度小于乙的速度过一段时间后两者速度相等,则两者之间的距离 (填最大或最小)。
2、追及问题的特征及处理方法:“追及”主要条件是:两个物体在追赶过程中处在同一位置,常见的情形有三种:⑴ 初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙,一定能追上,追上前有最大距离的条件:两物体速度 ,即v v 乙甲。
⑵ 匀速运动的物体甲追赶同向匀加速运动的物体乙,存在一个能否追上的问题。
⑶ 匀减速运动的物体追赶同向的匀速运动的物体时,情形跟⑵类似。
判断方法是:假定速度相等,从位置关系判断。
①当甲乙速度相等时,甲的位置在乙的后方,则追不上,此时两者之间的距离最小。
②当甲乙速度相等时,甲的位置在乙的前方,则追上,此情况还存在乙再次追上甲。
③当甲乙速度相等时,甲乙处于同一位置,则恰好追上,为临界状态。
解决问题时要注意二者是否同时出发,是否从同一地点出发。
追击问题分析方法:⑴ 要抓住一个条件,两个关系:一个条件是两物体的速度满足的临界条件,如两物体距离最大、最小,恰好追上或恰好追不上等。
两个关系是时间关系和位移关系,通过画草图找两物体的位移关系是解题的突破口。
⑵若被追赶的物体做匀减速运动,一定要注意追上前该物体是否已经停止运动。
⑶仔细审题,充分挖掘题目中的隐含条件,同时注意v t 图象的应用。
【例1】物体A 、B 同时从同一地点,沿同一方向运动,A 以10m/s 的速度匀速前进,B 以2m/s 2的加速度从静止开始做匀加速直线运动,求A 、B 再次相遇前两物体间的最大距离.【解析一】 物理分析法A 做 υA =10 m/s 的匀速直线运动,B 做初速度为零、加速度a =2 m/s 2的匀加速直线运动.根据题意,开始一小段时间内,A 的速度大于B 的速度,它们间的距离逐渐变大,当B 的速度加速到大于A 的速度后,它们间的距离又逐渐变小;A 、B 间距离有最大值的临界条件是υA =υB . ① 设两物体经历时间t 相距最远,则υA =at ② 把已知数据代入①②两式联立得t =5 s 在时间t 内,A 、B 两物体前进的距离分别为 s A =υA t =10×5 m=50 ms B =12at 2=12×2×52m =25 mA 、B 再次相遇前两物体间的最大距离为 Δs m =s A -s B =50 m -25 m =25 m 【解析二】 相对运动法因为本题求解的是A 、B 间的最大距离,所以可利用相对运动求解.选B 为参考系,则A 相对B 的初速度、末速度、加速度分别是υ0=10 m/s 、υt =υA -υB =0、a =-2 m/s 2. 根据υt 2-υ0=2as .有0-102=2×(-2)×s AB 解得A、B 间的最大距离为s AB =25 m . 【解析三】 极值法物体A 、B 的位移随时间变化规律分别是s A =10t ,s B =12at 2=12×2×t 2 =t 5.则A 、B 间的距离Δs =10t -t 2,可见,Δs 有最大值,且最大值为Δs m =4×(-1)×0-1024×(-1) m =25 m【解析四】 图象法根据题意作出A 、B 两物体的υ-t 图象,如图1-5-1所示.由图可知,A 、B 再次相遇前它们之间距离有最大值的临界条件是υA=υB ,得t 1=5 s .A 、B 间距离的最大值数值上等于ΔO υA P 的面积,即Δs m =12×5×10 m=25 m .【答案】25 m【实战演练1】(2011·新课标全国卷)甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。
专题:追击相遇问题和竖直上抛运动祥解

hBC= 1/2 gt2 2 = 45m
hAC= hBC- hm = 45-20 = 25 m
C
v
5秒末物体的位置C在A点下方25 m 或位移竖直向下
v= gt2 =30m/s 方向竖直向下
解二: 画出运动示意图如图示,选竖直向上为正方向 B
A → B →C 全过程综合考虑, 是匀减速运动
h= v0 t - 1/2 gt 2
t t x 5s 3s 8s v1
解题方法小结
方法一:物理分析法(一图三式法) (1)时间关系 (2)位移关系式 (3)速度关系式
方法二:利用二次函数求极值的方法求解(由于在匀变 速直线运动的位移表达式中有时间的二次方)
方法三:图象法(利用图象法分析,避开复杂的计算、 快速求解)
在“追及和相遇”问题中
练习1、一车从静止开始以1m/s2的加速度前进,车后相距x0 为25m处,某人同时开始以6m/s的速度匀速追车,能否追上? 如追不上,求人、车间的最小距离。
x0 v=6m/s
a=1m/s2
解析:依题意,人与车运动的时间相等,设为t, 当人追上车时,两者之间的位移关系为:
x车+x0= x人 即: at2/2 + x0= v人t
竖直上抛运动的运动分析
上升阶段
下降阶段
性质: a=g匀变速直线运动
竖直上抛运动的分析方法
v=0
v v
v0 v0
分段研究
上 升
设 v v0 gt1 0
向 上 为 正
H
v0t
1 2
gt12
下 降
设 向 下 为 正
v gt2
h
1 2
gt
2 2
v
例析追击和相遇问题的解题思想和方法

例析追击和相遇问题的解题思想和方法作者:刘玲来源:《中学物理·高中》2013年第12期追击和相遇是一类常见的运动学问题.解答此类问题的关键条件是:两物体能否在同一时刻到达同一位置.可见,相遇的物体必然存在以下两个关系:一是相遇位置与各物体的初始位置之间存在一定的位移关系.二是相遇物体的运动时间也存在一定的关系.对于两个物体同向运动,一类问题是速度大者减速(如匀减速直线运动)追速度小者(匀速运动),另一类问题速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动).常用的解题方法有:①列式计算法:抓住两物体速度相等时的位移之间的关系这个临界条件,根据相遇的时间关系、速度关系和位移关系,列式计算出结果.③图象法:将两者的速度-时间图象在同一坐标系中画出,然后利用图象求解.④相对运动法:巧妙地选取参考系,找出两物体的运动关系进行求解.1速度大者减速追速度小者对于第一类问题,速度大者减速追速度小者,这类问题常见有以下四种情况.1.1匀减速追匀加速例题1在光滑的水平轨道上有两个半径都是r的小球A和B,质量分别为m和2m,当两球心的距离大于L(L比2r大得多)时,两球之间无相互作用力.当两球心间的距离等于或小于L时,两球之间存在相互作用的恒定斥力F.设A球从远离B球处以速度v0沿两球心连线向原来静止的B球运动,欲使两球不发生接触,v0必须满足什么条件?我们用上述四种方法来解此题.变式一客车从静止开始以加速度a作匀加速直线运动的同时,在车尾的后面离车头为s远处有一乘客以某一恒定速度正追赶这列客车.已知司机从车头反光镜内能看到离车头最远距离为s0,同时司机从反光镜中看到该人的像必须持续时间在t0内才会注意到该人,这样才能制动客车使车停下来,该乘客要想乘上这列客车,追赶客车匀速运动的速度v所满足条件的表达式是什么?1.4匀减速追匀减速例题4摩托车以速度v1沿平直公路行驶,突然驾驶员发现正前方离摩托车s处,有一辆汽车正以速度v2开始减速,且v1分析与解我们选用相对运动法来解此题.以前方减速运动的汽车为参照物,则摩托车相对汽车的相对初速度v0r=v1-v2,相对汽车的相对加速度ar=a1-a2,摩托车刚好与汽车不相碰时,摩托车相对汽车的相对速度vtr=0,摩托车相对汽车的相对位移sr=s.。
追击、相遇问题(带详解)

追击和相遇问题1、两辆完全相同的汽车,沿水平直路一前一后匀速行驶,速度均为v0.若前车突然以恒定的加速度刹车,在它刚停住时,后车以前车刹车的加速度开始刹车.已知前车在刹车过程中所行驶的距离为x,若要保证两辆车在上述情况中不相撞,则两车在匀速行驶时保持的距离至少应为A.1xB.2xC.3xD.4x2.汽车A在红绿灯前停住,绿灯亮起时起动,以0.4 m/s2的加速度做匀加速运动,经过30 s后以该时刻的速度做匀速直线运动.设在绿灯亮的同时,汽车B以8 m/s的速度从A 车旁边驶过,且一直以相同的速度做匀速直线运动,运动方向与A车相同,则从绿灯亮时开始A.A车在加速过程中与B车相遇B.A、B相遇时速度相同C.相遇时A车做匀速运动D.两车不可能再次相遇3、A、B两车沿同一直线向同一方向运动,A车的速度v A=4 m/s,B车的速度v B=10 m/s.当B车运动至A车前方7 m处时,B车以a=2 m/s2的加速度开始做匀减速运动,从该时刻开始计时,则A车追上B车需要的时间是__ __s ,在A车追上B车之前,二者之间的最大距离是_ __ m.4.同一直线上的A、B两质点,相距s,它们向同一方向沿直线运动(相遇时互不影响各自的运动),A做速度为v的匀速直线运动,B从此时刻起做加速度为a、初速度为零的匀加速直线运动.若A在B前,两者可相遇______次,若B在A前,两者最多可相遇______次.5.从同一地点以30 m/s的速度先后竖直上抛两个物体,抛出时间相差2 s,不计空气阻力,两物体将在何处何时相遇?6.从相距30 km的甲、乙两站每隔15 min同时以30 km/h的速率向对方开出一辆汽车.若首班车为早晨5时发车,则6时从甲站开出的汽车在途中会遇到多少辆从乙站开出的汽车?7.如图1-2-1所示,A、B两物体相距s=7 m,A正以v1=4 m/s的速度向右做匀速直线运动,而物体B此时速度v2=10 m/s,方向向右,做匀减速直线运动(不能返回),加速度大小a=2 m/s2,从图示位置开始计时,问在什么情况下,经多少时间A追上B.图1-2-18. A球自距地面高h处开始自由下落,同时B球以初速度v0正对A球竖直上抛,空气阻力不计.问:(1)要使两球在B球上升过程中相遇,则v0应满足什么条件?(2)要使两球在B球下降过程中相遇,则v0应满足什么条件?9、一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3 m/s2的加速度开始加速行驶,恰在这时一辆自行车以6 m/s的速度匀速驶来,从后边超过汽车.试求:汽车从路口启动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?10、火车以速率V1向前行驶,司机突然发现在前方同一轨道上距车为S处有另一辆火车,它正沿相同的方向以较小的速率V2作匀速运动,于是司机立即使车作匀减速运动,加速度大小为a,要使两车不致相撞,求出a应满足关式.11、[易错题]甲、乙两质点同时开始在彼此平行且靠近的两水平轨道上同时运动,甲在前,乙在后,相距s .甲初速度为零,加速度为a ,做匀加速直线运动;乙以速度0v 做匀速运动,关于两质点在相遇前的运动,某同学作了如下分析:设两质点相遇前,它们之间的距离为s ∆,则t v s at s 0221-+=∆,当a v t 0=时,两质点间距离s ∆有最小值,也就是两质点速度相等时,两质点之间距离最近.你觉得他的分析是否正确?如果认为是正确的,请求出它们的最小距离;如果认为是不正确的,请说明理由并作出正确的分析.12、如下图所示,小球甲从倾角θ=30°的光滑斜面上高h =5 cm 的A 点由静止释放,同时小球乙自C 点以速度v 0沿光滑水平面向左匀速运动,C 点与斜面底端B 处的距离L =0.4 m .甲滑下后能沿斜面底部的光滑小圆弧平稳地朝乙追去,甲释放后经过t =1 s 刚好追上乙,求乙的速度v 0.13、在水平轨道上有两列火车A 和B 相距x ,A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动,而B 车同时做初速度为零、加速度为a 的匀加速直线运动,两车运动方向相同.要使两车不相撞,求A 车的初速度v 0满足什么条件.14、一列货车以28.8 km/h的速度在平直铁路上运行,由于调度失误,在后面600 m处有一列快车以72 km/h的速度向它靠近.快车司机发觉后立即合上制动器,但快车要滑行2000 m才停止.试判断两车是否会相碰.15、公共汽车从车站开出以4 m/s的速度沿平直公路匀速行驶,2 s后一辆摩托车从同一车站开出匀加速追赶,加速度为2 m/s2,试问:(1)摩托车出发后,经多少时间追上汽车?(2)摩托车追上汽车时,离出发处多远?(3)摩托车追上汽车前,两者最大距离是多少?16、一列火车以v1的速度直线行驶,司机忽然发现在正前方同一轨道上距车为s处有另一辆火车正沿着同一方向以较小速度v2做匀速运动,于是他立即刹车,为使两车不致相撞,则a应满足什么条件?1、【解析】两车同时刹车,则两车将滑行相同的距离s 而停止,由于前车刹车停止后后车接着刹车,所以后车比前车多运动的位移(即题中所求最小间距)即为前车刹车时间内后车以原速运动的位移.由刹车过程的平均速度等于原速的21,故前车刹车过程中,后车以原速运动的位移为2s . 【答案】 B2、【解析】 若A 车在加速过程中与B 车相遇,设运动时间为t ,则:21at 2=v B t ,解得:t =4.0822⨯=a v B s=40 s >30 s ,可见,A 车加速30 s 内并未追及B 车.因加速30 s 后,v A =12 m/s >v B =8 m/s ,故匀速运动过程中可追及B 车. 【答案】 C3、【解析】 设在B 车减速过程中A 车追及B 车,其间历时为t ,则:v A t =v B t -21at 2+7,代入数据解得:t =7 s(取有意义值).而B 车减速至零,历时t 0=av B=5 s <t ,故上解错误.正确的解答应为:v A t =av B 22+7,所以:t =AB v a v 7)2(2+=8 s 两车等速时间距最大,B 车减速至A 、B 等速历时: t 1=2410-=-a v v A B s=3 s ,所以A 、B 两车最大间距为: Δs m =v B t 1-21at 12+7-v A t 1=10×3 m-21×2×32 m+7 m-4×3 m =16 m 【答案】 8;164、【解析】 若A 车在前匀速运动,B 车在后匀加速追赶A 车,两车等速时相距最远(间距大于s ),故B 车追及A 车时必有v B >v A ,以后B 车在前,两车间距逐渐增大,不可能再相遇. 若B 车在前匀加速运动,A 车在后匀速运动,若追及时两车恰等速,因以后v B >v A ,不可再次相遇,即只能相遇1次;但若A 车追及B 车时v A >v B ,相遇后A 车超前,但由于B 车速度不断增大,仍能再次追及A 车,即能相遇2次. 【答案】 1;25、【解析】 设第一物体上抛t s 后相遇,则: 30t -21×10t 2=30×(t -2)- 21×10×(t -2)2解得:t =4 s,相遇高度h =30t -21×10t 2=40 m. 【答案】 距地40 m ,第一物体抛出后4 s 相遇6、【解析】 每车在两站间运动时间t =vs=1 h.当6时某车从甲站开出时,乙站的首发车已进甲站,此时路上已有3辆车在路途中,且乙站恰有一车待发.当该车行至乙站时历时1 h ,乙站将又发出4辆车,故最多可有7辆车相遇. 【答案】 7辆7、【解析】 物体B 的运动时间为t B =210=a v A s=5 s在此时间内B 前进了 s B =v ·t B =210×5 m=25 m ; 这时A 前进了 s A =v A t B =4×5 m=20 m可见在此时间内A 没有追上B ,必须在B 停止后,A 才能追上B .故A 追上B 的时间为t =4257+=+A B v s s s=8 s 【答案】 8 s 8、【解析】 两球相遇时位移之和等于h .即:21gt 2+(v 0t -21gt 2)=h 所以:t =0v h . 而B 球上升的时间:t 1=g v 0,B 球在空中运动的总时间: t 2=gv02 (1)欲使两球在B 球上升过程中相遇,则有: t <t 1,即0v h <gv0 , 所以v 0>gh (2)欲使两球在B 球下降过程中相遇,则有: t 1<t <t 2 即:g v 0<0v h <gv02 所以:22gh<v 0<gh 【答案】 (1)v 0>gh (2)22gh<v 0<gh 9、解析:【方法一:公式法】画出汽车和自行车的行程草图如图所示,当汽车的速度与自行车的速度相等时,两车之间的距离最大.设经过时间t 两车之间的距离最大.则有:v 汽=at =v 自 所以t =v 自a =63 s =2 sΔs m =s 自-s 汽=v 自t -12at 2=6×2 m-12×3×22m =6 m【方法二:图象法】画出自行车和汽车的速度-时间图象如图所示,自行车的位移s 自等于其图线与时间轴围成的矩形的面积,而汽车的位移s 汽则等于其图线与时间轴围成的三角形的面积.两车之间的距离则等于图中矩形的面积与三角形面积的差,不难看出,当t =t 0时矩形与三角形的面积之差最大. v -t 图象的斜率表示物体的加速度由a =6t 0=3得t 0=2 s 当t =2 s 时两车的距离最大:Δs m =12×2×6 m=6 m【方法三:二次函数极值法】设经过时间t 汽车和自行车之间的距离为Δs ,则: Δs =v 自t -12at 2=6t -32t 2当t =-62×(-32)=2 s 时Δs 有极大值 : Δs m =-624×(-32)m =6 m.【方法四:相对运动法】 选自行车为参考系,则从开始运动到两车相距最远这段过程中,以汽车相对地面的运动方向为正方向,汽车相对此参考系的各个物理量分别为:v 0=-6 m/s ,a =3 m/s 2,v =0对汽车,由公式v =v 0+at 得 t =v -v 0a =0-(-6)3s =2 s 又知:v 2-v 02=2as所以有s =v 2-v 022a =0-(-6)22×3m =-6 m , 相距最远为6 m 【答案:2 s , 6 m 】10、解析:设经过t 时刻两车相遇,则有21221at t V S t V -=+,整理得:02)(2122=+-+S t V V at ,要使两车不致相撞,则上述方程无解,即08)(442122<--=-=∆aS V V ac b ,解得SV V a 2)(221-≥. 答案:S V V a 2)(221-≥[规律总结]无论那种追及或相遇问题,都可以建立位移和时间关系方程进行求解,在分析时注意区分几种追碰(或规避)情况的条件:(1)两物体同方向运动且开始相距一定距离,设前后物体的加速度分别为1a 、2a ,以下几种情况能追及(碰):①二者同向加速,12a a >,如果二者速度相等时距离等于零,则能追上;若二者速度相等时距离不等于零则以后无法追上;;②二者同向加速,12a a <;③前一物体减速,后一物体加速,一定能追及;④前一物体加速,后一物体减速,如果二者速度相等时不能追上则以后无法追及;⑤二者均减速运动,12a a <,如果二者速度相等时不能追及则无法追及;12a a >,二者不相撞的安全条件是二者速度等于零时后一物体恰好追上前一物体.(2)两物体相反方向运动,列写位移和时间关系方程即可求解.11、解析:不正确.在两质点相遇之前,它们之间的距离s ∆也可能不断减小,直到0=∆s (相遇),而不存在先变小后变大的情况,这完全取决于两质点之间的初始距离s 与0v 、a 之间的大小关系.由s t v at s +-=∆0221可解得:判断式as v 220-=∆.当as v 22≥,即avs 220≤时,甲、乙之间的距离始终在减小,直至相遇(最小距离0=∆s ),两质点相遇前不会出现s ∆最小的情况.当as v 22<,即avs 220>时,甲与乙不可能相遇,当avt 0=时,两质点之间的距离最近,a v s s 220min -=∆. 答案:(略)12、【解析】设小球甲在光滑斜面上运动的加速度为a ,运动时间为t 1,运动到B处时的速度为v 1,从B 处到追上小球乙所用时间为t 2,则 : a =g sin 30°=5 m/s 2由h sin 30°=12at 21 得:t 1=4h a=0.2 s t 2=t -t 1=0.8 s , v 1=at 1=1 m/s , v 0t +L =v 1t 2代入数据解得: v 0=0.4 m/s. 【答案】 0.4m/s13、在水平轨道上有两列火车A 和B 相距x ,A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动,而B 车同时做初速度为零、加速度为a 的匀加速直线运动,两车运动方向相同.要使两车不相撞,求A 车的初速度v 0满足什么条件.【解析】 A 、B 车的运动过程(如右图),利用位移公式、速度公式求解.对A 车有: x A =v 0t +12×(-2a )×t2v A =v 0+(-2a )×t对B 车有: x B =12at 2,v B =at 两车有: x =x A -x B 追上时,两车不相撞的临界条件是v A =v B 联立以上各式解得v 0=6ax故要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤6ax . 【答案】 v 0≤6ax14、【解析】 两车速度相等恰追及前车,这是恰不相碰的临界情况,因此只要比较两车等速时的位移关系,即可明确是否相碰.因快车减速运动的加速度大小为: a =2000220222⨯=s v 快 m/s 2=0.1 m/s 2. 故快车刹车至两车等速历时: t =1.0820-=-a v v 货快 s=120 s. 该时间内两车位移分别是: s 快=v 快t -21at 2=20×120 m-21×0.1×1202 m=1680 ms 货=v 货t =8×120 m=960 m因为s 快>s 货+s 0=1560 m,故两车会发生相撞. 小结:该题还有多种讨论方法,如讨论两车相遇时速度关系或利用相对运动知识求解,请同学们练习.。
类型06追及相遇问题的解决方法(解析版)

类型06 追及相遇问题的解决方法知识点一、追及问题的两类情况 (1)知识点二、相遇问题的两类情况 (1)题型01:实际问题中追及相遇问题 (2)题型02:与图像结合的追及相遇问题 (4)知识点一、追及问题的两类情况(1)若后者能追上前者,追上时,两者处于同一位置,且后者速度一定不小于前者速度。
(2)若后者追不上前者,则当后者速度与前者速度相等时,两者相距最近。
知识点二、相遇问题的两类情况(1)同向运动的两物体追及即相遇。
(2)相向运动的物体,当各自发生的位移大小之和等于开始时两物体间的距离时即相遇。
热点题型一实际问题中追及相遇问题1.牢记“一个思维流程”2.掌握“三种分析方法”(1)分析法应用运动学公式,抓住一个条件、两个关系,列出两物体运动的时间、位移、速度及其关系方程,再求解。
(2)极值法设相遇时间为t,根据条件列出方程,得到关于t的一元二次方程,再利用数学求极值的方法求解。
在这里,常用到配方法、判别式法、不等式法等。
(3)图象法在同一坐标系中画出两物体的运动图象。
位移图象的交点表示相遇,速度图象抓住速度相等时的“面积”关系找位移关系。
【典例1】(2021·长春第一中学模拟)汽车A 以v A =4 m/s 的速度向右做匀速直线运动,发现前方相距x 0=7 m 处、以v B =10 m/s 的速度同向运动的汽车B 正开始匀减速刹车直到静止后保持不动,其刹车的加速度大小a =2 m/s 2.从此刻开始计时,求: (1)A 追上B 前,A 、B 间的最远距离是多少? (2)经过多长时间A 恰好追上B? 解题关键——画运动示意图 汽车A 和B 运动的过程如图所示.【答案】 (1)16 m (2)8 s【解析】(1)当A 、B 两汽车速度相等时,两车间的距离最远,即 v =v B -at =v A ,解得t =3 s 此时汽车A 的位移x A =x A t =12 m 汽车B 的位移x B =v B t -12at 2=21 m 故最远距离Δx max =x B +x 0-x A =16 m .(2)汽车B 从开始减速直到静止经历的时间t 1=v Ba =5 s 运动的位移x ′B =v 2B 2a=25 m汽车A 在t 1时间内运动的位移x ′A =v A t 1=20 m 此时相距Δx =x ′B +x 0-x ′A =12 m 汽车A 需再运动的时间t 2=Δxv A=3 s故A 追上B 所用时间t =t 1+t 2=8 s .【变式2】 (一题多解)在水平轨道上有两列火车A 和B 相距s ,A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动,而B 车同时做初速度为零、加速度为a 的匀加速直线运动,两车运动方向相同。
第四讲2:追及和相遇问题的求解方法

t)
302 2a
30(240 30) a
追上条件为x2=x1+1000 m
a= 9=2.25 m/s2
4
(2)摩托车与汽车速度相等时相距最远设此时刻为T,最大距离为xM
即V汽=aT
得 T V汽 25 100 s
aa 9
汽车做匀加速最大时间为
Tm
Vm a
40 s f 3
T
xmax
1000 V汽T
选自行车为参照物,以汽车相对地面的运动方向为
正方向,汽车相对自行车沿反方向做匀减速运动
v0=-6m/s,a=3m/s2,两车相距最远时vt=0
对汽车由公式
vt v0 at
由于不涉及位移,所 以选用速度公式。
t vt v0 0 (6) s 2s
a
3
对汽车由公式
vt2 v02 2as
由于不涉及“时间”, 所以选用速度位移公式。
由题意和a1 1m / s2可知:经过 6s人和车的速度相等.
s 1 6 6m 18m 25m 2
所以人不能追上汽车.人和车间的最小距离
Lmin s0 s 25m 18m 7m
解法4:巧选参考系法
若选汽车为参考系(即假设汽车不动),则人做初速度为 v0=v2=6m/s,加速度为a1=-1m/s2的匀减速直线运动.当人的速度减 小到零时,人就追不上车了. 运动的示意图如图所示,
v2t
1 2
at 2
s0
将v2 6m / s、a1 1m / s2、s0 25m代入上式可得:
t2 12t 50 0
由于方程根的判别式 b2 4ac 56 0.
故能够追上车的方程无解,即不能追上,
设人和车间的距离为L,则有
追击和相遇问题

追击和相遇问题1. 相遇和追击问题的实质研究的两物体能否在相同的时刻到达相同的空间位置的问题。
2. 解相遇和追击问题的关键画出物体运动的情景图,理清三大关系 (1)时间关系 :0t t t B A ±=(2)位移关系:0A B x x x =±(3)速度关系:两者速度相等。
它往往是物体间能否追上或(两者)距离最大、最小的临界条件,也是分析判断的切入点。
3. 相遇和追击问题剖析: (一)追及问题1、追及问题中两者速度大小与两者距离变化的关系。
甲物体追赶前方的乙物体,若甲的速度大于乙的速度,则两者之间的距离 。
若甲的速度小于乙的速度,则两者之间的距离 。
若开始甲的速度小于乙的速度过一段时间后两者速度相等,则两者之间的距离 (填最大或最小)。
2、追及问题的特征及处理方法:“追及”主要条件是:两个物体在追赶过程中处在同一位置,常见的情形有三种:⑴ 初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙,一定能追上,追上前有最大距离的条件:两物体速度 ,即v v =乙甲。
⑵ 匀速运动的物体甲追赶同向匀加速运动的物体乙,存在一个能否追上的问题。
判断方法是:假定速度相等,从位置关系判断。
①当甲乙速度相等时,甲的位置在乙的后方,则追不上,此时两者之间的距离最小。
②当甲乙速度相等时,甲的位置在乙的前方,则追上,此情况还存在乙再次追上甲。
③当甲乙速度相等时,甲乙处于同一位置,则恰好追上,为临界状态。
解决问题时要注意二者是否同时出发,是否从同一地点出发。
⑶ 匀减速运动的物体追赶同向的匀速运动的物体时,情形跟⑵类似。
3、分析追及问题的注意点:⑴ 要抓住一个条件,两个关系:一个条件是两物体的速度满足的临界条件,如两物体距离最大、最小,恰好追上或恰好追不上等。
两个关系是时间关系和位移关系,通过画草图找两物体的位移关系是解题的突破口。
⑵若被追赶的物体做匀减速运动,一定要注意追上前该物体是否已经停止运动。
追击及相遇问题的处理方法

追击及相遇问题的处理方法一、追及和相遇问题的求解方法两个物体在同一直线上运动,往往涉及追及,相遇或避免碰撞等问题,解答此类问题的关键条件是:两物体能否同时达到空间某位置。
基本思路是:①分别对两物体进行研究;②画出运动过程示意图;③列出位移方程④找出时间关系,速度关系⑤解出结果,必要时进行讨论。
方法是:(1)临界条件法:当二者速度相等时,二者相距最远(最近)。
(2)图象法:画出x-t图象或v-t图象,然后利用图象进行分析求解。
(3)数学判别式法:设相遇时间为t,根据条件列方程,得到关于t的一元二次方程,用判别式进行讨论,若Δ>0,即有两个解,说明可以相遇两次;若Δ=0,说明刚好追上或相遇;若Δ<0,说明追不上或不能相遇。
1、追及问题:追和被追的两物体的速度相等(同向运动)是能否追上及两者距离有极值的临界条件。
第一类:速度大者减速(如匀减速直线运动)追速度小者(如匀减速直线运动)①当两者速度相等时,追者位移追者位移仍小于被追者位移,则永远追不上,此时两者之间有最小距离。
②若两者位移相等,且两者速度相等时,则恰能追上,也是两者避免碰撞的临界条件。
③若两者位移相等时,追着速度仍大于被追者的速度,则被追者还有一次追上追者的机会,当速度相等时两者之间距离有一个最大值。
在具体求解时,可以利用速度相等这一条件求解,也可以利用二次函数的知识求解,还可以利用图象等求解。
第二类:速度小者加速(如初速度为零的匀加速直线运动)追速度大者(匀速直线运动)。
①当两者速度相等时有最大距离。
②当两者位移相等时,则追上。
具体的求解方法与第一类相似,即利用速度相等进行分析还可利用二次函数图象和图象图象。
2、相遇问题①同向运动的两物体追及即相遇。
②相向运动的物体,当各自发生的位移大小之和等于开始时两物体间的距离时相遇二、分析追及,相遇问题时要注意1、分析问题是,一个条件,两个关系。
一个条件是:两物体速度相等时满足的临界条件,如两物体的距离是最大还是最小及是否恰好追上等。
追击相遇问题

遇两次 ②若甲乙在同一处,则甲恰能 追上乙 ③若甲在乙后面,则甲追不上 乙,此时是相距最近的时候 情况同上
若涉及刹车问题,要先 求停车时间,以作判别!
(2)相遇 ①同向运动的两物体的追击即相遇 ②相向运动的物体,当各自位移大小之和
等于开始时两物体的距离,即相遇
(3)相撞
两物体“恰相撞”或“恰不相撞”的临界 条件: 两物体在同一位置时,速度恰相同 若后面的速度大于前面的速度,则相撞。 3、解题方法 (1)画清行程草图,找出两物体间的位移关系 (2)仔细审题,挖掘临界条件,联立方程 (3)利用二次函数求极值、图像法、相对运动 知识求解
例2:A火车以v1=20m/s速度匀速行驶,司机发现前方 同轨道上相距100m处有另一列火车B正以v2=10m/s速 度匀速行驶,A车立即做加速度大小为a的匀减速直线 运动。要使两车不相撞,a应满足什么条件?
方法一:公式法 两车恰不相撞的条件是两车速度相同时相遇。 由A、B 速度关系: v1
1 2 由A、B位移关系:v1t at v2t x0 2
x汽
△x
1 2 3 2 x v自t at 6t t 2 2
当t 6 3 2 ( ) 2 2s时
x自
x m
62 3 4 ( ) 2
6m
那么,汽车经过多少时间能追上自行车?此时汽车的速度是多 大?汽车运动的位移又是多大?
3 2 T 4s v汽 aT 12m / s x 6t t 0 2 1 2 s汽 aT =24 m 2
vt v0 2ax0
2 t 2 0 2
v v 0 10 2 2 a m / s 0.5m / s 2 x0 2 100
追及问题公式和相遇问题公式解题思路是什么

追及问题公式和相遇问题公式解题思路是什么
追及问题公式和相遇问题公式:追击问题:路程=速度差×追击时间;相遇问题:路程=速度和×相遇时间;相遇问题的关系式是:速度和×相遇时间=路程;路程÷速度和=相遇时间;路程÷相遇时间=速度和。
要注意追及、相遇问题中的“一个条件、两个关系”
追及问题公式和相遇问题公式
追击问题:路程=速度差×追击时间;
相遇问题:路程=速度和×相遇时间;
相遇问题的关系式是:
速度和×相遇时间=路程;
路程÷速度和=相遇时间;
路程÷相遇时间=速度和。
追及、相遇问题的解题思路
一、追及、相遇问题中的“一个条件、两个关系”
(1)一个条件:即两者速度相等,它往往是物体间能够追上、追不上或两者距离最大、最小的临界条件,也是分析判断的切入点.
(2)两个关系:即时间关系和位移关系,这两个关系可通过运动示意图得到.
二、追及问题的大致两种常见情形:
(1)“慢”匀加速追“快”匀速时,两者间距先增大后减小,v相同时相距最远,最终必定相遇反超;
(2)“快”匀减速追“慢”匀速时,两者间距越来越小,v相同时相距最近,若速度相等时间距为零,称为“恰好不相撞”,之后慢慢拉开间距。
(3)若物体A追物体B,开始时两个物体相距x0且vA>vB,有三种常见情景:
(a)A追上B时,必有xA-xB=x0,且vA≥vB。
(b)要使两物体恰好不相撞,两物体同时到达同一位置时速度相同,必有xA-xB=x0,vA=vB。
(c)若使两物体保证不相撞,则要求当vA=vB时,xA-xB<x0,且之后vA≤vB。
追及和相遇问题的解题方法

当:t b 2s时x有最大值 2a
此时:x 4ac b2 6m 4a
(2)当汽车追上自行车时:
x 0
所以 : - 3 t'2 6t' 0 2
即:t' 4s
此时:v汽 =at' 12m / s
规律总结: (1)相遇条件:两者到达同一位置。 (2)产生最大或最小距离的条件:
两者速度相等。
(1)写出前面的分析过程,并得出结论
(2)当人、车之间的距离最小时:
v1 v2即at 5m / s 所以t 5s
则有:x
1 2
at 2
x0
v1t
1 2
1
25
20
25
7.5m
追及和相遇问题的解题方法: 第一:数学解析法 第二:物理分析法 第三:v-t图像法
例题2: 方法一:物理分析法
(1)当汽车与自行车同速时,即v汽=v自时,两车相距最远
at v自
所以:t v自 2s a
而:x
v自t
1 2
at 2
6m
(2)当汽车追上自行车时,x汽=x自,
1 2
at '2
v自t '
所以:t' 2v自 4s a
此时:v'汽 at' 12m / s
方法二:数学解析法
(1)两车之间的距离为:
x
v自t
1 2
at 2
3 2
t2
6t(开口向下的抛物线)
5t
2(0 开口向上的抛物线)
若两者距离最小,则:
x= 4ac b2 7.5m 4a
方法二:物理分析法
分析过程:
开始人在车后,两者相距20m。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对题目图形的理解,务必做到间变化的关系式为 y = k1 x ,由于甲图过点(1.5,15) ,解出 k = 10 ,代 回上式可得甲的路程 - 时间关系函数为 y1 = 10 x 。 从图中可以看出乙的曲线呈现分段变化, 设第一段时乙的关系函数为 y2 = k2 x ,则当 x ∈ [0,1.5] 时,将已知点(1.5,30)代入,得 到乙的关系函数为 y2 = 20 x 。在第二段中,当 x ∈ [1.5, 7.5] 时,设其关系函数表达式为
例析追击和相遇问题的解题方法
一、追击类问题 例 1 甲乙两人同时去 B 地,甲骑自行车,乙骑摩托车中途摩托车出现故障改步行,下 图是他们的路程随时间变化的图线。(1)求出甲乙两人路程与时间的关系函数;(2)甲到达终 点用了多长时间?(3)两人何时相距最远,最远距离是多少?
解析
(1)对于第一问,欲求甲乙的路程 - 时间关系函数,利用图中给出的数据即可求
y3 = k3 x + b ,将点(1.5,,30) 、 (7.5,60)代入得到表达式 y3 = 5 x + 22.5 ,综上可知乙
的路程 - 时间关系函数为
0 ≤ x ≤ 1.5 20 x, 。(2)已知甲的路程 - 时间关系函数, 5 x + 22.5, 1.5 < x ≤ 7.5
将 y = 60 代入,即可求出对应的时间 x = 6 。(3)从路程 - 时间关系图的几何意义出发,甲 乙两人的距离即是两图线之间的纵向距离,观察图形,两人距离最值可能出现在 x = 1.5 及
小亮之间的距离为 s ,小明行走时间为 x , y1、y2 与 x 之间的函数图象如图 1, s 与 x 之间 的部分图形如图 2。(1)求小亮从乙到甲的 y2 与 x 之间的函数关系;(2)求小亮由甲返回到与 小明相遇的 s 与 x 的函数关系;(3)补全图 2 的信息,并求出 a 值。
解析
图 1 是小明与小亮的路程 - 时间图象,结合题目背景可知, AB 段是小亮从乙
a = 2000 /(200 + 50) = 8 。 GF 段: :当 x = 10 时,小亮到达甲地,此后 14 分钟,小亮停
留在甲地,此时,两人之间的距离 s 满足关系: s = 500 + 50 x(10 ≤ x ≤ 24) 。 FM 段:此 时,小亮出发往乙地,直至与小明相遇,两人之间的距离。满足关系式 s = −150 x + 4800 , 最终状态两人相遇即 s = 0 ,此段的时间 x ∈ [24,32] 。 MC 段:此时两人已经相遇,且同 时步行至乙地,故两人之间的距离 s 始终为 0。至此,对两人的运动过程的分析全部完成, 将对应的关系式与区间段代入图形即可得到对应的图 2。 点拨 遇到复杂类型的相遇追击问题,切忌慌乱,此时可以多读题目,将题目背景与图 形进行反复关联对照。同时,将已知的信息尽可能多的标注在图形上,从而提高审题效率。 一次函数类的相遇与追击问题常常与学生的生活实际相联系, 有条件时我们不妨安排学 生进行模拟实验,在生动趣味的实验过程中深化学生理解。在教学过程中,尽可能追求学生
x = 6 处,代入计算可知,当 x = 1.5 时,两人距离最远,最远为15km 。
点拨 对于一次函数的追击类问题, 只要围绕图形结合题设便可迅速求解。 值得注意的 是必须看清图形坐标轴信息,理清图形语言的几何意义,为解题提供捷径。 二、相遇类问题 例 2 甲乙两地之间有一条笔直的公路,小明从甲地出发沿公路步行前往乙地,同时小 亮从乙地出发沿公路骑自行车前往甲地,小亮到达甲地后停留一段时间,原路原速返回,追 上小明后两人一起步行到乙地。设小明与甲地的距离为 y1 ,小亮与甲地的距离为 y2 ,小明
地到甲地的过程,设其关系式为 y2 = kx + b ,将已知点代人可得 k = −200 、b = 2000 ,得 到其关系式为 y2 = −200 x + 2000 。 (2) BE 段 为 小 亮 在 甲 地 停 留 的 过 程 , ED 段 则 是 小 亮 与 小 明 相 遇 的 过 程 , 设
yDE = kx + b , 已知小亮 的骑行 速度,结 合已知 点 E (24, 0) ,可得 DE 段 的关 系式 为 y DE = 200 x − 4800 ,同时可以得到 yOC = 50 x 。此时,小亮与小明相遇的 s 与 x 的关系即
是 OC 与 DE 之间的纵坐标之差, s = 50 x − 200( x − 24) = −150 x + 4800 。 (3) 首 先 , a 值 表 示 两 人 第 一 次 相 遇 时 间 , 已 知 两 地 距 离 与 两 人 速 度 ,
