B-灰色灾变预测模型
灰色预测模型公式

灰色预测模型公式灰色预测模型是一种基于历史数据和现有数据的预测方法,它可以用来预测未来某个事件或指标的发展趋势。
灰色预测模型的核心思想是利用系统自身的信息和规律,通过建立灰色微分方程来进行预测。
灰色预测模型的公式可以表示为:$$\hat{X}_{0}^{(k)} = (X_{0}^{(1)} + X_{0}^{(2)} + ... + X_{0}^{(k)}) / k$$$$\hat{X}_{i}^{(k)} = (X_{0}^{(1)} + X_{0}^{(2)} + ... + X_{0}^{(k)}) / k$$$$\hat{X}_{i+1}^{(1)} = aX_{i}^{(1)} + b$$$$\hat{X}_{i+1}^{(k+1)} = aX_{i}^{(k+1)} + b$$其中,$X_{0}^{(k)}$表示观测数据的累加生成序列,$\hat{X}_{i}^{(k)}$表示预测值,$a$和$b$为待确定的系数。
灰色预测模型的核心思想是将数据分为两个部分:系统的发展规律部分和随机波动部分。
系统的发展规律部分可以通过灰色微分方程进行建模和预测,而随机波动部分则通过随机项来表示。
灰色预测模型的建模步骤如下:1. 数据预处理:对原始数据进行平滑处理,消除随机波动的影响,得到累加生成序列。
2. 确定发展规律:根据累加生成序列,建立灰色微分方程,估计系统的发展规律。
3. 模型参数估计:通过最小二乘法估计模型的参数,确定$a$和$b$的值。
4. 模型检验和优化:对模型进行检验和优化,确保预测结果的准确性和可靠性。
5. 模型预测:利用建立好的灰色预测模型,对未来的数据进行预测。
灰色预测模型在实际应用中具有广泛的应用价值。
它可以用来预测各种经济指标、环境数据、自然灾害等,为决策提供科学依据。
同时,灰色预测模型还可以用于评估和分析系统的可持续发展能力,帮助企业和机构合理规划和管理资源。
灰色预测模型是一种基于历史数据和现有数据的预测方法,它通过利用系统自身的信息和规律,建立灰色微分方程来进行预测。
灰色理论预测模型
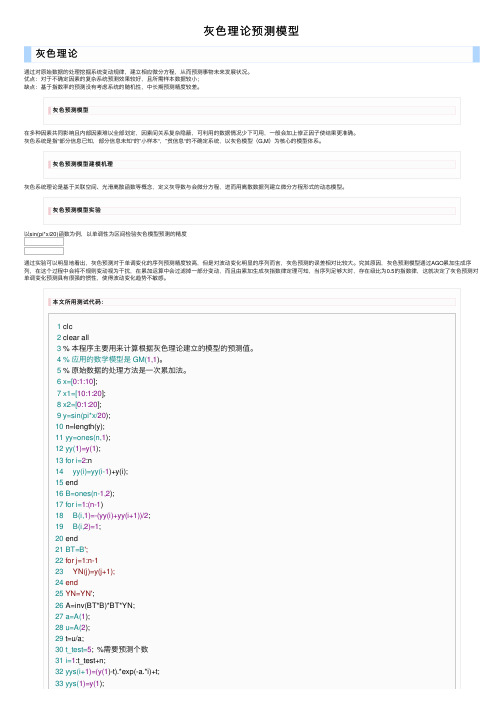
灰⾊理论预测模型灰⾊理论通过对原始数据的处理挖掘系统变动规律,建⽴相应微分⽅程,从⽽预测事物未来发展状况。
优点:对于不确定因素的复杂系统预测效果较好,且所需样本数据较⼩;缺点:基于指数率的预测没有考虑系统的随机性,中长期预测精度较差。
灰⾊预测模型在多种因素共同影响且内部因素难以全部划定,因素间关系复杂隐蔽,可利⽤的数据情况少下可⽤,⼀般会加上修正因⼦使结果更准确。
灰⾊系统是指“部分信息已知,部分信息未知“的”⼩样本“,”贫信息“的不确定系统,以灰⾊模型(G,M)为核⼼的模型体系。
灰⾊预测模型建模机理灰⾊系统理论是基于关联空间、光滑离散函数等概念,定义灰导数与会微分⽅程,进⽽⽤离散数据列建⽴微分⽅程形式的动态模型。
灰⾊预测模型实验以sin(pi*x/20)函数为例,以单调性为区间检验灰⾊模型预测的精度通过实验可以明显地看出,灰⾊预测对于单调变化的序列预测精度较⾼,但是对波动变化明显的序列⽽⾔,灰⾊预测的误差相对⽐较⼤。
究其原因,灰⾊预测模型通过AGO累加⽣成序列,在这个过程中会将不规则变动视为⼲扰,在累加运算中会过滤掉⼀部分变动,⽽且由累加⽣成灰指数律定理可知,当序列⾜够⼤时,存在级⽐为0.5的指数律,这就决定了灰⾊预测对单调变化预测具有很强的惯性,使得波动变化趋势不敏感。
本⽂所⽤测试代码:1 clc2 clear all3 % 本程序主要⽤来计算根据灰⾊理论建⽴的模型的预测值。
4 % 应⽤的数学模型是 GM(1,1)。
5 % 原始数据的处理⽅法是⼀次累加法。
6 x=[0:1:10];7 x1=[10:1:20];8 x2=[0:1:20];9 y=sin(pi*x/20);10 n=length(y);11 yy=ones(n,1);12 yy(1)=y(1);13 for i=2:n14 yy(i)=yy(i-1)+y(i);15 end16 B=ones(n-1,2);17 for i=1:(n-1)18 B(i,1)=-(yy(i)+yy(i+1))/2;19 B(i,2)=1;20 end21 BT=B';22 for j=1:n-123 YN(j)=y(j+1);24 end25 YN=YN';26 A=inv(BT*B)*BT*YN;27 a=A(1);28 u=A(2);29 t=u/a;30 t_test=5; %需要预测个数31 i=1:t_test+n;32 yys(i+1)=(y(1)-t).*exp(-a.*i)+t;33 yys(1)=y(1);34 for j=n+t_test:-1:235 ys(j)=yys(j)-yys(j-1);36 end37 x=1:n;38 xs=2:n+t_test;39 yn=ys(2:n+t_test);40 det=0;41 for i=2:n42 det=det+abs(yn(i)-y(i));43 end44 det=det/(n-1);4546 subplot(2,2,1),plot(x,y,'^r-',xs,yn,'b-o'),title('单调递增' ),legend('实测值','预测值');47 disp(['百分绝对误差为:',num2str(det),'%']);48 disp(['预测值为: ',num2str(ys(n+1:n+t_test))]);495051 %递减52 y1=sin(pi*x1/20);53 n1=length(y1);54 yy1=ones(n1,1);55 yy1(1)=y1(1);56 for i=2:n157 yy1(i)=yy1(i-1)+y1(i);58 end59 B1=ones(n1-1,2);60 for i=1:(n1-1)61 B1(i,1)=-(yy1(i)+yy1(i+1))/2;62 B1(i,2)=1;63 end64 BT1=B1';65 for j=1:n1-166 YN1(j)=y1(j+1);67 end68 YN1=YN1';69 A1=inv(BT1*B1)*BT1*YN1;70 a1=A1(1);71 u1=A1(2);72 t1=u1/a1;73 t_test1=5; %需要预测个数74 i=1:t_test1+n1;75 yys1(i+1)=(y1(1)-t1).*exp(-a1.*i)+t1;76 yys1(1)=y1(1);77 for j=n1+t_test1:-1:278 ys1(j)=yys1(j)-yys1(j-1);79 end80 x21=1:n1;81 xs1=2:n1+t_test1;82 yn1=ys1(2:n1+t_test1);83 det1=0;84 for i=2:n185 det1=det1+abs(yn1(i)-y1(i));86 end87 det1=det1/(n1-1);8889 subplot(2,2,2),plot(x1,y1,'^r-',xs1,yn1,'b-o'),title('单调递增' ),legend('实测值','预测值');90 disp(['百分绝对误差为:',num2str(det1),'%']);91 disp(['预测值为: ',num2str(ys1(n1+1:n1+t_test1))]);9293 %整个区间93 %整个区间94 y2=sin(pi*x2/20);95 n2=length(y2);96 yy2=ones(n2,1);97 yy2(1)=y2(1);98 for i=2:n299 yy2(i)=yy2(i-1)+y2(i);100 end101 B2=ones(n2-1,2);102 for i=1:(n2-1)103 B2(i,1)=-(yy2(i)+yy2(i+1))/2;104 B2(i,2)=1;105 end106 BT2=B2';107 for j=1:n2-1108 YN2(j)=y2(j+1);109 end110 YN2=YN2';111 A2=inv(BT2*B2)*BT2*YN2;112 a2=A2(1);113 u2=A2(2);114 t2=u2/a2;115 t_test2=5; %需要预测个数116 i=1:t_test2+n2;117 yys2(i+1)=(y2(1)-t2).*exp(-a2.*i)+t2;118 yys2(1)=y2(1);119 for j=n2+t_test2:-1:2120 ys2(j)=yys2(j)-yys2(j-1);121 end122 x22=1:n2;123 xs2=2:n2+t_test2;124 yn2=ys2(2:n2+t_test2);125 det2=0;126 for i=2:n2127 det2=det2+abs(yn2(i)-y2(i));128 end129 det2=det2/(n2-1);130131 subplot(2,1,2),plot(x2,y2,'^r-',xs2,yn2,'b-o'),title('全区间' ),legend('实测值','预测值'); 132 disp(['百分绝对误差为:',num2str(det2),'%']);133 disp(['预测值为: ',num2str(ys2(n2+1:n2+t_test2))]);。
B-灰色灾变预测模型

灰色灾变预测模型1 茶园沟泥石流灾变预测模型灰色灾变预测模型基本思路是把无明显规律的时间序列,经过一次累加生成有规律的时间序列,为建立GM(1, 1)灰色模型提供中间信息,同时弱化原序列的随机性,然后采用一阶单变量动态模型GM(1, 1)进行拟合,用模型推求出来的生成数回代计算值,作累减还原运算,最后对还原值进行精度检验并进行预测。
本文以茶园沟泥石流为例,茶园沟曾1887年、1900年、1934年、1936年、1947年、1972年以及2003年暴发大规模泥石流(表1)表1茶园沟泥石流灾变日期及相应序号本文通过采用1887年、1990年、1934年、1936年和1947年这5a灾变时间建立灾变预测模型,采用1972年和2003年这两年的灾变日期对预测结果进行检验。
根据表1建立茶园沟泥石流的灾变日期集:P=[p(1),p(2),p(3),p(4),p(5)]=[1 14 48 50 61]将日期集P中数据作一次AGO(Accumulated GeneratingOperation)累加生成:P(1)(1) =1P(1)(2) =P(1)(1) +p(2) =15P(1)(3) =P(1)(2) +p(3) =63P(1)(4) =P(1)(3) +p(4) =113P(1)(5) =P(1)(4) +p(5) =174构造茶园沟累加数据矩阵B和常数向量Yn:用最小二乘法求得灰参数a,u:即a =-0.2937,u =22.8044,u /a =-77.6573。
将灰参数代入时间微分方程: dP(1)/dt+aP(1)=u解微分方程求得时间函数:将a =-0.2937,u =22.8044,u /a =-77.6573代入上式函数,即得茶园沟泥石流灾变预测模型:2 茶园沟泥石流灾变预测模型精度检验预测模型的精度直接关系到预测结果的可信度。
因此,通下式计算出模型还原值并同实际值对比后,分别采用参差检验法(表2)和后验差检验法(表3)对预测模型进行检验.表2参差检验结果表3后验差检验结果根据表5中误差计算结果,计算出茶园沟泥石流灾变预测后验差比值C为根据后验差检验方法,小误差概率p为即由表2可知,所有∣q(t)∣均小于15.5773,所以,茶园沟泥石流灰色灾变预测小误差概率p =100% =1。
灰色预测模型2015

? 灰色系统是通过对原始数据的整理来寻找其变化规 律的,这是一种 就数据寻找数据的现实规律 的途径, 称为灰色序列生成。
? (灰色系统理论认为,尽管客观表象复杂,数理离 乱,但总是有整体功能的,因此必然蕴含某种内在 规律。关键在于如何选择适当的方式去挖掘和利用
它。一切灰色序列都能 通过某种生成弱化其随机性,
显现其规律性 。)
? 灰色理论中 常用的生成方法 有:
累加生成( AGO),即累加生成算子;
累减生成(IAGO)或逆累加生成以及均值生成 Z。
? 生成法如下:
? 设原始数据列为:x(0) ? {x(0) (1),x(0) (2), , x(0) (n)},则
? ? ? ? a? ?
k?2
k?2
n
(n ? 1)
z(1) (k)
2
?
? ?
n
k?2
2
z(1)
(k
)
? ?
k?2
? k? 2
?
? ? ? ? ? ? n
n
x(0) (k) ?
z(1) (k) 2 ?
n
n
z(1) (k) ?
z(1) (k)
b? ? k? 2
k?2
k?2
k?2
? ? ? ? n
(n ? 1)
其中x(0)(k)>=0,k=1,2, …,n; X(1)为X(0)的1-AGO序列:
X(1) ? (x(1)(1),x(1)(2),???, x(1)(n))
k
? 其中x(1) (k) ? x(0)(i), k ? 1,2,???, n ; Z(1)为X(1)的紧邻均值生成序
灰色灾变预测模型及其应用

灰色灾变预测模型及其应用
陈业华;邱菀华
【期刊名称】《北京航空航天大学学报》
【年(卷),期】1998(024)001
【摘要】灰色是信息不完全系统,不少论文提出了“灰数”、“灰平面”、“灰色统计”等一系列全新概念,为确定性,信息不完全数的研究提供了一种新的分析处理方法灰色方法即是对一些离散的原始数据采集累加生成及其逆进行处理,使之转化艇微分方程等方法来建模的有序数列的新方法。
【总页数】4页(P79-82)
【作者】陈业华;邱菀华
【作者单位】北京航空航天大学;北京航空航天大学
【正文语种】中文
【中图分类】O22
【相关文献】
1.基于灰色灾变预测模型的农业旱灾社会风险预警研究 [J], 谷洪波;麻湘琳
2.稻纵卷叶螟灰色灾变长期预测模型探讨 [J], 徐晨光;郭海波
3.基于灰色灾变及拓扑预测的干旱预测模型 [J], 阎苗渊;马细霞;杨丽莉;程东风
4.电器产品的灰色灾变预测模型 [J], 李玲玲;孙训俊;孙东旺;韩俊杰
5.社区矫正人员重新犯罪的灰色动态灾变预测模型 [J], 中央司法警官学院社区矫正课题组
因版权原因,仅展示原文概要,查看原文内容请购买。
数学建模之灰色预测模型

数学建模之灰色预测模型一、灰色预测模型简介(P372)特点:模型使用的不是原始数据列,而是生成的数据列。
优点:不需要很多数据,一般只用4个数据就能解决历史数据少,序列的完整性和可靠性低的问题。
缺点:只适用于中短期的预测和指数增长的预测。
1、GM(1,1)预测模型GM(1,1)表示模型为一阶微分方程,且只含有一个变量的灰色模型。
1.1模型的应用 ①销售额预测②交通事故次数的预测③某地区火灾发生次数的预测④灾变与异常值预测,如对旱灾,洪灾,地震等自然灾害的时间与程度进行预报。
(百度文库)⑤基于GM(1,1)模型的广州市人口预测与分析(下载的文档) ⑥网络舆情危机预警(下载的文档) 1.2步骤①级比检验与判断由原始数据列(0)(0)(0)(0)((1),(2),,())x x x x n =计算得序列的级比为(0)(0)(1)(),2,3,,.()x k k k n x k λ-==若序列的级比()k λ∈ 2212(,)n n e e-++Θ=,则可用(0)x 作令人满意的GM(1,1)建模。
光滑比为(0)1(0)1()()()k i x k p k xi -==∑若序列满足[](1)1,2,3,,1;()()0,,3,4,,;0.5.p k k n p k p k k n ϕϕ+<=-∈=<则序列为准光滑序列。
否则,选取常数c 对序列(0)x 做如下平移变换(0)(0)()(),1,2,,,y k x k c k n =+=序列(0)y 的级比0(0)(1)(),2,3,,.()y y k k k n y k λ-=∈Θ=②对原始数据(0)x 作一次累加得 (1)(1)(1)(1)(0)(0)(0)(0)(0)((1),(2),,())(11+(2),,(1)()).x x x x n x x x x x n ==++(),()建立模型:(1)(1),dx ax b dt+= (1)③构造数据矩阵B 及数据向量Y(1)(1)(1)(2)1(3)1,()z z B z n ⎡⎤- ⎢⎥- ⎢⎥=⎢⎥ ⎢⎥⎢⎥- 1⎣⎦(0)(0)(0)(2)3()x x Y x n ⎡⎤⎢⎥⎢⎥=⎢⎥ ⎢⎥⎢⎥⎣⎦() 其中:(1)(1)(1()0.5()0.5(1),2,3,,.z k x k x k k n =+-=)④由1ˆˆ()ˆT T auB B B Y b -⎡⎤==⎢⎥⎣⎦求得估计值ˆa= ˆb = ⑤由微分方程(1)得生成序列预测值为ˆ(1)(0)ˆˆˆ(1)(1)k 0,1,,1,,ˆˆak b b xk x e n a a -⎛⎫+=-+=- ⎪ ⎪⎝⎭,则模型还原值为(0)(1)(1)ˆˆˆ(1)(1),1,2,,1,.x k x k x k n +=+-=-⑥精度检验和预测残差(0)(0)ˆ()()(),1,2,,,k x k xk k n ε=-=3、波形预测波形预测, 是对一段时间内行为特征数据波形的预测。
人口预测模型灰色预测

灰色理论概况社会、经济、农业、工业、生态、生物等许多系统,是根据研究对象所属的领域和范围命名的,而灰色系统却是按颜色命名的。
用“黑’’表示信息未知,用“白”表示信息完全明确,用“灰"表示部分信息明确、部分信息不明确。
相应地,信息完全明确的系统称为白色系统,信息未知的系统称为黑色系统,部分信息明确、部分信息不明确的系统成为灰色系统。
灰色系统理论的研究对象是“部分信息已知、部分信息未知"的“小样本"、“贫信息"不确定性系统,它通过对“部分"已知信息的生产、开发实现对现实世界的确切描述和认识。
在人们的生活、经济活动或科研活动中,经常会遇到信息不完全的情况。
例如,在农业生产中,即使是播种面积、、化肥、灌溉等信息完全明确,但由于劳动力技术水平、自然环境、气候条件、市场行情等信息不明确,仍难以准确地预计出产量、产值;在证券市场上,即使最高明的系统分析人员亦难以稳操胜券,因为预测不准金融政策、利率政策、企业改革、政治风云和国际市场变化及其某些板块价格波动对其他板块之影响的确切信息。
灰色系统理论经过20年的发展其主要内容包括以灰色哲学为基础的思想体系,以灰色代数系统、灰色方程、灰色矩阵等为基础的理论体系,以灰色序列生成为基础的方法体系,以灰色关联空间为依托的分析体系,以灰色模型(GM)为核心的模型体系,以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系。
灰色系统分析除灰色关联分析外,还包括灰色聚类和灰色统计评估等方面 的内容。
灰色模型按照五步建模思想构建,通过灰色生成或序列算子的作用弱化随机行,挖机潜在的规律,经过差分方程与微分方程之间的互换,实现了利用离散的数据序列建立连续的动态微分方程。
灰色预测是基于GM 模型作出的定量预测,有(1,1)GM )模型、残差(1,1)GM 模型、新陈代谢(1,1)GM 模型、灰色Verhulst 模型、离散灰色模型等几种类型。
灰色预测模型理论及其应用

灰色预测模型理论及其应用灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测. 尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测.灰色预测模型只需要较少的观测数据即可,这和时间序列分析,多元回归分析等需要较多数据的统计模型不一样. 因此,对于只有少量观测数据的项目来说,灰色预测是一种有用的工具.本文主要围绕灰色预测GM(1,1)模型及其应用进行展开。
一、灰色系统及灰色预测的概念1.1灰色系统灰色系统产生于控制理论的研究中。
若一个系统的内部特征是完全已知的,即系统的信息是充足完全的,我们称之为白色系统。
若一个系统的内部信息是一无所知,一团漆黑,只能从它同外部的联系来观测研究,这种系统便是黑色系统。
灰色系统介于二者之间,灰色系统的一部分信息是已知的,一部分是未知的。
区别白色和灰色系统的重要标志是系统各因素间是否有确定的关系。
特点:灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定型系统的研究对象。
1.2灰色预测灰色系统分析方法是通过鉴别系统因素之间发展趋势的相似或相异程度,即进行关联度分析,并通过对原始数据的生成处理来寻求系统变动的规律。
生成数据序列有较强的规律性,可以用它来建立相应的微分方程模型,从而预测事物未来的发展趋势和未来状态。
灰色预测是用灰色模型GM(1,1)来进行定量分析的,通常分为以下几类:(1) 灰色时间序列预测。
用等时距观测到的反映预测对象特征的一系列数量(如产量、销量、人口数量、存款数量、利率等)构造灰色预测模型,预测未来某一时刻的特征量,或者达到某特征量的时间。
(2) 畸变预测(灾变预测)。
通过模型预测异常值出现的时刻,预测异常值什么时候出现在特定时区内。
(3) 波形预测,或称为拓扑预测,它是通过灰色模型预测事物未来变动的轨迹。
灰色预测模型原理

灰色预测模型原理灰色预测模型(Grey Prediction Model)是一种基于灰色系统理论和数学建模方法的预测模型。
灰色系统理论是我国学者黄金云教授于1982年提出的一种系统理论,它是研究非确定性和不完备信息系统的一种新方法,可用于研究多变量、小样本和非线性系统。
灰色预测模型主要基于灰色数学建模方法,通过对已知的部分序列数据进行建模和预测,来推测未知的序列数据趋势。
它适用于研究数据量小、信息不完备、非线性关系复杂的系统。
下面将简要介绍灰色预测模型的原理、模型建立过程以及一些应用案例。
1. 灰色预测模型的原理灰色预测模型的核心思想是通过对已知数据进行灰色关联度的度量,从而建立出合适的数学模型,进行未来数据的预测。
其基本原理可以概括为以下五个步骤:(1)建立灰色微分方程:根据原始数据的特点,确定合适的灰色微分方程,通常使用一阶或高阶灰色微分方程。
(2)求解灰色微分方程:根据所选择的灰色微分方程,求解其参数,得到模型的特征参数。
(3)模型检验:检验所建立的灰色预测模型的拟合程度和误差是否符合要求。
(4)进行灰色关联度分析:根据已知数据的变化规律,计算各个因素的灰色关联度,确定相关因素的重要性。
(5)进行预测:利用建立好的灰色预测模型,对未来的数据进行预测和分析,得出预测值。
2. 模型建立过程灰色预测模型的建立过程中,通常包括以下几个步骤:(1)数据的建立与处理:对原始数据进行筛选、预处理和归一化处理,以满足模型的要求。
(2)建立灰色微分方程:从已知数据中提取主要特征,并根据数据的特点选择合适的灰色微分方程。
(3)求解灰色微分方程:根据所选的灰色微分方程,通过累加生成序列、求解参数等方法,得到模型的特征参数。
(4)模型的检验:根据已知数据的拟合程度和误差范围,评估所建立的灰色预测模型的准确性和可靠性。
(5)模型的应用与预测:利用已建立的模型进行未来数据的预测和分析,得出预测结果。
3. 应用案例灰色预测模型在实际应用中具有广泛的应用范围,以下是一些常见的应用案例:(1)经济领域:用于对经济指标、市场需求、价格变动等进行预测,为经济决策提供参考。
灰色预测模型-2022年学习资料

常见的几种灰生成类型:-1.累加生成算子AGO-2.逆累加生成算子(IAGO-3.均值生成算子MEAN-4 级比生成算子-8
1.累加生成算子AGO-定义它是对原序列中的数据依次累加以得到-生成序列。令x为原序列-X=x1,x2.L ,x n-我们说X四是X0的AGO序列,并记为-X=AGO X0-当且仅当-X0=(x01,x02,L,x n)-并满足xk=∑xm-k=1,2,L,n-m=-9
灰色预测模型灰色预测模型ppt课件
1、-灰色系统介绍-■-灰色系统是由华中科技大学的邓聚龙教授80-年代初所创立,在短短的三十年里已得到了长 -的发展。-灰色系统研究的是“部分信息明确,部分信息-未知”的“小样本,贫信息”不确定性问题,并-依据信息 盖,通过序列算子的作用探索事物运-动的现实规律。其特点是“少数据建模”,着重-研究“外延明确,-内涵不明确 的对象。-2
3、灰数及其运算-只知道大概范围而不知道其确切值的数称为灰-数,通常记为:“⑧”-例如:-1.头发的多少才 是秃子。应该是个区间范-围。模糊-2.多少层的楼房算高楼,中高楼,低楼。-3.多么重才算胖子?。-5
灰数的种类:-a、仅有下界的灰数。-有下界无上界的灰数记为:⑧∈[a,∞]-b、仅有上界的灰数。-有上界无 界的灰数记为:⑧∈[∞,b]-c、区间灰数-既有上界又有下界的灰数:⑧∈[a,b]-d、连续灰数与离散灰数 在某一区间内取有限个值的灰数称为离散灰-数,取值连续地充满某一区间的灰数称为连续-6
灰生成技术-灰色序列生成-是一种通过对原始数据的挖掘、整理来寻求数据变化-的现实规律的途径,简称灰生成。生成特点-在保持原序列形式的前提下,改变序列中数据的值与-性质。一切灰色序列都能通过某种生成弱化其随机性, 显现其规律性。-灰生成的作用-1.统一序列的目标性质,为灰决策提供基础。-2.将摆动序列转换为单调增长序列 以利于灰建模。-3.揭示潜藏在序列中的递增势态,变不可比为可比序列。
数学建模——灰色预测模型

数学建模——灰色预测模型灰色预测模型(Grey Forecasting Model)是一种用于预测不确定性数据的数学模型。
它适用于那些缺乏充分历史数据、不具备明显的规律性趋势或周期性的情况。
灰色预测模型基于灰色系统理论,通过分析数据的变化趋势和规律,来进行预测。
该模型在处理少量数据、缺乏趋势规律的情况下,具有一定的优势。
灰色预测模型的基本思想:灰色预测模型基于“白化(Whitening)”和“黑化(Blackening)”的思想,将不确定性数据分为“白色”和“黑色”两部分。
其中,“白色”代表已知数据,具有规律性和趋势,可以进行预测;而“黑色”代表未知数据,缺乏规律,需要进行预测。
通过建立数学模型,将“白色”和“黑色”数据进行融合,得出预测结果。
灰色预测模型的基本步骤:1.建立灰色数列:将原始数据分成“白色”和“黑色”两部分,构建灰色数列。
2.建立灰色微分方程:对“白色”数列进行微分,得到一阶或高阶微分方程。
3.求解微分方程:求解微分方程,得到预测模型的参数。
4.进行预测:利用已知的模型参数,对“黑色”数据进行预测,得出未来的趋势。
示例:用灰色预测模型预测销售量假设你是一家新开设的小型餐厅的经营者,你希望预测未来三个月的月销售量。
然而,你的餐厅刚刚开业不久,历史销售数据有限,且不具备明显的趋势。
这种情况下,你可以考虑使用灰色预测模型来预测销售量。
步骤:1.建立灰色数列:将已知的销售数据分为“白色”(已知数据)和“黑色”(未知数据)两部分。
2.建立灰色微分方程:对“白色”销售数据进行一阶微分,得到灰色微分方程。
3.求解微分方程:根据灰色微分方程的形式,求解微分方程,得到模型的参数。
4.进行预测:利用求解得到的模型参数,对“黑色”销售数据进行预测,得到未来三个月的销售量趋势。
这个例子中,灰色预测模型可以帮助你基于有限的历史销售数据,预测未来的销售趋势。
虽然该模型的精确度可能不如其他更复杂的方法,但在缺乏充足数据时,它可以提供一种有用的预测工具。
灰色预测模型介绍.

数学模型与数学实验数课程报告题目:灰色预测模型介绍专业:班级:姓名:学号:二0一一年六月1. 模型功能介绍预测模型为一元线性回归模型,计算公式为Y=a+b。
一元非线性回归模型:Y=a+blx+b2x2+…+bmxm。
式中:y为预测值;x为自变量的取值;a,b1,b2……bm为回归系数。
当自变量x与因变量y之间的关系是直线上升或下降时,可采用一元线性预测模型进行预测。
当自变量x和因变量y之间呈曲线上升或下降时,可采用一元非线性预测模型中的y=a+b1x+b2x2+…+bmxm这个预测模型。
当自变量x和因变量y之间关系呈上升一下降一再上升一再下降这种重复关系时,可采用一元线性预测模型中的Y=a+bx这个模型来预测。
其中我要在这里介绍灰色预测模型。
灰色预测是就灰色系统所做的预测,灰色系统(Grey System)理论[]1是我国著名学者邓聚龙教授20世纪80年代初创立的一种兼备软硬科学特性的新理论[95]96]。
所谓灰色系统是介于白色系统和黑箱系统之间的过渡系统,其具体的含义是:如果某一系统的全部信息已知为白色系统,全部信息未知为黑箱系统,部分信息已知,部分信息未知,那么这一系统就是灰色系统。
一般地说,社会系统、经济系统、生态系统都是灰色系统。
例如物价系统,导致物价上涨的因素很多,但已知的却不多,因此对物价这一灰色系统的预测可以用灰色预测方法。
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
灰色系统的基本原理公理1:差异信息原理。
“差异”是信息,凡信息必有差异。
公理2:解的非唯一性原理。
信息不完全,不明确地解是非唯一的。
公理3:最少信息原理。
灰色系统理论的特点是充分开发利用已有的“最少信息”。
灰色预测模型ppt课件

.
灰色建模实例
北方某城市1986-1992年交通噪声平均声级数据
序号
1 2 3 4
年份
1986 1987 1988 1989
Leq 序号
年份
Leq
71.1 5
1990
71.4
72.4 6
1991
72.0
72.4 7
1992
71.6
72.1
表:某城市近年来交通噪声数据[dB(A)]
.
第一步:级比检验,建模可行性分析
.
4、灰生成技术
灰色序列生成 是一种通过对原始数据的挖掘、整理来寻求数据变化 的现实规律的途径,简称灰生成。
灰生成特点 在保持原序列形式的前提下,改变序列中数据的值与 性质。一切灰色序列都能通过某种生成弱化其随机性,
显现其规律性。
灰生成的作用 1.统一序列的目标性质,为灰决策提供基础。 2.将摆动序列转换为单调增长序列,以利于灰建模。 3.揭示潜藏在序列中的递增势态,变不可比为可比序列。
(k2,3,L,7),故可以用X ( 0 ) 作满意的GM(1, 1)
建模。
.
第二步: 用GM(1,1)建模
1. 对原始数据 X ( 0 )作一次累加:
k
x(1)(k) x(0)(m) (k1,2,L,7) m1
得:
X ( 1 ) x ( 1 )1 ,x ( 1 )2 ,L ,x ( 1 )7
.
例2 令原始序列X ( 0 )为
X ( 0 ) x ( 0 ) 1 ,x ( 0 ) 2 , x ( 0 ) 3 , x ( 0 ) 4 , x ( 0 ) 5
(1,1,1,1,1) A G O X (0 ) X (1 ) (1 ,2 ,3 ,4 ,5 )
关于“灰色预测模型”讲解

集成学习可以通过组合多个基模型的预测结果来提高整体 预测性能。可以将灰色预测模型作为基模型之一,与其他 预测方法一起构建集成学习模型。
与模糊逻辑融合
模糊逻辑能够处理不确定性和模糊性问题,可以与灰色预 测模型相结合,提高模型在处理不确定信息时的预测性能 。
THANKS
感谢观看
灰色差分方程
灰色预测模型的核心是建立灰色差分方程,通过对原始数据序列进行累加或累减 生成,构造出具有指数规律的数据序列,进而建立相应的微分方程进行求解。
适用范围及优势
适用范围
小样本建模
适应性强
预测精度高
灰色预测模型适用于数据量较 少、信息不完全、具有不确定 性和动态性的系统。它可以在 数据序列较短、波动较大、趋 势不明显的情况下,进行有效 的预测和分析。
04
灰色预测模型检验与评 估
残差检验法
01
02
03
残差计算
通过比较实际值与预测值 之间的差异,计算残差序 列。
残差分析
对残差序列进行统计分析 ,包括计算均值、方差等 指标,以评估模型的预测 精度。
残差图
绘制实际值与预测值的散 点图,以及残差序列的折 线图,直观展示模型的拟 合效果。
后验差检验法
金融市场分析
灰色预测模型可以用于分析金融市场的波动性和 趋势,帮助投资者做出更明智的投资决策。
3
物价水平预测
利用灰色预测模型可以对物价水平进行短期和长 期预测,为政府制定物价调控政策提供依据。
社会领域应用案例
人口数量预测
通过收集历史人口数据,利用灰色预测模型可以对未来人 口数量进行预测,为政府制定人口政策提供参考。
关于“灰色预测模型 ”讲解
灰色预测模型的优化及其应用

偏残差灰色预测模型的优化
1 2 3
偏残差灰色预测模型的基本原理
通过对原始数据序列的偏残差进行修正,提高灰 色预测模型的精度。
优化方法一
考虑非等间距序列:在偏残差灰色预测模型中考 虑非等间距序列的影响,可以更准确地反映原始 数据的变化规律。
优化方法二
引入非线性函数:在偏残差灰色预测模型中引入 非线性函数,可以更准确地描述原始数据序列的 变化规律。
05
结论
研究成果总结
灰色预测模型在处理具有不完整、不确定信息的问题上具有优势,能够克服数据量 小、信息不完全等限制。
通过引入优化方法,灰色预测模型在预测精度、稳定性和泛化性能等方面都得到了 显著提升。
灰色预测模型在多个领域具有广泛的应用价值,如经济、环境、医学等,为相关领 域的科学研究提供了新的思路和方法。
灰色神经网络预测模型的优化
01
灰色神经网络预测模型的基本原理
利用神经网络的自学习能力,对灰色预测模型进行优化。
02
优化方法一
选择合适的网络结构:根据历史数据选择合适的网络结构,可以提高灰
色神经网络预测模型的泛化能力。
03
优化方法二
采用集成学习算法:将多个灰色神经网络模型的预测结果进行集成,可
以提高预测精度。
灰色预测模型与其他模型的组合研究
01
02
03
集成学习
将灰色预测模型与其他预 测模型进行集成,通过集 结多个模型的优点,提高 预测精度。
混合模型
将灰色预测模型与其他模 型进行混合,以充分利用 各种模型的优势,提高预 测性能。
多模型融合
将多个灰色预测模型进行 融合,通过综合多个模型 的预测结果,提高预测精 度。
基于大数据和人工智能的灰色预测模型研究
灰色预测模型ppt

灰色系统理论与概率论、模糊数学一起并称为研究不确定系统的三种常用方 法。它们的研究对象都具有不确定性,但研究对象在不确定上的区别派生出三种 各具特色的不确定学科。三者的主要区别如下表所示:
项目 研究对象 基础集合 方法依据 途径手段 数据要求 目标 特色 灰色系统 贫信息不确定 灰色朦胧集 信息覆盖 灰序列生成 任意分布 现实规律 概率论 随机不确定 康托集 概率分布 概率统计 典型分布 历史统计规律 模糊数学 认知不确定 模糊集 隶属度函数 边界取值 隶属度可知 认知表达 经验(数据)
=(10771,11204,11487,11778,12076,12382,12695,13016,13347,13684)
精度检验
通过计算得出:(1)平均相对误差为
0
(2)X (0) 与 X 的绝对关联度为 0.993 0.90 s (3)均方差比为 c 2 0.24 0.35
其中, x (1) (k )
x ( 0) (i ), k 1,2,, n
i 1
k
在灰色系统中,累加算子的逆算子就是累减算子,累减生成对累加生成起还原作 用。
3.灰色系统预测模型
灰色预测的概念
灰色预测法是一种对含有不确定因素的系统进行预测的方法。灰色预测的理 论步骤如下:
进行关联 分析,并 对原始数 据进行生 成处理
灰 色 系 统 系统内一部分信息已 知,一部分信息未知, 系统内各因素间具有 不确定的关系。
白 色 系 统
系统的内部特征是 完全已知的,即系 统信息是完全充分 的。
黑 系统内部信息对外 色 界来说是一无所知 系 的。 统
1.灰色系统理论
灰色预测模型

dx
(t)
(1)
ax
(t)b,
dt
解为
b
a
(
t
1
) b
x(
t)
(
x(
1
))
e
.
a
a
(
1
)
(
0
)
(3)
于是得到预测值
b
b
(
1
)
(
0
)
ak
ˆ
x(
k
1
)
(
x(
1
)
)
e
,
k
1
,
2
,
,
n
1
,
a
a
从而相应地得到预测值:
(
0
)
(
1
)
(
1
)
ˆ
ˆ
ˆ
x
(
k
1
)
x
(
k
1
)
x
(
k
lim
dt
t
t 0
而 ( 1)( x ( k )) x ( k ) x ( k 1 ), 相当于
t 1
(3)加权邻值生成
(
0
)
(
0
)
(
0
)
(
0
)
x
(
x
(
1
),
x
(
2
),
,
x
(
n
))
设原始数列为
灰色预测模型.ppt

则GM(1,1)模型相应的微分方程为:
d X1 1 aX d t
其中:α 称为发展灰数;μ 称为内生控制灰数。
设 ˆ
a ˆ 为待估参数向量,
,可利用
最小二乘法求解。解得:
ˆ B B B Y n
T 1 T
求解微分方程,即可得预测模型:
1 0 ak ˆ X k 1 X 1 e a a
k 0 , 1 , 2 ..., n
二、模型检验 灰色预测检验一般有残差检验、关联度检 验和后验差检验。
(1)残差检验
ˆ 1i, 按预测模型计算 X
ˆ 1 i X 并将
T
利用公式求得:
0 .29075 0 . 87215
将以上两个参数带入公式中得:
1 0 ak ˆ X k 1 X 1 e a a
0 0 0 0 X k X 1 , X 2 ,..., X n
则关联系数定义为:
0 0 0 0 ˆ ˆ min min X k X k max max X k X k ( k ) 0 0 0 0 ˆ ˆ X k X k max max X k X k
序列进行数据处理,经过数据处理后的时
间序列即称为生成列。
(1)数据处理方式
灰色系统常用的数据处理方式有累加
和累减两种。 累加
累加是将原始序列通过累加得到生成列。
累加的规则: 将原始序列的第一个数据作为生成
列的第一个数据,将原始序列的第二个
数据加到原始序列的第一个数据上,其
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色灾变预测模型
1茶园沟泥石流灾变预测模型
灰色灾变预测模型基本思路是把无明显规律的时间序列,经过一次累加生成有规律的时间序列,为建立GM(1, 1)灰色模型提供中间信息,同时弱化原序列的随机性,然后采用一阶单变量动态模型GM(1, 1)进行拟合,用模型推求出来的生成数回代计算值,作累减还原运算,最后对还原值进行精度检验并进行预测。
本文以茶园沟泥石流为例,茶园沟曾1887年、1900年、1934年、1936
年、1947年、1972年以及2003年暴发大规模泥石流(表1)
表1茶园沟泥石流灾变日期及相应序号
本文通过采用1887年、1990年、1934年、1936年和1947年这5a灾变时间建立灾变预测模型,采用1972年和2003年这两年的灾变日期对预测结果进行检验。
根据表1建立茶园沟泥石流的灾变日期集:
P=[p(1),p (2),p (3),p(4),p(5)] =[1 14 48 50 61]
将日期集P 中数据作一次AGO(Accumulated GeneratingOperation) 累加生成:
P(1)(1) =1
P(1)(2) =P ⑴(1) +p(2) =15
P(1)(3) =P (1) (2) +p(3) =63
P⑴⑷=P (1) (3) +p⑷=113
P ⑴(5) =P ⑴⑷+p(5) =174
构造茶园沟累加数据矩阵B和常数向量Yn:
-39
-KN
-143 5
41
/J(4l5<
1户⑸6
用最小二乘法求得灰参数a,u:
-0 293]
22 8044」
即 a =-0.2937,u =22.8044,u /a 二77.6573。
将灰参数代入时间微分方程:dP(1)/dt+aP⑴=u
解微分方程求得时间函数:
/J 1J( / 4- 1丿二1J ( I ) - Lt /a J e at+ u /a
将a =-0.2937,u =22.8044,u /a =-77.6573 代入上式函数,即得茶园沟泥石流灾变预测模型
P ** (/+ 1丿=7R 6573e - 77 6573
2茶园沟泥石流灾变预测模型精度检验
预测模型的精度直接关系到预测结果的可信度。
因此,通下式计算出模型还
' f 3/ + r 1 r4f/
士。
