建筑制图基础形考作业
建筑制图基础形考作业一答案

《建筑制图基础》形考作业一答案
一、根据立体图中各点的空间位置,画出他们的投影图。
二、已知ABC三点的两面投影,求出第三面投影,并作出立体图。
三、已知点B在点A左方25 mm,下方10mm,前方18mm , 求出B点的三面投影,并完成A点的地三面投影。
四、画出直线的三面投影,判断各直线对投影面的相对位置,并标注各特殊位置直线对投影面的倾角的真实大小。
(1)AB是水平线
(2)CD是侧垂线
(3)EF是正平线(4)EF是侧平线
五、画出平面的第三面投影,判断各平面对投影面的相对位置,并标出各特殊位置平面对投影面的倾角的真实大小。
(1)三角形是正平面
(2)三角形是一般位置平面
(3)四边形是正垂面(4)平面图形是侧垂面
六、在三角形ABC内取一点D,使其距H面12mm,距V面20mm.
七、在三角形ABC内作一距V面15mm,的正平线。
八、完成五边形的正面投影(已知AB为侧平线)
九、在AB线段上取一点C,使得AC:CB=2:3。
十、已知C点在AB线段上,求C点的水平投影(用两种方法)
十一、已知MN两点在ABC平面上,补求它们的底二面投影。
十二、已知AB 、CD 两直线相交于K点,求AB直线的正面投影。
十三、已知AB线段的正面投影和对V面的倾角为30°,补全其水平投影。
《建筑制图基础形成性考核册》1-4作业答案
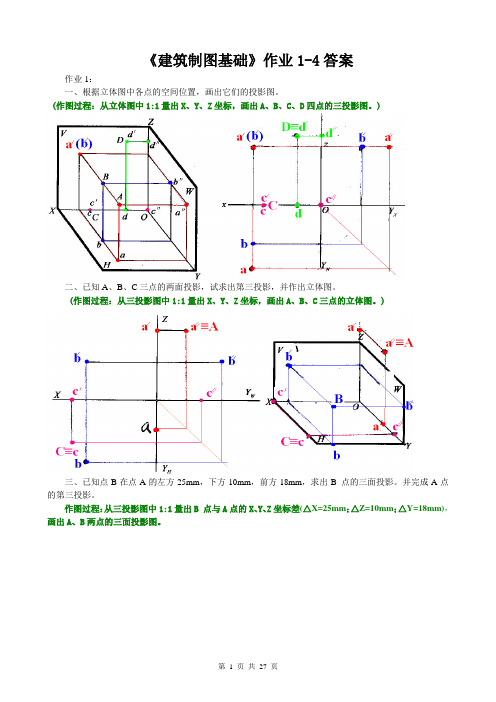
《建筑制图基础》作业1-4答案作业1:一、根据立体图中各点的空间位置,画出它们的投影图。
(作图过程:从立体图中1:1量出X、Y、Z坐标,画出A、B、C、D四点的三投影图。
)二、已知A、B、C三点的两面投影,试求出第三投影,并作出立体图。
(作图过程:从三投影图中1:1量出X、Y、Z坐标,画出A、B、C三点的立体图。
)三、已知点B在点A的左方25mm,下方10mm,前方18mm,求出B 点的三面投影。
并完成A点的第三投影。
作图过程:从三投影图中1:1量出B 点与A点的X、Y、Z坐标差(△X=25mm;△Z=10mm;△Y=18mm),画出A、B两点的三面投影图。
四、画出直线的第三投影,判断各直线对投影面的相对位置,并标出各特殊位置直线对投影面倾角的真实大小。
答案:见教材第43页表3-2。
五、画出平面的第三投影,判断各平面对投影面的相对位置,并标出各特殊位置平面对投影面倾角的真实大小。
答案:见教材第58页表3-4。
六、在三角形ABC内取一点D,使其距H面12mm,距V面20mm。
答案:七、在三角形ABC内作一距V面15mm的正平线。
答案:八、完成五边形的正面投影(已知AB为侧平线)答案:(作图方法:在平面内作辅助线法解题)九、在AB线段上取一点C,使得AC︰CD=2︰3十、已知C点在AB线段上,求C点的水平投影(用两种方法)。
十一、已知M、N两点在ABC平面上,补求它们的第二投影。
十二、已知AB、CD两直线相交于K点,求AB直线的正面投影。
十三、已知AB线段的正面投影和对V面的倾角β=30°,补全其水平投影。
十四、求点A到直线CD的垂直距离。
十五、求直线AB与P面的交点,并判别直线AB的可见性。
十六、求直线MN与ABC平面的交点,并判别直线MN的可见性。
《建筑制图基础》作业2一、求下列立体的第三面投影及表面上各已知点和直线的三面投影。
(1)求六棱柱表面A点、B点的三投影。
(2)二、求下列曲面立体的第三面投影及其表面上各已知点和直线的三面投影。
国家开放大学电大《建筑制图基础》形成性考核册作业1答案

国家开放大学学习指南形考作业参考答案作业一一、单项选择(每题5分,共计10分)1、请将你认为不适合描述为国家开放大学特色的选项选择出来。
()a. 国家开放大学是一所在教与学的方式上有别与普通高校的新型大学b. 国家开放大学是一所与普通高校学习方式完全相同的大学c. 国家开放大学可以为学习者提供多终端数字化的学习资源d. 国家开放大学是基于信息技术的特殊的大学2、请将不能客观地描述国家开放大学学习方式的选项选择出来。
()a. 在网络上阅读和学习课程教学资源b. 在课程平台上进行与老师与同学们的交流讨论c. 只有在面对面教学的课堂上才能完成学习任务d. 利用pad、手机等设备随时随地学习二、判断题(每题2分,共计10分)1、制定时间计划,评估计划的执行情况,并根据需要实时地调整计划,是管理学习时间的有效策略。
(对)2、远程学习的方法和技能比传统的课堂学习简单,学习方法并不重要。
(错)3、在国家开放大学的学习中,有课程知识内容请教老师,可以通过发email、QQ群、课程论坛等方式来与老师联络。
(对)4、在网络环境下,同学之间、师生之间无法协作完成课程讨论。
(错)5、纸质教材、音像教材、课堂讲授的学习策略都是一样的。
(错)作业二一、单选题(每题2分,共5题,共计10分)1、开放大学学制特色是注册后年内取得的学分均有效。
()选择一项:a. 10b. 8c. 5d. 32、不是专业学位授予的必备条件。
()a. 被评为优秀毕业生b. 课程学习成绩达到学位授予的相关要求c. 通过学位英语考试d. 毕业论文成绩达到学位授予相关要求3、是专业学习后期需要完成的环节。
()a. 了解教学计划b. 专业综合实践c. 入学教育d. 入学测试4、转专业后,学籍有效期从开始计算。
()a. 入学注册时b. 转专业后学习开始的时间c. 转专业批准的时间d. 提出转专业申请的时间5、不是目前国家开放大学设有的学习层次。
()a. 小学、初中b. 专升本科c. 中专d. 专科二、判断题(每题2分,共5题,共计10分)1、办理转专业相关事宜时,拟转入专业与转出专业应属于同等学历层次,本科转专业还应是同科类相近专业。
电大建筑制图基础形成性考核作业3

空间分析:
空间分析:
五、作出指定剖切位置的断面图。 空间分析:
画出轴测图(先补侧平面)
O X
Z
O Y
三、补全下列剖面图中所缺的图线.
空间分析:
三、补全下列剖面图中所缺的图线.
空间分析:
空间分析:
空间分析:
(4)
四、在指定位置上,作出1-1 、 2-2剖面图。 空间分析:
四、在指定位置上,作出1-1 、 2-2剖面图。 空间分析:
空间分析:
空间分析:
正等轴测图的轴间角 和变形系数 ∠XOY=∠YOZ=∠ZOX=1 20°
p=q=r≈1
一、画出下列形体的正等轴测图 (1)
空间分析:
Z
O Y
X
空间分析:
非对称形体的坐标取法
Z
O Y
X
空间分析: 此形体前后对称。
Z
O Y
X
(4)
Z
O
X
Y
画出轴测图(用堆积组合法)
Z
O Y
X
பைடு நூலகம்案:
二、补画下列形体的第三视图,并画出三正等轴测图 补画第三视图: (先补侧平面)
XXX《建筑制图基础》形考作业答案

XXX《建筑制图基础》形考作业答案一、根据立体图中各点的空间位置,绘制它们的投影图。
作图过程:根据立体图中的X、Y、Z坐标,绘制A、B、C、D四点的三视图。
二、已知A、B、C三点的两面投影,求出第三个投影,并绘制立体图。
作图过程:根据三视图中的X、Y、Z坐标,绘制A、B、C三点的立体图。
三、已知点B在点A的左侧25mm,下方10mm,前方18mm,求出B点的三视图。
并绘制A点的第三投影。
作图过程:根据三视图中B点与A点的X、Y、Z坐标差(△X=25mm;△Z=10mm;△Y=18mm),绘制A、B两点的三视图。
四、绘制直线的第三视图,判断各直线对投影面的相对位置,并标出各特殊位置直线对投影面倾角的真实大小。
参考教材第43页表3-2.五、绘制平面的第三视图,判断各平面对投影面的相对位置,并标出各特殊位置平面对投影面倾角的真实大小。
参考教材第58页表3-4.六、在三角形ABC内取一点D,使其距H面12mm,距V面20mm。
七、在三角形ABC内绘制一条距离V面15mm的正平线。
八、完成五边形的正面投影(已知AB为侧平线)。
作图方法:使用辅助线法解题。
九、在AB线段上取一点C,使得AC︰CD=2︰3.十、已知C点在AB线段上,求C点的水平投影(使用两种方法)。
十一、已知M、N两点在ABC平面上,求它们的第二投影。
十二、已知AB、CD两直线相交于K点,求AB直线的正面投影。
十三、已知AB线段的正面投影和对V面的倾角β=30°,补全其水平投影。
十四、求点A到直线CD的垂直距离。
十五、求直线AB与P面的交点,并判断直线AB的可见性。
十六、求直线MN与ABC平面的交点,并判断直线MN 的可见性。
一、求六棱柱表面A点、B点的三面投影。
二、求下列曲面立体的第三面投影及其表面上各已知点和直线的三面投影。
三、完成被切割的平面立体的三面投影。
四、完成被切割的曲面立体的三面投影。
五、已知四坡屋面的倾角α=30及檐口线的H投影,求屋面交线的H投影和屋面的V投影。
电大建筑制图基础形成性考核册作业答案(完整版)

1 4
空间分析: 两面共线;正平面上的线是正平线。
七、在三角形ABC内作一距V面15mm的正平线。
15
、完成五边形的正面投影 (已知AB为侧平线)作图方法:在平面内作辅助线法解题
见教材第50页a图3- 18。
九、 在直线AB线段上取一点C,使得AC:CD=2:3
19
十二、 已知AB、CD两直线相交于K点, 求AB直线的正面投影。
作图方法: 见教ቤተ መጻሕፍቲ ባይዱ第51页图3-19。
方法二:由平行投影的定比性
20
H■一、已知M、N两点在ABC平面上,补求 它们的第二投影。作图方法:在三角形平面上作辅助线法。
十四、 求点A 到直线CD 的垂直距离。
21
十四、 求点A到直线CD的垂直距离。(提示:CD直线是水平线,水平投影为CD直线实长)
16
十三、 已知AB线段的正面投影和对V面的倾角p=30°, 补全其水平投影。
十三、 已知AB线段的正面投影和对v面的 倾角B=30°,补全其水平投影。
作图方法: 用直角三形法作图求解。见教材第49页图3-16。
17
a18
答案:
十、 已知C点在AB线段上,求C点的水 平投影(用两种方法)。
方法一:补出第三投影。
(4)EF 是
线
6
__
五、画出平面的第三投影,判断各平面对投影面的相对 位置,并标出各特殊位置平面对投影面倾角的真实大小。(1)三角形是 面
答案:见教材第43页表3-2。(4)EF 是侧平线线
7
一般位置平面的投影图 投影为小于三角形实形的类似形
答案:见教材第58页表3-4。(1)三角形是止平面
建筑制图基础▲(20春)第2学期形考作业2答卷

24.水平面的正面投影反映实形。
答案:错误
25.在建筑立面图中,定位轴线及编号应全部详细标示出。
答案:错误
26.建筑立面图中,建筑的外形轮廓线用细实线绘制。
答案:错误
5.()是指直线或平面相对另一直线或平面的倾斜程度。
A.斜度
B.弧度
C.角度
D.锥度
答案:A
6.下列选项中,不可能是圆锥体截交线的是()。
A.等腰三角形
B.圆
C.椭圆
D.正方形
答案:D
7.下面关于水平线的论述,错误的是()。
A.在H面投影反映实长
B.在V面投影反映实长
C.在V面投影平行于OX轴
D.在W面投影平行于OY轴
答案:B
8于投影面的点
B.位于投影轴的点
C.位于垂直投影面直线上的点
D.位于原点的点
答案:C
9.一个垂直于圆柱轴线的平面与圆柱相交,其截交线是()。
A.双曲线
B.抛物线
C.圆
D.椭圆
答案:C
10.下列图示内容中,不属于建筑平面图的内容的是()。
A.新建建筑定位
B.墙柱的位置
C.楼梯的安排
D.门窗的位置
答案:A
二、多选题 (共 6 道试题,共 30 分)
11.给水排水工程包括()。
A.给水工程
B.排水工程
C.暖通工程
D.环境工程
答案:AB
12.关于点的两面投影规律,下面说法正确的是()。
A.点的两面投影连线垂直于投影轴
B.点的两面投影连线平行于投影轴
建筑制图基础形考作业一答案

《建筑制图基础》形考作业一答案
一、根据立体图中各点的空间位置,画出他们的投影图。
二、已知ABC三点的两面投影,求出第三面投影,并作出立体图。
三、已知点B在点A左方25 mm,下方10mm,前方18mm , 求出B点的三面投影,并完成A点的地三面投影。
四、画出直线的三面投影,判断各直线对投影面的相对位置,并标注各特殊位置直线对投影面的倾角的真实大小。
(1)AB是水平线
(2)CD是侧垂线
(3)EF是正平线(4)EF是侧平线
五、画出平面的第三面投影,判断各平面对投影面的相对位置,并标出各特殊位置平面对投影面的倾角的真实大小。
(1)三角形是正平面
(2)三角形是一般位置平面
(3)四边形是正垂面(4)平面图形是侧垂面
六、在三角形ABC内取一点D,使其距H面12mm,距V面20mm.
七、在三角形ABC内作一距V面15mm,的正平线。
八、完成五边形的正面投影(已知AB为侧平线)
九、在AB线段上取一点C,使得AC:CB=2:3。
十、已知C点在AB线段上,求C点的水平投影(用两种方法)
十一、已知MN两点在ABC平面上,补求它们的底二面投影。
十二、已知AB 、CD 两直线相交于K点,求AB直线的正面投影。
十三、已知AB线段的正面投影和对V面的倾角为30°,补全其水平投影。
建筑制图基础实训形考作业一

建筑制图基础实训
小作业一
1、写出图中指出的图线的名称,以及当b=0.7时的线宽。
2、注出窗立面图的比例。
3、根据所给的比例,注出外墙板长河高的
实际尺寸。
窗立面图
外墙板立面图1:60
4、作出下列建筑形体的剖面图与断面图。
(1)作1—1剖面图。
(2)作形体的半剖面图。
(3)补绘1—1剖面图。
(4)补绘2—2剖面图(雨篷的材料为钢筋混凝土)。
1
2 2 1
2—2剖面图
1 1
2 2 1—1剖面
2---2 剖面图
1
1
1 1
剖面图
2 (5)补绘2-2剖面图
(6)补绘1—1、2—2、3—3断面图。
2
3 3 1 1
2
(7)补画1—1阶梯剖面图。
5、简答题
(1)土木工程制图中的图线有几种?其用途有何不同?
(2)标注尺寸时,绘制45°短线的起止符号应注意哪些问题?
(3)图名有何作用?在注写图名时要注意哪些规定?
(4)剖面图与断面图的主要区别是什么?两者又有何联系?
(5)简化画法意义何在?常用的简化画法有几种?其使用条件是什么?。
国家开放大学建筑制图基础形考作业答案

国家开放大学建筑制图基础形考作业答案一、单选题1、下列哪个选项不属于正投影图的基本特性?()A.真实性B.积聚性C.平行性D.相似性答案:D2、在三面投影体系中,V面投影是水平投影的()A.对称平面B.垂直平面C.平行平面D.投影面垂直面答案:C3、在三面投影体系中,V面投影反映空间几何元素在()方位的投影。
A.水平面B.侧平面C.正平面D.任意平面答案:C4、在三面投影体系中,H面投影反映空间几何元素在()方位的投影。
A.正平面B.侧平面C.水平面D.任意平面答案:A5、在三面投影体系中,W面投影反映空间几何元素在()方位的投影。
A.正平面B.侧平面C.水平面和正平面D任意平面答案:B6、在三面投影体系中,空间几何元素在三个投影面上的投影能反映出它们的()。
A.形状和大小B.形状C.大小D.位置关系答案:A7、下列哪个选项不属于三面投影体系中的三个投影面?()A.V面B.H面C.W面D.X轴Y轴Z轴答案:D8、下列哪个选项不属于点的坐标?()A.x坐标B.y坐标C.z坐标D.y坐标或z坐标答案:D9、下列哪个选项不属于线的坐标?()A.x坐标B.y坐标C.z坐标D.线段长度答案:D10、下列哪个选项不属于面的坐标?()A.x坐标B.y坐标C.z坐标D.面的形状和大小答案:D二、判断题1、点是空间中最简单的几何元素,是组成线、面的基本单元。
()正确错误2、点的投影一定是点的连线与投影轴的交点。
()正确错误3、点的直角坐标与点的投影在形状和大小上完全一致。
()正确错误4、空间两直线平行,则它们的投影一定平行且反映实长。
()正确错误5、空间两直线相交,则它们的投影一定相交于一点。
()正确错误6、两直线的V面投影重合,则它们一定平行于H面。
()正确错误7、两直线的H面投影重合,则它们一定平行于W面。
()正确错误8、两直线或平行或相交,则它们的投影一定平行。
()正确错误9、平面的直角坐标与平面的投影在形状和大小上完全一致。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
答案: (B在点A的左方25mm,下方10mm, 前方18mm)
四、画出直线的第三投影,判断各直线对
投影面的相对位置,并标出各特殊位置直线对投 影面倾角的真实大小。
答案:(见教材第43页表3-2)
α=0°
βγ
答案:见教材第45页表3-3。
α=0°
β=0 ° γ=90 °
正平线
e′
a′ Z a〞
c′ X
c
b′
b〞
c〞
aO
YW
b YH
c
b a
答案:见教材第60页图3-31。
在投影图上不反
映空间平面与投影 面夹角的真实大小 。但可作最大斜度 线的方法求解α、β 、γ角的真实大小。
c″
d″
b″
a″
答案:见教材第60页表3-5。
β=90° γ
α
答案:见教材第60页表3-5。
β
α
γ=90°
六、在三角形ABC内取一点D,使其距H 面12mm,距V面20mm。
空间分析:三面共点(D点)
B
D
Q
C
P
A
六、在三角形ABC内取一点D,使其距H 面12mm,距V面20mm。
d′
Pv
20 12
QH
d
七、在三角形ABC内作一距V面15mm的正平线。
空间分析:两面共线;正平面上的线是正平线。
c
十二、已知AB、CD两直线相交于K点, 求AB直线的正面投影。
d′
k′
十一、已知M、N两点在ABC平面上,补求
它们的第二投影。
作图方法:
在三角形平面上作辅助线法。
n′
m
十四、求点A到直线CD的垂直距离。
十四、求点A到直线CD的垂直距离。 (提示:CD直线是水平线,水平投影为CD直线实长)
作图步骤: 1.求距离的投影; 2.求距离的实长
距离实长
1、求出距离的投影。
答案:Leabharlann 2、用直角三角形法求距离实长。十五、求直线AB与P面的交点,并判别 直线AB的可见性。
空间分析:
P
十五、求直线AB与P面的交点,并判别
直线AB的可见性。
解题步骤:
1. 求交点;
2. 可见性判别。
十六、求直线MN与ABC平面的交点,并 判别直线MN的可见性。
建筑制图基础 作业 1 解析
一、根据立体图中各点的空间位置,画出它们的投影图。
a′
az
a″
ax
a
ay
二、已知A、B、C三点的两面投影,试求出 第三投影,并作出立体图。
a′ a″
a
a
c
b
答案:
三、已知点B在点A的左方25mm,下方10mm, 前方18mm,求出B 点的三面投影。并完成A点的第 三投影。
七、在三角形ABC内作一距V面15mm的正平线。 PH
15
c′
八、完成五边形的正面投影
b′
(已知AB为侧平线)
作图方法:
在平面内作辅助线法解题
九、在直线AB线段上取一点C,使得AC:CD=2:3
见教材第50页 图3-18。
C′
C
十三、已知AB线段的正面投影和对 V面的倾角β=30°,补全其水平投影。
完
十三、已知AB线段的正面投影和对V面的 倾角β=30°,补全其水平投影。
30 °
作图方法:
用直角三形法 作图求解。
见教材第49页 图3-16。
b
答案:
十、已知C点在AB线段上,求C点的水 平投影(用两种方法)。
方法一:补出第三投影。
Z a″ c″ b″
c YH
方法二:由平行投影的定比性
作图方法: 见教材第51页图3-19。
直线MN是正垂线; 三角形ABC是一般位置平面。
交点是直线上的点; 也是三角形平面上的点。 同时交点也在三角形平面上的辅助线上。
空间分析:
十六、求直线MN与ABC平面的交点,并
判别直线MN的可见性。
解题步骤:
1.在正面投影的三 角形平面上作辅助 线求三角形水平投 影的交点;
2.可见性判别。
第一次形成性考核 作业评讲
α
β =0°
γ
f′
(见教材第43页表3-2)
答案:见教材第43页表3-2。
五、画出平面的第三投影,判断各平面对投影面的相对 位置,并标出各特殊位置平面对投影面倾角的真实大小。
a
bc
答案:见教材第58页表3-4。
α=90°
β=0 °
γ=90 °
一般位置平面的投影图
投影为小于三角形实形的类似形
