拉格朗日插值法
拉格朗日插值法 python

一、引言拉格朗日插值法是一种常用的插值方法,在数据分析和数值计算中有着广泛的应用。
它通过构造一个满足已知数据点的多项式函数来近似未知函数,从而可以在给定数据点之间进行插值预测。
在Python语言中,通过利用NumPy库和SciPy库提供的相关函数,我们可以很方便地实现拉格朗日插值法,进行数据的插值计算和预测。
本文将介绍拉格朗日插值法的原理和实现过程,并结合Python代码进行具体的演示和应用。
二、拉格朗日插值法的原理拉格朗日插值法是一种基于多项式插值的方法,它可以通过已知数据点构造一个多项式函数,从而实现数据的插值预测。
假设我们有n个已知数据点{(x1, y1), (x2, y2), ... , (xn, yn)},我们希望通过这些数据点来构造一个多项式函数P(x),使得P(xi)=yi,i=1,2,...,n。
具体地,多项式函数P(x)可以表示为:P(x) = Σ(yi * Li(x))其中Li(x)是拉格朗日基函数,它可以表示为:Li(x) = Π((x-xj)/(xi-xj)), j≠i, i=1,2,...,n通过对已知数据点的多项式函数P(x)进行构造和拟合,我们就可以实现对未知函数值的插值预测。
三、拉格朗日插值法的实现在Python语言中,我们可以利用NumPy库和SciPy库提供的相关函数,很方便地实现拉格朗日插值法。
具体实现过程如下:1. 导入NumPy库和SciPy库import numpy as npfrom scipy.interpolate import lagrange2. 定义已知数据点x = np.array([1, 2, 3, 4, 5])y = np.array([2, 3, 5, 7, 11])3. 调用lagrange函数进行插值计算poly = lagrange(x, y)4. 进行插值预测x_pred = 6y_pred = poly(x_pred)通过以上代码,我们就可以利用Python语言实现拉格朗日插值法的计算和预测。
重心拉格朗日插值法

重心拉格朗日插值法【实用版】目录1.拉格朗日插值法的概述2.拉格朗日插值法的基本原理3.拉格朗日插值法的应用实例4.拉格朗日插值法的优点与局限性正文【拉格朗日插值法的概述】拉格朗日插值法是一种数学插值方法,由 18 世纪意大利数学家约瑟夫·拉格朗日(Joseph-Louis Lagrange)提出。
它是一种基于基函数和待求值点权重的插值方法,可以广泛应用于数值计算、工程技术、物理学等领域。
【拉格朗日插值法的基本原理】拉格朗日插值法的基本原理是:假设已知 n 个自变量 x 的值和相应的因变量 y 的值,构建 n 个线性方程,求解这 n 个线性方程得到 n 个基函数,将这 n 个基函数与 x 的值相乘并求和,得到待求函数在 x 处的近似值。
具体来说,拉格朗日插值法的计算步骤如下:1.确定插值节点:首先,根据已知的自变量 x 的值和相应的因变量 y 的值,选取 n 个插值节点。
2.构建线性方程:对于每个插值节点,构建一个线性方程。
线性方程的形式为:y = a0 + a1x1 + a2x2 +...+ anxn,其中 a0, a1, a2,..., an 为待求系数,x1, x2,..., xn 为插值节点的自变量值,y 为对应的因变量值。
3.求解线性方程:解这 n 个线性方程,得到 n 个基函数:β0(x), β1(x),..., βn(x)。
其中,βi(x) = a0 + a1x1 + a2x2 +...+ anxn,i = 0, 1,..., n。
4.计算插值结果:将 n 个基函数与 x 的值相乘并求和,得到待求函数在 x 处的近似值:y(x) ≈β0(x) + β1(x)x1 + β2(x)x2 +...+ βn(x)xn。
【拉格朗日插值法的应用实例】拉格朗日插值法广泛应用于数值计算、工程技术、物理学等领域。
例如,在计算机图形学中,拉格朗日插值法可以用于计算光线与物体的交点,从而实现光线追踪渲染;在数值分析中,拉格朗日插值法可以用于求解微分方程的数值解等。
拉格朗日差值法

拉格朗日插值法就是构造一个多项式,使得恰好在每一个x处取到对应的y
首先,n+1个点(xi,yi)若xi不同,则可以确定唯一的最高幂次不超过n的多项式。
而如果题目直接或是间接给出了n+1个点,让我们求由这些点构成的多项式在某一个位置的取值,那么应用拉格朗日插值可以在O(n2 )的时间内解决这一问题
思路如下:
对于这个函数,要想在k=x[i]的时候取到y[i],并且y[i]仅在这一情况对答案有影响,就要构造出一项K[i]y[i],使得x仅在取到x[i]时K为1,其他情况K[i]为0。
于是,仿照中国剩余定理的思路,有了如下构造方式:
(1)首先,x≠x[i]时K[i]为0,就要让x取到除去x[i]外的任何值都为0,于是有了“累乘‘k-x[j]’”的思路;
(2)其次,如果简单地将y[i]与累乘‘k-x[j]’结合,则x=x[i]时
该项为“累乘x[i]-x[j]",所以需要在每一项下面加上"除以x[i]-x[j]”
(3)最后将每一项加和,得到上式
拓展:x取值连续时的做法
有时候,问题仅要求求解x连续的情况。
那么如果仅有一个k值需要代入f(k),就可以用下面的方法将复杂度变为
O(n)
对于分子,维护出k的前缀积和后缀积,即:
由于最终求得的值一定为正数,故需判断一下正负号。
如果N-i为奇数,则分母要取负数(因为fac(N-i)表示的是绝对值,N-i为偶数的时候恰好所有负号消掉了)。
计算方法插值法-Lagrange插值

b
a
x2
用 的值作为f(x)的近似值,不仅希望 能较好地逼近f(x),而且还希望它计算简单 。
评论:
由于代数多项式具有数值计算和理论分析方便的优点。所以本章主要介绍利用代数多项式进行插值,即代数插值。
定义:若存在一个次数不超过n次的多项式
使得满足:
则称P(x)为f(x)的n次插值多项式。
因为 ,所以方程组有解唯一解:
系数矩阵
可用于求2次插值多项式
仿照线性插值,现在试图用基函数的方法确定2次插值多项式
显然 应该有以下的形式
由 确定系数
从而导出
求二次式 ,使满足条件:
01
02
类似地可以构造出插值多项式
于是确定了3个抛物插值的基函数:
x0
x2
x1
x
y
1
y=l0(x)
y=l1(x)
y=l2(x)
3个抛物插值的基函数
取已知数据 作为线性组合系数,将基函数 线性组合可得
容易看出,P(x)满足条件
即
一般形式的拉格朗日插值多项式
已知: 2个插值点可求出一次插值多项式,而 3个插值点可求出二次插值多项式。
…
…
插值点增加到n+1个时,可通过n+1个不同的已知点 来构造一个次数为n的代数多项式P(x)。先构造一个特殊n次多项式 的插值问题,使其在各节点 上满足
对于线性插值,误差公式:
01
对于抛物插值(2次插值),误差公式:
02
例2.8 已知x0 =100, x1 =121,用线性插值近似计算 的时候,估计在x=115时的截断误差.
解: 由插值余项公式知
得
拉格朗日插值法的应用

拉格朗日插值法的应用概述拉格朗日插值法是一种常用的数值分析方法,广泛应用于数据拟合、泛函逼近、差值计算等领域。
本文将从数学原理、计算方法、应用案例等角度全面探讨拉格朗日插值法的应用。
数学原理拉格朗日插值法的基本思想是构造一个多项式,使得该多项式在给定插值节点上的函数值与已知函数值完全一致。
假设给定 n+1 个节点(x0, y0), (x1, y1),…,(xn, yn),要求通过这些节点构造一个多项式 P(x),使得对于任意 x,都有 P(xi) = yi。
计算方法利用拉格朗日插值法,可以得到如下的插值多项式:P(x) = Σ( yi * L(x) / L(xi) ),其中L(x) = Π( x - xj ) / Π( xi -xj ) ,j!=i。
在计算插值多项式时,首先需要计算 Lagrange 插值基函数 L(x)。
然后,依次计算每个节点对应的函数值乘以相应的基函数L(x)的比值,最后将所有结果相加,即可得到插值多项式 P(x)。
应用案例1. 数据拟合拉格朗日插值法可以用于数据拟合,通过已知数据点,构造插值多项式,从而估计数据在其他位置的值。
例如,给定一组实验数据点(x0, y0), (x1, y1),…,(xn, yn),假设我们想要估计在 x=3 的位置的函数值。
我们可以通过拉格朗日插值法构造插值多项式 P(x),然后计算 P(3),得到估计值。
2. 泛函逼近拉格朗日插值法可以用于对函数的逼近。
假设给定一个函数 f(x),我们想要找到一个函数 g(x) 来逼近 f(x)。
可以将 f(x) 的若干个节点上的函数值作为已知数据点,通过拉格朗日插值法构造插值多项式 P(x),从而得到逼近函数 g(x)。
在实际应用中,通常会选择合适的插值节点,以确保逼近结果的准确性。
3. 差值计算差值是拉格朗日插值法的一种重要应用。
给定一个连续函数 f(x) 和一个节点序列(x0, x1, …, xn),我们可以通过拉格朗日插值法构造插值多项式 P(x),从而通过插值多项式来逼近函数 f(x)。
拉格朗日插值法要求点的顺序

拉格朗日插值法要求点的顺序篇一拉格朗日插值法要求点的顺序咱们今天就来好好唠唠拉格朗日插值法要求点的顺序这个事儿。
为啥要谈这个呢?你想想啊,在处理各种数学问题的时候,要是这顺序搞不对,那不是乱套了嘛!就像你做饭,先放盐还是先放醋,顺序错了,味道能好吗?咱先说说这第一个要求。
对于拉格朗日插值法,**要求点的输入顺序必须是按照横坐标的大小进行排列的**。
比如说,你有一堆点 (1, 2) 、(3, 4) 、(2, 5) ,那得先把它们按照横坐标 1、2、3 这样从小到大排好。
这一点可重要了,要是顺序乱了,那算出来的结果能对吗?再来说说第二个要求。
**不仅要按横坐标大小排,还得注意不能有重复的横坐标值**。
这就好比你去买东西,同一样东西买两次,那不是浪费嘛!要是有重复的横坐标,这插值法还怎么插得准呢?还有啊,**每个点的坐标都得准确无误**。
要是你把 (1, 2) 写成 (1, 3) ,那可就差之毫厘谬以千里啦!你说要是不按照这些要求来,会咋样?那结果肯定是一塌糊涂,就像你闭着眼睛走路,能不摔跤吗?所以啊,大家都得把这些要求记在心里,可别马虎大意!总之,按照这些要求来操作拉格朗日插值法,才能得出准确可靠的结果,为咱们解决更多的数学难题助力!篇二拉格朗日插值法要求点的顺序嘿,朋友们!今天咱们来深入聊聊拉格朗日插值法要求点的顺序。
这可不是小事儿,搞不好会出大乱子的!为啥要强调这个顺序呢?你想啊,如果在建筑工地上,砖头乱放,能盖出结实的房子吗?同理,拉格朗日插值法的点顺序不对,也得不到正确的结果。
首先,**点的顺序得严格遵循横坐标的递增或者递减规律**。
比如说,如果是递增,那就是 1、2、3 这样排,递减就得是 3、2、1 来。
可不能一会儿增一会儿减,乱了套!然后呢,**重复的横坐标绝对不允许出现**。
这就好像考试不能作弊一样,是铁律!要是有重复的,那这插值法还怎么准确计算?还有个关键的,**点的坐标精度得有保证**。
拉格朗日插值法ppt课件

在节点xi处的函数值必然相等 但在节点 P(x外 )的值可能就会 f(x偏 ) 离 因此 P(x)近似代f(替 x)必然存在着误差 8
整体误差的大小反映了插值函数的好坏 为了使插值函数更方便在计算机上运算,一般插值函 数都使用代数多项式和有理函数
本章讨论的就是代数插值多项式
二、代数插值多项式的存在唯一性
n1(x) n1(xj )(xxj )
j0,1,2,,n -------(7')
显l然 0(x)l,1(x)l,2(x) , ,ln(x)线性(无 请同学关 们思考)
且
l j ( xi )
1 0
i j i j
i,j0,1,2,,n -------(8)
16
如果 l0(x)l用 1 ,(x)l2 ,(x) ,,ln(x)作 yf(x)的插值 而Pn(x) 为f(x)的插值多 ,则 项式
6
问题
• 是否存在唯一 • 如何构造 • 误差估计
如函 ys数 ixn ,若给 [0,]上 定 5个等分点
其插值函数的图象如图
7
yy
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 0
0.522
22..55
33
xxx
33..55
对于被插 f(x)和 函插 数值P(函 x) 数
一、插值余项
从上,节 yf可 (x)的 L 知 ag插 ran 值 ge
满足
n
Ln(x) yjlj(x) j0
L n(x i)f(x i) i 0 ,1 , ,n
但 x[a,b]
Ln(x)f(x) 不会完全成立
因此,插值多项式存在着截断误差,那么我们怎样估 计这个截断误差呢?
《拉格朗日插值法》课件

根据已知的插值点和插值函数的性质 ,确定多项式的阶数。
求解插值多项式的系数
求系数
通过已知的插值点和构造的插值多项式,求解出多项式的系数。
验证解的正确性
通过已知的插值点和求解出的系数,验证解的正确性。
04
拉格朗日插值法的应用实例
在数值分析中的应用
数值积分
拉格朗日插值法可用于数值积分,通过插值多项式对被积函数进行近似,进而求得积分的近似值。
全局插值能力较弱
拉格朗日插值法主要适用于局部插值,对于全局插值问题可能不太 适用。
06
拉格朗日插值法的改进与发
展
改进方法
提高精度
通过增加插值基函数的数量, 可以更精确地逼近函数,从而
提高插值的精度。
处理异常值
引入稳健性估计方法,对异常 值进行识别和处理,以提高插 值的稳定性。
优化算法
改进算法以提高计算效率,减 少计算量,使得插值过程更加 快速和高效。
图像处理
在图像处理中,可以使用拉格朗日插值法对图像进行放大、缩小或旋转等变换,保持图 像的清晰度和连贯性。
三维模型重建
在三维模型重建中,可以使用拉格朗日插值法对点云数据进行插值,得到连续光滑的三 维模型表面。
05
拉格朗日插值法的优缺点
优点
01
02
03
简单易行
拉格朗日插值法是一种直 观且易于理解的方法,不 需要复杂的数学工具即可 实现。
工程
用于解决各种实际问题,如机 械振动、流体动力学和电路分 析等。
物理学
用于模拟和预测各种物理现象 ,如力学、电磁学和量子力学 等。
02
拉格朗日插值法的基本概念
拉格朗日插值法的定义
用拉格朗日插值法

用拉格朗日插值法
拉格朗日插值法是经典的插值原理,是一种根据一组已知数据,用拉格朗日插值函数(Lagrange Polynomials)求未知数据的一种方法。
这种方法的基本思想是:设n个点(x1,y1),(x2,y2),..., (xn,yn)是一组给定的数据点,Pn(x)是构造出来的关于变量x的n 阶多项式,称为插值函数,它可以通过这些已知数据点,以最佳方式拟合这些数据点,而且在这多点之间插值时,需要保证在插值点处取到准确值,即Pn(xi)=yi。
设Pn(x)=f1(x)f2(x)…fn(x);其中,f1(x),f2(x)…fn(x)是拉格朗日插值函数,满足在每个插值点xi 处有功能值等于已知值yi。
拉格朗日(Lagrange)插值

18
x1 x2 利用 x0 = π , x1 = π L1 ( x ) = x π / 4 × 1 + x π / 6 × 1 6 4 π / 6 π / 4 2 π / 4 π / 6 2 π sin 50 0 ≈ L1 ( 5 ) ≈ 0.77614 这里 f ( x) = sin x , f (2) (ξ x ) = sinξ x , ξ x ∈(π , π ) 内插通常优于外插。 ) 18 内插通常优于外插。2选择 6 3 ( f (ξ x ) 而 1要计算的3x 所在的区间的x π )( x π ) , R1 ( x) = ( < sinξ x < 2 2 2! 6 4 端点,插值效果较好。 端点,插值效果较好。 sin 50° = 0.7660444… 0.01319 < R1 ( 5π ) < 0.00762 18
+1)
( n + 1) ! Nhomakorabeax
Rn ( x) =
(n + 1) !
∏( x x )
i i =0
注:
M n +1 n 作为误差估计上限。 将 ( n + 1)! ∏ | x x i | 作为误差估计上限。 i =0
通常不能确定 ξx , 而是估计
f ( n + 1 ) ( x ) ≤ M n + 1, x∈(a,b) ∈
这样求Lagrange插值多项式计算量大,不便于实际应用。 Lagrange插值多项式计算量大 注: 这样求Lagrange插值多项式计算量大,不便于实际应用。 过两点直线。 一次多项式插值 --- 过两点直线。 过三点抛物线。 二次多项式插值 --- 过三点抛物线。 则插值多项式不唯一 不唯一。 若不将多项式次数限制为 n ,则插值多项式不唯一。
拉格朗日插值法
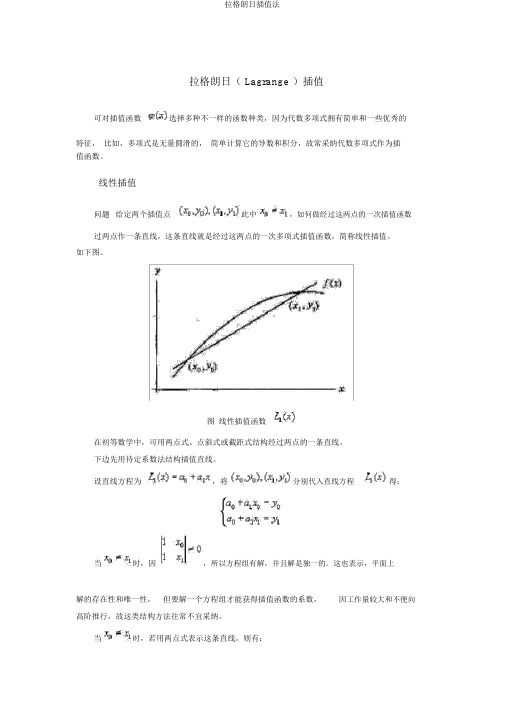
拉格朗日( Lagrange )插值可对插值函数选择多种不一样的函数种类,因为代数多项式拥有简单和一些优秀的特征,比如,多项式是无量圆滑的,简单计算它的导数和积分,故常采纳代数多项式作为插值函数。
线性插值问题给定两个插值点此中,如何做经过这两点的一次插值函数过两点作一条直线,这条直线就是经过这两点的一次多项式插值函数,简称线性插值。
如下图。
图线性插值函数在初等数学中,可用两点式、点斜式或截距式结构经过两点的一条直线。
下边先用待定系数法结构插值直线。
设直线方程为,将分别代入直线方程得:当时,因,所以方程组有解,并且解是独一的。
这也表示,平面上解的存在性和唯一性,但要解一个方程组才能获得插值函数的系数,因工作量较大和不便向高阶推行,故这类结构方法往常不宜采纳。
当时,若用两点式表示这条直线,则有:()这类形式称为拉格朗日插值多项式。
,,称为插值基函数,计算,的值,易见()在拉格朗日插值多项式中可将看做两条直线,的叠加,并可看到两个插值点的作用和地位都是同等的。
拉格朗日插值多项式型式免去认识方程组的计算,易于向高次插值多项式型式推行。
线性插值偏差定理记为以为插值点的插值函数,。
这里,设一阶连续可导,在上存在,则对随意给定的,起码存在一点,使()证明令,因是的根,所以可设对任何一个固定的点,引进协助函数:则由定义可得别在和和,即。
,这样起码有上应用洛尔定理,可知和,对3个零点,不失一般性,假设在每个区间起码存在一个零点,不如记为在上应用洛尔定理,获得,分在上起码有一个零点,。
此刻对求二次导数,此中的线性函数),故有代入,得所以即二次插值问题给定三个插值点,, 此中互不相等,如何结构函数的二次的(抛物线)插值多项式平面上的三个点能确立一条次曲线,如下图。
图三个插值点的二次插值仿制线性插值的拉格朗日插值,即用插值基函数的方法结构插值多项式。
设每个基函数是一个二次函数,对来说,要求是它的零点,所以可设同理,也相对应的形式,得将代入,得同理将代入获得和的值,以及和的表达式。
重心拉格朗日插值法

重心拉格朗日插值法
摘要:
1.拉格朗日插值法的概念
2.拉格朗日插值法的基本原理
3.拉格朗日插值法的应用实例
4.拉格朗日插值法的优缺点
正文:
拉格朗日插值法是一种数学上的插值方法,其概念源于18 世纪意大利数学家拉格朗日提出的一种用于估算函数值的技巧。
拉格朗日插值法通过构造一组基函数,利用这些基函数的线性组合来逼近目标函数,从而达到插值的目的。
拉格朗日插值法的基本原理可以概括为:首先选择一组插值节点,然后根据插值节点构造基函数,接着用基函数的线性组合来表示目标函数,最后通过求解线性方程组得到目标函数在任意点的值。
拉格朗日插值法在实际应用中有很多实例,例如在数值分析中,可以用拉格朗日插值法求解微分方程的数值解;在工程领域,可以用拉格朗日插值法对非线性函数进行拟合,从而优化设计方案。
拉格朗日插值法具有一些优点,例如具有较高的插值精度,可以很好地逼近大多数函数;同时,拉格朗日插值法具有较好的稳定性,不容易出现震荡现象。
然而,拉格朗日插值法也存在一些缺点,例如计算过程中需要求解线性方程组,当插值节点较多时,计算量会显著增加,从而降低计算效率。
总之,拉格朗日插值法是一种实用的数学方法,广泛应用于各个领域。
拉格朗日插值法

01
收敛性分析是研究拉格朗日插值法的一个重要方面,它涉及到该方法在何种条 件下能够准确地逼近未知函数。
02
在理论上,如果已知数据点足够多且分布均匀,那么拉格朗日插值多项式就能 够很好地逼近未知函数。
03
然而,在实际应用中,由于计算复杂度和数据可获取性的限制,我们通常只能 使用有限数量的数据点进行插值。因此,收敛性分析对于确定拉格朗日插值法 的精度和适用范围具有重要意义。
拉格朗日插值法的几何意义
从几何意义上讲,拉格朗日插值 法是通过在已知数据点上放置一 个多项式曲线,使得该曲线尽可
能接近原始数据点。
这意味着,拉格朗日插值多项式 在每个已知数据点上取值为零, 而在其他点上取值与原函数相近。
这种几何意义有助于我们更好地 理解拉格朗日插值法的原理和应
用。
拉格朗日插值法的收敛性分析
在实际应用方面,可以考虑如何 优化拉格朗日插值法的计算效率 和存储需求,以适应大规模数据 处理的需要。此外,可以探索拉 格朗日插值法在其他领域的应用, 例如金融、生物信息学和环境科 学等。
另外,随着人工智能和机器学习 技术的不断发展,可以考虑如何 利用这些技术来改进拉格朗日插 值法,例如通过神经网络或其他 机器学习方法来自动选择合适的 插值模型和参数。这将有助于提 高插值精度和泛化能力,并减少 人工干预和主观判断的误差。
03
拉格朗日插值法还有一些局限性,例如对于非线性数据的 插值效果较差,且容易受到数据异常值的影响。为了解决 这些问题,研究者们提出了许多改进的方法,如样条插值 、克里格插值和局部加权散点平滑插值等。
对未来研究的建议和展望
未来研究可以进一步探讨拉格朗 日插值法的理论性质,例如其收 敛性和稳定性等。此外,可以研 究如何将拉格朗日插值法与其他 数学方法或机器学习方法相结合, 以提高其预测精度和泛化能力。
拉格朗日多项式插值法

拉格朗日多项式插值法拉格朗日多项式插值法是一种数值计算方法,广泛应用于数学、物理、工程等领域。
它的基本思想是通过一些已知点的函数值来逼近未知函数值,这些已知点可以是离散的或连续的函数值。
在本文中,将详细阐述拉格朗日多项式插值法的步骤和实现过程。
Step 1:确定插值点和插值函数拉格朗日多项式插值法的第一步是选择插值点。
插值点是已知函数值的一组点,通常为离散的。
在选择插值点时,需要根据实际问题进行选择。
选择的插值点应尽可能分布均匀,以提高插值的精度。
然后,在这些插值点上构建插值函数,也就是通过这些点拟合出一条曲线。
Step 2:计算拉格朗日插值多项式的每一项然后,我们需要计算拉格朗日插值多项式的每一项。
拉格朗日插值多项式是一个多项式函数,用来拟合已知函数值的曲线。
在计算多项式的每一项时,需要用到插值点的坐标和函数值。
Step 3:将每一项相加得到拉格朗日插值多项式将每一项相加得到拉格朗日插值多项式,从而得到一个函数与原函数的误差最小。
Step 4:用拉格朗日插值多项式拟合未知函数值用拉格朗日插值多项式拟合未知函数值,将插值函数代入拉格朗日插值公式中计算即可得到未知函数值的近似值。
以上就是拉格朗日多项式插值法的基本步骤,下面将具体介绍如何利用这些步骤实现拉格朗日插值多项式的算法。
实现过程:1.定义插值点的坐标和函数值;2.计算拉格朗日多项式的每一项系数,每一项系数由插值点的函数值和坐标决定;3.将每一项系数相加,得到拉格朗日插值多项式;4.用拉格朗日插值多项式拟合未知函数值,即将未知函数的自变量带入拉格朗日插值多项式中计算。
在实现过程中,需要注意以下几点:1. 插值点的数量要足够多,以保证插值的精度;2. 插值点要均匀分布,尽可能覆盖整个函数区间;3. 对于高次多项式,容易产生龙格现象,需要进行截断。
拉格朗日多项式插值法的优点是计算简单,容易理解,可以应用于一些简单的数学问题的解决;缺点是插值点的选取与插值函数相关,且插值点的数量和位置对插值精度影响较大。
拉格朗日插值法(图文详解)

拉格朗⽇插值法(图⽂详解)拉格朗⽇插值⼊门由⼩学知识可知,n个点(x_i,y_i)可以唯⼀地确定⼀个多项式现在,给定n个点,请你确定这个多项式,并将k代⼊求值求出的值对998244353取模Input第⼀⾏两个正整数n,k,含义如题接下来n⾏,每⾏两个正整数x_i,y_i含义如题。
n≤2000,xi,yi,k≤998244353Output⼀个整数表⽰答案Sample Input3 1001 42 93 16Sample Output10201//样例⼀中的三个点确定的多项式是f(x)=x^2+2x+1,将100代⼊求值得到10201int re=1;while(y){if(y&1) re=(x*re)%mod;x=(x*x)%mod;y>>=1;}return re;}int read(){int x=0,f=1;char ch=getchar();while(!isdigit(ch)){if(ch=='-')f=-f;ch=getchar();}while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}return x*f;}signed main(){n=read(),k=read();for(int i=1;i<=n;i++)a[i]=read(),b[i]=read();for(int i=1;i<=n;i++){int tmp=1;for(int j=1;j<=n;j++)if(i!=j)tmp=tmp*(a[i]+mod-a[j])%mod; //分母tmp=quickpow(tmp,mod-2);for(int j=1;j<=n;j++)if(i!=j) tmp=tmp*(k+mod-a[j])%mod; //分⼦tmp=tmp*b[i]%mod;ans=(ans+tmp)%mod;}printf("%lld\n",ans);return 0;}#include<bits/stdc++.h>using namespace std;const int mod=998244353;int x[2010],y[2010],a=1,b=0;int powmod(int a,int b){int ans=1;while(b){if(b&1)ans=1ll*ans*a%mod;a=1ll*a*a%mod;b>>=1;}return ans;}int main(){int n,k;scanf("%d%d",&n,&k);for(int i=1;i<=n;i++)scanf("%d%d",x+i,y+i);for(int i=1;i<=n;i++){int a1=1,b1=1;//a1代表分母,b1代表分⼦b1=1ll*b1*y[i]%mod;for(int j=1;j<=n;j++)if(j!=i){b1=1ll*b1*(k-x[j])%mod;a1=1ll*a1*(x[i]-x[j])%mod;}b=(1ll*a1*b+1ll*a*b1)%mod;a=1ll*a*a1%mod;//b/a+b1/a1=(b*a1+a*b1)/(a*a1)}a=(a+mod)%mod,b=(b+mod)%mod;printf("%lld\n",1ll*b*powmod(a,mod-2)%mod);//因为带了除法,所以分母会⽐较⼤,于是在前⾯边乘边取模,最后取逆元return 0;}参考资料。
曲线插值法计算公式

曲线插值法计算公式
曲线插值法计算公式是一种用于通过已知数据点之间的连续曲线来预测未知数
据点的方法。
它在数学、工程和科学领域中得到广泛应用。
以下是一些常见的曲线插值法计算公式。
1. 拉格朗日插值法:拉格朗日插值法通过构造一个多项式来逼近给定的数据点。
设有n+1个数据点(xi, yi),那么拉格朗日插值多项式可以表示为:
P(x) = Σ(i=0 to n) yi * Li(x)
其中Li(x)是拉格朗日基函数,
Li(x) = Π(j=0 to n, j ≠ i) (x - xj) / (xi - xj)
拉格朗日插值法的优点是简单易用,但随着数据点数量的增加,计算复杂度
也会增加。
2. 牛顿插值法:牛顿插值法使用差商的概念,在给定的数据点上构造一个差分
多项式。
设有n+1个数据点(xi, yi),那么牛顿插值多项式可以表示为:
P(x) = f[x0] + (x-x0)f[x0,x1] + (x-x0)(x-x1)f[x0,x1,x2] + ... + (x-x0)(x-x1)...(x-xn-1)f[x0,x1,...,xn]
其中f[xi]表示差商,可以通过递归的方式计算得出:
f[xi] = yi
f[xi,xi+1,...,xi+k] = (f[xi+1,xi+2,...,xi+k] - f[xi,xi+1,...,xi+k-1]) / (xi+k - xi)
牛顿插值法的优点是计算效率高,且在数据点改变时只需要重新计算差商,
而不用重新计算全部数据。
以上是两种常见的曲线插值法计算公式。
根据实际情况,可以选择合适的方法
进行数据点的插值计算。
python实现拉格朗日插值法

python实现拉格朗日插值法Python实现拉格朗日插值法拉格朗日插值法是一种常用的数值插值方法,用于通过已知数据点的横坐标和纵坐标,求解给定横坐标下的纵坐标值。
在Python中,我们可以通过一些简单的步骤来实现拉格朗日插值法。
一、理论介绍拉格朗日插值法的核心思想是通过已知数据点的线性组合去逼近未知点的函数值。
具体而言,就是通过已知数据点的横坐标和纵坐标,构造一个一阶多项式来逼近未知点。
拉格朗日插值法的公式如下:f(x) = Σ[Li(x) * yi] (i=0,1,2,...,n)其中,f(x)表示插值函数,Li(x)表示拉格朗日插值多项式的基函数,yi表示已知数据点的纵坐标。
二、Python实现下面我们来一步一步实现拉格朗日插值法的Python代码。
步骤1:导入所需的库首先,我们需要导入numpy库,用于进行数值计算。
numpy库是Python 中进行科学计算的基础库,提供了很多数值计算的函数和工具。
import numpy as np步骤2:定义拉格朗日插值函数接下来,我们需要定义一个函数,用于实现拉格朗日插值的计算。
该函数需要传入已知数据点的横坐标和纵坐标数组,以及待求解点的横坐标。
def lagrange_interpolation(x, y, x0):n = len(x) - 1result = 0.0for i in range(n+1):basis = 1.0for j in range(n+1):if j != i:basis *= (x0 - x[j]) / (x[i] - x[j])result += basis * y[i]return result步骤3:输入已知数据点然后,我们需要输入已知数据点的横坐标和纵坐标。
可以通过列表或数组的形式进行输入。
x = [1, 2, 3, 4, 5]y = [2, 3, 4, 3, 2]步骤4:输入待求解点接下来,我们需要输入待求解点的横坐标。
拉格朗日插值法公式

拉格朗日插值法公式设有n+1个不同的数据点{(x0, y0),(x1, y1),...(xn, yn)},要求构造一个多项式P(x),满足P(xi) = yi (i=0,1,...,n),则拉格朗日插值多项式可以表示为:P(x) = L0(x)y0 + L1(x)y1 + ... + Ln(x)yn其中,Lk(x)是拉格朗日插值基函数,定义为:Lk(x) = Π (x-xj) / (xi-xj) (i!=j, i,j=0,1,...,n)即为连乘积的形式。
下面以具体的例子来说明拉格朗日插值法的计算过程。
假设我们有以下5个数据点:{(0,1),(1,2),(2,5),(3,10),(4,16)},我们要求在这些点上构造一个多项式函数P(x)。
首先,我们需要计算每个数据点对应的拉格朗日插值基函数。
由于共有5个数据点,我们需要计算5个基函数L0(x),L1(x),L2(x),L3(x),L4(x)。
L0(x)=(x-1)(x-2)(x-3)(x-4)/(0-1)(0-2)(0-3)(0-4)=x(x-1)(x-2)(x-3)(x-4)/24L1(x)=(x-0)(x-2)(x-3)(x-4)/(1-0)(1-2)(1-3)(1-4)=-(x)(x-2)(x-3)(x-4)/6L2(x)=(x-0)(x-1)(x-3)(x-4)/(2-0)(2-1)(2-3)(2-4)=(x)(x-1)(x-3)(x-4)/2L3(x)=(x-0)(x-1)(x-2)(x-4)/(3-0)(3-1)(3-2)(3-4)=-(x)(x-1)(x-2)(x-4)/2L4(x)=(x-0)(x-1)(x-2)(x-3)/(4-0)(4-1)(4-2)(4-3)=x(x-1)(x-2)(x-3)/24接下来,我们将每个数据点对应的函数值乘以对应的基函数,并相加即可得到最终的多项式函数:P(x)=L0(x)y0+L1(x)y1+L2(x)y2+L3(x)y3+L4(x)y4将数据代入计算:P(x)=(x(x-1)(x-2)(x-3)(x-4)y0/24)+(-(x)(x-2)(x-3)(x-4)y1/6)+((x)(x-1)(x-3)(x-4)y2/2)+(-(x)(x-1)(x-2)(x-4)y3/2)+(x(x-1)(x-2)(x-3)y4/24)简化后,最终得到P(x)=x^4-4x^3+6x^2-4x+1这个多项式P(x)在给定的5个数据点上与原函数相同,可以用于数据拟合、函数逼近和曲线绘制等应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拉格朗日(Lagrange)插值
可对插值函数选择多种不同的函数类型,由于代数多项式具有简单和一些良好的
特性,例如,多项式是无穷光滑的,容易计算它的导数和积分,故常选用代数多项式作为插值函数。
线性插值
问题给定两个插值点其中,怎样做通过这两点的一次插值函数过两点作一条直线,这条直线就是通过这两点的一次多项式插值函数,简称线性插值。
如图所示。
图线性插值函数
在初等数学中,可用两点式、点斜式或截距式构造通过两点的一条直线。
下面先用待定系数法构造插值直线。
设直线方程为,将分别代入直线方程得:
当时,因,所以方程组有解,而且解是唯一的。
这也表明,平面上两个点,有且仅有一条直线通过。
用待定系数法构造插值多项式的方法简单直观,容易看到解的存在性和惟一性,但要解一个方程组才能得到插值函数的系数,因工作量较大和不便向高阶推广,故这种构造方法通常不宜采用。
当时,若用两点式表示这条直线,则有:
()
这种形式称为拉格朗日插值多项式。
,,称为插值基函数,计算,
的值,易见
()
在拉格朗日插值多项式中可将看做两条直线,的叠加,并可看到两个插值点的作用和地位都是平等的。
拉格朗日插值多项式型式免除了解方程组的计算,易于向高次插值多项式型式推广。
线性插值误差
定理记为以为插值点的插值函数,。
这里
,设一阶连续可导,在上存在,则对任意给定的,至少存在一点,使
()
证明令,因是的根,所以可设
对任何一个固定的点,引进辅助函数:
则。
由定义可得,这样至少有3个零点,不失一般性,假定,分别在和上应用洛尔定理,可知在每个区间至少存在一个零点,不妨记为和,即和,对在上应用洛尔定理,得到在上至少有一个零点,。
现在对求二次导数,其中的线性函数),故有
代入,得
所以
即
二次插值
问题给定三个插值点,,其中互不相等,怎样构造函数
的二次的(抛物线)插值多项式
平面上的三个点能确定一条次曲线,如图所示。
图三个插值点的二次插值
仿造线性插值的拉格朗日插值,即用插值基函数的方法构造插值多项式。
设
每个基函数是一个二次函数,对来说,要求是它的零点,因此可设
同理,也相对应的形式,得
将代入,得
同理将代入得到和的值,以及和的表达式。
也容易验证:
插值基函数仍然满足:
二次插值函数误差:
上式证明完全类似于线性插值误差的证明,故省略。
插值作为函数逼近方法,常用来作函数的近似计算。
当计算点落在插值点区间之内时叫做内插,否则叫做外插。
内插的效果一般优于外插。
例给定。
构造线性插值函数并用插值函数计算和
解:构造线性插值函数:
分别将代入上式,得
,准确值
,准确值
例给定。
构造二次插值函数并计算。
解:
,准确值
例要制做三角函数的函数值表,已知表值有四位小数,要求用线性插值引起的
截断误差不超过表值的舍入误差,试决定其最大允许步长。
解:设最大允许步长
次拉格朗日插值多项式
问题给定平面上两个互不相同的插值点,有且仅有一条通过这两点的直线;给定平面上三个互不相同的插值点,有且仅有一条通过这三个点的二次曲线;给定平面上个互不相同的插值点,互
不相同是指互不相等,是否有且仅有一条不高于次的插值多项式曲线,如果曲线存在,那么如何简单地作出这条次插值多项式曲线
分析:次多项式,它完全由个系数决定。
若曲线通过给定平面上个互不相同的插值点,则应满足,事实上一个插值点就是一个插值条件。
将依次代入中得到线性方程组:
()
方程组的系数行列式是范德蒙(Vandermonde)行列式:
当互异时,,所以方程组()的解存在且惟一。
即问题的解存在而且惟一。
通过求解()得到插值多项式,因其计算量太大而不可取,仿照线性以及二次插值多项式的拉格朗日形式,我们可构造次拉格朗日插值多项式。
对于个互不相同的插值节点,由次插值多项式的惟一性,可对每个插值节点作出相应的次插值基函数。
要求是,的零点,因此可设
由将代入,得到
()
作其组合:
()
那么不高于次且满足,故就是关于插值点的插值多项式,这种插值形式称为拉格朗日插值多项式。
称为关于节
点的拉格朗日基函数。
例给出下列插值节点数据,做三次拉格朗日插值多项式,并计算()。
解:拉格朗日插值基函数为:
三次拉格朗日插值多项式:
n次插值多项式的误差
定理设是上过的次插值多项式,
互不相等,当时,则插值多项式的误差:
其中
证明*:记。
由于,因而
是的根,于是可设
下面的目标是算出,为此引入变量为的函数:
()
令,得
令,由定义即
至少有个零点,由于,由洛尔定理,在相邻的两个零点之间至少有一个零点,即至少有个零点。
同理再对应用洛尔定理,即
至少有个零点,反复应用洛尔定理得到至少有一个零点。
另一方面,对求阶导数,有
令,有
得到
()
由于的零点与的零点有关,因而为的函数。
若|可表示为
()
由()式可以看到,当是不高于次的多项式时,,即。
对于函数,关于节点的拉格朗日插值多项式就是其本身,故拉格朗日基函数满足
令,得到。
定理给出了当被插函数充分光滑时的插值误差或称插值余项表达式,但是,在实际计算中,并不知道的具体表示,难以得到的形式或较精确的界限,因此也难以得到界。
在实际计算中,可对误差运用下面的事后估计方法。
给出个插值节点,任选其中的个插值节点,不妨取,构造一个次插值多项式,记为。
在个插值节点中另选
个插值点,不妨取,构造一个次插值多项式,记为。
由定理2可得到
()
()
设在插值区间内连续而且变化不大,有,则
从而可得到
()
()
拉格朗日插值多项式的算法
下面用伪码描述拉格朗日插值多项式的算法。
1:输入:插值节点控制数,插值点序列,要计算的函数点,及变量。
2:FOR i :=0,1,…,n //i控制拉格朗日基函数序列
{tmp:=1;
FOR j:=0,1,…,i-1,i+1,…,n
{ //对于给定,计算拉格朗日基函数
;
} // tmp表示拉格朗日基函数
}
3:输出的计算结果。
