matlab插值曲线拟合解析
matlab插值法拟合曲线

matlab插值法拟合曲线
在MATLAB中,一维插值函数为interp1(),其调用格式为:
Y1=interp1(X,Y,X1,method)。
其中,X、Y是两个等长的已知向量,分别表示采样点和采样值;X1是一个向量或标量,表示要插值的点;method参数用于指定插值方法,常用的取值有以下四种:
1. linear:线性插值,默认方法。
将与插值点靠近的两个数据点用直线连接,然后在直线上选取对应插值点的数据。
2. nearest:最近点插值。
选择最近样本点的值作为插值数据。
3. pchip:分段3次埃尔米特插值。
采用分段三次多项式,除满足插值条件,还需满足在若干节点处相邻段插值函数的一阶导数相等,使得曲线光滑的同时,还具有保形性。
4. spline:3次样条插值。
每个分段内构造一个三次多项式,使其插值函数除满足插值条件外,还要求在各节点处具有连续的一阶和二阶导数。
曲线拟合可以使用cftool工具,首先导入X和Y的数据,然后可以选择残差图和置信区间分布图。
用MATLAB解插值和曲线拟合问题

f=10-(10-x(1))*exp(-t/x(2));
t=[0.5 1 2 3 4 5 7 9];
v=[6.36 6.48 7.26 8.22 8.66 8.99 9.43 9.63];
x0=[0,0.05];
x=lsqcurvefit('curvefun4',x0,t,v)
Interp1(x,y,cx,’method’)
在MATLAB的线性最小二乘拟合中,用得较多的是多项式拟合,其命令为:
A=polyfit(x,y,m)
二.上机内容
1、在飞机的机翼加工时,由于机翼尺寸很大,通常在图纸上只能标出部分关键点的数据.某型号飞机的机翼上缘轮廓线的部分数据如下。用插值法求x每改变0.1时的y值,画出图形表示。
x 0 4.74 9.05 19 38 57 76 95 114 133152 171 190
y 0 5.23 8.1 11.97 16.15 17.1 16.34 14.63 12.16 6.697.03 3.99 0
2、已知观测数据点如表所示:
用3次多项式函数拟合这些数据点,画出图形。
3、教材习题1,用griddata插值函数,三次插值。
注:上机作业文件夹以自己的班级姓名学号命名,文件夹包括如下上机报告和Matlab程序。
上机报告模板如下:
佛山科学技术学院
上 机报 告
课程名称数学应用软件
上机项目用MATLAB解插值和曲线拟合问题
专业班级
一.上机目的
熟练掌握多种插值方法:线性插值,三次样条插值,三次插值和最近邻点插值(linear、spline、cubic、nearest)
f=curvefun4(x,t)
MATLAB中的曲线拟合与插值

MATLAB 中的曲线拟合和插值在大量的使用领域中,人们经常面临用一个分析函数描述数据(通常是测量值)的任务。
对这个问题有两种方法。
在插值法里,数据假定是正确的,要求以某种方法描述数据点之间所发生的情况。
这种方法在下一节讨论。
这里讨论的方法是曲线拟合或回归。
人们设法找出某条光滑曲线,它最佳地拟合数据,但不必要经过任何数据点。
图11.1说明了这两种方法。
标有'o'的是数据点;连接数据点的实线描绘了线性内插,虚线是数据的最佳拟合。
11.1 曲线拟合曲线拟合涉及回答两个基本问题:最佳拟合意味着什么?应该用什么样的曲线?可用许多不同的方法定义最佳拟合,并存在无穷数目的曲线。
所以,从这里开始,我们走向何方?正如它证实的那样,当最佳拟合被解释为在数据点的最小误差平方和,且所用的曲线限定为多项式时,那么曲线拟合是相当简捷的。
数学上,称为多项式的最小二乘曲线拟合。
如果这种描述使你混淆,再研究图11.1。
虚线和标志的数据点之间的垂直距离是在该点的误差。
对各数据点距离求平方,并把平方距离全加起来,就是误差平方和。
这条虚线是使误差平方和尽可能小的曲线,即是最佳拟合。
最小二乘这个术语仅仅是使误差平方和最小00.20.40.60.81-2024681012xy =f (x )Second O rder C urv e Fitting图11.1 2阶曲线拟合在MATLAB 中,函数polyfit 求解最小二乘曲线拟合问题。
为了阐述这个函数的用法,让我们以上面图11.1中的数据开始。
» x=[0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1]; » y=[-.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];为了用polyfit ,我们必须给函数赋予上面的数据和我们希望最佳拟合数据的多项式的阶次或度。
如果我们选择n=1作为阶次,得到最简单的线性近似。
matlab 插值拟合

MATLAB 插值拟合介绍MATLAB是一种用于科学计算和工程应用的高级编程语言和环境。
它提供了许多功能强大的工具箱,可以用于各种数学计算、数据分析和图形绘制任务。
其中之一是插值拟合,它可以通过已知数据点之间的数学插值来估计未知数据点的值。
在本文中,我们将深入探讨MATLAB中的插值拟合方法以及如何使用它们来解决实际问题。
一、插值的概念插值是一种通过已知数据点之间的数学插值来估计未知数据点的值的方法。
它在许多领域中都有广泛的应用,如信号处理、图像处理、数据分析等。
插值的目标是在已知数据点之间建立一个连续的函数,以便可以在这些点之外对函数进行求值。
二、MATLAB中的插值方法MATLAB提供了多种插值方法,可以根据需要选择合适的方法。
下面介绍几种常用的插值方法:1. 线性插值线性插值是一种简单而直观的插值方法。
它假设在两个已知数据点之间的值是线性变化的,并使用直线来连接这些点。
MATLAB中的interp1函数可以实现线性插值。
2. 多项式插值多项式插值是一种更高阶的插值方法,它通过在已知数据点上构造一个多项式函数来逼近未知数据点。
MATLAB中的polyfit函数可以用于拟合多项式,并使用polyval函数进行插值。
3. 三次样条插值三次样条插值是一种更加平滑的插值方法,它通过在每个已知数据点附近构造一个三次多项式函数来逼近未知数据点。
MATLAB中的spline函数可以实现三次样条插值。
4. 二维插值除了在一维数据上进行插值外,MATLAB还提供了在二维数据上进行插值的方法。
例如,interp2函数可以用于二维线性插值,griddata函数可以用于二维三次插值。
三、插值拟合的实际应用插值拟合在许多实际问题中都有广泛的应用。
下面介绍几个常见的应用场景:1. 曲线拟合插值拟合可以用于拟合实验数据或观测数据的曲线。
通过选择适当的插值方法,可以找到最佳拟合曲线,从而更好地理解数据的趋势和规律。
2. 图像处理图像处理中经常需要对像素之间的值进行插值,以便进行放大、缩小或平滑处理。
在Matlab中如何进行数据插值与拟合

在Matlab中如何进行数据插值与拟合引言:数据处理是科学研究与工程开发中不可或缺的环节之一。
而数据插值和拟合则是数据处理中常用的技术手段。
在Matlab这一强大的数值分析工具中,提供了丰富的函数与工具箱,使得数据插值与拟合变得更加便捷高效。
本文将详细阐述在Matlab中如何进行数据插值与拟合,并介绍几个常用的插值与拟合方法。
一、数据插值数据插值是通过已知的有限个数据点,推导出数据点之间未知位置上的数值。
在Matlab中,可以利用interp1函数进行数据插值。
假设我们有一组离散的数据点,存储为两个向量x和y。
那么,可以通过以下步骤进行数据插值:1. 调用interp1函数,并传入x和y作为输入参数。
```matlabxi = linspace(min(x), max(x), n);yi = interp1(x, y, xi, '方法');```其中,xi是插值点的位置,min和max分别是x向量的最小值和最大值,n是插值点的数量。
'方法'是要使用的插值方法,可以选择线性插值(method='linear')、样条插值(method='spline')等。
2. 绘制插值结果曲线。
```matlabplot(x, y, 'o', xi, yi)legend('原始数据','插值结果')```使用plot函数可以绘制原始数据点和插值结果的曲线。
通过设置不同的插值方法和插值点的数量,可以探索不同的插值效果。
二、数据拟合数据拟合是通过已知的一组数据点,找到一个符合数据趋势的函数模型。
在Matlab中,可以利用polyfit函数进行多项式拟合。
假设我们有一组离散的数据点,存储为两个向量x和y。
那么,可以通过以下步骤进行数据拟合:1. 调用polyfit函数,并传入x和y作为输入参数。
```matlabp = polyfit(x, y, n);```其中,n是多项式的次数,p是拟合多项式的系数。
Matlab中的曲线拟合与插值技巧

Matlab中的曲线拟合与插值技巧在数据科学和工程领域中,曲线拟合和插值技术是常用的数学方法。
在Matlab 中,有许多工具和函数可用于处理这些技术。
本文将讨论Matlab中的曲线拟合和插值技巧,并介绍一些实际应用案例。
一、曲线拟合技术曲线拟合是根据已知数据点来构造一个与这些点最匹配的曲线模型。
在Matlab 中,常用的曲线拟合函数包括polyfit和lsqcurvefit。
1. polyfit函数polyfit函数是Matlab中一个功能强大的多项式拟合函数。
它可以拟合多项式曲线模型,并通过最小二乘法找到最佳拟合系数。
例如,我们有一组数据点(x,y),我们想要拟合一个二次多项式曲线来描述这些数据。
可以使用polyfit函数:```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];degree = 2;coefficients = polyfit(x, y, degree);```在上述例子中,degree参数设置为2,表示拟合一个二次多项式曲线。
polyfit 函数将返回一个包含拟合系数的向量,可以用来构造拟合曲线。
2. lsqcurvefit函数lsqcurvefit函数是Matlab中一个用于非线性最小二乘拟合的函数。
与polyfit函数不同,lsqcurvefit函数可以用于拟合任意曲线模型,不局限于多项式。
例如,我们想要拟合一个指数函数曲线来拟合数据:```matlabx = [1, 2, 3, 4, 5];y = [1.1, 2.2, 3.7, 6.5, 12.3];model = @(params, x) params(1)*exp(params(2)*x);params0 = [1, 0];estimated_params = lsqcurvefit(model, params0, x, y);```在上述例子中,model是一个函数句柄,表示要拟合的曲线模型。
MATLAB中的数据插值与拟合方法介绍

MATLAB中的数据插值与拟合方法介绍概述数据处理是科学研究和工程实践中的重要环节之一。
对于实验或观测数据,我们常常需要通过插值和拟合方法来获取更加精确和连续的函数或曲线。
在MATLAB中,有多种方法和函数可以用于实现数据插值和拟合,本文将介绍其中的一些常用方法。
一、数据插值数据插值是指利用有限个数据点,通过某种方法构建一个连续的函数,以实现在这些点之间任意位置的数值估计。
在MATLAB中,常用的数据插值方法有线性插值、多项式插值、三次样条插值等。
1. 线性插值线性插值是最简单的插值方法之一,假设我们有两个数据点 (x1, y1) 和 (x2, y2),要在这两个点之间插值一个新的点 (x, y),线性插值即为连接 (x1, y1) 和 (x2, y2) 这两个点的直线上的点(x, y)。
在MATLAB中,可以通过interp1函数进行线性插值。
2. 多项式插值多项式插值是使用一个低次数的多项式函数来拟合数据的方法。
在MATLAB 中,可以通过polyfit函数进行多项式拟合,然后利用polyval函数来进行插值。
具体的插值效果与所选用的多项式阶数有关。
3. 三次样条插值三次样条插值算法利用相邻数据点之间的三次多项式来拟合数据,从而构成一条光滑的曲线。
在MATLAB中,可以通过spline函数进行三次样条插值。
二、数据拟合除了插值方法外,数据拟合也是处理实验或观测数据的常见方法之一。
数据拟合是指通过选择一个特定的数学模型,使该模型与给定的数据点集最好地拟合。
在MATLAB中,常用的数据拟合方法有多项式拟合、指数拟合、非线性最小二乘拟合等。
1. 多项式拟合在MATLAB中,可以使用polyfit函数进行多项式拟合。
该函数通过最小二乘法来拟合给定数据点集,并得到一个多项式函数。
根据所选用的多项式阶数,拟合效果也会有所不同。
2. 指数拟合指数拟合常用于具有指数关系的数据。
在MATLAB中,可以通过拟合幂函数的对数来实现指数拟合。
matlab 插值拟合

matlab 插值拟合插值拟合是一种常用的数值分析方法,它通过已知的一些离散数据点,来构造一个函数,使得该函数通过这些数据点,并且在数据点之间的取值也能较好地拟合实际情况。
在MATLAB 中,可以使用interp1函数进行插值拟合。
interp1函数是MATLAB中用于一维数据插值的函数,它可以根据给定的数据点,通过线性插值、多项式插值、样条插值等方法,生成一个插值函数。
它的基本语法如下:YI = interp1(X,Y,XI,method)其中,X和Y是已知的数据点的横纵坐标,XI是需要插值的点的横坐标,method是插值方法。
下面将对这些参数进行解释。
X是已知数据点的横坐标,可以是一个向量或矩阵。
若X是向量,则X和Y的长度必须相等;若X是矩阵,则X和Y的行数必须相等。
X的元素必须按照升序排列。
Y是已知数据点的纵坐标,可以是一个向量或矩阵。
若Y是向量,则X和Y的长度必须相等;若Y是矩阵,则X和Y的行数必须相等。
XI是需要插值的点的横坐标,可以是一个向量或矩阵。
若XI 是向量,则返回的YI也是向量,长度与XI相等;若XI是矩阵,则返回的YI也是矩阵,行数与XI的行数相等。
XI的元素可以是任意实数,不一定需要在X定义的范围内。
method是插值方法,可以选择的参数有:- 'linear':线性插值,即通过两个最近的数据点在其之间进行线性插值计算。
- 'nearest':最近邻插值,即将每个需要插值的点与最近的数据点进行匹配。
- 'spline':样条插值,利用样条函数拟合数据点,生成平滑的曲线。
- 'pchip':分段三次Hermite插值,利用分段三次Hermite曲线拟合数据点。
- 'v5cubic':使用v5版本算法生成的3次样条。
除了上述的基本插值方法,还可以使用更高级的插值方法,如二维和多维插值等。
此外,interp1函数还提供了一些其他的参数和选项,如出界值处理、插值半径等,可以根据具体需求进行调整。
Matlab中的插值与拟合方法介绍

Matlab中的插值与拟合方法介绍在数据分析与处理的过程中,插值与拟合是非常重要的工具。
Matlab作为一种常用的数据处理与分析工具,提供了许多插值与拟合函数,方便用户进行数据处理和分析。
本文将介绍Matlab中的插值和拟合方法,并提供相应的示例和应用场景。
一、插值方法1. 线性插值线性插值是最简单的插值方法之一,通过连接已知数据点的直线进行插值。
在Matlab中,可以使用interp1函数进行一维线性插值。
下面以一个简单的例子来说明线性插值的应用:```x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];xi = 2.5;yi = interp1(x, y, xi)```在这个例子中,已知一组数据点(x, y),要求在x=2.5处的插值结果。
通过interp1函数,可以得到插值结果yi=5。
线性插值适用于数据点较少且近邻点的变化趋势比较明显的情况。
2. 三次样条插值三次样条插值是一种更精确的插值方法,它利用多个小区间的三次多项式进行插值。
在Matlab中,可以使用interp1函数的'spline'选项进行三次样条插值。
以下是一个示例:```x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];xi = 2.5;yi = interp1(x, y, xi, 'spline')```通过设置'spline'选项,可以得到插值结果yi=5.125。
三次样条插值适用于数据点较多且变化较为复杂的情况。
3. 二维插值除了一维插值,Matlab还提供了二维插值函数interp2,用于处理二维数据的插值问题。
以下是一个简单的二维插值示例:```x = 1:4;y = 1:4;[X, Y] = meshgrid(x, y);Z = X.^2 + Y.^2;xi = 2.5;yi = 2.5;zi = interp2(X, Y, Z, xi, yi)```在这个例子中,首先生成一个二维数据矩阵Z,然后利用interp2函数在给定的坐标(xi, yi)处进行插值,得到插值结果zi=12.25。
matlab 插值法拟合

matlab 插值法拟合Matlab是一款强大的数学软件,拥有丰富的函数库,可以进行各种数学计算和数据处理。
其中,插值法是一种常用的数值计算方法,可以通过已知数据点的信息,来估计在数据点之间的数值。
本文将介绍Matlab中的插值法及其应用。
插值法在科学计算和工程领域中有着广泛的应用。
它可以用来估计任意点的函数值,基于已知数据点之间的关系。
在Matlab中,插值法可以通过interp1函数实现。
该函数可以采用不同的插值方法,例如线性插值、拉格朗日插值和样条插值等。
线性插值是最简单的插值方法之一。
它假设函数在两个数据点之间的变化是线性的,并根据这个假设进行插值计算。
在Matlab中,可以使用interp1函数的默认设置来进行线性插值。
例如,给定一组已知数据点的横坐标和纵坐标,我们可以使用interp1函数来估计在两个数据点之间的任意点的函数值。
拉格朗日插值是一种更高阶的插值方法,它通过已知数据点来构造一个多项式函数,并使用这个函数来进行插值计算。
在Matlab中,可以使用interp1函数的'Lagrange'选项来进行拉格朗日插值。
该方法可以得到更精确的插值结果,特别是在数据点较密集的情况下。
样条插值是一种更加平滑的插值方法,它通过拟合一组分段函数来进行插值计算。
在Matlab中,可以使用interp1函数的'spline'选项来进行样条插值。
样条插值可以得到光滑的插值曲线,适用于需要光滑过渡的情况。
除了interp1函数之外,Matlab还提供了其他一些插值函数,例如interp2、interp3和interpn等。
这些函数可以用于二维或多维数据的插值计算。
它们可以根据给定的数据点,在不同的维度上进行插值,得到更加准确的插值结果。
在实际应用中,插值法常常用于数据处理和函数逼近。
例如,在图像处理中,可以使用插值法来放大或缩小图像。
在信号处理中,可以使用插值法来重建缺失的信号。
matlab曲线拟合,插值

南京航空航天大学 matlab 曲线拟合,插值
相关知识
在生产和科学实验中,自变量 与因变量 间的函数关系 有时不能写出解析表达式,而
1、 画出原始数据图; 2、 画出加密后的地貌图,并在图中标出原始数据
二、拟合 曲线拟合
已知离散点上的数据集 ,即已知在点集 上的函数值 ,构造一个解析函数(其图形为 一曲线)使 在原离散点 上尽可能接近给定的 值,这一过程称为曲线拟合。最常用的曲线拟 合方法是最小二乘法,该方法是寻找函数 使得 最小。 MATLAB 函数:p=polyfit(x,y,n)
3
南京航空航天大学 matlab 曲线拟合,插值
92 96 97 98 96 93 95 84 82 81 84 85 85 81 82 80 80 81 85 90 93 95 84 86 81 98 99 98 97 96 95 84 87 80 81 85 82 83 84 87 90 95 86 88 80 82 81 84 85 86 83 82 81 80 82 87 88 89 98 99 97 96 98 94 92 87
x=1900:2010;
y=interp1(year,product,x,'cubic');
plot(year,product,'o',x,y); 计算结果为:p1995=252.9885。
2、二维插值
1
南京航空航天大学 matlab 曲线拟合,插值
已知离散点上的数据集 ,即已知在点集 上的函数值 ,构造一个解析函数(其图形为
MATLAB中的插值与拟合方法详解

MATLAB中的插值与拟合方法详解篇一:介绍插值与拟合的概念及应用领域在科学研究和工程应用中,我们经常会遇到需要通过有限个已知数据点来推算出其它位置或数值的问题。
这种问题的解决方法通常可以分为两种:插值和拟合。
插值是指根据已知的离散数据点,在未知位置或数值上推算出一个函数值;而拟合则是根据已知的离散数据点,寻找一个函数模型来近似表示这些数据。
插值方法适用于数据点之间具有明显的数值关系的情况,如各种物理现象的测量数据、曲线绘制等。
拟合方法则适用于数据点之间存在较大离散度或复杂的关联关系的情况,例如统计分析、数据回归、信号处理等。
MATLAB作为一种强大的数值计算和可视化工具,提供了丰富的插值和拟合方法函数,使得我们能够更加高效地进行数据处理和分析。
接下来我们将详细介绍MATLAB中常用的插值和拟合方法。
篇二:插值方法详解插值方法在MATLAB中有多种实现方式,常用的有线性插值、多项式插值和样条插值。
1.线性插值线性插值是一种简单直接的插值方法,在已知的数据点间通过直线的插值来估计未知点的数值。
在MATLAB中,可以使用interp1函数来进行线性插值的计算。
该函数利用输入的数据点和未知点的坐标,返回未知点的插值结果。
2.多项式插值多项式插值是一种通过多项式函数来拟合数据点的插值方法。
MATLAB中的polyfit函数可以用来进行多项式的拟合计算。
这个函数通过最小二乘法来寻找一个多项式函数,使得该函数与给定的数据点最为接近。
3.样条插值样条插值是一种更加精确的插值方法,在MATLAB中可以使用interp1函数的'spline'选项来进行样条插值的计算。
样条插值通过分段函数形式来拟合数据,可以得到更加平滑和连续的插值结果。
篇三:拟合方法详解拟合方法主要有线性拟合、非线性拟合以及多项式拟合等。
1.线性拟合线性拟合是一种基于线性模型的拟合方法,它适用于数据点之间存在明确线性关系的情况。
在MATLAB中,可以使用polyfit函数来进行线性拟合计算。
Matlab数学建模学习笔记——插值与拟合
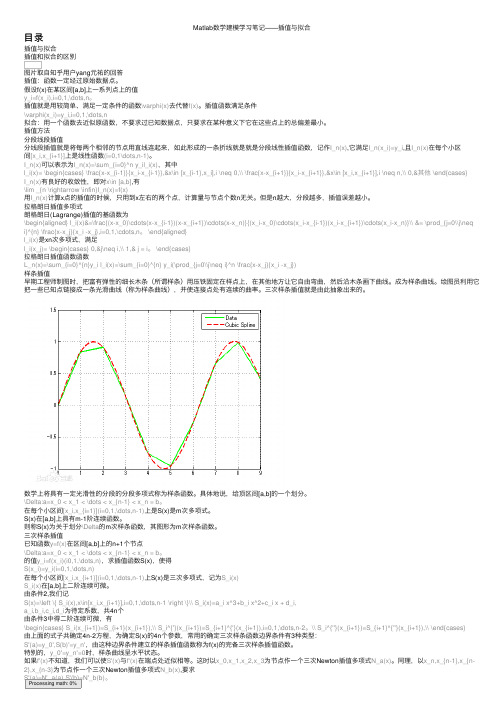
Matlab数学建模学习笔记——插值与拟合⽬录插值与拟合插值和拟合的区别图⽚取⾃知乎⽤户yang元祐的回答插值:函数⼀定经过原始数据点。
假设f(x)在某区间[a,b]上⼀系列点上的值y_i=f(x_i),i=0,1,\dots,n。
插值就是⽤较简单、满⾜⼀定条件的函数\varphi(x)去代替f(x)。
插值函数满⾜条件\varphi(x_i)=y_i,i=0,1,\dots,n拟合:⽤⼀个函数去近似原函数,不要求过已知数据点,只要求在某种意义下它在这些点上的总偏差最⼩。
插值⽅法分段线段插值分线段插值就是将每两个相邻的节点⽤直线连起来,如此形成的⼀条折线就是就是分段线性插值函数,记作I_n(x),它满⾜I_n(x_i)=y_i,且I_n(x)在每个⼩区间[x_i,x_{i+1}]上是线性函数(i=0,1\dots,n-1)。
I_n(x)可以表⽰为I_n(x)=\sum_{i=0}^n y_il_i(x),其中l_i(x)= \begin{cases} \frac{x-x_{i-1}}{x_i-x_{i-1}},&x\in [x_{i-1},x_i],i \neq 0,\\ \frac{x-x_{i+1}}{x_i-x_{i+1}},&x\in [x_i,x_{i+1}],i \neq n,\\ 0,&其他 \end{cases}I_n(x)有良好的收敛性,即对x\in [a,b],有\lim _{n \rightarrow \infin}I_n(x)=f(x)⽤I_n(x)计算x点的插值的时候,只⽤到x左右的两个点,计算量与节点个数n⽆关。
但是n越⼤,分段越多,插值误差越⼩。
拉格朗⽇插值多项式朗格朗⽇(Lagrange)插值的基函数为\begin{aligned} l_i(x)&=\frac{(x-x_0)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)}{(x_i-x_0)\cdots(x_i-x_{i-1})(x_i-x_{i+1})\cdots(x_i-x_n)}\\ &= \prod_{j=0\\j\neq i}^{n} \frac{x-x_j}{x_i -x_j},i=0,1,\cdots,n。
Matlab 曲面插值和拟合

Matlab 曲面插值和拟合插值和拟合都是数据优化的一种方法,当实验数据不够多时经常需要用到这种方法来画图。
在matlab 中都有特定的函数来完成这些功能。
这两种方法的确别在于:当测量值是准确的,没有误差时,一般用插值;当测量值与真实值有误差时,一般用数据拟合。
插值:对于一维曲线的插值,一般用到的函数yi=interp1(X,Y,xi,method) ,其中method包括nearst,linear,spline,cubic。
对于二维曲面的插值,一般用到的函数zi=interp2(X,Y,Z,xi,yi,method),其中method也和上面一样,常用的是cubic。
拟合:对于一维曲线的拟合,一般用到的函数p=polyfit(x,y,n)和yi=polyval(p,xi),这个是最常用的最小二乘法的拟合方法。
对于二维曲面的拟合,有很多方法可以实现,但是我这里自己用的是Spline Toolbox里面的函数功能。
具体使用方法可以看后面的例子。
对于一维曲线的插值和拟合相对比较简单,这里就不多说了,对于二维曲面的插值和拟合还是比较有意思的,而且正好胖子有些数据想让我帮忙处理一下,就这个机会好好把二维曲面的插值和拟合总结归纳一下,下面给出实例和讲解。
原始数据x=[1:1:15];y=[1:1:5];z=[0.2 0.24 0.25 0.26 0.25 0.25 0.25 0.26 0.26 0.29 0.25 0.29;0.27 0.31 0.3 0.3 0.26 0.28 0.29 0.26 0.26 0.26 0.26 0.29;0.41 0.41 0.37 0.37 0.38 0.35 0.34 0.35 0.35 0.34 0.35 0.35;0.41 0.42 0.42 0.41 0.4 0.39 0.39 0.38 0.36 0.36 0.36 0.36;0.3 0.36 0.4 0.43 0.45 0.45 0.51 0.42 0.4 0.37 0.37 0.37];z是一个5乘12的矩阵。
matlab 插值拟合

matlab 插值拟合插值拟合是一种数值分析方法,用于找到一条通过给定数据点的曲线或曲面。
这个曲线或曲面可以通过插值拟合来近似描述数据点之间的关系。
MATLAB是一个强大的数值计算工具,它提供了一些内置的函数和工具箱来进行插值拟合。
在MATLAB中,可以使用interp1函数进行一维插值拟合,使用interp2函数进行二维插值拟合,使用interp3函数进行三维插值拟合。
这些函数的基本用法如下:1. 一维插值拟合:```x = 0:0.1:1; % 自变量 x 的取值范围y = sin(x); % 因变量 y 的取值xq = 0:0.01:1; % 插值点的取值范围yq = interp1(x, y, xq, 'spline'); % 三次样条插值拟合plot(x,y,'o',xq,yq) % 绘制原始数据点和拟合曲线```2. 二维插值拟合:```[X,Y] = meshgrid(-2:0.25:2); % 自变量 x 和 y 的取值范围Z = X.*exp(-X.^2-Y.^2); % 因变量 z 的取值[Xq,Yq] = meshgrid(-2:0.1:2); % 插值点的取值范围 Zq = interp2(X,Y,Z,Xq,Yq,'cubic'); % 立方插值拟合surf(X,Y,Z); % 绘制原始数据点的三维图像hold on;surf(Xq,Yq,Zq) % 绘制插值拟合的三维图像```3. 三维插值拟合:```[X,Y,Z,V] = flow; % 通过内置的流动数据生成示例数据Xq = -2:0.1:2; % 插值点的取值范围Yq = -2:0.1:2;Zq = -2:0.1:2;Vq = interp3(X,Y,Z,V,Xq,Yq,Zq,'spline'); % 三次样条插值拟合slice(X,Y,Z,V,[-2,0,2], [-2,0,2],[-2,0,2]); % 绘制原始数据点的切片图hold on;slice(Xq,Yq,Zq,Vq,[-2,0,2], [-2,0,2],[-2,0,2]) % 绘制插值拟合的切片图```除了上述基本的插值函数,MATLAB还提供了一些其他的插值拟合函数和工具箱,如scatteredInterpolant、griddedInterpolant和Curve Fitting Toolbox等,用于处理更复杂的插值拟合问题。
曲线的插值与拟合matlab

在数学和统计学领域中,曲线的插值与拟合是一项重要的技术,它在数据分析、图像处理、工程计算等领域都有着广泛的应用。
曲线的插值与拟合可以帮助我们从有限的数据点中还原出连续的曲线,以便更好地理解数据的规律和特性。
1. 插值与拟合的概念在开始深入探讨曲线的插值与拟合之前,让我们先来了解一下这两个概念的含义。
插值是指通过已知数据点之间的连续函数,以得到介于已知数据点之间的数据点的值。
而拟合则是指通过已知数据点,找到拟合曲线以最好地逼近这些数据点。
2. 曲线插值的方法在实际操作中,我们可以使用不同的方法进行曲线的插值。
常见的方法包括线性插值、多项式插值、样条插值等。
在Matlab中,有丰富的函数库可以用来进行不同类型的曲线插值,例如interp1, interp2, interpn等,这些函数可以很方便地实现曲线的插值操作。
(1)线性插值线性插值是一种简单直接的插值方法,它通过已知的两个数据点之间的直线来逼近新的数据点。
虽然线性插值操作简单,但在一些情况下并不能很好地逼近数据的真实规律。
(2)多项式插值多项式插值是一种常用的插值方法,它通过已知数据点构造一个多项式函数来逼近数据。
在Matlab中,可以使用polyfit和polyval函数来实现多项式插值操作,通过调整多项式的阶数可以得到不同精度的逼近结果。
(3)样条插值样条插值是一种更加复杂但精确度更高的插值方法,它通过已知的数据点构造出一系列的局部插值函数来逼近数据。
在Matlab中,可以使用spline函数来进行样条插值操作,通过调整插值节点的数量和类型可以得到不同精度的逼近结果。
3. 曲线拟合的方法除了插值方法之外,曲线的拟合也是一种常用的数据处理方法。
在实际操作中,我们可以使用不同的方法来进行曲线的拟合。
常见的方法包括最小二乘法拟合、多项式拟合、非线性拟合等。
在Matlab中,有丰富的函数库可以用来进行不同类型的曲线拟合,例如polyfit, lsqcurvefit, nlinfit等,这些函数可以很方便地实现曲线拟合操作。
MATLAB中的数据插值与曲线拟合技术

MATLAB中的数据插值与曲线拟合技术概述:数据插值和曲线拟合是在科学研究和工程实践中常用的技术手段。
在MATLAB中,有丰富的函数库和工具箱可用于实现各种插值和拟合算法。
本文将介绍MATLAB中的一些常见的数据插值和曲线拟合技术,并分析它们的原理和适用场景。
一、数据插值技术:1. 线性插值:线性插值是最简单且常用的数据插值技术之一,它通过在已知数据点之间的直线上进行插值。
MATLAB中的interp1函数可以实现线性插值,其基本原理是根据已知数据点的横纵坐标值,计算出待插值点的纵坐标值。
2. 拉格朗日插值:在拉格朗日插值中,我们通过一个多项式函数来描述已知数据点之间的曲线。
MATLAB中的polyfit和polyval函数可以帮助我们实现拉格朗日插值。
首先,polyfit函数用于拟合一个多项式函数,然后polyval函数可以根据拟合得到的多项式计算插值点的纵坐标值。
3. 样条插值:样条插值是一种光滑插值技术,通过使用多个低次多项式来拟合数据点之间的曲线。
MATLAB中的spline函数可以实现样条插值。
该函数将已知数据点的横纵坐标传入,然后自动计算出曲线段之间的控制点,并进行插值操作。
二、曲线拟合技术:1. 多项式拟合:多项式拟合是一种常用的曲线拟合技术,它通过拟合一个多项式函数来逼近已知数据点。
MATLAB中的polyfit和polyval函数同样可以应用于多项式拟合,我们可以选择合适的多项式阶次进行拟合。
2. 非线性拟合:有些数据集并不能用简单的多项式函数进行拟合,可能需要更复杂的非线性函数来逼近。
在MATLAB中,我们可以使用curve fitting工具箱中的fit函数来实现非线性拟合。
该函数可以根据给定的模型类型和数据集,自动拟合出最优的曲线。
3. 递归最小二乘拟合:递归最小二乘拟合是一种高级的数据拟合算法,可以有效地处理大型数据集。
MATLAB中的regress函数可以进行递归最小二乘拟合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四种插值方法比较
函数
格式
zi=interp2(x,y,z,xi,yi)
功能
二维插值。Z为由已知点的值组成的 矩阵,参量x与y是与z同维的已知点 的矩阵,且必须是单调的。xi与yi为 需要插值的点。若xi与yi中有在x与y 范围之外的点,则相应地返回NaN。
zi=interp2(z,xi,yi) Interp2
包角系 数
0.91
0.92
0.93
0.95
0.96
0.98
0.99
1
>>a1=[90,100,110,120,125,130,135,140,145,150,155,160,165,170,175,180]; >>a2=[0.69,0.74,0.78,0.82,0.84,0.86,0.88,0.89,0.91,0.92,0.93,0.95,0.96,0.98,0.99 ,1]; >>ka=interp1(a1,a2,133.5) >>ka=0.8740
例4
对
y
1
1 x2
在[-5,
5]上,
用n=11个等距分点作分段线
性插值和三次样条插值, 用m=21个插值点作图,比较结果.
xy
y1
y2
0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000 3.5000 4.0000 4.5000 5.0000
例3. 已知实验数据如表。
x
0
0.25 0.50 0.75 1.00
y
0.9162 0.8109 0.6931 0.5596 0.4055
计算插值点x0=0.6处的函数值y0。
>> x=[0 0.25 0.50 0.75 1.00]; >> y=[0.9162 0.8109 0.6931 0.5596 0.4055]; >> x0=0.6; >> y01=interp1(x,y,x0); >> y02=interp1(x,y,x0,'nearest'); >> y03=interp1(x,y,x0,'pchip'); >> y04=interp1(x,y,x0,'spline'); >> y01,y02,y03,y04
例2. 在普通V带设计中,带轮的包角α与包角系数ka之间的关系如 表所示。求α=133.5°时的包角系数ka。
包角与包角系数
包角 (°)
90 100 110 120 125 130 135 140
包角系 数
0.69
0.74
0.78
0.82
0.84
0.86
0.88
0.89
包角 (°)
145 150 155 160 165 170 175 180
MATLAB对已知数据集外部点上函数值的预测都返回NaN, 但可通过为interp1函数添加‘extrap’参数指明也用于外插。 MATLAB的外插结果偏差较大。
例1
对
f
x
1
1 9
x2
在[-1,
1]上,
用n=20的等距分点
进行线性插值, 绘制 f(x)及插值函数的图形.
解 在命令窗口输入:
x=-1:0.1:1; y=1./(1+9*x.^2); xi=-1:0.1:1; yi=interp1(x,y,xi); plot(x,y,'r-',xi,yi,'*')
三、插值、曲线拟合
插值就是已知一组离散的数据点集,在集合内部某两 个点之间预测函数值的方法。
插值法是实用的数值方法,是函数逼近的重要方法。在 生产和科学实验中,自变量x与因变量y的函数y = f(x)的关 系式有时不能直接写出表达式,而只能得到函数在若干个 点的函数值或导数值。当要求知道观测点之外的函数值时, 需要估计函数值在该点的值。
解 在命令窗口输入:
n=11, m=21 x=-5:10/(m-1):5 y=1./(1+x.^2) z=0*x x0=-5:10/(n-1):5 y0=1./(1+x0.^2) y1=interp1(x0,y0,x) y2=interp1(x0,y0,x,'spline') [x' y' y1' y2'] plot(x,z,'r',x,y,'k:',x,y1,'b',x,y2,'g') gtext('Piece.linear.'),gtext('Spline'),gtext('y=1/(1+x^2)')
y01 = 0.639700000000000
y02 = 0.693100000000000
y03 = 0.641818996851421
y04 = 0.641831200000000
例4
对
y
1
1 x2
在[-5,
5]上,
用n=11个等距分点作分段线
性插值和三次样条插值, 用m=21个插值点作图,比较结果.
Matlab常用数据插值函数及功能
函数
格式
功能
yi=interp1(x,y,xi)
一维插值。对一组点(x,y)进行插 值,计算插值点xi的函数值。
yi=interp1(y,xi) Interp1
此格式默认x=1:n,其中n是向量 y的长度,y为矩阵时,
n=size(y,1)
yi=interp1(x,y,xi,method) Method为指定的插值算法。 Nearest最近邻点插值,linear线 性插值(默认方式),spline三次 样条函数插值,cubic三次插值。
沿着指定的方向dim进行计算。
三次样条数据插值。用三次样条插 值计算出由向量x与y确定的一元函 数在点xx处的值yy。
返回由向量x与y确定的分段样条多 项式的系数矩阵pp。
注意:
(1)只对已知数据点集内部的点进行的插值运算称为内插, 可比较准确的估测插值点上的函数值。
(2)当插值点落在已知数据集的外部时的插值称为外插, 要估计外插函数值很难。
此格式默认x=1:n、y=1:m,其中 [m,n]=size(z)。再按 zi=interp2(x,y,z,xi,yi)情形进行计算。
zi=interp2(x,y,z,xi,yi,method)
用指定的算法method计算二维插值。 Linear双线性插值(默认方式), Nearest最邻近插值,spline三次样条 插值,cubic双三次插值。
函数
格式
y=interpft(x,n) Interpft
y=interpft(x,n,dim)
yy=spline(x,y,xx) splቤተ መጻሕፍቲ ባይዱne
pp=spline(x,y)
功能 一维Fourier插值。适用于周期函数生 成数据的插值。X为抽样序列,n为 需要计算的等距点数,y为n点的插 值计算结果。
