线性系统理论MATLAB大作业
单纯形法MATLAB程序(线性与非线性规划大作业)

单纯形法程序整理.txt [hB,lB]=size(B);%测算B的行、列数 for j=1:hB if(A(B(j,1),B(j,2))~=1)%如果主元不为1,将对应行除以主元化为1 A(B(j,1),:)=A(B(j,1),:)/A(B(j,1),B(j,2)); end for i=1:hA%将其他元化为零 if(i==B(j,1)) continue; end A(i,:)=A(i,:)-A(B(j,1),:)*A(i,B(j,2)); end end end %————————————————% %% 子程序-选主元 function [r,s]=SubFc_XuanZhuYuan(TableK,h,l) %选主元素 % 选出表矩阵TableK中的主元素 %% 选列主元 t=0; for i=1:l if(TableK(h+1,i)<=t) t=TableK(h+1,i);%记录判别数最小值 s=i;%记录下标 end end if(t==0) error('判别数全为正'); end %% 选行主元 for i=1:h%检查元素是否为负,并赋予t初值 if(TableK(i,s)>0) t=TableK(i,l+1)/TableK(i,s); break; end if(i==h)%若元素全为负,则报错 error('主列元素全为非正,规划问题有无界解!'); end end %k=1; for i=1:h %若未知数出现负值,则是初始迭代标准性表产生的,应更换初始主元; if(TableK(i,l+1)<0) error('b向量出现负值,更换初始主元'); end if(TableK(i,s)<=0)%排除A表负元素 continue; end if(TableK(i,l+1)/TableK(i,s)<=t) t=TableK(i,l+1)/TableK(i,s);%记录判别数最小值 r=i;%记录下标 end end %补充判据 k=1; 第 2 页
华电线性系统理论大作业

而前文已经得出导轨的动能 Tw ,因此两式相加得系统的动能 T 为:
2 2 2 2 1 x T Tb Tw m x x2 a Ib I w a 2 R
是导轨相对于水平线的倾斜角。
图 1.球杆系统简图
2.2 拉格朗日法建模
为了对球杆系统进行研究, 我们先对其进行建模, 一般来说, 这种球杆系统, 运用拉格朗日方程建立其数学模型比较方便,拉格朗日方程如下:
d T T V R U t dt q q ' q ' q
v v' w r
其中 v ' 是小球相对于导轨的线速度,其数值等于 x ,负号是指方向与规定 的正方向相反, 指的是导轨的角速度,即 a ,r 是小球的质心在坐标系中的位 置向量,计算式如下:
R x 0 x x a v 0 0 R xa a 0 0 0
其中 T 为系统的动能,包括小球的转动的动能,导轨转动的动能等,V 为系 统的势能, 包括重力势能弹性势能等等, 能量耗散函数为 R ,q
q1 , q2 ....qk
T
1
为广义坐标向量,其中 k 代表系统的自由度,即完全描述系统运动特性需要的坐 标数目,关于自由度在下文会具体分析, u 为作用于系统的外力。 以下为各个变量所表示的物理意义,M:导轨的质量,g:重力加速度 r:小 球的半径 I b :球的惯性力矩, I w :杆的惯性力矩,x:球的相对横坐标,y:球 的相对纵坐标, :小球相对于导轨的转角,a:导轨与水平线的夹角,球杆系 统受力分析如下:
MATLAB期末大作业

MATLAB期末⼤作业学号:姓名:《Matlab/Simulink在数学计算与仿真中的应⽤》⼤作业1.假设地球和⽕星绕太阳运转的半径分别为r和2r,利⽤comet指令动画显⽰从地球到⽕星的转移轨迹(r可以任意取值,要求实时显⽰探测器、太阳、地球和⽕星的位置)。
解函数function comet(varargin)[ax,args,nargs] = axescheck(varargin{:});error(nargchk(1,3,nargs,'struct'));% Parse the rest of the inputsif nargs < 2, x = args{1}; y = x; x = 1:length(y); endif nargs == 2, [x,y] = deal(args{:}); endif nargs < 3, p = 0.10; endif nargs == 3, [x,y,p] = deal(args{:}); endif ~isscalar(p) || ~isreal(p) || p < 0 || p >= 1error('MATLAB:comet:InvalidP', ...'The input ''p'' must be a real scalar between 0 and 1.'); End指令 %particle_motiont = 0:5:16013;r1=6.7e6;%随便给定参数%---------------------------r2=2*r1;g=9.8;R=6.378e6;m=g*R^2;%内轨道v_inner=sqrt(m/r1);w_inner=v_inner/r1;x_inter=r1*cos(w_inner*t);y_inter=r1*sin(w_inner*t);%外轨道v_outer=sqrt(m/r2);w_outer=v_outer/r2;x_outer=r2*cos(w_outer*t);y_outer=r2*sin(w_outer*t);%控制器转移轨道a=(r1+r2)/2;E=-m/(2*a);V_near=sqrt(m*(2/r1-2/(r1+r2)));%转移轨道在近地点的速度V_far=sqrt(m*(2/r2-2/(r1+r2)));%转移轨道在远地点的速度h=r1*V_near;%由于在近地点的速度垂直于位置失量, h是转移轨道的⽐动量矩e=sqrt(1+2*E*h^2/m^2);%e为椭圆轨迹的偏⼼率TOF=pi*sqrt(a^3/m);%转移轨道是椭圆的⼀半及飞⾏时间是周期的⼀半(开普勒第三定律) w=pi/TOF;%椭圆轨迹的⾓速度c=a*e;b=sqrt(a^2-c^2);x_ellipse=a*cos(w*t)-0.5*r1;y_ellipse=b*sin(w*t);%动画显⽰运动轨迹x=[x_inter;x_outer;x_ellipse]';y=[y_inter;y_outer;y_ellipse]';comet(x,y)%---------------------------动态图像如下:2.利⽤两种不同途径求解边值问题dfdxf gdgdxf g f g=+=-+==34430001,,(),()的解.途径⼀:指令syms f g[f,g]=dsolve('Df=3*f+4*g,Dg=-4*f+3*g','f(0)=0,g(0)=1'); disp('f=');disp(f)disp('g=');disp(g)结果(Matlab 7.8版本)f=i/(2*exp(t*(4*i - 3))) - (i*exp(t*(4*i + 3)))/2g=exp(t*(4*i + 3))/2 + 1/(2*exp(t*(4*i - 3)))(Matlab 6.5版本)f=exp(3*t)*sin(4*t)g=exp(3*t)*cos(4*t)>>途径⼆:%problem2function dy=problem2(t,y)dy = zeros(2,1);dy(1) = 3*y(1)+4*y(2);dy(2) = -4*y(1)+3*y(2);[t,y] = ode45('problem2',[0 2],[0 1]);plot(t,y(:,1),'r',t,y(:,2),'b');图23.假设著名的Lorenz 模型的状态⽅程表⽰为-+-=+-=+-=)()()()()()()()()()()()(322133223211t x t x t x t x t x t x t x t x t x t x t x t x σρρβ其中,设28,10,3/8===σρβ。
matlab期末大作业

matlab期末⼤作业MATLAB语⾔及控制系统仿真期末⼤作业姓名:熊睿班级:K0312417学号:K031241742⽇期:2014/10/18⼤作业题⽬:⼀、已知单位负反馈系统的开环传递函数为)10)(5(100)(++=s s s Ks G ,K 分别取0.5和3两种情况。
1、分别在MATLAB 命令窗⼝或Simulink 模型窗⼝,建⽴K 取不同值时控制系统的模型;2、在第1问建⽴的模型基础上,要求分别在MATLAB 命令窗⼝或Simulink 模型窗⼝中绘制并观察该系统的单位阶跃响应曲线、单位斜坡响应曲线和单位加速度响应曲线;(注意:要求将K 取不同值时系统的单位阶跃响应绘制在⼀张图中并进⾏必要的标注)3、计算两种K 值所对应系统的时域性能指标(包括调节时间、上升时间、超调量、峰值时间);4、绘制系统的伯德图和奈奎斯特曲线;5、判断当K 取7.8时系统的稳定性,如果不稳定,进⾏校正直到系统稳定为⽌。
(提⽰:可使⽤rltool ⼯具)要求:有详细的建模过程、绘图过程和分析过程,最后要求进⾏总结。
⼆、写⼀份800字左右的MATLAB 学习体会和总结。
⼀、已知单位负反馈系统的开环传递函数为)10)(5(100)(++=s s s Ks G ,K 分别取0.51、分别在MATLAB 命令窗⼝或Simulink 模型窗⼝,建⽴K 取不同值时控制系统的模型;根据题⽬,在simulink 中建⽴程序图,如图○1,利⽤To workspace 将数据导⼊workspace 中,在cammond window 中⽤plot 函数画出两个不同增益的系统的阶跃响应。
如图○2 命令窗⼝中的程序:plot(tout,Y,’r ’,tout ’Y2,’k ’)图○11234567891000.511.5时间(秒)幅值阶跃响应曲线K=0.5K=3图○22、在第1问建⽴的模型基础上,要求分别在MATLAB命令窗⼝或Simulink模型窗⼝中绘制并观察该系统的单位阶跃响应曲线、单位斜坡响应曲线和单位加速度响应曲线;(注意:要求将K取不同值时系统的单位阶跃响应绘制在⼀张图中并进⾏必要的标注)根据题⽬:在1中所创建的程序图的基础下,对K=0.5的系统分别接⼊单位阶跃、单位斜坡和单位加速度输⼊。
MATLAB大作业
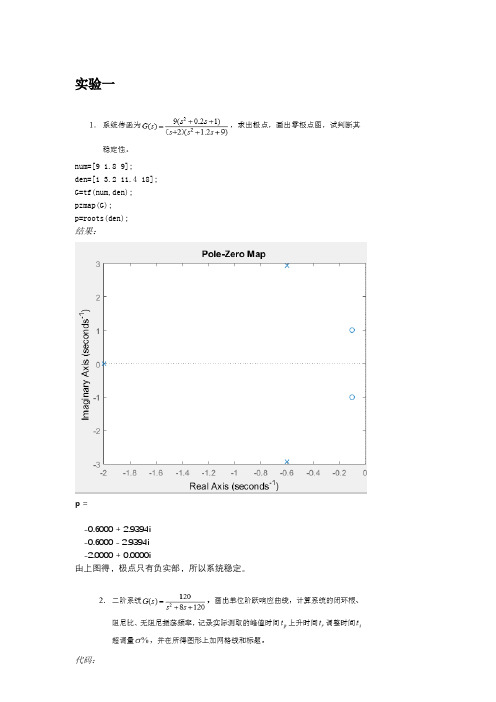
实验一num=[9 1.8 9];den=[1 3.2 11.4 18];G=tf(num,den);pzmap(G);p=roots(den);结果:p =-0.6000 + 2.9394i-0.6000 - 2.9394i-2.0000 + 0.0000i由上图得,极点只有负实部,所以系统稳定。
代码:num=[120];den=[1 8 120];step(num,den);title('step response of G(s)=120/s^2+8s+120');grid on;G=tf(num,den);[wn z p]=damp(G);运行结果截图:由上图可得,系统的闭环根s=-4.0000±10.1980i,阻尼比ξ=0.3651,无阻尼自然震荡频率w n=10.9545 t p=0.311, t s=0.987, t r=0.129, 超调量σ%=29.2%实验二代码:z=[-100];p=[-1 -10 -0.125];k=31.6;sys=zpk(z,p,k);figure(1);nyquist(sys);grid on;title('Nyquist Plot'); figure(2);title('Bode Diagram'); bode(sys);运行结果截图:由上图可得,系统的相位裕度Pm=-41.4dB,幅值裕度Gm=-27dB, 系统不稳定近似折线特性与原图对比:代码:z=[-100];p=[-1 -10 -0.125];k=31.6;sys=zpk(z,p,k);figure(1);bode(sys);grid;figure(2);w=logspace(-3,4,100);[w,L]=Asymptote(sys,w);semilogx(w,L);grid;运行结果截图:渐进折线与波德图中的幅频特性曲线很接近,两张图大概在10-1之前的斜率均为零,在101左右穿过零分贝线代码:Gc1=tf([1],[1]);Gc2=tf([3.333 1],[100 1]);z=[];p=[0 -10 -20];k=100;G=zpk(z,p,k);G11=series(Gc1,G);G22=series(Gc2,G);figure;bode(G,G11);grid on;title('²¨ÌØͼÇúÏ߱ȽÏ');figure;bode(G,G22);grid on;title('²¨ÌØͼÇúÏ߱ȽÏ');bode(G,G11,G22);grid on;title('²¨ÌØͼÇúÏ߱ȽÏ');figure;margin(G);grid on;figure;margin(G11);grid on;figure;margin(G22);grid on;运行结果截图:原系统与加入控制器(1)系统的B ODE图比较原系统稳定裕度值加入控制器(1)的稳定裕度值原系统与加入控制器(2)系统的B ODE图比较加入控制器(2)的稳定裕度值(2)控制器减小了系统的幅值裕量和相位裕量,系统的稳定性变差了。
线性系统设计作业

线性系统理论设计作业专业:学号:姓名:指导老师:解:1、①将惯性环节等效变换并带入数据得到如下所示:系统不加扰动和任何反馈及校正装置时,在t=0s 时,加上阶跃输入u=1500,得到波形如下:可以看出输出不能跟随输入变化,而且稳态误差较大,不能符合系统控制要求。
令n x =1;d U x =2 ;d I x =3得状态空间表达式如下:Y = []x 001②判断系统稳定性,在MATLAB 中输入以下程序:>> A=[0 0 18.086;0 -588.235 0;-8.1012 59.524 -25];P=poly(A);roots(P)运行结果如下:ans =-588.2350-15.6196-9.3804可以看到特征方程的所有特征值均为负实数,所以系统是稳定的。
③判断系统的能控性与能观性,在MATLAB 中输入以下程序: A=[0 0 18.086;0 -588.235 0;-8.1012 59.524 -25];B=[0;23529.412;0];C=[1 0 0];M=ctrb(A,B)RM=rank(M)N=obsv(A,C)RN=rank(N)运行结果如下:M =1.0e+009 *0 0 0.02530.0000 -0.0138 8.14170 0.0014 -0.8589RM =3N =1.0e+003 *0.0010 0 00 0 0.0181-0.1465 1.0766 -0.4522RN =3>>从计算结果可以看出,系统能控性矩阵和能观测性矩阵的秩都是3,为满秩,因此该系统是可控的,也是能观测的。
MATLAB实验练习题计算机南邮MATLAB数学实验大作业答案

“M A T L A B ”练习题 要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根。
(先画图后求解)(要求贴图)>>solve('exp(x)-3*x^2',0)ans=-2*lambertw(-1/6*3^(1/2))-2*lambertw(-1,-1/6*3^(1/2))-2*lambertw(1/6*3^(1/2))2、求下列方程的根。
1)5510x x ++=a=solve('x^5+5*x+1',0);a=vpa(a,6)a=1.10447+1.05983*i-1.00450+1.06095*i-.-1.00450-1.06095*i1.10447-1.05983*i2)1sin 02x x -=至少三个根 >>fzero('x*sin(x)-1/2',3)ans=2.9726>>fzero('x*sin(x)-1/2',-3)ans=-2.9726>>fzero('x*sin(x)-1/2',0)ans=-0.74083)2sin cos 0x x x -=所有根>>fzero('sin(x)*cos(x)-x^2',0)ans=>>fzero('sin(x)*cos(x)-x^2',0.6)ans=0.70223、求解下列各题:1)30sin lim x x x x ->- >>symx;ans=1/62)(10)cos ,x y e x y =求 >>symx;>>diff(exp(x)*cos(x),10)ans=(-32)*exp(x)*sin(x)3)21/20(17x e dx ⎰精确到位有效数字)>>symx;>>vpa((int(exp(x^2),x,0,1/2)),17)ans=0.4)42254x dx x +⎰ >>symx;>>int(x^4/(25+x^2),x)ans=125*atan(x/5)-25*x+x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩所确定的函数的一阶导数dy dx 与二阶导数22d y dx 。
[vip专享]MATLAB在线性系统理论中的应用
![[vip专享]MATLAB在线性系统理论中的应用](https://img.taocdn.com/s3/m/84bf29aa5727a5e9846a618d.png)
8
0
0
0
2
0
0
0
1
u1 2 0 0 0
x1
x2
x3
0.5 0.4375 0.75
u1 0
x4 -1.5
0 0 0
x4 0.75
43m1m“-”J520Gm01m24“492k-Z(1)g2L3-”3060@k%3-g“/1”7mD2%BJ/Tg0d1-ZP318¬-A_2"o70)Xc0?y258z6n”217 NE)
1 -2 0 2 -2 -2 4 -2 -4 j=
200 011 001
Example 6 从状态转移矩阵到传递函数的转化
举例:clear
a=[0 1 0;0 0 1;-6 -11 -6]; b=[0;0;1]; c=[ 1 1 1]; d=[0]; v=ss(a,b,c,d) [num,den]=ss2tf(a,b,c,d); printsys(num,den) [z,p,k]=ss2zp(a,b,c,d); zpk(z,p,k) x0=[2;0;1]; figure(1) step(v) figure(2) initial(v,x0) t=0:0.1:60; u=t; figure(3) lsim(v,u,t); %figure(3)
0.31 z^3 + 0.57 z^2 + 0.38 z + 0.89 ----------------------------------------z^4 + 3.23 z^3 + 2.98 z^2 + 2.22 z + 0.47
Sampling time: 0.1 Pzmap(gyu)%绘制零极点分布图
MATLAB 在线性系统理论中的应用
MATLAB在线性系统理论中的应用

MATLAB在线性系统理论中的应⽤MATLAB在线性系统理论中的应⽤第⼀章传递函数与状态空间表达式1.1 传递函数与状态空间表达式之间的转换⽤ss命令来建⽴状态空间模型。
对于连续系统,其格式为sys=ss(A,B,C,D),其中a,b,c,d 为描述线性连续系统的矩阵。
当sys1是⼀个⽤传递函数表⽰的线性定常系统时,可以⽤命令sys=ss(sys1)将其转换成为状态空间形式,也可以⽤命令sys=ss(sys1,’min’)计算出系统sys的最⼩实现。
example1:系数传递函数到状态空间表达式>>num=[1 7 24 24];den=[1 10 35 50 24];g=tf(num,den);sys=ss(g)the answer is:a =x1 x2 x3 x4x1 -10 -4.375 -3.125 -1.5x2 8 0 0 0x3 0 2 0 0x4 0 0 1 0b =u1x1 2x2 0x3 0x4 0c =x1 x2 x3 x4y1 0.5 0.4375 0.75 0.75d =u1y1 0Continuous-time model.example2:由传递函数系数,将离散系统脉冲传递函数模型转换成状态空间表达式>>num=[0.31 0.57 0.38 0.89];den=[1 3.23 3.98 2.22 0.47];Transfer function:0.31 z^3 + 0.57 z^2 + 0.38 z + 0.89-----------------------------------------z^4 + 3.23 z^3 + 2.98 z^2 + 2.22 z + 0.47Sampling time: 0.1Pzmap(gyu)%绘制零极点分布图sys=ss(gyu)%将离散系统脉冲传递函数模型转换成状态空间表达式。
The answer is:a =x1 x2 x3 x4x1 -3.23 -1.49 -1.11 -0.235x2 2 0 0 0x3 0 1 0 0x4 0 0 1 0b =u1x1 1x2 0x3 0x4 0c =x1 x2 x3 x4y1 0.31 0.285 0.19 0.445d =u1Discrete-time model.Example 3:⽤s求逆矩阵法从系统矩阵a,b,c,d求得传递函数>>syms s;a=[0 1;-2 -3];b=[1 0;1 1 ];c=[2 1;1 1;-2 -1];d=[3 0;0 0;0 1];i=[1 0;0 1];f=inv(s*i-a)g=simple(simple(c*f*b)+d)The answer is:f =[ (s+3)/(s^2+3*s+2), 1/(s^2+3*s+2)][ -2/(s^2+3*s+2), s/(s^2+3*s+2)]g =[ 3/(s+1)+3, 1/(s+1)][ 2/(s+2), 1/(s+2)][ -3/(s+1), -1/(s+1)+1]Example 4 eig()指令,求特征根矩阵和特征向量矩阵函数eig()Example 5 约旦标准型函数jordan()>> a=[0 1 0;0 0 1;2 -5 4]a =0 1 00 0 12 -5 4>> [q,j]=jordan(a)q =1 -2 02 -2 -24 -2 -4j =2 0 00 1 1a=[0 1 0;0 0 1;-6 -11 -6];b=[0;0;1];c=[ 1 1 1];d=[0];v=ss(a,b,c,d)[num,den]=ss2tf(a,b,c,d);printsys(num,den)[z,p,k]=ss2zp(a,b,c,d);zpk(z,p,k)x0=[2;0;1];figure(1)step(v)figure(2)initial(v,x0)t=0:0.1:60;u=t;figure(3)lsim(v,u,t);%figure(3)第⼆章状态转移矩阵与状态⽅程的解Example 1Collect函数的作⽤是合并同类项,ilaplace()函数的作⽤的求取laplace反变换,函数det ()的作⽤是求⽅阵的⾏列式。
华工自动化线性系统第一次 大作业

求的方法有时域的求解方法和频域的求解方法。 方法1:根据或者的定义直接计算:
=I+++…++…= 从公式可以看出,右边是一个无穷项的和,要精确计算出
结果是很困难的,所以无论是手工计算还是利用电脑计算,都 不可能取无穷项计算,通常是取有限项,得到一个近似的值, 以满足不同的精度要求即可.对于不同的精度要求,n的值会不 同。在工程上,只要取它的前几项就可以满足要求,本方法易 于理解,适合计算机编程。 方法2:利用拉氏反变换法求:
版本)正在进行着陆(速度V=16英里/小时)。描述飞机纵向 运动的状态空间方程
给出如下:
控制输入是升降舵角度和向量的状态变量分别是速度的变化, 迎角,俯仰速率和俯仰度。
该飞机的纵向模式称为短周期和长周期。在长周期特征 值,这也是一种复杂的共轭特征值接近虚轴,造成长周期运 动,在水平面缓慢地震荡。
二、状态转移矩阵的重要性与意义
线性系统理论大作业
专业:控制理论与控制工程 学号与姓名:
一、飞行器原理及结构和空间坐标系
为了进行控制系统设计的目的,飞机动力学经常称为飞行 姿态的一些操作状态进行线性化,它假设飞机的速度(马赫 数)和姿态是不变的。控制面(The control surfaces)和发动 机推力装置设置或修改,以达到这些状态,我们设计控制系统 就是为了维护这些条件,例如,强制将到这些状态的扰动(偏 差)变为零。
syms M s d1 t XT X0; A=[-0.0507 -3.861 0 -32.2;-0.00117 -0.5164 1 0;-0.000129 1.4168 -0.4932 0;0 0 1 0]; disp('矩阵A的行列式如下:'); d1=det(A); I=eye(4); disp('[sI-A]^(-1)为:'); B=(s*I-A); C=inv(B); digits(4) C=vpa(C) disp('状态转移阵为'); D=ilaplace(C); digits(4); M=vpa(D) X0=[0;0;0;0]; B=[0;-0.0717;-1.645;0]; XT=M*(X0+B) %求解系统的状态响应。 %画图 subplot(2,2,1) %画出x(t)d第一个分量X1(t),并把它显示在左上 角。 ezplot(XT(1,1),[0,2]) subplot(2,2,2) %画出x(t)d第二个分量X2(t),并把它显示在右上 角。 ezplot(XT(2,1),[0,2])
Matlab语言及应用大作业02答案

MATLAB语言及应用大作业姓名:学号:班级:1.利用plot函数在区间[0,2π]同时绘制x=sin(t)和y=cos(t),z=sin(t)+cos(t)的图形。
要求:1)对图像x轴和y轴分别标注“时间”和“函数值”2)对曲线加图例标注,图例位置自动定位(12分)。
>> t=[0:0.1*pi:2*pi];>> x=sin(t);>> y=cos(t);>> z=sin(t)+cos(t);>> plot(t,x,t,y,t,z)>> xlabel('时间')>> ylabel('函数值')>> legend('x=sin(t)','y=cos(t)','z=sin(t)+cos(t)')2. 求2!+4!+6!+8!+10! (12分)sum=0;for i=2:2:10pdr=1;for k=2:ipdr=pdr*k;endsum=sum+pdr;end在M文件编辑窗口编写上述程序,保存为exam02.m文件;在MATLAB命令窗口执行命令:>>exam02>>sumsum =36698663.编写m 函数,计算函数值(12分)221,10002,,0≥<≤<≤<⎪⎪⎩⎪⎪⎨⎧-=x x x x x x y 编写函数代码function f=exam03(t) if(t<0) f=0;elseif(t>=0)&(t<1) f=t;elseif(t>=1)&(t<=2) f=2-t; else f=0; end在M 文件编辑窗口编写上述程序,保存为exam03.m 文件在MATLAB 命令窗口输入: >> x=1;>> y=exam07(x) y = 14.计算下面矩阵的特征值、特征向量、迹和秩。
线性系统大作业1

xdot(1)=-R/L*x(1)-1/L*x(2)+1/L*f(t);
xdot(2)=1/C*x(1);
function in=f(t)
in=(t>0)*2;
end
end
仿真求解状态方程代码如下:
L=1;
C=0.1;
R=1.5;
[t,x]=ode45('funcforex14',[-1,10],[0;1],[],R,L,C);
的根。方阵A有n个特征值;实际物理系统中,A为实数方阵,故特征值或为实数,或为成对共轭复数;如A为实数对称方阵,则其特征值都是实数。
4.2系统的不变量与特征值的不变性
同一系统,经非奇异变換后,得
公式(4.1)
其特征方程为
公式(4.2)
公式(4.1)与公式(4.2)形式虽然不同,但实际是相等的,即系统的非奇异变换,其特征值是不变的。可以证明如下:
xlabel('t/ms');ylabel('电压/V');title('系统响应');
[t,x]=ode45('funcforex13',[-1,10],[0;1],[],R,L,C);
figure(1);plot(t,x(:,1),'k');hold on;xlabel('time sec');
figure(1);plot(t,x(:,1),'r');hold on;xlabel('time sec');grid;
xlabel('t/ms');ylabel('电压/V');title('齐次性');
MATLAB结课大作业

一、判断系统稳定性的方法,并举例说明。
方法一:用Nyquist稳定判据判断系统的稳定性Nyquist稳定判据:若想使得闭环系统稳定,则开环系统G(S)H(S)的Nyquist曲线逆时针绕临界点(-1,j0)点的圈数R必需等于G(S)H(S)(系统的开环传函)位于S的右半平面开环极点数P。
即:Z=P-R Z=0 稳定;Z≠0 不稳定,Z为闭环正实部根的个数。
方法二:用Bode图判断系统的稳定性函数调用格式为:margin( )或[Gm Pm wcp wcg]=margin(G)对于最小相位系统:当相角裕度P m(γ)>0o 或幅值裕度G m(h) >1时,表示系统稳定当相角裕度P m(γ)<0o 或幅值裕度G m(h) <1时,表示系统不稳定幅值裕度G m(h)、相角裕度P m(γ)越大,系统稳定程度越好。
在使用时,G m(h)、P m(γ)是成对使用的,有时仅使用一个裕度指标P m(γ)。
方法三:用代数稳定判据法判断系统的稳定性(1)系统数学模型为传递函数形式G(S)=tf(num,den):执行语句:roots(G.den{1});注:“{}”表示维数(2)系统数学模型为零极点增益形式G(S)=zpk(z,p,k);执行语句:G.p{1};(3)系统数学模型为状态空间形式G(S)=ss(A,B,C,D);执行语句:eig(G.A);注:eig()表示计算系统的极点方法四:用根轨迹法判断系统的稳定性若根轨迹在参数取值过程中,部分在左半平面,部分在右半平面,则系统的稳定性与可变参数的取值有关。
函数命令调用格式:[k poles]=rlocfind(G)方法五:用单位阶跃响应曲线判定系统稳定性例:已知系统的开环传函为:5(S+2)G(S)= ----------------------------(S+10)(S³+3S²+2S+5)判断系统的稳定性解:方法一:用Nyquist稳定判据判断系统的稳定性>>G=tf(5*[1 2],conv([1 10],[1 3 2 5]));>>roots(G.den{1})Ans=-10.0000-2.9042-0.0479+1.3112i-0.0479-1.3112i>>nyquist(G)执行以上程序得到nyquist图可以看出,nyquist曲线包围临界点的圈数R=0。
MATLAB程序设计期末大作业

MATLAB程序设计期末大作业姓名:班级:学号:指导教师:题目1给定如图1所示的单位负反馈系统。
图1在系统中分别引入不同的非线性环节(饱和、死区、与滞环),观察系统的阶跃响应,并且分析比较不同的非线性环节对系统性能的影响。
解:1、利用MATLAB中的simulink工具箱,对题设控制系统进行建模,如图1 所示。
则没有任何非线性环节的系统,其阶跃响应曲线如图2 所示。
图22、在系统中加入饱和非线性环节,系统框图如图3所示。
其中,饱和非线性环节的输出上限为0.1,输出下限为-0.1;阶跃信号幅值为1。
图3利用simulink进行仿真,得到的阶跃响应曲线如图4所示。
图4为了比较当饱和非线性环节输出上下限变化时系统阶跃响应的不同,可以利用simulink中的to workspace模块,将多次仿真的结果记录到工作空间的不同数组中,并且绘制到同一幅图像上。
此时,系统框图如图5所示。
图5将4种情况下系统的阶跃响应曲线绘制在同一幅图像中,代码如下:>> plot(tout,out2);>> plot(tout,out2);>> hold on;>> grid on;>> gtext('0.1');>> plot(tout,out1);>> plot(tout,out3);>> gtext('0.2');>> plot(tout,out4);>> gtext('0.5');运行程序,结果如图6所示。
图6从图6中可以看出:当饱和非线性环节的输出范围较窄时,系统的阶跃响应速度较慢,上升时间长;同时,超调量较小,振荡不明显;随着输出范围的扩大,系统的响应速度加快,上升时间大大减小,同时伴有显著的振荡。
这是因为饱和环节会对信号起到限幅作用;不难想象,限制作用越强,系统的输出越不容易超调,响应也会越慢,这从图6也可以看出这一趋势。
matlab的大作业

华东交通大学matlab 大作业(matlab在信号与系统中的应用)班级:姓名:学号:前言此次的大作业内容是matlab在信号与系统中的应用。
在信号与系统中有各种各样的信号还有系统要分析,而matlab特别适用与信号通过系统的分析。
而且本人对于matlab在信号与系统中的运用蛮感兴趣的,况且当初学习时对于其在信号与系统中的运用不是很了解,故借此机会,也顺便再系统地学习和掌握matlab在信号与系统的运用。
这次设计的程序主要是围绕用matlab求解信号与系统中一些信号描述、零输入响应的求解、冲激响应的求解、卷积的计算、零状态响应的求解、傅里叶的分析(包括方波分解为正弦波之和非周期信号的频谱分析,以及用傅里叶变换计算滤波器的响应和输出)。
接下来就描述一下设计的程序。
一、程序描述Chengxu1是对于信号与系统中的一些信号的描述。
包括单位冲激函数、单位阶跃函数、复数指数信号。
程序中,t0,tf,dt,分别指的是t的起点、终点、间隔。
t1指的是在冲激函数在t1处冲激,在t1处是阶跃函数的转折点。
用matlab来描述这些信号,是根据这些信号的特点来一一描述的。
而且此次的画图用的是stairs而不是plot。
是因为要描述的是连续信号中的不连续点,故用stairs,若要波形光滑些,则用plot效果更好一些。
就如冲激函数和阶跃函数的波形对比如下(此处所取的是t0=0,tf=5,dt=0.05,t1=1):用plot所画用stairs所画此外,复数指数信号可以分解为余弦和正弦信号,他们分别是复数信号的是实部和虚部,即相位差为90度。
图如下(此处alpha=-0.5,w=10):Chengxu2是求解LTI 系统的零输入,题型为:描述n 阶线性时不变连续系统的微分方程为已知y 及其各阶导数的初始值为 求系统的零输入响应。
可以根据具体的函数求解其零输入。
Chengxu3是求解阶LTI 系统的冲激响应,是求解系统函数为: 的冲激响应。
MATLAB处理线性系统数学模型

实验一用MATLAB处理线性系统数学模型[说明]一个控制系统主要由被控对象、测量装置、控制器和执行器四大部分构成。
MATLAB软件的应用对提高控制系统的分析、设计和应用水平起着十分重要的作用。
采用MATLAB软件仿真的关键问题之一是在MATLAB软件平台上怎样正确表示被控对象的数学模型。
[实验目的]1.了解MATLAB软件的基本特点和功能;2.掌握线性系统被控对象传递函数数学模型在MATLAB环境下的表示方法及转换;3.掌握多环节串联、并联、反馈连接时整体传递函数的求取方法;4.掌握在SIMULINK环境下系统结构图的形成方法及整体传递函数的求取方法;5.了解在MATLAB环境下求取系统的输出时域表达式的方法。
[实验指导]一、被控对象模型的建立在线性系统理论中,一般常用的描述系统的数学模型形式有:(1)传递函数模型——有理多项式分式表达式(2)传递函数模型——零极点增益表达式(3)状态空间模型(系统的内部模型)这些模型之间都有着内在的联系,可以相互进行转换。
1、传递函数模型——有理多项式分式表达式设系统的传递函数模型为1110111......)()()(a s a s a s a b s b s b s b s R s C s G n n n n m m m m ++++++++==----对线性定常系统,式中s 的系数均为常数,且a n 不等于零。
这时系统在MATLAB 中可以方便地由分子和分母各项系数构成的两个向量唯一地确定,这两个向量常用num 和den 表示。
num=[b m ,b m-1,…,b 1,b 0]den=[a n ,a n-1,…,a 1,a 0]注意:它们都是按s 的降幂进行排列的。
分子应为m 项,分母应为n 项,若有空缺项(系数为零的项),在相应的位置补零。
然后写上传递函数模型建立函数:sys=tf(num,den)。
这个传递函数便在MATLAB 平台中被建立,并可以在屏幕上显示出来。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
兰州理工大学2015级线性系统理论大作业线性系统理论Matlab 实验报告1、在造纸流程中,投料箱应该把纸浆流变成2cm 的射流,并均匀喷洒在网状传送带上。
为此,要精确控制喷射速度和传送速度之间的比例关系。
投料箱内的压力是需要控制的主要变量,它决定了纸浆的喷射速度。
投料箱内的总压力是纸浆液压和另外灌注的气压之和。
由压力控制的投料箱是个耦合系统,因此,我们很难用手工方法保证纸张的质量。
在特定的工作点上,将投料箱线性化,可以得到下面的状态空间模型:u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡-+-=0001.0105.0002.002.08.0. []21,x x y =其中,系统的状态变量x1=液面高度,x2=压力,系统的控制变量u1=纸浆流量u2=气压阀门的开启量。
在上述条件下,试设计合适的状态变量反馈控制器,使系统具有实特征根,且有一个根大于5解:本题目是在已知状态空间描述的情况下要求设计一个状态反馈控制器,从而使得系统具有实数特征根,并要求要有一个根的模值要大于5,而特征根是正数时系统不稳定,这样的设计是无意义的,故而不妨采用状态反馈后的两个期望特征根为-7,-6,这样满足题目中所需的要求。
要对系统进行状态反馈的设计首先要判断其是否能控,即求出该系统的能控性判别矩阵,然后判断其秩,从而得出其是否可控。
Matlab 判断该系统可控性和求取状态反馈矩阵K 的程序,如图1所示,同时求得加入状态反馈后的特征根并与原系统的特征根进行了对比。
图1系统能控性、状态反馈矩阵和特征根的分析程序上述程序的运行结果如图2所示:图2系统能控性、反馈矩阵和特征根的运行结果图2中为图1matlab 程序的运行结果,经过判断得知系统是可控的,同时极点的配置个数与系统状态相符,求得了状态反馈矩阵K 的值,并把原系统的特征根(rootsold )和加入状态反馈后的特征根(rootsnew )进行对比。
同时通过特征值可以看出该系统是稳定的。
2、描述恒速制导导弹的运动方程为:u x x ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0001000015.000100000005.00005.0-1.0-00010. []x y 01000= 运用ctrb 函数计算系统的能控型矩阵,并验证系统是不可控的;计算从u 到Y 的传递函数,并消去传递函数中的分子和分母公因式,由此可以得到能控的状态空间模型。
在消去了公因子之后,请用tf2ss 函数确定新的状态变量模型;证明(b)中得到的状态变量模型是能控的;说明恒速制导导弹是否稳定?讨论状态变量模型的能控性和复杂性的关系(假设用状态变量的数目来度量复杂性)。
解:该题是通过描述的恒速制导导弹的运动方程求解相应问题。
(a )运用ctrb 函数计算系统的能控性矩阵,并判断该系统不可控,详细matlab 程序和判断结果如图3和图4所示。
图3是判断该系统能控性的matlab 程序,通过求得能控性矩阵Qc ,并通过秩判据来判定该系统是否能控。
图3系统能控性的判别程序判定的结果如图4所示:图4系统的能控性矩阵和能控性判定结果通过matlab分析求得了系统的能控性矩阵Qc,同时通过秩判据判定该系统不可控。
(b)、(c)计算u到y的传递函数,并通过tf2ss函数确定新的状态变量模型,同时判断该模型是能控的。
具体程序如图5所示,判断的结果如图6示。
图5确定新状态空间并判定能控性的程序图6系统的传递函数、新的状态空间模型和能控性判定结果分析得知u到y的传递函数可通过状态空间描述的矩阵求得,同时通过tf2ss 函数确定了新的状态空间(A1,B1,C1,D1),运用函数ss求得新模型的状态方程,再通过能控型矩阵判定系统的能控性。
显然得到系统是可控的,同时还要声明通过传递函数求得空间描述和通过状态矩阵求得结果不同,从而验证了传递函数对系统的内部描述不完整。
(d)判断恒速制导导弹系统稳定性以下通过求得矩阵的特征值即传递函数的极值点来判断该系统是否稳定。
图7是求取极值点的程序,通过roots和eig函数来求取,目的进行必要的对比。
图8是通过两种途径获得的系统的极值点。
图7求取极值点的源程序图8是图7程序的运行结果:图8系统的传递函数和极值点从求得的结果中可以看出其特征值的根的实部都不是正数,从而就说明了该系统在李雅普洛夫意义下是稳定的。
图9 系统的单位阶跃响应通过程序给系统一个单位阶跃信号,从上图可以看出系统不是严格收敛的,而是发散的。
(e )状态变量模型的能控性和复杂性的关系(用状态变量的数目来度量复杂性)。
讨论状态变量模型的能控性与复杂性的关系。
很直观地讲,一个系统要能控,必须要其能控型判别矩阵的秩等于系统的阶数也即就是状态变量的数目,但是反过来,系统越复杂,状态变量的个数越多,能控型判别矩阵要求满足的秩也就越大,也即意味着越难达到要求,从而其能控性也就越不容易满足。
从而可以得出结论,即越复杂的系统越不容易达到完全可控。
3、垂直起降的飞机的线性化模型为:=Ax+B1u1+B2u2其中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=01004200.17070.0.3681.01002.00208.40024.00100.10482.04555.00188.00271.00366.0A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=05200.55446.34422.01B , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=04900.45922.71761.02B 系统的状态变量为水平速度1x (节)、垂直速度2x (节)、倾斜率3x (度/秒)和倾斜角4x (度);系统的控制输入为1u 和2u ,其中1u 用于控制垂直运动,2u 用于控制水平运动。
(a) 计算系统矩阵A 的特征值,并由此判断系统是否稳定;(b) 利用poly 函数确定A 的特征多项式,计算特征根,并与(a)中得到的特征根相比较;(c) 当只有1u 发挥作用时,系统能控吗?当只有2u 发挥作用时,结果又如何?请比较解释你的结论。
解:通过给定的垂直起降的飞机的线性化模型分析系统的属性(a)计算系统矩阵A的特征值,并根据特征值判断系统是否稳定图10矩阵A的特征值和u1、u2分别作用的能控性判别程序(b)利用poly函数确定A的特征多项式,计算特征值,并与(a)中的结果进行对比(c)当只有u1作用时,系统能控性;只有u2作用时,系统能控性。
针对以上三点问题,通过图10所示的matlab程序来判断所有问题,最终的结果在图11中显示。
求取矩阵A的特征值和u1、u2分别作用时系统可控性的运行结果:图11特征值、特征多项式和u1、u2分别作用的能控性结果其中roots1是通过eig函数求得的状态矩阵A的特征值,显然有两个特征值具有正实部,故系统不稳定;Q1是通过poly函数确定的A的特征多项式,roots2是通过roots函数求得的A矩阵的特征多项式的根,经过对比发现roots1和roots2的数值一样;只有u1或者u2作用是通过能控型矩阵Qc,用秩判据得到系统都是可控的。
dimA是通过size函数求得矩阵A的维数。
对比的当u1与u2发挥作用时所对应的能控型判别矩阵的秩都为4,即其秩等于系统的阶数也就是矩阵A的维数,从而说明在这两种情况下,系统均为能控。
4、为了探究月球背面(远离地球的一面)的奥秘,人们付出了不懈的努力。
例如,在地球-太阳-月球系统中,人们希望通信卫星能定点在不受月球遮挡的轨道上,并为此开展了广泛的论证研究工作。
图中给出了预期卫星轨道的示意图,从地球上看上去,卫星轨道的光影恰似环绕月球的外层光晕,因此这种轨道又称为光晕轨道。
轨道控制的目的是,使通信卫星在地球可见的光晕轨道上运行,从而保证通信链路的畅通,所需的通信链路包括从地球到卫星和从卫星到月球背面共两段线路。
卫星绕定点位置运动时,经过标准化和线性化的漂移运动方程为:1230001000000000100000000010007.3809000201000 2.1904020001000 3.1904000001x x u u u ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦其中,状态变量x 是卫星在三个方向上的位置和速度漂移,输入(1,2,3)i u i =分别是轨控发动机在ξ、η和ζ方向上产生的加速度。
(a) 卫星的定点位置是否稳定?(b) 如果只有1u 发挥作用,卫星是否能控? (c) 如果只有2u 发挥作用,卫星是否能控?(d) 如果只有3u 发挥作用,卫星是否能控?(e) 如果能够测得η方向的位置漂移,请确定由2u 到该位置漂移量的传递函数。
(提示:可以令观测输出为[]010000y x =)(f) 用tf2ss 函数,计算(e)中得到的传递函数的状态变量模型,并验证该轨迹子系统是能控系统;(g) 采用状态反馈2u Kx =-,设计合适的反馈控制器,使(f)中得到的系统的闭环极点为1,21s j =-±和3,410s =-。
解:在给定的卫星绕定点位置运动时的标准化和线性化的漂移运动方程,通过matlab 分析一下几点问题。
图12系统稳定性和u1、u2、u3分别作用时的能控性(1)关于卫星的定点位置的稳定性和分别只有u1或者u2或者u3作用时,卫星的能控性通过图12的程序来判断,判断结果在图13中显示。
卫星定位系统的稳定性和u1、u2、u3分别作用时的能控性判别结果如图13所示图13系统特征根和u1、u2、u3分别作用的能控性判别结果图14系统极值点分布图通过图13可以看出系统的极值点(roots1)中有大于零的点,直观的从图14的系统极值点分布图中看出在虚轴的右半平面上有一个极值点,所以系统是不稳定的;从图13中还可以发现系统在只有u1或者u2或者u3作用时,均不可控。
(2)确定由u2到漂移量的传递函数并确定传递函数所对应的状态变量模型,然后验证其为能控系统。
执行程序如图15所示,该程序用于求解传递函数和状态模型,并验证该模型的能控性。
运行的结果如图16所示。
图15传递函数、状态变量模型和能控性求解程序以上程序中求得了新系统的传递函数以及状态空间模型,并通过求取系统的能控性矩阵,根据秩判据判定系统的可控性,由if语句来选取,把最终结果显示在命令窗口。
图15程序的运行结果如图16所示:图16传递函数、状态空间描述和能控性的结果图16中显示了由u2到n方向的位置漂移量的传递函数,以及通过tf2ss函数得到该传递函数的状态变量模型,最后验证得到该模型是能控的。
(3)在给定状态空间描述的基础上采用状态反馈u2=-Kx,使得(1)中得到的模型的闭环极点为-1+j,-1-j,-10,-10.具体程序如图17所示,运行的结果如图18,图19所示。
