数据结构与算法分析C版答案
数据结构与算法分析 C++版答案

Data Structures and Algorithm 习题答案Preface ii1 Data Structures and Algorithms 12 Mathematical Preliminaries 53 Algorithm Analysis 174 Lists, Stacks, and Queues 235 Binary Trees 326 General Trees 407 Internal Sorting 468 File Processing and External Sorting 54 9Searching 5810 Indexing 6411 Graphs 6912 Lists and Arrays Revisited 7613 Advanced Tree Structures 82iii Contents14 Analysis Techniques 8815 Limits to Computation 94PrefaceContained herein are the solutions to all exercises from the textbook A Practical Introduction to Data Structures and Algorithm Analysis, 2nd edition.For most of the problems requiring an algorithm I have given actual code. Ina few cases I have presented pseudocode. Please be aware that the code presented in this manual has not actually been compiled and tested. While I believe the algorithmsto be essentially correct, there may be errors in syntax as well as semantics. Most importantly, these solutions provide a guide to the instructor as to the intendedanswer, rather than usable programs.1Data Structures and AlgorithmsInstructor’s note: Unlike the other chapters, many of the questions in this chapter are not really suitable for graded work. The questions are mainly intended to get students thinking about data structures issues.1.1This question does not have a specific right answer, provided the student keeps to the spirit of the question. Students may have trouble with the concept of “operations.”1.2This exercise asks the student to expand on their concept of an integer representation.A good answer is described by Project 4.5, where a singly-linkedlist is suggested. The most straightforward implementation stores each digitin its own list node, with digits stored in reverse order. Addition and multiplicationare implemented by what amounts to grade-school arithmetic. Foraddition, simply march down in parallel through the two lists representingthe operands, at each digit appending to a new list the appropriate partial sum and bringing forward a carry bit as necessary. For multiplication, combine the addition function with a new function that multiplies a single digitby an integer. Exponentiation can be done either by repeated multiplication (not really practical) or by the traditional Θ(log n)-time algorithm based on the binary representation of the exponent. Discovering this faster algorithm will be beyond the reach of most students, so should not be required.1.3A sample ADT for character strings might look as follows (with the normal interpretation of the function names assumed).Chap. 1 Data Structures and Algorithms// Concatenate two stringsString strcat(String s1, String s2);// Return the length of a stringint length(String s1);// Extract a substring, starting at ‘start’,// and of length ‘length’String extract(String s1, int start, int length);// Get the first characterchar first(String s1);// Compare two strings: the normal C++ strcmp function.Some// convention should be indicated for how to interpretthe// return value. In C++, this is 1for s1<s2; 0 for s1=s2;// and 1 for s1>s2.int strcmp(String s1, String s2)// Copy a stringint strcpy(String source, String destination)1.4The answer to this question is provided by the ADT for lists given in Chapter 4.1.5One’s compliment stores the binary representation of positive numbers, and stores the binary representation of a negative number with the bits inverted. Two’s compliment is the same, except that a negative number has its bits inverted and then one is added (for reasons of efficiency in hardware implementation).This representation is the physical implementation of an ADT。
数据结构与算法分析:C语言描述(原书第2版简体中文版!!!)PDF+源代码+习题答案

数据结构与算法分析:C语⾔描述(原书第2版简体中⽂版!!!)PDF+源代码+习题答案转⾃:/Linux/2014-04/99735.htm数据结构与算法分析:C语⾔描述(原书第2版中⽂版!!!) PDF+源代码+习题答案数据结构与算法分析:C语⾔描述(原书第2版)是《data structures and algorithm analysis in c》⼀书第2版的简体中译本。
原书曾被评为20世纪顶尖的30部计算机著作之⼀,作者mark allen weiss在数据结构和算法分析⽅⾯卓有建树,他的数据结构和算法分析的著作尤其畅销,并受到⼴泛好评.已被世界500余所⼤学⽤作教材。
在本书中,作者更加精炼并强化了他对算法和数据结构⽅⾯创新的处理⽅法。
通过c程序的实现,着重阐述了抽象数据类型的概念,并对算法的效率、性能和运⾏时间进⾏了分析。
数据结构与算法分析:C语⾔描述(原书第2版) PDF下载:百度⽹盘免费下载地址:(本⼈是从这⾥下载的,感谢原博主)全书特点如下: ●专⽤⼀章来讨论算法设计技巧,包括贪婪算法、分治算法、动态规划、随机化算法以及回溯算法 ●介绍了当前流⾏的论题和新的数据结构,如斐波那契堆、斜堆、⼆项队列、跳跃表和伸展树 ●安排⼀章专门讨论摊还分析,考查书中介绍的⼀些⾼级数据结构 ●新开辟⼀章讨论⾼级数据结构以及它们的实现,其中包括红⿊树、⾃顶向下伸展树。
treap树、k-d树、配对堆以及其他相关内容 ●合并了堆排序平均情况分析的⼀些新结果⽬录出版者的话专家指导委员会译者序前⾔第1章引论第2章算法分析第3章表、栈和队列第4章树第5章散列第6章优先队列(堆)第7章排序第8章不相交集ADT第9章图论算法第10章算法设计技巧第11章摊还分析第12章⾼级数据结构及其实现索引。
《数据结构、算法与应用(C++语言描述)》习题参考答案doc

第1章概论1.数据、数据元素、数据结构、数据类型的含义分别是什么?数据:对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并由计算机程序处理的符号的总称。
数据元素:数据的基本单位,在计算机程序中通常作为一个整体考虑。
数据结构:数据元素之间的关系+运算,是以数据为成员的结构,是带结构的数据元素的集合,数据元素之间存在着一种或多种特定的关系。
数据类型:数据类型是用来区分不同的数据;由于数据在存储时所需要的容量各不相同,不同的数据就必须要分配不同大小的内存空间来存储,所有就要将数据划分成不同的数据类型。
数据类型包含取值范围和基本运算等概念。
2.什么是数据的逻辑结构?什么是数据的物理结构?数据的逻辑结构与物理结构的区别和联系是什么?逻辑结构:数据的逻辑结构定义了数据结构中数据元素之间的相互逻辑关系。
数据的逻辑结构包含下面两个方面的信息:①数据元素的信息;②各数据元素之间的关系。
物理结构:也叫储存结构,是指逻辑结构的存储表示,即数据的逻辑结构在计算机存储空间中的存放形式,包括结点的数据和结点间关系的存储表示。
数据的逻辑结构和存储结构是密不可分的,一个操作算法的设计取决于所选定的逻辑结构,而算法的实现依赖于所采与的存储结构。
采用不同的存储结构,其数据处理的效率是不同的。
因此,在进行数据处理时,针对不同问题,选择合理的逻辑结构和存储结构非常重要。
3.数据结构的主要操作包括哪些?对于各种数据结构而言,他们在基本操作上是相似的,最常用的操作有:●创建:建立一个数据结构;●清除:清除一个数据结构;●插入:在数据结构中增加新的结点;●删除:把指定的结点从数据结构中删除;●访问:对数据结构中的结点进行访问;●更新:改变指定结点的值或改变指定的某些结点之间的关系;●查找:在数据结构中查找满足一定条件的结点;●排序:对数据结构中各个结点按指定数据项的值,以升序或降序重新排列。
4.什么是抽象数据类型?如何定义抽象数据类型?抽象数据类型(Abstract Data Type 简称ADT)是指一个数学模型以及定义在此数学模型上的一组操作。
《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著 课后习题答案 二

《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著课后习题答案二5Binary Trees5.1 Consider a non-full binary tree. By definition, this tree must have some internalnode X with only one non-empty child. If we modify the tree to removeX, replacing it with its child, the modified tree will have a higher fraction ofnon-empty nodes since one non-empty node and one empty node have been removed.5.2 Use as the base case the tree of one leaf node. The number of degree-2 nodesis 0, and the number of leaves is 1. Thus, the theorem holds.For the induction hypothesis, assume the theorem is true for any tree withn − 1 nodes.For the induction step, consider a tree T with n nodes. Remove from the treeany leaf node, and call the resulting tree T. By the induction hypothesis, Thas one more leaf node than it has nodes of degree 2.Now, restore the leaf node that was removed to form T. There are twopossible cases.(1) If this leaf node is the only child of its parent in T, then the number ofnodes of degree 2 has not changed, nor has the number of leaf nodes. Thus,the theorem holds.(2) If this leaf node is the child of a node in T with degree 2, then that nodehas degree 1 in T. Thus, by restoring the leaf node we are adding one newleaf node and one new node of degree 2. Thus, the theorem holds.By mathematical induction, the theorem is correct.32335.3 Base Case: For the tree of one leaf node, I = 0, E = 0, n = 0, so thetheorem holds.Induction Hypothesis: The theorem holds for the full binary tree containingn internal nodes.Induction Step: Take an arbitrary tree (call it T) of n internal nodes. Selectsome internal node x from T that has two leaves, and remove those twoleaves. Call the resulting tree T’. Tree T’ is full and has n−1 internal nodes,so by the Induction Hypothesis E = I + 2(n − 1).Call the depth of node x as d. Restore the two children of x, each at leveld+1. We have nowadded d to I since x is now once again an internal node.We have now added 2(d + 1) − d = d + 2 to E since we added the two leafnodes, but lost the contribution of x to E. Thus, if before the addition we had E = I + 2(n − 1) (by the induction hypothesis), then after the addition we have E + d = I + d + 2 + 2(n − 1) or E = I + 2n which is correct. Thus,by the principle of mathematical induction, the theorem is correct.5.4 (a) template <class Elem>void inorder(BinNode<Elem>* subroot) {if (subroot == NULL) return; // Empty, do nothingpreorder(subroot->left());visit(subroot); // Perform desired actionpreorder(subroot->right());}(b) template <class Elem>void postorder(BinNode<Elem>* subroot) {if (subroot == NULL) return; // Empty, do nothingpreorder(subroot->left());preorder(subroot->right());visit(subroot); // Perform desired action}5.5 The key is to search both subtrees, as necessary.template <class Key, class Elem, class KEComp>bool search(BinNode<Elem>* subroot, Key K);if (subroot == NULL) return false;if (subroot->value() == K) return true;if (search(subroot->right())) return true;return search(subroot->left());}34 Chap. 5 Binary Trees5.6 The key is to use a queue to store subtrees to be processed.template <class Elem>void level(BinNode<Elem>* subroot) {AQueue<BinNode<Elem>*> Q;Q.enqueue(subroot);while(!Q.isEmpty()) {BinNode<Elem>* temp;Q.dequeue(temp);if(temp != NULL) {Print(temp);Q.enqueue(temp->left());Q.enqueue(temp->right());}}}5.7 template <class Elem>int height(BinNode<Elem>* subroot) {if (subroot == NULL) return 0; // Empty subtreereturn 1 + max(height(subroot->left()),height(subroot->right()));}5.8 template <class Elem>int count(BinNode<Elem>* subroot) {if (subroot == NULL) return 0; // Empty subtreeif (subroot->isLeaf()) return 1; // A leafreturn 1 + count(subroot->left()) +count(subroot->right());}5.9 (a) Since every node stores 4 bytes of data and 12 bytes of pointers, the overhead fraction is 12/16 = 75%.(b) Since every node stores 16 bytes of data and 8 bytes of pointers, the overhead fraction is 8/24 ≈ 33%.(c) Leaf nodes store 8 bytes of data and 4 bytes of pointers; internal nodesstore 8 bytes of data and 12 bytes of pointers. Since the nodes havedifferent sizes, the total space needed for internal nodes is not the sameas for leaf nodes. Students must be careful to do the calculation correctly,taking the weighting into account. The correct formula looks asfollows, given that there are x internal nodes and x leaf nodes.4x + 12x12x + 20x= 16/32 = 50%.(d) Leaf nodes store 4 bytes of data; internal nodes store 4 bytes of pointers. The formula looks as follows, given that there are x internal nodes and35x leaf nodes:4x4x + 4x= 4/8 = 50%.5.10 If equal valued nodes were allowed to appear in either subtree, then during a search for all nodes of a given value, whenever we encounter a node of that value the search would be required to search in both directions.5.11 This tree is identical to the tree of Figure 5.20(a), except that a node with value 5 will be added as the right child of the node with value 2.5.12 This tree is identical to the tree of Figure 5.20(b), except that the value 24 replaces the value 7, and the leaf node that originally contained 24 is removed from the tree.5.13 template <class Key, class Elem, class KEComp>int smallcount(BinNode<Elem>* root, Key K);if (root == NULL) return 0;if (KEComp.gt(root->value(), K))return smallcount(root->leftchild(), K);elsereturn smallcount(root->leftchild(), K) +smallcount(root->rightchild(), K) + 1;5.14 template <class Key, class Elem, class KEComp>void printRange(BinNode<Elem>* root, int low,int high) {if (root == NULL) return;if (KEComp.lt(high, root->val()) // all to leftprintRange(root->left(), low, high);else if (KEComp.gt(low, root->val())) // all to rightprintRange(root->right(), low, high);else { // Must process both childrenprintRange(root->left(), low, high);PRINT(root->value());printRange(root->right(), low, high);}}5.15 The minimum number of elements is contained in the heap with a single node at depth h − 1, for a total of 2h−1 nodes.The maximum number of elements is contained in the heap that has completely filled up level h − 1, for a total of 2h − 1 nodes.5.16 The largest element could be at any leaf node.5.17 The corresponding array will be in the following order (equivalent to level order for the heap):12 9 10 5 4 1 8 7 3 236 Chap. 5 Binary Trees5.18 (a) The array will take on the following order:6 5 3 4 2 1The value 7 will be at the end of the array.(b) The array will take on the following order:7 4 6 3 2 1The value 5 will be at the end of the array.5.19 // Min-heap classtemplate <class Elem, class Comp> class minheap {private:Elem* Heap; // Pointer to the heap arrayint size; // Maximum size of the heapint n; // # of elements now in the heapvoid siftdown(int); // Put element in correct placepublic:minheap(Elem* h, int num, int max) // Constructor{ Heap = h; n = num; size = max; buildHeap(); }int heapsize() const // Return current size{ return n; }bool isLeaf(int pos) const // TRUE if pos a leaf{ return (pos >= n/2) && (pos < n); }int leftchild(int pos) const{ return 2*pos + 1; } // Return leftchild posint rightchild(int pos) const{ return 2*pos + 2; } // Return rightchild posint parent(int pos) const // Return parent position { return (pos-1)/2; }bool insert(const Elem&); // Insert value into heap bool removemin(Elem&); // Remove maximum value bool remove(int, Elem&); // Remove from given pos void buildHeap() // Heapify contents{ for (int i=n/2-1; i>=0; i--) siftdown(i); }};template <class Elem, class Comp>void minheap<Elem, Comp>::siftdown(int pos) { while (!isLeaf(pos)) { // Stop if pos is a leafint j = leftchild(pos); int rc = rightchild(pos);if ((rc < n) && Comp::gt(Heap[j], Heap[rc]))j = rc; // Set j to lesser child’s valueif (!Comp::gt(Heap[pos], Heap[j])) return; // Done37swap(Heap, pos, j);pos = j; // Move down}}template <class Elem, class Comp>bool minheap<Elem, Comp>::insert(const Elem& val) { if (n >= size) return false; // Heap is fullint curr = n++;Heap[curr] = val; // Start at end of heap// Now sift up until curr’s parent < currwhile ((curr!=0) &&(Comp::lt(Heap[curr], Heap[parent(curr)]))) {swap(Heap, curr, parent(curr));curr = parent(curr);}return true;}template <class Elem, class Comp>bool minheap<Elem, Comp>::removemin(Elem& it) { if (n == 0) return false; // Heap is emptyswap(Heap, 0, --n); // Swap max with last valueif (n != 0) siftdown(0); // Siftdown new root valit = Heap[n]; // Return deleted valuereturn true;}38 Chap. 5 Binary Trees// Remove value at specified positiontemplate <class Elem, class Comp>bool minheap<Elem, Comp>::remove(int pos, Elem& it) {if ((pos < 0) || (pos >= n)) return false; // Bad posswap(Heap, pos, --n); // Swap with last valuewhile ((pos != 0) &&(Comp::lt(Heap[pos], Heap[parent(pos)])))swap(Heap, pos, parent(pos)); // Push up if largesiftdown(pos); // Push down if small keyit = Heap[n];return true;}5.20 Note that this summation is similar to Equation 2.5. To solve the summation requires the shifting technique from Chapter 14, so this problem may be too advanced for many students at this time. Note that 2f(n) − f(n) = f(n),but also that:2f(n) − f(n) = n(24+48+616+ ··· +2(log n − 1)n) −n(14+28+316+ ··· +log n − 1n)logn−1i=112i− log n − 1n)= n(1 − 1n− log n − 1n)= n − log n.5.21 Here are the final codes, rather than a picture.l 00h 010i 011e 1000f 1001j 101d 11000a 1100100b 1100101c 110011g 1101k 11139The average code length is 3.234455.22 The set of sixteen characters with equal weight will create a Huffman coding tree that is complete with 16 leaf nodes all at depth 4. Thus, the average code length will be 4 bits. This is identical to the fixed length code. Thus, in this situation, the Huffman coding tree saves no space (and costs no space).5.23 (a) By the prefix property, there can be no character with codes 0, 00, or 001x where “x” stands for any binary string.(b) There must be at least one code with each form 1x, 01x, 000x where“x” could be any binary string (including the empty string).5.24 (a) Q and Z are at level 5, so any string of length n containing only Q’s and Z’s requires 5n bits.(b) O and E are at level 2, so any string of length n containing only O’s and E’s requires 2n bits.(c) The weighted average is5 ∗ 5 + 10 ∗ 4 + 35 ∗ 3 + 50 ∗ 2100bits per character5.25 This is a straightforward modification.// Build a Huffman tree from minheap h1template <class Elem>HuffTree<Elem>*buildHuff(minheap<HuffTree<Elem>*,HHCompare<Elem> >* hl) {HuffTree<Elem> *temp1, *temp2, *temp3;while(h1->heapsize() > 1) { // While at least 2 itemshl->removemin(temp1); // Pull first two treeshl->removemin(temp2); // off the heaptemp3 = new HuffTree<Elem>(temp1, temp2);hl->insert(temp3); // Put the new tree back on listdelete temp1; // Must delete the remnantsdelete temp2; // of the trees we created}return temp3;}6General Trees6.1 The following algorithm is linear on the size of the two trees. // Return TRUE iff t1 and t2 are roots of identical// general treestemplate <class Elem>bool Compare(GTNode<Elem>* t1, GTNode<Elem>* t2) { GTNode<Elem> *c1, *c2;if (((t1 == NULL) && (t2 != NULL)) ||((t2 == NULL) && (t1 != NULL)))return false;if ((t1 == NULL) && (t2 == NULL)) return true;if (t1->val() != t2->val()) return false;c1 = t1->leftmost_child();c2 = t2->leftmost_child();while(!((c1 == NULL) && (c2 == NULL))) {if (!Compare(c1, c2)) return false;if (c1 != NULL) c1 = c1->right_sibling();if (c2 != NULL) c2 = c2->right_sibling();}}6.2 The following algorithm is Θ(n2).// Return true iff t1 and t2 are roots of identical// binary treestemplate <class Elem>bool Compare2(BinNode<Elem>* t1, BinNode<Elem* t2) { BinNode<Elem> *c1, *c2;if (((t1 == NULL) && (t2 != NULL)) ||((t2 == NULL) && (t1 != NULL)))return false;if ((t1 == NULL) && (t2 == NULL)) return true;4041if (t1->val() != t2->val()) return false;if (Compare2(t1->leftchild(), t2->leftchild())if (Compare2(t1->rightchild(), t2->rightchild())return true;if (Compare2(t1->leftchild(), t2->rightchild())if (Compare2(t1->rightchild(), t2->leftchild))return true;return false;}6.3 template <class Elem> // Print, postorder traversalvoid postprint(GTNode<Elem>* subroot) {for (GTNode<Elem>* temp = subroot->leftmost_child();temp != NULL; temp = temp->right_sibling())postprint(temp);if (subroot->isLeaf()) cout << "Leaf: ";else cout << "Internal: ";cout << subroot->value() << "\n";}6.4 template <class Elem> // Count the number of nodesint gencount(GTNode<Elem>* subroot) {if (subroot == NULL) return 0int count = 1;GTNode<Elem>* temp = rt->leftmost_child();while (temp != NULL) {count += gencount(temp);temp = temp->right_sibling();}return count;}6.5 The Weighted Union Rule requires that when two parent-pointer trees are merged, the smaller one’s root becomes a child of the larger one’s root. Thus, we need to keep track of the number of nodes in a tree. To do so, modify the node array to store an integer value with each node. Initially, each node isin its own tree, so the weights for each node begin as 1. Whenever we wishto merge two trees, check the weights of the roots to determine which has more nodes. Then, add to the weight of the final root the weight of the new subtree.6.60 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15-1 0 0 0 0 0 0 6 0 0 0 9 0 0 12 06.7 The resulting tree should have the following structure:42 Chap. 6 General TreesNode 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Parent 4 4 4 4 -1 4 4 0 0 4 9 9 9 12 9 -16.8 For eight nodes labeled 0 through 7, use the following series of equivalences: (0, 1) (2, 3) (4, 5) (6, 7) (4 6) (0, 2) (4 0)This requires checking fourteen parent pointers (two for each equivalence),but none are actually followed since these are all roots. It is possible todouble the number of parent pointers checked by choosing direct children ofroots in each case.6.9 For the “lists of Children” representation, every node stores a data value and a pointer to its list of children. Further, every child (every node except the root)has a record associated with it containing an index and a pointer. Indicatingthe size of the data value as D, the size of a pointer as P and the size of anindex as I, the overhead fraction is3P + ID + 3P + I.For the “Left Child/Right Sibling” representation, every node stores three pointers and a data value, for an overhead fraction of3PD + 3P.The first linked representation of Section 6.3.3 stores with each node a datavalue and a size field (denoted by S). Each child (every node except the root)also has a pointer pointing to it. The overhead fraction is thusS + PD + S + Pmaking it quite efficient.The second linked representation of Section 6.3.3 stores with each node adata value and a pointer to the list of children. Each child (every node exceptthe root) has two additional pointers associated with it to indicate its placeon the parent’s linked list. Thus, the overhead fraction is3PD + 3P.6.10 template <class Elem>BinNode<Elem>* convert(GTNode<Elem>* genroot) {if (genroot == NULL) return NULL;43GTNode<Elem>* gtemp = genroot->leftmost_child();btemp = new BinNode(genroot->val(), convert(gtemp),convert(genroot->right_sibling()));}6.11 • Parent(r) = (r − 1)/k if 0 < r < n.• Ith child(r) = kr + I if kr +I < n.• Left sibling(r) = r − 1 if r mod k = 1 0 < r < n.• Right sibling(r) = r + 1 if r mod k = 0 and r + 1 < n.6.12 (a) The overhead fraction is4(k + 1)4 + 4(k + 1).(b) The overhead fraction is4k16 + 4k.(c) The overhead fraction is4(k + 2)16 + 4(k + 2).(d) The overhead fraction is2k2k + 4.6.13 Base Case: The number of leaves in a non-empty tree of 0 internal nodes is (K − 1)0 + 1 = 1. Thus, the theorem is correct in the base case.Induction Hypothesis: Assume that the theorem is correct for any full Karytree containing n internal nodes.Induction Step: Add K children to an arbitrary leaf node of the tree withn internal nodes. This new tree now has 1 more internal node, and K − 1more leaf nodes, so theorem still holds. Thus, the theorem is correct, by the principle of Mathematical Induction.6.14 (a) CA/BG///FEDD///H/I//(b) CA/BG/FED/H/I6.15 X|P-----| | |C Q R---| |V M44 Chap. 6 General Trees6.16 (a) // Use a helper function with a pass-by-reference// variable to indicate current position in the// node list.template <class Elem>BinNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>BinNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’/’) {curr++;return NULL;}BinNode<Elem>* temp = new BinNode(inlist[curr++], NULL, NULL);temp->left = converthelp(inlist, curr);temp->right = converthelp(inlist, curr);return temp;}(b) // Use a helper function with a pass-by-reference // variable to indicate current position in the// node list.template <class Elem>BinNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>BinNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’/’) {curr++;return NULL;}BinNode<Elem>* temp =new BinNode<Elem>(inlist[curr++], NULL, NULL);if (inlist[curr] == ’\’’) return temp;45curr++ // Eat the internal node mark.temp->left = converthelp(inlist, curr);temp->right = converthelp(inlist, curr);return temp;}(c) // Use a helper function with a pass-by-reference// variable to indicate current position in the// node list.template <class Elem>GTNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>GTNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’)’) {curr++;return NULL;}GTNode<Elem>* temp =new GTNode<Elem>(inlist[curr++]);if (curr == ’)’) {temp->insert_first(NULL);return temp;}temp->insert_first(converthelp(inlist, curr));while (curr != ’)’)temp->insert_next(converthelp(inlist, curr));curr++;return temp;}6.17 The Huffman tree is a full binary tree. To decode, we do not need to know the weights of nodes, only the letter values stored in the leaf nodes. Thus, we can use a coding much like that of Equation 6.2, storing only a bit mark for internal nodes, and a bit mark and letter value for leaf nodes.7Internal Sorting7.1 Base Case: For the list of one element, the double loop is not executed and the list is not processed. Thus, the list of one element remains unaltered and is sorted.Induction Hypothesis: Assume that the list of n elements is sorted correctlyby Insertion Sort.Induction Step: The list of n + 1 elements is processed by first sorting thetop n elements. By the induction hypothesis, this is done correctly. The final pass of the outer for loop will process the last element (call it X). This isdone by the inner for loop, which moves X up the list until a value smallerthan that of X is encountered. At this point, X has been properly insertedinto the sorted list, leaving the entire collection of n + 1 elements correctly sorted. Thus, by the principle of Mathematical Induction, the theorem is correct.7.2 void StackSort(AStack<int>& IN) {AStack<int> Temp1, Temp2;while (!IN.isEmpty()) // Transfer to another stackTemp1.push(IN.pop());IN.push(Temp1.pop()); // Put back one elementwhile (!Temp1.isEmpty()) { // Process rest of elemswhile (IN.top() > Temp1.top()) // Find elem’s placeTemp2.push(IN.pop());IN.push(Temp1.pop()); // Put the element inwhile (!Temp2.isEmpty()) // Put the rest backIN.push(Temp2.pop());}}46477.3 The revised algorithm will work correctly, and its asymptotic complexity will remain Θ(n2). However, it will do about twice as many comparisons, since it will compare adjacent elements within the portion of the list already knownto be sorted. These additional comparisons are unproductive.7.4 While binary search will find the proper place to locate the next element, it will still be necessary to move the intervening elements down one position in the array. This requires the same number of operations as a sequential search. However, it does reduce the number of element/element comparisons, and may be somewhat faster by a constant factor since shifting several elements may be more efficient than an equal number of swap operations.7.5 (a) template <class Elem, class Comp>void selsort(Elem A[], int n) { // Selection Sortfor (int i=0; i<n-1; i++) { // Select i’th recordint lowindex = i; // Remember its indexfor (int j=n-1; j>i; j--) // Find least valueif (Comp::lt(A[j], A[lowindex]))lowindex = j; // Put it in placeif (i != lowindex) // Add check for exerciseswap(A, i, lowindex);}}(b) There is unlikely to be much improvement; more likely the algorithmwill slow down. This is because the time spent checking (n times) isunlikely to save enough swaps to make up.(c) Try it and see!7.6 • Insertion Sort is stable. A swap is done only if the lower element’svalue is LESS.• Bubble Sort is stable. A swap is done only if the lower element’s valueis LESS.• Selection Sort is NOT stable. The new low value is set only if it isactually less than the previous one, but the direction of the search isfrom the bottom of the array. The algorithm will be stable if “less than”in the check becomes “less than or equal to” for selecting the low key position.• Shell Sort is NOT stable. The sublist sorts are done independently, andit is quite possible to swap an element in one sublist ahead of its equalvalue in another sublist. Once they are in the same sublist, they willretain this (incorrect) relationship.• Quick-sort is NOT stable. After selecting the pivot, it is swapped withthe last element. This action can easily put equal records out of place.48 Chap. 7 Internal Sorting• Conceptually (in particular, the linked list version) Mergesort is stable.The array implementations are NOT stable, since, given that the sublistsare stable, the merge operation will pick the element from the lower listbefore the upper list if they are equal. This is easily modified to replace“less than” with “less than or equal to.”• Heapsort is NOT stable. Elements in separate sides of the heap are processed independently, and could easily become out of relative order.• Binsort is stable. Equal values that come later are appended to the list.• Radix Sort is stable. While the processing is from bottom to top, thebins are also filled from bottom to top, preserving relative order.7.7 In the worst case, the stack can store n records. This can be cut to log n in the worst case by putting the larger partition on FIRST, followed by the smaller. Thus, the smaller will be processed first, cutting the size of the next stacked partition by at least half.7.8 Here is how I derived a permutation that will give the desired (worst-case) behavior:a b c 0 d e f g First, put 0 in pivot index (0+7/2),assign labels to the other positionsa b c g d e f 0 First swap0 b c g d e f a End of first partition pass0 b c g 1 e f a Set d = 1, it is in pivot index (1+7/2)0 b c g a e f 1 First swap0 1 c g a e f b End of partition pass0 1 c g 2 e f b Set a = 2, it is in pivot index (2+7/2)0 1 c g b e f 2 First swap0 1 2 g b e f c End of partition pass0 1 2 g b 3 f c Set e = 3, it is in pivot index (3+7/2)0 1 2 g b c f 3 First swap0 1 2 3 b c f g End of partition pass0 1 2 3 b 4 f g Set c = 4, it is in pivot index (4+7/2)0 1 2 3 b g f 4 First swap0 1 2 3 4 g f b End of partition pass0 1 2 3 4 g 5 b Set f = 5, it is in pivot index (5+7/2)0 1 2 3 4 g b 5 First swap0 1 2 3 4 5 b g End of partition pass0 1 2 3 4 5 6 g Set b = 6, it is in pivot index (6+7/2)0 1 2 3 4 5 g 6 First swap0 1 2 3 4 5 6 g End of parition pass0 1 2 3 4 5 6 7 Set g = 7.Plugging the variable assignments into the original permutation yields:492 6 4 0 13 5 77.9 (a) Each call to qsort costs Θ(i log i). Thus, the total cost isni=1i log i = Θ(n2 log n).(b) Each call to qsort costs Θ(n log n) for length(L) = n, so the totalcost is Θ(n2 log n).7.10 All that we need to do is redefine the comparison test to use strcmp. The quicksort algorithm itself need not change. This is the advantage of paramerizing the comparator.7.11 For n = 1000, n2 = 1, 000, 000, n1.5 = 1000 ∗√1000 ≈ 32, 000, andn log n ≈ 10, 000. So, the constant factor for Shellsort can be anything less than about 32 times that of Insertion Sort for Shellsort to be faster. The constant factor for Shellsort can be anything less than about 100 times thatof Insertion Sort for Quicksort to be faster.7.12 (a) The worst case occurs when all of the sublists are of size 1, except for one list of size i − k + 1. If this happens on each call to SPLITk, thenthe total cost of the algorithm will be Θ(n2).(b) In the average case, the lists are split into k sublists of roughly equal length. Thus, the total cost is Θ(n logk n).7.13 (This question comes from Rawlins.) Assume that all nuts and all bolts havea partner. We use two arrays N[1..n] and B[1..n] to represent nuts and bolts. Algorithm 1Using merge-sort to solve this problem.First, split the input into n/2 sub-lists such that each sub-list contains twonuts and two bolts. Then sort each sub-lists. We could well come up with apair of nuts that are both smaller than either of a pair of bolts. In that case,all you can know is something like:N1, N2。
数据结构与算法分析c语言描述中文答案

数据结构与算法分析c语言描述中文答案一、引言数据结构与算法是计算机科学中非常重要的基础知识,它们为解决实际问题提供了有效的工具和方法。
本文将以C语言描述中文的方式,介绍数据结构与算法分析的基本概念和原理。
二、数据结构1. 数组数组是在内存中连续存储相同类型的数据元素的集合。
在C语言中,可以通过定义数组类型、声明数组变量以及对数组进行操作来实现。
2. 链表链表是一种动态数据结构,它由一系列的节点组成,每个节点包含了数据和一个指向下一个节点的指针。
链表可以是单链表、双链表或循环链表等多种形式。
3. 栈栈是一种遵循“先进后出”(Last-In-First-Out,LIFO)原则的数据结构。
在C语言中,可以通过数组或链表实现栈,同时实现入栈和出栈操作。
4. 队列队列是一种遵循“先进先出”(First-In-First-Out,FIFO)原则的数据结构。
在C语言中,可以通过数组或链表实现队列,同时实现入队和出队操作。
5. 树树是一种非线性的数据结构,它由节点和边组成。
每个节点可以有多个子节点,其中一个节点被称为根节点。
在C语言中,可以通过定义结构体和指针的方式来实现树的表示和操作。
6. 图图是由顶点和边组成的数据结构,它可以用来表示各种实际问题,如社交网络、路网等。
在C语言中,可以通过邻接矩阵或邻接表的方式来表示图,并实现图的遍历和查找等操作。
三、算法分析1. 时间复杂度时间复杂度是用来衡量算法的执行时间随着问题规模增长的趋势。
常见的时间复杂度有O(1)、O(log n)、O(n)、O(n^2)等,其中O表示“量级”。
2. 空间复杂度空间复杂度是用来衡量算法的执行所需的额外内存空间随着问题规模增长的趋势。
常见的空间复杂度有O(1)、O(n)等。
3. 排序算法排序算法是对一组数据按照特定规则进行排序的算法。
常见的排序算法有冒泡排序、插入排序、选择排序、快速排序、归并排序等,它们的时间复杂度和空间复杂度各不相同。
数据结构与算法分析课后习题答案

数据结构与算法分析课后习题答案【篇一:《数据结构与算法》课后习题答案】>2.3.2 判断题2.顺序存储的线性表可以按序号随机存取。
(√)4.线性表中的元素可以是各种各样的,但同一线性表中的数据元素具有相同的特性,因此属于同一数据对象。
(√)6.在线性表的链式存储结构中,逻辑上相邻的元素在物理位置上不一定相邻。
(√)8.在线性表的顺序存储结构中,插入和删除时移动元素的个数与该元素的位置有关。
(√)9.线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。
(√)2.3.3 算法设计题1.设线性表存放在向量a[arrsize]的前elenum个分量中,且递增有序。
试写一算法,将x 插入到线性表的适当位置上,以保持线性表的有序性,并且分析算法的时间复杂度。
【提示】直接用题目中所给定的数据结构(顺序存储的思想是用物理上的相邻表示逻辑上的相邻,不一定将向量和表示线性表长度的变量封装成一个结构体),因为是顺序存储,分配的存储空间是固定大小的,所以首先确定是否还有存储空间,若有,则根据原线性表中元素的有序性,来确定插入元素的插入位置,后面的元素为它让出位置,(也可以从高下标端开始一边比较,一边移位)然后插入x ,最后修改表示表长的变量。
int insert (datatype a[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满,无法插入*/else {i=*elenum;while (i=0 a[i]x)/*边找位置边移动*/{a[i+1]=a[i];i--;}a[i+1]=x;/*找到的位置是插入位的下一位*/ (*elenum)++;return 1;/*插入成功*/}}时间复杂度为o(n)。
2.已知一顺序表a,其元素值非递减有序排列,编写一个算法删除顺序表中多余的值相同的元素。
数据结构C语言版习题参考答案

附录习题参考答案习题1参考答案1.1.选择题(1). A. (2). A. (3). A. (4). B.,C. (5). A. (6). A. (7). C. (8). A. (9). B. (10.)A.1.2.填空题(1). 数据关系(2). 逻辑结构物理结构(3). 线性数据结构树型结构图结构(4). 顺序存储链式存储索引存储散列表(Hash)存储(5). 变量的取值范围操作的类别(6). 数据元素间的逻辑关系数据元素存储方式或者数据元素的物理关系(7). 关系网状结构树结构(8). 空间复杂度和时间复杂度(9). 空间时间(10). Ο(n)1.3 名词解释如下:数据:数据是信息的载体,是计算机程序加工和处理的对象,包括数值数据和非数值数据。
数据项:数据项指不可分割的、具有独立意义的最小数据单位,数据项有时也称为字段或域。
数据元素:数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理,一个数据元素可由若干个数据项组成。
数据逻辑结构:数据的逻辑结构就是指数据元素间的关系。
数据存储结构:数据的物理结构表示数据元素的存储方式或者数据元素的物理关系。
数据类型:是指变量的取值范围和所能够进行的操作的总和。
算法:是对特定问题求解步骤的一种描述,是指令的有限序列。
1.4 语句的时间复杂度为:(1) Ο(n2)(2) Ο(n2)(3) Ο(n2)(4) Ο(n-1)(5) Ο(n3)1.5 参考程序:main(){int X,Y,Z;scanf(“%d, %d, %d”,&X,&Y,Z);if (X>=Y)if(X>=Z)if (Y>=Z){ printf(“%d, %d, %d”,X,Y,Z);}else{ printf(“%d, %d, %d”,X,Z,Y);}else{ printf(“%d, %d, %d”,Z,X,Y);}elseif(Z>=X)if (Y>=Z){ printf(“%d, %d, %d”,Y,Z,X);}else{ printf(“%d, %d, %d”,Z,Y,X);}else{ printf(“%d, %d, %d”,Y,X,Z);}}1.6 参考程序:main(){int i,n;float x,a[],p;printf(“\nn=”);scanf(“%f”,&n);printf(“\nx=”);scanf(“%f”,&x);for(i=0;i<=n;i++)scanf(“%f ”,&a[i]);p=a[0];for(i=1;i<=n;i++){ p=p+a[i]*x;x=x*x;}printf(“%f”,p)’}习题2参考答案2.1选择题(1). C. (2). B. (3). B. (4). B. 5. D. 6. B. 7. B. 8. A. 9. A. 10. D.2.2.填空题(1). 有限序列(2). 顺序存储和链式存储(3). O(n) O(n)(4). n-i+1 n-i(5). 链式(6). 数据指针(7). 前驱后继(8). Ο(1) Ο(n)(9). s->next=p->next; p->next=s ;(10). s->next2.3. 解题思路:将顺序表A中的元素输入数组a,若数组a中元素个数为n,将下标为0,1,2,…,(n-1)/2的元素依次与下标为n,n-1,…, (n-1)/2的元素交换,输出数组a的元素。
算法与数据结构C语言习题参考答案1-5章

绪论1.将下列复杂度由小到大重新排序:A.2n B.n! C.n5D.10 000 E.n*log2 (n)【答】10 000< n*log2(n)< n5< 2n < n!2.将下列复杂度由小到大重新排序:A.n*log2(n) B.n + n2 + n3C.24D.n0.5【答】24< n0.5< n*log2 (n) < n + n2 + n33.用大“O”表示法描述下列复杂度:A.5n5/2 + n2/5 B.6*log2(n) + 9nC.3n4+ n* log2(n) D.5n2 + n3/2【答】A:O (n5/2) B:O (n) C:O (n4) D:O (n2)4.按照增长率从低到高的顺序排列以下表达式:4n2 , log3n, 3n , 20n , 2000 , log2n , n2/3。
又n!应排在第几位?【答】按照增长率从低到高依次为:2000, log3n, log2n , n2/3 , 20n , 4n2 , 3n。
n!的增长率比它们中的每一个都要大,应排在最后一位。
5. 计算下列程序片断的时间代价:int i=1;while(i<=n){printf(“i=%d\n”,i);i=i+1;}【答】循环控制变量i从1增加到n,循环体执行n次,第一句i的初始化执行次数为1,第二句执行n次,循环体中第一句printf执行n次,第二句i从1循环到n,共执行n次。
所以该程序段总的时间代价为:T(n) = 1 + n + 2n = 3n+ 1 = O(n)6. 计算下列程序片断的时间代价:int i=1;while(i<=n){int j=1;while(j<=n){int k=1;while(k<=n){printf(“i=%d,j=%d,k=%d\n”,I,j,k);k=k+1;}j=j+1;}i=i+1;}【答】循环控制变量i从1增加到n,最外层循环体执行n次,循环控制变量j从1增加到n,中间层循环体执行n次,循环控制变量k从1增加到n,最内层循环体执行n次,所以该程序段总的时间代价为:T(n) = 1 + n + n{1 + n + n[1 + n + 2n +1] +1 +1}+ 1= 3n3 + 3n2 +4n +2= O(n3)2. 线性表1.试写一个插入算法int insertPost_seq(palist, p, x ),在palist所指顺序表中,下标为p的元素之后,插入一个值为x的元素,返回插入成功与否的标志。
算法与数据结构C语言版课后习题参考答案(机械工业出版社)1绪论习题详细答案

第1章概论习题参考答案一、基础知识题1.简述下列概念数据,数据元素,数据类型,数据结构,逻辑结构,存储结构,算法。
【解答】数据是信息的载体,是描述客观事物的数、字符,以及所有能输入到计算机中并被计算机程序识别和处理的符号的集合。
数据元素是数据的基本单位。
在不同的条件下,数据元素又可称为元素、结点、顶点、记录等。
数据类型是对数据的取值范围、数据元素之间的结构以及允许施加操作的一种总体描述。
每一种计算机程序设计语言都定义有自己的数据类型。
“数据结构”这一术语有两种含义,一是作为一门课程的名称;二是作为一个科学的概念。
作为科学概念,目前尚无公认定义,一般认为,讨论数据结构要包括三个方面,一是数据的逻辑结构,二是数据的存储结构,三是对数据进行的操作(运算)。
而数据类型是值的集合和操作的集合,可以看作是已实现了的数据结构,后者是前者的一种简化情况。
数据的逻辑结构反映数据元素之间的逻辑关系(即数据元素之间的关联方式或“邻接关系”),数据的存储结构是数据结构在计算机中的表示,包括数据元素的表示及其关系的表示。
数据的运算是对数据定义的一组操作,运算是定义在逻辑结构上的,和存储结构无关,而运算的实现则依赖于存储结构。
数据结构在计算机中的表示称为物理结构,又称存储结构。
是逻辑结构在存储器中的映像,包括数据元素的表示和关系的表示。
逻辑结构与计算机无关。
算法是对特定问题求解步骤的一种描述,是指令的有限序列。
其中每一条指令表示一个或多个操作。
一个算法应该具有下列特性:有穷性、确定性、可行性、输入和输出。
2.数据的逻辑结构分哪几种,为什么说逻辑结构是数据组织的主要方面?【解答】数据的逻辑结构分为线性结构和非线性结构。
(也可以分为集合、线性结构、树形结构和图形即网状结构)。
逻辑结构是数据组织的某种“本质性”的东西:(1)逻辑结构与数据元素本身的形式、内容无关。
(2)逻辑结构与数据元素的相对位置无关。
(3)逻辑结构与所含数据元素的个数无关。
算法与数据结构C语言版课后习题答案(机械工业出版社)第3,4章习题参考答案

算法与数据结构C语⾔版课后习题答案(机械⼯业出版社)第3,4章习题参考答案第3章栈和队列⼀、基础知识题3.1有五个数依次进栈:1,2,3,4,5。
在各种出栈的序列中,以3,4先出的序列有哪⼏个。
(3在4之前出栈)。
【解答】34215 ,34251,345213.2铁路进⾏列车调度时,常把站台设计成栈式结构,若进站的六辆列车顺序为:1,2,3,4,5,6,那么是否能够得到435612, 325641, 154623和135426的出站序列,如果不能,说明为什么不能;如果能,说明如何得到(即写出"进栈"或"出栈"的序列)。
【解答】输⼊序列为123456,不能得出435612和154623。
不能得到435612的理由是,输出序列最后两元素是12,前⾯4个元素(4356)得到后,栈中元素剩12,且2在栈顶,不可能让栈底元素1在栈顶元素2之前出栈。
不能得到154623的理由类似,当栈中元素只剩23,且3在栈顶,2不可能先于3出栈。
得到325641的过程如下:1 2 3顺序⼊栈,32出栈,得到部分输出序列32;然后45⼊栈,5出栈,部分输出序列变为325;接着6⼊栈并退栈,部分输出序列变为3256;最后41退栈,得最终结果325641。
得到135426的过程如下:1⼊栈并出栈,得到部分输出序列1;然后2和3⼊栈,3出栈,部分输出序列变为13;接着4和5⼊栈,5,4和2依次出栈,部分输出序列变为13542;最后6⼊栈并退栈,得最终结果135426。
3.3若⽤⼀个⼤⼩为6的数组来实现循环队列,且当前rear和front的值分别为0和3,当从队列中删除⼀个元素,再加⼊两个元素后,rear和front的值分别为多少?【解答】2和43.4设栈S和队列Q的初始状态为空,元素e1,e2,e3,e4,e5和e6依次通过栈S,⼀个元素出栈后即进队列Q,若6个元素出队的序列是e3,e5,e4,e6,e2,e1,则栈S的容量⾄少应该是多少?【解答】43.5循环队列的优点是什么,如何判断“空”和“满”。
数据结构与算法分析c第三版答案

数据结构与算法分析c第三版答案【篇一:数据结构第三章习题答案】txt>#include iostream#include stringusing namespace std;bool huiwen(string s){int n=s.length();int i,j;i= 0;j=n-1;while(ij s[i]==s[j]){ i++;j--;}if(i=j) return true;else return false;}int main(){string s1;cins1;couthuiwen(s1);return 0;}=============(2)设从键盘输入一整数的序列:a1, a2, a3,…,an,试编写算法实现:用栈结构存储输入的整数,当ai≠-1时,将ai进栈;当ai=-1时,输出栈顶整数并出栈。
算法应对异常情况(入栈满等)给出相应的信息。
#include iostreamusing namespace std;#define overflow -2#define ok 1#define error 0typedef int selemtype;typedef int status;typedef struct{selemtype a[5];int top;} sqstack;status initstack(sqstack s){s.top=0;return ok;}status push(sqstack s,selemtype e){if (s.top4){coutoverlow!endl;return error;}else s.a[s.top++]=e;return ok;}status pop(sqstack s,selemtype e){if (s.top==0) {coutunderflowendl; return error;}e=s.a[--s.top];couteendl;return ok;}int main(){sqstack s;initstack(s);int n,x,e1;coutn=?endl;cinn;for(int i=0;in;i++){ cinx;if(x!=-1 )push(s,x);else pop(s,e1); }return 0;}============(3)假设以i和o分别表示入栈和出栈操作。
数据结构与算法分析c语言描述中文答案

数据结构与算法分析c语言描述中文答案【篇一:数据结构(c语言版)课后习题答案完整版】选择题:ccbdca6.试分析下面各程序段的时间复杂度。
(1)o(1)(2)o(m*n)(3)o(n2)(4)o(log3n)(5)因为x++共执行了n-1+n-2+??+1= n(n-1)/2,所以执行时间为o(n2)(6)o(n)第2章线性表1.选择题babadbcabdcddac 2.算法设计题(6)设计一个算法,通过一趟遍历在单链表中确定值最大的结点。
elemtype max (linklist l ){if(l-next==null) return null;pmax=l-next; //假定第一个结点中数据具有最大值 p=l-next-next; while(p != null ){//如果下一个结点存在if(p-data pmax-data) pmax=p;p=p-next; }return pmax-data;(7)设计一个算法,通过遍历一趟,将链表中所有结点的链接方向逆转,仍利用原表的存储空间。
void inverse(linklist l) { // 逆置带头结点的单链表 l p=l-next; l-next=null; while ( p) {q=p-next; // q指向*p的后继p-next=l-next;l-next=p; // *p插入在头结点之后p = q; }}(10)已知长度为n的线性表a采用顺序存储结构,请写一时间复杂度为o(n)、空间复杂度为o(1)的算法,该算法删除线性表中所有值为item的数据元素。
[题目分析] 在顺序存储的线性表上删除元素,通常要涉及到一系列元素的移动(删第i个元素,第i+1至第n个元素要依次前移)。
本题要求删除线性表中所有值为item的数据元素,并未要求元素间的相对位置不变。
因此可以考虑设头尾两个指针(i=1,j=n),从两端向中间移动,凡遇到值item的数据元素时,直接将右端元素左移至值为item的数据元素位置。
数据结构与算法(C语言篇)第2章 习题答案[2页]
![数据结构与算法(C语言篇)第2章 习题答案[2页]](https://img.taocdn.com/s3/m/d29cd81a82c4bb4cf7ec4afe04a1b0717fd5b30a.png)
习题答案1.填空题(1)线性(2)顺序表(3)单链表(4)数据域、指针域(5)头结点(6)一定(7)不一定2.思考题(1)线性表采用顺序存储通常被称为顺序表。
顺序表指的是集合中数据元素之间的逻辑结构为线性结构,并且数据元素按照逻辑顺序依次存放在地址连续的存储单元中。
一般情况下,线性表中的所有数据结点的类型是相同的。
在C语言中,通常使用一维数组和结构体来表示顺序表。
(2)线性表采用链式存储通常被称为单链表。
单链表指的是集合中数据元素之间的逻辑结构为线性结构,但是数据元素所在的存储单元在内存地址上是不连续的。
单链表中的结点都是由两部分组成,一部分为数据域(data);另一部分为指针域(next)。
简单地说,data域用来存放结点的数据,而next域存放的是一个指针,该指针保存的是下一个结点所在的内存地址,或者说该指针指向下一个结点。
(3)在单链表中,如果需要查找某一个结点的后继时,直接通过指针移动到下一个结点即可。
但是要查找某一结点的前驱时,则需要从结点头开始。
为了提高数据操作的效率,引入双向循环链表。
双向循环链表中结点的结构与单链表不同,每一个结点都有一个指向前一个结点的指针和一个指向后一个结点的指针。
4.编程题(1)int seqlist_insert(seqlist_t *l, int value){if(seqlist_full(l)){ //判断是否为满printf("seqlist full\n");return -1;}l->last++; //数组下标加1,表示要插入数据l->data[l->last] = value; //将需要插入的数据赋值到数组中,表示插入数据 return 0;}(2)int linklist_head_insert(linklist_t *h, datatype_t value){linklist_t *temp;//为新插入的数据结点申请空间temp = (linklist_t *)malloc(sizeof(linklist_t));temp->data = value; //为新插入结点的数据域赋值数据temp->next = h->next; //将头结点指针指向的下一个结点的地址赋值给新结点的指针 h->next = temp; //将头结点指针指向新的结点return 0;}(3)void dlinklist_insert(dlinklist_t *dl, datatype_t value){//使用malloc函数为新插入的结点申请空间dlinklist_t *temp = (dlinklist_t *)malloc(sizeof(dlinklist_t));//为新插入的结点赋值temp->data = value;//获取第一个有数据的结点的地址,地址为dl->next//如果此时只有一个头结点,则假设存在有数据的结点dlinklist_t *pnext = dl->next;//将头结点与新插入的结点建立关系dl->next = temp;temp->prior = dl;//将头结点的下一个结点与新插入的结点建立关系temp->next = pnext;pnext->prior = temp;return ;}(4)使用递归的方法,函数调用自己本身,形成一个函数的复用//参数为指向头结点的指针int show_reverse_linklist(linklist_t *h){if(h->next == NULL){printf(“%d ”, h->data);return 0;}show_reverse_linklist(h->next);printf(“%d ”, h->data);return 0;}。
算法与数据结构C语言习题参考答案6-9章

1. 现在有一个已排序的字典,请改写二分法检索算法,使之当排序码key在字典中重复出现时算法能找出第一个key出现的元素下标(用*position来保存)。
保持算法时间代价为O(log n)。
【答】思路一般的二分法检索算法只要找出关键码key在字典中的一个下标。
在比较的过程中,一旦发现相等,记录下当前下标mid就符合要求。
程序如下:数据结构字典采用6.1.4节中的顺序表示法。
typedef int KeyType;typedef int DataType;二分法检索算法int binarySearch(SeqDictionary * pdic, KeyType key, int * position) {int low, mid, high;low = 0;high = pdic->n - 1;while (low <= high){mid = (low + high) / 2;if (pdic->element[mid].key = = key) {*position = mid;return TRUE;}elseif (pdic->element[mid].key > key)high = mid - 1;elselow = mid + 1;}*position = low;return FALSE;}改写后的算法想要找出关键码key在字典中第一次出现的下标。
在比较中,如果遇到相等(key与pdic->element[mid].key相等),则需要分情形讨论。
(1)如果当前下标mid等于0,或者key与pdic->element[mid-1].key不等,那么mid 一定是key第一次出现的下标,返回mid即可。
(2)如果情形(1)不成立,那么mid一定大于等于key第一次出现的下标,需要在low 和mid-1之间继续进行搜索,找出key第一次出现的下标。
数据结构c语言版课后习题答案完整版

数据结构c语言版课后习题答案完整版Document serial number【KKGB-LBS98YT-BS8CB-BSUT-BST108】第1章绪论5.选择题:CCBDCA6.试分析下面各程序段的时间复杂度。
(1)O(1)(2)O(m*n)(3)O(n2)n)(4)O(log3(5)因为x++共执行了n-1+n-2+……+1= n(n-1)/2,所以执行时间为O(n2)(6)O(n)第2章线性表1.选择题babadbcabdcddac2.算法设计题(6)设计一个算法,通过一趟遍历在单链表中确定值最大的结点。
ElemType Max (LinkList L ){if(L->next==NULL) return NULL;pmax=L->next; 法设计题(2)回文是指正读反读均相同的字符序列,如“abba”和“abdba”均是回文,但“good”不是回文。
试写一个算法判定给定的字符向量是否为回文。
(提示:将一半字符入栈)根据提示,算法可设计为:合应用题(1)已知模式串t=‘abcaabbabcab’写出用KMP法求得的每个字符对应的next和nextval函数值。
-1到9,列下标从1到11,从首地址S开始连续存放主存储器中,主存储器字长为16位。
求:①存放该数组所需多少单元②存放数组第4列所有元素至少需多少单元③数组按行存放时,元素A[7,4]的起始地址是多少④ 数组按列存放时,元素A[4,7]的起始地址是多少每个元素32个二进制位,主存字长16位,故每个元素占2个字长,行下标可平移至1到11。
(1)242 (2)22 (3)s+182 (4)s+142(4)请将香蕉banana 用工具 H( )—Head( ),T( )—Tail( )从L 中取出。
L=(apple,(orange,(strawberry,(banana)),peach),pear)H (H (T (H (T (H (T (L )))))))(5)写一个算法统计在输入字符串中各个不同字符出现的频度并将结果存入文件(字符串中的合法字符为A-Z 这26个字母和0-9这10个数字)。
数据结构(C语言版)(第2版)课后习题答案

精品文档考试教学资料施工组织设计方案数据结构(C语言版)(第2版)课后习题答案李冬梅2015.3目录第1章绪论 (1)第2章线性表 (5)第3章栈和队列 (13)第4章串、数组和广义表 (26)第5章树和二叉树 (33)第6章图 (42)第7章查找 (54)第8章排序 (65)第1章绪论1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储结构、抽象数据类型。
答案:数据:是客观事物的符号表示,指所有能输入到计算机中并被计算机程序处理的符号的总称。
如数学计算中用到的整数和实数,文本编辑所用到的字符串,多媒体程序处理的图形、图像、声音、动画等通过特殊编码定义后的数据。
数据元素:是数据的基本单位,在计算机中通常作为一个整体进行考虑和处理。
在有些情况下,数据元素也称为元素、结点、记录等。
数据元素用于完整地描述一个对象,如一个学生记录,树中棋盘的一个格局(状态)、图中的一个顶点等。
数据项:是组成数据元素的、有独立含义的、不可分割的最小单位。
例如,学生基本信息表中的学号、姓名、性别等都是数据项。
数据对象:是性质相同的数据元素的集合,是数据的一个子集。
例如:整数数据对象是集合N={0,±1,±2,…},字母字符数据对象是集合C={‘A’,‘B’,…,‘Z’,‘a’,‘b’,…,‘z’},学生基本信息表也可是一个数据对象。
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合。
换句话说,数据结构是带“结构”的数据元素的集合,“结构”就是指数据元素之间存在的关系。
逻辑结构:从逻辑关系上描述数据,它与数据的存储无关,是独立于计算机的。
因此,数据的逻辑结构可以看作是从具体问题抽象出来的数学模型。
存储结构:数据对象在计算机中的存储表示,也称为物理结构。
抽象数据类型:由用户定义的,表示应用问题的数学模型,以及定义在这个模型上的一组操作的总称。
具体包括三部分:数据对象、数据对象上关系的集合和对数据对象的基本操作的集合。
数据结构c语言版试题大全(含答案)
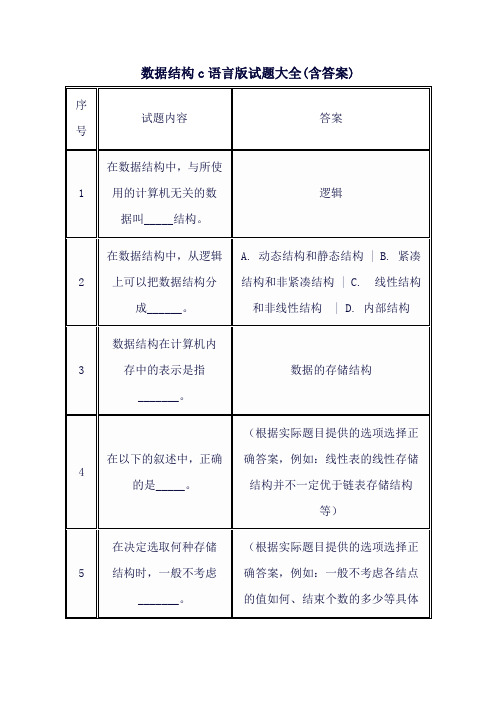
数据元素之间的关系
7
下面说法错误的是_______。
(1)算法原地工作的含义是指不需要任何额外的辅助空间 (2)在相同的规模n下,复杂度O(n)的算法在时间上总是优于复杂度O(2n)的算法。(3)所谓时间复杂度是指最坏情况下,估计算法执行时间的一个上界。(4)同一个算法,实现语句的级别越高,执行效率越低(此选项错误,因为执行效率与实现语句的级别不一定直接相关)
push和pop
37
在C语言中,使用____关键字可以为结构体成员创建一个别名。
typedef
38
二叉搜索树的特点是,对于任意节点,其左子树中的所有节点的值都____该节点的值,而其右子树中的所有节点的值都____该节点的值。
小于,大于
39
图的遍历算法主要有____和____两种。
深度优先搜索,广度优先搜索
15
数据采用链式存储结构时,要求______。
结点的最后一个数据域是指针类型
16
数据的运算______。
效率与采用何种存储结构有关
17
下列说法中,不正确的是______。
数据项可由若干个数据元素构成
18
不是算法的基本特性______。
长度有限
19
计算机中算法指的是解决某一问题的有限运算序列,它必须具备输入、输出、______。
数据的存储结构
4
在以下的叙述中,正确的是_____。
(根据实际题目提供的选项选择正确答案,例如:线性表的线性存储结构并不一定优于链表存储结构等)
5
在决定选取何种存储结构时,一般不考虑_______。
(根据实际题目提供的选项选择正确答案,例如:一般不考虑各结点的值如何、结束个数的多少等具体数据特性)
数据结构(C语言版)习题及答案第二章

数据结构(C语⾔版)习题及答案第⼆章习题2.1选择题1、线性表的顺序存储结构是⼀种(A)的存储结构,线性表的链式存储结构是⼀种(B)的存储结构。
A、随机存取B、顺序存取C、索引存取D、散列存取2、对于⼀个线性,既要求能够进⾏较快的插⼊和删除,⼜要求存储结构能够反映数据元素之间的逻辑关系,则应该选择(B)。
A、顺序存储⽅式B、链式存储⽅式C、散列存储⽅式D、索引存储⽅式3、已知,L是⼀个不带头结点的单链表,p指向其中的⼀个结点,选择合适的语句实现在p结点的后⾯插⼊s结点的操作(B)。
A、p->next=s ; s->next=p->next ;B、s->next=p->next ; p->next=s ;C、p->next=s ; s->next=p ;D、s->next=p ; p->next=s ;4、单链表中各结点之间的地址( C D)。
A、必须连续B、部分地址必须连续C、不⼀定连续D、连续与否都可以5、在⼀个长度为n的顺序表中向第i个元素(0A、n-iB、n-i+1C、n-i-1D、i2.2填空题1、顺序存储的长度为n的线性表,在任何位置上插⼊和删除操作的时间复杂度基本上都⼀样。
插⼊⼀个元素⼤约移动表中的(n/2)个元素,删除⼀个元素时⼤约移动表中的((n-1)/2)个元素。
2、在线性表的顺序存储⽅式中,元素之间的逻辑关系是通过(物理顺序)来体现的;在链式存储⽅式,元素之间的逻辑关系是通过(指针)体现的。
3、对于⼀个长度为n的单链表,在已知的p结点后⾯插⼊⼀个新结点的时间复杂度为(o(1)),在p结点之前插⼊⼀个新结点的时间复杂度为(o(n)),在给定值为e的结点之后插⼊⼀个新结点的时间复杂度为(o(n))。
4、在双向链表中,每个结点包含两个指针域,⼀个指向(前驱)结点,另⼀个指向(后继)结点。
5、对于循环链表来讲,逐个访问各个结点的结束判断条件是(设P为指向结点的指针,L为链表的头指针,则p->next= =L)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据结构与算法分析C版答案Modified by JEEP on December 26th, 2020.Data Structures and Algorithm 习题答案Preface ii1 Data Structures and Algorithms 12 Mathematical Preliminaries 53 Algorithm Analysis 174 Lists, Stacks, and Queues 235 Binary Trees 326 General Trees 407 Internal Sorting 468 File Processing and External Sorting 549Searching 5810 Indexing 6411 Graphs 6912 Lists and Arrays Revisited 7613 Advanced Tree Structures 82iii Contents14 Analysis Techniques 8815 Limits to Computation 94PrefaceContained herein are the solutions to all exercises from the textbook A PracticalIntroduction to Data Structures and Algorithm Analysis, 2nd edition. For most of the problems requiring an algorithm I have given actual code. Ina few cases I have presented pseudocode. Please be aware that the code presentedin this manual has not actually been compiled and tested. While I believe the algorithmsto be essentially correct, there may be errors in syntax as well as semantics.Most importantly, these solutions provide a guide to the instructor as to the intendedanswer, rather than usable programs.1Data Structures and AlgorithmsInstructor’s note: Unlike the other chapters, many of the questions in this chapterare not really suitable for graded work. The questions are mainly intended to getstudents thinking about data structures issues.This question does not have a specific right answer, provided the studentkeeps to the spirit of the question. Students may have trouble with the conceptof “operations.”This exercise asks the student to expand on their concept of aninteger representation.A good answer is described by Project , where a singly-linkedlist is suggested. The most straightforward implementation storeseach digitin its own list node, with digits stored in reverse order. Addition and multiplicationare implemented by what amounts to grade-school arithmetic. For addition, simply march down in parallel through the two lists representingthe operands, at each digit appending to a new list the appropriate partialsum and bringing forward a carry bit as necessary. For multiplication, combinethe addition function with a new function that multiplies a single digitby an integer. Exponentiation can be done either by repeated multiplication(not really practical) or by the traditional Θ(log n)-time algorithm based onthe binary representation of the exponent. Discovering this faster algorithmwill be beyond the reach of most students, so should not be required.A sample ADT for character strings might look as follows (with the normalinterpretation of the function names assumed).Chap. 1 Data Structures and AlgorithmsSomeIn C++, this is 1for s1<s2; 0 for s1=s2;int strcmp(String s1, String s2)One’s compliment stores the binary representation of positive numbers, andstores the binary representation of a negative number with the bits inverted.Two’s compliment is the same, except that a negative number has its bitsinverted and then one is added (for reasons of efficiency in hardware implementation).This representation is the physical implementation of an ADTdefined by the normal arithmetic operations, declarations, and other supportgiven by the programming language for integers.An ADT for two-dimensional arrays might look as follows.Matrix add(Matrix M1, Matrix M2);Matrix multiply(Matrix M1, Matrix M2);Matrix transpose(Matrix M1);void setvalue(Matrix M1, int row, int col, int val);int getvalue(Matrix M1, int row, int col);List getrow(Matrix M1, int row);One implementation for the sparse matrix is described in Section Another implementationis a hash table whose search key is a concatenation of the matrix coordinates.Every problem certainly does not have an algorithm. As discussed in Chapter 15,there are a number of reasons why this might be the case. Someprobl ems don’thave a sufficiently clear definition. Some problems, such as the halting problem,are non-computable. For some problems, such as one typically studied by artificialintelligence researchers, we simply don’t know a solution.We must assume t hat by “algorithm” we mean something composed of steps areof a nature that they can be performed by a computer. If so, than any algorithmcan be expressed in C++. In particular, if an algorithm can be expressed in anyother computer programming language, then it can be expressed in C++, since all(sufficiently general) computer programming languages compute the same set offunctions.The primitive operations are (1) adding new words to the dictionary and (2) searchingthe dictionary for a given word. Typically, dictionary access involves some sortof pre-processing of the word to arrive at the “root” of the word.A twenty page document (single spaced) is likely to contain about 20,000 words. Auser may be willing to wait a few seconds between in dividual “hits” of mis-spelledwords, or perhaps up to a minute for the whole document to be processed. Thismeans that a check for an individual word can take about 10-20 ms. Users willtypically insert individual words into the dictionary interactively, so this process cantake a couple of seconds. Thus, search must be much more efficient than insertion.The user should be able to find a city based on a variety of attributes (name, location,perhaps characteristics such as population size). The user should also be able to insertand delete cities. These are the fundamental operations of any database system:search, insertion and deletion.A reasonable database has a time constraint that will satisfy the patience of a typicaluser. For an insert, delete, or exact match query, a few seconds is satisfactory. If thedatabase is meant to support range queries and mass deletions, the entire operationmay be allowed to take longer, perhaps on the order of a minute. However, the timespent to process individual cities within the range must be appropriately reduced. Inpractice, the data representation will need to be such that it accommodates efficientprocessing to meet these time constraints. In particular, it may be necessary to supportoperations that process range queries efficiently by processing all cities in therange as a batch, rather than as a series of operations on individual cities.Students at this level are likely already familiar with binary search. Thus, theyshould typically respond with sequential search and binary search. Binary searchshould be described as better since it typically needs to make fewer comparisons(and thus is likely to be much faster).The answer to this question is discussed in Chapter 8. Typical measures of costwill be number of comparisons and number of swaps. Tests should include runningtimings on sorted, reverse sorted, and random lists of various sizes. Chap. 1 Data Structures and AlgorithmsThe first part is easy with the hint, but the second part is rather difficult to do withouta stack.a) bool checkstring(string S) {int count = 0;for (int i=0; i<length(S); i++)if (S[i] == ’(’) count++;if (S[i] == ’)’) {if (count == 0) return FALSE;count--;}}if (count == 0) return TRUE;else return FALSE;}b) int checkstring(String Str) {Stack S;int count = 0;for (int i=0; i<length(S); i++)if (S[i] == ’(’)(i);if (S[i] == ’)’) {if ()) return i;();}}if ()) return -1;else return ();Answers to this question are discussed in Section .This is somewhat different from writing sorting algorithms for a computer, sinceperson’s “working space” is typically limited, as is their ability to physically manipulatethe pieces of paper. Nonetheless, many of the common sorting algorithms havetheir analogs to solutions for this problem. Most typical answerswill be insertionsort, variations on mergesort, and variations on binsort.Answers to this question are discussed in Chapter 8.2Mathematical Preliminaries(a) Not reflexive if the set has any members. One could argue it is symmetric,antisymmetric, and transitive, since no element violate any ofthe rules.(b)Not reflexive (for any female). Not symmetric (consider a brother and sister). Not antisymmetric (consider two brothers). Transitive (for any3 brothers).(c)Not reflexive. Not symmetric, and is antisymmetric. Not transitive (only goes one level).(d)Not reflexive (for nearly all numbers). Symmetric since a+ b= b+ a,so not antisymmetric. Transitive, but vacuously so (there can be no distinct a, b,and cwhere aRband bRc).(e)Reflexive. Symmetric, so not antisymmetric. Transitive (but sort of vacuous).(f)Reflexive – check all the cases. Since it is only true when x= y,itis technically symmetric and antisymmetric, but rather vacuous. Likewise,it is technically transitive, but vacuous.In general, prove that something is an equivalence relation by proving that itis reflexive, symmetric, and transitive.(a)This is an equivalence that effectively splits the integers into odd andeven sets. It is reflexive (x+ xis even for any integer x), symmetric(since x+ y= y+ x) and transitive (since you are always adding twoodd or even numbers for any satisfactory a, b,and c).(b)This is not an equivalence. To begin with, it is not reflexive for anyinteger.(c)This is an equivalence that divides the non-zero rational numbers intopositive and negative. It is reflexive since x˙x>0. It is symmetric sincexy˙= yx˙. It is transitive since any two members of the given class satisfy the relationship.5Chap. 2 Mathematical Preliminaries(d)This is not an equivalance relation since it is not symmetric. For example,a=1and b=2.(e)This is an eqivalance relation that divides the rationals based on theirfractional values. It is reflexive since for all a,=0. It is symmetricsince if=xthen=.x. It is transitive since any two rationalswith the same fractional value will yeild an integer.(f)This is not an equivalance relation since it is not transitive. For example,4.2=2and 2.0=2,but 4.0=4.A relation is a partial ordering if it is antisymmetric and transitive.(a)Not a partial ordering because it is not transitive.(b)Is a partial ordering bacause it is antisymmetric (if ais an ancestor ofb, then bcannot be an ancestor of a) and transitive (since the ancestorof an ancestor is an ancestor).(c)Is a partial ordering bacause it is antisymmetric (if ais older than b,then bcannot be older than a) and transitive (since if ais older than band bis older than c, ais older than c).(d)Not a partial ordering, since it is not antisymmetric for any pair of sisters.(e)Not a partial ordering because it is not antisymmetric.(f)This is a partial ordering. It is antisymmetric (no violations exist) andtransitive (no violations exist).A total ordering can be viewed as a permuation of the elements. Since thereare n!permuations of nelements, there must be n!total orderings.This proposed ADT is inspired by the list ADT of Chapter 4.void clear();void insert(int);void remove(int);void sizeof();bool isEmpty();bool isInSet(int);This proposed ADT is inspired by the list ADT of Chapter 4. Note that whileit is similiar to the operations proposed for Question , thebehaviour issomewhat different.void clear();void insert(int);void remove(int);void sizeof();7bool isEmpty();long ifact(int n) {The iterative version requires careful examination to understand what it does, or to have confidence that it works as claimed.(b)Fibr is so much slower than Fibi because Fibr re-computes thebulk of the series twice to get the two values to add. What is much worse, the recursive calls to compute the subexpressions also re-computethe bulk of the series, and do so recursively. The result is an exponentialexplosion. In contrast, Fibicomputes each value in the seriesexactly once, and so its running time is proportional to n.void GenTOH(int n, POLE goal, POLE t1, POLE t2,POLE* curr) {if (curr[n] == goal) Put others on t1.GenTOH(n-1, t1, goal, t2, curr);move(t2, goal);GenTOH(n-1, goal, t1, t2, curr); In theory, this series approaches, but never reaches,0, so it will go on forever. In practice, the value should become computationallyindistinguishable from zero, and terminate. However, this is terrible programming practice.Chap. 2 Mathematical Preliminariesvoid allpermute(int array[], int n, int currpos) {if (currpos == (n-1)} {printout(array);return;}for (int i=currpos; i<n; i++) {swap(array, currpos, i);allpermute(array, n, currpos+1);swap(array, currpos, i); The idea is the print out theelements at the indicated bit positions within the set. If we do this for valuesin the range 0 to 2n.1, we will get the entire powerset.void powerset(int n) {for (int i=0; i<ipow(2, n); i++) {for (int j=0; j<n; j++)if (bitposition(n, j) == 1) cout << j << " ";cout << endl;}Proof: Assume that there is a largest prime number. Call it Pn,the nthlargest prime number, and label all of the primes in order P1 =2, P2 =3,and so on. Now, consider the number Cformed by multiplying all of the nprime numbers together. The value C+1is not divisible by any of the nprime numbers. C+1is a prime number larger than Pn, a contradiction.Thus, we conclude that there is no largest prime number. .Note: This problem is harder than most sophomore level students can handle.√Proof: The proof is by contradiction. Assume that 2is rational. By definition,there exist integers pand qsuch that√p2=,qwhere pand qhave no common factors (that is, the fraction p/qis in lowestterms). By squaring both sides and doing some simple algebraic manipulation,we get2p2=2q222q= pSince p2 must be even, pmust be even. Thus,9222q=4(p)222q=2(p)2This implies that q2 is also even. Thus, pand qare both even, which contra√dicts the requirement that pand qhave no common factors. Thus, 2mustbe irrational. .The leftmost summation sums the integers from 1 to n. The second summationmerely reverses this order, summing the numbers from n.1+1=ndown to n.n+1=1. The third summation has a variable substitution ofi, with a corresponding substitution in the summation bounds. Thus, it is also the summation of n.0=nto n.(n.1)=1.Proof:(a) Base case.For n=1, 12 = [2(1)3 +3(1)2 +1]/6=1. Thus, theformula is correct for the base case.(b) Induction Hypothesis.2(n.1)3 +3(n.1)2 +(n.1)i2 =.6i=1(c) Induction Step.i2 i2 +n2=i=1 i=12(n.1)3 +3(n.1)2 +(n.1)2=+n62n3 .6n2 +6n.2+3n2 .6n+3+n.1 2=+n62n3 +3n2 +n=.6Thus, the theorem is proved by mathematical induction. .Proof:(a) Base case.For n=1, 1/2=1.1/2=1/2. Thus, the formula iscorrect for the base case.(b) Induction Hypothesis.11=1..2i=1Chap. 2 Mathematical Preliminaries(c) Induction Step.1 11=+iin222i=1 i=111=1.+n221=1..n2Thus, the theorem is proved by mathematical induction. . Proof:(a) Base case. For n=0, 20 =21 .1=1. Thus, the formula is correctfor the base case.(b) Induction Hypothesis.2i=2n.1.i=0(c) Induction Step.2i=2i+2ni=0 i=0n=2n.1+2n+1 .1=2.Thus, the theorem is proved by mathematical induction. .The closed form solution is 3n+, which I deduced by noting that 3F (n).2n+1 .3F(n)=2F(n)=3. Now, to verify that this is correct, use mathematical induction as follows.For the base case, F(1)=3= .2The induction hypothesis is that =(3n.3)/2.i=1So,3i=3i+3ni=1 i=13n.3n= +32n+1 .33= .2Thus, the theorem is proved by mathematical induction.11nTheorem (2i)=n2 +n.i=1(a) Proof: We know from Example that the sum of the first noddnumbers is ith even number is simply one greater than the ithodd number. Since we are adding nsuch numbers, the sum must be ngreater, or n2 +n. .(b) Proof: Base case: n=1yields 2=12 +1, which is true.Induction Hypothesis:2i=(n.1)2 +(n.1).i=1Induction Step: The sum of the first neven numbers is simply the sum of the first n.1even numbers plus the nth even number.2i=( 2i)+2ni=1 i=1=(n.1)2 +(n.1)+2n=(n2 .2n+1)+(n.1)+2n= n2 .n+2n= n2 +n.nThus, by mathematical induction, 2i=n2 +n. .i=1Proof:52Base case. For n=1,Fib(1) = 1 <n=2,Fib(2) = 1 <(5).3Thus, the formula is correct for the base case.Induction Hypothesis. For all positive integers i<n,5 iFib(i)<().3Induction Step. Fib(n)=Fib(n.1)+Fib(n.2)and, by the InductionHypothesis, Fib(n.1)<(5) and Fib(n.3355Fib(n) <() +()3355 5<() +()333Chap. 2 Mathematical Preliminaries85= ()3355<()2()33n5= .3Thus, the theorem is proved by mathematical induction. .Proof:12(1+1)23 =(a) Base case. For n=1, 1=1. Thus, the formula is correct4for the base case.(b) Induction Hypothesis.22(n.1)ni3 = .4i=0(c) Induction Step.n2(n.1)n2i33=+n4i=02n4 .2n3 +n3=+n4n4 +2n3 +n2=4n2(n2 +2n+2)=42n2(n+1)=4Thus, the theorem is proved by mathematical induction..(a) Proof: By contradiction. Assume that the theorem is false. Then, eachpigeonhole contains at most 1 pigeon. Since there are nholes, there isroom for only npigeons. This contradicts the fact that a total of n+1pigeons are within the nholes. Thus, the theorem must be correct. .(b) Proof:i. Base case.For one pigeon hole and two pigeons, there must betwo pigeons in the hole.ii. Induction Hypothesis.For npigeons in n.1holes, some holemust contain at least two pigeons.13iii. Induction Step. Consider the case where n+1pigeons are in nholes. Eliminate one hole at random. If it contains one pigeon, eliminate it as well, and by the induction hypothesis some otherhole must contain at least two pigeons. If it contains no pigeons, then again by the induction hypothesis some other hole must contain at least two pigeons (with an extra pigeon yet to be placed). Ifit contains more than one pigeon, then it fits the requirements of the theorem directly..(a)When we add the nth line, we create nnew regions. But, we startwith one region even when there are no lines. Thus, the recurrence is F(n)=F(n.1)+n+1.(b) This is equivalent to the summation F(n)=1+ i=1 ni.(c) This is close to a summation we already know (equation .Base case: T(n.1)=1=1(1+1)/2.Induction hypothesis: T(n.1)=(n.1)(n)/2.Induction step:T(n)= T(n.1)+n=(n.1)(n)/2+n= n(n+1)/2.Thus, the theorem is proved by mathematical induction.If we expand the recurrence, we getT(n)=2T(n.1)+1=2(2T(n.2)+1)+1)=4T(n.2+2+1.Expanding again yieldsT(n)=8T(n.3)+4+2+1.From this, we can deduce a pattern and hypothesize that the recurrence isequivalent tonT(n)= .12i=2n.1.i=0To prove this formula is in fact the proper closed form solution, we use mathematicalinduction.Base case: T(1)=21 .1=1.14Chap. 2 Mathematical PreliminariesInduction hypothesis: T(n.1)= .1.Induction step:T(n)=2T(n.1)+1= 2 .1) + 1=2n.1.Thus, as proved by mathematical induction, this formula is indeed the correctclosed form solution for the recurrence.(a)The probability is for each choice.(b)The average number of “1” bits is n/2, since each position has probability of being “1.”(c)The leftmost “1” will be the leftmost bit (call it position 0) with probability; in position 1 with probability , and so on. The numberof positions we must examine is 1 in the case where the leftmost “1” isin position 0; 2 when it is in position 1, and so on. Thus, the expectedcost is the value of the summationni.2ii=1The closed form for this summation is 2 .n+2, or just less than two.2nThus, we expect to visit on average just less than two positions. (Studentsat this point will probably not be able to solve this summation,and it is not given in the book.)There are at least two ways to approach this problem. One is to estimate thevolume directly. The second is to generate volume as a function of weight.This is especially easy if using the metric system, assuming that the humanbody is roughly the density of water. So a 50 Kilo person has a volumeslightly less than 50 liters; a 160 pound person has a volumeslightly lessthan 20 gallons.(a) Image representations vary considerably, so the answer will vary as aresult. One example answer is: Consider VGA standard size, full-color (24 bit) images, which is 3 ×640 ×480, or just less than 1 Mbyte perimage. The full database requires some 30-35 CDs.(b)Since we needed 30-35 CDs before, compressing by a factor of 10 is not sufficient to get the database onto one CD.[Note that if the student picked a smaller format, such as estimating thesize of a “typical” gif image, the result might well fit onto a single CD.](I saw this problem in John Bentley’s Programming Pearls.) Approach 1:The model is Depth X Width X Flow where Depth and Width are in miles and Flow is in miles/day. The Mississippi river at its mouth is about 1/4 milewide and 100 feet (1/50 mile) deep, with a flow of around 15miles/hour =360 miles/day. Thus, the flow is about 2 cubic miles/day.Approach 2: What goes out must equal what goes in. The model is AreaXRainfall where Area is in square miles and Rainfall is in (linear) miles/day.The Mississipi watershed is about 1000 X 1000 miles, and the average rainfalis about 40 inches/year ≈.1 inches/day ≈.000002 miles/day (2 X .Thus, the flow is about 2 cubic miles/day.Note that the student should NOT be providing answers that look like theywere done using a calculator. This is supposed to be an exercise in estimation!The amount of the mortgage is irrelevant, since this is a question about rates.However, to give some numbers to help you visualize the problem, pick a$100,000 mortgage. The up-front charge would be $1,000, and the savingswould be 1/4% each payment over the life of the mortgage. The monthly charge will be on the remaining principle, being the highest at first and graduallyreducing over time. But, that has little effect for the first few years.At the grossest approximation, you paid 1% to start and will save1/4% eachyear, requiring 4 years. To be more precise, 8% of $100,000 is $8,000, while7 3/4% is $7,750 (for the first year), with a little less interestpaid (and thereforesaved) in following years. This will require a payback period ofslightlyover 4 years to save $1000. If the money had been invested, then in 5 yearsthe investment would be worth about $1300 (at 5would be close to 51/2years.Disk drive seek time is somewhere around 10 milliseconds or a little lessin 2000. RAM memory requires around 50 nanoseconds – much less thana microsecond. Given that there are about 30 million seconds in a year, amachine capable of executing at 100 MIPS would execute about 3billionbillion (3 .1018) instructions in a year.Typical books have around 500 pages/inch of thickness, so one million pagesrequires 2000 inches or 150-200 feet of bookshelf. This would be in excess of50 typical shelves, or 10-20 bookshelves. It is within the realm of possibilitythat an individual home has this many books, but it is rather unusual.A typical page has around 400 words (best way to derive this is to estimatethe number of words/line and lines/page), and the book has around 500 pages,so the total is around 200,000 words.16Chap. 2 Mathematical PreliminariesAn hour has 3600 seconds, so one million seconds is a bit less than300 hours.A good estimater will notice that 3600 is about 10% greater than 3333, so theactual number of hours is about 10% less than 300, or close to 270. (The realvalue is just under 278). Of course, this is just over 11 days.Well over 100,000, depending on what you wish to classify as a cityor town.The real question is what technique the student uses.(a) The time required is 1 minute for the first mile, then 60/59 minutesfor the second mile, and so on until the last mile requires 60/1=60 minutes. The result is the following summation.60 6060/i=60 1/i=60H60.i=1 i=1(b)This is actually quite easy. The man will never reach his destination, since his speed approaches zero as he approaches the end of the journey.3Algorithm AnalysisNote that nis a positive integer.5nlog nis most efficient for n=1.2nis most efficient when 2 ≤n≤4.10nis most efficient for all n>5. 20nand 2nare never moreefficient than the other choices.Both log3 nand log2 nwill have value 0 when n=1.Otherwise, 2 is the most efficient expression for all n>1.2/32 3n2 log3nlog2 nn20n4nn!.(a)n+6 inputs (an additive amount, independent of n).(b)8ninputs (a multiplicative factor).(c)64ninputs.100n.10n.√About (actually, 3 100n).n+6.(a)These questions are quite hard. If f(n)=2n= x, then f(2n)=22n=2(2n)2 = x.(b)The answer is 2(nlog2 3). Extending from part (a), we need some way tomake the growth rate even higher. In particular, we seek some way to log2 3 =make the exponent go up by a factor of 3. Note that, if f(n)=n)=2log2 3log2 3 =3xy, then f(2nn. So, we combine this observationwith part (a) to get the desired answer.First, we need to find constants cand nosuch that 1 ≤c×1 for n>n0.This is true for any positive value c<1 and any positive value of n0 (sincenplays no role in the equation).Next, we need to find constants cand n0 such that 1 ≤c×nfor n>n0.This is true for, say, c=1 and n0 =1.1718Chap. 3 Algorithm AnalysisOther values for n0 and care possible than what is given here.(a)The upper bound is O(n) for n0 >0 and c= c1. The lower bound isΩ(n) for n0 >0 and c= c1.(b)The upper bound is O(n3) for n0 >c3 and c= c2 +1. The lowerbound is Ω(n3) for n0 >c3 and c= c2.(c)The upper bound is O(nlog n) for n0 >c5 and c= c4 +1. The lowerbound is Ω(nlog n) for n0 >c5 and c= c4.(d)The upper bound is O(2n) for n0 >c7100 and c= c6 +lower bound is Ω(2n) for n0 >c7100 and c= c6. (100 is used forconvenience to insure that 2n>n6)(a) f(n)=Θ(g(n)) since log n2 = 2 log n.(b)f(n) is in Ω(g(n)) since ncgrows faster than log ncfor any c.(c)f(n) is in Ω(g(n)). Dividing both sides by log n, we see that log n grows faster than 1.(d)f(n) is in Ω(g(n)). If we t ake both f(n) and g(n) as exponents for 2, 2we get 2non one side and 2log2 n=(2log n)2 = n2 on the other, and ngrows slower than 2n.(e)f(n) is in Ω(g(n)). Dividing both sides by log nand throwing awaythe low order terms, we see that ngrows faster than 1.(f)。
