统计学 第九章 分类数据分析
《分类数据分析》PPT课件 (2)

精选课件ppt
2
分类数据分析的应用范围
政治学领域:研究政治立场是否影响政治派别。 社会学和心理学领域:分析不同类别的人不同的心理
特征。 公共政策分析领域:研究不同政策在不同地区产生的
效果。 文化传播领域:研究人们对媒体的看法。 分类数据分析是社会科学中最重要的课题之一。一方
面因为它的用途广泛,另一方面因为它解决的是基本 问题
PRE是不对称的,即需要区分自变量和 因变量。
在样本高度不均匀时,会出现不独立但 是结果为0的情况。
精选课件ppt
31
Goodman and Kruskal’s Lambda
Lambda方法是PRE方法的一种,原理是分别计算在 两种情况下预测错误的比例,然后进行比较。
X
c
d
Totals
Y
a
0.3 0.1 0.4
民主党
X:党派 独立党
共和党
革命的
Y:
场 立
中立的
保守的
33% (193)
41% (241)
26% (153)
100% (587)
30% (161)
37% (199)
34% (182)
100% (542)
11% (46)
33% (134)
56% (229)
100% (409)
400 574 564 1538
y
j1
(1Pm)
j1 (1Pm)
J
J
(1Pm)(1 Pim ) 1 (1Pm)
J
( nmj ) nm
ˆy
j 1
(n nm )
精选课件ppt
33
Lambda的方差
J
贾俊平《统计学》(第5版)课后习题-第9章 分类数据分析【圣才出品】

第9章 分类数据分析一、思考题1.简述列联表的构造与列联表的分布。
答:列联表是由两个以上的变量进行交叉分类的频数分布表。
列联表的分布可以从两个方面看,一个是观察值的分布,又称为条件分布,每个具体的观察值就是条件频数;一个是期望值的分布。
2.用一张报纸、一份杂志或你周围的例子构造一个列联表,说明这个调查中两个分类变量的关系,并提出进行检验的问题。
答:对三个生产厂甲、乙、丙提供的学习机的A、B、C三种性能进行质量检验,欲了解生产厂家同学习机性能的质量差异是否有关系。
抽查了450部学习机次品,整理成为如表9-2所示的3×3列联表。
表9-2根据抽查检验的数据表明:次品类型与厂家(即哪一个厂)生产是无关的(即是相互独立的)。
建立假设:H0:次品类型与厂家生产是独立的,H1:次品类型与厂家生产不是独立的。
可以计算各组的期望值,如表9-3所示(表中括号内的数值为期望值)。
表9-3 各组的期望值计算表所以2222(2017)(4033)(7058)9.821173358χ---=+++=…。
而自由度等于(R -1)(C -1)=(3-1)×(3-1)=4,若以0.01的显著性水平进行检验,查χ2分布表得20.01(4)13.277χ=。
由于220.019.821(4)13.277χχ=<=,故接受原假设H 0,即次品类型与厂家生产是独立的。
3.说明计算2χ统计量的步骤。
答:计算2χ统计量的步骤:(1)用观察值o f 减去期望值e f ;(2)将(o f -e f )之差平方;(3)将平方结果2)(e o f f -除以e f ;(4)将步骤(3)的结果加总,即得:22()o e ef f f χ-=∑。
4.简述ϕ系数、c 系数、V 系数的各自特点。
答:(1)ϕ相关系数是描述2×2列联表数据相关程度最常用的一种相关系数。
它的计算公式为:ϕ,式中,∑-=ee of f f 22)(χ;n 为列联表中的总频数,也即样本量。
第九章聚类分析

• 例:下表是同一批客户对经常光顾的五座商场在购物环境和
服务质量两方面的平均得分,现希望根据这批数据将五座商
7、如果参与聚类分析的变量存在数量级上的差异, 应在Transform Values框中的Standardize选项 中选择消除数量级差的方法。并指定处理是针对变 量的还是针对样本的。By variable表示针对变量, 适于 Q 型聚类分析;By case 表示针对样本,适 于R型聚类分析。
8、单击Statistics按钮指定输出哪些统计量
R型聚类:对变量进行聚类,使具有相似性的变量聚集在 一起,差异性大的变量分离开来,可在相似变量中选择 少数具有代表性的变量参与其他分析,实现减少变量个 数,达到变量降维的目的。
凝聚方式聚类:其过程是,首先,每个个体自成一类; 然后,按照某种方法度量所有个体间的亲疏程度,并将 其中最“亲密”的个体聚成一小类,形成n-1个类;接下 来,再次度量剩余个体和小类间的亲疏程度,并将当前 最亲密的个体或小类再聚到一类;重复上述过程,直到 所有个体聚成一个大类为止。可见,这种聚类方式对n个 个体通过n-1步可凝聚成一大类。
平方欧式距离(Squared Euclidean distance ) 切比雪夫(Chebychev)距离
max xi yi max( 7366 , 6864 )
Block距离
k
xi yi 73 66 68 64 i1
2、计数变量个体间距离的计算方式
卡方(Chi-Square measure)距离 Phi方(Phi-Square measure)距离
统计学(第六版)第九章分类数据分析(课后习题答案)
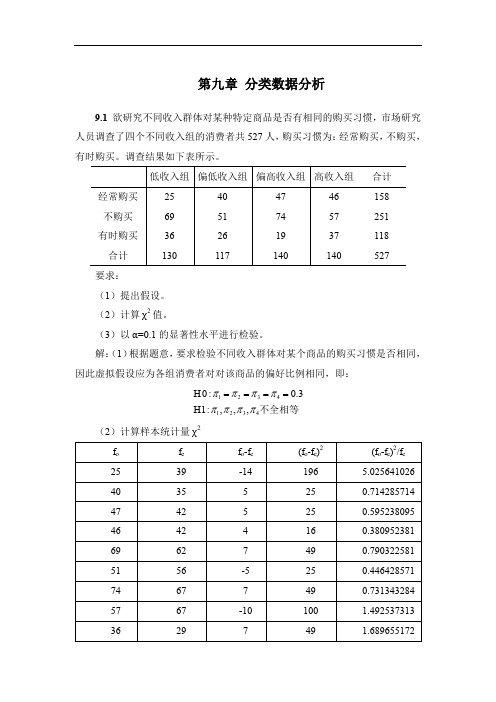
H 0 : 1 2 3 4 0.3 H1: 1 , 2 , 3 , 4不全相等
(2)计算样本统计量 χ2 fo 25 40 47 46 69 51 74 57 36 fe 39 35 42 42 62 56 67 67 29 fo-fe -14 5 5 4 7 -5 7 -10 7 (fo-fe)2 196 25 25 16 49 25 49 100 49 (fo-fe)2/fe 5.025641026 0.714285714 0.595238095 0.380952381 0.790322581 0.446428571 0.731343284 1.492537313 1.689655172
9.2 从总体中随机抽取了 n=200 的样本,调查后按不同属性归类,得到如下 结果: n1=28,n2=56,n3=48,n4=36,n5=32 依据经验数据,各类别在总体中的比例分别为: π1=0.1,π2=0.2,π3=0.3,π4=0.2,π5=0.2 以 α=0.1 的显著性水平进行检验, 说明现在的情况与经验数据相比是否发生 了变化(用 P 值) 解:虚拟假设 H0:样本数据的各类数据的比例与总体中各类数据的比例相同 H1:样本数据的各类数据的比例与总体中各类数据的比例不同 计算样本统计量 χ2 fo 28 56 48 36 32 fe 20 40 60 40 40 fo-fe 8 16 -12 -4 -8 (fo-fe)2 64 256 144 16 64 (fo-fe)2/fe 3.2 6.4 2.4 0.4 1.6 14 χ2 的自由度为(5-1)=4,P=0.007 远小于显著性水平 α=0.1,故拒绝 H0,现 在的情况与经验数据相比已经发生了变化(显著差异) 。
26 19 37
贾俊平《统计学》(第五版)考研真题(含复试)与典型习题详解 分类数据分析

合计
赞成
35
30
65
反对
15
20
35
合计
50
50
100
如果要检验男女教师对教师体制改革的看法是否相同,提出的原假设为( )。
A.H0:π1=π2=35 B.H0:π1=π2=50 C.H0:π1=π2=65
6 / 19
圣才电子书
D.H0:π1=π2=0.65
十万种考研考证电子书、题库视频学习平台
156 162
圣才电子书
A.0.6176
十万种考研考证电子书、题库视频学习平台
B.1.2352
C.2.6176
D.3.2352
【答案】B
【解析】 2 检验可以用于变量间拟合优度检验和独立性检验,可以用于测定两个分类 变量之间的相关程度。用 fo 表示观察值频数,用 fe 表示期望值频数,则 2 统计量为:
圣才电子书
十万种考研考证电子书、题库视频学习平台
第 9 章 分类数据分析
一、单项选择题
1.列联分析是利用列联表来研究( )。
A.两个数值型变量的关系
B.两个分类变量的关系
C.两个数值型变量的分布
D.一个分类变量和一个数值型变量的关系
【答案】B
【解析】列联表是由两个以上的变量进行交叉分类的频数分布表,列联分析是利用列联
【解析】表中的行是态度变量,这里划分为三类,即赞成,中立和反对;表中的列是单 位变量,这里划分为两类,即男同学和女同学,即 3×2 列联表。
5.一所大学为了解男女学生对后勤服务质量的评价,分别抽取了 300 名男学生和 240
名女学生进行调查,得到的结果如表 9-2 所示。
表 9-2 关于后勤服务质量评价的调查结果
贾俊平《统计学》复习笔记课后习题详解及典型题详解 第9章~第10章【圣才出品】

第9章分类数据分析9.1复习笔记一、分类数据与χ2统计量1.分类数据按照所采用的计量尺度不同,可以将统计数据分为分类数据、顺序数据和数值型数据。
分类数据和顺序数据都是只能归于某一类别的非数字型数据,它们是对事物进行分类的结果,其结果均表现为类别,用文字来表述,不过顺序数据的类别是有序的;数值型数据是按数字尺度测量的观测值,其结果表现为具体的数值。
分类数据是对事物进行分类的结果,其特征是,调查结果虽然用数值表示,但不同数值描述了调查对象的不同特征。
数值型数据可以转化为分类数据。
分类数据的结果是频数,χ2检验是对分类数据的频数进行分析的统计方法。
2.χ2统计量χ2统计量可以对分类数据做拟合优度检验和独立性检验,可以用于测定两个分类变量之间的相关程度。
若用f o 表示观察值频数,用f e 表示期望值频数,则χ2统计量可以写为:22()o e e f f f χ-=∑χ2检验:χ2检验是利用随机样本对总体分布与某种特定分布拟合程度的检验,也就是检验观察值与理论值之间的紧密程度。
χ2检验主要用于拟合优度检验和独立性检验。
(1)χ2统计量的特征①χ2≥0,因为它是对平方值结果的汇总;②χ2统计量的分布与自由度有关;③χ2统计量描述了观察值与期望值的接近程度。
两者越接近,即f o-f e的绝对值越小,计算出的χ2值越小;反之,f o-f e的绝对值越大,计算出的χ2值也越大。
χ2检验正是通过对χ2的计算结果与χ2分布中的临界值进行比较,做出是否拒绝原假设的统计决策。
(2)χ2分布与自由度的密切关系自由度越小,χ2的分布就越向左边倾斜;随着自由度的增加,χ2分布的偏斜程度趋于缓解,逐渐显露出对称性,随着自由度的继续增大,χ2分布将趋近于对称的正态分布。
(3)应用χ2检验统计量的注意事项①各组的理论频数f e不得小于总频数n;②总频数应较大,至少大于50;③如果某组理论频数小于5,可将相邻的若干组合并,直至理论频数大于5为止;④倘若有两个以上的单元,如果20%的单元期望频数f e小于5,则不能应用χ2检验。
分类数据分析

赞成 反对
合计
男学生 45 105 150
女学生 42 78 120
合计 87 183 270
9 - 18
c 统计量
统计学
STATISTICS (第四版)
概述
c2检验(Chi-square test)是现代统计 学的创始人之一,英国人K . Pearson( 1857-1936)于1900年提出的一种具有广 泛用途的统计方法,因此又称为Pearson c2检验。可用于两个或多个率或构成比间 的比较,定性资料的关联度分析,拟合 优度检验等等。
一分公司
二分公司 三分公司 四分公司
赞成该方 案
反对该方 案
实际频数 期望频数 实际频数 期望频数
68
75
57
79
100*66.4%=66
150*66.4%=80
90*66.4%=6 0
110*66.4%=73
32
75
33
31
100*33.6%=34
150*33.6%=40
90*33.6%=3 0
110*33.6%=37
n
9 -9
统计学
STATISTICS (第四版)
列联表的结构
(r c 列联表的一般表示)
列(cj)
列(cj)
行(ri)
j =1
j =2
…
i =1
f11
f12
…
i=2
f21
f22
…
:
:
:
:
合计
c1
c2
…
fij 表示第 i 行第 j 列的观察频数
合计
r1 r2
:
n
9 - 10
贾俊平《统计学》章节题库(分类数据分析)详解【圣才出品】

第9章分类数据分析一、单项选择题1.列联分析是利用列联表来研究()。
A.两个数值型变量的关系B.两个分类变量的关系C.两个数值型变量的分布D.一个分类变量和一个数值型变量的关系【答案】B【解析】列联表是由两个或以上的变量进行交叉分类的频数分布表,列联分析是利用列联表来研究两个分类变量之间的关系。
2.列联表中的每个变量()。
A.只能有一个类别B.只能有两个类别C.对类别没有限制D.可以有两个或两个以上的类别【答案】D3.设列联表的行数为3,列数为4,则χ2检验的自由度为()。
A.3B.4C.6D.12【答案】C【解析】列联分析中,χ2检验的自由度=(行数-1)(列数-1)=(R-1)(C-1)=(3-)×(4-1)=6。
4.一所大学准备采取一项学生对餐厅改革意见的调查,为了解男女学生对这一措施的看法,分别抽取了300名男学生和240名女学生进行调查,得到的结果如表9-1所示。
这个表格是()。
A.4×3列联表B.3×2列联表C.2×3列联表D.3×4列联表【答案】B【解析】表中的行是态度变量,这里划分为三类,即赞成、中立和反对;表中的列是单位变量,这里划分为两类,即男同学和女同学,因此这个表格是3×2列联表。
5.一所大学为了解男女学生对后勤服务质量的评价,分别抽取了300名男学生和240名女学生进行调查,得到的结果如表9-2所示。
这个列联表的最下边一行称为()。
A.总频数B.条件频数C.行边缘频数D.列边缘频数【答案】D6.某中学为了解教师对新课标改革的看法,分别抽取了300名男教师和240名女教师进行调查,得到的结果如表9-3所示。
这个列联表的最右边一列称为()。
A.总频数B.条件频数C.行边缘频数D.列边缘频数【答案】C7.某大学为了解学生对研究生奖学金制度改革的看法,分别抽取了300名男研究生和240名女研究生进行调查,得到的结果如表9-4所示。
数据分类分析方法

数据分类分析方法
数据分类分析方法是统计学中的一种方法,用于将数据按照一定的规则进行分类和分组。
常用的数据分类分析方法包括聚类分析、判别分析和决策树等。
1. 聚类分析:聚类分析是一种将数据按照相似性进行分组的方法。
根据数据之间的相似性度量,将数据分为若干个簇(cluster)。
常用的聚类算法有k-means 算法和层次聚类算法。
2. 判别分析:判别分析是一种用于区分或分类不同数据的方法。
通过寻找最佳的判别函数,将数据分为不同的类别。
常用的判别分析方法有线性判别分析(LDA) 和逻辑回归(logistic regression)。
3. 决策树:决策树是一种以树形结构表示分类规则的方法。
通过根据不同特征对数据进行划分,最终将数据分为不同的类别。
常用的决策树算法有ID3、C
4.5和CART。
这些方法可根据实际需求选择使用,根据数据的特征和问题的要求,选择合适的方法进行数据分类分析。
贾俊平《统计学》章节题库(分类数据分析)【圣才出品】

观察值
105
78
期望值
102
8l
根据这个列联表计算的 Χ2 统计量为( )。
A.0.6176
B.1.6176
C.0.3088
D.1.3088
【答案】A
【解析】 2 f0 fe 2 45 482 42 392 105 1022 78 812
87
反对
105
78
183
合计
150
120
270
这个列联表的最下边一行称为( )。
A.列边缘频数
B.行边缘频数
3 / 25
圣才电子书
C.条件频数
十万种考研考证电子书、题库视频学习平台
D.总频数
【答案】A
7.一所大学准备采取一项学生在宿舍上网收费的措施,为了解男女学生对这一措施的
2.设 R 为列联表的行数,C 为列联表的列数,则 Χ2 分布的自由度为( )。 A.R B.C C.R×C D.(R-1)×(C-1) 【答案】D
【解析】 2 检验的自由度=(行数-1)(列数-1)=(R-1)(C-1)。
1 / 25
圣才电子书 十万种考研考证电子书、题库视频学习平台
看法,分别抽取了 150 名男学生和 120 名女学生进行调查,得到的结果如下:
男学生
女学生
合计
赞成
45
42
87
反对
105
78
183
合计
150
120
270
根据这个列联表计算的赞成上网收费的行百分比分别为( )。
A.51.7%和 48.3%
B.57.4%和 42.6%
C.30%和 70%
D.35%和 65%
统计学第9章分类数据分析

可解释性
分类结果应具有可解释性,能够清晰地说明各类 别的特征和差异,方便用户理解和应用。
避免过拟合
在训练分类模型时,应避免过拟合现象,确保模 型泛化能力良好,能够适用于不同的数据集和场 景。
交叉验证
采用交叉验证方法评估分类模型的性能,以客观 地评价分类结果的准确性和可靠性。
谢谢聆听
02
目的:通过频数分布表,可以直观地了解数据的分布情况 ,发现数据的异常值和缺失值,以及数据的离散程度和集 中趋势。
03
制作步骤
04
1. 将数据按照某一属性进行分类。
05
2. 统计每一类别的频数和频率。
06
3. 制作频数分布表,包括类别、频数、频率和累积频数 、累积频率等列。
列联表分析
定义:列联表分析是一种将两个或多 个分类变量进行联合,并分析它们之
社会阶层划分
通过分类数据分析,将社会人群划分为不同的阶层,分析不同阶 层的社会特征和行为模式。
人口普查
分类数据分析可以用于人口普查数据的分析和处理,提供更准确 的人口统计信息。
舆情分析
通过分类数据分析,了解公众对某一事件或话题的态度和意见, 为政策制定和舆论引导提供依据。
06 分类数据分析的注意事项
优势比和相对风险
基本概念
相对风险
优势比(Odds Ratio)和相对风险 (Relative Risk)是衡量分类数据关 联强度的指标。
表示暴露于某因素下发生事件的相对危 险度,计算方法为相对风险=暴露组的 事件发生率/非暴露组的事件发生率。
优势比
表示一个事件发生的相对概率,计算 方法为优势比=事件组的发生概率/非 事件组的发生概率。
分类数据分析
目录
第9章 分类数据分析 - S

57/124 =0.46
列联表中变量的相互独立性 列联表中的两个变量,如果一个变量的值 在改变,而另一个变量的值并没有随之产 生变化,或变化的很细微,则说明这两个 变量相互独立。
• 【例1】一集团公司在四个不同地区设有分 公司,现从四个分公司抽取进行调查。调 查结果如下
• 1.假定行变量和列变量是独立的
中年 10/40 =0.25
青年 2/57 =0.04
边缘和 32/124 =0.26
5/27 =0.18 2/27 =0.08
20/40 =0.50 10/40 =0.25
35/57 =0.61 20/57 =0.35
60/124 =0.48 32/124 =0.26
关于Y的 条件分布
在x取固定值 的时候,y的 分布。
• 如果存活状况与性别无关,男性与女性的 幸存比例应该相等。
自由度为:分类变量类型的个数-1
决策:拒绝H0 结论:有证据表明存活状况与性别显著相关
• 9.2 列联分析:独立性分析 • 9.2.1列联表
关于X的 条件分布
在y取固定 值的时候x 的分布。
爱好的 条件分 布 戏曲 歌舞 球赛
老年 20/27 =0.74
子 脑力 体力 农业 边缘和 父 脑力 20 10 5 35 体力 5 30 5 40 农业 5 10 50 65 边缘和 30 50 60 140
【例3】 我省在残疾人中进行了抽样调查,共抽取 4028名残疾人。他们的性别与文化程度的 分布如下表所示。问残疾人的文化程度是 否与性别相关(α=0.05)?
2 检验需要注意的问题
2 a使用 检验时,期望频次不能过小,否则会 2 使计算出的 值过大,导致错误地拒绝原假
分类数据分析

数据异常值处理
识别并处理异常值,以避免对数据分 析产生负面影响。
数据标准化
将数据转换为统一的标准,以便进行 比较和分析。
数据编码
将分类变量转换为数值型变量,以便 进行数学运算和分析。
数据分组与分类
聚类分析
将相似的数据点聚集在一起,形成不同的组 或集群。
分类分析
根据已知结果对数据进行分类,如预测市场 细分或客户类型。
分类报告与解释
分类报告
详细描述分类模型的性能指标、特征重要性、过拟合 与欠拟合情况等,帮助用户全面了解模型表现。
可解释性
通过可视化、特征重要性分析等方法,帮助用户理解 模型决策过程,提高分类结果的透明度和可信度。
05
分类数据分析应用场景
市场营销细分
目标受众识别
通过分类数据分析,识别不同消费者群体的 特征,以便针对不同群体制定更有针对性的 营销策略。
要点二
详细描述
首先,收集信用卡交易数据,包括交易时间、交易地点、 交易金额等。然后,利用分类算法对数据进行处理和分析 ,识别出欺诈行为的特征和模式。最后,根据分类结果, 采取相应的措施(如拒绝交易、冻结账户等),以减少欺 诈行为的发生和保护相关利益。
电影推荐系统案例
总结词
通过分类数据分析,为用户推荐适合他们口味的电影, 提高电影观看体验。
分类数据分析
• 分类数据分析概述 • 数据收集与整理 • 分类算法与模型 • 分类结果评估与优化 • 分类数据分析应用场景 • 案例分析
01
分类数据分析概述
定义与特点
定义
分类数据分析是一种统计学方法,用 于将数据分成不同的类别或组,以便 更好地理解数据的结构和模式。
特点
分类数据分析具有简单易行、直观明 了的特点,能够揭示数据中的潜在类 别和结构,为决策提供有力支持。
贾俊平《统计学》(第7版)考点归纳和课后习题详解(含考研真题)-第九章至第十一章【圣才出品】

第9章分类数据分析9.1考点归纳【知识框架】【考点提示】(1)χ2统计量的计算公式及应用(计算题考点);(2)拟合优度检验(一个分类变量)和独立性检验(两个分类变量)(简答题、计算题考点);(3)列联表中的相关测量:三个系数的计算公式、特点及应用(选择题、简答题、计算题考点)。
【核心考点】考点一:χ2统计量(1)χ2统计量计算公式22()o e ef f f χ-=∑f o 表示观察值频数,用f e 表示期望值频数。
(2)χ2统计量的特征①χ2≥0;②χ2统计量的分布与自由度有关;③χ2统计量描述了观察值与期望值的接近程度。
(3)χ2分布与自由度的关系χ2分布随着自由度的增加而向右倾斜,且逐渐趋近于对称的正态分布。
考点二:列联表中的相关测量表9-1列联表的测量指标【真题精选】当列联表中的两个变量相互独立时,计算的相关系数c()。
[中国海洋大学2018研]A.等于1B.大于1C.等于0D.小于0【答案】C【解析】两个随机变量独立,则这两个随机变量不相关,反之不成立。
9.2课后习题详解一、思考题1.简述列联表的构造与列联表的分布。
答:(1)列联表的构造:列联表是将两个以上的变量进行交叉分类的频数分布表。
(2)列联表的分布:列联表的分布可以从两个方面看,一个是观察值的分布,又称为条件分布,每个具体的观察值就是条件频数;一个是期望值的分布。
2.用一张报纸、一份杂志或你周围的例子构造一个列联表,说明这个调查中两个分类变量的关系,并提出进行检验的问题。
答:(1)构造列联表:对三个生产厂甲、乙、丙提供的学习机的A、B、C三种性能进行质量检验,欲了解生产厂家同学习机性能的质量差异是否有关系。
抽查了450部学习机次品,整理成为如表9-2所示的3×3列联表。
表9-2(2)提出检验问题根据抽查检验的数据表明:次品类型与厂家(即哪一个厂)生产是无关的(即是相互独立的)。
(3)进行检验建立假设:H0:次品类型与厂家生产是独立的;H1:次品类型与厂家生产不是独立的。
统计学课件第9篇章分类数据分析

谢谢聆听
其他回归模型
总结词
除了线性回归分析和Logistic回归分析之外,还有许多其他类型的回归模型可 供选择。
详细描述
这些模型包括岭回归、套索回归、多项式回归、逐步回归等,每种模型都有其 特定的适用场景和假设条件。选择合适的回归模型需要考虑数据的特征、模型 的预测精度和解释性等因素。
06 分类数据分析的实际应用
市场细分分析
市场细分
通过分类数据分析,将市场划分为不 同的细分市场,以便更好地理解客户 需求和行为,从而制定更有效的营销 策略。
消费者行为研究
通过分析消费者的购买行为、偏好和 态度,了解不同细分市场的消费者需 求和趋势,以优化产品设计和市场定 位。
人口统计学研究
人口普查
利用分类数据分析对人口普查数据进行处理和分析,了解人口分布、年龄结构、 性别比例等人口统计学特征。
05 分类数据的回归分析
线性回归分析
总结词
线性回归分析是一种通过建立自变量与因变量之 间的线性关系来预测因变量的方法。
总结词
线性回归分析的假设包括线性关系、误差项独立 同分布、误差项无偏和误差项同方差。
详细描述
线性回归分析基于最小二乘法原理,通过拟合一 条直线来描述自变量和因变量之间的关系。这种 方法适用于因变量是连续变量的数据,并且自变 量和因变量之间存在线性关系。
选择合适的图形类型,将频数分布表 中的数据按照分类变量进行分组并绘 制图形。
相对频率与累积频率
相对频率
01
某一组的频数与总频数之比,用于表示该组在总体中的相对重
要程度。
累积频率
02
某一组的相对频率与前面所有组的相对频率之和,用于表示该
组及之前所有组在总体中的相对重要程度。
分类数据分析-PPT精选文档

150
干扰因素和解决办法
边际分布不均匀(如表6): 调整数据 将表格标准化 选择对边际总数不敏感的测量方法 行列不相等: 选择可以达到最大值的测量方法。
表6:不同边际分布,相同相关程度
(a)
X 60% (60) Y 30% (30) 10% (10) Totals 100% (100) 20% (200) 60% (600) 20% (200) 100% (1000) 10% (10) 30% (30) 60% (60) 100% (100) Totals 270 60% (180) Y 30% (90) 10% (30) Totals 100% (300) X 20% (120) 60% (360) 20% (120) 100% (600) 10% (30) 30% (90) 60% (180) 100% (300)
百分比法
X 0.9 (45) 0.1 (5) 1.0 (50) 0.4 (20) 0.6 (30) 1.0 (50) 0.9-0.4=0.5
Y
差额比率法
X:党派
民主党
Y: 立 场 革命的 保守的 193 153 346
共和党
46 229 275 239 382 621
n 11 n 21 ˆ n 12 n 22
差额比率法的性质
a X 75 Y 10 85 15 100 115 Y 750 100 850 b X 15 100 115
ˆ 50 ˆ 3 . 91
ˆ 50 ˆ 3 . 91
193 1.26 153 6.28 46 0.20 229
差额比率法的性质
a 100 25 125 50 200 250 25 200 225 b 100 50 150
《分类数据分析》课件

分类算法如逻辑回归、 支持向量机等被广泛应 用于疾病预测中。通过 对疾病相关数据的特征 进行提取和选择,利用 分类算法建立预测模型 ,对疾病的发生和发展 趋势进行预测。
经过训练的预测模型能 够准确地对疾病的发生 和发展趋势进行预测, 为疾病的预防和治疗提 供科学依据,提高人们 的健康水平。
05
总结与展望
分类数据分析实践
数据准备
数据清洗
去除异常值、缺失值和重复值,确保数据质量 。
数据转换
对数据进行必要的转换,如编码、归一化等, 以适应模型需求。
数据分割
将数据集分为训练集、验证集和测试集,以便于模型训练和评估。
数据探索与特征工程
数据探索
了解数据的基本特征和分布,识别潜在的问题和机会 。
特征选择
选择与目标变量相关的特征,去除无关或冗余的特征 。
实际效果
利用分类数据分析技术对客户 进行细分,将客户划分为不同 的群体,以便更好地了解客户 需求并提供个性化服务。
客户细分是将客户划分为不同 群体的过程,有助于企业更好 地了解客户需求、偏好和行为 模式,从而制定更加精准的市 场策略。
分类算法如聚类算法、决策树 等被广泛应用于客户细分中。 通过对客户数据的特征进行提 取和选择,利用分类算法进行 聚类分析,将客户划分为不同 的群体。
基于强化学习的分类数据分析方法
未来发展方向与趋势
• 强化学习作为一种机器学习方法 ,通过与环境的交互进行学习, 可以应用于分类数据分析中,以 提高分类性能和泛化能力
未来发展方向与趋势
数据隐私保护与安全分类分析
随着数据隐私和安全问题的日益突出,如何在保护数据隐私的同时进行分类分析成为未来的研究重点
疾病诊断
利用分类数据分析进行医学诊断,根据患者的症状和体征将其归类为 不同的疾病类型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( fo fe ) fe
2
7
2
9.1 χ2 统计量
分布与自由度的关系
8
9.2 拟合优度检验
9.2 拟合优度检验
9
9.2 拟合优度检验
样题
【例】1912年4月15日,豪华巨轮泰坦尼克号与 冰山相撞沉没。当时船上共有共2208人,其中男 性1738人,女性470人。海难发生后,幸存者为 718人,其中男性374人,女性344人,以的显著
j =1j=2…Fra bibliotek… … : …
15
合计
i =1 i=2 : 合计
f11 f21
:
f12 f22
:
r1 r2
:
c1
c2
n
fij 表示第 i 行第 j 列的观察频数
9.3独立性检验(例题分析)
样题
【例】一种原料来自三个不同的地区,原料质量被分成三 个不同等级。从这批原料中随机抽取500件进行检验,结 果如表9-3所示,要求检验各个地区和原料质量之间是否 存在依赖关系? ( 0.05)
140 171 189
合计
162
188
28
150
500
9.4列联表中的相关测量(例题分析)
答案
解:已知n=500,=19.82,列联表为33
习题
C
2
19.82 0.199 n 500
2 n
2
19.82 0.195 19.82 500
V
n min (r 1), (c 1)
3.
4. 5. 6.
列变量的类别用 c 表示, cj 表示第 j 个类别
每种组合的观察频数用 fij 表示 表中列出了行变量和列变量的所有可能的组合,所以称为列联表 一个 r 行 c 列的列联表称为 r c 列联表
14
9.3列联表(contingency table)
列(cj) 行(ri)
列(cj)
于是自由度df=2-1=1,经查分布表,
(0.1)
(1)=2.706,故拒绝H0,说明存活状况与性别显著相关
12
9.2 拟合优度检验
9.3 列联分析:独立性检验
13
9.3列联表的结构(r 和 c 列联表的一般表示)
1. 2.
由两个以上的变量交叉分类的频数分布表 行变量的类别用 r 表示, ri 表示第 i 个类别
之间完全相关 列联表中变量的位置可以互换,的符号 没有实际意义,故取绝对值即可
23
9.4 φ 相关系数
将入 相关系数的计算公式得
2 ad bc n (a b)(c d )( a c)(b d )
ad 等于 bc , = 0,表明变量X 与 Y 之间
不同行和列的列联表计算的列联系数不 便于比较 当列联表中有一维为2,min[(r-1),(c1)]=1,此时V=
26
9.4 φ 、C、V 的比较
1. 2.
同一个列联表,、C、V 的结果会不同 不同的列联表,、C、V 的结果也不同
3.
在对不同列联表变量之间的相关程度进行
比较时,不同列联表中的行与行、列与列 的个数要相同,并且采用同一种系数
2
22
9.4 φ 相关系数
将入 相关系数的计算公式得
2 ad bc n (a b)(c d )( a c)(b d )
ad 等于 bc , = 0,表明变量X 与 Y 之间独立 若 b=0 ,c=0,或a=0 ,d=0,意味着各观察频
数全部落在对角线上,此时|| =1,表明变量X 与 Y
1 φ 相关系数
2 列联相关系数
3 V 相关系数
18
9.4 列联表中的相关测量
1.
品质相关 • 对品质数据(分类和顺序数据)之间 相关程度的测度
2.
列联表变量的相关属于品质相关
3.
列联表相关测量的统计量主要有
• • •
相关系数
列联相关系数
V 相关系数
19
9.4 φ 相关系数(correlation coefficient)
计算公式为
2 V n min (r 1), (c 1)
式中: min ( r 1), (c 1) 表示取( r 1), (c 1)中较小的一个
2. 3. 4.
5. 6.
V 的取值范围是 0V1 V = 0表明列联表中的两个变量独立 V=1表明列联表中的两个变量完全相关
独立 若 b=0 ,c=0,或a=0 ,d=0,意味着各 观察频数全部落在对角线上,此时|| =1,表 明变量X 与 Y 之间完全相关 列联表中变量的位置可以互换,的符号没有 实际意义,故取绝对值即可
24
9.4 φ 相关系数
1. 2. 用于测度大于 22 列联表中数据的相关程 度 计算公式为
习题
答案
解:H0:地区和原料等级之间是独立的(不存在依赖关 系)、H1:地区和原料等级之间不独立 (存在依赖关系) 0.05(4)=9.488故拒绝H0,接受H1 ,即地区和原料等 级之间存在依赖关系,原料的质量受地区的影响
16
9.4 列联表中的相关测量
9.4 列联表中的相关测量
17
9.4 列联表中的相关测量
27
9.4列联表中的相关测量(例题分析)
样题
【例】一种原料来自三个不同地区,原料质量被分 成三个不同等级。从这批原料中随机抽取 500 件进 行检验,结果如下表。分别计算 系数、C 系数和V 系数,并分析相关程度
地区
甲地区 乙地区 丙地区
习题
一级
二级
三级
合计
52 60 50
64 59 65
24 52 74
e11 e12
将各期望频数代入 的计算公式 得
( a e11 ) 2 (b e12 ) 2 (c e21 ) 2 ( d e22 ) 2 e11 e12 e21 e22 n( ad bc ) 2 ( a b)( c d )( a c)(b d )
习题
性水平检验存活状况与性别是否有关。 ( 0.05)
10
9.2 拟合优度检验
答案
解:要回答观察频数与期望频数是否一致, 检验如下假设: H0:观察频数与期望频数一致
习题
H1:观察频数与期望频数不一致
11
9.2 拟合优度检验
自由度的计算为df=R-1,R为分类变量类型的个数。在
本例中,分类变量是性别,有男女两个类别,故R=2,
3.使用分类或顺序尺度
•你吸烟吗? •1.是;2.否
•你赞成还是反对这一改革方案?
•1.赞成;2.反对 4.对分类数据的描述和分析通常使用列联表
5.可使用检验
5
9.1 理解分类数据与χ2 统计量
1
2
分类数据
χ2 统计量
6
9.1 χ2 统计量
统计量
1. 用于检验分类变量拟合
优度
2.
计算公式为
2
19.82 0.141 500 2
结论:三个系数均不高,表明产地和原料等 级之间的相关程度不高
29
1.
测度22列联表中数据相关程度
2.
对于 22 列联表, 系数的值在
0~1之间
3.
相关系数计算公式为
2
n
2 ( f e ) 2 r c ij ij 式中: i 1 j 1 e ij n为实际频数的总个数,即样本容量
20
9.4 φ 相关系数(原理分析)
一个简化的 22 列联表
统计学
第九章 分类数据分析
学习目标
本章学习目标
理解分类数据与χ 2 统计量 掌握拟合优度检验及其应用
掌握独立性检验及其应用
掌握测度列联表中的相关性
2
9.1 理解分类数据与χ 2 统计量
3
9.1 理解分类数据与χ2 统计量
1
2
分类数据
χ2 统计量
4
1.分类变量的结果表现为类别
•例如:性别 (男, 女) 2.各类别用符号或数字代码来测度
C
2
2 n
C 的取值范围是 0C<1 C = 0表明列联表中的两个变量独立 C 的数值大小取决于列联表的行数和列数,
并随行数和列数的增大而增大 根据不同行和列的列联表计算的列联系数不 便于比较
25
9.4 V 相关系数(V correlation coefficient)
1.
因素 Y y1 y2 合计
因素 X x1 x2
合计
a c a+c
b d b+d
21
a+b c+d n
9.4 φ 相关系数
列联表中每个单元格的期望频数分 别为
( a b)( a c ) n ( a b)(b d ) n e21 e22 ( a c )( c d ) n (b d )( c d ) n
