灰度直方图均衡化与规定化
图像处理6灰度直方图和直方图均衡化

图像处理6灰度直⽅图和直⽅图均衡化灰度直⽅图介绍灰度直⽅图(Gray histogram)是关于灰度级分布的函数,是对图像中灰度级分布的统计。
灰度直⽅图是将数字图像中的所有像素,按照灰度值的⼤⼩,统计其出现的频率。
灰度直⽅图是灰度级的函数,它表⽰图像中具有某种灰度级的像素的个数,反映了图像中某种灰度出现的频率。
如果将图像总像素亮度(灰度级别)看成是⼀个随机变量,则其分布情况就反映了图像的统计特性,这可⽤probability density function (PDF)来刻画和描述,表现为灰度直⽅图。
实现以下代码便于理解灰度直⽅图的计算,其中histogram函数是基于numpy简化的,运⾏结果如下。
# coding: utf8from skimage import dataimport matplotlib.pyplot as pltimport numpy as npdef histogram(a, bins=10, range=None):"""Compute the histogram of a set of data."""import numpy as npfrom numpy.core import linspacefrom numpy.core.numeric import (arange, asarray)# 转成⼀维数组a = asarray(a)a = a.ravel()mn, mx = [mi + 0.0 for mi in range]ntype = np.dtype(np.intp)n = np.zeros(bins, ntype)# 预计算直⽅图缩放因⼦norm = bins / (mx - mn)# 均分,计算边缘以进⾏潜在的校正bin_edges = linspace(mn, mx, bins + 1, endpoint=True)# 分块对于⼤数组可以降低运⾏内存,同时提⾼速度BLOCK = 65536for i in arange(0, len(a), BLOCK):tmp_a = a[i:i + BLOCK]tmp_a_data = tmp_a.astype(float)# 减去Range下限,乘以缩放因⼦,向下取整tmp_a = tmp_a_data - mntmp_a *= normindices = tmp_a.astype(np.intp)# 对indices标签分别计数,标签等于bins减⼀indices[indices == bins] -= 1n += np.bincount(indices, weights=None,minlength=bins).astype(ntype)return n, bin_edgesif__name__ =="__main__":img=data.coffee()fig = plt.figure()f1 = fig.add_subplot(141)f1.imshow(img)f1.set_title("image")f2 = fig.add_subplot(142)arr=img.flatten()n, bins, patches = f2.hist(arr, bins=256, facecolor='red')f2.set_title("plt_hist")f3 = fig.add_subplot(143)hist, others = np.histogram(arr, range=(0, arr.max()), bins=256)f3.plot(others[1:],hist)f3.set_title("np_hist1")f4 = fig.add_subplot(144)hist, others = histogram(arr, range=(0, arr.max()), bins=256)f4.plot(others[1:], hist)f4.set_title("np_hist2")plt.show()关于bincount函数,可以参考Xurtle的博⽂https:///xlinsist/article/details/51346523bin的数量⽐x中的最⼤值⼤1,每个bin给出了它的索引值在x中出现的次数。
利用直方图均衡化和规定化进行图像增强的算法设计 数字图像处理毕业论文

目录第1章绪论 (1)1.1 数字图像处理的研究背景 (1)1.2 数字图像处理的研究内容 (1)1.3 DSP系统简介 (2)1.4 图像增强简介 (4)第2章DSP系统 (5)2.1 DSP芯片 (5)2.1.1 DSP芯片的特点 (6)2.1.2 图像处理系统中DSP芯片的选择 (7)2.2 基于DSP的图像处理系统 (8)第3章图像增强 (9)3.1 图像增强的基本概念 (9)3.2 图像增强的方法 (9)3.2.1 图像锐化 (10)3.2.1.1 图像锐化原理 (10)3.2.1.2 拉普拉斯算子 (11)3.2.1.3 基于DSP的算法实现 (12)3.2.1.4 图片锐化效果比较 (14)3.2.2 Sobel边缘检测算法 (16)3.2.2.1 Sobel边缘检测算法原理 (16)3.2.2.2 Sobel边缘检测算法的变异及实现 (16)3.2.3 直方图均衡化算法 (20)3.2.3.1 直方图均衡化 (20)3.2.3.2 直方图规定化 (21)3.2.3.3实验结果及分析 (23)第4章直方图均衡化和规定化算法的DSP实现 (25)4.1 算法的DSP实现与优化 (25)4.1.1 算法开发硬件平台选择 (25)4.1.2 算法的实现与优化 (26)4.2 实验及结果分析 (27)结论 (31)致谢 (32)参考文献 (33)第1章绪论1.1 数字图像处理的研究背景数字图像处理又称为计算机图像处理,它最早出现于20世纪50年代,当时的电子计算机已经发展到一定水平,人们开始利用计算机来处理图形和图像信息。
数字图像处理作为一门学科大约形成于20世纪60年代初期。
图像处理的基本目的是改善图像的质量,它以人为对象,以改善人的视觉效果为目的。
图像处理中,输入的是质量低的图像,输出的是改善质量后的图像,常用的图像处理方法有图像增强、复原、编码、压缩等。
图像处理技术在许多应用领域受到广泛重视并取得了重大的开拓性成就,属于这些领域的有航空航天、生物医学工程、工业检测、机器人视觉、公安司法、军事制导、文化艺术等,使图像处理成为一门引人注目、前景远大的新型学科。
利用直方图均衡化和直方图规定化对图像进行增强

利用直方图均衡化和直方图规定化对图像进行增强利用直方图均衡化和直方图规定化对图像进行增强4.1 利用直方图均衡化对图像进行增强通过灰度变换将一幅图像转换为另一幅具有均衡直方图的图像,即在一定灰度范围内具有相同的象素点数的图像的过程。
其“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直方图均衡化就是对图像进行非线性拉伸,重新分配图像像素值,使一定灰度范围内的像素数量大致相同。
直方图均衡化就是把给定图像的直方图分布改变成“均匀”分布直方图分布。
主要缺点:1、变换后图像的灰度级减少,某些细节消失;2、某些图像,如直方图有高峰,经处理后对比度不自然的过分增强。
算法如下:为讨论方便,以r 和s 分别表示归一化了的原图像灰度和经直方图修正后的图像灰度。
即1,0≤≤s r在[0,1]内设有变换S=T(r)且该函数单调递增,1)(0≤≤r T ,于是有反变换)(1s T r -=有概率论知,如果已知随即变量r 的概率密度)(r p r ,而随机变量s 是r 的函数。
则s 的概率密度)(s p s 可以有)(r p r 求出。
[])()()()()(1s T ds d r p ds dr r p dr r p ds d s p r r r r s -∞-===?从上式可以看出通过变换函数)(r T 可以控制图像灰度级的概率密度函数,从而改变图像灰度层次,这就是直方图修正技术的基础。
因为归一化规定 1)(=s p s有1式有 dr r p ds r )(=两边积分得 dr r p r T s rr )()(0?==上式就是所求得的变换函数。
它表明当变换函数)(r T 是原图像直方图累积分布函数时,能达到直方图均衡化的目的。
离散形式可表示为:∑∑=====ki i k i i r k k n n r p r T s 00)()(可见均衡后的各像素的灰度值k s 可直接由原图像的直方图算出。
直方图均衡化计算
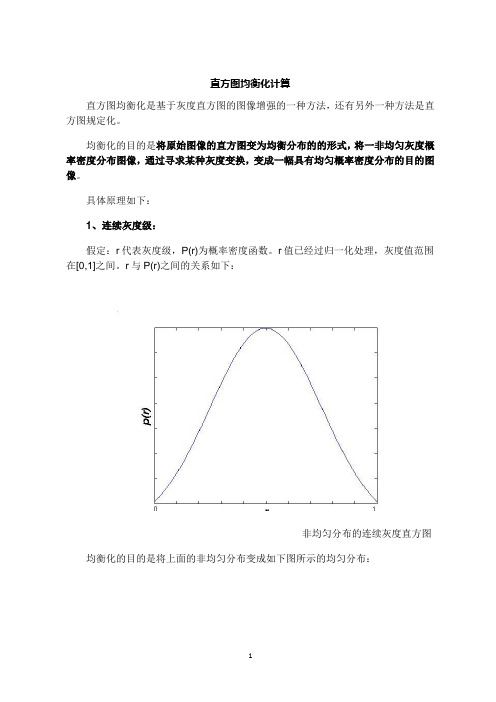
直方图均衡化计算直方图均衡化是基于灰度直方图的图像增强的一种方法,还有另外一种方法是直方图规定化。
均衡化的目的是将原始图像的直方图变为均衡分布的的形式,将一非均匀灰度概率密度分布图像,通过寻求某种灰度变换,变成一幅具有均匀概率密度分布的目的图像。
具体原理如下:1、连续灰度级:假定:r代表灰度级,P(r)为概率密度函数。
r值已经过归一化处理,灰度值范围在[0,1]之间。
r与P(r)之间的关系如下:非均匀分布的连续灰度直方图均衡化的目的是将上面的非均匀分布变成如下图所示的均匀分布:均匀分布的连续灰度直方图我们接下来要做的是要找到一种变换S=T(r)使直方图变平直,为使变换后的灰度仍保持从黑到白的单一变化顺序,且变换范围与原先一致,以避免整体变亮或变暗,需要有如下规定:(1)在0 <= r <= 1中,T(r)是单调递增函数,且0 <= T(r) <= 1;(2)反变换r=(s),(s)也为单调递增函数,且0 <= s <= 1。
直方图均衡化变换公式推导图示因为灰度变换不影响像素的位置分布,而且也不会增减像素数目,所以有如下的推导公式:2、离散灰度级:设一幅图像的像素总数为n,分为L个灰度级,其中::表示第K个灰度级出现的个数。
:第K个灰度级出现的概率。
(0<=<=1, k=0,1,2,...,L-1),公式如下:计算的基本步骤如下:(1)求出图像中所包含的灰度级,一般都经过归一化处理,范围在[0,1]之间,也可以定在[0,L-1]之间。
(2)统计各灰度级的像素数目(k=0,1,2,...,L-1)。
(3)计算图像直方图。
(4)计算变换函数,即:(5)用变换函数计算映射后输出的灰度级。
(6)统计映射后新的灰度级的像素数目。
(7)计算输出图像的直方图。
根据上面推导出来的公式以及计算步骤,我们可以结合栗子来加深理解~~~eg:设图像有64*64=4096的像素,有8个灰度级,灰度分布如下所示:由上图我们知道该图像的,和,下一步我们要做的就是通过变换函数求,即:依次可求得,,,,。
灰度直方图均衡化与规定化

一、课程设计目的(1)进一步掌握matlab的用法;(2)在实践中深入理解图像显示的方法;(3)学会用matlab对图像进行显示。
二、课程设计要求(1)根据题目,查阅有关资料,掌握图像显示技术;(2)学习MATLAB软件,掌握MATLAB各种函数的使用;(3)根据图像显示原理,运用MATLAB进行编程,仿真调制过程,记录并分析仿真结果;(4)形成设计报告。
三、设计方案一般情况下,如果图像的灰度分别集中在比较窄的区间,从而引起图像细节的模糊,为了使图像细节清晰,并使目标得到突出,达到图像增强的目的,可通过改善各部分亮度的比例关系,即通过直方图的方法来实现.直方图的方法是以概率论为基础的.常用的方法有直方图均衡化和直方图规定化.(1)直方图均衡化直方图均衡化又称直方图平坦化,是将一已知灰度概率密度分布的图像经过某种变换,变成一幅具有均匀灰度概率密度分布的新图像.其结果是扩展了像元取值的动态范围,从而达到增强图像整体对比度的效果.直方图均衡化的具体实现步骤如下:1).列出原始图像的灰度级,-=Lfj1,,1,j2).统计各灰度级的像素数目=L,-nj1,,,1j3).计算原始图像直方图各灰度级的频数=Lj=P(-fnn/,)11,,,fjj4).计算累积分布函数1,,,1,0,)()(0-==∑=L k j f P f C k j j f5).应用以下公式计算映射后的输出图像的灰度级,P 为输出图像灰度级的个数,其中INT 为取整符号1,,1]5.0)()[(min min max -=++-=P i g f C g g INT g i6).统计映射后各灰度级的像素数目 ni, i=0,1,…,k,…P-1.7). 计算输出直方图Pg(gi)=ni/n, i=0,1,…,P-1.8). 用fj 和gi 的映射关系修改原始图像的灰度级,从而获得直方图近似为均匀分布的输出图像(2) 直方图规定化直方图均衡化的优点是能自动增强整个图像的对比度,但它的具体增强效果不易控制,处理的结果总是得到全局的均衡化的直方图.实际工作中,有时需要变换直方图使之成为某个特定的形状,从而有选择地增强某个灰度值范围内的对比度,这时可采用比较灵活的直方图规定化方法.直方图规定化增强处理的步骤如下:令Pr (r )和Pz (z )分别为原始图像和期望图像的灰度概率密度函数。
【数字图像处理】直方图的均衡与规定化
【数字图像处理】直⽅图的均衡与规定化很多情况下,图像的灰度级集中在较窄的区间,引起图像细节模糊。
通过直⽅图处理可以明晰图像细节,突出⽬标物体,改善亮度⽐例关系,增强图像对⽐度。
直⽅图处理基于概率论。
直⽅图处理通常包括直⽅图均衡化和直⽅图规定化。
直⽅图均衡化可实现图像的⾃动增强,但效果不易控制,得到的是全局增强的结果。
直⽅图规定化可实现图像的有选择增强,只要给定规定的直⽅图,即可实现特定增强的效果。
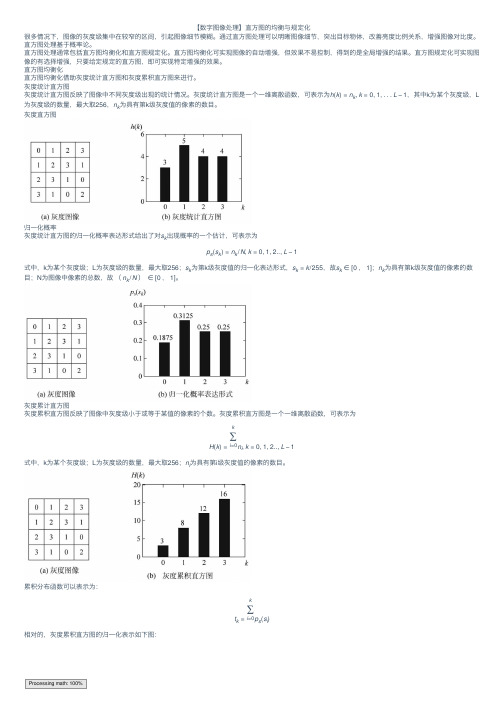
直⽅图均衡化直⽅图均衡化借助灰度统计直⽅图和灰度累积直⽅图来进⾏。
灰度统计直⽅图灰度统计直⽅图反映了图像中不同灰度级出现的统计情况。
灰度统计直⽅图是⼀个⼀维离散函数,可表⽰为h (k )=n k ,k =0,1,...L −1,其中k 为某个灰度级,L 为灰度级的数量,最⼤取256,n k 为具有第k 级灰度值的像素的数⽬。
灰度直⽅图归⼀化概率灰度统计直⽅图的归⼀化概率表达形式给出了对s k 出现概率的⼀个估计,可表⽰为p s (s k )=n k /N ,k =0,1,2..,L −1式中,k 为某个灰度级;L 为灰度级的数量,最⼤取256;s k 为第k 级灰度值的归⼀化表达形式,s k =k /255,故s k ∈[0,1];n k 为具有第k 级灰度值的像素的数⽬;N 为图像中像素的总数,故(n k /N )∈[0,1]。
灰度累计直⽅图灰度累积直⽅图反映了图像中灰度级⼩于或等于某值的像素的个数。
灰度累积直⽅图是⼀个⼀维离散函数,可表⽰为H (k )=k ∑i =0n i ,k =0,1,2..,L −1式中,k 为某个灰度级;L 为灰度级的数量,最⼤取256;n i 为具有第i 级灰度值的像素的数⽬。
累积分布函数可以表⽰为:t k =k ∑i =0p s (s i )相对的,灰度累积直⽅图的归⼀化表⽰如下图:Processing math: 100%原理步骤直⽅图均衡化主要⽤于增强动态范围偏⼩的图像的反差。
图像直方图均衡的标准化与规定化处理

图像直方图均衡的标准化处理均衡化基本原理:对在图像中像素个数多的灰度值(即对画面其主要作用的灰度值)进行展宽,而对像素个数少的灰度值进行归并,从而达到清晰图像的目的。
代码:img=imread('tim.jpg');figure,imshow(img);[m,n]=size(img); %测量图像尺寸参数h=zeros(1,256) %预创建存放灰度出现概率的向量for k=0:255h(k+1)=length(find(img==k))/(m*n);endfigure,bar(0:255,h,'k') %绘制直方图title('原图像直方图')xlabel('灰度值')ylabel('出现概率')S1=zeros(1,256);for i=1:256for j=1:iS1(i)=h(j)+S1(i); %计算SkendendS2=round(S1*256); %将Sk归到相近级的灰度for i=1:256heq(i)=sum(h(find(S2==i))); %显示均衡化后的直方图endfigure,bar(0:255,heq,'k') %显示灰度变化曲线title('均衡化后的直方图')xlabel('灰度值')ylabel('出现概率')figure,plot(0:255,S2,'r') %显示灰度变化曲线legend('灰度变化曲线')xlabel('原图像灰度级')ylabel('均衡化后灰度级')TR=img;for i=0:255TR(find(img==i))=S2(i+1); %将各个像素归一化后的灰度值付给这个像素endfigure,imshow(TR) %将各个像素归一化后的灰度值赋给这个像素 title('均衡化后图像')imwrite(TR,'tim.jpg');实验效果图:原图像原图像直方图标准化后图像标准化后直方图:灰度变化曲线图像直方图均衡的规定化处理直方图规定化的基本原理:有目的地增强某个灰度区间的图像,即能够人为地修正直方图的形状,使之与期望的形状相匹配。
图像增强知识点总结

图像增强知识点总结在图像增强领域,有许多常见的方法和技术,比如灰度变换、直方图均衡化、滤波、锐化、维纳滤波等。
这些方法都有各自的特点和应用场景,下面我们将一一介绍这些知识点。
1. 灰度变换灰度变换是图像增强中最基本的方法之一,它通过对图像的灰度级进行变换,来改善图像的质量。
常见的灰度变换包括线性变换和非线性变换。
线性变换通常使用线性函数来对图像进行变换,而非线性变换则使用非线性函数。
2. 直方图均衡化直方图均衡化是一种常见的图像增强方法,它通过对图像的灰度分布进行重新分配,来增强图像的对比度和清晰度。
直方图均衡化可以有效地增加图像的动态范围,从而使图像更加有吸引力。
3. 滤波滤波是图像增强中常用的方法之一,它通过对图像进行滤波操作,来去除图像的噪声和增强图像的细节。
常见的滤波方法包括均值滤波、中值滤波、高斯滤波等,它们都有各自的适用场景和特点。
4. 锐化锐化是图像增强中常用的方法之一,它通过增强图像的边缘和细节,来使图像更加清晰和鲜明。
常见的锐化方法包括拉普拉斯锐化、梯度锐化等,它们都可以有效地改善图像的质量。
5. 维纳滤波维纳滤波是一种基于统计模型的图像增强方法,它通过对图像进行频域滤波操作,来去除图像的噪声和增强图像的对比度。
维纳滤波可以在去噪和保留图像细节之间取得平衡,从而使图像更加清晰和有吸引力。
6. 小波变换小波变换是一种常用的图像增强方法,它可以将图像分解成不同频率的子带,从而使图像的低频部分和高频部分可以分别进行增强。
小波变换可以有效地增强图像的细节和对比度,从而使图像更加清晰和有吸引力。
7. 自适应增强自适应增强是一种基于局部特性的图像增强方法,它可以根据图像的局部特点来选择适当的增强方法和参数。
自适应增强可以在不同的图像区域使用不同的增强方法,从而使图像在不同区域上都能得到最佳的增强效果。
总结来说,图像增强是图像处理领域中一个重要的研究方向,它可以帮助我们改善图像的质量、清晰度和对比度,使图像更加鲜明、有吸引力。
四、灰度直方图是数字图像处理的重要工作。请简述灰度直方图规定化

其中,n 表示图像中像素的总数,n k 是在图像中出现这种灰度级的次数,L 表示灰度级四、灰度直方图是数字图像处理的重要工作。
请简述灰度直方图规定化、 均衡化的基本原理。
并以分辨率为 5*4,图像的深度6bit 的图像为例,自举例说明直方图均衡化的计算过 程。
解答:数字图像的直方图是作为图像每一个灰度级的统计概率分布 ”它提供了图像灰度分布的 概貌,直方图增强技术正是利用修改给定图像直方图的方法来增强图像的 ,最后得到的图像 增强程度取决于我们所采用的直方图。
令变量 r 和S 分别代表图像增强前后的像素灰度级, 相应灰度级分布的概率密度分别为P (r)和P S (s) o为讨论方便,假设像素灰度值已经归一化在区间[0,1],在灰度级坐标中r=0表示黑,r=1表示白。
对区间[0,1]内任一个r 值按变换函数:S = T(r)( 1)进行变换,T (r )满足两个条件:(1)单值单调递增函数;(2) 0 < T (r )< 1。
条件(1)使灰度级保持从黑到白的次序,条件( 2)保证映射变换后像素灰度值在允许的范围内。
从S 到r 的反变换为:r =T/(S ) , 0< s w 1 o和(2)o 由概率理论知,若P (r)和变换函数s = T(r)drP s (S )=[ P r (r) ]r»s)ds直方图增强技术就是通过变换函数 的外貌。
对于连续图像,变换函数为:rs=T(r) = 0 P(r)dr,0 <r <1此式右边为累积分布函数(CDF ,由该式对r 求导有:ds C 、 ——=P(r) dr代入(3)得到:(6)这说明,在变换后变量S 在定义域内,P s (s)是均匀概率密度。
在图像增强意义上,这 相当于像素的动态范围增加。
对于离散图像,灰度级r k 的概率值为:P r (r k )=nk ,0 <r k <1,k =0,1,2,•.…,L-1n(2)同样,规定变量s 也满足条件(1) 已知,r =T 」(s)是单值单调增加函数,则有:T (r )控制图像灰度级的概率密度函数而改变图像的数目,P r (r k )为第k 级灰度级的概率。
数字图像处理_直方图均衡化

图像变换是数字图像处理中的一种综合变换,如直方图变换。
使用C语言对位图文件的头信息进行读取,从而对图像进行直方图均衡化处理和灰度变换。
直方图均衡化大多数原始的遥感图像由于其灰度分布集中在较窄的范围内,使图像的细节不够清晰,对比度较低。
为了使图像的灰度范围拉开或使灰度均匀分布,从而增大反差,使图像细节清晰,以达到增强的目的,通常采用直方图均衡化及直方图规定化两种变换。
本文主要介绍直方图均衡化并进行实验。
直方图均衡化的概念直方图均衡化(Histogram Equalization)又称直方图平坦化,实质上是对图像进行非线性拉伸,重新分配图像象元值,使一定灰度范围内象元值的数量大致相等。
这样,原来直方图中间的峰顶部分对比度得到增强,而两侧的谷底部分对比度降低,输出图像的直方图是一个较平的分段直方图:如果输出数据分段值较小的话,会产生粗略分类的视觉效果。
直方图均衡化理论假设灰度级为归一化至范围[0,1]内的连续量,并令Pr (r)表示某给定图像中的灰度级的概率密度函数(PDF),其下标用来区分输入图像和输出图像的PDF。
假设我们对输入灰度级执行如下变换,得到(处理后的)输出灰度级s:S=T(r)=∫0r Pr(w)dw式中w 是积分的哑变量。
可以看出,输出灰度级的概率密度函数是均匀的,即a.当0≤s≤1 时,Ps(s)=1b.当s 为其他时,Ps(s)=0换言之,前述变换生成一幅图像,该图像的灰度级较为均衡化,且覆盖了整个范围[0,1]。
灰度级均衡化处理的最终结果是一幅扩展了动态范围的图像,它具有较高的对比度。
该变换函数只不过是一个累积分布函数(CDF)。
直方图均衡化算法直方图均衡化算法将原图像的直方图改变为在整个灰度范围内基本均匀地分布的形式,由此扩大了像素灰度的动态范围,从而增强了图像的对比度。
直方图均衡化算法步骤为:1) 给出原始图像的所有灰度级k S (k=0,1,…,L-1)。
2) 统计原始图像各灰度级的像素数k n 。
直方图均衡化及规定化

直方图均衡化
直方图均衡化示意图
图(a) 原图灰度级直方图;图(b) 累积变换后的直方图; 图(c) 均衡化后的直方图;
直方图均衡化
直方图均衡化
直方图规定化
直方图规定化的原因: 在实际应用中,希望能够有目的地增强某 个灰度区间的图像, 即能够人为地修正直 方图的形状, 使之与期望的形状相匹配, 这就是直方图规定化的基本思想。
s G( z ) ( L 1) q(t )dt
0 z
3.由于它们的直方图均衡化图像理论上是一样的,即:
G( z ) s T (r ), z G 1[T (r )] G 1[s]
于是就得到了根据指定直方图来变换图像的直方图匹配变换。
直方图规定化
直方图规定化
直方图规定化
原图 均衡化的图像
直方图规定化
例如:Pr (r)为原图像的灰度密度函数, Pz (z)为希 望得到的增强图像的灰度密度函数,二者的直方图 如下:
直方图规定化
直方图规定化基本步骤:
1.先对原图做直方图均衡化,得到
s T (r ) ( L 1) p(t )dt
0 r
2.再对规定的直方图均衡化,得到
就给出了一个函数图形,称为直方图。
直方图未规范化 规范化直方图均衡化均衡化的原因: 大多数自然图像,其灰度分布集中在较窄的区间,引起 图像细节不够清晰,采用直方图修正后可使图像的灰度间距 拉开或使灰度分布均匀,从而增大反差,使图像细节清晰,
达到增强的目的。
直方图均衡化
直方图均衡化处理的“中心思想”: 把原始图像的灰度直方图从比较集中的某个灰度区间
变成在全部灰度范围内的均匀分布。
直方图均衡化就是对图像进行非线性拉伸,重新分配
实验一 图像的灰度变换及直方图均衡化

实验一:图像灰度变换及直方图均衡化实验一、实验目的:1. 掌握灰度直方图的概念及其计算方法;2. 掌握利用图像灰度变换实现对图像的增强处理;3. 掌握利用直方图直方图均衡化和直方图规定化实现对图像的增强处理;4. 熟悉MA TLAB中图像增强的相关函数。
二、实验设备:1. 硬件设备:计算机;2. 软件环境:Windows+Matlab编程与仿真环境;3. 其他设备:记录用的纸、笔,以及U盘等存储设备。
三、实验原理:灰度直方图(histogram)是灰度级的函数,它表示图像中具有每种灰度级的像素的个数,反映图像中每种灰度出现的频率。
一般来说,灰度直方图的横坐标是灰度级,纵坐标是该灰度级出现的概率,是图像的最基本的统计特性。
从概率论的观点来理解,灰度出现的频率可看作其出现的概率,这样直方图就对应于概率密度函数PDF(Probability Density Function),而概率分布函数就是直方图的累积和,即概率密度函数的积分。
1. 直方图均衡化直方图均衡化是通过灰度变换将一幅图像转换另一幅具有均衡直方图,即在每个灰度级上都具有相同的像素点数的过程。
设灰度变换s=T(r)为斜率有限的非减连续可微函数,它将输入图像A(x,y)转换为输出图像B(x,y),输入图像的直方图为H a(r),输出图像的直方图为H b(s),它们的关系如下:图1.1 输入图像和输出图像直方图之间的关系图直方图均衡化的基本思想是把原始图像的直方图变换成均匀分布的形式图像灰度值的动态范围,从而达到了增强图像整体对比度的效果。
具体方法为:①列出原始图像的灰度级Sk, k=0,1…L-1,其中L是灰度级的个数;②统计原始图像各灰度级的像素数目nk;③计算原始图像直方图各灰度级的频率数;④计算原始图像的累计直方图;⑤取整计算;⑥确定映射关系;⑦统计新直方图各个灰度级的像素数目nk;⑧计算新的直方图。
2. 灰度变换灰度变换是图像增强的另一种重要手段,它可使图像动态范围加大,使图像对比度扩展,图像更加清晰,特征更加明显。
直方图均衡化

图像的灰度直方图是一个1-D的离散函数
h h ((ff)) n nf f ff 0, 0, 1, 1, ,, L L 1 1
灰度累积直方图也是一个1-D的离散函数
c( f ) n i
i 0 f
f 0, 1,
, L 1
直方图均衡化
直方图均衡化主要用于增强动态范围偏小的图像 的反差。
直方图均衡化
原始图像各灰度级对应的概率分布
例
灰度级
0
1
2
3
4
5
6
7
像素
概率
790
1023 850
656
329
245
122
0.03
81
0.02
0.19 0.25
0.21 0.16
0.08 0.06
18
直方图均衡化
图像直方图均衡化过程如下:
(1)得到变换后的值:
例解:
t 0 T ( s0 ) t1 T (s1 )
我们注意到在暗色的图像中,直 方图的组成成分集中在灰度级低 (暗)的一侧;反之,明亮的图 像的直方图的组成成分则集中在 灰度级高(亮)的一侧;动态范 围小,也就是对比度小,这种图 像直方图集中于灰度级的中部; 动态范围正常的图像直方图的成 分覆盖了灰度级很宽的范围。 直观上,若一图像像素占有全部 可能的灰度级并且分布均匀,则 图像有高的对比度和多变的灰度 色调,即,可通过改变直方图的 形状来达到增强图像对比度。
nk Pr ( rk ) 0 rk 1 n k 0, 1, 2 , , l 1
式中,nk为图像中出现rk 这种灰度的像素数,n 是 图像中像素总数,而 n k 就是概率论中所说的频数。 n 在直角坐标系中作出 rk 与Pr(rk) 的关系图形,这个图 形称为直方图。
【数字图像处理】灰度直方图、直方图均衡化、直方图规定化

【数字图像处理】灰度直⽅图、直⽅图均衡化、直⽅图规定化灰度直⽅图 ⼀幅图像由不同灰度值的像素组成,图像中灰度的分布情况是该图像的⼀个重要特征。
图像的灰度直⽅图就描述了图像中灰度分布情况,能够很直观的展⽰出图像中各个灰度级所占的多少。
图像的灰度直⽅图是灰度级的函数,描述的是图像中具有该灰度级的像素的个数:其中,横坐标是灰度级,纵坐标是该灰度级出现的频率。
灰度直⽅图的计算公式如下:p(rk)=nk/MN其中,rk是像素的灰度级,nk是具有灰度rk的像素的个数,MN是图像中总的像素个数。
直⽅图均衡化 Histogram Equalization假如图像的灰度分布不均匀,其灰度分布集中在较窄的范围内,使图像的细节不够清晰,对⽐度较低。
通常采⽤直⽅图均衡化及直⽅图规定化两种变换,使图像的灰度范围拉开或使灰度均匀分布,从⽽增⼤反差,使图像细节清晰,以达到增强的⽬的。
直⽅图均衡化,对图像进⾏⾮线性拉伸,重新分配图像的灰度值,使⼀定范围内图像的灰度值⼤致相等。
这样,原来直⽅图中间的峰值部分对⽐度得到增强,⽽两侧的⾕底部分对⽐度降低,输出图像的直⽅图是⼀个较为平坦的直⽅图。
均衡化算法直⽅图的均衡化实际也是⼀种灰度的变换过程,将当前的灰度分布通过⼀个变换函数,变换为范围更宽、灰度分布更均匀的图像。
也就是将原图像的直⽅图修改为在整个灰度区间内⼤致均匀分布,因此扩⼤了图像的动态范围,增强图像的对⽐度。
通常均衡化选择的变换函数是灰度的累积概率,直⽅图均衡化算法的步骤:计算原图像的灰度直⽅图 P(Sk)=nknP(Sk)=nkn,其中nn为像素总数,nknk为灰度级SkSk的像素个数计算原始图像的累积直⽅图 CDF(Sk)=∑i=0knin=∑i=0kPs(Si)CDF(Sk)=∑i=0knin=∑i=0kPs(Si)Dj=L⋅CDF(Si)Dj=L⋅CDF(Si),其中 DjDj是⽬的图像的像素,CDF(Si)CDF(Si)是源图像灰度为i的累积分布,L是图像中最⼤灰度级(灰度图为255)灰度直⽅图均衡化实现的步骤1.统计灰度级中每个像素在整幅图像中的个数2.计算每个灰度级占图像中的概率分布3.计算累计分布概率4.计算均衡化之后的灰度值5.映射回原来像素的坐标的像素值⽰例说明来看看通过上述步骤怎样实现的拉伸。
直方图均衡化及直方图规定化

《数字图像处理》实验报告(二)学号:____________ 姓名:__________ 专业:____ 课序号:__________计算机科学与技术学院实验2直方图均衡化一、实验学时:4学时(本部分占实验成绩的40%)二、实验目的:1、理解直方图均衡化的原理及步骤;2、编程实现图像(灰度或彩色)的直方图均衡化。
三、必须学习和掌握的知识点:直方图均衡化是一种快速有效且简便的图像空域增强方法,在图像处理中有着非常重要的意义,因此要求掌握。
四、实验题目:编程实现灰度图像的直方图均衡化处理。
要求给出原始图像的直方图、均衡化图像及其直方图和直方图均衡化时所用的灰度级变换曲线图。
五、思考题:(选做,有加分)实现对灰度图像的直方图规定化处理。
六、实验报告:请按照要求完成下面报告内容并提交源程序、可执行程序文件和实验结果图像。
1、请详细描述本实验的原理:1.直方图均衡化概述图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。
直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。
直方图拉伸是通过对比度拉伸对直方图进行调整,从而“扩大”前景和背景灰度的差别,以达到增强对比度的目的,这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。
直方图均衡化的英文名称是Histogram Equalization.直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。
这种方法通常用来增加许多图像的局部对比度,尤其是当图像的有用数据的对比度相当接近的时候。
通过这种方法,亮度可以更好地在直方图上分布。
这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
2基本思想直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直方图均衡化和直方图规定化-实验报告
一、实验目的掌握直方图均衡化和直方图规定化的图像增强方法掌握图像平滑滤波和锐化滤波的模板计算方法二、实验内容:1. 使用IPT中imhist,histeq函数进行直方图的均衡化和规定化,并显示结果2. 编写myhisteq函数实现直方图均衡化,与1中结果进行对比3. 给读取的图像叠加椒盐噪音(imnoise),分别使用均值滤波和中值滤波进行去噪,并对比图像处理的结果(使用IPT函数)4. 自定义3*3模板矩阵F,编写myfilter函数实现模板和图像的卷积运算,设计模板矩阵,实现图像的平滑和锐化。
三、实验代码及结果(1) 直方图的均衡化和规定化clc;clear;I= imread('H:\image\jpg\flower.jpg');I= rgb2gray(I) ; %将图像转换为灰度图像J= histeq( I) ; %对I 进行直方图均衡化figure,subplot( 2,2,1) ,imshow(I) ,title('原始图像') ;subplot (2,2,2), imshow(J), title('直方图均衡化后的图像');subplot( 2,2,3) ,imhist(I, 64), title( '原始的直方图');subplot( 2,2,4) ,imhist(J,64) ,title(' 均衡化后的直方图');clc;clear;I= imread('H:\image\jpg\flower.jpg');I= rgb2gray(I) ; %将图像转换为灰度图像h=0:255;h=1-h/255;J= histeq( I,h) ;figure,subplot( 2,3,1) ,imshow(I) ,title('原图像') ; subplot( 2,3,2) ,imhist(I, 64), title( '原图像的直方图'); subplot (2,3,3), stem(h), title('目标直方图');subplot( 2,3,4) ,imshow(I, 64), title( '规定化后的图像'); subplot( 2,3,5) ,imhist(J,64) ,title(' 规定化后的直方图');二、myhisteq函数实现直方图均衡化I = imread('j:\image\jpg\flower.jpg');I = rgb2gray(I);[height,width] = size(I);figuresubplot(2,2,1)imshow(I)%显示原始图像title('原图像');subplot(2,2,2)imhist(I)%显示原始图像直方图title('原图像直方图');%进行像素灰度统计;s = zeros(1,256);%统计各灰度数目,共256个灰度级for i = 1:heightfor j = 1: widths(I(i,j) + 1) = s(I(i,j) + 1) + 1;%对应灰度值像素点数量增加一endend%计算灰度分布密度p = zeros(1,256);for i = 1:256p(i) = s(i) / (height * width * 1.0);end%计算累计直方图分布c = zeros(1,256);c(1) = p(1);for i = 2:256c(i) = c(i - 1) + p(i);end%累计分布取整,将其数值归一化为1~256c = uint8(255 .* c + 0.5);%对图像进行均衡化for i = 1:heightfor j = 1: widthI(i,j) = c(I(i,j)+1);endendsubplot(2,2,3)imshow(I)%显示均衡化后的图像title('均衡化后图像');subplot(2,2,4)imhist(I)%显显示均衡化后的图像的直方图title('均衡化后图像的直方图');三、使用均值滤波和中值滤波进行去噪I= imread('j:\image\jpg\flower.jpg');I= rgb2gray(I) ; %将图像转换为灰度图像I1 = imnoise(I,'salt & pepper',0.02);%0.02是噪声强度,其值越大噪声越多h=fspecial('average',5);J1=filter2(h,I1,'valid');J2= imfilter(I1,h,'full');figure,subplot(3,3,1),imshow(I1);title('原始椒盐噪声图像图1');subplot(3,3,2),imshow(uint8(J1));title('filter2均值滤波图2');subplot(3,3,3),imshow(J2);title('imfilter均值滤波图3');J3 = medfilt2(I1,[5,5]);subplot(3,3,4),imshow(J3),title('中值滤波效果图4');G1= histeq(I1);subplot(3,3,5),imhist(G1,64),title('原图均衡化后的直方图');G2= histeq(J1);subplot(3,3,6),imhist(uint8(G2),64),title('图2均衡化后直方图'); G3= histeq(J2);subplot(3,3,7),imhist(G3,64),title('图3均衡化后直方图');G4= histeq(J3);subplot(3,3,8),imhist(G4,64),title('图4均衡化后直方图');问题:对于filter2均值滤波均衡化直方图不显示,不知道原因。
直方图修正法

直方图修正法分为直方图均衡化和直方图规定化目的:采用直方图修整后可使图像的灰度间距拉开或使灰度分布均匀,从而增大反差,使图像细节清晰,从而增强图像。
1.直方图均衡化通过对原图像进行某种变换使原图像的灰度直方图修正为均匀的直方图的一种方法以r 和s 分别表示归一化了的原图像灰度和经直方图修正后的图像灰度。
即 1,0≤≤s r 在[]1,0区间内的任一个r ,经变换T (r )都可产生一个S ,且 S=T(r)T(r)为变换函数,应满足下列条件:(1)在10≤≤r 内为单调递增函数(保证灰度级从黑到白的次序不变);(2)在10≤≤r 内,有1)(0≤≤r T 。
(确保映射后的像素灰度在允许的范围内) 由概率论理论可知,如果已知随机变量r 的概率密度为)(r p r ,而随机变量s 是r 的函数,则s 的概率密度)(s p s 可以由)(r p r 求出。
假定随机变量s 的分布函数用)(s F s 表示,根据分布函数定义,则有⎰⎰∞-∞-==s r r s s dr r ds s s p p F )()()([])()(1s dsd s T p p r s -=⇒ (1) 因为归一化假定 1)(=s p s由(1)得dr r ds p r )(= 两边积分得 ⎰==rrdr r r T s p 0)()( (变换函数) 上式表明当变换函数T (r )是原图像直方图累积分布函数时,能达到直方图均衡化的目的。
对于灰度级为离散的数字图像,用频率来代替概率。
∑∑=====k j k j j j r k k n r T n r p s 00)()(1,,2,1,0,10-=≤≤L k r k2.直方图规定化(直方图匹配)使原图像灰度直方图变成规定形状的直方图而对图像作修正的增强方法。
假设)(r p r 和)(z p z分别表示已归一化的原图像灰度概率密度函数和希望得到的图像概率密度函数。
首先对原图像进行直方图均衡化处理,即求变换函数:⎰==rrdr r r T s p 0)()( 假定已得到了所希望的图像,对它也进行均衡化处理,即⎰==zzdr r z G v p 0)()( (2) 它的逆变换是 )(1v z G -=即由均衡化后的灰度级得到希望图像的灰度级。
【OpenCV】图像增强---灰度变换、直方图均衡化

【OpenCV】图像增强---灰度变换、直⽅图均衡化图像增强的⽬的:改善图像的视觉效果或使图像更适合于⼈或机器的分析处理。
通过图像增强,可以减少图像噪声,提⾼⽬标与背景的对⽐度,也可以增强或抑制图像中的某些细节。
---------------------------------------------------------------------------------------------------灰度变换:把原图像的像素灰度经过某个函数变换成新图像的灰度。
可分为直线灰度变换法和直⽅图修正法。
直线灰度变换法:线性、分段线性、⾮线性变换。
直⽅图修正法:直⽅图均衡化、直⽅图规定化。
---------------------------------------------------------------------------------------------------图像直⽅图:是对像素的某种属性(如灰度、颜⾊、梯度等)分布进⾏统计分析的重要⼿段。
灰度直⽅图:是灰度级的函数,它反映了图像中每⼀灰度级出现的次数或频率。
直⽅图均衡化:把原始图像的直⽅图变换为均匀分布的形式,从⽽增加图像灰度的动态范围,以达到增强图像对⽐度的效果。
经过均衡化处理的图像,其灰度级出现的概率相同,此时图像的熵最⼤,图像所包含的信息量最⼤。
【注意,离散后是每块区域的概率相等,均衡化后并不是条直线哦。
】 细节概念等省略......---------------------------------------------------------------------------------------------------线性灰度增强、对数变换、指数变换、直⽅图均衡化。
代码见下(代码略粗糙...)【ImageEnhance.cpp部分代码】1//线性灰度增强2bool CImageEnhance::GrayLinearTransform(Mat &src, Mat &dst, uchar c, uchar d)3 {4int b=0,a=255;5 dst = src.clone();6int row = dst.rows, col = dst.cols * dst.channels();7 uchar *cc = dst.data;8for(int i = 0; i < row; ++i) {9for(int j = 0; j < col; ++j) {10int val = *cc;11if(a > val) a = val;12if(b < val) b = val;13 cc++;14 }15 }16 cc = dst.data;17float k = float(d - c)/(b-a);18//CString c1; c1.Format(_T("a=%d,b=%d,c=%d,d=%d,k=%.2f\n"), a,b,c,d,k);MessageBox(c1);19for(int i = 0; i < row; ++i) {20for(int j = 0; j < col; ++j) {21int val = *cc;22int s = (int)(k*(val - a) + c);23 *cc = s;24 cc++;25 }26 }27return true;28 }29//对数变换30bool CImageEnhance::GraynoLinearlog(Mat &src, Mat &dst) {31 dst = src.clone();32int row = dst.rows, col = dst.cols * dst.channels();33 uchar *cc = dst.data;34double k = 255 / log10(256.0);35for(int i = 0; i < row; ++i) {36for(int j = 0; j < col; ++j) {37int val = *cc;38 *cc = k * log10(1.0*(val + 1));39 cc++;40 }41 }42return true;43 }44//指数变换45bool CImageEnhance::GraynoLinearindex(Mat &src, Mat &dst) {46 dst = src.clone();47int row = dst.rows, col = dst.cols * dst.channels();48 uchar *cc = dst.data;49double k = 1.0 / 255;50for(int i = 0; i < row; ++i) {51for(int j = 0; j < col; ++j) {52int val = *cc;53 *cc = k * val * val;54 cc++;55 }56 }57return true;58 }5960 MatND CImageEnhance::getHist1(Mat& image)61 {62 MatND hist;63int channels[] = {0};64int dims = 1;65int histSize[] = {256}; //直⽅图箱⼦的个数66float granges[] = {0, 255};67const float *ranges[] = {granges}; //像素值范围68//计算直⽅图69 calcHist(&image, 1, channels, Mat()/*不使⽤掩码*/, hist, dims/*这是⼀维的直⽅图*/, histSize, ranges);70return hist; //这⾥得到的hiat是256⾏⼀列的Mat71 }7273//直⽅图均衡化74bool CImageEnhance::Equalize_hist(cv::Mat& src,cv::Mat& dst)75 {76//CMFC_Test_lyyDlg pic;77 MatND hist;78int channels[] = {0};79int dims = 1;80int histSize[] = {256}; //直⽅图箱⼦的个数81float granges[] = {0, 255};82const float *ranges[] = {granges}; //像素值范围83//计算直⽅图84 Mat image = src.clone();85 calcHist(&image, 1, channels, Mat()/*不使⽤掩码*/, hist, dims/*这是⼀维的直⽅图*/, histSize, ranges);8687//MatND hist = getHist1(src);//pic.getHist(dst);88float s[256];89float p[256];9091 cv::Mat lookup(cv::Size(1, 256), CV_8U);92int pixNum = src.cols * src.rows;//总像素个数93for (int i =0; i <256; i++) {94 s[i] = hist.at<float>(i) / pixNum;95if (i ==0) {96 p[i] = s[i];97 }98else {99 p[i] = p[i -1] + s[i];100 }101 }102for (int i =0; i <256; i++) {103 lookup.at <uchar>(i) = static_cast<uchar>(p[i]*255.0);104 }105106 cv::LUT(src, lookup, dst);//创建矩阵,把⼀个像素值映射到另⼀个像素值107return true;108 }ImageEnhance.cpp效果如下:原图像:线性灰度增强:我这⾥默认a和b表⽰原图像灰度值的最⼩与最⼤值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、课程设计目的(1)进一步掌握matlab的用法;(2)在实践中深入理解图像显示的方法;(3)学会用matlab对图像进行显示。
二、课程设计要求(1)根据题目,查阅有关资料,掌握图像显示技术;(2)学习MATLAB软件,掌握MATLAB各种函数的使用;(3)根据图像显示原理,运用MATLAB进行编程,仿真调制过程,记录并分析仿真结果;(4)形成设计报告。
三、设计方案一般情况下,如果图像的灰度分别集中在比较窄的区间,从而引起图像细节的模糊,为了使图像细节清晰,并使目标得到突出,达到图像增强的目的,可通过改善各部分亮度的比例关系,即通过直方图的方法来实现.直方图的方法是以概率论为基础的.常用的方法有直方图均衡化和直方图规定化.(1)直方图均衡化直方图均衡化又称直方图平坦化,是将一已知灰度概率密度分布的图像经过某种变换,变成一幅具有均匀灰度概率密度分布的新图像.其结果是扩展了像元取值的动态范围,从而达到增强图像整体对比度的效果.直方图均衡化的具体实现步骤如下:1).列出原始图像的灰度级=L,-fj,,1,1j2).统计各灰度级的像素数目=Lj,-n1,,1,j3).计算原始图像直方图各灰度级的频数=L (-=jnfnP/),11,,,fjj4).计算累积分布函数1,,,1,0,)()(0-==∑=L k j f P f C k j j f5).应用以下公式计算映射后的输出图像的灰度级,P 为输出图像灰度级的个数,其中INT 为取整符号1,,1]5.0)()[(min min max -=++-=P i g f C g g INT g i6).统计映射后各灰度级的像素数目 ni, i=0,1,…,k,…P-1.7). 计算输出直方图Pg(gi)=ni/n, i=0,1,…,P-1.8). 用fj 和gi 的映射关系修改原始图像的灰度级,从而获得直方图近似为均匀分布的输出图像(2) 直方图规定化直方图均衡化的优点是能自动增强整个图像的对比度,但它的具体增强效果不易控制,处理的结果总是得到全局的均衡化的直方图.实际工作中,有时需要变换直方图使之成为某个特定的形状,从而有选择地增强某个灰度值范围内的对比度,这时可采用比较灵活的直方图规定化方法.直方图规定化增强处理的步骤如下:令Pr (r )和Pz (z )分别为原始图像和期望图像的灰度概率密度函数。
如果对原始图像和期望图像均作直方图均衡化处理,应有⎰==x r dr r P r T S 0)()( (1) ⎰==xz dzz p Z G V 0)()( (2) )(1V G Z -= (3)由于都是进行均衡化处理,处理后的原图像概率密度函数Ps (S )及理想图像概率密度函数PV (V )是相等的。
于是,我们可以用变换后的原始图像灰度级S 代替(2)式中的V 。
即Z = G - 1(S ) (4)这时的灰度级Z 便是所希望的图像的灰度级。
此外,利用(1)与(3)式还可得到组合变换函数Z = G - 1[T (r )] (5) 对连续图像,重要的是给出逆变换解析式。
对离散图像而言,有n n Z P ii Z =)( (6)∑-===10)()(l i i z i i Z P Z G V (7))]([)(11i i i r T G S G Z --== (8)四、设计内容%----------------------------选择图片路径及显示---------------------------%global f%选择图片路径[filename,pathname]= ... %...表示与下行连接uigetfile({'*.bmp';'*.jpg';'*gif';'*tif'},'选择图片');%打开文件类型,对话框名称f=imread([pathname filename]);axes(handles.axes1); %在axes1显示原图像imshow(f) ;title('原始图像');%------------------设置下拉菜单分别选择显示图像------------%global fva=get(handles.popupmenu1,'Value');val=get(hObject,'Value');switch val %用switch 语句设置选项case 1 %原图像直方图I=double(f);[m,n]=size(I);H=zeros(1,256);for i=1:mfor j=1:nH(I(i,j)+1)=H(I(i,j)+1)+1;endends=zeros(1,256);t=zeros(1,256);for i=1:256 s(i)=H(i)/(m*n);for j=1:it(i)=t(i)+s(j);endendaxes(handles.axes2);plot(s);title('原图像直方图');case 2 %均衡化后图像及直方图I=double(f);[m,n]=size(I);H=zeros(1,256);for i=1:mfor j=1:nH(I(i,j)+1)=H(I(i,j)+1)+1;endends=zeros(1,256);t=zeros(1,256);for i=1:256 s(i)=H(i)/(m*n);for j=1:it(i)=t(i)+s(j);endendt1=round(t*(256-1)+0.5);H1=zeros(1,256);for i=1:256H1(t1(i))=H1(t1(i))+s(i);endaxes(handles.axes4);bar(H1);title('均衡化后直方图');I2=t1(I+1)-1;axes(handles.axes3);imshow(uint8(I2));title('均衡化后图像');case 3 %规定化后图像及直方图I=f;J=I;New=I;L=256; %灰度级Ps=zeros(L,1); % 存储原图像直方图概率数据 nk=zeros(L,1); % 存储原图像直方图数据nk2=zeros(L,1); % 存储直方图规定化后的图像的直方图 Rk=zeros(L,1); % 存储原图像累积直方图数据Ps2=zeros(L,1);Rk2=zeros(L,1);[row,col]=size(I); % 计算图像数据矩阵的行列数n=row*col; %总像素个数for i = 1:rowfor j = 1:colnum = double( I(i,j))+1; %获取像素灰度级nk(num) = nk(num)+1; %统计nkendend%计算直方图概率估计for i=1:LPs(i)=nk(i)/n;%计算累积直方图if i==1Rk(i)=Ps(i);else 1<=256Rk(i)=Rk(i-1)+Ps(i);end%规定化直方图Ps2Temp=[0.05,zeros(1,9),0.05,zeros(1,9),0.05,zeros(1,9),0.05,zeros(1,9),0.05,zeros(1,9),0.05,zeros(1,9),0.05,zeros(1,39),0.05,zeros(1,19),0.05,zeros(1,19),0.05,zeros(1,19),ones(1,80).*0.0045,ones(1,16).*0.0088];Ps2=Ps2Temp';%计算规定化累积直方图for c=1:Lif c==1Rk2(c)=Ps2(c);elseRk2(c)=Rk2(c-1)+Ps2(c);endend%计算原图像与目标图像累计直方图数值的差的绝对值double ScMin=zeros(256,256);for Y=1:Lfor X=1:LScMin(X,Y)=abs(Rk(Y)'-Rk2(X)');endend%建立映射HisM=zeros(L:1);for P=1:Lmin = 0;minV=ScMin(1,P);for Q=1:Lif(minV>ScMin(Q,P))minV=ScMin(Q,P);min = Q;endendHisM(P)= min;end%将原图像的每个像素灰度转换为直方图均衡化后的灰度for x = 1:rowfor y = 1:colNum = double( I(x,y))+1;if Num==iNew(x,y)=HisM(i);endendendend%计算直方图规定化后的直方图for p = 1:rowfor q = 1:colNN = double( New(p,q))+1;nk2(NN) = nk2(NN)+1;endendaxes(handles.axes5);imshow(New),title('规定化后图像');axes(handles.axes6);plot(Ps2),title('规定化后直方图');end;%--------------------直接调用函数-----------------------------------------%global fva=get(handles.popupmenu2,'Value');val=get(hObject,'Value');switch valcase 1axes(handles.axes1); %在axes1显示图像imshow(f);title('原图像');axes(handles.axes2);h=imhist(f,256);plot(h)ylim('auto'); %自动设定Y轴坐标范围和刻度title('原始直方图')case 2j=histeq(f);axes(handles.axes3);imshow(j) ;title('均衡化图像');axes(handles.axes4);h=imhist(j,256);plot(h)ylim('auto');title('均衡化图像直方图')case 3hgram=50:2:250k=histeq(f,hgram);axes(handles.axes5);imshow(k) ;title('规定化图像');axes(handles.axes6);h=imhist(k,256);plot(h)ylim('auto');title('规定化图像直方图')end;五、实验结果GUI界面设计:选择图片路径:直接调用函数均衡化和规定化:原图像与均衡化和规定化后对比:六、结果分析通过直接调用函数和编程对图像进行处理的结果对比,可以看出实验结果和理论结果基本一致;在编程处理中,可以自定义对规定化中的直方图(Ps2Temp)进行修改,从而得到所希望的图像增强效果.七、总结分析一周的数字图像处理课程设计,最大的收获是初步的掌握的Matlab软件的使用,通过这次课程设计,我学会如何利用MATLAB制作视图界面(GUI),并通过视图界面对数字图像进行处理,方便快捷,而且美观。
