4 方差分析--医学统计
医学统计学 -第08章 方差分析

第一节 方差分析的基本思想
看一个例子
例8-1 为研究钙离子对体重的影响作用,某研究者将36 只肥胖模型大白鼠随机分为三组,每组12只,分别给 予高脂正常剂量钙(0.5%)、高脂高剂量钙(1.0%)和高 脂高剂量钙(1.5%)三种不同的饲料,喂养9周,测其 喂养前后体重的差值。问三组不同喂养方式下大白鼠 体重改变是否不同?
• 三种喂养方式体重改变的平均值各不相同,这种变异 称为组间变异
•
是组内均值
X
与总均值
i
X
之差的平方和
360
340
组间变异反映了:
320
三种喂养方式的差异(影响), 300
同时也包含了随机误差。
280
260
240
k ni
220
SS组间
(Xi X )2
200
i1 j
180
X甲
X
X乙
X丙
甲
乙
丙
3、组内变异(SS组内,variation within groups)
0.05
2、根据公式计算SS、MS及F值,列于方差分析表内(计 算过程省略)
变异来源 总变异 组间 组内(误差)
完全随机设计的方差分析表
平方和 SS 自由度
均方MS
47758.32
35
31291.67
2
15645.83
16466.65
33
498.99
F值
31.36
3、确定P值,作出判断
分子自由度=k-1=2,分母自由度=n-k=33,查F 界值表(方差分析用)
表 8-1 三种不同喂养方式下大白鼠体重喂养前后差值(g)
正常钙(0.5%) 高剂量钙(1.0%) 高剂量钙(1.5%)
方差分析原理

方差分析原理方差分析(Analysis of Variance,简称ANOVA)是一种统计方法,用于比较两个或多个样本均值之间的差异。
它能够帮助我们确定多个样本的均值是否存在显著差异,并进一步了解差异来自于哪些因素。
本文将介绍方差分析的原理和应用。
一、方差分析的背景在实际问题中,我们常常需要比较不同样本的均值,以了解它们之间是否存在差异。
例如,我们想要知道不同药物对治疗某种疾病的疗效是否有差别,或者不同教学方法对学生成绩是否有影响等。
这时候,我们需要用到方差分析这个统计工具。
二、方差分析的基本原理方差分析的基本原理是通过比较组内变异(Within-group variation)与组间变异(Between-group variation)的大小来判断多个样本的均值是否存在显著差异。
组内变异指的是同一组内个体(观察值)之间的差异,也可以看作是测量误差或个体内部差异。
组间变异指的是不同组之间的差异,也可以理解为组与组之间的差别。
我们的目标是判断组间变异是否显著大于组内变异。
统计学家通过构建方差分析的假设检验来实现这一目标。
假设检验的零假设(null hypothesis)是所有样本的均值相等,备择假设(alternative hypothesis)则是至少存在一个样本的均值与其他样本不同。
三、方差分析的步骤进行方差分析时,一般需要按照以下步骤进行:1. 提出假设:定义零假设和备择假设。
2. 选择显著性水平:通常为0.05,表示我们要找到的结论是在5%的显著水平下成立。
3. 收集数据:需要收集多个组别的数据,并记录下来。
4. 计算方差:通过计算组内变异和组间变异。
5. 计算F统计量:F统计量用于判断组间变异是否显著大于组内变异,可以通过计算组间均方与组内均方之比得到。
6. 判断:根据F统计量与给定显著性水平的临界值进行比较,如果F统计量大于临界值,则拒绝零假设,表示至少存在一个样本均值与其他不同。
7. 进行事后分析(post hoc analysis):如果方差分析的结果是显著的,我们可以进行事后分析,以确定具体哪些组别之间存在差异。
医学统计学(方差分析)
各种变异的表示方法
04
列举存在的变异及意义
各种变异的表示方法
SS总 总 MS总
SS组内 组内 MS组内
SS组间 组间 MS组间
三者之间的关系: SS总= SS组内+ SS组间 总= 组内+ 组间
F=MS组间/MS组内
自由度: 组间=组数-1
组内=N-组数
通过这个公式计算出统计量F,查表求出对应的P值,与进行比较,以确定是否为小概率事件。
01
计算 C=(Σx) 2/N=(3309.5) 2/30=365093 SS总=Σx2-C=372974.87-365093=7881.87
α=0.05
02
SS组内=SS总-SS组间=7881.87-2384.026=5497.84
Ν总=N-1=29, Ν组间=k-1=2, Ν组内=N-k=30-3=27
159.0
111.0
115.0
合计Σxij
1160
921.5
1228
3309.5(Σx)
ni
11
9
10
30(N)
均数
105.45
102.39
122.80
110.32()
糖尿病
IGT
正常人
xij
106.5
Σ
Σxij2
123509.52
144.0
105.2
124.5
117.0
109.5
105.1
110.0
96.0
76.4
109.0
115.2
95.3
103.
95.3
医学统计学方差分析

SS误差 = SS总- SS处理- SS区组
处理=k-1,
区组= b-1
(1)F处理= MS处理/ MS误差 (2) F区组= MS区组/ MS误差
误差= 总 - 处理- 区组
(1) H0: 三种方法治疗后血红蛋白增加量总体均数相等 H1: ……不等或不全相等
(2) H0:各区组血红蛋白增加量总体均数相等 H1: ……不等或不全相等
问题
某医师用A、B和C三种方案治疗婴幼儿贫血患 者,治疗一个月后,血红蛋白的增加克数如下表,问三 种治疗方案对婴幼儿贫血的疗效是否相同?
表 5 .1 三 种 方 案 治 疗 后 血 红 蛋 白 增 加 量 ( g / L )
A
B
C
24
20
20
36
18
11
25
17
6
14
10
3
26
19
0
34
24
-1
23
4
5
合计
n
7
6
8
21
Σ jΧ
182
108
48
338
Σ jΧ 2
5054
2050
608
7712
X
26
18
6
22.8
第四章 方差分析
Analysis of variance ANOVA
第四章 方差分析
•方差分析的基本思想
•应用与资料要求 • 完全随机设计资料的方差分析 •随机区组设计资料的方差分析 •拉丁方设计资料的方差分析 •交叉设计资料的方差分析 •多个样本均数间的多重比较 •析因设计资料的方差分析 •正交设计资料的方差分析 •多元方差分析 •常用的数据转换方法 •课堂讨论
医学统计学 方差分析

100.66
110.31
4
367.60
5
80.57
97.90
115.76
103.56
4
397.79
6
102.77
81.20
90.30
138.54
4
412.81
ni
6
6
6
6
24( n )
Xi
550.01
537.30
618.19
726.28
2431.78( X )
Xi
91.67
89.55
103.03
2 =32 得: F0.05(2,32) 3.30, F0.01(2,32) 5.34 ,P<0.01。按 =0.05 水准,拒绝 H0 ,
差别有统计学意义,可以认为喂养三种不同饲料的大鼠红细胞数的总体均数不 全相同。
随机区组设计的两因素方差分析
例9.2 利用随机区组设计研究不同温
度对家兔血糖浓度的影响,某研究者进行 了如下实验:将 24只家兔按窝别配成6个 区组, 每组 4 只, 分别随机分配到温度 15℃、 20℃、 25℃、 30℃的4个处理组 中,测量家兔的血糖浓度值(mmol/L),结 果如下表9.4所示,分析4种温度下测量家 兔的血糖浓度值是否不同?
23
3742.5521
3
1247.5174 8.2717
1491.2744
5
298.2549 1.9776
2262.2511
15
150.8167
P
<0.01 >0.05
3. 确定 P 值,作出统计推断
根据处理组 F 值的分子的自由度处理 ,分母的自由度 误差 ;区组 F 值的分子的 自由度区组 ,分母的自由度 误差 查 F 界值表(附表 4),得到处理组和区组的 P 值。 根据表 9.6,按 =0.05 水准,对于不同区组间,不拒绝 H0 ,尚不能认为不同窝 别家兔血糖浓度值不同;对于不同处理组间,拒绝 H0 ,接受 H1 ,差异具有统 计学意义,可以认为 4 种温度下家兔血糖浓度值不全相同,即处理组 4 个总体 均数中至少有 2 个不同。
方差分析-4

第四章 多个样本均数比较的
方差分析
analysis of variance, ANOVA
第六节
多个样本均数间的多重比较
(multiple comparison)
当方差分析的结果为拒绝H0,接 受H1时,只说明g个总体均数不全相 等。若想进一步了解哪两个总体均
数不等,需进行多个样本均数间的
SXiX j =
0.43
1 30
1 30
=0.17
2.72 3.43
LSD-t = =
=-4.18
0.17
以 ν=116 查附表 2 的 t 界值表,得 P<0.05。按
0.05 水准,拒绝 H0,接受 H1,差别有统计学意
义。可认为降血脂新药 2.4g 组的低密度脂蛋白含量
检验统计量t的计算公式
LSD t Xi X j , SXiX j
误差
SXiX j
MS误差
1 ni
1 nj
MS误差:完全随机设计方差分析的误差均方
检验界值查p804附表2 tM界S误差 值表MS组内
LSD-t 检验与两样本均数比较的 t 检验区别 在于两样本均数差值的标准误 SXiX j 和自由度 ν 的计算上。
检验统计量的计算公式
Dunnett t X i X 0 S
X i X 0
误差
SXiX0
MS误差
1 ni
1 n0
,
Xi , ni 为第 i 个实验组的样本均数和样本例数; X 0 , n0 为对照组的样本均数和样本例数。
医学统计学--方差分析

笃学
精业
修德
6
厚生
2)组间变异
各处理组间的均数大小也不同,这种变异称 为组间变异。其大小可用组间均数与总均数的 离均差平方和表示:
k
SS组间 ni(xi x)2 i1
自由度 组间k1
笃学
精业
修德
7
厚生
3)组内变异 各处理组内部观察值也大小不等,这种变异称
为组内变异。其大小可用个体观察值与组均数的
பைடு நூலகம்i1 j1
i1 j1
k
k ni
ni(xi x)2
(xij xi)2
i1
i1 j1
ss组间ss组内
总 = N-1= (k-1)+(N-k) = 组间+组内
笃学
精业
修德
9
厚生
通过上述分解可以看出,方差分析的基本思想 就是根据资料的设计类型,将全部观测值的总 变异按影响结果的诸因素分解为相应的若干部 分变异,构造出反映各部分变异作用的统计量, 在此基础上,构建假设检验统计量,以实现对 总体参数的推断。
=0.05
(2) 计算检验统计量F值; (3) 查F界值表、确定P值并作出推断结果。
笃学
精业
修德
16
厚生
第二节 完全随机设计的方差分析
完全随机设计(completely random design) 不考虑个体差异的影响,仅涉及一个处理因素, 所以亦称单因素实验设计或单因素方差分析 (one-way ANOVA)。在实验研究中按随机化原 则将受试对象随机分配到一个处理因素的多个 水平中去,然后观察各组的试验效应;
笃学
精业
修德
11
厚生
F MS 组间 MS 组内
医学统计学方差分析

定义与原理
方差分析适用于多个组间的均值比较。当数据不符合正态分布或方差不齐时,可以经过适当的转换或采用非参数方法进行比较。
方差分析可以用于实验设计中的多因素分析,例如研究不同药物、剂量、时间等因素对生物指标的影响。
方差分析的数学模型与假设
02
线性模型
方差分析常用于处理一个或多个分组间的均值差异,因此需要构建线性模型来描述数据。线性模型中,每个组的观察值与该组的均值呈线性关系。
随机误差项
在方差分析中,每个观察值被认为是由固定效应(组均值)和随机效应(随机误差项)组成的。随机误差项是随机变量,且独立同分布,服从正态分布。
《医学统计学方差分析》
xx年xx月xx日
CATALOGUE
目录
方差分析概述方差分析的数学模型与假设方差分析的步骤与实例方差分析的优缺点与注意事项方差分析在医学中的应用与案例方差分析的发展趋势与未来展望
方差分析概述
01
方差分析(ANOVA)是一种统计方法,用于比较三个或更多组数据的均值差异。其原理是通过将数据的总变异分解为组间变异和组内变异,然后比较这两部分的变异是否具有显著性。
要点一
要点二
精度高
方差分析通过将每个观察值与各组均值进行比较,能够更准确地确定组间差异。
适用于多因素分析
方差分析可以同时考虑多个因素对实验结果的影响,适用于多因素的研究设计。
要点三
缺点
对数据正态性和独立性要求较高
方差分析要求数据符合正态分布,且各组观察值独立,否则可能导致分析结果的偏差。
对样本含量要求较高
方差分析对样本含量要求较高,样本含量过小可能导致统计效能较低。
《医学统计学》医统-第八章方差分析

编辑课件
公共卫生系 流行病与统计学教研室
祝晓明
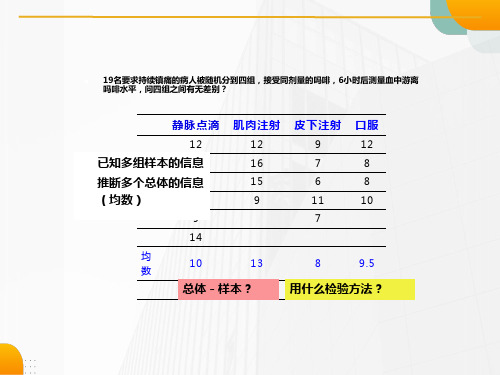
例 8-1 在评价某药物耐受性及安全性的I 期临床试验中,对符合纳入标准的30名健 康自愿者随机分为3组每组10名,各组注 射剂量分别为0.5U、1U、2U,观察48小 时部分凝血活酶时间(s)试问不同剂量的 部分凝血活酶时间有无不同?
编辑课件
编辑课件
• 方差分析
F=3.55, F>F0.05(2,18),P<0.05,三组大鼠 MT 含量的总体均值不全相同。
编辑课件
第三节 多个样本均数的两两比较
证实性研究
探索性研究
证实性研究 与探索性研究
编辑课件
Dunnett-t 检验 LSD-t 检验
SNK-q检验 Tukey检验 Schéffe检验
两个均数的比较时,同一资料所得结果与t检验等
价,即有如下关系 t 2 。F
2.方差分析的基本思想:将全部观测值的总变异按 影响因素分解为相应的若干部分变异,在此基础 上,计算假设检验的统计量 F 值,实现对总体均 数是否有差别的推断。
编辑课件
3. 方差分析有多种设计类型,但基本思想和计算步骤 相同,只是分组变量的个数不同,使用统计软件很容 易实现。 4.多重比较有多种方法,如 Dunnett-t 检验、LSD-t检 验、SNK-q (Student-Newman-Keuls)法 、Tukey法、 Schéffe法、Bonferroni t 检验和 Sidak t 检验。学习 中注意各种方法的适用性。
k1
的
2 分布, 2
2 ,
,认为方差不齐。
编辑课件
例8-1 资料方差齐性检验 提出检验假设,确定检验水准 H0:σ12=σ22=σ32 H1:三组方差不全相等 α=0.05
医学统计学:04 方差分析

1.4 f( F)
1.2
1.0
0.8
0.6
0.4
0.2
0.0
0
1
F 分布曲线
1 1, 2 5
1 5, 2 5
1 10,2 10
2F
3
4
F 界值表
附表4 F界值表(方差分析用,单侧界值) 上行:P=0.05 下行:P=0.01
分母自由度
υ2
1
161 1
4052
18.51 2
98.49
4.21 27
• 随机区组设计又称随机单位组设计、配伍组设计,也叫双因 素方差分析(two--way ANOVA)。是配对设计的扩展。
具体做法:
① 将受试对象按性质(如性别、年龄、病情等) (这些性质是
非处理因素,可能影响试验结果)相同或相近者组成m个单位 组(配伍组),每个单位组中有k个受试对象,分别随机地分 配到k个处理组。
2
7
33.4
18
2
8
38.3
19
2
9
38.4
20
2
10
39.8
21
3
1
32.9
22
3
2
37.9
23
3
3
30.5
24
3
4
31.1
25
3
5
34.7
26
3
6
37.6
27
3
7
40.2
28
3
8
38.1
29
3
9
32.4
30
3
10
35.6
35.51667
(Xij X )2
医学统计学方差分析 (2)

湿重,例2为抑菌圈的直径;
因素:影响试验指标的条件称为因素----例1为组别,
例2为药物(及剂量)、菌株来源;
水平:因素所处的状态称为该因素的水平----例1组别
这个因素有3个不同的水平;例2药物(及剂量) 因素有4个水平,菌株来源有7个水平。
在一项试验中,如果影响试验指标的因素只有 一个,则称该试验为单因素试验(例1);如果影响试 验指标的因素有多个,则称该试验为多因素试验(例 2)。
…
μg
数
22
假定处理组各水平Aj均为正态总体N(μj,σ2),区组 各水平Bk均为正态总体N(βk,σ2),方差分析的任务是:
对假设:
进行检验。
H0:μ1= μ2= …=μg H0:β1= β2 =…= βn
与完全随机设计的情形类似,我们将总平方和
分解为:
S S 总 S S 处 理 组 S S 区 组 + S S 误 差
方差分析----
多个样本均数比较的假设检验
1. 基本概念 t检验解决了推断两个总体均数是否相等的问题,
但实际工作中还会遇到需要推断多个总体均数是否相 等的问题。如:
Ex1 为研究煤矿粉尘作业环境对尘肺的影响,将18只
大鼠随机分到甲、乙、丙三个组,每组6只,分别在
地面办公楼、煤碳仓库和矿井下染尘,12周后测量大
s nj
SS总 (xij x)26.5628 j1 i1
s
SS组 间 nj(x•j x)22.5278 j1
S S 组 内 S S 总 S S 组 间 6 . 5 6 2 8 2 . 5 2 7 8 4 . 0 3 5 0
16
M S组 间 SsS 组 1 间2.3 5 27 181.264 M S组 内 S nS 组 内 s4 1.8 03 5 3 00.269
医学统计课件人卫6版第八章方差分析

总
组间+组内
2024/11/10
西安医学院公共卫生系
01
假设μ1=μ2 即患者与健康人血磷值相同,
02
那么两者的组间变异应该等于组内变异。
03
此时,令F=MS组间 / MS组内 ,
04
则F值理论上应为1。
05
若μ1≠μ2,组间变异便会↑,F↑。
06
查F界值表(附表4),
07
得P值,下结论。
完全随机设计的方差分析
完全随机设
1 计方差分析 中变异的分 解:
组间变异:
4 包括随机误 差和处理因 素的影响
2 总变异分为 两部分
组内变异:
3 反映随机误 差
完全随机设 计的单因素
5 方差分析 (one-way ANOVA)
——成组设
6 计的多个样 本均数的比 较
2024/11/10
西安医学院公共卫生系
二.分析计算步骤:以P47例6.1为例
该设计是将受试对象先按配比条件配成配 伍组(如动物实验时,可按同窝别、同性 别、体重相近进行配伍),每个配伍组有 三个或三个以上受试对象,再按随机化原 则分别将各配伍组中的受试对象分配到各 个处理组。
同一受试对象不同时间(或部位)重复多次 测量所得到的资料称为重复测量数据 (repeated measurement data),对该 类资料不能应用随机区组设计的两因素方差 分析进行处理,需用重复测量数据的方差分 析。
01 例 1 . 某 克 山 病 区 测 得 1 1 例 克 山病患者与13名健康人的血 磷值(mmol/L)如下,问 该地急性克山病患者与健康 人的血磷值是否不同?
02 患 者 x 1 : 0 . 8 4 , 1 . 0 5 , 1.20,1.20,1.39, 1.53,1.67,1.80, 1.87,2.07,2.11。
医学统计学教学课件-方差分析 PPT

B 组(24h)
11.14 11.60 11.42 13.85 13.53 14.16 6.94 13.01 14.18 17.72
C 组(96h)
合计
10.85
8.58
7.19
9.36 i为组的编号,A,B,C
9.59
8.81 j为组内为个体编号,
8.22 1,2,…,10
9.95
11.26
8.68
与总均数 X 间的差别
2. 组间变异( between group variation ) 各
组的均数
X
与总均数
i
X
间的差异
3. 组内变异(within group variation )每组的
10个原始数据与该组均数X i 的差异
下面先用离均差平方和(sum of squares of
deviations from mean,SS)表示变异的大小
3. 组内变异
在同一处理组内,虽
然每个受试对象接受的处
理相同,但测量值仍各不
相同,这种变异称为组内
变异。SS组内仅仅反映了随
mi
机误差的影响。也称SS误差
k ni
k
SS组内
(XijXi)2 (ni 1)Si2
i1 j1
i1
组间 =Nk
S 组 = ( 7 S . 7 内 8 . 0 6 ) 2 ( 7 4 . 7 8 . 0 1 ) 2 4 ( 8 . 6 9 . 2 8 ) 2 1 5 . 0 1
ni
T3 X 3 j j 1
k ni
X X ij i1 j1
ni
Qi
X
2 ij
j 1
ni
方差分析定义和应用-方差分析

第 1 页
第1章绪论4章 方差分析
《医学统计学》目录 第2 页
第1章 绪论 第2章 定量资料的统计描述 第3章 总体均数的区间估计和假设检验 第4章 方差分析 第5章 定性资料的统计描述 第6章 总体率的区间估计和假设检验 第7章 二项分布与Poisson分布 8章 秩和检验 第9章 直线相关与回归 第10章 实验设计 第11章 调查设计 第12章 统计表与统计图
第1章绪论4章 方差分析
第14 页
5.
正交试验设计的方差分析 如果要分析的因素有三个或三个以上,可进行 正交试验设计(orthogonal experimental design)的方差分析。
当分析因素较多时,试验次数会急剧增加,用此设计进行分析则更能体现出 其优越性。该设计利用正交表来安排各次试验,以最少的试验次数,得到 最佳的分析组合结果。
3. 主要原理:将各组数据的总变异按设计及研究目的分 为若干部分,再计算各部分的均方,两均方之比为F值。 F值与F临界值比较,决定P值大小,并根据P值大小推 断结论。
第1章绪论4章 方差分析
第6 (二)主要用途及应用条件有:
页
1. 进行两个或两个以上样本均数的比较; 2. 可以同时分析一个、两个或多个因素对试验结果的作用和影响; 3. 分析多个因素的独立作用及多个因素之间的交互作用; 4. 进行两个或多个样本的方差齐性检验等。 5. 应用条件:方差分析对分析数据的要求及条件比较严格,即要求各样
第1章绪论4章 方差分析
第3
第4章 方差分析 目录
页
第一节 方差分析的基本思路 第二节 单因素方差分析 第三节 双因素方差分析 第四节 多个样本均数间两两比较 第五节 多个方差齐性检验 第六节 变量变换
医学统计学方差分析

医学统计学方差分析方差分析是一种统计学方法,用于比较三个或三个以上的组之间的平均值是否存在显著差异。
在医学研究中,方差分析常用于比较不同治疗方法或不同个体群体之间的差异,以确定是否存在统计学上的显著差异。
方差分析的基本原理是比较组间离散程度与组内离散程度的比值,即组间均方与组内均方的比值。
组间方差表示不同组之间的差异性,组内方差表示同一组内个体之间的变异程度。
如果组间离散程度显著大于组内离散程度,即组间均方大于组内均方,就可以得出组间存在显著差异的结论。
在医学研究中,方差分析可以应用于很多不同的情况。
举例来说,我们可以使用方差分析来比较不同药物对同一疾病的治疗效果,或者比较不同药物剂量对同一疾病的治疗效果。
我们还可以使用方差分析比较不同年龄组、性别组或不同地区患者之间的其中一种疾病发病率。
方差分析的核心是比较组间差异与组内差异。
组间差异可以通过计算组间均方来得到。
组间均方的计算公式为组间平方和除以组间自由度。
组间平方和是每个组内数据与该组均值之差的平方的总和。
组间自由度等于组数减1、组内差异可以通过计算组内均方来得到。
组内均方的计算公式为组内平方和除以组内自由度。
组内平方和是每个组内数据与该组均值之差的平方的总和。
组内自由度等于总体样本量减去组数。
计算得到组间均方和组内均方之后,即可计算F值。
F值等于组间均方除以组内均方。
F值的计算结果可以与F分布的临界值进行比较,以判断组间均方是否显著大于组内均方。
如果F值大于F分布的临界值,就可以得出组间存在显著差异的结论。
除了F值,方差分析还可以计算一些其他的统计量。
例如,可以计算每个组的均值和标准差,以了解不同组之间的差异程度。
还可以计算方差分析表,其中包含了组间平方和、组间自由度、组间均方、组内平方和、总平方和、总自由度、组内自由度和组内均方等统计量。
需要注意的是,在进行方差分析之前,需要检验数据的正态性和方差齐性。
正态性检验可通过绘制正态概率图、Shapiro-Wilk检验或Kolmogorov-Smirnov检验进行。
【医学统计学】方差分析(ANOVA)PPT

P
总 组间 组内(误差)
54.4522 58 8.6054 2 4.30275.2555 0.0081
45.8468 56 0.8187
F 分布
➢方差比的分布
F
MSBetween MSWithin
~ F(1 , 2 )
F 分布
1.0
1=1, 2=10
0.8
0.6
1=5, 2=10
0.4
SStotal
2
X ij X
total= N-1
59
2
SST Xij 1.334 54.4522
j1
组间变异—— SS组间
▪ Sum of squares between groups
X1
X2
X3
X
n1( X1 X )2 n2( X2 X )2 n3( X3 X )2
➢ 随机的含义:机会均等 不可预测
❖因素 (factor)
所要检验的对象:治疗方案
❖ 水平(level)
因素的具体表现:方案A、方案B、方案C
❖ 试验(Trial)
单因素三水平的试验
基本步骤
➢建立检验假设,确定检验水准 ➢计算检验统计量(列方差分析表) ➢计算 P 值 ➢结论
建立假设,确定检验水准
多重比较(multiple comparison)
▪ 多组间的两两比较为什么不能用 t 检验?
进行一次假设检验,犯第一类类错误的概率:
进行多次(k)假设检验,至少犯一次第一类错误的概 率:
1-(1-)k
组数为3, k=3, 1-(1-0.05)k=0.1426 组数为4, k=6, 1-(1-0.05)k=0.2649 组数为5, k=10, 1-(1-0.05)k=0.4013
医学统计学方差分析

21
表2
变异来源 组间 组内 总变异 SS
例1 的方差分析表
DF MS F值 14.32 P值 <0.05
119.8314 2 59.916 112.9712 27 4.184 232.8026 29
按=0.05水准,拒绝H0,接受H1,认为三组 的差别具有统计学意义,不同时期切痂对大鼠 肝脏的ATP含量有影响。
B(75) E(81) A(81) D(87) E(73) B(74) F(68) C(69)
C(64) F(72) D(77) A(82)
35
3. 假设检验 例3
变异来源 药液( B ) 家兔( R ) 部位( C ) 误差( E ) 总( T)
方差分析表
df
5 5 5
SS
657.336 251.663 65.337
脏三磷酸腺苷(ATP)的影响,将30只雄 性大鼠随机分为3组,每组10只:A组 为烫伤组,B组为烫伤后24h(休克期) 切痂组,C组为烫伤后96h(非休克期) 切痂组。全部动物统一在烫伤后168h 处死并测量其肝脏的ATP含量,结果见 下表。试问三组的ATP总体均数是否有 差别?
3
表1 大鼠烫伤后肝脏ATP 的测量结果(m g )
A
X1
●●●●●●
B
X
●●●●●●
X2
●●●●●●
X3
●●●●●●
X4
●●●●●●
X5
13
组间变异<组内变异
B X A
● ● ● ● ● ●
X1
● ● ● ● ● ●
X2
● ● ● ● ● ●
医学统计学方差分析

i1 j1
X甲 X乙
X ij X丙
甲
乙
丙
基本思想:总变异的分解
SS总=SS组间+SS组内 自由度的分解
总组间组内
第一节 完全随机设计的方差分析
基本思想:各变异的平均变异,即均方
组间均方:
MS组间
SS组间
组间
组内(误差)均方:MS组内
SS组内
组内
第一节 完全随机设计的方差分析
基本思想:统计量F值
变异分解
110
总变异(SS总)
100
全部测量值大小不同 90
,这种变异称为总变异 80
,以各测量值Xij与总均
数间的差异度量。
70 60
50
40
k ni
SS总
(XijX)2
30
i1 j1
X
甲
乙
丙
组间变异(SS组间) • 组内均值 与总均值 之差的平方和
110
k
SS组间 ni(Xi X)2
100 90
F处理
MS处理 MS误差
F处理>Fα(k-1,(k-1)(m-1)),P<α,认为比较组总体均值不 全相同
F处理<Fα(k-1,(k-1)(m-1)),P>α,尚不能认为比较组总体 均值不同
第二节 随机区组设计的方差分析
基本思想:统计量F值
F区组
MS区组 MS误差
F区组>Fα(m-1,(k-1)(m-1)),P<α,认为各区组总体均值不 全相同
Sidak t检验 Bonferroni t 检验
第三节 多个样本均数的两两比较
SNK (Student-Newman-Keuls) 法的检验统计量 为q ,故又称为q检验
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
心脏病 136.00 152.50 167.10 177.40 153.30 150.00 168.20 164.00 150.00
高血压 184.00 157.00 190.00 169.00 191.00 173.00 151.00 181.00 172.00 195.00
SPSS软件实现
例7-1-1的SPSS操作方 法 1)建立数据库 将血压值组命名为bp。 将分组命名为
• 按α =0.05的水准,药物A与药物B交互效应A*B的F 值为1.146,P>0.05,无统计学意义,不拒绝H0, 即尚不能认为两种药物间存在交互作用。
• 药物A的P<0.05,拒绝H0,有统计学意义;
• 药物B的P>0.05,不拒绝H0,无统计学意义。
• 结论为药物A对晚期胃癌患者镇痛有作用,药物B
对晚期胃癌患者镇痛无作用
4 重复测量设计的方差分析
重复测量资料(repeated measurement data)是由在不同时间点上对同一对象的同 一观察指标进行多次测量所得。是在科研 工作中常见的方法,常用来分析在不同时 间点上该指标的差异
• 例7-5-2 某研究者欲了解一套新的锻炼方
法的减肥效果,该研究者在某小学随机抽
• (2)点击Plots选项,把A添加到Horizontal Axis ,把B添加到Spearate Lines,点击Add选项,
点击Continue,点击OK
3)主要的输出结果和解释 • 在输出的结果中给出了析因分析的基本结果。结 果主要包括A、B及A*B的平方和,均方和。各组F 值以及P值。
2 随机区组方差分析
属于两因素方差分析(two-way ANOVA)
用于多个样本均数的比较
两因素:研究因素和配伍组(区组)因素
研究因素有k个水平,共有n个区组
例7-2-1 某研究者用甲乙丙三种不同的饲料
喂养鼠,目的是了解不同饲料增重的效果
有无差异,采用随机区组设计的方法,以
窝别作为划分区组的特征,以消除遗传因
取了12名肥胖学生,随机分成两组,第一
组每天下午按新的锻炼方法锻炼,第二组
不参与新的锻炼方法,并于实验开始的第1、
2、3个月予以评价学生体重减重情况
表7-5-3 12名学生体重减重情况(斤)
测试时间 受试对象 1 2 3 4 5 6 7 8 9 10 11 12 组别 第1月 1 1 1 1 1 1 2 2 2 2 2 2 15 13 10 12 8 9 10 8 12 16 14 12 第2月 12 8 6 11 6 5 8 4 6 10 10 8 第3月 6 4 2 4 2 1 4 1 2 9 9 8
5 多个均数之间的两两比较
Dunnett-t 检验:它适用于k-1个试验组与一个 对照组均数差别的多重比较。 Bonfferoni 法 、SNK、LSD:适用于k个试验 组间均数差别的多重比较。
例7-5-2的SPSS操作方法
• 1)建立数据库
将锻炼方式命名为group,令锻炼=1,不锻炼=2;
将第1月、第2月与第3月体重减重分别命名为“one”、 “two”和“three”
2)SPSS软件实现方法
• (1)点击Analyze选项中的
General Linear Model
的Repeated Measures;
3)主要的输出结果和解释
在输出的结果中给出了随机区组设计的基本结果。 结果主要包括处理nutrition及区组block的平方 和,均方和。各组F值以及P值。 结果显示区组F值为13.521,P<0.001,有统计学 意义,拒绝H0,即可以认为八个区组之间的体重 有差异。 进一步想了解具体哪些区组有差异,可以进行SNK 检验。处理组F值为2.719,P为0.101,无统计学 意义,不拒绝H0,即可以认为处理组间体重相等
丙 62.50 62.40 58.60 73.50 79.30 37.40 51.20 46.20
例7-2-1的SPSS操作方法
• 1)建立数据库
将饲料命名为“nutrition”,其中
“1”表示甲饲料ห้องสมุดไป่ตู้“2”表示乙 饲料,“3”表示丙饲料。 将区组命名为“block”,其中“1” 表示第一区组,“2”表示第二
区组,以此类推。
将鼠增重体重命名为“weight”
2)SPSS软件实现方法
(1)点击Analyze选项中的General Linear Model的
Univariate,将weight导入到Dependent Variate框中,将
类型block和nutrition导入到Fixed Factor(s)框中
素对体重增长的影响,测得鼠体重增加,
请做分析
表 7-2-1
三种饲料喂养鼠所增体重(克)
区组号 1 2 3 4 5 6 7 8
甲 49.10 49.80 55.10 63.50 72.20 41.40 61.90 42.20
乙 56.20 48.50 54.80 64.20 66.40 45.70 53.00 37.80
定义trial到Define
factors框中,Numbers
of levers为3,点击add
添加,点击Define。
• 在左边的选项框中,选择“one”、“two”、 “three”进入Within-Subjects Variables中;
• 将组别选入Between-Subjects Factors,点击OK
(2)点击model,选择
custom自定义模型,
在Build Term(s)中选 择Main effects,将左 边框中的block和 nutrition两组添加到右 边Model,点击 Continue
• 点击进入Post Hoc Multiple Comparisons for Observed Means对话框,在Factor中选择nutrition进入右边Post Hoc Tests for对话框,并选择SNK进行均数两两比较,点击Continue
• 涉及一个研究因素
• 因素有K(K≥2)个水平或状态
• 例7-1-1某研究者从某社区随机抽取了11名
正常人、9名心脏病患者和10名高血压患者
进行血压测定,问三种人的收缩压有无差
别?
表 7-1-1 正常人、血压异常和高血压患者的血压测定结果 (mmHg) 三组样本人群
正常人 107.70 125.20 112.50 96.00 115.20 95.30 113.00 120.00 125.60 111.00 106.50
有统计学意义,故可认为不同测试时间点间体重减重不同, 受时间影响。 • 测试时间组factor1与组别交互组间F为4.386,P为0.026, 拒绝H0,具有统计学意义,故可认为测试时间组factor1
与组别之间有交互作用。
• 组别F值为0.397,P为0.543,不拒绝H0,无统计学意义, 故不能认为锻炼组和不锻炼组的减肥效果有差异
“group”,各组分别
用数字1、2和3表示
2)进行正态性检验
先:data,split file,将分组变量作为拆分变量
再:analyze,noparametric test,1-sample k-s test,检验效应变量
3)进行方差分析
(1)点击Analyze选项中的Compare Means
的One-way Anova,将bp导入到
Dependent List框中,将类型group导
入到 Factor框中。点击进入Post Hoc
Multiple Comparisons,选择SNK,点
击continue
• 点击Option,在Option对话框中选择Homogeneity
of variance test,点击continue,选择OK
3)主要的输出结果和解释
• 按α=0.05标准,方差齐性Levene检验显示
P>0.05,故可以认为bp三组数据方差齐性,由组
间与组内均方算出得F值为74.888,P为0.000,
拒绝H0,差异有统计学意义,所以可以认为bp三 组之间的血压均值不全相等。为了进一步了解三 组间均值两两比较情况,SNK检验显示1、2组, 1、3组和2、3组之间差异均有统计学意义,可以 认为它们血压均值完全不相等
例7-5-1 某研究者想了解药物A和药物B对于晚期 胃癌患者的镇痛作用,以及两者不同剂量之间有
无交互作用。A药使用两种剂量治疗,分别是
5mg和10mg,B药使用两种剂量治疗,分别是
10mg和20mg。研究者将12名病情相似的患者随
机分为四组,分别接受A药和B药不同剂量组合下 的用药治疗,测得的镇痛时间
3 析因设计方差分析
析因设计是在两个或多个实验因素的各水平组合
的基础上,研究各实验因素的主效应以及各因素 之间的交互作用。方差分析中,影响观察指标的 因素称为因子(factor);因子所处的状态称为因 子的一个水平(level of factor);各因子水平
的组合称为处理(treatment)
3)主要的输出结果和解释
• 球形检验结果见图7-6-18,可见卡方为0.153,P为 0.926,表明符合球形分布,以一元方差结果为准
• Sphericity Assumed即为球形分布假设成立时得结果,就 是本例中所要看的。
• 测试时间factor1组中F为129.068,P<0.05,拒绝H0,具
第七章
方差分析
主要内容
完全随机设计方差分析(one-way anova) 随机区组设计方差分析(two-way anova) 析因设计方差分析(factorial design) 重复设计方差分析(repeated measures anova) 多个均数之间的两两比较
