水流状态与沿程阻力系数
水力学(8)

一、是非题 1、达西定律适用于所有的渗流。 2、闸孔出流的流量与闸前水头的1/2次方成正比。 3、渐变流过水断面上各点的测压管水头都相同。 4、粘滞性是引起液流运动能量损失的根本原因。 5、直立平板静水总压力的作用点就是平板的形心。 6、层流的沿程水头损失系数仅与雷诺数有关。 7、水力粗糙管道是表示管道的边壁比较粗糙。 8、水头损失可以区分为沿程水头损失和局部水头损失。 9、满宁公式只能适用于紊流阻力平方区。 10、紊流光滑区的沿程水头损失系数仅与雷诺数有关。 11、满宁公式只能适用于紊流阻力平方区。
du dy
产生水 流阻力
损耗机 械能hw
图示
沿程水头损失hf 水头损失的分类
图示
各种局部水头损失的总和 局部水头损失 hj
某一流段的总水头损失: hw hf hj
各分段的沿程水头损失的总和
举例
返回
沿程水头损失与切应力的关系 1
2 τ0 FP1=Ap1 1 Z1 O L α
F L 0
f (Re, 0 )
r0 15 r0 15 r0 15
r
层流时,
64 Re
r0 15 r0 15
水力光滑壁面, 称为紊流光滑区
f (Re)
r0 15
水力粗糙壁面, 称为紊流粗糙区
lgRe
f( 0)
r
返回
计算沿程水头损失的经验公式——谢齐公式
列X方向的动量方程式
p1 A2 p2 A2 gA2 L cos Q(V2 V1 )
化简整理得: z1 z2 所以有
hj 1
g hj
V2 V1 h j 2 2 22g V12 V22 (V2 g (V2 V1 )V V ) 1 2
第3章-给水排水管网水力学基础讲解

图3.1 圆形管道非满管流和满管流示意图 (a)非满管流;(b)满管流
图3.2 圆形管道充满度示 意图
3.3.1 非满流管道水力计算公式 管渠流量公式:
q
Av
A
R
2 3
I
1 2
式中
A―过水断面面积(m2);
n
I―水力坡度,对于均匀流,为管渠底坡。
N mn
d ( din ) m i 1
当并联管道直径相同时,等效直径:
n
d (N)m di
kqNn l
d
m N
干管配水情况
3.4.2 沿线均匀出流的简化
给水管网中的配水管沿线向用户供水,如图3.6所示。假设沿线出流是 均匀的,则管道内任意断面x上的流量可以表示为:
qx
qt
沿程水头损失计算公式的指数形式为:
或
或 hf sf qn
式中,k、n、m─指数公式的参数。见表3.6; α―比阻,即单位管长的摩阻系数, α =k/Dm; sf―摩阻系数,sf= α l=kl/Dm。
沿程水头损失指数公式的参数
表3.6
3.3 非满流管渠水力计算
在排水管网中,污水管道一般采用非满管流设计,雨水管网一般采用 满管流设计,如图3.1所示。在两者的运行过程中,大多数时间内,均 处于非满管流状态。
第3章 给水排水管网水力学基础
3.1 给水排水管网水流特征
3.1.1 管网中的流态分析
在水力学中,水在圆管中的流动有层流、紊流及过渡流三种流态,可以根据雷诺数 Re进行判别,其表达式如下:
Re
VD
式中,V-管内平均流速(m/s);D-管径(m);ν-水的运动粘性系数,当水温为 10oC时,ν=1.308 x 10-6m2/s,当水温为30oC时,ν=0.804 x 10-6m2/s,当水温为 50oC时,ν=0.556 x 10-6m2/s。 当Re小于2000时为层流,当Re大于4000时为紊流,当Re介于2000到4000之间时, 水流状态不稳定,属于过渡流态。
水力学常用知识讲解(笔记)

《水力学》学习指南第一章绪 论(一)液体的主要物理性质1.惯性与重力特性:掌握水的密度ρ和容重γ;2.粘滞性:液体的粘滞性是液体在流动中产生能量损失的根本原因。
描述液体内部的粘滞力规律的是牛顿内摩擦定律 :注意牛顿内摩擦定律适用范围:1)牛顿流体, 2)层流运动3.可压缩性:在研究水击时需要考虑。
4.表面张力特性:进行模型试验时需要考虑。
下面我们介绍水力学的两个基本假设: (二)连续介质和理想液体假设1.连续介质:液体是由液体质点组成的连续体,可以用连续函数描述液体运动的物理量。
2.理想液体:忽略粘滞性的液体。
(三)作用在液体上的两类作用力第二章 水静力学水静力学包括静水压强和静水总压力两部分内容。
通过静水压强和静水总压力的计算,我们可以求作用在建筑物上的静水荷载。
(一)静水压强:主要掌握静水压强特性,等压面,水头的概念,以及静水压强的计算和不同表示方法。
1.静水压强的两个特性:(1)静水压强的方向垂直且指向受压面(2)静水压强的大小仅与该点坐标有关,与受压面方向无关,2.等压面与连通器原理:在只受重力作用,连通的同种液体内, 等压面是水平面。
(它是静水压强计算和测量的依据)3.重力作用下静水压强基本公式(水静力学基本公式)p=p 0+γh 或 其中 : z —位置水头,p/γ—压强水头(z+p/γ)—测压管水头请注意,“水头”表示单位重量液体含有的能量。
4.压强的三种表示方法:绝对压强p ′,相对压强p , 真空度p v , ↑ 它们之间的关系为:p= p ′-p a p v =│p │(当p <0时p v 存在)↑相对压强:p=γh,可以是正值,也可以是负值。
要求掌握绝对压强、相对压强和真空度三者的概念和它们之间的转换关系。
1pa(工程大气压)=98000N/m 2=98KN/m2下面我们讨论静水总压力的计算。
计算静水总压力包括求力的大小、方向和作用点,受压面可以分为平面和曲面两类。
《流体力学》实验指导书
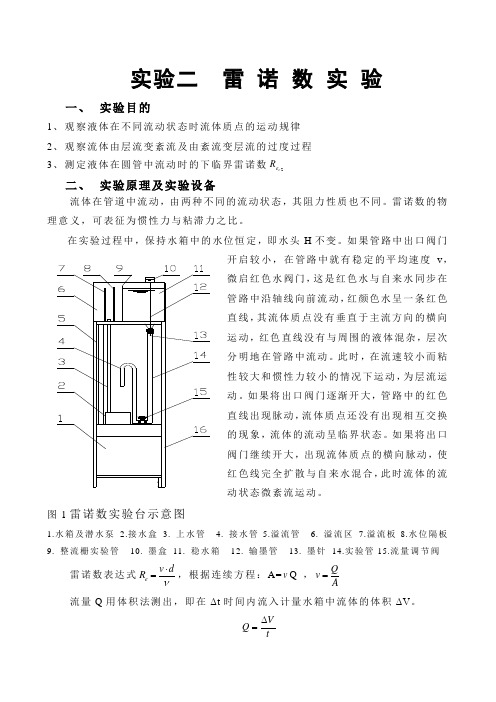
实验二 雷 诺 数 实 验一、 实验目的1、 观察液体在不同流动状态时流体质点的运动规律2、 观察流体由层流变紊流及由紊流变层流的过度过程3、 测定液体在圆管中流动时的下临界雷诺数2c e R二、 实验原理及实验设备流体在管道中流动,由两种不同的流动状态,其阻力性质也不同。
雷诺数的物理意义,可表征为惯性力与粘滞力之比。
在实验过程中,保持水箱中的水位恒定,即水头H 不变。
如果管路中出口阀门开启较小,在管路中就有稳定的平均速度v ,微启红色水阀门,这是红色水与自来水同步在管路中沿轴线向前流动,红颜色水呈一条红色直线,其流体质点没有垂直于主流方向的横向运动,红色直线没有与周围的液体混杂,层次分明地在管路中流动。
此时,在流速较小而粘性较大和惯性力较小的情况下运动,为层流运动。
如果将出口阀门逐渐开大,管路中的红色直线出现脉动,流体质点还没有出现相互交换的现象,流体的流动呈临界状态。
如果将出口阀门继续开大,出现流体质点的横向脉动,使红色线完全扩散与自来水混合,此时流体的流动状态微紊流运动。
图1雷诺数实验台示意图1.水箱及潜水泵2.接水盒3. 上水管4. 接水管5.溢流管6. 溢流区7.溢流板8.水位隔板9. 整流栅实验管 10. 墨盒 11. 稳水箱 12. 输墨管 13. 墨针 14.实验管15.流量调节阀雷诺数表达式e v dR ν⋅=,根据连续方程:A=v Q ,Qv A=流量Q 用体积法测出,即在Δt 时间内流入计量水箱中流体的体积ΔV 。
tVQ ∆=42d A π=式中:A —管路的横截面积;d —实验管内径;V —流速;ν—水的粘度。
三、实验步骤1、准备工作:将水箱充满,将墨盒装上墨水。
启动水泵,水至经隔板溢流流出,将进水阀门关小,继续向水箱供水,并保持溢流,以保持水位高度H 不变。
2、缓慢开启阀门7,使玻璃管中水稳定流动,并开启红色阀门9,使红色水以微小流速在玻璃管内流动,呈层流状态。
3、开大出口阀门15,使红色水在玻璃管内的流动呈紊流状态,在逐渐关小出口阀门15,观察玻璃管中出口处的红色水刚刚出现脉动状态但还没有变为层流时,测定此时的流量。
沿程阻力简便计算

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载沿程阻力简便计算地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第六章流动阻力和水头损失学习要点:熟练地掌握水头损失的分类和计算、层流与紊流的判别及其流速分布规律;掌握流动阻力的分区划分、各个分区内沿程水头损失系数的影响因素,了解紊流脉动现象及其切应力的特征、人工加糙管道与工业管道实验结果的异同、沿程水头损失系数计算的经验公式、几种特殊的管路附件的局部水头损失系数等。
实际流体具有粘性,在通道内流动时,流体内部流层之间存在相对运动和流动阻力。
流动阻力做功,使流体的一部分机械能不可逆地转化为热能而散发,从流体具有的机械能来看是一种损失。
总流单位重量流体的平均机械能损失称为水头损失,只有解决了水头损失的计算问题,第四章得到的伯努利方程式才能真正用于解决实际工程问题。
第一节水头损失及其分类流动阻力和水头损失的规律,因流体的流动状态和流动的边界条件而异,故应对流动阻力的水头损失进行分类研究。
一、水头损失分类流体在流动的过程中,在流动的方向、壁面的粗糙程度、过流断面的形状和尺寸均不变的均匀流段上产生的流动阻力称之为沿程阻力,或称为摩擦阻力。
沿程阻力的影响造成流体流动过程中能量的损失或水头损失(习惯上用单位重量流体的损失表示)。
沿程阻力均匀地分布在整个均匀流段上,与管段的长度成正比,一般用表示。
图6—1 水头损失另一类阻力是发生在流动边界有急变的流场中,能量的损失主要集中在该流场及附近流场,这种集中发生的能量损失或阻力称为局部阻力或局部损失,由局部阻力造成的水头损失称为局部水头损失。
通常在管道的进出口、变截面管道、管道的连接处等部位,都会发生局部水头损失,一般用表示。
水力学第四章层流、紊流,液流阻力和水头损失

3.7d
结论2:
•紊流光滑区水流沿程水头损失系数只取决于雷诺数,粗糙度不 起作用。容易得出光滑区紊流沿程损失与流速的1.75次方成正 比。 •紊流粗糙区水流沿程水头损失系数只取决于粗糙度,由于粗糙 高度进入流速对数区,阻力大大增加,这是不难理解的。容易 得出粗糙区紊流沿程损失与流速的2.0次方成正比。 •在紊流光滑区与粗糙区之间存在紊流过渡粗糙区,此时沿 程损失系数与雷诺数和粗糙度都有关。 •尼古拉兹试验反映了圆管流动的全部情况,在其试验结果图上 能划分出层流区,过渡区、紊流光滑区、紊流过渡粗糙区,紊 流粗糙区。紊流粗糙区通常也叫做‘阻力平方区’。
ro gJ 2 2 gJ 4 1 4 gJ 4 Q (ro r )2 rdr (ro ro ) d 0 4v 4v 2 128v
上式为哈根——泊肃叶定律:圆管均匀层流的流量Q与管径d 的四次方成比例。 3、断面平均流速: V
Q gJ 2 1 ro umax A 8 2
1 1 1 1 1 , , , , 及 30 61 .2 120 252 507 1
1 1 1 1 1 1 , , , , 及 30 61 .2 120 252 507 10
层流时,
64 Re
f (Re)
1 1 1 1 1 1 , , , , 及 30 61.2 120 252 507 1014
1 u u x x dt 0 T0
2、紊流的切应力 由相邻两流层间时均流速相对运动
所产生的粘滞切应力
紊流产生附加切应力
du l t v Re
t v Re 2
纯粹由脉动流速所产生 的附加切应力
dy ( du 2 ) dy
普朗特 混合长 Re 与 du 有关,根据质点脉动引起动量交换(传递),又称为动量传递理论 dy 理论
水流阻力系数的确定方法

水流阻力系数的确定方法
水流阻力系数的确定方法有多种,以下列举三种常用的方法:
1.理论公式法:根据流体力学原理,当流体在直管中流动时,阻力系数可以表示
为ξ=fi⋅dL,其中fi为摩擦系数,L为直管的长度,d为直管的内径。
当流体的流动状态为层流时,摩擦系数可以从流体力学推导而得:fi=Re64。
而当流体的流动状态为湍流时,摩擦系数无法采用理论分析方法完全推导而得,一般需要实验的方法。
2.实验测定法:通过实验测量得到水流的阻力系数。
在实验中,可以设置一系列
不同管径和流速的直管,记录每个管径和流速下的压力降和流速,然后根据公式Δp=ξ⋅ρ⋅2u2计算阻力系数。
3.经验数据法:根据实际应用中的经验数据确定水流阻力系数。
在实际应用中,
可以通过对已有的管道系统进行测量和计算,得到水流阻力系数的经验值。
这些经验值可以作为新管道系统设计时的参考。
需要注意的是,水流阻力系数的确定方法应根据具体情况选择。
在工程应用中,一般采用实验测定法和经验数据法来确定水流阻力系数。
同时,对于特殊的水流条件或需要精确计算的情况,可以采用理论公式法进行计算。
给水排水管网水力学基础

θ=3.4173(弧度),充满度y/D=0.5687 ,流速v=1.355(m/s)
沿程阻力系数常用公式: (续)
(4)巴甫洛夫斯基(Н.Н.Павловский)公式 :
将曼宁公式中的常数指数1/6改进为曼宁粗糙系数n和水力半径R的函数 。
1 y C R n
代入公式(3.2),得:
式中, y 2.5 n 0.13 0.75 R ( n 0.10) n――曼宁粗糙系数 。
3.4
管道的水力等效简化
水力等效简化原则: 经过简化后的管网对象与原来的实际对象具有相同的水力特性。如两条并联管 道简化成一条后,在相同的总输水流量下,应具有相同的水头损失。
3.4.1 串联或并联管道的简化 管道串联:如图3.4所示,两条或两条以上管道串联,可将它们等效为一条直 径为d,长度为l 的管道。根据水力等效原则,有:
图3.2 圆形管道充满度示 意图
3.3.1 非满流管道水力计算公式 管渠流量公式:
A q A v R I n
2 3
1 2 式中
A―过水断面面积(m2); I―水力坡度,对于均匀流,为管渠底坡。
非满流管道水力计算参数公式:
设管径为D,管内水深为y,充满度为y/D, 由管中心到水面线两端的夹角计算公式:
N kq nli kq nl hf m m d i 1 di
管道串联等效直径: 管道并联:两条或两条以上管道并联,长度相等,可
通过试验研究紊流流动过程中的沿程阻力系数
λ值与理论分析所得的值完全相符
• Ⅱ区.过渡区(不稳定区、临界区) ( 2320
<Red< 4000 ) λ = f(Re) 规律不明显,实用意义不大。
• Ⅲ区.水力光滑区λ = f(Re) 4-32,4-37
• Ⅳ区.紊流过渡区, λ = f(Re, Δ/d) 4-34
• Ⅴ区.粗糙区(平方区), λ = f(Δ/d) ,该
区的雷诺数和流速都很大,在工程上比较常见。 4-33
• Ⅴ区.粗糙区(平方区), λ = f(Δ/d) ,该
区的雷诺数和流速都很大,在工程上比较常见。
4-33
• 液流在该区流动时,对给定的管道, λ值为固 定常数
• 但工程上对该区的水流,习惯上用谢才公式,
• 为了探求紊流的沿程阻力系数λ的规律,水 力学者们进行了大量试验研究,目前,对 流速分布公式尚无纯理论解。
• 尼古拉兹采用管壁贴均匀砂的办法,进行 试验给出了结果,其中,尼古拉兹对人工 粗糙的管道的研究结果,被广泛用于工程 实践。下面介绍其试验结果。
• 水流边壁表面是粗糙不平的,可用粗糙度∆反映, 即壁面的凸起高度。
Ⅰ区.层流区(Re <2320)
• λ与∆/d无关,而与Re 成反比,此区沿程水 头损失与流速v成正比。
Ⅱ区.过渡区( 2320 <Re < 4000 )
紊流区 (Re >4000)
• R规e 律>4:000时,水流进入充分紊流状态,λ出现三种
• Ⅲ区.水力光滑区;该区各种不同相对粗糙度的
λ均沿图中直线段变化,这表明λ仍与∆ /d无关, 只与Re 相关
• 在尼古拉兹以后,很多学者对实际使用的 管道(粗糙度不是人为的)进行了大量实 验,证实了尼古拉兹图的正确性。
关于管道沿程阻力系数问题的分析

关于管道沿程阻力系数问题的分析江山;张海金;齐鹏【摘要】引用水力学基础理论,列出各种流态情况下的沿程阻力系数公式,并提出利用EXCEL软件来求解柯列勃洛克公式,从而为管道沿程阻力系数系数计算提供了一种简便方法,即利用Excel中求解勃洛克公式的简便方法.【期刊名称】《黑龙江水利科技》【年(卷),期】2012(040)010【总页数】2页(P177-178)【关键词】紊流;沿程阻力系数;Excel;柯列勃洛克公式【作者】江山;张海金;齐鹏【作者单位】绥化水文局,黑龙江绥化152000;绥化水文局,黑龙江绥化152000;绥化水文局,黑龙江绥化152000【正文语种】中文【中图分类】TV131.220 引言在管道水力系统中,沿程水头损失计算是水力计算的一个重要环节。
在实际工程中,为方便计算,不管是层流和紊流,管线的沿程水头损失都是采用层流时所求的沿程阻力系数来进行计算,而大多数情况下管道中水流流态都是紊流的,紊流状态下的沿程阻力系数与层流状态下的沿程阻力系数是有所差别的,其公式也不一样。
因此,本文分别分析了各种水流状态下沿程阻力系数求解公式,并利用Excel软件介绍了一种求解柯列勃洛克公式的简便方法。
1 阻力系数公式1.1 层流状态下沿程阻力系数公式层流状态下,沿程阻力系数只与雷诺数有关,与管壁粗糙程度无关,其计算公式一般由谢才公式得来:式中:g为重力加速度;C为谢才系数。
谢才系数公式可由曼宁公式算出:式中:R为水力半径;n为管道的糙率。
1.2 紊流状态下沿程阻力系数公式紊流中沿程阻力系数与雷诺数及粗糙度之间的理论,在理论上至今没有完全解决,1933年,尼古拉兹根据大量人工粗糙管试验发表了反映圆管流动情况的实验结果。
描绘出了尼古拉兹实验曲线图。
人们在后来的研究中依据普朗特混合长度理论和尼古拉兹试验数据提出了紊流沿程阻力系数的半经验公式。
1.2.1 紊流光滑管区在Re=5×10 ~3×10情况下,沿程阻力系数满足尼古拉兹光滑管公式:1.2.2 紊流粗糙管区此区黏性底层失去意义,绝对粗糙度对水头损失起决定作用。
水流状态与沿程阻力系数11.13
1、按平均水温60℃计,密度ρ=983.28,运动粘度ν=0.478,管壁粗糙度k=0.2(室内钢管)、0.5(室外钢管)、0.05(塑料管)。 2、流速V=353.68G/(d2ρ),雷诺数Re=1000Vd/ν,沿程阻力系数λ由流态及管壁状态和运动粘度决定,比摩阻R=500λρV2/d。 3、当Re≤2300,为层流λ=64/Re。当Re>2300为紊流:Re<20d/k(或V≤11ν/k)为紊流光滑区,λ=0.3164/Re0.25;当20d/k<Re<250d/k (或11ν/k<V≤445ν/k)
过渡区 过渡区 过渡区 过渡区 过渡区
0.055 0.059 0.067 0.077 0.091
4.264 4.134 3.878 3.616 3.324
##### ##### ##### ##### #####
###### ###### ###### ###### ######
0.0550 0.0585 0.0665 0.0765 0.0905
建筑热水设计——钢管考虑结垢时(比较保守)V<0.44m/s时为过渡区,V≥0.44m/s时为粗糙区 0.01 0.21 1440.0 DN40 38.50 983.24 0.35 1.0 0.478 28147 770 9625 DN32 0.01 0.21 1080.0 33.25 983.24 0.35 1.0 0.478 24443 665 8313 0.01 0.21 540.0 DN25 24.50 983.24 0.32 1.0 0.478 16586 490 6125 0.01 0.21 198.0 DN20 18.75 983.24 0.20 1.0 0.478 7947 375 4688 DN15 0.01 0.21 108.0 13.25 983.24 0.22 1.0 0.478 6134 265 3313
水力学课件第五章

紊流
管中为石油时
vd 100 2 333.3 2300 Re 0.6 ν
层流
作业
1、2
均匀流沿程水头损失与切应力的关系
沿程水头损失与切应力的关系 在管道恒定均匀流中,取总流流段1-1到2-2,各 作用力处于平衡状态:F=0。
P1
1
0 0
2
P2 2 z2
z1 z2 sin l
p1 p2 hf g g
m 13600 ( 1)hp ( 1) 0.3 4.23m 900
设流动为层流
4Q v 2.73m / s 2 d
l v 2 64 l v 2 64 l v 2 hf d 2 g Re d 2 g vd d 2 g
Re
d 1.175 0.075 979 < 2300 4 0.9 10
层流
1 2 1 Q 1.175 d 3600 1.175 3.14 0.075 2 3600 18.68m 3 / h 4 4
2、求沿程水头损失
64 64 0.0654 Re 979
T
T
u x u x u x
T
1 1 1 ' ux (ux ux )dt ux dt ux dt ux ux 0 T0 T0 T0
其它运动要素也同样处理:
1 p T 1 p T
T
pdt
0 T 0
p p p
pdt 0
脉动值说明:
—局部损失系数(无量纲)
一般由实验测定
实际液体流动的两种形态
雷诺试验
实验条件:
沿程阻力系数计算公式

沿程阻力系数计算公式沿程阻力系数是流体力学中一个重要的概念,它在管道流动、水利工程等领域都有着广泛的应用。
要搞清楚沿程阻力系数的计算公式,咱们得先从一些基础的知识说起。
想象一下,水在一根长长的管道里流动,就好像一群小朋友在一条长长的走廊里奔跑。
这时候,水和管道内壁之间就会产生一种摩擦力,这种摩擦力会阻碍水的流动,这就是沿程阻力。
沿程阻力系数呢,简单来说,就是用来衡量这种阻力大小的一个参数。
它的计算公式有很多种,不同的情况可能会用到不同的公式。
比如,对于层流(就是水流动得很平稳、很有秩序),沿程阻力系数可以用 64/Re 来计算,这里的 Re 是雷诺数。
雷诺数反映了流体的流动状态,是一个很重要的参数。
再比如,对于紊流(水流动得比较混乱、没有规律),情况就复杂一些啦。
这时候,沿程阻力系数的计算可能会用到尼古拉兹公式或者莫迪图。
我记得有一次在课堂上,给学生们讲解沿程阻力系数的时候,有个小家伙特别积极,一直追问我:“老师,那这个系数在实际生活中有啥用啊?”我就给他举了个例子,我说:“你想想看,咱们家里的自来水管,水从水厂通过长长的管道流到咱们家里,如果不考虑沿程阻力系数,那水的压力和流量可能就不对啦,咱们打开水龙头可能就没水或者水流特别小。
”这小家伙一听,眼睛瞪得大大的,好像一下子明白了。
在实际工程中,准确计算沿程阻力系数非常重要。
比如说在设计输油管道的时候,如果沿程阻力系数算错了,那可能会导致油泵的功率不够,油输送不出去,这可就麻烦大啦!所以啊,同学们,咱们一定要把沿程阻力系数的计算公式搞清楚,这样以后才能在实际问题中运用自如,解决各种和流体流动相关的难题。
总之,沿程阻力系数的计算公式虽然看起来有点复杂,但只要咱们认真学习,多做练习,多联系实际,就一定能够掌握它,为我们解决更多的实际问题提供有力的工具。
希望大家都能在流体力学的世界里畅游,不断探索,不断进步!。
水力学 液流形态和水头损失

第三章 液流形态和水头损失考点一 沿程水头损失、局部水头损失及其计算公式1、沿程水头损失和局部水头损失计算公式(1)水头损失的物理概念定义:实际液体运动过程中,相邻液层之间存在相对运动。
由于粘性的作用,相邻流层之间就存在内摩擦力。
液体运动过程中,要克服这种摩擦阻力就要做功,做功就要消耗一部分液流的机械能,转化为热能而散失。
这部分转化为热能而散失的机械能就是水头损失。
分类:液流边界状况的不同,将水头损失分为沿程水头损失和局部水头损失。
(2)沿程水头损失:在固体边界平直的水道中,单位重量的液体自一个断面流至另一个断面损失的机械能就叫做该两个断面之间的水头损失,这种水头损失是沿程都有并随沿程长度增加而增加的,所以称作沿程水头损失,常用h f 表示。
沿程水头损失的计算公式为达西公式对于圆管 gv d L h f 22λ= 对于非圆管 gv R L h f 242λ= 式中,λ为沿程阻力系数,其值与液流的流动形态和管壁的相对粗糙度d /∆有关,其中∆称为管壁的绝对粗糙度,)(Re,df ∆=λ; L 为管长;d 为管径;v 为管道的断面平均流速;R 为水力半径; v 为断面平均流速。
(3)局部水头损失:当液体运动时,由于局部边界形状和大小的改变,液体产生漩涡,或流线急剧变化,液体在一个局部范围之内产生了较大的能量损失,这种能量损失称作局部水头损失,常用h j 表示。
局部水头损失的计算公式为 gv h j 22ζ= 式中,ζ为局部阻力系数;其余符号同前。
(4)总水头损失对于某一液流系统,其全部水头损失h w 等于各流段沿程水头损失与局部水头损失之和,即 ∑∑+=ji fi w h h h2、湿周、水力半径(1)湿周χ:液流过水断面与固体边界接触的周界线,是过水断面的重要的水力要素之一。
其值越大,对水流的阻力和水头损失越大。
(2)水力半径R : 过水断面面积与湿周的比值,即 χAR =单靠过水断面面积或湿周,都不足以表明断面几何形状和大小对水流水头损失的影响。
流体力学实验

一 实验目的
标定文丘里流量计的流量系数。 验证能量方程的正确性。
二 实验装置
在文丘里流量计的两个测量断面上,分别有 4个测压孔与相应的均压环连通,经均压环 均压后的断面压强由气—水多管压差计9测 量(亦可用电测仪量测)。再装置图如下图 所示:
二 实验装置
供水流量由无级调速器调控使恒压水箱4始 终保持微溢流的程度,以提高进口前水体稳 定度。本恒压水箱还设有多道稳水隔板,可 使稳水时间缩短到3 ~5分钟。有色水经有 色水水管5注入实验管道8,可据有色水散开 与否判别流态。为防止自循环水污染,有色 指示水采用自行消色的专用色水。
三 实验操作
的液面高差Δh。
令
则上式可写成
三 实验原理
因此,测出测压计水位高差Δh后,即可求出 计算流量Q。 由于实际上所取的两个断面之间存在着水头 损失,所以实际流量Q 一般要略小于计算流量Q,若令
则μ是一小于1的数,称为流量系数。
三 实验原理
本实验的目的就是用实验的方法确定流量系 数μ的具体数值。实际流量Q 用体积法测定。 V为Δt时间内由管道流入计量箱内的体积。
流体力学实验
目录
雷诺实验 文丘里实验 沿程阻力系数的测定 沿程阻力系数的测定
雷诺实验
一 实验目的
1、实际观察流体的两种型态,加深对层流和 紊流的认识。 2、测定液体(水)在园管中流动的临界雷诺 数—即下临界雷诺数,学会其测定的方法。
二 实验装置
1.自循环供水器;2.实验台;3.可控硅无级调速器; 4.恒压水箱;5.有色水水管;6.稳水孔板;7.溢流板; 8.实验管道;9.实验流量调节阀。
涵洞设计细则(7)

计 算
相同数值。
图7.3.3多级跌水布置图式
七
4) 急流槽的水力计算
涵
急流槽是由进口、陡坡槽身、消能设施和出口等
洞 水
四部分组成,如图7.3.4所示
力
计
算
图7.3.4急流槽
①
急流槽的宽度一般与涵洞孔径大致相同,或
七 涵
根据需要通过的设计流量计算确定。
洞
②
急流槽中水流在整个槽身长度内处于急流状
水 力
2) 根据公路等级,求得涵洞规定设计洪水频
率的设计流量,并初拟涵洞的类型、洞口式
样和孔径后,应进行水力计算;验算涵内流
速、水深和涵前壅水位。
七
3) 涵洞水力计算图示应采用无压力式,并应符 涵
合4.3.7条规定;仅在特殊情况下,有充分的技
洞 水
术经济比较依据时,方可采用半压力式或压力 力
式涵洞。
计 算
七
表7.3.2消力槛的淹没系数σs值
涵 洞
水
力
计
算
③ 消力槛高P1的确定
Ⅰ 根据公式(7.3.2-1)(7.3.2-3)、表7.3.2,
先假定σs =1求得消力槛淹没系数σs,判断出槛 水流情况。当为自由出流时,则P1值即为所求得
的值;当为淹没出流时,可重新假定P1值,
七
计试算算σs值。H试10 算中hc-以P1公 式2g (qh72c.32.2-1)的变形式
态,起点断面水深为临界水深hk,随后各断面水 计
深小于临界水深hk,即出现降水曲线。
算
③ 按均匀流公式试算槽中正常水深h0、流速V0,
最后验算流量并检验与设计流量差不大于±5%。
④ 降水曲线范围内可按分段求和法计算完整的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
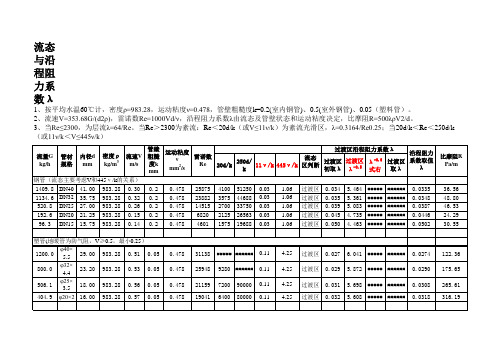
1、按平均水温60℃计,密度ρ=983.28,运动粘度ν=0.478,管壁粗糙度k=0.2(室内钢管)、0.5(室外钢管)、0.05(塑料管)。 2、流速V=353.68G/(d2ρ),雷诺数Re=1000Vd/ν,沿程阻力系数λ由流态及管壁状态和运动粘度决定,比摩阻R=500λρV2/d。 3、当Re≤2300,为层流λ=64/Re。当Re>2300为紊流:Re<20d/k(或V≤11ν/k)为紊流光滑区,λ=0.3164/Re0.25;当20d/k<Re<250d/k (或11ν/k<V≤445ν/k)
管壁 运动粘度 流速V 粗糙 雷诺数 ν Re 度k m/s 20d/k 2 mm /s mm 钢管(流态主要考虑V和445ν /k的关系) 1409.8 DN40 41.00 983.28 0.30 0.2 0.478 25875 4100 1134.6 DN32 35.75 983.28 0.32 0.2 0.478 23882 3575 520.8 DN25 27.00 983.28 0.26 0.2 0.478 14515 2700 192.6 DN20 21.25 983.28 0.15 0.2 0.478 6820 2125 96.3 DN15 15.75 983.28 0.14 0.2 0.478 4601 1575 流量G kg/h 管材 规格 内径d mm 密度ρ 3 kg/m 塑管(地暖管为防气阻,V≥0.5,最小0.25) φ40× 1200.0 29.00 983.28 0.51 0.05 5.5 φ32× 800.0 23.20 983.28 0.53 0.05 4.4 φ25× 506.1 18.00 983.28 0.56 0.05 3.5 404.9 φ20×2 16.00 983.28 0.57 0.05 流态特征
过渡区 过渡区 过渡区 过渡区 过渡区
0.055 0.059 0.067 0.077 0.091
4.264 4.134 3.878 3.616 3.324
##### ##### ##### ##### #####
###### ###### ###### ###### ######
0.0550 0.0585 0.0665 0.0765 0.0905
85.77 106.80 139.74 82.32 164.42
过渡区 0.027 过渡区 0.029 过渡区 0.031 过渡区 0.032
6.041 ##### ###### 5.872 ##### ###### 5.698 ##### ###### 5.608 ##### ######
0.0274 0.0290 0.0308 0.0318
122.36 175.65 265.61 316.19
建筑热水设计——钢管考虑结垢时(比较保守)V<0.44m/s时为过渡区,V≥0.44m/s时为粗糙区 0.01 0.21 1440.0 DN40 38.50 983.24 0.35 1.0 0.478 28147 770 9625 DN32 33.25 983.24 0.35 1.0 0.01 0.21 1080.0 0.478 24443 665 8313 0.01 0.21 540.0 DN25 24.50 983.24 0.32 1.0 0.478 16586 490 6125 0.01 0.21 198.0 DN20 18.75 983.24 0.20 1.0 0.478 7947 375 4688 DN15 13.25 983.24 0.22 1.0 0.01 0.21 108.0 0.478 6134 265 3313
250d/ k 51250 44688 33750 26563 19688 11ν /k 0.03 0.03 0.03 0.03 0.03 沿程阻力 流态 过渡区 过渡区 λ -0.5 过渡区 系数取值 445ν /k 区判断 λ 初取λ λ -0.5 式右 取λ 1.06 1.06 1.06 1.06 1.06 过渡区 过渡区 过渡区 过渡区 过渡区 0.034 0.035 ቤተ መጻሕፍቲ ባይዱ.039 0.045 0.050 5.464 5.361 5.083 4.735 4.463 ##### ##### ##### ##### ##### ###### ###### ###### ###### ###### 0.0335 0.0348 0.0387 0.0446 0.0502 过渡区沿程阻力系数λ 比摩阻R Pa/m
36.56 48.80 46.53 24.29 30.55
0.478 0.478 0.478 0.478
31138 25948 21159 19041
##### ###### 9280 ###### 7200 6400 90000 80000
0.11 0.11 0.11 0.11
4.25 4.25 4.25 4.25
