工程光学-光的衍射 习题课
习题课 光的衍射

L
2 1
红
紫 50mm
f
习题课 光的衍射
例4
四.典型例题
波长为400~~700nm的一束可见光垂直入射到
一缝宽为1.0×10-4cm的透射光栅上,其中波长为600
nm的光的第四级谱线缺级,会聚透镜的焦距为1m, 求: (1)此光栅每厘米有多少狭缝? (2)波长为600nm的光在屏上呈现的光谱线的全部
(2) d sin sin k
kmax
3d sin 90 sin 30 5.09 5 2 d
(取整)
习题课 光的衍射
四.典型例题
例3. 一束4000 A ~ 7000 A的可见光垂直地射到光栅常数 为0.002mm的透射平面光栅上,为了在投影物镜L的焦平 面上得到该波长的第一级光谱的长度为50mm,问物镜 L 的焦距至少应是多少毫米? 解:1 4000 A 与2 7000 A
级数
(3)第二级光谱在屏上的线宽
(4)第二级光谱与第一,第三级重叠部分的线宽度
习题课 光的衍射
解:(1).由缺级条件: k d 4 即 k a
四.典型例题
d 4a 4 10 cm
4
1 N 2500条 cm d
(2). kmax
4 4 10 sin 90 6取整 5 6 10
习题课 光的衍射 一.基本规律
1.惠更斯-菲涅尔原理
一.基本规律
k ( ) 2r E ( p) c cos(t )ds s r
2.单缝公式
2k ( ) 2 a sin { ( 2k 1) 2
工程光学-光的衍射习题课

工程光学光的衍射习题解答1、氦氖激光器发出的波长的单色光垂直入射到半径为1cm的圆孔,在光轴(它通过孔中心并垂直孔平面)附近离孔z处观察衍射,试求出夫琅和费衍射区的大致范围?解:2、钠灯发出波长为589nm的平行光垂直照射在宽度为0.01mm的单逢上,以焦距为600mm的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半角宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;(3)相邻暗纹之间的距离?解:3、在夫琅和费单缝衍射实验中,以波长为600nm的单色光垂直入射,若缝宽为1mm,则第1极小和第2极小的角位置分别出现在哪里?4、分析如图所示夫琅和费衍射装置如有以下变动时,衍射图样会发生怎样的变化?1)增大透镜L2的焦距;2)减小透镜L2的口径;3)衍射屏作垂直于光轴的移动(不超出入射光束照明范围)。
答:1)增大透镜L2的焦距,将使接收屏上衍射图样的间隔增大。
因有公式,此时衍射角不变,条纹间隔增大;2)增大透镜L2的口径,不会改变衍射图样的分布,但进入系统的光束宽度增加,可使光强增加;3)衍射屏垂直于系统光轴方向移动时,衍射图样不会改变,因为衍射屏移动前后光的入射角不变,缝宽不变,由衍射公式知其接收屏上的光强分布不变;5、在双缝夫琅和费实验中,所用的光波波长,透镜焦距,观察到两相临亮条纹间的距离,并且第4级亮纹缺级。
试求:(1)双缝的逢距和逢宽;(2)第1,2,3级亮纹的相对强度。
解:(1) (1)双缝的缝距和逢宽;又将代入得(2)(2)第1,2,3级亮纹的相对强度。
当m=1时当m=2时当m=3时代入单缝衍射公式当m=1时当m=2时当m=3时6、一块光栅的宽度为10cm ,每毫米内有500条逢,光栅后面放置的透镜焦距为500nm。
问:(1)它产生的波长的单色光的1级和2级谱线的半宽度是多少?(2)若入射光线是波长为632.8nm 和波长与之相差0.5nm的两种单色光,它们的1级和2级谱线之间的距离是多少?解:由光栅方程知,,这里的,确定了谱线的位置(1)(1)它产生的波长的单色光的1级和2级谱线的半宽度是多少?(此公式即为半角公式)(2)若入射光线是波长为632.8nm和波长与之相差0.5nm的两种单色光,它们的1级和2级谱线之间的距离是多少?由公式(此公式为线色散公式)可得。
光学 第2章 光的衍射7(习题课)

习题课
1、在杨氏双缝实验装置中,双缝相距0.5mm,接收
屏距双缝1m,点光源距双缝30cm,它发射出 500 nm 的单色光。试求:
(1)屏上干涉条纹的间距。
(2)若点光源由轴上向下平移2mm,屏上干涉条纹向 什么方向移动?移动多少距离?
2
2、若在牛顿环装置中的透镜与玻璃片之间充以折射 率为n某种液体,现测到第10级亮环的直径由1.40cm 变成1.27cm,试求该液体的成分的光波照射, 1 2 如果产生的衍射图样中λ1的第一极小与λ第二 2 极小重合,试问: (1)这两种波长之间有何关系 (2)是否还有其他的极小也重合?
4
4、波长为600nm的单色光垂直入射到一光栅上,测得第
2级主极大的衍射角为30°,且第三级是缺级.求
(1) 光栅常量d等于多少?
(2) 透光缝可能的最小宽度b等于多少?
(3) 在选定了上述b和d之后,可能观察到的全部主极大
的级次.
5
5、波长为632.8nm的单色平行光垂直入射到一圆孔上 在孔中心轴上距孔r0 = 1m处的P0点出现一亮点,假定 这时小圆孔截取的波面对P0点恰好露出一个半波带 求:()小圆孔的半径R h = ? 1 (2)由P0点沿中心轴从远处向圆孔移动时,第一个暗点 到圆孔的距离是多少?
6
光的衍射习题课ppt课件

Ae
A2
Ao
A1
N2
过该装置。
b sin k
b sin (2k b sin
1)
2
(3) 条纹宽度
k 1,2暗纹中心 k 1,2明纹中心 中央明纹
中央明条宽度:角宽度
0
2b
线宽度 x0
2 b
f
明条纹宽度 x f
b
2.衍射光栅
(1)光栅衍射是单缝衍射和各缝干涉的总 效果
(2)光栅方程
(b b)sin k k 0,1,2,
已知 (b b) sin 2 2
(b b) sin 3 3
得 b b 6 104 m
又因第4级缺级,则由 k
b
b
k
,
得
b b 4
b
b 1.5104 m
b
(2)设 90,则 (b b) sin k
可以见到 2k 1 21 (k=10条),包括零
级明纹,但是:由于有缺级,(4,8) ,则
可见到17条(实际15条)
(3)此时屏上条纹不再对称, 在一侧有
(b b) sin 30 (b b) sin k
当 90时,k 15
另一侧有 (b b)(sin 30 sin ) k
90时,k 5
考虑到第4,8,12及-4
i
为缺级以及实际效果,共
观察到15条明纹,全部级
x o
k 4, 4 333nm
f
可允许在屏上x=1.5mm处的明纹为波长
600nm的第二级衍射和波长为420nm的第三
级衍射
(2)此时单缝可分成的波带数 分别是 k 2,时 为 2k 1 5
k 3,时 为 2k 1 7
工程光学-郁道银-第13章光的衍射课后习题答案
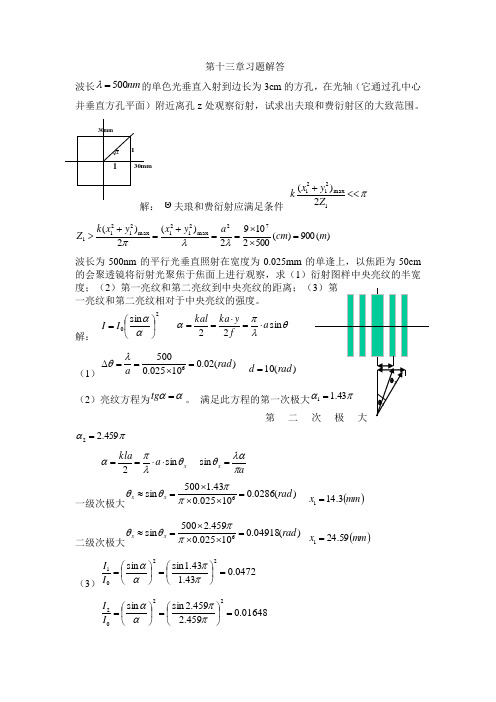
1θ2θ2mm3011mm 30第十三章习题解答波长nm 500=λ的单色光垂直入射到边长为3cm 的方孔,在光轴(它通过孔中心并垂直方孔平面)附近离孔z 处观察衍射,试求出夫琅和费衍射区的大致范围。
解: 夫琅和费衍射应满足条件 π<<+1max 21212)(Z y x k)(900)(50021092)(2)(72max 2121max 21211m cm a y x y x k Z =⨯⨯==+=+>λλπ波长为500nm 的平行光垂直照射在宽度为0.025mm 的单逢上,以焦距为50cm的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;(3)第一亮纹和第二亮纹相对于中央亮纹的强度。
解: 20sin ⎪⎭⎫⎝⎛=ααI I θλπαs i n 22a f y ka kal ⋅=⋅==(1))(02.010025.05006rad a=⨯==∆λθ )(10rad d =(2)亮纹方程为αα=tg 。
满足此方程的第一次极大πα43.11= 第二次极大πα459.22=x a k l a θλπαs i n 2⋅⋅==a x πλαθ=sin 一级次极大)(0286.010025.043.1500sin 6rad x x =⨯⨯⨯=≈ππθθ ()mm x 3.141=二级次极大)(04918.010025.0459.2500sin 6rad x x =⨯⨯⨯=≈ππθθ ()mm x 59.241=(3)0472.043.143.1sin sin 2201=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=ππααI I01648.0459.2459.2s i n s i n 2202=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=ππααI I10.若望远镜能分辨角距离为rad 7103-⨯的两颗星,它的物镜的最小直径是多少?同时为了充分利用望远镜的分辨率,望远镜应有多大的放大率?解:D λθ22.10= )(24.21031055022.179m D =⨯⨯⨯=--⨯-=⨯⨯⨯⨯⨯=''=Γ969310180606060067πϕ11. 若要使照相机感光胶片能分辨m μ2线距,(1)感光胶片的分辨率至少是没毫米多少线;(2)照相机镜头的相对孔径f D至少是多大?(设光波波长550nm ) 解:)(50010213mm N 线=⨯=-3355.01490=≈'NfD12. 一台显微镜的数值孔径为0。
光的衍射习题课

解:倾角入射时光栅方程 d sin sin0 m
sin m d sin0
sin m d sin0 m d 1 2 1
m d 1 2 1 m 2.1 m d 1 2 1 m 6.3
m 6 ,5 ,4 ,3 ,2 ,1 , 0 , 1 ,2
B. 2, 5, 8, 11…… D. 3, 6, 9, 12……
m1
2
750
5
4. 如图所示,波长为 = 480nm 的平行光束 垂直照射到宽度为a=0.40mm的单缝上,单 缝后透镜的焦距为f = 60cm,当单缝两边缘 点AB射向P点的两条光线在P点的位相差为 时 ,P点的明暗程度和离透镜焦点 O 的距离 等于多少?
解 : 由光栅衍射方程
d sin 1 k11 d sin 2 k22
当两谱线重合时即1= 2, 所以 k11 k22 解得
k1 2 660 3 6 9 k2 1 440 2 4 6
当第二次重合时是
k1 6 k2 4
即k1 = 6, k2 = 4
3.某元素的特征光谱中含有波长分别为 λ1 = 450nm和 λ 2 = 750nm 的光谱线,在光栅光谱中,这两种波长的谱线有重叠现象,重叠 处 λ 2 的谱线的级次将是( D ) d sin m m ; m2 1 450 3
1 1 2 2
A. 2, 3, 4, 5…… C. 2, 4, 6, 8……
由光栅方程可知
d sin 600 61
6 4400 107 d 3.05 103 mm 0.866
10.波长= 600nm的单色光垂直入射到一光栅上, 测得第二级主极 大的衍射角为300, 且第三级是缺级。 a) 光栅常数d 等于多少? b) 透光缝可能的最小宽度a等于多少? c) 在选定了上述d 和a之后, 求屏幕上可能呈现的主极大的极次。 解:(1)由光栅衍射主极大公式 dsin k
第十一章【光的衍射】习题课

(A)振动振幅之和;
(B)光强之和; (C)振动振幅之和的平方; (D)振动的相干叠加。
E
CK ( ) dS cos(t - 2r )
r
[D]
en
dS · r
Q
dE(p) p
S
2.一束波长为的平行单色光垂直入射到一单缝 AB 上,
在屏幕 D 上形成衍射图样,如果 P 是中央亮纹一侧 第二个暗纹所在的位置,则BC 的长度为
单缝衍射、衍射光栅 习题课
一、惠更斯--菲涅耳原理
惠更斯原理:波在媒质中传播到的各点,都可 看成新的子波源。
惠更斯原理只能解释波的衍射,不能给出波强。 菲涅耳原理:波传播到某一点的光强为各个子波在
观察点的干涉叠加。
菲涅耳:提出子波相干叠加的概念
惠更斯—菲涅耳原理
波传到的任何一点都是子波波源,各子波在空 间某点的相干叠加,就决定了该点波的强度。
BP
AP
BC
3
6
2
BP AP BC 2.5 5
2
暗条纹 明条纹
L
D
P
F 屏
4、在单缝夫琅禾费衍射实验中,屏上第三级暗纹对应 的单缝处的波面可划分为几个半波带?若将缝宽缩小 一半,原来第三级暗纹处将是什么条纹?
暗纹条件: 半波带数目
bsin 2k k(k 1,2,3)
2
6个半波带
缝宽变化前: bsin 3
明纹中心
2k 1
个半波带
A C
b
B L
f
o
x
P
3 2 1
1
I
2
3
•明纹、暗纹位置 f k (k 1,2 ) 暗纹
x b f(k 1) (k 1,2 ) 明纹
23光衍射习题课

13、对某一定波长的垂直入射光,衍射光栅的屏幕上只能出现 零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该 (A) 换光栅常数小的光栅. (B) 换光栅常数大的光栅. (C) 将光栅向靠近屏幕的方向移动. (D) 将光栅向远离屏幕的方向移动. B 解: (a b) sin900
(a b) sin k , km
1 d:光栅常数: 若每厘米刻有N条刻痕,则 d cm N 2.光栅衍射的暗纹条件
d sin k
m N
k 0,1,2,
d sin
m 1,2,, ( N 1)
在几乎黑暗的背景上出现了一系 列又亮又细且分得开的明条纹。
3.光栅衍射明纹的特点
4.条纹缺级问题
k 1,2, 明纹 a sin k ' k ' 1,2, 暗纹
17、波长λ=550 nm(1nm=10−9 m)的单色光垂直入射于光栅常数 d=2×10-4 cm的平面衍射光栅上,可能观察到的光谱线的最大 级次为 (A) 2. (B) 3. (C) 4. (D) 5.
2 103 解: d sin90 k , k 3.6 3 550
D
22
某元素的特征光谱中含有波长分别为λ1= 450nm 和λ2=
750nm 的光谱线,在光栅光谱中,这两种波长的谱线有重
叠现象,重叠处λ2 的谱线的级数为:
(A) 2,3,4,5 (B) 2,5,8,11
解: d sin
(C) 2,4,6,8
(D) 3,6,9,12
k11 k22
1 3 k2 k1 k1 2 5
D
k1 5、 、 、 时, 10 15 k2 3、 9 6、
光的衍射习题1

第二章光的衍射(1)一、选择题1.根据惠更斯—菲涅耳原理,若已知光在某时刻的阵面为S,则S的前方某点P的光强度决定于波阵面S上所有面积元发出的子波各自传到P点的(A) 振动振幅之和(B) 光强之和(C) 振动振幅之和的平方(D) 振动的相干叠加2.在如图所示的单缝夫琅和费衍射装置中,将单缝宽度a同时使单缝沿y轴正方向作为微小位移,则屏幕C(A) 变窄,同时向上移;(B)(C) 变窄,不移动;(D) 变宽,同时向上移;(E) 变宽,不移动。
3.波长λ=5000Ǻ的单色光垂直照射到宽度a=0.25mm的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹。
今测的屏幕上中央条纹一侧第三个暗条纹和另一侧第三个暗条纹之间的距离为d=12mm,则凸透镜的焦距f为(A) 2m (B) 1m (C) 0.5m (D) 0.2m (E) 0.1m4.在透光缝数为的光栅衍射实验里,缝干涉的中央明纹中强度的最大值为一个缝单独存在时单缝衍射中央明纹强度最大值的(A) 1倍(B) N倍(C)2N倍(D) N2倍5.波长为4.26Ǻ的单色光,以70º角掠射到岩盐晶体表面上时,在反射方向出现第一级级大,则岩盐晶体的晶格常数为(A) 0.39Ǻ (B) 2.27Ǻ (C) 5.84λǺ (D) 6.29Ǻ二、填空题1.惠更斯—菲涅耳原理的基本内容是:波阵面上各面积元所发出的子波在观察点P的______,决定了P点的合震动及光强。
2.在单缝夫琅和费衍射实验中,设第一级安稳的衍射角很小,若钠黄光(λ≈5890Ǻ)中央明纹宽度为4.0mm,则λ=4420Ǻ的蓝紫色光的中央明纹宽度为_____.3.一束单色光垂直入射在光栅上,衍射光谱中共出现5条明纹。
若已知此光栅缝宽度与不透明部分宽度相等,那么在中央明纹一侧的两条明纹分别是第_____级和第_____级谱线。
4.单色平行光垂直照射一侧狭缝,在缝后远处的屏上观察到夫琅和费衍射图样,现在把缝宽加倍,则透过狭缝的光的能量变为_____倍,屏上图样的中央光强变为_____倍5.一双缝衍射系统,缝宽为a,两缝中心间距为d。
课时作业4:4.5-4.6 光的衍射 光的偏振 激光

5光的衍射6光的偏振激光考点一光的衍射1.一束红光射向一块有双缝的不透光的薄板,在薄板后的光屏上呈现明暗相间的干涉条纹.现将其中一条窄缝挡住,让这束红光只通过一条窄缝,则在光屏上可以看到()A.与原来相同的明暗相间的条纹,只是亮条纹比原来暗些B.与原来不相同的明暗相间的条纹,中央亮条纹较宽C.只有一条与缝宽对应的亮条纹D.无条纹,只存在一片红光答案 B解析因产生了干涉现象,说明两缝都很窄,能够满足使红光发生明显衍射的条件,即挡住一条窄缝后,在屏上得到的是红光的单缝衍射图样,故选B.2.某同学使用激光器做光源,在不透光的挡板上开一条宽度为0.05 mm的窄缝(水平),进行光的衍射实验,如图1所示,则他在光屏上看到的条纹是()图1答案 D解析单缝衍射条纹中间宽,两侧越来越窄,又由于单缝是水平的,故衍射条纹也是水平的,D对.3.下列四种明暗相间的条纹,分别是红光、蓝光各自通过同一种双缝干涉仪器和同一个单缝衍射仪器形成的图样(灰黑色部分表示亮条纹;保持缝到屏距离不变).其中属于蓝光的衍射图样的是()答案 B解析双缝干涉的图样是明暗相间的条纹,所有条纹宽度相同且等间距,所以A、C选项中的图样为干涉图样,单缝衍射条纹是中间明亮且宽大,越向两侧宽度越小越暗,而波长越长,中央亮条纹宽度越大,红光的波长大于蓝光的波长,所以B项为蓝光的衍射图样,故B正确.4.在一束单色光的传播方向上分别放置单缝、双缝、小圆孔和小圆板后,在光屏上得到如图2甲、乙、丙、丁四幅图样,关于光屏前传播方向上放置的装置,以下说法正确的是()图2A.甲是单缝、乙是双缝B.乙是双缝、丙是小圆孔C.丁是小圆孔、甲是双缝D.丙是小圆孔、丁是小圆板答案 D考点二光的偏振5.(多选)如图所示,一束自然光通过偏振片照射到光屏上,则图中光屏上发亮的有(偏振片上用箭头表示其透振方向)()答案ABD解析自然光通过偏振片后成为偏振光,当偏振光的振动方向与偏振片的透振方向平行时能够通过,垂直时不能通过,所以A、B、D正确.6.(多选)当以入射光线为轴转动偏振片时,通过偏振片观察电灯、烛焰、月球、反光的黑板,看到现象有何不同()A.观察电灯和烛焰时,透射光的强弱随偏振片的旋转而变化B.观察电灯和烛焰时,透射光的强弱不随偏振片的旋转而变化C.观察月球和反光的黑板时,透射光的强弱不随偏振片的旋转而变化D.观察月球和反光的黑板时,透射光的强弱随偏振片的旋转而变化答案BD解析通过偏振片去观察电灯、烛焰时,透射光的强弱不随偏振片的旋转而变化.因为灯光、烛光都是自然光,沿各个方向振动的光的强度相同,因此当偏振片旋转时,透射出来的光波的振动方向虽然改变了,但光的强弱没有改变.月球和黑板反射的光已经是偏振光,它通过偏振片透射过来的光线和强弱都会随偏振片的旋转发生变化,故B、D正确,A、C错误.7.(2020·郑州七中期中)在日落时分拍摄水面下的景物时,应在照相机镜头前装一个偏振片,其目的是()A.减少阳光在水面上的反射光B.最大限度地阻止阳光在水面上的反射光进入照相机镜头C.增强光由水面射入空气中的折射光进入镜头的强度D.减弱光由水面射入空气中的折射光进入镜头的强度答案 B解析日落时分的阳光照射到水面上时,反射光很强,照相机镜头对着水面时,进入镜头的光线既有阳光经水面的反射光,又有由水中折射入空气的折射光,折射光线进入镜头所摄得的照片才是水下景物的像.在镜头上安装一个偏振片,转动偏振片方向使其透振方向与反射光的偏振方向垂直,即可最大限度地阻止反射光进入镜头,增强图像的清晰度.B正确.考点三激光及其应用8.(2020·上海市南洋模范中学期中)在激光的伤害中,以机体中眼睛的伤害最为严重.激光聚于感光细胞时,产生过量热量而引起的蛋白质凝固变性是不可逆的损伤,一旦损伤以后就会造成眼睛的永久失明,激光对眼睛的危害如此之大的主要原因是()A.单色性好B.高能量C.相干性好D.平行度好答案 B解析由题意可知,激光聚于感光细胞时产生过量热量而引起的蛋白质凝固变性是造成眼睛失明的原因,说明引起这一现象的主要原因是激光的高能量,故B正确,A、C、D错误.9.(多选)以下说法正确的是()A.激光是一种人工产生的相干光,具有高度的相干性B.由于激光的方向性好,所以激光不能发生衍射现象C.光纤通信是激光和光导纤维相结合的产物D.普通摄像技术所记录的只是光波的强弱信息,而全息摄像技术还可以记录光波的相位信息答案ACD10.(多选)沙尘暴是由于土地的沙化引起的一种恶劣的气象现象,发生沙尘暴时能见度只有几十米,天空变黄发暗,这是由于在这种情况下()A.只有波长较短的一部分光才能到达地面B.只有波长较长的一部分光才能到达地面C .只有频率较高的一部分光才能到达地面D .只有频率较低的一部分光才能到达地面答案 BD解析 根据光发生明显衍射现象的条件知,发生沙尘暴时,只有波长较长的一部分光能到达地面,据λ=c f知,到达地面的光是频率较低的一部分光,故选项B 、D 正确. 11.(多选)鉴别奶粉的质量,奶粉的碳水化合物(糖)的含量是一个重要指标,可以用“旋光法”来测量糖溶液的浓度,从而鉴定含糖量.偏振光通过糖的水溶液后,偏振方向会相对于传播方向向左或向右旋转一个角度α,这一角度α称为“旋光度”,α的值只与糖溶液的浓度有关,将α的测量值与标准值相比较,就能确定被测样品的含糖量了.如图3所示,S 是自然光源,A 、B 是偏振片,转动B ,使到达O 处的光最强,然后将被测样品P 置于A 、B 之间,则下列说法正确的是( )图3A .到达O 处的光的强度会明显减弱B .到达O 处的光的强度不会明显减弱C .将偏振片B 转动一个角度,使得O 处光的强度最大,偏振片B 转过的角度等于αD .将偏振片A 转动一个角度,使得O 处光的强度最大,偏振片A 转过的角度等于α 答案 ACD解析 自然光通过偏振片后得到振动方向与偏振片的透振方向平行的偏振光,该偏振光经被测样品后,其偏振方向发生了偏转,即相对于光的传播方向向左或向右旋转一个角度α,到达B 的光的偏振方向与B 的透振方向不完全一致,故O 处光的强度会明显减弱,故A 正确,B 错误;若将A 或B 转动一个角度,使得O 处光的强度最大,说明它们转过的角度等于α,故C 、D 正确.。
工程光学习题参考答案第十二章-光的衍射

第十二章 光的衍射1. 波长为500nm 的平行光垂直照射在宽度为0.025mm 的单缝上,以焦距为50cm 的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;(3)第一亮纹和第二亮纹的强度。
解:(1)零强度点有sin (1,2, 3....................)a n n θλ==±±± ∴中央亮纹的角半宽度为0aλθ∆=∴亮纹半宽度290035010500100.010.02510r f f m a λθ---⨯⨯⨯=⋅∆===⨯ (2)第一亮纹,有1sin 4.493a παθλ=⋅= 同理224.6r mm =(3)衍射光强20sin I I αα⎛⎫= ⎪⎝⎭,其中sin a παθλ= 当sin a n θλ=时为暗纹,tg αα=为亮纹 ∴对应 级数 α 0II0 0 11 4.493 0.047182 7.725 0.01694 . . . . . . . . .2. 平行光斜入射到单缝上,证明:(1)单缝夫琅和费衍射强度公式为20sin[(sin sin )](sin sin )a i I I a i πθλπθλ⎧⎫-⎪⎪=⎨⎬⎪⎪-⎩⎭式中,0I 是中央亮纹中心强度;a 是缝宽;θ是衍射角,i 是入射角(见图12-50) (2)中央亮纹的角半宽度为λθ∆=图12-50 习题3图解:设直径为a ,则有f d aλ=4.利用第三节的结果导出外径和内径分别为a 和b 的圆环(见图12-51)的夫琅和费衍射强度公式,并求出当2ab =时,(1)圆环衍射与半径为a 的圆孔衍射图样的中心强度之比;(2)圆环衍射图样第一个暗环的角半径。
∴P 当(12449416a ca ⎫-=⎪⎭ ∴()()09016aI I = (2)第一暗纹有()()22110a J ka b J kb ka kb θθθθ-= 查表可有 3.144ka θ=4. (1)一束直径为2mm 的氦氖激光(632.8nm λ=)自地面射向月球,已知地面和月球相距33.7610km ⨯,问在月球上得到的光斑有多大?(2)如果用望远镜用作为扩束器将该扩展成直径为4m 的光束,该用多大倍数的望远镜?将扩束后的光束再射向月球,在月球上的光斑为多大? 解:(1)圆孔衍射角半宽度为0.61aλθ=∴传到月球上时光斑直径为(2)若用望远镜扩束,则放大倍数为2000倍。
工程光学习题解答第十一章_光的衍射

第十一章 光的衍射1. 波长为500nm 的平行光垂直照射在宽度为0.025mm 的单缝上,以焦距为50cm 的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;(3)第一亮纹和第二亮纹的强度。
解:(1)零强度点有sin (1,2, 3....................)a n n θλ==±±± ∴中央亮纹的角半宽度为0aλθ∆=∴亮纹半宽度290035010500100.010.02510r f f m a λθ---⨯⨯⨯=⋅∆===⨯ (2)第一亮纹,有1sin 4.493a παθλ=⋅= 9134.493 4.493500100.02863.140.02510rad a λθπ--⨯⨯∴===⨯⨯ 21150100.02860.014314.3r f m mm θ-∴=⋅=⨯⨯==同理224.6r mm =(3)衍射光强20sin I I αα⎛⎫= ⎪⎝⎭,其中sin a παθλ= 当sin a n θλ=时为暗纹,tg αα=为亮纹 ∴对应 级数 α 0II0 0 11 4.493 0.047182 7.725 0.01694 . . . . . . . . .2. 平行光斜入射到单缝上,证明:(1)单缝夫琅和费衍射强度公式为20sin[(sin sin )](sin sin )a i I I a i πθλπθλ⎧⎫-⎪⎪=⎨⎬⎪⎪-⎩⎭式中,0I 是中央亮纹中心强度;a 是缝宽;θ是衍射角,i 是入射角(见图12-50) (2)中央亮纹的角半宽度为cos a iλθ∆=证明:(1))即可(2)令(sin sin ai πθπλ==± ∴对于中央亮斑 sin sin i aλθ-=3. 在不透明细丝的夫琅和费衍射图样中,测得暗条纹的间距为1.5mm ,所用透镜的焦距为30mm ,光波波长为632.8nm 。
光的衍射习题课

d k k , k 1,2, a 当d n时, 明纹所缺级次为:k = n , 2n , … a
17 设光栅平面、透镜均与屏幕平行。则当入射 的平行单色光从垂直于光栅平面入射变为斜入射 时,能观察到的光谱线的最高级数 : [ B ] (A)变小 ; (B)变大 ; (C)不变; (D)k的改变无法确定 。 分析:当平行单色光垂直于光栅平面入射时
3 3 于是 a 0 2 si n30
2
15 测量单色光的波长时,下列方法中哪一种方 法最为准确? [ D ] (A)双缝干涉 ; (B)牛顿环 ; (C)单缝衍射 ; (D)光栅衍射 .
16 一束平行单色光垂直入射在光栅上,当光栅 常数(a+b)为下情况时(a 代表每条缝的宽度), k =3、6、9等级次的主极大均不出现? : [ B ] (A)a + b = 2a ; k 2k' 2 ,4 ,6 , (B)a + b = 3a ; k 3k' 3 ,6 ,9 , (C)a + b = 4a ; k 4k' 4 ,8 ,12 , (D)a + b = 6a 。 k 6k' 6 ,12 , 分析: 明纹缺级级次:
(b)d / a 4,4缺级 (d )d/a 3 , 3缺级
(4)见图4.2
589.3 10 arcsi n ( k ) 2 2.0 10 / 6000
9
arcsi n ( 0.1768 k) 1, 取 k = 0 , 1 , 2 , 3 , 4 , 5 。 ∵ si n
相应的角位置值: 00 , 10011, 20042,
0 0 32 2 , 45 , 62 7 0
光的衍射习题(课堂PPT)

4.将透镜向上作小位移时,透镜中心位置向上移动, 将使条纹向上平移。
5、单缝的宽度b=0.40 mm,以波长λ=589nm的单色光垂直照射,设 透镜的焦距f=1.0m.求: (1)第一级暗纹距中心的距离; (2)第二级明纹距中心的距离;
解:由单缝衍射的暗纹条件 bsin 1kl
得
: 1sin1
kl
其条纹间距 Δx = x2 – x1 = 2·7×10-3 m
(2)当光垂直照射光栅时 ,屏上第 k 级明纹的位置为
dx'/ f klx ' k l f 而光栅常数 d = 10-2 /10-3 m
d
当 λ1 = 400nm 和 k = 1 时 , x’1 = 2×10-2 m ;。 当 λ2 = 760nm 和 k = 1 时 , x’2 =3·8×10-2 m 。
屏中心多远 ?这两条明纹之间的距离又是多少 ?
解: (1)当光垂直照射单缝时 ,屏上第 k 级明纹的位置
bx/ f (2k1)l
2
x (2k 1) l f
2b
当 λ1 =400nm 和 k = 1 时 ,x1 = 3·0×10-3 m
当 λ2 =760nm 和 k = 1 时 ,x2 =5·7×10-3 m
x
0 .1
得 D = 1.34m
注:嫦娥1号的绕月轨道离月球表面 200公里,对月球表面的分辨率为 120m,嫦娥2号的绕月轨道离月球表面 100公里,对月球表面的分辨率为7m.
8.以氢放电管发出的光垂直照射在某光栅上,在衍射角 =41 的
方向上看到l1656.2nm 和 l2410.1nm 的谱线相重合,求光栅常
纹位置一样.求前一种单色光的波长.
由衍射明纹条件
光的衍射习题(附答案)1(1)

光的衍射(附答案)一.填空题1.波长λ = 500 nm(1 nm = 10−9 m)的单色光垂直照射到宽度a = 0.25 mm的单缝上,单缝后面放置一凸透镜,在凸透镜的焦平面上放置一屏幕,用以观测衍射条纹.今测得屏幕上中央明条纹之间的距离为d = 12 mm,则凸透镜的焦距f为1 m.2.在单缝夫琅禾费衍射实验中,设第一级暗纹的衍射角很小,若钠黄光(λ1 ≈589 nm)中央明纹宽度为4.0 mm,则λ2 ≈ 442 nm(1 nm = 10−9 m)的蓝紫色光的中央明纹宽度为3.0 mm.3.平行单色光垂直入射在缝宽为a = 0.15 mm的单缝上,缝后有焦距为f = 400mm的凸透镜,在其焦平面上放置观察屏幕.现测得屏幕上中央明纹两侧的两个第三级暗纹之间的距离为8 mm,则入射光的波长为500 nm(或5×10−4mm).4.当一衍射光栅的不透光部分的宽度b与透光缝宽度a满足关系b = 3a 时,衍射光谱中第±4, ±8, …级谱线缺级.5.一毫米内有500条刻痕的平面透射光栅,用平行钠光束与光栅平面法线成30°角入射,在屏幕上最多能看到第5级光谱.6.用波长为λ的单色平行红光垂直照射在光栅常数d = 2 μm(1 μm = 10−6 m)的光栅上,用焦距f = 0.500 m的透镜将光聚在屏上,测得第一级谱线与透镜主焦点的距离l = 0.1667 m,则可知该入射的红光波长λ=632.6或633nm.7.一会聚透镜,直径为3 cm,焦距为20 cm.照射光波长550nm.为了可以分辨,两个远处的点状物体对透镜中心的张角必须不小于2.24×10−5rad.这时在透镜焦平面上两个衍射图样中心间的距离不小于4.47μm.8.钠黄光双线的两个波长分别是589.00 nm和589.59 nm(1 nm = 10−9 m),若平面衍射光栅能够在第二级光谱中分辨这两条谱线,光栅的缝数至少是500.9.用平行的白光垂直入射在平面透射光栅上,波长为λ1 = 440 nm的第3级光谱线将与波长为λ2 =660 nm的第2级光谱线重叠(1 nm = 10−9 m).10.X射线入射到晶格常数为d的晶体中,可能发生布拉格衍射的最大波长为2d.二.计算题11.在某个单缝衍射实验中,光源发出的光含有两种波长λ1和λ2,垂直入射于单缝上.假如λ1的第一级衍射极小与λ2的第二级衍射极小相重合,试问:(1) 这两种波长之间有何关系?(2) 在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合?解:(1) 由单缝衍射暗纹公式得a sinθ1= 1 λ1a sinθ2= 2 λ2由题意可知θ1 = θ2, sinθ1= sinθ2代入上式可得λ1 = 2 λ2(2) a sinθ1=k1λ1=2k1λ2(k1=1, 2, …)sinθ1=2k1λ2/ aa sinθ2=k2λ2(k2=1, 2, …)sinθ2=2k2λ2/ a若k2= 2 k1,则θ1= θ2,即λ1的任一k1级极小都有λ2的2k1级极小与之重合.12.在单缝的夫琅禾费衍射中,缝宽a = 0.100 mm,平行光垂直如射在单缝上,波长λ= 500 nm,会聚透镜的焦距f = 1.00 m.求中央亮纹旁的第一个亮纹的宽度Δx.解:单缝衍射第1个暗纹条件和位置坐标x1为a sinθ1= λx1 = f tanθ1≈f sinθ1≈f λ/ a (∵θ1很小)单缝衍射第2个暗纹条件和位置坐标x2为a sinθ2 = 2 λx2 = f tanθ2≈f sinθ2≈ 2 f λ/ a (∵θ2很小)单缝衍射中央亮纹旁第一个亮纹的宽度Δx1 = x2− x1≈f (2 λ/ a −λ/ a)= f λ/ a=1.00×5.00×10−7/(1.00×10−4) m =5.00mm.13.在单缝夫琅禾费衍射中,垂直入射的光有两种波长,λ1 = 400 nm,λ2 = 760nm(1 nm = 10−9 m).已知单缝宽度a = 1.0×10−2 cm,透镜焦距f = 50 cm.(1)求两种光第一级衍射明纹中心间的距离.(2)若用光栅常数a= 1.0×10-3cm的光栅替换单缝,其它条件和上一问相同,求两种光第一级主极大之间的距离.解:(1) 由单缝衍射明纹公式可知a sinφ1=12(2 k + 1)λ1 =12λ1(取k = 1)a sinφ2=12(2 k + 1)λ2=32λ2tanφ1= x1/ f,tanφ2= x1/ f由于sinφ1≈ tanφ1,sinφ2≈ tanφ2所以x1= 32f λ1 /ax 2=32f λ2 /a则两个第一级明纹之间距为Δx1= x2− x1=32fΔλ/a = 0.27 cm(2) 由光栅衍射主极大的公式d sinφ1= k λ1= 1λ1d sinφ2= k λ2= 1λ2且有sinφ = tanφ= x / f所以Δx1= x2− x1= fΔλ/a = 1.8 cm14.一双缝缝距d = 0.40 mm,两缝宽度都是a = 0.080 mm,用波长为λ = 480 nm(1 nm = 10−9 m)的平行光垂直照射双缝,在双缝后放一焦距f = 2.0 m的透镜.求:(1) 在透镜焦平面的屏上,双缝干涉条纹的间距l;(2) 在单缝衍射中央亮纹范围内的双缝干涉数目N和相应的级数.解:双缝干涉条纹(1) 第k级亮纹条件:d sinθ=kλ第k级亮条纹位置:x1= f tanθ1≈f sinθ1≈k f λ/ d相邻两亮纹的间距:Δx= x k +1− x k = (k + 1) fλ/ d −k λ/ d= f λ/ d = 2.4×10−3 m = 2.4 mm (2) 单缝衍射第一暗纹:a sinθ1= λ单缝衍射中央亮纹半宽度:Δx0 = f tanθ1≈ f sinθ1≈ k f λ / d = 12 mmΔx/ Δx = 5∴双缝干涉第±5级主极大缺级.∴在单缝衍射中央亮纹范围内,双缝干涉亮纹数目N = 9分别为k = 0, ±1, ±2, ±3, ±4级亮纹或根据d /a= 5指出双缝干涉缺第±5 级主极大,同样可得出结论。
23光衍射习题课

a+b 解: k = k′ a
k ′ = 1,2,3 L a+b =3 a
B
18
k = 3,6,9 L 时
13、一束白光垂直照射在一光栅上,在形成的同一级光栅光谱 、一束白光垂直照射在一光栅上, 中,偏离中央明纹最远的是 (A) 紫光. (B) 绿光. (C) 黄光. (D) 红光. 紫光. 绿光. 黄光. 红光. D 解:(a + b ) sin = kλ , sin ∝ λ , λ红 最大 14、对某一定波长的垂直入射光,衍射光栅的屏幕上只能出现 、对某一定波长的垂直入射光, 零级和一级主极大,欲使屏幕上出现更高级次的主极大, 零级和一级主极大,欲使屏幕上出现更高级次的主极大,应该 (A) 换光栅常数小的光栅. (B) 换光栅常数大的光栅. 换光栅常数小的光栅. 换光栅常数大的光栅. (C) 将光栅向靠近屏幕的方向移动. 将光栅向靠近屏幕的方向移动. (D) 将光栅向远离屏幕的方向移动. 将光栅向远离屏幕的方向移动. B (a + b ) sin 900 解: (a + b ) sin = kλ , k m = ∝ (a + b) 15、若用衍射光栅准确测定一单色可见光的波长,在下列各 、若用衍射光栅准确测定一单色可见光的波长, 种光栅常数的光栅中选用哪一种最好? 种光栅常数的光栅中选用哪一种最好? (A) 5.0×10-1 mm. (B) 1.0×10-1 mm. × . × . (C) 1.0×10-2 mm. (D) 1.0×10-3 mm. × . × .
D
12、一束平行单色光垂直入射在光栅上,当光栅常数(a + b)为下 、一束平行单色光垂直入射在光栅上,当光栅常数 为下 列哪种情况时(a代表每条缝的宽度 代表每条缝的宽度), 列哪种情况时 代表每条缝的宽度 ,k=3、6、9 等级次的主极 、 、 大均不出现? 大均不出现? (A) a+b=2 a. (B) a+b=3 a. + . + . (C) a+b=4 a. (D) a+b=6 a. + . + .
光的衍射部分习题课

2.4 10 7 弧度
这个值就是所要求望远镜最小可分辨的角距 离.设望远镜的口径为D,取可见光平均波 长=550nm,由瑞利判据得
物理科学与信息工程学院
1.22 D
可计算出望远镜的口径为:
1.22 550 10 D 2.4 107
2a
2k+1= 3;5;7…
物理科学与信息工程学院
7. 夫琅和费圆孔衍射
爱里斑的半角宽度:
1.22
D
sin N sin
2
8. 平面衍射光栅
光强分布公式
sin I I0
2
其中
a sin
d sin
~
~
~
4. 根据惠更斯-菲涅耳原理处理 问题的方法
a. 菲涅耳半波带法;b. 振幅矢量图解法; c. 积分法。
物理科学与信息工程学院
5. 运用菲涅耳半波带法处理 圆孔和圆屏衍射
着重解释轴线上的光强分布,属于定性或半定量 方法。 实际应用:菲涅耳波带片。
1 1 K ( ) r0 R
2
a10 k 1 ak 0 AP (1) 2 2
2
sin
物理科学与信息工程学院
解 对 于 光 栅 A , d = 2 ×103 毫 米 , N = w/d = 2 ×104.由光栅方程求出第二级衍射主极大的衍射角:
sin
1
2 30 0 d
物理科学与信息工程学院
角色散为
k 2 D d cos 2 10 3 10 6 cos 30 0 1.155 10 3 rad / nm.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程光学 光的衍射 习题解答
1、氦氖激光器发出的波长nm 8.632=λ的单色光垂直入射到半径为1cm
的圆孔,在光轴(它通过孔中心并垂直孔平面)附近离孔z 处观察衍
射,试求出夫琅和费衍射区的大致范围?
解: π<<+1
max 21212)(Z y x k 2、钠灯发出波长为589nm 的平行光垂直照射在宽度为0.01mm 的单逢上,以焦距为600mm 的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半角宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;
(3)相邻暗纹之间的距离?
解: 2
0sin ⎪⎭
⎫ ⎝⎛=ααI I θλπαs i n 22a f y ka kal ⋅=⋅== 3、在夫琅和费单缝衍射实验中,以波长为600nm 的单色光垂直入射,若缝宽为1mm ,则第1极小和第2极小的角位置分别出现在哪里?
4、分析如图所示夫琅和费衍射装置如有以下变动时,衍射图样会发
生怎样的变化?
1)增大透镜L2的焦距;
2)减小透镜L2的口径;。
答:1)增大透镜L 2的焦距,将使接收屏上衍射图样的间隔增大。
因有公式'f e θ=,此时
衍射角θ不变,条纹间隔e 增大;
2)增大透镜L 2的口径,不会改变衍射图样的分布,但进入系统的光束宽度增加,
可使光强增加;
3)衍射屏垂直于系统光轴方向移动时,衍射图样不会改变,因为衍射屏移动前后
光的入射角不变,缝宽不变,由衍射公式知其接收屏上的光强分布不变;
5、 在双缝夫琅和费实验中,所用的光波波长nm 8.632=λ,透镜焦距cm f 50=,观察到两相临亮条纹间的距离mm e 5.1=,并且第4级亮纹缺级。
试求:(1)双缝的逢距和逢宽;(2)第1,2,3级亮纹的相对强度。
解:(1) (1)双缝的缝距和逢宽;
λθm d =⋅sin )2,1,0(⋅⋅⋅±±=m
又f
x =θsin f d m x λ=∴ f d e λ= )(21.05005.1108.6326
mm e f
d =⨯⨯==∴-λ ()d
a
m n =⋅ 将41m n =⎧⎨=⎩代入得 4
1)(053.04=⇒==d a mm d a (2)(2)第1,2,3级亮纹的相对强度。
当m=1时 d
λθ=1s i n 当m=2时 d
λθ2s i n 2= 当m=3时 d
λθ3s i n 3= 代入单缝衍射公式 202)s i n (ββ
I N I = θλ
πβs i n a ⋅=
∴ 当m=1时 81.0)4(21)()(sin sin 2222201===⎪⎭
⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛⋅=πππλλπλλπd a d a d a d a I I 当m=2时 405.0)42(122s i n 22202==⎪⎭
⎫ ⎝⎛⎪⎭⎫ ⎝⎛=πππd a d a I I 当m=3时 09.04343sin 2203=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=ππI I
6、 一块光栅的宽度为10cm ,每毫米内有500条逢,光栅后面放置的透镜焦距为500nm 。
问:(1)它产生的波长nm 8.632=λ的单色光的1级和2级谱线的半宽度是多少?(2)若入射光线是波长为632.8nm 和波长与之相差0.5nm 的两种单色光,它们的1级和2级谱线之间的距离是多少?
解:)(102500
13mm d -⨯==
4105500100⨯=⨯=N 由光栅方程 λθm d =sin 知
3164.010
1028.632sin 631=⨯⨯==-d λθ ,9486.0cos 1=θ 6328.02sin 2==d λθ ,774.0cos 2=θ 这里的1θ,2θ确定了谱线的位置
(1)(1)它产生的波长nm 8.632=λ的单色光的1级和2级谱线的半宽度是多少?
θλθcos Nd =
∆(此公式即为半角公式) )(1067.69486
.010*******.632cos 663411rad Nd --⨯=⨯⨯⨯⨯⨯==∆θλ
θ )(1017.8774
.01021058.632cos 63422rad Nd -⨯=⨯⨯⨯⨯==∆θλθ )(1034.3311mm f dl -⨯=∆=θ
)(1008.4322mm f dl -⨯=∆=θ
(2)若入射光线是波长为632.8nm 和波长与之相差0.5nm 的两种单色光,它们的1级和2级谱线之间的距离是多少?
由公式 θ
λcos d m f d dl ⋅=(此公式为线色散公式)
可得
)(131.09486
.010********.0cos 13611mm d f d dl =⨯⨯⨯⨯⨯=⋅⋅=--θλ )(32.0774
.010********.0cos 23622mm d f d dl =⨯⨯⨯⨯⨯=⋅⋅=--θλ。
