多属性决策方法 (1)
多属性决策——精选推荐
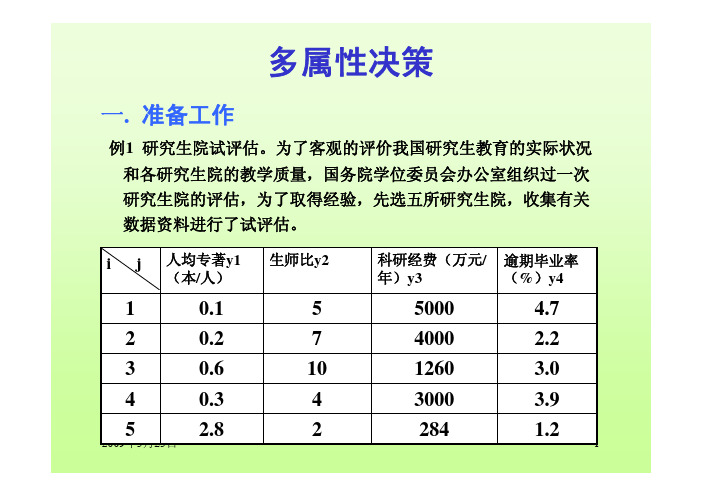
2009年5月25日1多属性决策一. 准备工作例1 研究生院试评估。
为了客观的评价我国研究生教育的实际状况和各研究生院的教学质量,国务院学位委员会办公室组织过一次研究生院的评估,为了取得经验,先选五所研究生院,收集有关数据资料进行了试评估。
1.228422.853.9300040.34 3.01260100.63 2.2400070.224.7500050.11逾期毕业率(%)y4科研经费(万元/年)y3生师比y2人均专著y1(本/人)i j2009年5月25日2……………………………………………………决策矩阵1yjyny 1x 11y jy 1ny 1ix mx 1i y ijy in y 1m y mjy mny 多属性决策问题记作MA ,可供选择的方案集为用表示方案的n 个属性,其中是第个方案的第个属性值当目标函数为时,}{,,1m x ...x X =),...,(1in i i y y Y =i x ij y i j i f nj m i x f y i j ij ,...1;,...,1),(===1. 数据预处理(规范化)1)属性类型效益型;成本型;既非效益又非成本型2)非量纲化3)归一化4)数据预处理的本质是要给出某个目标的属性值在决策人评价方案优劣时的实际价值。
5)常用数据预处理方法2009年5月25日32009年5月25日4线性变换原始的决策矩阵Y={ },变换后的决策矩阵记为Z={ },设是决策矩阵第列中的最大值,是决策矩阵第列中的最小值。
若为效益性属性,则若为成本型属性,则ij z ij y nj m i ,...,1,,...,1==max jyj minj yj j j max /j ij ij yy z =max /1jij ij yy z −=]/[minij jijy y z =′2009年5月25日5标准0-1变换若为效益性属性,则若为成本型属性,则j j min max min jjj ij ij yyy y z −−=min max max jjijj ij yyy y z −−=2009年5月25日6最优值为给定区间的变换适用于既非效益型又非成本型的属性 设给定的最优属性区间为,为无法容忍下限,为无法容忍上限,则],[*0jj y y j y ′j y ′′()()jjijjy y y y ′−−−001()()**1jjjij y y yy −′′−−10j ij j yy y <<′*0jij j y y y ≤≤j ij jy y y ′′<<*其他=ij z2009年5月25日7[]6,512=′′j y 1.024681012ijz ijy jy ′j y ′′*jy 0j y 2=′j y ij生师比y 2z 2145235710421.00000.83330.33330.66660.0000例设研究生院的生师比最佳区间为2009年5月25日8向量规范化∑==mi ijijij yy z 12无论是成本型还是效益型属性,均可用上式变换向量规范化的最大特点是,规范化后,各方案同一属性值的平方和为12009年5月25日9专家打分数据的预处理假设各位专家意见的重要性相同,则每个专家在评价中理应发挥同样的作用,但是,对同一被评价对象的同一指标,由于不同专家的打分习惯不同,所给分值所在区间往往会有很大差别。
多属性决策方法应用一例

信 息 技 术14科技资讯 SCIENCE & TECHNOLOGY INFORMATIONDOI:10.16661/ki.1672-3791.2017.32.014多属性决策方法应用一例①夏正喜(九江职业技术学院信息工程学院 江西九江 332007)摘 要:本文针对网络购物网店选择的问题,提出了一种基于OWA算子和语言OWA算子的综合多属性群决策方法,首先利用OWA 进行纵向集结,然后利用CWAA算子对纵向集结结果进行横向集结;不仅能充分考虑决策者的自身重要性程度,而且尽可能地消除个别决策者受个人感情等主观因素的影响因素,并增加中间值的作用,从而增强决策结果的合理性。
关键词:网络购物 多属性决策 OWA算子 CWAA算子中图分类号:G64 文献标识码:A 文章编号:1672-3791(2017)11(b)-0014-02①基金项目:江西省高校人文社会科学研究项目(项目编号:GL1578)。
随着电子商务的发展,网络购物已经伴随着人们的日常生活,然而如何在众多网络商店中选择一个较满意的网店也是一种学问,通常我们都是听朋友的推荐、根据该网店的知名度和顾客对该网店的评价等众多因素综合考虑的。
其实网友在网上购物最关心的问题主要有:价格、质量、服务、安全、时间。
要综合考虑各方面信息来选择商家,这是一个多属性决策的问题,为此本文引入多属性决策算子:OWA算子和语言OWA算子(CWAA算子)来解决。
1 问题的分析与求解选取了4个网店进行分析,考虑价格、质量、服务、安全、时间这5个因素,对一般客户,v i p 客户,专家,较固定客户进行问卷调查。
设C=(一般客户,v ip客户,专家,较固定客户),网店集为1234(x ,x ,x ,x )X =;对定性指标的描述,一般直接用“满意、较满意、一般、较不满意、不满意”等模糊语言形式给出,对定量指标转化为定性指标,S={满意、较满意、一般、较不满意、不满意}。
多属性决策的方法

多属性决策的方法
多属性决策的方法有很多,以下是几种常见的方法:
1. 加权评分法(Weighted Scoring Method):根据不同属性的重要性,为每个属性赋予一个权重值,然后对每个方案进行评分计算,最后按照评分高低进行决策。
2. 层次分析法(Analytic Hierarchy Process,AHP):通过构建层次结构,将复杂的决策问题分解成多个层次,通过比较不同层次的属性之间的相对重要性,最终确定最优决策。
3. 电子表格法(Spreadsheet Method):将不同方案的各属性值记录在电子表格中,根据设定的权重进行计算得出综合评分,通过比较评分高低进行决策。
4. TOPSIS法(Technique for Order Preference by Similarity to Ideal Solution):通过计算方案与理想解和负理想解之间的相似性,确定每个方案的综合评分,最终选择最接近理想解且最远离负理想解的方案。
5. 折衷编程法(Compromise Programming):根据决策者的偏好和目标,建立数学模型,通过最大化总效益和最小化总成本的折衷,找到最优的决策方案。
以上方法各有特点,适用于不同的决策问题和决策者的需求。
在实际应用中,可
以根据具体情况选择合适的方法进行多属性决策。
决策理论与方法之多属性决策

决策理论与方法之多属性决策多属性决策是决策理论与方法中的一种重要决策方法,主要用于解决具有多个评价指标的决策问题。
在实际生活和工作中,我们常常需要面对的是多因素影响下的决策问题。
多属性决策方法的应用可以帮助我们全面、客观、科学地对待问题,提高决策的准确性和决策结果的有效性。
多属性决策方法的核心思想是将决策问题中的多个属性进行定量化,并将各个属性的权重进行合理分配,最终得出综合评价结果,从而选择最优的决策方案。
在多属性决策中,常用的方法包括层次分析法、利用等价关系建立模型、TOPSIS方法等。
层次分析法是一种常用的多属性决策方法,其主要思想是将决策问题拆分成若干个子问题,并构建层次结构,通过比较不同层次的准则,得出最终的决策结果。
该方法的优点是能够考虑多个属性的重要性,并将其量化成权重,从而进行综合评估。
但是,层次分析法需要进行一系列的判断和计算,比较繁琐,容易受到主管者主观判断的影响。
利用等价关系建立模型是另一种常用的多属性决策方法,其主要思想是通过对各个属性之间的关系进行建模,从而得出最终的决策结果。
该方法的优点是能够考虑属性之间的相互影响,更加真实地反映决策问题的本质。
但是,建立等价关系模型需要对问题有一定的了解和分析能力,并且需要进行一定的计算,对于一些复杂问题来说,可能会存在一定的困难。
TOPSIS方法(Technique for Order Preference by Similarity to an Ideal Solution)是一种较为常用的多属性决策方法,其主要思想是将各个决策方案与最佳解和最差解进行比较,通过计算得出每个方案与最佳解和最差解的接近程度,并根据接近程度确定优劣排序。
TOPSIS方法具有计算简单、易于理解和应用的优点,但是在实际应用中,需要对决策问题进行一定的约束条件和假设。
综上所述,多属性决策方法是一种重要的决策理论和方法,可以帮助我们解决多因素影响下的决策问题。
决策专题二_多属性决策分析方法

各方案的相对贴近度为
=0.643, =0.268, =0.613,
用理想解法各方案的排序结果是
=0.312,
•
第二节 模糊综合评价方法
对方案、人才、成果的评价,人们的考虑的因素很多, 而且有些描述很难给出确切的表达,这时可采用模糊评价 方法。它可对人、事、物进行比较全面而又定量化的评价
,是提高领导决策能力和管理水平的一种有效方法。
•模糊的评级; •模糊数的运算;
•
模糊综合评价的基本步骤:
(1)首先要求出模糊评价矩阵P,其中Pij表示方案X在第i 个指标处于第j级评语的隶属度,当对多个指标进行综合 评价时,还要对各个指标分别加权,设第i个指标权系数 为Wi,则可得权系数向量: A=(W1,W2,…Wn)
•
(2)利用矩阵的模糊乘法得到综合模糊评价向量B
评语集合: V={很好,较好,一般,不好};
•
首先对图像进行评价: 假设有30%的人认为很好,50%的人认为较好,20%的 人认为一般,没有人认为不好,这样得到图像的评价结果 为
(0.3, 0.5, 0.2 , 0) 同样对声音有:0.4, 0.3, 0.2 , 0.1) 对价格为: (0.1, 0.1, 0.3 , 0.5) 所以有模糊评价矩阵:
因此,克服指标间不可公度的困难,协调指标间的矛盾 性,是多属性综合评价要解决的主要问题。
•
(一)决策矩阵
设有 个备选方案 个决策指标
决策矩阵
•
(二)决策矩阵的标准化
➢ 由于指标体系中指标不同的量纲,例如,产值的单位为万 元,产量的单位为万吨,投资回收期的单位为年等,这给 综合评价带来许多困难。
所谓理想解,是设想各指标属性都达到最满意的解;所谓 负理想解,也是设想指标属性都达到最不满意的解。
几种典型类型的多属性决策方法

(1)基于所有方案的综合属性值最大的组合赋权法
考虑所有方案的综合属性值越大越好建立如下最优化模型:
壹差名∑舌∑i=1k=l乃砟蟛=∑∑%w:=∑∑∑,:,砟w;,=l。
,=l
,
∑《=1
k=l
0≤xk≤1
通过构造Lagrange函数求解此模型:
令
解得:
三:芝兰圭勺%嘭+要(圭《一)三=∑∑∑勺%w;+三(∑《一),=lJ=1.k=l。
Z1
k=lk=l要:兰墨乃矿+他:o%mlj=li。
盖=圭c圭纠川
∑∑,;,蟛i=1j=l。
铲丽惦(著舌勺嘭)2
由E=互t坼旷即可求得组合权重。
(2)基于与理想点的偏离程度最小的组合赋权法
考虑所有方案距离理想点越近越好建立如下优化模型:
1(1一_)诈w;
=∑∑%)wj=∑∑∑(1一%)诈w;i=1j=li=l,=1k=l
,
盯∑《=1
k=l
0≤xk≤1
通过构造Lagrange函数求解此模型:
三:圭芝圭(1一。
)稚嘭+S-(Z7x;一1)三=∑∑∑(1—0)稚w:+一1)i=1j=lk=l一k=l。
多属性决策方法概要

多属性决策方法概要多属性决策方法是一种用于解决具有多个属性、多个可选方案的决策问题的方法。
在实际生活和工作中,我们常常面临着这样的问题,例如选择一种产品、确定一个项目的优先级或者评估不同的投资选择等。
在这些问题中,每个可选方案都有多个属性或者指标来描述其特点,而我们需要通过一定的决策方法来帮助我们做出合理的选择。
本文将介绍几种常见的多属性决策方法。
1.权重法:权重法是一种常用的多属性决策方法,它通过为每个属性指定一个权重来反映其重要性,然后根据各个属性的得分和权重的乘积来评估每个方案的综合得分。
具体来说,首先需要确定各个属性的权重,可以通过专家来评估或者采用层次分析法等方法。
然后,对每个属性进行评分,可以使用定性评价或者定量评价的方法。
最后,将每个属性的得分与其权重相乘,并将所有属性的加权得分相加,得到每个方案的综合得分。
根据综合得分的大小,选择综合得分最高的方案。
2.理想解法:理想解法是一种基于每个属性的最小值或最大值来确定方案的方法。
具体来说,首先需要将每个属性的值标准化,例如将其转换为[0,1]区间上的值。
然后,计算每个方案与理想解法之间的距离,可以使用欧式距离或者其他距离度量方法。
最后,根据与理想解法之间的距离的大小,选择距离最小或距离最大的方案作为最优方案。
3.TOPSIS法:TOPSIS法是一种常用的多属性决策方法,它综合考虑了每个方案与理想解法的距离以及与负理想解法的距离。
具体来说,首先需要将每个属性的值标准化,例如将其转换为[0,1]区间上的值。
然后,利用标准化后的属性值计算每个方案与理想解法之间的距离和方案与负理想解法之间的距离。
最后,根据与理想解法的距离和与负理想解法的距离的比较,计算每个方案的综合得分,并选择综合得分最高的方案作为最优方案。
4. Borda计分法:Borda计分法是一种常用的多属性决策方法,它基于每个方案在每个属性上的排名来评估方案的综合得分。
具体来说,首先对每个属性的得分进行排序,然后根据每个方案在每个属性上的排名分配得分。
第四讲各种多属性决策方法

学校序号 1 2 3 4 5 6
费用/(万元) 60 50 44 36 44 30
平均就读距离/(km) 1.0 0.8 1.2 2.0 1.5 2.4
例2 研究生院评估。为了客观地评价我国研究生教育的实际状 况和各研究生院的教学质量,国务院学位委员会办公室组织过 一次研究生院的评估。为了取得经验,先选5所研究生院,收 集有关数据资料进行了试评估。下表中所给出的是为了介绍各 种数据预处理方法的需要而选的几种典型属性和经过调整了的 数据。
一、多属性决策问题的准备工作
1、决策矩阵 设可供选择的方案集为: X {X1, X 2 ,, X m}
方案的属性集为: Y {y1, y2 ,, yn}
决策矩阵为: y11 y1 j y1n
yi1
yij
yin
ym1 ymj ymn
例1学校扩建问题。设某地区现有6所学校,由于无法完 全容纳该地区适龄儿童,需要扩建其中的一所。在扩建 时既要满足学生就近入学的要求,又要使扩建的费用尽 可能小。(至于所扩建学校的教学质量我们稍后再考 虑。)经过调研,获得如下表所示的决策矩阵。
z ij
y max j
yij
y max j
y min j
(3) (4)
3、最优值为给定区间时的变换 设给定的最优属性区间为[yj0,yj*],yj’为无法容忍下
限,yj’’为无法容忍上限,则
1
(
y
0 j
yij
)
/(
y
0 j
y
' j
)
若y
' j
yij
y
0 j
1
zij
1 ( yij
y
* j
几类多属性决策方法研究

几类多属性决策方法研究多属性决策是现代决策科学的重要组成部分,广泛应用于各种领域。
在多属性决策过程中,由于需要考虑多个属性或因素,因此需要采用一定的方法对它们进行综合分析和评估。
本文将介绍几类多属性决策方法,并通过案例或数据进行实证研究,以增加文章的可信度和说服力。
让我们确定本文的主题和核心要表达的观点。
本文旨在探讨多属性决策方法的研究,重点介绍几种经典的多属性决策方法,包括加权平均法、层次分析法、灰色关联度法等。
通过比较和分析这些方法的特点和适用范围,帮助读者更好地理解和应用多属性决策方法。
在确定了主题后,我们需要围绕主题展开情节。
引入加权平均法。
加权平均法是一种简单而常用的多属性决策方法,其基本思想是将每个属性或因素进行加权平均,得到一个综合评价分数。
该方法的特点是计算简单、易于理解,但忽略了不同属性之间的差异性,可能会影响决策的准确性。
为了证明这一观点,我们可以通过一个实际案例来说明。
假设有三个方案A、B、C,分别在价格、质量、可靠性三个属性上进行评估。
通过加权平均法计算综合得分,价格权重为3,质量权重为3,可靠性权重为4。
经过计算,A的综合得分为87,B的综合得分为90,C的综合得分为85。
因此,根据加权平均法,B为最优方案。
但实际上,在价格和质量属性上,A比B更具优势,因此A可能是更优秀的方案。
接下来,我们引入层次分析法。
层次分析法是一种系统化的多属性决策方法,它将决策问题分解为若干层次,每个层次包含多个属性或因素。
通过两两比较各属性或因素的重要性,得出每个层次中各属性的权重,最终得出综合评价分数。
该方法的特点是系统性强、逻辑清晰,能够充分考虑每个属性或因素的重要性。
但需要注意的是,层次分析法的可靠性取决于专家对各属性重要性的判断是否准确。
为了验证该方法的有效性,我们通过一个实际案例来说明。
假设有三个方案A、B、C,分别在价格、质量、可靠性三个属性上进行评估。
通过层次分析法计算综合得分,价格权重为27,质量权重为36,可靠性权重为37。
多属性决策1-基础篇

9.1 多目标决策的特点
一、多目标决策的例子:买车决策 二、多目标决策的目标准则体系 三、评价准则和效用函数 四、目标准则体系的风险因素处理 五、多目标决策问题的分类 六、多目标决Байду номын сангаас的求解过程
一、多目标决策的例子: 买车决策
例1:买车决策问题。
➢单目标决策1(价格): 价格(C)<价格(T)<价格(V)<价格(M) ➢单目标决策2(油耗): 油耗(T)<油耗(V)<油耗(C)<油耗(M) ➢单目标决策3(舒适度):舒适(M)>舒适(V)>舒适(T)>舒适(C)
选优法(Dominance)又称优势法,是利用非劣解 的概念(也称优势原则)淘汰一批劣解。
若方案集X中的方案xi与方案xk相比,方案xi至 少有一个属性值严格优于方案xk,而且方案xi 的其余所有属性值均不劣于方案xk,则称方案xi 比方案xj占优势,处于劣势的方案xk可从方案 集X中删除。
从大批方案中选取少量方案时,可以用选优法 淘汰全部劣解。
二、 满意值法
例子1: 买车。切除值:价格高于30万的不与考虑
三、 逻辑和法
逻辑和法(Disjunctive)意义为“或门”,该方法与满意值法的思路正 好相反。
不失一般性,设各属性均为效益型。逻辑和法首先为每个属性规定 一个阀值yj* ( j=1,..,n)。只要当方案xi有某个属性值yij优于相应阀值yj*, 即yij≥ yj* ( j=1,..,n),方案xi就被保留。
方案1
方案2
……
方案n
1) 单层次目标准则体系
各个目标都属于同一层次,每个目标无须分解就可以 用单准则给出定量评价。
总目标
决策理论与方法之多属性决策

决策理论与方法之多属性决策多属性决策是决策理论与方法中的一个重要分支,主要用于处理具有多个属性或标准的决策问题。
多属性决策注重综合各个属性或标准的信息,通过量化和加权的方式,对各个选择方案进行评价,从而找到最符合决策者要求的最佳方案。
多属性决策的基本框架包括问题定义、属性权重确定、方案评价和最优方案选择四个主要步骤。
问题定义是多属性决策的起点。
在这一步骤中,决策者需要明确决策的目标和各个属性或标准的要素。
例如,若要选取一家供应商,决策者可以将供应商的价格、品质、交货期等作为属性。
属性权重确定是多属性决策的关键步骤。
由于各个属性可能具有不同的重要性,因此需要对不同属性进行加权处理。
传统的方法包括主观加权法和客观加权法。
主观加权法主要依赖于决策者主观意愿,通过对不同属性进行比较排序来设定权重;客观加权法则基于统计分析或数学建模等方法,通过数据处理来确定各属性权重。
方案评价是对各个选择方案进行量化评价的过程。
在这一步骤中,可以使用评价函数、模型或指标来对各个属性进行量化和评估。
评价函数可以是线性函数、指数函数或对数函数等,可根据具体的决策问题选择适合的函数。
模型方法基于专家判断、经验法则或历史数据等,通过建立模型来对方案进行评价。
指标方法则是利用指标体系来评价方案的好坏。
最优方案选择是多属性决策的最终目标。
在这一步骤中,通常会使用其中一种决策方法或算法来确定最佳方案。
常用的方法包括加权总分法、熵权法、TOPSIS法和灰色关联法等。
加权总分法是最简单直观的方法,将各个属性的分数按权重加总,得到最终的总分,从而选择总分最高的方案。
熵权法则通过考虑属性之间的相关性,将熵指标作为属性权重的度量,从而选择最小熵的方案。
TOPSIS法则将方案与最佳方案和最差方案进行比较,根据各个属性的正负向离差距离,确定每个方案的综合指标,从而选择综合指标最大的方案。
灰色关联法则通过计算各个方案与最佳方案之间的关联度,从而选择关联度最高的方案。
多属性决策讲义课件

5
第一节 多属性决策问题
定性指标量化处理方法
将定性指标按性质划分为若干级别,分别赋予不同的量值。 一般可以划分为五个级别,最优值10分,最劣值0分。其余 级别赋予适当的分值。也可以划分为其他级别和赋予其他分 值,方法类似,视具体情况而定。具体分值见表。
等级 分值
指标 机型
A1 A2 A3 A4
最大速度 最大范围 最大负载 费用 可靠性
马赫
公里
千克 106美元
2.0
1500 20000 5.5 一般
2.5
2700 18000 6.5
低
1.8
2000 21000 4.5
高
2.2
1800 20000 5.0 一般
灵敏度
很高 一般
高 一般
4
第一节 多属性决策问题
,熵越大;反之,不确定性越小,熵越小。
m
e k pi ln pi i 1
(1)对决策矩阵用线性比例变换法进行标准化处理,得标准
化矩阵Y=( yij )m*n,并进行归一化处理,得
pij
yij
m
,(i 1, 2,, m; j 1, 2,, n)
yij
i 1
21
第二节 确定权重的常用方法
m
最大速度 最大范围 最大负载 费用 可靠性
马赫
公里
千克 106美元
2.0
1500
20000
5.5
5
2.5
2700
18000
6.5
3
1.8
2000 21000
4.5
7
2.2
1800
20000
多属性决策分析

多属性决策分析引言多属性决策分析是一种决策分析方法,用于处理在决策过程中有多个属性或准则的情况。
在实际生活中,我们常常面临需要权衡多个属性或准则的决策,例如选择购买的产品、选择投资项目等。
多属性决策分析方法可以帮助我们在复杂多变的决策环境中做出更准确和合理的决策。
基本概念在多属性决策分析中,我们首先需要定义决策问题中的属性或准则。
属性可以是各种各样的特征或指标,例如价格、质量、服务等。
每个属性都可以用一个评价指标来度量,这些指标可以是定量的(例如价格)也可以是定性的(例如服务)。
然后,我们需要为每个属性确定权重或重要性,用于衡量其在决策过程中的相对重要程度。
方法多属性决策分析方法有很多种,其中一种常用的方法是加权求和法。
该方法将每个属性的值乘以其权重,并将它们相加以得到最终的决策值。
具体步骤如下:1.确定决策问题的属性或准则,并为每个属性确定评价指标。
2.为每个属性确定权重或重要性。
可以使用专家判断、问卷调查、层次分析法等方法来确定权重。
3.对于每个属性,根据其评价指标对各个选项进行评价,并将评价结果转化为数值。
4.将每个属性的评价结果乘以其权重,并将它们相加以得到最终的决策值。
5.根据最终的决策值,选择得分最高的选项作为最优决策。
除了加权求和法外,还有其他一些常用的多属性决策分析方法,例如层次分析法、灰色关联分析法等。
这些方法根据不同的决策问题和决策环境可以选择不同的方法进行分析。
示例假设我们要选择一款笔记本电脑进行购买,我们关注的属性包括价格、配置、品牌和售后服务。
我们采用加权求和法进行分析,将权重分别设置为0.3、0.4、0.2和0.1。
对于价格属性,我们将价格分为五个等级:1000元以下、1000-2000元、2000-3000元、3000-4000元和4000元以上。
我们根据电脑的价格将其评价分别设为5、4、3、2和1。
对于配置属性,我们将配置分为五个等级:高配、中高配、中配、中低配和低配。
多属性决策分析方法概述

多属性决策分析方法概述多属性决策分析是一种用于解决决策问题的方法,能够同时考虑多个属性或指标,帮助决策者找到最优的方案或做出合理的决策。
在实际应用中,多属性决策分析被广泛应用于各种领域,如企业管理、金融投资、市场营销、工程项目等。
基于价值函数的方法首先要确定决策问题的目标和属性或指标,然后通过构造或归纳得到价值函数,根据价值函数计算出方案的效用值,最后对方案进行排序或筛选。
常见的基于价值函数的方法有加权得分法、受益成本分析法、利益相关者分析法等。
加权得分法是一种简单而直观的方法,它将每个属性或指标的重要性用权重表示,通过计算每个方案在每个属性或指标上的得分乘以权重,得到方案的总得分,然后根据总得分进行排序或筛选。
受益成本分析法是一种经济学上常用的方法,它通过对每个方案的效益与成本进行比较,计算出效益成本比或效益净现值,来评估方案的投资价值和可行性。
利益相关者分析法是一种针对决策问题中的利益相关者的需求进行评估和分析的方法,它通过对每个方案在每个利益相关者需求上的满足程度进行评估,计算出方案的综合满意度,来评估方案的可行性和可接受性。
基于对比矩阵的方法是一种将多属性决策问题转化为矩阵运算和数值计算的方法,通过构建对比矩阵和权重向量,来计算出方案的优劣程度。
常见的基于对比矩阵的方法有层次分析法、模糊综合评判法、灰色关联分析法等。
层次分析法是一种常用的多属性决策分析方法,它通过构建层次结构和对比矩阵,对每个属性或指标进行两两比较,得到权重向量,然后根据权重向量计算出方案的综合得分,最后对方案进行排序或筛选。
模糊综合评判法是一种将模糊数学理论应用于多属性决策分析的方法,它通过构建模糊评价矩阵和模糊综合评判矩阵,计算出方案的模糊综合得分,最后对方案进行排序或筛选。
灰色关联分析法是一种将灰色关联度理论应用于多属性决策分析的方法,它通过构建灰色关联矩阵和关联度向量,计算出每个方案与最优方案之间的关联度,最后对方案进行排序或筛选。
多属性决策(第一章)

zij
yij y y
max j
y
min j min j
对成本型属性j,令
zij
y y
max j max j
yij
min j
y
3 区间型属性的变换 ' y , y y • 设给定的最优属性区间为 , 为无 j '' 法容忍下限,y j为无法容忍上限,则
0 j * j
有以下几种。
• 1 线性变换 • 原始的决策矩阵为 Y y ,变换后的决策矩阵记 ,n y 为 Z z ,i 1,, m, j 1,。设 是决策矩阵第j列中 y min 的最大值, 是决策矩阵第j列中的最小值。若j j 为效益型属性,则 max •
ij
ij
max j
illj德尔菲法又名专家意见法是依据系统的程序采用匿名发表意见的方式即团队成员之间不得互相讨论不发生横向联系只能与调查人员发生关系以反覆的填写问卷以集结问卷填写人的共识及搜集各方意见可用来构造团队沟通流程应对复杂任务难题的管理技德尔菲法delphimethod是在20世纪40年代由o
第一章 决策概念与过程
四 权值确定方法--最小二乘法
首先由决策人把目标的重要性作成对比较,设有n个 1 C n(n 1) 次,把第j个目标的相 目标,则需比较 2 对重要性记为 aij ,并认为,这就是属性i的权 i a 和属性j的权 j 之比的近似值, n个目标 的成对比较的结果为矩阵A:
2ห้องสมุดไป่ตู้n
1 y 0j yij y 0j y 'j 1 zij * '' * 1 yij y j y j y j 0
多属性决策方法

多属性决策方法在许多实际问题中,我们需要从多个选择中挑选出一个最优解。
这些问题通常涉及到多个决策属性,例如成本、质量、可靠性、时间等等。
这些属性之间相互影响,有时候还会存在不确定性和模糊性。
如何有效地进行多属性决策,是一个十分重要的问题。
本文将介绍三种常见的多属性决策方法,分别是层次分析法、灰色关联度法和熵权法。
一、层次分析法层次分析法是一种按照结构层次进行分析的方法,它将复杂的多属性决策问题分解为若干层次,从而进行简化。
这种方法侧重于对决策问题中各个因素之间的相对重要性进行比较和排序,以确定最佳决策方案。
下面是层次分析法的基本思路:1.确定决策目标2.分解目标成为若干个层次,找出每个层次的准则和子准则3.构造层次结构模型4.构造判断矩阵,通过专家评价确定每个准则和子准则之间的相对重要性5.计算权重并得出最终方案这里简单介绍一下层次分析法的计算过程。
设有n个决策准则和n个决策方案,判断矩阵为A=(a[i,j]),其中a[i,j]表示准则i相对于准则j的重要程度。
首先,计算每个准则相对于其他所有准则的权重向量W=[w1,w2,…,wn],其中wi表示准则i对应的权重,wi的大小与其在判断矩阵A中所处的位置有关。
然后,计算每个方案的得分向量V=[v1,v2,…,vn],其中vi表示方案i在各个准则下的得分。
最终得到所有方案的加权得分,选择加权得分最大的方案作为最优决策方案。
二、灰色关联度法灰色关联度法是一种基于灰色系统理论的多属性决策方法。
其基本思路是将多个决策属性放在同一等级上,通过对各个属性值之间的相对关系进行量化,来评价方案的综合表现。
具体做法是首先将各个属性标准化,使得它们的取值范围相同。
然后,计算每个属性值与其他属性值之间的相对关系,从而得到各个方案的关联度。
最终选择关联度最大的方案作为最优决策方案。
三、熵权法熵权法是一种基于信息熵的多属性决策方法。
其基本思路是将每个属性的信息熵看做是一个衡量不确定性的指标,然后通过权重分配来最小化所有属性的信息熵的加权和,从而得到最优决策方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•教育投入:学术资源、师资资源、物质资源
•
财力资源、学生情况
•1.学术资源 •(1)博士点总数及学科分布; •(2)硕士点总数及学科分布; •(3)国家重点学科数及学科分布; •(4)国家重点实验室、国家工程研究中心、国家人文社科重点研究基地 •数及学科分布; •(5)国家级科技奖励。 •2.师资资源 •(1)具有博士的教师比例或教师在其领域获得最高学位的比例; •(2)专任教师与学生比; •(3)长江学者特聘教授人数或两院院士人数; •(4)教师平均工资。
• 非量纲化 • 归一化
•决策理论与方法
•6
常用的数据预处理方法
•决策理论与方法
•7
线性变换——例子
•决策理论与方法
•8
常用的数据预处理方法
•决策理论与方法
•9
标准0-1变换
•决策理论与方法
•10
最优值为给定区间时的变换
•决策理论与方法
•11
最优值为给定区间时的变换
•决策理论与方法
•12
•此时所选取的综合指标,相当于在原指标的基础上, 进行了坐标旋转,使得第一个指标的方差最大(含有 最多的信息)。
•32
•主成分的推导
设有n个项目,p个指标,相应的指标矩阵为:
x11 x12 x1 p
X
(X1,
X 2 ,
,
Xp)
x21 x22 ... ... ...
•25
•教育产出:研究成果、成果转化、人才培养
•
校友捐赠、声望声誉
•1.研究成果 •(1)课题批准总数及级别; •(2)索引情况:SCI/EI/ISTP/ •CSTP/SSCI/A&HCI/CSSCI人均数; •(3)获国家和国际奖励。 •2.科技成果转化 •(1)成果转化率; •(2)成果转化效益。 •3.人才培养 •(1)7月~9月前毕业生一次就 业率(毕业率); •(2)7月前毕业生考取其他院校 研究生人数及比率;
x2 p ...
,
xn1
xn2
xnp
•综合指标 F a1 x1 a2 x2 a p x p X,
为 其中组合系数为 (a1, a2 , , a p )'
p
且要求 ( , ) ' ai2 1 i 1
•33
其中组合系数为 (a1, a2 , , a p )', 使 var( F )最大,
•财力资源、物质资源 •科研成果、成果转化 •人才培养、校友捐赠
•相互关联
•基本思想
•主成分分析就是设法将原来众多具有一定相关性的 指标(比如 p个指标),重新组合成一组相互无关 的综合指标来代替原来指标。通常数学上的处理就 是将原来 p个指标作线性组合,作为新的综合指标。
•30
•第一综合指标 F1 a11x1 a12 x2 a1 p x p
j 1,2, , p
•指标
•项目
a11 a12 a1 p
a21 a22 a2 p
an1
an2
anp
•36
(a1, a2 , , a p )
•指标间的差异
•标准化
xij
aij a j var(a j )
其中
aj
xnj
( x1, x2 , , x p )
•37
•2) 计算相关系数矩
阵
r11 r12 r1 p
•相关系数矩 阵
R
r21
r22
r2 p
rp1 rp2 rpp
rij为向
量xi
和x
的相
j
关系数
,
rij
cov( xi , x j ) var( xi ) var( x j )
•中国大学排行榜问题
•n所大学 • p个指 标
•29
•清华、北大、复旦、南开… ... 江西 财大等 •学术资源 x1、师资资源 x2、物质资源 x3、财力资源 x4、学生情况 x5、科研 成果 x6、成果转化 x7、人才培养 x8、 校友捐赠 x9、
•……..
•多数情况下,不同指标之间是有一定相关性.
j 1
p
p
var( F ) k juj W k juj
j1
j1
p
p
p
k juj k j juj k j j
j1
j1
j1
•34
u1时, var( F ) 最大, 且 max var( F ) 1
1 n
n i 1
aij,var(a j )
1 n1
n
(aij
i 1
a j )2
x11 x12 x1 p
•标准化数据矩阵
X
x21
x22
x2 p
xn1
xn2
xnp
x1 j
xj
x2 j
W
(w1, w2 ,L
,
wn
)T
,其中,
n
wj
1。
j 1
步骤二:对决策矩阵 X (xij )mn 作标准化处理,标准化矩阵为
Y ( yij )mn ,并且标准化之后的指标均为正向指标。
n
步骤三:求出各决策方案的线性加权指标值 ui wj yij 1 i m。 j 1
步骤四:以线性加权指标值 ui 为依据,选择线性加权指标值最大者为
n
最满意的答案,即
u(a* )
max
1 i m
ui
max 1 i m
w j yij 。
j 1
二、理想解法
• 理想解法又称为TOPSIS(Technique for Order Preference b这种方法通过构造多属性问题的理想解和负理想解, 并以靠近理想解和远离理想解两个基准作为评价各 可行方案的依据。理想解法又成为双基点法。
• 理想解:设想各指标属性都达到最满意的解。 • 负理想解:设想指标属性都达到最不满意的解。
三、功效系数法
• 功效系数法是将各决策指标的相异度量转化为相应 的无量纲的功效系数,再进行综合评价的多属性决 策方法。
var( F ) var( X ) ' var( X ) 'W
若W的特征根为1 2 p 0,
W var( X ) 协方差矩阵
对应的正交特征向量组为:u1, u2 ,
,
u
,
p
且
Wu j
juj
p
p
令
kjuj 且
k
2 j
1
j 1
•26
•(3)毕业生国外院校奖学金获 得者与录取人数及比率;
•(4)留学生比例(在同专业学 生中的比例;来自五大洲的比 例);
•(5)国家级大赛学生获奖情况 (电子设计、数模、桃战杯,英 语演讲、机器人大赛等)。
•4.校友捐赠 •校友平均捐赠率。 •5.声望或声誉 •知名学者专家、校长、官员、企 业家问卷调查。
•特征向量矩阵 U (u1,u2, ,up )
•4)求主成分的贡献率,确定因子 •如果 k 超过0.85,
p
fi i / i i 1
则说明前k个主成分 基本包含了全部指
k
•特征值的累积贡献率 k fi i 1
标具有的信息,因 此可以只选前k个主
因此F1 Xu1, var( F1) 1 •同理,有 F2 Xu2 , F3 Xu3 , , Fp Xup
var( Fj ) j , j 1,2, , p
此时,称F1为第一主成分,F2为第二主成分,...,Fn为第n主成分
p
称f j j / i为第j个主成分的贡献率
• 功效系数法的基本步骤是:
– 步骤一:确定决策指标体系 – 步骤二:计算各指标的功效系数 – 步骤三:计算各方案的总功效系数 – 步骤四:以总功效系数为判据,对各方案进行排序。
功效系数越大,方案越优;反之,方案越劣。
•案例
•主成分分析
•中国大学排行榜
•中国大学排行榜 —— • 网大排行榜 • 武书连排行榜(广东管理科学学 院) • 中国校友会排行榜
如何取a11、a12、 、a1 p
F1的方差var( F1)最大
•第二综合指标 F2 a21x1 a22 x2 a2 p x p
F2的方差var( F2 )最大吗? 还要要求F1和F2不相关,即cov(F1, F2 ) 0, 即正交
•以此类推,可以创建第三、第四、以至第 p个综合指 标,同时后面的主成分也要前面所有的主成分正交
•如此多的指标(40多个),都与学校的排名和声誉有 关但又可能互相重叠交叉,如何处理这些指标才 够客观合理。
•其他类 •似问题
•企业生产率评价 •品牌知名度评价 •各地区居民消费评价
•等 等
•27
•主成分分析法 •(PCA)
•28
•Karl Parson在1901年引进的,针对非随机向量 •Hotelling 1933年将这个方法推广到随机向量.
1 n
xi n k1 xki
1 n
cov( xi ,
xj
)
n
1
( xki
k 1
xi )( xkj
