数据拟合MATLAB实验作业
实验二讲稿:MATLAB拟合

YOUR LOGO
THANK YOU
汇报人:XX
汇报时间:20XX/01/01
拟合过程中要关注参数的取 值范围和物理意义
拟合结果的评价与验证
拟合效果的评估
残差分析:计算残差平方和, 评估拟合效果
诊断图:绘制诊断图,检查异 常值和拟合趋势
拟合统计量:计算拟合优度统 计量,评估拟合效果
预测误差:预测未来数据,评 估预测误差
异常值的处理
识别:通过图形或统计方法识别异常值 处理:根据实际情况选择删除或保留异常值 重新拟合:在处理异常值后重新进行拟合 验证:验证拟合结果是否符合预期
MATLAB拟合的注意事项
04
数据的预处理
数据清洗:去除异常值、缺失值和重复值 数据转换:将数据转换为适合拟合的形式,如对数转换、多项式转换等 数据缩放:将数据缩放到合适的范围,以提高拟合精度 数据分割:将数据分成训练集和测试集,以评估模型的泛化能力
拟合参数的选择
参数初始值的设定要合理
根据数据特点选择合适的拟 合函数
适用场景:当标准拟合函数无法满足需求时,可以使用自定义函数拟合
步骤:编写自定义函数,并使用MATL AB的fminsearch或fminunc等优化 函数进行拟合 注意事项:自定义函数需要符合数学函数的规范,且需要能够计算函数的 导数
MATLAB拟合的实例
03
一元线性拟合
实例数据:一元线性数据集
拟合的步骤
导入数据
设定拟合模型
执行拟合操作
评估拟合结果
MATLAB拟合的常用方法
02
多项式拟合
定义:多项式拟合是一种通过多项式逼近数据的方法,通过最小化误差平方和来求解最 佳拟合多项式
实现方式:使用MATLAB中的polyfit函数进行多项式拟合,该函数可以求解一元或多 元多项式拟合
实验数据的拟合

一、实验目的
学会MATLAB软件中利用给定数据进行拟合运算的 方法。
二、相关知识
在上一个实验中,我们已经讨论了在生产和科学实 验中,需要利用插值和拟合的场合,本实验讨论拟 合。在MATLAB中,拟合也有相应的函数来完成。 我们首先来讨论拟合的数学定义。
已知离散点上的数据集 {(x1, y1), (x2, y2 ), , (xn, yn )},即 已知在点集 {x1, x2 , , xn}上的函数值 {y1, y2, , yn} , 构造一个解析函数 f (x)(其图形为一曲线),使 f (x)
T/C 31 32 31 29 27 25 24 22 20 18 17 16
考虑下列类型函数,得到残差。并作图比较效果: (1)二次多项式函数; (2)三次多项式函数; 3.简述插值与拟合的区别。 4.完成实验报告。
2.假定某天的气温变化记录如下表,试用最小二 乘法找出这一天的气温变化规律。
t/h 0 1 2 3 4 5 6 7 8 9 10 11 12
T/C 15 14 14 14 14 15 16 18 20 22 23 25 28
t/h 13 14 15 16 17 18 19 20 21 22 23 24
c=lsqcurvefit(fun,c0,x,y)
说明:polyfit求出已知数据x,y的n阶拟合多项式
f (x) 的系数p,x,y都是向量,x的分量必须单调。
lsqcurvefit用作各种类型曲线的拟合,用最小二乘 法寻找符合经验公式的最优曲线。可用非线性函数 的数据拟合。
例1:求如下给定数据的拟合曲线, x=[0.5,1.0,1.5,2.0,2.5,3.0], y=[1.75,2.45,3.81,4.80,7.00,8.60]。
用MATLAB进行数据拟合

k1 e k2
式中, 表示应力, 单位是 N/m2; 表示应变.
已知应力-应变关系可以用一条指数曲线来描述, 即假设
k1 e k2
式中, 表示应力, 单位是 N/m2; 表示应变.
解 选取指数函数作拟合时, 在拟合前需作变量代换,
化为 k1, k2 的线性函数.
于是,
ln
ln k1 k2
y
+
+
+
+
+ (xi +i,yi)
+
+
y=f(x) +
x i 为点(xi,yi) 与曲线 y=f(x) 的距离
拟合与插值的关系
问题:给定一批数据点,需确定满足特定要求的曲线或曲面 解决方案: •若要求所求曲线(面)通过所给所有数据点,就是插值问题; •若不要求曲线(面)通过所有数据点,而是要求它反映对象 整体的变化趋势,这就是数据拟合,又称曲线拟合或曲面拟合。
线性最小二乘法的求解:预备知识
超定方程组:方程个数大于未知量个数的方程组
r11a1
r12a2
r1m am
y1
(n m)
rn1a1 rn2a2 rnmam yn
即 Ra=y
r11 r12 r1m
a1
y1
其中 R
,
a
,
y
rn1 rn2 rnm
am
yn
超定方程一般是不存在解的矛盾方程组。
函数插值与曲线拟合都是要根据一组数据构造一个函数作 为近似,由于近似的要求不同,二者的数学方法上是完全不同 的。
实例:下面数据是某次实验所得,希望得到X和 f之间的关系?
x1 2 4
matlab 拟合
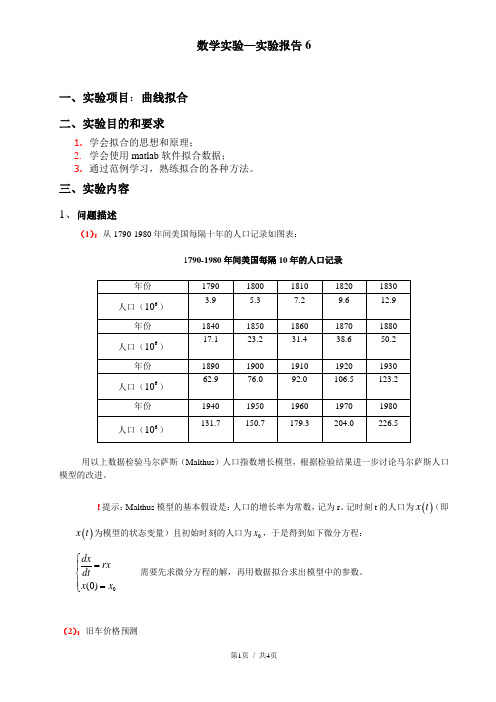
数学实验—实验报告6一、实验项目:曲线拟合 二、实验目的和要求1. 学会拟合的思想和原理;2. 学会使用matlab 软件拟合数据;3. 通过范例学习,熟练拟合的各种方法。
三、实验内容 1、问题描述(1):从1790-1980年间美国每隔十年的人口记录如图表:1790-1980年间美国每隔10年的人口记录用以上数据检验马尔萨斯(Malthus )人口指数增长模型,根据检验结果进一步讨论马尔萨斯人口模型的改进。
!提示:Malthus 模型的基本假设是:人口的增长率为常数,记为r 。
记时刻t 的人口为()x t (即()x t 为模型的状态变量)且初始时刻的人口为0x ,于是得到如下微分方程: 0(0)dx rxdtx x ⎧=⎪⎨⎪=⎩ 需要先求微分方程的解,再用数据拟合求出模型中的参数。
(2):旧车价格预测某年美国旧车价格的调查资料如下表,其中i x 表示轿车的使用年数,i y 表示相应的平均价格,试分析用什么形式的曲线来拟合上述的数据,并预测使用4.5年后轿车的平均价格大致为多少?美国旧车价格的调查数据i x 1 2 3 4 5 6 7 8 9 10 i y 2615 1943 1494 1087 765 538 484 290 226 204 2、实验步骤: 题一:代码:>> x=dsolve('Dx=r*x','x(0)=x0','t') x =x0*exp(r*t) 即()0rtx t x e =!上式取对数,f rt c =+ 代换12f a t a =+ 其中1r a = 20ax e =>> popul=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.4 226.5];>> data=1790:10:1980;>> a=polyfit(data,log(popul),1); >> r=a(1); >> r r =0.0214 >> x0=exp(a(2)) x0 =1.2422e-016>> y=x0*exp(r*data); >> plot(data,y) >> hold on>> plot(data,popul,'ro'); >> xlabel('年份');>> ylabel('人口数量(10^6 )');>> title('1790-1980年间美国人口变化'); >> grid17801800182018401860188019001920194019601980050100150200250300350年份人口数量(106 )1790-1980年间美国人口变化分析:开始时,人口数量增长符合马尔萨斯(Malthus )人口指数增长模型,但1940年之后,增长速度变慢,而马尔萨斯模型中增长速度变大,与实际不符。
MATLAB中简单的数据拟合方法与应用实例①

MATLAB中简单的数据拟合方法与应用实例仅供努力学习matlab的同学们参考参考,查阅了M多资料,总结了以下方法按步骤做能够基本学会matlab曲线拟合的1.1数据拟合方法1.1.1多项式拟合1.多项式拟合命令polyfit(X,Y,N):多项式拟合,返回降幂排列的多项式系数。
Polyval(P,xi):计算多项式的值。
其中,X,Y是数据点的值;N是拟合的最高次幂;P是返回的多项式系数;xi是要求的横坐标拟合命令如下:x=[1 2 3 4 5 6 7 8 9];y=[9 7 6 3 -1 2 5 7 20];P=polyfit(x,y,3);xi=0:.2:10;yi=polyval(P,xi);plot(xi,yi,x,y,'r*');拟合曲线与原始数据如图1-1图1-12图形窗口的多项式拟合1)先画出数据点如图1-2x=[1 2 3 4 5 6 7 8 9];y=[9 7 6 3 -1 2 5 7 20];plot(x,y,'r*');图1-22)在图形窗口单击Tools—Basic Fitting,如图1-3勾选.图1-3图1-3右方分别是线性、二阶、三阶对数据进行多项式拟合。
下面的柱状图显示残差,可以看出,三阶多项式的拟合效果是最好的。
1.1.2指定函数拟合已知M组数据点和对应的函数形式f t (t)=acos(kt)eXY编写M文件:syms tx=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.08;0.032;-0.015;-0.02];f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});cfun=fit(x,y,f)xi=0:.1:20;yi=cfun(xi);plot(x,y,'r*',xi,yi,'b-');图1-4运行程序,在命令窗口可达到以下运行结果,图像如图1-4Warning: Start point not provided, choosing random start point.> In fit>handlewarn at 715In fit at 315In Untitled2 at 5cfun =General model:cfun(t) = a*cos(k*t)*exp(w*t)Coefficients (with 95% confidence bounds):a = 0.9987 ( 0.9835, 1.014)k = 1.001 (0.9958, 1.006)w = -0.2066 (-0.2131, -0.2002)从结果可以看出,拟合的曲线为:(0.2066) ()0.9987cos(1.001)*tf t t e-=。
实验一 用Matlab数据拟合.

练习:练习1.已知观测数据点如表所示x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17求用三次多项式进行拟合的曲线方程.求用三次多项式进行拟合的曲线方程2.已知观测数据点如表所示x 1.6 2.7 1.3 4.1 3.6 2.3 y 17.7 49 13.1 189.4 110.8 34.5 0.6 4 4.9 409.1 3 65 2.4 36.9的值,求a, b, c的值使得曲线f(x=aex+bsin x+c lnx与已知数据的值点在最小二乘意义上充分接近.点在最小二乘意义上充分接近
例4已知观测数据点如表所示x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 35 8.56 9.69 11.25 13.17的值,求三个参数a, b, c的值使得曲线f(x=aex+bx2+cx3与的值已知数据点在最小二乘意义上充分接近.已知数据点在最小二乘意义上充分接近说明:说明最小二乘意义上的最佳拟合函数为f(x= 3ex+ 4.03x2 + 0.94 x3.此时的残差是:此时的残差是0.0912.
编写下面的程序调用拟合函数.编写下面的程序调用拟合函数x=0:0.1:1; y=[3.1,3.27,3.81,4.5,5.18,6,7.05,8.56,9.69,11.25,13.17]; x0=[0,0,0]; [beta,r,J]=nlinfit(x',y','nihehanshu',x0;程序运行后显示beta = 3.0022 4.0304 0.9404
MATLAB 数据拟合

Matlab 数据拟合1.最小二乘法数据拟合2.非线性曲线拟合3.神经网络对实验数据进行拟合(线型拟合:最小二乘法数据拟合和神经网络对实验数据进行拟合对数据x=0:0.1:1,y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]进行拟合;非线性拟合:x=100:100:1000;y=4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59;对函数kt)(-=中的a,b,k进行拟合)*+ebaxf02.01线性最小二乘法拟合Exa:拟合2次线性多项式先描点确定大概用几次多项式x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; plot(x,y,'*')方法一:用MATLAB已有程序x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; A=polyfit(x,y,2);z=polyval(A,x);plot(x,y,'k+',x,z,'r')A =-9.8108 20.1293 -0.0317最小二乘法编程子函数:function c=lspoly1(x,y,M)n=length(x);B=zeros(1:M+1);F=zeros(n,M+1);for k=1:M+1F(:,k)=x'.^(k-1);endA=F'*F;B=F'*y';c=(A\B)'主程序:x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];lspoly1(x,y,2)c =-0.0317 20.1293 -9.8108ans =-0.0317 20.1293 -9.8108方法二:用超定方程组x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; R=[(x.^2)' x' ones(11,1)];A=R\y'A =-9.810820.1293-0.03172非线性最小二乘法拟合2.1 用MA TLAB提供了两个求非线性最小二乘拟合的函数:lsqcurvefit和lsqnonlin,两个命令都要先建立M文件fun.m,在其中定义函数f(x).例子:用下面一组数据拟合中的参数a,b,kx=100:100:1000y=4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59kt)(-+=*aef02.0bxa.用命令lsqcurvefitM文件curvefun1.m :function f=curvefun1(x,tdata)f=x(1)+x(2)*exp(-0.02*x(3)*tdata)x(1)=a;x(2)=b;x(3)=k;主程序tdata=100:100:1000cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59];x0=[0.2,0.05,0.05];x=lsqcurvefit ('curvefun1',x0,tdata,cdata)f= curvefun1(x,tdata)b.用命令lsqnonlinM文件curvefun2.m:function f=curvefun2(x)tdata=100:100:1000;cdata=1e-03*[4.54,4.99,5.35,5.65,5.90,6.10,6.26,6.39,6.50,6.59];f=x(1)+x(2)*exp(-0.02*x(3)*tdata)- cdata主程序x0=[0.2,0.05,0.05];x=lsqnonlin('curvefun2',x0)f= curvefun2(x)3神经网络数据拟合x=0:0.1:1;y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2]; net=newff([0,1],[2,1],{'tansig','purelin'}); %设置神经网络net.trainParam.goal=0.0000001; %设置训练误差net.trainParam.epochs=1000; %设定最大训练步数net=train(net,x,y); %训练网络y1=sim(net,x0); %输出数据plot(x,y,'o', x0,y1,'r')。
在Matlab中数据拟合的研究应用1

在Matlab 中数据拟合的研究应用而解决数据拟合问题最重要的方法变是最小二乘法,矛盾方程组和回归分析。
而本论文主要研究的就是最小二乘法。
在科学实验,统计研究以及一切日常应用中,人们常常需要从一组测定的数据(例如N 个点((,)(0,1,,)i i x y i m = )去求得自变量x 和因变量y 的一个近似解表达式()y x ϕ=,这就是由给定的N 个点(,)(0,1,,)i i x y i m = 求数据拟合的问题。
插值法虽然是函数逼近的一种重要方法,但他还存在以下的缺陷:一是由于测量数据的往往不可避免地带有测试误差,而插值多项式又通过所有的点(,)i i x y ,这样就使插值多项式保留了这些误差,从而影响了逼近精度。
此时显然插值效果是不理想的。
二是如果由实验提供的数据较多,则必然得到次数较高的插值多项式,这样近似程度往往既不稳定又明显缺乏实用价值。
因此,怎样从给定的一组实验数据出发,寻求已知函数的一个逼近函数()y x ϕ=,使得逼近函数从总体上来说与已知函数的偏差按某种方法度量能达到最小而又不一定过全部的点(,)i i x y ,这就需要介绍本论文主要研究的最小二乘法曲线拟合法。
一.数据拟合的原理及依据1.最小二乘法的基本原理从整体上考虑近似函数()p x 同所给数据点(,)i i x y (,)(0,1,,)i i x y i m = 误差()(0,1,,)i i i r p x y i m =-= 的大小,常用的方法有以下三种:一是误差()(0,1,,)i i i r p x y i m =-= 绝对值的最大值0max i i mr ≤≤,即误差向量01(,,,)tm r r r r = 的∞-的范数;二是误差绝对值的和0mi i r =∑,即误差向量r 的1-范数;前两种方法简单,自然,但不便于微分运算,后一种方法相当于考虑2-的范数的平方,因此在曲线拟合中常采用误差平方和20mi i r =∑来度量误差01(,,,)m r r r r = 的整体大小。
高等数学MATLAB实验四 数据拟合问题 实验指导书

实验四 数据拟合问题实验目的:1、加深对函数基本概念的理解;2、掌握利用函数解决实际问题的方法;3、掌握MA TLAB 软件中有关函数、绘图等命令实验要求:掌握函数基本知识,熟悉MA TLAB 中绘图命令plot 。
实验内容:某研究所为了研究氮肥(N )的施肥量与土豆产量的关系,做了十次实验,实验数据见表1-1,其中hm 表示公顷,t 表示吨,kg 表示千克,试分析氮肥的施肥量与土豆产量之间的关系。
表1-1 氮肥施肥量与土豆产量关系的实验数据实验方案设y 代表土豆产量,x 代表氮肥的施肥量。
显然,y 与x 之间应该有某种关系,假设y 与x 之间的关系为函数关系,则问题就转化为已知数据点(,)i i x y ,寻找函数()y y x =,这就是数据拟合问题。
所谓数据拟合,就是从一组实验数据点(,)i i x y 出发,寻找函数()y y x =的一个近似表达式()y f x =(称为经验公式)。
从几何上看,就是希望根据给定的这些数据点(,)i i x y ,求曲线()y y x =的一条近似曲线()y f x =。
近似曲线()y f x =不必过每一个数据点,但如果近似曲线的效果要好的话,那么数据点(,)i i x y 离近似曲线的距离应该尽量小,用偏差平方和函数2(())i i iW f x y =-∑来刻画近似曲线的效果,偏差平方和函数越小则近似曲线的拟合效果越好,因此最好的近似曲线应该满足2min(())iiif x y -∑。
多项式函数由于性质良好,计算方便,常常用来进行数据拟合。
可以考虑采用2{1,,}x x 作为基函数来拟合这组数据(即用二次多项式函数2012a a x a x ++作为经验公式),此时偏差平方和函数为22012()i iW a a x a x y =++-∑,其中n 为数据点的数目,要使偏差平方和函数W 最小,需要201211123012111123420121111n n ni i ii i i n n n ni i i i i i i i i n n n n i i i i ii i i i na a x a x y a x a x a x x y a x a x a x x y ===========⎧++=⎪⎪⎪++=⎨⎪⎪++=⎪⎩∑∑∑∑∑∑∑∑∑∑∑(该方程组称为法方程组),将实验数据(,)i i x y 代入上式,解得014.7391a =, 10.1973139a =, 20.000339492a =-,即拟合函数为214.73910.19731390.000339492y x x =+-。
matlab 数据 曲线拟合

matlab 数据曲线拟合全文共四篇示例,供读者参考第一篇示例:Matlab是一款功能强大的数据分析和曲线拟合工具,广泛应用于科学研究、工程设计、金融分析等领域。
在实际工作中,我们经常需要对实验数据进行处理和分析,而曲线拟合是其中一个常见的操作。
本文将介绍在Matlab中如何进行数据曲线拟合,并通过实例详细说明其使用方法。
我们需要准备一组实验数据,这些数据通常是以表格的形式存储在Excel或文本文件中。
假设我们有一组随机产生的数据点,存储在一个文本文件中,每行包含一对(x, y)坐标。
我们可以通过Matlab的文件读取函数将这些数据导入到Matlab中,然后进行曲线拟合分析。
接下来,我们需要选择适合数据走势的拟合模型。
根据实际情况,可以选择线性函数、多项式函数、指数函数、对数函数等不同类型的拟合模型。
在Matlab中,使用`polyfit`函数可以进行多项式拟合,使用`expfit`函数可以进行指数拟合,使用`fit`函数可以进行其他自定义的拟合操作。
以多项式拟合为例,我们假设要对一组数据进行二次多项式拟合。
通过`load`函数读取数据文件,然后将数据分成两个数组`x`和`y`,分别表示x坐标和y坐标。
接下来,使用`polyfit`函数进行拟合操作,语法如下:```matlabp = polyfit(x, y, 2);````2`表示进行二次多项式拟合。
拟合结果会保存在向量`p`中,`p`的元素表示拟合多项式的系数。
完成拟合操作后,我们可以利用拟合结果绘制曲线图。
通过`polyval`函数,可以根据拟合结果生成拟合曲线的y坐标值,并与原始数据一起绘制在图上,以便进行对比和分析。
除了多项式拟合之外,Matlab还提供了许多其他灵活的拟合方法。
对于非线性数据,可以使用`fit`函数进行非线性拟合。
该函数允许用户根据实际数据特点选择不同的拟合模型,并进行参数估计和优化。
在实际应用中,曲线拟合是数据分析的重要环节之一。
实验五用Matlab数据拟合PPT文档21页

此时的残差是: 0.0912.
拟合函数为: f(x)= 3ex+ 4.03x2 + 0.94 x3.
练习:
1. 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17 求用三次多项式进行拟合的曲线方程.
编写下面的程序调用拟合函数.
x=0:0.1:1; y=[3.1,3.27,3.81,4.5,5.18,6,7.05,8.56,9.69,11.25,13.17]; x0=[0,0,0]; [beta,r,J]=nlinfit(x',y','nihehanshu',x0);
程序运行后显示
beta = 3.0022 4.0304 0.9404
例4 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17
求三个参数 a, b, c的值, 使得曲线 f(x)=aex+bx2+cx3 与 已知数据点在最小二乘意义上充分接近. 说明: 最小二乘意义上的最佳拟合函数为
用Matlab进行数据拟合
1. 多项式曲线拟合: polyfit.
p=polyfit(x,y,m) 其中, x, y为已知数据点向量, 分别表示横,纵坐 标, m为拟合多项式的次数, 结果返回m次拟合 多项式系数, 从高次到低次存放在向量p中.
实验五 用Matlab数据拟合

2. 已知观测数据点如表所示 x 1.6 2.7 1.3 4.1 3.6 2.3 y 17.7 49 13.1 189.4 110.8 34.5
0.6
4
4.9
409.1
3
65
2.4
36.9
求a, b, c的值, 使得曲线 f(x)=aex+bsin x+c lnx 与已知数据 点在最小二乘意义上充分接近.
例4 已知观测数据点如表所示
x 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 y 3.1 3.27 3.81 4.5 5.18 6 7.05 8.56 9.69 11.25 13.17 求三个参数 a, b, c的值, 使得曲线 f(x)=aex+bx2+cx3 与 已知数据点在最小二乘意义上充分接近.
1.55
500 106
2.47
2. 93
3. 03
2.89
1000 106 1500 106 2000 106 2375 106
3 1.953 103 1.517 103 1.219 10
/ / N / m 2 3.103 103 2.465 103
解: 描出散点图, 在命令窗口输入: t=[0:1:16] y=[30.0 29.1 28.4 28.1 28.0 27.7 27.5 27.2 27.0 26.8 26.5 26.3 26.1 25.7 25.3 24.8 24.0] plot(t,y,'*')
a=polyfit(t,y,1) a= -0.3012 29.3804 hold on
beta
= 3.0022 4.0304 0.9404
matlab实验报告 插值和拟合
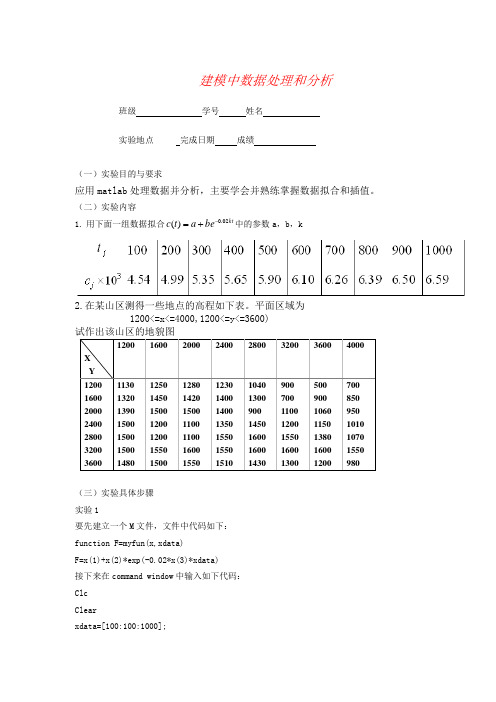
建模中数据处理和分析班级 学号 姓名 实验地点 完成日期 成绩(一)实验目的与要求应用matlab 处理数据并分析,主要学会并熟练掌握数据拟合和插值。
(二)实验内容1. 用下面一组数据拟合ktbea t c 02.0)(-+=中的参数a ,b ,k2.在某山区测得一些地点的高程如下表。
平面区域为 1200<=x<=4000,1200<=y<=3600) 试作出该山区的地貌图X Y 120016002000240028003200360040001200 1130 1250 1280 1230 1040 900 500 700 1600 1320 1450 1420 1400 1300 700 900 850 2000 1390 1500 1500 1400 900 1100 1060 950 2400 1500 1200 1100 1350 1450 1200 1150 1010 2800 1500 1200 1100 1550 1600 1550 1380 1070 3200 1500 1550 1600 1550 1600 1600 1600 1550 36001480 1500 1550 1510 1430 1300 1200 980(三)实验具体步骤 实验1要先建立一个M 文件,文件中代码如下: function F=myfun(x,xdata) F=x(1)+x(2)*exp(-0.02*x(3)*xdata) 接下来在command window 中输入如下代码: Clc Clearxdata=[100:100:1000];ydata=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59]/1000; x0=[0.2 0.05 0.05];[x,resnorm]=lsqcurvefit(@myfun,x0,xdata,ydata) 接着MATLAB 会进行若干次运算,并给出结果:所以拟合的结果是a=0.0063,b=-0.0034,c=0.2542 然后,我们作图看看拟合的结果,输入代码plot(xdata,0.0063-0.0034*exp(-0.02*0.2542*xdata),xdata,ydata,'o') 得到图像如下:实验二建立一个m 文件,在其中输入代码如下: x=1200:400:4000;y=1200:400:3600;100200300400500600700800900100044.555.566.57x 10-3temps=[1130 1250 1280 1230 1040 900 500 700;1320 1450 1420 1400 1300 700 900 850;1390 1500 1500 1400 900 1100 1060 950;1500 1200 1100 1350 1450 1200 1150 1010;1500 1200 1100 1550 1600 1550 1380 1070;1500 1550 1600 1550 1600 1600 1600 1550;1480 1500 1550 1510 1430 1300 1200 980];mesh(x,y,temps)xi=1200:30:4000;yi=1200:30:3600;zi=interp2(x,y,temps,xi',yi,'cubic');mesh(xi,yi,zi)meshz(xi,yi,zi)colordef black运行后打开图形窗口的属性设置对话框,对背景,颜色等属性进行设置,得到下图:(四)实验结果实验中顺利得到拟合结果以及一个三维图像,虽然过程艰辛,但结果十分美好。
matlab_数学实验_实验报告_数据拟合

数据的分析之数据的拟合一、实验项目:Matlab 数据拟合 二、实验目的和要求1、掌握用matlab 作最小二乘多项式拟合和曲线拟合的方法。
2、通过实例学习如何用拟合方法解决实际问题,注意差值方法的区别。
3、鼓励不囿于固定的模式或秩序,灵活调整思路,突破思维的呆板性,找到打破常规的解决方法。
并在文献检索 动手和动脑等方面得到锻炼。
三、实验内容操作一:Malthus 人口指数增长模型用以上数据检验马尔萨斯人口指数增长模型,根据检验结果进一步讨论马尔萨斯人口模型的改进。
马尔萨斯模型的基本假设是人口的增长率为常数,记为r 。
记时刻t 的人口为()x t ,且初始时刻的人口为x 0,于是得到如下微分方程(0)dx rxdtx x ⎧=⎪⎨⎪=⎩ 需要先求微分方程的解,再用数据拟合模型中的参数。
一、分析有这个方程很容易解出0()*rtx t x e =r>0时,是表示人口箭杆指数规律随时间无限增长,称为指数增长模型。
将上式取对数,可得y=rt+a ,y=lnx ,a=lnx0 二、用matlab 编码t=1790:10:1980;x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92 106.5 123.2 131.7 150.7 179.3 204.0 226.5]; p=polyfit(t,log(x),1); r=p(1) x0=exp(p(2)) x1=x0.*exp(r.*t); plot(t,x,'r',t,x1,'b')三、结果和图像 0.0214r =0 1.2480016x e =-17801800182018401860188019001920194019601980050100150200250300350操练二:旧车价格预测分析用什么形式的曲线来拟合数据,并预测使用4、5年后的轿车平均价格大致为多少。
matlab中的数据拟合
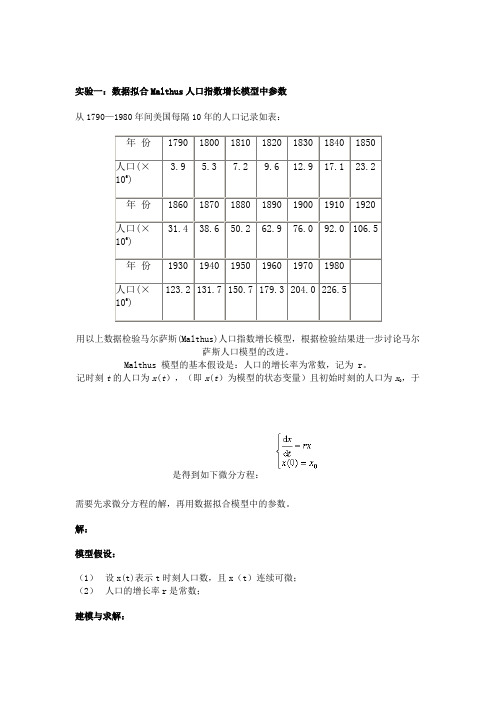
实验一:数据拟合Malthus人口指数增长模型中参数从1790—1980年间美国每隔10年的人口记录如表:年份1790 1800 1810 1820 1830 1840 1850 人口(×3.9 5.3 7.2 9.6 12.9 17.1 23.2106)年份1860 1870 1880 1890 1900 1910 1920 人口(×31.4 38.6 50.2 62.9 76.0 92.0 106.5106)年份1930 1940 1950 1960 1970 1980123.2 131.7 150.7 179.3 204.0 226.5人口(×106)用以上数据检验马尔萨斯(Malthus)人口指数增长模型,根据检验结果进一步讨论马尔萨斯人口模型的改进。
Malthus 模型的基本假设是:人口的增长率为常数,记为 r。
记时刻t的人口为x(t),(即x(t)为模型的状态变量)且初始时刻的人口为x0,于是得到如下微分方程:需要先求微分方程的解,再用数据拟合模型中的参数。
解:模型假设:(1)设x(t)表示t时刻人口数,且x(t)连续可微;(2)人口的增长率r是常数;建模与求解:由可以得到其解为:x(t)=x0 *exp(r*t)对上式两边取对数可得:ln x(t)=ln x0+rt=> y=a+rt (y=ln x(t),a=ln x0)Matlab计算:t=[0:19];x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5];plot(t,x,'+') %画散点图y=log(x);p=polyfit(t,y,1)p =0.2142 1.7213故y=0.2142t+1.7213ln x0 =1.7213 => x0=5.5918x(t)=5.5918*exp(0.2142t)所得的拟合图形为:实验二:经济增长模型增加生产、发展经济所依靠的主要因素有增加投资、增加劳动力以及技术革新等,在研究国民经济产值与这些因素的数量关系时,由于技术水平不像资金、劳动力那样容易定量化,作为初步的模型,可认为技术水平不变,只讨论产值和资金、劳动力之间的关系。
06Matlab插值与拟合实验

460
750 1500 1050 1000 900 380 750 550 300 100 4800
370
550 1550 1150 1050 930 780 650 480 350 150 5200
350
500 1500 1200 1100 950 750 550 350 320 250 5600
f=a1+a2/x + + +
f=aebx +
+
-bx f=ae + +
+ +
+ + +
+
+ +
课堂上机3:化学反应拟合实验
在某化学反应里,测得生成物的质量浓度y(10^(-3)g/cm^3)与时 间t的关系如下表。为了研究该化学反应的性质,如反应速度等, 欲求y与t之间的连续函数关系式y=f(t)。 分别用 ①线性函数 ②y=a*exp(b/t) ③y=t/(a*t+b) 来拟合下表数据,哪个函数拟合效果最好。
Method的方法
nearest:最近点插值法 linear:线性插值,用直线连接数据点 spline:样条插值,用三次样条曲线 cubic:立方插值,用三次曲线
比较不同方法插值效果
x=0:10;y=sin(x);xi=0:.25:10; yi1 = interp1(x,y,xi,'nearest'); yi2 = interp1(x,y,xi,'linear'); yi3 = interp1(x,y,xi,'spline'); yi4 = interp1(x,y,xi,'cubic'); plot(x,y,'o',xi,yi1,':',xi,yi2,'-',xi,yi3,'k.',xi,yi4,'--') legend(‘原始数据’,‘最近点插值’,‘线性插值’,‘样条插 值’,‘立方插值’)
matlab数据拟合

title('从 0:00 到 23:00 之间的温度变化')
2.拟合图像:
温 度 (℃ )
从 0:00到 23:00之 间 的 温 度 变 化 32
30 实测温度
28
26
24
22
20
18 拟合温度
16
14
12
0
5
10
15
20
25
时 间 (h)
3.使用五次多项式程序代码为:
t=[ 0 2 4 6 8 10 12 14 16 18 20 22]; h=[18.5 20.4 22.8 25.6 30.9 27.4 22.0 15.3 13.5 12.7 13.5 15.4]; Y=polyfit(t,h,5); tt=0:0.5:24; hh=polyval(Y,tt) plot(tt,hh,'-b',t,h,'k:'),text(9.5,29,'实测温 度'); text(15,16.5,'拟合温度'); xlabel('时间(h)'); ylabel('温度(℃)'); title('从0:00到23:00之间 的温度 变化')
