第9章怎样研究算法遗传算法示例练习题答案解析(学习资料)
遗传算法详解

串3、4配对;然后,随机选取交叉点,设位串1、2的交叉点为k=4,
二者只交换最后一位,从而生成两个新的位串,即 串 串 1 2 : : 1 01 11 00 0 1 0 1 01 11 00 01 0 新 新 1 2串 串
1. 复制
复制(又称繁殖),是从一个旧种群(old population) 中选择生命力强的字符串(individual string)产生新种群 的过程。或者说,复制是个体位串根据其目标函数f(即 适值函数)拷贝自己的过程。直观地讲,可以把目标函数 f看作是期望的最大效益的某种量度。根据位串的适值所 进行的拷贝,意味着具有较高适值的位串更有可能在下一 代中产生一个或多个子孙。显然,在复制操作过程中,目 标函数(适值)是该位串被复制或被淘汰的决定因素。
复制操作的初始种群(旧种群)的生成往往是随机产生 的。例如,通过掷硬币20次产生维数n=4的初始种群如下 (正面=1,背面=0):
01101
11000
01000
10011
显然,该初始种群可以看成是一个长度为五位的无符 号二进制数,将其编成四个位串,并解码为十进制的数:
位串1:
01101
13
位串2:
5.1.1 基本遗传学基础
遗传算法是根据生物进化的模型提出的一种优化算法。 自然选择学说是进化论的中心内容,根据进化论,生物的 发展进化主要由三个原因,即遗传、变异和选择。
遗传是指子代总是和亲代相似。遗传性是一切生物所 共有的特性,它使得生物能够把其特性、性状传给后代。 遗传是生物进化的基础。
变异是指子代和亲代有某些不相似的现象,即子代永 远不会和亲代完全一样。它是一切生物所具有的共有特性, 是生物个体之间相互区别的基础。引起变异的原因主要是 生活环境的影响及杂交等。生物的变异性为生物的进化和 发展创造了条件。
遗传算法(大作业)
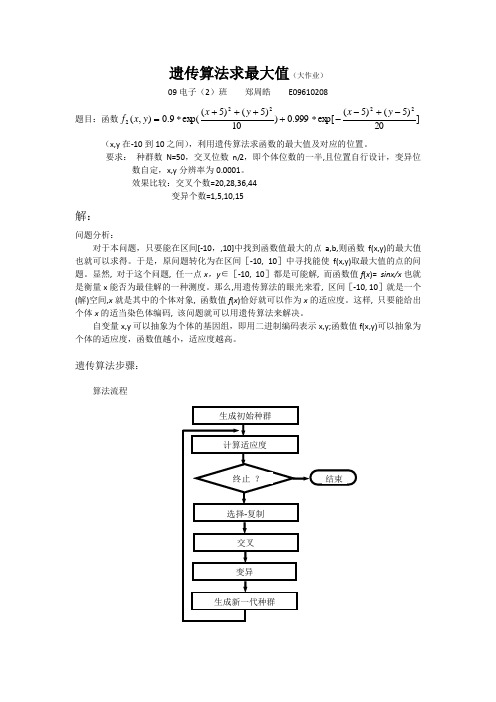
遗传算法求最大值(大作业)09电子(2)班 郑周皓 E09610208 题目:函数]20)5()5(exp[999.0)10)5()5(exp(9.0),(22222-+--*++++*=y x y x y x f (x,y 在-10到10之间),利用遗传算法求函数的最大值及对应的位置。
要求: 种群数N=50,交叉位数n/2,即个体位数的一半,且位置自行设计,变异位数自定,x,y 分辨率为0.0001。
效果比较:交叉个数=20,28,36,44变异个数=1,5,10,15解:问题分析:对于本问题,只要能在区间[-10,,10]中找到函数值最大的点a,b,则函数f(x,y)的最大值也就可以求得。
于是,原问题转化为在区间[-10, 10]中寻找能使f(x,y)取最大值的点的问题。
显然, 对于这个问题, 任一点x ,y ∈[-10, 10]都是可能解, 而函数值f (x )= sinx/x 也就是衡量x 能否为最佳解的一种测度。
那么,用遗传算法的眼光来看, 区间[-10, 10]就是一个(解)空间,x 就是其中的个体对象, 函数值f (x )恰好就可以作为x 的适应度。
这样, 只要能给出个体x 的适当染色体编码, 该问题就可以用遗传算法来解决。
自变量x,y 可以抽象为个体的基因组,即用二进制编码表示x,y;函数值f(x,y)可以抽象为个体的适应度,函数值越小,适应度越高。
遗传算法步骤:算法流程第1步在论域空间U上定义一个适应度函数f(x),给定种群规模N,交叉率P c和变异率P m,代数T;取适度函数为f(x)=sinx/x,种群规模N=50,用popsize表示。
x,y的精度为0.0001 .交叉率(crossover rate):参加交叉运算的染色体个数占全体染色体总数的比例,记为Pc,取值范围一般为0.4~0.99,根据要求本例中选为20/50、28/50、36/50、44/50。
变异率(mutation rate):发生变异的基因位数所占全体染色体的基因总位数的比例,记为Pm,取值范围一般为0.0001~0.1,根据要求本例中选为1/50、5/50、10/50、15/50。
数学建模遗传算法例题

数学建模遗传算法例题数学建模是一种重要的实践活动,通过运用数学工具和方法对实际问题进行建模和求解。
而遗传算法则是一种基于生物进化原理的优化算法,能够通过模拟自然选择、交叉和变异等过程来搜索全局最优解。
在数学建模中,遗传算法也是一种常用的求解工具。
下面以一个简单的例题来介绍遗传算法在数学建模中的应用。
假设有一个机器人需要从起点出发沿着一条直线路径到达终点,并且需要尽量减少行驶路程。
此外,机器人有两种可选的行驶策略:一种是直行,另一种是先左转再右转。
由于机器人的行驶方向只能是水平或竖直,因此左转和右转的方向只有两种。
问题:如何确定机器人应该采用哪种行驶策略,并如何规划其行驶路径?解决此问题的一种方法是使用遗传算法。
具体步骤如下:1. 定义遗传算法的编码和解码方式因为机器人只有两种行驶策略,因此可以用一个二进制字符串来表示机器人的行驶方案。
例如,'01'表示机器人先左转再右转,“10”表示机器人直行。
因此,一个长度为N的二进制字符串可以代表机器人在N个路口的行驶方案。
2. 定义适应度函数适应度函数用于评估染色体的优劣程度。
在此例中,适应度函数应为机器人到达终点的路程长度。
因此,需要计算出每个染色体对应的机器人行驶方案下的总路程长度作为其适应度值。
3. 初始化种群初始化一个大小为M的随机种群,每个染色体为长度为N的二进制字符串。
4. 选择操作选择操作是指通过适应度函数对染色体进行选择,保留适应度较高的染色体,淘汰适应度较低的染色体。
在此例中,可以采用轮盘赌选择算法对染色体进行选择。
5. 交叉操作交叉操作是指将两个染色体的部分基因进行交换,产生新的后代染色体。
在此例中,可以采用单点交叉算法,即随机选择一个位置将两个染色体划分成两部分,然后交换这两部分,从而产生新的后代染色体。
6. 变异操作变异操作是指随机改变染色体中的一个基因,从而产生一个新的染色体。
在此例中,可以选择随机选择一个基因位置,将其取反,从而产生一个新的染色体。
遗传算法与优化问题的求解

遗传算法与优化问题的求解遗传算法是一种基于生物进化理论的启发式优化算法,具有广泛的应用领域,包括工程、经济、物流以及机器学习等。
它通过模拟自然选择、遗传变异和遗传交叉等过程,不断搜索并改善问题的解,以找到满足约束条件的最佳解决方案。
本文将重点探讨遗传算法的基本原理、应用案例,并分析其优势和限制。
一、遗传算法的基本原理遗传算法的基本原理可以总结为以下几个步骤:1. 初始化种群:将问题转化为染色体编码,通过随机生成一组个体作为初始种群。
2. 适应度评估:根据问题的特定目标函数,对每个个体的适应度进行评估,以衡量其解决问题的能力。
3. 选择操作:根据适应度大小,利用选择算子选择一部分优秀个体作为父代,进行繁殖。
4. 遗传操作:通过交叉和变异操作,生成一定数量的子代个体。
交叉操作模拟基因的组合,变异操作模拟基因的突变。
5. 替代策略:将子代替换部分父代,保持种群的规模不变。
6. 终止条件:根据设定的终止条件,如达到最大迭代次数或找到满足要求的解,终止算法。
否则,返回第3步。
二、遗传算法的应用案例1. 旅行商问题(TSP): TSP是一个著名的组合优化问题,要求在给定城市之间找到最短路径。
遗传算法可以通过将城市顺序编码为染色体,并使用交叉和变异操作改善解的质量。
2. 排课问题:在学校的课程安排中,合理地安排教室、时间和教师是一项复杂而关键的任务。
遗传算法可以通过将课程、教室和时间等信息编码为染色体,并通过优化适应度函数寻找最佳解决方案。
3. 员工排班问题:在企业中,合理安排员工的工作时间和休假时间是一项具有挑战性的问题。
遗传算法可以通过将员工的工作时间分配编码为染色体,并通过交叉和变异操作生成新的排班安排,以优化员工满意度和工作效率。
三、遗传算法的优势和限制1. 优势:a. 全局搜索能力强:遗传算法能够避免陷入局部最优解,通过多样化的交叉和变异操作,搜索整个解空间。
b. 对问题结构没有要求:遗传算法不依赖于问题的特定形式,适用于各种类型的优化问题。
【智能算法】超详细的遗传算法(GeneticAlgorithm)解析和TSP求解代码详解

回到3.1中提的求一元函数最大值的问题。在上面我们把极大值比喻为山峰,那么,袋鼠的位置坐标可以比喻为区间[-1, 2]的某一个x坐标 (有了x坐标,再通过函数表达式可以算出函数值 <==> 得到了袋鼠染色体编码,解码得到位置坐标,在喜马拉雅山脉地图查询位置坐标算 出海拔高度)。这个x坐标是一个实数,现在,说白了就是怎么对这个x坐标进行编码。下面我们以二进制编码为例讲解,不过这种情况下以 二进制编码比较复杂就是了。(如果以浮点数编码,其实就很简洁了,就一浮点数而已。)
就像0和1两种碱基,然后将他们串成一条链形成染色体。一个位能表示出2种 状态的信息量,因此足够长的二进制染色体便能表示所有的特征。这便是二进制编码。如下:
1110001010111
它由二进制符号0和1所组成的二值符号集。它有以下一些优点:
image 当指针在这个转盘上转动,停止下来时指向的个体就是天选之人啦。可以看出,适应性越高的个体被选中的概率就越大。
遗传算法的交叉操作,是指对两个相互配对的染色体按某种方式相互交换其部分基因,从而形成两个新的个体。 适用于二进制编码个体或浮点数编码个体的交叉算子: 1. 单点交叉(One-point Crossover):指在个体编码串中只随机设置一个交叉点,然后再该点相互交换两个配对个体的部分染色体。 2. 两点交叉与多点交叉:
(1) 两点交叉(Two-point Crossover):在个体编码串中随机设置了两个交叉点,然后再进行部分基因交换。 (2) 多点交叉(Multi-point Crossover) 3. 均匀交叉(也称一致交叉,Uniform Crossover):两个配对个体的每个基因座上的基因都以相同的交叉概率进行交换,从而形成两 个新个体。 4. 算术交叉(Arithmetic Crossover):由两个个体的线性组合而产生出两个新的个体。该操作对象一般是由浮点数编码表示的个体。 咳咳,根据国际惯例。还是抓一个最简单的二进制单点交叉为例来给大家讲解讲解。 二进制编码的染色体交叉过程非常类似高中生物中所讲的同源染色体的联会过程――随机把其中几个位于同一位置的编码进行交换,产生新 的个体。
《遗传算法详解》课件

遗传算法具有全局搜索能力、对问题 依赖性小、可扩展性强、鲁棒性高等 特点。
遗传算法的基本思想
初始化
随机生成一组解作为初始种群。
适应度评估
根据问题的目标函数计算每个解 的适应度值。
选择操作
根据适应度值的大小,选择优秀 的解进行遗传操作。
迭代更新
重复以上过程,直到满足终止条 件。
变异操作
对某些基因进行变异,增加解的 多样性。
《遗传算法详解》 ppt课件
• 遗传算法概述 • 遗传算法的基本组成 • 遗传算法的实现流程 • 遗传算法的优化策略 • 遗传算法的改进方向 • 遗传算法的未来展望
目录
Part
01
遗传算法概述
定义与特点
定义
遗传算法是一种模拟生物进化过程的 优化算法,通过模拟基因遗传和变异 的过程来寻找最优解。
Part
05
遗传算法的改进方向
混合遗传算法的研究
混合遗传算法
结合多种优化算法的优点,提高遗传算法的全局搜索能力和收敛速 度。
混合遗传算法的原理
将遗传算法与其他优化算法(如梯度下降法、模拟退火算法等)相 结合,利用各自的优势,弥补各自的不足。
混合遗传算法的应用
在许多实际问题中,如函数优化、路径规划、机器学习等领域,混 合遗传算法都取得了良好的效果。
自适应交叉率
交叉率控制着种群中新个体的产生速度。自适应交叉率可以根据种群中个体的适应度差 异进行调整,使得适应度较高的个体有更低的交叉率,而适应度较低的个体有更高的交 叉率。这样可以提高算法的搜索效率。
自适应变异率
变异率决定了种群中新个体的产生速度。自适应变异率可以根据种群中个体的适应度进 行调整,使得适应度较高的个体有更低的变异率,而适应度较低的个体有更高的变异率
遗传算法的分析

遗传算法遗传算法(Genetic Algorithm)目录[隐藏]∙ 1 遗传算法的概念∙ 2 遗传算法与自然选择∙ 3 遗传算法的基本原理∙ 4 遗传算法的步骤和意义∙ 5 遗传算法的特点∙ 6 遗传算法在神经网络中的应用∙7 遗传算法案例分析o7.1 案例一:遗传算法在装箱环节中的应用[1]∙8 参考文献[编辑]遗传算法的概念遗传算法是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。
它是由美国的J.Holland教授1975年首先提出,其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,能自动获取和指导优化的搜索空间,自适应地调整搜索方向,不需要确定的规则。
遗传算法的这些性质,已被人们广泛地应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。
它是现代有关智能计算中的关键技术之一。
[编辑]遗传算法与自然选择达尔文的自然选择学说是一种被人们广泛接受的生物进化学说。
这种学说认为,生物要生存下去,就必须进行生存斗争。
生存斗争包括种内斗争、种间斗争以及生物跟无机环境之间的斗争三个方面。
在生存斗争中,具有有利变异的个体容易存活下来,并且有更多的机会将有利变异传给后代;具有不利变异的个体就容易被淘汰,产生后代的机会也少的多。
因此,凡是在生存斗争中获胜的个体都是对环境适应性比较强的。
达尔文把这种在生存斗争中适者生存,不适者淘汰的过程叫做自然选择。
它表明,遗传和变异是决定生物进化的内在因素。
自然界中的多种生物之所以能够适应环境而得以生存进化,是和遗传和变异生命现象分不开的。
正是生物的这种遗传特性,使生物界的物种能够保持相对的稳定;而生物的变异特性,使生物个体产生新的性状,以致于形成新的物种,推动了生物的进化和发展。
遗传算法是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型。
它的思想源于生物遗传学和适者生存的自然规律,是具有“生存+检测”的迭代过程的搜索算法。
遗传算法复习资料.doc

1轮盘赌选择是指个体选中并遗传到下一代群体中的概率,与该个体的适应度大小成正比。
其工作过程是这样的:设想群体全体成员的适应性分数有一张饼图来代表,这张饼图就和用于赌博的转轮形状一样。
我们要为群体中每一染色体指定饼图中一个小块。
为了选取一个染色体,你要做的就是旋转这个轮子并把一个小球抛入其中,让小球翻来翻去地跳动,知道轮盘停止时,看小球停止在哪一块上,就选中与它对应的那个染色体。
2作业车间调度问题可以描述为:给定一个工件的集合和一个机器的集合,每个工件包括了多道工序,每道工序需要在一台给定的机器上非间断的加工某一段时间;每台机器一次最多只能加工一道工序;调度就是把工序分配给机器上某个时间段。
问题的目标是找到最小时间长度的调度。
3适应度函数是度量个体适应度的函数。
它来度量群体中各个给在优化计算中有可能达到或接近于或有助于找到最优解的优良程度。
实用度较高的个体遗传到下一代的概率就较大;而适应度较低的个体遗传到下一代的概率就相对小一些。
4小生境小生境是指特定坏境中的一种组织的功能,把有共同特征的组织称作物种。
生物学中,小生境是指特定环境下的一种生存环境。
生物在其进化过程中,一般总是与自己相同的物种生活在一起,共同繁衍后台;他们也都是在某一特定的地理区域中生存。
例如,热带鱼不能再叫冷的地带生存,而北极熊也不能在热带生存。
更特别的例了,人类有个别的部落至今还仍存在鲜为人知的某个闭塞的原始环境中,他们的智力或进化水平也许比不上现代开放环境中的人,但在这个部落内部,也不失有一些优秀分了。
5二倍体算子6使用基本遗传算法进行运算必须提前设定几个参数,每个参数的取值范围是多少?选择操作在遗传算法中的作用是什么?能举出2种常用的选择算法,并能详细说遗传算法中需要选择的运行参数主要有个体编码串长度(使用二进制编码来表示个体时,编码串长度的选取与问题所要求的求解精度有关)、群体大小M(20-100)、交叉概率Pm (O.OOOl-O.l)、终止代数T(100-1000)、代沟G(常见=1.0)选择操作就是确定如何从父代群体中按某种方法选择哪些个体遗传到下一代群体中的一种遗传运算。
遗传算法9PPT课件

01
02
03
二进制编码
使用0和1组成的二进制串 表示染色体,常见于优化 二进制问题。
实数编码
使用实数表示染色体,适 用于连续问题优化。
排列编码
将问题解的排列作为染色 体,适用于组合优化问题。
初始种群的产生
随机生成
随机生成一定数量的染色体作为初始 种群。
启发式方法
根据问题特性,采用启发式方法生成 初始种群。
PART 01
遗传算法概述
定义与特点
定义
遗传算法是一种基于生物进化原 理的优化算法,通过模拟自然选 择和遗传机制,在搜索空间中寻 找最优解。
特点
遗传算法具有全局搜索、并行性 、自适应性、鲁棒性和可扩展性 等特点,适用于解决复杂的、非 线性、多峰值优化问题。
遗传算法的基本思想
编码
将问题的解空间映射 到基因空间,将问题 的解表示为基因序列。
可以根据个体的适应度和种群 的多样性,自适应地调整选择 概率、交叉概率和变异概率等 参数。
可以根据问题的特性和求解要 求,自适应地调整算法的搜索 空间和搜索方式。
多目标优化策略
针对多目标优化问题,采用多目标遗 传算法,通过同时优化多个目标函数, 找到Pareto最优解集。
可以采用多目标进化算法,如NSGAII、SPEA等,以找到更全面和均衡的 解集。
适应度函数的设计
问题相关
适应度函数需与问题目标紧密相关,反映解的优劣。
归一化处理
对适应度值进行归一化处理,便于后续操作。
选择操作
轮盘赌选择
根据适应度值大小,通过轮盘赌方式选择染色体。
锦标赛选择
从种群中随机选取一定数量的染色体进行比较,选择最佳个体。
交叉操作
遗传算法求解实例

yjl.m :简单一元函数优化实例,利用遗传算法计算下面函数的最大值f (x) =xsin( 10 二* x) 2.0,x • [-1,2]选择二进制编码,种群中个体数目为40,每个种群的长度为20,使用代沟为0.9,最大遗传代数为25len lbub scale lbin译码矩阵结构: FieldD code译码矩阵说明:len -包含在Chrom中的每个子串的长度,注意sum(len)=length(Chrom);lb、ub -行向量,分别指明每个变量使用的上界和下界;code -二进制行向量,指明子串是怎样编码的,code(i)=1为标准二进制编码,code(i)=0则为格雷编码;scale -二进制行向量,指明每个子串是否使用对数或算术刻度,scale(i)=0为算术刻度,scale(i)=1则为对数刻度;lbin、ubin -二进制行向量,指明表示范围中是否包含每个边界,选择lbin=0或ubin=0,表示从范围中去掉边界;lbin=1或ubin=1则表示范围中包含边界;注:增加第22 行:variable=bs2rv(Chrom, FieldD);否则提示第26 行plot(variable(l), Y, 'bo');中variable(I)越界yj2.m :目标函数是De Jong函数,是一个连续、凸起的单峰函数,它的M文件objfun1包含在GA工具箱软件中,De Jong函数的表达式为:n2f (x) = ' X j , 一512 乞X j E 512i d这里n是定义问题维数的一个值,本例中选取n=20,求解min f (x),程序主要变量:NIND (个体的数量):=40;MAXGEN (最大遗传代数):=500;NVAR (变量维数):=20 ;PRECI (每个变量使用多少位来表示):=20;GGAP (代沟):=0.9注:函数objfun1.m 中switch改为switch1,否则提示出错,因为switch为matlab保留字,下同!yj3.m :多元多峰函数的优化实例,Shubert函数表达式如下,求min f (x)【shubert.m 】f(x 「X 2)= 7 i cos[( i T)*X t i]*7 i cos[( i ■ 1) * x 2 - i] ,- 10 乞 X t , x 2 乞 10i丄i注:第10行各变量的上下限改为[-10;10],原来为[-3;3];第25行改为:[Y, l]=min(ObjV);原来为[Y, I]=min(ObjVSel);以此将染色体的个 体值与shubert()函数值对应起来, 原表达式不具有 shubert()函数自变量和应变量的对应关系yj4.m :收获系统最优控制,收获系统(Harvest)是一个一阶的离散方程,表达式为x(k T) = a*x(k) - u (k) , k =1, 2,…,N-s.t. x(0)为初始条件x(k)三R 为状态变量u(k 厂R ■为控制输入变量精确优化解:用遗传算法对此问题求解, x(0) =100 , > -1.1,控制步骤N=20 ,决策变量u (k) 个数 NVAR=20, u(k) •二[0,200 ]注:第 20行语句原为:Chrom=crtrp(NIND,FieldDD);改为:Chrom=crtrp(SUBPOP*NIND,FieldDD);运行提示:Warning: File: D:\MA TLAB6p5\toolbox\gatbx\CRTRP .M Line: 34 Column: 19 Variable 'nargin' has bee n previously used as a function n ame. (Type "warni ngoff MATLAB:mir_warni ng_variable_used_as_fu nctio n"tosuppress this warnin g.)yj5.m :装载系统的最优问题,装载系统是一个二维系统,表达式如下X 1 ( k ' 1) = X 2 (k)丄 丄1x 2(k -1) =2 * x 2 (k) —X t (k)^u(k)N目标函数: 1Nf (x,u) - -X t (N 1)u (k)2N k 亠N _1理论最优解: min f (x, u) = _ 1 ■_ - — k 23 6N 2 N k 二目标函数: Nf(x,u)工 J u(k)k40.4 20x( N ) - x(0)k =1, 2,…,Nmax f (x)=Nx(0)(a -1) ~N 」 a (a -1)用遗传算法对此问题求解,x(0) =[0 0],控制步骤N=20,决策变量u(k)个数NVAR=20 , u(k)三[0,10]注:增加第32-35行语句,功能为实现每隔MIGGEN=20代,以迁移率MIGR=0.2在子种群之间迁移个体,增加这几行语句之前求得目标函数最小值为-0.1538,增加这几行语句之后求得目标函数最小值为-0.1544,目标函数理论最优值为-0.1544.yj6.m :离散二次线性系统最优控制问题,其一维二阶线性系统表达式如下:x(k 1)=a*x(k) b*u(k) , k =1, 2,…,N目标函数:N2 2 2f(x,u) =q*x(n 亠1)亠二[s * x( k)亠r*u(k)]k z1参数设置:求min f (x, u)yj7.m :目标分配问题描述为:m个地空导弹火力单元对n批空袭目标进行目标分配。
算法】超详细的遗传算法(GeneticAlgorithm)解析

算法】超详细的遗传算法(GeneticAlgorithm)解析01 什么是遗传算法?1.1 遗传算法的科学定义遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。
其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
1.2 遗传算法的执行过程(参照百度百科)遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。
每个个体实际上是染色体(chromosome)带有特征的实体。
染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。
因此,在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码。
初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。
第9章如何研究算法遗传算法例如练习题答案解析

第9章如何研究算法:遗传算法例如1、P类问题、NP类问题、NPC类问题是运算机科学领域关于可求解性可计算性很重要的概念。
关于P、NP和NPC类问题,回答以下问题。
(1)以下说法不正确的选项是_____。
(A) P类问题是运算性能够在有限时刻内能够求解的问题;(B) NP类问题是运算性能够在有限时刻内能够验证“解”的正确性的问题;(C) NPC类问题是对问题的每一个可能解,运算机都能够在有限时刻内验证“解”的正确性的问题,被称为NP完全问题;(D)上述说法有不正确的;答案:D说明:此题考核P类问题、NP类问题、NPC类问题的概念。
P类问题指运算性能够在有限时刻内求解的问题,(A)正确;NP类问题指尽管在多项式时刻内难于求解但不难判定给定一个解的正确性问题,(B)正确;NPC问题指NP问题的所有可能答案都能够在多项式时刻内进行正确与否的验算,称为NP-Complete问题,(C)正确;(A)(B)(C)都正确,因此(D)错误。
具体内容请参考第九章视频之“可求解与难求解问题”和第九章课件。
(2)可解性问题是指能够找到多项式时刻复杂性算法进行求解的问题,难解性问题是指找不到多项式时刻复杂性算法进行求解的问题。
以下说法不正确的选项是_____。
(A) P类问题是可解性问题,NP类问题是难解性问题。
(B) NP类问题不必然是难解性问题,因为P类问题也必然是NP类问题;(C) NP类问题不确信是不是是P类问题,但NPC类问题必然是难解性问题;(D)上述说法有不正确的;答案:A说明:此题考核对可解性问题和难解性问题概念的明白得。
P类问题指运算性能够在有限时刻内求解的问题,因此是可解性问题;NP类问题指尽管在多项式时刻内难于求解但不难判定给定一个解的正确性问题,但P类问题是NP类问题的一个子集,因此NP类问题不必然是难解性问题;NPC问题指NP问题的所有可能答案都能够在多项式时刻内进行正确与否的验算,称为NP-Complete问题,是难解性问题,综上,(A)错误。
遗传算法优化问题的研究

遗传算法优化问题的研究在计算机领域,优化问题一直是研究的热点之一。
遗传算法(Genetic Algorithm,GA)是一种模拟自然进化过程的优化算法,其能够快速地找到问题的全局最优解,受到了广泛的研究和应用。
一、遗传算法的基本原理遗传算法的基本原理是模拟生物进化中的自然选择、交叉和变异等机制。
它通过不断地对问题的解进行遗传操作来达到优化的目的,主要包括以下几个步骤:1.初始化种群:根据问题的不同,通过一定的方法初始化一定数量的初始种群。
2.选择操作:根据每个个体的适应度(即问题的解的评价指标),选择一定数量的个体进行交叉和变异操作。
3.交叉操作:选择一对父代个体,通过交叉操作生成一定数量的子代个体。
4.变异操作:对一定数量的子代个体进行变异操作,使得具有一定概率的基因发生变化从而产生新的个体。
5.重复以上操作直到满足终止条件:其中的终止条件可以是最大迭代次数、达到一定适应度、相邻几代适应度变化小于所设定的值等。
二、遗传算法的优点遗传算法具有以下几个优点:1.全局搜索:由于遗传算法是模拟进化过程的全局搜索算法,所以它可以在搜索空间中进行全局搜索,得到问题的全局最优解。
2.鲁棒性:遗传算法对于初始种群的选择、交叉和变异等操作不太敏感,因此具有较好的鲁棒性。
3.并行性:遗传算法的并行性非常强,可以采用多线程或多台计算机并行计算,提高计算效率。
4.动态适应性:遗传算法可以根据问题的不同,在求解过程中对基因操作的概率进行动态调整,提高算法的适应性。
三、遗传算法的应用遗传算法在许多领域中得到了广泛的应用,包括优化问题(如函数最优化、组合优化、排样问题等)、机器学习、控制优化、图像处理、模式识别等领域。
在工程领域中,遗传算法被应用于结构优化、产品设计、工艺优化、航空航天等领域。
例如,在飞行器设计中,通过采用遗传算法进行结构优化,可以提高飞行器的性能和可靠性。
同时,在金融领域中,遗传算法也得到了广泛的应用。
例如,在股票选举、分析和交易中,可以采用遗传算法进行股票筛选和交易策略的优化。
遗传算法计算步骤

遗传算法的计算步骤例1:设2()20.5f x x x =-++,求 max (), [1,2]f x x ∈-.(1)编码和产生初始群体首先第一步要确定编码的策略,也就是说如何把1-到2这个区间内的数用计算机语言表示出来.编码时要注意以下三个原则:完备性:问题空间中所有点(潜在解)都能成为GA 编码空间中的点(染色体位串)的表现型;健全性:GA 编码空间中的染色体位串必须对应问题空间中的某一潜在解; 非冗余性:染色体和潜在解必须一一对应.这里我们通过采用二进制的形式来解决编码问题,将某个变量值代表的个体表示为一个{0,1}二进制串.当然,串长取决于求解的精度.如果要设定求解精度到六位小数,由于区间长度为2(1)3--=,则必须将闭区间 [1,2]-分为6310⨯等分.因为216222097152231024194304=<⨯<= 所以编码的二进制串至少需要22位.将一个二进制串(b 21b 20b 19…b 1b 0)转化为区间[1,2]-内对应的实数值很简单,只需采取以下两步:1)将一个二进制串(b 21b 20b 19…b 1b 0)代表的二进制数化为10进制数:21212019102100()(2)'i i i b b b b b b x =⋯=⋅=∑2)'x 对应的区间[1,2]-内的实数:12)1(2'122---⋅+-=x x 例如,一个二进制串a=<1000101110110101000111>表示实数0.637197.'x =(1000101110110101000111)2=2288967637197.01232288967122=-⋅+-=x 二进制串<0000000000000000000000>,<1111111111111111111111>,则分别表示区间的两个端点值-1和2.利用这种方法完成了遗传算法的第一步——编码,这种二进制编码的方法完全符合上述的编码的三个原则.首先我们来随机的产生一个个体数为4个的初始群体如下:pop(1)={<1101011101001100011110>, %% a1<1000011001010001000010>, %% a2<0001100111010110000000>, %% a3<0110101001101110010101>} %% a4化成十进制的数分别为:pop(1)={ 1.523032,0.574022 ,-0.697235 ,0.247238 }接下来我们就要解决每个染色体个体的适应值问题了.(2)定义适应函数和适应值 由于给定的目标函数2()20.5f x x x =-++在[1,2]-内的值有正有负,所以必须通过建立适应函数与目标函数的映射关系,保证映射后的适应值非负,而且目标函数的优化方向应对应于适应值增大的方向,也为以后计算各个体的入选概率打下基础.对于本题中的最大化问题,定义适应函数()g x ,采用下述方法:min min (), ()0()0,f x F f x F g x -->⎧=⎨⎩若其他 式中min F 既可以是特定的输入值,也可以是当前所有代或最近K 代中()f x 的最小值,这里为了便于计算,将采用了一个特定的输入值.若取min 1F =-,则当()1f x =时适应函数()2g x =;当() 1.1f x =-时适应函数()0g x =.由上述所随机产生的初始群体,我们可以先计算出目标函数值分别如下 f [pop(1)]={ 1.226437 , 1.318543 , -1.380607 , 0.933350 }然后通过适应函数计算出适应值分别如下取min 1F =-,g[pop(1)]= { 2.226437 , 2.318543 , 0 , 1.933350 }(3)确定选择标准这里用到了适应值的比例来作为选择的标准,得到的每个个体的适应值比例叫作入选概率.其计算公式如下:对于给定的规模为n 的群体pop={123,,,,n a a a a },个体i a 的适应值为()i g a ,则其入选概率为1()(),1,2,3,,()i s i n ii g a P a i n g a ===⋯∑由上述给出的群体,我们可以计算出各个个体的入选概率.首先可得 41() 6.478330i i g a==∑, 然后分别用四个个体的适应值去除以41()i i g a =∑,得:P (a 1)=2.226437 / 6.478330 = 0.343675 %% a 1P (a 2)=2.318543 / 6.478330 = 0.357892 %% a 2P (a 3)= 0 / 6.478330 = 0 %% a 3P (a 4)=1.933350 / 6.478330 = 0.298433 %% a 4(4)产生种群计算完了入选概率后,就将入选概率大的个体选入种群,淘汰概率小的个体,并用入选概率最大的个体补入种群,得到与原群体大小同样的种群.由初始群体的入选概率我们淘汰掉a 3,再加入a 2补足成与群体同样大小的种群得到newpop(1)如下:newpop(1)={<1101011101001100011110>, %% a 1<1000011001010001000010>, %% a 2<1000011001010001000010>,%% a2<0110101001101110010101>} %% a4(5)交叉交叉也就是将一组染色体上对应基因段的交换得到新的染色体,然后得到新的染色体组,组成新的群体(Matlab程序参见附录9).我们把之前得到的newpop(1)的四个个体两两组成一对,重复的不配对,进行交叉.(可以在任一位进行交叉)<110101110 1001100011110>,<1101011101010001000010>交叉得:<100001100 1010001000010>,<1000011001001100011110><10000110010100 01000010>,<1000011001010010010101>交叉得:<01101010011011 10010101>,<0110101001101101000010>通过交叉得到了四个新个体,得到新的群体jchpop (1)如下:jchpop(1)={<1101011101010001000010>,<1000011001001100011110>,<1000011001010010010101>,<0110101001101101000010>}这里采用的是单点交叉的方法,当然还有多点交叉的方法,这里就不着重介绍了.(6)变异变异也就是通过一个小概率改变染色体位串上的某个基因.现把刚得到的jchpop(1)中第3个个体中的第9位改变,就产生了变异,得到了新的群体pop(2)如下:pop(2)= {<1101011101010001000010>,<1000011001001100011110>,<1000011011010010010101>,<0110101001101101000010> }然后重复上述的选择、交叉、变异直到满足终止条件为止.(7)终止条件遗传算法的终止条件有两类常见条件:(1)采用设定最大(遗传)代数的方法,一般可设定为50代,此时就可能得出最优解.此种方法简单易行,但可能不是很精确(Matlab程序参见附录1);(2)根据个体的差异来判断,通过计算种群中基因多样性测度,即所有基因位相似程度来进行控制.。
从原理到实例·遗传算法详解

从原理到实例·遗传算法详解前言自上一期的文章《算法时代的到来》发表后,同学们反响激烈。
有担心职业发展前景的,有讨论哪款软件应用算法最好的,也有想立志从事算法研究的。
一石激起千层浪,大家对电机的算法优化应用的兴趣被激起来了。
算法优化不是新事物,已经在很多领域里应用,杨思超博士一直从事遗传算法的研究工作,有幸我们请到他为大家进一步讲解遗传算法的原理。
什么是优化?优化,就是“把某个东西变得更好”。
在生活中,寻找最优方案的例子无处不在:1. 爬山时,从那一侧开始,选择怎样的路径能最快登顶同时又相对安全?2. 工厂在总工时,材料成本一定,怎样生产A,B,C三个产品来达到利润最大化?3. 机械人的各个关节怎样配合来达到平衡的同时,能最高效敏捷的运动?那通常怎么去找到最快最好的方式呢?咱们首先想到的方法是:要看路径最短那咱们就把所有的路径都走一遍就是了嘛。
也就是经典的枚举法。
诚然,当我们的时间和金钱成本足够多的情况下,利用枚举法找到的方案一定是最有说服力的。
这样原始的方法在现今追求快节奏低成本的社会环境里是越来越没有其立足之地了。
取而代之的是依靠各种优化算法来寻找答案:我们往往能成百上千倍的缩短寻找时间和成本,化不可能为可能。
优化算法和咱们电机设计也密不可分在研发一款新产品时,设计师会从任务需求出发,在满足性能指标的前提下设法寻找某种目标下的最优方案,可以是成本最低,也可以是安全性最高,体积最小,效率最高等等。
为了实现优化,首先我们会定下优化目标(效率最优,成本最低,体积最小),同时明确约束条件(转矩脉动小于2%,效率大于95%,电压小于50V,热负荷小于3000等等)。
然后我们可以设置优化的变量(整体三维尺寸,气隙半径,定转子槽型,磁钢形状,材料牌号,电机拓扑等等),再丢给软件优化,经过一段时间后,软件输出结果,我们挑选,对比并最终敲定方案。
作为设计师,通常我们的关注点在“优化的结果”而不是“优化的过程”。
大学计算机基础第九章习题与解析

第9章怎样研究算法:遗传算法示例1、P类问题、NP类问题、NPC类问题是计算机科学领域关于可求解性可计算性很重要的概念。
关于P、NP和NPC类问题,回答下列问题。
(1)下列说法不正确的是_____。
(A) P类问题是计算机可以在有限时间内能够求解的问题;(B) NP类问题是计算机可以在有限时间内能够验证“解”的正确性的问题;(C) NPC类问题是对问题的每一个可能解,计算机都可以在有限时间内验证“解”的正确性的问题,被称为NP完全问题;(D)上述说法有不正确的;答案:D解释:本题考核P类问题、NP类问题、NPC类问题的概念。
P类问题指计算机可以在有限时间内求解的问题,(A)正确;NP类问题指虽然在多项式时间内难于求解但不难判断给定一个解的正确性问题,(B)正确;NPC问题指NP问题的所有可能答案都可以在多项式时间内进行正确与否的验算,称为NP-Complete问题,(C)正确;(A)(B)(C)都正确,所以(D)错误。
具体内容请参考第九章视频之“可求解与难求解问题”以及第九章课件。
(2)可解性问题是指能够找到多项式时间复杂性算法进行求解的问题,难解性问题是指找不到多项式时间复杂性算法进行求解的问题。
下列说法不正确的是_____。
(A) P类问题是可解性问题,NP类问题是难解性问题。
(B) NP类问题不一定是难解性问题,因为P类问题也一定是NP类问题;(C) NP类问题不确定是否是P类问题,但NPC类问题一定是难解性问题;(D)上述说法有不正确的;答案:A解释:本题考核对可解性问题和难解性问题概念的理解。
P类问题指计算机可以在有限时间内求解的问题,所以是可解性问题;NP类问题指虽然在多项式时间内难于求解但不难判断给定一个解的正确性问题,但P类问题是NP类问题的一个子集,所以NP类问题不一定是难解性问题;NPC问题指NP问题的所有可能答案都可以在多项式时间内进行正确与否的验算,称为NP-Complete问题,是难解性问题,综上,(A)错误。
遗传算法例题分析

6 0.58 1.97 0.22 1.23
7 1 2 0 1
∑ f (x )
i
平均值 最大值 最小值
f
293 576 64
f max
f min
(3)计算适应度。衡量字符串(染色体)好坏 计算适应度。衡量字符串(染色体) 的指标是适应度(Fitness),它通常也就是遗传算 的指标是适应度(Fitness),它通常也就是遗传算 ), 法中的目标函数。适应度是今后优胜劣汰的主要判据。 法中的目标函数。适应度是今后优胜劣汰的主要判据。 在本例中,适应度比较简单,用 x 计算。当x值 在本例中,适应度比较简单, 计算。 13、24、 19时的适应度分别为 169、576、64、 时的适应度分别为: 为13、24、6、19时的适应度分别为:169、576、64、 361( 的第4 361(表2-1的第4列)。 表1-1中还列举当前适应度的总和 即f
(2)形成初始群体。遗传算法中,常用随机 形成初始群体。 遗传算法中, 的方法产生初始群体, 的方法产生初始群体,即随机生成一组任意排列 的字符串。群体中个体的数目通常也是固定的。 的字符串。群体中个体的数目通常也是固定的。 本例中,采用随机产生的方法, 本例中,采用随机产生的方法,假设得出拥 有 4 个 个 体 的 初 始 群 体 , 即 : 01101 、 11000 、 01100、10011。它们的x值相应为:13、24、 01100、10011。它们的x值相应为:13、24、8、 19(见表2 19(见表2-1)。
i 1 2
2
(及平均值 x ∑ ( x ) + f ( x ) + f ( x ) + f ( x ) = 1170 f = ∑ f ( x ) 4 = 293
组合优化问题的遗传算法求解策略研究

组合优化问题的遗传算法求解策略研究遗传算法是人工智能领域中一种常用的优化算法,广泛应用于解决各种计算问题。
本文将着重探讨遗传算法在组合优化问题上的求解策略,包括问题建模、适应度函数设计、群体选择、交叉和变异等方面的应用与改进。
1. 组合优化问题及其建模组合优化问题是指求解一组对象(如图、文本等)在特定条件下的最优组合方案问题。
以图的顶点覆盖问题为例,给定一个无向图$G=(V,E)$,找到一组节点$C \subseteq V$,使得图中每条边至少有一个端点属于集合$C$,且$C$的大小最小。
这是一个典型的NP完全问题,传统算法需要枚举所有可能的组合方案,时间复杂度为$O(2^n)$。
因此,我们需要一种高效的算法来解决这一问题。
将问题转化为求最小化某一目标函数的形式。
对于顶点覆盖问题,可将$C$看做染色体,$C$中每个元素(节点)看做染色体上的一个基因,基因的取值为0或1,表示该节点是否被选中。
这样,问题就转化为求解一个01串,使得染色体上取值为1的基因组成的节点集合$C$覆盖了所有边,且$C$的大小最小。
2. 适应度函数设计适应度函数是遗传算法中的核心概念,用于衡量染色体的优劣程度。
适应度函数的设计是遗传算法的关键步骤之一。
对于组合优化问题,适应度函数的设计应该体现出所求问题的特征。
例如,在顶点覆盖问题中,将染色体上取值为1的基因组成的节点集合$C$作为顶点覆盖集,适应度函数可定义为$1/|C|$,因为$C$的大小越小,则该染色体的适应度值越大。
3. 群体选择群体选择也是遗传算法的核心步骤之一,用于选取适应度值较高的染色体,并从其中产生新一代染色体。
对于组合优化问题,可选用轮盘赌算法来进行群体选择。
轮盘赌算法的基本思想是将染色体的适应度函数值作为轮盘上的扇形面积,较高适应度值的染色体所占的扇形面积更大,从而更有可能被选中。
4. 交叉和变异交叉和变异是遗传算法中的两个重要操作,用于产生新一代染色体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
