大学经济数学.ppt
合集下载
第六章 定积分 《经济数学》PPT课件

6.4.2 定积分的分部积分法
设函数u=u(x),v=v(x)在区间[a,b]上有连续导数,则有 (uv)'=u'v+uv',即uv'=(uv)'-u'v,等式两端在[a,b]上的定积分为 ,即:
➢ 这就是定积分的分部积分公式.
06 P A R T
6.5
广义积分
前面我们是在有限区间上讨论有界函数的定积分.但是,无论在理
CHAPTER
06
第6章 定 积分
PART
06
6.1
定积分的概念
6. 1. 2 定积分的定义
➢ 定义6-1 设函数f(x)在区间[a,b]上有定义,用点
a=x0<x1<x2<…<xn=b将区间[a,b]任意分成n个小区间[xi-
1,xi](i=1,2,…,n),其长度为Δxi=xi-xi-1,在每个小区间[xi-1,xi]上
一个有效数为6位数的近似值.
• 注意:对于分段函数不能求其积分的精确值,但可求近似值,即再
用“N”命令.
由定理可知,在运用换元法计算定积分时应注意以下两点:
用变量代换x=φ(t)把原来变量x代换成新变量t 时,积分限一定要换成相应于新变量t的积分限;
求出f[φ(t)]φ'(t)的一个原函数F[φ(t)]后,不需要 再把t变换成原来变量x的函数,而只需把新变量t 的上、下限分别代入F[φ(t)]中,然后求出增量即 可.
பைடு நூலகம்
的值与
被积函数f(x)和积分区间[a,b]有关,而与积分变量用什么字母表
示无关,即:
➢ (2)定义中假定a<b,如果b<a,我们规定
,特
PPT教程:经济数学(第二版)

xn dn (w1,, wn ; c)
反函数 Inverse Function
• 当n=m,如果存在g 使得
f1(x1, x2 ,, xn ) y1 f2 (x1, x2 ,, xn ) y2
x1 g1( y1,, yn ) x2 g2 ( y1,, yn )
fn (x1, x2 ,, xn ) yn xn gn ( y1,, yn )
x1 xn 1
0
海森矩阵 Hessian Matrix
2 f
x12
Hf
(x)
2 f x1xn
2 f xnx1
2 f xn 2
隐函数定理 Implicit Function
如果 • (1) 函数F (x,y)在(x0,y0)附近连续, • (2)偏导数Fx (x,y)和Fy (x,y) 存在且连续, • (3)F (x0,y0)=0, • (4) Fy (x0,y0) ≠0, 则 F (x,y)=0唯一确定一个隐函数 y=f (x) ,使得
B
C
A
凹函数另一定义
• 凹函数:集合S为凸集,x1、x2 S,有 f ( x2) f (x1)+ f '(x1) (x2 - x1)
C A
x1
x2
1
回顾:凸函数 Convex
• 凸函数:集合S为凸集,x1、x2 S,(0,1), 有 f ( x1 + (1-) x2) f (x1)+ (1-) f ( x2)
拟凸函数和拟凹函数判断法则
如果函数f (x) 二次可导,
0
f1 B f2
fn
f1 f2 fn f11 f12 f1n f21 f22 f2n
fn1 fn2 fnn
0 B1 f1
反函数 Inverse Function
• 当n=m,如果存在g 使得
f1(x1, x2 ,, xn ) y1 f2 (x1, x2 ,, xn ) y2
x1 g1( y1,, yn ) x2 g2 ( y1,, yn )
fn (x1, x2 ,, xn ) yn xn gn ( y1,, yn )
x1 xn 1
0
海森矩阵 Hessian Matrix
2 f
x12
Hf
(x)
2 f x1xn
2 f xnx1
2 f xn 2
隐函数定理 Implicit Function
如果 • (1) 函数F (x,y)在(x0,y0)附近连续, • (2)偏导数Fx (x,y)和Fy (x,y) 存在且连续, • (3)F (x0,y0)=0, • (4) Fy (x0,y0) ≠0, 则 F (x,y)=0唯一确定一个隐函数 y=f (x) ,使得
B
C
A
凹函数另一定义
• 凹函数:集合S为凸集,x1、x2 S,有 f ( x2) f (x1)+ f '(x1) (x2 - x1)
C A
x1
x2
1
回顾:凸函数 Convex
• 凸函数:集合S为凸集,x1、x2 S,(0,1), 有 f ( x1 + (1-) x2) f (x1)+ (1-) f ( x2)
拟凸函数和拟凹函数判断法则
如果函数f (x) 二次可导,
0
f1 B f2
fn
f1 f2 fn f11 f12 f1n f21 f22 f2n
fn1 fn2 fnn
0 B1 f1
大学数学与经济学讲座PPT课件

详细描述
数学模型能够将复杂的经济问题简化为易于理解和分析的数学形式,帮助研究者 深入了解经济现象的本质和内在规律。此外,数学模型还可以预测经济趋势和政 策效果,为政府和企业决策提供科学依据。
经济学中的常用数学模型
总结词
在经济学中,有许多常用的数学模型,如线性回归模型、时间序列模型、博弈论模型等。这些模型各有特点和应 用范围,能够针对不同的经济问题提供有效的分析工具。
03
经济学基础
经济学的定义与重要性
经济学定义
经济学是一门研究人类经济行为和现 象的学科,主要探讨如何利用有限的 资源来满足人类无限的需求。
经济学的重要性
经济学为人类提供了一种理解经济现 象和问题的框架,有助于我们做出更 好的决策,提高社会整体福利。
经济学的主要分支
微观经济学
研究个体经济单位(如家庭、企业)的经济 行为和资源配置。
表述方式。通过数学模型,可以更好地理解和预测经济现象,提高经济
决策的科学性。
02
经济学中的数学方法
在经济学中,数学方法的应用非常广泛,如微积分、线性代数、概率论
和统计学等。这些方法为经济学研究提供了强大的工具,帮助研究者深
入探索经济现象的本质和规律。
03
讲座收获
通过本次讲座,听众对数学在经济学中的应用有了更深入的理解,掌握
宏观经济学
研究整个经济系统的运行和政策制定,包括 国家层面的经济活动和政策。
发展经济学
研究经济发展和贫困问题的根源及解决方案。
国际经济学
研究国家之间的经济关系和互动,包括贸易、 投资和汇率。
经济学的应用
政策制定
政府通过制定经济政策来影响国家的 经济发展和民生福祉。
企业决策
数学模型能够将复杂的经济问题简化为易于理解和分析的数学形式,帮助研究者 深入了解经济现象的本质和内在规律。此外,数学模型还可以预测经济趋势和政 策效果,为政府和企业决策提供科学依据。
经济学中的常用数学模型
总结词
在经济学中,有许多常用的数学模型,如线性回归模型、时间序列模型、博弈论模型等。这些模型各有特点和应 用范围,能够针对不同的经济问题提供有效的分析工具。
03
经济学基础
经济学的定义与重要性
经济学定义
经济学是一门研究人类经济行为和现 象的学科,主要探讨如何利用有限的 资源来满足人类无限的需求。
经济学的重要性
经济学为人类提供了一种理解经济现 象和问题的框架,有助于我们做出更 好的决策,提高社会整体福利。
经济学的主要分支
微观经济学
研究个体经济单位(如家庭、企业)的经济 行为和资源配置。
表述方式。通过数学模型,可以更好地理解和预测经济现象,提高经济
决策的科学性。
02
经济学中的数学方法
在经济学中,数学方法的应用非常广泛,如微积分、线性代数、概率论
和统计学等。这些方法为经济学研究提供了强大的工具,帮助研究者深
入探索经济现象的本质和规律。
03
讲座收获
通过本次讲座,听众对数学在经济学中的应用有了更深入的理解,掌握
宏观经济学
研究整个经济系统的运行和政策制定,包括 国家层面的经济活动和政策。
发展经济学
研究经济发展和贫困问题的根源及解决方案。
国际经济学
研究国家之间的经济关系和互动,包括贸易、 投资和汇率。
经济学的应用
政策制定
政府通过制定经济政策来影响国家的 经济发展和民生福祉。
企业决策
经济数学ppt课件

向量与线性变换
总结词
向量是具有大小和方向的量,线性变换是向量空间中的一种变换。
详细描述
向量是具有大小和方向的量,它可以用来表示经济变量,如需求量、供给量等。线性变 换是向量空间中的一种变换,它可以用来描述经济变量之间的线性关系,如价格和需求
量之间的比例关系。在经济问题中,线性变换可以用来描述经济增长、消费变化等。
06 案例分析
经济增长模型的数学分析
总结词
经济增长模型是研究一个国家或地区 在一定时期内经济增长的规律和影响 因素的数学模型。
公式和定理
经济增长模型通常使用微分方程、差 分方程等数学工具来描述经济增长的 过程,并运用数学定理和公式来求解 。
详细描述
经济增长模型通过建立数学方程来描 述一个国家或地区经济增长的过程, 并分析影响经济增长的各种因素,如 劳动力、资本、技术等。
详细描述
市场供需模型通常包括供给曲线和需求曲线,通过分析这些曲线的形 状和交点来研究市场均衡和价格形成机制。
公式和定理
市场供需模型通常使用线性方程、不等式等数学工具来描述供给和需 求的关系,并运用数学定理和公式来求解市场均衡点。
应用实例
市场供需模型可以用于分析商品或服务的价格波动、预测市场趋势以 及制定价格策略等。
特征值与特征向量
总结词
特征值和特征向量是矩阵分析中的重要概念 ,它们可以用来描述线性变换的性质。
详细描述
特征值和特征向量是矩阵分析中的重要概念 ,它们可以用来描述线性变换的性质。在经 济问题中,特征值和特征向量可以用来描述 经济系统的动态性质,如经济增长的稳定性 、市场波动的幅度等。通过分析特征值和特 征向量的性质,可以对经济系统的未来发展
不定积分与定积分
第五章 不定积分 《经济数学》PPT课件

然成立.
一般有下面的定理: ➢ 定理5-1 设∫f(u)du=F(u)+C,u=φ(x),且u=φ(x)有连续导函数,
则:∫f[φ(x)]φ'(x)dx=F[φ(x)]+C (5.1) ➢ 事实上:
➢ 当我们要求某个不定积分∫g(x)dx而又不能直接用基本积分公 式时,如果被积函数g(x)可以写成f[φ(x)]φ'(x)的形式,而∫f(u)du 又比较容易求出,那么,我们就可以应用公式(5.1)求得∫g(x)dx,即:
CHAPTER
05
第5章 不定 积分
PART
05
5.1
不定积分的概念
5. 1. 1 原函数的概念
在现实生活中,往往会有这样的问题:已知一个函数的导数,而要求这个函数的 本身.例如,社会学家已知人口的增长率而希望利用这一信息来预测今后的人 口水平;物理学家已知一个物体的运动速度而希望计算它的路程函数;经济学 家则希望从已知的通货膨胀率来估计今后的物价水平等等.
➢ 由不定积分的定义可知: ∫cos xdx=sin x+C.
PART
05
5.2
基本积分公式
由导数的基本公式可以得到相应的基本积分公式如下:
PART
05
5.3
不定积分的性质
性质1 ∫kf(x)dx=k∫f(x)dx (k为不等于零的常数) 性质2 ∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx 由性质1、2可得推论: • ∫[k1f1(x)+k2f2(x)+…+knfn(x)]dx=k1∫f1(x)dx+k2∫f2(x)dx+
以化难为易.
5. 1. 2 不定积分的定义
➢ 定义5-2 若函数F(x)是函数f(x)的一个原函数,则称f(x)的原函 数全体F(x)+C(C为任意常数)为函数f(x)的不定积分,记做∫f(x)dx, 即:∫f(x)dx=F(x)+C
一般有下面的定理: ➢ 定理5-1 设∫f(u)du=F(u)+C,u=φ(x),且u=φ(x)有连续导函数,
则:∫f[φ(x)]φ'(x)dx=F[φ(x)]+C (5.1) ➢ 事实上:
➢ 当我们要求某个不定积分∫g(x)dx而又不能直接用基本积分公 式时,如果被积函数g(x)可以写成f[φ(x)]φ'(x)的形式,而∫f(u)du 又比较容易求出,那么,我们就可以应用公式(5.1)求得∫g(x)dx,即:
CHAPTER
05
第5章 不定 积分
PART
05
5.1
不定积分的概念
5. 1. 1 原函数的概念
在现实生活中,往往会有这样的问题:已知一个函数的导数,而要求这个函数的 本身.例如,社会学家已知人口的增长率而希望利用这一信息来预测今后的人 口水平;物理学家已知一个物体的运动速度而希望计算它的路程函数;经济学 家则希望从已知的通货膨胀率来估计今后的物价水平等等.
➢ 由不定积分的定义可知: ∫cos xdx=sin x+C.
PART
05
5.2
基本积分公式
由导数的基本公式可以得到相应的基本积分公式如下:
PART
05
5.3
不定积分的性质
性质1 ∫kf(x)dx=k∫f(x)dx (k为不等于零的常数) 性质2 ∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx 由性质1、2可得推论: • ∫[k1f1(x)+k2f2(x)+…+knfn(x)]dx=k1∫f1(x)dx+k2∫f2(x)dx+
以化难为易.
5. 1. 2 不定积分的定义
➢ 定义5-2 若函数F(x)是函数f(x)的一个原函数,则称f(x)的原函 数全体F(x)+C(C为任意常数)为函数f(x)的不定积分,记做∫f(x)dx, 即:∫f(x)dx=F(x)+C
《经济数学第二版》教学课件

关注数学教育的发展趋势,及时更新教学内 容和方法
THANKS
理解向量、矩阵的基本概念和性质,掌握矩阵的运算和逆矩阵的计算。
行列式与特征值
理解行列式的概念和性质,掌握行列式的计算和应用,理解特征值的概念和计算方法。
数理经济学
边际分析
理解边际分析的基本概念和方法,掌握边 际函数和边际曲线的计算和应用。
VS
最优化理论
理解最优化理论的基本概念和方法,掌握 静态最优和动态最优的计算和应用。
期末考试成绩
01
考试成绩分析
通过分析学生的考试成绩,可以了解 学生对课程的总体掌握情况和学习效 果。
02
成绩分布
通过统计成绩分布,可以看出学生在 班级中的学习水平和层次。
03
最高分、最低分与平 均分
通过比较最高分、最低分和平均分, 可以了解班级的整体学习情况和课程 的教学效果。
学生评价与反馈
问卷调查
问题式教学
问题设置合理
问题分析与讨论
问题解决与反思
设置的问题与课程内容紧密相 关,具有针对性和启发性。
通过引导学生对问题进行深入 的分析和讨论,帮助学生更好 地理解和掌握课程内容。
在问题分析和讨论的基础上, 引导学生解决问题并进行反思 ,提高学生的思维能力和解决 问题的能力。
实验教学
实验内容丰富
决实际问题。
能够在团队中扮演不同的角色, 与他人协作完成复杂任务。
善于倾听和表达,能够有效地与 团队成员沟通和分享经验。
05
教学评价与反馈
学生平时表现
出勤率
通过考察学生的出勤率,可以了解学生对课程的投入程度和态度。
课堂参与度
在课堂上积极发言、提问、参与讨论等表现可以反映学生的积极参与程度和对课程的理解程度。
THANKS
理解向量、矩阵的基本概念和性质,掌握矩阵的运算和逆矩阵的计算。
行列式与特征值
理解行列式的概念和性质,掌握行列式的计算和应用,理解特征值的概念和计算方法。
数理经济学
边际分析
理解边际分析的基本概念和方法,掌握边 际函数和边际曲线的计算和应用。
VS
最优化理论
理解最优化理论的基本概念和方法,掌握 静态最优和动态最优的计算和应用。
期末考试成绩
01
考试成绩分析
通过分析学生的考试成绩,可以了解 学生对课程的总体掌握情况和学习效 果。
02
成绩分布
通过统计成绩分布,可以看出学生在 班级中的学习水平和层次。
03
最高分、最低分与平 均分
通过比较最高分、最低分和平均分, 可以了解班级的整体学习情况和课程 的教学效果。
学生评价与反馈
问卷调查
问题式教学
问题设置合理
问题分析与讨论
问题解决与反思
设置的问题与课程内容紧密相 关,具有针对性和启发性。
通过引导学生对问题进行深入 的分析和讨论,帮助学生更好 地理解和掌握课程内容。
在问题分析和讨论的基础上, 引导学生解决问题并进行反思 ,提高学生的思维能力和解决 问题的能力。
实验教学
实验内容丰富
决实际问题。
能够在团队中扮演不同的角色, 与他人协作完成复杂任务。
善于倾听和表达,能够有效地与 团队成员沟通和分享经验。
05
教学评价与反馈
学生平时表现
出勤率
通过考察学生的出勤率,可以了解学生对课程的投入程度和态度。
课堂参与度
在课堂上积极发言、提问、参与讨论等表现可以反映学生的积极参与程度和对课程的理解程度。
经济数学课件完整版

0.2.6
fprintf语句
fprintf 为 输 出 命 令 , 其 格 式 为 :fprintf('text
format',val),
其中,text为需要输出的文本内容,val 为需要输
出的变量值,format是对变量值val的显示格式说
明.说明val的值为整数时用%d;说明val的值为以
科学记数法显示时用%e;说明val的值以浮点数
1.0 学习任务1 等额本金还款法还房贷
等额本金还款法是在还款期内把贷款总额按还款期数(贷款分几次还清就是几期)均分,每期偿
还同等数额的本金和剩余贷款在该期所产生的利息.
若贷款总额为b,银行月利率(年利率的1/12)为r,每月一期,总还款期数为n,第k期的还款额记为
f(k),请完成如下任务:
的定义域是各部分的自变量取值集合的并集.求分段函数
的函数值f(x0)时,要根据x0所在的范围选用相应的解析式,
其图形要在同一坐标系中分段作出.
1.1 函数及其性质
显示时用%f,如果该语句的输出完成后需要换行
的话用\n说明.
0.2 数学软件MATLAB的基本用法
0.2.7
平面图形
在MATLB系统中,用plot(x,y)绘制平面曲线y=f(x)的图形,
其中x是自变量的取值范围;y是对应于自变量x函数值.
自变量x的取值常用如下两种形式给出:
(1)x = a∶d∶b,表示自变量x从a开始,以d为间距,在闭区
Out[3]=1.74755
(*这里的1.74755是系统给出的运算结果*)
更一般地,用N [exp,n]得到表达式具有n位有效数字的数值结果.
0.1 数学软件Mathematica的基本用法
fprintf语句
fprintf 为 输 出 命 令 , 其 格 式 为 :fprintf('text
format',val),
其中,text为需要输出的文本内容,val 为需要输
出的变量值,format是对变量值val的显示格式说
明.说明val的值为整数时用%d;说明val的值为以
科学记数法显示时用%e;说明val的值以浮点数
1.0 学习任务1 等额本金还款法还房贷
等额本金还款法是在还款期内把贷款总额按还款期数(贷款分几次还清就是几期)均分,每期偿
还同等数额的本金和剩余贷款在该期所产生的利息.
若贷款总额为b,银行月利率(年利率的1/12)为r,每月一期,总还款期数为n,第k期的还款额记为
f(k),请完成如下任务:
的定义域是各部分的自变量取值集合的并集.求分段函数
的函数值f(x0)时,要根据x0所在的范围选用相应的解析式,
其图形要在同一坐标系中分段作出.
1.1 函数及其性质
显示时用%f,如果该语句的输出完成后需要换行
的话用\n说明.
0.2 数学软件MATLAB的基本用法
0.2.7
平面图形
在MATLB系统中,用plot(x,y)绘制平面曲线y=f(x)的图形,
其中x是自变量的取值范围;y是对应于自变量x函数值.
自变量x的取值常用如下两种形式给出:
(1)x = a∶d∶b,表示自变量x从a开始,以d为间距,在闭区
Out[3]=1.74755
(*这里的1.74755是系统给出的运算结果*)
更一般地,用N [exp,n]得到表达式具有n位有效数字的数值结果.
0.1 数学软件Mathematica的基本用法
第六章 定积分 《经济数学》PPT课件

(2)该定理初步揭示了定积分与原函数之间的 内在联系,因此,我们就有可能通过原函数来计 算定积分.
【例 6-2】求 d x et2 dt dx 0
解: d x et2 dt ex2 dx 0
【例 6-3】若 f (x) 是连续函数,求 d
b
f (t)dt .
dx x
解: d dx
b
f (t)dt
证:因为函数 f (x) 在闭区间[a,b] 上连续,
所以在[a,b] 上必有最大值 M 和最小值 m .
根据性质 6 有 m(b a)
b
f (x)dx M (b a)
a
即 m 1
b
f (x)dx M
ba a
由闭区间上连续函数的性质可知,在[a,b] 上至少存
在一点 ,使 1
b
f (x)dx f ( ) 成立.
关,而与积分变量用什么字母表示无关.
b
b
即 a
f (x)dx a
f (u)du
(2)定义中假定 a b,如果 b a ,我们规定
b f (x)dx a f (x)dx .
a
b
特别地,当 a b 时,规定 b f (x)dx 0 . a
(3)若函数 f (x) 在[a,b] 上连续,或 f (x)
0
0
由复合函数的求导法则,得
d x2
d(u) du
dx 0 sin tdt
du
dx
sin u 2x
2xsin x
(二)牛顿——莱布尼兹公式
定理(微积分基本定理) 设 f (x) 在闭区间[a,b] 上连续, F(x) 是 f (x) 的一个原函数,则有
b
f (x)dx F (b) F (a) . a
【例 6-2】求 d x et2 dt dx 0
解: d x et2 dt ex2 dx 0
【例 6-3】若 f (x) 是连续函数,求 d
b
f (t)dt .
dx x
解: d dx
b
f (t)dt
证:因为函数 f (x) 在闭区间[a,b] 上连续,
所以在[a,b] 上必有最大值 M 和最小值 m .
根据性质 6 有 m(b a)
b
f (x)dx M (b a)
a
即 m 1
b
f (x)dx M
ba a
由闭区间上连续函数的性质可知,在[a,b] 上至少存
在一点 ,使 1
b
f (x)dx f ( ) 成立.
关,而与积分变量用什么字母表示无关.
b
b
即 a
f (x)dx a
f (u)du
(2)定义中假定 a b,如果 b a ,我们规定
b f (x)dx a f (x)dx .
a
b
特别地,当 a b 时,规定 b f (x)dx 0 . a
(3)若函数 f (x) 在[a,b] 上连续,或 f (x)
0
0
由复合函数的求导法则,得
d x2
d(u) du
dx 0 sin tdt
du
dx
sin u 2x
2xsin x
(二)牛顿——莱布尼兹公式
定理(微积分基本定理) 设 f (x) 在闭区间[a,b] 上连续, F(x) 是 f (x) 的一个原函数,则有
b
f (x)dx F (b) F (a) . a
第二章 极限与连续 《经济数学》PPT课件

由函数连续的定义可知,如果函数f(x)在点x0处满足下列条件之一: • (1)函数f(x)在点x0处无定义; • (2)lim(x→x0) f(x)不存在; • (3)lim(x→x0 ) f(x)存在,但不等于f(x0). 则点x0就是函数f(x)的间断点. 如图2-13所示的是几种在点x=x0处不连续的函数.
值无限趋近于一个确定的常数A,则称常数A为函数在自变量x趋向于无穷大时的
极限.记做:
Lim(x→∞)f(x)=A 或 f(x)→A (x→∞)
• 当自变量x大于0而绝对值无限增大时,如果函数y=f(x)的对应值无限趋近于一个
确定的常数A,则称常数A为函数在自变量x趋向于正无穷大时的极限.记做:
lim (x→+∞)f(x)=A 或 f(x)→A (x→+∞)
形的面积时,实际上采用的就是求极限的办法.而我国魏晋时期的大数学家刘徽(公元3世纪)就曾 用圆的内接正多边形来逼近圆的方法,计算的圆周率精确到小数点后4位的数值:3.1416. • 设有一圆,首先作内接正六边形,把它的面积记为A1;再作内接正十二边形,其面积记为A2;再作内 接正二十四边形,其面积记为A3;循此下去,每次边数加倍,一般地,把内接正6×2n-1边形的面积记 为An(n∈N).这样,就得到一系列内接正多边形的面积: • A1,A2,A3,…,An,…
2.1.2 无穷小与无穷大
3)无穷小的阶 ➢ 有限个无穷小的代数和与积仍是无穷小,但是两个无穷小的商则
会出现不同的情况.例如,当x→0时,2x,x2,sin x都是无穷小,但它 们两两之比的极限会出现各种不同情况,这反映了不同的无穷小 趋向于零的快慢程度.由于两个无穷小之商一般不能立刻判断其 极限是否存在,所以我们通常称这种极限为未定式极限.
值无限趋近于一个确定的常数A,则称常数A为函数在自变量x趋向于无穷大时的
极限.记做:
Lim(x→∞)f(x)=A 或 f(x)→A (x→∞)
• 当自变量x大于0而绝对值无限增大时,如果函数y=f(x)的对应值无限趋近于一个
确定的常数A,则称常数A为函数在自变量x趋向于正无穷大时的极限.记做:
lim (x→+∞)f(x)=A 或 f(x)→A (x→+∞)
形的面积时,实际上采用的就是求极限的办法.而我国魏晋时期的大数学家刘徽(公元3世纪)就曾 用圆的内接正多边形来逼近圆的方法,计算的圆周率精确到小数点后4位的数值:3.1416. • 设有一圆,首先作内接正六边形,把它的面积记为A1;再作内接正十二边形,其面积记为A2;再作内 接正二十四边形,其面积记为A3;循此下去,每次边数加倍,一般地,把内接正6×2n-1边形的面积记 为An(n∈N).这样,就得到一系列内接正多边形的面积: • A1,A2,A3,…,An,…
2.1.2 无穷小与无穷大
3)无穷小的阶 ➢ 有限个无穷小的代数和与积仍是无穷小,但是两个无穷小的商则
会出现不同的情况.例如,当x→0时,2x,x2,sin x都是无穷小,但它 们两两之比的极限会出现各种不同情况,这反映了不同的无穷小 趋向于零的快慢程度.由于两个无穷小之商一般不能立刻判断其 极限是否存在,所以我们通常称这种极限为未定式极限.
第一章 函数 《经济数学》PPT课件

【例1-1】某班级的全体学生组成一个集合.该班的学生都是这个集合 的元素.
【例1-2】自然数的全体组成一个集合.每一个自然数都是这个集合的 元素.
【例1-3】直线x+3y+3=0上所有的点组成一个集合.这里直线的每个 点是这个集合的元素.
➢ 习惯上,我们用英文大写字母 A 、B、C、X、Y等表示集合,用英文小 写字母a、b、c、x、y等表示集合的元素.如果a是集合A的元素,则记 作a∈A,读作a属于A.如果a不是集合A的元素,则记作a∉A,读作a不属 于A.
1. 2. 1 函数的概念
➢ 问题3:图1-5反映了上海证券交易所的上证指数从201×年10 月1日到201×年12月31日的60个交易日的变化情形,由此图可 以看出在这段时间中上证指数随时间的变化.
➢ 从图1-5中我们可以看到,有日期t和指数I两个变量,当变量t在某 一范围内变化时(201×年第四季度有60个交易日),指数I随着日 期t的变化而变化,并且当t取某一日期时,有唯一上证指数I与之相 对应.
➢ 补集有以下性质:A∪A ̅=I;(2)A∩A ̅=Φ . 【例1-14】设全体学生为全集I,如果男生为集合A,则A ̅表示为
女生集合.
1. 1. 5 集合的运算律
1)交换律
运 算 律
3)分配律
2)结合律
4)对偶律(德•摩根公式)
1. 1. 6
实数集
人们对数的认识从自然数发展到有理数(包括正负整数,正负分 数及零),再由有理数发展到无理数(例如e,π,√3等),如果令p,q为 整数,且q≠0,则一般有理数可用p/q表示,无理数不能用p/q表示.
1},A∩B={x|0<x≤3}. 【例1-13】 设A为全体有理数集合,B为全体无理数集合,则:A∪B为全
【例1-2】自然数的全体组成一个集合.每一个自然数都是这个集合的 元素.
【例1-3】直线x+3y+3=0上所有的点组成一个集合.这里直线的每个 点是这个集合的元素.
➢ 习惯上,我们用英文大写字母 A 、B、C、X、Y等表示集合,用英文小 写字母a、b、c、x、y等表示集合的元素.如果a是集合A的元素,则记 作a∈A,读作a属于A.如果a不是集合A的元素,则记作a∉A,读作a不属 于A.
1. 2. 1 函数的概念
➢ 问题3:图1-5反映了上海证券交易所的上证指数从201×年10 月1日到201×年12月31日的60个交易日的变化情形,由此图可 以看出在这段时间中上证指数随时间的变化.
➢ 从图1-5中我们可以看到,有日期t和指数I两个变量,当变量t在某 一范围内变化时(201×年第四季度有60个交易日),指数I随着日 期t的变化而变化,并且当t取某一日期时,有唯一上证指数I与之相 对应.
➢ 补集有以下性质:A∪A ̅=I;(2)A∩A ̅=Φ . 【例1-14】设全体学生为全集I,如果男生为集合A,则A ̅表示为
女生集合.
1. 1. 5 集合的运算律
1)交换律
运 算 律
3)分配律
2)结合律
4)对偶律(德•摩根公式)
1. 1. 6
实数集
人们对数的认识从自然数发展到有理数(包括正负整数,正负分 数及零),再由有理数发展到无理数(例如e,π,√3等),如果令p,q为 整数,且q≠0,则一般有理数可用p/q表示,无理数不能用p/q表示.
1},A∩B={x|0<x≤3}. 【例1-13】 设A为全体有理数集合,B为全体无理数集合,则:A∪B为全
大学经济数学PPT课件

第14页/共51页
y 反函数y ( x)
Q(b, a)
直接函数y f ( x)
o
P(a, b)
x
直接函数与反函数的图形关于直线 y x对称.
第15页/共51页
(2)复合函数
例:设 y u, u 1 x2 ,
y 1 x2
定义 2: 设函数 y f (u)的定义域 D f , 而函数 u ( x)的值域为 Z , 若 Df Z , 则称 函数 y f [( x)]为 x的复合函数.
x 自变量, u 中间变量, y 因变量,
第16页/共51页
注意: 1.不是任何两个函数都可以复合成一个复 合函数的;
例如:y u ,u x2 1
2.复合函数可以由两个以上的函数经过复 合构成.
例如: y = cot x , 2
y=
u,
u
=
cot
v, v
=
x. 2
第17页/共51页
4. 初等函数
x 1
x1
ƒ(x)在 x0 处的右极限. 记为
lim
x x0
f (x)
A或
f ( x0+0)
A.
第39页/共51页
左极限和右极限统称为单侧极限.它们之间有如下关系:
定理2. 函数y = ƒ(x)当 x→x0 时极限存在且为A的充要条 件是函数y = ƒ(x)的左极限和右极限都存在且等于A。即
lim f ( x) A lim f ( x) lim f ( x) A
第17初等函数第18指数函数第19对数函数第20三角函数正弦函数第21sin余弦函数第22cos正切函数第23余切函数第24正割函数第25余割函数第26反三角函数第27arcsinarcsin反正弦函数第28arccosarccos反余弦函数第29arctanarctan反正切函数幂函数指数函数对数函数三角函数和反三角函数统称为基本初等函数
y 反函数y ( x)
Q(b, a)
直接函数y f ( x)
o
P(a, b)
x
直接函数与反函数的图形关于直线 y x对称.
第15页/共51页
(2)复合函数
例:设 y u, u 1 x2 ,
y 1 x2
定义 2: 设函数 y f (u)的定义域 D f , 而函数 u ( x)的值域为 Z , 若 Df Z , 则称 函数 y f [( x)]为 x的复合函数.
x 自变量, u 中间变量, y 因变量,
第16页/共51页
注意: 1.不是任何两个函数都可以复合成一个复 合函数的;
例如:y u ,u x2 1
2.复合函数可以由两个以上的函数经过复 合构成.
例如: y = cot x , 2
y=
u,
u
=
cot
v, v
=
x. 2
第17页/共51页
4. 初等函数
x 1
x1
ƒ(x)在 x0 处的右极限. 记为
lim
x x0
f (x)
A或
f ( x0+0)
A.
第39页/共51页
左极限和右极限统称为单侧极限.它们之间有如下关系:
定理2. 函数y = ƒ(x)当 x→x0 时极限存在且为A的充要条 件是函数y = ƒ(x)的左极限和右极限都存在且等于A。即
lim f ( x) A lim f ( x) lim f ( x) A
第17初等函数第18指数函数第19对数函数第20三角函数正弦函数第21sin余弦函数第22cos正切函数第23余切函数第24正割函数第25余割函数第26反三角函数第27arcsinarcsin反正弦函数第28arccosarccos反余弦函数第29arctanarctan反正切函数幂函数指数函数对数函数三角函数和反三角函数统称为基本初等函数
经济数学第四章ppt课件
第一 lim ln(cot x) . x0 ln x
解
lim
ln(cot
x)
lim
1 cot
x
( csc2
x)
lim
x
( lim x )( lim 1 ) 1
x0 ln x
x0
1
x0 sin x cos x
x0 sin x x0 cos x
x
关于 x→∞时的未定式 型,上述洛比达法则同样适合.
f (x x) f (x) f / (x x)x. 这里 是介于 0 与 1 之间的一个数,也就是说,函数 f(x)在 x 处的改变量 y f / (x x)x , 0< <1.(微分中值定理.)
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
页码:11
例 3 求 lim sin mx . x0 sin nx
解 lim sin mx lim m cos mx m . x0 sin nx x0 n cos nx n
上述关于
x
x0
时未定式
0 0
型的洛比达法则,对于
x→∞时未定式
0 0
型同样适合.
关于
x
x0
时未定式
型的情形,有如下定理.
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
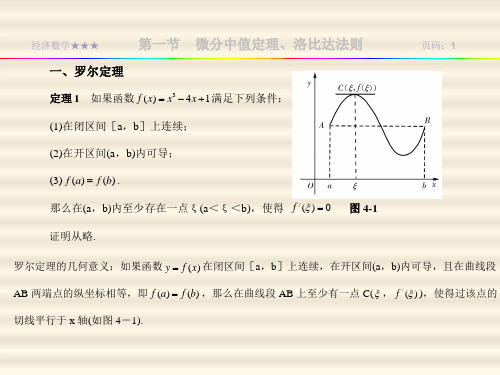
(3) f (a) f (b) .
那么在(a,b)内至少存在一点ξ(a<ξ<b),使得 f / ( ) 0 图 4-1
证明从略.
页码:1
罗尔定理的几何意义:如果函数 y f (x) 在闭区间[a,b]上连续,在开区间(a,b)内可导,且在曲线段 AB 两端点的纵坐标相等,即 f (a) f (b) ,那么在曲线段 AB 上至少有一点 C( , f / ( ) ),使得过该点的 切线平行于 x 轴(如图 4-1).
第四章 导数的应用 《经济数学》PPT课件

4.3.1
函数的极值
1) 极值的定义 ➢ 如图所示,函数f(x)有两个极大值f(x2),f(x4),三个极小值
f(x1),f(x3),f(x5),但这并不意味着f(x2)或f(x1)是函数f(x)在定义 域中的最大值或最小值,而只是对xi附近局部范围来说的,如图42所示的函数f(x),其极小值f(x5)甚至比极大值f(x2)大.
的灵敏程度,这就是经济量的弹性.一般来说,商品的需求量对市 场价格的反应是很灵敏的,反映当商品价格变动时需求量变动的 强弱程度的量就是需求弹性. • 设需求函数Q=f(P),这里P表示产品的价格,记该商品在点P0处的 需求弹性或需求弹性系数为: 记需求弹性函数为: • 在经济上表示,当产品的价格为P时,价格变动1%,需求量将变化 η%.
PART
04
4.5
导数在经济中的应用
4.5.1 导数的概念在经济中的应用
1) 边际分析 ➢ 在第1章中,我们介绍了几个经济中常用的函数: • 成本函数C(Q):给出生产Q单位产品的总成本. • 收益函数R(Q):给出销售Q单位产品的总收益. • 利润函数L(Q)=R(Q)-C(Q):给出生产Q单位产品并全部销售出去后的总利润. ➢ 这三个函数中的自变量Q只能取非负整数,但对现代企业而言,产品的生产、
一般地,函数在给定的区间上的最大值与最小值可能在区间内部 的点处取得,也可能在区间的端点处取得.如果函数的最大值与最 小值是在区间内部的点处取得,那么这个最大值(或最小值)一定 也是极大值(或极小值).因此,对于在给定区间上的函数,可直接求 出极值可疑点(驻点和导数不存在的点)及区间端点处的函数值, 比较这些数值的大小,即可求出函数的最大值与最小值.
4.3.2 函数的最大(小)值
在第2章中我们曾经指出,闭区间上的连续函数一定存在最大值 和最小值.与极值概念不同的是,极值是一个局部性的概念,而最 大值(或最小值)是全局性的概念.最大值(或最小值)是函数在所 考察的区间内全部函数值中的最大者(或最小者),而极值只是函 数在极值点的某个邻域内的最大值或最小值.
第三章 导数与微分 《经济数学》PPT课件

CHAPTER
03
第3章 导数与 微分
PART
03
3.1
导数
导数是数学中的一个分支——微积分的两个基本概念之一,它
表示一个函数的因变量相对于自变量的变化的快慢程度,即因变 量关于自变量的变化率.事物总是在不断地运动和变化的,而描述 这种运动和变化离不开变化率,导数就是对现实生活中各种各样 的变化率的一种统一的数学抽象.导数是微积分以及实际生活中 应用极其广泛的概念,其应用范围包括函数性态的描述、曲线的 描绘、最优化问题的讨论以及变化率的分析等.
,
即函数在点x=0处的右导数不存在,所以函数f(x)在点x=0处的导
数不存在.
3. 1. 5
高阶导数
在本小节中,我们将讨论一个量的变化率的变化率.这样的变化率 有很多种,例如,汽车的加速度是它的速度关于时间的变化率,而 速度本身又是路程关于时间的变化率.如果路程的单位是千米,时 间的单位是小时,那么速度(路程关于时间的变化率)的单位是千 米/小时,而加速度(速度的变化率)的单位则是千米/小时2.
上述有关变化率的变化率的问题,在经济上是常用的.例如,在通 货膨胀时期,你可以听到经济部门的报告指出,“尽管通货膨胀率 在增长,但其增长速度在减缓”,就是指物价在上涨,但已经不比 以前那样增长得快了.
3. 1. 5
高阶导数
1) 高阶导数的概念 ➢ 设函数y=f(x)关于x的变化率由其导函数f '(x)给出.类似地,函数f
3.2 1 微分的定义
关于微分定义的几点说明: ➢ (1)函数的微分dy是Δx的一次函数,它不仅与Δx有关,而且与x也
有关.函数的微分dy与Δy只差一个比Δx高阶的无穷小,它是Δy的 主要部分,所以也称微分dy是函数改变量Δy的线性主部. ➢ (2)若函数y=f(x)在x处的改变量Δy可以表示成Δx的线性函数 k(x)Δx与一个比Δx高阶的无穷小之和Δy=k(x)Δx+o(Δx),则称 函数y=f(x)在点x处可微. ➢ (3)由于自变量x的微分dx=(x)'Δx=Δx,故dx可理解为自变量x的 改变量Δx.于是dy=f '(x)Δx=f '(x)dx,即函数的微分等于函数的 导数乘上自变量的微分.
03
第3章 导数与 微分
PART
03
3.1
导数
导数是数学中的一个分支——微积分的两个基本概念之一,它
表示一个函数的因变量相对于自变量的变化的快慢程度,即因变 量关于自变量的变化率.事物总是在不断地运动和变化的,而描述 这种运动和变化离不开变化率,导数就是对现实生活中各种各样 的变化率的一种统一的数学抽象.导数是微积分以及实际生活中 应用极其广泛的概念,其应用范围包括函数性态的描述、曲线的 描绘、最优化问题的讨论以及变化率的分析等.
,
即函数在点x=0处的右导数不存在,所以函数f(x)在点x=0处的导
数不存在.
3. 1. 5
高阶导数
在本小节中,我们将讨论一个量的变化率的变化率.这样的变化率 有很多种,例如,汽车的加速度是它的速度关于时间的变化率,而 速度本身又是路程关于时间的变化率.如果路程的单位是千米,时 间的单位是小时,那么速度(路程关于时间的变化率)的单位是千 米/小时,而加速度(速度的变化率)的单位则是千米/小时2.
上述有关变化率的变化率的问题,在经济上是常用的.例如,在通 货膨胀时期,你可以听到经济部门的报告指出,“尽管通货膨胀率 在增长,但其增长速度在减缓”,就是指物价在上涨,但已经不比 以前那样增长得快了.
3. 1. 5
高阶导数
1) 高阶导数的概念 ➢ 设函数y=f(x)关于x的变化率由其导函数f '(x)给出.类似地,函数f
3.2 1 微分的定义
关于微分定义的几点说明: ➢ (1)函数的微分dy是Δx的一次函数,它不仅与Δx有关,而且与x也
有关.函数的微分dy与Δy只差一个比Δx高阶的无穷小,它是Δy的 主要部分,所以也称微分dy是函数改变量Δy的线性主部. ➢ (2)若函数y=f(x)在x处的改变量Δy可以表示成Δx的线性函数 k(x)Δx与一个比Δx高阶的无穷小之和Δy=k(x)Δx+o(Δx),则称 函数y=f(x)在点x处可微. ➢ (3)由于自变量x的微分dx=(x)'Δx=Δx,故dx可理解为自变量x的 改变量Δx.于是dy=f '(x)Δx=f '(x)dx,即函数的微分等于函数的 导数乘上自变量的微分.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经济数学
第一章 函数的极限与连续
函数的极限与连续
函数的极限 XXXXX
极限的运算 函数的连续性
函数的概念 函数的极限 无穷小与无穷大 极限的运算法则 两个重要极限
广州大学纺织服装学院
数学建模案例
数学模型的概念 数学建模过程
经济数学
1.1 函数的极限
一、 函数的概念 二、 函数的极限 三、 无穷小与无穷大
lim
x x0
f (x)
A或
f ( x0+0)
A.
广州大学纺织服装学院
经济数学
左极限和右极限统称为单侧极限.它们之间有如下关系:
定理2. 函数y = ƒ(x)当 x→x0 时极限存在且为A的充要条 件是函数y = ƒ(x)的左极限和右极限都存在且等于A。即
lim f ( x) A lim f ( x) lim f ( x) A
变量 x 在U (xˆ0 ,d)内无限接近于 x0时,相应的函数值无限接近于 确定的常数 A,那么常数 A 就叫函数 f (x)当 x ® x0 时的极限,记
作 lim f (x) A 或 f (x) x® x0
A( x
x0 )
例如 lim x 1 , limarctan x 0 .
x1
x0
广州大学纺织服装学院
说明函数在 x0点的极限是否存在与函数在 x0 处有无定义无 关.这是因为函数在 x0点的极限是函数在 x0 附近的变化趋势, 而不是在 x0处函数值。
广州大学纺织服装学院
经济数学
3. 函数ƒ(x)的左、右极限 如 y x ( x 0) 则只能考察 x 从 0 的右侧趋于
0 时的极限. 因而必须引进左、右极限的概念.
-x f (x)
y
y f (x)
f (x)
o
xx
奇函数
广州大学纺织服装学院
经济数学
(4)函数的周期性:
对于函数f(x) ,若存在一个不为零的数l,使得 关系式 f (x l) f (x) 对于定义域内任何x值都成立, 则 f(x)叫做周期函数,l 称为是f(x)的周期。
(通常说周期函数的周期是指其最小正周期).
广州大学纺织服装学院
1、函数的概念
经济数学
定义 1 设数集 D R,则称映射 f : D R为定义
在 D上的函数.
即对于每个数 x D, 变量 y按照一定法则总有
确定的数值和它对应,则称 y是 x的函数,记作
y f (x)
因变量
自变量
当x0 D时, 称f ( x0 )为函数在点x0处的函数值. 数集D叫做这个函数的定义域
空心领域:U (xˆ0, )
1. x→∞ 时函数ƒ(x)的极限 (1) 设函数ƒ(x),当x>0且无限增大时,函数ƒ(x)趋
于一个确定的常数A,则称函数ƒ(x)当 x→∞ 时以A为
极限.记
lim f (x) A 或 f (x) A(x ).
x
如: lim 1 0, lim ex 0, lim arctan x .
3l
l
2
2
l 2
3l 2
广州大学纺织服装学院
经济数学
3、反函数与复合函数
(1) 反函数 设函数的定义域为D,值域为W. 若对∀y∈W,D上 都有唯一确定一个数值 x 与 之对应,且ƒ(x)=y. 若把 y 看作自变量, x 看作因变量,则称函数 x=f-1(y)为函数 y =ƒ(x) 的反函数.而原函数 y =ƒ(x)为直 接函数; x , y 互换便有y=φ(x) (y=f-1(x)), 从而函数与 反函数定义域、值域及图象间有一定的关系.
o
x1 x2
x
I
广州大学纺织服装学院
经济数学 (3)函数的奇偶性:
设D关于原点对称, 对于x D, 有 f ( x) f ( x) 称 f ( x)为偶函数;
y y f (x)
f (x)
f (x)
-x o x
x
偶函数
广州大学纺织服装学院
经济数学
设D关于原点对称, 对于x D, 有 f ( x) f ( x) 称 f ( x)为奇函数;
(1) 左极限
当x 从 x0 左侧(小于)趋于x0 时 , ƒ(x)以A为极限. 则
A是ƒ(x)在 x0处的左极限. 记为
lim
x x0
f (x)
A
或 f ( x0-0) A.
(2)右极限
当x从 x0 右侧(大于)趋于x0 时 , ƒ(x)以A为极限. 则A是
ƒ(x)在 x0 处的右极限. 记为
1 x2
D :[1,1] D : (1,1)
广州大学纺织服装学院
经济数学
几个特殊的函数举例
(1)符号函数
y
1 当x 0
y
sgn x
0
当x 0
1 当x 0
1
o
x
-1
x sgn x x
广州大学纺织服装学院
经济数学
(3)取整函数 y=[x]
y
[x]表示不超过 x的最
4
大整数
3
2
-4 -3 -2 -1 1o-11 2 3 4 5 x
x x0
x x0
x x0
此定理给出了怎样利用单侧极限判断函数极限 存在的方法; 特别对分段函数适用.
广州大学纺织服装学院
例5
设ƒ(x)=|x|
,求
lim
x0
f
( x).
解
因
x
x
x
, x0 , x0
则
f (0 ) lim f ( x) lim x 0,
x0
x0
f (0 ) lim f ( x) lim ( x) 0.
广州大学纺织服装学院
y 反函数y ( x)
经济数学
Q(b, a)
直接函数y f ( x)
o
P(a, b)
x
直接函数与反函数的图形关于直线 y x对称.
广州大学纺织服装学院
经济数学
(2)复合函数
例:设 y u, u 1 x2 ,
y 1 x2
定义 2: 设函数 y f (u)的定义域 D f , 而函数 u ( x)的值域为 Z , 若 Df Z , 则称 函数 y f [( x)]为 x的复合函数.
广州大学纺织服装学院
反余弦函数 y arccos x
经济数学
y arccos x
广州大学纺织服装学院
反正切函数 y arctan x
经济数学
y arctan x
广州大学纺织服装学院
反余切函数 y arccot x
经济数学
y arccot x
幂函数,指数函数,对数函数,三角函数和反三 角函数统称为基本初等函数.
经济数学
4. 初等函数
(1) 幂函数 y x (是常数)
y
y x2
1
y x y x
(1,1)
y 1 x
o1
x
广州大学纺织服装学院
经济数学
(2) 指数函数 y a x (a 0, a 1) y ex
y (1)x a
• (0,1)
y ax (a 1)
广州大学纺织服装学院
经济数学
(3) 对数函数 y log a x (a 0, a 1) y = lnx
y M
y=f(x)
o
x
有界 X
y M
x0
o
X
x 无界
-M
-M
广州大学纺织服装学院
经济数学
(2)函数的单调性:
设函数 f ( x)的定义域为D, 区间I D, 如果对于区间 I 上任意两点 x1及 x2 , 当 x1 x2时, 恒有 (1) f ( x1 ) f ( x2 ),
则称函数 f ( x)在区间I上是单调增加的 ;
y
y f (x) f (x2 )
f (x1)
o
广州大学纺织服装学院
x1
x2
x
I
经济数学
如果对于区间 I 上任意两点 x1及 x2 , 当 x1 x2时, 恒有 (2) f ( x1 ) f ( x2 ), 则称函数 f ( x)在区间 I上是单调减少的;
y
y f (x)
Байду номын сангаас
f (x1)
f (x2 )
y f ( x) ( x 0)的解析表达式.
广州大学纺织服装学院
经济数学
思考题1解答
设 1u x
则 f u 1
u
1 1 u2
1
1 u2 , u
故 f ( x) 1 1 x2 . ( x 0) x
广州大学纺织服装学院
经济数学
二、函数的极限
领域:设δ是某个正数,称开区间(x0- δ, x0+ δ)为 以为x0中心,以δ为半径的邻域,简称点x0的邻域, 记为U(x0, δ)
余切函数 y cot x
经济数学
y cot x
广州大学纺织服装学院
正割函数 y sec x
经济数学
y sec x
广州大学纺织服装学院
余割函数 y csc x
经济数学
y csc x
广州大学纺织服装学院
(5) 反三角函数 反正弦函数 y arcsin x
经济数学
y arcsin x
经济数学
例4 (1) lim C C (C为常数); x x0
(2)
lim (ax
x x0
b)
ax0
b;
特别地:lim x x0
x
x0 ,
当n为正整数时, lim x x0
xn
x0n ,
当x0
第一章 函数的极限与连续
函数的极限与连续
函数的极限 XXXXX
极限的运算 函数的连续性
函数的概念 函数的极限 无穷小与无穷大 极限的运算法则 两个重要极限
广州大学纺织服装学院
数学建模案例
数学模型的概念 数学建模过程
经济数学
1.1 函数的极限
一、 函数的概念 二、 函数的极限 三、 无穷小与无穷大
lim
x x0
f (x)
A或
f ( x0+0)
A.
广州大学纺织服装学院
经济数学
左极限和右极限统称为单侧极限.它们之间有如下关系:
定理2. 函数y = ƒ(x)当 x→x0 时极限存在且为A的充要条 件是函数y = ƒ(x)的左极限和右极限都存在且等于A。即
lim f ( x) A lim f ( x) lim f ( x) A
变量 x 在U (xˆ0 ,d)内无限接近于 x0时,相应的函数值无限接近于 确定的常数 A,那么常数 A 就叫函数 f (x)当 x ® x0 时的极限,记
作 lim f (x) A 或 f (x) x® x0
A( x
x0 )
例如 lim x 1 , limarctan x 0 .
x1
x0
广州大学纺织服装学院
说明函数在 x0点的极限是否存在与函数在 x0 处有无定义无 关.这是因为函数在 x0点的极限是函数在 x0 附近的变化趋势, 而不是在 x0处函数值。
广州大学纺织服装学院
经济数学
3. 函数ƒ(x)的左、右极限 如 y x ( x 0) 则只能考察 x 从 0 的右侧趋于
0 时的极限. 因而必须引进左、右极限的概念.
-x f (x)
y
y f (x)
f (x)
o
xx
奇函数
广州大学纺织服装学院
经济数学
(4)函数的周期性:
对于函数f(x) ,若存在一个不为零的数l,使得 关系式 f (x l) f (x) 对于定义域内任何x值都成立, 则 f(x)叫做周期函数,l 称为是f(x)的周期。
(通常说周期函数的周期是指其最小正周期).
广州大学纺织服装学院
1、函数的概念
经济数学
定义 1 设数集 D R,则称映射 f : D R为定义
在 D上的函数.
即对于每个数 x D, 变量 y按照一定法则总有
确定的数值和它对应,则称 y是 x的函数,记作
y f (x)
因变量
自变量
当x0 D时, 称f ( x0 )为函数在点x0处的函数值. 数集D叫做这个函数的定义域
空心领域:U (xˆ0, )
1. x→∞ 时函数ƒ(x)的极限 (1) 设函数ƒ(x),当x>0且无限增大时,函数ƒ(x)趋
于一个确定的常数A,则称函数ƒ(x)当 x→∞ 时以A为
极限.记
lim f (x) A 或 f (x) A(x ).
x
如: lim 1 0, lim ex 0, lim arctan x .
3l
l
2
2
l 2
3l 2
广州大学纺织服装学院
经济数学
3、反函数与复合函数
(1) 反函数 设函数的定义域为D,值域为W. 若对∀y∈W,D上 都有唯一确定一个数值 x 与 之对应,且ƒ(x)=y. 若把 y 看作自变量, x 看作因变量,则称函数 x=f-1(y)为函数 y =ƒ(x) 的反函数.而原函数 y =ƒ(x)为直 接函数; x , y 互换便有y=φ(x) (y=f-1(x)), 从而函数与 反函数定义域、值域及图象间有一定的关系.
o
x1 x2
x
I
广州大学纺织服装学院
经济数学 (3)函数的奇偶性:
设D关于原点对称, 对于x D, 有 f ( x) f ( x) 称 f ( x)为偶函数;
y y f (x)
f (x)
f (x)
-x o x
x
偶函数
广州大学纺织服装学院
经济数学
设D关于原点对称, 对于x D, 有 f ( x) f ( x) 称 f ( x)为奇函数;
(1) 左极限
当x 从 x0 左侧(小于)趋于x0 时 , ƒ(x)以A为极限. 则
A是ƒ(x)在 x0处的左极限. 记为
lim
x x0
f (x)
A
或 f ( x0-0) A.
(2)右极限
当x从 x0 右侧(大于)趋于x0 时 , ƒ(x)以A为极限. 则A是
ƒ(x)在 x0 处的右极限. 记为
1 x2
D :[1,1] D : (1,1)
广州大学纺织服装学院
经济数学
几个特殊的函数举例
(1)符号函数
y
1 当x 0
y
sgn x
0
当x 0
1 当x 0
1
o
x
-1
x sgn x x
广州大学纺织服装学院
经济数学
(3)取整函数 y=[x]
y
[x]表示不超过 x的最
4
大整数
3
2
-4 -3 -2 -1 1o-11 2 3 4 5 x
x x0
x x0
x x0
此定理给出了怎样利用单侧极限判断函数极限 存在的方法; 特别对分段函数适用.
广州大学纺织服装学院
例5
设ƒ(x)=|x|
,求
lim
x0
f
( x).
解
因
x
x
x
, x0 , x0
则
f (0 ) lim f ( x) lim x 0,
x0
x0
f (0 ) lim f ( x) lim ( x) 0.
广州大学纺织服装学院
y 反函数y ( x)
经济数学
Q(b, a)
直接函数y f ( x)
o
P(a, b)
x
直接函数与反函数的图形关于直线 y x对称.
广州大学纺织服装学院
经济数学
(2)复合函数
例:设 y u, u 1 x2 ,
y 1 x2
定义 2: 设函数 y f (u)的定义域 D f , 而函数 u ( x)的值域为 Z , 若 Df Z , 则称 函数 y f [( x)]为 x的复合函数.
广州大学纺织服装学院
反余弦函数 y arccos x
经济数学
y arccos x
广州大学纺织服装学院
反正切函数 y arctan x
经济数学
y arctan x
广州大学纺织服装学院
反余切函数 y arccot x
经济数学
y arccot x
幂函数,指数函数,对数函数,三角函数和反三 角函数统称为基本初等函数.
经济数学
4. 初等函数
(1) 幂函数 y x (是常数)
y
y x2
1
y x y x
(1,1)
y 1 x
o1
x
广州大学纺织服装学院
经济数学
(2) 指数函数 y a x (a 0, a 1) y ex
y (1)x a
• (0,1)
y ax (a 1)
广州大学纺织服装学院
经济数学
(3) 对数函数 y log a x (a 0, a 1) y = lnx
y M
y=f(x)
o
x
有界 X
y M
x0
o
X
x 无界
-M
-M
广州大学纺织服装学院
经济数学
(2)函数的单调性:
设函数 f ( x)的定义域为D, 区间I D, 如果对于区间 I 上任意两点 x1及 x2 , 当 x1 x2时, 恒有 (1) f ( x1 ) f ( x2 ),
则称函数 f ( x)在区间I上是单调增加的 ;
y
y f (x) f (x2 )
f (x1)
o
广州大学纺织服装学院
x1
x2
x
I
经济数学
如果对于区间 I 上任意两点 x1及 x2 , 当 x1 x2时, 恒有 (2) f ( x1 ) f ( x2 ), 则称函数 f ( x)在区间 I上是单调减少的;
y
y f (x)
Байду номын сангаас
f (x1)
f (x2 )
y f ( x) ( x 0)的解析表达式.
广州大学纺织服装学院
经济数学
思考题1解答
设 1u x
则 f u 1
u
1 1 u2
1
1 u2 , u
故 f ( x) 1 1 x2 . ( x 0) x
广州大学纺织服装学院
经济数学
二、函数的极限
领域:设δ是某个正数,称开区间(x0- δ, x0+ δ)为 以为x0中心,以δ为半径的邻域,简称点x0的邻域, 记为U(x0, δ)
余切函数 y cot x
经济数学
y cot x
广州大学纺织服装学院
正割函数 y sec x
经济数学
y sec x
广州大学纺织服装学院
余割函数 y csc x
经济数学
y csc x
广州大学纺织服装学院
(5) 反三角函数 反正弦函数 y arcsin x
经济数学
y arcsin x
经济数学
例4 (1) lim C C (C为常数); x x0
(2)
lim (ax
x x0
b)
ax0
b;
特别地:lim x x0
x
x0 ,
当n为正整数时, lim x x0
xn
x0n ,
当x0
