离散汉密尔顿图
应用离散数学图论欧拉图与哈密尔顿图题库试卷习题及答案
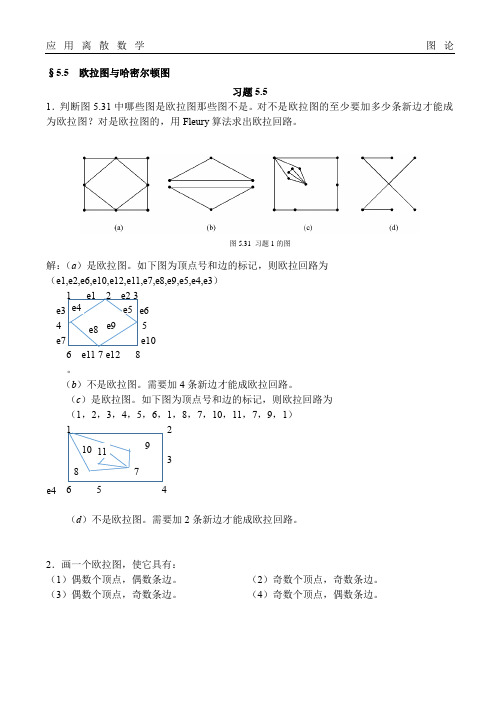
§5.5 欧拉图与哈密尔顿图习题5.51.判断图5.31中哪些图是欧拉图那些图不是。
对不是欧拉图的至少要加多少条新边才能成为欧拉图?对是欧拉图的,用Fleury算法求出欧拉回路。
图5.31 习题1的图解:(a)是欧拉图。
如下图为顶点号和边的标记,则欧拉回路为(e1,e2,e6,e10,e12,e11,e7,e8,e9,e5,e4,e3)e645e106 e117 e12 8。
(b)不是欧拉图。
需要加4条新边才能成欧拉回路。
(c)是欧拉图。
如下图为顶点号和边的标记,则欧拉回路为(1,2,3,4,5,6,1,8,7,10,11,7,9,1)236 5 4(d)不是欧拉图。
需要加2条新边才能成欧拉回路。
2.画一个欧拉图,使它具有:(1)偶数个顶点,偶数条边。
(2)奇数个顶点,奇数条边。
(3)偶数个顶点,奇数条边。
(4)奇数个顶点,偶数条边。
解 四个图按顺序分别如下:3.在k (k ≥2)个长度大于或等于3的无公共点的环型图之间至少加多少条边才能使它们组成一个简单欧拉图。
解:环形图中每个点的度是2,要形成欧拉回路,就要使新图是一个连通图,并且每个点的度仍保度偶数,因此,要让新图是欧拉图,则至少要加k 条边。
4.证明:可以从连通图中任意一点出发,经过这个图中每条边恰好两次,回到出发点。
解 将每条边都增加一条平行边,则得到一个多重图,此多重图的每个顶点的度数都是偶数,所以存在欧拉闭迹。
在欧拉闭迹中,将经过平行边改成第二次经过原来的边,定理即得证。
5.完全图p K 是欧拉图吗?是哈密尔顿图吗?完全二部图n m K ,是欧拉图吗?是哈密尔顿图吗?解 (1)K p ⎩⎨⎧不是欧拉图是欧拉图 为偶数时当为奇数时当p p K p (p ≥3)为哈密尔顿图((v 1,v 2,v 3,……,v p )即是一个哈密尔顿回路)。
(2)因为K m,n 中顶点的度数要么为m ,要么为n ,所以K m,n ⎩⎨⎧不是欧拉图是欧拉图 为奇数时或当为偶数时和当n m n m因为K m,n 的顶点数为m+n ,而任意两点的度数之和为2m 或2n 或m+n 。
第七章 2汉密尔顿图

L: v1
vp
2021/2/16
7-2 汉密尔顿图 2021/2/16
7-2 汉密尔顿图
如果 v p 不邻接于 vl1, vm1,..., v j1,..., vt1 中的任意一个结点,则 deg(vp ) p 1 k ,
deg(u)+deg(v)≥ n, 则G是汉密尔顿图。
2021/2/16
11
7-2 汉密尔顿图
设G=〈V ,E〉是有n个结点的简单图, (1) 如果任两结点u,v∈V, 均有
deg(u)+deg(v)≥ n-1, 则在G中存在一条汉密尔顿路;
(1)证明:首先证明图 G 连通。用反证法进行证明。假设图 G 不连通,则图 G 至少
deg(v1) k , deg(vp ) deg(v1) p 1 k k p 1 n 1 , 这 与 前 提 条 件
deg u +deg v n-1矛盾。因此 v p 必然邻接于 vl1, vm1,..., v j1,..., vt1 中的任意一个结
点。回路 L1 一定存在。 STEP 3:打开回路,得到基本路径 L2。
有两个连通分支 G1 和 G2 。G1=<V1, E1> ,G2=<V2 , E2> 。| V1 | n1 ,| V2 | n2 。在G1 中取 一 个 结 点 v1 , deg(v1) n1 1 , 在 G2 中 取 一 个 结 点 v2 , deg(v2 ) n2 1 。
deg(v1) deg(v2 ) n1 1 (n2 1) n1 n2 2 n 2 ,与 deg u+deg v n-1 矛
因此该定理不能证明彼得森图是非 汉密尔顿图。但彼得森图是非汉密尔 顿图。
离散数学第七章图论习题课ppt课件

24
设G是一个n阶无向简单图,n是大于等于3的 奇数。证明图G与它的补图中度数为奇数的结 点个数相等。
证明: 因为G是n阶无向简单图,且n是大于等于3的奇数,
故无向图的结点数为奇数,则所对应的n阶完全图 中每个结点的度数为n-1即为偶数, 利用奇数+奇数=偶数,偶数+偶数=偶数,所以, 在G中结点度数为奇数的结点,在其补图中的度 数也应为奇数,故G和其补图的奇数结点个数也 是相同的。
25
P286 1、在无向图G中,从结点u到结点v有一条长度为 偶数的通路,从结点u到结点v又有一条长度为奇 数的通路,则在G中必有一条长度为奇数的回路。
(4) D中长度为4的回路有多少条? 答: 长度为4的回路为11条。
(5) D中长度4的通路有多少条?其中有几条是回路? 答:长度4的通路88条,其中22条为回路。
(6) 写出D的可达矩阵。 44的全1矩阵。
17
简单无向图 G 必有2结点同度数。
证: 令 G={v1,…,vn},
(2) n阶非连通的简单图的边数最多可为n-1阶连通图 加上一个孤立点,所以边数为(n-1)(n-2)/2,最少为0。
20
一个图如果同构于它的补图,则该图称为自补图。
1)一个图是自补图,其对应的完全图的边数必为偶数; 2)证明:若n阶无向简单图是自补图,则n=4k或n=4k+1
(k为正整数)。 解:
平面图的对偶图
无向树及其性质 根树及其应用
地图着色与平 面图着色
3
4
一、无向图与有向图
(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案

(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案(精华版)国家开放大学电大本科《离散数学》网络课形考网考作业及答案 100%通过考试说明:2020年秋期电大把该网络课纳入到“国开平台”进行考核,该课程共有5个形考任务,针对该门课程,本人汇总了该科所有的题,形成一个完整的标准题库,并且以后会不断更新,对考生的复习、作业和考试起着非常重要的作用,会给您节省大量的时间。
做考题时,利用本文档中的查找工具,把考题中的关键字输到查找工具的查找内容框内,就可迅速查找到该题答案。
本文库还有其他网核及教学考一体化答案,敬请查看。
课程总成绩 = 形成性考核×30% + 终结性考试×70% 形考任务1 单项选择题题目1 若集合A={ a,{a},{1,2}},则下列表述正确的是().选择一项:题目2 若集合A={2,a,{ a },4},则下列表述正确的是( ).选择一项:题目3 设集合A={1 , 2 , 3 , 4}上的二元关系R={<1, 1>,<2, 2>,<2, 3>,<4, 4>},S={<1, 1>,<2, 2>,<2, 3>,<3, 2>,<4, 4>},则S是R的()闭包.选择一项:B. 对称题目4 设集合A={1, 2, 3},B={3, 4, 5},C={5, 6, 7},则A∪B–C=( ).选择一项:D. {1, 2, 3, 4} 题目5 如果R1和R2是A上的自反关系,则R1∪R2,R1∩R2,R1-R2中自反关系有()个.选择一项:C. 2 题目6 集合A={1, 2, 3, 4}上的关系R={<x,y>|x=y且x, y∈A},则R的性质为().选择一项:D. 传递的题目7 若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是( ).选择一项:题目8 设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为().选择一项:C. 8 题目9 设A={1, 2, 3, 4, 5, 6, 7, 8},R是A上的整除关系,B={2, 4, 6},则集合B的最大元、最小元、上界、下界依次为 ( ).选择一项:B. 无、2、无、2 题目10 设集合A ={1 , 2, 3}上的函数分别为:f = {<1, 2>,<2, 1>,<3, 3>},g = {<1, 3>,<2, 2>,<3, 2>},h = {<1, 3>,<2,1>,<3, 1>},则h =().选择一项:D. f◦g 判断题题目11 设A={1, 2}上的二元关系为R={<x, y>|xA,yA, x+y =10},则R的自反闭包为{<1, 1>, <2, 2>}.()选择一项:对题目12 空集的幂集是空集.()选择一项:错题目13 设A={a, b},B={1, 2},C={a, b},从A到B的函数f={<a, 1>, <b, 2>},从B到C的函数g={<1, b>, <2, a >},则g° f ={<1,2 >, <2,1 >}.()选择一项:错题目14 设集合A={1, 2, 3, 4},B={2, 4, 6, 8},下列关系f = {<1, 8>, <2, 6>,<3, 4>, <4, 2,>}可以构成函数f:.()选择一项:对题目15 设集合A={1, 2, 3},B={2, 3, 4},C={3, 4, 5},则A∩(C-B )= {1, 2, 3, 5}.()选择一项:错题目16 如果R1和R2是A上的自反关系,则、R1∪R2、R1∩R2是自反的.()选择一项:对题目17 设集合A={a, b, c, d},A上的二元关系R={<a, b>, <b, a>, <b, c>, <c, d>},则R具有反自反性质.()选择一项:对题目18 设集合A={1, 2, 3},B={1, 2},则P(A)-P(B )={{3},{1,3},{2,3},{1,2,3}}.()选择一项:对题目19 若集合A = {1,2,3}上的二元关系R={<1, 1>,<1, 2>,<3, 3>},则R是对称的关系.()选择一项:错题目20 设集合A={1, 2, 3, 4 },B={6, 8, 12}, A到B的二元关系R=那么R-1={<6, 3>,<8,4>}.()选择一项:对形考任务2 单项选择题题目1 无向完全图K4是().选择一项:C. 汉密尔顿图题目2 已知一棵无向树T中有8个顶点,4度、3度、2度的分支点各一个,T的树叶数为( ).选择一项:D. 5 题目3 设无向图G的邻接矩阵为则G的边数为( ).选择一项:A. 7 题目4 如图一所示,以下说法正确的是 ( ) .选择一项:C. {(d, e)}是边割集题目5 以下结论正确的是( ).选择一项:C. 树的每条边都是割边题目6 若G是一个欧拉图,则G一定是( ).选择一项:B. 连通图题目7 设图G=<V, E>,v∈V,则下列结论成立的是 ( ) .选择一项:题目8 图G如图三所示,以下说法正确的是 ( ).选择一项:C. {b, c}是点割集题目9 设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).选择一项:A. (a)是强连通的题目10 设有向图(a)、(b)、(c)与(d)如图六所示,则下列结论成立的是( ).选择一项:D. (d)只是弱连通的判断题题目11 设图G是有6个结点的连通图,结点的总度数为18,则可从G中删去4条边后使之变成树.( ) 选择一项:对题目12 汉密尔顿图一定是欧拉图.( ) 选择一项:错题目13 设连通平面图G的结点数为5,边数为6,则面数为4.( ) 选择一项:错题目14 设G是一个有7个结点16条边的连通图,则G为平面图.( ) 选择一项:错题目15 如图八所示的图G存在一条欧拉回路.( ) 选择一项:错题目16 设图G如图七所示,则图G的点割集是{f}.( ) 选择一项:错题目17 设G是一个图,结点集合为V,边集合为E,则( ) 选择一项:对题目18 设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.( ) 选择一项:错题目19 如图九所示的图G不是欧拉图而是汉密尔顿图.( ) 选择一项:对题目20 若图G=<V, E>,其中V={ a, b, c, d },E={ (a, b), (a, d),(b, c), (b, d)},则该图中的割边为(b, c).( ) 选择一项:对形考任务3 单项选择题题目1 命题公式的主合取范式是( ).选择一项:题目2 设P:我将去打球,Q:我有时间.命题“我将去打球,仅当我有时间时”符号化为( ).选择一项:题目3 命题公式的主析取范式是( ).选择一项:题目4 下列公式成立的为( ).选择一项:题目5 设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().选择一项:题目6 前提条件的有效结论是( ).选择一项:B. ┐Q 题目7 命题公式(P∨Q)→R的析取范式是 ( ).选择一项:D. (┐P∧┐Q)∨R 题目8 下列等价公式成立的为( ).选择一项:题目9 下列等价公式成立的为( ).选择一项:题目10 下列公式中 ( )为永真式.选择一项:C. ┐A∧┐B ↔ ┐(A∨B) 判断题题目11 设个体域D={1, 2, 3},A(x)为“x小于3”,则谓词公式(∃x)A(x) 的真值为T.( ) 选择一项:对题目12 设P:小王来学校, Q:他会参加比赛.那么命题“如果小王来学校,则他会参加比赛”符号化的结果为P→Q.( ) 选择一项:对题目13 下面的推理是否正确.( ) (1) (∀x)A(x)→B(x) 前提引入(2) A(y)→B(y) US (1) 选择一项:错题目14 含有三个命题变项P,Q,R的命题公式P∧Q的主析取范式(P∧Q∧R)∨(P∧Q∧┐R).( ) 选择一项:对题目15 命题公式P→(Q∨P)的真值是T.( ) 选择一项:对题目16 命题公式┐P∧P的真值是T.( ) 选择一项:错题目17 谓词公式┐(∀x)P(x)(∃x)┐P(x)成立.( ) 选择一项:对题目18 命题公式┐(P→Q)的主析取范式是P∨┐Q.( ) 选择一项:错题目19 设个体域D={a, b},则谓词公式(∀x)(A(x)∧B(x))消去量词后的等值式为(A(a)∧B(a))∧(A(b)∧B(b)).( ) 选择一项:对题目20 设个体域D={a, b},那么谓词公式(∃x)A(x)∨(∀y)B(y)消去量词后的等值式为A(a)∨B(b).( ) 选择一项:错形考任务4 要求:学生提交作业有以下三种方式可供选择:1. 可将此次作业用A4纸打印出来,手工书写答题,字迹工整,解答题要有解答过程,完成作业后交给辅导教师批阅. 2. 在线提交word文档. 3. 自备答题纸张,将答题过程手工书写,并拍照上传形考任务 5 网上学习行为(学生无需提交作业,占形考总分的10%)附:元宇宙(新兴概念、新型虚实相融的互联网应用和社会形态)元宇宙(Metaverse)是整合了多种新技术而产生的新型虚实相融的互联网应用和社会形态,通过利用科技手段进行链接与创造的,与现实世界映射与交互的虚拟世界,具备新型社会体系的数字生活空间。
离散数学中汉密尔顿回路求解思路

离散数学中汉密尔顿回路求解思路离散数学是研究离散结构及其关系的一门学科,其中汉密尔顿回路问题是研究图论中的重要问题之一。
本文将探讨汉密尔顿回路的求解思路,并介绍常用的算法。
一、汉密尔顿回路概述汉密尔顿回路是指图中经过每个顶点一次且只一次的回路,也称为哈密顿回路。
对于给定的图,求解是否存在汉密尔顿回路的问题被称为汉密尔顿回路问题。
该问题的解决对于理论研究和实际应用具有重要意义。
二、暴力搜索算法暴力搜索算法是最直观、最简单的求解汉密尔顿回路的方法。
其基本思路是对图中的每一条路径进行遍历,判断是否满足汉密尔顿回路的条件。
该算法的时间复杂度为O(n!),因为需要对所有可能的路径进行枚举。
然而,由于其时间复杂度过高,在大型图中求解问题时效率低下。
三、回溯算法回溯算法是一种通过试错的方式来搜索解空间的方法。
对于汉密尔顿回路问题,回溯算法的基本思路是从图中的某个顶点开始遍历,按照某种策略选择下一个未被访问的顶点,直到回到起始顶点形成回路。
如果当前路径无法满足汉密尔顿回路的条件,则回溯到上一个顶点,换一个未被访问的顶点进行尝试。
通过不断地回溯和尝试,最终找到汉密尔顿回路。
四、分支限界算法分支限界算法是一种通过剪枝和优先队列等手段来减少搜索空间的方法。
在求解汉密尔顿回路问题时,分支限界算法主要通过定义优先级函数和界函数来判断当前路径是否有可能成为汉密尔顿回路。
如果当前路径无法满足界函数的条件,那么该路径可以被剪枝。
通过不断地剪枝和选择有希望成为汉密尔顿回路的路径,最终找到问题的解。
五、动态规划算法动态规划算法是一种以递推的方式来求解问题的方法。
在求解汉密尔顿回路问题时,动态规划算法将问题划分为多个子问题,并通过求解子问题的最优解来推导出整体的最优解。
具体而言,该算法通过定义状态转移方程和初始化条件来求解汉密尔顿回路问题。
动态规划算法的优势在于可以通过存储已解决子问题的结果来减少重复计算,提高求解效率。
六、启发式算法启发式算法是一种通过启发式规则和策略来搜索解空间的方法。
6汉密尔顿图
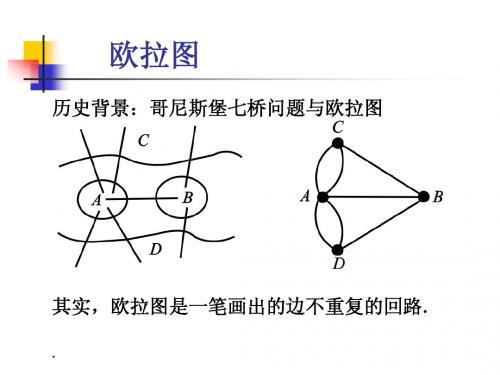
例15.3
设图为G2,则G2=<V1,V2,E>,其中 V1={a,g,h,i,c},V2={b,e,f,j,k,d}, 易知,p(G2-V1)=|V2|=6>|V1|=5, 由定理15.6可知,G2不是哈密顿图, 但G2是半哈密顿图。 baegjckhfid为G2中一条哈密顿通路。 设图为G3,G3=<V1,V2,E>,其中 V1={a,c,g,h,e},V2={b,d,i,j,f}, G3中存在哈密顿回路。 如 abcdgihjefa, 所以G3是哈密顿图。33Fra bibliotek极大路径
是一条路径,如果的始点和终点都不 与外的顶点相邻,则称是一条极大路 径。 极大:不能再向外延伸
34
无向半汉密尔顿图的充分条件
定理15.7 设G是n阶无向简单图,若对于G中任意不相邻的顶点
vi,vj,均有 d(vi)+d(vj)≥n-1
则G中存在哈密顿通路。
(15.1)
证明 首先证明G是连通图.否则G至少有两个连通分支, 设G1,G2是阶数为n1,n2的两个连通分支,设v1∈V(G1), v2∈V(G2),因为G是简单图,所以 dG(v1)+dG(v2)=dG1(v1)+dG2(v2)≤n1-1+n2-1≤n-2 这与(15.1)矛盾,所以G必为连通图.
35
定理15.7
下面证G中存在哈密顿通路。 设Г=v1v2„vl为G中用“扩大路径法”得到的“极大路 径”,即Г的始点v1与终点vl不与Г外的顶点相邻.显然有 l≤n. (1)若l=n,则Г为G中哈密顿通路。
(2)若l<n,这说明Г不是哈密顿通路,即G中还存在着Г外的 顶点.但可以证明G中存在经过Г上所有顶点的圈.
离散数学形考任务2图论部分概念及性质
离散数学形考任务2图论部分概念及性质
单项选择题
●如图所示,以下说法正确的是( ).答案是:e是割点
●如图一所示,以下说法正确的是( ) .答案是:{(d, e)}是边割集
●若G是一个汉密尔顿图,则G一定是( ).答案是:连通图
●若G是一个欧拉图,则G一定是( ).答案是:连通图
●设G是连通平面图,有v个结点,e条边,r个面,则r= ( ).答案是:e-v+2
●设G是有n个结点,m条边的连通图,必须删去G的( )条边,才能确定G的一棵
生成树.答案是:m-n+1
●设图G=<V, E>,vV,则下列结论成立的是( )
●设无向图G的邻接矩阵为则G的边数为( ).答案是:7
●设无向图G的邻接矩阵为则G的边数为( ).答案是:7
●设有向图(a)、(b)、(c)与(d)如图所示,则下列
结论成立的是( ).答案是:(a)是强连通的
●设有向图(a)、(b)、(c)与(d)如图所示,则下列
结论成立的是( ).答案是:(d)只是弱连通的
●图G如图三所示,以下说法正确的是( ).答案是:{b, c}是点割集
●图G如图四所示,以下说法正确的是( ) .答案是:{(a, d) ,(b, d)}是边割
集。
离散数学 7-3 图的矩阵表示

所以用此定理来证明某一特定图不是汉密尔顿图并不是
总是有效的。例如,著名的彼得森(Petersen)图,在图中删 去任一个结点或任意两个结点,不能使它不连通;删去3个结 点,最多只能得到有两个连通分支的子图;删去4个结点,只 能得到最多三个连通分支的子图;删去5个或5个以上的结点,
e3
v3
1 1 0 0 0
0 1 1 0 0
0 0 1 1 0
1 0 0 1 0
1 0 1 0 0
v3 0 v4 0 v5 0
无向图的关联矩阵反映出来图的性质:
每一条边关联两个结点,故每一列中只有两个1。
每一行中元素之和等于该行对应的结点的度数。
一行中元素全为0,其对应结点为孤立点。
两个平行边其对应的两列相同。 同一个图当结点或边的编号不同时,其对应的矩 阵只有行序列序的差别。
证明思路:1) 先证必要性: G有欧拉路 G连通 且(有0个 或 2个奇数度结点) 设G的欧拉路是点边序列v0e1v1e2… ekvk,其中结点可能重复, 但边不重复。因欧拉路经过(所有边)所有结点,所以图G 是连通的。 对于任一非端点结点vi,在欧拉路中每当vi出现一次,必关 联两条边,故vi虽可重复出现,但是deg(vi)必是偶数。对于端 点,若v0=vk ,则deg(v0)必是偶数,即G中无奇数度结点 。若 v0≠vk ,则deg(v0)必是奇数, deg(vk)必是奇数,即G中有两个奇 数度结点 。必要性证完。
e3
v3
0 0 0
-1 1 0 0
-1 1 0 0
有向图的关联矩阵的特点:
(1)每一列中有一个1和一个-1,对应一边一个始 点、一个终点,元素和为零。 (2)每一行元素的绝对值之和为对应点的度数。-1 的个数等于入度,1的个数等于出度。
离散数学专业名词

第一章集合论、逻辑与算法基础1.1集合set(集合)power set(幂)complement of a set(补集)roster method(枚举法)universalset set(全集)symmetric difference(对称差集)set-builder method(集合构造方法)Venn diagrams(文氏图)ordered pair(有序对)subset(子集)union of sets(并集)Cartesian product(笛卡尔积)superset(父集)intersection of sets(交集)diagonal of a set(对角集)proper subset(真子集)disjoint sets(不相交集)ordered n-tuples(有序n元组)equal sets(相等集合)index set(索引集)n-flod Cartesian product(n次笛卡尔积)empty (null)set(空集)set difference(差集)bit string(位串)finite set(有限集)mutually disjoint(互不相交)length(长度)infinite set(无限集)pairwise disjoint(互不相交)singleton set(单体集合)relative complement(相对补集)1.2数理逻辑statement(命题)condition(条件)converse(逆命题)proposition(命题)biimplication(双向蕴涵)inverse(反命题)truth value(真值)biconditional(双向条件)contrapositive(逆否命题)negation(非)logical connectives(逻辑连接词)statement formula(命题公式)conjunction(合取)well-formed formulas(良态公式)formula(公式)disjunction(析取)tautology(重言式)implication(蕴涵)contradiction(矛盾式)1.3论证有效性proof(证明)modus tollens(否定法)disjunctive addition(析取加法)argument(论证)disjunctive syllogisms(析取三段论)conjunctive addition(合取加法)conclusion(结论)hypothetical syllogism(假设三段论)logically valid(逻辑有效)premise(前提)dilemma(二难推论)modus ponens(断言法)conjunctive simpli fications(合取简化)1.4量词与一阶逻辑statement logic(命题逻辑)predicate(谓词)domain(域)propositional logic(命题逻辑)propositional function(命题函数)free vricable(自由变量)n-place predicate(n位谓词)bound variable(约束变量)first-order logic(一阶逻辑)universal quantifier(全称量词)counterexample(反例)existential quantifier(存在量词)disproof(反证)1.5证明方法theorem(定理)indirect proof(间接证明)proof by contradiction(反证法)proof by direct method(直接证明方法)direct proof(直接证明)1.6 算法algorithm(算法)two-way selection(双路选择)list(列表)input(输入)if two-dimensional array(二维数组)output(输出)thenread precision(精度)else printuniqueness(唯一性)whilesubproprams(子程序)finiteness(有限性)do proceduregenerality(通用性)forfunction assignment operator(赋值运算符)begin constant polynomial(常量多项式)assignment statement(赋值语句)enddegree(次数)control structures(控制结构)return one-way selection(单路选择)arrays(数组)第三章关系与偏序集3.1关系与偏序集binary relation (二元关系)directed graph representation(有向图表示)digraph (有向图)relation (关系)vertex(顶点)adjacent to (与...相邻)R-related (R-相关)directed edge(有向边)adjacent from(从...相邻)related (相关)directed arc(有向弧)loop (环)empty relation (空关系)arrow diagram (矢量图)domain (域)universal relation (全称关系)directed graph(有向图)range (值域)image (映像) equivalence class (等价类)transitive closure (传递闭包)inverse (逆)R-class(R-类)directed walk (有向通路)composition (复合)reflexive (自反)R-equivalence class (R-等价类)walk (通路)partition (划分)vertices of the walk (通路顶点)transitive (传递)equivalence relation induced by the partition (划分推出的等价关系)terminal vertex (终止顶点)equivalence relation (等价关系)internal vertices (内部顶点)equality relation (相等性关系)reflexive closure (自反闭包)path (路径)congruence modulo m (模m同余)symmetric closure (对称闭包)3.2偏序集antisymmetric (反对称)lexicographic order (词典序)topological ordering (拓扑排序)partial order (偏序)dictionary order (字典序)upper bound(上界)partially ordered set (偏序集)closed (闭合)poset (偏序集)least upper bound(lub)(最小上界)covers (覆盖)lower bound (下界)dual (序偶)Hasse diagram (哈赛图)greatest lower bound (glb)(最大下界)comparable (可比)minimal element (极小元)lattice (格)linearly ordered set (线性有序集)maximal element (极大元)distributive (可分配性)totally ordered set (完全有序集)greatest element (最大元)complement (补元)chain (链)least element (最小元)Boolean algebra (布尔代数)product partial order (积偏序)compatible (兼容,相容)第四章矩阵与关系闭包4.1矩阵matrix(矩阵)diagonal matrix(对角矩阵)join(并)rectangular array(矩阵阵列)identity matrix(单位矩阵)Boolean meet(布尔交)element(元素)sum(和)meet(交)entry(项)difference(差)join of meet expression(相交表达式的并)equal(等于)multiplication(乘法)Boolean product(布尔积)square matrix(方阵)transpose(转置)product(积)zero matrix(零矩阵)symmetric(对称)diagonal element(对角元素)Boolean join(布尔并)4.2 关系矩阵与闭包matrix of a relation(关系矩阵)Warshall’s algorithm(Warshall算法)第五章函数5.1 函数function(函数)target(目标)onto(满射)well defined(合理定义)range(值域)surjective(满射)single valued(单值)numeric functions(数字函数)surjection(满射)image(映像)identity function(恒等函数)one-to-one correspondence(一一映射)preimage(预映像,前射,前像,原像)constant function(常数函数)bijective(双射)mapped(映射)one-one(单射函数)bijection(双射)domain(域)injective(内射)composition(复合)codomain(合域)injection(内射)5.2 特殊函数与集合的基数inverse function(逆函数)images(映像)cardinality(基数)left invertible(左可逆)direct image(直接映像)equivalent(等价)left inverse(左逆)inverse image(逆映像)equipotent(幂等)right invertible(右可逆)floor(下限)countable(可数)right inverse(右逆)ceiling(上限)uncountable(不可数)restriction(限制)floor function(弱取整函数)extension(扩展)ceiling function(强取整函数)5.3 序列与字符串sequence(序列)sum of the terms(项之和)index(索引)nth term of the sequence(序列第n项)summation symbol(求和符号)subscript(下标)finite sequence(有限序列)string(字符串)infinite sequence(无限序列)word(字符)integer sequence(整数序列)dummy variable(哑变量)alphabet(字母表)arithmetic progression(AP)(等差数列)lower limit(下限)length(长度)first term(首项)upper limit(上限)empty string(空字符串)common difference(公差)general term(通项)empty word(空串)geometric progression(GP)(等比数列)product of the terms(项之积)concatenation(接合)common ratio(公比)product symbol(求积符号)5.4 二元运算binary operation(二元运算)mathematical system(数学系统)idempotent(幂等)close under(在……下闭合)groupoid(群)idempotent semigroup(幂等半群)associative(可结合)identity(单位元)band(带)commutative(可交换)semigroup(半群)free semigroup generated by(由……生成的自由半群)Cayley multiplication table(Cayley乘法表)monoid(幺半群)free monoid generated by(由……生成的自由幺半群)Cayley table(Cayley表)transformation semigroup(变换半群)第六章同余6.1同余Congruent (同余)congruence class modulo (模m的同余类)6.3线性同余linear congruence in one variable (一个变量x的线性同余式)inverse (逆)residue representation (余数表示)unique modulo (唯一模)modular representation (模表示)round-robin tournament (循环赛)hashing (散列)hash address (散列地址)linear probing (线性探测)hash table (散列表)hashing function (散列函数)probe sequence (探测数列)hash function (散列函数)collision (冲突)double hashing (双重散列)6.4特殊同余定理Euler phi-function (欧拉phi函数)ciphertext (密文)encryption key (加密钥匙)plaintext(明文)decryption function (加密函数)decryption key (揭秘钥匙)第十章图论10.1图的定义与符号graph (图)parallel (平行边)arc(弧)set of vertices (顶点集合)isolated vertex (顶点孤立)Staring vertex (始点)set of edges (边集)degree (度)terminating vertex (终点)incidence function (关联函数)k-regular graph (k-正则图)in-degree (入度)end vertices (端点)even degree vertex (偶度顶点)out-degree (出度)endpoints(端点)odd degree vertex (奇度顶点)simple graph (简单图)incident (关联)degree sequence (度数列) complete graph(完全图)Adjacent (相邻)directed graph(有向图)triangle (三角形)loop (环)digraph (有向图)bipartite graph (二分图)incidence table (关联表)directed edge(有向边)Bipartition (二分)complete bipartite (完全二分)subgraph (子图)Complement of a graph(补图)Ramsey number (Ramsey数)10.2通路,路径与圈walk (通路)initial vertex (始点)terminal vertex(终点)directed walk (有向通路)length of a walk (通路长度)length of a directed walk (有向通路长度)u-v walk (u-v通路)u-v directed walk (u-v 有向通路)closed walk (闭合通路)closed directed walk (闭合有向通路)open walk (开放通路)open directed walk (开放有向通路)trail (迹) path (路径)trivial walk (平凡通路)trivial path (平凡路径)trivial trail (平凡迹)nontrivial walk (非平凡通路)nontrivial path (非平凡路径)nontrivial trial (非平凡迹)circuit (回路)cycle (圈)k-cycle (k圈)even cycle (偶数圈)odd cycle (奇数圈)subwalk (子通路)reduction of P by Q(P用Q简化)decomposition (分解)connected (连接)connected graph (连接图,连通图)disconnected graph (不连接图,不连通图)component (分支)distance (距离)matching (匹配)M-saturated (M-饱和)M-unsaturated (M-不饱和)perfect matching (完美匹配)maximum matching(最大匹配)neighbors (邻居)10.3图的矩阵表示adjacency (相邻矩阵)incidence matrix(关联矩阵)10.4特殊回路Euler circuit (欧拉回路)Euler trail (欧拉迹)Hamiltonian graph (汉密尔顿图)Euler graph (欧拉图)Hamiltonian cycle (汉密尔顿圈)Hamiltonian path (汉密尔顿路径)10.5同构isomorphic (同构)different (不同)10.6图算法weight (权)weighted graph (加权图)weight matrix (加权矩阵)length of a path (路径长度)shortest path algorithm (最短路径算法)greedy algorithm (贪婪算法)topological ordering (拓扑排序)immediate successor (直接后继)queue (队列)rear (队尾)10.7 平面图和图着色planar graph(平面图)exterior face(外面)proper vertex coloring(正常顶点着色)plane graph(平面图)interior face(内面)chromatic number(色数)planar representation of a graph(图的平面表示)subdivision of a graph(图的细分)edge coloring(边着色)faces(面)homeomorphic(同胚)proper edge coloring(正常边着色)boundary(边界)vertex coloring(顶点着色)chromatic index(色索引)第十一章树与网络11.1 树tree(树)acyclic graph(无环图)11.2 有根树rooted tree(有根树)binary tree(二叉树)postorder traversal(后序遍历)lever(层)trivial tree(平凡树)inorder sequence(中序顺序)child(子节点)left child(左子节点)preorder sequence(前序顺序)terminal vertex(终点)right child(右子节点)postorder sequence(后序顺序)leaf(叶子)left subtree(左子树)binary search tree(二叉搜索树)internal vertex(内顶点)right subtree(右子树)infix(中缀)descendant(后代)full binary tree(完全二叉树)prefix(前缀)ordered rooted tree(有序有根树)inorder traversal(中序遍历)postfix(后缀)height(高度)preorder traversal(前序遍历)expression tree(表达式树)11.3 生成树spanning tree(生成树)minimal spanning tree(最小生成树)weighted tree(加权树)Prim’s algorithm(Prim算法)weight(权)11.4 网络single-source,single-sink network(单元单汇网络)flow conservation(流量守恒)quasipath(拟路径)source(源)flow in edge(边流)forward arc(正向弧)target(目标)flow into(流入)backward arc(反向弧)sink(汇)flow out of(流出)slack(松弛)s-t network(s-t网络)conservation of flow(流量守恒)F-saturated(F-饱和)capacity(容量)value of a flow(流值)F-unsaturated(F-不饱和)transport network(传输网络)s-t cut of network(网络的s-t分割)flow augmenting(流增广)network(网络)capacity of an s-t cut(s-t分割容量)patent(父节点)flow(流)minimal cut(最小分割)immediate predecessor(直接前驱)capacity constraint(容量限制)maximal flow(最大流)。
离散数学第8章 图论

软件学院
图论原理 两个图同构的必要条件: 1.结点个数相等. 2.边数相等. 3.度数相同的结点数相等. 4.对应的结点的度数相等. 下面是同构的图:
a b c e d 3 5 1 4 2 b c d a f e 2 4 6 1 3 5
软件学院
图论原理
软件学院
图论原理
图的同构 设G=<V,E>和G’=<V’,E’>是图,如果存在双射f:VV’ 且任何 vi,vj∈V,若边(vi,vj)∈E,当且仅当 边(f(vi),f(vj))∈E’, (则称G与G’同构,记作G≌G’. (同构图要保持边的“关联”关系) 例如:右边所示的两个图: a b 1 4 G=<V,E> G’=<V’,E’> c d 3 2 构造映射f:VV’ a 1 b 2 c 3 d 4 a 1 b 2 c 3 d 4
c
d
v2
v4 v6 G2
v3
v5
f g h G1
软件学院
图论原理
欧拉通路的判定方法: 定理:无向连通图G中结点a和b间存在欧拉通路的充分必要 条件是a与b的次数均为奇数而其他结点的次数均为偶数。 如果G有两个奇数度结点:就从一个奇数度结点出发,每当到 达一个偶数度结点,必然可以再经过另一条边离开此结点, 如此重复下去,经过所有边后到达另一个奇数度结点 如果G无奇数度结点,则可以从任何一个结点出发,去构造一 条欧拉路. a b 1 2 c d 4 3
v3
是一个结点,则称此路 是一个回路. 如果一条路中所有边都不同,则称此路为迹或简单通路. 如果一条回路中所有边都不同,则称此回路为闭迹或简 单回路. 如果一条路中所有结点都不同,则称此路为基本通路. 如果一条回路中所有结点都不同,则称此路为基本回路. 一条基本通路一定是简单通路,但是一条简单通路不 一定是基本通路
国开电大2024秋《离散数学》形考任务1-6以及大作业

国开大学、各地开放大学形考、终考、期末复习资料答案由【电大题园】微信公众号提供,禁止复制盗取。
答案由【电大题园】微信公众号提供,禁止复制盗取。
答案由【电大题园】微信公众号提供,禁止复制盗取。
国开电大2024秋《离散数学》形考任务1-6以及大作业离散数学(本)·形考任务一1.若集合A={ a,{a},{1,2}},则下列表述正确的是( ).A.{a,{a}}ÎAB.{1,2}ÏAC.{a}ÍAD.ÆÎA正确答案:C2.若集合A={1, 2, 3, 4},则下列表述正确的是().A.{1, 2}ÎAB.{1, 2, 3 } Í AC.AÌ{1, 2, 3 }D.{1, 2, 3}ÎA正确答案:B3.若集合A={2,a,{ a },4},则下列表述正确的是( ).A.{a,{ a }}ÎAB.ÎAC.{2}ÎAD.{ a }ÍA正确答案:D4.若集合A={1,2},B={1,2,{1,2}},则下列表述正确的是( ).A.AÌB,且AÎBB.BÌA,且AÎBC.AÌB,且AÏBD.AËB,且AÎB正确答案:A5.若集合A={a,b},B={a,{a,b}},则下列表述正确的是( ).A.AÌBB.BÌAC.AÏBD.AÎB正确答案:D6.若集合A的元素个数为5,则其幂集的元素个数为().A.5B.16C.32D.64正确答案:C7.设集合A={1, 2, 3, 4, 5, 6},B={1, 2, 3},A到B的关系R={<x,y>| x A,yB且x=y2},则R=( ).A.{<1, 1>, <2, 4>}B.{<1, 1>, <4, 2>}C.{<1, 1>, <6, 3>}D.{<1, 1>, <2, 1>}8.设集合A={2, 4, 6, 8},B={1, 3, 5, 7},A到B的关系R={<x,y>|xA, y B且 y=x +1},则R= ().A.{<2, 3>, <4,5>, <6, 7>}B.{<2, 1>, <4, 3>, <6, 5>}C.{<2, 1>, <3, 2>, <4, 3>}D.{<2, 2>, <3, 3>, <4, 6>}正确答案:A9.设A={1, 2, 3},B={1, 2, 3, 4},A到B的关系R={〈x,y〉| xÎA,yÎB,x=y},则R= ( ) .A.{<1, 2>, <2, 3>}B. {<1, 1>, <1, 2>, <1, 3>, <1, 4>, <1, 5>}C. {<1, 1>, <2, 1>}D.{<1, 1>, <2, 2>, <3, 3 >}正确答案:D10.设A={a,b,c},B={1,2},作f:A→B,则不同的函数个数为()A.2B.3C.6D.8正确答案:D11.空集的幂集是空集.()A.正确B.错误12.存在集合A与B,可以使得AÎB与AÍB同时成立.A.正确B.错误正确答案:A13.集合的元素可以是集合.A.正确B.错误正确答案:A14.如果A是集合B的元素,则A不可能是B的子集.A.正确B.错误正确答案:B15.设集合A={a},那么集合A的幂集是{Æ, {a}}A.正确B.错误正确答案:A16.若集合A的元素个数为4,则其幂集的元素个数为16A.正确B.错误正确答案:A17.设A={1, 2, 3},B ={1, 2, 3, 4},A到B的关系R ={<x,y> |xÎA,yÎB,x>y},则R ={<2,1>, <3, 1>, <3, 2 >}A.正确B.错误正确答案:A18.设A={1, 6,7},B={2, 4,8,10},A到B的关系R={〈x,y〉|xÎA,yÎB,且x=y},则R={<2, 2>, <4, 4>, <8, 8>, <10, 10>}A.正确B.错误正确答案:B19.设A={a,b,c},B={1,2,3},作f:A→B,则共有9个不同的函数.A.正确B.错误正确答案:B20.设A={1,2},B={ a,b,c },则A´B的元素个数为8.()A.正确B.错误正确答案:B离散数学(本)·形考任务二1.n阶无向完全图Kn的边数是().A.nB. n(n-1)/2C. n-1D.n(n-1)正确答案:B2.n阶无向完全图Kn每个结点的度数是().A.nB. n(n-1)/2C.n-1D.n(n-1)正确答案:C3.已知无向图G的结点度数之和为20,则图G的边数为().A.5B.15C.20D.10正确答案:D4.已知无向图G 有15条边,则G的结点度数之和为().A.10B.20C.30D.5正确答案:C5.图G如图所示,以下说法正确的是( ) .A.{(a, e)}是割边B.{(a, e)}是边割集C.{(a, e) ,(b, c)}是边割集D.{(d,e)}是边割集正确答案:D6.若图G=<V,E>,其中V={ a,b,c,d },E={ (a,b), (b,c) , (b,d)},则该图中的割点为().A.aB.bC.cD.d正确答案:B7.设无向完全图K有n个结点(n≥2),m条边,当()时,K 中存在欧拉回路.A.m为奇数B.n为偶数C.n为奇数D.m为偶数正确答案:C8.设G是欧拉图,则G的奇数度数的结点数为( )个.A.0B.1C.2D.4正确答案:A9.设G为连通无向图,则()时,G中存在欧拉回路.A.G不存在奇数度数的结点B.G存在偶数度数的结点C.G存在一个奇数度数的结点D.G存在两个奇数度数的结点正确答案:A10.设连通平面图G有v个结点,e条边,r个面,则.A.v + e - r=2B.r +v - e =2C.v +e - r=4D.v +e – r = –4正确答案:B11.已知图G中有1个1度结点,2个2度结点,3个3度结点,4个4度结点,则G的边数是15.( )A.正确B.错误正确答案:A12. 设G是一个无向图,结点集合为V,边集合为E,则G的结点度数之和为2|E|.( )A.正确B.错误正确答案:A13. 若图G=<V,E>,其中V={ a,b,c,d },E={ (a,b), (a,d),(b,c), (b,d)},则该图中的割边为(b,c).( )A.正确B.错误正确答案:A14. 边数相等与度数相同的结点数相等是两个图同构的必要条件.A.正确B.错误正确答案:A15. 若图G中存在欧拉路,则图G是一个欧拉图.A.正确B.错误正确答案:B16. 无向图G存在欧拉回路,当且仅当G连通且结点度数都是偶数.( )A.正确B.错误正确答案:A17. 设G是具有n个结点m条边k个面的连通平面图,则n-m=2-k.A.正确B.错误正确答案:A18.设G是一个有6个结点13条边的连通图,则G为平面图.A.正确B.错误正确答案:B19. 完全图K5是平面图.A.正确B.错误正确答案:B20. 设G是汉密尔顿图,S是其结点集的一个子集,若S的元素个数为6,则在G-S中的连通分支数不超过6A.正确B.错误正确答案:A离散数学(本)·形考任务三1.无向图G是棵树,边数为12,则G的结点数是().A.12B.24C.11D.13正确答案:D2.无向图G是棵树,边数是12,则G的结点度数之和是().A.12B.13C.24D.6正确答案:C3.无向图G是棵树,结点数为10,则G的边数是().A.9B.10C.11D.12正确答案:A4.设G是有10个结点,边数为20的连通图,则可从G中删去()条边后使之变成树.A.12B.9C.10D.11正确答案:D5.设G是有n个结点,m条边的连通图,必须删去G的( )条边,才能确定G 的一棵生成树.A.m-n+1B.m-nC.m+n+1D.n-m+1正确答案:A6.设A(x):x是金属,B(x):x是金子,则命题“有的金属是金子”可符号化为().A.(x)(A(x)∧B(x))B.┐("x)(A(x)→B(x))C.(x)(A(x)∧B(x))D.┐(x)(A(x)∧┐B(x))正确答案:C7.设A(x):x是学生,B(x):x去跑步,则命题“所有人都去跑步”可符号化为().A.($x)(A(x)∧B(x))B.("x)(A(x)→B(x))C.($x)(A(x)∧┐B(x))D.("x)(A(x)∧B(x))正确答案:B8.设A(x):x是书,B(x):x是数学书,则命题“不是所有书都是数学书”可符号化为().A.┐("x)(A(x)→B(x))B.┐($x)(A(x)∧B(x))C.("x)(A(x)∧B(x))D.┐($x)(A(x)∧┐B(x))正确答案:A9.("x)( P(x,y)∨Q(z))∧($y) (R(x,y) → ("z) Q(z))中量词“"”的辖域是().A.P(x,y)B.P(x,y)∨Q(z)C.R(x,y)D.P(x,y)∧R(x,y)正确答案:B10.设个体域D={a,b,c},那么谓词公式($x)A(x)∨("y)B(y)消去量词后的等值式为( ).A.(A(a)∨A(b)∨A(c))∨(B(a)∧B(b)∧B(c))B.(A(a)∧A(b)∧A(c))∨(B(a)∨B(b)∨B(c))C.(A(a)∨A(b)∨A(c))∨(B(a)∨B(b)∨B(c))D.(A(a)∧A(b)∧A(c))∨(B(a)∧B(b)∧B(c))正确答案:A11.若无向图G的边数比结点数少1,则G是树.A.正确B.错误正确答案:B12.无向图G是树当且仅当无向图G是连通图.A.正确B.错误正确答案:B13.无向图G是棵树,结点度数之和是20,则G的边数是9A.正确B.错误正确答案:B14.设G是有8个结点的连通图,结点的度数之和为24,则可从G中删去5条边后使之变成树.A.正确B.错误正确答案:A15.设个体域D={1,2,3},则谓词公式("x)A(x)消去量词后的等值式为A(1)∧A(2)∧A(3).A.正确B.错误正确答案:A16.设个体域D={1, 2, 3, 4},则谓词公式($x)A(x)消去量词后的等值式为A(1 ) ∨A(2) ∨ A(3) ∨ A(4)A.正确B.错误正确答案:A17.设个体域D={1, 2},则谓词公式("x)P(x) ∨($x)Q(x)消去量词后的等值式为(P (1)∧P (2)) ∨(Q(1)∨Q(2)).A.正确B.错误正确答案:A18.("x)(P(x)∧Q(y)→R(x))中量词“"” 的辖域为(P(x)∧Q(y)).A.正确B.错误正确答案:B19. ("x)(P(x)∧Q(y))→R(x)中量词“"” 的辖域为(P(x)∧Q(y)).A.正确B.错误正确答案:A20.设A(x):x是人,B(x):x是学生,则命题“有的人是学生”可符号化为┐( x)(A(x)∧┐B(x))A.正确B.错误正确答案:B大作业1. 在线提交word文档第一部分一、公式翻译题(每小题2分,共10分)1.将语句“我会英语,并且会德语.”翻译成命题公式.参考答案:设p.我学英语Q:我学法语则命题公式为:pΛQ2.将语句“如果今天是周三,则昨天是周二.”翻译成命题公式.参考答案:设P:今天是周三Q:昨天是周二则命题公式为:P→Q3.将语句“小王是个学生,小李是个职员.”翻译成命题公式.参考答案:设P:小王是个学生Q:小李是个职员则命题公式为:P∧Q4.将语句“如果明天下雨,我们就去图书馆.”翻译成命题公式.参考答案:设P:如果明天下雨Q:我们就去图书馆则命题公式为:P→Q5.将语句“当大家都进入教室后,讨论会开始进行.”翻译成命题公式.参考答案:设P:当大家都进入教室后Q:讨论会开始进行则命题公式为:P→Q二、计算题(每小题10分,共50分)1.设集合A={1, 2, 3},B={2, 3, 4},C={2, {3}},试计算(1)A-C;(2)A∩B;(3)(A∩B)×C.参考答案:(1)A-C={l,3};(2)A∩B={2,3};(3)(A∩B)×C= { <2,2>,<2, {3} > ,<3,2> ,<3, {3} >}.2. 设G=<V,E>,V={v1,v2,v3,v4,v5},E={(v1,v3) , (v1,v5) , (v2,v3) , (v3,v4) , (v4,v5) },试(1)给出G的图形表示;(2)求出每个结点的度数;(3)画出其补图的图形.参考答案:(1)关系图编辑(2)deg(v1)=3deg(v2)=2deg(v3)=3deg(v4)=2deg(v5)=2(3)补图编辑3.试画一棵带权为1, 2, 3, 3, 4的最优二叉树,并计算该最优二叉树的权.参考答案:编辑权为1×3+2×3+3×2+3×2+4×2=294.求出如下所示赋权图中的最小生成树(要求写出求解步骤),并求此最小生成树的权.编辑参考答案:解:用Kruskal 算法求产生的最小生成树,步骤为:w(v2,v6)=1 选(v2,v6)w(v4,v5)=1 选(v4,v5)w(v1,v6)=2 选(v1,v6)w(v3,v5)=2 选(v3,v5)w(v2,v3)=4 选(v2,v3)最小生成树如图所示:编辑最小生成树的权w(T)=1+1+2+2+4=10. 5. 求P→(Q∧R) 的析取范式与合取范式. 参考答案:解:(P∨Q)→R⇔┐(P∨Q)∨R⇔(┐P∧┐Q)∨R(析取范式)⇔(┐P∨R)∧(┐Q∨R)(合取范式)。
离散数学-几种特殊图

第四讲几种特殊图一、小结本讲主要介绍欧拉图与汉密尔顿图、平面图与着色以及一些相关的概念与结论等。
1.欧拉图的概念给定无孤立结点图G ,若存在一条路经过图G的每条边一次且仅一次,则该路称为欧拉路;若存在一条回路经过图G的每条边一次且仅一次,在该回路称为欧拉回路;具有欧拉回路的图称为欧拉图;具有欧拉路但无欧拉回路的图称为半欧拉图。
规定平凡图为欧拉图。
2.欧拉路与回路存在的充要条件无向图G具有一条欧拉路,当且仅当G是连通的,且有零个或2个奇数度数的结点。
无向图G具有一条欧拉回路,当且仅当G是连通的,并且它的结点度数都是偶数的。
3.汉密尔顿图的概念给定图G ,若存在一条路经过图G的每个结点一次且仅一次,则该路称为汉密尔顿路;若存在一条回路经过图G的每个结点一次且仅一次,则该回路称为汉密尔顿回路;具有汉密尔顿回路的图称为汉密尔顿图;具有汉密尔顿路但无汉密尔顿回路的图称为半汉密尔顿图。
4.汉密尔顿回路存在的必要条件若图G=<V,E>中具有一条汉密尔顿回路,则对于结点集V的每个非空子集S均有W(G-S)£|S|成立,其中W(G-S)是(G-S)中连通分支数。
5.汉密尔顿路存在的充分条件设G=<V,E>是具有n个结点的简单图,若在G中每一对结点度数之和大于等于n - 1,则在G中存在一条汉密尔顿路。
6.平面图的概念设G=<V,E>是一个无向图,如果能把G的所有结点与边画在平面上,并且使得任何两条边除端点外没有其他的交点,则称G是一个平面图(也称可平面图).显然平面图的边与边只在结点处相交。
将平面图“图示在平面上”,有时也说成“将平面图嵌入一平面”。
7.平面图的面、边界、面的次数等概念设G是一个连通平面图,如果由图中的边所包围的一个区域内既不包含图的结点,也不包含图的边,则这个区域称为G的一个面,包围该面的所有边所构成的回路称为这个面的边界。
面r的边界的回路长度称为该面的次数,记为deg(r)。
自考离散数学02324真题含答案(2009.4-2016.4年整理版)

全国2009年4月自学考试离散数学试题(附答案)课程代码:02324一、单项选择题(本大题共15小题,每小题1分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列为两个命题变元P,Q的小项是()A.P∧Q∧⎤ P B.⎤ P∨QC.⎤ P∧Q D.⎤ P∨P∨Q2.下列语句中是真命题的是()A.我正在说谎B.严禁吸烟C.如果1+2=3,那么雪是黑的D.如果1+2=5,那么雪是黑的3.设P:我们划船,Q:我们跑步。
命题“我们不能既划船又跑步”符号化为()A.⎤ P∧⎤ Q B.⎤ P∨⎤ QC.⎤(P↔Q)D.⎤(⎤ P∨⎤ Q)4.命题公式(P∧(P→Q))→Q是()A.矛盾式B.蕴含式C.重言式D.等价式5.命题公式⎤(P∧Q)→R的成真指派是()A.000,001,110,B.001,011,101,110,111C.全体指派D.无6.在公式(x∀)F(x,y)→(∃y)G(x,y)中变元x是()A.自由变元B.约束变元C.既是自由变元,又是约束变元D.既不是自由变元,又不是约束变元7.集合A={1,2,…,10}上的关系R={<x,y>|x+y=10,x∈A,y∈A},则R的性质是()A.自反的B.对称的C.传递的、对称的D.反自反的、传递的8.若R和S是集合A上的两个关系,则下述结论正确的是()A.若R和S是自反的,则R∩S是自反的B.若R和S是对称的,则R S是对称的C.若R和S是反对称的,则R S是反对称的D.若R和S是传递的,则R∪S是传递的9.R={<1,4>,<2,3>,<3,1>,<4,3>},则下列不是..t(R)中元素的是()A.<1,1> B.<1,2>C.<1,3> D.<1,4>10.设A={{1,2,3},{4,5},{6,7,8}},下列选项正确的是()A.1∈A B.{1,2,3}⊆AC.{{4,5}}⊂A D.∅∈A11.在自然数集N上,下列运算是可结合的是()A.a*b=a-2b B.a*b=min{a,b}C.a*b=-a-b D.a*b=|a-b|12.在代数系统中,整环和域的关系是()A.整环一定是域B.域不一定是整环C.域一定是整环D.域一定不是整环13.下列所示的哈斯图所对应的偏序集中能构成格的是()A.B.C.D.14.设G为有n个结点的简单图,则有()A.Δ(G)<n B.Δ(G)≤nC.Δ(G)>n D.Δ(G)≥n15.具有4个结点的非同构的无向树的数目是()A.2 B.3C.4 D.5二、填空题(本大题共10小题,每小题2分,共20分)请在每小题的空格中填上正确答案。
离散数学 第4-5章

例题6: 1 2 带权图如右,求图的最小生成树 6 5 e 4 解:选取含最大边(c,d)的回路cdec, 3 删去其中权数最大的边(c,d),然后 b 1 c 再选取含最大边(a,b)的回路abea,删去其中权数最 大的边(a,b),再选取含最大边(c,e)的回路bceb,删 去其中权数最大的边(c,e),再选取含最大边(a,d)的 回路adea,删去其中权数最大的边(a,d),即得最小 a 生成树。 d 1 T=<{a,b,c,d,e},{(c,b),(b,e),(e,a),(e,d)}>。 e 2
汉密尔顿图的判定:
必要条件但不是充分条件定理: 1。在汉密尔顿图G中删除结点集V1后,G-V1的 连通分支数W (G V1 ) | V 1|。不满足这一条件的图一 定不是汉密尔顿图。 充分条件但不是必要条件定理: 2。如果无向简单图G中任何一对结点的度数之和 都大于等于结点数,则G中存在一条汉密尔顿回路。
例题4: 下列结论不正确的是( D )。 A)无向连通图G是欧拉图的充分必要条件是G不 含奇数度结点 B)非平凡连通图G有欧拉通路的充分必要条件是 G最多有两个奇数度结点 C)有向连通图D是欧拉图的充分必要条件是D的 每个结点的入度等于出度 D)有向连通图D是有向欧拉图的充分必要条件是 除两个结点外,每个结点的入度等于出度
例题3: 设G是无向图如右(彼得森图), 说明G不是欧拉图。 解:因为无向图G中所有的 结点的度数全为奇数,所以 G不是欧拉图。 2。无向连通图存在欧拉通路的充分必要条件是图 中只有两个奇数度的结点。 3。当n为奇数时,完全无向图Kn是欧拉图。例 如K3、K5等。 4。当n为偶数时,完全无向图Kn不是欧拉图,也 不存在欧拉通路。
g
例题8: 设图G如右,作图G 的嵌入图,说明图G是 平面图。 解: 图G的嵌入图如下, 故图G是平面图。
《离散数学》第七章_图论-第3-4节

图的可达性矩阵计算方法 (3) 无向图的可达性矩阵称为连通矩阵,也是对称的。 Warshall算法
例7-3.3 求右图中图G中的可达性矩 阵。 分析:先计算图的邻接矩阵A布尔乘法的的2、 v1
3、4、5次幂,然后做布尔加即可。
解:
v4
v2
v3 v5
P=A∨ A(2) ∨ A(3) ∨A(4)∨A(5)
图的可达性矩阵计算方法(2)
由邻接矩阵A求可达性矩阵P的另一方法: 将邻接矩阵A看作是布尔矩阵,矩阵的乘法运算和加 法运算中,元素之间的加法与乘法采用布尔运算 布尔乘:只有1∧1=1 布尔加:只有0∨0=0 计算过程: 1.由A,计算A2,A3,…,An。 2.计算P=A ∨ A2 ∨ … ∨ An P便是所要求的可达性矩阵。
v4
v3
v2
G中从结点v2到结点v3长度 为2通路数目为0,G中长 度为2的路(含回路)总数 为8,其中6条为回路。 G中从结点v2到结点v3长度 为3的通路数目为2, G中 长度为3的路(含回路)总
图的邻接矩阵的 应用 (2)计算结点vi与vj之间的距离。
中不为0的最小的L即为d<vi,vj>。
(一)有向图的可达性矩阵
可达性矩阵表明了图中任意两个结点间是否至少存在一条 路以及在任何结点上是否存在回路。
定义7-3.2 设简单有向图G=(V,E),其中V={v1, v2,…,vn },n阶方阵P=(pij)nn ,称为图G的可达 性矩阵,其中第i行j列的元素
p ij =
1 1 1 1 P v3 1 1 v4 0 0 v5 0 0 v1 v2 1 1 1 1 1 1
0 1 A(G)= 1 0 0 1 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 1 0
4.4-Hamilton图_ou_简

关于Hamilton路和Hamilton回路的性质
5. 若图中有n个点,则 Hamilton路恰有n-1条边, Hamilton 回路恰有n条边。 6. Hamilton路是图G的支撑子树, Hamilton回路是图G的支撑子图。
二、H路、H图的必要条件
定理4.4.1 如果图G=(P, L)是Hamilton图,则
3 7
6
5 8 3
例:
右图“度序列”: (3, 3, 3, 5, 5, 6, 7, 8, 8) m=3时, d3 =3 ≤3, d9-3=d6 =6 <6;前者 成立,后者不成立, m=4时, d4 =5 ≤4, d9-4=d5 =5 <5;都不 成立; 从而,这是H图. Note:定理4.4.4强于定理4.4.2
比较H路、H回路与Euler路
Euler路未必简单有向路; H路一定为简单路,H回路为回路。 H路着眼于无重复地遍历图中诸点; Euler路着眼于无重复地遍历有向图中诸弧。 H路、 H回路是G的支撑子图, H路是G的支撑树; Euler路未必为G的支撑子图。 存在Euler路,未必存在 H回路。 存在H回路,未必存在Euler路。
§4.4 Hamilton图
Hamilton回路问题 沿着正十二面体的棱寻找一条旅行路线,通过每个城市恰好一次又回 到出发城市。
§4.4.1 Hamilton路及必要条件
一、H路、H回路
定义4.4.1 设G=(P, L)是有限图,且|P(G)|≥3, (v1, … , vn)是G中一条路。如果G中每点恰在此路中出 现一次,则称此路为Hamilton路。 如果G中每点,除v1外,恰在此路中出现一次,而 v1=vn,则此路称为Hamilton回路。 定义4.4.2 设G=(P, L)是有限图,如果G中有一条 Hamilton回路,则称G为Hamilton图。 显然,由m个节点构成的完全图Km是Hamilton图。
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Sir William Rowan Hamilton, 1857, Icosian game: 是否存在一条回路,使它含有图中的所有顶点 一次且仅一次?
1
马的周游路线(knight’s tour)
棋盘上马的周游路线(knight’s tour on a chessboard)
2
汉密尔顿图
1. 周游世界,汉密尔顿通(回)路,汉密尔顿 图 2. 判定汉密尔顿图的必要条件 3. 判定汉密尔顿图的充分条件 4. 旅行商问题
3
Willam Rowan Hamilton
Willam Rowan Hamilton(1805~1865):
爱尔兰神童(child prodigy), 三一学院(Trinity College), 光学(optics) 1827, Astronomer Royal of Ireland. 1837, 复数公理化, a+bi, (a,b) 四元数(quaternion): a+bi+cj+dk, 放弃乘 法交换律!
8
无向半汉密尔顿图的必要条件
推论: 设G=<V,E>是无向半汉密尔顿图, 则对V的任意非空真子集V1有 p(G-V1)≤|V1|+1 证明: 设P是G中任意汉密尔顿通路, 当V1 中顶点都在P内部且都不相邻时, p(PV1)= |V1|+1最大; 否则, p(P-V1)≤|V1|. P 是G的生成子图, 所以p(G-V1)≤p(PV1)≤|V1|+1. #
路径--极大路径--圈--更长路径 ---更长极大路径--更长圈--更长路径--……--汉密尔顿通路(构造法)
16
极大路径
Γ是一条路径,如果Γ的始点和终点都不 与Γ外的顶点相邻,则称Γ是一条极大路 径。 极大:不能再向外延伸
17
定理15.7(证明(1)(3))
证明: (1) G连通: ∀u∀v( (u,v)∉E→ ∃w((u,w)∈E∧(w,v)∈E ) n-2
设二部图G=<V1, V2, E>, |V1|≤|V2|, |V1|≥2, |V2|≥2
若G是汉密尔顿图,则|V1|=|V2|; 若G是半汉密尔顿图,则|V1|=|V2|-1; 若|V2| ≥ |V1|+2;若G不是半汉密尔顿图, 也不是汉密尔顿图
14
反例: 非充分条件
上述条件只是必要条件,而不是充分条件 反例: Petersen图
27
TSP的复杂性
蛮力法(brute force): 穷举所有的可能进 行验证或比较, 复杂性为2n以上. TSP: n!条H通路, (n-1)!/2条H回路 目前还不知道TSP是否有多项式时间算法, TSP , 大多数学者认为没有. 证明? P=?NP问题: 计算机科学的核心问题, 奖 金$1,000,000
15,18-20
32
24
应用举例
例:七天内安排七门课的考试,使得同一位教 师所担任的两门课程不在相邻的两天考试,若 无教师担任多于四门课程,则可以合理安排。 每个顶点对应一门考试课程,两个顶点之间有 边当且仅当对应两课程由不同教师担任,每个 顶点的度数至少是3,任两个顶点度数之和至 少为6,因此一定存在一条汉密尔顿通路。
30
作业2:
2、今有a,b,c,d,e,f,g7个人,已知下列 事实:
a会讲英语; b会讲英语和汉语; c会讲英语、意大利语和俄语; d会讲日语和汉语; e会讲德语和意大利语; f会讲法语、日语和俄语; g会讲法语和德语。
试问这7个人应如何排座位,才能使每个人都 能和他身边的人交谈?
31
作业3:
v0 v0 vi vi+1 vk vk
19
无向汉密尔顿图的充分条件
推论1: 设G是n(≥3)阶无向简单图,若对G 中任意不相邻顶点u与v有 d(u)+d(v)≥n 则G是汉密尔顿图. 证明: 由定理15.7知G连通且有汉密尔顿 通路Γ=v0v1…vn. (1) 若(v0,vn)∈E,则得汉 密尔顿回路C=v0v1…vnv0. (2) 若 (v0,vk)∉E,则与定理15.7证明(2b)类似,也 存在汉密尔顿回路. # v0 vn
6
汉密尔顿图(Hamilton)的思考
n阶简单图是汉密尔顿图,要求m≥n ——要有尽可能多的边
K3,3
K5
7
无向汉密尔顿图的必要条件
定理15.6: 设G=<V,E>是无向汉密尔顿 图,则对V的任意非空真子集V1有 p(G-V1)≤|V1| 证明: 设C是G中任意汉密尔顿回路, 当V1 中顶点在C中都不相邻时, p(C-V1)=|V1| 最大; 否则, p(C-V1)<|V1|. C是G的生成 子图, 所以p(G-V1)≤P(C-V1)≤|V1|. #
v0 vi vi+1 vn
20பைடு நூலகம்
无向汉密尔顿图的充分条件
推论2: 设G是n(≥3)阶无向简单图,若对G 中任意顶点u有 d(u)≥n/2 则G是汉密尔顿图. G . 推论3:Kn(n>2)为汉密尔顿图
21
图的闭包C(G)
定义:给定简单图G=<V,E>,|V|=n, 将图G中度数之和至少为n的非邻接顶点 连接起来得到图G ',对G '重复上述步骤, 直到不再有这样的顶点对为止,所得到 的图称为G 的闭包,记作C(G) 。
9
推论(证明二)
推论: 设G=<V,E>是无向半汉密尔顿图, 则对V的任意非空真子集V1有 p(G-V1)≤|V1|+1 证明二: 设P是G中任意汉密尔顿通路, 两 个端点是u与v. 令G1=G∪(u,v), 由定理3 有 p(G-V1) ≤ p(G1-V1)+1 ≤ |V1|+1. #
10
举例1
(3) 由圈得更长路径: 由连通性
18
定理15.7(证明(2))
证明: (2) 由极大路径得圈: 设极大路径 Γ=v0v1…vk, k≤n-2. (2a) 若(v0,vk)∈E,则得圈 C=v0v1…vkv0. (2b) 若(v0,vk)∉E,则 ∃i( 1≤i≤k-1∧(vi,vk)∈E∧(v0,vi+1)∈E ), 否则, d(v0)+d(vk)≤d(v0)+k-d(v0) =k ≤n-2(矛盾). 于是得圈C=v0…vivkvk-1…vi+1v0. #
22
定理5
定理5: 无向n阶简单图G是汉密尔顿图 ⇔ C(G)是汉密尔顿图.
23
引理
引理: 设u,v是无向n阶简单图G中两个不 相邻顶点,且d(u)+d(v)≥n, 则 G是汉密尔顿图 ⇔ G∪(u,v)是汉密尔顿图. 证明: (⇒)显然 (⇐) 设C是G∪(u,v)中的汉密尔顿回路. (1) C不经过(u,v): C是G中汉密尔顿回路. (2) C经过(u,v): C-(u,v)是G中汉密尔顿通 路, 与定理15.7证明(2b)类似, G中有汉密 尔顿回路. #
4
马的周游路线(knight’s tour)
Leohard Euler, 1759, 详细分析
5
汉密尔顿图(Hamilton)
汉密尔顿通路(Hamilton path): 经过图中 所有顶点的初级通路 汉密尔顿回路(Hamilton circuit/cycle): 经过图中所有顶点的初级回路 汉密尔顿图(Hamiltonian): 有汉密尔顿回 路的图 半汉密尔顿图(semi- Hamiltonian): 有汉 密尔顿通路但没有汉密尔顿回路的图
25
有向汉密尔顿图的充分条件
n(n>1)阶竞赛图中都有汉密尔顿通路。 证明:归纳法
v‘r-1 v‘2 v‘1 vk+1 vk+1
26
v‘1 v‘r
v‘2 vk+1 v‘2
v‘k
v‘1
v‘k
旅行商问题(TSP)
旅行商问题(Travling Salesman Problem): 给定n个城市之间的所有距离, 求推销员 走遍所有城市的最短路线 又名货郎担问题,巡回售货员问题,TSP TSP: 给定带权完全图G=<V,E,W>,求最 短汉密尔顿回路.
a
e b c d
f 二部图{a,f}和{b,c,d,e}
11
举例2
a e h b g j c 二部图{a,c,g,h,i}和{b,d,e,f,j,k} 半汉密尔顿图
12
f i k d
举例3
a b c g j d e 二部图{a,c,g,h,e}和{b,d,f,i,j} 汉密尔顿图
13
i h f
二部图与汉密尔顿图
Petersen图满足: ∀V1≠∅, p(G-V1)≤|V1| Petersen图不是汉密尔顿图: 穷举 Petersen图是半汉密尔顿图
15
无向半汉密尔顿图的充分条件
定理15.7: 设G是n(≥2)阶无向简单图,若对G中 任意不相邻顶点u与v有 d(u)+d(v)≥n-1 则G是半汉密尔顿图. 证明: (1) G连通 (2) 由极大路径得圈 (3) 由圈得更长路径
28
总结
周游世界,汉密尔顿通(回)路,汉密尔顿图 判定汉密尔顿图的必要条件 判定汉密尔顿图的充分条件 旅行商问题
29
作业1:
1、画一个无向图,使它是: (1)既是欧拉图,又是汉密尔顿图; (2)是欧拉图,而不是汉密尔顿图; (3)是汉密尔顿图,而不是欧拉图; (4)既不是欧拉图,也不是汉密尔顿图。
