概率论-第二十一讲--欧拉图与哈密尔顿图(略)

16
二、哈密尔顿图
例5. 证明下图中没有汉密尔顿路径。 图中，3个顶点标记为A，5个顶点 A 标记为B，相差2个，不可能存在 一条汉密尔顿路径。 B B 如果在标记过程中，遇到相邻结 点出现相同标记时，如果有一个 结点的度数为2，可在此对应边上 A A 增加一个结点，并标上相异标 A 记。 B B B B B
11
二、哈密尔顿图
定理3：若无向图G=<V,E>是哈密尔顿图， V1是V的任意非空 真子集，则 ω(G- V1)≤| V1 |。 证明：设C是G的一条哈密尔顿回路，对于V的每个非空真子集 V1有：ω(C-V1) ≤|V1|
ω(C- V1)是C删去V1中所有顶点及关联的边后所得图
的连通分支数。 又因为C - V1是G - V1的生成子图，故有
13
二、哈密尔顿图
定义3：若无向图G＝<V,E>的顶点集合V可以划分成两个子集X 和Y，使G中的每一条边e的一个端点在X中，另一个端点 在Y中，则称G为二部图或偶图。二部图可记为 G＝<X,E,Y>，X和Y称为互补结点子集。 二部图不会有自回路。
14
二、哈密尔顿图
定理4：设二部图G=<X, E, Y>，设|X|=m，|Y|=n。若m≠n，则G 必不是汉密尔顿图。 证明：方法1. 用汉密尔顿图的性质证明。 因为|X|≠|Y|，不妨设|X|<|Y|。 显然有ω(G-X)=|Y|>|X|， 这与汉密尔顿图的必要条件ω(G-X)≤|X|矛盾。 因此G必不是汉密尔顿图。
定理2：一个有向连通图具有欧拉路径，当且仅当它 的每个顶点的引入次数等于引出次数，可能 有两个顶点除外，其中一个的引入次数比它 的引出次数大1，另一个的引入次数比它的 引出次数小1。 推论： 一个有向连通图具有欧拉回路，当且仅当它 的每个顶点的引入次数等于引出次数。
5
一、欧拉图
例2
(a)
(b)
(c)
15
二、哈密尔顿图
定理4：设二部图G=<X, E, Y>，设|X|=m，|Y|=n。若m≠n，则G 必不是汉密尔顿图。 证明：方法2. 用二部图的性质证明。 因为|X|≠|Y|,不妨设 |X|<|Y|。 假设G是汉密尔顿图，则G中存在汉密尔顿回路C。因为 |X|<|Y|，所以在C中必然存在u,v∈Y，且u,v在C中邻接。因 此边(u, v) ∈E，这与二部图中任何一条边一个端点在X中另 一个端点在Y中矛盾。 因此G必不是汉密尔顿图。 推论：设二部图G=<X, E, Y>，设|X|=m，|Y|=n。若|m-n|>1， 则G中必不存在汉密尔顿路径。
10
二、哈密尔顿图
目前还没有找到一个简明的条件来作为哈密尔顿回路存 在的充要条件。 必要条件： 定理3：若无向图G=<V,E>是哈密尔顿图， V1是V的任意非空 真子集，则 ω(G- V1)≤| V1 |。 | V1 |：V1的基数，
ω(G- V1)：G删去V1中所有顶点及关联的边后所得图
的连通分支数。
欧拉图与哈密尔顿图
一、欧拉图
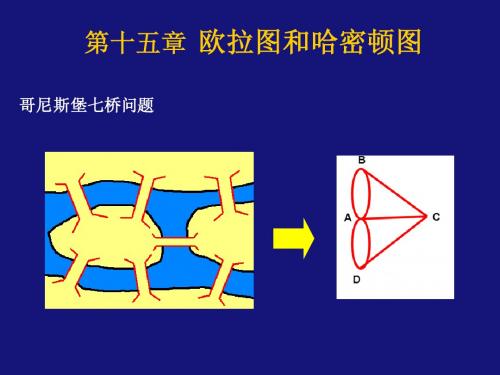
Konigsberg(哥尼斯堡)七桥问题：
1
一、欧拉图
定义1：设G=<V,E>是不含孤立顶点的无向图， 若G中存在一条路径经过G中每条边一次且仅一次的路径， 称为欧拉路径； 若G中存在一条回路经过G中每条边一次且仅一次的回路称 为欧拉回路；具有欧拉回路的图称为欧拉图。 即“一笔画问题”，每条边画且仅画一次，一笔画完。若回 到出发点，则为欧拉图；回不到出发点，则有欧拉路径。
7
二、哈密尔顿图
环球航行问题： 英国数学家Hamilton１８５９年提出的一种 游戏。一个实心的正十二面体的20个顶点标上世 界著名大城市的名字，要求游戏者从某一城市出 发，遍历各城市一次且仅一次，最后回到原地。 即“周游世界”问题。
8
二、哈密尔顿图
9
二、哈密尔顿图
定义2：在无向图G=<V,E>中， 经过G中的每个顶点一次且仅一次的路径称为哈密尔 顿路径。 经过G中的每个顶点一次且仅一次的回路称为哈密尔 顿回路。具有哈密尔顿回路的图称为哈密尔顿图。
2
一、欧拉图
定理1：无向连ቤተ መጻሕፍቲ ባይዱ图G具有一条欧拉路径，当且仅当 G具有零个或者两个奇数次数的顶点。 推论：无向连通图G具有一条欧拉回路，当且仅当 其顶点次数都是偶数。
3
一、欧拉图
例1
(a) (a)是欧拉图；
(b)
(c)
(b)不是欧拉图，但存在欧拉路径； (c)既不是欧拉图，也不存在欧拉路径。
4
一、欧拉图
A 若图具有哈密尔顿路径，则A和B 数目要么相等，要么相差1。 （逆不成立）
17
二、哈密尔顿图
充分条件： 定理4：设G=<V,E>是具有n≥3个顶点的简单无向图， 若在G中每一对顶点的次数之和大于等于n， 则在G中存在一条哈密尔顿回路。 定理5：设G=<V,E>是具有n≥3个顶点的简单无向图， 若在G中每一对顶点的次数之和大于等于n-1， 则在G中存在一条哈密尔顿路径。 注意：定理4、5的逆定理不成立。
ω(G- V1)≤ ω(C- V1) ≤ | V1 | 。
该定理可用来判定某些无向图不是哈密尔顿图。
12
二、哈密尔顿图
例4(a)
V
令V1＝{v}, ω(G- V1)=2>|V1| 所以G非哈密尔顿图。
G
(b) 任意非空集 V 1 ⊆ V 有 ω(G- V1) ≤ | V1 | 但G却非哈密尔顿图－－典型例子。 说明定理3逆定理不成立。
18
二、哈密尔顿图
判断下图是不是哈密尔顿图?
图中 (1), (3),不是哈密尔顿图,(2) 为哈密尔顿图。
19
作业 P262 8-2习题 14，15
20
(a)是欧拉图； (b)不是欧拉图，但存在欧拉路径； (c)既不是欧拉图，也不存在欧拉路径。
6
一、欧拉图
例3. 一块多米诺骨牌排是由两个半面组成的。这些方块被 表明1、2、3、4、5、6个点或空白。问：是否可能将 28块不同的多米诺骨牌排成一个圆环,使得在这个排列 中,每两块相邻的多米诺骨牌其相邻的两个半面是相同 的。 解：构造一个具有7个顶点的图,这些顶点对应于空白、1、 2、3、4、5和6,在每两个顶点之间都有一条边,我们把 这条边当作一块多米诺骨牌,并且把这条边相关联的两 个顶点当作它的两个半面。图中28条边恰好对应28块 不同的多米诺骨牌，因此圆环排列问题对应于图中是 否存在一条欧拉回路，因为每个顶点的度数都为8，所 以欧拉回路是存在的。