研究生《机械系统动力学》试卷及答案
合肥工业大学机械动力学基础试题(含部分答案)

②由动能定理可知: E = m1 x12
1 2
其中 x1 a , x2 b , 为杆转过的角度. J eq m1a 2 m2b2 再求等效刚度, keq x 2
1 2
1 2 1 2 2 kx2 kb keq kb2 2 2
④推导出用单元节点位移表示的单元应变、单元应力表达式,再利用虚功方程建立单元节 点力阵与节点位移列阵之间的关系,形成单元的刚度方程式。 ⑤根据系统的动能与势能,得到各单元的刚度矩阵和质量矩阵。 ⑥考虑整体结构的约束情况,修正整体刚度方程,求解单元节点的运动方程。 ⑦由单元节点的运动方程“装配”成为全系统的运动方程。 (6)简述机械系统的三要素及动力学模型。 (2012) 答:三要素:惯性、弹性、阻尼. 动力学模型:①集中参数模型,由惯性元件、弹性元件和阻尼元件等离散元件组成;②有 限单元模型,由有限个离散单元组成,每个单元则是连续的;③连续弹性体模型将实际结 构简化成质量和刚度均匀分布或按简单规律分布的弹性体. 3. 试求图示振动系统的运动微分方程和固有频率。 (图 3、图 5 作纯滚动)
不作用外载荷时的力矩平衡可列为: ∴系统固有频率为:
M J
eq
keq 0
keq J eq
kb 2 . m1a 2 m2b 2
③由于 m作纯滚动,则运动微分方程可表示为: J kx r 0 ,其中 J 为 m相对于接地 点的转动惯量, J
kk mx kx 0 ,即: mx 1 2 k3 cos 2 x 0 k1 k2
∴系统固有频率为:n
k m
k1k2 k3 cos 2 k k k (k k 2 ) cos 2 k1 k 2 . = 1 2 3 1 m m(k1 k 2 )
第11章机械系统动力学

第十一章机械系统动力学11-1填充题(1) _____________________________ 机器速度波动的类型有______________________________ 和两种。
前者一般采用的调节方法是_______ ,后者一般采用的调节方法是_________ 。
(2)用飞轮进行调速时,若苴它条件不变,则要求的速度不均匀系数越小,飞轮的转动惯量将越—。
在满足同样的速度不均匀系数条件下,为了减小飞轮的转动惯量,应将飞轮安装在___________ 轴上。
(3)___________________________________________________ 最大盈亏功是指机械系统在一个运动循环中的与 _________________________________________________ 之差的最大值。
(4) ____________________________________________________________________________ 某机械主轴实际转速在其平均转速的±3%范围内变化,则其速度不均匀系数忌___________________________ 。
(5)某机器的主轴平均角速度^lOOrad/s,机器运转的速度不均匀系数飪0.05,则该机器的最大角速度如《等于_______ r ad/s,最小角速度轴加等于 ________ rad/s。
11-2选择题(1)_______________________________________________________________________________________ 在周期性速度波动中,一个周期内等效驱动力做功瞅1与等效阻力做功M的疑值关系是__________________A.Wd>Wr;B.恥<昭;C. WWr:D.肌=%(2)在机械系统的启动阶段,系统的动能______ ,并且 _____ 。
第14章知识资料机械系统动力学(1)

2
m m (vv ) 等效质量:
n
e i 1
J
si
(i
v
)2
n
i 1
i
si
F F v 等效力:
n
e i 1
M(i vi )
(
iห้องสมุดไป่ตู้
si
v
)
c
osi
机械系统运动方程式的建立
等效构件为回转件时机械系统的运动方程简化式为:
经过推导,可得M以ed微 分 M形e式dt表示d的J e机2 械2 系统运动方程式为:
Wm a x
m2 J
20 π 202 0.3
0.52
max
m
(1
) 2
25.2
rad/s
m in
m (1
)
2
14.8
rad/s
ωmax发生在 32处;
ωmin 发生在
处。
五、试题自测及答案(1 、2、3、4)
1.一重力G1=450N的飞轮支承在轴径直径d=80 mm的轴
承 上 , 在 轴 承 中 摩 擦 阻 力 矩 作 用 下 , 飞 轮 转 速 在 14s 内 从 200 r/min 均匀地下降到150 r/min。若在飞轮轴上再装上
以积分方式表示的机械系统运动方程式为:
F s
s0
e
ds
s s0
(Fd
Fr
)ds
1 2
mv2
1 2
m0v02
以上两个公式在具体应用时要看使用哪个方程更简单。
机器运转的速度波动
机器速度波动的原因是其驱动功与阻抗功并不时时相 等。或者说,其等效驱动力矩与等效阻力矩并不时时相等, 其转动惯量也不能随等效力矩作相应的变化,致使机器出 现盈功或亏功,产生速度的波动。
最新研究生《机械系统动力学》试卷及答案

太原理工大学研究生试题姓名: 学号: 专业班级: 机械工程2014级1 圆柱型仪表悬浮在液体中,如图1所示。
仪表质量为m ,液体的比重为ρ,液体的粘性阻尼系数为r ,试导出仪表在液体中竖直方向自由振动方程式,并求固有频率。
(10分)2 系统如图2所示,试计算系统微幅摆动的固有频率,假定OA 是均质刚性杆,质量为m 。
(10分)3 图3所示的悬臂梁,单位长度质量为ρ,试用雷利法计算横向振动的周期。
假定梁的变形曲线为⎪⎭⎫ ⎝⎛-=x L y y M 2cos 1π(y M 为自由端的挠度)。
(10分)4 如图4所示的系统,试推导质量m 微幅振动的方程式并求解θ(t)。
(10分)5 一简支梁如图5所示,在跨中央有重量W 为4900N 电机,在W 的作用下,梁的静挠度δst=0.2cm ,粘性阻尼使自由振动10周后振幅减小为初始值的一半,电机n=600rpm 时,转子不平衡质量产生的离心惯性力Q=1960N ,梁的分布质量略去不计,试求系统稳态受迫振动的振幅。
(15分)6 如图6所示的扭转摆,弹簧杆的刚度系数为K ,圆盘的转动惯量为J ,试求系统的固有频率。
(15分)7如图7一提升机,通过刚度系数m N K /1057823⨯=的钢丝绳和天轮(定滑轮)提升货载。
货载重量N W 147000=,以s m v /025.0=的速度等速下降。
求提升机突然制动时的钢丝绳最大张力。
(15分)8某振动系统如图8所示,试用拉个朗日法写出动能、势能和能量散失函数。
(15分)太原理工大学研究生试题纸图1 图2 图3图4 图5 图6图7 图8。
2014级研究生《机械系统动力学》试题A(word文档良心出品)

太原理工大学研究生试题A姓名: 学号: 专业班级: 机械工程2014级 课程名称: 《机械系统动力学》 考试时间: 120分钟 考试日期: 2015.12.11 题号 一 二 三 四 五 六 七 八 总分 分数1 求图1系统的当量刚度,悬臂梁端点的刚度分别为K 1和K 3。
(10分)2 系统如图2所示,假定水平杆OB 是无质量的刚性杆,试导出系统的自由振动方程式并求固有频率。
(10分)3 图3所示半径为r ,重量为W 的圆柱体在一个半径为R 的圆柱面内作无滑动的滚动,试导出圆柱体对圆柱面最低位置o 作微幅摆动的振动方程式。
(10分)4 计算图4所示系统的衰减振动频率并确定临界阻尼值。
已知:K=7056N/cm ,r=35.28N.s/cm ,m=17.64kg ,a=127cm, L=254cm 。
(10分)5 如图5所示,质量为m 的缸体与刚度为K 的弹簧相联,活塞的运动y=Asin ωt ,缸体与活塞间的粘性阻尼系数为r ,试确定缸体受到粘性阻尼力作用产生的振幅及它与活塞的相位关系。
(15分)6 如图6所示的系统,在重量mg=88.2N 作用下弹簧压缩了δst=0.25cm ,支承运动xH=Hcos ωt 。
当支承不动时,质量自由振动两相邻振幅之比Ai/Ai+1=0.8,试作出在0<ω/p <2范围内的幅频响应曲线。
(15分)7 质量弹簧系统如图7所示,其质量m 的振动方程为pt A x sin =(cm )。
弹簧单位长度质量为cm kg /02.0=ρ、长度cm L 50=,振动圆频率s rad p /6=,最大振幅cm A 5.0=。
试推导出弹簧的最大动能公式并根据以上数值求出max k T 。
(15分)8 如图8所示的系统,假定刚性杆的质量为m ,试求出在激振力t Q ωsin 0作用下,?=p ,?=n ,?=q (符号含义与教科书相同)(15分)太原理工大学研究生试题纸图1 图2 图3 图4 图5 图6LxKmabLr KθQ0sinωto图7 图8。
2014级研究生《机械系统动力学》试题B

太原理工大学研究生试题B姓名: 学号: 专业班级: 机械工程2014级1 求图1系统的当量刚度,钢丝绳的刚度为K 1,滑轮的质量忽略不计。
(10分)2 系统如图2所示,圆盘的转动惯量为I ,其旋转轴线与垂直方向成α角安装,圆盘上有一偏心质量m ,偏心距为a ,求系统微幅振动的频率。
(10分)3 试求图3所示系统的固有频率。
略去转轴和中间齿轮的转动惯量,已知:I1=235.2kg.cm2,I2=98kg.cm2, L1=75cm, L2=75cm, D1=15cm, D2=7.5cm, d1=5cm, d2=4cm 。
(10分)4 重量为W 的薄板挂在弹簧的下端,在空气中上下振动时,周期为T 1;在液体中上下振动时,周期为T 2。
假定空气阻尼略去不计,液体阻力表示为,其中2A 为薄板的总面积,为其运动速度。
试证明液体的粘性系数:2122212T T T AgT W -=πμ,见图4。
(10分) 5 如图5所示的单摆,其质量为m ,摆杆是无质量的刚性杆,长为L 。
它在粘性液体中摆动,粘性阻尼系数为r ,悬挂点O 的运动x(t)=Asin ωt ,试写出单摆微幅摆动的方程式并求解。
(15分)6 机器和机座由弹簧和阻尼支承如图6所示。
机器产生的惯性激振力频率ω=43rad /s ,机器与机座的重量为2450N,选择阻尼系数r=2.94N.s /cm 的材料制作隔振器(即阻尼器的阻尼系数r=2.94N.s /cm)。
问隔振系数η<0.1时,弹簧刚度K 应该多大? (15分)7 统如图7所示,其滑轮质量为M ,忽略绳的弹性和M 的转动(只考虑M 的上下振动),试用能量法确定系统的固有频率。
(15分)8如图8所示的振动系统,其支承的振动位移t H x H ωsin =,试求支承的最大振动力幅0Q 。
(15分)太原理工大学研究生试题纸图1 图2 图3图4 图5 图6图7 图8。
【2017年整理】机械动力学复习题
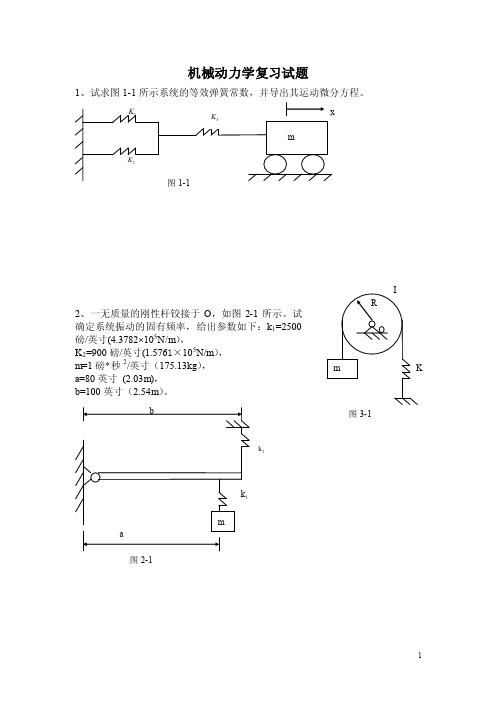
机械动力学复习试题1、试求图1-1所示系统的等效弹簧常数,并导出其运动微分方程。
2、一无质量的刚性杆铰接于O ,如图2-1所示。
试确定系统振动的固有频率,给出参数如下:k 1=2500磅/英寸(4.3782×105N/m ),K 2=900磅/英寸(1.5761×105N/m ), m=1磅*秒2/英寸(175.13kg ), a=80英寸 (2.03m), b=100英寸(2.54m )。
2k图3-1图2-13、试求出图3-1所示系统的固有频率。
弹簧是线性的,滑轮对中心0的转动惯量为I。
设R=2500磅/英寸(4.3782×105N/m),I=600磅*英寸*秒2(67.79N*m*s2),m=2.5磅*秒2/英寸(437.82kg),R=20英寸(0.5/m)4、一台质量为M的机器静止地置于无质量的弹性地板上,如图4-1所示。
当一单位载荷作用于中心点时的挠度为x st。
今在机器上放有一总质量为ms并带有两个旋转的不平衡质量的振动器提供一铅垂的谐波力mlw2sinwt,这里,转动的频率w是可以改变的。
试说明怎样用此振动器来测定系统弯曲振动的固有频率。
5,、图5-1中所示的系统模拟一在粗糙道路上运动的车辆,速度为均匀,即V=常数。
试计算其响应Z(t)和传给车辆的力。
图5-16,、试导出如图6-1所示系统的运动微分方程,并求解位移X1(t)。
图6-17、转动惯量分别为I1和I2的两个圆盘安装在扭转刚度分别为GJ1和GJ2的圆轴上如图7-1。
导出这两个圆盘的转动微分方程。
8、导出图8-1所示系统当θ为微小角时的运动微分方程。
GJ 1GJ 21()t θ2()t θM 2(t)M 1(t)I 1I 29、如图9-1所示在风洞中试验的机翼截面。
设机翼的总质量为m,绕其质心C 的转动惯量为I C,试导出器运动微分方程。
K1C O图9-1C图10-110、导出图10-1所示的三重摆的运动方程。
机械系统动力学试题a2008答案

机械系统动力学试题A平分标准1 填空(20)(每空2分)离散线性系统的数学模型可用线性常微分方程描述。
LTI系统为线性时不变系统。
静态设计主要考虑静态载荷作用,动态设计主要考虑振动与动态载荷作用。
系统有离散系统和连续系统。
确定性系统在随机激励下,响应是随机的。
重力场的势函数为-mgy 。
广义坐标为完全决定系统状态的独立参数。
牛顿力学的主要不便是处理约束反力不方便。
连续系统的自由度数为无穷多。
2 用拉格朗日方程建立单摆运动方程(20)。
解:3 写出建立拉格朗日方程的步骤(20)。
解:(1)确定系统自由度数,选取广义坐标(5);(2)计算系统动能E(5);(3)计算系统的广义力Q(5);(4)将动能和广义力代入格郎日方程,得系统运动微分方程(5)。
4如图,推导杆的纵向振动微分方程(20)。
解:微元所受的合力为:dx x F F T ∂∂=(2) 因为 xu AE A F T ∂∂==σ(3) 所以 dx xu AE dx x F F T 22∂∂=∂∂=(5) 微元的质量为:dx A M ρ=(2)代入牛顿定律得:dx tu A dx x u AE 2222∂∂=∂∂ρ(3) 222221t u c x u ∂∂=∂∂即(4) ρE c =2其中(1)5 等效力学模型微分方程中,已知等效转动惯量为常数,等效力矩为)(ϖe e M M =,0=t 时,0=ϖ,求时间和角速度的关系(20)。
解:等效力学模型微分方程为:e e e M dt d d dJ dt d J =⎪⎭⎫ ⎝⎛+22221ϕϕϕ(5) 因等效转动惯量为常数,故有:e e M dtd J =22ϕ(2) 即:e e M dtd J =ω,)(ϖe e M M =(3) 分离变量得:)(ϖωe e M d J dt =(5) 积分并应用初始条件,得:⎰=ωϖω0)(e e M d J t (5)。
2014年机械动力学基础考试题 参考答案

2014年机械动力学基础考试题参考答案一、判断题(每个1分,共10分)1、串联弹簧的等效刚度比原来各弹簧的刚度都要小,并联弹簧的等效刚度比原来各弹簧的刚度都要大。
√2、多自由度振动系统的运动微分方程组中,各方程间的耦合是振动系统的固有性质。
×3、自由振动系统的振幅、初相角及振动频率是系统的固有特征,与初始条件无关。
×4、固有振型关于质量矩阵、刚度矩阵和阻尼矩阵均具有正交性。
×5、单自由度无阻尼振动系统作用一简谐激励,若初始条件为0,即000x x==,系统不会有自由振动项。
×6、一般情况下,两自由度线性系统的自由振动是简谐振动。
×7、共振时无阻尼系统的振幅将随时间无限增大,响应滞后激励的相位角为π2。
√8、对于多自由度线性系统,当激振频率与其中任一固有频率相等时,系统都会发生共振。
√9、一般来说,系统的固有频率和固有振型的数目与系统的自由度数目相同。
√10、杜哈梅积分将激励视为非常短的脉冲的叠加,适用于单自由度有阻尼的质量-弹簧系统对任意激励的响应。
√二、简答题(每题5分,共计25分)(1)什么是机械振动?举例说明振动的优、缺点。
答:机械振动是指物体(或物体系)在平衡位置(或平均位置)附近来回往复的运动。
第二问为开放题(2)简述机械振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
答:实际阻尼是指振动系统的真实阻尼值,用于度量系统自身消耗振动能量的能力;临界阻尼是概念阻尼,是指一个特定的阻尼值,大于或等于该阻尼值,系统的运动不是振动,而是一个指数衰运动;阻尼比(相对阻尼系数)等于实际阻尼与临界阻尼之比(3)写出拉格朗日方程的表达式,并解释各符号所代表的含义。
拉格朗日方程的表达式为:)()(d d t Q q Uq T q T t j jj j =∂∂+∂∂-∂∂ (j =1,2,…,n )。
式中,,j j q q 为振动系统的广义坐标和广义速度;T 为系统的动能;U 为系统的势能;Q j (t )为对应与广义坐标q j 的除有势力以外的其他非有势力的广义力;n 为系统的自由度数目。
[机械系统动力学考试题2014年]
![[机械系统动力学考试题2014年]](https://img.taocdn.com/s3/m/76ad7cffaeaad1f346933f8a.png)
机械系统动力学课程第一部分开卷考试题(2014年硕士研究生课适用、共六题)一、下图所示为一对心曲柄滑块机构。
曲柄以转速ω1=100 rad / s 作等速回转运动,曲柄长度r = 50.8 mm ,质心与其回转中心A 重合。
连杆长度l =203 mm ,连杆质心S 2到铰链B 的距离mm BS 8.502=,连杆质量kg m 36.12=,对其质心的转动惯量220102.0m kg J •=。
滑块质量kg m 907.03=,其质心与铰链C 重合。
(1)列出动态静力分析方程,绘出摆动力对A 点的摆动力矩与惯性载荷相对应的那一部分平衡力矩随曲柄位置1θ变化的情况;(2)对计算结果的某些现象、或各尺寸参数、质量分布等问题,提出一个讨论问题,并阐述自己的观点。
(15分)二、列出曲柄导杆机构(右下图)的完全平衡方程,并推出平衡条件,写出在杆1和3上所加项式运动规律。
要求有详细的推导步骤;(2)试简述使用高次方多项式作为凸轮从动件运动规律有何特点?(10分)五、已知一曲柄压机简图如题三图所示,l 1 =50 mm ,l 2 =300 mm ,J 1 = 8 kgm 2 , m 3 = 2 kg ,不计杆2质量,曲柄受驱动力矩M 1 = 158.5-10ω N •m ,工作阻力F 3为:⎩⎨⎧=)(m N)(m N 160F 333向上运动向下运动设当φ1 = 0°时,ω1 = 15.5 1/s 。
现求以杆1为等效构件,用经典四阶龙格库塔法,以Δφ =5°计算φ1 =0°~720°对应的ω1,dt d 1ω的值,绘出线图。
(10分)打印格式:No. φ1 ω1 dω1/dt0 0 15.5 · 1 5 · ·2 10 · ·六、请检索文献,完成一篇3000字左右的“综述”,内容是平面连杆机构弹性动力学分析近年来的研究方法和应用。
机械系统动力学习题2010.

⎨ ⎪⎩−KB1
+ (2K
−
2mω2
)B2
=
P0
得
解该方程组,
B1
=
(2K
−
KP0 mω2)(2K −
2mω2 )
−
K
2
B2
=
(2K
−
(2K − mω2 )P0 mω2)(2K − 2mω2) − K
2
所以,受迫响应为
x1
=
(2K
−
KP0 mω2)(2K −
2mω2 )
−
K
2
sinωt
及
x2
=
(2K
所以碰撞后的系统可视为低阻尼状态
•
碰撞初始位置: x0 = 0, x0 = v = 0
•
所以 A =
x0
+
x0
+ξwn x0 wd
=
x0 = 0.082 m wn 1 −ξ2
Td
2π ==
wd
wn
2π 1−ξ2
= 1.4
s
所以在相撞后的约 Td ≈0.35 s 达到最大振幅 Ae−ξwnt ≈0.07 m
整理,得
ωn4
−
1 M
[k
(M +
+ l
m)
g
]ωn
2
+
kg Ml
=0
解:取质量块的位移 x1 , x2 为广义坐标, 对 m1, m2 分别进行受力分析,根据牛顿定律,有
⎧ ••
⎪m1 x1 = K2 ( x2 − x1 ) − K1 x1
⎨
⎪ ⎩
m2
••
x2
=
北交机电考研试题及答案

北交机电考研试题及答案一、选择题(每题2分,共10分)1. 下列关于机械设计的说法中,错误的是()。
A. 机械设计需要考虑材料的力学性能B. 机械设计不需要考虑成本C. 机械设计需要考虑零件的加工工艺性D. 机械设计需要考虑产品的使用环境答案:B2. 在机电一体化系统中,传感器的作用是()。
A. 执行控制命令B. 转换信号C. 进行数据处理D. 驱动机械部件答案:B3. 下列关于伺服电机的描述中,正确的是()。
A. 伺服电机的控制精度较低B. 伺服电机的响应速度较慢C. 伺服电机的控制精度较高D. 伺服电机的输出力矩较小答案:C4. 在机械制造过程中,数控机床通常用于()。
A. 手工加工B. 批量生产C. 单件生产D. 非金属材料加工答案:B5. 机械系统动力学分析的主要目的是()。
A. 确定零件的尺寸B. 评估系统的性能C. 确定零件的材料D. 评估系统的可靠性答案:B二、填空题(每题2分,共10分)1. 在机械设计中,为了提高零件的疲劳强度,通常采用_________。
答案:表面硬化处理2. 伺服电机的控制精度高,通常用于_________控制系统。
答案:高精度3. 数控机床的编程语言通常采用_________。
答案:G代码4. 机械系统的动力学分析中,_________是描述系统动态响应的重要参数。
答案:阻尼比5. 在机械制造中,_________是保证加工精度的关键因素之一。
答案:夹具设计三、简答题(每题5分,共20分)1. 简述机械设计中的可靠性设计原则。
答案:机械设计中的可靠性设计原则主要包括:确保零件的强度和刚度满足要求;选择合适的材料和加工工艺;进行合理的结构设计以减少应力集中;进行必要的可靠性分析和试验。
2. 解释伺服电机与普通电机的主要区别。
答案:伺服电机与普通电机的主要区别在于:伺服电机具有高精度的控制能力,可以实现精确的位置、速度和力矩控制;伺服电机通常采用闭环控制,能够实时反馈和调整输出;伺服电机的响应速度快,适用于要求快速响应的场合。
(完整word版)西北工业大学机械系统动力学试题(含答案)(word文档良心出品)

考试科目: 机械系统动力学 课程编号:056022 开课学期: 2014-2015学年第二学期 考试时间:2015/07/08 说 明:所有答案必须写在答题册上,否则无效。
共6 页 第 1页1. 用加速度计测出某结构按频率82 Hz 简谐振动时的最大加速度为50g (2/980s cm g =). 求该振动的振幅及最大速度.解答: 已知振动频率 82f Hz =,最大加速度max 50a g =,振动角频率2164f ωππ==rad/s将简谐振动表述为正弦函数 sin()x A t ωϕ=+ ,则其速度为 cos()x A t ωωϕ=+ ,加速度为 2sin()x A t ωωϕ=-+振幅 m a x 22509.80.185(164)a A cm ωπ⨯=== 最大速度 max 1.8516495.1/v A cm s ωπ==⨯=2. 一个机器内某零件的振动规律为0.4sin 0.3cos x t t ωω=+,x 的单位是cm ,10/s ωπ=。
这个振动是否简谐振动? 求出它的振幅、最大速度及最大加速度,并用旋转矢量表示这三者之间的关系。
解答:频率相同的简谐振动合成的振动仍是简谐振动,显然该振动为简谐振动。
0.4sin 0.3cos sin()x t t A t ωωωϕ=+=+其中,振幅 0.5A == ,相角为 10.3370.4tg ϕ-==︒ 最大速度 max 0.5105v A ωππ==⨯=最大加速度 22max 0.5(10)500a A ωπ==⨯=振幅、最大速度和最大加速度之间的旋量关系可表示为图0 所示:图0 振幅、最大速度和最大加速度间的旋量关系表示3. 将图1所示的锯齿波展为富里叶级数, 并画出频谱图.考试科目: 机械系统动力学 课程编号:056022 开课学期: 2014-2015学年第二学期 考试时间:2015/07/08 说 明:所有答案必须写在答题册上,否则无效。
机械系统动力学试题

机械系统动力学试题一、 简答题:1.机械振动系统的固有频率与哪些因素有关?关系如何?2.简述机械振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
3.简述无阻尼单自由度系统共振的能量集聚过程。
4. 简述线性多自由度系统动力响应分析方法。
5. 如何设计参数,使减振器效果最佳?二、 计算题:1、 单自由度系统质量Kg m 10=, m s N c /20∙=, m N k /4000=, m x 01.00=,00=∙x ,根据下列条件求系统的总响应。
(a ) 作用在系统的外激励为t F t F ωcos )(0=,其中N F 1000=,s rad /10=ω。
(b ) 0)(=t F 时的自由振动。
2、 质量为m 的发电转子,它的转动惯量J 0的确定采用试验方法:在转子径向R 1的地方附加一小质量m 1。
试验装置如图2所示,记录其振动周期。
a )求发电机转子J 0。
b )并证明R 的微小变化在R 1=(m/m 1+1)·R 时有最小影响。
3、 如图3所示扭转振动系统,忽略阻尼的影响J J J J ===321,K K K ==21(1)写出其刚度矩阵;(2)写出系统自由振动运动微分方程; (2)求出系统的固有频率;(3)在图示运动平面上,绘出与固有频率对应的振型图。
1θ(图2)(图3)4、求汽车俯仰振动(角运动)和跳振(上下垂直振动)的频率以及振动中心(节点)的位置(如图4)。
参数如下:质量m=1000kg,回转半径r=0.9m,前轴距重心的距离l1=0.1m,后轴距重心的距离l2=1.5m,前弹簧刚度k1=18kN/m,后弹簧刚度k2=22kN/m(图4)5、如5图所示锻锤作用在工件上的冲击力可以近似为矩形脉冲。
已知工件,铁锤与框架的质量为m1=200 Mg,基础质量为m2=250Mg,弹簧垫的刚度为k1=150MN/m,土壤的刚度为k2=75MN/m.假定各质量的初始位移与速度均为零,求系统的振动规律。
机械动力学——两自由度系统习题

解:
以 0 为零势能点
系统势能:U (m1 m2 )gl(1 cos)
系统动能: T
1 2
m1 2l 2
1 2
m2 (l 2 2
x 2
2xl
cos )
1 4
m2 x 2
U x
0
U
(m1 m2 )gl sin
T 0 x
T x
3 2
m2
x
m2l
cos
d dt
T x
3 2
m2x
m2l cos
解:
(1)系统水平方向运用动量定理: d[m1x m(x l cos )] 2kx dt
m1 mx ml cos ml sin2 2kx 0
对 m 进行受力分析,沿垂直于杆的方向:
ml m cosx mg sin ml 2 ml cosx mgl sin 0
因为自由微振动 cos 1 、 sin 、2 0 ,得微分方程组:
k
k
k k
12
0 0
K M 0
频率方程
自然频率:
1 I 22 2Ik k 2 0 2
12
1
2
(2
2
)k
I
(2 2)k
I
固有振型:
1211
1
2
,
1222
1
2
主振型图:
2 1
-3/11-
机械系统动力学作业 4
3. 如图所示,一质量为 m1 的水平台用两根长度为 l 的绳子悬挂起来,其上有一半 径为 r,质量为 m2 的圆柱体,沿水平台作无滑动滚动。试用 和 x 为广义坐标建立 系统的运动微分方程。
弹簧无初始应力,
机械系统动力学复习题2014
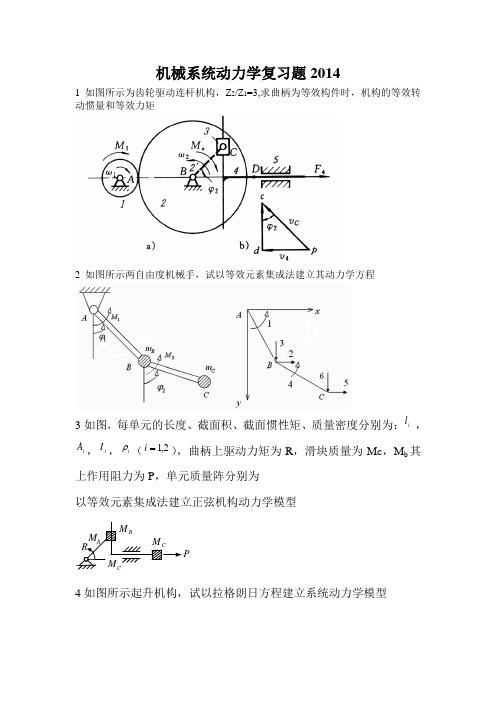
机械系统动力学复习题2014
1如图所示为齿轮驱动连杆机构,Z 2/Z 1=3,求曲柄为等效构件时,机构的等效转动惯量和等效力矩
2 如图所示两自由度机械手,试以等效元素集成法建立其动力学方程
3如图,每单元的长度、截面积、截面惯性矩、质量密度分别为: i l ,i A ,i I ,i ρ(2,1=i ),曲柄上驱动力矩为R ,滑块质量为Mc ,M b 其上作用阻力为P ,单元质量阵分别为
以等效元素集成法建立正弦机构动力学模型
P
4如图所示起升机构,试以拉格朗日方程建立系统动力学模型
5以拉格朗日方程建立系统的振动模型
6 如图所示系统,受到P1=0,t
sin
=的作用,求振动方程、系统固有频率
Pω
P
2
及模态阵。
7已知刚度阵K和质量阵m,试用静力凝聚法求自振频率
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡------=1111121211331236][k ⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡=0000000000200001][m
8试述多柔体系统动力学分析方法和KED 方法的异同.
9求解多自由度振动系统时, 自由度缩减方法主要有那些?试述其中两种的基本思路与实施步骤。
10 简述KED 方法的基本假定和分析过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
太原理工大学研究生试题
姓名: 学号: 专业班级: 机械工程2014级 课程名称: 《机械系统动力学》 考试时间: 120分钟 考试日期: 2015.12.11 题号 一 二 三 四 五 六 七 八 总分 分数
1 圆柱型仪表悬浮在液体中,如图1所示。
仪表质量为m ,液体的比重为ρ,液体的粘性阻尼系数为r ,试导出仪表在液体中竖直方向自由振动方程式,并求固有频率。
(10分)
2 系统如图2所示,试计算系统微幅摆动的固有频率,假定OA 是均质刚性杆,质量为m 。
(10分)
3 图3所示的悬臂梁,单位长度质量为ρ,试用雷利法计算横向振动的周期。
假定梁的
变形曲线为⎪⎭
⎫ ⎝⎛
-=x L y y M 2cos 1π(y M 为自由端的挠度)。
(10分)
4 如图4所示的系统,试推导质量m 微幅振动的方程式并求解θ(t)。
(10分)
5 一简支梁如图5所示,在跨中央有重量W 为4900N 电机,在W 的作用下,梁的静挠度δst=0.2cm ,粘性阻尼使自由振动10周后振幅减小为初始值的一半,电机n=600rpm 时,转子不平衡质量产生的离心惯性力Q=1960N ,梁的分布质量略去不计,试求系统稳态受迫振动的振幅。
(15分)
6 如图6所示的扭转摆,弹簧杆的刚度系数为K ,圆盘的转动惯量为J ,试求系统的固有频率。
(15分)
7如图7一提升机,通过刚度系数m N K /1057823⨯=的钢丝绳和天轮(定滑轮)提升货载。
货载重量N W 147000=,以s m v /025.0=的速度等速下降。
求提升机突然制动时的钢丝绳最大张力。
(15分)
8某振动系统如图8所示,试用拉个朗日法写出动能、势能和能量散失函数。
(15分)
太原理工大学研究生试题纸
图1 图2 图3
图4 图5 图6
m 1
m 2
x 1x 2Q 1sin ωt
Q 2sin ωt
k 1r 1
k 2r 2
k 3r 3
图7 图8。
