一维非定常对流扩散方程非均匀网格上的高精度紧致差分格式
非均匀结构网格上MUSCL和WENO格式的精度

非均匀结构网格上MUSCL和WENO格式的精度
刘君;刘瑜
【期刊名称】《气体物理》
【年(卷),期】2024(9)3
【摘要】基于一维均匀网格条件下构造的差分格式,在实际应用中须推广到非均匀或者曲线网格上,坐标变换过程引入几何诱导误差。
目前常用收敛解误差随着网格细化变化的精度测试方法评估差分格式的精度。
在二维柱坐标均匀网格上,采用1阶迎风、2阶MUSCL和5阶WENO计算流场参数为常数的自由流问题,按照精度测试方法比较收敛曲线斜率,发现1阶迎风的网格收敛精度是2阶的,5阶WENO 的网格收敛精度不到1阶。
理论分析表明,这种精度测试方法与差分格式精度定义不等价,而且所采用的数据无法反映差分格式的固有缺陷,因此,不能用来作为差分格式精度评价指标。
很多研究WENO的文献经常模拟双Mach反射问题、二维Riemann问题等经典算例,把接触间断是否演变成不稳定涡结构作为特征,理论上可以证明涡结构是非物理现象,因此用是否出现涡结构作为算法高精度的论据并不合适。
【总页数】11页(P66-76)
【作者】刘君;刘瑜
【作者单位】宁波大学机械与力学学院
【正文语种】中文
【中图分类】O35
【相关文献】
1.一维非定常对流扩散方程非均匀网格上的高精度紧致差分格式
2.二维非结构网格上的高精度有限体积WENO格式
3.一种非均匀网格上的高精度紧致差分格式
4.二维泊松方程非均匀网格上的高精度紧致差分格式
5.非结构网格上求解二维H-J方程的一种WENO格式
因版权原因,仅展示原文概要,查看原文内容请购买。
一维对流扩散方程的4种差分格式的Jacobi迭代收敛性比较

(. 1 宁夏 大 学 数 学计 算机 学 院 , 宁夏 银 川 70 2 ; 2 复旦 大 学 数 学科 学 学 院 , 海 5 0 1 . 上
摘
要 : 对 一 维 常 系数 对 流扩 散 方程 采 用 不 同的 差 分 格 式 离散 后 所 得 到 的线 性 系统 , 过 直 接 估 计 Jc b 迭 代 针 通 ao i
考虑 一维对 流扩散模 型方 程 :
~
1 谱 半 径
() 1
+“ 一 f( £ , x, )
当系数 ££ ) 小 时 , (>0 很 该方程 常作 为奇异 摄动 问题
定 义 y / 2 ) 网格 雷 诺 数 , y 1时 , = (e 为 当 > 称
的模型方 程. 而此 时 , 于 该方 程 , 典 的 中心 差 分 对 古 格 式 ( 称 为 C ) 用 J c b 迭 代 方 法 求 解 会 不 简 DS 采 ao i
的数 值震 荡 , 但其 数值 精 度 只有 一 阶. 文献 [ ] 1 中四 阶紧致差 分格式 ( 简称 为 HO s 通 过添加 人工黏性 c) 项抑 制 了迭代 的数值 震 荡 , 随着 扩 散 系数 的减小 但 其收敛变得很慢 , 而文献[ ] 2 中指数型高 阶紧致差分格 式( 简称为 E C ) 0 HO S  ̄ 在集 中 了以上 3 格式 的高精 种 度、 高稳定性优点的同时克服 了数值上 的震荡 , 不但具
为 阶三 对角矩 阵 , 则存 在 实的非 奇异对 角 矩阵 Q, 使 得 Q Q为实对称 矩 阵 , 且仅 当 对 每个 i1 A 当 ( ≤ i )有 b C ≤ , i >0或 b 一C一0 所得 对 称 矩阵 为 … .
A=ti一1 7 2 y 一 1. =r = [ —2 , +2 , ] 定理 2 对 任何 网格 雷诺 数 y 点 Jc b 迭代矩 , ao i 阵 的谱半径 为
一维非稳态对流-扩散方程的隐式中心差分格式

一维非稳态对流-扩散方程的隐式中心差分格式一维非稳态对流-扩散方程描述了在一维空间中同时存在对流和扩散过程的物理现象。
这个方程在很多工程和科学领域都有广泛的应用,如热传导、质量传输和流体力学等。
对方程进行数值求解可以得到物理现象的定量解,进而对系统行为进行预测和优化。
对于一维非稳态对流-扩散方程的数值解法中,中心差分格式是一种常用的方法。
中心差分格式是基于中心差分近似的方法,该方法精确地处理了对流和扩散效应,并适用于广泛的问题。
其中,隐式格式是一种特殊的中心差分格式,它在处理高度非稳态情况下的数值解具有优势。
在一维非稳态对流-扩散方程的隐式中心差分格式中,我们假设空间网格的节点为x_i,时间步长为Δt。
方程的解u(x,t)在网格节点x_i处的近似值为u_i^n,其中n表示时间步数。
根据对流和扩散项的中心差分近似,方程可以离散为如下的格式:(u_i^{n+1}-u_i^n)/Δt=α(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1})/(Δx^2)-β(u_{i+1}^{n+1}-u_{i-1}^{n+1})/(2Δx)其中,α表示扩散系数,β表示对流系数,Δx表示空间步长。
在隐式中心差分格式中,时间步n+1的解u_i^{n+1}是未知的,我们将其视为待求解的值。
通过将方程的右侧扩散和对流项全部取为n+1步的值,从而得到一个关于u_i^{n+1}的线性方程。
因此,我们可以得到如下的表达式:u_i^{n+1}=(αΔt/(Δx^2)-βΔt/(2Δx))u_{i-1}^{n+1}+(1-2αΔt/(Δx^2))u_i^{n+1}+(αΔt/(Δx^2)+βΔt/(2Δx))u_{i+1}^{n+ 1}这个方程可以用矩阵的形式表示为:AU^{n+1}=BU^n其中,U^{n+1}是一个列向量,包含了所有网格节点i处的解u_i^{n+1};U^n是一个列向量,包含了所有网格节点i处的解u_i^n;A和B是相关系数矩阵,具体的表达式为:A=[1-2αΔt/(Δx^2),αΔt/(Δx^2)+βΔt/(2Δx),0, 0[αΔt/(Δx^2)-βΔt/(2Δx),1-2αΔt/(Δx^2),αΔt/(Δx^2)+βΔt/(2Δx), 0[0,αΔt/(Δx^2)-βΔt/(2Δx),1-2αΔt/(Δx^2), 0...[0,...,0,αΔt/(Δx^2)-βΔt/(2Δx),1-2αΔt/(Δx^2)]B = identity matrix通过求解这个线性方程组,就可以得到隐式中心差分格式下的数值解。
求解一维扩散反应方程的隐式高精度紧致差分格式

求解一维扩散反应方程的隐式高精度紧致差分格式1概述一维扩散反应方程是描述许多物理过程的数学方程之一,如化学反应、热传导等。
在求解这样的方程时,我们需要寻找适合的数值解法。
本文将介绍一种隐式高精度紧致差分格式,用于求解一维扩散反应方程。
2一维扩散反应方程一维扩散反应方程可表示为:$$\frac{\partial u}{\partial t}=D\frac{\partial^2u}{\partial x^2}+\rho u(1-u)$$其中,$u(x,t)$表示物理量的变量,$D$为扩散系数,$\rho$为反应速率常数。
初始条件为$u(x,0)=u_0(x)$,边界条件为$u(0,t)=u(L,t)=0$,其中$L$为区间长度。
3差分方法为了求解上述方程的数值解,我们需要使用差分方法。
差分方法可以将连续的偏微分方程转化为离散的方程,从而得到数值解。
这里我们采用一阶差分法和二阶差分法分别对时间和空间进行离散化。
时间离散化:$$\frac{\partial u(x,t)}{\partialt}\approx\frac{u(x,t+\Delta t)-u(x,t)}{\Delta t}$$空间离散化:$$\frac{\partial^2u(x,t)}{\partialx^2}\approx\frac{u(x+\Delta x,t)-2u(x,t)+u(x-\Deltax,t)}{\Delta x^2}$$将上述两个式子带入到原方程中,得到离散化形式:$$\frac{u_i^{n+1}-u_i^n}{\Delta t}=D\frac{u_{i+1}^n-2u_i^n+u_{i-1}^n}{\Delta x^2}+\rho u_i^n(1-u_i^n)$$其中,$n$表示时间步长,$i$表示空间位置。
4隐式高精度紧致差分格式在上述差分方法中,我们采用了一阶差分法和二阶差分法,这种方法的精度有限。
为了提高求解的精度,可以采用更高阶的差分方法。
解一维和二维对流扩散方程的单调差分格式

一维对流扩散方程是指一维均匀的边界层上的传质过程的数学模型,常用于描述对流扩散过程中的温度、湿度、速度等场的分布情况。
一维对流扩散方程的数学形式为:∂φ/∂t+U∂φ/∂x=D∂^2φ/∂x^2其中φ表示传质物质的浓度,t表示时间,x表示空间坐标,U表示对流速度,D表示扩散系数。
二维对流扩散方程是指二维均匀的边界层上的传质过程的数学模型,常用于描述对流扩散过程中的温度、湿度、速度等场的分布情况。
二维对流扩散方程的数学形式为:∂φ/∂t+U∂φ/∂x+V∂φ/∂y=D∂^2φ/∂x^2+D∂^2φ/∂y^2其中φ表示传质物质的浓度,t表示时间,x和y分别表示两个空间坐标,U和V分别表示两个方向上的对流速度,D表示扩散系数。
单调差分格式是一种常用的数值求解方法,它通过进行差分运算来求解微分方程的数值解。
在求解一维和二维对流扩散方程时,可以使用单调差分格式来解决。
具体来说,可以将空间坐标和时间分别离散化,将对流扩散方程转化为一个线性方程组,然后使用单调差分格式来解决。
单调差分格式的具体形式取决于方程的类型和离散化的方式,但一般来说,它都是将微分方程的差分形式写成一个线性方程组的形式。
例如,在求解一维对流扩散方程时,可以使用下面的单调差分格式:φ_i^{n+1}=φ_i^n+Δt(D(φ_{i+1}^n-2φ_i^n+φ_{i-1}^n)/Δx^2+U(φ_ {i+1}^n-φ_{i-1}^n)/2Δx)其中φ_i^n表示第i个网格点在时间步n的浓度值,Δx和Δt分别表示网格的空间步长和时间步长。
同样的,在求解二维对流扩散方程时,可以使用下面的单调差分格式:φ_i^n=φ_i^n+Δt(D(φ_{i+1,j}^n+φ_{i-1,j}^n+φ_{i,j+1}^n+φ_{i,j-1}^ n-4φ_i^n)/Δx^2+U(φ_{i+1,j}^n-φ_{i-1,j}^n)/2Δx+V(φ_{i,j+1}^n-φ_ {i,j-1}^n)/2Δy)其中φ_i^n表示第(i,j)个网格点在时间步n的浓度值,Δx和Δy分别表示网格在x和y方向上的空间步长,Δt表示时间步长。
一维非定常对流扩散方程非均匀网格上的高阶紧致差分格式

西安理工 大学学报 J o u r n a l o f X i ’ a n U n i v e r s i t y o f T e c h n o l o g y ( 2 0 1 3 )V o 1 . 2 9 N o . 4 文章编号 : 1 0 0 6 - 4 7 1 0 ( 2 0 1 3 ) 0 4 - 0 4 7 5 - 0 6
t h e 1 D u n s t e a d y c o n v e c t i o n d i f f u s i o n e q u a t i o n .Th e s c h e me i s t he s e c o n d o r d e r a c c u r a c y or f t i me a n d t h e
A Hi g h Or d e r Co m pa c t Di fe r e n c e Sc h e me o n No n- Uni f o r m Gr i ds f o r t h e 1 D Un s t e a d y Co nv e c t i o n Di fu s i o n Eq ua t i o n
4 7 5
一
维 非 定 常对 流 扩 散 方 程 非 均 匀 网格 上 的高 阶紧致 差 分格 式
非定常对流扩散方程的高阶差分格式

摘
要 :对流扩散 方程 主要 包含对流和扩散两项。在数值 计算中 , 方程 中的扩散项一般 采用具有优 良物理特性和计算
精度 的中心差分 离散格 式 , 而对对流项的处理就稍显 困难 , 处理不 当便会产 生数值震 荡或数值 弥散 , 给数值计算 带来
OU 0U 2
= s
度 的差 分 格式 , 志 峰 和陈 国谦 [ 通 过 引入 一个 综 杨 8 ] 合 变 换 , 对 流 扩 散 方 程 变 为纯 扩 散 方 程 , 后 利 将 然 用 求解 扩 散方 程 的 已有 四阶格 式 , 终建 立 了求 解 最 对 流扩 散方程 的一 种两 层 四阶 紧致 隐格式 。本 文构 造 了一 种 精度 高 的 紧致 隐式 差 分格 式 , 过 引入 指 通 数 变换 将 对 流扩 散方 程 变为 扩 散方 程 , 后 采用 时 然
困难 。针 对 对 流 扩 散 方 程 , 过 引入 指数 变 换将 对 流 扩散 方程 变 为 扩散 方程 , 免 对对 流项 的 直接 处理 。利 用 四阶 紧 通 避
致差 分格 式 , 首先建立三类特殊方程 的高精度 差分格式 , 此基础上建 立一 维非定常含源对流扩散 方程 的高阶格式 , 在 并进行稳定性分析 , 所得格式精度 高且绝对稳定。数值 算例表 明了该格式的有效性。
钭 撑虫崴 缸
、01 3 No. J , .4 3 un. 201 2
编辑 部 网址 :h t / t / p: www. u b t m s wp x .o
文 章 编 号 :17 —5 8 (0 20 —0 4 —0 6 4 0 62 1 )3 15 5 中图分类号 :T 3 2 E 1
非均匀网格上对流扩散反应方程的一种差分

Vo .2 1 8、NO.6 NO .2 7 V 00
非均 匀 网格 上 对 流 扩散 反 应 方程 的一 种 差 分
田 芳
( 宁夏大学 数学计算机学院, 宁夏 银川 7 0 2 5 0 1) ( - i t n f x . uc ) E ma : i _ l a  ̄n ue . d n
A b t a t A i h a c r c o s r c h g c u a y c mp to n t i e e t c e eo o — n f r r d f ro e d me so a c a f f i df r n h m nn n u i m g i n i n in l ai e s o o c n e to — fu i n r a to qu to s p o o e Nu r c lr s ls s o t t t e p e e t s h me ha o v c i n di so - e i n e a i n i r p s d c me i a e u t h w ha h r n c e s s p e e a l r p r i fis h g c r y h g e o u i n f r t e l r e g a e tc a e ft e un n wn r f r b e p o e te o i h a u a , i h r s l to h a g di n h ng o h k o s t c c o r s q a tt , e n l s ia l r t e b u d r a e , t . u n i b i g wel u t b e f h o n a y l y r e c y o Ke y wor On - m e so a o v to — i u i n e u to Hi h a c r y c m p to n t i e e t ds e di n i n lc n e i n d f so q a i n; g u a o c c c c a ff ie d f r n i sh m e c e ;No - io m i Bo n a y l y r n un f r g d; u d r a e r
求解对流扩散方程的紧致二级四阶Runge—Kutta差分格式

d o i : 1 2 . 3 9 6 9 / j . i s s n . 1 6 7 2— 8 5 1 3 . 2 0 1 5 . 0 5 . 0 O 9
C N5 3—1 1 9 2 / N I S S N 1 6 7 2—8 5 1 3
O u +k O u
a
,
一
1 u ( x 0 d ( x, 力, )= ) ∈力,
t u ( 0 , )= ( 1 , t )=0 , ∈a , t ≥0 .
0 纛 2 u
㈩ 、
1 格式的构造与截断误差
将 区域 ×[ O, ] 进 行剖 分 , 记 ^和 . r 分别 是 方 向和 t 方 向的 网格 步长 , 其 中 = 1
) 应 用 于一 维对 流扩散 方程 , 对 空 间 变量 应 用 紧致
差 分格 式 , 时 间变量 z 采 用二级 四阶 R u n g e— K u t t a方 法 , 提 出 了精 度 为 0 ( r + h ) 的绝对稳 定 的 差分 格式 , 讨论 了稳 定性. 最后通 过数 值算例 说 明该格 式 的有效性 .
=
+ o ( 一 t t ) , ’
( 8 )
A- 1 眺 ( t )
( 9 )
5
1
6 l 2 1 5
A =
l 2 6
.
1
‘ l 2
l
对角 占优 矩 阵 , 因此非 奇异.
( 9 )式用 二级 四阶隐式 R u n g e—K u t t a格式 ( 7 )得 到如下 格式
紧致差分格式

紧致差分格式紧致差分格式(Compactly Supported Finite Difference Formulation)是一种常用的数值计算方法,用于求解偏微分方程的数值解。
它的特点是既能有效地处理高阶精度问题,又能保证数值解的稳定性和收敛性。
紧致差分格式最大的特点是它的数值计算节点只限于离散空间范围内的邻近节点。
也就是说,只有最近的节点之间进行计算,而不受整个空间范围的限制。
这种局部性的计算方式使得紧致差分格式具有较高的计算效率和灵活性。
在实际应用中,紧致差分格式广泛应用于流体力学、热传导等领域的数值计算中。
例如,在模拟流体的传输过程中,可以通过紧致差分格式将流体动力学方程转化为有限差分方程,从而得到流体在空间和时间上的数值解。
紧致差分格式的求解过程主要包括两个步骤:离散化和迭代求解。
首先,通过将原始的偏微分方程转化为差分方程,将问题在空间和时间上离散化。
其次,通过迭代求解逼近数值解。
在迭代求解的过程中,需要设置适当的边界条件和初始条件,以确保数值解的准确性。
紧致差分格式的优点是可以获得较高的数值精度和稳定性。
由于它的节点计算只限于离散空间范围内的邻近节点,可以在不增加计算复杂度的情况下提高数值解的精度。
与其他数值方法相比,紧致差分格式更加准确和可靠。
然而,紧致差分格式也有一些限制。
首先,它对初始条件和边界条件较为敏感,不同的条件可能会导致不同的数值解。
其次,紧致差分格式对问题的网格剖分要求较高,过于粗糙或者过于细致的网格都可能导致数值解的不准确性。
总之,紧致差分格式是一种重要的数值计算方法,广泛应用于偏微分方程的数值求解中。
它的局部性计算方式使得其具有较高的计算效率和灵活性,同时能够保证数值解的准确性。
但在使用时需要注意初始条件和边界条件的设置,以及合理选择网格剖分,以获得更为可靠和准确的数值解。
对流扩散方程高精度有限差分方法

致 谢研究生的学习生活就要结束了,而大学最后的一段学习生活也已宣告尾声。
在本文完成之际,我特别向所有曾经给予我帮助、鼓励和支持的人们表示衷心的感谢。
在此,我首先要向我的导师张佐刚教授表示最衷心的感谢。
从入学之初到毕业论文完成的整个过程中,我都一直得到张老师细致入微的关心和照顾,无论是在学习上还是在生活上都给了我莫大的支持和鼓励。
另外,在论文写作过程中,张老师对我悉心的教诲和严格的要求足以让我受益终生,我深深地被老师严谨的治学精神和一丝不苟的生活态度所折服,他一丝不苟的育人作风更是为我以后的学习工作树立了榜样。
这里我还要特别感谢高雷阜教授在平时一直给予的默默关心,在导师繁忙的时候,给予了我无私的帮助,同时也是他为我们提供了一个方便优越的学习环境,使论文得以顺利完成。
最后还要感谢辽宁工程技术大学理学院所有的老师,是他们在传授我知识的同时培养了我良好的数学思维和数学的思考方式,还有理学院所有的同学,他们在日常的学习生活中给了我无数的帮助和启发。
祝福所有的老师和同学身体健康,工作和学业一切顺利!摘 要对流扩散方程作为流体力学中的基本方程之一,目前求解的数值方法有很多,主要包括有限单元法、有限体积法、有限分析法和有限差分法。
其中,有限差分法作为一种重要的数值离散方法,在科学研究和工程计算中都得到了广泛的应用。
而在有限差分法中,高精度有限差分方法又以其涉及网格点少、边界无需特殊处理、具有较高的计算精度等优点,成为学者们争相研究的热点问题。
本文首先分析了高精度差分格式的研究意义、国内外的研究现状、研究过程中存在的一系列问题和发展的趋势。
然后结合均匀网格上和非均匀网格上差分算子的定义式,具体介绍了一些传统的关于对流扩散方程的差分格式和目前已经得到一定发展的主要的高精度差分格式。
通过对这些差分格式的研究学习,了解了很多高精度差分格式的主要构造方法,从中也得到了一些启发。
并且通过对一些差分方法的优点和局限性的分析,改进了文献中的一些高精度差分格式的构造方法,分别应用待定系数法、降维法等数学思想,给出了均匀网格上简单对流方程的一种高精度差分格式,以及非均匀网格上二维对流扩散反应方程的一种高精度紧致差分格式,并给出了相应的数值算例,证明了该格式较好的计算效果。
【国家自然科学基金】_高精度紧致差分格式_基金支持热词逐年推荐_【万方软件创新助手】_20140801
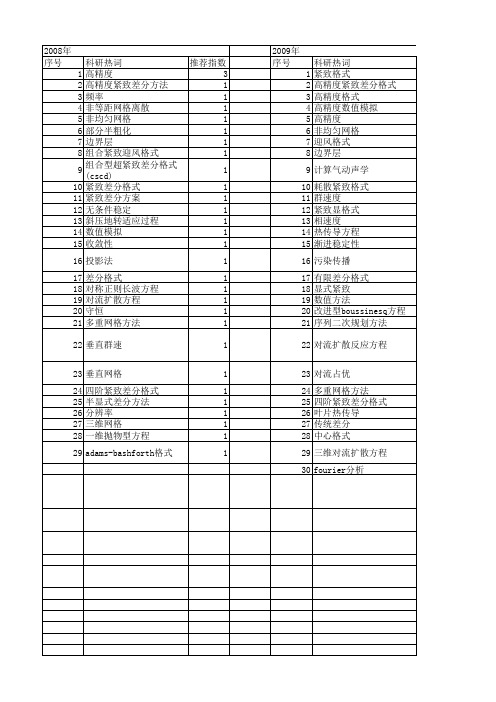
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35
科研热词 推荐指数 高精度 6 richardson外推法 4 高阶紧致格式 3 非均匀网格 2 边界层 2 对流扩散方程 2 高精度紧致差分格式 1 高精度紧致差分方法 1 隐式紧致格式 1 隐式差分 1 调制对传波 1 行进波 1 紧致格式 1 紧致差分格式 1 稳定性 1 泊松方程 1 有限差分法 1 对传波 1 定常行进波 1 定常对流扩散方程 1 交替方向隐式格式 1 二维波动方程 1 stationary traveling wave 1 soret效应 1 soret effect 1 1 schrsoinger equation 1 schrodinger方程 1 richardson extrapolation method 1 poiseuille流动 1 modulated eounterpropagating wave 1 high-order compact scheme 1 high order compact scheme 1 high accuracy 1 counterpropagating wave 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 推荐指数 非均匀网格 3 高阶紧致差分格式 2 高精度紧致格式 2 预报校正 2 非线性对流扩散方程 2 紧致差分格式 2 二维热传导方程 2 高精度紧致差分格式 1 高精度 1 预条件技术 1 非定常对流扩散方程 1 边界层问题 1 边界层 1 自然对流 1 线性多步法 1 涡量-流函数方法 1 扩散反应方程 1 多重网格方法 1 四阶紧致格式 1 加权隐式差分格式 1 二维对流扩散方程 1 不可压navier-stokes/boussinesq方程组 1 一维定常对流扩散方程 1 richardson外推法 1 richardson 外推法 1 maccormack方法 1 fgmres迭代法 1 adi方法 1 adi 方法 1
一维定常对流扩散反应方程的高精度紧致差分格式

一维定常对流扩散反应方程的高精度紧致差分格式祁应楠;武莉莉【摘要】针对一维定常对流扩散反应方程,提出了一种四阶精度的有理型紧致差分格式,其局部截断误差为O(h4);然后通过Richardson外推技术和算子插值法将本文格式的精度提高到六阶.因为格式仅涉及到3个网格基架点,所以对于Dirichlet 边值问题,由差分格式可得三对角线性方程组,可采用追赶法进行求解.最后通过数值算例验证了本文方法的精确性和可靠性.【期刊名称】《华中师范大学学报(自然科学版)》【年(卷),期】2017(051)001【总页数】6页(P1-6)【关键词】对流扩散反应方程;高阶紧致格式;Richardson外推;有限差分法【作者】祁应楠;武莉莉【作者单位】宁夏师范学院数学与计算机科学学院,宁夏固原756000;宁夏师范学院数学与计算机科学学院,宁夏固原756000【正文语种】中文【中图分类】O241.8对流扩散反应问题是流体力学、传热学、传质学等学科以及环境、化工等应用领域中经常遇到的典型问题之一,由于问题的准确解往往很难获得,所以人们经常采用数值方法来寻求问题的近似解.目前,所流行的近似计算方法包括有限差分法、有限元法和边界元法等.其中有限差分方法是一种常用的数值计算方法.目前,国内外已经有许多有关该问题高阶紧致差分格式的研究报道.如:魏剑英[1]针对一维对流扩散方程,提出了一种指数型高阶紧致差分格式.王彩华[2]利用泰勒展开公式和数项级数收敛性给出了一线性对流扩散问题的一类高精度紧致差分格式.田芳和田振夫[3]基于非均匀网格上函数的泰勒级数展开,构造了非均匀网格上的高精度紧致差分格式.Sun和Zhang[4]构造了定常对流扩散反应方程的多项式型四阶紧致差分格式,并用Richardson外推法[5]和算子插值技术将格式的精度提高到了六阶.Tian和Dai [6]构造对流扩散问题的指数型格式,其空间具有四阶精度.文献[7]研究了非定常对流扩散方程的有理型高阶紧致差分格式并得到了很好的计算效果.杨志峰等[8]构造了含源项非定常对流扩散问题的紧致四阶格式.文献[9-11]研究了利用样条插值的方法来构造高精度紧致差分格式.文献[12]通过消除对流项,并利用Pade格式,构造了一维非定常对流扩散反应方程无条件稳定的四阶紧致差分格式.文献[13]针对非定常对流扩散方程,对空间采用三点紧致差分格式,并对时间采用单对角隐式Runge-Kutta方法进行离散,得到了截断误差为O(τ4+h4)的无条件稳定的隐格式.文献[14]通过简单的分裂算法及增加特殊网格点的方法,对时间的处理采用C-N格式与向后欧拉结合的技巧,推导出求解高维非定常对流扩散反应方程的隐式差分格式.本文针对一维定常对流扩散反应方程,基于截断误差余项修正思想,并结合原方程本身,推导得到了求解该方程的一种四阶精度的有理型紧致差分格式.然后采用Richardson外推法和算子插值技术将格式的精度提高到六阶.最后给出了数值算例. 本文讨论的方程模型为两点边值问题:其中,边界条件为:u(0)=q0,u(L)=qL.这里,a,p(x),b(x)分别为扩散、对流和反应项系数.且a>0,p(x)和b(x)均为关于空间变量x的光滑函数.首先将定义域[0,L]离散为:0=x0<x1<x2<…<xN=L,记为网格数,空间步长定义为.为了方便书写,用ui表示表示,依此类推.将式(1)改写为:由此定义空间一阶和二阶导数的中心差分算子为:将式(1)利用中心差分代替,并利用关于u的一阶数和二阶导数的定义,可得:).如果略去i和i项,及高阶截断误差项O(h4),即可得到二阶中心差分格式.为了得到高精度的差分格式,将式(5)中的三阶和四阶导数项进行处理,为此对式(2)两边同时关于x求一阶导和二阶导数可得:.将式(6)代入式(7)消去xi化简可得:.将式(6)和式(8)代入式(5)可得:fi+O(h4).将式(3)和式(4)代入式(9),略去高阶项后化简整理可得:其中式(10)即为多项式型四阶紧致(FOC)差分格式,此格式色散误差和耗散误差较大.为了能精确数值求解此类方程,我们推导一种有理型的四阶紧致差分格式.将式(2)代入式(6)可得:.在式(15)中令,则式(15)可简化为:将式(2)和式(15)代入式(7),整理可得:.令则式(17)可化简为:将式(16)和式(18)代入式(5),整理可得:其中,.接着,将式(19)中的一阶导数用中心差分代替加×(5),利用式(3)和(4)对u的一阶和二阶导数进行离散,整理可得:).将式(15)和式(17)代入式(20)加×(5),同样利用u的一阶和二阶导数进行离散,整理可得:).令则式(21)可化简为:(γ4f+γ5fx+γ6fxx)i+O(h4).然后,略去式(22)中i和i项,并将式(3)和式(4)代入式(22),化简整理可得有理型的高阶紧致差分格式:,其中,.此格式的高阶截断误差为O(h4),即此格式具有四阶精度.本文格式之所以称之为有理型格式,是因为其差分算子的系数为有理型函数,记为RHOC.从推导过程可以看出,FOC格式只是其中的一种特殊情况,有理型格式的推导更具有广泛性.结合原方程可得到具有不同性质的高精度格式,对于不同性质的问题可选用与之相适应的格式进行求解,此类格式均为三个网格基架点,只发生系数的变化.下面使用Richardson外推方法[5]将本文的四阶格式RHOC提高到六阶精度.◆………… ◆——◆0 1 2 ……N/2◆—●—◆…… ◆—●—◆0 1 2 3 4……N-1 N首先,用格式(23)分别在粗网格和细网格上计算一遍可得粗网格和细网格具有四阶精度的近似解.然后利用Richardson外推公式:可得到在粗网格具有六阶精度的解,其中和分别为粗网格和细网格上的解,即通过Richardson外推公式(24)可将细网格上偶数点(菱形点)的精度提高到六阶.为了使细网格上奇数点(圆点)的精度也达到六阶,使用算子插值法.由式(23)可得:).由于细网格上偶数点(菱形点)已经算出,因此只须采用式(26)计算奇数点(圆点),即可得如下算子插值公式:.通过式(26)利用细网格上具有六阶精度的偶数点来计算奇数点,从而可使得细网格上点的精度均为六阶,整个过程我们将其记为RRHOC,其算法步骤如下:1) 在粗网格上用格式(23)计算一遍,可得;2) 在细网格上用格式(23)计算一遍,可得;3) 通过外推式(24)将细网格上偶数点(菱形点)的精度计算至六阶,4) 通过式(26)将细网格上奇数点(圆点)的精度计算至六阶.为了验证本文格式的精确性和可靠性,分别采用RHOC格式和RRHOC格式对以下两个有精确解的问题进行数值实验,并与中心差分格式、多项式型四阶紧致格式(FOC) [4]和六阶格式(REC) [4]的计算结果进行比较.其中,L∞范数误差和收敛阶(Rate)的定义如下:L∞范数误差,其中,Ui表示点xi处的精确解,ui表示点xi处的数值解,L∞(uh1)和L∞(uh2)分别表示网格步长为h1和h2时对应的L∞范数误差.问题1:该问题的精确解为:u(x)=ex.取:a=1,b(x)=x2+1,f(x)=x2ex.问题2:该问题的精确解为:u(x)=e-4πsin(x).取:a=1,p(x)=1,b(x)=1,f(x)=e-4π(cos x+2sin x).对于问题1和问题2,表1和表3列出了取不同步长h时,采用中心差分格式、FOC格式[4]与本文RHOC格式计算的L∞范数误差和Rate(收敛阶).不难得到,本文所提的四阶精度的有理型格式(RHOC)格式比多项式型格式(FOC) 和中心差分格式均具有更高的准确度.而且,当网格数不断增加时,RHOC格式的L∞范数误差比中心差分格式小四个数量级不等,比同是四阶的FOC格式计算结果更精确.表2和表4列出了取不同网格步长h时,REC格式[4]与本文RHOC格式的最大绝对误差和收敛阶,从表中可以看出经过外推和算子插值之后的REC格式和本文RHOC格式均有六阶精度,但是本文RHOC格式的计算误差明显优于REC格式[4].本文基于中心差分格式的截断误差余项修正,并利用原方程本身,提出了数值求解一维两点边值问题的一种紧致的高精度差分方法,由理论推导可知所提格式为四阶精度.然后采用Richardson外推法和算子插值技术将格式的精度提高到六阶.最后,采用本文两种方法计算了两个数值算例,并与传统的中心差分格式以及文献[4]中的FOC格式和REC格式进行了对比,充分体现了本文方法的精确性和有效性. 【相关文献】[1] 魏剑英. 定常对流扩散反应方程的指数型高阶差分格式[J].宁夏大学学报(自然科学版), 2012,33(2):140-143.[2] 王彩华. 一维对流扩散方程的一类新型高精度紧致差分格式[J].水动力学研究与进展, 2004,19(5):655-663.[3] 田芳,田振夫. 定常对流扩散反应方程非均匀网格上的高精度紧致差分格式[J].宁夏师范学院学报(自然科学版), 2009, 26(2):219-225.[4] SUN H, ZHANG J. A High order finite difference discretization strategy based on extrapolation for convection diffusion equations[J].Numer Methods Partial Differential Eq,2004, 20(1):18-32[5] CHENEY W, KINCARD D. Numerical Mathematics and Computing[M]. 4th Ed. CA:Brooks/Cole Publishing,Pacific Grove,CA. 1999.[6] TIAN Z F, DAI S Q. High-order compact exponential finite difference methods for convection-diffusion type problems[J]. J Comput Phys, 2007, 220:952-974.[7] 赵飞,蔡志权,葛永斌. 一维非定常对流扩散方程的有理型高阶紧致差分格式[J].江西师范大学学报(自然科学版), 2014, 38(4):413-418.[8] 杨志峰,陈国谦. 含源项非定常对流扩散问题紧致四阶差分格式[J].科学通报, 1993,38(2):113-116.[9] LANG F G, XU X P. Quintic B-spline collocation method for second order mixed boundary value problem[J]. Computer Physics Communications. 2012, 183:913-921.[10] GOH J, MAJID A A, ISMAIL A I M. A quartic B-spline for second-order singular boundary value problems[J]. Computers and Mathematics with Applications. 2012,64:115-120.[11] 林建国,许维德,陶尧森.含源项非定常非线性对流扩散方程的三次样条四阶差分格式[J].水动力学研究与进展(A辑), 1994, 9(2):599-602.[12] 杨录峰,李春光.一种求解对流扩散反应方程的高阶紧致差分格式[J]. 宁夏大学学报(自然科学版), 2013, 34(2): 101-104.[13] PIAO X, CHOI H J, KIM S D, et al. A fast singly diagonally implicit Runge-Kutta method for solving 1D unsteady convection-diffusion equations[J]. Numercal Methods for Partial Differential Equations,2013(30):788-812.[14] ADEM K. Finite difference approximations of multidimensional unsteady convection-diffusion-reaction equations[J]. Journal of Computational Physics, 2015, 285:331-349.。
对流扩散方程的非一致网格有限差分方法

中 图分 类号 :O 4 . 2 18
文 献 标 识 码 :A 源自No — n f r fnie dif r n e s h m e m e h d f r c n e to - i f so q a i ns n u i o m i t f e e c c e t o o o v c i n d f u i n e u to C AO a g n Gu n ma ,WANG a h a C i u ,QIH a t o ia
( . l g f t e t a S in e Tini r l ie s y Tini 0 3 7 Chn ; 1 Col e o e Ma h ma i l c c , a j No ma Unv r i , a j 3 0 8 , ia c e n t n 2 C l g f lcr ncI f r t n S i c ,T a j iest ,Ti j 0 0 2 C i a . o l eo e to i no mai c n e ini Un v r i e E o e n y a i 3 0 7 , hn ) nn
场 理论 、 体力学 、 流 弹性力 学 、 量子力 学 、 电子 器件 模 拟、 化学 反应 、 制 理 论及 其 他 同类 领 域. 一 般 模 控 其
型的形 式为 :
一 £ 口 z) 6 z) 一 厂 z) z∈ ( 6 , ( ( U )+ ( U ( , 口, ) ( )=口 甜 6 : , n = , ( )= = = () 1
V0 . 0 NO 1 13 . Jn 0 0 a .2 1
文 章 编 号 : 6 11 1 ( 0 0 0 — 0 70 1 7 -1 4 2 1 ) 10 0 —4
【计算机应用】_差分格式_期刊发文热词逐年推荐_20140724
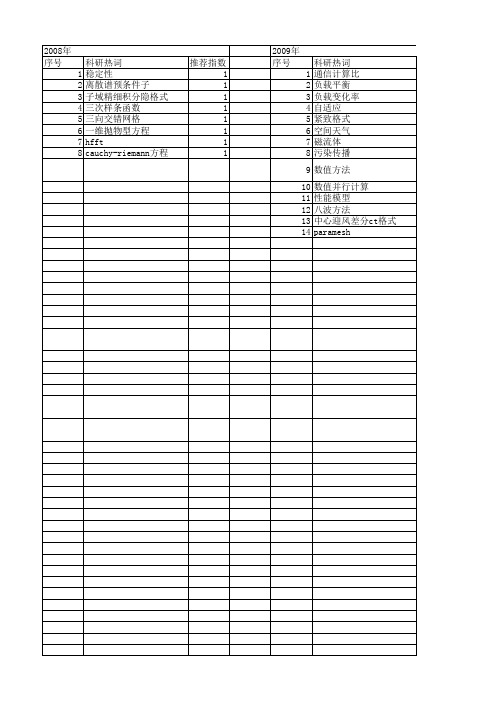
科研热词 通信计算比 负载平衡 负载变化率 自适应 紧致格式 空间天气 磁流体 污染传播 数值方法 数值并行计算 性能模型 八波方法 中心迎风差分ct格式 par1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 推荐指数 频偏估计 1 解调 1 联合紧致差分格式 1 紧致差分格式 1 稳定性 1 直接法 1 甚高频数据广播信号 1 有限差分法 1 收敛性 1 广义极小剩余法 1 巴黎期权特性 1 定价模型 1 唯一性 1 同步 1 可转债 1 richardson外推 1 helmholtz方程 1 euler-lagrange分裂格式 1 black-scholes方程 1
2008年 序号 1 2 3 4 5 6 7 8
科研热词 稳定性 离散谱预条件子 子域精细积分隐格式 三次样条函数 三向交错网格 一维抛物型方程 hfft cauchy-riemann方程
推荐指数 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
科研热词 解的存在唯一性 紧致差分格式 收敛性 有限差分 高精度紧致差分格式 高精度
推荐指数 3 3 3 2 1 1 1 非线性schroedinger方程 1 非线性schr(o)dinger方程 1 非线性 1 非定常 1 紧致交错网格 1 涡量-速度法 1 格子波尔兹曼方法 1 有限差分法 1 广义分布函数 1 对角占优 1 对流扩散方程 1 完全匹配层 1 交替方向隐式格式 1 井间地震 1 二维波动方程 1 不可压navier-stokes方程组 1 一维burgers守恒型方程 1 weno差分格式 1 unique solvability 1 tti介质 1 nonlinear schrsdinger equation1 linearized compact difference 1 scheme convergence 1
非均匀网格上三维对流扩散方程高精度紧致差分方法

采 用 BC Sa ( ) 代 法 求 解. 值 算 例表 明 , 网格 节 点 数 相 同 的 情 况 下 , 于非 均 匀 网格 的 计 算格 式 较 均 匀 网 iG tb 2 迭 数 在 基 格 格 式 具 有 高精 度 、 高分 辨 率 的 优 点 , 于合 边界 层 的 对 流扩 散 问题 有很 好 的适 应 性 . 对
献 [— 1 ] 对 文献 E ] 9 0针 8 中坐 标 变换 的不 足 , 接在 直
非 均匀 网格 上推导 了二 维对 流扩散 方程 的高精 度 紧 致差 分格 式. 文 基 于 降 维 法 的思 想 [ 以 非 均 匀 本 1 , 网格 上一 维 对 流 扩 散 方 程 的 高精 度 差 分 格 式 l _ 1 为
数值 求解 对流 扩散 方 程 的基 本 差 分 格 式 ( 古 典 中 如
1 非 均匀 网格 上 的差 分 算 子
不失 一般性 , 虑求 解 区域 ∈ [ , 3 将 其剖 考 O1 ,
心差 分格 式 和迎风 格式 ) 都存 在着 不 同方面 的缺 陷 , 不 能满 足实 际计算 和模 拟 的需要 . 因此 , 对高 精度 紧 致 差分 格 式 的研 究受 到 研究 者 的普 遍重 视 l .目 1 ]
前 大多 数 高精度 格 式 均基 于 均 匀 网格 构 造 , 于 对 对 流 占优 和计 算 区域 内含边界 层 问题 的求解并 不 能达 到 理论 上 的精度 . 献 [ ] 用 坐 标 变换 技 术 , 出 文 8采 提 了非均 匀 网 格 上 求 解 含 边 界 层 对 流 扩 散 问 题 的方 法 , 方法 的计算 结 果很 好 , 也 存 在 一些 不 足 , 该 但 主 要有 : ①对 原求 解方 程做 变换 增加 了离散 项 , 式 的 格 推导 过程 复杂 ;② 要 求 所选 用 的 变换 显 式 可 逆 . 文
一维对流方程的差分格式

一维对流方程的差分格式∂u/∂t+c∂u/∂x=0其中u是流体密度,t是时间,x是空间位置,c是流体速度。
为了离散化这个方程,我们将时间和空间范围分为小区间,然后在这些离散点上近似连续方程。
我们可以使用中心差分、向前差分或向后差分等方法来近似对流方程。
中心差分格式是一种常用的差分格式,通过使用当前时间步和两个相邻时间步的值来近似时间导数,使用当前空间点和两个相邻空间点的值来近似空间导数。
假设我们在时间方向上将时间分为n个步长Δt,将空间方向上将空间分为m个步长Δx,那么时间和空间步长分别为Δt = t_max / n 和Δx = x_max / m。
在中心差分格式中,时间导数可以使用向前差分或向后差分来计算。
使用向前差分有:∂u/∂t≈(u_i,j-u_i-1,j)/Δt使用向后差分有:∂u/∂t≈(u_i+1,j-u_i,j)/Δt空间导数可以使用中心差分来计算:∂u/∂x≈(u_i+1,j-u_i-1,j)/(2Δx)结合时间导数和空间导数的近似,我们可以得到中心差分格式的一般形式:(u_i,j+1-u_i,j)/Δt+c(u_i+1,j-u_i-1,j)/(2Δx)=0通过对该方程进行变形,可以得到u_i,j+1的计算公式:u_i,j+1=u_i,j-cΔt/(2Δx)(u_i+1,j-u_i-1,j)在空间和时间方向上进行迭代,可以逐步求解一维对流方程。
除了中心差分,还存在其他差分格式,如向前差分和向后差分。
向前差分格式使用当前时间和前一时间步的值来近似时间导数,向后差分格式使用当前时间和后一时间步的值来近似时间导数。
中心差分格式的优点是它具有二阶精度,即误差随着步长的平方而减少。
然而,该格式可能会出现数值耗散或数值扩散的问题,特别是在高梯度区域。
在实际应用中,选择正确的差分格式对于获得准确的数值解至关重要。
一维对流方程的差分格式提供了一种近似求解连续方程的方法,使得我们能够使用计算机来解决复杂的流体力学问题。
《一维Sine-Gordon方程高阶紧致有限体积方法》范文

《一维Sine-Gordon方程高阶紧致有限体积方法》篇一一、引言Sine-Gordon方程是一种重要的非线性偏微分方程,在物理学的多个领域中有着广泛的应用,如基本粒子理论、统计力学、固体物理等。
为了精确地模拟Sine-Gordon方程的动态行为,本文提出了一种高阶紧致有限体积方法。
该方法不仅具有较高的计算精度,而且可以有效地处理复杂的边界条件和初始条件。
二、Sine-Gordon方程及其性质Sine-Gordon方程是一个二阶非线性偏微分方程,具有周期性解和孤立波解等特性。
在物理学中,它被用来描述一些基本粒子的相互作用、非线性晶格的振动以及一维波传播等问题。
在求解过程中,需要对该方程进行数值模拟,而数值方法的选择对结果的准确性和可靠性具有重要影响。
三、高阶紧致有限体积方法为了解决Sine-Gordon方程的数值模拟问题,本文提出了一种高阶紧致有限体积方法。
该方法基于有限体积法的基本思想,通过引入高阶紧致格式,提高了数值解的精度和稳定性。
具体而言,该方法在空间域和时间域上进行了离散化处理,并对每个离散点进行高阶近似。
这样可以在保证计算精度的同时,有效降低计算复杂度。
四、方法实现高阶紧致有限体积方法的实现过程主要包括以下步骤:1. 空间域和时间域的离散化:将求解区域划分为若干个离散点,每个离散点代表一个网格单元。
在时间域上,采用等距离划分的方式,以便于计算时间步长和迭代过程。
2. 高阶紧致格式的引入:在每个网格单元内,采用高阶紧致格式对Sine-Gordon方程进行离散化处理。
这样可以有效地减小数值误差,提高计算精度。
3. 迭代过程:根据离散化后的Sine-Gordon方程,进行迭代计算。
在每个时间步长内,根据当前时刻的解和已知的初始条件、边界条件等信息,更新下一时刻的解。
4. 边界条件和初始条件的处理:针对不同的物理问题,需要设置不同的边界条件和初始条件。
在本文的方法中,通过引入适当的边界条件和初始条件处理方法,保证了计算结果的准确性和可靠性。
关于非均匀网格高精度格式的误差分析方法

关于非均匀网格高精度格式的误差分析方法王秋菊;任玉新【摘要】The derivation of truncation error on non-uniform grid for cubic spline reconstruction in finite volume framework is analyzed in this paper.The basic rule for the derivation of truncation error on non-uni-form grid is proposed which is that all derivations in the truncation error analysis should base on the same stencil.If this rule is not satisfied,the truncation error will not be self-consistent.Furthermore,the third-order discretization of the diffusion terms is obtained based on the correct truncation error analysis which makes both the convection and diffusion terms to achieve consistent third-order accuracy.%以三次样条重构有限体积方法为例,研究非均匀网格上截断误差的分析方法。
通过推导得到了分析非均匀网格上截断误差的基本准则,即在非均匀网格的截断误差分析中,要保证不显式或者隐含地改变数值方法对应的模板点———当不满足这一准则时,误差分析会得到不自洽的结果;而满足这一准则时,可保证分析结果的正确性。
利用正确的误差分析结果,可发展进一步提高计算精度的措施。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一维非定常对流扩散方程非均匀网格上的高精度紧致差分格式黄雪芳;郭锐;葛永斌【摘要】A high accuracy compact finite difference scheme with non-uniform grids is pro-posed to solve unsteady convection diffusion equations, which are used to describe boundary layer problems or locally large gradient problems, etc. The new method starts from the dis-cretization of the steady convection diffusion equation. Firstly, the spatial derivatives are discretized by using the Taylor series expansion on non-uniform grids. Then, the second order backward Eulerian difference formula is used to discretize the temporal derivative term. The three-level full implicit compact difference scheme on non-uniform grids for solving the one-dimensional unsteady convection diffusion equation is derived. The new scheme has the second order accuracy in time and the third to fourth order accuracy in space and is unconditionally stable. Finally, some numerical experiments are conducted to demonstrate the high accuracy and the advantages in solving boundary layer problems or locally large gradient problems.%本文在非均匀网格上给出了求解非定常对流扩散方程的一种高精度紧致差分格式,特别适合边界层和大梯度等问题的求解。
从稳态对流扩散方程入手,首先,基于非均匀网格上的泰勒级数展开对空间导数项进行离散,然后对时间项采用二阶向后欧拉差分公式,从而得到一维非定常对流扩散方程在非均匀网格上的三层全隐式紧致差分格式。
新格式在时间具有二阶精度,空间具有三到四阶精度,并且是无条件稳定的。
最后,通过数值实验验证了本文格式的精确性,以及在处理诸如边界层和大梯度问题上的优势。
【期刊名称】《工程数学学报》【年(卷),期】2014(000)003【总页数】10页(P371-380)【关键词】非定常对流扩散方程;非均匀网格;高精度紧致格式;全隐式;边界层【作者】黄雪芳;郭锐;葛永斌【作者单位】宁夏大学数学计算机学院,银川750021;宁夏大学数学计算机学院,银川 750021;宁夏大学数学计算机学院,银川 750021【正文语种】中文【中图分类】O241.821 引言对流扩散方程是一类重要的运动模型方程,它可以描述诸如质量、热量、能量及速度等的对流和扩散过程,由于实际问题往往比较复杂,精确解很难求出,因此研究其精确稳定的数值求解方法具有十分重要的意义.国内外已提出了很多求解该类方程的有限差分方法,田振夫和冯秀芳提出了一种数值求解对流扩散方程的指数型交替组显方法,该方法具有固有并行性,而且无条件稳定[1];Ding和Zhang对时间项采用半离散和Padé逼近方法,对空间项利用文献[2]中的多项式紧致差分,构造了一种空间四阶和时间五阶的差分格式[3].文献[4,5]分别利用四阶紧致差分公式和四阶紧致指数格式构造了非定常对流扩散方程的高精度紧致差分格式;Mohebbi和Dehghan采用四阶紧致有限逼近和C1连续三次样条插值方法,提出了求解一维热传导方程和对流扩散方程的高阶紧致解法[6].这些格式都是基于均匀网格的,对于解光滑问题可以得到非常精确的计算结果,但对于大梯度问题及边界层问题,采用均匀网格的计算效果往往不理想.因此,发展高效的非均匀网格上的高精度紧致差分格式就成为有限差分方法发展的必然趋势[7-10].对定常对流扩散方程,建立在非均匀网格上的差分格式,文献[7–9]已经有相关报道,非定常对流扩散方程在非均匀网格上的高精度紧致差分方法却鲜有报道.本文针对一维非定常对流扩散方程,对空间导数利用泰勒级数展开进行离散,以及二阶向后欧拉差分方法对时间导数进行离散,得到了求解非定常对流扩散方程在非均匀网格上的三层高精度紧致全隐差分格式.2 一维对流扩散方程高精度紧致差分格式其中u(x,t)是未知函数,a为扩散项系数,p(x,t)为对流项系数,源项f(x,t)为已知函数,假设u(x,t),p(x,t)和f(x,t)均为求解区域上关于变量x和t的足够光滑函数.将空间区域[a1,a2]剖分为N个子区间,定义空间步长xb=xi−xi−1,xf=xi+1−xi,1≤i≤N−1,当xb=xf时,网格为均匀剖分.对时间方向采用均匀网格剖分,步长用τ表示.为方便差分格式推导,首先考虑如下一维定常对流扩撒方程考虑如下一维变系数非定常对流扩散方程u,p,s均为x的函数,分别将u(xi+1),u(xi−1)在点x(i)处作泰勒展开,得(3)与(4)式相减可得(3)和(4)式分别乘xb,xf相加得定义x方向非均匀网格上的一阶和二阶中心差分算子将上述定义的差分算子代入一阶和二阶导数,则(2)式可写成如下形式其中对原方程(1)关于x求导,得到u关于x的三阶和四阶导数,代入τi,并将si用代替,略去截断误差项则(9)式变为其中考虑方程在n+1时刻的值,对利用二阶向后欧拉差分离散,即将代入(11)式,略去时间高阶项,可得其中用分别表示函数u(x,t)在点(xi,tn),(xi−1,tn),(xi+1,tn)处的近似解,将及差分算子的定义代入(13)式,化简整理可得到一维非定常对流扩散方程(1)在非均匀网格上的高精度紧致差分格式对应系数为其中n≥1.易得此格式的截断误差项由给出,时间为二阶精度,当xf=xb时,空间为四阶精度,当x f̸=xb时,空间为三阶精度,且该格式为无条件稳定的,这在后面的数值实验部分将给出数值验证.这是一个三层格式,要进行计算,除了需知道初始时刻的值外,还需知道第一时间层上的值.对此,采用向后差分处理时间导数,即用代替(12)式,并令n=0,同理可得到计算第一个时间步的差分离散格式对应系数为其中利用格式(16)完成第1个时间步的计算后,即可使用格式(14)计算第2个时间步以后的值,直到所需时刻.尽管格式(16)时间方向仅有一阶精度,但由于在计算过程中其只用于完成第一个时间步的计算,不会影响格式的整体精度.同时可以看到,在每个时间层上其对应方程组均为三对角方程组,可用追赶法进行求解.3 数值实验为验证本文格式的精确性和有效性,我们对如下三个算例进行数值求解.问题1[4]初始条件为:u(x,0)=0.边界条件为:u(0,t)=0,u(1,t)=1,其精确解由以下式子给出该问题在x=1处有跳跃边界层,对其空间区域[0,1]采用以下变换函数生成非均匀网格N为网格剖分子区间的个数,θ是角度的控制,θ=π时网格在边界处分布密集;当θ=2π时网格在区域中间分布密集.−1≤λ≤1称作伸缩变换系数,该参数可以调节网格点在某一局部区域网格点的密集程度,λ=0时网格剖分为均匀网格.对问题1,令θ=π,选取适当的变换系数λ使网格在x=1处分布密集,定义网格比η= τN2.表1和表2给出了T=1.0,η=1,Re取100和1000时,分别运用本文差分格式和Crank-Nicolson方法进行计算,得到数值解与精确解的最大绝对误差和空间收敛阶结果,其中非均匀网格分布均选取结果最好时对应的变换系数λ(算例2和算例3下同);图1和图2给出了问题1的精确解和数值解的比较.由计算结果可以看出,本文非均匀网格在精度上优势明显,其在较少网格数下即能达到较高的计算精度,且收敛阶均能达到四阶精度.表1: 问题1在不同网格数下的最大绝对误差及收敛阶(Re=100)网格数 Crank-Nicolson格式本文格式均匀网格本文格式非均匀网格(λ=0.69)最大绝对误差Order 最大绝对误差 Order 最大绝对误差Order 20 4.353×10−1 9.774×10−2 1.120×10−3 40 1.938×10−1 1.17 1.566×10−2 2.64 4.440×10−5 4.66 805.574×10−2 1.80 1.329×10−3 3.56 2.515×10−6 4.14 160 1.213×10−2 2.20 7.767×10−5 4.10 1.615×10−7 3.96表2: 问题1在不同网格数下的最大绝对误差及收敛阶(Re=1000)网格数 Crank-Nicolson格式本文格式均匀网格本文格式非均匀网格(λ=0.93)最大绝对误差Order 最大绝对误差 Order 最大绝对误差Order 40 8.518×10−1 6.188×10−13.632×10−3 80 7.241×10−1 0.23 3.833×10−1 0.69 1.384×10−44.71 1605.171×10−1 0.49 1.512×10−1 1.34 7.432×10−6 4.22 320 2.634×10−1 0.97 3.049×10−1 2.31 4.470×10−7 4.06图1: 当Re=100,(a):N=10,λ=0.54;(b):N=40,λ=0.69时,问题1数值解和精确解的比较图2:当Re=1000,(a):N=40,λ=0.93;(b):N=100,λ=0.93时,问题1数值解和精确解的比较另外,令N=160,Re分别取100和1000时,运用本文非均匀网格差分格式计算,可得η分别取10,100,1000,最大绝对误差均与η=1时结果一致,由此也可以验证本文差分格式为无条件稳定的.问题2[6]其初始条件如下:u(x,0)=αe−cx .√精确解为:,其边界条件由精确解给出.对此问题,令采用(17)式给出的变换函数,令θ=π.表3和表4给出了问题2在T=1,τ=2h,Re分别取100和1000时运用本文格式计算得到的平均误差结果,并与文献[6]及Crank-Nicolson格式的计算结果进行比较.计算结果表明,在相同的网格数下,本文非均匀网格格式采用合理的网格分布,可以得到较Crank-Nicolson格式,文献[6]中格式和本文均匀网格格式更为精确的计算结果.表5给出了问题2在网格剖分固定,不同时间步长下计算所得平均误差及时间收敛阶,可以看出本文差分格式时间上基本能达到二阶精度.表3:问题2的平均误差(Re=100)16 8.420×10−2 1.321×10−2 1.155×10−21.256×10−4(λ = −0.64)32 9.981×10−2 1.232×10−3 1.150×10−31.497×10−5(λ = −0.69)64 1.064×10−1 8.811×10−5 8.612×10−51.665×10−6(λ = −0.73)128 1.088×10−1 5.698×10−6 6.118×10−62.808×10−7(λ = −0.82)表4:问题2的平均误差(Re=1000)16 1.414×10−2 2.883×10−1 2.530×10−1 8.113×10−2(λ = −0.17)32 2.289×10−2 7.616×10−2 7.135×10−28.502×10−3(λ = −0.72)64 2.973×10−2 1.519×10−2 1.471×10−21.131×10−5(λ = −0.92)128 3.374×10−22.425×10−3 2.385×10−37.902×10−7(λ = −0.92)表5: 当N=2408,λ=0时,问题2在不同时间步长下的平均误差及收敛阶 8 16 6.980×10−8 1.50 3.439×10−8 2.04 1 1.980×101.413×10 1 32 1.920×10−8 1.86 1.072×10−8 1.68 1−9 −9问题3 变系数非定常对流扩散问题其精确解为:右端项f(x,t)及初边值条件均由精确解确定.随着a取值变小,该问题精确解在x=0处呈现出大梯度变化,表6给出了T=1.0,τ=时,a取10−4和10−5两种情况下采用均匀网格和非均匀网格计算得到的最大绝对误差.其中非均匀网格剖分同样采用(17)式给出的变换函数,令θ=2π,并选取相应的变换函数将区间[0,1]扩展到[−1,1],得到区域中间密集的网格分布.图3给出了N=32时,a 取10−4和10−5时均匀网格和非均匀网格数值解与精确解的比较,可以看出,在相同网格数下,高雷诺数问题采用均匀网格格式时,其数值解在大梯度附近区域发生振荡,而非均匀网格格式与精确解吻合得很好.表6: 问题3的最大绝对误差16 4.126×10−1 7.996× 10−2(λ =0.79)5.745×10−1 1.851× 10−1(λ =0.93)32 1.763×10−1 4.876× 10−2(λ =0.77) 5.780×10−1 7.034× 10−2(λ =0.93)646.127×10−2 3.950× 10−2(λ =0.8) 3.517×10−1 4.305× 10−2(λ =0.92)图3:当N=32,(a):a=10−4,λ=0.77;(b):a=10−5,λ=0.77时,问题3数值解和精确解的比较本文提出了数值求解一维非定常对流扩散方程在非均匀网格上的高精度紧致差分格式,该格式在时间和空间上分别能达到二阶和四阶精度,在求解大梯度和边界层问题时计算效果优于均匀网格.本文格式建立在非均匀网格上,在实际的流场计算中更为实用,针对不同的问题,通过合理地调节网格疏密,可以得到更高的计算精度.最后数值实验验证了本文方法的精确性和有效性.4 结论参考文献:[1]田振夫,冯秀芳.对流扩散方程的一种新的显式方法[J].工程数学学报,2000,17(4):65-69 Tian Z F,Feng X F.A new explicit method with exponential-type for the convection-di ff usion equation[J].Chinese Journal of Engineering Mathematics,2000,17(4):65-69[2]Karaa S,Zhang J.High order ADI method for solving unsteady convection-di ff usion problems[J].Journal of ComputationalPhysics,2004,198(1):1-9[3]Ding H,Zhang Y.A new di ff erence scheme with high accuracy and absolute stability for solving convectiondi ff usion[J].Journal of Computational and Applied Mathematics,2009,230(2):600-606[4]Tian Z F,Yu P X.A high-order exponential scheme for solving 1D unsteady convection-di ff usion equations[J].Journal of Computational and Applied Mathematics,2011,235(8):2477-2491[5]葛永斌,田振夫,吴文权.含源项非定常对流扩散方程的高精度紧致隐式差分方法[J].水动力学研究与进展(A辑),2006,21(5):619-625 Ge Y B,Tian Z F,Wu WQ.A high-order compact implicit di ff erence method for the unsteady convectiondi ff usion equation with source term[J].Journal of Hydrodynamics,2006,21(5):619-625[6]Mohebbi A,Dehghan M.High-order compact solution of the one-dimensional heat and advection-di ff usion equations[J].Applied Mathematics Modelling,2010,34(10):3071-3084[7]Kalita J C,Dass A K,Dalal D C.A transformational-free HOC scheme for steady convection-di ff usion on non-uniform grids[J].International Journal for Numerical Methods in Fluids,2004,44(1):33-53[8]田芳,田振夫.非均匀网格上求解对流扩散问题的高阶紧致差分方法[J].宁夏大学学报(自然科学版),2009,30(3):209-212 Tian F,Tian Z F.A high-order compact fi nite di ff erence method for convection di ff usion problems on non-uniform grids[J].Journal of Ningxia University(Natural Science Edition),2009,30(3):209-212[9]曹广满,王彩华,齐海涛.对流扩散方程的非一致网格有限差分方法[J].天津师范大学学报(自然科学版),2010,30(1):7-10 Cao G M,Wang C H,Qi H T.Non-uniform fi nite di ff erence scheme method for convection-di ff usion equations[J].Journal of Tianjin Normal University(Natural Science Edition),2010,30(1):7-10[10]田芳,田振夫.定常对流扩散反应方程非均匀网格上高精度紧致差分格式[J].工程数学学报,2009,26(2):219-225 Tian F,Tian Z F.A high accuracy compact di ff erence scheme for convection di ff usion reaction equation on non-uniform grid[J].Chinese Journal of EngineeringMathematics,2009,26(2):219-225。
