典型优化问题的遗传算法求解—8选址分配问题
使用Matlab进行遗传算法优化问题求解的方法

使用Matlab进行遗传算法优化问题求解的方法引言在现代科技发展的背景下,优化算法成为解决各种问题的重要工具之一。
遗传算法作为一种生物启发式算法,具有全局寻优能力和适应性强的特点,在许多领域中被广泛应用。
本文将介绍如何使用Matlab进行遗传算法优化问题求解,包括问题建模、遗传算子设计、遗传算法编码、适应度评价和求解过程控制等方面。
一、问题建模在使用遗传算法求解优化问题之前,我们首先需要将问题定义为数学模型。
这包括确定问题的目标函数和约束条件。
例如,假设我们要最小化一个多变量函数f(x),其中x=(x1,x2,...,xn),同时还有一些约束条件g(x)<=0和h(x)=0。
在Matlab中,我们可通过定义一个函数来表示目标函数和约束条件。
具体实现时,我们需要在目标函数和约束函数中设置输入参数,通过调整这些参数进行优化。
二、遗传算子设计遗传算法的核心是遗传算子的设计,包括选择(Selection)、交叉(Crossover)、变异(Mutation)和替代(Replacement)等。
选择操作通过一定的策略从种群中选择出适应度较高的个体,作为进行交叉和变异的父代个体。
交叉操作通过将两个父代个体的基因片段进行交换,产生新的子代个体。
变异操作通过改变个体某些基因的值,引入新的基因信息。
替代操作通过选择适应度较低的个体将其替换为新产生的子代个体。
三、遗传算法编码在遗传算法中,个体的编码方式决定了问题的解空间。
常见的编码方式有二进制编码和实数编码等。
当问题的变量是二进制形式时,采用二进制编码。
当问题的变量是实数形式时,采用实数编码。
在Matlab中,我们可以使用矩阵或向量来表示个体的基因型,通过制定编码方式来实现遗传算法的编码过程。
四、适应度评价适应度评价是遗传算法中判断个体优劣的指标。
在适应度评价过程中,我们将问题的目标函数和约束条件应用于个体的解,计算得到一个适应度值。
适应度值越大表示个体越优。
matlab遗传算法求解配送中心选址问题案例讲解

matlab遗传算法求解配送中心选址问题案例讲解遗传算法是一种基于生物进化原理的优化算法,可以用于求解各种复杂的问题,包括配送中心选址问题。
下面是一个使用MATLAB实现遗传算法求解配送中心选址问题的案例讲解。
一、问题描述假设有一组客户和一组候选的配送中心,每个客户都有一个需求量,配送中心有一个最大容量。
目标是选择一些配送中心,使得所有客户的需求量能够被满足,同时总成本最低。
二、算法实现1. 初始化种群在MATLAB中,可以使用rand函数随机生成一组候选配送中心,并使用二进制编码来表示每个配送中心是否被选中。
例如,如果候选配送中心有3个,则可以生成一个长度为3的二进制串来表示每个配送中心的状态,其中1表示被选中,0表示未被选中。
2. 计算适应度值适应度值是评估每个解的质量的指标,可以使用总成本来表示。
总成本包括建设成本、运输成本和库存成本等。
在MATLAB中,可以使用自定义函数来计算适应度值。
3. 选择操作选择操作是根据适应度值的大小选择解的过程。
可以使用轮盘赌选择、锦标赛选择等算法。
在MATLAB中,可以使用rand函数随机选择一些解,并保留适应度值较大的解。
4. 交叉操作交叉操作是将两个解的部分基因进行交换的过程。
可以使用单点交叉、多点交叉等算法。
在MATLAB中,可以使用自定义函数来实现交叉操作。
5. 变异操作变异操作是对解的基因进行随机修改的过程。
可以使用位反转、位变异等算法。
在MATLAB中,可以使用rand函数随机修改解的基因。
6. 终止条件终止条件是判断算法是否结束的条件。
可以使用迭代次数、最优解的变化范围等指标来判断终止条件。
在MATLAB中,可以使用自定义函数来实现终止条件的判断。
三、结果分析运行遗传算法后,可以得到一组最优解。
可以根据最优解的适应度值和总成本进行分析,并确定最终的配送中心选址方案。
同时,也可以使用其他评价指标来评估算法的性能,如收敛速度、鲁棒性等。
LabVIEW中的遗传算法和优化问题求解

LabVIEW中的遗传算法和优化问题求解LabVIEW(Laboratory Virtual Instrument Engineering Workbench)是一种广泛应用于工程、科学和教育领域的可视化开发环境和图形编程语言,它的强大功能和灵活性使得它在工程领域中被广泛使用。
在LabVIEW中,遗传算法(Genetic Algorithm)被广泛应用于优化问题的求解。
遗传算法是一种基于生物进化理论的优化算法,它通过模拟生物进化的过程,通过选择、交叉和变异的操作来搜索最优解。
在LabVIEW 中,遗传算法通过使用遗传算法工具箱来实现。
使用遗传算法求解优化问题的一般步骤如下:1. 定义问题:首先需要明确优化问题是什么,以及问题的目标函数是什么。
例如,我们要最小化一个函数或者使得某个约束条件满足等。
2. 设计编码方案:遗传算法是基于染色体编码的,我们需要设计一个合适的编码方案来表示问题的解空间。
例如,可以使用二进制编码、实数编码或者排列编码等。
在LabVIEW中,可以使用BitArray或者RealArray来表示染色体。
3. 初始化种群:种群是遗传算法的基本单位,它由多个个体组成。
在LabVIEW中,可以使用一个数组来表示一个种群,数组的每个元素表示一个个体。
4. 评价个体适应度:每个个体都有一个适应度值,表示其在问题中的优劣程度。
在LabVIEW中,可以根据定义的目标函数来计算个体的适应度值。
5. 选择操作:根据个体的适应度值,选择一定数量的个体用于后续的交叉和变异操作。
选择操作根据适应度值的大小来进行,适应度值越大的个体被选中的概率越高。
6. 交叉操作:选择的个体通过染色体的交叉操作来生成新的个体。
交叉操作类似于生物中的基因交换过程,在LabVIEW中可以使用Crossover函数来实现。
7. 变异操作:对于新生成的个体,通过染色体的变异操作来引入新的基因变化。
变异操作类似于生物中的基因突变过程,在LabVIEW中可以使用Mutation函数来实现。
考虑竞争和新鲜度的生鲜配送站选址问题研究

考虑竞争和新鲜度的生鲜配送站选址问题研究作者:张镛基岑仲迪来源:《物流科技》2024年第11期摘要:针对生鲜配送站多建乱建所带来选址成本居高不下的问题,在考虑固定建设成本、运营成本、配送成本的情况下,将新鲜度作为惩罚成本建立了模型的成本函数,引入竞争函数解决配送站建造位置过于拥挤的问题,以此为基础构建了多目标选址模型。
收集宁波市数据形成算例,使用改进遗传算法对模型进行求解,得到了算例生鲜配送站的最佳选址方案,并通过与仅考虑成本情况下模型结果进行对比分析得到竞争和新鲜度对选址的影响。
关键词:生鲜商品;新鲜度;配送站选址;竞争;改进遗传算法中图分类号:F252.14文献标志码:ADOI:10.13714/ki.1002-3100.2024.11.005Abstract: To address the problem of excessive and haphazard construction of fresh food delivery stations, we have developed a cost function for our model that incorporates the penalty cost of freshness, taking into account fixed construction costs, operational costs, and delivery costs. In order to address the issue of overcrowded locations for building delivery stations, we have introduced a competition function into the model. Based on these considerations, we have constructed a multi-objective site selection model. We have employed an improved genetic algorithm to solve the model and obtain the optimal site selection solution for the fresh food delivery stations in our case study. Furthermore, we have conducted a comparative analysis by comparing the results of our model considering both competition and freshness with the results obtained from a model that solely considers costs. This analysis provides insights into the impact of competition and freshness on site selection.Key words: fresh food products; freshness; site selection for delivery stations; competition; improved genetic algorithm0 引言隨着科学技术和新零售模式的发展,生鲜电商迎来了发展的黄金时期。
遗传算法求解优化问题实例

遗传算法求解优化问题实例
一个常见的优化问题是旅行商问题(Traveling Salesman Problem,TSP)。
给定一组城市和每对城市之间的距离,旅行商问题要求找到一条经过所有城市一次且回到起点的最短路径。
以下是使用遗传算法求解TSP的实例:
1. 随机生成一个初始种群,种群中的每个个体表示一条路径。
每个个体由一个城市序列表示,例如[1, 2, 3, ..., n],其中n是城市的数量。
2. 计算种群中每个个体的适应度。
适应度可以定义为路径的总长度,即经过所有城市的距离之和。
3. 选择适应度较高的个体作为父代,进行交叉和变异操作以生成新的子代。
交叉操作可以是将两条路径的一部分交换,变异操作可以是随机改变路径中的一个或多个城市顺序。
4. 计算新生成的子代的适应度。
5. 重复步骤3和4,直到达到终止条件(例如达到最大迭代次数)。
6. 返回适应度最好的个体作为最优解,即最短路径。
遗传算法的优势在于可以在大规模问题中寻找较好的解,虽然不一定能找到最佳解,但可以得到相对较优的解。
军事物流选址分配模型及遗传算法优化

关键 词 : 军事物 流 ; 中心选 址 ; 务 需求分 配 ; 传 算法 ; 服 遗 拉格 朗 日松 弛 法
中图分 类号 : 2 1 9 O 1 . 文献标 识码 : A 文章编 号 :6 1 6 3 2 0 ) 1— 10— 4 17 —0 7 (0 7 0 0 1 0
O p i i a i n o he M o e fM i t r g si s Ce e c to nd tm z to ft d lo l a y Lo itc nt r Lo a i n a i A lo a i n o e v c i g G e tc A l o ihm l c to f S r i e Usn nei g rt
3 De at n fS in e sac . pr meto ce csRee rh,I fr t nEn ie r g U ies y h n zo 5 0 2, hn ) nomai gn ai nv ri ,Z e gh u4 0 0 C ia o n t Absr c On c n iin t a a h lg si sc ne a ii a e v c a c t t a t: o d to h te c o it e trf clt h s a s r ie c pa i c y y,a m o e fmii r d lo lt y a
2 Nain lDee e y L b r tr fB i d P o e sn f in l ,C e g u 6 0 4 C ia . t a o fn e Ke a o aoy o l r c s i g o g a s h n d 1 0 1, h n ; n S
维普资讯
第 8卷 第 1 期
20 0 7年 3月
组合优化问题的遗传算法求解

组合优化问题的遗传算法求解一、简介组合优化问题指的是在有限个元素中选取某些元素,以达到最优化的目标。
组合优化问题的求解在实际中应用广泛,如旅行商模型、调度问题、网络优化等领域。
但是这类问题求解面临着复杂度高、难以精确求解等困难。
在这种情况下,遗传算法是一种有效的求解方法。
遗传算法是一种基于达尔文进化论的计算方法,通过模拟生物进化的方式求解组合优化问题。
本文将介绍遗传算法在组合优化问题求解中的应用,着重介绍遗传算法基本框架、编码方法、适应度函数的构建以及遗传算法的优化策略等。
二、遗传算法基本框架遗传算法的求解过程主要包括初始种群生成、适应度评价、选择操作、交叉操作和变异操作等基本步骤。
(1)初始种群生成遗传算法首先需要生成一定数量的初始种群,初始种群可以通过随机生成或其他启发式算法生成。
例如,在旅行商问题中,初始种群可以随机生成多条路径。
(2)适应度评价适应度函数是遗传算法的核心,适应度函数的构建直接关系到遗传算法的性能。
适应度函数是对每个染色体的优劣进行量化评价,用以指导后续优化操作。
适应度函数构建需要根据问题特点进行设计。
(3)选择操作选择操作是指将上一代种群中的某些个体复制到下一代种群中,个体复制的概率与其适应度大小有关。
适应度越高的个体被选择的概率越大,从而使适应度高的个体更有机会进化到下一代。
选择操作可以通过轮盘赌选择、锦标赛选择等方式实现。
(4)交叉操作交叉操作是指对选择后的个体进行杂交,交叉操作是遗传算法的核心,它通过随机杂交个体的染色体,产生新的杂交染色体,从而增加搜索空间。
交叉操作可分为单点交叉、多点交叉、均匀交叉等。
(5)变异操作变异操作是指在交叉操作之后对个体发生变异,从而产生新的个体。
变异操作是通过随机改变染色体中的基因,从而增加多样性。
变异操作可以是简单变异、非一致变异、高斯变异等。
以上是遗传算法的基本框架,遗传算法的性能因素有适应度函数的设计、进化代数、群体大小、交叉概率、变异概率等。
线性规划问题中的遗传算法求解研究

线性规划问题中的遗传算法求解研究遗传算法在线性规划问题中的应用研究引言线性规划是一种常见的优化问题,它的目标是在一组线性约束条件下,寻找使得目标函数最大或最小的变量值。
传统的解决线性规划问题的方法包括单纯形法、内点法等。
然而,随着计算机技术的发展,人工智能算法也开始在解决这类问题上发挥作用。
其中,遗传算法作为一种模仿生物进化过程的优化算法,被广泛应用于线性规划问题中。
一、遗传算法的基本原理遗传算法是一种仿生优化算法,它模拟生物进化的过程,通过不断的选择、交叉和变异等操作,逐步优化解空间中的解。
其基本原理包括以下几个步骤:1. 初始化种群:随机生成一组初始解,每个解都代表线性规划问题的一个可能解。
2. 适应度评估:计算每个解的适应度,即目标函数值。
适应度越高,说明解越优。
3. 选择操作:根据适应度对解进行选择,高适应度的解更有可能被选中,从而保留下来。
4. 交叉操作:选取两个解进行基因的交叉,生成新的解。
交叉操作可以保留两个解中优秀的特征,有利于搜索更优解。
5. 变异操作:对新生成的解进行基因突变,引入随机因素,增加搜索的多样性。
变异操作有助于跳出局部最优解,寻找全局最优解。
6. 重复以上步骤,直到满足停止条件。
二、遗传算法在线性规划问题中的求解过程1. 根据线性规划问题的约束条件和目标函数,确定决策变量的范围和约束条件。
2. 初始化种群:随机生成一组初始解作为种群。
3. 计算适应度:对于每个解,计算目标函数的值作为适应度。
4. 选择操作:根据适应度,选择一部分解作为下一代种群,保留适应度较高的解。
5. 交叉操作:选取两个解,通过交叉操作生成新的解。
可以使用单点交叉、多点交叉等不同的交叉方式。
6. 变异操作:对新生成的解进行变异操作,引入随机因素,增加解空间的多样性。
7. 重复进行步骤4至步骤6,直到满足停止条件。
8. 输出最优解:根据迭代过程中的适应度值,选择最优解作为线性规划问题的解。
三、遗传算法在线性规划问题中的优势1. 全局搜索能力:遗传算法能够通过交叉和变异操作进行全局搜索,避免陷入局部最优解。
基于遗传算法的最优化问题求解

基于遗传算法的最优化问题求解遗传算法是一种启发式算法,受到进化生物学中的自然选择和遗传机制启发而设计。
它可以用于解决许多最优化问题,比如函数优化、组合优化和排程优化等。
本文将介绍遗传算法的基本原理和应用,并探讨如何使用遗传算法来求解最优化问题。
1. 遗传算法的基本原理遗传算法的基本过程包括初始化种群、选择、交叉、变异和替换等步骤。
首先,通过随机生成一组个体来构建初始种群。
个体通常是由一组变量表示的解向量。
接下来,通过选择操作从当前种群中选择出适应度较高的个体作为父代。
选择操作可以使用各种方法,如轮盘赌选择、竞争选择和排名选择等。
然后,通过交叉操作将父代个体的基因片段进行交换和组合,产生一组新的个体。
交叉操作可以使用单点交叉、多点交叉或均匀交叉等方法。
随后,对新个体进行变异操作,通过改变个体的基因值来引入新的多样性。
变异操作可以是改变一个基因位的值,或者改变一组基因位的值。
最后,使用替换操作将新个体替换掉部分原始种群中的个体,以形成下一代种群。
以上步骤可以循环迭代执行,直到满足终止条件,如达到最大迭代次数或找到满意的解。
2. 遗传算法的应用遗传算法在各种最优化问题中都有广泛的应用。
函数优化是最常见的应用领域之一。
遗传算法可以通过调整自变量的取值来最小化或最大化特定的目标函数。
它的优势在于能够通过遍历解空间,找到全局最优解或接近最优解的解。
组合优化是另一个常见的应用领域。
组合优化问题通常涉及在给定约束条件下,选择一组对象或变量来满足特定的目标。
例如,旅行商问题就是一个经典的组合优化问题,遗传算法可以用于找到旅行商的最短路径。
排程优化也是遗传算法的重要应用领域之一。
排程问题涉及将若干任务安排在一定时间内,以最大化或最小化某种指标。
遗传算法可以用于求解复杂的排程问题,如工厂作业调度、航班排班和员工排班等。
此外,遗传算法还可以应用于参数优化、神经网络训练和机器学习等问题。
3. 使用遗传算法求解最优化问题的步骤使用遗传算法求解最优化问题通常包括以下步骤:首先,需要定义问题的目标函数和约束条件。
典型优化问题的遗传算法求解— 选址分配问题

典型优化问题的模型与算法-R03
19
图形描述
设施的选址和客户的分配
C3 c13
C1 (u1, v1) c11
F1 (x1, y1)
…
d1
cmn (xi, yi)
Fm dm
Cn (uj, vj)
m : 设施总数
n : 客户总数
Fi: 第i 个设施, i=1,2,…,m Cj: 第 j 个客户, j=1,2,…,n
j 1
m
gm j (z) zij 1, j 1,2,, n i 1
zij 0 or 1, i 1,2,, m, j 1,2,, n
变量:
zij: 0-1 决策变量 zij=1, 顾客 j 由设施 i 服务;否则 zij=0
Fi = (xi, yi) :设施 i 的未知位置,决策变量 参数:
学校、消防站、公园等, 此类基础设施对于“最佳选址”理解的共同点在于,使供
需点之间的“总距离”或者“平均距离”最小。
除此以外,这个基本模型经过扩展还可以有更广泛的 应用范围,如:
优化城市零售商业网点空间分布(通过最大化惠顾人流量来 实现)、
优化制造业场所空间分布(通过最小化运输成本实现)、 优化公共服务设施空间分布(通过最优化服务质量实现)、 ……
单韦伯 (single Weber)问题
在欧几里德空间上典型的单韦伯(single Weber) 问题是
寻找一个位置,使从代表顾客位置的一些固定点到它 的距离和最小。
问题描述:
有 m 个“设施”需要选址,n 个已知位置的“顾客” 分;我们配每需给个要不设找同施到的具设有施的,能每力个为顾a客i,的i=需1,2求,…为,mbj,j=1,2,…,n
如地震、海啸、流行病、
基于遗传算法的多目标优化问题求解

基于遗传算法的多目标优化问题求解随着现代科技的飞速发展和生产制造业与服务业的日益繁荣,多目标优化问题已成为了一个重要的研究方向。
多目标优化问题指的是需要在同时优化多个目标指标的情况下进行决策的问题,例如在生产制造业中需要同时考虑成本和质量等多个指标。
解决这种问题的有效手段便是遗传算法,本文将介绍基于遗传算法的多目标优化问题求解。
一、遗传算法的核心思想遗传算法是一种模拟遗传学和自然选择过程的优化方法,其核心思想是通过模拟“基因”的遗传变异和自然选择过程来寻找问题的最优解。
遗传算法的具体实现过程主要包括以下几个步骤:1. 初始化种群:遗传算法需要初始化一个种群来表示问题的解集合,一般采用随机生成的方式进行初始化。
2. 选择操作:通过“适者生存”的原则,在种群中选择若干个较为适应的个体,作为下一代种群的父母。
3. 变异操作:对父母进行个体基因的随机变异,以增加种群的遗传多样性。
4. 交叉操作:采用不同的交叉方式将父母基因进行组合,生成新的下一代个体。
5. 筛选操作:从父母和子代中选择较优的个体,更新种群,并进行下一次迭代。
通过上述过程,遗传算法能够搜索到问题的最优解,其中适应度函数的设定是非常重要的一步,它用来评估个体的适应度程度。
二、多目标优化问题的遗传算法求解在多目标优化问题的求解中,适应度函数也需要进行改进,一般将每个目标指标的值单独计算,再考虑其权重关系。
例如在生产制造业中,成本和质量两个指标的权重往往不同,需要根据实际情况进行调整。
另外,遗传算法中的选择操作也需要进行改进,常用的多目标选择方法有以下两种:1. 非支配排序:通过将每个个体与其余个体进行比较,将其分为不同的等级,并选取前面的等级的个体作为父母进行交叉和变异操作。
2. 拥挤度计算:通过计算每个个体在解空间中的拥挤度,选择拥挤度较大的个体作为下一代的父母,以增加解空间的遍历能力。
多目标优化问题的遗传算法求解需要注意以下几个问题:1. 避免陷入局部最优解:在遗传算法中,子代可能比父代更劣,因此需要加入一定的随机因素来跳出局部最优解。
遗传算法求解多目标优化问题

遗传算法求解多目标优化问题随着科技的发展和社会的进步,人们对各种问题的优化需求越来越高。
在现实生活中,我们常常面临多个目标之间的冲突,需要找到一种解决方案,能够在多个目标之间取得平衡。
在这种情况下,多目标优化问题应运而生。
多目标优化问题(Multi-Objective Optimization Problem,简称MOP)是指在具有多个冲突目标的复杂系统中寻找最优解的问题。
解决MOP问题的方法有很多种,其中一种被广泛应用的方法就是遗传算法。
遗传算法是一个基于自然进化过程的优化算法,通过模拟自然进化的过程来搜索最优解。
它将问题的解表示为一个个体(也称为染色体),通过交叉和变异等遗传操作产生下一代的个体,不断迭代,最终找到较好的解。
在使用遗传算法求解多目标优化问题时,需要采取一些特定的策略和算子来克服多目标之间的冲突。
下面我将介绍一些常见的策略和算子。
第一,适应度函数的设计。
在单目标优化问题中,适应度函数往往只有一个目标。
而在多目标优化问题中,适应度函数需要同时考虑多个目标的性能。
常用的适应度函数设计方法有线性加权和Chebyshev方法。
线性加权方法将各个目标按一定权重加权求和,而Chebyshev方法则选取各个目标值中最大的值作为适应度值。
第二,选择操作的策略。
在遗传算法中,选择操作是保留适应度较高的个体,淘汰适应度较低的个体。
针对多目标优化问题,常用的选择操作策略有非支配排序和拥挤度算子。
非支配排序方法将个体划分为不同的层级,每一层级的个体相对于其他层级的个体来说都是非支配的。
拥挤度算子则是通过计算个体在解空间中的密度来保留具有多样性的解。
第三,交叉和变异操作的设计。
在多目标优化问题中,交叉和变异操作需要保证生成的新个体能够在多个目标之间取得平衡。
常用的交叉操作有模拟二进制交叉(SBX)和离散型交叉。
SBX方法通过对父代染色体的值进行交叉,产生子代染色体的值。
离散型交叉则从父代染色体中随机选择一个目标值来构建子代染色体。
基于遗传算法的最优化问题求解方法

基于遗传算法的最优化问题求解方法随着人工智能技术的不断发展和普及,最优化问题在工程、经济、管理等领域中得到了广泛应用。
最优化问题是指在一定的限制条件下,寻找最佳的决策方案,从而能够获得最优的效果。
为了解决最优化问题,人们在不断探索新的算法和方法。
其中,基于遗传算法的最优化问题求解方法备受关注。
遗传算法是一种基于生物进化思想的计算机算法,具有全局优化、可适应性强、鲁棒性好等特点,因此在最优化问题的求解中扮演着重要的角色。
一、遗传算法的概念和基本原理遗传算法是模拟生物进化过程的计算机算法。
它是从自然界中生物进化的过程中发掘出来的一种求解最优化问题的方法。
遗传算法的基本原理是模拟生物进化过程的三个操作:选择、交叉和变异。
1.选择操作选择操作是指根据个体适应度大小,按照一定的概率选择优秀个体,淘汰劣质个体。
具体实现方法是在种群中随机选择两个个体比较它们的适应度,然后根据某种方法保留优秀个体并淘汰劣质个体,以此来生成新的种群。
选择操作是遗传算法中最重要的操作之一,它直接影响到算法的性能。
2.交叉操作交叉操作是指将已选择的优秀个体进行交叉从而生成新的个体。
具体实现方法是在两个被选择的个体之间随机选取交叉点,并交换两个个体之间的某些基因信息。
目的是为了保留经过选择操作后的优秀个体,并且在新的个体中引入多样性,增加种群的搜索范围,从而增强算法的全局搜索能力。
3.变异操作变异操作是指在某些条件下,对已经生成的新个体进行个别基因的改变。
具体实现方法是选取某个新个体的一个基因进行随机改变操作,例如随机增加、删除或修改某个基因的值。
变异操作是为了增加多样性,避免算法陷入局部最优解,从而提高算法的全局寻优能力。
二、遗传算法的优点和不足遗传算法具有一系列的优点,主要包括以下方面。
1.全局最优性遗传算法具有全局寻优能力,它能够搜索全部解空间,并找到全局最优解。
这是由于它采用了随机寻优方法,能够避免陷入局部最优解。
2.可适应性强遗传算法能够自适应地调整参数,以适应问题的复杂性和难度,在不同的环境下优化效果也不同。
遗传算法在求解函数优化问题中的应用研究

《 装备制造技术)0 1 ) 1 年第 6 2 期
的“ 函数” 优化 , 这里所指的函数 , 主要是强调 函数的 数学特征 , 函数的连续性 、 如 凹凸性 、 多峰性 、 多维性 等。通常 , 标 函数优化问题可以描述为以下步骤 : 目 () 1 步骤 1 ——确定需要赋值 的自变量 五。在 函 数优化 问题里 , 我们称这些变量为设计变量 。 可能会
图 2 最 大 值 随计 算 计算循环次数 的增加 , 其
结 果 慢慢 的逼 近 最 大值 ,但 是 当达 到一 定 的 程度 之
() 3 步骤 3 ——确定作用 于 自( 设计) 变量上 的限 后 ,计算 的结果就会在最大值 附近波动 。本算例可 当循环次数达 到 10次时 , 5 结果已经非常接近最 制条件 即约束条件 ,把它们写成等式或不等式 的形 知 , 大值 , 当计算循环 次数再继续增大时, 那么结果只能 式。从而可得到 目标 函数为
E up n Ma ua tn e h oo yNo6,01 q ime t n fcr gT c n lg . 2 i 1
遗传 算法在 求解 函数优化 问题 中的应 用研 究
郑 美 茹
( 陕西铁路工程职业技术学院 机电工程系 , 陕西 渭南 74 0 100)
摘 要 : 绍 了遗 传算法是 一种借 鉴生物界 自然选择和优化机制发展起 来的高度 并行 、 介 随机 、 自适应搜 索算 法。 阐述 了
有 n个 这 样 的 变量 , 常 用 通
这些 变 量 ;
, , , 来 表 示 。 … ‰
0 5 1 0 1 0 2 0 2 0 3 0 3 0 4 0 4 05 o 0 0 5 0 5 0 5 0 5 o
计算循环次数 , v
典型优化问题的模型与算法作业题
P1 1 2 3 4 5 6 7
a1=7 1
4 b1=11 P2 3 2 5 1 7 4 6
a2=15 2 a3=17 3
5 b2= 3 6 b3=9 7 b4=16
4
3
1
2
现
提交内容:
实验报告的电子文档 源代码及其全部工程文件、数据文件(ZIP形式) 发送到:liushuan@
典型优化问题的模型与算法
2
6 7
5
典型优化问题的模型与算法
1
实验
内容:
以某一典型优化问题为例,构造“具体”模型,采用 遗传算法进行求解。
基本要求:
列出具体模型;
设计染色体编码、交叉算子、变异算子、适值函数、 选择策略、种群初始化方法等;
给出程序设计说明(类,函数,流程图等); 给出多种条件下的仿真结果对比分析。 采用VB、VC、C#、JAVA等任一种软件开发语言实
粒子群优化算法优化算法智能优化算法多目标优化算法最优化算法最优化理论与算法传统优化算法球的光照模型算法遗传算法函数优化蚁群优化算法
典型优化问题的模型与算法—作业题
1. 有界背包是指有多种物品且每种物品都有多个的背包问题。试建 立数学模型、说明问题的特点,并设计一种求解此问题的完整的 遗传算法。
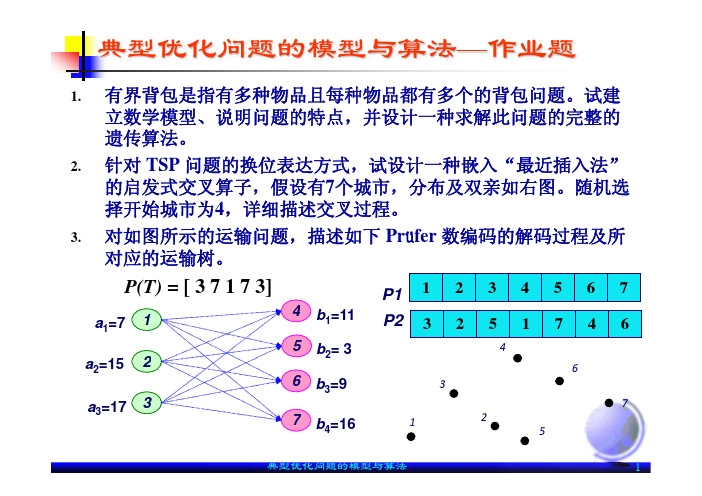
2. 针对 TSP 问题的换位表达方式,试设计一种嵌入“最近插入法” 的启发式交叉算子,假设有7个城市,分布及双亲如右图。随机选 择开始城市为4,详细描述交叉过程。
遗传算法求解多目标优化问题有效性评价

遗传算法求解多目标优化问题有效性评价引言:多目标优化问题是在实际工程和科学中普遍存在的一类问题,它们涉及到多个矛盾的目标同时优化的情况。
遗传算法(Genetic Algorithm)作为一种常用的优化方法,能够有效地应对复杂的多目标优化问题,并求解出一组帕累托最优解集。
然而,在实际应用中,我们需要对遗传算法求解多目标优化问题的有效性进行评价,以便确认其在不同问题上的适用性和性能。
效果评价指标:评价遗传算法求解多目标优化问题的有效性需要借助一些评价指标。
以下是一些常用的评价指标:1. Pareto前沿:Pareto前沿是指多目标优化问题中,所有非支配解形成的边界。
2. 趋近度:趋近度指标衡量了计算得到的帕累托前沿与真实前沿之间的差异。
常用的趋近度度量方法包括Hypervolume指标、Generational Distance指标等。
3. 均匀度:均匀度指标能够反映解集空间分布的均匀性。
Flow Distance指标和Spacing指标是常用的均匀度度量方法。
4. 支配度评价:支配度评价指标体现了解集质量的综合表现。
解集中的个体数目越多越好,且个体尽量要有较大的各目标函数值。
评价方法:针对遗传算法求解多目标优化问题的有效性评价,可以采用以下方法:1. 可视化分析:通过绘制Pareto前沿图,直观地观察计算得到的解的分布情况、密度以及分布范围等。
可以借助散点图、等高线图等方法绘制多目标优化问题的解集,以便直观地评估算法的求解效果。
2. 比较分析:将遗传算法与其他多目标优化算法进行比较,如粒子群优化算法、模拟退火算法、遗传模拟退火算法等。
通过比较不同算法的求解效果,评估遗传算法在不同问题上的表现。
3. 统计分析:使用一些常用的评价指标,如趋近度指标、均匀度指标、支配度指标等,可以对遗传算法求解多目标优化问题的结果进行量化评价。
通过统计分析和对比,得到算法在不同问题上的性能评估。
实例分析:为了更好地说明遗传算法求解多目标优化问题的有效性评价,我们以一个实例进行分析。
基于MATLAB遗传算法的物流中心选址问题研究

基于MATLAB遗传算法的物流中心选址问题研究一、本文概述随着电子商务的飞速发展和全球供应链的日益紧密,物流中心选址问题在运筹学和运营管理领域中的重要性日益凸显。
合理的物流中心选址不仅能够降低运输成本、提高物流效率,还能对整个供应链的顺畅运行产生深远影响。
因此,研究物流中心选址问题,寻求科学的优化方法,具有重要的理论价值和实际应用意义。
本文旨在运用MATLAB遗传算法对物流中心选址问题进行深入研究。
遗传算法作为一种模拟生物进化过程的优化算法,具有全局搜索能力强、鲁棒性高等优点,适用于解决复杂的组合优化问题。
本文将通过MATLAB编程实现遗传算法,构建物流中心选址问题的数学模型,并通过案例分析验证算法的有效性和实用性。
具体而言,本文将首先介绍物流中心选址问题的背景和研究意义,阐述物流中心选址问题的特点和难点。
然后,将详细介绍遗传算法的基本原理和实现步骤,包括染色体编码、初始种群生成、适应度函数设计、选择操作、交叉操作和变异操作等。
在此基础上,本文将构建物流中心选址问题的数学模型,包括目标函数和约束条件,并利用MATLAB编程实现遗传算法求解。
本文将通过案例分析,对比不同算法下的优化结果,验证遗传算法在物流中心选址问题中的优越性和实用性。
通过本文的研究,旨在为物流中心选址问题提供一种科学有效的优化方法,为企业决策提供参考依据,推动物流行业的智能化和高效化发展。
也希望能够为相关领域的学术研究提供有益的参考和借鉴。
二、物流中心选址问题的数学模型在物流系统中,选址问题是一个典型的组合优化问题,涉及多个因素的权衡和决策。
物流中心选址问题的目标是找到一个或多个合适的地点,以便在满足客户需求的最小化物流成本。
这个问题可以通过构建数学模型进行求解。
我们需要定义问题的决策变量。
在这个问题中,决策变量是物流中心的位置。
我们可以使用坐标系统来表示这些位置,例如二维平面上的点(x, y)。
如果有多个物流中心,那么决策变量将是一个向量,包含每个物流中心的坐标。
遗传算法求解选址问题的python代码

遗传算法求解选址问题的python代码选址问题是一种组合优化问题,其中目标是最小化总成本,总成本通常由多个因素决定,例如运输成本、设施成本等。
遗传算法是一种启发式搜索算法,可以用于求解这类问题。
以下是一个使用遗传算法求解选址问题的Python代码示例:```pythonimport numpy as npimport random定义适应度函数def fitness_func(individual):计算总成本total_cost = 0for i in range(len(individual) - 1):total_cost += abs(individual[i] - individual[i + 1])total_cost += abs(individual[-1] - individual[0])return total_cost定义遗传算法参数pop_size = 100 种群大小chrom_length = 10 染色体长度(即候选地址数量)num_generations = 100 迭代次数mutation_rate = 变异率初始化种群pop = (0, chrom_length, (pop_size, chrom_length))进行迭代进化for generation in range(num_generations):计算适应度值fitness = ([fitness_func(chrom) for chrom in pop]) 选择操作:轮盘赌选择法idx = (pop_size, size=pop_size, replace=True, p=fitness/()) pop = pop[idx]交叉操作:单点交叉for i in range(0, pop_size, 2):if () < :cross_point = (1, chrom_length-1)temp = pop[i][:cross_point] + pop[i+1][cross_point:]pop[i] = temppop[i+1] = temp[::-1]变异操作:位反转变异法for i in range(pop_size):if () < mutation_rate:flip_point = (0, chrom_length-1)pop[i][flip_point] = pop[i][flip_point] + (1 if pop[i][flip_point] % 2 == 0 else -1) % chrom_length```。
如何利用遗传算法进行优化问题求解

如何利用遗传算法进行优化问题求解遗传算法是一种模拟自然选择和遗传机制的优化算法,被广泛应用于各种优化问题的求解。
它模拟了生物进化的过程,通过不断迭代和优胜劣汰的选择机制,逐步找到问题的最优解。
本文将介绍遗传算法的基本原理和应用,以及如何利用遗传算法解决优化问题。
一、遗传算法的基本原理遗传算法的基本原理是基于达尔文的进化论和孟德尔的遗传学原理。
它通过模拟自然界中的遗传机制,将问题的解表示为染色体,并通过交叉、变异等操作对染色体进行进化,以求得最优解。
遗传算法的基本流程如下:1. 初始化种群:随机生成一组初始解,称为种群。
2. 评估适应度:根据问题的评价函数,计算每个个体的适应度,用于衡量个体对问题的解的贡献。
3. 选择操作:根据适应度选择一部分个体作为父代,用于产生下一代。
4. 交叉操作:通过交叉操作,将父代个体的染色体片段互换,产生新的个体。
5. 变异操作:对新的个体进行变异操作,以增加种群的多样性。
6. 评估适应度:计算新的个体的适应度。
7. 判断终止条件:判断是否达到终止条件,如找到最优解或达到迭代次数。
8. 返回结果:返回最优解或近似最优解。
二、遗传算法的应用遗传算法广泛应用于各种优化问题的求解,如旅行商问题、车辆路径规划、资源分配等。
下面以旅行商问题为例,介绍如何利用遗传算法进行求解。
旅行商问题是指给定一组城市和每对城市之间的距离,求解一条最短路径,使得每个城市只访问一次,并返回起点城市。
遗传算法可以通过优化路径的顺序,找到最短路径。
首先,将每个城市表示为染色体的一个基因,染色体的长度为城市的个数。
然后,通过交叉和变异操作,生成新的个体。
交叉操作可以通过将两个个体的染色体片段互换,生成新的个体。
变异操作可以通过随机选择染色体的一个基因,将其替换为其他城市,增加种群的多样性。
通过不断迭代和优胜劣汰的选择机制,遗传算法可以逐步找到最优解。
在每次迭代中,根据问题的评价函数,计算每个个体的适应度。
运筹优化中的遗传算法应用案例分析

运筹优化中的遗传算法应用案例分析遗传算法是一种模拟自然界进化过程的优化方法,通过模拟生物遗传和进化规律,在问题求解过程中寻找最优或接近最优解。
在运筹优化领域,遗传算法被广泛应用于多个方面,如旅行商问题、资源分配问题、生产调度问题等。
本文将对几个运筹优化中的遗传算法应用案例进行分析,以展示遗传算法在实践中的应用效果和优势。
首先要介绍的是旅行商问题(TSP)。
旅行商问题是一个经典的求解最短路径问题,即找出一条路径使得旅行商可以依次访问多个城市,并回到起点城市,且所走过的总路径最短。
遗传算法可以通过定义适应度函数以及遗传操作(选择、交叉、变异)来求解该问题。
通过遗传算法的迭代过程,逐渐优化路径,并最终得到全局最优解。
第二个案例是资源分配问题。
在生产调度和资源分配中,经常需要考虑如何合理利用有限的资源来最大化利益。
遗传算法可以通过优化资源分配方案,同时考虑到资源约束和利益最大化的目标。
通过对资源的分配和利用情况进行建模,并通过遗传算法优化模型,可以提高资源的利用效率,并达到最优的资源分配方案。
第三个案例是生产调度问题。
在制造业中,生产调度是一个重要的问题,涉及到如何合理安排生产任务、机器设备的时间利用、产品的交付时间等方面。
遗传算法可以通过建立合适的数学模型,考虑到各种约束条件,并通过遗传算法的迭代优化过程,自动找到最优的生产调度方案。
除了上述案例,遗传算法还可以应用于其他运筹优化问题,如货车路径优化、物流配送最优化、航班调度等。
通过合理的建模和设计,将问题转化为适应度函数的形式,可以利用遗传算法求解这些复杂的运筹优化问题。
遗传算法之所以在运筹优化中得到广泛应用,是因为它具有以下几个优势:首先,遗传算法具有全局搜索的能力。
遗传算法通过种群的多样性保持,在搜索空间中进行全局搜索,能够找到接近全局最优解的解。
这对于那些问题空间复杂、搜索空间庞大的问题特别有效。
其次,遗传算法具有自适应性。
通过不断迭代的过程,遗传算法可以根据问题的具体情况,自动调整参数和权重,使得算法能够适应不同问题的求解过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
di: 建立第 i 个设施的费用 cij: 第 i 个设施向第 j 个客户提供服务的费用 Fi=(xi, yi): 设备 i 的已知位置 Cj=(uj, uj): 客户 j 的已知位置
典型优化问题的模型与算法-R03
20
数学模型
mn
m
min f (x) cij xi来自 di yii1 j1
x i
是
[ xmin , xmax ]
之间的随机数
y i
是 [ ymin , ymax ] 之间的随机数
典型优化问题的模型与算法-R03
14
GA求解
评价
对于指定的染色体 vk,设施的位置是固定的 我们可将最优分配的距离和映射为 vk 的适值 为计算距离和,需要解决分配子问题。
对于固定的设施选址问题,采用拉格朗日松弛法解决分 配子问题
j 1
m
gm j (z) zij 1, j 1,2,, n i 1
zij 0 or 1, i 1,2,, m, j 1,2,, n
变量:
zij: 0-1 决策变量 zij=1, 顾客 j 由设施 i 服务;否则 zij=0
Fi = (xi, yi) :设施 i 的未知位置,决策变量 参数:
位学者。他证明目标函数既不是凹的也不是凸 的,并存在许多局部最优解。
典型优化问题的模型与算法-R03
5
分类
按能力分类:
有能力约束的LAP 无能力约束的LAP
按阶段分类:
单阶段LAP 多阶段LAP
其它分类:
有障碍的LAP 平衡的LAP
典型优化问题的模型与算法-R03
6
问题的扩展
一般的选址-分配模型致力于为这样一些基础设施寻找 最佳选址,如:
例如:
v1 [(x11, y11),(x21, y21),(x31, y31)] [(1.3, 3.8),(2.5, 0.4),(3.1, 1.7)]
典型优化问题的模型与算法-R03
11
GA求解
初始化
最优选址应在包括所有顾客的矩形区域内,因此设施 初始选址可以从这个矩形区域内任取位置。
y ymax
选址层
在选址层,采用进化方法搜索整个选址区域。通过这种方法,整个 可选址区域可以被有效地搜索以找到全局或近全局最优解。
染色体表达
因为选址变量是连续的,所以采用浮点值染色体。染色体 表达如下:
vk [(x1k , y1k ), (x2k , y2k ),, (xik , yik ),, (xmk , ymk )]
yi : 0-1 决策变量 yi=1,设施 i 被建立,否则 yi=0
典型优化问题的模型与算法-R03
C3
C1
F1 xmin
Cn (un, vn)
Fm (xm, ym)
C2 xmax
ymin
x
典型优化问题的模型与算法-R03
12
GA求解
交叉
对于实数编码,可以采用线性凸组合交叉 (Linear Convex
Combination)
假设选择具有如下染色体的两个双亲产生后代
v1 [(x11, y11), (x21, y21),, (xi1, yi1),, (xm1, ym1)]
ai: 第 i 个设施的能力 bj: 第 j 个顾客的需求 Fi=(xi, yi): 设备 i 的未知位置,决策变量 Cj=(uj, vj): 顾客 j 的已知位置
典型优化问题的模型与算法-R03
3
数学模型
mn
min
f (F, z)
t(Fi , C j ) zij
i1 j1
n
s. t.
gi (z) bj zij ai , i 1,2,, m
只能用于小规模问题。
典型优化问题的模型与算法-R03
10
GA求解
Gong, Gen, Xu 和 Yamazaki 提出了一种解决具有能力 约束的选址-分配问题的混和进化方法
这种方法将问题分为两层:
分配层
在分配层,因为这一子问题需经常解决,所以采用拉格朗日松弛法 解决这个一般指派问题,以尽快获得解。
城市电网变电站选址问题
变、配电站设施;小区顾客;输电线(距离 )最短
海上溢油应急点选址优化
应急服务点设施;发生溢油较高的区域顾客 ;到达发生事故点的距离之和最小
公路养护资源的选址和配置问题
养护点设施;路段顾客;目标是工作量均衡
典型优化问题的模型与算法-R03
8
应用
C3
F1
C1
Cn
… Fm
典型问题
选址-分配问题
(Location Allocation Problem)
东北大学 系统工程研究所 2014.09
典型优化问题的模型与算法-R03
选址-分配问题
选址-分配 (location-allocation) 问题
也称作多韦伯 (multi-Weber ) 问题或 P 中位 (P-median ) 问题。
强烈变异(violent mutation):采用与初始化过程相同的 方法产生后代
v
v
Subtle mutation Violent mutation
[1, 2 ,..., 2m1, 2m ], i 是 (- , )(i 1,2,...,2 m)之间的随机数 是一个较小的正数
Θ [(1x ,1y ),(2x ,2y ),...,(mx ,my )]
t(Fi,Cj): 由设施 i 到顾客 j 的欧几里得距离。
t(Fi ,Cj ) (xi uj )2 (yi vj )2
保证不超过每个 设施的服务能力
保证每个顾客只 由一个设施服务
Cj (uj, vj) bj
ai Fi (xi, yi)
……
典型优化问题的模型与算法-R03
4
特点
非线性规划问题 既有 0-1 变量,又有实数变量 分配子问题是一个一般的指派问题 NP-难的问题 Cooper 是正式认识并描述多韦伯问题的第一
禁止邻域的定义:
适值意义上的邻域
eval(vk ) eval(v) 较小的正参数
选址意义上的邻域
vk v 较小的正参数
其中 vk已被选入下一代,v 尚未选入下一代的染色体。
典型优化问题的模型与算法-R03
17
典型问题
无能力约束的选址-分配问题
(Uncapacitated Location Allocation Problem)
如地震、海啸、流行病、
设备选址
如电力、通信、交通系统中相关设备或站址 的选取和定位
典型优化问题的模型与算法-R03
9
一般求解方法
Cooper 提出了一种称作选择选址-分配(alternative location-allocation) 的 启发式,这是一种最好的启发方法
随着非线性规划技术的发展,通过松弛整数分配约束,同时考虑选址变量 和分配变量,产生了一些新的方法。
学校、消防站、公园等, 此类基础设施对于“最佳选址”理解的共同点在于,使供
需点之间的“总距离”或者“平均距离”最小。
除此以外,这个基本模型经过扩展还可以有更广泛的 应用范围,如:
优化城市零售商业网点空间分布(通过最大化惠顾人流量来 实现)、
优化制造业场所空间分布(通过最小化运输成本实现)、 优化公共服务设施空间分布(通过最优化服务质量实现)、 ……
典型优化问题的模型与算法-R03
19
图形描述
设施的选址和客户的分配
C3 c13
C1 (u1, v1) c11
F1 (x1, y1)
…
d1
cmn (xi, yi)
Fm dm
Cn (uj, vj)
m : 设施总数
n : 客户总数
Fi: 第i 个设施, i=1,2,…,m Cj: 第 j 个客户, j=1,2,…,n
v2 [(x12 , y12 ), (x22 , y22 ),, (xi2 , yi2 ),, (xm2 , ym2 )]
后代染色体中的基因由下面等式确定
xi1 i xi1 (1 i ) xi2
yi1 i yi1 (1 i ) yi2
xi 2 (1 i ) xi1 i xi2
设施的位置(选址) 顾客对设施的分配
使顾客和服务他们的设施间的距离总和最小。
典型优化问题的模型与算法-R03
2
图形描述
(u1, v1)
C3
C1 b1
F1 a1
(x1, y1)
…
C2
(un, vn) Cn
bn
am Fm (xm, ym)
m : 设施总数
n : 顾客总数
Fi: 第i 个设施, i=1,2,…,m Cj: 第 j 个顾客, j=1,2,…,n
Harris 等发现当可能解的数量是一个类型 II 的 Sterling 数时,可行解的数 量相当少。他们发现任何可行解中顾客的子集必须包括在非重叠凸域内, 他们提出了一种算法,利用问题这一凸域特性产生所有可行解,并通过对 这些解的完全枚举找到最优解。
Qstresh 提出了基于通行线 (passing line) 解决两设施韦伯问题的不同算法。 Rosing 基于 Harris 的思想提出了关于一般多韦伯问题的优化方法,然而,
单韦伯 (single Weber)问题
在欧几里德空间上典型的单韦伯(single Weber) 问题是
寻找一个位置,使从代表顾客位置的一些固定点到它 的距离和最小。
问题描述:
有 m 个“设施”需要选址,n 个已知位置的“顾客” 分;我们配每需给个要不设找同施到的具设有施的,能每力个为顾a客i,的i=需1,2求,…为,mbj,j=1,2,…,n
i 1
n
