制图-第三章基本体及其表面交线
合集下载
工程制图 04-第三章-1基本立体及其表面交线(截交线)
例5.求三棱锥被P平面截切后的三投影。 平面截切后的三投影
s’
P
s’’
1’’
解题步骤：
分析：截平面斜切三 棱锥其截交线应 为封闭三角形. 利用棱线法求截交线 即：求三棱锥各棱线 与截平面的交点
1’
2’
2’’3’(3’’) Nhomakorabeaa’
b’
3
c’
a’’ (c’’)
b’’
a
1
求截切体的第三投影 即: 由二投影求出第 三投影。 完成被截立体的投影 即:判别可见性后再 按虚实加深图线 擦去被截掉部分
c
P
k a b
1
例4. 圆柱上线段的投影（P78例3-7）。
b’ B k’ C K d’ (b’’) (d’’)
k’’
S
C’ C’’
作图步骤： （1）在已知投影上取若干点，包 括特殊点（c’，k’，b’）和一般点 d’等; （2）画有积聚性的投影; （3）光滑连接侧投影各点， 并判断可见性。
c k d
请点击解答显示其内容请点击解答显示其内容请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示后视图形请点击鼠标左键显示后视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示侧视图形请点击鼠标左键显示侧视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示后视图形请点击鼠标左键显示后视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示右视图形请点击鼠标左键显示右视图形请点击鼠标左键显示左视图形请点击鼠标左键显示左视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示俯视图形请点击鼠标左键显示右视图形请点击鼠标左键显示右视图形
机械制图 第三章 立体及立体表面交线
第三章立体及立体表面交线目的要求：1）掌握平面立体和回转体的投影特性，以及表面取点线的方法2）熟悉立体表面上常见交线的画法（截交线、相贯线）重点难点：1）掌握和熟练运用各种立体的投影特性求解表面取点线的方法2）熟练求解立体表面上截交线和相贯线授课学时：8学时主要作图练习：1）完成平面立体、回转体的三面投影，平面立体、回转体表面找点、找线。
2）单个截平面截棱柱、棱锥后的三面投影。
3）多个截平面（切口）截棱柱、棱锥的三面投影，尤其是长方体截切后的三面投影。
4）单个和多个截平面截切圆柱、圆锥、圆球后的三面投影，尤以带槽的圆柱和圆球为主。
5）圆柱与圆柱相贯、同轴回转体相贯的各种情况作图、综合作图。
6）授课内容：机件形状是多种多样的，经过分析，都是由一些基本几何体所组成。
而几何体又是由一些表面所围成，根据这些表面的性质，几何体可分为两类：平面立体——由若干个平面所围成的几何体，如棱柱、棱锥等。
曲面立体——由曲面或曲面与平面所围成的几何体，最常见的是回转体，如圆柱、圆锥、圆球、圆环等。
用投影图表示一个立体，就是把围成立体的这些平面和曲面表达出来，然后根据可见性判别哪些线是可见的，哪些线是不可见的，把其投影分别画成粗实线和虚线，即可得立体的投影图。
§3-1 平面立体的投影平面立体各表面都是平面图形，各平面图形均由棱线围成，棱线又由其端点确定。
因此，平面立体的投影是由围成它的各平面图形的投影表示的，其实质是作各棱线与端点的投影。
一、棱柱以正六棱柱为例，其顶面、底面均为水平面，它们的水平投影反映实形，正面及侧面投影积聚为一直线。
棱柱有六个侧棱面，前后棱面为正平面，它们的正面投影反映实形，水平投影及侧面投影积聚为一直线。
棱柱的其它四个侧棱面均为铅垂面，水平投影积聚为直线，正面投影和侧面投影为类似形。
图3-1 正六棱柱的投影二、棱锥以四棱锥为例，其底面为一长方形，呈水平位置，水平投影反映底面的实形。
左右两个棱面是正垂面，其正面投影积聚为直线，水平和侧面投影均为类似三角形，前后两个棱面为侧垂面，其侧面投影积聚为直线，水平和正面投影同样为类似的三角形。
工程制图PPT【第3章 基本体的投影及表面交线】
e’
e”
b” b’
[例]完成圆锥被切割后的水平投影和侧面投影。
5’6’ 3 ’4’ 1 ’2 ’
6” 4”
2”
5” 3”
1”
2
4
6
5
1
3
圆球的截交线
投影面平行面与球相交
截交线总是圆
[例] 完成圆球被正垂面切割后的水平投影和侧面投影。
b’
b”
g’h’ c’d ’ e’f ’
a’
h” d”
f”
g” c”
结论1
结论2
相贯线向大圆柱 的轴线方向凸起
两圆柱相交
[例]求两圆柱的相贯
线。
1 ’ 5’ 6’ 3 ’ 2 ’4’
1 ”3” 5”6”
4”
2”
01 分析形状 02 作特殊点
03 作一般点
4
1
3
5
6
2
Ⅳ Ⅲ
Ⅰ Ⅴ
Ⅵ Ⅱ
04 判断可见性 05 平滑连接 06 整理轮廓
两圆柱正交产生相贯线的形式 两外表面相交 外表面与内表面相交 两内表面相交
外表面与内表面相交
1’
3’
2 ’4’
1 ”3”
4”
2”
4
1
3
2
两内表面相交
1’
3’
2 ’4’
1 ”3” 2”
4”
4
1
3
2
求圆柱被穿竖孔和横孔后的相贯线
圆柱与圆锥相交 [例]求圆柱与圆锥正交时相贯线的投影。
3’
4’
5’7’
6’8’
1 ’2’
3“4”
7”8“
5”6“
1”
2”
工程制图习题集答案-第3章(基本体及其表面截交线)
第三章 基本体及其截交线
3-11完成被切圆柱的水平投影
第三章 基本体及其截交线
3-12完成缺口圆柱的水平投影
第三章 基本体及其截交线
3-13完成穿孔圆柱的第三面投影
第三章 基本体及其截交线
3-14完成被切圆锥的水平投影和侧面投影
分析：此为圆锥被一正垂面所截，截交线的形状应为椭圆，其水平投影和侧面投影均为类似形（椭圆） 作图要点：取椭圆截交线上的若干点，根据正面投影分别求出各点的另两面投影，即求特殊点（截交线上最前最后、最高最低点）和取一般点（采用纬圆法或直素线法求作圆锥表面点的水平投影和侧面投影）；然后依次光滑连接各点得到截交线投影；最后补全圆锥的三面投影
第三章 基本体及其截交线
3-10完成被切圆柱的侧面投影
分析：圆柱被一正垂面截切，其截交线为一椭圆。因圆柱面的水平投影具有积聚性，截平面与圆柱面的交线的水平投影积聚在圆上。而侧面投影为一椭圆 作图要点说明：需求出椭圆截交线上的若干个点的投影。先求特殊点（最左最右点、最前最后点）；再取一般点，根据两面投影求其侧面投影。然后依次光滑连接各点，最后补全和完善侧面投影''
b'
b''
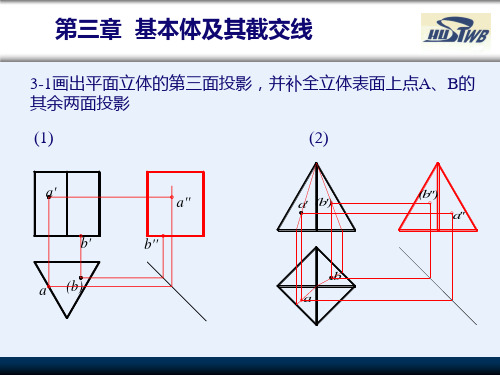
3-1画出平面立体的第三面投影，并补全立体表面上点A、B的其余两面投影
(1)
(2)
第三章 基本体及其截交线
(1)
第三章 基本体及其截交线
3-2完成被切棱柱的第三面投影
分析：四棱柱的所有棱面都被一正垂面截切，因为四个棱面均为铅垂面，其水平投影具有积聚性，另截平面与上底面也形成一交线。根据已知两面投影可直接求出截平面与四棱柱的五个交点的侧面投影，然后依次连接各点即为截交线。最后补全棱线棱面的侧面投影（不可见轮廓线用虚线表示）
机械制图第3章
第 3 章 基本体及其表面交线
3.3 平面与立体相交
平面与平面体相交 3.3.1 平面与平面体相交 平面与立体表面相交而产生的交线称为截交线。 这个截 交线是一个平面多边形,此多边形的各个顶点就是截平面与平 面体的棱线的交点, 称为贯穿点。在求作棱柱或棱锥的截交线 时,常常先求出贯穿点, 即侧棱线或底棱与截平面的交点, 然 后依次连成截交线。 棱柱的截交线 1. 棱柱的截交线 例 3-1 图3-7所示的L形棱柱被正垂面P切割, 求作切割后 棱柱的三视图。
第 3 章 基本体及其表面交线
图 3-1 正三棱柱及其表面上点的投影
第 3 章 基本体及其表面交线 投影分析 1. 投影分析 如图3-1所示,正三棱柱的两端面(顶面和底面)平行于水平 面, 后侧棱面平行于正面, 另外两个棱面垂直于水平面。 在这 种位置下, 三棱柱的投影特征是: 顶面和底面的水平投影重合, 并反映实形——正三角形。三个侧棱面的水平投影积聚为三角 形的三条边。
第 3 章 基本体及其表面交线
图 3-10 正垂面切割三棱锥的截交线的作图步骤
第 3 章 基本体及其表面交线 作图 作图 (1) 根据三棱锥的三视图以及p′的位置, 由s′a′和s′c′与p′的交 点d′和f′，分别在sa、 sc和s″a″、s″c″上直接求出d、 f和d″、 f″, 如图3-10(a)所示。 (2) 由于SB是侧平线, 因此必须由s′b′与p′的交点e′在s″b″ 上求出e″, 再由45°线或利用宽相等的投影关系在sb上求出e, 如 图3-10(b)所示。 (3) 连接各点的同面投影即为所求交线的三面投影,擦去作 图线, 将切割后三棱锥的图线描深, 如图3-10(c)所示。
第 3 章 基本体及其表面交线 2. 作图方法 作图方法 画圆锥的三视图时, 应先画各投影的中心线, 再画底面圆的 各投影, 然后画出锥顶的投影和等腰三角形, 完成圆锥的三视图。 3. 圆锥体表面上点的投影 圆锥体表面上点的投影 如图3-5所示,已知圆锥体表面上点M的正面投影m′,求作m和 m″。根据M点的位置和可见性, 可确定点M在前、左方圆锥面上, 点M的三面投影均为可见。
第3章 基本体的投影及表面交线
机械制图与AutoCAD基础课程配套课件
1
第3章 基本体的投影及表面交线
3.1基本体的投影
一、平面立体的投影及其表面取点
平面立体由若干个平面多边形所围成的。因此，绘制平面立体的 投影，就是绘制它的所有多边形表面的投影，也就是绘制多边形各个 边和各个顶点的投 反映底面实形的投影，根据投影 规律画两底的其他投影，最后再 根据投影规律画侧棱的各个投影 （注意区分可见性）。如果某个 投影的图形对称，则应该画出对 称中心线 。
a' c'(d')
b'
a"
d"
c"
b"
d
b
a
c
（a）求特殊点
g'(h')
h"
g"
h g
（c）求一般点
e'(f')
f"
e"
f
e
（b）求最右点
a' e'(f')
c'(d') g'(h') b'
f"
d" h"
a" e"
c" g" b"
df h
b
a
g
ce
（d）光滑连接
四、相贯线的特殊情况 1.两轴线平行共底的圆柱相交，其相贯线是两条平行于轴线的直线，
2. 辅助平面法
辅助平面法就是利用三面共点的原理求相贯线上的一 系列的点，即假想用一个辅助平面截切两相贯回转体 ，得两条截交线，两截交线的交点，即为两相贯立体 表面共有的点，也是辅助平面上的点。为了能方便地 作出相贯线上的点，最好选用特殊位置平面（投影面 的平行面或垂直面）作为辅助平面，并使辅助平面与 两回转体交线的投影为最简单（为直线或圆）。
机械制图第三章 基本体及立体表面交线
第三章
基本体及立体表面交线
第一节 平面立体的投影
任何立体都是由表面（平面或曲面）所围成。 单一的几何立体称为基本体。 表面全部为平面的立体称为平面立体，如棱柱、棱锥、棱 台等。 表面为曲面或既有曲面又有平面的立体称为曲面立体，常 见的曲面立体是回转体，如圆柱、圆锥、球和圆环等，如 图3-1所示。
常 见 的 基 本 立 体
图3-21 圆锥体表面取点
(2) 辅助纬圆法。
(b)
图3-22 圆锥体表面取点
图3-23
常见圆锥的三面投影示例
三、圆球
球面是由母线圆（或半圆）绕其直径旋转而成。
图3-24 圆球的形成
1. 圆球的投影分析 圆球的三面投影均为与其直径相等的圆。它们分别
是球三个不同方向的轮廓圆的投影。
图3-25 圆球的投影分析
图3-15 圆柱体的三视图
画圆柱体投影时，一般先画出轴线和圆的中心 线及投影为圆的那个投影，然后画出其余投影。
*轮廓素线与圆柱体的对应
(a)
图3-16 圆柱体的轮廓素线分析
(b)
3. 圆柱面上取点
已知圆柱表面上点 M 、N 的正面 投影，求作它们的水平及侧面投影。
图3-17 圆柱体表面取点、取线
(d)
第二节 回转体的投影
表面由平面与曲面围成，或全部由曲面围成的立体称 为曲面立体。
常见曲面是回 转面，它是由一直 线或曲线以一定直 线为轴线回转形成。 由回转曲面组成的 立体，称回转体， 如圆柱体、圆锥体、 球体等。
图3-13 回转体的形成
一、圆柱体
圆柱体是由顶面、底面和圆柱面所组成。 圆柱面上任意一条平行于轴线的直线，称为圆柱面的素线。
棱柱的投影特征： 一面投影为多边形，其边是各棱面的积聚性投影；另两
基本体及立体表面交线
第一节 平面立体的投影
任何立体都是由表面（平面或曲面）所围成。 单一的几何立体称为基本体。 表面全部为平面的立体称为平面立体，如棱柱、棱锥、棱 台等。 表面为曲面或既有曲面又有平面的立体称为曲面立体，常 见的曲面立体是回转体，如圆柱、圆锥、球和圆环等，如 图3-1所示。
常 见 的 基 本 立 体
图3-21 圆锥体表面取点
(2) 辅助纬圆法。
(b)
图3-22 圆锥体表面取点
图3-23
常见圆锥的三面投影示例
三、圆球
球面是由母线圆（或半圆）绕其直径旋转而成。
图3-24 圆球的形成
1. 圆球的投影分析 圆球的三面投影均为与其直径相等的圆。它们分别
是球三个不同方向的轮廓圆的投影。
图3-25 圆球的投影分析
图3-15 圆柱体的三视图
画圆柱体投影时，一般先画出轴线和圆的中心 线及投影为圆的那个投影，然后画出其余投影。
*轮廓素线与圆柱体的对应
(a)
图3-16 圆柱体的轮廓素线分析
(b)
3. 圆柱面上取点
已知圆柱表面上点 M 、N 的正面 投影，求作它们的水平及侧面投影。
图3-17 圆柱体表面取点、取线
(d)
第二节 回转体的投影
表面由平面与曲面围成，或全部由曲面围成的立体称 为曲面立体。
常见曲面是回 转面，它是由一直 线或曲线以一定直 线为轴线回转形成。 由回转曲面组成的 立体，称回转体， 如圆柱体、圆锥体、 球体等。
图3-13 回转体的形成
一、圆柱体
圆柱体是由顶面、底面和圆柱面所组成。 圆柱面上任意一条平行于轴线的直线，称为圆柱面的素线。
棱柱的投影特征： 一面投影为多边形，其边是各棱面的积聚性投影；另两
工程制图 第三章
⑵ 圆锥的投影
投影特性： 当圆锥的轴线垂直某一个投影面 时，则圆锥在该投影面上的投影是 与其底面全等的圆形，另外两个投 影为等腰三角形。
⑶圆锥面上取点
★辅助直线法 如何在圆锥面上作直线？ 过锥顶作一条素线 ★辅助圆法 圆的半径？
s
●
●
s
m
(n)
●
(n)
m
n●
s
m
3．圆球
⑴ 圆球的形成
完成开槽半圆球的水平投影和侧面投影
水平面截圆球的截交线的投影，在俯视 两个侧平面截圆球的截交线的投影，在 图上为部分圆弧，在侧视图上积聚为直线 侧视图上为部分圆弧，在俯视图上积聚为 直线
3.3 相贯线的性质及画法
两立体相交称为相贯，其表面产生的交线称为相贯线 相贯线特性
共有性 相贯线是两立体表面上的共有线，也是两 立体表面的分界线
1. 棱柱
棱柱的投影
六棱柱表面特征：
平面立体
①六个棱面为矩形，均垂直于顶面
和底面，且两两对应平行； ②顶面和底面均为正六边形，且相 互平行； ③棱线相互平行，且垂直于顶（底） 面。
六棱柱的三视图 作图步骤：
⑴画三面投影的对称中心线。
⑵画顶面（底面）的三面投
影。 ⑶分别连接上、下底面对应 顶点的同面投影，并判别可 见性。
辅助平面的选择原则 使辅助平面与两回转体表面截交线 的投影简单易画，例如直线或圆，一 般选择投影面平行面
例3.8 求轴线相互垂直的圆锥和圆柱的相贯线
● ● ● ●
●
● ● ●
解题步骤
●
●
★ 求特殊点 ★ 用辅助平面法求中间点
● ●
●
★ 光滑连接各点
《机械制图》教案——第三章 立体投影及表面交线
第三章基本立体的投影、截交线、相贯线§1立体的投影1．1平面立体的投影本节教学目标：掌握平面立体的投影特性和作图方法；掌握拉伸体的形成、投影及画法；熟悉平面立体表面中特殊位置的点、线的三面投影及画法。
重点：平面立体的投影特性及表面取点、取线的投影。
难点：平面立体表面中特殊位置处点、线的投影。
引入：通过对前面知识的学习已经知道，很多的机械零件都是由一些简单的基本形体组成，比如螺栓，我们可以将它分成正六棱柱、圆柱体和圆锥台三部分。
如果我们要绘制此螺栓的三视图，同学们都应该知道必须要绘制正六棱柱、圆柱体和圆锥台的三视图。
任何一个复杂的物体都可以看成由基本体组成，按组成基本体表面的性质进行分类，基本体可分为平面体和曲面体。
平面立体侧表面的交线称为棱线若平面立体所有棱线互相平行，称为棱柱。
若平面立体所有棱线交于一点，称为棱锥。
1.1.1棱柱的投影1. 以正六棱柱为例，分析平面立体的结构，（1）正六棱柱共有几个表面？有何关系？（2）正六棱柱共有几条侧棱？有何关系？提问：1）不同位置的投影有什么不同？2）应怎样放置最合理？提示：使尽可能多的表面和棱线处于特殊位置。
2.投影特性分析（1）投影分析：上、下两个底面——平行的两个侧面——其余的几个侧面（2）三面投影图分析（3）绘图步骤：1）建立投影面系；2）根据三等原则绘制三面投影；3）区分可见性。
3. 棱柱体的投影特性（重点：学生应掌握）（1）当棱柱的底面平行于某一投影面时，棱柱的投影在该面上为与底面相等的正多边形。
（2）另两面投影为几个相邻的矩形线框。
4. 棱柱表面取点、线重点：所取的点、线属于棱柱的哪个面上？进而再求三面投影。
***若点所在平面的投影可见，点的投影可见；若平面的投影积聚成直线，点的投影也可见。
例：例：已知四棱柱，试完成其Ｖ、Ｈ投影。
（图7-1）图7-1四棱柱的投影1.1.2棱锥的投影棱锥的投影是棱锥各顶点同面投影连线的集合。
1. 棱锥的定义2. 棱锥的形体分析（1）投影分析：下底面——顶点——其余的几个侧面（2）三面投影图分析（3）绘图步骤：1）建立投影面系；2）根据三等原则绘制三面投影；3）区分可见性。
14级汽修第三章基本体及其表面的交线第二节回转体及三视图
•工程上常见的回转体有圆柱、圆锥、球、圆环等。
(a) 圆柱 环
பைடு நூலகம்
(b) 圆锥
(c) 圆球
(d) 圆
图3-6 常见的回转体
绘制回转体的投影，即是绘制回转体的回转面和平面的投影，也就是绘制 回转体的轮廓线、尖顶的投影以及转向轮廓线。
O
1.圆柱体
⑴ 圆柱体的组成 由圆柱面和两个底面组成。 圆柱面是由直线AA1绕与 它平行的轴线OO1旋转而成。 直线AA1称为母线。 圆柱面上与轴线平行的任 一直线称为圆柱面的素线。 ⑵ 圆柱体的三视图 圆柱面的俯视图积聚成一 个圆，在另两个视图上分别以 两个方向的轮廓素线的投影表 示。
1.圆锥面的形成
圆锥面---一直线绕与它相交的轴线回转 而成。 圆锥立体分析:当圆锥的轴线是铅垂线时, 底面为水平面，圆锥面上的所有素线 都是通过锥顶的直线。
S O
⑴ 圆锥体的特征 由圆锥面和底面组成。
圆锥面是由直线SA 绕与它相交的轴线OO1旋 转而成。 S称为锥顶，直线SA 称为母线。圆锥面上过锥 顶的任一直线称为圆锥面 的素线。
图3-11 圆锥的投影
三、圆球-----由球面围成
球面---半圆绕其直径为轴线回转 一周而成。
图3-13 圆球的形成
1.球的投影
图3-14 圆球的投影
三.圆球
2.圆球的三视图
三个视图分别为三 个和圆球的直径相等的 圆，它们分别是圆球三 个方向轮廓线的投影。
(a)
(b)
(c) 图3-14 圆球的投影
A
O1 A1
2.圆柱体的三视图
转向轮 廓素线
圆柱的投影分析: • 顶面、底面的水平投影重 合为一圆，正面投影和侧 面投影分别重影为两直线； • 圆柱面的水平投影积聚为 一圆，正面投影和侧面投 影分别画出转向轮廓素线 的投影。
(a) 圆柱 环
பைடு நூலகம்
(b) 圆锥
(c) 圆球
(d) 圆
图3-6 常见的回转体
绘制回转体的投影，即是绘制回转体的回转面和平面的投影，也就是绘制 回转体的轮廓线、尖顶的投影以及转向轮廓线。
O
1.圆柱体
⑴ 圆柱体的组成 由圆柱面和两个底面组成。 圆柱面是由直线AA1绕与 它平行的轴线OO1旋转而成。 直线AA1称为母线。 圆柱面上与轴线平行的任 一直线称为圆柱面的素线。 ⑵ 圆柱体的三视图 圆柱面的俯视图积聚成一 个圆，在另两个视图上分别以 两个方向的轮廓素线的投影表 示。
1.圆锥面的形成
圆锥面---一直线绕与它相交的轴线回转 而成。 圆锥立体分析:当圆锥的轴线是铅垂线时, 底面为水平面，圆锥面上的所有素线 都是通过锥顶的直线。
S O
⑴ 圆锥体的特征 由圆锥面和底面组成。
圆锥面是由直线SA 绕与它相交的轴线OO1旋 转而成。 S称为锥顶，直线SA 称为母线。圆锥面上过锥 顶的任一直线称为圆锥面 的素线。
图3-11 圆锥的投影
三、圆球-----由球面围成
球面---半圆绕其直径为轴线回转 一周而成。
图3-13 圆球的形成
1.球的投影
图3-14 圆球的投影
三.圆球
2.圆球的三视图
三个视图分别为三 个和圆球的直径相等的 圆，它们分别是圆球三 个方向轮廓线的投影。
(a)
(b)
(c) 图3-14 圆球的投影
A
O1 A1
2.圆柱体的三视图
转向轮 廓素线
圆柱的投影分析: • 顶面、底面的水平投影重 合为一圆，正面投影和侧 面投影分别重影为两直线； • 圆柱面的水平投影积聚为 一圆，正面投影和侧面投 影分别画出转向轮廓素线 的投影。
工程制图5第三章基本立体表面交线-相贯线
•
加强自身建设，增强个人的休养。202 0年11 月4日下 午12时 0分20. 11.420. 11.4
•
精益求精，追求卓越，因为相信而伟 大。202 0年11 月4日星 期三下 午12时 0分13 秒12:00:1320.1 1.4
•
专业精神和专业素养，进一步提升离 退休工 作的质 量和水 平。202 0年11 月下午1 2时0分 20.11.4 12:00N ovember 4, 2020
2.作图方法
求交线的实质是求各侧平面与回转面的交线。 • 分析各棱面与回转体表面的相对位置，从而确
定交线的形状。 • 求出各棱面与回转体表面的交线。 • 连接各段交线，并判断可见性。
11
例1：补全主视图
投空影间分分析析：：
由四于棱相柱贯的线四是个两侧立面体分表别与 面圆的柱共面有相线交，，所前以后相两贯侧线面的与圆 侧柱面轴投线影平积行聚，在截一交段线圆为弧两上段，直 水线平；投左影右积两聚侧在面矩与形圆上柱。轴线垂 直，截交线为两段圆弧。
封闭性—相贯线一般是封闭的空间折线（通常 由直线和曲线组成）或空间曲线。
7
8
求相贯线步骤
⒈ 交线分析
⑴ 空间分析： 分析相交两立体的表面形状， 形体大小及
相对位置，预见交线的形状。
⑵ 投影分析： 是否有积聚性投影？找出相贯线的已知投影，
预见未知投影，从而选择解题方法。
9
⒉ 作图
当相贯线的投影为非圆曲线时，其作图步骤为：
a'
b'
•• 1'
c'
• (d')
•• 2'
d" • a" (•b")1• "•(2c"")
工程制图习题集答案—第章(基本体及其表面截交线)
3-10完成被切圆柱的侧面投影
分析：圆柱被一正垂面截切， 其截交线为一椭圆。因圆柱面 的水平投影具有积聚性，截平 面与圆柱面的交线的水平投影 积聚在圆上。而侧面投影为一 椭圆
作图要点说明：需求出椭圆截 交线上的若干个点的投影。先 求特殊点（最左最右点、最前 最后点）；再取一般点，根据 两面投影求其侧面投影。然后 依次光滑连接各点，最后补全 和完善侧面投影中的转向轮廓 线
第三章 基本体及其截交线
3-11完成被切圆柱的水平投影
第三章 基本体及其截交线
3-12完成缺口圆柱的水平投影
(1)Βιβλιοθήκη (2)第三章 基本体及其截交线
3-13完成穿孔圆柱的第三面投影
(1)
(2)
第三章 基本体及其截交线
3-14完成被切圆锥的水平投影和侧面投影
(1)
分析：此为圆锥被一正垂面 所截，截交线的形状应为椭
第三章 基本体及其截交线
3-2完成被切棱柱的第三面投影
(2)
(3)
第三章 基本体及其截交线
3-3画出被切平面立体的第三面投影
(1)
(2)
第三章 基本体及其截交线
3-4已知切割后三棱锥的正面投 影，补全水平投影，画出侧面 投影
3-5补全四棱台切口的水平投影， 画出侧面投影
第三章 基本体及其截交线
(1)
a'
(b') c'
b
a (c)
a'' b''
c''
(2)
a' b'
c'
a (c)
b
(a'') b"
c"
电子课件-《机械制图(第三版) 》-A03-2612 制图-第三章
二、斜二轴测图
将坐标轴O0Z0放置成铅垂位置，并使坐标面X0O0Z0平 行于轴测投影面V，用斜投影法将物体连同其坐标轴一起 向V面投射，所得到的轴测图称为斜轴测图。
图3－48 斜二轴测图
1．轴间角和轴向伸缩系数
轴向伸缩系数p1=r1=1；
轴间角∠XOZ=90°。
轴测轴OY的方向和轴向伸缩系数q1，可随着投射方 向的变化而变化。为了绘图简便，国家标准规定，选取 轴间角∠XOY=∠YOZ=135°，q1=0.5。
一、平面切割平面体 二、平面切割回转曲面体
一、平面切割平面体
【例3－1】画出图示平面切割体的三视图。
图3－17 平面切割体的作图步骤
【例3－2】已知切割四棱柱的正面投影，参照 立体图，求作水平和侧面投影。
图3－18 四棱柱开通槽
二、平面切割回转曲面体
平面切割曲面体时，截交线的形状取决于曲面体表面 的形状以及截平面与曲面体的相对位置。
回转面——由一条母线（直线或曲线）围 绕轴线回转而形成的表面。
回转体——由回转面围成或回转面与平面 围成的立体。如圆柱、圆锥、球等。
1．圆柱 圆柱体由圆柱面与上、下两底面围成。圆柱面 可看作一条直母线绕与其平行的轴线回转而成。
圆柱面上任意一条平 行于轴线的直线，称为圆 柱面的素线。
图3－8 圆柱体的三视图
【例3－8】绘制如图所示连杆头的三视图。
§3－3 两回转体相交的投影作图
两回转体相交，常见的是圆柱与圆柱相 交、圆锥与圆柱相交以及圆柱与圆球相交， 其交线称为相贯线。
一、圆柱与圆柱相交 二、相贯线的特殊情况 三、综合举例
一、圆柱与圆柱相交
【例3－9】两个直径不等的圆柱正交，求作相 贯线的投影。
第三章 基本体及其表面交线
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
轴向伸缩系数p=r=1；
轴间角∠XOZ=90°。
平面切割回转曲面体
1．平面与圆柱相交
平面与圆柱相交时，根据平面与圆柱轴线相对位置的 不同可形成三种不同形状的截交线。
【例3－3】如图所示为圆柱被正垂面斜切，已知 主、俯视图，求作左视图。
解题步骤
【例3－4】求作带切口圆柱的侧面投影。
解题步骤
【例3－5】补全接头的三面投影。
解题步骤
2．平面与圆锥相交
（2）棱锥表面上的点
三棱锥表面上点的投影
二、回转体
回转面——由一条母线（直线或曲线）围 绕轴线回转而形成的表面。
回转体——由回转面围成或回转面与平面 围成的立体。如圆柱、圆锥、圆球等。
1．圆柱体 圆柱体由圆柱面与上、下两端面围成。圆柱面
可看做是由一条直母线绕与其平行的轴线回转而成。
圆柱面上任意一条平 行于轴线的直线，称为圆 柱面的素线。
图3－8 圆柱体的三视图
圆柱表面上点的投影
2．圆锥 圆锥由圆锥面和底面围成。圆锥面可看做是由
一条直母线绕与其相交的轴线回转而成。
图3－9 圆锥体的三视图
圆锥表面上点的投影
3．球 圆球的表面可看做是由一条圆母线绕其直径回
转而成。
图3－11 球的三视图
球面上点的投影
§3－2 切割体的投影作图
截交线的基本特性： （1）截交线为封闭的平面图形。 （2）截交线既在截平面上，又在立体表面
（1）物体上互相平行的线段，轴测投影仍互 相平行。平行于坐标轴的线段，轴测投影仍平行 于相应的轴测轴，且同一轴向所有线段的轴向伸 缩系数相同。
（2）物体上不平行于轴测投影面的平面图形， 在轴测图上变成原形的类似形。
二、正等轴测图（正等测）
1．轴间角和轴向伸缩系数
正等轴测图——当物体上三根坐标轴与轴测投影面的 倾角均相等时，用正投影法得到的投影，简称正等测。
【例3－7】如图所示，已知半球开槽的主视图， 补全俯视图，并作出左视图。
解题步骤
【例3－8】绘制如图所示连杆头的三视图。
解题步骤
§3－3 两回转体相交的投影作图
两回转体相交，常见的是圆柱与圆柱相 交、圆锥与圆一、圆柱与圆柱相交 二、相贯线的特殊情况 三、综合举例
一、轴测图的基本知识 二、正等轴测图（正等测） 三、斜二轴测图
一、轴测图基本知识
轴测图——将物体连同其直角坐标系，沿不平行于任 一坐标面的方向，用平行投影法投射在单一投影面上所得 到的具有立体感的图形，又称作轴测投影。
轴测投影面 轴测轴 轴间角 原点 轴向伸缩系数
轴测图的形成
2．轴测投影的基本性质
二、相贯线的特殊情况
1．相贯线为平面曲线
同轴回转体的相贯线——圆
两回转体公切于一个球面的相贯线——椭圆
2．相贯线为直线
相交两圆柱轴线平行的相贯线——直线
相交两圆锥共顶的相贯线——直线
三、综合举例
【例3－10】已知相贯体的俯、左视图，求作主视 图。
图3－37 已知俯、左视图，求作主视图
§3－4 立体的轴测图
上，是截平面与立体表面的共有线，截交线上的 点均为截平面与立体表面的共有点。
一、平面切割平面体 二、平面切割回转曲面体
一、平面切割平面体
六棱柱被切割 正四棱锥被切割
【例3－1】画出图示平面切割体的三视图。
图3－17 平面切割体的作图步骤
【例3－2】已知切割四棱柱的正面投影，参照立 体图，求作水平和侧面投影。
第三章 基本体及其表面交线
§3－1 §3－2 §3－3 §3－4
基本体的三视图 切割体的投影作图 两回转体相交的投影作图 立体的轴测图
§3－1 基本体的三视图
平面立体——表面全由平面围成的立体，如 棱柱、棱锥等。
曲面立体——表面全由曲面或由曲面和平面 所围成的立体，如圆柱、圆锥、球、环等。
一、平面立体 二、回转体
图3－18 四棱柱开通槽
二、平面切割回转曲面体
平面切割曲面体时，截交线的形状取决于曲面体表面 的形状以及截平面与曲面体的相对位置。
平面与回转曲面体相交时，其截交线一般为封闭的平 面曲线，特殊情况下是直线，或直线与平面曲线组成的封 闭的平面图形。
作图的基本方法：求出曲面体表面上若干条素线与截 平面的交点，然后顺次光滑连接即得截交线。
图3－39 正等轴测图的轴间角和轴向伸缩系数
2．正等测画法 （1）正六棱柱
图3－40 正六棱柱的正等测画法
【例3－12】作楔形块的正等轴测图。
解题步骤
（2）圆柱 【例3－13】作竖直正圆柱的正等轴测图。
图3－43 圆柱的正等测画法
（3）圆角 【例3－14】作圆角的正等轴测图。
图3－45 圆角的正等测画法
一、平面立体
1．棱柱
棱柱——由两个多边形端面和若干矩形平面（侧面） 组成，棱柱的侧面棱线互相平行。
（1）棱柱的三视图
图3－3 正六棱柱三视图的画法步骤
正五棱柱三视图作图步骤
（2）棱柱表面上的点
棱柱表面上点的投影
2．棱锥
棱锥——底面是多边形，侧面为三角形，棱线 交于一点。
（1）棱锥的三视图
四棱锥三视图作图步骤
根据截平面对圆锥轴线的位置不同，截交线有五种情 况：椭圆、圆、双曲线、抛物线和相交两直线。
作图步骤：先作出截交线上的特殊点，再作出若干中 间点，然后光滑连成曲线。
【例3－6】补全正平面切割圆锥后的正面投影。
解题步骤
3．平面与圆球相交
平面切割圆球时，其交 线均为圆，圆的大小取决于 平面与球心的距离。当平面 平行于投影面时，在该投影 面上的交线圆的投影反映实 形，另外两个投影面上的投 影积聚成直线。
（4）半圆头板 【例3－15】作半圆头板的正等轴测图。
图3－46 半圆头板的正等测画法
二、斜二轴测图
将坐标轴O0Z0放置成铅垂位置，并使坐标面X0O0Z0平 行于轴测投影面V，用斜投影法将物体连同其坐标轴一起 向V面投射，所得到的轴测图称为斜轴测图。
图3－47 斜二轴测图
1．轴间角和轴向伸缩系数
一、圆柱与圆柱相交
【例3－9】两个直径不等的圆柱正交，求作相贯 线的投影。
解题步骤
圆柱穿孔后相贯线的投影
两圆柱正交时相贯线的变化规律
国家标准规定，允许采用简化画法作出相贯线的投影，
即以圆弧代替非圆曲线。当轴线垂直相交且平行于正面的 两个不等径圆柱相交时，相贯线的正面投影以大圆柱的半 径为半径画圆弧即可。
轴间角∠XOZ=90°。
平面切割回转曲面体
1．平面与圆柱相交
平面与圆柱相交时，根据平面与圆柱轴线相对位置的 不同可形成三种不同形状的截交线。
【例3－3】如图所示为圆柱被正垂面斜切，已知 主、俯视图，求作左视图。
解题步骤
【例3－4】求作带切口圆柱的侧面投影。
解题步骤
【例3－5】补全接头的三面投影。
解题步骤
2．平面与圆锥相交
（2）棱锥表面上的点
三棱锥表面上点的投影
二、回转体
回转面——由一条母线（直线或曲线）围 绕轴线回转而形成的表面。
回转体——由回转面围成或回转面与平面 围成的立体。如圆柱、圆锥、圆球等。
1．圆柱体 圆柱体由圆柱面与上、下两端面围成。圆柱面
可看做是由一条直母线绕与其平行的轴线回转而成。
圆柱面上任意一条平 行于轴线的直线，称为圆 柱面的素线。
图3－8 圆柱体的三视图
圆柱表面上点的投影
2．圆锥 圆锥由圆锥面和底面围成。圆锥面可看做是由
一条直母线绕与其相交的轴线回转而成。
图3－9 圆锥体的三视图
圆锥表面上点的投影
3．球 圆球的表面可看做是由一条圆母线绕其直径回
转而成。
图3－11 球的三视图
球面上点的投影
§3－2 切割体的投影作图
截交线的基本特性： （1）截交线为封闭的平面图形。 （2）截交线既在截平面上，又在立体表面
（1）物体上互相平行的线段，轴测投影仍互 相平行。平行于坐标轴的线段，轴测投影仍平行 于相应的轴测轴，且同一轴向所有线段的轴向伸 缩系数相同。
（2）物体上不平行于轴测投影面的平面图形， 在轴测图上变成原形的类似形。
二、正等轴测图（正等测）
1．轴间角和轴向伸缩系数
正等轴测图——当物体上三根坐标轴与轴测投影面的 倾角均相等时，用正投影法得到的投影，简称正等测。
【例3－7】如图所示，已知半球开槽的主视图， 补全俯视图，并作出左视图。
解题步骤
【例3－8】绘制如图所示连杆头的三视图。
解题步骤
§3－3 两回转体相交的投影作图
两回转体相交，常见的是圆柱与圆柱相 交、圆锥与圆一、圆柱与圆柱相交 二、相贯线的特殊情况 三、综合举例
一、轴测图的基本知识 二、正等轴测图（正等测） 三、斜二轴测图
一、轴测图基本知识
轴测图——将物体连同其直角坐标系，沿不平行于任 一坐标面的方向，用平行投影法投射在单一投影面上所得 到的具有立体感的图形，又称作轴测投影。
轴测投影面 轴测轴 轴间角 原点 轴向伸缩系数
轴测图的形成
2．轴测投影的基本性质
二、相贯线的特殊情况
1．相贯线为平面曲线
同轴回转体的相贯线——圆
两回转体公切于一个球面的相贯线——椭圆
2．相贯线为直线
相交两圆柱轴线平行的相贯线——直线
相交两圆锥共顶的相贯线——直线
三、综合举例
【例3－10】已知相贯体的俯、左视图，求作主视 图。
图3－37 已知俯、左视图，求作主视图
§3－4 立体的轴测图
上，是截平面与立体表面的共有线，截交线上的 点均为截平面与立体表面的共有点。
一、平面切割平面体 二、平面切割回转曲面体
一、平面切割平面体
六棱柱被切割 正四棱锥被切割
【例3－1】画出图示平面切割体的三视图。
图3－17 平面切割体的作图步骤
【例3－2】已知切割四棱柱的正面投影，参照立 体图，求作水平和侧面投影。
第三章 基本体及其表面交线
§3－1 §3－2 §3－3 §3－4
基本体的三视图 切割体的投影作图 两回转体相交的投影作图 立体的轴测图
§3－1 基本体的三视图
平面立体——表面全由平面围成的立体，如 棱柱、棱锥等。
曲面立体——表面全由曲面或由曲面和平面 所围成的立体，如圆柱、圆锥、球、环等。
一、平面立体 二、回转体
图3－18 四棱柱开通槽
二、平面切割回转曲面体
平面切割曲面体时，截交线的形状取决于曲面体表面 的形状以及截平面与曲面体的相对位置。
平面与回转曲面体相交时，其截交线一般为封闭的平 面曲线，特殊情况下是直线，或直线与平面曲线组成的封 闭的平面图形。
作图的基本方法：求出曲面体表面上若干条素线与截 平面的交点，然后顺次光滑连接即得截交线。
图3－39 正等轴测图的轴间角和轴向伸缩系数
2．正等测画法 （1）正六棱柱
图3－40 正六棱柱的正等测画法
【例3－12】作楔形块的正等轴测图。
解题步骤
（2）圆柱 【例3－13】作竖直正圆柱的正等轴测图。
图3－43 圆柱的正等测画法
（3）圆角 【例3－14】作圆角的正等轴测图。
图3－45 圆角的正等测画法
一、平面立体
1．棱柱
棱柱——由两个多边形端面和若干矩形平面（侧面） 组成，棱柱的侧面棱线互相平行。
（1）棱柱的三视图
图3－3 正六棱柱三视图的画法步骤
正五棱柱三视图作图步骤
（2）棱柱表面上的点
棱柱表面上点的投影
2．棱锥
棱锥——底面是多边形，侧面为三角形，棱线 交于一点。
（1）棱锥的三视图
四棱锥三视图作图步骤
根据截平面对圆锥轴线的位置不同，截交线有五种情 况：椭圆、圆、双曲线、抛物线和相交两直线。
作图步骤：先作出截交线上的特殊点，再作出若干中 间点，然后光滑连成曲线。
【例3－6】补全正平面切割圆锥后的正面投影。
解题步骤
3．平面与圆球相交
平面切割圆球时，其交 线均为圆，圆的大小取决于 平面与球心的距离。当平面 平行于投影面时，在该投影 面上的交线圆的投影反映实 形，另外两个投影面上的投 影积聚成直线。
（4）半圆头板 【例3－15】作半圆头板的正等轴测图。
图3－46 半圆头板的正等测画法
二、斜二轴测图
将坐标轴O0Z0放置成铅垂位置，并使坐标面X0O0Z0平 行于轴测投影面V，用斜投影法将物体连同其坐标轴一起 向V面投射，所得到的轴测图称为斜轴测图。
图3－47 斜二轴测图
1．轴间角和轴向伸缩系数
一、圆柱与圆柱相交
【例3－9】两个直径不等的圆柱正交，求作相贯 线的投影。
解题步骤
圆柱穿孔后相贯线的投影
两圆柱正交时相贯线的变化规律
国家标准规定，允许采用简化画法作出相贯线的投影，
即以圆弧代替非圆曲线。当轴线垂直相交且平行于正面的 两个不等径圆柱相交时，相贯线的正面投影以大圆柱的半 径为半径画圆弧即可。