函数极限的柯西准则(老黄学高数第101讲)
函数极限的柯西收敛准则

写完之后我想看看其他人是怎么证明的搜索了一下拉格朗日中值定理的辅助函数的构造结果发现自己写的这篇博客居然排名第一
函数极限的柯西收敛准则
以下内容来自中科大数学分析教程P73,定理2.4.7 函数在x_{0}点的极限的定义 若存在l,\forall \epsilon>0,\exists\delta>0,使得当|x-x_{0}|<\delta 则有|f(x)-l|<\epsilon,即称l为f(x)当x趋近于x_{0}的极限 定理:函数f(x)在x_{0}处有极限的充要条件是\forall \epsilon>0,\exists\delta>0, \quad\quad 使得任意x_{1},x_{2}\in U(x_{0},\delta)时,有 \quad\quad |f(x_{1})-f(x_{2})|<\epsilon 证明: 1.必要性 若f(x)在x_{0}点的极限为l,即\forall \frac{\epsilon}{2}>0,\exists\delta,当x_{1},x_{2}\in U(x_{0},\delta) 有|f(x_{1})-l|<\frac{\epsilon}{2},|f(x_{2})-l|<\frac{\epsilon}{2} 则:|f(x_{1})-f(x_{2})|=|f(x_{1})+l-l-f(x_{2})| \quad\quad \leqslant |f(x_{1})-l|+|f(x_{2})-l| \ห้องสมุดไป่ตู้uad\quad\leqslant\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon
谈谈数学分析中的几类柯西准则

谈谈数学分析中的几类柯西准则【摘要】本文主要论述了数列的柯西收敛准则,函数极限存在的柯西准则,级数收敛的柯西准则,函数列一致收敛的柯西准则,函数项级数一致收敛的柯西准则,平面点列的柯西准则,含参量反常积分一致收敛的柯西准则的应用并进行了总结和证明,并通过大量的例题体现了它们的地位和作用.柯西收敛准则是证明收敛与发散的基本方法,并且通过此种方法还推出了很多简单的方法,由此可见柯西准则的重要地位,此种方法的优越性也是显而易见的,就是通过本身的特征来判断是否收敛,这就给证明带来了方便,本文将这几种准则作了以下总结,并且探讨了它们之间的一些关系.【关键词】柯西准则,一致收敛,级数Some Canchy criteria in the Mathematical Analysis【Abstract】This passeage discusses the sequence of cauchy criterion function limit, the convergence of cauchy criterion, the convergence of the series, the function of cauchy criterion listed uniform convergence of cauchy criterion function series, uniform convergence of cauchy criterion, plane of cauchy criterion, some abnormal integral parameter uniform convergence of cauchy criterion and summarized and proof, and through a lot of sample reflected their status and role. Cauchy convergence criteria is proved the convergence and spread the basic method and through this method also launched many simple method, thus the important position of cauchy criterion, this kind of method is obvious superiority of the characteristics of itself, through to judge whether to prove the convergence, and this will bring convenience to the standards for the following summary, and probes into some of the relationship between them.【Key words】cauchy criterion, uniform convergence, series目录1 引言 (1)2数列的柯西收敛准则 (1)3函数极限存在的柯西准则 (2)4级数收敛的柯西准则 (3)4.1 级数的定义 (3)4.2 级数收敛的柯西准则及其应用 (3)5函数列一致收敛的柯西准则 (5)5.1 函数列的定义 (5)5.2 函数列的一致收敛及其应用 (5)6函数项级数一致收敛的柯西准则 (7)6.1 函数项级数定义 (7)6.2 函数项级数的一致收敛 (7)7含参量反常积分的一致收敛的柯西准则 (8)7.1 含参量反常积分的定义 (8)7.2 含参量无穷积分的一致收敛概念及柯西准则 (8)8 柯西准则在数学分析中的作用 (11)9参考文献 (13)1 引言柯西准则是数学分析的基础理论,贯穿于整个数学分析内容之中.在数学分析中,凡涉及到“收敛”与“一致收敛”概念的,都有与内容相应的柯西收敛(或一致收敛)准则,其最大优点是不需要借助于数列(或函数)以外的任何信息,只依据各项的特点,它具有整齐完美的形式,在分析中有很重要的理论价值.由于柯西准则的内容多,又分布在教材的不同地方,在学习时感到空洞,抓不住实质,更不能很好地应用它们,下面根据自己的学习经验,谈点体会.2 数列的柯西准则定理2.1 (柯西收敛准则) 数列{}n a 收敛的充要条件是:对任给的0ε>,存在正整数N ,使得当,n m N >时有 n m a a ε-<. 例1 证明:任一无限十进小数120.na bb b =的n 位不足近似(1,2,)n =所组成的数列1121222,,,,101010101010nn b b b b b b ++++ (1) 满足柯西条件(从而必收敛),其中k b 为0,1,2,,9中的一个数,k=1,2,.证 记122101010nn n b b b a =+++.不妨设n m >,则有 1212101010m m nn m m m nb b b a a ++++-=+++ 11911(1)101010m n m +--≤+++1111(1)101010m n m mm -=-<<. 对任给的0ε>,取1N ε=,则对一切n m N >>有n m a a ε-<. 这就证明了数列(1)满足柯西条件. 例2 已知1sin 2nn k k kx ==∑,求证lim n n x →∞存在. 证明:设n m >,11sin 122nnn m k k k m k m k x x =+=+-=≤∑∑11111(1)222m n m +--=+++1111112212m m m +≤⋅=<-.所以10,{}N εε∀>∃=,当n m N >>时,1n m x x mε-<<,由柯西收敛准则,所以lim n n x →∞存在.3 函数极限存在的柯西准则定理 3.1(柯西准则) 设函数f 在00(;')U x δ内有定义.0lim ()x x f x →存在的充要条件是:任给0ε>,存在正数(')δδ<,使得对任何00',"(;)x x U x δ∈有(')(")f x f x ε-<.证 必要性 设0lim ()x x f x A →=,则对任给的0ε>,存在正数(')δδ<,使得对任何00(;)x U x δ∈有()2f x A ε-<.于是对任何00',"(;)x x U x δ∈有(')(")(')(")22f x f x f x A f x A εεε-≤-+-<+=.充分性 设数列00{}(;)n x U x δ⊂且0lim n n x x →∞=.按假设,对任给的0ε>,存在正数(')δδ<,使得对任何00',"(;)x x U x δ∈,有(')(")f x f x ε-<.对上述的0δ>,存在0N >,使得当,n m N >时有00,(;)n m x x U x δ∈,从而有 ()()n m f x f x ε-<.于是,按数列的柯西准则,数列{()}n f x 的极限存在,记为A ,即lim ()n n f x A →∞=.按照函数极限的柯西准则,我们能写出极限0lim ()x x f x →不存在的充要条件:存在00ε>,对任何0δ>(无论δ多么小),总可以找到00',"(;)x x U x δ∈,使得0(')(")f x f x ε-≥.例3 证明极限01lim sin x x→不存在.证 取01ε=,对任何0δ>,设正整数1n δ>,令11',"2x x n n πππ==+ 则有00',"(;)x x U x δ∈,而011sin sin 1'"x x ε-==.于是按柯西准则,极限01lim sin x x →不存在.4 级数收敛的柯西准则4.1 级数的定义给定一个数列{n u },对它的各项依次用“+”号连接起来的表达式 12n u u u ++++(2)称为数项级数或无穷级数(也常称级数),其中n u 称为数项级数(2)的通项 4.2 级数收敛的柯西准则及其应用定理4.2 级数收敛的充要条件是:任给正数ε,总存在正整数N ,使得当m>N 以及对任意的正整数p ,都有 12m m m p u u u ++++++<ε根据定理4.2,我们立刻可写出级数发散的充要条件:存在某正数0ε,对任何正整数N ,总存在正整数0m (>N)和0p ,有 0000120m m m p u u u ε++++++≥ (3)由定理4.2立即可得如下推论,它是级数收敛的一个必要条件.推论 若级数(2)收敛,则l i mn n u →∞=0. 例4讨论调和级数1+11123n++++的敛散性解 这里调和级数显然满足推论的结论,即1l i m l i m 0n n n u n→∞→∞==. 但令p=m 时,有 122111122m m m u u u m m m+++++=+++++ ≥111222m mm+++=12.因此,取0ε=12,对任何正整数N ,只要m>N 和p=m 就有(5)式成立.所以调和级数是发散的.例5 应用级数收敛的柯西准则证明级数21n∑收敛.证 由于12m m m p u u u ++++++=222111(1)(2)()m m m p ++++++ <111(1)(1)(2)(1)()m m m m m p m p +++++++-+=11m m p -+ <1m. 因此,对任给正数ε,取N=1ε⎡⎤⎢⎥⎣⎦,使当m>N 及对任意正整数p ,由上式就有12m m m p u u u ++++++<1m<ε. 依定理4.2推得级数21n∑是收敛的. 例6 设11111!2!!n x n =++++,证明{}n x 收敛.证明 ,n p N ∀∈,111111(1)!(2)!()!(1)(1)(2)(1)()n p n x x n n n p n n n n n p n p +-=+++<++++++++++-+ 1111111111121n n n n n p n p n np n=-+-++-=-<++++-++. 0ε∀>,11,n n εε<>,取1[]N ε=,于是0ε∀>,1[]N ε∃=,,n N p N ∀>∀∈,有n p n x x ε+-<,故{}n x 收敛.5函数列一致收敛的柯西准则5.1 函数列收敛的定义设函数列{}n f 与函数f 定义在同一数集D 上,若对任给的正数ε,总存在某一正整数N ,使得当n>N 时,对一切x D ∈,都有 ()()n f x f x ε-<, 则称函数列{}n f 在D 上一致收敛于f ,记作()()n f x f x ⇒ ()n →∞,x D ∈.由定义看到,如果函数列{}n f 在D 上一致收敛,那么对于所给的ε,不管D 上哪一点x ,总存在公共的()N ε(即N 的选取仅与ε有关,与x 的取值无关),只要n>N ,都有|()()n f x f x ε-<.由此看到函数列{}n f 在D 上一致收敛,必在D 上每一点都收敛.反之,在D 上每一点都收敛的数列{}n f ,在D 上不一定收敛. 5.2 函数列的一致收敛及其应用定理5.2 (函数列一致收敛的柯西准则) 函数列{n f }在数集D 上一致收敛的充要条件是:对任给正数ε,总存在正数N ,使得当n ,m>N 时,对一切x D ∈,都有()()n m f x f x ε-<. (4)证 [必要性] 设()()n f x f x ⇒ (n →∞),x D ∈,即对任给0ε>,存在正数N ,使得当n>N 时,对一切x D ∈,都有()()2n f x f x ε-<. (5)于是当n ,m>N ,由(5)就有()()()()()()n m n m f x f x f x f x f x f x -≤-+-<22εε+=ε.[充分性] 若条件(4)成立,由数列收敛的柯西准则,{}n f 在D 上任一点都收敛,记其极限函数为()f x ,x D ∈.现固定式中的n ,让m →∞,于是当n>N 时,对一切x D ∈都有()()n f x f x ε-≤. 由定义可得,()()n f x f x ⇒ ()n →∞,x D ∈. 根据一致收敛定义可推出下述定理:函数列{}n f 在区间D 上一致收敛于f 的充要条件是:l i m s u p ()()0n n x Df x f x →∞∈-=. (6) 证 [必要性] 若()()n f x f x ⇒ ()n →∞,x D ∈.则对任给的正数ε,存在不依赖于x 的正整数N ,当n>N 时,有 ()()n f x f x ε-<,x D ∈. 由上确界的定义,亦有sup ()()n x Df x f x ε∈-≤.这就证得(6)式成立.[充分性] 由假设,对任给的0ε>,存在正整数N ,使得当n>N 时,有s u p ()()n x Df x f x ε∈-<. (7)因为对一切x D ∈,总有 ()()s u p ()()n n x Df x f x f x f x ∈-≤-. 故由(7)式得()()n f x f x ε-<.于是{}n f 在D 上一致收敛于f .在判断函数列是否一致收敛上定理 5.2更为方便一些(其缺点是必须事先知道它的极限函数),由, 所以在(,)-∞+∞上,sin 0nxn ⇒()n →∞. 例7 证明:若对,0,n n N a x I ∀∈∃>∀∈,有1()()n n n f x f x a +-≤,且1n n a ∞=∑收敛,则函数列{()}n f x 在区间I 上一致收敛. 证明: ,,n p N x I ∀∈∀∈,111()()()()()()n p n n p n p n n n p n f x f x f x f x f x f x a a +++-++--≤-++-≤++(,)sin 1lim sup 0lim 0n n x nx nn →∞→∞∈-∞+∞-==因为1n n a ∞=∑收敛,故0,,n N p N ε∀>∃∈∀∈,有1n p n a a ε+-++<.于是,0,,,n N p N x I ε∀>∃∈∀∈∀∈,有 11()()n p n n p n n p n f x f x a a a a ε++-+--≤++=++<.所以{()}n f x 在区间I 上一致收敛.6 函数项级数一致收敛的柯西准则6.1 函数项级数定义定义1 设{()}n u x 是定义在数集E 上的一个函数列,表达式 12()()()n u x u x u x ++++,x E ∈ (8)称为定义在E 上的函数项级数,简记为1()nn k u x =∑或()n u x ∑.称1()()nn k k S x u x ==∑, x E ∈,n=1,2,(9)为函数项级数(10)的部分和函数列定义2 设{()}n S x 是函数项级数()n u x ∑的部分和函数列.若{()}n S x 在数集D 上一致收敛于函数()S x ,则称函数项级数()n u x ∑在D 上一致收敛于函数()S x ,或称()n u x ∑在D 上一致收敛. 6.2 函数项级数的一致收敛定理6.2(一致收敛的柯西准则) 函数项级数()n u x ∑在数集D 上一致收敛的充要条件为:对任给的正数ε,总存在某正整数N ,使得当n>N 时,对一切x D ∈和一切正整数p ,都有()()n p n S x S x ε+-<,或 12()()()n n n p u x u x u x ε++++++<.此定理中当p=1时,得到函数项级数一致收敛的一个必要条件.推论 函数项级数()n u x ∑在数集D 上一致收敛的必要条件是函数列{()}n u x 在D 上一致收敛于零.设函数项级数()n u x ∑在D 上的和函数为()S x ,称()()()n n R x S x S x =- 为函数项级数()n u x ∑的余项.7 含参量反常积分的一致收敛的柯西准则7.1 含参量反常积分的定义设函数(,)f x y 定义在无界区域{(,),}R x y a x b c y =≤≤≤<+∞上,若对每一个固定的[,]x a b ∈,无穷积分(,)cf x y dy +∞⎰(10)都收敛,则它的值是x 在[,]a b 上取值的函数,当记这个函数为()I x 时,则有 ()(,)cI x f x y d y +∞=⎰,[,]x a b ∈, (11)称(10)式为定义在[,]a b 上的含参量x 的无穷限无穷积分,或简称含参量无穷积分. 如同无穷积分与数项级数的关系那样,含参量无穷积分与函数项级数在所研究的问题与论证方法上也极为相似.7.2 含参量无穷积分的一致收敛概念及柯西准则定义 若含参量无穷积分(10)与函数()I x 对任给的正数ε,总存在某一实数N>c ,使得当M>N 时,对一切[,]x a b ∈,都有(,)()Mcf x y d yI x ε-<⎰,即(,)Mf x y d y ε+∞<⎰,则称含参量无穷积分(10)在[,]a b 上一致收敛于()I x ,或简单地说含参量无穷积分(10)在[,]a b 上一致收敛.定理7.3 (一致收敛的柯西准则) 含参量无穷积分(10)在[,]a b 上一致收敛的充要条件是:对任给的正数ε,总存在某一实数M c >,使得当12,A A M >时,对一切[,]x a b ∈,都有21(,)A A f x y d y ε<⎰. (12)例8 证明含参量无穷积分s i n xydy y+∞⎰(13) 在[,)δ+∞上一致收敛(其中0δ>),但在(0,)+∞内不一致收敛. 证 作变量代换u xy =,得s i n s i n AA x x y u d y d u yu +∞+∞=⎰⎰, (14)其中A>0.由于0sin udu u+∞⎰收敛,故对任给正数ε,总存在正数M ,当'A M >时,就有's i n A udu uε+∞<⎰. 取A M δ>,则当MA δ>时,对一切0x δ≥>,由(14)式有s i n Axydy yε+∞<⎰, 所以(13)在0x δ≥>上一致收敛.现在证明(13)在(0,)+∞内不一致收敛.由一致收敛定义,只要证明:存在某一正数0ε,使对任何实数M(>c),总相应地存在某个A M >及某个[,]x a b ∈,使得0(,)Af x y d y ε+∞≥⎰.由于非正常积分0sin udu u+∞⎰收敛,故对任何正数0ε与M ,总存在某个(0)x >,使得00s i n s i n Mxu u du du u uε+∞+∞-<⎰⎰,即0000sin sin sin Mx uu u du du du u u uεε+∞+∞+∞-<<+⎰⎰⎰. (15) 现令001sin 2udu uε+∞=⎰,由(14)及不等式(15)的左端就有000s i n s i n 2MM x x y u d y d u yu εεε+∞+∞=>-=⎰⎰. 所以(13)在(0,)+∞内不一致收敛.关于含参量无穷积分一致收敛性与函数项级数一致收敛之间的联系有下述定理.定理 含参量无穷积分(10)在[,]a b 上一致收敛的充要条件是:对任一趋于+∞的递增数列{}n A (其中1A c =),函数项级数111(,)()n nA n A n n f x y dy u x +∞∞===∑∑⎰(16)在[,]a b 上一致收敛.证 [必要性]由(10)在[,]a b 上一致收敛,故对任给的0ε>,必存在M c >,使当m n A A M >>时,对一切[,]x a b ∈,总有"'(,)A A f x y d y ε<⎰. (17)又由()n A n →+∞→∞,所以对正数M ,存在正整数N ,只要当m n M >>时,就有m n A A M >>.由(17)对一切[,]x a b ∈,就有 11()()(,)(,)m n mnA A n m A A u x u x f x y dy f x y dy ++++=++⎰⎰=1(,)m nA A f x y dy ε+<⎰.这就证明了级数(16)在[,]a b 上一致收敛.[充分性] 用反证法.假如(10)在[,]a b 上不一致收敛,则存在某个正数0ε,使得对于任何实数M c >,存在相应的"'A A M >>和'[,]x a b ∈,使得"0'(',)A A f x y d y ε≥⎰.现取1max{1,}M c =,则存在211A A M >>及1[,]x a b ∈,使得2110(,)A A f x y dy ε≥⎰.一般地,取2(1)max{,}(2)n n M n A n -=≥,则有221n n n A A M ->>及[,]n x a b ∈,使得2210(,)n n A n A f x y dy ε-≥⎰. (18)由上述所得到的数列{}n A 是递增数列,且lim n n A →∞=+∞.现考察级数111()(,)n nA n A n n u x f x y dy +∞∞===∑∑⎰.由(18)式知存在正数0ε,对任何正整数N ,只要n M >,就有某个[,]n x a b ∈,使得21220()(,)n nA n n n A u x f x y dy ε+=≥⎰.这与级数(16)在[,]a b 上一致收敛的假设矛盾.故含参量无穷积分(10)在[,]a b 上一致收敛.例9 若无穷积分()af x dx ∞⎰收敛,函数()f x 在[,)a +∞单调,则lim ()0x xf x →+∞=.证 不妨设函数()f x 在[,)a +∞上单调递减,已知无穷积分()af x dx ∞⎰收敛,我们有()0f x ≥,[,)x a ∈+∞.由已知条件无穷积分()a f x dx ∞⎰收敛,根据柯西收敛准则0,ε∀>..1p A ∀>和2p A >,有12()p p f x dx ε<⎰.于是122,,2xx A p p x ∀>==取,因为()f x 单调递减,得到2122()()()()02p xxx x p xf x dx f t dt f x dt f x ε>=≥=≥⎰⎰⎰. 即lim ()0x xf x →+∞=.8 柯西准则在数学分析中的作用8.1 柯西准则在实数完备性理论中的作用实数完备性是数学分析的基础,其六大定理即确界原理、单调有界定理、区间套定理、有限覆盖定理、聚点定理、柯西准则,建立了实数完备性理论的骨架.作为六大定理之一的柯西准则,起着至关重要的作用,由该准则人手,可依次推出其它五个定理.由广义积分收敛的柯西准则易推出广义积分的绝对收敛判别法及比较判别法. 8.2 用柯西准则判断敛散性的优越性作为判别敛散性的工具,柯西准则较其它判别法具有更多的优点.其一,条件的充分必要性决定其适用范围更广,更普遍;其二,柯西准则只利用题目本身的条件,不必借助极限结果,以下举两个例子说明之.例10 若数列{}n a 收敛,则数列{}n a 必收敛. 证 0ε∀>{}n a 收敛,由柯西准则',,N N m n N ∴∃∈∀>,有m n a a ε-< 从而m n m n a a a a ε-<-<,由柯西准则数列{}n a 收敛.例11 设函数列{()}n f x 在D 上一致收敛,则函数级数11(()())n n n f x f x ∞+=-∑在D 上一致收敛.证 设1()()()n n n u x f x f x +=- 0ε∀>因为 {()}n f x 在D 上一致收敛,由函数列一致收敛的柯西准则: 所以 'N N ∃∈,当n N >时,',p N x D ∀∈∀∈,有()()n p n f x f x ε+-< 从而 11()()()()()n n n p n p n u x u x u x f x f x ε++-++++=-<.由函数级数的柯西一致收敛准则得:11(()())n n n f x f x ∞+=-∑在D 上一致收敛 。
柯西极限存在准则

柯西极限存在准则
极限存在准则又叫柯西收敛原理,给出了收敛的充分必要条件;数列{Xn}收敛的充分必要条件是:对于任意给定的ε,存在着这样的N,使得当m>N,n>N时就有|Xn-Xm|<ε这个准则的几何意义表示,数列{Xn}收敛的充分必要条件是:对于任意给定的正数ε,在上一切具有足够大号码的点Xn中,任意两点间的距离小于ε .
充分性证明:
1、首先证明Cauchy列有界
取ε=1,根据Cauchy列定义,存在自然数N,对一切n>N,有
Ian-aN+1I<1;
令M=max{|a1|,|a2|,…,|aN|,|aN+1|+1}
则对一切n,成立|an|≤M;
所以Cauchy列有界;
2、其次在证明收敛
因为Cauchy列有界,所以根据Bolzano-Weierstrass定理有界数列有收敛子列存在一个子列ajn以A为极限;那么下面就是要证明这个极限A也就是是Cauchy列的极限;注意这种证明方法是实数中常用的方法:先取点性质,然后根据实数稠密性,考虑点领域的性质,然后就可以证明整个实数域的性质了
因为Cauchy列{an}的定义,对于任意的ε>0,都存在N,使得m、n>N时有
|am-an|<ε/2
取子列{ajn}中一个jk,其中k>N,使得
|ajk-A|<ε/2
因为jk>=k>N,所以凡是n>N时,我们有
|an-A|<=|an-ajk|+|ajk-A|<ε/2+ε/2=ε
这样就证明了Cauchy列收敛于A.
即得结果:Cauchy列收敛。
函数极限的归结原则(老黄学高数第96讲)

依次取δ=δ’,δ’/2, …δ’/n,…,相应存在x1,x2,…,xn…
使得0<|xn-x0|<δ’/n ,而|f(xn)-A|≥ε0, n=1,2,…
与题设矛盾! ∴
f(x)=A.
注: 1、归结原则可简述为:
f(x)=A对任何xn→x0(n→∞)有
f(xn)=A.
注: 2、若有以x0为极限的数列{xn},使 f(xn)不存在, 或两个以x0为极限的数列{x’n}与{x”n},使
对任何包含于U(+∞)且以+∞为极限的数列{xn},
极限
f(xn)都存在且相等.
请叙述函数极限其它形式的归结原则.
2、设f(x)=xcosx,试作数列:
(1){xn}使得xn→+∞(n→∞),f(xn)→0(n→∞); (2){yn}使得yn→+∞(n→∞),f(yn)→+∞(n→∞); (3){zn}使得zn→+∞(n→∞),f(zn)→-∞(n→∞).
3、证明 cosx不存在. 证:设x’n=2nπ,x”n=nπ+ , 则x’n→+∞,x”n→+∞ (n→∞), 而cos x’n=1,cos x”n=0 (n→∞), ∴ cosx不存在.
(归结原则):设f在U⁰(x0;δ’)内有定义。
f(x)存在的充要条件是:对任何包含于U⁰(x0;δ’)
且以x0为极限的数列{xn}, f(xn)都存在且相等.
[充分性]若对任意的{xn}⊂U⁰(x0;δ’)且 xn=x0,有
f(xn)=A,但
f(x)≠A,则存在ε0>0,
对任意δ>0,总有x’∈U⁰(x0;δ),使|f(x’)-A|≥ε0.
f(x’n)与 f(x”n)都存在但不相等,则 f(x)也不存在.
数列极限的柯西收敛准则

数列极限的柯西收敛准则柯西准则是柯西极限存在准则,又叫柯西收敛原理。
其是可以用来判断某个式子是否收敛的充要条件包括但是不限于数列,主要应用在数列,数项级数,函数,反常积分,函数列和函数项级数等方面。
每个方面都对应一个柯西准则,不同方面的柯西准则要用不同样式的柯西极限存在准则来进行计算。
柯西准则是数学的一方面,数学是研究数量、结构、变化、空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种。
数学透过抽象化和逻辑推理的使用,由计数、计算、量度和对物体形状及运动的观察而产生。
数学已成为许多国家及地区的教育范畴中的一部分。
它应用于不同领域中,包括科学、工程、医学、经济学和金融学等。
数学家也研究纯数学,就是数学本身的实质性内容,而不以任何实际应用为目标。
中国古代,数学叫作算术,又称算学,最后才改为数学.中国古代的算术是六艺之一(。
数学源于人类早期的生产活动,古巴比伦人从远古时代已经开始已经累积了一定的数学知识,并能够应用领域实际问题.从数学本身看看,他们的数学知识也只是观测和经验税金,没综合结论和证明,但也必须充分肯定他们对数学所作出的贡献.基础数学的知识与运用是个人与团体生活中不可或缺的一部分.其基本概念的精炼早在古埃及、美索不达米亚及古印度内的古代数学文本内便可观见.从那时开始,其发展便持续不断地有小幅度的进展.但当时的代数学和几何学长久以来仍处于独立的状态.代数学可以说道就是最为人们广为拒绝接受的“数学”.可以说道每一个人从小时候已经开始学数数起至,最先碰触至的数学就是代数学.而数学做为一个研究“数”的学科,代数学也就是数学最重要的组成部分之一.几何学则就是最早已经开始被人们研究的数学分支.。
数学公式知识:柯西中值定理的定义、证明及其应用

数学公式知识:柯西中值定理的定义、证明及其应用柯西中值定理,又称柯西中值定理,是微积分学中的一个重要定理,它指出了连续函数在闭区间上必然存在一点,对于这一点的导数等于函数在这一区间上的平均增量。
这个定理被柯西首先在1823年提出,并且在实际问题中有着广泛的应用。
柯西中值定理的定义首先我们来看一下柯西中值定理的定义。
设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)内可导。
那么存在一个点c∈(a,b),使得:f'(c) = (f(b) - f(a))/(b - a)这里f'(c)表示函数f(x)在点c处的导数。
换句话说,柯西中值定理指出即使在一个闭区间上连续的函数,在这个区间内必然存在至少一个点,使得该点的导数等于函数在这个区间上的平均增量。
柯西中值定理的证明接下来我们来证明柯西中值定理。
首先我们对于函数f(x)在闭区间[a, b]上连续进行加强,使用连续性的性质,我们可以得到:max(f(x)) ≤ f(x) ≤ min(f(x)) (x∈[a,b])然后我们来考虑f(b) - f(a)和f'(c)的关系。
使用微积分的中值定理,我们可以得到:f(b) - f(a) = f'(c)(b - a)结合以上两个式子,我们可以得到:f'(c) = (f(b) - f(a))/(b - a)这就是柯西中值定理的证明。
证明过程可以看出,柯西中值定理的核心思想是把函数在闭区间上的平均增量和在其中某个点的导数联系了起来,这是微积分中一个非常重要的观念。
柯西中值定理的应用柯西中值定理在微积分中有着广泛的应用,特别是在求解实际问题中的一些情况。
下面我们来看一些柯西中值定理的应用。
1.速度和加速度的关系假设我们研究一辆汽车在某一段路程上的运动情况,我们可以把汽车在这段路程上的速度看作是一个连续函数。
使用柯西中值定理,我们可以证明存在一个时间点,汽车在这个时间点的速度等于整段路程上的平均速度。
(仅供参考)柯西收敛准则

例3 设数列满足条件 : an1 an r n , n 1, 2,,
其中 r (0,1). 求证 {an}收敛.
证 an p an an1 an an2 an1 an p an p1
r n r n1
由于
lim
n
rn 1r
rn 0, 于是
p1
r n (1 r p ) 1r
定理1 对于级数 un, 将它的所有正项保留而
n1
将负项换为0, 组成一个级数记为 vn 将它
n1
的所以负项变号(乘上因子-1)而将正项换为0, 也组
成一个正项级数记 wn
n1
vn
un
un 2
un , un 0, un
0 0
wn
un
un 2
un , un 0 0, un 0
(1)若级数 un 绝对收敛, 则级数 vn wn 都收敛;
(
1
1 2
1
,
{ xn} 收敛 .
2
2016/6/14
二 函数极限的柯西收敛准则
lim
n
xn
a
xn f (n)
lim f (n) a
n
lim f ( x) A
x
当 n,m > N 时, 总有
当 n , m > N 时, 总有
当x1, x2 X时,
总有
lim f ( x) A
x x0
当0 x1 x0 ,
0 x2 x0 时,总有
lim f ( x) A
x x0
当0 x1 x0 ,
0 x2 x0 时,总有
lim f ( x)不存在
x x0
尽管
0 0
第十讲柯西收敛准则

第十讲柯西收敛准则柯西收敛准则是数学分析中一个重要的收敛判定准则,通过它我们可以判断一个数列是否收敛。
在数学分析中,数列是由一系列有序的数按照一定规律排列而成的,我们通常关心的是这个数列是否有一个极限值。
柯西收敛准则是通过数列中各项之间的距离来判断数列的收敛性。
柯西收敛准则的原理是:对于一个数列{an},如果对于任意给定的正数ε,总存在一个正整数N,使得当n>N时,所有后续项an与前项之间的差值小于ε,那么数列{an}就是收敛的。
具体来说,柯西收敛准则可以形式化为以下定义:对于一个数列{an},如果对于任意给定的正数ε,都存在一个正整数N,使得当n,m>N时,有,an - am,<ε,那么数列{an}就是收敛的。
其中,ε表示误差范围,N表示柯西收敛序列中的一些位置。
柯西收敛准则的直观解释是:当数列中的元素逐渐靠近一些极限值时,元素之间的距离也会逐渐变小,直到无限接近于零。
也就是说,如果数列是收敛的,那么无论选择多小的误差范围ε,我们总可以找到一个足够大的位置N,使得大于该位置的所有后续项都在ε的误差范围之内。
柯西收敛准则可以应用于各种不同类型的数列,比如数列中的元素可以是实数,复数,还可以是无限级数或者函数序列等等。
它在数学分析中的应用非常广泛,特别是在序列极限的证明中,经常可以用到柯西收敛准则进行推导和判断。
柯西收敛准则的证明可以通过数列的有界性以及数学分析中的等式推导和不等式性质来进行。
首先,根据柯西收敛准则的定义,我们可以推导出数列是有界的,即存在一个常数M,使得对于所有的n,有,an,<= M。
其次,通过等式推导和不等式性质,我们可以得到:,an - am, <= ,an - an+1, + ,an+1 - an+2, + ... + ,am-1 - am。
由于an满足柯西收敛准则,所以取n > N时,保证,an - am,小于给定误差ε。
于是,通过上述等式和不等式,我们可以得到从n > N开始,数列中的任意两项an和am之间的差值都小于ε,即数列满足柯西收敛准则。
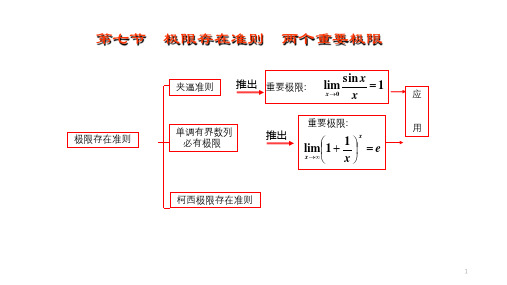
高等数学 第1章 第七节 极限存在准则 两个重要极限
则
lim
n
x n1
lim n
6 xn ,
A
6 A,
解得 A 3或A 2,(舍去)
lim n
xn
3.
14
3.两个重要极限的应用
例6: 求 lim tan x 1
x0 x
可作为公式
lim
x
s
in u x ux
1
lim ux 0
x
解: lim tan x lim sin x 1 lim sin x lim 1 11 1 x0 x x0 x cos x x0 x x0 cos x
1 n2 1
n2
1
22
n2
1
n2
n n2 1
,
1
lim 1 0, n 2n
lim n n n2 1
lim n
n
1
1
由夹逼定理知:
n2
0 0, 10
lim n
n
1 2
1
n2
1 22
n2
1 n2
存在, 且
lim n
n
1 2
1
n2
1
22
n2
1
n2
0.
8
例2 用夹逼准则证明:
lim sin x 1.
1yn xn zn n 1,2,3,,
2
lim
n
yn
a,
lim
n
z
n
a,
则数列x
n
的
极
限
存
在,
且
lim
n
xn
a.
准则1 若
1当x
U
x
一、柯西(Cauchy)中值定理

B
A
D
F ( 2 )F ( b )
o
F ( a ) F ( 1 ) F ( x )
x
f (b) f (a ) ( x ) f ( x ) f (a ) [ F ( x ) F (a )]. F (b) F (a ) ( x ) 满足罗尔定理的条件 ,
则在(a , b)内至少存在一点 , 使得 () 0.
tan x x 求 lim 2 . x 0 x tan x
2 sec x 1 tan x x lim 原式 lim 3 x 0 x 0 3 x2 x
tan x 1 2 sec x tan x 1 lim . lim x 0 3 x 0 x 3 6x
2
关于 型的极限,有下述定理
这种极限称为未定式本节我们就利用cauchy中值定理来建立求未定式极限的lhospital法则利用这一法则可以直接求型未定式解法洛必达法则定义称为那末极限tanlimsinlnsinlnlimbxax那末或为无穷大存在都存在且定理定义这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则
本节我们就利用Cauchy中值定理来建立求未定式 极限的L.Hospital法则,利用这一法则,可以直接求
,
0 和 这两种基本未定式的极限,也可间接求出 0
0 , ,00 , 0 ,1 等其它类型的未定式的极限
0 三、 型及 型未定式解法 : 洛必达法则 0
定义 如果当x a (或x )时,两个函数f ( x )
及 F ( x ) 都存在且 F ( x ) 0; f ( x ) ( 3) lim 存在(或为无穷大); x a F ( x ) f ( x) f ( x ) 那末 lim lim . x a F ( x ) x a F ( x )
柯西中值定理和不定式极限

1 ln(1 x ) 1 e elim . x 0 2x 2
前页 后页 返回
2. 型不定式极限 定理6.7 若函数 f 和 g 满足:
(i) lim f ( x ) lim g( x ) ;
x x0 x x0
(ii) 在点 x0 的某右邻域 U ( x0 ) 内二者均可导,
k AB
f (b) f (a ) . g(b) g(a )
v
P ( g( ) , f ( ))
B( g (b ) , f (b ))
A ( g(a ) , f (a ))
O
u
前页 后页 返回
证 作辅助函数
f (b) f (a ) F ( x ) f ( x ) f (a ) ( g( x ) g(a )). g(b) g(a )
我们再举一例:
arctan x . 例8 求极限 A lim x arctan 2 x π π 解 因为 lim arctan x , lim arctan 2 x , x 2 x 2
前页 后页 返回
所以 A = 1. 若错误使用洛必达法则: arctan x 1 1 4 x2 lim lim 2, 2 x arctan 2 x x 1 x 2 这就产生了错误的结果. 这说明: 在使用洛必达法 0 则前,必须首先要判别它究竟是否是 或 型. 0 3. 其他类型的不定式极限
证 我们补充定义 f ( x0 ) g( x0 ) 0, 所以 f , g
前页 后页 返回
在点 x0 连续. 任取 x U ( x0 ), 则在区间[ x0 , x ]
( [ x , x0 ] )上应用柯西中值定理, 有
柯西极限存在准则

柯西极限存在准则
柯西极限体系是一套可以用来定义和推理不同类型极限的数学体系,是到如今为止唯一权威的无穷极限性定义,由美国数学家约翰·科西(John Cauchy)于19世纪40年代末首先提出的。
它要求可以把每个极限看做某个方向的极限,而每个方向上的极限又应当符合以下两个共同特性:
1、极限:如果人们从某一方向而来,他们发现它在每一个越过方向上都是有某种程度的分类,即每当准确的特定的方向越过特定的角度时,极限也会发生变化。
2、独立:这一分类只与此方向有关,而不是其他方向的分类。
因此,每种部分的极限可以独立计算,不需要考虑其他极限的情况。
由此,它将一个未知函数的极限分解为不同方向上的不同极限,而且这些极限可以独立计算,以得出最终结果。
虽然科西体系本身早已成为极限计算的核心,但由于核心原理不易于理解,现代数学课程也少有涉及科西的迹象,导致它很少被人了解和使用。
柯西中值定理和不定式极限汇总

柯西中值定理和不定式极限汇总不定式极限是微积分中的一个概念,用于描述函数在无穷远处的变化趋势。
不定式极限通常用符号∞来表示,表示函数在无穷远处的极限值。
不定式极限可以是无穷大、无穷小或无穷远。
现在我们来详细介绍柯西中值定理。
设函数f(x)在闭区间[a, b]上连续,在开区间(a, b)内可导。
根据柯西中值定理,存在一个xi∈(a, b),使得f'(x_i) = \frac{f(b)-f(a)}{b-a}\]其中,f'(xi)表示函数在(xi, f(xi))处的瞬时变化率,也就是导数。
我们通过一个例子来具体说明柯西中值定理的应用。
例1:设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,并且f(a)=f(b)。
证明:存在一个点c∈(a,b),使得f'(c)=0。
证明:根据柯西中值定理,存在一个点c∈(a,b),使得f'(c) = \frac{f(b)-f(a)}{b-a} = \frac{0}{b-a} = 0\]因此,存在一个点c∈(a,b),使得f'(c)=0,即证明了结论。
除了柯西中值定理,微积分中还有其他的一些重要定理,如拉格朗日中值定理、罗尔定理等。
这些定理的应用可以帮助我们更好地理解函数的性质和变化规律,为解决问题提供了有力的工具。
总结起来,柯西中值定理是微分学中的一个重要定理,它可以描述函数在一个区间上的平均变化率与其在该区间上其中一点处的瞬时变化率之间的关系。
柯西中值定理在求解函数的最大值、最小值以及判断函数在一些点上的性质时起着重要的作用。
除了柯西中值定理,微积分中还有其他的一些重要定理,它们的应用可以帮助我们更好地理解函数的性质和变化规律,为解决问题提供有力支持。
实变函数三大基本定理

实变函数三大基本定理实变函数是数学中的重要概念,它的研究过程中涉及到多个定理和概念。
今天,让我们来一起了解实变函数的三大基本定理。
一、极限定理实变函数的极限定理是指,如果一个函数在某个点处存在极限,那么这个点就称为这个函数的极限点,而且极限点的值必须是函数在这个点处的唯一极限。
这一基本定理的具体表达式有很多,其中最常见的是柯西准则和斯特朗定理。
柯西准则是指,如果在函数f(x)的定义域内,对于任意ε > 0,总存在一个小于ε的δ > 0,使得当0 < |x - a| < δ时,有|f(x) - L| < ε,则称函数f(x)在x = a处的极限是L。
斯特朗定理是指,如果一个函数在区间[a,b]上连续,且在[a,b]上的任意一个点x0的导数存在,则函数在[a,b]上满足柯西准则。
二、中值定理中值定理是指,如果一个函数在某个区间[a,b]上连续,且在(a,b)内可导,那么它在[a,b]上至少存在一个点c,使得f'(c) = (f(b) -f(a)) / (b - a)。
有了中值定理,我们可以更好地了解函数的变化规律,为后面的研究打下基础。
三、泰勒公式泰勒公式是一种常见的数值分析方法,它用一系列导数来逼近一个函数的值。
具体地讲,如果一个函数在某个闭区间上多次可导,那么这个函数可以被一组多项式所逼近。
这个多项式是以函数在某个点的导数为系数的多项式。
泰勒公式的概念非常重要,它在实际工程应用中发挥了重要的作用。
综上所述,实变函数的三大基本定理——极限定理、中值定理和泰勒公式——在实际的数学运算中都起到了至关重要的作用,是我们系统学习实变函数的重要组成部分。
如果你正在研究实变函数,这三个基本定理是你必须掌握的关键知识点。
函数极限的柯西收敛准则

函数极限的柯西收敛准则函数极限是微积分学中的重要内容,它描述了函数在某一点处的趋近性质。
柯西收敛准则是判定函数极限存在与否的一种准则,它告诉我们如何根据函数的收敛性质来判断函数极限的存在性。
本文将围绕柯西收敛准则展开讨论,并详细解释该准则的原理和应用。
柯西收敛准则是由法国数学家柯西提出的,它是基于数列收敛性质推广而来的。
在数列收敛的情况下,柯西收敛准则告诉我们,当数列中的元素足够接近时,它们的极限存在且唯一。
同样地,对于函数而言,柯西收敛准则也可以用来判断函数极限的存在性。
柯西收敛准则的表述如下:对于任意给定的正数ε,存在正数δ,使得当函数f(x)中的任意两个自变量x1和x2满足|x1-x2|<δ时,对应的函数值f(x1)和f(x2)满足|f(x1)-f(x2)|<ε。
换句话说,对于任意给定的精度ε,只要自变量足够接近,函数值也会足够接近。
柯西收敛准则的原理是基于函数的连续性和函数极限的定义。
在数学中,连续性描述了函数在某一点处的光滑性,而函数极限描述了函数在某一点处的趋近性。
柯西收敛准则将这两个性质结合起来,通过自变量的足够接近来推断函数值的足够接近。
柯西收敛准则的应用非常广泛。
在实际问题中,我们经常需要判断函数极限的存在性并进行相关的计算。
通过柯西收敛准则,我们可以确定自变量的取值范围,从而得到函数极限的近似值。
这对于优化问题、数值计算和科学研究等领域都具有重要意义。
举个例子来说明柯西收敛准则的应用。
考虑函数f(x) = 1/x,在x 趋于无穷大时,该函数的极限应为0。
为了验证这个结论,我们可以使用柯西收敛准则。
对于任意给定的正数ε,我们需要找到一个正数δ,使得当|x1-x2|<δ时,|f(x1)-f(x2)|<ε成立。
由于f(x) = 1/x是一个单调递减的函数,所以只需考虑x1>x2的情况。
假设x1>x2,则有f(x1)-f(x2) = 1/x1-1/x2 = (x2-x1)/(x1*x2)。
柯西准则

2n+ + 1
2n+p +..+
第一节、数列的柯西准则与函数的一致连续性13
1 (1 1 )
2n 2p = . . 1
2n <
ε >0, N ε1 ,
=.. ..
. .
1 . <n
对任意取当n > N时, 对任意正整数
p, 有
. n p n x x ε + . <
→+∞
= .
总有
1 2 当x , x > X时,
0
lim ( )
x x
f x A
→
= .
总有
1 0 当0 < x . x <δ ,
2 0 0 < x . x <δ时,
0
lim ( )
x x
f x A
→
= .
总有
1 0 当0 < x . x <δ ,
n p n x x + . 1 2
1 2
2 2 2
sin( ) sin( ) sin( )
n n n p
n n n p
+ + +
= + + + +..+ +
1
1
2n+ ≤ ( ) 1 2 1
1 1 1 1 1
2n+ 2 2 2p. 2 = + + +..+
故数列{ } n x 收敛.
3
例4 若xn+1.xn <cn, 且sn=c1+c2+..+cn,
数学分析6.2柯西中值定理和不定式极限(讲义)

第六章微分中值定理及其应用2 柯西中值定理和不定式极限(讲义)一、柯西中值定理定理6.5:(柯西中值定理)若函数f和g满足:1、在[a,b]上都连续;2、(a,b)上都可导;3、f’(x)和g’(x)不同时为零;4、g(a)≠g(b),则存在ξ∈(a,b),使得=.证:记F(x)=f(x)-f(a)-(g(x)-g(a)),根据罗尔中值定理,至少存在一点ξ∈(a,b),使得F’(ξ)=f’(ξ)-g’(ξ)=0.∵g’(ξ)≠0;∴=.注:当g’(ξ)=0时,则=,且f(a)≠f(b).柯西中值定理的几何含义:将f,g看作x的参量方程,在uOv 平面上表示一段曲线,由表示连接曲线两端的弦的斜率,而=|x=ξ则表示曲线上与x=ξ相对应的一点(g(ξ),f(ξ))处的切线斜率。
因此柯西中值定理公式表示上述切线与连接曲线两端的弦互相平行.例1:证明:设函数f在[a,b](a>0)上连续,在(a,b)内可导,则存在ξ∈(a,b),使得f(b)-f(a)=ξf’(ξ)ln.证:∵设g(x)=lnx,则f,g在[a,b](a>0)上符合柯西中值定理;∴存在ξ∈(a,b),使得=,即ξf’(ξ)=,∴f(b)-f(a)=ξf’(ξ)ln.二、不定式极限两个无穷小量或两个无穷大量之比的极限统称为不定式极限,以导数为工具研究不定式极限的方法通称为洛必达法则。
1、型不定式极限定理6.6:若函数f和g满足:1、f(x)=g(x)=0;2、在点x0的某空心邻域U0(x0)内两者都可导,且g’(x)≠0;3、=A(A可为实数或±∞或∞),则==A.证:补充定义f(x0)=g(x0)=0,使f,g在点x0处都连续,任取x∈U0(x0),则f,g在[x0,x](或[x,x0])上符合柯西中值定理,∴存在ξ∈(x0,x)(或(x,x0)),使得==.当x→x0时,ξ→x0,∴===A.例2:求.证:设f(x)=1+cosx,g(x)=tan2x,则==-=. 又f,g在x0=π的邻域内满足定理6.6,∴==.例3:求.解法1:记f=e x-,g=ln(1+x2),则f’=e x-,g’= f,g在U(0,)符合洛必达法则,∴=====1.解法2:由ln(1+x2)~x2(x→0),得=====1.例4:求.解:令t=,则当x→0+时,t→0+.∴===-1.2、型不定式极限定理6.7:若函数f和g满足:1、f(x)=g(x)=∞;2、在点x0的某右邻域U0+(x0)内两者都可导,且g’(x)≠0;3、=A(A可为实数或±∞或∞),则==A. 证:设A为实数,∵=A,∴对∀ε>0,存在x1∈U0+(x0),对一切x∈(x0,x1),有<ε.∵在U0+(x0, x1)内f,g都可导,且g’(x)≠0;∴f和g在区间[x,x1]上满足柯西中值定理,故必存在ξ∈(x,x1)⊂(x0,x1),使得=,∴<ε. 又=.∵<|A|+ε,∴有界,∵f(x)=g(x)=∞,∴=0.∴存在δ>0,使当x0<x<x0+δ< x1时,有<ε.∴对一切满足不等式x0<x<x0+δ的x,有≤+<ε. ∴=A.注:1、类似地可证明当A=±∞或∞时的情形;2、对x→x0,x→x0+,x→x0-,x→±∞或x→∞,结论都成立。
2009-12-19 柯西准则

柯西准则柯西准则主要用来判断极限存在性,有数列极限的柯西准则和函数极限的柯西准则. 它们之间也有密切的联系. 实际上,函数极限的柯西准则可以通过归结原则用数列极限的柯西准则来证明,这一点也充分表明归结原则作为联系函数极限与数列极限的桥梁的意义.数列极限的柯西准则 数列{a n }极限存在的充要条件是,对∀ε>0,总是∃N >0,对∀n , m >N ,有|a n -a m |<ε.需要注意的是,这里的极限是指狭义的有限极限,不包括无穷大的情形. 另外,数列{a n }不一定要从n =1开始就有定义,可以是从某一项开始才有定义.(1)0lim ()x x f x →存在 “对∀ε>0,总是∃δ>0,对∀x 1, x 2∈0(;)o U x δ,有|f (x 1)-f (x 2)|<ε”. (2)0lim ()x x f x +→存在 “对∀ε>0,总是∃δ>0,对∀x 1, x 2∈0(;)o U x δ+,有|f (x 1)-f (x 2)|<ε”. (3)0lim ()x x f x -→存在 “对∀ε>0,总是∃δ>0,对∀x 1, x 2∈0(;)o U x δ-,有|f (x 1)-f (x 2)|<ε”. (4)lim ()x f x →∞存在 “对∀ε>0,总是∃M >0,对∀x 1, x 2∈(;)U M ∞,有|f (x 1)-f (x 2)|<ε”.(5)lim ()x f x →+∞存在 “对∀ε>0,总是∃M >0,对∀x 1, x 2∈(;)U M +∞,有|f (x 1)-f (x 2)|<ε”. (6)lim ()x f x →-∞存在 “对∀ε>0,总是∃M >0,对∀x 1, x 2∈(;)U M -∞,有|f (x 1)-f (x 2)|<ε”. 需要注意的是,这里的极限是指狭义的有限极限,不包括无穷大的情形. 下面我们用数列极限的柯西准则与归结原则来证明函数极限的柯西准则.(1)0lim ()x x f x →存在 “对∀ε>0,总是∃δ>0,对∀x 1, x 2∈0(;)o U x δ,有|f (x 1)-f (x 2)|<ε”. 证明 必要性. 若0lim ()x x f x →存在,设0lim ()x x f x A →=. 那么,对∀ε>0,总是∃δ>0,对∀x ∈0(;)o U x δ,有|f (x )-A |<ε/2. 从而对∀x 1, x 2∈0(;)o U x δ,有|f (x 1)-A |<ε/2,|f (x 2)-A |<ε/2,于是|f (x 1)-f (x 2)|≤ |f (x 1)-A |+|f (x 2)-A |<ε.充分性. 设数列{x n }满足“以x 0为极限且n 超过某值时总有x n ≠x 0”. 任给ε>0. 由假设知∃δ>0,对∀x 1, x 2∈0(;)o U x δ,有|f (x 1)-f (x 2)|<ε. 对于δ>0,由于{x n }以x 0为极限并且n 超过某值时总有x n ≠x 0,于是∃N >0,对∀n , m >N ,有x n , x m ∈0(;)o U x δ,从而有|f (x n )-f (x m )|<ε.这就是说,任给ε>0,总是∃N >0,对∀n , m >N ,|f (x n )-f (x m )|<ε. 由数列极限的柯西准则知数列{f (x n )}的极限存在,记为A .注意到,满足“以x 0为极限且n 超过某值时总有x n ≠x 0”的数列{x n }不是唯一的. 假设另一个数列{y n }也满足同样条件,也就是“以x 0为极限且n 超过某值时总有y n ≠x 0”,根据上面的分析,我们有数列{f (y n )}的极限存在,记作B . 我们再构造一个新的数列{z n }:x 1, y 1, x 2, y 2, x 3, y 3……容易知道,这个数列也满足“以x 0为极限且n 超过某值时总有z n ≠x 0”,根据上面的分析,我们有数列{f (z n )}的极限存在,从而它的两个子列{f (x n )}与{f (y n )}的极限相等.这样我们就证明了,对于任意的以x 0为极限且n 超过某值时总有x n ≠x 0的数列{x n },有lim ()n n f x →∞存在且相等. 根据归结原则,我们有0lim ()x x f x →存在. (2)0lim ()x x f x +→存在 “对∀ε>0,总是∃δ>0,对∀x 1, x 2∈0(;)o U x δ+,有|f (x 1)-f (x 2)|<ε”. 证明 必要性. 若0lim ()x x f x +→存在,设0lim ()x x f x A +→=. 那么,对∀ε>0,总是∃δ>0,对∀x ∈0(;)o U x δ+,有|f (x )-A |<ε/2. 从而对∀x 1, x 2∈0(;)o U x δ+,有|f (x 1)-A |<ε/2,|f (x 2)-A |<ε/2,于是|f (x 1)-f (x 2)|≤ |f (x 1)-A |+|f (x 2)-A |<ε.充分性. 设数列{x n }满足“以x 0为极限且n 超过某值时总有x n >x 0”. 任给ε>0.由假设知∃δ>0,对∀x 1, x 2∈0(;)o U x δ+,有|f (x 1)-f (x 2)|<ε. 对于δ>0,由于{x n }以x 0为极限并且n 超过某值时总有x n >x 0,于是∃N >0,对∀n , m >N ,有x n , x m ∈0(;)o U x δ+,从而有|f (x n )-f (x m )|<ε.这就是说,任给ε>0,总是∃N >0,对∀n , m >N ,|f (x n )-f (x m )|<ε. 由数列极限的柯西准则知数列{f (x n )}的极限存在,记为A .注意到,满足“以x 0为极限且n 超过某值时总有x n >x 0”的数列{x n }不是唯一的. 假设另一个数列{y n }也满足同样条件,也就是“以x 0为极限且n 超过某值时总有y n >x 0”,根据上面的分析,我们有数列{f (y n )}的极限存在,记作B . 我们再构造一个新的数列{z n }:x 1, y 1, x 2, y 2, x 3, y 3……容易知道,这个数列也满足“以x 0为极限且n 超过某值时总有z n >x 0”,根据上面的分析,我们有数列{f (z n )}的极限存在,从而它的两个子列{f (x n )}与{f (y n )}的极限相等.这样我们就证明了,对于任意的以x 0为极限且n 超过某值时总有x n >x 0的数列{x n },有lim ()n n f x →∞存在且相等. 根据归结原则,我们有0lim ()x x f x +→存在. (3)0lim ()x x f x -→存在 “对∀ε>0,总是∃δ>0,对∀x 1, x 2∈0(;)o U x δ-,有|f (x 1)-f (x 2)|<ε”. 证明 必要性. 若0lim ()x x f x -→存在,设0lim ()x x f x A -→=. 那么,对∀ε>0,总是∃δ>0,对∀x ∈0(;)o U x δ-,有|f (x )-A |<ε/2. 从而对∀x 1, x 2∈0(;)o U x δ-,有|f (x 1)-A |<ε/2,|f (x 2)-A |<ε/2,于是|f (x 1)-f (x 2)|≤ |f (x 1)-A |+|f (x 2)-A |<ε.充分性. 设数列{x n }满足“以x 0为极限且n 超过某值时总有x n <x 0”. 任给ε>0.由假设知∃δ>0,对∀x 1, x 2∈0(;)o U x δ-,有|f (x 1)-f (x 2)|<ε. 对于δ>0,由于{x n }以x 0为极限并且n 超过某值时总有x n <x 0,于是∃N >0,对∀n , m >N ,有x n , x m ∈0(;)o U x δ-,从而有|f (x n )-f (x m )|<ε.这就是说,任给ε>0,总是∃N >0,对∀n , m >N ,|f (x n )-f (x m )|<ε. 由数列极限的柯西准则知数列{f (x n )}的极限存在,记为A .注意到,满足“以x 0为极限且n 超过某值时总有x n <x 0”的数列{x n }不是唯一的. 假设另一个数列{y n }也满足同样条件,也就是“以x 0为极限且n 超过某值时总有y n <x 0”,根据上面的分析,我们有数列{f (y n )}的极限存在,记作B . 我们再构造一个新的数列{z n }:x 1, y 1, x 2, y 2, x 3, y 3……容易知道,这个数列也满足“以x 0为极限且n 超过某值时总有z n <x 0”,根据上面的分析,我们有数列{f (z n )}的极限存在,从而它的两个子列{f (x n )}与{f (y n )}的极限相等.这样我们就证明了,对于任意的以x 0为极限且n 超过某值时总有x n <x 0的数列{x n },有lim ()n n f x →∞存在且相等. 根据归结原则,我们有0lim ()x x f x -→存在. (4)lim ()x f x →∞存在 “对∀ε>0,总是∃M >0,对∀x 1, x 2∈(;)U M ∞,有|f (x 1)-f (x 2)|<ε”. 证明 必要性. 若lim ()x f x →∞存在,设lim ()x f x A →∞=. 那么,对∀ε>0,总是∃M >0,对∀x ∈(;)U M ∞,有|f (x )-A |<ε/2. 从而对∀x 1, x 2∈(;)U M ∞,有|f (x 1)-A |<ε/2,|f (x 2)-A |<ε/2,于是|f (x 1)-f (x 2)|≤ |f (x 1)-A |+|f (x 2)-A |<ε.充分性. 设数列{x n }满足“以∞为极限”. 任给ε>0. 由假设知∃M >0,对∀x 1, x 2∈(;)U M ∞,有|f (x 1)-f (x 2)|<ε. 对于M >0,由于{x n }以∞为极限,于是∃N >0,对∀n , m >N ,有x n , x m ∈(;)U M ∞,从而有|f (x n )-f (x m )|<ε.这就是说,任给ε>0,总是∃N >0,对∀n , m >N ,|f (x n )-f (x m )|<ε. 由数列极限的柯西准则知数列{f (x n )}的极限存在,记为A .注意到,满足“以∞为极限”的数列{x n }不是唯一的. 假设另一个数列{y n }也满足同样条件,也就是“以∞为极限”,根据上面的分析,我们有数列{f (y n )}的极限存在,记作B . 我们再构造一个新的数列{z n }:x 1, y 1, x 2, y 2, x 3, y 3……容易知道,这个数列也满足“以∞为极限”,根据上面的分析,我们有数列{f (z n )}的极限存在,从而它的两个子列{f (x n )}与{f (y n )}的极限相等.这样我们就证明了,对于任意的以∞为极限的数列{x n },有lim ()n n f x →∞存在且相等. 根据归结原则,我们有lim ()x f x →∞存在. (5)lim ()x f x →+∞存在 “对∀ε>0,总是∃M >0,对∀x 1, x 2∈(;)U M +∞,有|f (x 1)-f (x 2)|<ε”. 证明 必要性. 若lim ()x f x →+∞存在,设lim ()x f x A →+∞=. 那么,对∀ε>0,总是∃M >0,对∀x ∈(;)U M +∞,有|f (x )-A |<ε/2. 从而对∀x 1, x 2∈(;)U M +∞,有|f (x 1)-A |<ε/2,|f (x 2)-A |<ε/2,于是|f (x 1)-f (x 2)|≤ |f (x 1)-A |+|f (x 2)-A |<ε.充分性. 设数列{x n }满足“以+∞为极限”. 任给ε>0. 由假设知∃M >0,对∀x 1, x 2∈(;)U M +∞,有|f (x 1)-f (x 2)|<ε. 对于M >0,由于{x n }以+∞为极限,于是∃N >0,对∀n , m >N ,有x n , x m ∈(;)U M +∞,从而有|f (x n )-f (x m )|<ε.这就是说,任给ε>0,总是∃N >0,对∀n , m >N ,|f (x n )-f (x m )|<ε. 由数列极限的柯西准则知数列{f (x n )}的极限存在,记为A .注意到,满足“以+∞为极限”的数列{x n }不是唯一的. 假设另一个数列{y n }也满足同样条件,也就是“以+∞为极限”,根据上面的分析,我们有数列{f (y n )}的极限存在,记作B . 我们再构造一个新的数列{z n }:x 1, y 1, x 2, y 2, x 3, y 3……容易知道,这个数列也满足“以+∞为极限”,根据上面的分析,我们有数列{f (z n )}的极限存在,从而它的两个子列{f (x n )}与{f (y n )}的极限相等.这样我们就证明了,对于任意的以+∞为极限的数列{x n },有l i m ()n n f x →∞存在且相等. 根据归结原则,我们有lim ()x f x →+∞存在. (6)lim ()x f x →-∞存在 “对∀ε>0,总是∃M >0,对∀x 1, x 2∈(;)U M -∞,有|f (x 1)-f (x 2)|<ε”. 证明 必要性. 若lim ()x f x →-∞存在,设lim ()x f x A →-∞=. 那么,对∀ε>0,总是∃M >0,对∀x ∈(;)U M -∞,有|f (x )-A |<ε/2. 从而对∀x 1, x 2∈(;)U M -∞,有|f (x 1)-A |<ε/2,|f (x 2)-A |<ε/2,于是|f (x 1)-f (x 2)|≤ |f (x 1)-A |+|f (x 2)-A |<ε.充分性. 设数列{x n }满足“以-∞为极限”. 任给ε>0. 由假设知∃M >0,对∀x 1, x 2∈(;)U M -∞,有|f (x 1)-f (x 2)|<ε. 对于M >0,由于{x n }以-∞为极限,于是∃N >0,对∀n , m >N ,有x n , x m ∈(;)U M -∞,从而有|f (x n )-f (x m )|<ε.这就是说,任给ε>0,总是∃N >0,对∀n , m >N ,|f (x n )-f (x m )|<ε. 由数列极限的柯西准则知数列{f (x n )}的极限存在,记为A .注意到,满足“以-∞为极限”的数列{x n }不是唯一的. 假设另一个数列{y n }也满足同样条件,也就是“以-∞为极限”,根据上面的分析,我们有数列{f (y n )}的极限存在,记作B . 我们再构造一个新的数列{z n }:x 1, y 1, x 2, y 2, x 3, y 3……容易知道,这个数列也满足“以-∞为极限”,根据上面的分析,我们有数列{f (z n )}的极限存在,从而它的两个子列{f (x n )}与{f (y n )}的极限相等.这样我们就证明了,对于任意的以-∞为极限的数列{x n },有l i m ()n n f x →∞存在且相等. 根据归结原则,我们有lim ()x f x →-∞存在. 可以看到,函数极限的6条柯西准则的证明是完全类似的,这也从某种程度上体现了函数6种极限的某种内在一致性.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
而
=1=ε0.
根据柯西准则,极限
不存在.
1、(1)叙述极限 (2)根据柯西准则叙述
f(x)的柯西准则; f(x)不存在的充要条件,
并(-∞)内有定义.
f(x)在的充要条件是:任给ε>0,存在正数M,
使得对任何x’<-M, x”<-M,都有|f(x’)- f(x”)|<ε.
请自行叙述其它类型函数极限的柯西准则以及极限 不存在的充要条件.
1、(1)叙述极限 (2)根据柯西准则叙述
f(x)的柯西准则; f(x)不存在的充要条件,
并应用它证明 sinx不存在.
取ε0= 1/2,对任给正数M,有自然数n≥M,
取x1= -nπ,x2= -nπ-π/2,有x1<-n≤-M, x2<-n≤-M,
D(x)不存在.
1、(1)叙述极限 (2)根据柯西准则叙述
f(x)的柯西准则; f(x)不存在的充要条件,
并应用它证明 sinx不存在.
(2)设f为定义在U(-∞,a]上的函数,若存在正数ε0,
对任给正数M>a,总存在x1,x2,尽管x1<-M, x2<-M,
而|f(x1)- f(x2)|≥ε0,则称
f(x)不存在.
(柯西准则):设f在U⁰(x0;δ’)内有定义。 f(x)存在的充要条件是:任给ε>0,存在正数δ(<δ’),
使得对任何x’, x”∈U⁰(x0;δ)有|f(x’)- f(x”)|<ε. [充分性]若任给ε>0,存在正数δ(<δ’),使得 对任何x’, x”∈U⁰(x0;δ)有|f(x’)- f(x”)|<ε.则对任何数列 {xn}⊂U⁰(x0;δ’)且 xn=x0,对δ,有N>0,使 当n,m>N时,有xn,xm∈U⁰(x0;δ),且|f(xn)- f(xm)|<ε. 根据数列的柯西收敛准则,可设数列{f(xn)}收敛于A, 由{xn}的任意性及归结原则,知 f(x)=A,得证!
而|sinx1-sinx2|=1>ε0,∴
sinx不存在.
2、设D(x)为狄利克雷函数,x0∈R. 证明 D(x)不存在. 证:已知狄利克雷函数:D(x)=
取ε0=1/2,对任何δ>0,在U⁰(x0,δ)中必有 有理数x’和无理数x”,使D(x’)=1,D(x”)=0,
则|D(x’)-D(x”)|=1>ε0,∴
注: f(x)不存在的充要条件:
存在ε0>0,对任何δ>0(无论δ多么小), 总可以找到x’, x”∈U⁰(x0;δ),使得|f(x’)- f(x”)|≥ε0.
利用柯西准则,证明极限
不存在.
证:取ε0=1,对任何δ>0,设n>1/δ,
令x’n= , x”n=
,则有x’n, x”n∈U⁰(0;δ),
老黄学高数
第101讲 函数极限
的柯西准则
(柯西准则):设f在U⁰(x0;δ’)内有定义。 f(x)存在的充要条件是:任给ε>0,存在正数δ(≤δ’),
使得对任何x’, x”∈U⁰(x0;δ)有|f(x’)- f(x”)|<ε. 证: [必要性]若 f(x) =A,∀ε>0,有正数δ(≤δ’),
使对任何x∈U⁰(x0;δ),有|f(x)-A|<ε/2 .于是对任何 x’, x”∈U⁰(x0;δ)有|f(x’)-f(x”)|≤|f(x’)-A|+|f(x”)-A|<ε. 必要性得证!
