5非线性光学 四波混频
非线性光学复习总结

一.非线性基本概念线性极化率的基本概念:一、电场的复数表示法:E(r,t)=1/2E(r,ω)exp(-iωt)+c.c. (1)E(r,t)=Re{E(r,ω)exp(-iωt)} (2)E(r,t)=1/2E(r,ω)exp(-iωt) (3)以上三者物理含义是一致的,其严格数学表示是(1)式。
(注意是数学表达式,所以这种表示法主要还是为了运算的方便,具体那些系数、共轭神马的物理意义是其次的,不用太纠结。
)称为复振幅,代表频率为的简谐振动,的频率仅是数学描述,物理上不存在。
1/2是归一化系数。
对于线性算符,可采用(3)式进行简化计算,然后加c.c.或Re{ }即可对非线性算符,必须采用(1)式的数学形式计算二、因果性原理:某时刻的电场只能引起在此时刻以后介质的响应,而对此时刻以前的介质响应没有贡献。
也可以这样说,当光在介质中传播时,t时刻介质所感应的极化强度P(t)不仅与t时刻的光电场有关,也与此前的光电场有关。
(先有电场E,后有极化P)与此相关的是时间不变性原理:在某时刻介质对外电场的响应只与此前所加电场的时间差有关,而与所取的时间原点无关。
于是,极化强度表达的思路即是先找到时刻t之前附近的一段微小时间t-τ=dτ内电场的作用,再对从电场产生开始以来的时间进行积分,求得总的效应。
τ时刻电场,影响其后的极化:t时刻的极化,来自其前面时刻的电场贡献:或t时刻的极化,来自前面时刻的电场贡献:三、线性极化率:其中四、介电常数(各向同性介质):五、色散:由于因果性原理,导致必然是频率的函数,即介质的折射率和损耗都随光波长变化,称为色散现象。
正常色散:折射率随波长增加而减小。
六、KK关系:以上两式为著名的KK色散关系,由K-K关系课件,只要知道极化率的实部和虚部中任何一个与频率的函数关系(光谱特性)就可通过此关系求出另外一个。
线性极化率张量同样满足真实性条件:,所以,这两式是线性极化率的KK关系。
七、极化率的一维谐振子经典模型:没希望考了。
光子学四波混频技术的研究与应用

光子学四波混频技术的研究与应用光子学四波混频技术简介光子学四波混频技术(Phenomenon of Four Wave Mixing,FWM)是一种非线性光学过程,通过使用光纤、激光器、光源和光探测器等设备,可以实现三个或更多光信号的混频,最终产生新的频率与调制信号。
FWM技术产生的新信号,不仅具有与原信号不同的频率,还具有根据原信号的幅度和相位关系,而形成的非线性扰动产生的新频率与既有频率之间存在着特定的相互关系。
FWM技术的应用FWM技术在通讯、光电子学、量子信息、光谱学等领域都有广泛的应用。
其中,FWM技术在通信领域的应用,可以实现紧凑型、低成本且高速率的光通信系统。
此外,FWM还可在生物医学成像、量子量测和光声成像等领域应用。
例如,这项技术可以通过准确测量光子的数量,产生高分辨率的生物化学成像。
在光学传感领域,由于FWM技术可监测和测量温度、压力、流速、水平和其他物理量的变化,而被广泛应用。
此外,该技术还可以实现基于光子信号的微型传感器,用于监测环境的变化。
光子学四波混频技术的研究过去的几十年中,FWM技术得到了广泛的研究,并结合了不同的技术和原理来进一步规范化,在实现实时通讯、光传感、光量子计算等技术方面已经取得了很大的进展。
例如,研究人员已经成功开发出紧凑型的FWM光滤波器,可以提高光子信号的效率和可靠性。
这些成果和技术的开发,将在今后的光通讯和光电子学领域发挥重要作用。
在物理学和电子学领域,又有一些有趣的研究进展:例如,研究人员用于有效的减少光子信号的色散,或用于在量子技术等领域实现频谱管理。
未来展望随着科学技术的进步和创新,FWM技术将继续发展和应用。
未来,我们可以期望这项技术实现更高效、可靠和高分辨率的光子元件与光子传输,进一步推进通讯和传感技术的发展。
在量子技术和纳米技术中,FWM技术将逐渐得到广泛的应用。
这个技术的广泛应用将带来更快速、可靠、高安全性的通讯和其他应用,同时推动人类的科技、工业和文化的前进。
第四章三次谐波与四波混频

分类: 分类:
2、非参量过程---非参量过程---介质在与光场相互作用后的终态与初态不同了, 介质在与光场相互作用后的终态与初态不同了,发生 质间的能量转移。 了光场与介 质间的能量转移。
受激拉曼散射(SRS)、受激布里渊散射(SBS)。 受激拉曼散射(SRS)、受激布里渊散射(SBS)。 双光子吸收(TPA)。 双光子吸收(TPA)。 饱和吸收(SA)。 饱和吸收(SA)。
实现三次谐波的困难
(1)晶体中的激光损伤强度阈值较低,无法使用高强度的入射激光。 晶体中的激光损伤强度阈值较低,无法使用高强度的入射激光。 (2)晶体中的双折射特性难以实现三次谐波所要求的位相匹配。 晶体中的双折射特性难以实现三次谐波所要求的位相匹配。 所以,一般难以在晶体中直接实现三次谐波(THG), 所以,一般难以在晶体中直接实现三次谐波(THG),方解石直接实现 THG相位匹配的晶体 THG相位匹配的晶体。 相位匹配的晶体。 −6 目前实验结果: 4mm长方解石晶体中以 目前实验结果:在4mm长方解石晶体中以 3 × 10 的转换效率得到了 三次谐波输出。 三次谐波输出。 (3) 对紫外光吸收较强
三次谐波
实现三次谐波的介质 I. 晶体: 晶体:
χ (3) ~ 10− 20 − 10− 23 ( SI制) χ (3) ( SI ) = χ ( 2) ~ 10 −11 − 10−13 ( SI制)
4π ×10 −8 χ ( 3) (esu ) 9 4π χ ( 2) ( SI ) = ×10 − 4 χ ( 2 ) (esu ) 3
三阶非线性光学效应概述
主要特点: 及耦合波方程描述。 主要特点:1、基于 χ (3) 及耦合波方程描述。 2、无论介质有何种对称性,总存在一些非零的 无论介质有何种对称性, χ ( 3) 张量元,原则上三阶非线性光学效应可 张量元, 所有介质中观察到 中观察到。 在所有介质中观察到。 3、比二阶效应弱几个数量级( χ (3) << χ ( 2) ),更难 比二阶效应弱几个数量级( ), 于观察。 于观察。 4、三阶效应中参与相互作用的有四个光电场, 三阶效应中参与相互作用的有四个光电场, 现象更加丰富。 现象更加丰富。
四波混频
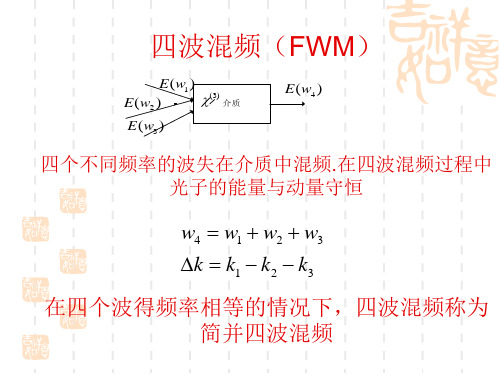
E ( w1 ) χ(3) E ( w2 )
E ( w3 )
E ( w4 )
四个不同频率的波失在介质中混频.在四波混频过程中 光子的能量与动量守恒
w4 = w1 + w2 + w3 ∆k = k1 − k2 − k3
在四个波得频率相等的情况下,四波混频称为 简并四波混频
虽然简并四波混件下,必须保证 。
改变信道间距
用适当不等间距的波长信道配置设计来实现 ,通常选择通 道频率,使产生的新频率分量大部分落在通道滤波器通带 之外,这种技术用于10个信道,每个信道速率为10G/s 以下 的系统可大大减小四波混频的影响 加大信道间距也可抑 制四波混频的效率,却是以牺牲系统带宽为代价的 实际上 , 采用部分等间距信道更为有意义,其核心在于使通道间隔 相对远的信道之间的四波混频所产生的频率分量落在信道 滤波器通带内,由于四波混频的效率随着波长间隔加大而 降低,引入的恶化并不严重,这样可使系统容纳更多的波长。
∆k = k4 − (k1 − k2 − k3 ) = 0
考虑一种特殊情况,如下图,存在两对波矢方向相反的光,输 出为-k‘,它们满足如下相位匹配条件 k ' + (−k ' ) = k + (−k ) 。
简并四波混频的相位匹配
四波混频效应
这种简并四波混频非线性过程与典型的全息照过程很 相似。可以将k‘当做物光,k当做参考光,两者在介质 中互相干涉,形成全息图,如果全息图被记录下来了, 在参考光k的照射下,沿物光k’相反的方向-k‘可见物得 虚像。若挡住物光k’,在另一参考光-k的照射下,会 产生-k‘方向的赝像,该赝像就是原物光的相位共轭光。 虽然全照息过程和四波混频过程都产生相位共轭光, 但两者根本不同之处:全息照相的记录和重现过程在 时间上式分段进行的,而四波混频的相位共轭光与原 入射光几乎是同时产生。
四波混频相互作用方式

四波混频相互作用方式
四波混频相互作用方式是指在物理中存在着四个波的相互作用方式。
这种相互作用方式主要有以下四种:
1. 双光子吸收(Two-photon absorption, TPA):两个光子被共同吸收并相互作用。
这种过程可以用来产生高能量的激发态或者光学非线性响应。
2. 光折变(Optical parametric amplification, OPA):在非线性材料中,光子可以通过与压缩光波或者拉伸光波相互作用,使得一个光子被分裂成两个较低能量的光子。
3. 光学双光子激发(Two-photon excitation, TPE):两个光子被共同吸收,并且可以用来激发分子的高能激发态。
4. 光学参量振荡(Optical parametric oscillation, OPO):当在非线性光学晶体中注入一个光泵浦波时,会产生一个激光输出波和一个较低频率的副波。
这种过程可以用来产生较宽的频率输出范围。
关于四波混频的理论探讨

关于四波混频的理论探讨
黄湘宁
【期刊名称】《青海大学学报(自然科学版)》
【年(卷),期】2008(026)006
【摘要】文中以三阶非线性光学为基础,从求解耦合波方程出发,讨论了几种在克尔介质中四波混频相位共轭过程,给出了相位共轭反射率和透射率,通过做出解的图像,分析了介质反向相位共轭波的光强分布,并确定为工作在最理想情况下非线性耦合系数与介质长度的乘积所应满足的要求.
【总页数】5页(P70-74)
【作者】黄湘宁
【作者单位】青海师范大学实验教学管理中心,青海,西宁,810008
【正文语种】中文
【中图分类】O437
【相关文献】
1.基于氧化镁晶体中级联四波混频过程的紫外飞秒光脉冲产生 [J], 陈忠;华林强;张津;龚成;柳晓军
2.基于简并四波混频的双信道双频段增益谱 [J], 王丹;郭瑞翔;戴玉鹏;周海涛
3.超长距10 G光传输系统带内四波混频现象研究 [J], 张菡;熊铖;李由
4.基于级联四波混频过程的量子导引 [J], 翟淑琴;康晓兰;刘奎
5.几种信道间隔方案对四波混频效应的抑制研究 [J], 申静;邵立蓉
因版权原因,仅展示原文概要,查看原文内容请购买。
四波混频

非线性光学中,四波混频是介质中四个光波相互作用所引起的非线性光学效应,它起因于介质的三阶非线性极化。 四波混频相互作用的方式一般可分为以下三类:
一,三个泵浦场的作用情况;二,输出光与一个光具有相同模式的情况;三,后向参量放大和振荡
由于四波混频在所有介质中都能很容易的观察到,而且变换形式很多,所以它已经得到了很多有意义的应用。例如,利用四波混频可以把可调谐相干光源的频率范围扩展到红外和紫外;在简笔的情况下,四波混频可用于自适应光学的波前再现;在材料应用中共振四波混频技术又非常有效的光谱和分析工具等待
发生四波混频的原因是入射光中的某一个波长上的变化,从而产生了新的波长的光波。
在DWDM系统中,当信道间距与光纤色散足够小且满足相位匹配时,四波混频将成为非线性串扰的主要因素。当信道间隔达到10GHZ 以下时,FWM 对系统的影响将最严重。
通信中,四波混频(Four-Wave Mixing,FWM) 亦称四声子混合,是光纤介质三阶极化实部作用产生的一种光波间耦合效应,是因不同波长的两三个光波相互作用而导致在其它波长上产生所谓混频产物,或边带的新光波,这种互作用可能发生于多信道系统的信号之间,可以产生三倍频、和频、差频等多种参量效应。
目前的DWDM系统的信道间隔一般在100GHZ ,零色散导致四波混频成为主要原因,所以,采用G.653 光纤传输DWDM系统时,容易产生四波混频效应,而采用G.652 或G.655 光纤时,不易产生四波混频效应。但G.652 光纤在1550nm 窗口存口存在一定的色散,传输10G信号时,应加色散补偿,G.655 光纤在1550nm 窗口的色散很小,适合10G DWDM 系统的传输。
四波混频对DWDM系统的影响主要表现在:(1)产生新的波长,使原有信号的光能量受到损失,影响系统的信噪比等性能;(2)如果产生的新波长与原有某波长相同或交叠,从而产生严重的串扰。四波混频的产生要求要求各信号光的相位匹配,当各信号光在光纤的零色散附近传输时,材料色散对相位失配的影响很小,因而较容易满足相位匹配条件,容易产生四波混频效应。
光通信中非线性效应对传输质量的影响分析

光通信中非线性效应对传输质量的影响分析光通信作为当代高速通信领域的重要技术之一,在实现高速、高容量的数据传输方面具有广阔的应用前景。
然而,光通信系统中的非线性效应却对传输质量产生了一定的影响。
本文将对光通信中的非线性效应进行分析,探讨其对传输质量的影响,并进一步讨论可能的解决方案。
在光通信系统中,非线性效应是指光信号在光纤中传输过程中由于介质的非线性光学特性而产生的影响。
主要的非线性效应包括自相位调制(SPM)、互相位调制(XPM)、四波混频(FWM)等。
这些非线性效应的产生主要是由于光强的非线性响应和相位调制引起的。
首先,非线性光学效应会引起光信号的失真。
在传输过程中,光信号会逐渐受到非线性效应的影响,导致光信号的波形发生畸变、脉冲展宽以及时域和频域的波形畸变。
这些失真现象会使得光信号的调制深度降低,误码率增加,从而影响传输质量。
其次,非线性效应还会引起相位噪声。
在光信号传输的过程中,光信号的相位会受到非线性因素的影响,导致相位噪声的增加。
相位噪声的存在会使得传输系统的时钟重置困难,影响数据的正确解调,降低传输质量。
此外,非线性光学效应还会引起其他的信号衰减和失真现象。
例如,光信号在光纤中的传输过程中会产生自发参量泵浦(ASE)噪声,使得信噪比下降;光信号的波形畸变也可能导致光信号的幅度和频谱的失真,进而影响传输质量。
针对光通信系统中非线性效应对传输质量产生的影响,我们可以采取一系列的解决方案来改善传输质量。
首先,我们可以采用优化调制格式的方式来减少非线性效应的影响。
例如,利用相位预编码技术(例如码间相位调制)可以降低非线性效应对传输质量的影响。
通过适当调制光信号的相位,可以减小非线性效应的产生。
其次,我们可以在光通信系统中引入非线性光纤来改善传输质量。
非线性光纤具有更大的非线性系数,可以提高光信号的光强,减小非线性效应的影响。
此外,利用非线性光纤的特性,我们还可以在传输过程中实现波长转换,从而减少非线性效应的累积。
四波混频
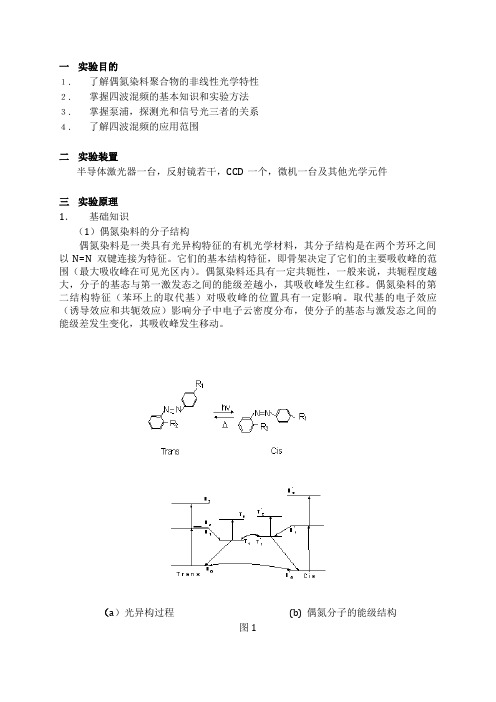
一实验目的1.了解偶氮染料聚合物的非线性光学特性2.掌握四波混频的基本知识和实验方法3.掌握泵浦,探测光和信号光三者的关系4.了解四波混频的应用范围二实验装置半导体激光器一台,反射镜若干,CCD一个,微机一台及其他光学元件三实验原理1.基础知识(1)偶氮染料的分子结构偶氮染料是一类具有光异构特征的有机光学材料,其分子结构是在两个芳环之间以N=N双键连接为特征。
它们的基本结构特征,即骨架决定了它们的主要吸收峰的范围(最大吸收峰在可见光区内)。
偶氮染料还具有一定共轭性,一般来说,共轭程度越大,分子的基态与第一激发态之间的能级差越小,其吸收峰发生红移。
偶氮染料的第二结构特征(苯环上的取代基)对吸收峰的位置具有一定影响。
取代基的电子效应(诱导效应和共轭效应)影响分子中电子云密度分布,使分子的基态与激发态之间的能级差发生变化,其吸收峰发生移动。
(a)光异构过程(b) 偶氮分子的能级结构图1(2)偶氮染料的光异构特性偶氮染料是一种偏振敏感的有机染料,它具有反式(trans)和顺式(cis)两种分子结构,如图1(a)所示(其中R1和R2表示不同的取代基,本实验所用甲基橙的取代基R1为NaO3S , R2 为N(CH3)2 )。
它们的分子主轴均为氮氮双键。
两者对应能态的能量是反式结构能量低,结构稳定;顺式结构能量高,结构不稳定,所以一般情况下偶氮分子多以稳定的反式结构存在。
图 1 (b) 是偶氮分子的能级结构图,由图可见,当用激光激发时,反式偶氮分子的基态粒子So吸收一个光子后,跃迁到第一激发态的某一振动能级Sv上,并迅速驰豫到第一激发态的最低能级S1上。
处于S1能级上的粒子可以进一步吸收一个光子并跃迁到第二重激发态S2上,也可经过系间跃迁无辐射驰豫到三重激发态T1上,这种跃迁由S1与T1间能级差决定。
差距越小,跃迁越容易。
T1态的粒子可以吸收光子跃迁到T2态上,也可通过无辐射跃迁回到So态上。
同时当激光强度达到一定值后,S2、T2等能级上的粒子还可以进一步吸收光子跃迁到更高一级激发态上去。
非线性光学课件-第三章

sech
x
1 cosh x
ex
2 ex
带h称为双曲函数
双曲正切,双曲正割
A1 ( z )
A1
(0)
s
ec
h
z Ls
A2 (z)
A1
(0)
tanh
z Ls
其中
Ls
cn deff A1(0)
Ls 称为相位匹配下二次谐 波产生的有效倍频长度
当z=Ls 时, tanh(1)= 0.762 sech(1)= 0.648
第三章 光学倍频、混频与参量转换
典型的非线性现象
1、光学倍频
二阶非线性 光学现象
介质不具有对称中 心的各向异性介质
2、光学和频、差频(三波混频)
3、光学参量振荡和放大 …
1、三次谐波
三阶非线性 光学现象
对介质对称无要求
2、四波混频 3、双光子吸收 4、光学自聚焦 5、受激散射 …
这些效应是产生光学变频的较成熟的手段之一,它为人们提供了一 种研究物态结构、分子跃迁驰豫和凝聚态物理构成的新的有效手段。
2
1
1,2为基波和谐波真空中的波长
n2 (2 ) n1(1)
只有满足上述条件,倍频最佳,但由于通 常n2(2)≠n1(1),所以只有采取特殊方法才 能做到。
3.1.2 光学二次谐波的基本理论
对于沿z方向传播的三波混频的耦合波方程
A3 z
i3D 2cn(3 )
(2) (3;1,2 ) :
A A ei(k3 k1k2 ) z
(注意是谐波之间同相位,不是谐波和基波同相位)
L
晶体
dz
z
O
在位置z处,在dz薄层介质内的振幅
光纤通信中的非线性光学效应研究与应用

光纤通信中的非线性光学效应研究与应用随着互联网和数字通信技术的快速发展,光纤通信已成为现代通信领域的重要组成部分。
而要实现高速、高带宽的光纤通信,非线性光学效应的研究与应用显得尤为重要。
本文将探讨光纤通信中的非线性光学效应的研究现状、原理及其应用。
一、非线性光学效应的概念和原理在光纤中,当光的强度达到一定程度时,光的电磁波属性将会发生明显改变,这种变化被称为非线性光学效应。
非线性光学效应中常见的有自相位调制(SPM)、自发强度调制(SIM)、四波混频(FWM)等。
非线性光学效应的原理是基于介质对光的响应与其光强的非线性关系。
光纤中的非线性效应是由非线性极化率所引起的,这种极化率与光强相关。
当光强增强时,非线性极化率的变化将会导致光的传输特性发生改变,进而影响光纤通信系统性能。
二、非线性光学效应的研究现状在过去的几十年里,非线性光学效应在光纤通信领域得到了广泛的研究与应用。
研究者通过对非线性光学效应的深入研究,不仅揭示了其物理机制,还提出了许多有效的光纤通信系统性能优化方法。
首先,研究者通过理论分析和实验验证,深入研究了非线性光学效应对光纤通信系统的影响机制。
他们发现,在高速、长距离光纤通信系统中,非线性光学效应会对光信号的传输质量产生显著的影响,导致信号的失真和衰减。
其次,研究者通过改变光纤材料的结构和光信号的调制方式,提出了一系列有效的非线性光学效应控制方法。
例如,通过控制光信号的光强分布,可以减小非线性光学效应的影响,提高传输系统的性能。
此外,研究者还通过引入非线性光学效应的特殊调制技术,提高了光纤通信系统的传输速率和容量。
光纤通信系统中的非线性光学效应可以用于实现光的调制、调制解调器和光时钟等功能,进一步提高了系统的性能和功能。
三、非线性光学效应的应用非线性光学效应在光纤通信中有着广泛的应用前景。
以下将介绍几个非线性光学效应在光纤通信系统中的具体应用。
1. 光纤光学参量放大器光纤光学参量放大器(OPA)是利用非线性光学效应的能力而设计的一种放大器。
四波混频

三次谐波与四波混频(2013年12月31)摘要:讨论了各向同性介质中的三阶非线性过程,以及四波混频和它的特殊情况。
关键词:三阶非线性过程,四波混频。
一、 各向同性介质中的三阶非线性过程只有不具有中心对称性的介质或者各向异性介质才具有二阶非线性,但是所有介质都存在着三阶非线性。
一般(3)χ比(2)χ小得多,故三阶效应要比二阶效应弱得多。
在三阶非线性现象中,也存在着光与介质不发生能量交换,而参与作用的光波之间发生能量交换的非线性效应,这被称为波动非线性效应。
设输入光场()E t 是由沿z 方向传播的三个不同频率的单色光场组成312123().i t i t i t E t E e E e E e c c ωωω---=+++ (1.1) 相应的各向同性介质中的三阶非线性极化强度为(3)(3)30()()P t E tεχ= (1.2) 将式(1.1)代入式(1.2),可见(3)()P t 是具有不同频率的(包括零频)的各项极化强度之和,可以写成(3)()()n i t n nP t P e ωω-=∑ (1.3)式中n 取±,负号表示复数共轭量,包括极化强度的各种频率成分:11211231231200,0,3,,,2ωωωωωωωωωωωω+++-+等。
这些频率项分别表示三次谐波、四波混频、相位共轭、光克尔效应、自聚焦、饱和吸收、双光子吸收、受激散射等三阶非线性光学效应。
三倍频效应是频率为ω的光场入射介质产生频率为3ω光场的过程,其极化强度为(3)(3)30(3)(3;,,)()P E ωεχωωωωω= (1.4) 这里D=1. 很少有晶体能实现三倍频的相位匹配,而且输入激光的强度往往受到光损伤的限制。
气体激光损伤极限强度比固体要高几个数量级,研究表明碱金属蒸汽在可见光区极化率(3)χ有很强的共振增强,因此具有较强的三倍频效应。
以功率比表示的三倍频的转换效率为222(3)223243039()sin ()2P P L kL c P c n n S ωωωωωωηχε∆== (1.5) 定义相干长度c c /,L=L kL /2/2c L k ππ=∆∆=当时,,三倍频效率很快下降;当0k ∆=,相位匹配,有最大的转换效率。
一、非线性光学及其现象

• 典型的有机二阶非线性光学材料包括: • (1)尿素及其衍生物; • (2)硝基苯衍生物,如MAP(2,4一二硝基苯丙氨 酸甲酯)、MNA(2一甲基4硝基苯胺)、CNA(2一氯 4.硝基苯胺)等; • (3)硝基吡啶氧类,如POM(3一甲基4.硝基吡啶 氧); • (4)二苯乙烯类,如MMONS(3一甲基4.甲氧基4 一硝基二苯乙烯); • (5)查耳酮类,如BMC(4一溴4 一甲氧基查耳酮); • (6)苯甲醛类,如MHBA(3一甲氧基4.羟基苯甲 醛); • (7)有机盐类。
产生光学克尔效应的非线性介质可以是液体、固体、气体或原子蒸气。产生的 物理机制、效应的强弱都可以很不相同。有时也可以同时来源于几种不同机制。 常见的物理机制有:①在光的作用下能级粒子数分布发生了改变。这适用于有 分立能级的原子、分子或固体体系。②在光的作用下电子云分布发生了变化。 这适用于原子或固体。③光场感生的电致伸缩效应。这适用于液体、固体和高 压气体。④光场引起分子取向发生变化。适用于由各向异性分子组成的有机液 体和溶液、分子晶体和液晶等。⑤光场引起分子排列发生变化。适用于例如液 态的惰性元素等。 通过对于来自光学克尔效应的双折射的测量,能够有效地测定各种介质的三阶 非线性极化率。由于不同介质产生的光学克尔效应有着不同的机制,通过光学 克尔效应的研究还可以进行各种不同物质的物性研究,测量不同的微观参量, 例如分子取向的弛豫时间等。
(1) ( 3) 0 ( ) 3 ( ,0,0) E0 E0 E e it c.c.
(5.1 - 1)
•
这表示由于三阶非线性极化的作 用, 恒定电场的存在使得介质的介电张量 ( 3) (5.1 - 2) 3 ,0)E0 E0 0 ( 元素 改变了 ,,0 且
四波 混频

A4 z
43
A4 t
i 2
43
2 A4 t 2
1 2
4
A4
i A4 2 2 A3 2 2P0 A4 iP0 A3*ei
3.相位匹配技术
物理机制:
✓ 相位匹配时,参量增益对应FWM的峰值,可写为
kM kW kNL 0
材料色散 波导色散 非线性效应 对于简并FWM,上述贡献分别为
✓ FWM的微观解释:在量子力学术语中,一个或几个光波的光子被湮灭, 同时产生了几个不同频率的新光子,且在此参量作用过程中,净能量 和动量是守恒的,这样的过程就称为四波混频过程。
2.四波混频的标量理论
✓ 在准连续条件下运转,则可忽略场分量的时间依赖关系:
E j (r) Fj (x, y) Aj (z),
人理解。 • (3)别人眼中的自己,才是真正存在的自己。学会以别人的
角度看问题,并据此改进自己在他们眼中的形象。 • (4)只能修正自己,不能修正别人。想成功地与人相处,让
别人尊重自己的想法,惟有先改变自己。 • (5)真诚坦白的人,才是值得信任的人。 • (6)真情流露的人,才能得到真情回报。
• 2.表达同理心七个步骤 • (1)问开放式的问句 • (2)放慢脚步 • (3)避免太快下判断 • (4)注意你的身体反应 • (5)了解过去 • (6)让故事说出来 • (7)设定界限
• 14.交谈时,我会注视对方的眼睛。
ABC
• 15.我很注意人们无意间身体姿态所流露的心情。 A B C
• 16.别人跟我讲话时,我会东张西望。
ABC
• 17.别人说我表情太严肃了。
ABC
• 18.别人不听我的劝告,我并不生气。
ABC
• 对于 1,2,4,5,7,12,13,14,15,18 题(共10 题),如果选A 则得1 分,选B 得2 分,选C 得3 分。对于3, 6,8,9,10,11,16,17 题(共8 题),如果选A 则得3
基于非线性光纤四波混频的波长转换

基于非线性光纤四波混频的波长转换作者:许建慧来源:《科技视界》 2013年第22期许建慧(广东宜通世纪科技股份有限公司,广东广州 510630)【摘要】波分复用的发展为通信网信息量的爆炸性增长提供了带宽支持,是未来大容量、高速率的光子网络的基础。
链路上的高速率对通信节点的吞吐和交换能力提出了要求,目前使用的O-E-O波长转换受电子瓶颈的约束,将无法应付未来100Gbit/s以上的网络速率,而全光波长转换器可以胜任。
基于高非线性光纤FWM的波长转换,结构简单且灵活,并由于非线性固有特征具备超高速、全透明转换能力,未来有着广阔的应用前景。
【关键词】FWM;波长转换;极化控制;相位匹配;零色散波长;双折射0 介绍WDM技术的进步促进了光纤物理链路上可用带宽快速发展,目前WDM的单通路传输速率商用化产品达到了40Gbit/s。
高容量的传输加大了交换负荷。
对于100Gbit/s的网络速率,电子交换显得很吃力,而光分组交换具有纳秒级甚至更高的交换速率,能够应付未来更高速率网络。
光分组交换是不含O-E-O的全光交换,交换的颗粒度达到数据包级,同时支持波长交换。
OXC是光波长交换中一个关键成员,其中的全光波长转换器能够解决OXC中的阻塞,即光域中的波长竞争,使波长可进行link-by-link的分配,增加了有限波长资源的利用率。
非线性光学领域的研究在最近十几年发展迅猛。
研究显示通过部署高比特率的多波长系统及光放大器产生的XPM,SPM及FWM等非线性效应[1]可用于全光波长转换,并都通过了实验证实,例如在SOA中[2]、在光纤中[3-4]和在晶体中[5]等等。
其中,基于光纤FWM的波长转换具飞秒响应、低插入损耗、非退化信号消光比及低噪声等固有特性,有希望实现Tbit/s的高速性能。
德国的Huettl 和丹麦的Galili已进行了联合实验:在1100m长的高非线性光纤中利用FWM实现了320Gbit/s差分四相移键控(QDPSK)信号的波长转换[6]。
非线性光学四波混频

(5.3 - 17)
2
1
在求解这些方程时, 为了克服有多个坐标量的困难, 我们引入共同坐标z。 对于平面波而言, 有
而由图5.3 - 6, 又有
4
3
(5.3 - 18)
于是, (5.3 - 17)式可以改写为
(5.3 - 19)
在一般情况下, DFWM相位共轭特性可以通过对(5.3 - 35)式进行数值计算给出。 图5.3 - 7~图5.3 - 10分别为对称激励情况下计算得到的特性曲线, 由这些曲线可以得到DFWM的如下特性:
02
5.3.2 简并四波混频(DFWN)理论
简并四波混频作用简并四波混频是指参与作用的四个光波的频率相等。 这时, 支配这个过程的三阶非线性极化强度一般有三个波矢不同的分量:
(5.3 - 1)
式中
简并四波混频的输出可以利用耦合波方程求解。其四波相互作用也可以理解为如下的全息过程:三个入射光波中的两个相互干涉,形成一个稳定光栅,第三个光波被光栅衍射,得到输出波。
图5.3 - 3 简并四波混频结构示意图
01
我们讨论的DFWM结构如图5.3 - 3所示, 非线性介质是透明、 无色散的类克尔介质, 三阶非线性极化率是χ(3) 。 在介质中相互作用的四个平面光波电场为
02
(5.3 - 3)
03
其中, E1、 E2是彼此反向传播的泵浦光, E3、 E4是彼此反向传播的信号光和散射光。 一般情况下, 信号光和泵浦光的传播方向有一个夹角, 它们的波矢满足
01
图5.3 - 4 振荡时, 介质中E3和E4的功率分布
01
图5.3 - 5 DFWN的放大特性
当(3π/4)>|g|L>(π/4)时, R>1。 此时, 可以产生放大的反射光, 在介质中E3和E4的功率分布如图5.3 - 5所示。
应用四波混频研究多普勒系统中的碰撞效应

密级:学校代码:10075分类号:学号:********理学硕士学位论文应用四波混频研究多普勒系统中的碰撞效应学位申请人:崔宇指导教师:孙江教授学位类别:理学硕士学科专业:光学授予单位:河北大学答辩日期:二零一五年六月Classified Index: COAD: 10075 U.D.C No: 20121049A Dissertation for the Degree of M. ScienceThe study of collision effects by nondegenerate four wave mixing in aDoppler systemCandidate:Cui YuSupervisor: Prof. Sun JiangAcademic Degree Applied for:Master of ScienceSpecialty:OpticalUniversity:Hebei UniversityDate of Oral Examination:June, 2015摘要碰撞效应是许多研究领域的基础。
近年来,随着碰撞效应在冷原子技术和量子信息与量子计算上的应用研究,原子碰撞效应再次吸引了大量的研究兴趣。
高分辨共振四波混频作为一种纯光学高阶全相干激光光谱学技术,具有广泛的应用领域。
本文将该技术应用于多普勒系统中的原子碰撞效应研究,与目前探测原子布居纵向弛豫的原子碰撞测量技术不同,共振四波混频可以研究碰撞对两能级间原子相干的横向弛豫的影响。
本论文采用共振双四波混频理论研究了多普勒展宽系统和多普勒缀饰系统中的双光子共振非简并四波混频和碰撞再构引起的非简并四波混频。
数值分析了压强、温度、碰撞展宽系数等参数对碰撞再构四波混频信号的影响。
发现随着缓冲气压的增强,由碰撞引起的能量转移现象引起的四波混频逐渐增强,它反映了非弹性碰撞引起的低能级上的原子布居情况。
因此,我们研究的双四波混频方法可以作为研究碰撞引起的能级再分布的有效手段。
光纤的非线性光学效应及其对光纤通信的影响

光纤的非线性光学效应及其对光纤通信的影响随着科学技术的发展,人们对物质和文化生活的要求不断提高,导致待传输的信息量(语音、图像、视频和数据等)爆炸式增长,光纤通信已成为大容量现代传输网的基本组成形式。
近些年由于掺铒光纤放大器(EDFA)的实用化,在信号的传输过程中,光纤的损耗对系统影响已不再是主要因素了,而光纤的非线性光学效应确引起人们的极大关注。
特别是在密集波分复用(DWDM)系统中,随着光纤中信道数量的增多,进入光纤的光功率将随之加大,光纤的非线性光学效应将成为影响系统性能的主要因素。
本文介绍了光纤中常见的几种非线性光学效应及其对光纤通信的影响。
标签:非线性光学效应受激散射效应非线性折射率效应交叉相位调制Abstract:With the development of science and technology,people’s material and cultural life is ever increasing,cause the amount of information to be transmitted(voice,image,video and data,etc.)explosive growth,large-capacity optical fiber communication has become a basic modern communication network composition form. In recent years because of EDFA practical,in the process of signal transmission fiber loss impact on the system is no longer a major factor,while the nonlinear optical effect indeed cause for concern. Especially in DWDM systems,with the increase in the number of channels in optical fibers,The optical power into the fiber increases,nonlinear optical effect will become a major factor affecting system performance. This article describes several common optical fiber nonlinear effects and their impact on the optical fiber communication Key words:nonlinear optical effects;stimulated scattering effects;nonlinear refractive index effects;cross-phase modulation中圖分类号:TN24 文献标识码:A 文章编号:1003-9082(2014)03-0009-03非线性光学效应是光场与传输介质相互作用时发生的一种物理效应,当光纤中传输的光功率较弱时,光纤呈现为线性系统,其各项特征参量随光场作线性变化,但在高强度的电磁场中,任何电介质(包括光纤)都会表现出非线性特性。
非相干光时延四波混频相干拍频调制的多能级理论研究

The Study of Multilevel Theory Interference-beat Modulation in Time-delay Four-wave Mixing with Incoherent Light
ZHANG Yang,LI Yuqiong,SHEN Jianqi
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093)
Abstract The development of the incoherent light time-delay four-wave mixing theory is described the differe- nce of the two-level theory and the theory of multilevel is analysed.The photon echo signal of the Er2O3 and CeO2 doped TeO2-Nb2O5-ZnO glass is also observed by the experiment of time-delay four-wave mixing with incoherent light,with the temperatures at 7.5K and 300K respectively.The Photon echo signal indicates the interference-beat modulation.The multi-level theory in the case of non-uniform broadening the theoretical formula is used to fit the ex- perimental results.The multi-level theory is used to explain the experimental results.The reference for the develop- ment of the incoherent light four-wave mixing theory is provided.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式中
Ps(3)
(k1
k1
ki
,
)
0
(3)
(
)E1(k1)E1(k1)E
i
(ki
)
Ps(3) (k1 k1 ki , ) 0 (3) ( )E1(k1)E1 (k1)Ei (ki )
Ps(3) (k1 k1 ki , ) 0 (3) ( )E1(k1)E1(k1)Ei (ki )
dE3 ( z ) dz
i0 2
2k3
0 (3){6[|
E1
|2
|
E2
|2 ]E3(z)
6E1E2 E4 ( z )}
dE4 ( z) dz
i0 2
2k4
0 (3){6[|
E1
|2
|
E2
|2 ]E4 (z)
6E1E2 E3 ( z )}
(5.3 - 8)
6E1(r)E2 (r)E3(r)}ei(tk4r) c.c. (5.3 - 5)
在考虑到慢变化振幅近似的条件下, 介质中光电场 复振幅的变化规律满足耦合波方程, 即
dEl (r) drl
i0 2
2ki
a()
PNL (, r)eiklr
(5.3 - 6)
1) 小信号理论
102
Is= 0 0.05
0.10
101
0.20
0.50
0.80 100
R
10-
1
0
1.0 2.0 3.0 4.0 5.0 6.0 7.0
Ip
图5.3 - 7 Is为参量时, R与Ip的关系曲线
102
0
0.40.6
0.2
0.8
101
0.90
0.95
则由(5.3 - 14)式得到 R tan2( g L)
(5.3 - 16)
在gL较小的情况下,随着gL的增大,R也增大。如果介质长
度一定,则g越大,R越大。g的大小反映了泵浦光对散射光 耦合的强弱。
(3) 由(5.3 - 16)式可见, 当|g|L≈π/2时, R→∞, 这相应于 振荡的情况。 在这种情况下, E3和E4在介质中的功率分布如 图5.3 - 4所示。
1.0 P4(|g|z)
P/P总
0.8
0.6
0.4 P3(|g|z)
0.2
|g|Lπ 2
P总 ∞
0 0.2 0.4 0.6 0.8 1.0 |g|z/|g|L
图5.3 - 4 振荡时, 介质中E3和E4的功率分布
当(3π/4)>|g|L>(π/4)时, R>1。 此时, 可以产生放大的 反射光, 在介质中E3和E4的功率分布如图5.3 - 5所 示。
(c)
图5.3 - 1 四波混频中的三种作用方式
1) 三个泵浦场的作用情况
在这种情况下, 作用的光波频率为ω1 , ω2和ω3, 得到的信 号光波频率为ωs, 这是最一般的三阶非线性效应。 2) 输出光与一个输入光具有相同模式的情况
在这种情况下, 例如输入信号光为Es0=E30 , ωs=ω3, 则 由于三阶非线性相互作用的结果, E3将获得增益或衰减。 3) 后向参量放大和振荡
如 果 介 质 中 的 四 个 光 电 场 满 足 |E1(r)|2 、 |E2(r)|2>>|E3(r)|2、 |E4(r)|2, 就可以忽略泵浦抽空效应。 在 这种情况下, 只需考虑E3(r)和E4(r)所满足的方程即可。 假 设E3(r)和E4(r)沿着z轴彼此相反方向传播,相应的耦合波方 程为
简并四波混频的输出可以利用耦合波方程求解。其四波相 互作用也可以理解为如下的全息过程:三个入射光波中的 两个相互干涉,形成一个稳定光栅,第三个光波被光栅衍 射,得到输出波。
例如:考虑到k1=-k1’,特殊情形下的三个稳定光栅。根据衍射 理 论 可 以 得 到 三 个 衍 射 波 , 其 波 矢 分 别 为 : ks=k1+k1’-ki ; ks=k1-k1’+ki;ks=-k1+k1’+ki
首先,普通全息的记录过程是通过参考光和信号光干涉、 对记录介质曝光,并调制其透明度实现的,所以,参考光 与信号光必须同频率,否则就会形成不稳定的运动光栅, 在曝光过程中会将全息图擦除掉。而在四波混频过程中, 相互作用的光波则不一定同频率。
第二,四波混频过程中的四个光波是通过三阶非线性极化 率发生相互作用的,在一般情况下,三阶极化率是一个张 量,它可以使不同偏振的光之间产生耦合。
这是四波混频中的一种特殊情况, 其中两个强光波作为 泵浦光场, 而两个反向传播的弱波得到放大。这与二阶非 线性过程中的参量放大相似,其差别只是这里是两个而不 是一个泵浦光场,两个弱光分别是信号光波和空闲光波。
在四波混频中,相位匹配时非常重要的条件,因为它可以 大大地增强信号光波的输出。
由于四波混频在所有介质中都能容易地被观测到,而且变 换形式很多,所以它可以得到许多很有意义的应用。例如, 利用四波混频可以把可调谐相干光源的频率范围扩展到红 外和紫外;在材料研究中,共振四波混频技术是非常有效 的光谱和分析工具。
(
z
)
(5.3 - 10)
式中
g
1 k
300 2 (3)E1E2
(5.3 - 11)
在这里已考虑到k3=k4=k。 假设边界条件为
可以解得
E3(z 0) E30
E4(z L) 0
(5.3 - 12)
E3 ( z )
cos[|g | (z cos(|g |
P4out
P3out
功率(任意单位)
P3in 0
z L
图5.3 - 5 DFWN的放大特性
2) 大信号理论[16, 17]
在DFWN过程中, 如果必须考虑泵浦抽空效应, 就应 当同时求解 (5.3 - 7)式的四个方程, 这就是大信号理论。
我们讨论的DFWM作用结构如图5.3 - 6所示, E1、 E2是彼此反向传播的泵浦光, E3, E4是彼此反向传播的信 号光和相位共轭光, 光电场仍采用(5.3 -3)式的形式。
5.3.2 简并四波混频(DFWN)理论 1. 简并四波混频作用 简并四波混频是指参与作用的四个光波的频率相
等。 这时, 支配这个过程的三阶非线性极化强度一般有 三个波矢不同的分量:
Ps(3) ( ) Ps(3) (k1 k1 ki , ) Ps(3) (k1 k ki , ) Ps(3) (k1 k ki ,)
dE1 ( z ) dz
iCE2(z)E3(z)E4 (z)
dE2 (z) dz
iCE1
(
z)
E3
(
z)
E4
(
z
)
dE3 ( z ) dz
iCE1(z)E2 (z)E4 (z)
dE4 (z) dz
iCE1
(
z)
E2
(
z
)
E3
(
z
)
(5.3 - 19)
2. 非共振型简并四波混频过程
在非共振型四波混频过程中, 光场将引起介质折射 率的变化。 通常所采用的介质, 大致分为两类: 一类对 本地场响应(光克尔效应[13] ), 另一类对非本地场响 应(热响应[12] 、 光折变效应[13, 14] 、 电致伸缩效 应[15]等)。 前者可以利用非线性极化率表征, 后者不 能直接利用非线性极化率表征。 这些介质中的四波混 频过程都可以通过耦合波方程描述。
E1
(3)
E4 z
E3
E2
z= 0
z= L
图5.3 - 6 非共线DFWM结构示意图
为了分析简单起见, 我们假设四个光电场同向线偏 振, 并且忽略光克尔效应引起的非线性折射率变化项。 在这种情况下, (5.3 - 7)式变为
dE1(r) dr1
i k1
300 2
(3)E2(r)E3(r)E4 (r)
(5.3 - 4)
如果这四个光波为同向线偏振光, 则可以根据非线性极化 强度的一般关系, 得到相应于某一分量的感应非线性极化 强度, 例如:
P4(r, t) 0 (3){3[2 | E1(r) |2 2 | E2(r) |2 2 | E3(r) |2 | E4(r) |2 ]E4(r)
由此可以得到如下结论:
(1) 在输入面(z=0)上, 通过非线性作用产生的反射光场
E4(0)正比于入射光场E*30 。 因此, 反射光E4(z<0)是入射光 E3(z<0)的背向相位共轭光。
(2) 若定义相位共轭(功率)反射率为
R
E4 (z 0) 2 E3(z 0) 2
(5.3 - 15)
(5.3 - 9)
并可以得到E′3 (z)和E′4 (z)满足的方程。 为了方便起 见, 在下面求解E′3 (z)和E′4 (z)的过程中, 我们略去右上角 的撇号, 将E′3 (z)和E′4 (z)满足的方程改写为
dE3 dz
igE4 ( z )
dE3 dz
igE4
5.3 四 波 混 频
5.3.1 四波混频概述
四波混频是介质中四个光波相互作用所引起的非线 性光学现象, 它起因于介质的三阶非线性极化。
四波混频相互作用的方式一般可分为如图5.3 - 1所 示的三类。
E1
E1
E1
E2 E3
Es
E3
