实验数据的表图表示
制作简单的数学表格和图表

目录
• 数学表格基础知识 • 使用Excel制作数学表格 • 制作条形图与柱形图 • 制作折线图和散点图 • 制作饼图和环形图 • 高级技巧:组合图表与动态图表制作
01
数学表格基础知识
表格定义及作用
表格定义
数学表格是一种用于整理和展示 数学数据的结构化形式,通常由 行和列组成,可以清晰地呈现数 据之间的关系和趋势。
数据验证公式
使用复杂的公式来定义数据验证规则,实现更高级的动态交互效果 ,例如根据用户输入的值自动筛选和展示相关数据。
分享与导出成果文件
1 2 3
导出为静态图片
将制作好的组合图表或动态图表导出为静态图片 ,如PNG、JPG等格式,方便在其他文档或平台 中分享和使用。
导出为动态GIF
将动态交互效果导出为GIF动图,保留图表的动 态展示效果,便于在网络社交媒体等平台上分享 和传播。
适用场景
环形图适用于需要同时展示多个分类数据占比,并且需要强调某个或某些分类的 情况。例如,在展示公司各部门销售占比时,可以使用环形图来突出表现销售占 比最高的部门。
实际操作:创建并编辑饼图或环形图
选择图表类型
在数据可视化工具中,选择饼图或环形图 作为要创建的图表类型。
导出和分享
完成图表编辑后,可以将其导出为图片或 PDF等格式,以便与他人分享和交流。
准备数据
准备好需要展示的数据,包括分类名称和 对应的数值。确保数据的准确性和完整性 。
调整图表元素
根据实际需求,调整图表的各个元素,例 如扇形的大小、颜色、标签等,以使图表 更加直观和易于理解。
创建图表
将数据导入到图表中,并根据需要对图表 进行进一步的编辑和美化,例如调整颜色 、添加标签和标题等。
1.压强

实验 液体深 橡皮膜在水 U形管两侧液面 序号 h/cm 中的方向 高度差/cm
1
向上
2
向上
3 实验结论:
向上
(3)探究:液体压强与液体密度的关系 实验数据表格:
实验 液体 液体深
序号
h/cm
1
水
2 盐水 实验结论:
总之:液体压强与
与
、
U形管两侧液面 高度差/cm
和
有关。
等无关
考点4 连通器
定义 原理 应用
>
果分别装的是酒;
液体则P甲
>P乙。 (填“>”、“<”或“=”)
10. 如右图所示,一木桶壁上有一 缺口,桶壁上最长的木板长为0.5 m, 缺口处的木板长为0.2 m,桶底内部 底面积为4×10-2 m2。当桶内装足 够多的水时,求:
(1)桶底受到水的压强约为多少Pa?
__p__表示
积
__p_=__FS___
之比,用符号
单位
p: 帕 斯 卡 (Pa); F: 牛顿 (N); S:米2(m2)
增大压强:①、受力面积一定时, 增大压力 ;
增大和减 小压强的
方法
②、压力一定时,
减小受力面 积
。
减小压强:①、受力面积一定时,__减__小__压__力
;
②、压力一定时, 减小受力面积 。
(填“正确”或“错误”)的,
等
6、(2014•宁夏)某同学探究液体内部压强的特点,实验 过程如图所示.
(1)实验前,要通过调试,保证压强计两边玻璃管中的液 面 相平 .
(2)如图所示,将压强计的探头放在水中的某一深度处,使
橡皮膜朝向不同的方向,这是为了探究,
同种液体,同一深度处,液体内部向各个方向压强的关系 。
实验数据的记录.

m
n xiyi xi yi n x ( xi )
2 i 1 i 1 i 1 n i i i 1 n 2
n
n
n
b
2 x i yi xi xiyi
n
n
n
n
i 1
n x 2 ( xi ) 2
i 1 i 1
i 1 n
i 1 n
i 1
1.234×103 1.234×105 1.234×10-1 1.234×10-4
2、有效数字的取舍原则:
(1) .在运算中舍去多余的数字时,采用“4舍6入5尾 留双”的法则; ( 2)在加减运算中,各值小数点后取的位数,以有 例如: 9.436 9.434 9.435 9.445 整化为三位有 效数字位数最少的为准; 效数字,则对应为 9.44 9.43 9.44 9.44 (3)在乘除运算中,各数以及结果所保留的有效 数字位数,以有效数字位数最少者为准; (4)在对数运算中,所取对数尾数应当与真数的 有效数字位数相同。例如: lg7.1×1028 =28.85 (5)常数л、е 及乘子、 等的有效数字位数可 根据需要保留。
(ⅰ)要能表示全部有效数字,以便从图解法求出 各量的准确度与测量的准确度相适应,为此 将测量误差较小的量取较大的比例尺。 (ⅱ)坐标轴上每小格的数值,应便于读数和计算, 一般取1、2、5或是1、2、5的10n倍,要避 免用3、6、7、9这样的数值及它的10n倍。 (ⅲ)在上述条件下,充分考虑利用图纸的全面 积,使全图布局合理。若图形为直线,应 使其直线与横纵坐标轴的夹角尽可能在45° 左右 。 •注:图形大小一般在10cm×10cm左右
例:现有下列实验数据:
x 1 3 8 10 13 y 3.0 4.0 6.0 7.0 8.0 15 17 20 9.0 10.0 11.0
实验数据处理的基本方法
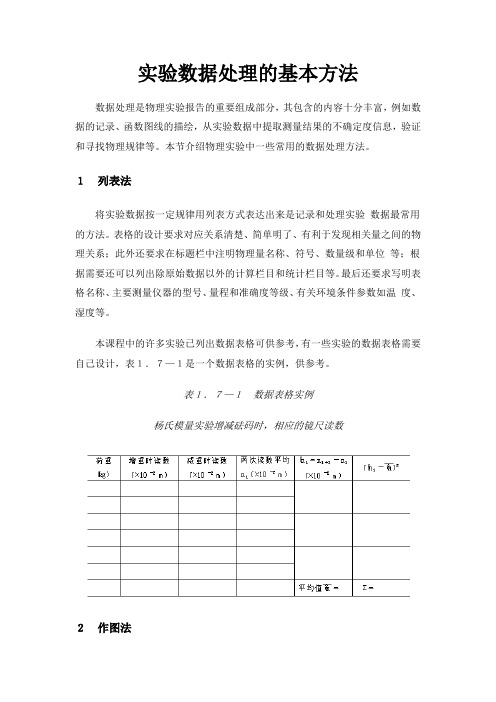
表1.7—1 数据表格实例
杨氏模量实验增减砝码时,相应的镜尺读数
2 作图法
作图法可以最醒目地表达物理量间的变化关系。从图线上还可 以简便求出实验需要的某些结果(如直线的斜率和截距值等),读出没有进行观测的对应点(内插法),或在一定条件下从图线的延伸部分读到测量范围以外的对应 点(外推法)。此外,还可以把某些复杂的函数关系,通过一定的变换用直线图表示出来。例如半导体热敏电阻的电阻与温度关系为,取对数后得到,若用半对数坐标纸,以lgR为纵轴,以1/T为横轴画图,则为一条直线。
1,2,3,4,5
6,7,8,9,10
用6减1,7减2,8减3,9减4,10减5,得到五个差值,取平均后再除以5(即除以两次5),这时就把这十个数中的误差对数据的影响全部计入了.
逐差法的使用条件是必须有偶数个数据,因为要写成两组对应的形式.
(4)描点和连曲线。根据实验数据用削尖的硬铅笔在图上描 点,点子可用“+”、“×”、“⊙”等符号表示,符号在图上的大小应与该两物理量的不确定度大小相当。点子要清晰,不能用图线盖过点子。连线时要纵观所有 数据点的变化趋势,用曲线板连出光滑而细的曲线(如系直线可用直尺),连线不能通过的偏差较大的那些观测点,应均匀地分布于图线的两侧。
(5)写图名和图注。在图纸的上部空旷处写出图名和实验条件等。此外,还有一种校正图线,例如用准确度级别高的电表校准低级别的电表。这种图要附在被 校正的仪表上作为示值的修正。作校正图除连线方法与上述作图要求不同外,其余均同。校正图的相邻数据点间用直线连接,全图成为不光滑的折线(见图1.7— 1)。这是因为不知两个校正点之间的变化关系而用线性插入法作的近似处理。
统计图表ppt.课件

案例五:产品满意度调查表
总结词
通过柱状图和饼图展示产品的满意度调查结 果,包括各评价维度的得分和占比。
详细描述
使用柱状图表示各评价维度的得分情况,使 用饼图展示各评价维度的占比,并添加相应 的文字说明和图表注解。
THANKS
感谢观看
统计图表的设计原则
01
明确目的
根据展示需求选择合 适的图表类型,确保 图表能够准确传达信 息。
02
简洁明了
避免过多的图表元素 和复杂的图表设计, 保持图表的简洁和易 读性。
03
数据可视化
将数据以直观、易懂 的方式呈现,突出关 键信息和数据变化。
04
对比与参照
合理运用对比和参照 ,帮助读者更好地理 解和分析数据。
科学研究
总结词
在科学研究中,统计图表是呈现实验结果和科学发现的常用 手段,有助于推动科学知识的传播和发展。
详细描述
利用曲线图记录实验过程中各项指标的变化趋势;通过表格 呈现详细的实验数据;使用流程图说明实验操作步骤和逻辑 关系等。
商业决策
总结词
在商业决策中,统计图表能够为决策 提供数据支持,帮助企业做出科学、 合理的决策,提高经营效率和盈利能 力。
统计图表PPT课件
目录
• 统计图表概述 • 常用统计图表 • 统计图表的应用场景 • 统计图表制作技巧 • 统计图表案例分析
01
统计图表概述
Chapter
统计图表的定义与作用
定义
统计图表是一种可视化工具,通过图形和表格的形 式展示数据,帮助人们快速理解和分析数据。
作用
统计图表能够清晰地呈现数据的分布、趋势和关系 ,提高数据的可读性和易理解性,有助于做出正确 的决策和判断。
刚体转动惯量测量数据表(可编辑)

刚体转动惯量的测量转动惯量是刚体转动时惯性大小的量度,它与刚体的质量、质量对轴的分布以及转轴位置有关。
如果刚体形状规则,质量分布均匀,可以直接计算出它绕特定轴的转动惯量。
但对于几何形状不规则和质量分布不均匀的刚体,只能用实验的方法来测量。
测量转动惯量的方法有很多种,如三线摆法、单悬扭摆法、双悬扭摆法、螺旋弹簧式扭摆法等,本实验介绍了利用螺旋弹簧式扭摆法来测量刚体的转动惯量。
一、实验目的1.观察扭摆振动现象。
2.用扭摆法测量不同形状刚体的转动惯量。
二、实验原理螺旋弹簧式扭摆如图6.1所示,在垂直轴上装有螺旋弹簧,用以产生恢复力矩。
在轴的上方可以装上各种待测刚体。
将刚体在水平面内转过某一角度θ后,在弹簧的恢复力矩的作用下,刚体就开始绕垂直转轴作往返扭转运动。
根据胡克定律,弹簧产生的恢复力矩M 与所转过的角位移θ成正比:θK M −= (1)式中,K 为弹簧的扭转系数,负号表示恢复力矩M 的方向与角位移θ的方向相反。
又根据转动定律,则有22dt d JJ M θβ== (2)其中,J 为刚体的转动惯量,β为角加速度。
联立式(1)、(2)可得:022=+θθJ Kdtd 令ω2=K /J ,上式变为:0222=+θωθdtd (3) 方程(3)表明扭摆运动具有角简谐振动的特征:角加速度与角位移成正比,而方向相反。
其通解为:)cos(0ϕωθθ+=t 式中,θ0为谐振动的角振幅,ϕ为初相位,ω为角速度。
扭摆的振动周期为:KJ T πωπ22==或 K J T 224π=(4) 上式表明,扭摆周期T 的平方与转动惯量J 成正比。
若单独测出扭摆周期,因扭摆系数K 是未知量,所以还不能由式(4)计算出转动惯量,为此,一般采用比较法求出K 。
实验中用一个几何形状规则的圆柱体,它的转动惯量J 1可以根据其质量和几何尺寸用理论公式直接计算得到。
设金属载物圆盘的转动惯量为J 0,转动的周期为T 0,若将圆柱体置于金属载物盘上,测出它的摆动周期T 1,则KJ T 0224π= KJ J T 012214+=π (5) 由式(5)可以确定K ,J 0。
实验六 图及其应用

实验六图及其应用数据结构实验六图及其应用1、实验目的? 熟练掌握图的两种存储结构(邻接矩阵和邻接表)的表示方法 ? 掌握图的基本运算及应用? 加深对图的理解,逐步培养解决实际问题的编程能力2、实验内容:采用邻接表或邻接矩阵方式存储图,实现图的深度遍历和广度遍历;用广度优先搜索方法找出从一顶点到另一顶点边数最少的路径。
1.问题描述:利用邻接表存储结构,设计一种图(有向或无向),并能够对其进行如下操作:1) 创建一个可以随机确定结点数和弧(有向或无向)数的图; 2) 根据图结点的序号,得到该结点的值;3) 根据图结点的位置的第一个邻接顶点的序号,以及下一个邻接顶点的序号;4) 实现从第v 个顶点出发对图进行深度优先递归遍历; 5) 实现对图作深度优先遍历;6) 实现对图进行广度优先非递归遍历; 编写主程序,实现对各不同的算法调用。
2.实现要求:(以邻接表存储形式为例)编写图的基本操作函数::对图的各项操作一定要编写成为C(C++)语言函数,组合成模块化的形式,每个算法的实现要从时间复杂度和空间复杂度上进行评价。
1)“建立图的邻接表算法”:CreateGraph(ALGraph *G) 操作结果:采用邻接表存储结构,构造没有相关信息的图G2)“邻接表表示的图的递归深度优先遍历算法”:DFSTraverse(ALGraphG,void(*Visit)(char*)) 初始条件:图G 已经存在;操作结果:返回图的按深度遍历的结果。
3)“邻接表表示的图的广度优先遍历算法”: BFSTraverse(ALGraphG,void(*Visit)(char*)) 初始条件:图G 已经存在;操作结果:返回图的按广度遍历的结果。
4)“邻接表从某个结点开始的广度优先遍历算法”:BFS(ALGraph G, int v)初始条件:图G 已经存在;操作结果:返回图从某个结点开始的按广度遍历的结果。
分析: 修改输入数据,预期输出并验证输出的结果,加深对有关算法的理解。
实验数据图示法和图解法
7
三、在选作图用数据时的注意点
1.较平直的曲线可均匀选取数据 弯曲的曲线则在曲率大处多取数据
2.尽可能重复测量每一对数据,求平 均值,用平均值在坐标上描点作图
3.尽可能一面测量多,取一数面据作图
均匀选数据
可及时发现问题进行补测数据或重复
测量,以免最后发现错误而前功尽弃
8
四、实验数据的图解法
(二变量关系的图示法研究)
●先用图示法给出y ~ x图线 ●再根据画出的图线的形状和规律
寻找经验公式 在 ●检研即验究经二测验变量公量各式x 组和是否合(yx的合适i , 关适的yi系,)数值时并学且关系要式确 以 定经x为验横公坐式标中,的y为某纵些坐常标数,画出图线
如何寻找经验公式并检验是否合适 如何确定经验公式中的某些常数
V
同一图上有几条图线时描点符号应不同并在
图纸上的空白位置
注明符号所代表的内容
5
d.联线
P
e.写图名 在图纸顶部附近空旷位置 写出简洁而完整的图名
.. .... . . . .
o
V
纵轴代表的物理量写在前面
横轴代表的物理量写在后面
中间用符号“~”联接
在图名的下方允许附加
必不可少的实验条件或图注
6
空气压强 ~ 温度图线 体积保持不变
9
●图示法的具体规则 a.选轴 b.定标尺 c.描点 d.联线 e.写图名
以空气压强~温度图线为例说明
2
●图示法的具体规则
a.选轴
P (, cmHg)
在在坐轴标的纸末上端近旁 注明以物横理轴量代表及自单变位量, 纵轴代表应变量 划单两位条用粗小细括适号当括的住线,表也示可纵用轴逗和号横分轴开
第2章 试验数据的表图表示

表格法的不足
从表格中不能给出所有的函数关系; 从表格中不易看出变量变化时函数的变化 规律,而只能大致估计出函数是递增的、 递减的或是周期性变化的等等。
2.2 图示法
2.2 图示法
试验数据图示法就是将试验数据用图形表 示出来,它能用更加直观和形象的形式, 将复杂的试验数据表现出来。通过数据图, 可以直观地看出试验数据变化的特征和规 律。它的优点在于形象直观,便于比较, 容易看出数据中的极值点、转折点、周期 性、变化率以及其它特性。试验结果的图 示法还可为后一步数学模型的建立提供依 据。
4.圆形图
它可以表示总体中各组成部分所占的比例。 圆形图只适合于包含一个数据系列的情况, 它在需要重点突出某个重要项时十分有用。 将饼图的总面积看成100%,按各项的的构 成比将圆面积分成若干份,每3.6°圆心角 所对应的面积为1%,以扇形面积的大小来 分别表示各项的比例。 图例
5.XY(散点图)
2mm 1 My (mm / y) 2y y
(2)坐标轴的分度应与试验数据的有效数字位数相匹配,即坐标读数的 有效数字位数与实验数据的位数相同; (3)推荐坐标轴的比例常数M=(1、2、5)³10± n (n为正整数), 而3、6、7、8等的比例常数绝不可用;
(4)纵横坐标之间的比例不一定取得一致,应根据具体情况选择,使曲 线的坡度介于30°~60°之间
2.2 图示法
图表是数字值的可视化表示。用于试验数 据处理的图形种类很多,EXCEL根据图形 的形状可以分为线图、柱形图、条形图、 饼图、环形图、散点图、直方图、面积图、 圆环图、雷达图、气泡图、曲面图等等。 图形的选择取决于试验数据的性质。 图表向导 举例
2.2.1 EXCEL常用图表类型介绍
新版数据分析常用的20种图表

03
用于展示两个变量之间的关系和分布。
常用20种图表简介
1 2
饼图(Pie Chart)
用于展示分类数据的占比情况。
直方图(Histogram)
用于展示连续变量的分布情况。
3
箱线图(Box Plot)
用于展示一组数据的分布情况,包括中位数、四 分位数和异常值。
常用20种图表简介
热力图(Heat Map)
相关系数热力图
• 相关系数热力图:用于展示多个变量之间的相关系数,通过颜色的深浅来表示相关系数的值,可以直观地观察出哪些变量 之间存在较强的相关性。
对应分析图
• 对应分析图:用于展示两个分类变量之间的关系,通过将分 类变量的各个类别映射到二维平面上,可以观察出类别之间 的相似性和差异性。
06
序列类图表
柱状图是以垂直的柱形来展示数 据,而条形图则是以水平的条形
来展示数据。
在使用柱状图和条形图时,需要 注意选择合适的柱形或条形宽度 和颜色,以便更好地展示数据的
差异和比较。
瀑布图
瀑布图是一种特殊的柱状图,主 要用于展示数据从一个初始值到
最终值的变化过程。
瀑布图的优点在于可以直观地展 示数据的增减变化和累计效果, 适用于财务分析、销售分析等场
和分析。
漏斗图
流程分析
漏斗图主要用于分析具有流程性质的数据,如用户转化路径、销 售流程等,可以直观地展示各个环节的转化率和流失情况。
环节对比
通过对比不同环节的转化率,可以找出流程中的瓶颈和问题所在, 为优化流程提供数据支持。
可定制化
漏斗图通常支持定制化设置,如调整环节顺序、设置颜色、添加标 签等,以满足不同场景下的分析需求。
小提琴图
第2章--试验数据的表图表示

表外附加通常放在表格的下方,主要是一些不便列在表内 的内容,如指标注释、资料来源、不变的试验数据等
注意事项 :
(1) 表格设计应该简明合理、层次清晰,以便于 阅读和使用;
(2) 数据表的表头要列出变量的名称、符号和单 位;
(3) 要注意有效数字位数; (4) 试验数据较大或较小时,要用科学记数法来
2.2 图示法
图表是数字值的可视化表示。用于试验数 据处理的图形种类很多,EXCEL根据图形 的形状可以分为线图、柱形图、条形图、 饼图、环形图、散点图、直方图、面积图、 圆环图、雷达图、气泡图、曲面图等等。 图形的选择取决于试验数据的性质。
图表向导 举例
2.2.1 EXCEL常用图表类型介绍
1.柱形图
公式(函数式):借助于数学方法将实验数据按一 定函数形式整理成方程,即数学模型。
2.1 列表法
将试验数据列成表格,便于随时检查结果是否正 确合理,及时发现问题,利于计算和分析误差, 并在必要时对数据随时查对。通过列表法可有助 于找出有关实验因素之间的规律性,得出定量的 结论或经验公式等。列表法是图示法和公式法的 基础,是工程技术人员经常使用的一种方法。列 表法常分为: ➢ 记录表 ➢ 结果表示表
中反映出关于研究结果的完整概念。 例如:
说明:
三部分组成:表名、表头、数据资料 必要时,在表格的下方加上表外附加
表名应放在表的上方,主要用于说明表的主要内容,为了 引用的方便,还应包含表号
表头通常放在第一行,也可以放在第一列,也可称为行标 题或列标题,它主要是表示所研究问题的类别名称和指标 名称
每个数据标志相关的可能误差量。 所谓趋势线,是用图形的方式显示数据的预测趋
实验设计与数据处理_复习总结

3、多元线性回归分析
(1)多元线性回归方程的建立与求解
(2)多元线性回归方程显著性R检验 (复SS相R关系数,F检验) (3)因素主次的判断 (3种方法) SS T
偏回归系数的标准化
偏回归系数的显著性检验(F检验) 偏回归系数的 t 检验
Pj b j
L jj L yy
tj Fj
4、非线性回归分析 (1)一元非线性回归分析 (2)一元多项式回归 (3)多元非线性回归
第六章 正交试验设计 1、基本概念 (1)正交表 等水平正交表符号 混合水平正交表符号 (2)等水平正交表的正交特性 (3)混合水平正交表的正交特性
2、正交试验设计的基本步骤 (六大步骤) (1)明确试验目的,确定评价指标; (2)挑选因素,确定水平; (3)选正交表,进行表头设计; (4)明确试验方案,进行试验,得到结果; (5)对试验结果进行统计分析; (6)进行验证试验,做进一步分析。
第四章 试验数据的回归分析
线性回归
一元线性回归 多元线性回归
回归分析 非线性回归
一元非线性回归 多元非(2)相关关系 (3)回归分析 2、一元线性回归分析 / 直线拟合 (1)回归方程的建立与求解 (2)一元线性回归效果的检验(相关系数,F检验)
r Lxy Lxx L yy
4、正交试验设计结果的方差分析法 (1)方差分析的基本步骤与格式 若某因素或交互作用的均方≤MSe,则应将它们归入误差列; (2)二水平正交试验的方差分析 二水平正交试验中,正交表中任一列(第j列)对应的离差平方和为:
SSj 1n(K1 K2)2
(3)三水平和四水平正交试验的方差分析
对于3水平和4水平正交试验的方差分析,任一列(第j列)的离差平方和为 :
第八章回归正交设计 1、一次回归正交设计的基本方法 (1)确定因素的变化范围 上水平、下水平、零水平xj0 、变化间距Δj (2) 因素水平的编码
用Excel软件进行实验数据处理

§2—5 用Excel软件进行实验数据处理Excel是一个功能较强的电子表格软件,具有强大的数据处理、分析和统计等功能。
它最显著的特点是函数功能丰富、图表种类繁多。
用户能在表格中定义运算公式,利用软件提供的函数功能进行复杂的数学分析和统计,并利用图表来显示工作表中的数据点及数据变化趋势。
在大学物理实验中,可帮助我们处理数据、分析数据、绘制图表。
Excel软件操作便捷、掌握容易,用于实验数据的处理非常方便。
下面简单介绍其在实验数据处理中的一些基本方法。
1.工作表、工作簿、单元格、区域等概念1)工作表启动Excel后,系统将打开一个空白的工作表。
工作表有256列,用字母A,B,C,…命名;有65536行,用数字1,2,3…命名。
2)工作簿一个Excel文件称为一个工作簿,一个新工作簿最初有3个工作表,标识为Sheetl,Sheet2,Sheet3,若标签为白色即为当前工作表,单击其他标签即可成为当前工作表。
3)单元格工作表中行与列交叉的小方格称为单元格,Excel中的单元格地址来自于它所在的行和列的地址,如第C列和第3行的交叉处是单元格C3,单元格地址称为单元格引用。
单击一个单元格就使它变为活动单元格,它是输入信息以及编辑数据和公式的地方。
4)表格区域表格区域是指工作表中的若干个单元格组成的矩形块。
指定区域:用表格区域矩形块中的左上角和右下角的单元格坐标来表示,中间用“:”隔开。
如A3:E6为相对区域,$A$3:$E$6为绝对区域。
$A3:$E6或A$3:E$6为混合区域。
5)工作表中内容的输入① 输入文本文本可以是数字、空格和非数字字符的组合,如:1234,1+2,A&ab、中国等,单击需输入的单元格,输入后,按方向键或回车键来结束。
② 输入数字在Excel中数字只可以为下列字符:30大学物理实验0123456789+ ,( ),*/%,E。
输入负数:在数字前冠以减号(—),或将其置于括号中。
图表的认识与图表的表示

自定义动画路径:对于某些图表元素,可以自定义动画路径,使元素按照特定的轨迹移动,增加动态效果的多样性和创意性。
图表的交互效果制作技巧
添加交互元素:如按钮、链接等,增强图表与用户的互动性。
动态数据展示:使用JavaScript等脚本语言,实现数据随时间变化的动态效果。
PART ONE
图表的基本概念
PART TWO
图表定义
图表是一种用图形表示数据的工具
图表可以分为多种类型,如柱状图、折线图和饼图等
图表可以清晰地传达信息和观点
图表可以直观地展示数据之间的关系和趋势
图表类型
柱状图:用于比较不同类别之间的数据
折线图:用于显示数据随时间变化的趋势
饼图:用于表示各部分在整体中所占的比例
特点:直观展示各部分在整体中的比例
适用场景:展示部分与整体的关系,如市场份额、用户比例等
表示步骤:确定数据比例-绘制圆形-按照比例划分扇形-标注数据和比例
散点图表示方法
添加标题
定义:散点图是用点的密度和变化趋势表示两指标之间直线和曲线关系的一种图形
添加标题
作用:用于展示两个变量之间的关系,通过观察散点图中点的分布情况,可以大致判断出两个变量之间是否存在某种关联关系以及关联关系的类型
确定图表的标题和图例
标题:简明扼要地概括图表内容
图例:解释图表中使用的符号或颜色代表的含义
图表的制作技巧
PART FIVE
图表的美化技巧
选择合适的图表类型:根据数据特点和需求选择合适的图表类型,如柱状图、折线图、饼图等。
调整图表颜色和字体:选择清晰、易于辨识的颜色和字体,使图表更加易于阅读和理解。
《统计学》数据的表格与图形表示

第三章数据的表格与图形表示
重点:理解“分布”的概念,可通过两种途径来表示分布:表格与图形
1、组织数值数据:有序数组和茎叶图
有序数组(Ordered Array)
对数据进行排序归类
(可用EXCEL或其它计算机软件处理)
茎叶表示 (Stem-and-leaf display)
垂直线左边的数字称为“首数”或“茎”
垂直线右边的数字称为“尾数”或“叶”
选择多少作为茎? 应根据形状。
实例: 美国59个增长共同基金(Mutual funds) 表3.1(p.55)及图3.1
(p.56).
2、数值数据的表格
频数分布 (Frequency Distribution)(p.61,表3.2)
1) 组数 ( Number of Class)
一般规则:5到15组(取决于观察值的数量)
2)组距 ( Class Interval)
组距=全距/组数
(1)和(2)是相关的,关键要考虑分布的形状
3)组界 ( Boundary of Class)
不重复而包括全部数值
(注意“互斥且完备”的含义)
频率分布(Relative Frequency Distribution)(表3.3, p.62)
百分比分布 (Percentage Distribution) (表3.4, p.63)
累积频率分布显示了从最低组到最高组频率如何累积 (表3.5, p.64)
先用频数分布建立累计频数分布
累积频率分布只计算频率分布的下界
3、数值数据的图形
04/26/22 商务统计基础(第3章)3-1。
表格数据的图形化上

注意事项
折线的起伏应该与数据的变化 趋势相符,同时要注意坐标轴
的刻度和标签的合理性。
饼图
适用场景
适用于展示数据的占比情况。
优点
可以直观地看出各个部分在整体中的 占比情况。
缺点
不适合展示过多的数据分类,容易导 致视觉混乱。
注意事项
饼图的扇区大小应该与数据的占比成 正比,同时要注意扇区的颜色和标签 的清晰度。
原理
适用场景
优点
实现工具
关系图通过节点和边来表示数据之间 的关系,节点表示实体,边表示实体 之间的关系。
能够直观地展示数据之间的关系和连 接情况。
其他高级图形化方法
等高线图
通过绘制等高线来表示数据的分布情况,适用于展示二维平面上的数 据分布。
散点图矩阵
通过绘制多个散点图来表示多个变量之间的关系,适用于展示多维数 据之间的关系。
操作简便
适用于小规模数据
对于数据量不大的情况,Excel能够满 足基本的图形化需求。
通过简单的拖拽和设置,即可快速生 成图表。
Python的matplotlib库
强大的数据可视化能力
01
matplotlib支持绘制各种复杂的图表,如散点图、箱线图、热
力图等。
编程实现灵活度高
02
用户可以通过编程方式自定义图表的样式、颜色、标签等,实
交互式图表
通过添加交互功能来增强图表的交互性和易用性,如添加鼠标悬停提 示、拖拽、缩放等功能。
动态图表
通过动态展示数据的变化过程来增强图表的表现力,如添加动画效果、 实时更新数据等。
04
表格数据图形化的实现工 具
Excel
数据可视化功能丰富
Excel提供了多种图表类型,如柱状图、 折线图、饼图等,方便用户根据需求 选择。
南通大学《试验设计与数据处理》复习要点

《试验设计与数据处理》复习要点第一章误差分析一、真值与平均值1、真值:指在某一时刻和某一状态下,某量的客观值或实际值。
2、平均值(1)算术平均值:x̅=x1+x2+⋯+x nn =∑x in同样试验条件下,多次试验值服从正态分布,算术平均值是这组等精度试验值中的最佳值或最可信赖值。
(2)加权平均值:x̅w=w1x1+w2x2+⋯+w n x nw1+w2+⋯+w n =∑w i x i∑w i(3)对数平均值:x̅L=x1−x2ln x1x2=x2−x1ln x2x1,试验数据的分布曲线具有对称性(4)几何平均值:lg x̅G=∑lg x̅in(5)调和平均值:H=n∑1x i二、误差的基本概念1、绝对误差=测得值-真值,结果可正可负。
2、相对误差=绝对误差/真值≈绝对误差/测得值,结果可正可负。
3、算术平均误差∆=∑|x i−x̅|n4、标准误差(1)样本标准差s=√∑(x i−x̅)2n−1=√∑x i2−(∑x i)2/nn−1(2)总体标准差σ=√∑(x i−x̅)2n =√∑x i2−(∑x i)2/nn三、误差来源及分类根据误差的性质或产生原因,可分为随机误差、系统误差、粗大(过失)误差。
1、随机误差:在一定试验条件下,以不可预知的规律变化着的误差;2、系统误差:在一定试验条件下,由某个或某些因素按照某一确定的规律起作用而形成的误差;3、粗大(过失)误差:一种显然与事实不符的误差。
四、试验数据的精准度1、精密度:反映随机误差大小的程度,是指在一定的试验条件下,多次试验值的彼此符合程度或一致程度;2、正确度:指大量测试结果的(算术)平均值与真值或接受参照值之间的一致程度,反映了系统误差的大小,是指在一定的试验条件下,所有系统误差的综合;3、准确度:反映系统误差和随机误差的综合,表示了试验结果与真值或标准值的一致程度。
五、试验数据误差的统计检验1、随机误差的检验随机误差的大小可用试验数据的精密程度来反映,而精密度的好坏又可用方差来度量,所以对测试结果进行方差检验,即可判断随机误差之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ppt课件
20
例: x
y
y
10 20 40 60 80 100 1000 2000 2 4 14 60 80 100 177 181
M
●
0.50
F
0.25
xB
0.75
xA
0.00
1.00 C
xC
图9 等边三角ppt形课件坐标图
15
(6)三维表面图(3D surface graph)
三元函数Z=f(X,Y)对应的曲面图,根据曲面图可以看出因 变量Z值随自变量X和Y值的变化情况
图10 三pp维t课表件 面图
16
(7)三维等高线图(contour plot) 三维表面图上Z值相等的点连成的曲线在水平面上的投影
图5 不同提取方法对两种原料有效成分提取率效果比较
ppt课件
11
(4)圆形图和环形图
①圆形图(circle chart) 也称为饼图(pie graph) 表示总体中各组成部分所占的
比例 只适合于包含一个数据系列的
情况 饼图的总面积看成100% ,每
3.6°圆心角所对应的面积为 1% ,以扇形面积的大小来分 别表示各项的比例
两个坐标轴的性质不同
➢ 数值轴 :表示数量性因素或变量
➢ 分类轴 :表示的是属性p因pt课素件 或非数量性变量
10
分类: ➢ 单式:只涉及一个事物或现象 ➢ 复式:涉及到两个或两个以上的事物或现象
超声波法
醇提法 碱提法
植物2 植物1
湿浸法
0 2 4 6 8 10 12 14 16 18 20 提取率(%)
ppt课件
3
(2)说明:
三部分:表名、表头、数据资料 必要时,在表格的下方加上表外附加 表名应放在表的上方,主要用于说明表的主要内容,为了
引用的方便,还应包含表号 表头常放在第一行或第一列,也称为行标题或列标题,它
主要是表示所研究问题的类别名称和指标名称 数据资料:表格的主要部分,应根据表头按一定的规律排
ppt课件
19
(1)选用坐标系的基本原则:
①根据数据间的函数关系
线性函数:普通直角坐标系 幂函数:双对数坐标系 指数函数:半对数坐标
②根据数据的变化情况
两个变量的变化幅度都不大,选用普通直角坐标系; 有一个变量的最小值与最大值之间数量级相差太大时,可以选用半对
数坐标; 两个变量在数值上均变化了几个数量级,可选用双对数坐标; 在自变量由零开始逐渐增大的初始阶段,当自变量的少许变化引起因
动态,可用于不同事物或现象的比较
ppt课件
6
图1 高吸水性树脂保水率与时间和温度的关系
ppt课件
7
效率η(%) 压头H(m)
100
30
80
25
20 60
15
40
η
10
20
H 5
0
0
0
5
10
15
20
25
30
35
流量qv(L/s)
图2 某离心泵特性曲线
ppt课件
8
(2)XY散点图(scatter diagram)
表示两个变量间的相互关系 散点图可以看出变量关系的统计规律
2.5
y
2.0
1.5
1.0
0.5 0 2 4 6 8 10
x
图3
散点图 ppt课件
9
(3)条形图和柱形图
12
10
提取率(%)
8
6 4
2
0 湿浸法
碱提法
醇提法
提取方法
超声波法
图4 不同提取方法提取率比较
用等宽长条的长短或高低来表示数据的大小,以反映各数 据点的差异
列 表外附加通常放在表格的下方,主要是一些不便列在表内
的内容,如指标注释、资料来源、不变的试验数据等
ppt课件
4
(3)注意 :
表格设计应简明合理、层次清晰,以便阅读和使用; 数据表的表头要列出变量的名称、符号和单位; 要注意有效数字位数; 试验数据较大或较小时,要用科学记数法来表示,并记入
应有图注。
ppt课件
18
2.2.2 坐标系的选择
坐标系(coordinate system) 笛卡尔坐标系(又称普通直角坐标系)、半对数坐
标系、对数坐标系、极坐标系、概率坐标系、三角形 坐标系 …... 对数坐标系(semi-logarithmic coordinate system) ➢ 半对数坐标系 ➢ 双对数坐标系
图11 三维等高线图
ppt课件
17
绘制图形时应注意 :
(1)在绘制线图时,要求曲线光滑,并使曲线尽可能通过较多 的实验点,或者使曲线以外的点尽可能位于曲线附近,并 使曲线两侧的点数大致相等;
(2)定,其坐标轴上必须标明该坐标所代表
的变量名称、符号及所用的单位,一般用纵轴代表因变量; (4)坐标轴的分度应与试验数据的有效数字位数相匹配; (5)图必须有图号和图题(图名),以便于引用,必要时还
ppt课件
图6 全球天然维生素E消费比例
12
②环形图(circular diagram)
图7 全球合成、天然维生素E消费比例比较
每一部分的比例用环中的一段表示
可显示多个总体各部分所占的相应比例 ,有利于比较
ppt课件
13
(5)三角形图(ternary)
常用于表示三元混合物各组分含量或浓度之间的关系
第2章 试验数据的表图表示法
ppt课件
1
2.1 列表法
将试验数据列成表格,将各变量的数值依照一定的形式和 顺序一一对应起来
(1)试验数据表 ①记录表 试验记录和试验数据初步整理的表格 表中数据可分为三类: ➢ 原始数据 ➢ 中间数据 ➢ 最终计算结果数据
ppt课件
2
②结果表示表 表达试验结论 应简明扼要
表头,注意表头中的与表中的数据应服从下式:数据的实 际值×10±n = 表中数据; 数据表格记录要正规,原始数据要书写得清楚整齐,要记 录各种试验条件,并妥为保管。
ppt课件
5
2.2 图示法
2.2.1 常用数据图
(1)线图(line graph/chart) 表示因变量随自变量的变化情况 线图分类: ➢ 单式线图:表示某一种事物或现象的动态 ➢ 复式线图:在同一图中表示两种或两种以上事物或现象的
三角形:等腰Rt△、等边△、不等腰Rt△等
顶点:纯物质
边:二元混合物
A
三角形内:三元混合物
●
xB=1- xA- xS
M
●
xA
B
S
xS
ppt课图件 8 等腰直角三角形坐标图
14
0.00 A
1.00
xB
xC
0.25 0.75
xB 0.50
x 0.50 A
E
0.75
xA
1.00
B
0.00
xC
0.25
