如何有效利用主成分分析进行综合评价
主成分分析方法及其应用效果评估

主成分分析方法及其应用效果评估主成分分析(Principal Component Analysis,简称PCA)是一种常用的数据降维技术,被广泛应用于数据分析、模式识别和机器学习等领域。
本文将介绍主成分分析的基本原理、具体方法以及其在实际应用中的效果评估。
一、主成分分析的基本原理主成分分析是一种统计分析方法,旨在将具有相关性的多个变量转化为一组线性无关的新变量,称为主成分。
通过降维,主成分分析可以有效减少数据的维度,并保留原始数据中的大部分信息。
主成分分析的基本原理是通过找到数据中的最大方差方向来构建主成分。
具体步骤如下:1. 标准化数据:对原始数据进行标准化处理,使得每个变量具有相同的尺度。
2. 计算协方差矩阵:计算标准化后数据的协方差矩阵。
3. 计算特征值与特征向量:对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。
4. 选择主成分:根据特征值的大小排序,选择前k个特征值对应的特征向量作为主成分。
5. 构建主成分:将选择的主成分按权重线性组合,得到原始数据的主成分。
二、主成分分析的具体方法主成分分析可以通过多种计算方法实现,其中最常用的是基于特征值分解的方法。
下面介绍主成分分析的具体计算步骤:1. 标准化数据:对原始数据进行标准化处理,使得每个变量具有均值为0、方差为1的特性。
2. 计算协方差矩阵:将标准化后的数据计算协方差矩阵。
3. 特征值分解:对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。
4. 选择主成分:根据特征值的大小选择前k个特征向量作为主成分。
5. 构建主成分:将选择的主成分按权重线性组合,得到原始数据的主成分。
三、主成分分析在实际应用中的效果评估在应用主成分分析时,我们需要对其效果进行评估,以确保选择的主成分能够充分保留原始数据的信息。
常用的效果评估方法有以下几种:1. 解释方差比(Explained Variance Ratio):解释方差比可以衡量每个主成分对原始数据方差的贡献程度。
主成分分析用于多指标评价的方法研究主成分评价

主成分分析用于多指标评价的方法研究主成分评价一、本文概述本文旨在探讨主成分分析(PCA)在多指标评价中的应用及其方法研究。
主成分分析作为一种广泛使用的统计分析工具,其主要目的是通过降维技术,将多个相关变量转化为少数几个独立的综合指标,即主成分,以便更好地揭示数据的内在结构和规律。
在多指标评价体系中,由于指标间可能存在的信息重叠和相关性,直接分析往往难以得出清晰的结论。
因此,利用主成分分析进行降维处理,提取出关键的主成分,对于简化评价过程、提高评价效率和准确性具有重要意义。
本文首先介绍主成分分析的基本原理和步骤,包括数据标准化、计算协方差矩阵、求解特征值和特征向量、确定主成分个数以及计算主成分得分等。
然后,结合具体案例,详细阐述主成分分析在多指标评价中的应用过程,包括评价指标的选择、数据的预处理、主成分的计算和解释等。
对主成分分析方法的优缺点进行讨论,并提出相应的改进建议,以期为多指标评价领域的研究和实践提供参考和借鉴。
通过本文的研究,旨在加深对主成分分析在多指标评价中应用的理解,提高评价方法的科学性和实用性,为相关领域的研究和实践提供有益的启示和帮助。
二、主成分分析的基本原理和方法主成分分析(Principal Component Analysis,PCA)是一种广泛应用于多变量数据分析的统计方法。
其基本原理是通过正交变换将原始数据转换为一系列线性不相关的变量,即主成分。
这些主成分按照其解释的原始数据方差的大小进行排序,第一个主成分解释的方差最大,之后的主成分依次递减。
通过这种方式,主成分分析可以在不损失过多信息的前提下,降低数据的维度,从而简化复杂的多变量系统。
数据标准化:需要对原始数据进行标准化处理,以消除量纲和数量级的影响。
标准化后的数据均值为0,标准差为1。
计算协方差矩阵:然后,计算标准化后的数据的协方差矩阵,以捕捉变量之间的相关性。
计算特征值和特征向量:接下来,求解协方差矩阵的特征值和特征向量。
主成分分析在煤矿安全评价中的应用

主成分分析在煤矿安全评价中的应用1.建立指标体系主成分分析可以通过对煤矿安全相关指标的分析,确定一个综合评价指标体系。
对于煤矿安全评价来说,可以将各类指标分为物理指标(如瓦斯浓度、煤尘浓度等)、技术指标(如瓦斯抽放量、通风量等)、管理指标(如事故率、投入产出比等)等。
通过主成分分析,可以将这些指标综合,得到一个综合评价指标,用于对煤矿安全状况进行评价和比较。
2.确定主要风险因素主成分分析可以通过对煤矿安全指标的分析,确定主要的风险因素。
通过主成分分析,可以对各个指标之间的关联关系进行分析,找出其中具有高度相关性的指标,并将其归纳为主要风险因素。
这样可以帮助煤矿安全管理者更好地了解煤矿安全的脆弱性,有针对性地采取措施来降低风险。
3.评估煤矿安全状况主成分分析可以通过对一段时间内煤矿安全实际数据的分析,评估煤矿的安全状况。
通过主成分分析,可以从多个角度对煤矿安全进行综合评价,从而得到一个客观的安全状况评估结果。
这样可以帮助煤矿安全管理者更好地了解煤矿当前的安全状况,及时采取措施来改善安全状况。
4.风险预警和预测主成分分析还可以通过对历史数据的分析,建立预测模型,用于煤矿安全风险的预警和预测。
通过主成分分析,可以提取出影响煤矿安全风险的关键因素,并建立模型进行预测。
这样可以帮助煤矿安全管理者提前预判潜在的安全风险,并采取措施来避免或减轻事故的发生。
5.优化煤矿管理策略主成分分析可以通过对煤矿安全指标的分析,帮助煤矿安全管理者优化管理策略。
通过主成分分析,可以找到关键的影响因素,并确定其权重,从而更好地分配资源和制定管理策略。
这样可以帮助煤矿安全管理者制定科学有效的管理措施,以提高煤矿的安全水平。
综上所述,主成分分析在煤矿安全评价中具有广泛的应用价值。
通过主成分分析,可以建立综合评价指标体系、确定主要风险因素、评估煤矿安全状况、进行风险预警和预测、优化管理策略等,从而提高煤矿的安全水平。
主成分分析法在综合评价学生成绩中的应用

学) 、 L ( 质量 工 程 I) 、 M( 全面质量 管理 ) 、 N( 机
取几个较少的综合指标 , 尽可能多地反映原来指 标 的信息。主成分分析法也是数学上处理降维的
一
种方 法 , 该方法既降低了数据“ 维数” , 同 时 保
法是适 合用 来综 合评 价学 生成绩 的一 种多 因素 评
价方 法 。
应用 S P S S 软件 , 首先将数据标准化 , 然后计 算各 门课成绩之 间的相关 系数矩阵, 分析结果表 明: ( 1 ) 在被统计 到的 l 7门课程 中, 虽然 c程序 设计 ( C ) 和管理学 ( G ) 的相关性为负 , 但是仅 为
留 了原数据 的大 部 分信 息 。因此 , 主成 分 分 析 方 法 常常被用 来处 理多 指标评 价 问题 。当第 一 主成
械设 计基 础 ) 、 O( 机 械 制 图 Ⅱ) 、 P( 试 验设 计 ( 双 语 Ⅱ) ) 、 Q( 可靠 性 工程 ) 。A—F为公 共 基 础课 , G、 H、 I 、 J 、 K、 N、 O为 学 科 基 础 课 , L 、 M、 P 、 Q 为专
G UAN L l 6oNG CHENG s
主成 分 分析 法在 综合 评 价 学 生成绩 中的 应 用
禹建 丽 , 郑芬芸 , 周 瑞芳 , 胡 紫研
摘 要: 应用 S P S S 数据处理软件对质量与可靠性工程专业学生的课程成绩进行主 成分分析 , 以2 0位 学生 l 7门课程 的成绩为样本进行研 究, 得 出了五个主 成 分的特 征 向量 , 累积 方差贡 献率 达到 8 1 . 2 5 1 %, 同 时给 出 了学生成 绩排
主成分分析综合评价应该注意的问题

主成分分析综合评价应该注意的问题众所周知,综合分析题在国家公务员考试与省级公务员考试中属于相对较难的题型,也是在考试中比较容易失分的题型,综合分析又分为4类题型:要素分析、词句理解、评价分析、比较分析。
接下来一起探讨一下评价分析题。
第一、认识评价分析【基准1】取值资料5提及“报复性看球”这一现象,恳请你根据取值资料4、5,对这一现象展开评析。
(15分后)要求:观点明确,分析透彻,条理清晰,不超过字。
【基准2】“取值资料3”中,郑女士指出:“京剧这个行当真的无法过分商业化,直播中多数人只看见京剧的皮毛和八卦而忽略了京剧艺术本身。
”恳请就她的观点谈谈你的观点。
(15分后)要求:观点明确,分析透彻,条理清晰,字数不超过字。
通过上面两道题,我们不难辨认出,题干中都就是建议学生对资料中发生的观点、现象展开分析,谈论观点、重新认识、看法,其实就是实地考察学生的评价能力。
答题建议中除了经常出现的常规建议之外还可以发生观点明晰这一建议,并且发生的频率比较低,这也属评价分析题的题干特征。
第二、学会评价分析的解题方法评价分析解题方法相比较词句认知来说,解题方法比较简单。
一共分成三步:分别就是抒发观点、论证观点、得出结论。
具体来说:1.表达观点(1)恰当:积极支持、赞成、恰当、认知、很关键等;(2)错误:片面、偏激、不科学、不支持、反对、存在……问题等;(3)部分恰当:不完全正确、须要实事求是对待、有利有弊;(4)不能判断:尚需观察、尚不能确定。
(备注:如果明确要求推论正误必须写下对或错)对观点(或社会现象)结合材料进行解释,材料中没有解释可以用自己的理解简单解释。
2.论证观点判断观点的理由:材料中的对表态有利的信息都是理由。
3.得出结论可针对观点(或社会现象)提出简单对策;可再次对观点进行肯定或总结。
第三、评价分析题完备的答题示范点1.执法部门的做法其出发点是好的,值得借鉴,但也存在问题,应进一步完善。
(表达观点)2.首先,广场晒谷可以化解农民晾干缺乏场地的问题,火车站边线偏远,农忙时节旅客较太少,农民晾干基本不能对旅客乘车和公共安全导致影响。
主成分分析和聚类分析在高职学生成绩综合评价中的应用

主成分分析和聚类分析在高职学生成绩综合评价中的应用作者:***来源:《计算机时代》2023年第11期关键词:主成分分析;聚类分析;学生成绩;综合评价中图分类号:G717 文献标识码:A 文章编号:1006-8228(2023)11-64-05 0 引言职业院校经常需要对学生成绩进行综合评价,以检测学校管理、教育教学和人才培养的成效,进而做出相应的调整及改进。
目前,学生成绩综合评价应用较多的方法是加权综合评分法或将各种成绩简单的相加,由于加权评分法中的权重设置容易受人为因素的影响,而各项成绩简单的相加又不能体现学生综合的学习能力,这些方法都存在各自的缺点[1],这里基于主成分分析给出一个简单实用的综合评价方法,并在此基础上进一步对学生成绩进行聚类分析,相对有效的解决了上述评价方法存在的问题,有利于因材施教,提升人才培养质量。
1 数学模型1.1 主成分分析基本思想主成分分析是一种数据“降维”分析方法。
其基本思想是将原来众多的具有一定相关性的指标,重新组合成一组新的互不相关的综合指标来代替原来指标。
通常数学上的处理就是将原来多个指标作线性组合,作为新的综合指标[2]。
问题是如何选取相应的线性组合。
代入数据计算学生各主成分得分如下表3 所示,由每位学生的主成分得分代入综合评价函数,可以得到综合得分,按照综合得分大小排序,就得到每位学生的名次,由于排名是通过统计分析计算得到,其排名结果将减少主观因素,反映某些实际情况。
結果分析:第一主成分中x1,x4,x5,x6,x7五个变量的系数比较大且都为正数,说明第一主成分主要由这五个变量决定,且与这五个变量的取值成正相关,从这五个变量分别所代表的课程(英语、高等数学、计算机基础、Linux 基础、Python 语言程序设计)来看,他们相对于其他两门课程(道德与法治、体育),是专业核心课,传统学分占比也较大,是反映高职学生技能水平和决定一位学生成绩的主要方面,得分较高,名次就较高,这与目前实际情况也是相符的。
基于主成分分析的我国各地区经济发展水平综合评价(2)

基于主成分分析的我国各地区经济发展水平综合评价摘要我国幅员辽阔,但是由于历史发展、地理位置、自然条件、人口、政策等因素影响,各地区经济发展水平存在很大差异。
本文通过建立我国各省、直辖市、自治区社会经济发展的综合评价指标体系,运用主成分分析方法,计算出各地区经济发展水平的综合得分,得出综合排名,并对结果作出分析,提出相应的建议对策,旨在促进区域共同发展。
关键词:经济发展水平;主成分分析法;对策AbstractChina area is very large,but because of the historical development , geographical location, natural conditions , population, policy and other factors, there is a big difference in the level of economic development of the region. This article through the establishment of a comprehensive evaluation system of provinces, municipalities and autonomous regions of socio-economic development , the use of principal component analysis method to calculate the level of economic development in all regions composite score , ranking results , and to analyze the results ,make recommendations measures to promote common development of the region.Keywords : the level of economic development;principal component analysis ;countermeasures引言地区经济发展是指一个地区从贫困、落后的状态向经济及社会生活现代化发展的过程。
主成分分析综合评价应该注意的问题

主成分分析综合评价应该注意的问题随着科学技术与质量活动的日益深入,统计学在质量评价管理中发挥了重要作用,以及汇总多维数据,将它们归纳为有限数量的衡量变量。
在这些方法中,主成分分析(PCA)是最常用的一种,它可以有效地压缩原始数据,并将其转换为可以三维可视化的表示形式。
PCA 是一种有用的工具,可以帮助改进和提高质量管理的工作效率和效果。
然而,在使用PCA进行综合评价时,应该注意一些问题,以确保评估的准确性和可靠性。
首先,评估者必须正确地确定动因和衡量变量的范围,它们是确定主要因素和价值的关键因素。
其次,应检查衡量变量之间的相关性,以确定其评价影响和贡献程度。
此外,应评估数据的质量,以确保数据准确,并采取必要措施来纠正任何质量问题。
最后,当选择PCA时,应检查数据中的噪声水平,排除有害因素并正确校准结果。
除了上述注意事项之外,PCA还可以用来识别待评价对象的关键特征,以及识别重要关联的变量和因素。
识别这些特征可以帮助理解影响指标的因素,从而有效地实施绩效评估。
此外,评估者还可以利用PCA来比较受评价对象之间的差异性,以及对其影响因素的衡量。
最后,需要强调的是,PCA并不能像多元统计分析那样涵盖更多的变量,但它可以帮助识别出评价的关键结构,从而有助于绩效管理的有效实施。
基于上述原因,在使用PCA进行综合评价时,必须首先认真考虑上述注意事项,以确保有效的绩效评估结果。
总而言之,PCA在质量管理中发挥了重要作用,但在使用PCA进行综合评价时,必须注意确定衡量变量范围、检查衡量变量相关性、评估数据质量、检查数据中的噪声水平等因素,以确保评估结果的准确性和可靠性。
而且,识别PCA所测量的特征可以有效实施绩效评估,而PCA还可以帮助比较受评价对象之间的差异性,以及对其影响因素的衡量。
此外,在实施PCA前,还需要深入了解PCA的本质,以及PCA评价的局限性,并提前了解不同因素对结果的影响,以获得准确判断。
因此,只有掌握这些问题,才能使PCA对绩效评价产生有效效果。
基于主成分分析的综合评价
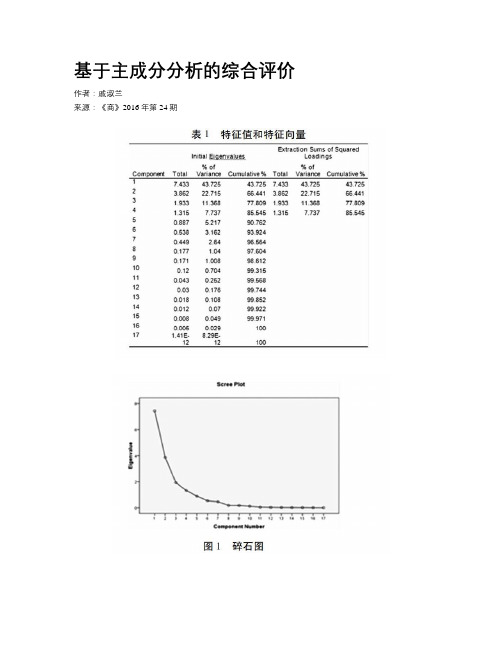
基于主成分分析的综合评价作者:戚淑兰来源:《商》2016年第24期摘要:研究综合评价研究问题关于社会、环境、经济等很多领域,是将事物的时效性,准确性,经济性以及满意性等方面进行评价的过程。
这要经过一定的途径将许多评价指标值合成一个综合性的评价指标值,从而进行综合评价。
主成分分析是一种重要的统计分析方法,它不仅可以想办法把原来很多具有一定相关关系的指标重新组合成一组新的且相互之间没有关系的指标,而且还能显示出比较客观的权重。
关键词:主成分分析;综合评价;环境污染;工业发展;spss.一、引言评价是一个综合咨询、计算和观测等方法的一个综合分析的过程。
但是这个过程需要评价者做出相应的指示。
综合评价就是将事物的准确性,时效性,经济性以及满意性等方面进行评价的过程。
但是评价者在评价这个过程中很容易主关干预,造成评价的结果偏离原来的结果。
多元统计分析是探讨多维变量总体,总体的每一个个体都可用p项指标来表示,虽然指标多能够描述详尽,显示细腻的一方面;但由于指标很多就较易造成分不清主次,对研究的对象很难做一个直接清楚的判断。
而主成分分析作为综合分析的一种统计方法,能够比较好的保证评价的结果是客观的。
主成分分析作为了一种比较科学的、客观的评价方法。
使综合评价的结果更加的科学,更加的实效。
二、研究背景人类的生产及生活过程与环境资源和生态环境有着很强的关系。
随着科学技术与经济的发展,人民生活水平的提高,工业的发达,废弃废料的排放造成很大程度的环境破坏和环境污染。
中国作为一个发展中国家,随着改革开放和经济的高速发展,环境污染也随之呈加剧之势。
经济发展与环境污染已经成为一个越来越重要的话题。
现在我们国家处于经济转型期,要把经济效益、环境保护以及产业结构相结合起来,形成经济新常态。
运用主成分分析综合评价的方法,寻找各省市经济发展、工业产值与环境污染状况之间的关系,而且对评价结论进行了解释。
三、主要思路经过探讨指标体系里面的结构关系就可以把许多个指标转换为相互之间没有关系的、含有初始指标的大部分内容的少数的几个综合性指标,运每个主成分的方差贡献率对那些指标加权得到综合评价得分。
主成分分析法在水质综合评价中的应用

主成分分析法在水质综合评价中的应用学习主成分分析法的目的是:对水质评价因子进行筛选、组合,用于水环境综合整治工程的指导。
本论文就是以主成分分析法为依据建立综合评价模型,利用神经网络算法确定各评价因子的权重。
在神经网络算法的基础上,选取C-C作为遗传算法的初始值,经过多次迭代后,最终确定评价指标。
1、评价体系设计理论评价体系设计理论包括:确定指标体系的原则与指标赋权方法;确定指标的筛选方法;构建权重集;构建评价模型。
2、主成分分析法及其应用根据前人研究结果得出,水环境质量的综合评价指标具有高度的相关性和重复性,通过聚类分析将各因子划分成不同的类别,选择相应的阈值作为主成分,并根据重要性排序法确定权重,从而确定出最优综合评价指标体系。
3、基于成分相似性度量和分析结果,建立了数据驱动的评价模型基于主成分分析法,确定因子的权重。
通过改变因子的评价方式,以及根据因子的重要性赋予不同权重,对上海市黄浦江两岸水质综合评价模型进行重新调整,实现了三类评价指标之间的互补性。
基于因子重要性赋予评价指标权重的步骤是:①评价指标的选取及水平权重的确定。
由于水质的复杂性,采用因子评价指标体系,可以保证较大的信息容量。
②对水质评价指标的确定。
主成分的选择是关键问题,也是最难处理的问题,即综合评价指标选取时存在一个怎样的阈值问题。
③基于相似性指标和重要性,确定综合评价模型的形式。
④对比实例验证模型的可靠性。
4、结果及讨论3、基于成分相似性度量和分析结果,建立了数据驱动的评价模型。
因此,建立评价模型过程中应该遵循从简单到复杂,由单因素逐步过渡到多因素的规律,才能使分析结果更接近真实情况。
4、结果表明,建立的模型能很好地反映水质质量的状况,尤其适用于短时间的水质评价,以便于快速进行环境整治工程的决策。
主成分分析与聚类分析在地区综合实力评价中的应用

主成分分析与聚类分析在地区综合实力评价中的应用【摘要】本文选取具有代表性的7类共17个指标作为我国31个省、市、自治区综合实力评价的原始指标,运用主成分分析得到综合评价函数,计算得到我国各省市的综合得分,并据此进行K均值聚类分析,将我国31个省、市、自治区划分为5个类型,根据聚类结果对其进行了简单评价。
【关键词】主成分分析聚类分析综合实力评价一、主成分分析法主成分分析也称主分量分析,由于多个变量之间往往存在着一定程度的相关性,人们希望通过线性组合的方式,从这些指标中尽可能快地提取信息。
主成分分析旨在保证原始数据信息损失最小的前提下,通过线性变换对高维变量空间进行降维处理,以少数的综合变量取代原有的多维变量。
由于主成分是通过正交变换得到的,因此各个主成分是互不相关的,且第一个主成分的方差最大,其余次之。
主成分分析能够从选定的指标体系中归纳出大部分信息,并且能够根据指标间的相对重要性进行客观加权,可以避免评价者的主观影响,因此主成分分析在综合评价中的应用越来越得到人们的重视。
根据主成分分析法进行综合评价的步骤如下:将原始数据标准化并建立变量的相关系数矩阵R;求出R的特征根λ1≥…≥λp≥0相应地特征向量为T1,T2…Tp;由累计方差贡献率确定主成分的个数(m),并写出主成分为:Y=T’X(1);以特征根维权,构造综合评价函数Z。
各个主成分的权重分别为wi=λt/ λi(i=1,2,…p)(2),Z=w1Y+w2Y+…+wPY=W’Y=W’T’X=(TW)’X=(3)。
二、聚类分析法聚类分析(cluster analysis)是一组将研究对象分为相对同质的群组(clusters)的统计分析技术。
本文采用聚类分析中的K均值聚类,以主成分分析得到的各地区的综合实力得分为聚类变量,以距离的远近亲疏为标准进行聚类,类数的确定参考系统聚类的结果。
三、综合实力指标的选取影响一个地区综合实力的指标有很多,本文参考国内外相关文献资料,综合考虑各种因素的影响力和数据的可得性,选择了以下七个方面的十七项指标作为综合评价的指标。
主成分分析方法在经济评价中的作用

4)主成分载荷
定义主成分载荷为第j个主成分与第i个原始变 量的相关系数,经推导可得:
lij ( yi , x j )
i ii
pij
其含义是:原变量xj 在第i个主成分上的载荷, 它反映了主成分yi与原变量xj之间的关联程度。
3. 利用主成分分析进行综合评价
人们进行综合评价时,都会遇到如何选择评价指标 体系和如何对这些指标进行综合的困难。
1)协方差矩阵及数据的协方差
注意1: 协方差矩阵计算的是不同维度(指标)之间的协方差,而 不是不同样本之间的。
注意2:协方差,反应了两个维度之间的线性相关程度。 协方差越大,则线性相关性越大,数据的维度冗余也越大。
注意3:协方差矩阵在对角线上的元素越大,表明信号越 强,变量的重要性越高;元素越小则表明可能是存在的 噪声或是次要变量。在非对角线上的元素大小则对应于 相关观测变量对之间冗余程度的大小。
第一个主成分,是输入样本协方差阵的具有最大特征 值对应的特征向量。
特征向量不唯一,如何选取呢?一般选取特征向量的元素 之和为正数的这个向量。
2. 主成分分析的数学知识
3) PCA中的主成分及贡献率
累积贡献率:前k个主成分共有多大的综合能力,用这k个
主成分的方差和在全部方差中所占比重来描述,称为累积
线性代数理论的经济学应用系列专题之
主成分分析方法 在经济评价中的应用
1. 概述
主成分分析Principle Component Analysis(PCA) , 是一种通过降维来简化数据结构的方法。
其目的是把多个变量化为少数几个综合变量(综合指标), 这几个综合变量可以反映原来多个变量的大部分信息,但 指标之间要相互独立,互不相关。主成分分析主要起着降 维和简化数据结构的作用。
主成分分析法与熵权topsis法综合评价医疗质量

中国卫生统计2019年12月第36卷第6期・919・主成分分析法与爛权TOPSIS 法综合评价医疗质量师先锋I 徐湘$秦伟$医疗质量反映了一所医院的整体医疗服务水平,合秩和比(RSR)法⑸对某医院2008 -2017年的主要医对于医疗质量客观合理的评价可以让医院管理者比较疗质量指标进行综合性评价,客观反映医院医疗质量和全面的了解医院现状,同时也可以为医院质量不断提 升提供决策依据。
由于反映医疗质量的指标种类繁 多,如果采用单项指标进行统计分析不够全面很难以做出客观科学的评价,如果采用单种评价方法进行综合性评价难以避免判断的主观性,如何科学合理的评 价医疗质量,寻求可以针对多指标进行客观性评价的 综合评价方法成为医院管理者的一项难题⑷。
近年 来,国内研究者在比较国内外医院质量评价模型的基础上,在制定适合国情医疗质量评价体系的研究方面 取得了一定的成果⑵,但并没有最终形成一个统一的体系可以合理有效的评价医疗质量。
本文采用 主成分分析法⑶和优劣距离法(爛权TOPSIS 法)⑷结表1某医院2008 -2017年医疗质量评价指标年度兀X 2X3X4&*6X720081694387. 3910. 2729. 7899. 2499. 9792. 6586. 3520091867293. 079. 5432.6499. 5099. 9693. 108& 71201020835100. 279.4035.3199. 7499. 9693.5086. 9220112295095. 839.7133. 9599. 7099.9094. 2386. 27201227427100. 509.4035. 8599. 6399. 9795.5684. 93201328215106. 339. 7336. 8899. 7999. 9797.0385.5020143047396. 589. 3735.6499. 82100.0098.0480. 9920152880784. 409. 5032. 3099. 72100.0097. 4381.9920163227892.049.0936. 2799. 0299. 9997. 3282. 2620173213691.699.0136. 1199.6199. 4297.6082. 582.方法(1) 主成分分析进行质量评价① 对于低优绝对指标利用采用倒数法(即100/X),低优相对数指标采用差数法(即1-X )进行指标的同趋势化处理。
基于主成分分析模型的我国商业银行绩效评估

基于主成分分析模型的我国商业银行绩效评估随着我国经济的快速发展,商业银行在推动经济发展、支持实体经济方面发挥着重要的作用。
为了有效评估商业银行的绩效,提高其运营效率和风险管理能力,需要建立科学合理的评估模型。
本文将基于主成分分析模型,来评估我国商业银行的绩效。
主成分分析是一种常用的多指标综合评估方法,它通过将多个指标综合成一个新的综合指标,从而减少指标数量和复杂度,并揭示指标之间的关系。
在商业银行的绩效评估中,我们可以选择几个重要的指标作为评估对象,如利润水平、资本充足率、不良贷款率、存贷款比等。
我们需要收集商业银行的相关数据,包括每家银行的利润、资本充足率、不良贷款率、存贷款比等指标。
然后,对这些数据进行标准化处理,以消除量纲差异和指标之间的差异。
标准化可以采用z-score方法,将每个指标减去平均值,再除以标准差。
接下来,我们使用主成分分析方法对标准化后的数据进行综合评估。
主成分分析的目标是找到少数几个具有代表性的主成分,这些主成分能够解释原始数据中大部分的变异。
我们可以通过主成分分析的结果,得到每个主成分的权重,并计算每家银行的综合评分。
我们根据得到的综合评分对商业银行进行绩效评估。
我们可以将商业银行划分为优秀、良好、一般和不良等几个不同的等级。
优秀的商业银行在各个指标上表现出色,并且综合评分较高,良好的商业银行在大部分指标上表现良好,综合评分较高,一般的商业银行在部分指标上表现一般,综合评分较低,不良的商业银行在多个指标上表现较差,综合评分较低。
基于主成分分析模型的绩效评估可以帮助我们快速了解商业银行的综合表现,并找出存在问题的指标,以便及时采取措施改进。
这种评估方法具有定量化的特点,能够客观评估商业银行的绩效,并为决策提供科学依据。
基于主成分分析的土壤肥力综合指数评价

3 国 家 “十 一 五 ”科 技 支 撑 计 划 资 助 项 目 ( 2006BAD05B07、 2007BAD89B16、2006BAD25B09) 。 3 3 通讯作者 E2mail: txhong@ hotmail. com 收稿日期 : 2009206209 接受日期 : 2009209209
主成分分析在综合评价中的应用

四川农业大学商学院课程论文《数据处理方法》课程论文论文题目:主成分分析在综合评价中的应用成员1:工作:分数:成员2:工作:分数:成员3:工作:分数:成员4:工作:分数:2013-5-14主成分分析在综合评价中的应用摘要本文根据2007年各地区国有及国有控股工业企业主要经济效益指标的统计数据,进行主成分分析并选取三个主成分,运用主成分对各地区进行综合排名。
运用K均值聚类,得出的结果与主成分综合排名进行比较,结果相当吻合,主成分分析可广泛运用于经济指标数据分析。
关键字:主成分分析经济效益指标综合排名分类Application of Principal Component Analysis in the analysis of Economic Data Xionghao, Information and Computing Science, 20109271Yang Xiaotao, Information and Computing Science, 20109281Zou Huimin, Financial Management, 20118795Zhao Wenqin, Financial Management, 20118793Abstract: according to the 2007 state-owned and state holding industrial enterprises in various areas of the main economic benefit index statistics, principal component analysis and three principal components and using the principal component comprehensive ranking for all regions. Using k-means clustering, and the results comparing with principal component comprehensive ranking and the results are consistent, principal component analysis data analysis can be widely used in economic indicators.Key words: principal component analysis ;Comprehensive ranking ;Classification1.问题描述经济数据分析结果对国家的宏观调控与企业决策有着至关重要的作用。
stata主成分分析综合得分

Stata主成分分析(PCA)是一种常用工具,被用来进行多元数据分析,可以通过减少变量数量而减少统计数据的负荷。
它找出与数据集最有
联系的核心有用特征,将原始变量合并成较少的几个新的变量,从而
捕捉到数据的最重要的信息。
因此,Stata主成分分析对研究和分析有重要的意义,因为研究人员可
以处理更复杂的数据集,并通过PCA获得更好的数据概括。
Stata主成分分析是一项复杂的统计分析,由于其结构及其原理的复杂性,也是一项具有挑战性的工作。
主成分分析不仅可以简化数据,而
且可以提供对原始数据的有效描述。
研究人员可以有效地估计数据的
核心特征,并减少变量的数量,以便分析结果的精度和准确性更高。
因此,Stata PCA可以帮助研究人员获得统计数据并像拼图一样组装他们。
研究人员可以深入了解数据集,而如果不使用PCA,分析数据将
变得复杂和困难,因为它会使研究变得更加复杂。
总之,Stata PCA作为一项重要的工具,可以帮助研究人员深入地理解
数据,同时减少数据分析的负担。
它可以帮助研究人员准确地把握数
据的核心特征,并减少变量的数量,提高分析精度。
主成分分析

主成分的几何解释
主成分分析用数学模型表达,即对X进行 正交变换,在几何上就是作一个坐标旋 转。因此,主成分分析在二维空间中有 明显的几何意义。 假设共有n个样品,每个样品都测量了两 个指标(X1,X2),它们大致分布在一 个椭圆内:
事实上,散点的分布总有可 能沿着某一个方向略显扩张, 这个方向就把它看作椭圆的 长轴方向。显然,在坐标系 x1Ox2中,单独看这n个点的 分量X1和X2,它们沿着x1方 向和x2方向都具有较大的离 散性,其离散的程度可以分 分 别用的X1方差和X2的方差测 定。如果仅考虑X1或X2中的 任何一个分量,那么包含在 另一分量中的信息将会损失, 因此,直接舍弃某个分量不 是“降维”的有效办法。
Y1 = T1′ X 。
第一主成分的约束条件
第二主成分为, 第二主成分为,满足 T2′T2 = 1 ,且 Cov(Y2 , Y1 ) = Cov(T2′ X, T1′ X) = 0 , 使得 D(Y2 ) = T2′ ΣT2 达到最大的 Y2 = T2′ X 。 一般情形, 主成分为, 一般情形,第 k 主成分为,满足 Tk ′Tk = 1 , 到最大的 Yk = Tk ′ X 。 ,使得 且 Cov(Yk , Yi ) = Cov(Tk ′ X, Ti′ X) = 0 ( i < k ) 使得 D(Yk ) = Tk ′ ΣTk 达 ,
在这p个新变量Y中可以找到m个(m<p) 的变量(y1,y2,…,ym)能解释原始数据 中大部分方差所包含的信息。此时我们 将原始的p个变量X缩减为m个新变量y, 通过m个新变量来传递原始变量的大部 分信息,同时缩减了数据的维数。
如何找到新变量Y及正交阵T
之前说过,这一组新的变量y1,y2,…,yp 要充分反映原变量的信息,且相互独立。 信息能否反映充分,我们用变量的离异 程度来衡量,即标准差或方差。因此寻 找主成分Y的问题转化为,在保证新变量 y1,y2,…,yp相互独立的条件下,求某一 个线性组合T,使D(Y)达到最大。
主成分分析在综合评价中的应用模型

主成分分析在综合评价中的应用张毅(长江大学信息与数学学院,湖北荆州 434023)[摘要] 应用主成分分析原理,以少数的综合变量取代原有的多维变量,使数据结构简化,把原指标综合成几个主成分,再以这几个主成分的贡献率为权数进行加权平均,构造出一个综合评价函数.文章应用该原理对23家电器企业的实力进行了综合评价,其结果是合理可信的.[关键词] 主成分分析;综合评价;排序[中图分类号] O29 [文献标识码] A [文章编号] 1008-4657(2005)06-0062-04 排序问题在我们日常生活中经常碰到,对单指标系统中的各样本点进行排序,按指标值的大小排序就可以了.而对多指标系统中的各样本点进行排序就不能按各指标值的大小这一简单原则进行了,一个常用的方法是对各指标进行总和平均后,按平均值的大小进行排序.但有时由于各指标间的量纲不一样,就不能进行加法运算了.再者,即使各指标间的量纲一致,可以作加法运算,而各指标反映系统侧面不同,对系统的作用不一样,作加法运算时,存在一个权系数的处理问题,而权系数的取定没有一个统一的标准,这样就不能得到统一的排序结果.同时,在很多情况下各指标间有一定的相关性,甚至是严重相关,从而使得这些指标所提供的信息在一定的程度上有所重叠,求和时系统信息会重叠计算,也不能得到令人信服的排序结果.本文利用主成分分析原理,对多维空间实行降维处理,在系统变异信息损失最小的情况下,得到线性无关的几个主成分,利用主成分得分,对系统中各样本点进行综合评价,这样就排除了各指标间由于量纲不同和信息重叠所造成的影响,不用人为规定权系数,排除主观因素的干扰,使得计算结果更加科学、真实可靠.1 应用实例我们对23家家电类上市公司2005年1月的财务指标作主成分分析,设定综合评价指数对23家公司进行排序,并用聚类分析验证了排序的正确性.这6项财务指标分别为:每股盈利x1(元),每股净资产x2(元),主营利润率x3(% ),净资产收益率x4(% ),负债率x5(% ),每股公积金x6(元).数据来源于武汉证券公司,数据如表1.表1 23家公司基本情况表公司名称x1x2x3x4x5x6科龙电器0. 06 2. 89 17. 95% 2. 11% 0. 75% 1. 5894康佳电器0. 03 5. 34 14. 75% 0. 64% 0. 65% 3. 0858ST华发0. 00 0. 82 -3. 91% -0. 31% 0. 44% 0. 3584TCL -0. 13 1. 98 14. 83% -5. 99% 0. 82% 0. 7662小天鹅0. 03 3. 16 22. 27% 1. 04% 0. 63% 2. 217862续表1 23家公司基本情况表公司名称x1x2x3x4x5x6美菱电器0. 02 2. 09 19. 31% 1. 08% 0. 64% 1. 3843美的电器0. 11 5. 62 17. 39% 1. 99% 0. 77% 2. 0633万家乐0. 00 1. 04 30. 98% 0. 04% 0. 81% 0. 1263ST湖山-0. 01 0. 68 11. 86% -1. 32% 0. 61% 0. 0377夏新电子0. 01 3. 07 21. 90% 0. 25% 0. 68% 0. 7019海信电器0. 05 4. 94 16. 35% 1. 05% 0. 40% 3. 0019ST博讯-0. 01 0. 08 3. 57% -1. 90% 0. 89% 0. 1052ST福日0. 21 2. 09 2. 33% 10. 11% 0. 68% 1. 1370浙江阳光0. 15 5. 26 19. 44% 2. 83% 0. 42% 2. 7996澳柯玛0. 02 3. 57 16. 50% 0. 51% 0. 70% 2. 4720广电信息0. 01 4. 47 4. 59% 0. 28% 0. 52% 2. 9576春兰股份0. 01 5. 81 10. 85% 0. 23% 0. 39% 2. 9625厦华电子0. 03 2. 20 11. 83% 1. 24% 0. 76% 2. 5512四川长虹0. 08 4. 45 14. 50% 1. 80% 0. 35% 1. 8879大显股份0. 01 2. 17 14. 51% 0. 59% 0. 39% 0. 5229宁波富达0. 01 1. 92 16. 22% 0. 59% 0. 61% 0. 2551青岛海尔0. 05 4. 83 11. 94% 1. 09% 0. 18% 2. 4520飞乐音响0. 02 1. 78 15. 84% 1. 17% 0. 53% 0. 3309首先,将数据标准化处理,然后将处理后的数据,利用SAS软件,可得指标x1,x2,x3,,,x6的相关系数矩阵为:R =1.00000.3793 1.0000-0.0627 0.1673 1.00000.9287 0.2122 -0.1150 1.0000-0.2134-0.4582 0.1825 -0.1637 1.00000.3316 0.8670 0.0329 0.2176 -0.3358 1.0000从相关系数矩阵可看出,x1与x4,x2与x6之间强相关,系统信息有重叠,计算出相关系数矩阵的特征值、特征向量及其贡献率如表2.表2 贡献率及累计贡献率主成分特征值贡献率累计贡献率1 2. 68060 0. 446767 0. 446772 1. 44684 0. 241140 0. 687913 1. 09278 0. 182130 0. 870044 0. 61751 0. 102918 0. 972955 0. 11415 0. 019024 0. 991986 0. 04813 0. 008021 1. 0000063由上表可知,当主成分个数为3时,累计贡献率已经有了87. 01%,所以主成分个数取三个即可.则其对应的主成分为:y1=0.484429x1+0.496377x2-0.025010x3+0.426082x4-0.335658x5+0.483393x6; y2=0.453670x1-0.432427x2-0.321221x3-0.209738x4+0.188846x5-0.396159x6; y3=0.196254x1+0.057543x2+0.804400x3+0.171089x4+0.530876x5+0.003727x6. 从上述公式可看出,第一主成分y1主要是由x1,x2,x4,x6的系数决定的,并且权重值相差不大,由各指标的实际意义,可知第一个主成分主要反映了企业的收益水平和资产的增利水平;第二主成分y2中,x1系数最大,x2系数最小,可知第二个主成分主要经营策划能力,即以少的资产获得较大的利润.第三主成分y2中x3的系数最大,x5的系数次之,其它系数较小,可知第三个主成分则集中反映了企业经营能力和负债偿还能力.评价系数W为:W =K1K1+K2+K3y1+K2K1+K2+K3y2+K3K1+K2+K3y3利用表2中的数据,可计算出y1,y2,y3,同时能计算出W,从而得出综合评价结果.排名如表3.表3 综合评价结果公司名称第一主成分第二主成分第三主成分综合评价结果名次科龙电器2. 21799 -1. 89662 0. 33603 0. 68362 12康佳电器4. 12284 -3. 5606 0. 44796 1. 224007 3ST华发0. 57366 -0. 48605 0. 01839 0. 163712 21TCL 1. 25058 -1. 29823 0. 2047 0. 32521 19小天鹅2. 62972 -2. 296 0. 38032 0. 793623 10美菱电器1. 70006 -1. 49789 0. 28997 0. 518531 15美的电器3. 82122 -3. 24103 0. 50011 1. 168614 4万家乐0. 56573 -0. 59752 0. 31389 0. 190604 20ST湖山0. 3399 -0. 35783 0. 13369 0. 103349 22夏新电子1. 85421 -1. 66867 0. 36146 0. 56532 14海信电器3. 89644 -3. 34864 0. 44079 1. 164996 5ST博讯0. 07269 -0. 1012 0. 03323 0. 016234 23ST福日1. 71762 -1. 20872 0. 2054 0. 589991 13浙江阳光4. 0147 -3. 36146 0. 50608 1. 235838 2澳柯玛2. 94768 -2. 56283 0. 35596 0. 877843 9广电信息3. 62206 -3. 11229 0. 31045 1. 062323 7春兰股份4. 28818 -3. 71432 0. 43716 1. 264044 1厦华电子2. 31406 -1. 97806 0. 24338 0. 690985 11四川长虹3. 14422 -2. 67179 0. 40044 0. 957878 8大显股份1. 3271 -1. 18356 0. 24859 0. 405473 16宁波富达1. 07506 -0. 97444 0. 24812 0. 333911 17青岛海尔3. 58354 -3. 06925 0. 39582 1. 072343 6飞乐音响1. 04913 -0. 93509 0. 23983 0. 329767 1864从表3中,我们可以看出,排在第一位的是春兰股份.春兰公司是我国白色家电的龙头企业,也是我国最早生产家用空调的企业之一,它现已成为中国家喻户晓的品牌,空调产品国内市场占有率始终名列前茅,洗衣机、摩托车等产品也具有较高的知名度和市场占有率,核心竞争力非常突出.排在第二位的是浙江阳光,浙江阳光股份公司主营业务是节能电光源、照明电器、仪器设备的开发、制造和销售,该公司强抓管理,降低成本,使产品的市场占有率进一步提高,经济效益稳步增长.排在最后一位的是ST博讯,由于上市当年就出现巨额亏损,引起股民哗然,被中国证监会查实有虚假上市行为,受到国务院的通报批评,并成为中国第一家被刑事起诉的上市公司.为了验证上述分析的正确性,下面我们用AVE法对上述23个公司进行聚类分析.从分类图和伪t2及伪F统计量可知, 23家上市公司可分为4类,分类情况如表4.表4 公司分类情况公司名称类别公司名称类别公司名称类别科龙电器3 ST湖山4春兰股份1康佳电器1夏新电子3厦华电子2ST华发4海信电器1四川长虹2TCL 3 ST博讯4大显股份3小天鹅2 ST福日3宁波富达3美菱电器3浙江阳光1青岛海尔1美的电器1澳柯玛2飞乐音响3万家乐4广电信息1从聚类进程图中,我们可以明显看出,公司可以分为四类(见表4):春兰股份、浙江阳光、美的电器、康佳电器、海信电器、青岛海尔为一类,是综合实力最强的公司,它们的评价系数排名也在前列.而ST华发、ST湖山、万家乐、ST博讯成一类,它们的评价系数排名排在后面,为实力较差的一类公司.2 结束语主成分分析法是一种多指标分析方法,目前已有不少研究者将它应用于社会中的很多方面.本文利用主成分分析法以及聚类分析对公司效益进行综合评价,其结果是合理的.利用主成分分析法进行综合评价可以消除评价指标之间的相关性;另外,在综合评价函数中,各主成分的权数为其贡献率,它反映了该主成分包含原始数据的信息量占全部信息量的比重,这样确定权数是客观、合理的,它克服了某些评价方法中人为确定权数的缺陷;这种方法的计算比较规范,便于在计算机上实现.[参考文献][1]范金城,梅长林.数据分析[M].北京:科学出版社, 2002.[2]何哓群.现代统计分析方法与应用[M].北京:中国人民大学出版社, 1998. 281-315.[3]王学仁,王松桂.实用多元统计分析[M].上海:上海科学技术出版社, 1990.[4]吴翎.应用数理统计[M].北京:国防科学技术大学出版社, 1995. 285-303.The Application ofPrincipalComponentAnalysis in the Comprehensive Assessment of SocietyZHANG Yi (YangtzeUniversity, Jingzhou,Hube,i 434000,China)Abstract:Ifwe apply the theory of principle component analysis, which can use less comprehensive variables to instead ofthemultivariate variables, thismethod can simplify the structure of the data and aggregate the original index into severalprincipal components. Regarding the contribution rate of this principal componentas right, countweighted average andmake up a compre-hensive function. This textapplies the theory ofprincipal componentanalysis to assess the evaluation of23 companies in real life, and the result is convincing.Key words:principle component analysis; comprehensive assessment; judge the value65。
主成分分析在电网线损管理综合评价中的应用分析

主成分分析在电网线损管理综合评价中的应用分析摘要:电网线损受各种因素的影响:电网结构特征;设备物理参数;电网运行特征;用电特征;以及各种自然状况。
传统的管理方式无法客观地评价其线损。
通过主成分分析的方法,能够满足各种不同的分析状况,也可以进行独立性较高的分析。
本文主要从主成分分析的评价方法,并根据其实际线损排序和理论排序的差异,对管理工作进行评价。
通过此次研究,我们探寻了该方法的实际可行性,以及效率的高低。
并结合同期线损系统的正式上线运行,通过该系统实时监测电网线损的情况,及时的对实际线损和理论线损作比对,通过比对得出的结论及时纠正管理线损存在的问题,有效且合理的的提高了降损的效率。
关键词:主成分分析;电网线损;管理方式;综合评价;同期;应用分析;合理降损电网的线损关系着企业的经济利益,它是电力系统在运行时非正常损耗的指标。
它的大小体现了电网的科学合理性,第一是电网结构的合理性;第二是电网生产方式的合理性;第三是其管理方式的合理性。
电网线损的大小并不是仅仅由管理的合理性来决定的,它也受其他因素的影响,例如电网本身的合理性。
因此,将管理等价为线损的数值大小是不科学的。
传统的电力企业评定线损的方式主要是根据过去一段时间的运行情况来判断。
这种方式对电力系统的探知不全面,导致管理工作失去了科学性。
另外电网线损数值较小,并不代表管理更加科学。
也有可能是电网本身的属性较好。
所以要对电网的成分进行分析,并不能单单靠线损数值来判定电网管理的开展优良程度。
目前,我国电力企业评价线损的主要方式有以下几种:电量比重评价;同类划分评价;最小方差评价;聚类分群评价。
第二种和第四种都是通过多维的角度来进行电网性能的评判,它在空间层面上对电网进行了总结,在在这个总结的集合内划分很多的有限元,对这些有限元进行评价。
这种方法忽略了各个指标的关联性,使得电网管理不够科学。
针对这一现象,我们提出了主成分分析方法。
这个方法是利用主成分评价电网的线损,它通过建立数学模型的方式反映电网的指标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何有效利用主成分分析进行综合评价 摘要:由于主成分分析在多元统计分析中的降维作用,使之在社会、经济、医疗、生化等各领域运用越来越广泛,但由于传统主成分分析方法的局限性导致了一些问题的产生。这些问题吸引了许多领域专家的关注,并具有针对性的提出了一些不同的改进方法。本文介绍了主成分分析的基本和性质,并整理了近年来主成分分析在综合评价应用中遇到的普遍问题并整理验证了认同率较强的一些改进方法,以供大家研究学习。 关键词: 主成分分析;综合评价;均值化
1引言 研究的背景和意义 随着生产力的不断进步,生产方式由外延式扩张转化为追求经济效益的内涵式发展,以致在生产过程中必须考虑经济效益的各个方面,如生产力水平、技术进步、资源占用等情况,并需要就综合各方面的因素进行综合评价。 评价是根据确定的目的来测定对象系统的属性,并将这种属性变为客观定量的计值或者主观效用行为,整个过程离不开评价者的参与,而综合评价作为评价的一种也需要评价者做出相应反应或指示,而很多综合评价过程易受到评价者的干预,使评价结果产生偏差。 主成分分析能将高维空间的问题转化到低维空间去处理【9】,使问题变得比较简单、直观,而且这些较少的综合指标之间互不相关,又能提供原有指标的绝大部分信息。而且,伴随主成分分析的过程,将会自动生成各主成分的权重,这就在很大程度上抵制了在评价过程中人为因素的干扰,因此以主成分为基础的综合评价理论能够较好地保证评价结果的客观性,如实地反映实际问题。主成分综合评价提供了科学而客观的评价方法,完善了综合评价理论体系,为管理和决策提供了客观依据,能在很大程度上减少了上述不良现象的产生。 所以在社会经济、管理、自然科学等众多领域的多指标体系中,如节约型社会指标体系、生态环境可持续型指标体系、和谐社会指标体系、投资环境指标体系等,主成分分析法常被应用于综合评价与监控【6】。 综上所述,对综合评价指标体系理论进行研究,既有理论上的必要性,更有实践中的迫切性。 研究的发展史 基于主成分分析的综合评价以主成分分析为理论基础,以综合评价为主线,着眼于作出合理公正的综合评价。以下从综合评价和主成分分析两个方面来讨论主成分综合评价的发展史。 综合评价是伴随着人类文明的产生、发展而产生、发展的。其基本思想是将反映研究对象数量特征的多个指标转化为一个综合指标,并据以对各个具体评价对象进行排序比较,从而做出好坏优劣的评价结论。 1888年,艾奇沃斯(Edgeworth)发表了论文《考试中的统计学》,提出了对考生中的不同部分应如何加权。1913年,斯皮而曼(sPe~an)发表了《和与差的相关性》一文,讨论了不同加权的作用。在20世纪30年代,瑟斯通(Thurstone)和利克特(Likert)又对定性记分方法的工作给予了新的推动。20世纪60年代,美国学者查德(L·A·zadaen)模糊集合理论,为模糊综合评价法奠定了基础。20世纪70一80年代,是现代科学评价蓬勃兴起的年代。在此期间,产生了多种应用广泛的评价方法,诸如ELECTRE法(1971一1977,1983)、多维偏好分析的线性规划法(LINMAP,1973)、层次分析法(AHP,1977)、数据包络分析法(DEA,1978)、逼近于理想解的排序法(TOPSIS,1981)等【7】。 主成分分析,首先是由英国的皮尔生(Kar卜Pearson)对非随机变量引入的,而后美国的数理统计学家赫特林在1933年将此方法推广到随机向量的情形团【8】。主成分分析的降维思想从一开始就很好地为综合评价提供了有力的理论和技术支持。 20世纪80~90年代,是现代科学评价在我国向纵深发展的年代,人们对包括主成分综合评价在内的评价理论、方法和应用开展了多方面的、卓有成效的研究,主要表现为:常规评价方法在国民经济、生产控制和社会生活中的广泛应用;多种评价方法的组合研究,综合应用及比较;新评价方法的研究和应用;评价方法的深入研究,如:评价属性集的设计、标准化变换、评价模型选择等等。 主成分做综合评价的研究现状 目前国内外关于综合评价的方法很多,在根据各指标间相关关系或各指标值的变异程度来确定权重系数的方法中,主成分分析法是应用尤为广泛。在使用该方法的早期,大多都是按照传统的主成分分析法做综合评价的步骤来计算综合得分来对样品排序,即利用主成分F1,F2,…,Fm做线性组合,并以每个主成分Fi的方差贡献率αi作为权重系数来构造一个综合评价函数: Y =α1F1 +α2F2 +…+αm F m 然而,随着传统主成分分析方法在综合评价中的进一步应用,人们发现此方法时经不起实践检验的。在实际应用中,经常发现运用此方法所得结果的解释往往与实际情况不符。举了一个简单的例子,假定高考中考试科目有四门:数学(x1)、语文(x2)、外语(x3)和物理(x4),满分都是相同的150分。考生的四门考试成绩必须综合成一个综合评价函数,一般取为总分ixi41。但从统计学的角度来看,可能取为*41ixi
更为合理,这里xi*是xi的标准化数值(x1* 、x2* 、x3* 、x4*有相同的均值和标准差)。如果我们使用传统的主成分分析法,根据上述综合评价函数F的得分来对学生进行排名,那就酿成大错了。 就此,一些学者提出了一些改进的方法,其中具有代表性的方法有:Yan(1998)提出,当第一主成分的方差比较大时,即贡献率较大时,用它做综合评价指标。如果觉得用一个主成分解释的方差不够大时,综合反映X1 ,X 2 ,…,Xp信息的能力不够,而用多个主成分构造综合评价函数又不合适时,可以像因子分析那样对主成分进行旋转。Hou(2006)也提出,当用第一主成分进行综合评价达不到理想结果时,可用分组主成分评价法。即先用因子分析法将p个变量分成k组,然后分别对各组变量进行主成分分析,只取每组的一主成分,求出各组第一主成分的得分Cj(j=1,2,…,k)以因子旋转后各因子的放差贡
献率为权重kjjjWj1建立综合评价函数:kjWjCjz1。最后根据各评价样本综合得分y来对样品
进行排序。但其可行性也受到了一些学者的质疑【4】。由此可见,主成分综合评价法是一片有待进一步深耕细作的热土。
2关于主成分分析基本知识 主成分分析 设要进行主成分分析的原指标有p个,记作x 1 ,x2 ,…,x p 。现有n个样品,相应的观测值为x ik , i =1,2,…,n,而k =1,2,…,p。 作标准化变换后,将Xk变换为Xk*,即
SkXk-XkXk*,k =1,2,…,m.
式中,Xk及Sk分别是xk的均值及标准差,x k*的均值为0、标准差为1. 主成分分析的原理是: 根据各样品原指标的观测值x ik或标准化变换后的观测值x ik*求出系数 a ik (k=1,2,…,p,j=1,2,…,m,m 建立用标准化变换后的指标x k*表示综合指标Fj的方程*xkakjFjk,也可建立用原指标Xk
表示综合指标Fj的方程*xkakjFjk。 对系数a ik由下列原则决定: (1)各个综合指标Fj彼此独立或不相关; (2)各个综合指标Fj所反映的各个样品的总信息等于原来p个指标Xk*所反映的各个样品的总信息,即p个Fj的方差λj之和等于p个Xk*的方差之和,也就是 Pjj
且λ1≥λ2 … ≥λP。
称上述彼此独立或不相关又不损失或损失很少原有信息的各个综合指标。yj为原指标 的主成分.其中,第一综合指标F1的方差最大,吸收原来p个指标的总信息最多,称第一主成分;第二综合指标F2的方差次之,吸收原来p个指标的总信息次之,称为第二主成分;同理,F3 F 4…Fp分别称为第三主成分、第四主成分……第p主成分。【9】 主成分分析能否旋转 主成分分析与因子分析的联系与区别 相当数量的应用文章对主成分分析与因子分析不加严格区分,因而对分析结果的解释非常模糊。文献【1】认为主成分分析与因子分析两者之间有联系,但也存在着明显的区别。 从联系上看,主成分分析和因子分析都是将多个相关变量(指标)转化为少数几个不相关变量的一种多元统计分析方法。其目的是使在高维空间中研究样本分布规律的问题,通过降维得到简化,并尽量保留原变量的信息量。两者都有消除相关、降维的功能。 主成分分析是通过变量变换把注意力集中到具有最大变差的那些主成分上,而视变量不大的主成分为常数予以舍弃;因子分析是通过因子模型把注意力集中到少数不可观测的公共因子上,而舍弃特殊因子。主成分个数与公共因子个数的选择准则通常是相同的。 主成分分析中主成分向量Y与原指标向量X的表达式为XLYT,式中ppijlL.;而因子分析中的因子模型为AFX,其中ε为特殊因子,0.mpijaA,当0D时,可采用主成分分析法估计A阵,则ijjijla。 对主成分分析中的主成分与因子分析中的公共因子的含义均需进行明确解释,否则,会遇到应用上的困难。 虽然主成分分析法与因子分析法有着密切的联系,但从应用上更需关注的是它们之间的区别。 1、 主成分分析的实质是P维空间的坐标旋转,并不改变样本数据结构,不能作为模型来描述;因子分析的实质是P维空间到M维空间的一种映射,需构造模型。 2、 主成分的个数与原变量个数相等,而公因子的个数小于原变量的个数。 3、 主成分分析是把主成分表示为原变量的线性组合,因子分析是把原变量表示为公共因子和特殊因子的线性组合。 4、 主成分分析由可观测的变量X直接求的主成分Y,并可逆;因子分析只能通过可观测的原变量去估计不可观测的公共因子F,不能用X表示F。 5、 主成分分析中的L阵是唯一的正交阵;因子分析中的A阵不唯一,也不一定是正交阵。 6、 主成分分析主要应用在综合评价和指标筛选上;因子分析除这两个作用以外,还可以应用于对样本或变量的分类。 能否对主成分实施旋转 对于主成分能否进行旋转这一问题,很多研究学者认为,当主成分不能很好解释综合评价结果时,可以像因子分析那样进行正交旋转,从而使主成分得到更好的解释。 关于主成分能否旋转的问题,文献【1】【4】【5】【7】【8】均做了论证,发现这种方法是不可行的。 论证具体如下: 主成分分析的实质是对原始指标变量进行线性变换,即F =XA,其中ppijaA.
显然A为正交矩阵,如果对主成分进行旋转,则有: 其中L是正交矩阵。由于X矩阵不变,其相关矩阵R对应的特征根和单位特征向量也不变,即说明矩阵A具有唯一性。由上式知:如果主成分能旋转则说明矩阵A不是唯一的。 从而我们可以得出:主成分不能进行旋转。
3 主成分分析做综合评价的局限性与改进方法 传统主成分分析做综合评价的一般步骤 (1)将原始数据标准化。将各样品指标值x i按iiiIXDXEXX*式转化成标准化指标Xi*,其中,E(Xi)和D(Xi)分别是Xi的均值和方差。Xi的均值是0,方差是1. (2)求各标准化指标Xi*的两两相关系数rij,并写出相关系数矩阵ppijrR][。
