武汉大学水力学教材答案第二章..
水力学第二章课后答案.docx
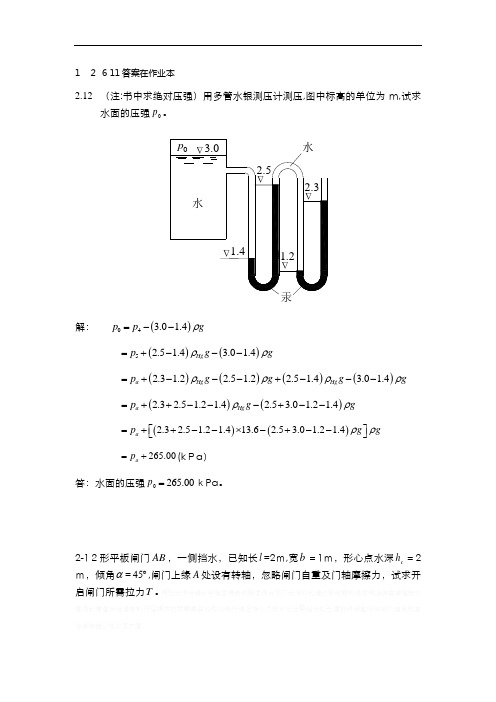
1 2 6 11答案在作业本2.12 (注:书中求绝对压强)用多管水银测压计测压,图中标高的单位为m,试求水面的压强0p 。
解:()04 3.0 1.4p p g ρ=--()()5 2.5 1.4 3.0 1.4Hg p g g ρρ=+---()()()()2.3 1.2 2.5 1.2 2.5 1.4 3.0 1.4a Hg Hg p g g g g ρρρρ=+---+--- ()()2.3 2.5 1.2 1.4 2.5 3.0 1.2 1.4a Hg p g g ρρ=++---+--()()2.3 2.5 1.2 1.413.6 2.5 3.0 1.2 1.4a p g g ρρ=++--⨯-+--⎡⎤⎣⎦ 265.00a p =+(k Pa )答:水面的压强0p 265.00=kPa 。
2-12形平板闸门AB ,一侧挡水,已知长l =2m,宽b =1m,形心点水深c h =2m,倾角α=︒45,闸门上缘A 处设有转轴,忽略闸门自重及门轴摩擦力,试求开启闸门所需拉力T 。
lbαB ATh c解:(1)解析法。
10009.80721239.228C C P p A h g bl ρ=⋅=⋅=⨯⨯⨯⨯=(kN )322221222 2.946122sin sin 4512sin 45sin C C D C C C bl I h y y h y A blαα=+=+=+=+=⨯⋅2-13矩形闸门高h =3m,宽b =2m ,上游水深1h =6m,下游水深2h =4.5m ,试求:(1)作用在闸门上的静水总压力;(2)压力中心的位置。
解:(1)图解法。
压强分布如图所示:∵ ()()12p h h h h g ρ=---⎡⎤⎣⎦()12h h g ρ=-()6 4.510009.807=-⨯⨯ 14.71=(kPa)14.713288.263P p h b =⋅⋅=⨯⨯=(kN )合力作用位置:在闸门的几何中心,即距地面(1.5m,)2b处。
《水力学》第二章答案

第二章:水静力学 一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h 高的水头具有大小为ρgh 的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4.在静水压强的基本方程式中C g p z =+ρ中,z 表示某点在基准面以上的高度,称为位置水头,g p ρ表示在该点接一根测压管,液体沿测压管上升的高度,称为测压管高度或压强水头,g p z ρ+称为测压管水头,即为某点的压强水头高出基准面的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A 是等压面,C-C,B-B 都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了Ap∆,水面以下同一高度的各点压强都增加Ap∆。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.图2-82-9.选择A2-10.(1)图a 和图b 静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
《水力学》第二章答案

第二章:水静力学一:思考题2-1.静水压强有两种表示方法,即:相对压强和绝对压强2-2.特性(1)静水压强的方向与受压面垂直并指向手压面;(2)任意点的静水压强的大小和受压面的方位无关,或者说作用于同一点上各方向的静水压强都相等. 规律:由单位质量力所决定,作为连续介质的平衡液体内,任意点的静水压强仅是空间坐标的连续函数,而与受压面的方向无关,所以p=(x,y,z)2-3答:水头是压强的几何意义表示方法,它表示h高的水头具有大小为p gh的压强。
绝对压强预想的压强是按不同的起点计算的压强,绝对压强是以0为起点,而相对压强是以当地大气压为基准测定的,所以两者相差当地大气压Pa.绝对压强小于当地大气压时就有负压,即真空。
某点负压大小等于该点的相对压强。
Pv=p'-pa2-4•在静水压强的基本方程式中z+〃=C中,z表示某点在基准面以上的高度,/pg称为位置水头,*表示在该点接一根测压管,液体沿测压管上升的高度,称为测p g压管高度或压强水头,z+亠称为测压管水头,即为某点的压强水头高出基准面p g的高度。
关系是:(测压管水头)=(位置水头)+(压强水头)。
2-5.等压面是压强相等的点连成的面。
等压面是水平面的充要条件是液体处于惯性坐标系,即相对静止或匀速直线运动的状态。
2-6。
图中A-A是等压面,C-C,B-B都不是等压面,因为虽然位置高都相同,但是液体密度不同,所以压强水头就不相等,则压强不相等。
2-7.两容器内各点压强增值相等,因为水有传递压强的作用,不会因位置的不同压强的传递有所改变。
当施加外力时,液面压强增大了坐,水面以下同一高度A的各点压强都增加坐。
A2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p・2-10・(1)图a和图b静水压力不相等。
因为水作用面的面积不相等,而且作用面的形心点压强大小不同。
所以静水压力Pa>Pb・(2)图c和图d静水压力大小相等。
武大水力学答案

第一章 导 论1、( √ )2、( × )3、( × )4、( 1 )5、( 2 )6、等于;相同;相反。
7、L/T 2 ;L 2/T ;M/LT 或FT/L 2。
8、变形; 弹性。
9、直线; 渠底。
10、连续介质。
11、相反;相同。
12、解:等速直线运动;F ∑=mgsin θ-τA=0 ; sin θ=135512522=+; A =0.40×0.45 ; τ =μd d u y =μu δ ; μ=mg A u sin θδ=0.1047 Pa ·s ;ν=μρ=1.102×10-4m 2/s 13、解:切应力分别为:(薄板上下表面)τ上=μ(du dy )上 =μu x τ下=μ(du dy )下=μu x∆- 薄板所受切应力 τ=τ上+τ下=μ(x u +)x-∆∆ 则薄板所受切力 T =τA =μ(x u +)x -∆∆A第二章 水静力学1、 ( )2、( )3、( )4、() 5、() 6、( ) 7、( ) 8、( ) 9、( ) 10、( )11、( 3 ) 12、( 3 ) 13、( 4 ) 14、( 3 ) 15、 ( 4 ) 16、( 2 ) 17、( 4 ) 18、( 2 ) 19、( 1 )20、( 2 )21、单位重量液体的总势能 22、单位重量液体的位置势能;单位重量液体的压强势能 。
23、0 ; 当地大气压强。
24、0.1 。
26、解:27、解:28、解:29、解:30、解: hpg==ρ200.H O232、解: h p p g =-a 0ρ= 0.663 m33、解:此时自由液面(等压面)是与水平面夹角为的斜面,将X =-a ,Y=0 ,Z=-g 代入欧拉方程dp=ρρ()(())X x Y y Z z a x g z d d d d d ++=-+-积分有 p =-++ρ()ax gz C在自由面上 p =0 ax gz C +=则 tan =a g h l = a h lg ==4.9 m/s 234、解: 先求出静水总压力P gh 1212=ρP ghL gL 22=+ρρsin 30L将 P 1,P 2对A 点求矩有222223121L g ghL h gh ρρρ+=⨯sin 3023L化简得 h h ()212-=8解此方程 h=3.759 m35、解:(1)(2) P gh g h h R g h h Rb x =+--+-122112121[()()]ρρρ =15.68 kNP gh Rb g h h Rb R b g z =+-+ρρπρ11212234() =33.58 kNP P P =+=x z 2237.06 kNθ==arctanz x P P 64.9736、解: 液体是质量力为 Z X Y =-+==(),g a 0 代入公式 d d p g a z =-+ρ()积分 p g a z c =-++ρ()z h =1 时 , p p =a ,, 代入方程则 c p g a h z p g a gh =++-=++a a ρρ()()()11 其中: h h z =-1,为任一点处的水深;g 为重力加速度。
水力学习题答案第二章

选择题(单选题)2.1静止流体中存在:(a)(a)压应力;(b)压应力和拉应力;(c)压应力和剪应力;(d)压应力、拉应力和剪应力。
2.2相对压强的起算基准是:(c)(a)绝对真空;(b)1个标准大气压;(c)当地大气压;(d)液面压强。
2.3金属压力表的读值是:(b)(a)绝对压强;(b)相对压强;(c)绝对压强加当地大气压;(d)相对压强加当地大气压。
2.4某点的真空度为65000Pa,当地大气压为,该点的绝对压强为:(d)(a)65000Pa;(b)55000Pa;(c)35000Pa;(d)165000Pa。
2.5绝对压强P abs与相对压强p、真空度P V、当地大气压P a之间的关系是:(c))P abs=P+P v ;a b P=P abs+P a ;(c)P V = P a-P abs ;(d)P = P V +P V。
(a2.6在密闭容器上装有U形水银测压计,其中1、2、3点位于同一水平面上,其压强关系为:(c)a P I> P2 > P3 ;(b)P1= P2= P3 ;(c)P1 < P2 < P3 ;(d)P2 < Pl < P3。
2.7用U形水银压差计测量水管内A、B两点的压强差,水银面高差h P=10cm, p A- p B为:(a); ( b); ( c); (d )。
2.8 露天水池,水深 5 m处的相对压强为:(b)(a) 5kPa; (b) 49kPa; (c) 147kPa; (d) 205kPa。
2.9垂直放置的矩形平板挡水,水深3m,静水总压力P的作用点到水面的距离y D为:(c)(a) 1.25m; ( b) 1.5m; (c) 2m; (d) 2.5m。
2.10圆形水桶,顶部及底部用环箍紧,桶内盛满液体,顶箍与底箍所受张力之比为:(a)(a) 1/2 ; ( b); (c) 2; (d) 3。
2.11在液体中潜体所受浮力的大小:(b)(a)与潜体的密度成正比;(b )与液体的密度成正比;(c)与潜体淹没的深度成正比;(d)与液体表面的压强成反比。
(完整)水力学第二章思考题答案

(完整)水力学第二章思考题答案2.1。
恒定流:如果在流场中任何空间点上所有的运动要素都不随时间而改变.非恒定流:如果在流场中任何空间点上有任何一个运动要素是随时间而变化。
均匀流:水流的流线为相互平行的直线.非均匀流:水流的流线不是相互平行的直线。
渐变流:水流的流线虽然不是相互平行的直线,但几乎近于平行的直线.急变流:水流的流线之间夹角很大或者流线的曲率半径很小.按运动要素是否彼此平行的直线分为均匀流和非均匀流,而非均匀流按流线的不平行和弯曲程度又分为渐变流和急变流。
渐变流重要性质为:过水断面上近似服从静压分布:Z+P/y=C2.2。
此时的A₁υ₁=A₂υ₂符合连续方程.两个断面无支流,且上游水位恒定,则下游通过的流量一定,则流量保持平衡,满足该公式。
2。
3能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’。
Ζ₁:位置水头;Ρ₁/ρg:压强水头;(μ₁)²/2g:流速水头;Ζ₂:单位位能;Ρ₂/ρg:单位压能;(μ₂)²/2g:单位动能;hw’:水头损失。
能量意义:在总流中任意选取两个过水断面,该两断面上液流所具有的总水头若为H₁和H₂,则:H₁=H₂+hw。
2.4这些说法都不对.对于理想液体来说,在无支流进去的情况下,其各断面的流量总和是相等的,根据能量方程:Ζ₁+Ρ₁/ρg+α₁(μ₁)²/2g=Ζ₂+Ρ₂/ρg+α₂(μ₂)²/2g+hw’,及连续方程:A ₁υ₁=A₂υ₂。
可以看出:只要其流量不改变,能量的总和就不会变。
则水是由流速大地方向流速小的地方流这种说法就是错误的。
总流的动量方程:ΣF=ρQ(Β₂υ₂-Β₁υ₁),也说明了这一点。
2.5总水头线:把各断面H=Ζ+Ρ/ρg+α(μ)²/2g描出的点子连接起来得到的线就是总水头线;测压管水头线:把各断面的(Ζ+Ρ/ρg)值的点子连接起来得到的线就是测压管水头线。
【精品作文】水力学第二章课后答案

m(g?a)
压强的传递有所改变。当施加外力时,液面压强增大了的各点压强都增加
?pA
?pA
,水面以下同一高度
。
2-8.(1)各测压管中水面高度都相等。
(2)标注如下,位置水头z,压强水头h,测压管水头p.
P
图2-8
2-9.选择A
2-10.(1)图a和图b静水压力不相等。因为水作用面的面积不相等,而且作用面的形心点压强大小不同。所以静水压力Pa>Pb.
(2)若容器盛的是汽油,则有
p?ρ?gh?0.75?9.8?1.5kPa?11.03kPa 0
2. 如图2-26所示封闭水箱两测压管的液面高程为:?液
面
高
程
为
?4?60cm
1
?100cm
,?
2
?20cm
,箱内少
。问
?3
为多?
解:由于水箱底部以上部分全都是水,且水银测压管开口与大气相通,故有
1-2.当空气温度从0℃增加至20℃时,运动粘度?增加15%,重度?减少10%,问此时动力粘度?增加多少(百分数)? [解] ?
?????(1?0.15)?原(1?0.1)?原
?1.035?原?原?1.035?原
???原1.035?原??原
???0.035
?原?原
此时动力粘度?增加了3.5%
习题2
1. 一封闭容器如图2-35所示,测压管液面高于容器液面,h=1.5m,,若容器盛
武汉大学水力学教材答案第二章..

第二章水静力学1、相对压强必为正值。
( )2、图示为一盛水容器。
当不计瓶重时, 作用于地面上的力等于水作用于瓶底的总压力。
( )3、静水总压力的压力中心就是受力面面积的形心。
( )4、二向曲面上的静水总压力的作用点就是静水总压力的水平分力与铅直分力的交点。
( )5、一个任意形状的倾斜平面与水面的夹角为α。
则该平面上的静水总压力P=ρgy D A sinα。
(y D为压力中心D的) ()b,长度L及倾角α均相等,则二板上的静水总压力作( )( )8、静水压强仅是由质量力引起的。
( )9、在一盛水容器的侧壁上开有两个小孔A、B,并安装一U 形水银压差计,如图所示。
由于A、B两点静水压强不∆h 的差值。
( )10、物体在水中受到的浮力等于作用于物体表面的静水总压力。
( )11、选择下列正确的等压面: ( )(3) C − C (4) D − D( )(1) 淹没面积的中心;(2) 压力体的中心;(3) 总压力的作用点;(4) 受压面的形心。
13、平衡液体中的等压面必为( )(1) 水平面;(2) 斜平面;(3) 旋转抛物面;(4) 与质量力相正交的面。
14、图示四个容器内的水深均为H,则容器底面静水压强最大的是( )(1) a ; (2) b ; (3) c ; (4) d 。
15、欧拉液体平衡微分方程( ) (1) 只适用于静止液体;(2) 只适用于相对平衡液体;(3) 不适用于理想液体;(4) 理想液体和实际液体均适用。
16、容器中盛有两种不同重度的静止液体,如图所示,作用在容器A B 壁面上的静水压强分布图应为( ) (1) a (2) d17、液体某点的绝对压强为58 kP a,则该点的相对压强为( )(1) 159.3 kP a;(2) 43.3 kP a;(3) -58 kP a(4) -43.3 kP a。
18、图示的容器a 中盛有重度为ρ1的液体,容器b中盛有密度为ρ1和ρ2的两种液体,则两个容器中曲面AB 上压力体及压力应为( )(1) 压力体相同,且压力相等;(2) 压力体相同,但压力不相等;(3) 压力体不同,压力不相等;1 m 时〔虚线位置〕,闸门上的静水总压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章水静力学1、相对压强必为正值。
( )2、图示为一盛水容器。
当不计瓶重时, 作用于地面上的力等于水作用于瓶底的总压力。
( )3、静水总压力的压力中心就是受力面面积的形心。
( )4、二向曲面上的静水总压力的作用点就是静水总压力的水平分力与铅直分力的交点。
( )5、一个任意形状的倾斜平面与水面的夹角为α。
则该平面上的静水总压力P=ρgy D A sinα。
(y D为压力中心D的) ()b,长度L及倾角α均相等,则二板上的静水总压力作( )( )8、静水压强仅是由质量力引起的。
( )9、在一盛水容器的侧壁上开有两个小孔A、B,并安装一U 形水银压差计,如图所示。
由于A、B两点静水压强不∆h 的差值。
( )10、物体在水中受到的浮力等于作用于物体表面的静水总压力。
( )11、选择下列正确的等压面: ( )(3) C − C (4) D − D( )(1) 淹没面积的中心;(2) 压力体的中心;(3) 总压力的作用点;(4) 受压面的形心。
13、平衡液体中的等压面必为( )(1) 水平面;(2) 斜平面;(3) 旋转抛物面;(4) 与质量力相正交的面。
14、图示四个容器内的水深均为H,则容器底面静水压强最大的是( )(1) a ; (2) b ; (3) c ; (4) d 。
15、欧拉液体平衡微分方程( ) (1) 只适用于静止液体;(2) 只适用于相对平衡液体;(3) 不适用于理想液体;(4) 理想液体和实际液体均适用。
16、容器中盛有两种不同重度的静止液体,如图所示,作用在容器A B 壁面上的静水压强分布图应为( ) (1) a (2) d17、液体某点的绝对压强为58 kP a,则该点的相对压强为( )(1) 159.3 kP a;(2) 43.3 kP a;(3) -58 kP a(4) -43.3 kP a。
18、图示的容器a 中盛有重度为ρ1的液体,容器b中盛有密度为ρ1和ρ2的两种液体,则两个容器中曲面AB 上压力体及压力应为( )(1) 压力体相同,且压力相等;(2) 压力体相同,但压力不相等;(3) 压力体不同,压力不相等;1 m 时〔虚线位置〕,闸门上的静水总压力。
( )(3) 不变;(4) 无法确定。
3 m 水柱高,当地大气压为一个工程大气压,其相应的绝对压强值等于( )(1) 3 m 水柱高;(2) 7 m 水柱高;(3) -3 m 水柱高;(4) 以上答案都不对。
21、液体中,测管水头(z + p/ρg) 的能量意义是______________________。
22、液体中,位置高度z 的能量意义是_______________;压强高度p/ρg 的能量意义是_______________。
23、真空压强的最小值是__________________;真空压强的最大值是___________________。
24、比重为0.81 的物体放入比重为0.9 的液体中,则出露部分体积与总体积之比为__________________。
25、容器A、B分别以加速度a和等角速度 运动,如图所示。
分别绘出液面下深度h处的等压面形状,并标明该等压面上任一质点的质量力F的方向。
2627、绘出图示圆柱体上水平压强分布图和压力体图。
并标出水压力铅直分力的方向。
28、三个圆球各充满液体后的测压管液面如图示,试绘出各球面的压力体图,并标出力的方向。
30、压力水箱上角装有一圆柱体压力表读数为19.60 kPa,箱中盛满水。
试绘出作用于圆柱面ABC上的水平压强分布图和压力体。
31、有一圆柱形容器,顶部设一通气管,如图所示。
已知圆柱半径 R =0.5 m ,通气管中的水面与容器顶盖齐平。
容器以等角速度ω=2π s -1绕铅垂中心轴旋转,求容器顶盖的总压力P 。
(N 937. 1P =)32、一封闭容器如图所示。
容器中水面的绝对压强 p 0=91.5Pa 。
中间插入一两端开口的玻璃管。
当空气恰好充 满全管而不流动时, 求管伸入水中的深度 h 。
(=h 0.663 m )33、在物体上装置一个直径很小的盛水 U 形管,以测定物体作直线运动的加速度(如图)。
若 L =0.3m ,h =0.15 m ,求物体的加速度 a 。
(a =4.9 m/s 2)α=120︒,如图所示可绕 A 轴转动,如图所受。
已知 L = 2 m 。
不计门重及摩擦力,求闸门开 始自动倾倒时的水深 h 。
(h=3.759 m )35、一曲面的形状为 3/4 个圆柱面,半径 R =0.8 m ,宽度(垂直于纸面)为1 m 。
圆心位于液面以下h =2.58 m ,如图所受。
容器中盛有密度为 ρ1=816 kg/m 3的液体,其深度 h 1=0.98 m ,其下为密度ρ2=1000 kg/m 3的液体。
(1) 绘制曲面的水平分力的压强分布图和垂直分力的压力体图。
(2) 求作用于曲面的静水总压力的大小和方向。
(kN 15.68P x ==; kN 33.58P z =;=P 37.06 kN ;=θ64.97︒)加速度 a 垂直向上运动,如图所示。
试导出液体中任一点压强 p 的表达式。
(h ga g p z a g p a )1()(++++-=ρρ)37、一容器左侧盛油,右侧盛水,上、下各接一水银压差计。
各液面标高如图所示。
已知油的密度ρ=816 kg/m 3。
求容器顶部压差计液面高差h 。
(h =0.2018 m )(不计重量)在密度分别为ρ1和ρ2的两种液体作用下处于平衡状态。
试导出D 与ρ1,ρ2,h 1,h 2之间的关系式。
( gg )gh gh (3D 211122ρ+ρρ-ρ=)39、一矩形水箱,箱中盛有液体,水箱沿倾斜角为θ的斜面以加速度a 向下滑动(如图)。
试确定箱内液体表面的 形状。
(液面方程为0=g)z -sin a (x )cos (a θ+θ ;液面对水平面的倾斜角θθ=βasin -g cos a x z =tan )40、图示为一空心弯管,下端插入水中,其水平段长度R =30 cm 。
当弯管绕铅直z 轴作等角速度旋转时,管内水 面上升至下游水面以上h =20 cm 。
求角速度ω。
(=ω 6.6 rad/s )41、在石油库斜壁的圆孔上装有一直径D =1.2 m 的半球形盖(如图)。
半球形盖中心O 点在液面下的深度H =4 m 。
斜壁与液面的夹角α=30︒,石油的密度ρ=900 kg/m 3。
求螺栓a 、b 上的总拉力。
(42.70kN )42、杯式水银真空计如图所示。
已知杯的直径D =60 mm ,管的直径d =6 mm 。
杯顶接大气时,测压管液面读数 为零。
杯顶封闭时,若测得测压管读数h =300 mm ,求杯中气体的真空压强。
(=0p 40.384 kPa )43、用U 形水银测压计测量A 点的静水压强,其读数为h ( mm ),如图所示。
令A 点压强不变,若将U 形管下将高 度H ( mm )。
则水银测压计读数放大为h +∆h( mm )。
试证明: ∆h=H/13.1。
44、蜡块A 沉浸在充满油和水的容器中,如图所示。
已知蜡块密度ρn =960 kg/m 3,油的密度ρ0=900 kg/m 3。
试确定蜡块沉没在水中和油中的体积占百分之几。
(V 6.0V 2=;V 4.0V 1=)45、在盛满液体的容器壁上装有一个均质圆柱体,如图所示。
由于圆柱体浸在液体中,必受到一个向上的浮力作用。
若摩擦力很小,在浮力产生的力矩的作用下,此圆柱体可绕O 轴不停转动,这种说法对不对?为什么?H 和 底面积 A 均相等时,问:(1) 容器底部所受的静水压强是否相等?(2) 底面所受的静水压力是否相等?(3) 桌面上受的压力是否相等?为什么?47、一圆锥形开口容器,下接一弯管。
当容器空着时,弯管上读数如图所示。
问圆锥内充满水后,弯管上读数为多少? (h=4.08m ,l=1.065m )48、图示一倒U 形差压计,左边管内为水,右边管内为相对密度(即比重)9.0s 1=的油。
倒U 形管顶部为相对密度8.0s 2=的油。
已知左管内A 点的压强2A m /KN 98p =,试求右边管内B 点的压强。
(p B =97.4Kpa )49、一容器如图所示,当A 处真空表读数为22cm 汞柱高,求E 、F 两管中的液柱高21h ,h 值。
并求容器左侧U 形管中的h 值。
(h 1=126cm , h 2=600.8cm , h=80.9cm )50、两液箱具有不同的液面高程,液体重度均为'γ,用两个测压计连接如图,试证:212211'h h h h +γ+γ=γ51、密闭容器盛水如图,已知m 3h =,,m 2h ,m 5.2h A B ==求容器内点A ,点B 及液面上的相对压强及绝对压强,并求图中所示y 值。
(p A =-19600pa , p B =24500pa , p 0=-29400pa ;绝对压强: p A =78400pa , p B =122500pa , p 0=63600pa ;y=3m )52、如图所示为一铅直安装的煤气管。
为求管中静止煤气的密度,在高度差m 20H =的两个断面安装U 形管测压计,内装水。
已知管外空气的密度3a m /kg 28.1=ρ,测压计读数为mm 115h ,mm 100h 21==。
与水相比,U 形管中气柱的影响可以忽略。
求管内煤气的密度。
(0.53Kg/m 3)53、试按图示复式水银测压计的读数计算出锅炉中水面上蒸汽的绝对压强p 。
已,m 3.2h ,m 2.1h ,m 5.2h ,m 4.1h ,m 3H 4321=====水银的相对密度6.13s =。
(362.8Kpa )54、如图所示为双液式微压计,A ,B 两杯的直径均为mm 50d 1=,用U 形管连接,U 形管直径mm 5d 2=,A 杯内盛有酒精,密度31m /kg 870=ρ,B 杯内盛有煤油32m /kg 830=ρ。
当两杯上的压强差0p =∆时,酒精与煤油的分界面在0-0线上。
试求当两种液体的分界面上升到0‘-0’位置、mm 280h =时p ∆等于多少?(156.6Pa )55、一水箱装置如图,箱底高出地面m 3h 2=,箱中水深m 2h 1=,其表面压强以绝对压强计为0.7个工程大气压,要求:(1)以地面为基准面,求出A 、B 两点的单位位能与单位压能,并在图上标明;(2)以水箱中水面为基准面,求出A 、B 两点的单位位能与单位压能,并在图上标明。
(Z A1=5m , Z B1=3m ,p A1/γ=-3m , p B1/γ=-1m ;Z A2=2m , Z B2=0m ,p A1/γ=-3m , p B1/γ=-1m )56、图示为一沉没于海中的潜艇的横断面图,气压计测出潜艇内的绝对压强cm 84p s =(水银柱),已知海水的相对密度03.1s =,试求潜艇的沉没深度y 。
