02平面力系
第二章平面力系

第二章平面力系教学目标:掌握平面力系向一点简化的一般结果和最终结果;掌握平面任意力系的平衡方程;掌握平面特殊力系的平衡方程。
重点、难点:平面力系平衡方程求解力学问题。
学时分配:8学时。
§2-1 平面任意力系的简化一 平面任意力系向一点简化——主矢与主矩设刚体上作用有n 各力1F 、2F 、…、n F 组成的平面任意力系,如图3-2a 所示,在力系所在平面内任取点O 作为简化中心,由力的平移定理将力系中各力矢量向O 点平移,如图3-2b 所示,得到作用于简化中心O 点的平面汇交力系1F '、2F '、…、n F ',和附加平面力偶系,其矩为1M 、2M 、…、n M 。
图3-2平面汇交力系1F '、2F '、…、n F '可以合成为力的作用线通过简化中心O 的一个力RF ',此力称为原来力系的主矢,即主矢等于力系中各力的矢量和。
有∑=''''ni 1=+++=+++=1212i n n RF F F F F F F F 平面力偶系1M 、2M 、…、n M 可以合成一个力偶,其矩为o M ,此力偶矩称为原来力系的主矩,即主矩等于力系中各力矢量对简化中心的矩的代数和。
有∑=ni n o (M =M ++M +M =M 1i o 21)F结论:平面任意力系向力系所在平面内任意点简化,得到一个力和一个力偶,如图所示,此力称为原来力系的主矢,与简化中心的位置无关;此力偶矩称为原来力系的主矩,与简化中心的位置有关。
利用平面汇交力系和平面力偶系的合成方法,可求出力系的主矢和主矩。
如图所示,建立直角坐标系oxy ,主矢的大小和方向余弦为212122)F ()F (=F F =F ni yi ni xi Ry RxR ∑∑==+'+'Rn1i yiRRy R n1i xi R RxF FF F cos ,F F F F )cos ∑∑===''=⋅=''=⋅)((j F i F R R主矩的解析表达式为∑=-=ni xi i yi i o )F y F (x M 1)(R F二 平面任意力系简化结果讨论(1)当00≠='o M ,RF 时,简化为一个力偶。
平面力系的概念

平面力系的概念平面力系是一个在平面内作用的力的集合。
在力学中,力是指物体与物体之间、物体与环境之间相互作用的效果。
平面力系是由多个力的向量合成而成的力的系统,它们都在一个平面内作用。
在平面力系中,每个力都有自己独特的方向和大小,同时也受到其他力的影响。
平面力系可以通过一个力的合力和力的力矩来描述。
合力是所有力合成的力的向量,而力矩是指力对给定点产生的转动效应。
在平面力系中,力的合力和力矩能够帮助我们理解平面上物体的平衡和运动。
在平面力系中,可以通过分解力来研究系统中的力。
根据牛顿第三定律,力总是成对出现的,一个力的作用与另一个力的反作用相等且方向相反。
因此,在平面力系中,我们可以将每个力都分解为两个力,一个垂直于参考轴的力和一个平行于参考轴的力。
这样的分解可以使我们更容易地分析力系。
平面力系也可以通过力的分解来求解复杂的问题。
通过使用向量分解技术,我们可以将一个力分解为多个分力,以帮助我们更好地理解和计算力的影响。
这种分解技术非常有用,尤其是在平面力系中涉及到复杂几何形状和不同角度的力时。
通过使用平面力系的概念,我们可以研究和解决许多力学中的问题。
例如,我们可以用平面力系的概念来解释物体在平面上的平衡。
当一个物体处于平衡状态时,它受到的所有合力和力矩都为零。
这意味着物体不会有任何线性和旋转方面的变化,它将保持静止或以恒定的速度运动。
另一个例子是使用平面力系来计算物体的加速度。
通过分解所有作用在物体上的力,并将它们的合力与物体的质量相除,我们可以得到物体的加速度。
这样,我们可以更好地理解和计算物体受到的作用力对其运动的影响。
除了平衡和运动问题,平面力系还可以用于其他许多力学应用。
例如,我们可以使用平面力系来研究机械系统的静力学平衡和稳定性。
平面力系的概念还可以应用于流体力学中,用于分析流体内部和外部的压力分布和力的传递。
总而言之,平面力系是力学中一个重要的概念,用于描述在平面内作用的力的集合。
它通过分解力和计算合力和力矩来帮助我们理解和解决各种平面平衡和运动问题。
02平面汇交力系
y
F
B
FBA
x
FBC
F
B
A
C D
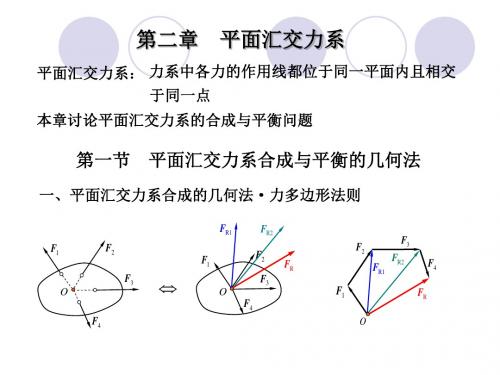
解: 1)首先选取销钉B 为研究对象, 画受力图 建立坐标轴,列平衡方程
Fix 0, Fiy 0,
FBA cos FBC cos 0 FBA sin FBC sin F 0
解得
F
FBC FBA 2sin
30
x
F3
45
F4
2 F4x F4 cos 45 4 2 2.83 kN
2 F4 y F4 sin 45 4 2 2.83 kN
二、平面汇交力系合成的解析法
1. 合力投影定理 力系的合力在任一坐标轴上的投影等于其各分力在同一轴上投 影的代数和,即
FRx Fix
F1
F2
FR
O
F3
O
F2
F3
FR1 FR2
F4
F1
FR
F4
O
任一平面汇交力系均可合成为一个作用线通过汇交点的合力。 合力的大小和方向由各分力矢依次首尾相连构成的开口多边形 的封闭边矢量确定。
对应的矢量关系式为
FR F1 F2
Fn Fi
二、平面汇交力系的平衡条件 平面汇交力系平衡的充要条件为其合力为零。
FRx 129.3 N
FRy 112.3 N
2)确定合力的大小和方向
FR FR2x FR2y 129.32 112.32 N 171.3 N
cos FRx 129.3 0.755
FR 171.3
cos FRy 112.3 0.656
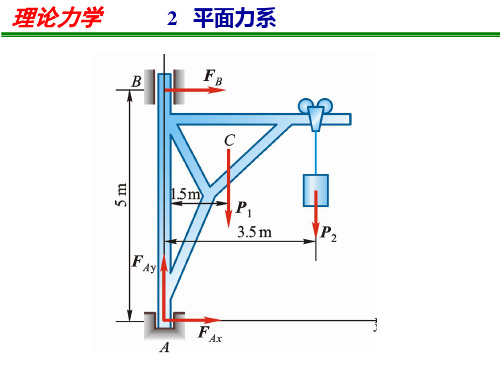
理论力学平面力系
理论力学
2 平面力系
2-2 平面力对点的矩
2-2 平面力对点之矩 --度量(力使物体绕O点)转动效应
力可以使物体移动 ——取决于力的大小、方向;
力可以使物体绕某一点转动——取决于: 1、定义:M O(F) F h
F Oh
为力F 对O点的矩,简称力矩:
O称为矩心、O 点与力F 所确 定的平面称为力矩作用面、O点 到力的作用线的距离h称为力臂.
理论力学
2 平面力系
理论力学
2 平面力系
2-1 平面汇交力系
工程中的力系几乎都是空间力系,但可以简化为平面力系来 研究。平面力系是指:所有力的作用线在同一平面内。
根据力作用线的情况又可分为平面汇交力系、平面平行力系、 平面任意(一般)力系。
2-1 平面汇交力系 1、平面汇交力系:各力作用在同一平面内,且作用线汇交
于一点,或作用在同一点。如图
F1
F2
F3 A
Fn
问题:1°汇交于一点的 n 个力对物体的作用效应可不 可以用一个合力来等效?
2°如果物体平衡,这个 n个力满足什么关系?
理论力学
2 平面力系
2-1 平面汇交力系
2、平面汇交力系的合成(求合力)的几力何多法边形法则
F1
F2
c F3 d
F2
FR2 FR1
a
j
x
O
Fx
Oi
F Fx x
Fx F cosa
F Fx Fy
Fy F cos b
因此,为方便计算,通常将坐标轴设为正交。
理论力学
2 平面力系
2-1 平面汇交力系
2°平面汇交力系合成的解析法
y
F1
FR
第二章 平面力系

平面力系
§2-1 一般概念
一.力系分类
平面力系(汇交力系、平行力系、一般力系) 空间力系
二.工程实例 在工程地质和工程建筑物中,常遇到
的一些平面力系问题,如:
铁路绗架、水坝、坝基 空间问题一般简化为平面问题处理
W1
W2
1m
§2-2 平面汇交力系的合成与分解
一、二力合成 1、几何法:已知作用在物体上的两个力,F1、F2 ,它们
5.力偶在任意坐标轴上的投影恒等于零.
§2-6 平面力系的合成
一、力的平移定理 作用在物体上的力可以平移到任意点,但必须附加上
一力偶,其矩大小等于此力对新作用点之矩。
M B M B (F ) F d (2 - 10)
二、平面任意力系向已知点简化(如下图)
1、简化方法:
2、简化结果:
主矢 FR Fi 主矩 M O M O (F i) (2 - 11)
P 2 10m
BT T
W1 R
N W2
T
P2
解:可以用解析法和图解法解此题 答案:T=7500KN,N=21500KN
§2-8 平面一般力系平衡条件和方程式
一、平面任意力系的平衡条件(充要条件)
R0, M00 二、平面任意力系平衡方程式 主矢
必有 主矩
R ( F x)2( F y)20
Fx 0
主矢与简化中心无关,主矩与简化中心有关
三、平面任意力系的合成
1、力和力偶合成一个力 2、合力矩定理:
平面力系的合力,对该平面任一点之矩,等于各分力 对同一点之矩的代数和。
n
M0 R m0(Fi) i1
3、简化结果分析,四种情况有三种结果
§2-7 重心
平面力系的名词解释

平面力系的名词解释平面力系是指作用于同一个物体的多个力构成的一个力的集合,这些力都在同一个平面上。
一、什么是平面力系?在物理学中,力是指导致物体产生运动、形变或其他物理效应的物理量。
平面力系是指在一个平面上所受到的多个力的集合,这些力不仅可以是同向或相反方向的,也可以是夹角形成的。
二、平面力系的特点1. 平面内的力:平面力系中的所有力都在同一个平面内,这是平面力系的一个重要特点。
2. 作用点:平面力系中的力的作用点可以在物体的任何位置,但必须在同一平面内。
3. 力的大小和方向:平面力系中的力可以是同向、相反或夹角形成的,它们的大小和方向会对物体产生不同的效果。
4. 平衡状态:平面力系中的力可以使物体保持静止或产生运动。
如果物体处于静止状态,那么力系中的力必须满足力的合力为零的条件;如果物体处于运动状态,那么力系中的力必须使物体产生加速度。
三、平面力系的分解与合力对于平面力系,我们可以使用矢量分解和合力的概念来研究力的效果。
矢量分解是将平面力系中的力分解为两个或多个分力,使得这些分力的合力等于原力系。
这使我们能够更好地理解和计算力的效果。
四、例子解析以下是一个例子,用于更好地理解平面力系的概念:假设有一辆汽车被两个力作用,一个向前的推力和一个向左的侧向力。
这两个力都在同一个平面内,即汽车的水平面上。
如果推力和侧向力的合力为零,那么汽车将保持在静止状态。
如果推力和侧向力的合力不为零,那么汽车将产生加速度,并朝合力的方向运动。
在这个例子中,我们可以通过将推力和侧向力进行矢量分解,计算出它们各自的效果,并最终得出整个力系对汽车的影响。
五、应用领域平面力系的概念在物理学和工程学中具有广泛的应用。
在机械、土木、航空等工程领域,研究平面力系可以帮助我们更好地理解和分析物体的运动和变形。
例如,在建筑结构的设计中,平面力系的分析可以用于确定材料的强度和结构的稳定性。
此外,在运动学和静力学中,平面力系的概念也被广泛应用。
02 平面力系题解

F AB
FCB
FT1
FT2
FT2
P
P
[解] 取滑轮 B 为研究对象,受力如图所示,列平衡方程:
F F
x
y
0 : FAB FCB cos 30 FT1 sin 30 0
0 : FCB sin 30 P FT 2 cos 30 0
x
FND
FBD D FBD
FAB
FBC
F
B
解:易知杆 AB、BC、BD 均为二力杆。 研究 OA,受力如图。
M
F
O
0 , FAB a cos M 0 , FAB
M a cos M a cos tan 2
研究节点 B,受力如图。
2.6
简支梁如图,梯形载荷的集度分别为 q1、q2,求支座 A、B 处的反力。
q1
A l
q2
B
F Ax A
F1
F2
B
FAy
l 2
2l 3
FB
[解] 研究 AB 梁, 梯形载荷可分解为集度 q1 的均布载荷和最大集度为 (q2 q1 ) 的线性载荷, 1 AB 梁受力如图,其中 F 1 q1 l , F2 (q2 q1 )l 2
x
y
0, FBx FC cos 60 0 0, FBy FC sin 60 q 6 0
MA F Ax
A
M B (b)
FBx 34.64 (kN); FBy 60 (kN);
5
FAy
FBy
FBx
班级
学号
哈工大理论力学 I 第8版_02_平面力系

12
三.力偶和力偶矩 1.力偶
由两个等值、反向、不共线的(平行)力组
成的力系称为力偶,记作 F , F
13
2.力偶矩 力偶中两力所在平面称为力偶作用面 力偶两力之间的垂直距离称为力偶臂 两个要素 a.大小:力与力偶臂乘积 b.方向:转动方向 力偶矩
M F d 2ABC
F n F n M n M O ( F n )
F R F i F i
M O M i M O ( Fi )
主矢 F R Fi
主矩 M O M O (Fi )
主矢与简化中心无关,而主矩一般与简化中心有关.
F R x ' F ix ' F ix F x
18
=
=
=
=
4.力偶没有合力,力偶只能由力偶来平衡.
19
五.平面力偶系的合成和平衡条件
已知:M 1 , M 2 , M n ;
任选一段距离d
M1 d
F1
M 1 F1d
M2 d
F2
M 2 F2d
Mn d
Fn
M n Fnd
=
=
20
FR F1 F2 Fn
FR F1 F2 Fn
第二章 平面力系
1
§2-1பைடு நூலகம்平面汇交力系
一.多个汇交力的合成
力多边形规则
2
FR1 F1 F2
3
FR2 FR1 F3 Fi i 1
n
FR Fi Fi i 1
力多边形 力多边形规则
3
二.平面汇交力系平衡的几何条件
02第2章 平面汇交力系

。 A FB
O
。
c
FB
a
FC FC
W
。
W
b
FC=bc=680 N FB=ca=310 N 所求插爪及轴承所受的力与它们对于系统的约束力FB 及FC大小相等、方向相反,均为压力。
9
§2-2 力在坐标轴上的投影
矢量 F 在轴上的投影不在 投影不在 是矢量而是代数量,并规定其 是矢量而是代数量 投影的指向与轴的正向相同时 指向与轴的正向相同时 为正值,反之为负值。 为正值 y b2 Fy a2 Fy βF α A Fx a1 Fx b1 B
F 4m B C F B C FA A 8m FD=bc=10 kN D A FA
θ
c
FD
b
D
a
θ
F
FD
FA=ca=22.5 kN,θ=26.5°
8
棘轮插爪构成的止逆装置,如图所示, 例2-2 棘轮插爪构成的止逆装置,如图所示,已知提 升重量W=500 N,d1=42 cm,d2=24 cm,a=12 升重量 , , , cm,h=5cm。求插爪及轴承所受的压力。 。求插爪及轴承所受的压力。
3
平面汇交力系: 平面汇交力系 各力的作用线位于同一平面内且汇交 于一点的力系。 研究方法: 研究方法: 几何法 解析法 解析法
平面汇交力系
4
§2-1 平面汇交力系合成 与平衡— 与平衡—几何法
一、合成的几何法
1.两个共点力的合成 1.两个共点力的合成 由力的平行四边形法则 平行四边形法则合成,也可用力的三角形法则 平行四边形法则 三角形法则 合成。 D C F2 FR A。 B F1 FRR F c b
6
二、平面汇交力系平衡的几何条件 平面汇交力系平衡的充要条件是: F2 F1
理论力学02平面力系的简化和平衡

第二章
平面力系的简化和平衡
2.1力的合成与分解: 1.平行四边形法则: 作用于物体上同一点的两个力可合成 一个合力,此合力也作用于该点,合力的 大小和方向由以原两力矢为邻边所构成的 平行四边形的对角线来表示。
④ R ≠0, MO ≠0,为最一般的情况。此种情况还可以继续简 化为一个合力 R 。
合力R 的大小等于原力系的主矢 合力R 的作用线到简化中心的距离
MO d R
结论:
平面任意力系的简化结果 :①合力偶MO ; ②合力 合力矩定理:由于主矩 而合力对O点的矩
R
M O mO ( Fi )
主矩:
M O M O ( F ) 3F1 1.5P 1 3.9P 2 2355kN m
(2)求合力及其作用线位置:
d x 3.514m 0 0 cos 90 70.84
(3)求合力作用线方程:
MO MO
' ' FR x FRy y FRx x FRy y FRx
二、汇交力系的合成 由几何法知合力等于各分力的矢量和,即
R F Fn F i 1 F 2 F 3
又 由于
Fi X ii Yi j Zi k Fxii Fyi j Fzi k
代入上式得 R
F i F
xi
yi
j Fzi k
根据合矢量投影定理得合力在坐标轴的投影
静力学-平面力系

03
平面力偶系合成与平衡
力偶概念及性质
力偶定义
由两个大小相等、方向相反且作用线平 行的力组成的力系。
VS
力偶性质
力偶没有合力,只能用力偶矩来度量其效 应;力偶对其作用面内任一点之矩恒等于 力偶矩,而与矩心的位置无关。
力偶矩计算与方向判断
力偶矩计算
力偶矩等于两力大小与两力作用线间距离的 乘积,即M=Fd。
计算方法
通过矢量运算,将力系中 的每个力分别投影到坐标 轴上,然后进行代数求和, 得到主矢和主矩。
简化结果讨论:合力、合力偶、平衡
合力
当主矢不为零时,力系可 简化为一个合力,其作用 点通过简化中心,大小和 方向由主矢确定。
合力偶
当主矢为零但主矩不为零 时,力系可简化为一个合 力偶,其力偶矩等于主矩。
全性。
建筑工程
在建筑结构中,框架结构和剪力 墙结构等常常受到空间平行力系 的作用。通过合理设计和施工, 可以确保建筑物的稳定性和承载
能力。
机械工程
在机械设计中,许多机构和构件 受到空间平行力系的作用。例如, 齿轮传动、带传动等机械传动中, 各构件受到的力和力矩往往构成
空间平行力系。
拓展思考
01
建立力学模型
摩擦角概念
当物体处于临界平衡状态时,摩擦力与正压力之间的夹 角称为摩擦角。
考虑滑动摩擦时物体平衡问题求解方法
确定研究对象和受力分析
选取研究对象,进行受力分析,画出受力图。
列平衡方程
根据静力学平衡条件,列出平衡方程。
引入滑动摩擦定律
在平衡方程中引入滑动摩擦定律,将摩擦力 表示为正压力的函数。
求解未知量
06
空间平行力系简介与拓展 思考
第二章 平面力系

FR F1 F2 Fn Fi
i 1
n
力FR对刚体的作用与原力系对该刚体的作用等效。所以 称此力为汇交力系的合力。
如力系中各力作用线均沿同一直线,则此力系为共线力系, 它是平面汇交力系的特殊情况。显然力系的合力大小和方向 取决于各分力的代数和,即 n
FR Fi
i 1
24
静力学
例题 1-5
平面力系
合力的大小:
2 Rx 2 Ry
FR F F 171.3 N
合力与轴x,y夹角的方向余弦为:
FRx cos( FR , i ) 0.754 FR
F2
y
F1
60
O
45
30
cos( FR , j )
FRy FR
45
x
F4
0.656
F3
平面力系
Fx Fx1 Fx 2 Fxn Fxi i 1 n Fy Fy1 Fy 2 Fyn Fyi i 1
n
合力矢FR的大小和方向余弦为
FR Fx2 Fy2 ( Fxi ) 2 ( Fyi ) 2
B
D
钢丝绳的另一端绕在铰车D上。 杆AB与BC铰接,并以铰链A,C 与墙连接。如两杆与滑轮的自重
4 .由力三角形图c可得:
I
F
q
FD
J
K
FB
(c)
sin 180 q FB F 750 N sin
11
静力学
例题 1-2
平面力系
水平梁AB中点C作用着力F,其大小等于2 kN,方向与梁
的轴线成60º 角,支承情况如图a 所示,试求固定铰链支座A和活动铰链支座B的约束源自。梁的自重不计。3,
02 平面一般力系

这是平面任意力系平衡方程的基本形式,也称为一 力矩式方程。
二、平面任意力系平衡问题的解题步骤
定。确定研究对象。 画。画出分离体受力图。 列。列平衡方程。 校。利用所学知识检查结果的正确性。
§4-3 平面平行力系的平衡方程及其应用
在平面平行力系中,若选择直角坐标轴的y(或x)轴与 力系各力作用线平行,则每个力在x(或y)轴上的投影 均为零,即∑Fx≡0(或∑Fy≡0)。于是平行力系只有两 个独立的平衡方程, 即 Fy 或 Fx 0
(a)
(b)
(c)
平面任意力系的简化,主矢与主矩 力系的主矢
y A1 F1 O A2 F2 An (a) Fn Mn MO
1
y
Fn FR
=
F1
M2 F2
x
=
O
O MO
FR
x
d
O
FR
O
d
O
FR (d)
FR (e)
(b)
(c)
平移力组成的平面汇交力系的合力, 称为原平面任意 力系的主矢。 作用点在简化中心O点,大小等于 各分力的矢量和,即
y a E1
a
F2
O
x
F3
F4
2.5 如练习2.5图所示三角支架的铰链A处销钉上悬挂一 重物G,各杆自重不计,已知G=10kN,试求杆AB、 AC所受的力。
B 6 0° G 3 0° C (a) A A B 6 0° 6 0° C
G (b )
2.6 构件的支承和载荷情况如练习2.6图所示,l=4m, 求支座A、B的约束反力。
一、平面一般力系的平衡方程 平面一般力系平衡的必要与充分条件为: FR′=0, MO=0。即
002理力-平面力系

已知F1=200N,F2=300N,F3=100N,F4=250N。
求图示平面汇交力系的合力。 解 根据公式可得
Fx Fx1 Fx 2 Fx 3 Fx 4 F1 cos 30o F2 cos 60o F3 cos 45o F4 cos 45o 129.3 N Fy Fy1 Fy 2 Fy 3 Fy 4 F1 sin 30o F2 sin 60o F3 sin 45o F4 sin 45o 112.3 N
作用点:
∴ tg
Ry Rx
tg
1
Y X
为该力系的汇交点。
四、平面汇交力系的平衡方程
从前述可知:平面汇交力系平衡的必要与充分条件是该力系 的合力为零。 即:
Rx X 0 Ry Y 0
R Rx R y 0
2 2
为平衡的充要条件,也叫平衡方程。
13
[例3]
0
16
[例6] 求当F力达到多大时,球离开地面?已知P、R、h。 解:先研究物块,受力如图,画力三角形。
解力三角形: 又:
N F cos
F R N h ( 2 R h)
R2 (R h)2 1 cos h(2R h) R R
17
再研究球,受力如图, 作力三角形,解力三角形。
m1 F1d1;
m2 F2 d 2
又m1 P1d
m2 P2d
R A P1 P2' RB P1' P2
合 矩 力
M RA d ( P P2' )d P d P2' d m1 m2 1 1
求出负值,说明物体受压力。
第2章平面一般力系

主矢作用在简化中心O点,与简化中心位置无关(为什么?)。 (3)将平面力偶系合成:
F'1 m1
R'
F' 2
=
m2
=
MO
mn
得到作用于力系平面内的一力偶,其力偶矩为: MO =m1+m2+…+mn
F' n
mO (F1 ) mO (F 2 ) ... mO (F n ) mO ( F i )
F'1 m1
R'
F' 2
=
m2
mn
F' n
(1)将各力平移至点O , 得一平面汇交力系和一平面力偶系。 (2)将平面汇交力系合成: R' F'1 F'2 ... F'n F 1 F 2 ... F n Fi 原力系中各力的矢量和称为力系的主矢量,简称主矢( 它是不是原力系的合力?),用 R' 表示,即 R' F i
1
第二章
系。
平面一般力系
平面一般力系:各力的作用线都在同一平面内且任意分布的力
平面一般力系包含以下几种特殊力系: (1)平面汇交力系:各力的作用线都在同一平面内且汇交于 一点的力系。
(2)平面平行力系:各力的作用线都在同一平面内且相互平 行的力系。
(3)平面力偶系:各力偶作用面共面。
2
第二章
平面一般力系
原力系中各力对简化中心之矩的代数和称为力系对简化中心 的主矩 (它是不是合力偶?) 主矩一般与简化中心的位置有关(why?)。
12
过O点建立直角坐标系,由矢量和投影定理,得主矢在x、y轴
上的投影为:
R'x X 1 X 2 X n X i ' Ry Y1 Y2 Yn Yi 则主矢的大小:
02平面汇交力系

§2-2
平面汇交力系合成与平衡 的解析法(坐标法)
一.力在坐标轴上的投影与力沿轴的分解 1、力在坐标轴上的投影 力在 x 轴上的投影: 力在 y 轴上的投影:
F1
O Fn R
合力R为力多边形的封闭边
若将合成过程中出现的各个“过程合力”略 去,则F1、F2、……Fn与它们的合力R就构成一 个力多边形。这种合成方法称为力多边形规则。
四、平面汇交力系平衡的几何条件
平衡几何条件: 即:力多边形自行封闭
例如:一平面汇交力系,作其力多边形
由图可知,该力多边形封闭,所以该平面汇交力系为平衡力系。
前章回顾
1、力、刚体、平衡、约束等概念 2、力学公理 3、约束及约束力
人体关 节.mpg
4、受力分析及受力图
力系分类
平面 力系分类 空面
任意 共线力系、平面力偶系 平面汇交力系:各力的作用线都在同一平 面内且 汇交于一点的力系。 研究方法:几何法,解析法。 汇交
平行
§2-1
平面汇交力系合成与平衡的
R
X Y
2
2
0
所以,平面汇交力系的平衡方程为 :
X 0 Y 0
[例2-7] 已知如图P、Q, 求平衡时 面的反力ND=? 解:研究球受力如图,
选投影轴列方程为
=? 地
X 0
T2cos T 0 1
①
②
Y 0
由①得
T2 sin Q N D 0
第二章 平面汇交力系
第二章 平面汇交力系
平面力系

证明:
F
F
F
F
Od A = O d A
=
mO A
F
F F F
m Fd m0F
§3–2
§2–7 力线平移定理
二、几个性质:
1、当力线平移时,力的大小、方向都不改变,但附
加力偶的矩的大小与正负一般要随指定O点的位
置的不同而不同。
2、力线平移的过程是可逆的,即作用在同一平面内 的一个力和一个力偶,总可以归纳为一个和原力 大小相等的平行力。
中心。
F1
F2
A1 O
A2
A3
F1
=
F2
m1
m2
O
m3
=
F3
F3
R
O
LO
§2–8 平面任意力系的简化•主矢与主矩
共点力系F1、 F2、 F3的合成结果为一作用点在 点O 的力R。这个力矢R 称为原平面任意力系的主矢。
R F1 F2 F3
F1 F2 F3
1 2 3 3 1 0.768
y
F2
60°
A
22
B
F3
2m
R Rx2 Ry2 0.794
cosR、x Rx 0.614
R
R , x 526'
cosR、y Ry 0.789
R
R , y 3754'
F1
A
B F2
C
F3
D
R
F4
E
§2–2 共点力系合成与平衡的几何法
F1
A
B F2
R
C
F3
D
F4
第二章 平面力系

第二章平面力系第1节平面汇交力系合成与平衡的几何法若作用在物体上的力,其作用线均分布在同一平面内,则该力系称为平面力系。
若作用在同一平面内的各力作用线均汇交于一点,则该力系称为平面汇交力系。
一、合成的几何法应用力多边形法则,合力矢即是力多边形的封闭边,合力作用线通过力系的汇交点。
如图2-1-1-1所示。
图2-1-1-1若有n个力,则合力矢可以表示为F R = F 1 + F 2 +⋯+ F n = ∑ i=1 n F i二、平衡的几何法平面汇交力系平衡的充要条件是:力多边形自行封闭。
如图2-1-1-2所示。
若矢量表示即为F R =0图2-1-1-2第2节平面汇交力系合成与平衡的解析法一、力在坐标轴上的投影力在坐标轴上的投影等于力的模乘以力与投影轴正向间夹角的余弦,如图2-2-1-1所示,它是一标量,即F x =Fcosθ; F y =Fcosβ力沿坐标轴的分力是一矢量,其合力与分力之间应满足力的平行四边形法则。
如图2-2-1-2所示。
当坐标轴为直角坐标轴时,力沿坐标轴分解的分力可以表示为F x = F x i; F y = F y i合力投影定理:合力在某轴上的投影等于各分力在同一轴上投影的代数和,即F x = ∑ i=1 n F xi ; F y = ∑ i=1 n F yi当投影轴x与y垂直时,其合力的大小与方向为F R = F x 2 + F y 2 , cos( F R ,i)= F x F R ; cos( F R ,j)= F y F R二、合成的解析法当为直角坐标轴时,可按以下方法来合成F R = F x 2 + F y 2 = ( ∑ F xi ) 2 + ( ∑ F yi ) 2cos( F R ,i)= F x F R = ∑ F xi F R ; cos( F R ,j)= F y F R = ∑ F yi F R三、平衡的解析法力系中各力在两个坐标轴上投影的代数和分别等于零,即∑ F x =0; ∑ F y =0上式称为平面汇交力系的平衡方程。
第二章 平面基本力系

平衡方程
Fx 0 Fy 0
第一节 平面汇交力系
例2-1 圆筒形容器重量为G,置于托轮A、B
上,如图所示,试求托轮对容器的约束反力。
第一节 平面汇交力系
解:取容器为研究对象,画受力图 容器自重G
托轮对容器是光 滑面约束,其约束 反力为FNA和FNB
FNA
FNB G
第一节 平面汇交力系
B F
a C
Fx
O
Fx
x
Fx=±Fcosa
Fy=±Fsina
y
b1
C
Fy
a1 B
Fx
A
F a
Fy
O
Fx
x
F Fx2 Fy2
tana Fy / Fx
第一节 平面汇交力系
2.合力投影定理
ad=ab+bc-cd 即 Fx=F1x+F2x+F3x Fy=F1y+F2y+F3y
第一节 平面汇交力系
c) 只要保持力偶矩的大小和力偶的转向不变,可 以同时改变力偶中力的大小和力偶臂的长短, 而不改变力偶对刚体的作用。
d) 力偶对其作用面内任一点之矩恒为常数,且等 于力偶矩,与矩心的位置无关。
第三节 平面力偶系
二. 平面力偶系的合成和平衡条件
1.平面力偶系的合成 平面力偶系:作用在物体上同一平面内的若干力偶的总称。
M o (Fn ) Fn h Fn r cosa
2)合力矩定理 将力Fn分解为切向力Ft和法(径)向力Fr, 即
Fn Ft Fr
由合力矩定理得:
M o (Fn ) M o (Ft ) M o (Fr ) Ft r 0
考研复习—工程力学——第2章 平面力系

负号表示合力偶为顺时针转向。
图2-10
第2章
2.3 平面任意力系的简化
2.3.1 力的平移定理
平移定理:作用在刚体上的力,可以平移至刚体内任一指定点,若不改变该力对于 刚体的作用则必须附加一力偶,其力偶矩等于原力对新作用点的矩。
Fx 0
RAx R By P 0
RAx P RBx 20 kN 10 kN 10 kN
M A (F) 0 RBy a P a F 2a 0
RBy 2F P 20 kN 20 kN 0
(2)画ACD杆及CEB杆受力图,如图(b)、图(c)所示。
(3)研究CEB杆,如图(c)所示,则有
例2-16:图所示梯子,AB一端靠在铅垂的墙壁上,另一端搁置 在水平地面上。假设梯子与墙壁间为光滑约束,而梯子与地面之间存 在摩擦。已知:摩擦因数为 ,梯子长度AB=L,梯子重力为W。求:( 1)若梯子在倾角 的位置保持平衡,求梯子与地面之间的摩擦力 和其 余约束力;(2)为使梯子不致滑倒,求倾角α的取值范围。
2 3 Fp
Fs1
Fs 2
1 3
Fp
(拉)
2 3
Fp (压)
(3)考察节点B的平衡: Fs3 0
第2章
2.7 考虑摩擦时的平衡问题
2.7.1 工程中的摩擦问题
1、摩擦平衡问题: 工程中有一类问题摩擦力不能忽略。例如车辆的制动、螺旋连接与锁 紧装置、楔紧装置、缆索滑动和传动系统等。这类平衡问题统称为摩擦平衡问题。
Fd fFN
第2章
2.7 考虑摩擦时的平衡问题
2.7.3 摩擦角与自锁现象
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FR F1 F2 Fn
=
=
=
M FR d
F1d F2 d Fn d
n i 1
M 1 M 2 M n
M Mi Mi
平面力偶系平衡的充要条件 M=0 即
Mi 0
§2-5 平面任意力系向作用面内一点简化
1、力的平移定理
§2-4 平面力偶理论
一.力偶和力偶矩 1.何谓力偶?
由两个等值、反向、不共线的(平行)力组成的 力系称为力偶,记作 F , F
2.力偶矩 力偶中两力所在平面称为力偶作用面。 力偶两力之间的垂直距离称为力偶臂。
两个要素
a.大小:力与力偶臂乘积
b.方向:转动方向
力偶矩
M F d 2 1 2 F d 2ABC
例2-7 已知: , , xB , yB , l; F
求: 平衡时,CD杆的拉力。 解: CD为二力杆,取踏板 由杠杆平衡条件
(3 3)
合力矩定理
M o ( FR ) M O M O ( Fi )
若为O1点,如何?
§2-7 平面任意力系的平衡条件和平衡方程
平面任意力系平衡的充要条件是: 力系的主矢和对任意点的主矩都等于零
即
因为
FR 0
FR
Mo 0
( Fx ) ( Fy )
2 2
M O M O ( Fi )
(坐标法)
一.力在坐标轴上的投影与力沿轴的分解
Fx F cosθ
Fy F cosβ
F Fx Fy
二.平面汇交力系合成的解析法 因为
FR Fi
由合矢量投影定理,得合力投影定理
FRx Fix
FRy Fiy
则,合力的大小为:
FR FRx FRy
Fix
Fx
FR
Fy cos( FR , j ) FR
2
(3 1)
M O M o ( Fi ) ( Fix Fiy Fiy Fix )
(3 2)
3、平面固定端约束
=
=
≠
=
§2-6 平面任意力系的简化结果分析
=
主矢
主矩
MO 0 MO 0 MO 0 MO 0
平面汇交力系
M 0 FR M 0 Fi
三、力矩与合力矩的解析表达式
M O F M O Fy M O Fx x F sin y F cos x Fy y Fx
M O FR M O Fi
M O FR xi Fiy yi Fix
A, B 两个取矩点连线,不得与投影轴垂直
M A 0 M B 0 M 0 C
三矩式
A, B, C
三个取矩点,不得共线
§2-8
平面平行力系的平衡方程
Fx 0
0 0 0 0
Fx 0
F1 cos F2 cos F3 cos 0 F1 sin F2 sin F3 sin 0
二. 力偶与力偶矩的性质
1.力偶在任意坐标轴上的投影等于零。
2.力偶对任意点取矩都等于力偶矩, 不因矩心的改变而改变。
M F d
M O F , F M O F M O F
1 1 1
F d x1 F x1 Fd
M O F , F F d x2 F x2
最后结果
合力
合力 合力偶 平衡
说明
合力作用线过简化中心
合力作用线距简化中心M O
FR
FR 0 FR 0
与简化中心的位置无关 与简化中心的位置无关
合力的概念:当主矩等于0时的主矢。
当说明合力时,必须指明合力大小和合力
的作用点。
其中
d
MO FR
M o FRd
FR FR FR
解得: FBC 27.32kN
例2-5 已知: F=3kN, l=1500mm, h=200mm.忽略自重; 求:平衡时,压块C对工件与地面的压力,AB杆 受力。
解:AB、BC杆为二力杆。
取销钉B。
用解析法
Fix 0
FBA cos θ FBC cos θ 0
得 FBA FBC
FR
2
2
方向为: cosF , i
R
cos FR , j
Fiy
FR
作用点为力的汇交点。
三.平面汇交力系的平衡方程
平衡条件
FR 0
平衡方程 Fx 0
Fy 0
§2-3 平面力对点之矩的概念和计算
一、平面力对点之矩(力矩) 力矩作用面
两个要素:
1.大小:力F与力臂的乘积 2.方向:转动方向
C A
例2-3 已知:图示平面共点力系; 求:此力系的合力。 解:用解析法
FRx F ix F1 cos 30 F2 cos 60 F3 cos 45 F4 cos 45 129.3N
FRy F iy F1 sin 30 F2 sin 60 F3 sin 45 F4 sin 45 112.3N
4、各杆件自重不计或均分布在节点上。
在上述假设下,桁架中每根杆件均为二力杆。
节点法与截面法
1、节点法
2、截面法
例2-1
已知: 求: P=20kN,R=0.6m, h=0.08m:
1.水平拉力F=5kN时,碾子对地面及障碍物的压力?
2.欲将碾子拉过障碍物,水平拉力F至少多大?
3.力F沿什么方向拉动碾子最省力,及此时力F多大?
解得 F P tan θ 11.55kN
3. 解得 Fmin P sin θ 10kN
例2-2 已知:AC=CB,P=10kN,各杆自重不计; 求:CD杆及铰链A的受力。 解:CD为二力杆,取AB杆,画受力图。 用几何法,画封闭力三角形。
或
按比例量得 F 28.3kN, F 22.4kN
=2( n 3 )
m 2n 3
m 2n 3
平面复杂(超静定)桁架
m 2n 3
平面简单(静定)桁架
m 2n 3
非桁架(机构)
关于平面桁架的几点假设:
1、各杆件为直杆, 各杆轴线位于同一平面内;
2、杆件与杆件间均用光滑铰链连接;
且位于桁架几何平面内; 3、载荷作用在节点上,
ABC ABD
=
=
=
=
4.力偶没有合力,力偶只能由力偶来平衡。
三.平面力偶系的合成和平衡条件 已知: M , M , M ;
1 2 n
任选一段距离d
M1 d M2 d
Mn d
F 1 F2
Fn
M 1 F1d M 2 F2 d
M n Fn d
=
=
FR F1 F2 Fn
Fy 0
平面平行力系的Biblioteka 程为两个,有两种形式 Fy 0 M A 0
各力不得与投影轴垂直
A, B
M A 0 M B 0
两点连线不得与各力平行
§2-9
物体系的平衡· 静定和超静定问题
§2-10 平面简单桁架的内力计算
总杆数 m
m3
总节点数 n
Fiy 0
FBA sin θ FBC sin θ F 0
解得 FBA FBC 11.35kN 选压块C
Fix 0 FCB cos θ FCx 0
解得 FCx
F 2 cotθ Fl 2h 11.25kN
Fiy 0
F CB sin FCy 0
M 0 F F h
M 0 F r F
二、汇交力系的合力矩定理
FR Fi F1 F2 Fn FR F1 F2 Fn
r FR r F1 r F2 r Fn
即
M O FR M O Fi
解得 FCy 1.5kN
例2-6
已知: F=1400N, θ 20 , r 60mm 求: M O F . 解: 直接按定义
M O F F h F r cos θ 78.93N m
按合力矩定理
M O F M O Ft M O Fr F cos θ r 78.93N m
有
Fx 0 Fy 0 M o 0
(3 4)
平面任意力系的平衡方程(一般式)
平面任意力系的平衡方程有三种形式, 一般式
二矩式
三矩式
平面任意力系平衡方程的三种形式
一般式 二矩式
Fx 0 Fy 0 M A 0
Fx 0 M A 0 M 0 B
R
M O M i M O ( Fi ) 能否称 M O为合力偶?
主矢 F F
R
i
主矩 M
O
M O ( Fi )
若选取不同的简化中心,对主矢、主矩有无影响?
如何求出主矢、主矩?
FRx Fix Fix Fx
FRy Fiy Fiy Fy
M B M B ( F ) Fd
2、平面任意力系向作用面内一点简化 ·主矢和主矩
F1 F1
F2 F2
M 1 M 0 ( F1 )
M 2 M 0 ( F2 )
Fn Fn
