珠海市2012～2013学年度第二学期期末学生学业质量监测高一数学

合集下载

珠海市2013-2014 学年度第二学期高三学生学业质量监测(珠海二模)

试卷类型：B 珠海市2013-2014 学年度第二学期高三学生学业质量监测语文试题本试卷共8 页，包括六个部分24 小题，满分150 分。

考试用时150 分钟。

注意事项：1．答卷前，考生首先检查答题卡是否整洁无缺损，监考教师分发的考生信息条形码是否正确；之后务必用黑色字迹的签字笔在答题卡指定位置填写自己的学校、姓名和考生号。

2．选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上。

不按要求填涂的答案无效。

3．非选择题必须用黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上。

请注意每题答题空间，预先合理安排；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．作答选做题时，请先用2B 铅笔填涂选做题的题号对应的信息点，再作答。

漏涂、错涂、多涂的答案无效。

5．考生必须保持答题卡的整洁。

考试结束后，将答题卡交回。

一、本大题4 小题，每小题3 分，共12 分。

1．下列词语中加点的字，每对读音都不相同．．．的一项是（）(3分)A．耿．直/梗．概勘．探/桑葚．当．政/安步当．车B．邋遢．/趿．拉呵．责/沉疴．咀嚼．/咬文嚼．字C．孝悌．/醍．醐顷．刻/倾．情集结．/开花结．果D．储．蓄/贮．备烘焙．/陪．衬解．救/解．甲归田2．下面语段中画线的词语，使用不恰当．．．的一项是（）(3 分)有些词语不带光环光晕，在颂扬赞美时往往可以不动声色、不着痕迹，效果较之正统颂词过犹不及。

不过，条件是恰如其分，一旦言过其实，颂词就会变为谀词，甚至沦为笑料。

从颂词到谀词，或许是一个滑行的过程，难以做到泾渭分明；但两者的根本区别还是不难厘定的，那就是颂在实处为颂，颂到虚处则为谀。

切记笔下生花之时莫离事实这个谱，是避免从颂词到谀词到笑料这条堕落路径的要诀。

A.过犹不及B.恰如其分C.泾渭分明D.厘定3．下列句子中，没有语病．．．．的一项是（）(3分)A．4 月17 日，广州恒大客场以一种令人意想不到的方式负于墨尔本胜利队，他们所欠缺的：一是战术不当，二是心理状态不稳。

广东省珠海市2013届高三上学期期末学业质量监测数学理试题

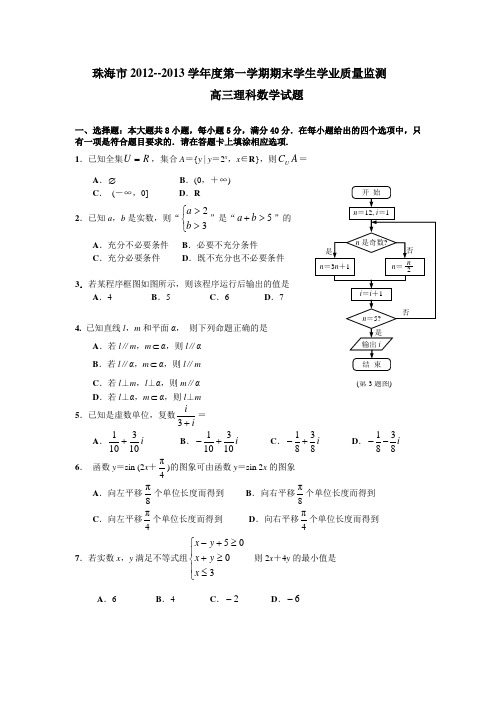
珠海市2012--2013学年度第一学期期末学生学业质量监测高三理科数学试题一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项. 1．已知全集R U =，集合A ＝{y | y ＝2x ，x ∈R }，则A C U ＝A ．∅B ．(0，＋∞)C ． (－∞，0]D ．R 2．已知a ，b 是实数，则“⎩⎨⎧>>32b a ”是“5>+b a ”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．若某程序框图如图所示，则该程序运行后输出的值是 A ．4 B ．5 C ．6 D ．74. 已知直线l ，m 和平面α，则下列命题正确的是A ．若l ∥m ，m ⊂α，则l ∥αB ．若l ∥α，m ⊂α，则l ∥mC ．若l ⊥m ，l ⊥α，则m ∥αD ．若l ⊥α，m ⊂α，则l ⊥m 5．已知是虚数单位，复数ii+3＝ A ．i 103101+ B ．i 103101+- C ．i 8381+- D ．i 8381--6．函数y ＝sin (2x ＋π4)的图象可由函数y ＝sin 2x 的图象 A ．向左平移π8个单位长度而得到 B ．向右平移π8个单位长度而得到 C ．向左平移π4个单位长度而得到 D ．向右平移π4个单位长度而得到7．若实数x ，y 满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 则2x ＋4y 的最小值是A ．6B ．4C ．2-D ．6-n ＝12, i ＝1n ＝3n ＋1开始 n 是奇数?输出i 结束是否 n ＝ n ＝5?是否n 2i ＝i ＋1 (第3题图)8．对于直角坐标平面内的任意两点11(,)A x y 、22(,)B x y ，定义它们之间的一种“距离”： ‖AB ‖=1212x x y y -+-，给出下列三个命题：①若点C 在线段AB 上，则‖AC ‖+‖CB ‖=‖AB ‖；②在△ABC 中，若∠C =90°，则‖AC ‖+‖CB ‖=‖AB ‖； ③在△ABC 中，‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A. 0B. 1C. 2D.3二、填空题：本大题共7小题，每小题5分，满分30分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置. （一）必做题（9-13题） 9．函数=y xxsin 的导函数='y ． 10．在递增等比数列{a n }中，4,2342=-=a a a ，则公比q ＝． 11．某学校三个社团的人员分布如下表（每名同学只参加一个社团）：学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则这三个社团人数共有_______________. 12．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝3π，3=b ，若△ABC 的面积为233 ，则c = ． 13．如图，F 1，F 2是双曲线C ：22221x y a b-=(a ＞0，b ＞0) 的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若 | AB | : | BF 2 | : | AF 2 |＝3 : 4 : 5，则双曲线的离心率为 .（二）选做题（14-15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在直角坐标系x O y 中，已知曲线1C ：⎩⎨⎧-=+=t y t x 212 , (为参数）与曲线2C ：⎩⎨⎧==θθsin 3cos 3y x ,（θ为参数）相交于两个点A 、B ，则线段AB 的长为 .合唱社粤曲社武术社高一 45 30 a高二 15 10 20xy OA BF 1F 2(第13题图)ODCB AP(第15题图）15．（几何证明选讲选做题）如图，PAB 、PCD 为⊙O 的两条割线，若PA=5，AB=7，CD=11，AC=2，则BD 等于 .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）设向量a ＝)sin ,2(θ，b ＝)cos ,1(θ，θ为锐角．（1）若a ·b ＝136，求sin θ＋cos θ的值；（2）若a ∥b ，求sin(2θ＋π3)的值．17．（本小题满分12分）某中学校本课程共开设了A ，B ，C ，D 共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：（1）求这3名学生选修课所有选法的总数；（2）求恰有2门选修课没有被这3名学生选择的概率；（3）求A 选修课被这3名学生选择的人数的数学期望.18．（本小题满分14分）已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形（1）求证：N B C BC 11//平面；（2）求证：BN 11C B N ⊥平面；（3）设M 为AB 中点，在BC 边上找一点P ，使MP //平面1CNB ,并求PCBP的值.88 4主视图侧视图俯视图44819．(本题满分14分)已知椭圆C ：)0(12222>>=+b a by a x ，左、右两个焦点分别为1F 、2F ，上顶点),0(b A ，21F AF ∆为正三角形且周长为6.（1）求椭圆C 的标准方程及离心率；（2）O 为坐标原点，P 是直线A F 1上的一个动点，求||||2PO PF +的最小值，并求出此时点P 的坐标．20．(本小题满分14分)已知函数21()22f x ax x =+，()g x lnx =. （1）如果函数()y f x =在[1,)+∞上是单调减函数，求a 的取值范围；（2）是否存在实数0a >，使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根？若存在，请求出a 的取值范围；若不存在，请说明理由．21．（本题满分14分）已知正项数列{}n a 的前n 项和为n S ，且(2)4n n n a a S += *()n ∈N . （1）求1a 的值及数列{}n a 的通项公式；（2）求证：33331231111532n a a a a ++++<*()n ∈N ；（3）是否存在非零整数λ，使不等式1121111(1)(1)(1)cos 21n n n a a a a a πλ+--⋅⋅-<+ 对一切*n ∈N 都成立？若存在，求出λ的值；若不存在，说明理由.ODCBAP(第15题图）珠海市2012~2013学年第一学期普通高中学生学业质量监测高三理科数学试题参考答案及评分标准一、选择题：CABD AADB 二、填空题： 9．函数=y xxsin 的导函数='y ． 10．在递增等比数列{a n }中，4,2342=-=a a a ，则公比q ＝． 11．某学校三个社团的人员分布如下表（每名同学只参加一个社团）：学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则这三个社团人数共有_______________. 12．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝3π，3=b ，若△ABC 的面积为233 ，则c = ．13．如图，F 1，F 2是双曲线C ：22221x y a b-=(a ＞0，b ＞0) 的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若 | AB | : | BF 2 | : | AF 2 |＝3 : 4 : 5，则双曲线的离心率为 .（二）选做题（14-15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在直角坐标系x O y 中，已知曲线1C ：⎩⎨⎧-=+=t y t x 212 , (为参数）与曲线2C ：⎩⎨⎧==θθsin 3cos 3y x ,（θ为参数）相交于两个点A 、B ，则线段AB 的长为 .15．（几何证明选讲选做题）如图，PAB 、PCD 为⊙O 的两条割线，若PA=5，AB=7，CD=11，AC=2，则BD 等于 .合唱社粤曲社武术社高一 45 30 a高二 15 10 20xy OA BF 1F 2(第13题图)9、2sin cos x xx x - 10、2 11、150 12、713、13 14、 4 15、 6 三、解答题：12+12+14+14+14+14=80 16．（本小题满分12分）设向量a ＝)sin ,2(θ，b ＝)cos ,1(θ，θ为锐角．（1）若a ·b ＝136，求sin θ＋cos θ的值；（2）若a ∥b ，求sin(2θ＋π3)的值．17．（本小题满分12分）某中学校本课程共开设了A ，B ，C ，D 共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：（1）求这3名学生选修课所有选法的总数；（2）求恰有2门选修课没有被这3名学生选择的概率；（3）求A 选修课被这3名学生选择的人数的数学期望.18．（本小题满分14分）已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形（1）求证：N B C BC 11//平面；（2）求证：BN 11C B N ⊥平面；（3）设M 为AB 中点，在BC 边上找一点P ，使MP //平面1CNB ,并求PCBP的值.19．(本题满分14分)88 4主视图侧视图俯视图448已知椭圆C ：)0(12222>>=+b a by a x ，左、右两个焦点分别为1F 、2F ，上顶点),0(b A ，21F AF ∆为正三角形且周长为6.（1）求椭圆C 的标准方程及离心率；（2）O 为坐标原点，P 是直线A F 1上的一个动点，求||||2PO PF +的最小值，并求出此时点P 的坐标．20．(本小题满分14分)已知函数21()22f x ax x =+，()g x lnx =. （1）如果函数()y f x =在[1,)+∞上是单调减函数，求a 的取值范围；（2）是否存在实数0a >，使得方程()()(21)g x f x a x '=-+在区间1(,)e e内有且只有两个不相等的实数根？若存在，请求出a 的取值范围；若不存在，请说明理由．21．（本题满分14分）已知正项数列{}n a 的前n 项和为n S ，且(2)4n n n a a S += *()n ∈N . （1）求1a 的值及数列{}n a 的通项公式；（2）求证：33331231111532n a a a a ++++<*()n ∈N ；（3）是否存在非零整数λ，使不等式1121111(1)(1)(1)cos 21n n n a a a a a πλ+--⋅⋅-<+ 对一切*n ∈N 都成立？若存在，求出λ的值；若不存在，说明理由.三、解答题：16．（本小题满分12分）解：（1）因为a ·b ＝2＋sin θcos θ＝136，所以sin θcos θ＝16． ……………… 3分所以 (sin θ＋cos θ)2＝1＋2 sin θcos θ＝43．又因为θ为锐角，所以sin θ＋cos θ＝233． ……………… 6分（2）解法一因为a ∥b ，所以tan θ＝2． ……………… 8分所以 sin2θ＝2 sin θcos θ＝ 2 sin θcos θ sin 2θ＋cos 2θ＝ 2 tan θ tan 2θ＋1＝45， cos2θ＝cos 2θ－sin 2θ＝cos 2θ－sin 2θ sin 2θ＋cos 2θ＝1－tan 2θ tan 2θ＋1＝－35．……………… 10分所以sin(2θ＋π3 )＝12sin2θ＋32cos2θ＝12×45＋32×(－35 )＝4－3310． ……………… 12分解法二因为a ∥b ，所以tan θ＝2． ……………… 8分所以 sin θ＝255，cos θ＝55．因此 sin2θ＝2 sin θcos θ＝45， cos2θ＝cos 2θ－sin 2θ＝－35． ……………… 10分所以sin(2θ＋π3 )＝12sin2θ＋32cos2θ＝12×45＋32×(－35 )＝4－3310． ……………… 12分17、（本小题满分12分）解析：(Ⅰ)每个学生有四个不同选择，根据乘法法则，选法总数N=64444=⨯⨯ …… 3分(Ⅱ) 恰有2门选修课这3名学生都没选择的概率为1694442332432223242=⨯⨯⨯⨯⨯==A C C P ……………… 7分(Ⅲ) 设A 选修课被这3名学生选择的人数为ξ，则ξ＝0,1,2,3＝64274333= P(ξ＝1)＝P(ξ＝0)6427433213=⋅C P(ξ＝2)＝64943313=⋅C P(ξ＝3)＝ 6414333=C ……………… 9分ξ的分布列是………… 10分43641364926427164270=⨯+⨯+⨯+⨯=ξE ………… 12分18.解：（1）证明：该几何体的正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，∴1,,BB BC BA 两两互相垂直。

数学文卷·2014届广东省珠海市高二下学期期末考试(2013.07)

17．若 OA = 3 + 4i ， OB = -1 - i ，其中 a，b Î R ，是虚数单位，则 AB =
．（用
复数代数形式表示）
18．下列结论：①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归
分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关
系的两个变量进行统计分析的一种常用方法．其中正确的是
（已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5
（1）试求出回归直线方程；
（2）请估计当施化肥量为 10 kg 时，水稻产量为多少？
（已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5
×2.5=125）
第 4 页共 12 页
25．（本小题 10 分）
已知二次函数 y = f (x) 的图像如图所示．（１）求函数 f (x) 的解析式；（2）求函数 f (x) 在区间[t,t + 2]上的最大值h(t) ；
»
2.778
由 P ( K 2 ³ 2.706 ) = 0.10 ，所以大概 90％认为药物有效．
………10 分
24．（本小题 10 分）
给出施化肥量（kg）对水稻产量（kg）影响的试验数据：
施化肥量 x 15
20
25
30
水稻产量 y 330 345 365 405
（1）试求出回归直线方程；
（2）请估计当施化肥量为 10 kg 时，水稻产量为多少？

2012-2013学年海珠区高一下学期期末教学质量检测数学试题

2012-2013学年海珠区高一下学期期末教学质量检测数学试题一、选择题（共10小题；共50分）1.A. B. C. D.2. 已知角的终边经过点，则的值是A. B. C. D.3. 若函数，则是A. 最小正周期为的奇函数B. 最小正周期为的奇函数C. 最小正周期为的偶函数D. 最小正周期为的偶函数4. 化简A. B. C. D.5. 等于______A. B. C. D.6. 在等差数列中，已知，则A. B. C. D.7. 将函数的图象向左平移个单位，再向上平移个单位，所得图象的函数解析式是A. B.C. D.8. 在中，是以为第三项，为第七项的等差数列的公差，是以为第三项，为第六项的等比数列的公比，则这个三角形是A. 钝角三角形B. 等腰直角三角形C. 锐角三角形D. 等腰三角形9. 函数＝在区间的简图为A. B.C. D.10. 在中，点在上，且，点为中点，若，，则A. B. C. D.二、填空题（共4小题；共20分）11. 已知，，三个正数成等比数列，其中，，则 ______．12. 已知，则的最小值为______．13. 在边长为的正三角形中，设，，，则______．14. 给出下列命题：①存在实数，使；②函数是偶函数；③是函数的一条对称轴的方程；④若，是第一象限的角，且，则 .其中正确命题的序号是______ .三、解答题（共6小题；共78分）15. 已知向量，（1）求；（2）当为何实数时，与平行，平行时它们是同向还是反向?16. 在假期社会实践活动中，小明参观了某博物馆．该博物馆大厅有一幅壁画，刚进入大厅时，他在点处看这幅壁画顶端点的仰角为，往正前方走后，在点处看壁画顶端点的仰角为（如图所示）.（1）求的长；（2）若小明身高为，求这幅壁画顶端点离地面的高度（精确到，其中）.17. 设等差数列的前项和为，等比数列的前项和为，已知，，.（1）求数列与的通项公式；（2）求与 .18. 已知函数．（1）求的最小正周期；（2）求的单调递增区间；（3）求在上的最值及取最值时的值．19. 在平面直角坐标系中，点满足约束条件：．（1）在给定的坐标系中画出满足约束条件的可行域（用阴影表示，并注明边界的交点）；（2）设，求的取值范围；（3）已知两点，，求的最大值．20. 数列满足：，，，为数列的前项和（1）求证：数列为等差数列；（2）设，求数列的前项和；（3）设（为非零整数，），试确定的值，使得对任意，有恒成立．答案第一部分1. B2. A3. D4. B5. D6. C7. B8. C9. A 10. D第二部分11.12.13.14. ②③第三部分15. （1）所以（2）设，则所以解得故时，与反向平行16. （1）在中，因为，所以由正弦定理，得，将代入上式，得（2）在中，因为，所以因为所以则所以答：的长为；壁画顶端点离地面的高度为 . 17. （1）设等差数列的公差为，等比数列的公比为 . 由，得，又，所以，所以由，得，所以（2）18. （1）的最小正周期．（2）因为，由，得，所以的单调增区间是．（3）因为，所以．所以．所以．当，即时，取得最小值．当，即时，取得最大值．19. （1）由得所以由得所以由得所以画出可行域，如右下图所示.（2）当直线与直线重合时，倾斜角最小且为锐角，此时当直线与直线重合时，倾斜角最大且为锐角，此时，所以的取值范围为（3）设，则，表示直线在轴上的截距，当直线经过点时，取到最大值，这时的最大值为 .20. （1）由，得，即，且所以数列是以为首项，公差为的等差数列．（2）由（1）知．所以，，，两式相减得所以（3）因为，所以要使，只要恒成立，即恒成立，即恒成立．当为奇数时，即恒成立当且仅当时，有最小值为，∴．当为偶数时，即恒成立当且仅当时，有最大值，∴．即，又为非零整数，则综上所述，存在，使得对任意，都有．。

珠海市2012届高一第二学期期末考试(数学)含答案与评分标准

珠海市2012届高一第二学期期末考试数学试卷时间：120分钟分值：150分参考公式：球的表面积24r S π=，球的体积334r V π=，圆锥侧面积rl S π=侧一、选择题：(本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，只有一项是符合题目要求的,请在答题卡相应位置填涂答案)1．已知向量(2,3)a =，(6,)b x =，且a b ⊥，则x 的值为( )A ．4B ．4-C ．9-D ．92．在ABC ∆中，a =3b =，120A =，则Ｂ的值为( )A ． 30B ． 45C ． 60D ． 903．数23可能是数列3,5,7,9,11,,中的第( )项A. 10B. 11C. 12D. 134．等差数列{}n a 的首项11=a ，公差3=d ，{}n a 的前n 项和为n S ，则=10S ( )A. 28B. 31C. 145D. 1605．已知两数2-与5-，则这两数的等比中项是( )A ．10B ．10-C ．10±D ．不存在6．已知数列{}n a 的通项公式是249n a n =-，则其前n 项和n S 取最小值时，n 的值是( )A ．23B ．24C ．25D ．267．若角βα,满足22παπ<<-，22πβπ<<-,则βα-的取值范围是 ( )A ．)0,(π-B ．),(ππ-C ．)2,23(ππ- D ．),0(π 8．不等式组300x x y x y ≤⎧⎪+≥⎨⎪-≥⎩表示的平面区域的面积等于( )A ．92B ．6C ．9D ．189．给出以下四个命题：①若一条直线a 和一个平面α平行，经过这条直线的平面β和α相交，那么a 和交线平行；②如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面； ③如果两条直线都平行于一个平面，那么这两条直线互相平行；④如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。

珠海市2012-2013学年度第一学期期末学生学业质量监测高三文科数学

珠海市2012~2013学年度第一学期期末学生学业质量监测高三文科数学试题一、选择题：本大题共10小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项.1．已知集合),1(+∞-=M ，集合{}0)2(|≤+=x x x N ，则N M ⋂= A ．]2,0[ B ． ),0(+∞ C ． ]0,1(- D ． )0,1(-2．已知a ，b 是实数，则“⎩⎨⎧>>32b a ”是“5>+b a ”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．若某程序框图如图所示，则该程序运行后输出的值是 A ．4 B ．5 C ．6 D ．74. 已知直线l ，m 和平面α，则下列命题正确的是 A ．若l ∥m ，m ⊂α，则l ∥α B ．若l ∥α，m ⊂α，则l ∥m C ．若l ⊥m ，l ⊥α，则m ∥α D ．若l ⊥α，m ⊂α，则l ⊥m5．已知是虚数单位，复数ii+3＝ A ．i 103101+ B ．i 103101+- C ．i 8381+- D ．i 8381--6．函数y ＝sin (2x ＋π4)的图象可由函数y ＝sin 2x 的图象 A ．向左平移π8个单位长度而得到 B ．向右平移π8个单位长度而得到 C ．向左平移π4个单位长度而得到 D ．向右平移π4个单位长度而得到7．已知a 、b 均为单位向量,)2()2(b a b a -⋅+=233-，a 与b 的夹角为 A ．30° B ．45° C ．135° D ．150°8．在递增等比数列{a n }中，4,2342=-=a a a ，则公比q ＝ A ．-1 B ．1 C ．2 D ．21(第3题图)9．若实数x ，y 满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-3005x y x y x 则2x ＋4y 的最小值是A ．6B ．4C ．2-D ．6-10．对于直角坐标平面内的任意两点11(,)A x y 、22(,)B x y ，定义它们之间的一种“距离”： ‖AB ‖=1212x x y y -+-，给出下列三个命题： ①若点C 在线段AB 上，则‖AC ‖+‖CB ‖=‖AB ‖； ②在△ABC 中，若∠C =90°，则‖AC ‖+‖CB ‖=‖AB ‖； ③在△ABC 中，‖AC ‖+‖CB ‖>‖AB ‖. 其中真命题的个数为A. 0B. 1C. 2D.3二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置. （一）必做题（11-13题）11．某学校三个社团的人员分布如下表（每名同学只参加一个社团）：学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从社团成员中抽取30人，结果合唱社被抽出12人，则这三个社团人数共有_______________. 12．在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知C ＝3π，3=b ，若△ABC 的面积为233 ，则c = ．13．如图，F 1，F 2是双曲线C ：22221x y a b-=(a ＞0，b ＞0)的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若 | AB | : | BF 2 | : | AF 2 |＝3 : 4 : 5，则双曲线的离心率为 .（二）选做题（14-15题，考生只能从中选做一题）14．（坐标系与参数方程选做题）在直角坐标系x O y 中，已知曲线1C ：⎩⎨⎧-=+=t y t x 212, (为参xyOA B F 1F 2(第13题图)第 3 页共 9 页(第15题图）数）与曲线2C ：⎩⎨⎧==θθsin 3cos 3y x ,（θ为参数）相交于两个点A 、B ，则线段AB 的长为 .15．（几何证明选讲选做题）如图，PAB 、PCD 为⊙O 的两条割线，若PA=5，AB=7，CD=11，AC=2，则BD 等于 .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）设向量a ＝)sin ,2(θ，b ＝)cos ,1(θ，θ为锐角．（1）若a ·b ＝136，求sin θ＋cos θ的值；（2）若a ∥b ，求sin(2θ＋π3)的值．17．（本小题满分12分）某种零件按质量标准分为5,4,3,2,1五个等级.现从一批该零件中随机抽取20个，对其等级进行统计分析，得到频率分布表如下：（1）在抽取的20个零件中，等级为5的恰有2个，求n m ,；（2）在（1）的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级恰好相同的概率.18．（本小题满分14分）已知某几何体的直观图和三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，（1）求证：N B C BC 11//平面；（2）求证：BN 11C B N ⊥平面；（3）求此几何体的体积.19．(本题满分14分)已知椭圆C ：)0(12222>>=+b a by a x ，左、右两个焦点分别为1F 、2F ，上顶点),0(b A ，21F AF ∆为正三角形且周长为6.（1）求椭圆C 的标准方程及离心率；（2）O 为坐标原点，直线A F 1上有一动点P ，求||||2PO PF +的最小值．20．（本题满分14分）已知函数()ln a xf x x x-=+，其中a 为常数，且0>a . （1）若曲线()y f x =在点（1，(1)f ）处的切线与直线121+=x y 垂直，求a 的值；（2）若函数()f x 在区间[1，2]上的最小值为21，求a 的值.21.（本题满分14分）在数列{}n a 中，*)(1,111N n a a a a n n n ∈+==+.（1）求证：数列⎭⎬⎫⎩⎨⎧n a 1是等差数列，并求数列{}n a 的通项公式；（2）设nnn a b ⋅=21，求数列}{n b 的前n 项和n T ；（3）设∑=+++=201312121i i i a a P ，求不超过P 的最大整数的值.主视图侧视图俯视图第 5 页共 9 页珠海市2012~2013学年第一学期普通高中学生学业质量监测高三文科数学试题参考答案及评分标准一、选择题：CABDA AACDB 二、填空题： 11、150 12、7 13、13 14、 4 15、 6三、解答题：本大题共6小题，满分80分． 16．（本小题满分12分）解：（1）因为a ·b ＝2＋sin θcos θ＝136，所以sin θcos θ＝16． ……………… 3分所以 (sin θ＋cos θ)2＝1＋2 sin θcos θ＝43．又因为θ为锐角，所以sin θ＋cos θ＝233． ……………… 6分（2）解法一因为a ∥b ，所以tan θ＝2． ……………… 8分所以 sin2θ＝2 sin θcos θ＝ 2 sin θcos θ sin 2θ＋cos 2θ＝ 2 tan θ tan 2θ＋1＝45， cos2θ＝cos 2θ－sin 2θ＝cos 2θ－sin 2θ sin 2θ＋cos 2θ＝1－tan 2θ tan 2θ＋1＝－35．……………… 10分所以sin(2θ＋π3 )＝12sin2θ＋32cos2θ＝12×45＋32×(－35 )＝4－3310． ……………… 12分解法二因为a ∥b ，所以tan θ＝2． ……………… 8分所以 sin θ＝255，cos θ＝55．因此 sin2θ＝2 sin θcos θ＝45， cos2θ＝cos 2θ－sin 2θ＝－35． ……………… 10分所以sin(2θ＋π3 )＝12sin2θ＋32cos2θ＝12×45＋32×(－35 )＝4－3310． ……………… 12分 17．（本小题满分12分）（Ⅰ）解：由频率分布表得 0.050.150.351m n ++++=，即 0.45m n +=. ………………2分由抽取的20个零件中，等级为5的恰有2个，得 1.0202==n . ………………4分所以0.450.10.35m =-=. ………………5分MB 1C 1NCBA（Ⅱ）解：由（Ⅰ）得，等级为3的零件有3个，记作123,,x x x ；等级为5的零件有2个，记作12,y y .从12312,,,,x x x y y 中任意抽取2个零件，所有可能的结果为：12131112232122313212(,),(,),(,),(,),(,),(,),(,),(,),(,),(,)x x x x x y x y x x x y x y x y x y y y共计10种. ………………9分记事件A 为“从零件12312,,,,x x x y y 中任取2件，其等级相等”.则A 包含的基本事件为12132312(,),(,),(,),(,)x x x x x x y y 共4个. ………………11分故所求概率为 4()0.410P A ==.………………12分 18.解：（1）证明：该几何体的正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，∴1,,BB BC BA 两两互相垂直。

广东省珠海市2012-2013学年高一下学期期末学业质量测监英语试题(B卷)

绝密★启用前试卷类型：B珠海市2012～2013学年度第二学期期末学生学业质量监测高一英语试题（本试卷分第一卷和第二卷两部分。

满分：135；考试用时：120分钟）注意事项：1. 答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。

用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。

2. 选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3. 非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4. 考生必须保持答题卡的整洁。

考试结束后，将答题卡交回。

第一卷第一部分单项填空：（共10小题；每小题2分，满分20分）从每小题所给的四个选项中选出一个最佳选项，并将答题卡上的相应选项涂黑。

1. ___________ you have your computer stolen. You forgot to lock the door when leaving.A. No excuseB. No surpriseC. No matterD. No wonder2. The students together with the head teacher _________ visit the Chime Long Paradise.A. is going toB. are going toC. is to beD. may going to3. “Where have you been? We thought that you were lost!”mother said angrily,_________ to Lily.A. pointingB. to pointC. having pointedD. pointed4. With the electricity ___________, all the machines stopped.A. cut offB. was cut offC. cut downD. was cut down5. We hope that we can _________ the world ________ wars, killers and everything else that is bad.A．get rid of; by B．be rid of; by C．rid; of D．get rid; of 6. Each of the students, working hard at his or her lessons, __________ to go to university.A. hopeB. hopesC. hopingD. to hope7. The reason __________ she gave for not finishing the homework is that she was ill.A. whyB. whatC. thatD. for8. ___________ she will go or not doesn’t matter much.A. WhenB. ThatC. IfD. Whether9. I met my old friend ____________ on my way home from school.A. by chanceB. on accidentC. by suddenD. on occasion10. I’m so busy today that I can’t __________ the house.A. help cleaningB. help cleanedC. help to cleanD. helped clean第二部分完形填空：（共15小题，每小题2分，满分30分）阅读下面的短文，然后从每小题所给的四个选项中选出一个最佳选项，并将答题卡上的相应选项涂黑。

广东省珠海市202-2013学年高一数学下学期期末考试试题(A卷)新人教A版

珠海市2012～2013学年度第二学期期末学生学业质量监测高一数学试题（A 卷）及参考答案时量：120分钟分值：150分．适用学校：全市各高中使用A 卷学校．内容：数学必修②第二章，数学必修③，数学必修④．一、选择题（本大题共12小题，每小题5分，共60分，每小题给出的四个选项中，只有一项是符合题目要求的）1.(平面向量) 已知平面向量(4,1)a =r ，(,2)b x =r ，且a r 与b r平行，则x =（）A B ．12- C ．8 D ．122.(三角函数) 4sin3π的值是（）A ．12 B ．12- C ．32 D ．32- 3.(一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是( ).至多有一次中靶 B. 两次都中靶 C. 只有一次中靶 D. 两次都不中靶4.(将两个数8,17a b ==交换,使17,8a b ==,下面语句正确一组是 ( )5.(某一个同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的对比表：摄氏温度/℃-5 047 12 15 19 23 27 31 36热饮杯数 156 150 132 128 130 116 104 89 93 76 54 某同学利用智能手机上的Mathstudio 软件研究，直接得到了散点图及回归方程（如右图所示），请根据结果预测，若某天的气温是3℃，大约能卖出的热饮杯数为（）. A. 143 B. 141 C. 138 D. 134 （单词提示：Linear 线性）a=b b=a （A ） c=b b=a a=c （B ） b=aa=b （C ）a=c c=b b=a （D ）6.(统计) 要从已编号（160-）的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验，用每部分选取的号码间隔一样的系统抽样方法确定所选取的6枚导弹的编号可能是（）A ．5,10,15,20,25,30B ．3,13,23,33,43,53C ．1,2,3,4,5,6D ．2,4,8,16,32,487.(平面向量) 如右下图所示，D 是ABC ∆的边AB 上的中点，记BC a =u u u r r ，BA c =u u u r r，则向量CD =u u u r（）A ．a -r 8.(A ．1639.(算法) A.1-10.(a 的值为（ 11.(，A ．y 1sin(26x π+D.sin(26y x π=+12.(三角变换) 已知(,0)2x π∈-，4cos 5x =，则=x 2tan （）A ．724B ．724-C ．247-D ． 247-二、填空题（本大题共8小题，每小题5分，共40分,请将正确答案填在答题卡上） 13.(圆的方程) 以(1,2),(5,6)A B --为直径两端点的圆的标准方程为．ACB14.(算法)二进制数定义为“逢二进一”，如2(1101)表示二进制数，将它转换成十进制形式，是321012120212⨯+⨯+⨯+⨯= 13，即2(1101)转换成十进制数是13，那么类似可定义k 进制数为“逢k 进一”，则8进制数8(102)转换成十进制数是_________ 15.(统计) 一个容量为20的样本数据，分组后组距与频数如下表：人，则高中部三、解答题（本大题共5小题，每题10分，共50分.请将详细解答过程写在答题卡上）21.(平面向量) 已知||4a =r ，||b =r ()(2)4a b a b +⋅-=r r r r .（1）求a b ⋅r r（2）求||a b +r r .22.(三角函数)已知函数sin()(0,0)2y A x A πωϕωϕ=+><<，的图形的一个最高点为，由这个最高点到相邻的最低点时曲线经过(6,0)，求这个函数的解析式.23.(统计)某学校900名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[13,14)，第二组[14,15)，…，第17,18，下图是按上述分组方法得到的频率分布直方图．五组[]（1（2（324.(概率)方案1方案2：奖.两个方案中，哪个方案中奖率更高？请说明理由.25.(三角变换)已知OPQ 是半径为1，圆心角为4π的扇形，C是扇形弧上的动点. ABCD是扇形的内接矩形，记COP θ∠=.（1）求当角θ取何值时，矩形ABCD 的面积最大？并求出这个最大值. （2）当矩形ABCD θ的值. 附加题：26. 在一次商贸交易会上，一商家在柜台开展促销抽奖活动，甲、乙两人相约同一天上午去该柜台参与抽奖.（1）若抽奖规则是从一个装有6个红球和4个白球的袋中有放回地取出2个球，当两个球同色时则中奖，求中奖概率；（2）若甲计划在9：00～9：40之间赶到，乙计划在9：20～10：00之间赶到，求甲比乙提前到达的概率.27．如图，已知在三角形ABC 中，3AB =,4AC =，5BC =.(1) 求向量AB AC BC ++u u u r u u u r u u u r的模；(2)若长为10的线段PQ 以点A 为中点，问BC PQ 与的夹角θ取何值时BP ⋅的值最大？并求这个最大值.28. 在三角形ABC 中（1）若4A B π+=，求(1tan )(1tan )A B ++的值.（2）若lg tan lg tan 2lg tan A C B +=，求证：32B ππ≤<.θOQDCPBA CAB珠海市2012～2013学年度第二学期期末学生学业质量监测高一数学试题及参考答案一、选择题1、C2、D3、D4、B5、B6、B7、B8、D9、B 10、B 11、C 12、C二、填空题（本大题共8小题，每小题5分，共40分,请将正确答案填在答题卡上） 13.22(2)(2)25x y -++= 14. 66 15.0.7 16. 10?i > 17.3600 18.π 19. (4,3)(4,3)--或 20.4[+2,+2]()33k k k Z ππππ∈1分） 3分） 4分）（（9221分）由周期公式可得到：216T πω==，又0ω>Q ，8πω∴=…………………………（4分）sin()8y x πϕ∴=+……………………………………………………………（5分）又函数图像过点sin(2)8πϕ=⨯+，即sin()14πϕ+=…………………………………（7分）又02πϕ<<Q4πϕ∴=…………………………………………………………………（9分）所以函数解析式是：sin()84y x ππ=+……………………………………（10分）23.解：（1）样本在这次百米测试中成绩优秀的人数=10.06503⨯⨯=（人）……………（2分）（2）学校900名学生中，成绩属于第四组的人数10.32900288⨯⨯=（人）………………………（2分）（3）由图可知众数落在第三组[15,16)，是151615.52+=………………………（5分）6分） 9分）24.解奖概率为S S 正方形圆（25分）（i ）2个球都是红色，包含的基本事件数为；………………………………（6分）（ii ）2个球都是白色，包含的基本事件数为2+13=.……………………………（7分）所以，中奖这个事件包含的基本事件数为1+3=4. 因此，中奖概率为42105=.…………（9分）由于235π>，所以方案1的中奖率更高. …………………………………………（10分）25.解：(1)在Rt OBC ∆中：cos OB θ=，sin BC θ=……………………（1分）在Rt OAD ∆中：tan 14AD OA π== 所以sin OA AD BC θ===…………………………………（2分）所以cos sin AB OB OA θθ=-=-……………………………………（3分）所以矩形ABCD 的面积(cos sin )sin S AB BC θθθ=⋅=-……………………（4分）6分） 7分） (2) 当S =8分）又因为32444πππθ<+<，所以2243ππθ+=，即524πθ=…………………（10分）附加题：26. 在一次商贸交易会上，一商家在柜台开展促销抽奖活动，甲、乙两人相约同一天上午去该柜台参与抽奖.（1）若抽奖规则是从一个装有6个红球和4个白球的袋中有放回地取出2个球，当两个球同色时则中奖，求中奖概率；（2）若甲计划在9：00～9：40之间赶到，乙计划在9：20～10：00之间赶到，求甲比乙提前到达的概率.解：（1）从袋中10个球中摸出2个，试验的结果共有1010100⨯=（种）……………………………（1分）中奖的情况分为两种：（i ）2个球都是红色，包含的基本事件数为6636⨯=；…………………………（2分）（ii ）2个球都是白色，包含的基本事件数为4416⨯=.…………………………（3分）所以，中奖这个事件包含的基本事件数为36+16=52. 因此,中奖概率为521310025=.………………………（4分）（2）设两人到达的时间分别为9点到10点之间的x 分钟、y 分钟.用(,)x y 表示每次试验的结果，则所有可能结果为{(,)|040,2060}x y x y Ω=≤≤≤≤；……………………………………………………………（5分）记甲比乙提前到达为事件A ，则事件A 的可能结果为{(,)|,040,2060}A x y x y x y =<≤≤≤≤. ………………………………………………………（6分）如图所示，试验全部结果构成区域Ω为正方形ABCD . 而事件A 所构成区域是正方形内的阴影部分. ………………………………………………………（8分）根据几何概型公式，得到2221402072()408S P A S -⨯===阴影正方形. 所以，甲比乙提前到达的概率为78. ………………………………（10分）27．如图，已知在三角形ABC 中，3AB =,4AC =，5BC =.(1) 求向量AB AC BC ++u u u r u u u r u u u r的模；(2)若长为10的线段PQ 以点A 为中点，问BC PQ 与的夹角θ取何值时CQ BP ⋅的值最大？并求这个最大值.C解：（1）AB AC BC ++=u u u r u u u r u u u r ………………………………（1分）=2分）=……………………（3分）=8=…………………………………………………………………………………（4分）（另解：用几何法，根据向量加法的平行四边形法则，画图，很快可得8AB AC BC ++=u u u r u u u r u u u r）（2）u 5分）==6分） === ==（8分）==25cos 25PQ BC =<⋅>-u u u r u u u r………………………………………………………（9分）当00PQ BC <⋅>=u u u r u u u r 即00θ=时，m ()0ax BP CQ ⋅=u u u r u u u r ……………………………（10分）28. 在三角形ABC 中（1）若4A B π+=，求(1tan )(1tan )A B ++的值.（2）若lg tan lg tan 2lg tan A C B +=，求证：32B ππ≤<.精品试卷解：（1）由4A B π+=得tan()1A B +=即tan tan 11tan tan A B A B+=-……………………………（1分）即tan tan 1tan tan A B A B +=-即tan tan +tan tan =1A B A B +…………………………………………………（2分）即tan (tan +1)(tan 1)=2A B B ++…………………………………………（3分）即(tan +1)(tan 1)=2B A +即(1tan )(1tan )2A B ++=…………………………………………………（4分）（2）由已知得：,,A B C 都为锐角，2tan tan tan A C B ⋅=…………………………………………（5分）Q 分） ∴∴7分）∴8分）即即即9分）。

珠海市2013届高三上学期期末学业质量监测数学理(3份)

海珠区2012-2013学年第二学期期末教学质量监测参考答案和评分标准

2012-2013学年第二学期期末教学质量监测高二化学参考答案一、单项选择题（本题包括15小题，每小题2分，共30分，每小题只有一个选项符合题意。

）二、双项选择题（本题包括5小题，每小题4分，共20分。

每小题有两个选项．．．．符合题意。

只选一个且正确的得2分，只要选错一个，该小题就为0分）三、填空题（本题包括4小题，共50分） 21．(13分)（1）① 3Pb ＋8HNO 3=3Pb(NO 3)2＋2NO ↑＋4H 2O （2分）PbO ＋2HNO 3=Pb(NO 3)2＋H 2O （2分） ② Pb 2＋＋ SO 42－=PbSO 4↓ （2分） HNO 3 （1分）（2）①PbO 2（1分）Pb －2e－= Pb 2＋（2分）②PbSO 4＋2H 2O －2e －=PbO 2＋4H ＋＋SO 42－（2分）小（1分）22．（ 8 分）。

（1）①（C 6H 10O 5）n + nH 2O nC 6H 12O 6 （2分）② C 6H 12O 6 2（2分）酸或酶③（2分）（2）BD （2分）23．( 16 分)（1）C 10H 16O （2分）， 13.5 （2分）。

（2）（3分）（反应物、产物结构书写错误得0分，漏写H 2O 得0分，写等号或可逆符号扣1分，漏写浓H 2SO 4或△扣1分）（3）+2Ag(NH 3)2OH+ 2Ag↓+3NH 3+ H 2O （3分）（反应物、产物书写错误或漏写得0分，没有配平扣1分，写等号或可逆符号扣1分，漏写Cu 或△扣1分）（4）（4分，各2分）（5）B 、C （2分，各1分）24．（ 13 分）（1）防止三氯化铝与乙酸酐水解(只答三氯化铝水解或乙酸酐水解也可) （2分）（2）萃取，分液；（2分）蒸馏（1分）（3）否（1分），乙醇与水混溶（1分）（4）否（1分），在洗涤的操作中，足量5%的氢氧化钠已将乙酸完全中和（2分）（5）将苯乙酮粗产品进行蒸馏．．，迅速将温度升高到202．．．℃．，收集馏分．．．．（3分） + H 2O浓H 2SO 4△Cu△。

【首发】广东省珠海市2012-2013学年高二下学期期末学业质量测监数学文试题(B卷)精校电子版缺答案

珠海市2012-2013学年度第二学期期末学业质量检测高二文科数学试题（B 卷）考试用时：120分钟总分：150分考试内容：数学选修1-2，数学选修4-4，函数部分内容.参考公式：用最小二乘法求线性回归方程系数公式 ∑∑==∧---=ni ini i ix xy y x xb 121)())((=1221ni ii nii x y nx yxnx==--∑∑，ˆay b x ∧=-. 随机变量))()()(()(22d b c a d c b a bc ad n K ++++-= （其中d c b a n +++=）临界值表一、选择题（本题共有12个小题，每小题5分,共60 分）． 1.函数)1ln()(-=x x f 的定义域是 A ． ),1(+∞ B ．),1[+∞ C ． ),0(+∞ D ．),0[+∞ 2.下列表述正确的是①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理；③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理；⑤类比推理是由特殊到特殊的推理. A ．①②③ B ．②③④ C ．②④⑤ D ．①③⑤ 3.已知i 是虚数单位，则2)2(i -=A ．2B ．2-C ．4D ．4- 4.复数i 52+-在复平面内对应的点位于A ．第二象限B ．第一象限C ．第四象限D ．第三象限5.已知⎪⎩⎪⎨⎧≤>=.0,2,0,log )(21x x x x f x ，则)2(-f 的值是A ．2-B ．2C ．21 D ．416.若直线的参数方程为)(132是参数t ty tx ⎩⎨⎧+=-=，则直线的斜率为A ．31-B ．31C ．3-D ．37.三段论：“①只有船准时起航，才能准时到达目的港；②这艘船是准时到达目的港；③所以这艘船是准时起航的”中的“小前提”是A ．①B ．②C ．①②D ．③8.以直角坐标系的原点为极点，x 轴的非负半轴为极轴，并在两种坐标系中取相同的长度单位，点M 的极坐标是)32,4(π，则点M 直角坐标是 A ．)32,2( B ．)32,2(- C ．)2,3( D ．)2,3(- 9.下列函数，奇函数是A ．x x f ln )(=B ．xe xf =)( C ．x x x f +=sin )(D ．2cos )(x x x f +=10.正弦曲线x y sin =通过坐标变换公式⎩⎨⎧==y Y xX 23，变换得到的新曲线为A ．3sin 2X Y = B ．X Y 3sin 2= C ．X Y 3sin 21= D ．3sin 21XY = 11．复数计算：i -31=A ．43i +B ．43i -C ．103i -D ．103i+12．三角形的内角和为180º，凸四边形内角和为360º，那么凸n 边形的内角和为 A ．︒⋅180n B ． ︒⋅-180)1(n C ．︒⋅-180)2(n D ．︒⋅+180)1(n 二、填空题（本题共有8个小题，每小题5分,共40 分）．13.在工商管理学中，MRP ( Material Requirement Planning ）指的是物资需求计划，基本MRP 的体系结构如下图所示．从图中可以看出，主生产计划受______________________的影响．14.右侧流程图输出的结果是_________．Ks5u15.将参数方程是参数）θθθ(,sin 1,cos 2⎩⎨⎧-=+=y x 化为普通方程为．（标准方程）16.化极坐标方程2sin 4cos 3=+θρθρ为直角坐标方程为．（一般方程）17.若i 43+=，i --=1，i 是虚数单位，则=_________．（用复数代数形式表示） 18．（相关关系）下列结论：①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法．其中正确的是．（将所有正确的序号填上）19.已知：2231=+，2597531=++++.由以上两式，可以类比得到：=++++++131197531_____.20．已知*+∈=+=N n a a a a n nn ,1,111，则=n a ．三、解答题（本题共有5个小题，每小题10分，共50分）． 21．（本小题10分）（证明不等式）已知：,1,0,0<>>mn n m 证明：m nm n >++11． 22．（本小题10分）（极坐标与参数方程）已知直线的参数方程：)(sin 21cos 22是参数θθθ⎩⎨⎧+-=+=y x ．（1）求圆的圆心坐标和半径；（2）设圆上的动点),(y x P ，求y x z +=的最大值．23．（本小题10分）为考察某种药物预防甲型H1N1流感的效果，进行动物试验，调查了100个样本，统计结果为：服用药的共有60个样本，服用药但患病的仍有20个样本，没有服用药且未患病的有20个样本.（Ⅰ）根据所给样本数据完成下面2×2列联表；（Ⅱ）请问能有多大把握认为药物有效？（参考数据：224576=）24.kg ）影响的试验数据：（1）试求出回归直线方程；（2）请估计当施化肥量为10时，水稻产量为多少？（已知：7.5×31.25+2.5×16.25+2.5×3.75+7.5×43.75=612.5,2×7.5×7.5+2×2.5×2.5=125）25．（本小题10分）（综合题）已知函数R x ax x x f ∈+=,)(2．Ks5u （１）若)()1(x f x f -=+，求a 的值；（２）当2=a 时，求)()(x xf x g =的单调区间．。

广东省珠海市高三数学下学期学生学业质量检测试题文(

珠海市2013—2014学年度第二学期高三学生学业质量监测数学（文）试题【试卷综析】试题的题型比例配置与高考要求一致，全卷重点考查中学数学主干知识和方法，侧重于中学数学学科的基础知识和基本技能的考查，侧重于知识交汇点的考查.直观感知、观察发现、归纳类比、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等核心数学能力，重点考察了数形结合、简单的分类讨论、化归等数学基本思想方法试题中无偏题，怪题，起到了引导高中数学向全面培养学生数学素质的方向发展的作用。

总之本次考前模拟训练数学试题遵照高考考试大纲和考试大纲说明的要求，从题型设置、考察知识的范围等方面保持稳定，试题难度适中，试题在考查高中数学基本概念、基本技能和基本方法等数学基础知识，突出三基，强化三基的同时，突出了对学生能力的考查，注重了对学科的内在联系和知识的综合、重点知识的考查.一、选择题：本大题共10小题，每小题5 分，满分 50分．在每小题给出的四个选项中，只有一项是符合题目要求的．请在答题卡上填涂相应选项．1．已知集合 A={0,1, 2,3} ，集合 {|||2}B x N x =∈≤ ，则A B I = A ．{ 3 } B ．{0，1，2} C ．{ 1，2}D ．{0，1，2，3}【知识点】集合的表示方法；交集. 【答案解析】B 解析：解：{}0,1,2B =Q {}0,1,2A B ∴⋂=【思路点拨】可以把B 集合中描述法表示了元素用列举法表示出来，然后按交集的定义进行求解即可.2．设复数z1=1+i ，z2=2+xi （x R ∈），若 12.z z R∈，则x =A ．－2B ．－1C ．1D ．2【知识点】复数代数形式的运算【答案解析】A 解析：解：因为()()1212z z i xi ⋅=++()()22x x i =-++R∈,所以20,x +=即x 2=-.故选A.【思路点拨】把复数乘积展开，化简为a+bi （a 、b ∈R ）的形式，可以判断所在象限． 3．不等式2230x x -++<的解集是A ．{}|1x x <-B ．3|2x x ⎧⎫>⎨⎬⎩⎭C ．3|12x x x ⎧⎫-<<⎨⎬⎩⎭ D ．3|12x x x ⎧⎫<->⎨⎬⎩⎭或【知识点】一元二次不等式的解法. 【答案解析】D 解析：解：原不等式为：()()22302310x x x x -->-+>即，解得：312x x <->或，所以选:D.【思路点拨】先利用不等式的性质，把原不等式化为二次项系数大于零的一元二次不等式，再利用三个二次的关系求解.4．通过随机询问100 名性别不同的小学生是否爱吃零食，得到如下的列联表：由22()()()()()n ad bc K a b c d a c b d -=++++算得22100(10302040) 4.76250503070K ⨯-⨯=≈⨯⨯⨯参照右上附表，得到的正确结论A ．在犯错误的概率不超过5%的前提下，认为“是否爱吃零食与性别有关”B ．在犯错误的概率不超过5%的前提下，认为“是否爱吃零食与性别无关”C ．有97．5%以上的把握认为“是否爱吃零食与性别有关”D ．有97．5%以上的把握认为“是否爱吃零食与性别无关” 【知识点】独立性检验的应用，【答案解析】A 解析：解：∵K2= 100(10×30−20×40)250×50×30×70≈4.762＞3.841，P （K2＞3.841）=0.05∴在犯错误的概率不超过5%的前提下，认为“是否爱吃零食与性别有关”．故选：A ．【思路点拨】根据P （K2＞3.841）=0.05，即可得出结论．【典型总结】本题考查独立性检验的应用，考查学生分析解决问题的能力. 5．右上图是一个几何体的三视图，由图中数据可知该几何体中最长棱的长度是A ．6B ．5C ．5D 13【知识点】三视图；三视图与原图的关系.【答案解析】 C 解析：解：由三视图知：几何体为三棱锥，如图：ACBS其中SA ⊥平面ABC ，AC ⊥平面SAB ，SA=2，AB=4，AC=3，∴BC=5，SC ==SB ==∴最长棱为5BC =故选：C ．【思路点拨】可根据三视图找到原图的线面关系，根据图中所给数据进行计算. 6．执行如右图所示的程序框图，则输出的 y =A ．12 B ．1 C ．－1 D ．2【知识点】循环结构的程序框图【答案解析】D 解析：解：第1次循环，y=2,i=1 第2次循环，y= y=2,i=1,i=2 第3次循环，y=-1,i=3 第4次循环，y=2,i=4 ...........框图的作用是求周期为3的数列，输出y 的值，满足2014≥2014，退出循环，循环次数是2014次，即输出的结果为2，故答案为：2．【思路点拨】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环计算循环变量y ，i 的值，并输出满足i ≥2014的值． 7.“(1)(1)0a b -->”是“a>1 且b>1”的A ．充要条件B ．充分但不必要条件C ．必要但不充分条件D ．既不充分也不必要条件【知识点】充分条件、必要条件、充要条件.【答案解析】 C 解析：解：因为命题：若a>1 且b>1则(1)(1)0a b -->是真命题，若(1)(1)0a b -->则>1 且b>1是假命题，所以选C.【思路点拨】如果命题“若A 则B ”成立，那么A 是B 的充分条件，B 是A 的必要条件.8.将函数 cos(2)6y x π=-的图像向右平移12π个单位后所得的图像的一个对称轴是A ．x=6πB ．4x π= C ．3x π= D ．2x π=【知识点】平移变换，三角函数的对称性.【答案解析】 A 解析：解：函数 cos(2)6y x π=-的图像向右平移12π个单位后为函数：cos 23y x π⎛⎫=- ⎪⎝⎭易知它一条对称轴为：x=6π. 【思路点拨】利用平移变换得到函数 cos(2)6y x π=-的图像向右平移12π个单位后的函数解析式cos 23y x π⎛⎫=- ⎪⎝⎭，然后确定正确选项. 9．变量 x y 、满足线性约束条件32021x y y x y x +-≤⎧⎪-≤⎨⎪≥--⎩，则目标函数 z =kx －y ，仅在点（0 , 2）取得最小值，则k 的取值范围是A ．k<－3B ．k>1C ．－3<k<1D ．—1<k<1 【知识点】线性规划；不等式表示平面区域.【答案解析】C 解析：解：作出不等式对应的平面区域，由z=kx-y 得y=kx-z ，要使目标函数y=kx-z 仅在点A （0，2）处取得最小值，则阴影部分区域在直线y=kx-z 的下方， ∴目标函数的斜率k 满足-3＜k ＜1，故选：C ．【思路点拨】可由数形结合的方法找出目标函数取最小值的位置，进而求出k 的值. 10．设函数()y f x =在R 上有定义，对于任一给定的正数P ，定义函数(),()(),()p f x f x pf x p f x p ≤⎧=⎨>⎩，则称函数()p f x 为 ()f x 的“P 界函数”．若给定函数2()21,2f x x x p =--=，则下列结论不成立的是A ．[(0)][(0)]p p f f f f =B ．[(1)][(1)]p p f f f f =C ．[(2)][(2)]p p f f f f =D ．[(3)][(3)]p p f f f f =【知识点】新定义函数；分段函数求值.【答案解析】 B 解析：解：因为2()21,2f x x x p =--=，所以()()2[(0)]11=2p f f f f =-=-，()[(0)]=[(0)]=1=2p f f f f f -.故A 正确. ()2[(1)](2)22p p f f f f =-=-=，()[(1)]=[(1)]=27p f f f f f -=故B 不正确.()[(2)]12f f f =-=，222[(2)][(2)](1)2p p f f f f f ==-=故C 正确.[(3)](2)1,f f f ==-222[(3)][(3)](2)1p p f f f f f ===-故D 正确.综上：选项B 不正确.【思路点拨】结合“P 界函数”的定义计算即可.二、填空题：本大题共5小题，考生做答 4小题，每小题 5 分，满分 20 分．其中第 14～15 题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．请将答案填在答题卡相应位置． 11．等差数列{}n a 的前n 项和为Sn ，且满足a1=2，a2+a4+a6=15，则S10= ．【知识点】等差数列的通项公式、前n 项和公式，等差数列的性质. 【答案解析】 65 解析：解：由a2+a4+a6=15得45a =，又a1=2，则公差1d =，所以1011021091652s =⨯+⨯⨯⨯=【思路点拨】利用等差数列的通项公式、前n 项和公式，等差数列的性质求解.12．函数3()2f x x x =- 在x=1处的切线方程为．【知识点】导数的几何意义.直线的点斜式方程.【答案解析】2y x =-解析：解：()232f x x '=-Q ，()11f '∴=所以切线方程为： ()()()111y f x '--=-，即：2y x =-【思路点拨】利用导数的几何意义，求函数在某点处的切线方程.13．已知菱形 ABCD 的边长为 a ， ∠DAB=60°，2EC DE =u u u r u u u r ，则 .AE DB u u u r u u u r的值为．【知识点】平面向量数量积的运算．【答案解析】23a -解析：解：如图所示12,,3EC DE DE DC =∴=u u u r u u u r u u u r u u u r Q 因为菱形 ABCD 的边长为a, ∠DAB=60° 21,cos1202DA DC a DA DC DA DC a ∴==⋅==-o u u u r u u u r u u u r u u u r u u u r u u u r ,,DB DA DC =+u u ur u u u r u u u rAE DB ∴⋅=u u u r u u u r 1()()()()3AD DE DA DC AD DC DA DC ++=++u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r221233DA DC DA DC =-+-⋅u u u r u u u r u u u r u u u r 222211333a a a a =-++=-. 【思路点拨】利用菱形的性质、向量的三角形法则及其平行四边形法则、数量积运算、向量共线定理即可得出．14．（坐标系与参数方程选做题）在极坐标系中，已知圆 C 的圆心为（2,2π），半径为 2，直线(0,)2R πθααρ=≤≤∈被圆C 截得的弦长为3，则α的值等于．【知识点】极坐标方程的意义.【答案解析】3π 解析：解：圆C 的普通方程为：()2224x y +-=，直线的方程为：tan y x α=⋅.圆心C （0,2）到直线的距离为121tan 1α=+2tan 3α=，所以tan 3,α=因为02πα≤≤所以tan 3α=所以3πα=.【思路点拨】把极坐标方程化为直角坐标方程求解.15．（几何证明选讲选做题）如图，CD 是圆O 的切线，切点为C ，点 B 在圆O 上，3BCD=60°，则圆O 的面积为________．【知识点】弦切角.【答案解析】4π 解析：解：因为弦切角等于同弧上的圆周角，∠BCD=60°，所以∠A=60°，则∠BOC=120°，因为所以圆的半径为2,所以圆的面积为：4π 【思路点拨】通过弦切角转化为，圆周角，然后求出圆心角，结合弦长，得到半径，然后求出圆的面积．三、解答题:本大题共 6 小题，满分 80 分．解答须写出文字说明、证明过程和演算步骤. 16．（本小题满分12 分）已知函数()sin 2cos cos 2sin ,,0,()42f x x x x R f πϕϕϕπ=+∈<<=-（1）求()f x 的表达式；（2）若5(),(,)23132f αππαπ-=∈，求cos α的值.【知识点】两角和的正弦公式；两角差的余弦公式.【答案解析】（1）()5sin 26f x x π⎛⎫=+⎪⎝⎭（2）526-解析：解：（1）42f π⎛⎫=- ⎪⎝⎭可得sin cos cos sin 22ππφφ+=，所以cos φ=。

广东省珠海市高一数学下学期期末考试试题(b卷)

珠海市2014～2015学年度第二学期期末学生学业质量监测高一数学试题（B 卷）试卷满分为150分，考试用时120分钟．考试内容：必修一、必修二．一、选择题（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项填涂在答题卡上）ABDDC BCADA DB 1．0400角终边所在象限（ A ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2. sin 225 的值为（B ）A ．2 B ． 2- C D.3．若A ，B 为对立事件，则( D )A ．()()1P A PB +< B ．()()1P A P B +>C ．()()1P A P B +≤D ．()()1P A P B += 4．在下列各图中，每个图的两个变量具有相关关系的图是（D ）（1）（2）（3）（4） A ．（1）（2） B ．（1）（3） C ．（2）（4） D ．（2）（3）5．某学校有高中学生900人，其中高一有400人，高二300人，高三200人，采用分层抽样的方法抽取一个容量为45的样本，那么高一、高二、高三各年级抽取的学生人数为( C )A ．30、10、5B ．25、15、5C ． 20、15、10D ．15、15、156. 已知角α的终边过点()4,3P -，则sin cos αα+的值是（ B ）A ．15 B ．15- C ．75 D ． 75- 7. 若扇形的周长为4cm ，半径为1cm ，则其圆心角的大小为（C ） A ．02 B ．04 C. 2 D ．47 8 994 4 6 4 7 38. 当输入1,20x y =-=时，右图中程序运行后输出的结果为( A )A ．3； 43 B. 43；3C.-18；16D. 16；-189. 要得到函数sin(2)3y x π=-的图象，只要将函数sin 2y x =的图象（ DA.向左平行移动3π个单位 B.向左平行移动6π个单位 C.向右平行移动3π个单位 D.向右平行移动6π个单位10. 右图是2015年举行的全国少数民族运动会上，七位评委为某民族舞蹈打出的分的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和中位数分别为（）。

广东省珠海市2012届高三数学第二次调研考试理 (2012珠海二模)新人教A版

珠海市2011-2012学年度第二学期高三质量监测理科数学一、选择题：（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的,请在答题卡相应位置填涂答案）１．已知全集U R =，集合{||1|1}A x x =-<，则A C U 等于（ C ） A.(-∞，0] B. [2，)+∞ C.(-∞，0][2，)+∞ D.[0，2]２．等比数列{}n a 中，112a =，又14234a a a a +=-，则公比q = A ．2- B． C ．2 D ．3３．在复平面内，复数6+5i, -2+3i 对应的点分别为A,B.若C 为线段AB 的中点，则点C 对应的复数是（） A.4+8i B.8+2i C.2+4i D.4+i ４．已知a 、b 是实数，则“a>1，b>2”是“a+b>3且ab>2”的A ．充分而不必要条件B ．必要而不充分条件C ．充分且必要条件D ．既不充分也不必要条5． ABC ∆中，角A B C 、、所对的边a b c 、、，若a =3A π=，cos B =，则b = A．5 B．5C．5 D．6．已知函数()f x 满足：当x ≥1时，()f x =)1(-x f ；当x ＜1时，()f x =x2，则)7(log 2f =A ．167B ．87C ．47D ．277．某班主任对全班50名学生进行了作业量多少的调查，数据如下表：不喜欢玩电脑游戏8 15 23 总数262450根据表中数据得到250181589505927232426k ().⨯⨯-⨯=≈⨯⨯⨯，参考下表：P (K 2≥k )0.050 0.025 0.010 0.001 k3.8415.0246.63510.828则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（） A ．97.5% B ．95% C ．90% D ．99.9%8．起点到终点的最短距离为（） ks5uA ．16B ．17C ． 18D ．19ks5u二、填空题：本大题共7小题，每小题5分，满分30分．其中14～15题是选做题，考生只能选做一题，两题全答的，只计算前一题得分．答案请填在答题卡上.9.（理科）某校高中部有三个年级，其中高三有学生1000人，现采用分层抽样法抽取一个容量为185的样本，已知在高一年级抽取了75人，高二年级抽取了60人，则高中部共有学生____人.10．（理科）已知单位向量a ，b ，其夹角为3π，则b a +=__________ 11．（理科）已知随机变量2~(2,)N ξσ，3(1)4P ξ>-=，(5)P ξ>= .12．下图是一个几何体的三视图，根据图中数据可得该几何体的表面积是_________；13．甲乙两艘船都要在某个泊位停靠，若分别停靠4小时、8小时，假定它们在一昼夜的时间段内任意时刻到达，则这两艘船中有一艘在停靠泊位时必须等待的概率为．0v 1v 2v 5v v 3v 4v 起点8终点422465763414．（坐标系与参数方程选做题）．如图，PA 是圆的切线，A 为切点，PBC 是圆的割线，且=BC PB 12，则PA BC = ． 15．（坐标系与参数方程选做题）曲线4cos 4πρθθ==关于直线对称的曲线的极坐标方程为。

广东省珠海市高二数学下学期期末考试试题(B卷)理(含解析)

珠海市2012-2013学年度第二学期期末学业质量检测高二理科数学试题（B 卷）一、选择题（共12题，每题5分）1．已知，现将两个数交换,使,下面语句正确的一组是( ) A ． B ．C ．D ．解：先把b 的值赋给中间变量c ，这样c=17，再把a 的值赋给变量b ，这样b=8，把c 的值赋给变量a ，这样a=17．故选C ．2．某工厂生产产品，用传送带将产品送到下一道工序，质检人员每隔十分钟在传送带的某一个位置取一件检验，则这种抽样方法是( )A ．简单随机抽样B ．系统抽样C ．分层抽样D ．非上述答案解：本题符合系统抽样的特征：总体中各单位按一定顺序排列，根据样本容量要求确定抽选间隔，然后随机确定起点，每隔一定的间隔抽取一个单位的一种抽样方式．故选B ． 3．一个工厂有若干个车间，今采用分层抽样法从全厂某天的2000件产品中抽取一个容量为200的样本进行质量检查，若一车间这一天生产了80件产品，则从该车间抽取的产品件数为（）A ． 2B ．4C ．6D ．84A ．0.18B ．0.40C ．0.50D ．0.38 解：由表中数据知分数在[90，120）中累积频数是20，样本总数是50，那么分数在[90，120）中的频率是200.450，故选B ． 5．在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3的概率是（）A ．101 B ．15 C ．103 D ．112解：所有的取法共有25C =10种，而取出的2个小球的数字之和等于3的取法只有一种：即取出的小球的编号为1、2．故取出的小球标注的数字之和为3的概率是110，故选A ． 6．执行右面的程序框图，如果输入的N 是6，那么输出的p 是( )A ．120B ． 720C ． 1440D ．50407．欧阳修《卖油翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿．可见“行行出状元”，卖油翁的技艺让人叹为观止．若铜钱是直径为3cm 的圆，中间有边长为1cm 的正方形孔，若你随机向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率（） A ．π94 B. π49 C.94π D.49π故选答案A8．（随机变量及其分布）已知随机变量X 服从正态分布N(3,1)，且(24)P X ≤≤=0.6826，则=>)4(X P （）A ．0.1585B ．0.1588C ．0.1587D ．0.1586故选答案C9．右图是2013赛季詹姆斯(甲）、安东尼（乙）两名篮球运动员连续参加的7场比赛得分的情况，如茎叶图表示，则甲乙两名运动员的中位数分别为（）A ．23、22B ．19、20C ．26、22D ．23、20解：由题意知，∵甲运动员的得分按照从小到大排列是 15，17，19，23，24，26，32．共有7个数字，最中间一个是23；乙运动员得分按照从小到大的顺序排列是 11，11，13，20，22，30，31．共有7个数据，最中间一个是20，∴甲、乙两名运动员比赛得分的中位数分别是23，20．故选D ． 10．（计数原理）从4名同学中选出3人，参加一项活动，则不同的方法有（）种 A ．3 B ．4 C ．6 D ．2411．6名同学从左到右站成一排，其中甲不能站在两头，不同的站法有（）种A ． 480B ． 240C ． 120D ．9612．为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为 ( )A．0.27,78 B．0.27,83 C．2.7,78 D．2.7,83故选答案A二、填空题（共8题，每题5分）13．（算法初步）将二进制数101(2)化为十进制结果为．14．（算法初步）用秦九韶算法求多项式f(x)＝0.5x5＋4x4－3x2＋x－1当x＝3的值时，a1 =_____________．解：∵f（x）=0.5x5+4x4-3x2+x-1=（（（（0.5x+4）x+0）x-3）x+1）x-1，故用秦九韶算法求多项式f（x）=0.5x5+4x4-3x2+x-1当x=3的值时，a1=1．故答案为：1．15．（记数原理）在大小相同的2个红球和2个白球中，若从中任意选取2 个，则所选取的2个球中恰好有1个红球的概率为__________．16．（记数原理）1名男同学和2名女同学站成一排，其中2名女同学相邻的排法有___________种.17．（概率）姚明比赛时罚球命中率为90%，则他在3次罚球中罚失1次的概率是．18．（随机变量分步列）离散型随机变量X 的分布列为:X2P41 2141则X 的期望___________.19．（统计）一组数据的平均数是2，方差是3，若将这组数据中的每一个数据都加上60，得到一组新数据，则所得新数据的平均数和方差分别是_______和_________．解：一组数据的平均数是2，方差是3，将这组数据中的每一个数据都加上60，得到一组新数据，由数据的平均数和方差的计算公式得：所得新数据的平均数为62，方差为3．故答案为：62； 3． 20．（统计案例）（统计案例）某班主任对全班50名学生进行了作业量多少的调查，数据如下表：为了检验“喜欢玩电脑游戏与认为作业多”是否有关系，根据表中数据，得到2=4.84值，对照临界值表，有的把握认为“喜欢玩电脑游戏与认为作业多”之间有相关关系．解：由表中数据可知Χ2=4.84， ∵4.84＞3.841，∴有1-0.05=95%的把握说喜欢玩电脑游戏与认为作业量的多少有关系．故答案为：95%．三、解答题（共4题，每题10分）21．(本题满分10分)某中学团委组织了“弘扬奥运精神，爱我中华”的知识竞赛，从参加考试的学生中抽出60名学生，将其成绩(均为整数)分成六段[40,50)，[50,60)，…，[90,100]后画出如下部分频率分布直方图．观察图形给出的信息，回答下列问题：(1)求第四小组的频率，并补全这个频率分布直方图；(2)估计这次考试的及格率(60分及以上为及格)和平均分(保留小数点后2位）．解：(1)设分数在［70,80)内的频率为错误！未找到引用源。