2018年高考数学新课标3理科真题及答案
2018年高考理科数学全国三卷试题和答案解析

2018年高考理科数学全国三卷试题和答案解析2018年高考理科全国三卷1.已知集合 $A=\{1,2,3,4\}。
B=\{2,3,4\}。
C=\{3,4\}。
D=\{4\}$,则 $(A\cup B)\cap (C\cup D)$ 的元素为 $\{3,4\}$。
2.设 $f(x)=\dfrac{1-x}{1+x}$,则 $f(f(x))=\dfrac{x-1}{x+1}$。
3.中国古建筑借助榫卯将木构件连接起来,构建的突出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头。
若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是选项 B。
4.若 $\log_2 a=3$,$\log_3 b=4$,$\log_5 c=5$,则$a^2bc=\dfrac{2^6\cdot 3^8\cdot 5^{10}}{15}$。
5.$x^6+(x+1)^6$ 的展开方式中 $x^2$ 的系数为 $40$。
6.直线 $y=x+1$,$y=-x+3$ 分别与 $x$ 轴,$y$ 轴交于两点,点在圆 $x^2+y^2=1$ 上,则面积 $S$ 的取值范围是$0<S<2\pi$。
7.函数 $f(x)=\sqrt{1-x^2}$,$g(x)=\dfrac{1}{2}$,则$h(x)=f(x)g(x)+\dfrac{1}{2}$ 的图像大致为一个半径为$\dfrac{1}{2}$,圆心在 $y$ 轴上方 $\dfrac{1}{2}$ 的圆。
8.某群体中的每位成员使用移动支付的概率为 $0.8$,各成员的支付方式相互独立。
设使用移动支付的人数为 $n$,则$P(n\leq 3)$ 的概率为 $0.008+0.096+0.345+0.409=0.858$。
9.已知 $\triangle ABC$ 中,$\angle A=120^\circ$,$AB=AC$,$BC=2$,则 $S_{\triangle ABC}=\sqrt{3}$,$\sinA=\dfrac{\sqrt{3}}{2}$,$\cos A=-\dfrac{1}{2}$。
2018年全国(三卷)高考数学(理)试题及答案

2018年全国(三卷)高考数学(理)试题及答案绝密★启用前2018年普通高等学校招生全国统一考试理科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合,,则A .B .C .D .{}|10A x x =-≥{}012B =,,AB ={}0{}1{}12,{}012,,A .10B .20C .40D .806.直线分别与轴,轴交于,两点,点在圆上,则面积的取值范围是A .B .C .D .7.函数的图像大致为8.某群体中的每位成员使用移动支付的概率都为,各成员的支付方式相互独立,设为该20x y ++=x y A B P ()2222x y -+=ABP △[]26,[]48,232⎡⎣2232⎡⎤⎣⎦422y xx =-++p X群体的10位成员中使用移动支付的人数,,,则A .0.7B .0.6C .0.4D .0.39.的内角的对边分别为,,,若的面积为,则A .B .C .D .10.设是同一个半径为4的球的球面上四点,为等边三角形且其面积为,则三棱锥体积的最大值为A .B .C .D . 11.设是双曲线()的左,右焦点,是坐标原点.过作的一条渐近线的垂线,垂足为.若,则的离心率为A B .2 C D2.4DX =()()46P X P X =<=p =ABC △A B C ,,a b c ABC△2224a b c +-C =π2π3π4π6A B C D ,,,ABC △93D ABC -12318324354312F F ,22221x y C a b-=:00a b >>,O 2F C P 16PF OP=C 53212.设,,则A .B .C .D . 二、填空题:本题共4小题,每小题5分,共20分。
2018年高考理科数学试题及答案-全国卷3

2018年普通高等学校招生全国统一考试(全国卷3)理科数学一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}|10A x x =-≥,{}012B =,,,则A B =A .{}0B .{}1C .{}12,D .{}012,, 2.()()1i 2i +-= A .3i --B .3i -+C .3i -D .3i +3.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是4.若1sin 3α=,则cos2α=A .89B .79C .79-D .89-5.522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为A .10B .20C .40D .806.直线20x y ++=分别与x 轴,y 轴交于A ,B 两点,点P 在圆()2222x y -+=上,则ABP △面积的取值范围是 A .[]26,B .[]48,C .232⎡⎤⎣⎦,D .2232⎡⎤⎣⎦, 7.函数422y x x =-++的图像大致为8.某群体中的每位成员使用移动支付的概率都为p ,各成员的支付方式相互独立,设X 为该群体的10位成员中使用移动支付的人数, 2.4DX =,()()46P X P X =<=,则p = A .0.7B .0.6C .0.4D .0.39.ABC △的内角A B C ,,的对边分别为a ,b ,c ,若ABC △的面积为2224a b c +-,则C =A .π2B .π3C .π4D .π610.设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为A .123B .183C .243D .54311.设12F F ,是双曲线22221x y C a b-=:(00a b >>,)的左,右焦点,O 是坐标原点.过2F 作C 的一条渐近线的垂线,垂足为P .若16PF OP =,则C 的离心率为 A .5B .2C .3D .212.设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C .0a b ab +<<D .0ab a b <<+二、填空题:本题共4小题,每小题5分,共20分。
2018年全国卷3理科数学试题和参考答案

20 20 20 20
故有 99% 的把握认为两种生产方式的效率有差异
【考点】茎叶图、均值及其意义、中位数、独立性检验
19. (12 分)
如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 CD 所在的平面垂直, M 是 CD 上 异于 C, D 的点.
(1) 证明:平面 AMD 平面 BMC ; (2) 当三棱锥 M ABC 体积的最大时,求面 M AB 与面 MCD 所成二面角的正弦值 .
在本试卷上无效 .
3. 考试结束后,将本试卷和答题卡一并交回 .
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的 .
1.已知集合 A x | x 1 0 , B 0, 1, 2 ,则 A B ( )
A. 0
B. 1
C. 1, 2
【答案】 C
【解析】 A : x 1, A B 1, 2
ABC 等边 S ABC 9 3
AB 6 ,
D
O
A
FE
B
C
在等边 ABC 中, BF
2 BE
3 AB
2 3,
3
3
在 Rt OFB 中,易知 OF
2 , DF
6 ,故 VD ABC max
1 9 3 6 18 3
3
【考点】外接球、椎体体积最值
11. 设 F1,
F2 是双曲线
x2 C : a2
的一条渐近线的垂线,垂足为
M
y1 y2 4m
x my 1,联立
可求
,由
y2 4 x
y1 y2 4
MB MA y1 y2
y1 y2 1 x1x2
x1 x2
2018年高考数学全国卷三理科试题(附答案)

2018年高考数学全国卷三理科试题(附答案) 2018年高考数学全国卷三理科考试已经落下帷幕,本试卷为考生带来了挑战,让大家从中更加深入的了解数学知识,本试卷的答案让大家从中收获了成长。
2018年高考数学全国卷三理科试题2018年高考数学全国卷三理科试题出炉,考生们做好了准备,及时解决遇到的问题,取得优异的成绩。
本次全国卷三包括4个部分组成,分别是选择题、填空题、解答题和分析题。
如下:一、选择题1. 若集合A={x|-2≤x≤2},集合B={x|x2<4},则A∩B= (A) {-2,2} (B) {-2,0,2} (C) {-1,1} (D) {0,2}2. 若平面上的两个点的坐标分别A(2,3),B(4,-3),那么它们之间的距离是(A)2(B)5(C)7(D)63. 若复数z1=1-i,z2=1+i,则z1、z2的共轭复数分别为(A)1-i,1+i(B)1+i,1-i(C)-1+i,-1-i(D)-1-i,-1+i4. 若函数y=3x3-6x2+9x+3在x=2处取得极值,则极大值为(A)-12(B)-9(C)15(D)185. 若两个圆O1,O2的半径分别是6,9,则O1, O2相切的条件是(A)r1=r2(B)r1+r2=15(C)r1-r2=3(D)r1+r2=3二、填空题1. 下列各式中,(1+√5)5次方的展开式中,常数项为a_1r_1+a_3r_3+a_5r_5,其中a_1,a_3,a_5分别为______,_______,_______。
答案:a_1=5 ; a_3=-5 ; a_5=12.函数f (x)=2x2+8x+9,x≤1时的最大值为_________。
答案:13三、解答题1.求实数a,b满足等式|a-3|-|b+3|=4的解。
答:解得a=-1、b=-72.曲线y=x3+3x2+3x+c的图象经过点(1,1),求参数c的值。
答:设y=x3+3x2+3x+c设点P(1,1)在曲线上,即1=1+3+3+cc=0四、分析题1.已知实数x,y满足约束条件2x+y≤12,x,y≥0,求此约束条件下的最大值。
2018高考全国3卷理科数学带答案

427.函数y x x2的图像大致为2018年普通高等学校招生全国统一考试理科数学注意事项:1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将本试卷和答案卡一并交回。
、选择题:本题共 12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合 题目要求的。
2. 1 i 2 iA. 3 iB. 3 iC. 3 iD. 3 i3. 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼 的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是55. x 2 2的展开式中x 4的系数为xA. 10B. 20C. 401 .已知集合A x|x 1 > 0 , B0 ,1,2,贝U AI BA. 0B.1C.1 , 2D.0, 1 ,2 A-,则 cos234.若 sin 00- 97- 900- 9A6 .直线x y 2 0分别与x 轴, y 轴交于A , B 两点,点P 在圆y 22上,则 ABP 面积的取值范围是 A. 2 , 6C. 2 ,32D. 2 2 , 3 2D. 80..p,各成员的支付方式相互独立,设X为该群体的&某群体中的每位成品使用移动支付的概率都为10位成员中使用移动支付的人数,DX 2.4 ,A. 0. 7B. 0. 6C. 0. 49. △ABC的内角A, B, C的对边分别为a , b , c,右D. 0. 32 2 2ABC的面积为 -一b一—,贝U C4B.-3C.-4D. J610.设A, B , C ,D是同一个半径为4的球的球面上四点, ABC为等边三角形且其面积为9. 3,则三棱锥D ABC体积的最大值为A. 12 3B. 18 3211.设h , F2是双曲线c:笃』a bC. 24.3D. 54 30, b 0 )的左,右焦点,O是坐标原点.过F2作C的一条渐近线的垂线, 垂足为P .若PF!■ 6 OP,贝U C的离心率为B. 2C.12 .设a log0.2 0.3 , b log2 0.3,则A. a b ab 0C. a b 0 ab 二、填空题:本题共4小题,每小题5分,B.D.共20分。
2018年全国新课标Ⅲ卷全国3卷高考理科数学试卷及参考答案与试题解析
2018年全国新课标Ⅲ卷全国3卷高考理科数学试卷及参考答案与试题解析一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5.00分)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )A.{0}B.{1}C.{1,2}D.{0,1,2}2.(5.00分)(1+i)(2-i)=( )A.-3-iB.-3+iC.3-iD.3+i3.(5.00分)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )A. B. C. D.4.(5.00分)若sinα=,则cos2α=( )A. B. C.- D.-5.(5.00分)(x2+)5的展开式中x4的系数为( )A.10B.20C.40D.806.(5.00分)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x-2)2+y2=2上,则△ABP面积的取值范围是( )A.[2,6]B.[4,8]C.[,3]D.[2,3]7.(5.00分)函数y=-x4+x2+2的图象大致为( )A. B. C.D.8.(5.00分)某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立.设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(x=4)<P(X=6),则p=( ) A.0.7 B.0.6 C.0.4 D.0.39.(5.00分)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为,则C=( )A. B. C. D.10.(5.00分)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且面积为9,则三棱锥D-ABC体积的最大值为( )A.12B.18C.24D.5411.(5.00分)设F1,F2是双曲线C:-=1(a>0.b>0)的左,右焦点,O是坐标原点.过F2作C的一条渐近线的垂线,垂足为P,若|PF1|=|OP|,则C的离心率为( )A. B.2 C. D.12.(5.00分)设a=log0.20.3,b=log20.3,则( )A.a+b<ab<0B.ab<a+b<0C.a+b<0<abD.ab<0<a+b二、填空题:本题共4小题,每小题5分,共20分。
2018年高考全国卷3理科数学试题及参考答案

2018年高考全国卷3理科数学试题及参考答案1.已知集合A={x∣x-1≥0},B={0,1,2},则A∩B=A{0}B{1}C{1,2}D{0,1,2}2.(1+i)(2-i)=A-3-i B-3+i C3-i D3+i3.中国古建筑借助棒卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头。
若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是A.AB.BC.CD.D4.若,则A B C D5.的展开式中的系数为A.10B.20C.40D.806.直线x+y+2=0分别与x轴,y交于A,.两点,点P在圆(x-2)²+y²=2上,则∆ABP面积的取值范围是A[2,6]B[4,8]C D7.函数y=-+x²+2的图像大致为A.BC.DA.AB.BC.CD.D8.某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<p(x=6),则p=<span="">A.0.7B.0.6C.0.4D.0.3,9.∆ABC的内角A,B,C的对边分别为a,b,c,若∆ABC的面积为则C=A B C D10.设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D-ABC体积的最大值为A12B18C24D5411.设F1、F2是双曲线的左、右焦点,O是坐标原点,过F2作C的一条渐近线的垂线,垂足为P,若,则C的离心率为A B2C D分值:5分查看题目解析>A.AB.BC.CD.D13、已知向a=(1,2),b=(2,-2),c=(1,),若c//(2a+b),则λ=__________14.曲线y=(ax+1)ex在点(0,1)处的切线的斜率为-2,则a=。
2018年全国统一高考数学真题试卷及答案解析【全国卷三】
2018年高考真题理科数学 (全国III卷)一、填空题:(本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.已知集合A={x∣x-1≥0},B={0,1,2},则A∩B=()A.{0}B.{1}C.{1,2}D.{0,1,2}2.(1+i)(2-i)=()A.-3-iB.-3+iC.3-iD.3+i3.中国古建筑借助棒卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头。
若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()4.若,则( )A. B. C. D.5.的展开式中的系数为( )A.10B.20C.40D.806.直线x+y+2=0分别与x轴,y交于A,.两点,点P在圆(x-2)²+y ²=2上,则∆ABP面积的取值范围是( )A.[2,6]B.[4,8]C.D.7.函数y=-+x²+2的图像大致为A . B.C. D.8.某群体中的每位成员使用移动支付的概率都为p,各成员的支付方式相互独立,设X为该群体的10位成员中使用移动支付的人数,DX=2.4,P(X=4)<p(x=6),则p=< span="">( )A .0.7 B.0.6 C.0.4 D.0.39.∆ABC的内角A,B,C的对边分别为a,b,c,若∆ABC的面积为,则C=( )A. B. C. D.10.设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为9,则三棱锥D-ABC体积的最大值为( )A.12B.18C.24D.5411.设F1、F2是双曲线的左、右焦点,O是坐标原点,过F2作C的一条渐近线的垂线,垂足为P,若,则C的离心率为( )A. B.2 C. D.二、填空题(本题共4小题,每小题5分,共20分。
2018年全国统一高考数学试卷(理科)(新课标ⅲ)(含解析版)

2018年全国统一高考数学试卷(理科)(新课标Ⅲ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)已知集合A={x|x﹣1≥0},B={0,1,2},则A∩B=()A.{0}B.{1}C.{1,2}D.{0,1,2} 2.(5分)(1+i)(2﹣i)=()A.﹣3﹣i B.﹣3+i C.3﹣i D.3+i3.(5分)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()A.B.C.D.4.(5分)若sinα=,则cos2α=()A.B.C.﹣D.﹣5.(5分)(x2+)5的展开式中x4的系数为()A.10B.20C.40D.806.(5分)直线x+y+2=0分别与x轴,y轴交于A,B两点,点P在圆(x﹣2)2+y2=2上,则△ABP面积的取值范围是()A.[2,6]B.[4,8]C.[,3]D.[2,3] 7.(5分)函数y=﹣x4+x2+2的图象大致为()A.B.C.D.<P(X=6),则p=()9.(5分)△ABC的内角A,B,C的对边分别为a,b,c.若△ABC的面积为,则C=()A.B.C.D.10.(5分)设A,B,C,D是同一个半径为4的球的球面上四点,△ABC为等边三角形且面积为9,则三棱锥D﹣ABC体积的最大值为()A.12B.18C.24D.5411.(5分)设F1,F2是双曲线C:﹣=1(a>0.b>0)的左,右焦点,O是坐标原点.过F2作C的一条渐近线的垂线,垂足为P,若|PF1|=|OP|,则C的离心率为()A.B.2C.D.12.(5分)设a=log2A.a+b<ab<0B.ab<a+b<0C.a+b<0<ab D.ab<0<a+b 二、填空题:本题共4小题,每小题5分,共20分。
完整版)2018年高考理科数学全国三卷试题及答案解析

完整版)2018年高考理科数学全国三卷试题及答案解析2018年高考理科全国三卷1.已知集合 A={1,2,3,4}。
B={2,3,4}。
C={3,4}。
D={4},则(A∩B)∪(C∩D) 的元素个数是多少?2.已知函数 f(x)=x^2-2x+1,g(x)=2x-1,则 f(g(x)) 的值为多少?3.中国古建筑借助榫卯将木构件连接起来,构建的突出部分叫榫头,凹进部分叫卯眼。
图中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是哪一个?4.若 a,b,c 是正整数,且 a^2+b^2=c^2,则 a+b+c 的值是多少?5.将 (2x-y+3z)^4 展开后,x^2y^2z^2 的系数是多少?6.平面直角坐标系中,直线与 x 轴交于 A,与 y 轴交于B,直线与 x 轴交于 C,与 y 轴交于 D。
点 P 在圆 x^2+y^2=1 上,且线段 AP 与线段 CD 相交于点 O。
则△AOD 的面积的取值范围是什么?7.已知函数 f(x)=x^3-3x,则 f(x+2)-f(x-2) 的图像大致是什么?8.某群体中的每位成员使用移动支付的概率为 p,各成员的支付方式相互独立。
设 N 为该群体的成员数,X 为使用移动支付的人数,则 P(X=k) 的值是多少?9.△ABC 中,∠A=60°,BC=2,AD 是 BC 的中线,点 E 在 AB 上,使得 AE=AD。
若△ADE 为等边三角形且其面积为 1/3,则△ABC 的面积是多少?10.设 V 是半径为 R 的球的球面上四点 A,B,C,D 所构成的四面体的体积,V 的最大值是多少?11.双曲线 H 的左、右焦点分别为 F1(-c,0)、F2(c,0),坐标原点为 O,过 F1 作 H 的一条渐近线,垂足为 P。
若 OP=2c,则 H 的离心率是多少?12.设函数 f(x)=x^3-ax^2+bx-1,若 f(x) 在点 x=1 处的切线的斜率为 3,在 x=2 和抛物线 y=x^2+cx+d 的零点个数为 2,过点 (2,0) 的直线 y=kx+m 与 y=f(x) 的交点为 (3,4),则 a,b,c,d 的值分别是多少?13.已知向量 a=3i+2j,b=-2i+5j,则 a·b 的值是多少?14.曲线 y=2x^3-3x^2+6x-1 的切线在点 (1,4) 处的斜率是多少?15.函数 f(x)=x^2-2x+3 在区间 [-1,3] 上的最小值是多少?16.已知点 A(1,0,0),B(0,1,0),C(0,0,1),D(1,1,1),且 AD 与平面 BCD 垂直,AD 的长度为 2.则 BD 的长度是多少?17.等比数列 {an} 的首项为 a1=2,公比为 q=1/2.求 S10 的值和 a10 的值。
2018年全国卷3高考理科数学试题解析版

C. 40
D. 80
【解析】分析:写出
,然后可得结果
详解:由题可得
令
,则
所以
故选 C.ຫໍສະໝຸດ 拓展:本题主要考查二项式定理,属于基础题。
6. 直线
分别与轴,轴交于,两点,点在圆
范围是
A.
B.
C.
D.
【答案】A
上,则
面积的取值
【解析】分析:先求出 A,B 两点坐标得到 再计算圆心到直线距离,得到点 P 到直线距
详解:由题可得
,即
故答案为
拓展:本题主要考查向量的坐标运算,以及两向量共线的坐标关系,属于基础题。
14. 曲线
在点
处的切线的斜率为 ,则 ________.
【答案】
【解析】分析:求导,利用导数的几何意义计算即可。
详解:
则
所以
故答案为-3.
拓展:本题主要考查导数的计算和导数的几何意义,属于基础题。
15. 函数
【答案】2
【解析】分析:利用点差法进行计算即可。
详解:设
则
所以
所以
取 AB 中点 因为
,分别过点 A,B 作准线 ,
的垂线,垂足分别为
因为 M’为 AB 中点,
所以 MM’平行于 x 轴
因为 M(-1,1)
所以 ,则
即
故答案为 2.
拓展:本题主要考查直线与抛物线的位置关系,考查了抛物线的性质,设
,利
详解:当 时, ,排除 A,B.
,当
时, ,排除 C
故正确答案选 D.
拓展:本题考查函数的图像,考查了特殊值排除法,导数与函数图像的关系,属于中档题。
8. 某群体中的每位成员使用移动支付的概率都为,各成员的支付方式相互独立,设为该群体
2018年高考全国3卷理科数学试题及答案解析
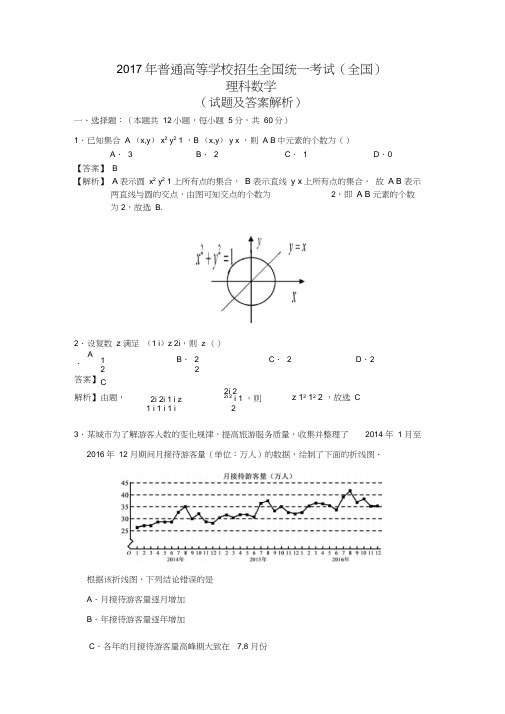
6 5 6 5∴S66a12d 1 622 24,故选A.
22
10.已知椭圆C:x2y21(a b 0)的左、右顶点分别为A1,A2,且以线段A1A2为直ab
径的圆与直线bx ay 2ab 0相切,则C的离心率为()
A.πB.3πC.πD.π
424【答案】B
【解析】由题可知球心在圆柱体中心,圆柱体上下底面圆半径r12 1 3,
22
23π则圆柱体体积Vπr2hπ,故选B.
4
9.等差数列an的首项为1,公差不为0.若a2,a3,a6成等比数列,则an前6项的和为()
A.24B.3C.3D.8
【答案】A
【解析】∵an为等差数列,且a2,a3,a6成等比数列,设公差为d.
A.
【答案】
【解析】
B.
)
C.40
D.80
C
由二项式定理可得,原式展开中含
2 2 3 3 3 2
x C522xyy C532x y
33
x y的项为
3 33 3
40x3y3,则x3y3的系数为40,故选C.
22
5.已知双曲线C:x2y21
a2b2
a 0,b 0)
的一条渐近线方程为
y5x,
y x,
2
且与椭圆
3
D.
x8π对称
3
7.执行右图的程序框图,为使输出
的最小值为()
A.
B.
C.
D.2
答案】D
解析】程序运行过程如下表所示:
S
M
t
初始状态
0
100
(完整)2018年高考理科数学全国3卷(附答案)
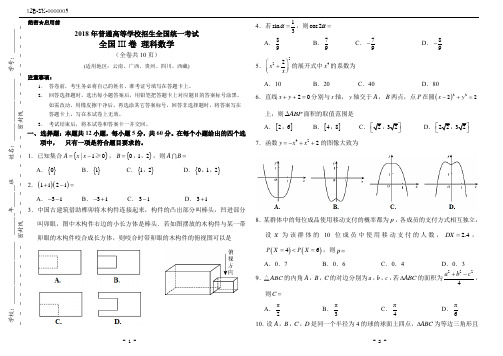
(2)求 中点 的轨迹的参数方程.
23.[选修4—5:不等式选讲](10分)
设函数 .
(1)画出 的图像;
(2)当 , ,求 的最小值.
绝密★启用前
2018年普通高等学校招生全国统一考试
理科数学试题参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
C
D
A
B
C
A
D
B
C
B
C
B
二、填空题
三、解答题:共70分。解答题应写出文字说明、证明过程或演算步骤。第17~21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
等比数列 中, .
(1)求 的通项公式;
(2)记 为 的前 项和.若 ,求 .
18.(12分)
某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
以上给出了4种理由,考生答出其中任意一种或其他合理理由均可得分.
(2)由茎叶图知 .
列联表如下:
超过
不超过
第一种生产方式
15
5
第二种生产方式
5
15
(3)由于 ,所以有99%的把握认为两种生产方式的效率有差异.
19.解:
(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC 平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(2018 年新课标Ⅲ理)已知集合 A ={x |x -1≥0},B ={0,1,2},则 A ∩B =()A .{0}B .{1}C .{1,2}D .{0,1,2}C 【解析】A ={x |x -1≥0}={x |x ≥1},则 A ∩B ={x |x ≥1}∩{0,1,2}={1,2}.2.(2018 年新课标Ⅲ理)(1+i)(2-i)=()A .-3-iB .-3+iC .3-iD .3+iD 【解析】(1+i)(2-i)=2-i +2i -i =3+i .3.(2018 年新课标Ⅲ理)中国古建筑借助榫卯将木构件连接起来 .构件的凸出部分叫榫头 ,凹进部分叫卯眼 ,图中木构件右边的小长方体是榫头 .若如图摆放的木构件与某一带卯眼的木 构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()AB C DA 【解析】由题意可知木构件与某一带卯眼的木构件咬合成长方体,小的长方体是榫头,从 图形看出轮廓是长方形,内含一个长方形,且一条边重合,另外 3 边是虚线.故选 A .14.(2018 年新课标Ⅲ理)若 sin α= ,则 cos 2α=()8 7 7A .B .C .-9 991 7B 【解析】cos 2α=1-2sin α=1-2× = .2 5.(2018 年新课标Ⅲ理) x +的展开式中 x 的系数为( )A .10B .20C .408D .-9D .802 3 29 925 4x2 2 C 【解析】 x + 的展开式的通项为 T =C (x ) =2 C x r +1 5 5.由 10-3r =4,解得 r2 =2.∴ x + 的展开式中 x 的系数为 2 C =40. 56.(2018 年新课标Ⅲ理)直线 x +y +2=0 分别与 x 轴,y 轴交于 A ,B 两点,点 P 在圆(x -2) + y=2 上, △则△ ABP 面积的取值范围是( )A .[2,6]B .[4,8]C .[ 2,3 2]D .[2 2,3 2]A 【解析】易得 A (-2,0),B (0,-2),|AB |=2 2.圆的圆心为(2,0),半径 r = 2.圆心(2,0)到直线 x +y +2=0 的距离 d = |2+0+2|=2 2,∴点 P 到直线 x +y +2=0 的距离 h 的取值范围 1 +1 1为[2 2-r ,2 2+r ],即[ 2,3 2].又△ ABP 的面积 S = |AB |·h = 2h ,∴S 的取值范围是 [2,6].7.(2018 年新课标Ⅲ理)函数 y =-x +x +2 的图象大致为( )A BCDD 【解析】函数过定点(0,2),排除 A ,B ;函数的导数 y ′=-4x +2x =-2x (2x -1),由 y ′>0解得 x <-2 2或 0<x < ,此时函数单调递增,排除 C .故选 D .2 28.(2018 年新课标Ⅲ理)某群体中的每位成员使用移动支付的概率都为 p ,各成员的支付方式相互独立.设 X 为该群体的 10 位成员中使用移动支付的人数,DX =2.4,P (X =4)<P (X =6),25 r 2 5 r r r r 10 3r- - x x25 4 2 2 x 22 2 2 24 2 3 2则 p =()A .0.7B .0.6C .0.4D .0.3B【解析】 某群体中的每位成员使用移动支付的概率都为 p ,为独立重复事件 ,满足 X ~1B (10,p ).由 P (X =4)<P (X =6),可得C p (1-p ) <C p (1-p ) ,解得 p > .因为 DX =2.4,所10 10 2以 10p (1-p)=2.4,解得 p =0.6 或 p =0.4(舍去).9.(2018 年新课标 Ⅲ理 △)△ ABC 的内角 A ,B ,C 的对边分别为 a ,b ,c .若△ ABC 的面积为a2+b 4-c ,则 C =( )π πA .B .2 3π C .4π D .61 a +b -c a +b -c C 【解析】S = ab sin C =,则 sin C = =cos C .因为 0<C <π,所以 π C = .410.(2018 年新课标Ⅲ理)设 A ,B ,C ,D 是同一个半径为 4 的球的球面上四点 △△ ABC 为等边三 角形且面积为 9 3,则三棱锥 D -ABC 体积的最大值为()A .12 3B .18 3C .24 3D .54 3B 【解析】 △由△ ABC 为等边三角形且面积为 9 3,得 S =3 4·|AB |=9 3,解得 AB =6.设半径为 4 的球的球心为 O △△ ABC 的外心为 O ′,显然 D 在 O ′O 的延长线与球的交点处(如 2 3图).O ′C = × ×6=2 3,OO ′= 4 -(2 3) =2,则三棱锥 D -ABC 高的最大值为 6,则三棱1 3 锥 D -ABC 体积的最大值为 × ×6 =18 3.3 4x y 11.(2018 年新课标Ⅲ理)设 F ,F 是双曲线 C : - =1(a >0,b >0)的左,右焦点,O 是坐标原点.1 2 a b过 F 作 C 的一条渐近线的垂线,垂足为 P ,若|PF |= 6|OP |,则 C 的离心率为()214 4 6 6 6 42 2 2 2 2 2 2 2 2 4 2bc △ ABC △ ABC 2 2 23 232 22 2A . 5B .2C . 3D . 2b bcC 【解析】双曲线 C 的一条渐近线方程为 y = x ,∴点 F 到渐近线的距离 d = =b ,a 2 2 2即|PF | =b ,∴|OP | =|OF | 22 -|PF | 2=c -b2b=a ,cos ∠PF O = .∵|PF | =6| OP |,∴|PF |2 c 11= 6a .△F △ PF 中,由余弦定理得|PF | =|PF | +|F F | -2|PF |·|F F |cos ∠PF O ,即 6a =b 12121 221 22b c+4c -2×b ×2c × =4c -3b =4c -3(c -a ),化简得 3a =c ,∴e = =c aca= 3.12.(2018 年新课标Ⅲ理)设 a =log 0.3,b =log 0.3,则( )0.2 2A .a +b <ab <0B .ab <a +b <0C .a +b <0<abD .ab <0<a +bB【 解 析 】 ∵a = log 0.3 = 0.2lg 0.3lg 0.3lg 0.3 lg 0.3 ,b = log 0.3 = ,∴a + b = - = -lg 5 2 lg 2lg 2lg 55 10lg 0.3·lg lg 0.3·lglg 0.3(lg 5-lg 2) 2 lg 0.3 lg 0.3 3 10 5 lg 0.3= ,ab =- · = .∵lg >lg ,lg 2·lg 5 lg 2·lg 5 lg 2 lg 5 lg 2·lg 5 3 2 lg 2·lg 5 <0,∴ab <a +b <0.故选 B .13.(2018 年新课标 Ⅲ 理 )已知向量 a =(1,2),b =(2, - 2),c =(1,λ). 若 c ∥(2a +b ),则 λ = ________.1 21 λ 1【解析】(2a +b )=2(1,2)+(2,-2)=(4,2),由 c ∥(2a +b ),得 = ,解得 λ= .14.(2018 年新课标Ⅲ理)曲线 y =(ax +1)e在点(0,1)处的切线的斜率为-2,则 a =________.-3 【解析】由 y =(ax +1)e ,可得 y ′=a e +(ax +1)e .∵y ′| =a +1,∴a +1=-2,解得 a =-3.π 15.(2018 年新课标Ⅲ理)函数 f (x )=cos 3x + 在[0,π]的零点个数为________.3【解析】令 f (x )=cos3x + =0,得 3x + = +k π(k ∈Z ),解得 x = + (k ∈Z ).当 k =0π 4π 7π 10π π时,x = ;当 k =1 时,x = ;当 k =2 时,x = ;当 k =3 时,x = .∵x ∈[0,π],∴x = ,或 x 4π 7π= ,或 x = .∴f (x )的零点的个数为 3.9 9a +b 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 224 2 2x xxxx =06ππ π π k π 6 6 2 9 3 9 9 9 9 916.(2018 年新课标Ⅲ理)已知点 M (-1,1)和抛物线 C :y =4x ,过 C 的焦点且斜率为 k 的直线 与 C 交于 A ,B 两点.若∠AMB =90°,则 k =________.2【解析】 ∵抛物线的焦点为 F (1,0),∴过 A ,B 两点的直线方程为 y = k (x -1).联立y =4x ,4+2k化简得 k x -2(2+k )x +k =0.设 A (x ,y ),B (x ,y ),则 x +x = ,x x= y =k(x -1),41.∴y +y =k (x +x -2) = ,y y =k (x -1)(x -1) = k [x x -(x +x ) +1] =- 4.∵M ( - 12 1 2 k 1 2 1 2 1 2 1 21,1),∴MA =(x +1,y -1),M B =(x +1,y -1).∵∠AMB =90°=0,∴MA ·MB =0,即(x +112214 1)(x +1)+(y -1)(y -1)=0,整理得 x x +(x +x )+y y -(y +y )+2=0,∴1+2+ -4- 21 2 1 2 1 2 1 2 1 2 k4k+2=0,即 k -4k +4=0,解得 k =2.17.(2018 年新课标Ⅲ理)等比数列{a }中,a =1,a =4a .n153(1)求{a }的通项公式;n(2)记 S 为{a }的前 n 项和.若 S =63,求 m . nnm【解析】(1)设等比数列{a }的公比为 q .n由 a =1,a =4a ,得 1×q =4×(1×q ),解得 q =±2. 153当 q =2 时,a =2 nn -1;当 q =-2 时,a =(-2) .n1×[1-(-2) ] 1-(-2) 1-(-2) (2)当 q =-2 时,S = = .由 S =63,得 =63,m ∈N ,无解;n 1-(-2) 3 m 3 1×(1-2 )当 q =2 时,S = =2 n 1-2-1.由 S =63,得 2 m m -1=63,解得 m =6.18.(2018 年新课标Ⅲ理)某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取 40 名工人,将他们随机分成两组,每组 20 人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生 产任务的工作时间(单位:min)绘制了如下茎叶图:2222 2 2 22 k 1 1 2 2 1 2 1 2 2 2 → → → →2 2 4 2 n 1 - n n mn n(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;(2)求 40 名工人完成生产任务所需时间的中位数 m ,并将完成生产任务所需时间超过 m 和 不超过 m 的工人数填入下面的列联表:超过 m不超过 m第一种生产方式第二种生产方式(3)根据(2)中的列联表,能否有 99%的把握认为两种生产方式的效率有差异?n(ad -bc )附:K= (a +b )(c +d)(a +c )(b +d )P (K ≥k )k0.0503.8410.0106.6350.00110.828【解析】(1)根据茎叶图中的数据知第一种生产方式的工作时间主要集中在 72~92 之间, 第二种生产方式的工作时间主要集中在 65~85 之间,∴第二种生产方式的工作时间较少,效率更高.(2)这 40 名工人完成生产任务所需时间按从小到大的顺序排列后,排在中间的两个数据是79+8179 和 81,m = =80.2由此填写列联表如下:第一种生产方式第二种生产方式总计超过 m15520不超过 m51520总计20204040(15×15-5×5) (3)K = =10>6.635,20×20×20×20∴有 99%的把握认为两种生产方式的效率有差异.⌒19.(2018 年新课标Ⅲ文)如图,边长为 2 的正方形 ABCD 所在的平面与半圆弧 所在平面垂2 2 22 2 CD⌒直,M是上异于C,D的点.(1)求证:平面AMD⊥平面BMC;(2)当三棱锥M﹣ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.【解析】(1)证明:在半圆中,DM⊥MC.⌒∵正方形ABCD所在的平面与半圆弧所在平面垂直,∴AD⊥平面DCM.又MC⊂平面DCM,∴AD⊥MC.又AD∩DM=D,∴MC⊥平面ADM.∵MC⊂平面MBC,∴平面AMD⊥平面BMC.(2)∵△ABC 的面积为定值,∴要使三棱锥M﹣ABC体积最大,则三棱锥的高最大,此时M 为圆弧的中点.以O为坐标原点,建立如图所示的空间直角坐标系.∵正方形ABCD的边长为2,∴A(2,-1,0),B(2,1,0),M(0,0,1),则平面MCD的一个法向量为m=(1,0,0).设平面MAB的一个法向量为n=(x,y,z),则A B=(0,2,0),AM=(-2,1,1).n·AB=2y=0,∴n·AM=-2x+y+z=0.令x=1,则y=0,z=2,∴n=(1,0,2).m·n15∴cos〈m,n〉===.|m|·|n|1×55设面MAB与面MCD所成的二面角为α,则sinα=525 1-=.55CDCD→→→→2xy 20.(2018 年新课标Ⅲ文)已知斜率为 k 的直线 l 与椭圆 C : + =1 交于 A ,B 两点,线段 AB4 3的中点为 M (1,m )(m >0).1(1)求证:k <- ;2(2)设 F 为 C 的右焦点,P 为 C 上一点,且F P +FA +FB =0,求证:|FA |,|FP |,|FB |成等差数列, 并求该数列的公差.【解析】(1)设 A (x ,y ),B (x ,y ).1122∵线段 AB 的中点为 M (1,m ),∴x +x =2,y +y =2m .1212xy 将 A (x ,y ),B (x ,y )代入 + =1 中,1 12 2 4 3化简得 3(x +x )(x -x )+4(y +y )(y -y )=0,即 6(x -x )+8m (y -y )=0,121212121212y -y 6 3 ∴k = =- =- .x -x 8m 4m 12 1 m 3点 M (1,m)在椭圆内,即 + <1(m >0),解得 0<m < .4 3 23 1∴k =- <- .4m 2(2)证明:设(x ,y ),可得 x +x =2.3312∵FP +FA +FB =0,F (1,0),∴x -1+x -1+x -1=0,y +y +y =0.123123∴x =1,y =-(y +y )=-2m .3312∵m >0,∴P 在第四象限.2 2 → → → → → →2 2 12 2 → → →3 3∴y =- ,m = ,k =-1.3 2 41 1 1 3 ∵|FA |=2- x ,|FB |=2- x ,|FP |=2- x = ,2 1 2 2 23 21则|FA |+|FB |=4- (x +x )=3.2 1 2 ∴2|FP |=|FA |+|FB |.y =-x + ,联立化简得 28x 2-56x +1=0.x y+ =1, 4 31∴x +x =2,x x = .1 2 1 2 283 21 ∴|x -x |= (x +x ) -4x x = .1 2 1 2 1 2 71 3 21 ∴该数列的公差 d 满足 2d =± |x -x |=± .2 1 2 143 21∴该数列的公差为± .2821.(2018 年新课标Ⅲ理)已知函数 f (x )=(2+x +ax )ln(1+x )-2x .(1)若 a =0,求证:当-1<x <0 时,f (x )<0;当 x >0 时,f (x)>0;(2)若 x =0 是 f (x )的极大值点,求 a .x【解析】(1)证明:当 a =0 时,f (x )=(2+x )ln(1+x )-2x (x >-1),则 f ′(x)=ln(1+x )- .1+x x x令 g (x )=f ′(x )=ln(1+x )- ,则 g ′(x )= .1+x (1+x )当 x ∈(-1,0)时,g ′(x )≤0;当 x ∈(0,+∞)时,g ′(x )≥0.∴f ′(x )在(-1,0)递减,在(0,+∞)递增.∴f ′(x )≥f ′(0)=0.∴f (x )=(2+x )ln(1+x )-2x 在(-1,+∞)上单调递增.又 f (0)=0,∴当-1<x <0 时,f (x )<0;当 x >0 时,f (x )>0.(2)由 f (x )=(2+x +ax )ln(1+x )-2x ,2+x +ax ax -x +(1+2ax )(1+x )ln(1+x ) 得 f ′(x )=(1+2ax )ln(1+x )+ -2= .1+x 1+x令 h (x )=ax -x +(1+2ax)(1+x )ln(1+x ),则 h ′(x )=4ax +(4ax +2a +1)ln(1+x ).→ → → 742 2 22 22 2 2 2当 a ≥0,x >0 时,h ′(x )>0,h (x )单调递增.∴h (x )>h (0)=0,即 f ′(x )>0.∴f (x )在(0,+∞)上单调递增,∴x =0 不是 f (x )的极大值点,不合题意.当 a <0 时,令 u (x )=h ′(x )=4ax +(4ax +2a +1)ln(1+x ),1-2a则 u ′(x )=8a +4a ln(1+x )+ ,显然 u ′(x )单调递减.1+x 1①令 u ′(x )=0,解得 a =- .∴当-1<x <0 时,u ′(x )>0;当 x >0 时,u ′(x )<0.∴h ′(x )在(-1,0)上单调递增,在(0,+∞)上单调递减.∴h ′(x )≤h ′(0)=0,则 h(x )在(0,+∞)上单调递减.又 h (0)=0,∴当-1<x <0 时,h (x )>0,即 f ′(x )>0;当 x >0 时,h (x )<0,即 f ′(x )<0. ∴f (x )在(-1,0)上单调递增,在(0,+∞)上单调递减.∴x =0 是 f (x )的极大值点,符合题意.1 ②若- <a <0,则 u ′(x )=1+6a >0,u ′1+6a - 4a -11 =(2a -1)(1-e +6a 4a )<0,∴u ′(x )=0 在(0,+∞)上有唯一一个零点,设为 x .∴当 0<x <x 时,u ′(x )>0,h ′(x )单调递增,h ′(x )>h ′(0)=0,即 f ′(x )>0.∴f (x )在(0,x )上单调递增,不合题意;1 ③若 a <- ,则 u ′(x )=1+6a <0,u ′ 1 e-1 =(1-2a )e >0,∴u ′(x )=0 在(-1,0)上有唯一一个零点,设为 x .1∴当 x <x <0 时,u ′(x )<0,h ′(x )单调递减,h ′(x )>h ′(0)=0,h (x )单调递增,h (x )<h (0)=0,即 f ′(x ) 1 <0.∴f (x )在(x ,0)上单调递减,不合题意.11综上,a =- .6x =cos θ,22.(2018 年新课标Ⅲ理)在平面直角坐标系 xOy 中,⊙O 的参数方程为(θ 为参数),y =si n θ过点(0,- 2)且倾斜角为 α 的直线 l 与⊙O 交于 A ,B 两点.(1)求 α 的取值范围;(2)求 AB 中点 P 的轨迹的参数方程.6 6 e6 2 2【解析】(1)将⊙O 的参数方程化为普通方程,得为 x +y =1,圆心为 O (0,0),半径 r =1. π 当 α= 时,过点(0,- 2)且倾斜角为 α 的直线 l 的方程为 x =0,成立;π 当 α≠ 时,过点(0,- 2)且倾斜角为 α 的直线 l 的方程为 y =tan α·x + 2.∵直线 l 与⊙O 交于 A ,B 两点,∴圆心 O (0,0)到直线 l 的距离 d =| 2| <1. 1+tan α ∴tan α>1,解得 tan α>1 或 tan α<-1. π π π 3π ∴ <α< 或 <α< .π 3π 综上,α 的取值范围为 , .(2)由(1)知直线 l 的斜率不为 0,设直线 l 的方程为 x =m (y + 2).设 A (x ,y ),B (x ,y ),P (x ,y ). 1 1 2 2 3 3x =m (y + 2), 联立 x +y =1, 化简得(m 2 +1)y +2 2m y +2m -1=0. 2 2m 2m -1 ∴y +y =- ,y y = . 1 2 m +1 1 2 m +12 2m ∴x +x =m(y + 2)+m (y + 2)=- +2 2m , 1 2 1 2 m +1x +x 2m y +y 2m x = = ,y = = . 3 2 m +1 3 2 m +12m m +1 ∴AB 中点 P 的轨迹的参数方程为 (m为参数),(-1<m <1). m +123.(2018 年新课标Ⅲ理)设函数 f(x )=|2x +1|+|x -1|.(1)画出 y =f (x )的图象;(2)当 x ∈[0,+∞)时,f (x )≤ax +b ,求 a +b 的最小值.112 2 2 2 22 4 2 2 44 42 2 2 2 22 2 2 23 2 2 1 2 1 2 2 2 x = , 22 2my = 21 【解析】(1)当 x ≤- 时,f (x )=-(2x +1)-(x -1)=-3x ;2 1 当- <x <1,f (x )=(2x +1)-(x -1)=x +2; 2当 x ≥1 时,f(x )=(2x +1)+(x -1)=3x .-3x ,x ≤- , 2∴f (x )= 1 x +2,- <x <1, 2 3x ,x ≥1.对应的图象如图所示.(2)当 x ∈[0,+∞)时,f (x )≤ax +b .当 x =0 时,f (0)=2≤0·a +b ,∴b ≥2;当 x >0 时,要使 f (x )≤ax +b 恒成立,则 f (x )的图象恒在直线 y =ax +b 的下方或在直线上. ∵f (x )的图象与 y 轴的交点的纵坐标为 2,且各部分直线的斜率的最大值为 3,1∴当且仅当a≥3且b≥2时,不等式f(x)≤ax+b在[0,+∞)上成立,∴a+b的最小值为5.。
