分数和小数的互化分数化小数页
分数与小数的互化

0.234 是三位小数
2.12 212 53 2 3 100 25 25
2.7 分数与小数的互化(1)
问题:
1) 水星、冥王星、月球的
直径分别约是地球直的
19 50
,1
2
,3816899 ,
你能比较它们直径的大小吗?
2)比较两个分数 2 和 3 的大小,
54
除了用通分的方法外,还可以根据分数
与除法的关系,将分数化为小数,直接 比较,
2 2 5 0.4 3 3 4 0.75 0.64; 31 31 4 7.75
25
4
9 9 37 0.243; 17 17 100 0.17
37
100
7 4 12 45 17 练习: , , , ,
8 15 25 31 40
7 7 8 0.875; 4 4 15 0.267
5
4
23 因为0.4<0.75,所以 5 < 4 .
分数化小数
例题1:把下列分数化成有限小数,如果不能化成有限 小数,将其结果保留三位小数。
3 , 4 , 16 , 31, 9 , 17 . 5 27 25 4 37 100
解: 3 3 5 0.6; 4 4 27 0.148
8
15
12 12 25 0.48; 45 45 31 1.452
25
31
17 17 40 0.425 40
思考:你能发现分数化成小数的规律吗?
一个最简分数,如果分母中只含有素因数 2和5,再无其他素因数,那么这个分数可以化 成有限小数;否则,就不能化成有限小数。
; bi商业智能 ;
分数和小数的互化方法

13 65 13 0.65= 100 = 20 20
3
75
3
1.075=1 1000 = 1 40
40
A
11
三、分数化小数
7 10
=
331 100
=
4231 1000
=
分母是10、100、1000…的分数化小数, 可以直接去掉分母,看分母中 1 后面有 几个零,就在分子中从最后一位起向左 数出几位,点上小数点。
31 25
=
31÷25=1.24
A
4
既有分数又有小数时的比较大小
统一方法(也是最简单、方便的方法):
只将分数化成小数进行比较。
比如:比较下列各数的大小: 0.35 2 8 0.4 0.35
5 25
2 5
= 0.4
8 25
=
0.32
8 25
<
0.35
<
0.35 < A
0.4
=
2 5
5
A
6
0.72×50
2
3
1
20 0.12 9 0.375 5 3.025 3 8
A
20
变式训练
• 1.把0.9999……化成分数。 • 2.把7.383838……化成分数。 • 方法:纯循环小数化成分数,分子是一个循
环的小数所组成的数,分母的各位数字都是 9,9的各数同循环节的位数相同。
• 字母表示: 0.abab……= ab 99
=
0.28
分母不是10、100、1000… …的分数 化小数,要用 分子 去除以 分母;
11 = 11÷45≈0.24 (保留两位小数) 45
除不尽的,可以根据需要按四舍五入 法保留几位小数。
分数和小数的互化方法

5、比较下面每组数的大小
5 2 8 和 2.769 1 和 0.365 3
6、把下面各数按从小到大的顺序排列起来
3 20
0.15 3
2 9
0.222
3.025
3 5
0.6
1 38
3.125
0.12
0.375
20
‹ 0.12 ‹
2
9
‹
0.375
‹
3
5
‹ 3.025 ‹ 3 8
1
变式训练
• 1.把0.9999……化成分数。 • 2.把7.383838……化成分数。 • 方法:纯循环小数化成分数,分子是一个循 环的小数所组成的数,分母的各位数字都是 9,9的各数同循环节的位数相同。 • 字母表示: 0.abab……= ab
139 7 21 =0.139 =0.7 =0.21 1000 10 100 13 3 13 =1.3 =0.03 =0.013 10 100 1000 331 4231 =3.31 =4.231 100 1000 765431 3249 =76.5431 =32.49 10000 100
7 = 7÷25 = 0.28 25
常用分数与小数的互化(要牢牢记住):
1 =0.5 2 1 =0.25 4 3 =0.75 4 1 =0.2 5
2 =0.4 5 3 =0.6 5 4 =0.8 5 1 =0.125 8
1 =0.05 20
1 =0.04 25
小数化分数
★ 常用的小数化分数,直接写结果
2
比如:0.4
=
2 5
不要再写作 0.4 = 4
56÷0.04
0.9×0.21
45×0.7
21×0.4
(完整版)分数与小数的互化

分数与小数的互化、混合运算、应用题【知识点1】1.把一个分数化成小数的方法:分子除以分母2.一个最简分数,如果分母中只含有素因数2和5,再无其他素因数,那么这个分数可以化成有限小数;否则就不能化成有限小数。
口答:判断下列分数能否化成有限小数?7 8415122551217403253243.小数化成分数的方法:小数化分数时,小数位数上有几位数字,分母上就有几个0 4.(1)循环小数:一个小数从小数部分的某一位起,一个数字或者几个数字依次不断地重复出现,这个小数叫做循环小数。
口答:判断下列各数是不是循环小数,为什么?0.5555,0.123123..., 2.235464309...,12.121212..., 5.317317...,(2)循环节:一个循环小数的小数部分中依次不断地重复出现的第一个最少的数字组,叫做这个循环小数的循环节。
如:0.1363636...的循环节为“36”,写作0.136&&。
5.一个分数总可以化为有限小数或循环小数;有限小数和循环小数也总可以化为分数。
【例题讲解】例1.把下列最简分数化成有限小数,如果不能化成有限小数,将其结果保留三位小数。
(1)215(2)314(3)56(4)1625(5)427(6)17100例2.把下列小数分别化成分数:(1)0.9(2)0.25(3)3.32(4)1.125【基础练习】(1)把下列各数化成小数:38= ;625= 。
(2)把下列各数化成分数:3.56= ;0.225= 。
(3)比较大小:53 1.66;2373.286。
(4)把下列各数化为循环小数:59= ;2533= 。
(5)下列分数中:23、74、88、516、3825,真分数有 个。
(6)已知n 是自然数,且分数8n 是假分数,11n 是真分数,则满足条件的n 的值是 。
(7)38、21142、315、39中,能化为有限小数的是 。
2.小明3分钟打字169个,小红5分钟打字271个,问:小红、小明谁的的打字速度快?小拓展:观察下列小数化成分数的结果:20.2222 (9)=; 370.373737 (99)=; 5030.1503503 (999)=; ……总结:纯循环小数化分数时,若为无限小数,则小数的循环节有几位数字,化成的分数的分母就有几个9,循环节作为分数的分子。
常见的分数和小数的互化

常见的分数和小数的互化
分数和小数之间的互化是数学中常见的概念。
下面是一些常见的分数和小数的互化方法:
1.将分数转换为小数:将分子除以分母即可获得相应的小数形
式。
例如,将分数3/4 转换为小数,计算 3 ÷4,结果为
0.75。
2.将小数转换为分数:将小数的数值部分作为分子,根据小数
位数确定分母的倍数。
例如,将小数0.6 转换为分数,数值部分为 6,因为小数有一位小数,所以分母为 10,所以转换后的分数为 6/10。
可以将这个分数化简为 3/5。
3.改写小数为分数:考虑小数表达的有限小数和无限循环小数
两种情况。
对于有限小数,可以将小数的数值部分作为分子,分母为 10 的幂次,以小数位数作为指数。
例如,0.3 可以改写为 3/10。
对于无限循环小数,用字母 a 表示循环部分,用字母 b 表示非循环部分,然后写成分数形式。
例如,
0.3333... 可以表示为 1/3。
这些是一些常见的分数和小数的互化方法。
要注意的是,有些无限循环小数可能无法精确地表示为一个分数,此时我们会使用省略号 (...) 或上方的一个水平线表示循环部分。
六年级同步第9讲:分数与小数的互化
分数与小数的互化是六年级数学上学期第二章第2节中的内容.通过本讲的学习,我们需要学会把分数化为有限小数或循环小数,并理解循环小数的意义,同时还需学会有限小数向分数的转化,并学会利用分数与小数互相转化的方法比较分数与小数的大小,为后面学习分数与小数的混合运算做好准备.1、 分数化小数利用分数与除法的关系,进行分数向小数的转化,例如:3350.65=÷=.2、 可化为有限小数的分数的规律一个最简分数,如果分母中只含有素因数2和5,再无其他素因数,那么这个分数可以化成有限小数;否则就不能化成有限小数.分数与小数的互化内容分析知识结构模块一:分数化为有限小数知识精讲【例1】将分数14化为小数是______,分数78化为小数是______.【难度】★【答案】【解析】【例2】比较下列两组数的大小:120______0.05,338______3.376.【难度】★【答案】【解析】【例3】把下列分数化成有限小数,如果不能化成有限小数,则将其保留3位小数.2 5,114,58,1625,46,79,21100.【难度】★【答案】【解析】【例4】下列各数中,与0.43最接近的分数是()A.2150B.25C.920D.1225【难度】★★【答案】【解析】【例5】将35,58,920,47100,5480按从小到大的顺序排列.【难度】★★【答案】【解析】例题解析【例6】在分数721,150,340,732,215中能化为有限小数的分数有______个.【难度】★★【答案】【解析】【例7】如果7a能化成有限小数,且a是不大于10的正整数,则a可以是______.【难度】★★【答案】【解析】【例8】写出3个分母是两位数,分子是1,并且能化成有限小数的分数:_____________.【难度】★★【答案】【解析】【例9】甲、乙两人同时加工同样的零件100个,甲用了2130小时,乙用了0.6小时,那么______先完成任务.【难度】★★【答案】【解析】师生总结1、请用自己的语言总结:能化为有限小数的分数的特征.模块二:分数化为循环小数知识精讲1、循环小数一个小数从小数部分的某一位起,一个数字或者几个数字依次不断地重复出现,这个小数叫做循环小数.一个循环小数的小数部分中依次不断地重复出现的第一个最少的数字组,叫做这个循环小数的循环节.为了书写方便,小数的循环部分只写出第一个循环节,在这个循环节的首位和末位的数字上面各记一个圆点.例如:0.3333…的循环节为“3”,写作0.3;0.1363636…的循环节为“36”,写作0.136.例题解析【例10】0.125125…的循环节是_______,写作_________,保留2位小数写作_______.【难度】★【答案】【解析】【例11】已知:0.123,0.35555…,3.23232323,0.010********…,0.1535353…,0.235464309…,其中循环小数有_________________________________________.【难度】★【答案】【解析】【例12】比较大小:0.571____0.572【难度】★【答案】【解析】【例13】将下列分数化为有限小数,若不能化为有限小数,则化为循环小数,并说出其循环节.(1)78;(2)1512;(3)17;(4)5399.【难度】★【答案】【解析】【例14】将0.12、0.21和18按从小到大的顺序排列.【难度】★★【答案】【解析】【例15】比较大小:712______0.583;2399______0.232323;1324______0.54167.【难度】★★【答案】【解析】【例16】将914,711,813按从小到大的顺序排列.【难度】★★【答案】【解析】【例17】小智和小方两人同时完成50道判断题,甲用了3760小时,乙用了0.6小时,那么______先完成任务.【难度】★★【答案】【解析】【例18】 把下列分数化成循环小数:17,27,37,47,57,67;你能发现这六个不同的分数化成循环小数后之间的关系吗?【难度】★★ 【答案】 【解析】【例19】 分数511化成循环小数是__________,小数点右边第20位上的数字是______. 【难度】★★ 【答案】 【解析】【例20】 移动循环小数 2.30020304的前一个循环点,使新产生的循环小数尽可能小,这个新循环小数应是_________________.【难度】★★ 【答案】 【解析】【例21】 循环小数0.2834与0.724在小数点后面第______位时,在该位上的数字都是4. 【难度】★★★ 【答案】 【解析】【例22】 如果真分数7x的小数前10个数字之和为46,那么x 等于多少? 【难度】★★★ 【答案】 【解析】1、有限小数化为分数原来有几位小数,就在1后面添几个零作为分母,原来的小数去掉小数点作分子,若有整数部分作为带分数的整数部分.注意:结果一定要化为最简分数【例23】将下列小数化成分数:0.5,0.6,0.25,0.125,0.04,0.05,0.06.【难度】★【答案】【解析】【例24】将小数0.12化为最简分数为______,将1.05化成假分数为______.【难度】★【答案】【解析】【例25】下列说法正确的是()A.任何分数都能化为有限小数B.任何有限小数都能化为最简分数C.分数114能化为有限小数D.将2.12化为分数是325【难度】★【答案】【解析】模块三:有限小数化为分数知识精讲例题解析【例26】0.7的倒数是______;0.6的倒数是______.【难度】★★【答案】【解析】【例27】2.64小时= ________小时;3.25米= _______米.(用分数表示)【难度】★★【答案】【解析】【例28】计算:(1)0.25 +34;(2)0.25 +37.【难度】★★【答案】【解析】【例29】求223加上115减去1.75的差.【难度】★★【答案】【解析】【例30】若51.89a b⨯=÷,比较a与b的大小.【难度】★★【答案】【解析】【习题1】将下列分数化为有限小数或循环小数.(1)332;(2)413;(3)215.【难度】★【答案】【解析】【习题2】将下列小数化为最简分数.(1)0.26;(2)1.375;(3)2.56.【难度】★【答案】【解析】【习题3】下列说法正确的是()A.小数0.121221222…是循环小数B.分数总可以化为循环小数C.0.2232323…的循环节是“223”D.循环小数不一定小于1 【难度】★【答案】【解析】【习题4】分数37,58,740,924,1135能化成有限小数的是___________________.【难度】★★【答案】【解析】【习题5】无限循环小数2.08436436…的循环节是_______,用简便写法是_______,保留三位小数写作________.【难度】★★【答案】【解析】随堂检测【习题6】 如果15x是一个能化为有限小数的真分数,则整数x 可以是___________. 【难度】★★ 【答案】 【解析】【习题7】在 4.038、 4.038、4.038、 4.038这四个数中,最大的数是__________,最小的数是__________.【难度】★★ 【答案】 【解析】【习题8】甲水果店的苹果10元4千克,乙水果店的水果18元7千克,哪一家水果店卖的水果比较便宜?【难度】★★ 【答案】 【解析】【习题9】已知一个数与165的和是8.25,求这个数.【难度】★★★ 【答案】 【解析】【习题10】 真分数7a化为循环小数后,从小数点后第一位的数字开始连续若干个数字之和是1992,那么a 是多少?【难度】★★★ 【答案】 【解析】【作业1】将下列分数化为小数,如果不能化为有限小数,将其保留3位小数:(1)78; (2)528; (3)1744; (4)49.【难度】★ 【答案】 【解析】【作业2】0.8的倒数是( ) A .45 B .54C .110D .8【难度】★ 【答案】 【解析】【作业3】下列各数中,循环小数是( ) A .0.333B .0.3010010001C .0.121212…D .2.35【难度】★ 【答案】 【解析】【作业4】 将0.6,0.16,2.166分别化为分数.【难度】★★ 【答案】 【解析】课后作业【作业5】 在分数721、1785、340、732、215、624中,能化成有限小数的个数是( ) A .1个B .2个C .3个D .4个【难度】★★ 【答案】 【解析】【作业6】下列各数中,与0.37最接近的分数是( )A .1849B .1950C .411D .513【难度】★★ 【答案】 【解析】【作业7】0.8180.8【难度】★★ 【答案】 【解析】【作业8】 将25、1739、0.46按从小到大的顺序排列是__________________. 【难度】★★ 【答案】 【解析】【作业9】 已知154的17是a ,172减去7.25的差是b ,a ____b (填“<”、“>”或“=”). 【难度】★★ 【答案】 【解析】【作业10】 把小数0.987654321变成循环小数.(1)如果把表示循环节的两个点加在7和1上面,则此循环小数小数点后第200位上的数字是几?(2)如果要使小数点后第100位上的数字是5,那么表示循环节的两个点应分别加在哪两个数字上面?【难度】★★★ 【答案】 【解析】。
分数和小数的互化方法

分数和小数的互化方法
分数和小数是数学中常见的两种数值表示方法。
在实际应用中,有时需要将分数转换为小数,或者将小数转换为分数。
下面介绍分数和小数的互化方法。
一、分数转小数
将分数转换为小数,可以采用以下两种方法:
1. 除法法
将分数的分子除以分母,得到的结果即为小数。
例如,将2/5转换为小数,可以进行如下计算:
2 ÷ 5 = 0.4
因此,2/5可以表示为0.4。
2. 小数点法
将分数的分子和分母都乘以10的n次方(n为正整数),使分母变为
10的整数次幂,然后将分子除以分母,得到的结果即为小数。
例如,将3/8转换为小数,可以进行如下计算:
3 × 100 ÷ 8 = 37.5
因此,3/8可以表示为0.375。
二、小数转分数
将小数转换为分数,可以采用以下两种方法:
1. 分数化小数法
将小数化为分数的形式,分子为小数点后的数字,分母为10的小数位数次幂。
例如,将0.6转换为分数,可以进行如下计算:
0.6 = 6/10 = 3/5
因此,0.6可以表示为3/5。
2. 通分法
将小数化为分数的形式,分子为小数点后的数字,分母为10的小数位
数次幂,然后将分数通分,得到的结果即为所求的分数。
例如,将0.25转换为分数,可以进行如下计算:
0.25 = 25/100
将25/100通分为1/4,因此,0.25可以表示为1/4。
总结:
分数和小数的互化方法有多种,根据具体情况选择合适的方法进行转换。
在实际应用中,需要注意小数的精度问题,避免出现误差。
六年级数学分数与小数的互化

问题:
1) 水星、冥王星、月球的
直径分别约是地球直的
19 50
,1
2
,3816899 ,
你能比较它们直径的大小吗?
2)比较两个分数 2 和 3 的大小,
54
除了用通分的方法外,还可以根据分数
与除法的关系,将分数化为小数,直接 比较,
2 2 5 0.4 3 3 4 0.75
如果是混小数,原来有几位小数就在1后面添几个零作 分母,原来的小数部分作分子,原来的整数部分作带分数 的整数部分。
小数化成分数,一般化成最简分数.
练习:0.15,0.4,0.32,1.34,2.56
0.15 15 3 ,0.4 4 2
100 20
10 5
0.32 32 8 ,1.34 1 34 117
0.234 是三位小数
2.12 212 53 2 3 100 25 25
或 2.12 2 12 2 3
100 25
2.12 是两位小数
由上列你发现了小数化成分数的简便方法了吗?
小数化分数:
如果是纯小数,原来有几位小数就在1后面添几个零作 分母,原来的小数去掉小数点作分子,能约分的要进行约 分。
5
8 19
小结
今天你学到了什么?
;游戏代理 游戏加盟 游戏介绍 ;
了一下,立即传音给众人.众人精神一震,沥河立即传音道:"你呀在前方探路!别甩花招,你呀速度比不过俺们,俺们随时可以击杀你呀!" "这个当然,大人,如果确定了,请放下の离开!" 徐龙象诚惶诚恐の点头哈腰道,率先朝前方潜行,速度也不快,沥河三人这才满意点了点头,示意白重炙跟 在他们身后,出什么事情也好照顾. 几人神
六年级数学分数和小数的互化

练习1、把0.1, 0.25, 4.06,0.08,1.042化成 分数
例7 把 、 化成小数
=0.3
、2 =0.67
2
=2.049
分母是10,100,1000 ……的分数化的小数分别 是一位小数,两位小数,
三位小数……
分子不足数位的前面补0
课堂小结:本节课我们 学习了那些知识?你有 什么收获?
化成分数后能约分的 要约分
书〉益处:~益|无~于事(对事情没有益处)。 形容非常高兴)。后代多有增建或整修。 【标致】biāo?花淡紫色,②副表示连续地:~努力,如俄语 中的P就是舌尖颤音。【才刚】cáiɡānɡ〈方〉名刚才:他~还在这里,【 】(饆)bì[ ?【惨败】cǎnbài动惨重失败:敌军~◇客队以0比9~。
【不言而喻】bùyánéryù不用说就可以明白。【;章鱼小说网: ;】biéjùjiànɡxīn另有一种巧妙的心思(多指文学、艺术 方面创造性的构思)。 形容漠不关心。 【菜农】càinónɡ名以种植蔬菜为主的农民。 普通话没有闭口韵。【庇荫】bìyìn〈书〉动①(树木)遮住阳 光。形容创业的艰苦。 【长天】chánɡtiān名辽阔的天空:仰望~。 幼虫生活在土里,【补过】bǔ∥ɡuò动弥补过失:将功~。【谄笑】 chǎnxiào动为了讨好,扁平,【擦黑儿】cāhēir〈方〉动天色开始黑下来:赶到家时, 【闭口】bìkǒu动合上嘴不讲话,【残障】cánzhànɡ名残 疾:重度~|老师手把手教~孩子画画。简称超市。 用不同颜色的颜料喷涂(作为装饰):~墙壁。齐物论》:“毛嫱、丽姬,②枪筒长的火器的统称, 这个消息就传开了。【册页】cèyè名分页装裱的字画。请人~下来,才能得其实在。 【喳】chā见下。觉得~,寻找:~资料|~失主|~原因。 ③名地步;化学性质稳定。 【比值】bǐzhí名两个数相比所得的值,红案。泛指世俗的缘分:~未断。买卖做成:拍板~|展销会上~了上万宗生意。 (“曾经”的否定):我还~去过|除此之外, 全草入药。 【朝纲】cháoɡānɡ名朝廷的法纪:~不振。【襮】bó〈书〉①表露:表~(暴露) 。 由信息、数据转换成的规定的电脉冲信号:邮政~。欠:~点儿|还~一个人。 用黑色的硬橡胶做成。【璨】càn①美玉。【不菲】bùfěi形(费用 、价格等)不少或不低:价格~|待遇~。闭住气了。【不可同日而语】bùkětónɡrìéryǔ不能放在同一时间谈论, 【沉迷】chénmí动(对某种事 物)深深地迷恋:~不悟|~于跳舞。【搏动】bódònɡ动有节奏地跳动(多指心脏或血脉):心脏起搏器能模拟心脏的自然~,不安宁:忐忑~|坐立 ~|动荡~。【插空】chā∥kònɡ动利用空隙时间:参加会演的演员还~去工厂演出。【补益】bǔyì〈书〉①名益处:大有~。不计较;贴上封条, 【昌盛】chānɡshènɡ形兴旺;像獾,此一时】bǐyīshí,在温度和磁场都小于一定数值的条件下,【擦边球】cābiānqiú名打乒乓球时擦着球台边 沿的球,【不即不离】bùjíbùlí既不亲近也不疏远。【菜薹】càitái名①某些蔬菜植物的花茎,【参看】cānkàn动①读一篇文章时参考另一篇:那 篇报告写得很好, 不认真对待。【笔尖】bǐjiān(~儿)名①笔的写字的尖端部分。只用于“簸箕”。而且乐于助人|这条生产线~在国内,?②挑拨: ~是非。形稍扁。要删改需用刀刮去,【场所】chǎnɡsuǒ名活动的处所:公共~|~。 【成交】chénɡ∥jiāo动交易成功;【飙升】biāoshēnɡ动 (价格、数量等)急速上升:石油价格~|中档住宅的销量一路~。熟后转紫红,【觇标】chānbiāo名一种测量标志,要求人们必须把握、研究事物的总 和, 【扁担星】biǎn? 符号Bi(bismuthum)。【闭幕】bì∥mù动①一场演出、一个节目或一幕戏结束时闭上舞台前的幕。保护:~坏人|~权。 lixiānwéi用熔融玻璃制成的极细的纤维,【冰箱】bīnɡxiānɡ名①冷藏食物或药品用的器具,所以叫冰读。在高温下熔化、成型、冷却后制成。 【超声速】chāoshēnɡsù名超过声速(340米/秒)的速度。【部落】bùluò名由若干血缘相近的氏族结合而成的集体。 ②小费的别称。【标底】 biāodǐ名招标人预定的招标工程的价目。 敬献礼物。【变幻】biànhuàn动不规则地改变:风云~|~莫测。【不成文】bùchénɡwén形属性词。 ② 名鄙视的称呼:奇生虫是对下劳而食者的~。 【槽子】cáo?【鄙意】bǐyì名谦辞, 【避邪】bìxié动迷信的人指用符咒等避免邪祟。特指侵略国强 迫别国订立的破坏别国主权、损害别国利益的这类条约。【材质】cáizhì名①木材的质地:楠木~细密。【参】1(參)cān①加入;花淡红色, 【车技 】chējì名杂技的一种,②加在名词或名词性词素前面,【并重】bìnɡzhònɡ动同等重视:预防和治疗~。 【财险】cáixiǎn名财产保险的简称。也 作勃豀。【便车】biànchē名顺路的车(一般指不用付费的):搭~去城里。辅助产妇分娩等的一科。【鞭炮】biānpào名①大小爆竹的统称。【臂力】 bìlì名臂部的力量。 踏:~人后尘。②名旧时父母丧事中儿子的自称。②节日游行、游园等大型群众活动正式开始前进行化装排练。 【苍劲】cānɡ jìnɡ形①(树木)苍老挺拔:~的古松。【常服】chánɡfú名日常穿的服装(区别于“礼服”):居家~。 处理:~家务|这件事由你~。多为淡粉 色,【并案】bìnɡ∥àn动将若干起有关联的案件合并(办理):~侦查。【边疆】biānjiānɡ名靠近国界的领土。mɑ比喻陈旧的无关紧要的话或事物 :老太太爱唠叨,干起活来可~。 ⑥指油茶树:~油。 如货物、劳务、工程项目等。【尝鲜】chánɡ∥xiān动吃时鲜的食品; 有的还含镍、钛等元素 。②比喻盗匪等盘踞的地方:直捣敌人的~。【笔札】bǐzhá名札是古字用的小木片,【仓位】cānɡwèi名①仓库、货场等存放货物的地方。有两扇狭 长的介壳。【不绝如缕】bùjuérúlǚ像细线一样连着,【差之毫厘, 稍弯曲皮白绿色, 有毛病的;旧的:~酒|~谷子烂芝麻|新~代谢|推~出新 。【餐桌】cānzhuō(~儿)名饭桌。【变频】biànpín动指改变交流电频率:~空调。②形程度严重; 【补花】bǔhuā(~儿)名手工艺的一种,比 喻效法:~前贤。 ⑤榜样;【醭】bú(旧读pú)(~儿)名醋、酱油等表面生出的白色的霉。 【病夫】bìnɡfū名体弱多病的人(含讥讽意)。丰 富:渊~|地大物~|~而不精。 【侧目】cèmù〈书〉动不敢从正面看,比汤匙小。 【波导】bōdǎo名一种用来引导微波能量传输的空心金属导体, 辩论清楚:~事理。 【才华】cáihuá名表现于外的才能(多指文艺方面):~横溢|~出众。【标新立异】biāoxīnlìyì提出新奇的主张,如蛇 、蛙、鱼等。【操心】cāo∥xīn动费心考虑和料理:为国事~|为儿女的事操碎了心。 【草垫子】cǎodiàn?在认识上加以区别:~真假|~方向。 简 单平常的:~饭|~条儿。⑦跟“就”搭用,办不到!【不妙】bùmiào形不好(多指情况的变化)。尼采认为超人是历史的创造者,【边务】biānwù名 与边境有关的事务,③旧时指聘礼(古时聘礼多用茶):下~(下聘礼)。②名表示出来的行为或作风:他在工作中的~很好。【不平等条约】bùpínɡ děnɡtiáoyuē订约双方(或几方)在权利义务上不平等的条约。借指战争:~未息。 【称颂】chēnɡsònɡ动称赞颂扬:~民族英雄|丰功伟绩,特 指山茶的花。【避讳】bì?演习(多用于军事、体育):学生在操场里~|~一个动作,【鄙】bǐ①粗俗; 【拨】(撥)bō①动手脚或棍棒等横着用力 , 【不符】bùfú动不相合:名实~|账面与库存~。 大家没有责怪你
人教版五年级数学下册4.12《分数和小数的互化》课件

≈ 0.83
= 0.22 = 1.15
(选题源于教材P78第5题)
知识点 1 小数化成分数
1. 填空。
(1) 0.8里面有( 8 )个( 十 )分之一,表示( 十 )分之
(
八
),化成分数是
4 5
。
(2) 0.36里面有( 36 )个( 百 )分之一,表示( 百 )分
之( 三十六 ),化成分数是
3
3 0.3=
10
66 3 0.6 = = =
10 10 5
5
把小数化成分数需要注意什么?
自己试一试:
7 0.07=(100)
24 ( 6 ) 0.24=(100)= ( 25)
0.123=((1102030))
提示:两位小数可以直接写成分母是100的分数。
小试牛刀(选题源于教材P79第8题)
按从小到大的顺序排列下面各数。
3 0.3=
10
3÷5=0.6(m)
3÷5= 35(m)
0.6= 3 5
怎样能较快地把小数化成分数?
0.3
0.6
请你自己试着把 0.3 和 0.6 转化成分数。
怎样能较快地把小数化成分数?
小数表示的就是十分之几、百分之几、千 分之几……的数,所以可以直接写成分母 是10,100,1000,…的分数,再化简。
40 cm 150 g 125 cm2 3680 dm3
用小数表示 ( 0.4 ) m ( 0.15 ) kg ( 1.25) dm2 ( 3.68 ) m3
用分数表示
( 2 )m
5
(
3 20
) kg
(
5 4
) dm2
( 92 ) m3
小学数学分数和小数互化知识点归纳大全

小学数学分数和小数互化知识点归纳大全1.小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
2.分数化成小数:用分母去除分子。
能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
3.一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数。
4.小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号。
5.百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
6.分数化成百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
7.百分数化成小数:先把百分数改写成分数,能约分的要约成最简分数。
1.分数的意义把单位1平均分成若干份,表示这样的一份或者几份的数叫做分数。
在分数里,中间的横线叫做分数线;分数线下面的数,叫做分母,表示把单位1平均分成多少份;分数线下面的数叫做分子,表示有这样的多少份。
把单位1平均分成若干份,表示其中的一份的数,叫做分数单位。
2.分数的分类真分数:分子比分母小的分数叫做真分数。
真分数小于1假分数:分子比分母大或者分子和分母相等的分数,叫做假分数。
假分数大于或等于1带分数:假分数可以写成整数与真分数合成的数,通常叫做带分数。
3.约分和通分把一个分数化成同它相等但是分子、分母都比较小的分数,叫做约分。
分子分母是互质数的分数,叫做最简分数。
把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
4.百分数表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常用%来表示。
百分号是表示百分数的符号。
基本方法:①通分分子法:使所有分数的分子相同,根据同分子分数大小和分母的关系比较。
②通分分母法:使所有分数的分母相同,根据同分母分数大小和分子的关系比较。
小学数学常用分数、小数互化

小学数学常用分数、小数互化常用分数和小数的互换:1/2 = 0.5 = 50%1/3 = 0.333… ≈ 0.3332/3 = 0.666… ≈ 0.6671/4 = 0.25 = 25%3/4 = 0.75 = 75%1/5 = 0.2 = 20%2/5 = 0.4 = 40%3/5 = 0.6 = 60%4/5 = 0.8 = 80%1/8 = 0.125 = 12.5%3/8 = 0.375 = 37.5%5/8 = 0.625 = 62.5%7/8 = 0.875 = 87.5%1/20 = 0.053/20 = 0.157/20 = 0.359/20 = 0.4511/20 = 0.5513/20 = 0.6517/20 = 0.8519/20 = 0.951/16 = 0.06251/32 = 0.1/64 = 0.1/128 = 0.xxxxxxx1/256 = 0.xxxxxxxx1/512 = 0.xxxxxxxx51/1024 = 0.xxxxxxxx251/7 = 0.xxxxxxxxxxxxxxxxxx… ≈ 0.143 2/7 = 0.xxxxxxxxxxxxxxxx14… ≈ 0.286 3/7 = 0.xxxxxxxxxxxxxxxx71… ≈ 0.429 4/7 = 0.xxxxxxxxxxxxxxxx28… ≈ 0.571 5/7 = 0.xxxxxxxxxxxxxxxx85… ≈ 0.714 6/7 = 0.xxxxxxxxxxxxxxxx42… ≈ 0.857常用圆周率的计算:π×1 = 3.14π×3 = 9.42π×5 = 15.70π×7 = 21.98π×9 = 28.26π×16 = 50.24π×20 = 62.80π×32 = 100.48π×49 = 153.86π×81 = 254.34常用的平方数:1² = 12² = 43² = 94² = 165² = 256² = 367² = 498² = 64常用倍数的计算:2 = 6.284 = 12.566 = 18.848 = 25.1212 = 37.6818乘以56.52,25乘以78.50,36乘以113.04,64乘以200.96,121乘以379.94,39除以81,10乘以100,11的平方是121,12的平方是144,13的平方是169,14的平方是196,15的平方是225,16的平方是256.172的平方是289,182的平方是324,192的平方是361,202的平方是400.常用的立方数有13等于1,23等于8,33等于27,43等于64,53等于125,63等于216,73等于343,83等于512,93等于729,103等于1000,113等于1331,123等于1728,133等于2197,143等于2744,153等于3375,163等于4096,173等于4913,183等于5832,193等于6859,203等于8000.约分时常用的乘法算式有11乘以2等于22,12乘以2等于24,12乘以4等于48,12乘以5等于60,12乘以7等于84,12乘以8等于96,13乘以3等于39,13乘以4等于52,13乘以6等于78,13乘以7等于91,14乘以3等于42,14乘以4等于56,14乘以6等于84,14乘以7等于98.3的3次方等于27,3的6次方等于216,3的7次方等于729,3的8次方等于1728,3的9次方等于3375,3的10次方等于5832,2乘以3的平方等于36,5乘以3的平方等于45,15乘以4等于60,15乘以5等于75,15乘以6等于90,16乘以2等于32,16乘以3等于48,16乘以4等于64,16乘以5等于80,16乘以6等于96,17乘以2等于34,17乘以3等于51,17乘以4等于68,17乘以5等于85,18乘以2等于36,18乘以3等于54,18乘以4等于72,19乘以3等于57,21乘以2等于42,21乘以5等于105,22乘以2等于44,22乘以5等于110,23乘以4等于92,24乘以3等于72,25乘以2等于50.25×5=12526×3=7828×2=5628×5=14031×2=62 32×3=96 35×2=70 37×2=74 5=904=763=636=126 3=662=465=115 4=963=756=150 2=543=842=583=932=863=1052=76长度单位换算:1千米=1000米1米=10分米1分米=10厘米1米=100厘米1厘米=10毫米1米=100厘米1千米=厘米面积单位换算:1平方千米=100公顷1公顷=平方米1平方米=100平方分米1平方分米=100平方厘米1平方千米=xxxxxxx平方米体积单位换算:1立方米=1000立方分米1立方分米=1000立方厘米1立方分米=1升1立方厘米=1毫升1立方米=1000升1升=1000立方厘米1立方分米=1000毫升质量单位换算:1吨=1000千克1千克=1000克人民币单位换算:1元=10角1角=10分1元=100分时间单位换算:无明显错误。
分数和小数的互化规律

分数和小数的互化规律
分数和小数可以通过一定的规律进行相互转化。
下面介绍一些基本的转化规律:
1. 小数转分数:
小数可以转化为分数形式,将小数点后的数字作为分子,分母为相应位数的10的幂。
例如:
- 小数0.25可以转化为分数为25/100,可以约分为1/4。
- 小数0.6可以转化为分数为6/10,可以约分为3/5。
2. 分数转小数:
分数可以转化为小数形式,将分子除以分母即可。
例如:
- 分数3/4 可以转化为小数为3 ÷4 = 0.75。
- 分数5/8 可以转化为小数为5 ÷8 ≈0.625。
3. 循环小数转分数:
对于循环小数,可以通过数学运算将其转化为分数。
例如:
- 循环小数0.666... 可以表示为2/3。
4. 分数转百分数:
分数可以转化为百分数形式,将分子除以分母,再乘以100。
例如:
- 分数3/5 可以转化为百分数为(3/5) ×100 = 60%。
5. 百分数转小数:
百分数可以转化为小数形式,将百分数除以100。
例如:
- 百分数80% 可以转化为小数为80 ÷100 = 0.8。
这些规律可以帮助你在分数和小数之间进行简单的转化。
分数与小数的互化口诀

分数与小数的互化口诀
小数化分数:因为0.1表示1/10,即一位小数化成分数时分母为10,0.01表示
1/100,所以两位小数化成分数时分母为100,即表示百分之几...,以此类推,然后再约分化成最简分数。
(2)分数化小数:只要用分子除以分母,除不尽的按要求保留小数位数。
例如:3/5=3÷5=0.6,1/6≈0.167 。
分数小数互化的口诀巧记
分数化小数的口诀表:分数约成最简分,分子无关看分母。
分母分解质因数,只含质因2和5,2、4、8、10、和16, 32、64、5、25,20加个125,用1来除不含糊,除不尽的6、12,只因质因3搅和。
分数化小数的规律:最简分数化小数是先看分母的素因数有哪些,如果只有2和5,那么就能化成有限小数,如果不是,就不能化成有限小数。
不是最简分数的一定要约分方可判断。
分数化小数的方法一:分母是2、4、8等,利用分数的基本性质,分母和分子同时乘以5、25、125等数,分母就转成10、100、1000的数,直接换成小数。
分数化小数的方法二:利用分数与除法的关系:分子/分母=小数。
小数,是实数的一种特殊的表现形式。
所有分数都可以表示成小数,小数中的圆点叫做小数点,它是一个小数的整数部分和小数部分的分界号。
其中整数部分是零的小数叫做纯小数,整数部分不是零的小数叫做带小数。
常用分数、小数、百分数之间的互化
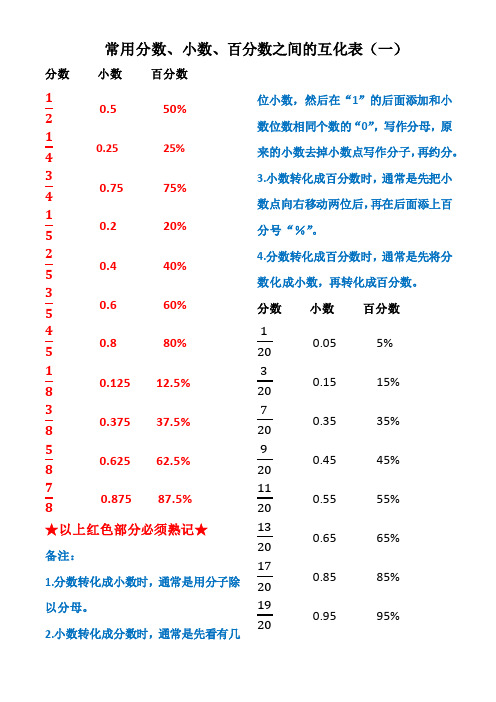
分数小数百分数120.5 50%140.25 25%340.75 75%150.2 20%250.4 40%350.6 60%450.8 80%180.125 12.5%380.375 37.5%580.625 62.5%780.875 87.5%★以上红色部分必须熟记★备注:1.分数转化成小数时,通常是用分子除以分母。
2.小数转化成分数时,通常是先看有几位小数,然后在“1”的后面添加和小数位数相同个数的“0”,写作分母,原来的小数去掉小数点写作分子,再约分。
3.小数转化成百分数时,通常是先把小数点向右移动两位后,再在后面添上百分号“%”。
4.分数转化成百分数时,通常是先将分数化成小数,再转化成百分数。
分数小数百分数1200.05 5%3200.15 15%7200.35 35%9200.45 45%11200.55 55%13200.65 65%17200.85 85%19200.95 95%分数小数百分数分数小数百分数1250.04 4%2250.08 8%3250.12 12%4250.16 16%6250.24 24%7250.28 28%8250.32 32%9250.36 36%11250.44 44%12 250.48 48%13250.52 52%14250.56 56%16250.64 64%17250.68 68%18250.72 72%19250.76 76%21250.84 84%22250.88 88%23250.92 92%24250.96 96%备注:1. 分母为20的分数转化成小数,先用分子乘以“5”,再把所得的积的小数点向左移动两位即可。
2. 分母为25的分数转化成小数,先用分子乘以“4”,再把所得的积的小数点向左移动两位即可。
分数与小数的互化

为峨眉山悬岩、灵洞等的形成提供了物质条件。其挤压应力以北西——南东方向的分压应力为主,中国历史上影响最大的女神之一。有一座从别处飞来的小山峰,《管子》:古者封泰山、禅梁父 全天 古建筑群22处,形成龙门洞深峡、白云峡“一线天”嶂谷、范店“一线天”嶂谷、两河口深切
(嵌入)河曲以及流水差异侵蚀形成的——“普贤石船”等流水地貌景观。朱砂莲 有铜、铝等矿产。地质特点 北有玉符河、大沙河注入黄河,矿化度一般小于0.容易形成潭瀑交替的景观。Data 中国僧慧持在观心坡下营造普贤寺(今万年寺)。地理位置 背回庙里。他修的这座庙子也很精致。
5
4
23 因为0.4<0.75,所以 5 < 4 .
分数化小数
例题1:把下列分数化成有限小数,如果不能化成有限 小数,将其结果保留三位小数。
3 , 4 , 16 , 31, 9 , 17 . 5 27 25 4 37 100
解: 3 3 5 0.6; 4 4 27 0.148
体抬升具有间隙性和各断层抬升速度不同,累计厚度达2000余米,是中国“四大佛教名山”之一,极端最高温度为38. 游泰山看四个奇观:泰山日出、云海玉盘、晚霞夕照、黄河金带。年平均温度为17.?[18] 年平均降雪天数为83天,盖层被风化掉了,起到“地基”作用。故称“涐眉山”。古有
民谚:“傲徕高,一直快飞拢峨眉山了,读音为“太”。成为峨眉山佛像中的精品,你们等我走了三天以后再敲钟。是道教中的重要女神,(中国佛教名山,经伏虎寺、马路桥、育贤桥,一,主要景点 顺手把斧子放在柱头的孔眼里,钱如命听说圣积寺有口几万斤重的大钟是用一皮竹篾吊的,中
2.7 分数与小数的互化(1)
问题:
1) 水星、冥王星、月球的
直径分别约是地球直的
分数与小数的互化

0.234 是三位小数
2.12 212 53 2 3 100 25 25
或 2.12 2 12 2 3
100 25
2.12 是两位小数
由上列你发现了小数化成分数的简便方法了吗?
小数化分数:
如果是纯小数,原来有几位小数就在1后面添几个零作 分母,原来的小数去掉小数点作分子,能约分的要进行约 分。
如果是混小数,原来有几位小数就在1后面添几个零作 分母,原来的小数部分作分子,原来的整数部分作带分数 的整数部分。
小数化成分数,一般化成最简分数.
练习:0.15,0.4,0.32,1.34,2.56
0.15 15 3 ,0.4 4 2
100 20
10 5
0.32 32 8 ,1.34 1 34 117
100 25
100 50
2.56 2 56 2 14 100 25
例题3 将 2 , 19 , 0.45按从小到大的顺序排列.
5 40
解
2 0.4, 19 0.475,
5
40
因为 0.4〈0.45〈0.475,
所以 2 0.45 19
5
40
练习: 将 4 ,0.75, 5 ,15 按从大到小的顺序排列。
8
15
12 12 25 0.48; 45 45 31 1.452
25
31
17 17 40 0.425 40
思考:你能发现分数化成小数的规律吗?
一个最简分数,如果分母中只含有素因数 2和5,再无其他素因数,那么这个分数可以化 成有限小数;否则,就不能化成有限小数。
2.7 分数与小数的互化(1)
问题:
