2012年初中毕业与升学统一考试数学试卷(黑龙江哈尔滨市)

2012年黑龙江省哈尔滨市中考数学试卷及解析

2012年黑龙江省哈尔滨市中考数学试卷及解析一、选择题（共10小题，每小题3分，满分30分）4．（3分）（2012•哈尔滨）如图所示的几何体是由六个小正方体组合而成的，它的左视图是（）C=90°，AC=4，AB=5，则sinB的值是（）5．（3分）（2012•哈尔滨）如图，在Rt△ABC中，∠B=6．（3分）（2012•哈尔滨）在10个外观相同的产品中，有2个不合格产品，现从中任意抽取1个进行检测，抽到不合格产品的概率是（）7．（3分）（2012•哈尔滨）如果反比例函数y=的图象经过点（﹣1，﹣2），则k的值是（）2=8．（3分）（2012•哈尔滨）将抛物线y=3x2向左平移2个单位，再向下平移1个单位，所得抛物线为9．（3分）（2012•哈尔滨）如图，⊙O是△ABC的外接圆，∠B=60°，OP⊥AC于点P，OP=2，则⊙O 的半径为（）4 6所对的弧都为OP=2，．10．（3分）（2012•哈尔滨）李大爷要围成一个矩形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边总长应恰好为24米，要围成的菜园是如图所示的矩形ABCD，设BC的边长为x米，AB 边的长为y米，则y与x之间的函数关系式是（）二、填空题（共10小题，每小题3分，满分30分）11．（3分）（2012•哈尔滨）把16000 000用科学记数法表示为 1.6×107．12．（3分）（2006•河南）函数y=中，自变量x的取值范围是x≠5．13．（3分）（2012•哈尔滨）化简：=3．14．（3分）（2012•哈尔滨）把多项式a3﹣2a2+a分解因式的结果是a（a﹣1）2．15．（3分）（2012•哈尔滨）不等式组的解集是＜x＜2．16．（3分）（2012•哈尔滨）一个等腰三角形的两边分别为5和6，则这个等腰三角形的周长是16或17．17．（3分）（2012•哈尔滨）一个圆锥的母线长为4，侧面积为8π，则这个圆锥的底面圆的半径是2．=18．（3分）（2012•哈尔滨）方程的解是x=6．19．（3分）（2012•哈尔滨）如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=105度．20．（3分）（2012•哈尔滨）如图，四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED=2∠CED，点G是DF的中点，若BE=1，AG=4，则AB的长为．AB===三、解答题（共8小题，满分60分）21．（6分）（2012•哈尔滨）先化简，再求代数式的值，其中x=cos30°+．x=cos30 =•=•x=+=×+=+=222．（6分）（2012•哈尔滨）图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，点A和点B在小正方形的顶点上．（1）在图1中画出△ABC（点C在小正方形的顶点上），使△ABC为直角三角形（画一个即可）；（2）在图2中画出△ABD（点D在小正方形的顶点上），使△ABD为等腰三角形（画一个即可）．23．（6分）（2012•哈尔滨）如图，点B在射线AE上，∠CAE=∠DAE，∠CBE=∠DBE．求证：AC=AD．24．（6分）（2012•哈尔滨）小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x（单位：cm）的边与这条边上的高之和为40cm，这个三角形的面积S（单位：cm）的变化而变化．（1）请直接写出S与x之间的函数关系式（不要求写出自变量x的取值范围）；（2）当x是多少时，这个三角形面积S最大？最大面积是多少？==，25．（8分）（2012•哈尔滨）虹承中学为做好学生“午餐工程”工作，学校工作人员搭配了A，B，C，D四种不同种类的套餐，学校决定围绕“在A，B，C，D四种套餐种类中，你最喜欢的套餐种类是什么？（必选且只选一种）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查问卷适当整理后绘制成如图所示的不完整的条形统计图，其中最喜欢D中套餐的学生占被抽取人数的20%，请你根据以上信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？（2）通过计算，补全条形统计图；（3）如果全校有2000名学生，请你估计全校学生中最喜欢B中套餐的学生有多少名？×=50026．（8分）（2012•哈尔滨）同庆中学为丰富学生的校园生活，准备从军跃体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元．（1）购买一个足球、一个篮球各需多少元？（2）根据同庆中学的实际情况，需从军跃体育用品商店一次性购买足球和篮球共96个，要求购买足球和篮球的总费用不超过5720元，这所中学最多可以购买多少个篮球？27．（10分）（2012•哈尔滨）如图，在平面直角坐标系中，点O为坐标原点，直线y=2x+4交x轴于点A，交y轴于点B，四边形ABCO是平行四边形，直线y=﹣x+m经过点C，交x轴于点D．（1）求m的值；（2）点P（0，t）是线段OB上的一个动点（点P不与0，B两点重合），过点P作x轴的平行线，分别交AB，OC，DC于点E，F，G，设线段EG的长为d，求d与t之间的函数关系式（直接写出自变量t的取值范围）；（3）在（2）的条件下，点H是线段OB上一点，连接BG交OC于点M，当以OG为直径的圆经过点M时，恰好使∠BFH=∠ABO，求此时t的值及点H的坐标．相似，根据相似三角形对应边成比例可得=，根据等边对等角的性质可得∠=，∴，BGP=∴∴=，=，BGP=∴OF==，BH===，=== BE=∴==，=∴=，=，28．（10分）（2012•哈尔滨）已知：在△ABC中，∠ACB=90°，点P是线段AC上一点，过点A作AB 的垂线，交BP的延长线于点M，MN⊥AC于点N，PQ⊥AB于点Q，AQ=MN．（1）如图1，求证：PC=AN；（2）如图2，点E是MN上一点，连接EP并延长交BC于点K，点D是AB上一点，连接DK，∠DKE=∠ABC，EF⊥PM于点H，交BC延长线于点F，若NP=2，PC=3，CK：CF=2：3，求DQ的长．AQ=MN=MAN==，∴，∴=∴=2NTC==2 PKC=AQ=MN=∴=，∴，∴=，即，∴==∴==，EG==，，∴=BD==AQ=MN=∴=，=∴=ABC=BP==3PBC==PBC=（（REF=EF==∴+（．。

2012年哈尔滨市道里区初中升学调研测试数学试卷(一)

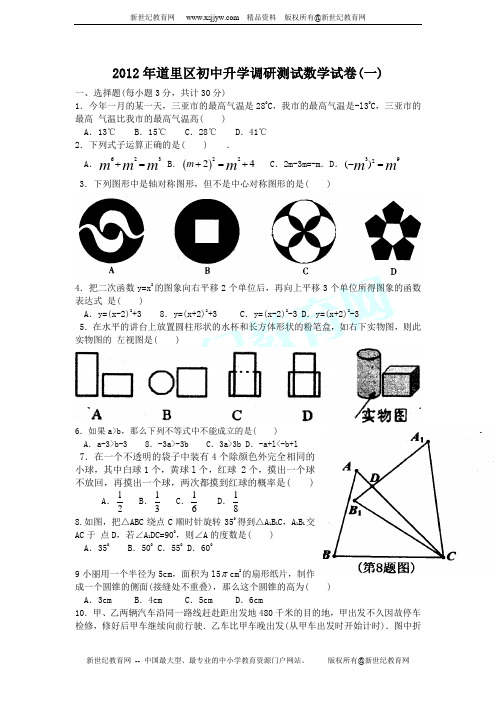
2012年道里区初中升学调研测试数学试卷(一)一、选择题(每小题3分，共计30分)1．今年一月的某一天，三亚市的最高气温是280C ，我市的最高气温是-l30C ，三亚市的最高气温比我市的最高气温高( )A ．13℃ B．15℃ C．28℃ D．41℃ 2．下列式子运算正确的是( ) ．A ．623m m m += B ．()2224m m +=+ C ．2m-3m=-m ．D ．392()m m -= 3．下列图形中是轴对称图形，但不是中心对称图形的是( )4．把二次函数y=x 2的图象向右平移2个单位后，再向上平移3个单位所得图象的函数表达式是( )A ．y=(x-2)2+3 8．y=(x+2)2+3 C ．y=(x-2)2-3 D ．y=(x+2)2-35．在水平的讲台上放置圆柱形状的水杯和长方体形状的粉笔盒，如右下实物图，则此实物图的左视图是( )6．如果a>b ，那么下列不等式中不能成立的是( )A ．a-3>b-3 8．-3a>-3b C ．3a>3b D ．-a+l<-b+l7．在一个不透明的袋子中装有4个除颜色外完全相同的小球，其中白球1个，黄球l 个，红球 2个，摸出一个球不放回，再摸出一个球，两次都摸到红球的概率是( )A ．12B ．13C ．16D ．188.如图，把△ABC 绕点C 顺时针旋转350得到△A 1B 1C ，A 1B 1交AC 于点D ，若∠A 1DC=900，则∠A 的度数是( )A ．350B ．500C ．550D ．6009小丽用一个半径为5cm ，面积为l5πcm 2的扇形纸片，制作成一个圆锥的侧面(接缝处不重叠)，那么这个圆锥的高为( ) A ．3cm B ．4cm C ．5cm D ．6cm10．甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，甲出发不久因故停车检修，修好后甲车继续向前行驶．乙车比甲车晚出发(从甲车出发时开始计时)．图中折线OABC 、线段DE 分别表示甲、乙两车所行路程y(千米)与时间x(小时)之间的函数关系对应的图象．根据图象中所提供的信息，有下列说法：①乙车比甲车晚2小时出发；②甲车修好后行驶了1．5小时与乙车在途中第二次相遇；③乙车行驶的平均速度为每小时48千米；④甲、乙两车到达目的地所用的时间相同．符合图象描述的说法有( ) A ．1个 B ．2个 C ．3个 D ．4个二、填空题(每小题3分，共计30分) 11．去年哈尔滨市地税收入约370亿元，将370亿元用科学记数法表示为元． 12．在函数y=22x x -+中，自变量x 的取值范围是 13．分解因式：a 3-9ab= ．14．若反比例函数y=5n x+的图象经过点(2，3)，则n 的值是． 15．某商场将一件商品在进价的基础上加价80％标价，再八折出售，售价为l44元，则这件商品的进价为元．16．如图，一艘渔船位于海洋观测站P 的北偏东600方向，渔船在A 处与海洋观测站P 的距离为80 海里，它沿正南方向航行一段时间后，到达位于海洋观测站P 的南偏东450方向上的B 处．则此时渔船所在的B 处与海洋观测站P 的距离为海里(结果保留根号)．．17．如图，直线y=kx+b 交坐标轴于A 、B 两点，A(-2，O)、B(0，3)，则不等式kx+b<0的解集是 18.观察下列图形：它们是按一定规律排列的，依照此规律，第8个图形中共有 ○ 个． 19．等腰△AB C 中，AB=AC ，BC=23，⊙0是△AB C 的外接圆，若⊙0的半径为2，则△ABC 的面积为20．如图，在AABC 中，∠ACB=900，∠ABC=300，AD 平分∠BAC 交BC 于点P ，∠BDC=600，若AB=43，则BD的长为．三、解答题(其中21～24题各6分，25-26题各8分，27-28题各l 0分。

数学考试后总结与反思

数学考试后总结与反思数学考试后总结与反思引导语：“考”与“试”是意义相近的两个概念，皆有考查、检测、考核等多重含义。

以下是店铺整理的数学考试后总结与反思，欢迎参考!数学考试后总结与反思1一、试卷分析：(一)命题：任课教师命题，年级统一考试。

(二)考试内容：北师版数学九年级上册第一至第四章。

(三)试题分析1、试卷在总体上体现了《新课程标准》的评价理念，重视了对学生学习数学知识与技能的结果和过程的评价，也关注了对学生在数学思考能力、计算能力和解决问题能力等方面发展状况的评价。

突出了数学思想方法的理解与应用;注重了数学与现实的练系;关注了对获取数学信息能力以及“用数学、做数学”的意识的考查;特别是重视几何推理书写及计算结果的准确为我们以后的教学起了较好的导向作用。

2、重视双基，突出重点知识考查试卷考查双基意图明显，所占分值较大。

试题对基础知识的考查既注意全面性，又突出重点。

在试卷中，对一元二次方程和平行四边行等主干知识进行了侧重考查。

3、重视与实际生活相联系，考查数学应用能力试题贴近学生的实际生活，体现了数学与生活的联系。

在考查中引导学生经历解决实际问题的过程，体验运用数学知识解决实际问题的情感，考查学生从实际问题中抽象数学模型的能力，培养用数学、做数学的意识。

4、重视数学思想方法的考查初中数学中常见的整体思想、分类讨论、探索开放等数学思想方法在试卷中得到充分体现。

5得分情况简析：从得分情况看，高分数段和较高分数段的学生约占三分之一，比较正常，中间状态的成绩所占比例太少，低分段的人所占比例太大。

从初一到现在，一直这样，令人担忧。

二、近期工作总结与反思及今后措施1、客观的认识一年一度的毕业会考与升学考试对我们学校的影响。

取得好的成绩是提高我校知名度和信誉度的主要途径，同时，也是检验我们教学效果的重要标尺。

2、帮助学生认识学习的重要性，在现在的年龄段就是学习，为以后的人生道路打好基础。

引导学生从自己的切身利益出发，正确给自己定位，树立近期目标和长远目标。

中国统一考试题库及答案

中国统一考试题库及答案一、单项选择题（每题2分，共20分）1. 中国统一考试中，以下哪项是考试的主要目的？A. 选拔优秀人才B. 测试学生的知识掌握程度C. 评估教学质量D. 促进教育公平答案：B2. 中国统一考试通常包括哪些科目？A. 语文、数学、英语B. 物理、化学、生物C. 政治、历史、地理D. 所有以上选项答案：D3. 在中国统一考试中，以下哪项不是考试的评分标准？A. 准确性B. 完整性C. 创新性D. 规范性答案：C4. 中国统一考试的组织机构是？A. 教育部B. 各省教育厅C. 各市教育委员会D. 各学校答案：A5. 中国统一考试的时间通常是在每年的？A. 3月B. 6月C. 9月D. 12月答案：B6. 在中国统一考试中，以下哪项是考试的基本原则？A. 公平、公正、公开B. 竞争、合作、发展C. 创新、实践、应用D. 以上都是答案：A7. 中国统一考试的成绩通常用于以下哪个目的？A. 选拔公务员B. 选拔研究生C. 高中毕业和大学入学D. 职业资格认证答案：C8. 在中国统一考试中，以下哪项是考试的准备阶段？A. 报名B. 考试C. 成绩公布D. 录取答案：A9. 中国统一考试的试卷通常由以下哪个机构负责命题？A. 教育部考试中心B. 各省教育厅命题组C. 各市教育委员会命题组D. 各学校命题组答案：A10. 中国统一考试的监考人员通常由以下哪个机构指派？A. 教育部B. 各省教育厅C. 各市教育委员会D. 各学校答案：C二、多项选择题（每题3分，共15分）11. 中国统一考试的考试形式包括以下哪些？A. 笔试B. 口试C. 实验操作D. 上机考试答案：A, B, C, D12. 中国统一考试的考试内容通常涵盖以下哪些方面？A. 基础知识B. 基本技能C. 综合应用D. 创新能力答案：A, B, C, D13. 在中国统一考试中，以下哪些因素可能影响考试的公平性？A. 考试环境B. 考试时间C. 考试难度D. 考试评分标准答案：A, B, C, D14. 中国统一考试的考试流程通常包括以下哪些步骤？A. 报名B. 考试C. 成绩公布D. 录取答案：A, B, C, D15. 中国统一考试的考试结果通常用于以下哪些方面？A. 学生自我评价B. 学校教学质量评估C. 学生升学和就业D. 教育政策制定答案：A, B, C, D三、判断题（每题1分，共10分）16. 中国统一考试是全国统一命题、统一考试时间、统一评分标准的考试。

2012年初中毕业与升学统一考试数学试卷(贵州贵阳市)(详细解析)

2012年初中毕业与升学统一考试数学试卷（贵州贵阳市）参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）（2012?贵阳）下列整数中，小于﹣3的整数是（）A．﹣4 B．﹣2 C．2D．3考点：有理数大小比较；绝对值。

专题：推理填空题。

分析：根据正数都大于负数，两个负数比较大小，其绝对值大的反而小，得出2和3都大于﹣3，求出|﹣3|=3，|﹣2|=2，|﹣4|=4，比较即可．解答：解：∵﹣4＜﹣3＜﹣2＜2＜3，∴整数﹣4、﹣2、2、3中，小于﹣3的整数是﹣4，故选A．点评：本题考查了绝对值和有理数的大小比较的应用，有理数的大小比较法则是：正数都大于0，正数大于一切负数，负数都小于0，两个负数比较大小，其绝对值大的反而小．2．（3分）（2012?贵阳）在5月份的助残活动中，盲聋哑学校收到社会捐款约110000元，将110000元用科学记数法表示为（）A．1.1×103元B．1.1×104元C．1.1×105元D．1.1×106元考点：科学记数法—表示较大的数。

分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：将110000用科学记数法表示为： 1.1×105．故选：C．点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．3．（3分）（2012?贵阳）下列四个几何体中，主视图、左视图与俯视图是全等图形的几何体是（）A．圆锥B．圆柱C．三棱柱D．球考点：简单几何体的三视图。

分析：根据几何体的三种视图，进行选择即可．解答：解：A、圆锥的主视图、左视图都是等腰三角形，俯视图是圆形，不符合题意，故此选项错误；B、圆柱的主视图、左视图可以都是矩形，俯视图是圆形，不符合题意，故此选项错误；C、三棱柱的主视图、左视图都是矩形，俯视图是三角形，不符合题意，故此选项错误；D、球的三视图都是圆形，故此选项正确．故选：D．点评：本题考查了几何体的三种视图，注意所有的看到的棱都应表现在三视图中．4．（3分）（2012?贵阳）如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（）A．∠BCA=∠F B．∠B=∠E C．B C∥EF D．∠A=∠EDF考点：全等三角形的判定。

中考真题电子版-数学哈尔滨-2012

哈尔滨市2012年初中升学考试数学12A(满分:120分时间:120分钟)第Ⅰ卷(选择题,共30分)一、选择题(每小题3分,共计30分)1.-2的绝对值是( )A.-12B.12 C.2 D.-22.下列运算中,正确的是( ) A.a 3·a 4=a 12 B.(a 3)4=a 12 C.a+a 4=a 5 D.(a+b)(a-b)=a 2+b 23.下列图形是中心对称图形的是( )4.如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )5.如图,在Rt △ABC 中,∠C=90°,AC=4,AB=5,则sin B 的值是( )A.23B.35C.34D.456.在10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,抽到不合格产品的概率是( ) A.110B.15C.25D.457.如果反比例函数y=k -1x 的图象经过点(-1,-2),则k 的值是( )A.2B.-2C.-3D.38.将抛物线y=3x 2向左平移2个单位,再向下平移1个单位,所得抛物线为( )A.y=3(x+2)2-1 B .y=3(x-2)2+1 C.y=3(x-2)2-1 D.y=3(x+2)2+19.如图,☉O 是△ABC 的外接圆,∠B=60°,OP ⊥AC 于点P,OP=2√3,则☉O 的半径为( )A.4√3B.6√3C.8D.1210.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD.设BC 边的长为x 米,AB 边的长为y 米,则y 与x 之间的函数关系式是( )A.y=-2x+24(0<x<12)B.y=-12x+12(0<x<24)C.y=2x-24(0<x<12)D.y=12x-12(0<x<24)第Ⅱ卷(非选择题,共90分)二、填空题(每小题3分,共计30分)11.把16 000 000用科学记数法表示为 . 12.在函数y=1x -5中,自变量x 的取值范围是 .13.化简:√9= .14.把多项式a 3-2a 2+a 分解因式的结果是 . 15.不等式组{2x -1>0,x -1<1的解集是 .16.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是 . 17.一个圆锥的母线长为4,侧面积为8π,则这个圆锥的底面圆的半径是 . 18.方程1x -1=32x+3的解是 .19.如图,平行四边形ABCD 绕点A 逆时针旋转30°,得到平行四边形AB'C'D'(点B'与点B 是对应点,点C'与点C 是对应点,点D'与点D 是对应点),点B'恰好落在BC 边上,则∠C= 度.20.如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连结DE 交AB 于点F,∠AED=2∠CED,点G 是DF 的中点,若BE=1,AG=4,则AB 的长为 .三、解答题(其中21~24题各6分,25~26题各8分,27~28题各10分,共计60分)21.(本题6分)先化简,再求代数式(1x +x+1x)÷x+2x2+x的值,其中x=√3cos30°+12.22.(本题6分)图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A 和点B在小正方形的顶点上.(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).23.(本题6分)如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.12B24.(本题6分)小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);(2)当x是多少时,这个三角形面积S最大?最大面积是多少?(参考公式:当x=-b2a时,二次函数y=ax2+bx+c(a≠0)有最小(大)值4ac-b24a)25.(本题8分)虹承中学为做好学生“午餐工程”工作,学校工作人员搭配了A,B,C,D四种不同种类的套餐,学校决定围绕“在A,B,C,D四种套餐中,你最喜欢的套餐种类是什么?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢D种套餐的学生占被抽取人数的20%,请你根据以上信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)通过计算,补全条形统计图;(3)如果全校有2000名学生,请你估计全校学生中最喜欢B种套餐的学生有多少名?26.(本题8分)同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.(1)购买一个足球、一个篮球各需多少元?(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?27.(本题10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交x轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.(1)求m的值;(2)点P(0,t)是线段OB上的一个动点(点P不与O,B两点重合),过点P作x轴的平行线,分别交AB,OC,DC于点E,F,G.设线段EG的长为d,求d与t之间的函数关系式(直接写出自变量t的取值范围);(3)在(2)的条件下,点H是线段OB上一点,连结BG交OC于点M,当以OG为直径的圆经过点M时,恰好使∠BFH=∠ABO,求此时t的值及点H的坐标.28.(本题10分)已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.(1)如图1,求证:PC=AN;(2)如图2,点E是MN上一点,连结EP并延长交BC于点K,点D是AB上一点,连结DK,∠DKE=∠ABC,EF⊥PM于点H,交BC延长线于点F,若NP=2,PC=3,CK∶CF=2∶3,求DQ 的长.哈尔滨市2012年初中升学考试一、选择题1.C因为-2的绝对值是2,所以选C.评析本题意在考查绝对值的概念,正确地理解并运用绝对值的概念是求解的关键.正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.2.B对于选项A:a3·a4=a3+4=a7,即选项A是错误的;对于选项B:(a3)4=a12,即选项B正确;对于选项C:由于a与a4不是同类项,所以不能合并,即选项C是错误的;对于选项D:(a+b)(a-b)=a2-b2,即选项D错误.故应选B.评析本题考查了整式的运算,关键是要能正确理解并灵活运用整式运算的有关法则.注意同底数幂的乘法法则是底数不变,指数相加,而不是相乘;幂的乘方法则是底数不变,指数相乘;合并同类项要遵循两个不变,即字母不变,相同字母的指数也不变;注意平方差公式的结构形式.3.A选项A旋转180°后可以与自身重合,所以A图案是中心对称图形,故应选A.评析本题意在考查中心对称图形的概念,正确地分析图案的特征,利用中心对称图形的概念判定是求解的关键.判断方法:如果这个图形绕某一点旋转180°后能与自身重合,则这个图形是中心对称图形.4.C这个几何体的左视图由三个小正方体搭成,故左视图是C选项.评析本题考查的是几何体的视图,关键是要分清上、下、左、右各个方位.主视图是指从立体图形的正面看到的平面图,左视图指从立体图形的左面看到的平面图,俯视图指从立体图形的上面看到的平面图.5.D Rt△ABC中,因为∠C=90°,AC=4,AB=5,所以由正弦的定义,得sin B=ACAB =45,故应选D.评析本题考查锐角三角函数的求法,关键是要正确理解锐角三角函数的概念.根据锐角三角函数的定义可求某个锐角的三角函数值:正弦:在直角三角形中,锐角α的对边与斜边之比叫做∠α的正弦,记作sinα,即sinα=∠α的对边斜边.余弦:在直角三角形中,锐角α的邻边与斜边之比叫做∠α的余弦,记作cosα,即cosα=∠α的邻边斜边.正切:在直角三角形中,锐角α的对边与邻边之比叫做∠α的正切,记作tanα,即tanα=∠α的对边∠α的邻边.6.B因为10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,所以抽到不合格产品的概率是210=15,故应选B.评析本题考查概率的概念,关键是要弄清楚出现可能结果的意义.古典概型E,设它的所有可能结果是n个等可能的情形,事件A包含其中的m个情形,则定义事件A的概率为:P(A)=mn.7.D因为反比例函数y=k-1x 的图象经过点(-1,-2),所以-2=k-1-1,得k=3,故应选D.评析本题考查反比例函数的知识,关键是能正确理解点与图象的关系.即已知点在反比例函数的图象上,那么这点的坐标一定满足该反比例函数的解析式,反之也成立.8.A因为抛物线y=3x2的顶点坐标为(0,0),所以向左平移2个单位,再向下平移1个单位的顶点坐标为(-2,-1),即所得抛物线为y=3(x+2)2-1,故应选A.评析本题考查了二次函数的图象的特征,关键是要正确理解平移的意义和二次函数顶点坐标的知识.二次函数图象的平移规律:左加右减,上加下减.9.A因为∠B=60°,所以∠AOC=120°,又因为OP⊥AC,所以∠AOP=∠COP=60°,所以∠OAP=30°,又因为OP=2√3,所以OA=4√3,即☉O的半径为4√3,故应选A.评析本题考查三角形的外接圆、圆周角、圆心角、弦心距、含有30°角的直角三角形的性质等知识,关键要能利用圆周角与圆心角的关系求出∠AOP的大小.从条件出发,将问题转化到含有30°角的直角三角形中求得☉O的半径.x+12,而菜园的一边利用足够长的墙,所以0<x<24,故应10.B根据题意,得x+2y=24,所以y=-12选B.评析本题考查的是矩形的长与宽之间的函数关系,关键是要掌握矩形的对边相等的性质.注意矩形的周长等于(长+宽)×2.二、填空题11.答案 1.6×107解析16000000=1.6×107.评析本题考查的是科学记数法的知识,关键是确定a和n.科学记数法的形式是a×10n,其中1≤|a|<10,指数n是整数位数减1.12.答案x≠5解析依题意,得x-5≠0,得x≠5,即自变量x的取值范围是x≠5.评析本题考查了函数自变量的取值范围,知道分式的分母不能为0是求解的关键.13.答案3解析因为32=9,所以9的算术平方根是3,即√9=3.评析本题考查二次根式的化简,关键是要能正确理解一个正数的算术平方根的意义.知道1~20的平方,可以顺利地求解此类问题.14.答案a(a-1)2解析a3-2a2+a=a(a2-2a+1)=a(a-1)2.评析本题考查因式分解的知识,掌握因式分解的一般方法是解决问题的关键.分解因式关键是选择合适的方法.分解因式的步骤是一提(提公因式)、二套(套公式)、三验(检验是否分解彻底).套公式时可根据需分解多项式的项数进行选择:如果是两项,一般是平方差公式;三项,一般是完全平方公式.15.答案12<x<2解析解不等式2x-1>0,得x>12,解不等式x-1<1,得x<2,所以不等式组{2x-1>0,x-1<1的解集是12<x<2.评析本题考查解不等式组,关键是先求出每个不等式的解集,最后确定不等式组的解集.不等式组解集的确定法则:同大取大、同小取小、大小小大取中间、大大小小是无解.16.答案16或17解析当5是等腰三角形的腰长时,那么6就是底边长,所以这个等腰三角形的周长是5+5+6=16;当6是等腰三角形的腰长时,那么5就是底边长,所以这个等腰三角形的周长是6+6+5=17.所以这个等腰三角形的周长是16或17.评析本题考查等腰三角形和三角形的三边关系,考虑到哪是底边,哪是腰是正确求解的关键.另外,遇到等腰三角形的边角问题时,一定要注意分情况讨论求解,才能避免错误.17.答案2解析设圆锥底面的半径为r,由S=12lr,得l=2×8π÷4=4π,而扇形的弧长等于圆锥的底面周长,所以2πr=4π,解得r=2.即这个圆锥的底面圆的半径是2.评析本题意在考查圆锥的侧面展开图的有关计算,关键要能正确理解母线、侧面积等. 18.答案x=6解析去分母,得2x+3=3(x-1),解得x=6,经检验,x=6是原方程的解.评析本题考查分式方程的解法,关键是要能通过去分母,将分式方程转化为整式方程,注意不要忘记验根.19.答案105解析因为旋转30°,所以∠BAB'=30°,又因为点B'在BC上,AB=AB',所以∠B=75°,因为四边形ABCD是平行四边形,所以AB∥CD,所以∠B+∠C=180°,所以∠C=105°.评析本题考查的是图形的旋转、等腰三角形和平行四边形的性质及平行四边形的有关计算,关键是要能正确理解旋转的特征和平行四边形的性质.旋转前后图形的形状、大小都不发生改变,而平行四边形的对边平行,邻角互补.20.答案 √15解析因为四边形ABCD 是矩形,所以∠ABE=∠BAD=90°,AD ∥BE,又因为点G 是DF 的中点,所以在Rt △DAF 中,AG=DG=FG,所以∠ADG=∠GAD=∠DEC,所以∠AGF=2∠ADG=2∠DEC,因为∠AED=2∠CED,所以∠AED=∠AGE,所以AE=AG,由AG=4,知AE=4,在Rt △ABE 中,因为BE=1,所以由勾股定理,得AB=√AE 2-BE 2=√42-12=√15. 评析本题意在考查矩形的性质、直角三角形斜边上中线的性质以及勾股定理.关键是要能将已知条件转化到直角三角形中来处理.将已知条件结合图形转化到直角三角形中来,以便于运用勾股定理求解. 三、解答题 21.解析原式=x+2x·x 2+x x+2=x+2x·x(x+1)x+2=x+1,(2分)∵x=√3cos 30°+12=√3×√32+12=32+12=2,(4分)∴原式=2+1=3.(6分)评析本题考查的是分式的化简与求值和特殊角的三角函数值,求解的关键是要能先对已知分式化简,并求出x 的具体值,最后再代入计算.注意运算顺序,先算括号里的,后算括号外的,除法运算转化为乘法运算,同时将异分母转化为同分母,当然也可以把除法转化为乘法后用乘法分配律进行计算,注意灵活运用分式的基本性质、因式分解、除法运算法则等进行变化. 22.解析 (1)正确画图(参考图1~图4,画出一个即可).(3分) (2)正确画图(参考图5~图8,画出一个即可).(6分)评析本题考查的是直角三角形、等腰三角形,关键是要在格点上寻求符合要求的点,这是一道开放型试题.23.证明 ∵∠ABC+∠CBE=180°, ∠ABD+∠DBE=180°,∠CBE=∠DBE, ∴∠ABC=∠ABD.(2分) 在△ABC 和△ABD 中,{∠CAE =∠DAE,AB =AB,∠ABC =∠ABD,∴△ABC ≌△ABD.(5分) ∴AC=AD.(6分)评析本题考查的是全等三角形的判定和性质.关键是要能正确地寻求满足三角形全等的条件.一般三角形全等的判定方法有:SAS,ASA,AAS,SSS;直角三角形除了用一般方法判定外还可以用HL.24.解析 (1)S=-12x 2+20x.(2分) (2)解法一:∵a=-12<0,∴S 有最大值, ∴当x=-b2a =-202×(-12)=20时,(4分)S 有最大值,为4ac -b 24a =4×(-12)×0-2024×(-12)=200.∴当x 为20 cm 时,三角形面积最大,最大面积是200 cm 2.(6分) 解法二:∵a=-12<0,∴S 有最大值, ∴当x=-b2a =-202×(-12)=20时,(4分)S 有最大值,为S=-12×202+20×20=200.∴当x 为20 cm 时,三角形面积最大,最大面积是200 cm 2.(6分)评析本题考查了利用二次函数解决生活中的问题,关键是要能依据题意,正确地寻找等量关系.25.解析 (1)40÷20%=200(名).∴在这次调查中,一共抽取了200名学生.(2分) (2)200-90-50-40=20(名).(4分) 正确画图.(5分)(3)解法一:2 000×50200=500(名).(7分) ∴估计全校最喜欢B 种套餐的学生有500名.(8分) 解法二:50200×100%=25%,(6分)2 000×25%=500(名).(7分)∴估计全校最喜欢B 种套餐的学生有500名.(8分)评析本题考查了统计的知识,关键是要能读懂题目,准确地从统计图中捕捉信息. 26.解析 (1)设购买一个足球需要x 元,购买一个篮球需要y 元.根据题意得 {3x +2y =310,2x +5y =500,(2分)解得{x =50,y =80.∴购买一个足球需要50元,购买一个篮球需要80元.(4分) (2)解法一:设购买a 个篮球,则购买(96-a)个足球. 80a+50(96-a)≤5 720,(6分) a ≤3023,(7分)∵a 为整数,∴a 最多是30.∴这所中学最多可以购买30个篮球.(8分) 解法二:设购买n 个足球,则购买(96-n)个篮球, 50n+80(96-n)≤5 720,(6分) n ≥6513.(7分)∵n 为整数,∴n 最少是66,96-66=30,∴这所中学最多可以购买30个篮球.(8分)评析本题考查的是用方程组和不等式解决问题.关键是要能寻求到等量关系和不等量关系.属中档题.27.解析 (1)解法一:如图,∵y=2x+4交x 轴和y 轴于A,B, ∴A(-2,0),B(0,4),∴OA=2,OB=4,∵四边形ABCO 是平行四边形, ∴BC=OA=2,过点C 作CK ⊥x 轴于K, 则四边形BOKC 是矩形,∴OK=BC=2,CK=OB=4, ∴C(2,4),(1分)代入y=-x+m 得4=-2+m, ∴m=6.(2分) 解法二:如图,∵y=2x+4交x 轴和y 轴于A,B, ∴A(-2,0),B(0,4),∴OA=2,OB=4, 延长DC 交y 轴于点N,∵y=-x+m 交x 轴和y 轴于D,N, ∴D(m,0),N(0,m),∴OD=ON, ∴∠ODN=∠OND=45°.∵四边形ABCO 是平行四边形, ∴BC ∥AO,BC=OA=2,∴∠NCB=∠ODN=∠OND=45°, ∴NB=BC=2.(1分) ∴ON=NB+OB=2+4=6, ∴m=6.(2分)(2)解法一:如图,延长DC 交y 轴于N,分别过点E,G 作x 轴的垂线,垂足分别是R,Q,则四边形ERQG、四边形POQG、四边形EROP是矩形,∴ER=PO=GQ=t,∵tan∠BAO=ERAR =OBOA,∴tAR=42,∴AR=12t.(3分)∵y=-x+6交x轴和y轴于D,N,∴OD=ON=6,∴∠ODN=45°,∵tan∠ODN=GQQD,∴DQ=t.(4分)又∵AD=AO+OD=2+6=8,∴EG=RQ=8-12t-t=8-32t,∴d=-32t+8(0<t<4).(6分)解法二:如图,∵EG∥AD,P(0,t),∴设E(x1,t),G(x2,t),把E(x1,t)代入y=2x+4得t=2x1+4,∴x1=t2-2,(3分)把G(x2,t)代入y=-x+6得t=-x2+6,∴x2=6-t,(4分)∴d=EG=x2-x1=(6-t)-(t2-2),∴d=-32t+8(0<t<4).(6分)(3)解法一:如图,∵四边形ABCO是平行四边形,∴AB∥OC,∴∠ABO=∠BOC,∵BP=4-t,∴tan∠ABO=EPBP =tan∠BOC=12,∴EP=2-t2,∴PG=d-EP=6-t.(7分)∵以OG 为直径的圆经过点M, ∴∠OMG=90°.(8分) ∵∠OPG=90°,∠MFG=∠PFO, ∴∠BGP=∠BOC,∴tan ∠BGP=BPPG =tan ∠BOC=12, ∴4-t 6-t =12,解得t=2.(9分)∵∠BFH=∠ABO=∠BOC,∠OBF=∠FBH, ∴△BHF ∽△BFO,∴BH BF =BFBO ,即BF 2=BH ·BO,∵OP=2,∴PF=1,BP=2,∴BF=√BP 2+PF 2=√5,∴5=BH×4, ∴BH=54,∴HO=4-54=114, ∴H (0,114).(10分) 解法二:如图,∵四边形ABCO 是平行四边形,∴AB ∥OC, ∴∠ABO=∠BOC.∵BP=4-t,∴tan ∠ABO=EPBP =tan ∠BOC=12, ∴EP=2-t2,∴PG=d-EP=6-t.(7分)∵以OG 为直径的圆经过点M, ∴∠OMG=90°.(8分) ∵∠OPG=90°,∠MFG=∠PFO, ∴∠BGP=∠BOC,∴tan ∠BGP=BPPG =tan ∠BOC=12, ∴4-t 6-t =12,解得t=2.(9分)∴OP=2,BP=4-t=2,∴PF=1, ∴OF=√12+22=√5=BF,∴∠OBF=∠BOC=∠BFH=∠ABO,∴BH=HF, 过点H 作HT ⊥BF 于点T, 则BT=12BF=√52,∴BH=BTcos ∠OBF =√522√5=54, ∴OH=4-54=114,∴H (0,114).(10分)解法三:如图,∵OA=2,OB=4,∴由勾股定理得AB=2√5. ∵P(0,t),∴BP=4-t,∵cos ∠ABO=BP BE =4-t BE =OBAB =2√5,∴BE=√52(4-t),(7分)∵以OG 为直径的圆经过点M,∴∠OMG=90°,(8分) ∵四边形ABCO 是平行四边形,∴AB ∥OC, ∴∠ABG=∠OMG=90°=∠BPG, ∴∠ABO+∠BEG=90°,∠BGE+∠BEG=90°, ∴∠ABO=∠BGE,∴sin ∠ABO=sin ∠BGE, ∴OA AB =BE EG =BEd,即=√52(4-t)8-3t2,∴t=2.(9分)∵∠BFH=∠ABO=∠BOC,∠OBF=∠FBH, ∴△BHF ∽△BFO,∴BH BF =BFBO ,即BF 2=BH ·BO,∵OP=2,∴PF=1,BP=2, ∴BF=√BP 2+PF 2=√5,∴5=BH×4,∴BH=54, ∴HO=4-54=114,∴H (0,114).(10分)评析本题考查了一次函数、平行四边形、矩形、相似三角形、圆以及锐角三角函数等知识,关键是要能正确地理解题意,通过适当的辅助线将问题转化.注意充分发挥方程思想、转化思想、数形结合思想.属中等偏难题. 28.解析 (1)证明:证法一:如图.∵BA ⊥AM,MN ⊥AP,∴∠BAM=∠ANM=90°, ∴∠PAQ+∠MAN=∠MAN+∠AMN=90°, ∴∠PAQ=∠AMN.(1分)∵PQ ⊥AB,MN ⊥AC,∴∠PQA=∠ANM=90°, ∵AQ=MN,∴△AQP ≌△MNA,(2分) ∴AN=PQ,AM=AP,∴∠AMB=∠APM. ∵∠APM=∠BPC,∠BPC+∠PBC=90°,∠AMB+∠ABM=90°, ∴∠ABM=∠PBC.(3分)∵PQ⊥AB,PC⊥BC,∴PQ=PC,(4分)∴PC=AN.(5分)证法二:如图.∵BA⊥AM,MN⊥AC,∴∠BAM=∠ANM=90°,∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,∴∠PAQ=∠AMN.(1分)∵PQ⊥AB,∴∠AQP=90°=∠ANM.∵AQ=MN,∴△PQA≌△ANM.(2分)∴AP=AM,PQ=AN,∴∠APM=∠AMP.∵∠AQP+∠BAM=180°,∴PQ∥MA,∴∠QPB=∠AMP.(3分)∵∠APM=∠BPC,∴∠QPB=∠BPC.∵∠BQP=∠BCP=90°,BP=BP,∴△BPQ≌△BPC,(4分)∴PQ=PC,∴PC=AN.(5分)(2)解法一:如图.∵NP=2,PC=3,∴由(1)知PC=AN=3,∴AP=NC=5,AC=8,∴AM=AP=5,∴AQ=MN=√AM2-AN2=4.(6分)∵∠PAQ=∠AMN,∠ACB=∠ANM=90°,∴∠ABC=∠MAN,∴tan∠ABC=tan∠MAN=MNAN =4 3 .∵tan∠ABC=ACBC,∴BC=6.(7分)∵NE∥KC,∴∠PEN=∠PKC,又∵∠ENP=∠KCP,∴△PNE∽△PCK,∴NECK =NPPC,∵CK∶CF=2∶3,设CK=2k,则CF=3k,∴NE2k =23,NE=43k,过N作NT∥EF交CF于T,则四边形NTFE是平行四边形,∴NE=TF=43k,∴CT=CF-TF=3k-43k=53k.∵EF⊥PM,∴∠BFH+∠HBF=90°=∠BPC+∠HBF,∴∠BPC=∠BFH.∵EF∥NT,∴∠NTC=∠BFH=∠BPC.∵tan∠NTC=tan∠BPC=BCPC =2,∴tan∠NTC=NCCT=2,∴CT=53k=52,∴k=32.(8分)∴CK=2×32=3,BK=BC-CK=3.∵∠PKC+∠DKE=∠ABC+∠BDK,∠DKE=∠ABC, ∴∠BDK=∠PKC,tan ∠PKC=PCKC =1,∴tan ∠BDK=1,过K 作KG ⊥BD 于G.∵tan ∠BDK=1,tan ∠ABC=43, ∴设GK=4n,则BG=3n,GD=4n,∴BK=5n=3,∴n=35,∴BD=4n+3n=7n=215.(9分) ∵AB=√AC 2+BC 2=10,AQ=4,∴BQ=AB-AQ=6, ∴DQ=BQ-BD=6-215=95.(10分)解法二:如图.∵NP=2,PC=3,∴由(1)知AN=PC=3, ∴AP=NC=5,AC=8,∴AM=AP=5, ∴AQ=MN=√AM 2-AN 2=4.(6分) ∵NM ∥BC,∴∠NMP=∠PBC.又∵∠MNP=∠BCP,∴△MNP ∽△BCP, ∴MN BC =NPPC ,∴4BC =23,∴BC=6.(7分)作ER ⊥CF 于R,则四边形NERC 是矩形, ∴ER=NC=5,NE=CR, ∵∠BHF=∠BCP=90°, ∴∠EFR=90°-∠HBF,∠BPC=90°-∠HBF, ∴∠EFR=∠BPC,∴tan ∠EFR=tan ∠BPC, ∴ER RF =BCPC ,即5RF =63,∴RF=52,∵NE ∥KC,∴∠NEP=∠PKC.又∵∠ENP=∠KCP,∴△NEP ∽△CKP,∴NE KC =NP PC =23, ∵CK ∶CF=2∶3,设CK=2k,CF=3k, ∴NE=CR=43k,CR=CF-RF=3k-52,∴3k-52=43k,∴k=32,(8分)∴CK=3,CR=2,∴BK=3.在CF 的延长线上取点G,使∠EGR=∠ABC, ∴tan ∠EGR=tan ∠ABC,∴ER RG =AC BC =43,∴RG=34ER=154,EG=√ER2+RG2=254,KG=KC+CR+RG=354,∵∠DKE+∠EKC=∠ABC+∠BDK,∠ABC=∠DKE,∴∠BDK=∠EKC,∴△BDK∽△GKE,∴BDKG =BK EG,∴BD·EG=BK·KG,∴BD×254=3×354,∴BD=215.(9分)∵AB=√AC2+BC2=10,AQ=4,∴BQ=AB-AQ=6,∴DQ=BQ-BD=6-215=95.(10分)解法三:如图.∵NP=2,PC=3,∴由(1)知AN=PC=3,∴AP=NC=5,AC=8,∴AM=AP=5,∴AQ=MN=√AM2-AN2=4.(6分)∵NM∥BC,∴∠EMH=∠PBC,∠PEN=∠PKC.又∵∠PNE=∠PCK,∴△PNE∽△PCK,△PNM∽△PCB,∴NECK =PNPC,MNBC=PNPC,∵CK∶CF=2∶3,设CK=2k,则CF=3k,∴NE2k =23,4BC=23,∴NE=43k,BC=6.(7分)∴BF=6+3k,ME=MN-NE=4-43k,tan∠ABC=ACBC =43,BP=√PC2+BC2=3√5,∴sin∠EMH=sin∠PBC=PCBP =√55,∵EF⊥PM,∴FH=BFsin∠PBC=√55(6+3k),EH=EMsin∠EMH=√55(4-43k).过E作ER⊥BF于R,则四边形NCRE是矩形,∴ER=NC=5.∵∠RFE+∠REF=∠RFE+∠PBC=90°,∴∠REF=∠PBC.∴tan∠REF=tan∠PBC=12,∵tan∠REF=RFRE,∴RF=52,∴EF=√ER2+RF2=5√52,∵EH+FH=EF,∴√55(4-43k)+√55(6+3k)=5√52,∴k=32,(8分)∴CK=2×32=3,BK=BC-CK=3.∵∠PKC+∠DKE=∠ABC+∠BDK,∠DKE=∠ABC,∴∠BDK=∠PKC.∵tan∠PKC=1,∴tan∠BDK=1,过K作KG⊥BD于G.∵tan∠BDK=1,tan∠ABC=43,∴设GK=4n,则BG=3n,GD=4n,∴BK=5n=3,∴n=35,∴BD=4n+3n=7n=215.(9分)∵AB=√AC2+BC2=10,AQ=4,∴BQ=AB-AQ=6,∴DQ=BQ-BD=6-215=95.(10分)评析本题综合考查了直角三角形、全等三角形、相似三角形、锐角三角函数、特殊四边形、勾股定理等知识.属难题.关键是要能充分利用图形的性质,添加适当的辅助线,将问题转化.另外,本题强化了全等三角形和相似三角形以及锐角三角形的功能地位,充分使用了几何知识来解决问题.。

2011年初中毕业升学考试(中考)数学试卷及答案

数学试卷第1页（共10页）准考证号：**市2011年初中毕业生学业考试数学试卷【说明】全卷分为第Ⅰ卷和第Ⅱ卷，第Ⅰ卷1－2页，第Ⅱ卷3－10页。

考试时间120分钟，满分150分。

考试结束后，第Ⅱ卷和答题卡按规定装袋上交。

第Ⅰ卷(选择题共40分)注意事项：1．答第Ⅰ卷前，考生务必将自己的学校、姓名、准考证号、考试科目填涂在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上。

3．考试结束后，本试卷由考场统一收回，集中管理。

一、选择题：本大题共10个小题，每小题4分，共40分，在每个小题给出的四个选项中，只有一个符合题目要求 1．－2的相反数A ．－2B ．2C ．2±D ．－2 2．下列分式是最简分式的Ａ．b a a 232 B ．a a a 32- C ．22b a b a ++ D ．222ba ab a -- 3．下列运算错误的是A ．235a a a ⋅=B ．347()m m =C ．3363282c b a bc a =）（ D ．624m m m ÷= 4．一幅扑克牌（不含大小王），任意抽取一张，抽中方块的概率是 A ．21 B ．521 C ．31 D ．415．函数31--=x x y 的自变量x 的取值范围是 A ．1x > B ．1x >且3x ≠ C ．1≥x D. 1≥x 且3x ≠数学试卷第2页（共10页）6．点（－2，3）关于原点对称的点的坐标是A ．(2,3)B ．(－2,－3)C ．(2,－3)D ．(－3,2) 7．如图：等腰梯形ABCD 中，AD ∥BC ，AB=DC ， AD=3，AB=4,∠B=60︒，则梯形的面积是 A.310 B.320 C.346+ D.3812+ 8．计算2sin30︒-sin 245︒+cot60︒的结果A.3321+ B.3321+ C.23+ D.23-1+ 9．如图：△ABC 中，DE ∥BC ，AD:DB=1:2,下列选项正确的是A ．DE:BC=1:2B ．AE:AC=1:3C ．BD:AB=1:3D ．S DE A ∆:S ABC ∆=1:4（第9题）（第10题）10．如图：在△ABC 中，∠ACB=90°,CD ⊥AB 于点D ，下列说法中正确的个数是①CD AB BC AC ⋅=⋅ ②DB AD AC ⋅=2③BA BD BC ⋅=2 ④DB AD CD ⋅=2A ．1个B ．2个C ．3个D ．4个CBEDABDAC数学试卷第3页（共10页）绝密★启用前【考试时间：2011年6月】**市2011年初中毕业生学业考试数学试卷第Ⅱ卷（非选择题共110分）注意事项：1．第Ⅱ卷共8页，用钢笔或中性笔直接答在试卷上。

2006-2012【哈尔滨中考数学试题及答案】

哈尔滨市 2006-2012 年初中升学考试数学试题
A．4
B． 10
C． 2 6
D． 4 3
10．在平面直角坐标系内，直线 y = 3 x + 3 与两坐标轴交于 A、B 两点，点 O 为坐标原点， 4
若在该坐标平面内有以点 P（不与点 A、B、O 重合）为顶点的直角三角形与 Rt△ABO 全等，且这个以点 P 为顶点的直角三角形与 Rt△ABO 有一条公共边，则所有符合条件的 P 点个数为（）
已知：二次函数 y = ax 2 + bx + c 的图象与 x 轴交于 A、B 两点，其中点 A 的坐标是（－ 1，0），与 y 轴负半轴交于点 C，其对称轴是直线 x = 3 ， tan ∠BAC = 2 。
2 （1）求二次函数 y = ax 2 + bx + c 的解析式；
（2）作圆 O’，使它经过点 A、B、C，点 E 是 AC 延长线上一点，∠BCE 的平分线 CD 交圆 O’于点 D，连结 AD、BD，求△ACD 的面积；
6．下列图形中，既是轴对称图形，又是中心对称图形的是（）
A．等边三角形 B．矩形
C．正五边形
7．下列命题中，正确命题的个数是（）
D．等腰梯形
①垂直于弦的直径平分这条弦
②平行四边形对角互补
③有理数与数轴上的点是一一对应的 ④相交两圆的公共弦垂直平分两圆的连心线
A．0 个
B．1 个
C．2 个
D．3 个
（3）若在甲育苗基地以相应的优惠方式购买一批该种树苗，又在乙育苗基地以相应的优惠方式购买另一批该种树苗，两批树苗共 2500 株，购买这 2500 株树苗所花的费用至少需要多少元？这时应在甲、乙两处分别购买该种树苗多少株？

盐城市二○一二年初中毕业与升学统一考试数学试卷

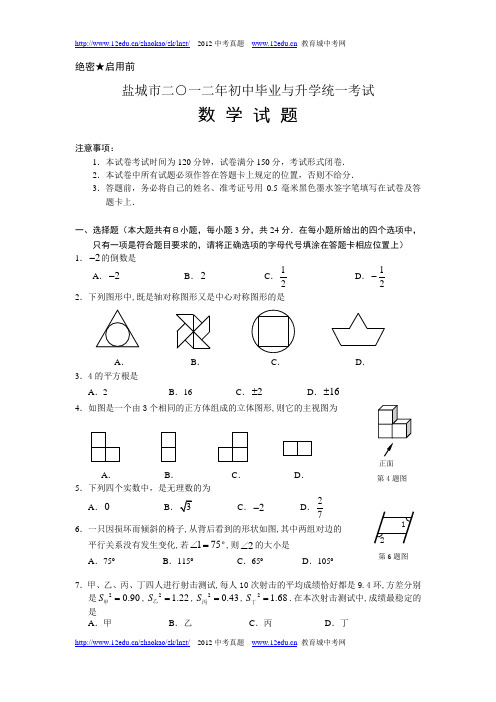
绝密★启用前盐城市二○一二年初中毕业与升学统一考试数学试题注意事项：1．本试卷考试时间为120分钟，试卷满分150分，考试形式闭卷． 2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．3．答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上．一、选择题（本大题共有８小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 1．2-的倒数是A ．2-B ．2C ．12D ．12-2．下列图形中,既是轴对称图形又是中心对称图形的是A ．B ．C ．D ． 3．4的平方根是A ．2B ．16C ．2±D ．16± 4．如图是一个由3个相同的正方体组成的立体图形,则它的主视图为A ．B ．C ．D ． 5．下列四个实数中，是无理数的为A ．0 BC ．2-D ．276．一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若175∠=º,则2∠的大小是A ．75ºB ．115ºC ．65ºD ．105º7．甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,方差分别是20.90S =甲,2 1.22S =乙,20.43S =丙,21.68S =丁.在本次射击测试中,成绩最稳定的是A ．甲B ．乙C ．丙D ．丁第6题图12第4题图正面8．已知整数1234,,,,a a a a ⋅⋅⋅满足下列条件：10a =,21|1|a a =-+,32|2|a a =-+, 43|3|a a =-+,…,依次类推,则2012a 的值为A ．1005-B ．1006-C ．1007-D ．2012-二、填空题（本大题共有10小题，每小题3分，共30分．不需写出解答过程，请将答案直接写在答题卡相应位置上） 9,则x 的取值范围是 ▲ . 10．分解因式:224a b -＝ ▲ .11．中国共产党第十八次全国代表大会将于2012年10月15日至18日在北京召开.据统计,截至2011年底,全国的共产党员人数已超过80 300 000,这个数据用科学计数法可表示为 ▲ .12．若1x =-,则代数式324x x -+的值为 ▲ .13．小勇第一次抛一枚质地均匀的硬币时正面向上,他第二次再抛这枚硬币时,正面向上的概率是 ▲ .14．若反比例函数的图象经过点(1,4)P -,则它的函数关系式是 ▲ .15．如图,在四边形ABCD 中,已知AB ∥DC ,AB DC =.在不添加任何辅助线的前提下,要想该四边形成为矩形,只需再加上的一个．．条件是 ▲ .(填上你认为正确的一个答案即可)16．如图,在ABC ∆中,D 、E 分别是边AB 、AC 的中点,50B ∠=º.现将ADE ∆沿DE折叠,点A 落在三角形所在平面内的点为1A ,则1BDA ∠的度数为 ▲ °. 17．已知1O 与2O 的半径分别是方程2430x x -+=的两根,且122O O t =+,若这两个圆相切．．,则t ＝ ▲ . 18．一批志愿者组成了一个“爱心团队”,专门到全国各地巡回演出,以募集爱心基金.第一个月他们就募集到资金1万元,随着影响的扩大,第n (n ≥2)个月他们募集到的资金都将会比上个月增加20%,则当该月所募集到的资金首次突破10万元时,相应的n 的值为 ▲ .(参考数据:51.22.5≈,61.2 3.0≈,71.2 3.6≈)三、解答题（本大题共有10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、推理过程或演算步骤） 19．（本题满分8分）（1）计算:01||2012sin 302---︒ （2）化简:2()(2)a b b a b -++第15题图AB CD第16题图B ACD EA 1解方程:321x x =+21．（本题满分8分）现有形状、大小和颜色完全一样的三张卡片,上面分别标有数字“1”、“2”、“3”.第一次从这三张卡片中随机抽取一张,记下数字后放回；第二次再从这三张卡片中随机抽取一张并记下数字.请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽取的数字大于第一次抽取的数字的概率.22．（本题满分8分）第三十届夏季奥林匹克运动会将于2012年7月27日至8月12日在英国伦敦举行,目前正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥运火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:(1) 接受问卷调查的学生共有___________名；(2) 请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小；(3) 若该校共有1200名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递路线达到“了解”和“基本了解”程度的总人数.23．（本题满分10分）如图所示,在梯形ABCD 中,AD ∥BC ,90BDC ∠=︒,E 为BC 上一点,BDE DBC ∠=∠. (1) 求证:DE EC =；(2) 若12AD BC =,试判断四边形ABED 的形状,并说明理由．第23题图ABCDE第22题图接受问卷调查的学生人数扇形统计图了解基本了解了解很少不了解50%接受问卷调查的学生人数折线统计图程度 5 10 1520 2530不了解了解很少基本了解了解如图所示,当小华站立在镜子EF 前A 处时,他看自己的脚在镜中的像的俯角为45︒；如果小华向后退0.5米到B 处,这时他看自己的脚在镜中的像的俯角为30︒.求小华的眼睛到地面的距离.(结果精确到0.1米,参考数据 1.73≈)25．（本题满分10分）如图①所示,已知A 、B 为直线l 上两点,点C 为直线l 上方一动点,连接AC 、BC ,分别以AC 、BC 为边向ABC ∆外作正方形CADF 和正方形CBEG ,过点D 作1DD l ⊥于点1D ,过点E 作1EE l ⊥于点1E .(1)如图②,当点E 恰好在直线l 上时(此时1E 与E 重合),试说明1DD AB =； (2)在图①中,当D 、E 两点都在直线l 的上方时,试探求三条线段1DD 、1EE 、AB 之间的数量关系,并说明理由；(3)如图③,当点E 在直线l 的下方时,请直接写出三条线段1DD 、1EE 、AB 之间的数量关系.(不需要证明)26．（本题满分10分）如图所示,AC AB ⊥,AB =,2AC =,点D 是以AB 为直径的半圆O 上一动点, DE CD ⊥交直线AB 于点E ,设(090)DAB αα∠=︒<<︒.(1)当18α=︒时,求 BD的长； (2)当30α=︒时,求线段BE 的长；(3)若要使点E 在线段BA 的延长线上,则α的取值范围是_________.(直接写出答案)图②图①第25题图l (E 1)AB CDFGE D 1 图③lE 1 ABC DFG ED 1 lE 1ABCD FG E D 1 第24题图 FE A B B 1 A 1 CD 30º45º27．（本题满分12分）知识迁移当0a >且0x >时，因为2≥0,所以ax x -≥0,从而ax x+≥当x =). 记函数(0,0)ay x a x x=+>>,由上述结论可知：当x =时,该函数有最小值为直接应用已知函数1(0)y x x =>与函数21(0)y x x=>, 则当x =_________时,12y y +取得最小值为_________. 变形应用已知函数11(1)y x x =+>-与函数22(1)4(1)y x x =++>-,求21y y 的最小值,并指出取得该最小值时相应的x 的值. 实际应用已知某汽车的一次运输成本包含以下三个部分：一是固定费用,共360元；二是燃油费,每千米为1.6元；三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x 千米,求当x 为多少时,该汽车平均每．．．千米．．的运输成本．．．．．最低？最低是多少元？ 28．（本题满分12分）在平面直角坐标系xOy 中,已知二次函数214y x mx n =++的图象经过点(2,0)A 和点3(1,)4B -,直线l 经过抛物线的顶点且与y 轴垂直,垂足为Q .(1) 求该二次函数的表达式；(2) 设抛物线上有一动点P 从点B 处出发沿抛物线向上运动,其纵坐标1y 随时间(t t ≥0)的变化规律为1324y t =-+.现以线段OP 为直径作C .①当点P 在起始位置点B 处时,试判断直线l 与C 的位置关系,并说明理由；在点P 运动的过程中,直线l 与C 是否始终保持这种位置关系? 请说明你的理由； ②若在点P 开始运动的同时,直线l 也向上平行移动,且垂足Q 的纵坐标2y 随时间t的变化规律为213y t =-+,则当t 在什么范围内变化时,直线l 与C 相交? 此时,若直线l 被C 所截得的弦长为a ,试求2a 的最大值.第28题备用图第28题图。

【初中数学】黑龙江省哈尔滨市2012年初中毕业学年调研测试数学试卷通用

哈尔滨市2012年初中毕业学年调研测试数学试卷一、选择题(每小题3分，共计30分) 1.－3的倒数是( ) A.－13 B.13C.3D.－3 2.下列运算中正确的是( )A.()222a b a b -=- B.224a a a += C.()326aa -=- D.226326a a a =3.抛物线()21y x =+的顶点坐标是( )A.(－1,0)B. (－1,1)C. (0,－1)D. (1,0)4.下列四个图形分别是等边三角形、等腰梯形、正方形、圆,它们全是轴对称图形,其中对称轴的条数最少的图形是( )A. B. C. D. 5.由5个大小相同的正方体组成的几何体如图所示,其主视图是( )A. B. C. D. 6.如果反比例函数ky x=的图象经过点(―3,―4),那么该函数的图象位于( )A.第一、二象限B. 第一、三象限C. 第二、四象限D. 第三、四象限7.如图,D 是等腰直角△ABC 内一点,BC 是斜边,如果将△ABD 绕点A 逆时针方向旋转到△ACD ′的位置(B 与C 重合,D 与D ′重合),则∠ADD ′的度数是( ) A.25° B.30° C.35° D.45°8.同时抛两枚质地均匀的正方体骰子,每个骰子的六个面分别刻有1到6的点数,下列事件中是不可能事件的是( )A.点数之和是12B.点数之和是13C. 点数之和大于4且小于8D. 点数之和小于3 9.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 于点E,则△CDE 的周长是( )A.8B.6C.9D.1010.春节期间,某商场搞优惠促销活动,其活动内容是:“凡在该商场一次性购物超过50元者,超过50元的部分按9折优惠”.在此活动中,李明到该商场为单位一次性买单价为30元的办公用品x 件(x ＞2),则应付款y(元)与商品件数x(件)的函数关系是( )等边三角形等腰梯形正方形圆 (第5题图)A.y=27x(x ＞2)B. y=27x ＋5(x ＞2)C. y=27x ＋50(x ＞2)D. y=27x ＋45(x ＞2) 二、填空题(每小题3分，共计30分)11.我国最长的河流——长江全长约为6300千米,用科学计数法可表示为千米.12.在函数y=x2x 6+中，自变量x 的取值范围是 .13.不等式组21210x x -<⎧⎨+>⎩的解集是 .14.把34xy xy -因式分解的结果是 .15.若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥底面的半径为 .16.如图,已知P 是正方形ABCD 对角线BD 上一点,且BP=BC,则∠ACP 的度数为度.17.等腰三角形一腰上的高与腰长之比为1:2,则该等腰三角形顶角的度数为度.18.如图,AB 和AC 分别是⊙O 的直径和弦,OD ⊥AC 于D,连接BD 、BC,AB=5,AC=4,则BD= .19.如图,D 为AB 的中点,将△ABC 沿过D 点的直线折叠,使点A 落在BC 边的点F 处,若∠B=50°,则∠BDF=度.20.已知,如图,在△ABC 中,AB=AC=10,延长AC 到E,使CE=AC,边B 点作BE 的垂线交AC 于D,若D 为AC 的中点,则BE 的长为 .三、解答题(其中21-24题各6分，25、26题各8分，27、28题各10分，共60分) 21.(本题6分)先化简，再求代数式22111x x x ---的值，其中x=2tan45°－1.22. (本题6分)图1、图2分别是6×5的,网格,网格中每个小正方形的边长均为1,线段AB 的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:(1)在图1中画一个以线段AB 为一边的菱形(非正方形),所画菱形各顶点必须在小正方形的顶点上.(2)在图2中画一个以线段AB 为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为52.23.(本题6分)如图,四边形ABCD 的对角线AC 和BD 相交于点O,∠1=∠2,∠3=∠4,求证:BO=DO.23.(本题6分)为了美化环境,计划将一个边长为4米的菱形草地ABCD 分割成如图所示的四块,其中四边形AEPM 和四边形NPFC 均为菱形,且∠A=120°,若AE 的长为x 米, 四边形BEPN 和四边形DMPF 的面积和为S 平方米.(1)请直接写出S 与x 之间的函数关系式(不要求写出自变量x 的取值范围); (2)根据(1)中的函数关系式,计算当x 为何值时S 最大,并求出最大值.【参考公式：二次函数y=ax 2+bx+c(a ≠0)，当x=-a b2时，y 最大(小)值=244ac b a】25.(本题8分)为了解某学校学生的个性特长发展情况,学校决定围绕“音乐、体育、美术、书法、其它活动项目中,你参加哪一项活动(每人只限一项)的问题”,在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题：(1)在这次调查中一共抽查了多少名学生?(2)求参加“音乐”活动项目的人数占抽查总人数的百分比.(3)若全校有2400名学生，请估计该校参加“美术”活动项目的人数.26.(本题8分)甲、乙两人从A 地前往B 地,AB 两地的路程为180千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到0.5小时. (1)求甲乙两人的速度分别是多少?(2)甲到达B 地后与乙同时按原速度返回A 地,若它们由B 地返回A 地的过程中所行走路程的和不少于150千米,则它们至少要行走多少小时?27.(本题10分)如图：在平面直角坐标系中，直线132y x =+与x 轴、y 轴分别交于A 、B 两点,直线8y kx =+与直线AB 相交于点D,与x 轴相交于点C,过D 作DE ⊥x 轴,E 为垂足,E 点的横坐标为2.(1)求直线CD 的解析式；(2)若点P 为x 轴上一点,P 点的坐标为(t,0),过P 作x 轴的垂线,交直线AB 于点Q,边Q 点作x轴的平行线交直线CD 于点M,设线段QM 的长为y,当－6＜t ＜2时,求y 与t 的函数关系式;(3)在(2)的条件下，当t 为何值时,过P 、Q 、M 三点的圆与直线AB 和直线CD 这两条直线只有三个公共点.28.(本题10分)已知: △ABC中,∠ACB=2∠ABC,AD为∠BAC的平分线,E为线段AC上一点,过E作AD的垂线交直线AB于F.(1)当E点与C点重合时(如图1)，求证：BF=DE；(2)连接BE交AD于点N,M是BF的中点,连接DM(如图2)，若DM⊥BF,DC=4,S△ABD:S△ACD=3:2,求DN的长.。

可数名词与不可数名词-讲义+练习题

可数名词和不可数名词一. 可数名词和不可数名词及其考点知识点题目训练1.可数名词与不可数名词的区别普通名词所表示的人或事物是可以按个数计算的，如果普通名词所表示的事物是不能按个数来计算的，这类名词就叫不可数名词。

找出不可数名词，在横线上打勾homework ______half ______advice______money ______ knowledge ______boot _____blood ______music ______ chicken ________heat _____mouth ______bread _______ information ______milk _____cow _______tear ________ 2.可数名词变复数的变法一、写出下列名词的复数形式1、orange 2、class 3、text 4、monkey 5、piano 6、child 7、shelf 8、bed 9、country 10、family 11、toy 12、foot 13、Japanese 14、radio 15、photo 16、army 17、tomato 18、fox 19、woman 20、knife 22、sheep 1.I’d like ____ noodles. ____ noodles. A. tomatoes and beef B. mutton and cabbages C. chicken and carrots D. onion and fish 2.He had something to write down and asked me for _____. A.a paper B.some papers C.some pieces of papers D.a D.a piece of paper 3.．The deer has four ______. A. foot B. feet C. feets D. Foots 4．Her two brothers are both ______. A. policeman B. policemans C. policemen D. policemens 5．There are four _____ and two ______ in the group. A. Japanese, Germen B. Japaneses, Germen C. Japanese, Germans 6.Two ______ would come to the village. A. woman-doctors B. women doctor C. women doctors D. woman doctors3.有些名词既是可数又是不可数 orange （橘汁）（橘汁） → oranges （橘子）（橘子）1—What color are they? — ________ . A. They arc oranges B. They're orange C. Those are orange 2. I see you have a few white________(hair). 3. Can you give me some bottles of ____ (orange), please? 4.- We are doing ____. A .our homework B. my homework C. one’s homework D. the homeworks 4.单数可数名词和冠词连用。

2012年哈尔滨中考数学真题卷含答案解析

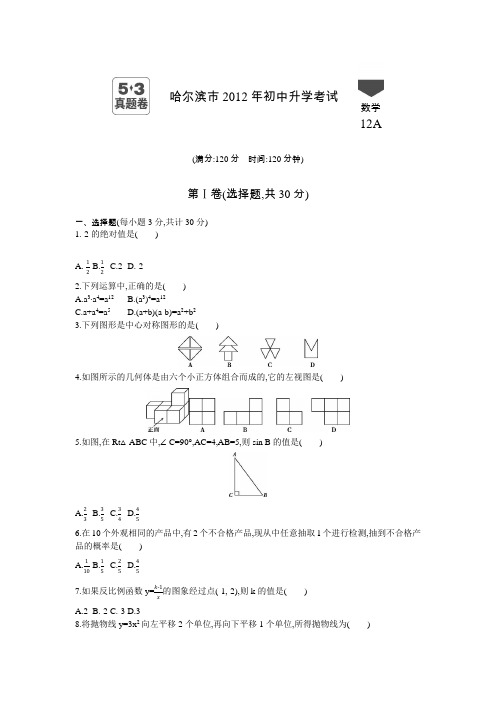
哈尔滨市2012年初中升学考试数学12A(满分:120分时间:120分钟)第Ⅰ卷(选择题,共30分)一、选择题(每小题3分,共计30分)1.-2的绝对值是( )A.-12B.12 C.2 D.-22.下列运算中,正确的是( ) A.a 3·a 4=a 12 B.(a 3)4=a 12 C.a+a 4=a 5 D.(a+b)(a-b)=a 2+b 23.下列图形是中心对称图形的是( )4.如图所示的几何体是由六个小正方体组合而成的,它的左视图是( )5.如图,在Rt △ABC 中,∠C=90°,AC=4,AB=5,则sin B 的值是( )A.23B.35C.34D.456.在10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,抽到不合格产品的概率是( ) A.110B.15C.25D.457.如果反比例函数y=k -1x 的图象经过点(-1,-2),则k 的值是( )A.2B.-2C.-3D.38.将抛物线y=3x 2向左平移2个单位,再向下平移1个单位,所得抛物线为( )A.y=3(x+2)2-1 B .y=3(x-2)2+1 C.y=3(x-2)2-1 D.y=3(x+2)2+19.如图,☉O 是△ABC 的外接圆,∠B=60°,OP ⊥AC 于点P,OP=2√3,则☉O 的半径为( )A.4√3B.6√3C.8D.1210.李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的矩形ABCD.设BC 边的长为x 米,AB 边的长为y 米,则y 与x 之间的函数关系式是( )A.y=-2x+24(0<x<12)B.y=-12x+12(0<x<24)C.y=2x-24(0<x<12)D.y=12x-12(0<x<24)第Ⅱ卷(非选择题,共90分)二、填空题(每小题3分,共计30分)11.把16 000 000用科学记数法表示为 . 12.在函数y=1x -5中,自变量x 的取值范围是 .13.化简:√9= .14.把多项式a 3-2a 2+a 分解因式的结果是 . 15.不等式组{2x -1>0,x -1<1的解集是 .16.一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是 . 17.一个圆锥的母线长为4,侧面积为8π,则这个圆锥的底面圆的半径是 . 18.方程1x -1=32x+3的解是 .19.如图,平行四边形ABCD 绕点A 逆时针旋转30°,得到平行四边形AB'C'D'(点B'与点B 是对应点,点C'与点C 是对应点,点D'与点D 是对应点),点B'恰好落在BC 边上,则∠C= 度.20.如图,四边形ABCD 是矩形,点E 在线段CB 的延长线上,连结DE 交AB 于点F,∠AED=2∠CED,点G 是DF 的中点,若BE=1,AG=4,则AB 的长为 .三、解答题(其中21~24题各6分,25~26题各8分,27~28题各10分,共计60分)21.(本题6分)先化简,再求代数式(1x +x+1x)÷x+2x2+x的值,其中x=√3cos30°+12.22.(本题6分)图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A 和点B在小正方形的顶点上.(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).23.(本题6分)如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.求证:AC=AD.12B24.(本题6分)小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);(2)当x是多少时,这个三角形面积S最大?最大面积是多少?(参考公式:当x=-b2a时,二次函数y=ax2+bx+c(a≠0)有最小(大)值4ac-b24a)25.(本题8分)虹承中学为做好学生“午餐工程”工作,学校工作人员搭配了A,B,C,D四种不同种类的套餐,学校决定围绕“在A,B,C,D四种套餐中,你最喜欢的套餐种类是什么?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查问卷适当整理后绘制成如图所示的不完整的条形统计图,其中最喜欢D种套餐的学生占被抽取人数的20%,请你根据以上信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)通过计算,补全条形统计图;(3)如果全校有2000名学生,请你估计全校学生中最喜欢B种套餐的学生有多少名?26.(本题8分)同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.(1)购买一个足球、一个篮球各需多少元?(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?27.(本题10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交x轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.(1)求m的值;(2)点P(0,t)是线段OB上的一个动点(点P不与O,B两点重合),过点P作x轴的平行线,分别交AB,OC,DC于点E,F,G.设线段EG的长为d,求d与t之间的函数关系式(直接写出自变量t的取值范围);(3)在(2)的条件下,点H是线段OB上一点,连结BG交OC于点M,当以OG为直径的圆经过点M时,恰好使∠BFH=∠ABO,求此时t的值及点H的坐标.28.(本题10分)已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.(1)如图1,求证:PC=AN;(2)如图2,点E是MN上一点,连结EP并延长交BC于点K,点D是AB上一点,连结DK,∠DKE=∠ABC,EF⊥PM于点H,交BC延长线于点F,若NP=2,PC=3,CK∶CF=2∶3,求DQ 的长.哈尔滨市2012年初中升学考试一、选择题1.C因为-2的绝对值是2,所以选C.评析本题意在考查绝对值的概念,正确地理解并运用绝对值的概念是求解的关键.正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.2.B对于选项A:a3·a4=a3+4=a7,即选项A是错误的;对于选项B:(a3)4=a12,即选项B正确;对于选项C:由于a与a4不是同类项,所以不能合并,即选项C是错误的;对于选项D:(a+b)(a-b)=a2-b2,即选项D错误.故应选B.评析本题考查了整式的运算,关键是要能正确理解并灵活运用整式运算的有关法则.注意同底数幂的乘法法则是底数不变,指数相加,而不是相乘;幂的乘方法则是底数不变,指数相乘;合并同类项要遵循两个不变,即字母不变,相同字母的指数也不变;注意平方差公式的结构形式.3.A选项A旋转180°后可以与自身重合,所以A图案是中心对称图形,故应选A.评析本题意在考查中心对称图形的概念,正确地分析图案的特征,利用中心对称图形的概念判定是求解的关键.判断方法:如果这个图形绕某一点旋转180°后能与自身重合,则这个图形是中心对称图形.4.C这个几何体的左视图由三个小正方体搭成,故左视图是C选项.评析本题考查的是几何体的视图,关键是要分清上、下、左、右各个方位.主视图是指从立体图形的正面看到的平面图,左视图指从立体图形的左面看到的平面图,俯视图指从立体图形的上面看到的平面图.5.D Rt△ABC中,因为∠C=90°,AC=4,AB=5,所以由正弦的定义,得sin B=ACAB =45,故应选D.评析本题考查锐角三角函数的求法,关键是要正确理解锐角三角函数的概念.根据锐角三角函数的定义可求某个锐角的三角函数值:正弦:在直角三角形中,锐角α的对边与斜边之比叫做∠α的正弦,记作sinα,即sinα=∠α的对边斜边.余弦:在直角三角形中,锐角α的邻边与斜边之比叫做∠α的余弦,记作cosα,即cosα=∠α的邻边斜边.正切:在直角三角形中,锐角α的对边与邻边之比叫做∠α的正切,记作tanα,即tanα=∠α的对边∠α的邻边.6.B因为10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,所以抽到不合格产品的概率是210=15,故应选B.评析本题考查概率的概念,关键是要弄清楚出现可能结果的意义.古典概型E,设它的所有可能结果是n个等可能的情形,事件A包含其中的m个情形,则定义事件A的概率为:P(A)=mn.7.D因为反比例函数y=k-1x 的图象经过点(-1,-2),所以-2=k-1-1,得k=3,故应选D.评析本题考查反比例函数的知识,关键是能正确理解点与图象的关系.即已知点在反比例函数的图象上,那么这点的坐标一定满足该反比例函数的解析式,反之也成立.8.A因为抛物线y=3x2的顶点坐标为(0,0),所以向左平移2个单位,再向下平移1个单位的顶点坐标为(-2,-1),即所得抛物线为y=3(x+2)2-1,故应选A.评析本题考查了二次函数的图象的特征,关键是要正确理解平移的意义和二次函数顶点坐标的知识.二次函数图象的平移规律:左加右减,上加下减.9.A因为∠B=60°,所以∠AOC=120°,又因为OP⊥AC,所以∠AOP=∠COP=60°,所以∠OAP=30°,又因为OP=2√3,所以OA=4√3,即☉O的半径为4√3,故应选A.评析本题考查三角形的外接圆、圆周角、圆心角、弦心距、含有30°角的直角三角形的性质等知识,关键要能利用圆周角与圆心角的关系求出∠AOP的大小.从条件出发,将问题转化到含有30°角的直角三角形中求得☉O的半径.x+12,而菜园的一边利用足够长的墙,所以0<x<24,故应10.B根据题意,得x+2y=24,所以y=-12选B.评析本题考查的是矩形的长与宽之间的函数关系,关键是要掌握矩形的对边相等的性质.注意矩形的周长等于(长+宽)×2.二、填空题11.答案 1.6×107解析16000000=1.6×107.评析本题考查的是科学记数法的知识,关键是确定a和n.科学记数法的形式是a×10n,其中1≤|a|<10,指数n是整数位数减1.12.答案x≠5解析依题意,得x-5≠0,得x≠5,即自变量x的取值范围是x≠5.评析本题考查了函数自变量的取值范围,知道分式的分母不能为0是求解的关键.13.答案3解析因为32=9,所以9的算术平方根是3,即√9=3.评析本题考查二次根式的化简,关键是要能正确理解一个正数的算术平方根的意义.知道1~20的平方,可以顺利地求解此类问题.14.答案a(a-1)2解析a3-2a2+a=a(a2-2a+1)=a(a-1)2.评析本题考查因式分解的知识,掌握因式分解的一般方法是解决问题的关键.分解因式关键是选择合适的方法.分解因式的步骤是一提(提公因式)、二套(套公式)、三验(检验是否分解彻底).套公式时可根据需分解多项式的项数进行选择:如果是两项,一般是平方差公式;三项,一般是完全平方公式.15.答案12<x<2解析解不等式2x-1>0,得x>12,解不等式x-1<1,得x<2,所以不等式组{2x-1>0,x-1<1的解集是12<x<2.评析本题考查解不等式组,关键是先求出每个不等式的解集,最后确定不等式组的解集.不等式组解集的确定法则:同大取大、同小取小、大小小大取中间、大大小小是无解.16.答案16或17解析当5是等腰三角形的腰长时,那么6就是底边长,所以这个等腰三角形的周长是5+5+6=16;当6是等腰三角形的腰长时,那么5就是底边长,所以这个等腰三角形的周长是6+6+5=17.所以这个等腰三角形的周长是16或17.评析本题考查等腰三角形和三角形的三边关系,考虑到哪是底边,哪是腰是正确求解的关键.另外,遇到等腰三角形的边角问题时,一定要注意分情况讨论求解,才能避免错误.17.答案2解析设圆锥底面的半径为r,由S=12lr,得l=2×8π÷4=4π,而扇形的弧长等于圆锥的底面周长,所以2πr=4π,解得r=2.即这个圆锥的底面圆的半径是2.评析本题意在考查圆锥的侧面展开图的有关计算,关键要能正确理解母线、侧面积等. 18.答案x=6解析去分母,得2x+3=3(x-1),解得x=6,经检验,x=6是原方程的解.评析本题考查分式方程的解法,关键是要能通过去分母,将分式方程转化为整式方程,注意不要忘记验根.19.答案105解析因为旋转30°,所以∠BAB'=30°,又因为点B'在BC上,AB=AB',所以∠B=75°,因为四边形ABCD是平行四边形,所以AB∥CD,所以∠B+∠C=180°,所以∠C=105°.评析本题考查的是图形的旋转、等腰三角形和平行四边形的性质及平行四边形的有关计算,关键是要能正确理解旋转的特征和平行四边形的性质.旋转前后图形的形状、大小都不发生改变,而平行四边形的对边平行,邻角互补.20.答案 √15解析因为四边形ABCD 是矩形,所以∠ABE=∠BAD=90°,AD ∥BE,又因为点G 是DF 的中点,所以在Rt △DAF 中,AG=DG=FG,所以∠ADG=∠GAD=∠DEC,所以∠AGF=2∠ADG=2∠DEC,因为∠AED=2∠CED,所以∠AED=∠AGE,所以AE=AG,由AG=4,知AE=4,在Rt △ABE 中,因为BE=1,所以由勾股定理,得AB=√AE 2-BE 2=√42-12=√15. 评析本题意在考查矩形的性质、直角三角形斜边上中线的性质以及勾股定理.关键是要能将已知条件转化到直角三角形中来处理.将已知条件结合图形转化到直角三角形中来,以便于运用勾股定理求解. 三、解答题 21.解析原式=x+2x·x 2+x x+2=x+2x·x(x+1)x+2=x+1,(2分)∵x=√3cos 30°+12=√3×√32+12=32+12=2,(4分)∴原式=2+1=3.(6分)评析本题考查的是分式的化简与求值和特殊角的三角函数值,求解的关键是要能先对已知分式化简,并求出x 的具体值,最后再代入计算.注意运算顺序,先算括号里的,后算括号外的,除法运算转化为乘法运算,同时将异分母转化为同分母,当然也可以把除法转化为乘法后用乘法分配律进行计算,注意灵活运用分式的基本性质、因式分解、除法运算法则等进行变化. 22.解析 (1)正确画图(参考图1~图4,画出一个即可).(3分) (2)正确画图(参考图5~图8,画出一个即可).(6分)评析本题考查的是直角三角形、等腰三角形,关键是要在格点上寻求符合要求的点,这是一道开放型试题.23.证明 ∵∠ABC+∠CBE=180°, ∠ABD+∠DBE=180°,∠CBE=∠DBE, ∴∠ABC=∠ABD.(2分) 在△ABC 和△ABD 中,{∠CAE =∠DAE,AB =AB,∠ABC =∠ABD,∴△ABC ≌△ABD.(5分) ∴AC=AD.(6分)评析本题考查的是全等三角形的判定和性质.关键是要能正确地寻求满足三角形全等的条件.一般三角形全等的判定方法有:SAS,ASA,AAS,SSS;直角三角形除了用一般方法判定外还可以用HL.24.解析 (1)S=-12x 2+20x.(2分) (2)解法一:∵a=-12<0,∴S 有最大值, ∴当x=-b2a =-202×(-12)=20时,(4分)S 有最大值,为4ac -b 24a =4×(-12)×0-2024×(-12)=200.∴当x 为20 cm 时,三角形面积最大,最大面积是200 cm 2.(6分) 解法二:∵a=-12<0,∴S 有最大值, ∴当x=-b2a =-202×(-12)=20时,(4分)S 有最大值,为S=-12×202+20×20=200.∴当x 为20 cm 时,三角形面积最大,最大面积是200 cm 2.(6分)评析本题考查了利用二次函数解决生活中的问题,关键是要能依据题意,正确地寻找等量关系.25.解析 (1)40÷20%=200(名).∴在这次调查中,一共抽取了200名学生.(2分) (2)200-90-50-40=20(名).(4分) 正确画图.(5分)(3)解法一:2 000×50200=500(名).(7分) ∴估计全校最喜欢B 种套餐的学生有500名.(8分) 解法二:50200×100%=25%,(6分)2 000×25%=500(名).(7分)∴估计全校最喜欢B 种套餐的学生有500名.(8分)评析本题考查了统计的知识,关键是要能读懂题目,准确地从统计图中捕捉信息. 26.解析 (1)设购买一个足球需要x 元,购买一个篮球需要y 元.根据题意得 {3x +2y =310,2x +5y =500,(2分)解得{x =50,y =80.∴购买一个足球需要50元,购买一个篮球需要80元.(4分) (2)解法一:设购买a 个篮球,则购买(96-a)个足球. 80a+50(96-a)≤5 720,(6分) a ≤3023,(7分)∵a 为整数,∴a 最多是30.∴这所中学最多可以购买30个篮球.(8分) 解法二:设购买n 个足球,则购买(96-n)个篮球, 50n+80(96-n)≤5 720,(6分) n ≥6513.(7分)∵n 为整数,∴n 最少是66,96-66=30,∴这所中学最多可以购买30个篮球.(8分)评析本题考查的是用方程组和不等式解决问题.关键是要能寻求到等量关系和不等量关系.属中档题.27.解析 (1)解法一:如图,∵y=2x+4交x 轴和y 轴于A,B, ∴A(-2,0),B(0,4),∴OA=2,OB=4,∵四边形ABCO 是平行四边形, ∴BC=OA=2,过点C 作CK ⊥x 轴于K, 则四边形BOKC 是矩形,∴OK=BC=2,CK=OB=4, ∴C(2,4),(1分)代入y=-x+m 得4=-2+m, ∴m=6.(2分) 解法二:如图,∵y=2x+4交x 轴和y 轴于A,B, ∴A(-2,0),B(0,4),∴OA=2,OB=4, 延长DC 交y 轴于点N,∵y=-x+m 交x 轴和y 轴于D,N, ∴D(m,0),N(0,m),∴OD=ON, ∴∠ODN=∠OND=45°.∵四边形ABCO 是平行四边形, ∴BC ∥AO,BC=OA=2,∴∠NCB=∠ODN=∠OND=45°, ∴NB=BC=2.(1分) ∴ON=NB+OB=2+4=6, ∴m=6.(2分)(2)解法一:如图,延长DC 交y 轴于N,分别过点E,G 作x 轴的垂线,垂足分别是R,Q,则四边形ERQG、四边形POQG、四边形EROP是矩形,∴ER=PO=GQ=t,∵tan∠BAO=ERAR =OBOA,∴tAR=42,∴AR=12t.(3分)∵y=-x+6交x轴和y轴于D,N,∴OD=ON=6,∴∠ODN=45°,∵tan∠ODN=GQQD,∴DQ=t.(4分)又∵AD=AO+OD=2+6=8,∴EG=RQ=8-12t-t=8-32t,∴d=-32t+8(0<t<4).(6分)解法二:如图,∵EG∥AD,P(0,t),∴设E(x1,t),G(x2,t),把E(x1,t)代入y=2x+4得t=2x1+4,∴x1=t2-2,(3分)把G(x2,t)代入y=-x+6得t=-x2+6,∴x2=6-t,(4分)∴d=EG=x2-x1=(6-t)-(t2-2),∴d=-32t+8(0<t<4).(6分)(3)解法一:如图,∵四边形ABCO是平行四边形,∴AB∥OC,∴∠ABO=∠BOC,∵BP=4-t,∴tan∠ABO=EPBP =tan∠BOC=12,∴EP=2-t2,∴PG=d-EP=6-t.(7分)∵以OG 为直径的圆经过点M, ∴∠OMG=90°.(8分) ∵∠OPG=90°,∠MFG=∠PFO, ∴∠BGP=∠BOC,∴tan ∠BGP=BPPG =tan ∠BOC=12, ∴4-t 6-t =12,解得t=2.(9分)∵∠BFH=∠ABO=∠BOC,∠OBF=∠FBH, ∴△BHF ∽△BFO,∴BH BF =BFBO ,即BF 2=BH ·BO,∵OP=2,∴PF=1,BP=2,∴BF=√BP 2+PF 2=√5,∴5=BH×4, ∴BH=54,∴HO=4-54=114, ∴H (0,114).(10分) 解法二:如图,∵四边形ABCO 是平行四边形,∴AB ∥OC, ∴∠ABO=∠BOC.∵BP=4-t,∴tan ∠ABO=EPBP =tan ∠BOC=12, ∴EP=2-t2,∴PG=d-EP=6-t.(7分)∵以OG 为直径的圆经过点M, ∴∠OMG=90°.(8分) ∵∠OPG=90°,∠MFG=∠PFO, ∴∠BGP=∠BOC,∴tan ∠BGP=BPPG =tan ∠BOC=12, ∴4-t 6-t =12,解得t=2.(9分)∴OP=2,BP=4-t=2,∴PF=1, ∴OF=√12+22=√5=BF,∴∠OBF=∠BOC=∠BFH=∠ABO,∴BH=HF, 过点H 作HT ⊥BF 于点T, 则BT=12BF=√52,∴BH=BTcos ∠OBF =√522√5=54, ∴OH=4-54=114,∴H (0,114).(10分)解法三:如图,∵OA=2,OB=4,∴由勾股定理得AB=2√5. ∵P(0,t),∴BP=4-t,∵cos ∠ABO=BP BE =4-t BE =OBAB =2√5,∴BE=√52(4-t),(7分)∵以OG 为直径的圆经过点M,∴∠OMG=90°,(8分) ∵四边形ABCO 是平行四边形,∴AB ∥OC, ∴∠ABG=∠OMG=90°=∠BPG, ∴∠ABO+∠BEG=90°,∠BGE+∠BEG=90°, ∴∠ABO=∠BGE,∴sin ∠ABO=sin ∠BGE, ∴OA AB =BE EG =BEd,即=√52(4-t)8-3t2,∴t=2.(9分)∵∠BFH=∠ABO=∠BOC,∠OBF=∠FBH, ∴△BHF ∽△BFO,∴BH BF =BFBO ,即BF 2=BH ·BO,∵OP=2,∴PF=1,BP=2, ∴BF=√BP 2+PF 2=√5,∴5=BH×4,∴BH=54, ∴HO=4-54=114,∴H (0,114).(10分)评析本题考查了一次函数、平行四边形、矩形、相似三角形、圆以及锐角三角函数等知识,关键是要能正确地理解题意,通过适当的辅助线将问题转化.注意充分发挥方程思想、转化思想、数形结合思想.属中等偏难题. 28.解析 (1)证明:证法一:如图.∵BA ⊥AM,MN ⊥AP,∴∠BAM=∠ANM=90°, ∴∠PAQ+∠MAN=∠MAN+∠AMN=90°, ∴∠PAQ=∠AMN.(1分)∵PQ ⊥AB,MN ⊥AC,∴∠PQA=∠ANM=90°, ∵AQ=MN,∴△AQP ≌△MNA,(2分) ∴AN=PQ,AM=AP,∴∠AMB=∠APM. ∵∠APM=∠BPC,∠BPC+∠PBC=90°,∠AMB+∠ABM=90°, ∴∠ABM=∠PBC.(3分)∵PQ⊥AB,PC⊥BC,∴PQ=PC,(4分)∴PC=AN.(5分)证法二:如图.∵BA⊥AM,MN⊥AC,∴∠BAM=∠ANM=90°,∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,∴∠PAQ=∠AMN.(1分)∵PQ⊥AB,∴∠AQP=90°=∠ANM.∵AQ=MN,∴△PQA≌△ANM.(2分)∴AP=AM,PQ=AN,∴∠APM=∠AMP.∵∠AQP+∠BAM=180°,∴PQ∥MA,∴∠QPB=∠AMP.(3分)∵∠APM=∠BPC,∴∠QPB=∠BPC.∵∠BQP=∠BCP=90°,BP=BP,∴△BPQ≌△BPC,(4分)∴PQ=PC,∴PC=AN.(5分)(2)解法一:如图.∵NP=2,PC=3,∴由(1)知PC=AN=3,∴AP=NC=5,AC=8,∴AM=AP=5,∴AQ=MN=√AM2-AN2=4.(6分)∵∠PAQ=∠AMN,∠ACB=∠ANM=90°,∴∠ABC=∠MAN,∴tan∠ABC=tan∠MAN=MNAN =4 3 .∵tan∠ABC=ACBC,∴BC=6.(7分)∵NE∥KC,∴∠PEN=∠PKC,又∵∠ENP=∠KCP,∴△PNE∽△PCK,∴NECK =NPPC,∵CK∶CF=2∶3,设CK=2k,则CF=3k,∴NE2k =23,NE=43k,过N作NT∥EF交CF于T,则四边形NTFE是平行四边形,∴NE=TF=43k,∴CT=CF-TF=3k-43k=53k.∵EF⊥PM,∴∠BFH+∠HBF=90°=∠BPC+∠HBF,∴∠BPC=∠BFH.∵EF∥NT,∴∠NTC=∠BFH=∠BPC.∵tan∠NTC=tan∠BPC=BCPC =2,∴tan∠NTC=NCCT=2,∴CT=53k=52,∴k=32.(8分)∴CK=2×32=3,BK=BC-CK=3.∵∠PKC+∠DKE=∠ABC+∠BDK,∠DKE=∠ABC, ∴∠BDK=∠PKC,tan ∠PKC=PCKC =1,∴tan ∠BDK=1,过K 作KG ⊥BD 于G.∵tan ∠BDK=1,tan ∠ABC=43, ∴设GK=4n,则BG=3n,GD=4n,∴BK=5n=3,∴n=35,∴BD=4n+3n=7n=215.(9分) ∵AB=√AC 2+BC 2=10,AQ=4,∴BQ=AB-AQ=6, ∴DQ=BQ-BD=6-215=95.(10分)解法二:如图.∵NP=2,PC=3,∴由(1)知AN=PC=3, ∴AP=NC=5,AC=8,∴AM=AP=5, ∴AQ=MN=√AM 2-AN 2=4.(6分) ∵NM ∥BC,∴∠NMP=∠PBC.又∵∠MNP=∠BCP,∴△MNP ∽△BCP, ∴MN BC =NPPC ,∴4BC =23,∴BC=6.(7分)作ER ⊥CF 于R,则四边形NERC 是矩形, ∴ER=NC=5,NE=CR, ∵∠BHF=∠BCP=90°, ∴∠EFR=90°-∠HBF,∠BPC=90°-∠HBF, ∴∠EFR=∠BPC,∴tan ∠EFR=tan ∠BPC, ∴ER RF =BCPC ,即5RF =63,∴RF=52,∵NE ∥KC,∴∠NEP=∠PKC.又∵∠ENP=∠KCP,∴△NEP ∽△CKP,∴NE KC =NP PC =23, ∵CK ∶CF=2∶3,设CK=2k,CF=3k, ∴NE=CR=43k,CR=CF-RF=3k-52,∴3k-52=43k,∴k=32,(8分)∴CK=3,CR=2,∴BK=3.在CF 的延长线上取点G,使∠EGR=∠ABC, ∴tan ∠EGR=tan ∠ABC,∴ER RG =AC BC =43,∴RG=34ER=154,EG=√ER2+RG2=254,KG=KC+CR+RG=354,∵∠DKE+∠EKC=∠ABC+∠BDK,∠ABC=∠DKE,∴∠BDK=∠EKC,∴△BDK∽△GKE,∴BDKG =BK EG,∴BD·EG=BK·KG,∴BD×254=3×354,∴BD=215.(9分)∵AB=√AC2+BC2=10,AQ=4,∴BQ=AB-AQ=6,∴DQ=BQ-BD=6-215=95.(10分)解法三:如图.∵NP=2,PC=3,∴由(1)知AN=PC=3,∴AP=NC=5,AC=8,∴AM=AP=5,∴AQ=MN=√AM2-AN2=4.(6分)∵NM∥BC,∴∠EMH=∠PBC,∠PEN=∠PKC.又∵∠PNE=∠PCK,∴△PNE∽△PCK,△PNM∽△PCB,∴NECK =PNPC,MNBC=PNPC,∵CK∶CF=2∶3,设CK=2k,则CF=3k,∴NE2k =23,4BC=23,∴NE=43k,BC=6.(7分)∴BF=6+3k,ME=MN-NE=4-43k,tan∠ABC=ACBC =43,BP=√PC2+BC2=3√5,∴sin∠EMH=sin∠PBC=PCBP =√55,∵EF⊥PM,∴FH=BFsin∠PBC=√55(6+3k),EH=EMsin∠EMH=√55(4-43k).过E作ER⊥BF于R,则四边形NCRE是矩形,∴ER=NC=5.∵∠RFE+∠REF=∠RFE+∠PBC=90°,∴∠REF=∠PBC.∴tan∠REF=tan∠PBC=12,∵tan∠REF=RFRE,∴RF=52,∴EF=√ER2+RF2=5√52,∵EH+FH=EF,∴√55(4-43k)+√55(6+3k)=5√52,∴k=32,(8分)∴CK=2×32=3,BK=BC-CK=3.∵∠PKC+∠DKE=∠ABC+∠BDK,∠DKE=∠ABC,∴∠BDK=∠PKC.∵tan∠PKC=1,∴tan∠BDK=1,过K作KG⊥BD于G.∵tan∠BDK=1,tan∠ABC=43,∴设GK=4n,则BG=3n,GD=4n,∴BK=5n=3,∴n=35,∴BD=4n+3n=7n=215.(9分)∵AB=√AC2+BC2=10,AQ=4,∴BQ=AB-AQ=6,∴DQ=BQ-BD=6-215=95.(10分)评析本题综合考查了直角三角形、全等三角形、相似三角形、锐角三角函数、特殊四边形、勾股定理等知识.属难题.关键是要能充分利用图形的性质,添加适当的辅助线,将问题转化.另外,本题强化了全等三角形和相似三角形以及锐角三角形的功能地位,充分使用了几何知识来解决问题.。

盐城市2012年初中毕业于升学统一考试数学试题与答案

盐城市2012年初中毕业于升学统一考试数学试题与答案一、选择题（每题3分，共24分）1．下列各式中，不成立的是（）．A．=3 B．－=－3 C．= D．- =32．近似数精确到了( )位A．百分B．万C．千D．十万3.如图，已知AC∥ED，∠C=26°，∠CBE=37°，则∠BED的度数是（）．A.63°B.83°C.73°D.53°4. 计算的结果是（）．A． B．C．D．5．如图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，这个几何体的主视图是（）.A．B．C．D．6．若关于的一元二次方程有两个不相等的实数根，则的取值范围是（）A．B．且C．D．且7．如图，已知⊙是以数轴的原点为圆心，半径为1的圆，,点在数轴上运动，若过点且与平行的直线与⊙有公共点, 设，则的取值范围是（）.A．O≤≤B．≤≤C．－1≤≤1 D．＞8. 如图，某一中学生耐力测试比赛中，甲、乙两学生测试的路程s（米）与时间t（秒）之间的函数关系的图象分别为折线OABC和线段OD，下列说法正确的是（）．科A．乙比甲先到终点B．乙测试的速度随时间增加而增大学C．比赛进行到29.4秒时，两人出发后第一次相遇D．比赛全程甲的测试速度始终比乙的测试速度快学二、填空题（每题3分，共21分）9．化简的结果是．10．分解因式把= ．11. 如图，在边长为1的等边△ABC中，中线AD与中线BE相交于点O，则OA长度为．12. 有一组数据如下：3、a、4、6、7，它们的平均数是5，那么这组数据的方差是．13. 如图，已知点A、B在双曲线（x＞0）上，AC⊥x轴于点C，BD⊥y轴于点D，AC与BD交于点P，P是AC的中点，若△ABP的面积为3，则k＝．14. 如图，直线经过⊙O的圆心O，且与⊙O交于A、B两点，点C在⊙O上，且= ，点P是直线上的一个动点（与圆心O不重合），直线CP与⊙O相交于点Q．且QP=QO，则∠OCP的度数为．15．如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为cm．三、解答下列各题（共75分）16．（本题6分）解不等式组并在数轴上表示不等式组的解集.17．（本题6分）如图，已知中，，，把一块含角的直角三角板的直角顶点放在的中点上（直角三角板的短直角边为，长直角边为），将直角三角板绕点按逆时针方向旋转至如图的位置，延长交于，延长交于，求证：.18．（本题7分）19．（本题7分）某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人，请用列表法或树状图法，求选出的恰为一男一女的概率．20．（本题6分）开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1支钢笔和3本笔记本；小亮用31元买了同样的钢笔2支和笔记本5本.校运会后，班主任拿出200元交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，要求笔记本数不少于钢笔数，请问钢笔最多能买多少支？21．（本题8分）如图，AB为⊙O的直径，DF⊥AB于点D，交弦AC于点E，FC=FE.求证：（1）FC是⊙O的切线；（2）若⊙O的半径为5，,求弦AC的长.22．（本题8分）如图所示，某居民楼Ⅰ高20米，窗户朝南。

2012年黑龙江省哈尔滨市中考数学试卷及解析

2012年黑龙江省哈尔滨市中考数学试卷及解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）（2012•哈尔滨）﹣2的绝对值是（）A．﹣B．C．2D．﹣2考点：绝对值。

1428548专题：计算题。

分析：根据绝对值的定义解答．解答：解：|﹣2|=2，，故选C．点评：本题考查了绝对值的性质﹣﹣﹣一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0．A．a3•a4=a12B．（a3）4=a12C．a+a4=a5D．（a+b）（a﹣b）=a2+b2考点：平方差公式；合并同类项；同底数幂的乘法；幂的乘方与积的乘方。

1428548专题：探究型。

分析：分别根据同底数幂的乘法、幂的乘方与积的乘方法则、合并同类项及平方差公式对各选项进行逐一解答即可．解答：解：A、a3•a4=a7，故本选项错误；B、（a3）4=a12，故本选项正确；C、a与a4不是同类项，不能合并，故本选项错误；D、（a+b）（a﹣b）=a2﹣b2，故本选项错误．故选B．点评：本题考查的是同底数幂的乘法、幂的乘方与积的乘方法则、合并同类项及平方差公式，熟知以上知识是解答此题的关键．3．（3分）（2012•哈尔滨）下列图形是中心对称图形的是（）A．B．C．D．考点：中心对称图形。

1428548分析：根据轴对称图形与中心对称图形的概念求解．解答：解：A、是轴对称图形，也是中心对称图形；B、是轴对称图形，不是中心对称图形；C、是轴对称图形，不是中心对称图形；D、既不是轴对称图形，又不是中心对称图形．故选A．点评：本题考查了中心对称图形．掌握好中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．4．（3分）（2012•哈尔滨）如图所示的几何体是由六个小正方体组合而成的，它的左视图是（）A．B．C．D．考点：简单组合体的三视图。

1428548专题：常规题型。

哈尔滨市中考考试说明

哈尔滨市中考考试说明一、考试性质初中毕业学业考试是义务教育阶段的终结性考试，目的是全面、准确地反映初中毕业生在学科学习目标方面所达到的水平。

考试结果既是衡量学生是否达到毕业标准的主要依据，也是高中阶段学校招生的重要依据。

二、指导思想学业考试命题应依据学科课程标准，加强试题与社会实际和学生生活的联系，注重考查学生对知识与技能的掌握情况，特别是在具体情境中综合运用所学知识分析和解决问题的能力，杜绝设置偏题、怪题，减少繁琐复杂的计算题。

试题难度应适当。

学业考试要坚持以学生为本，遵循科学性、公平性、公正性的原则。

按照国家的教育方针、课程计划和教学大纲（课程标准）的规定，全面考查学生的基础知识和基本能力，特别是思想政治素质、文化科学素质、身体心理素质等，促进学生生动活泼地主动发展，反映九年义务教育的本质。

三、基本要求导向性要求。

学业考试要有利于促进提高学生的综合素质，促进学生对知识与技能、过程与方法、情感态度价值观的学习和形成。

有利于激发学生的学习动力、学习兴趣，培养学生的创新精神和实践能力。

有利于学生认识社会、认识自我，形成科学的价值观念。

有利于全面提高教育教学质量，有利于课改的深入实施。

科学性要求。

学业考试要准确反映学生的学习水平，既便于高中阶段学校招生选拔，又便于对学生学习情况的整体监测和提高教学质量。

考试内容的呈现要清晰、明了，便于学生理解和应答。

学业考试成绩要具有可比性，以利于不同学校之间和同一学校不同年级之间的比较。

公平性要求。

学业考试要充分考虑城乡不同区域、不同类型学校之间的差异，在考试内容中增加与学生生活经验相关的题目，在试卷中提供与学生生活实际相联系的内容，努力使不同地域的初中学校的学生都能公平地参与考试。

要重视对物理、化学和生物实验的考查，增加学生动手实践能力的考查。

要充分考虑残疾学生等特殊群体的实际情况，积极创造条件，提供必要的考试环境和条件。

规范性要求。

学业考试的科目、内容、时间安排和试卷格式要规范。

黑龙江省龙东地区2012年中考数学试题(word版,答案扫描版)

2011年湖北省襄阳市中考数学试卷锦元数学工作室编辑一、选择题：（本大题共12个小题，每小题3分，共36分）在每小题给出的四个选项中，只有一项是符合题目要求的，请将其序号在答题卡上涂黑作答．1、（湖北襄阳3分）﹣2的倒数是A ．2-B ．2C ．12- D ．12【答案】C 。

【考点】倒数。

【分析】根据两个数乘积是1的数互为倒数的定义，直接得出结果：∵（－2）×（12-）=1，∴﹣2的倒数是12-。

故选C 。

2、（湖北襄阳3分）下列运算正确的是A ．2a a a -=B ．236()a a -=-C ．632x x x ÷=D ．222()x y x y +=+【答案】B 。

【考点】合并同类项，幂的乘方，同底数幂的除法，完全平方公式。

【分析】A ，2a a a -=-，故本选项错误；B ，幂指数的幂，指数相乘，故本答案正确；C ，同底数幂的除法底数不变指数相减，633x x x ÷=故本选项错误；D ，应该是完全平方式，222()2x y x xy y +=++，故本选项错误。

故选B 。

3、（湖北襄阳3分）若x y 、为实数，且110x y ++-=，则2011()x y 的值是 A 、0 B 、1 C 、﹣1 D 、﹣2011【答案】C 。

【考点】非负数的性质，算术平方根，绝对值，有理数的乘方。

【分析】根据非负数的性质，即几个非负数的和为0时，这几个非负数都为0，求出x y 、的值，再代入2011()x y进行计算即可： ∵1x +=0，∴x +1=0，解得x =﹣1；∵10y -=，∴y ﹣1=0，解得y =1。

∴201120111()11x y ⎛⎫==- ⎪-⎝⎭。

故选C 。

4、（湖北襄阳3分）如图，CD ∥AB ，∠1=120°，∠2=80°，则∠E 的度数是A 、40°B 、60°C 、80°D 、120°【答案】A 。

2024年黑龙江省哈尔滨市香坊区中考一模数学试题(解析版)

2024年香坊区初中毕业学年调研测试（一）数学试卷考生须知：1．本试卷满分为120分，考试时间为120分钟．2．答题前，考生先将自己的“姓名”、“考场”、“座位号”在答题卡上填写清楚．3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸上、试题纸上答题无效．4．选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、字迹清楚．5．保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀．第Ⅰ卷选择题（共30分）（涂卡）一、选择题（每小题3分，共计30分）．1. 下列各数中，最大的是（）A. B. 0 C. 2 D. 【答案】C【解析】【分析】首先化简绝对值，然后把选项中的4个数按从小到大排列，即可得出最大的数．∵，∴，∴最大的数是2．故选：C ．【点睛】本题考查了有理数的大小比较，一般地，正数大于零，零大于负数，两个负数，绝对值大的反而小．2. 我国平均每平方千米的土地一年从太阳得到的能量，相当于燃烧130000000kg 的煤所产生的能量．把130000000kg 用科学记数法可表示为（）A. kgB. kgC. kgD. kg 【答案】B【解析】【分析】本题主要考查了科学记数法．科学记数法的表现形式为的形式，其中，n 为整数，确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相3-1-11-=3012-<<-<71310⨯81.310⨯71.310⨯80.1310⨯10n a ⨯110a ≤<同．解：把130000000kg 用科学记数法可表示为kg ，故选：B ．3. 下列运算中，正确的是（）A. B. C. D. 【答案】D【解析】【分析】根据合并同类项可判断A ，根据完全平方公式可判断B ，根据单项式除以单项式可判断C ，根据积的乘方与幂的乘方运算可判断D ，从而可得答案．解：，不是同类项，不能合并，故A 不符合题意；，故B 不符合题意；，故C 不符合题意；，故D 符合题意；故选D【点睛】本题考查的是合并同类项，完全平方公式的应用，单项式除以单项式，积的乘方与幂的乘方运算的含义，熟记基础运算法则是解本题的关键．4. 如图所示几何体是由4个大小相同的小立方块搭成，其左视图是（）A. B. C. D.【答案】D【解析】【分析】根据左视图的定义“从主视图的左边往右边看得到的视图就是左视图”进一步分析即可得到答案．从主视图的左边往右边看得到的视图为：的81.310⨯3232a a a-=()222a b a b +=+322a b a a ÷=()2242a b a b =33a 2a ()2222a b a ab b +=++3222a b a ab ÷=()2242a b a b =故选：D .【点睛】本题考查了左视图的识别，熟练掌握相关方法是解题关键．5. 已知点在反比例函数的图像上，且，则下列结论一定正确的是（）A. B. C. D. 【答案】D【解析】【分析】把点A 和点B 的坐标代入解析式，根据条件可判断出、的大小关系．解：∵点，）是反比例函数的图像上的两点，∴，∵，∴，即，故D 正确．故选：D ．【点睛】本题主要考查反比例函数图像上点的坐标特征，掌握图像上点的坐标满足函数解析式是解题的关键．6. 如图，为的直径，直线与相切于点C ，连接，若，则的度数为（）A. B. C. D. 【答案】B ()()1122,,,A x y B x y 2y x =-120x x <<120y y +<120y y +>120y y -<120y y ->1y 2y ()11,A x y ()22,B x y 2y x=-11222x y x y ==-120x x <<210y y <<120y y ->AB O CD O AC 50ACD ∠=︒BAC ∠30︒40︒50︒60︒【分析】连接，先根据圆的切线的性质可得，从而可得，再根据等腰三角形的性质即可得．解：如图，连接，直线与相切，，，，，，，故选：B ．【点睛】本题考查了圆切线的性质、等腰三角形的性质，熟练掌握圆的切线的性质是解题关键．7. 随着5G 网络技术的发展，市场对5G 产品的需求越来越大，为满足市场需求，某大型5G 产品生产厂家更新技术后，加快了生产速度，现在平均每天比更新技术前多生产30万件产品，现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同，设更新技术前每天生产x 万件，依据题意得（）A. B. C. D. 【答案】B【解析】【分析】设更新技术前每天生产x 万件产品，则更新技术后每天生产（x+30）万件产品，根据工作时间=工作总量÷工作效率，再结合现在生产500万件产品所需时间与更新技术前生产400万件产品所需时间相同，即可得出关于x 的分式方程．解：设更新技术前每天生产x 万件产品，则更新技术后每天生产（x+30）万件产品，依题意，得：．的OC 90OCD ∠=︒40OCA ∠=︒OC CD O OC CD ∴⊥90OCD ∴∠=︒50ACD ∠=︒ 40OCA ∴∠=︒OA OC = 40BAC OCA ∴∠=∠=︒40050030x x =-40050030x x =+40050030x x =-40050030x x=+40050030x x =+【点睛】本题考查了由实际问题列分式方程，解题的关键是找准等量关系，正确列出分式方程．8. 小明、小红、小刚3位同学合影留念，3人随机站成一排，那么小明、小刚两人恰好相邻的概率是（）．A. B. C. D. 【答案】C【解析】【分析】本题考查了列表法或画树状图法求概率，写出所有可能的情况是解题关键．设小明、小红、小刚3位同学分别为A 、B 、C ，根据写出所有可能的排列情况，再找出小明、小刚两人恰好相邻的情况，利用概率公式求解即可．解：设小明、小红、小刚3位同学分别A 、B 、C ，则可能的情况有：、、、、、，共6种，其中小明、小刚两人恰好相邻的情况有：、、、，共4种，小明、小刚两人恰好相邻的概率是，故选：C 9. 如图，在中，D ，E ，F 分别是边，，上的点，，且，则的长为（）．A. 5B. 6C. 7D. 8【答案】D【解析】【分析】本题考查平行线分线段成比例，先得出，求出长，再利用平行四边形的判定和性质可得出答案．解：∵，∴，∵，为13122345ABC ACB BAC BCA CAB CBA ACB BAC BCA CAB ∴4263=ABC AB AC BC ,DE BC EF AB ∥∥:3:4,14BF FC AB ==EF ::3:4AE CE AD BD ==BD EF AB ::3:4BF CF AE CE ==DE BC∴．∴，∵，∴，又∵，∴是平行四边形，∴,故选D ．10. “五一节”期间，数学老师一家自驾游去了离家170千米的某地，下面是他们离家的距离y （千米）与汽车行驶时间x （小时）之间的函数图象．他们出发2.2小时时，离目的地还有（）千米．A. 12B. 24C. 146D. 164【答案】B【解析】【分析】本题考查了一次函数的应用，主要利用了待定系数法求一次函数解析式和函数值的求解，要注意求的是离目的地的距离，这也是本题容易出错的地方．设段图象的函数表达式为，利用待定系数法求一次函数解析式求出函数表达式，再把代入进行计算求出行驶的路程，再用全程减去行驶的路程计算即可得解．解：设段图象的函数表达式为，函数图象经过点，，，解得，，::3:4AE CE AD BD ==:4:7BD BD =14AB =8BD =,DE BC EF AB ∥∥BFED 8EF BD ==AB y mx b =+ 2.2x =AB ()0y mx b m =+≠ (1.5,90)A (2.5,170)B ∴ 1.5902.5170m b m b +=⎧⎨+=⎩8030m b =⎧⎨=-⎩8030(1.5 2.5)y x x ∴=-<≤当时，，千米．故选：B ．第Ⅱ卷非选择题（共90分）二、填空题（每小题3分，共计24分）．11. 在函数中，自变量的取值范围是________．【答案】【解析】【分析】根据分式的分母不为0，进行求解即可．解：由题意，得：，解得：；故答案为：．【点睛】本题考查求自变量的取值范围．熟练掌握分式的分母不为0，是解题的关键．12.的结果是________．【答案】【解析】【分析】本题主要考查了二次根式的减法，直接化简二次根式，进而合并得出答案．故答案为：13. 分解因式：=____.【答案】【解析】【分析】先提取公因式后继续应用平方差公式分解即可．2.2x =80 2.230146y =⨯-=17014624∴-=223y x =+x 32x ≠-230x +¹32x ≠-32x ≠--==3x 9x -()()x x 3x 3+-x．故答案为：14. 二次函数的最大值为___________．【答案】【解析】【分析】本题考查了二次函数的最值，掌握二次函数的顶点式的性质是解题关键．由二次函数的顶点式可知，抛物线开口向下，顶点坐标为，即可求解．解：，抛物线开口向下，顶点坐标为，即当时，二次函数有最大值，故答案为：．15. 某单位今年六月份面向社会提供就业岗位32个，并按计划逐月稳步增长，预计八月份将提供岗位50个．则七、八两个月提供就业岗位数量的月平均增长率为___________．【答案】【解析】【分析】本题考查了一元二次方程的应用，理解题意并根据题意建立等量关系是解题的关键．根据今年六月份提供就业岗位32个，并按计划逐月增长，预计八月份将提供岗位50个，列一元二次方程即可．解：月平均增长率为x ，根据题意得：，解得：或（舍）∴月平均增长率为，故答案为：．16. 如图，分别以等边的三个顶点为圆心，以边长为半径画弧，三段圆弧围成的封闭图形叫做“莱洛三角形”，它是工业生产中广泛使用的一种图形．若等边的边长为5，则该“莱洛三角形”的周长等于___________．()()()22x 9x x x 9x x 3x 3-=-=+-()()x x 3x 3+-()2323y x =---3-()2,3-()2323y x =--- ∴()2,3-2x =3-3-25%()232150x +=14x =94x =-25%25%ABC ABC【答案】【解析】【分析】本题考查了等边三角形的性质，弧长公式，熟练掌握等边三角形的性质和弧长公式是解题的关键．根据等边三角形的性质及弧长公式求解即可．解：∵等边三角形的边长为，，∴，∴该“莱洛三角形”的周长，故答案：．17. 已知是的边上的高，若，则的长为___________．【解析】【分析】本题考查了勾股定理，利用分类讨论的思想解决问题是解题关键．由勾股定理，得出，进而得到，分两种情况讨论：是锐角三角形和是钝角三角形，利用勾股定理分别求解即可．解：是的边上的高，，在中，，，，，①当是锐角三角形时，，为5π180n r l π=ABC 560ABC ACB BAC ∠=∠=∠=︒ 60551803AB BC ACl l l ππ⨯====5353ππ=⨯=5πCD ABC AB 31,2AB CD AD AC ===BC 2AC =3AB =ABC ABC CD ABC AB CD AB ∴⊥Rt ACD 1CD AD ==2∴==AC 32AB AC = 3AB ∴=ABC 2BD AB AD ∴=-=BC ∴==②当是钝角三角形时，，，综上可知，18. 在中，对角线和相交于点O ，，延长至点E ，连接交于点F ，若，则线段的长为___________．【解析】【分析】取中点，连接，过点作于点，证明四边形是菱形，进而得出，再利用三角形中位线定理，得到，，证明，推出，最后利用勾股定理求解即可．解：如图，取中点，连接，过点作于点，在中，对角线和相交于点O ，，，，，，，四边形是菱形，，ABC 4BD AD AB =+=BC ∴==BC ABCD Y AC BD 5,8,6AD AC BD ===BC OE CD 12E ACD ∠=∠OF CD M OM O ON BE ⊥N ABCD 4CE OC ==1522OM BC ==OM BC ∥FOM FEC ∽513OF OE =CD M OM O ON BE ⊥N ABCD Y AC BD 5,8,6AD AC BD ===4OA OC ∴==3OB OD ==5BC AD ==222OB OC BC ∴+=OB OC ∴⊥∴ABCD ACB ACD ∠=∠∴12E ACD ∠=∠，即，，，，点是的中点，点是的中点，是的中位线，，，，，，，，在中，，，在中，，【点睛】本题考查了菱形的判定和性质，三角形中位线定理，相似三角形的判定和性质，勾股定理等知识，正确作辅助线是解题关键．三、解答题（其中19~22题各7分，23题8分，24~26题各10分，共计66分）．12E ACB ∴∠=∠2ACB E ∠=ACB E COE ∠=∠+∠ E COE ∴∠=∠4CE OC ∴== M CD O BD OM ∴BCD △1522OM BC ∴==OM BC ∥FOM FEC ∴ ∽55248OF OM EF CE ∴===513OF OF OE OF EF ∴==+1122BOC S OB OC BC ON =⋅=⋅ 125OB OC ON BC ⋅∴==Rt ONC 165CN ===1636455EN CN CE ∴=+=+=Rt ONE OE ===551313OF OE ∴===19. 先化简，再求代数式的值，其中．【答案】，【解析】【分析】本题考查特殊角的三角函数值，分式的化简求值，熟练掌握运算法则是解答本题的关键．先化简括号内的式子，再算括号外的乘除法，最后将求出x 的值代入化简后的式子计算即可．解：原式，当时，原式．20. 如图，方格纸中每个小正方形的边长均为1个单位长度，线段和线段的端点均在小正方形的顶点上．（1）如图1，在方格纸中添加一条线段（点E 、F 在小正方形的顶点上），使它们构成轴对称图形；（2）如图2，在方格纸中找点M （点M 在小正方形的顶点上），使四边形是中心对称图形，并直接写出所画四边形的面积．【答案】（1）见解析（2）见解析，6【解析】【分析】本题考查了作图——轴对称图形和中心对称图形，割补法求面积，掌握轴对称图形和中心对称图形的定义是解题关键．（1）根据轴对称图形的定义作图即可；（2）根据中心对称图形的定义作图，再利用割补法求出面积即可．2222142442x x x x x xx x x+--⎛⎫-÷ ⎪--+-⎝⎭()2tan 45cos30x ︒=-︒12x -()()()2214222x x x x x x x x ⎡⎤+--=-÷⎢⎥---⎢⎥⎣⎦()()()222224422x x x x x x x x x x ⎡⎤---=-⋅⎢⎥---⎢⎥⎣⎦()()2241422x x x x x x x --=⋅=---()2tan 45cos30212x ⎛=-== ⎝︒︒==AB CD EF ABMC解：如图，即为所求做；【小问2】解：如图，四边形即为所求做；四边形的面积．21. 某学校开展了安全知识的宣传教育活动．为了解这次活动的效果，学校从全校1500名学生中随机抽取部分学生进行知识测试（测试满分100分，得分x 均为不小于60的整数），并将测试成绩分为四个等级：基本合格，合格，良好，优秀，制作了如下不完整统计图．请你根据图中提供的信息解答下列问题：（1）在这次调查中，一共抽取了多少名学生？（2）请通过计算补全条形统计图；（3）若全校学生都参加测试，请你估计该学校测试成绩优秀的学生有多少名．【答案】（1）一共抽取了200名学生（2）见（3）该学校测试成绩优秀的学生有300名ABMC ABMC 1111341222122212121262222=⨯-⨯⨯-⨯⨯-⨯⨯-⨯⨯=----=607()0x ≤<708()0x ≤<809()0x ≤<()90100x ≤≤【分析】本题考查的是频数分布直方图和扇形统计图，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．（1）基本合格的有30人，占比为，即可求解；（2）拿人数200人减去其余三个等级的人数即可；（3）拿总人数乘以样本中成绩优秀人数所占比例即可．【小问1】解：（名）答：一共抽取了200名学生．【小问2】解：，补全图形为：【小问3】解：（名）答：该学校测试成绩优秀的学生有300名．22. 如图，一种手机支架可抽象成如图2的几何图形，伸缩臂长度可调节，并且可绕点A 上下转动，转动角α变动范围是，手机支撑片可绕点B 上下转动，，转动角β变动范围是．小明使用该支架进行线上学习，当，且点C 离底座的高度不小于时，他才感觉舒适．15%3015%200÷=20030804050---=401500300200⨯=AB ()10cm 15cm AB ≤≤090α︒<≤︒EC 10cm BC =090β︒<≤︒30β≥︒7cm（1）如图2，当时，求托片底部点C 离底座的高度，并判断是否符合小明使用的舒适要求（参考数据：）．（2）如图3，当的情况下，要伸缩到多少厘米时才能满足点C 离底座的最低高度舒适要求．（精确到）【答案】（1）托片底部点C 离底座的高度为，不符合小明使用的舒适要求；（2）要伸缩到厘米时才能满足点C 离底座的最低高度舒适要求．【解析】【分析】本题考查了解直角三角形的应用，灵活运用三角函数是解题关键．（1）过点作于点，于点，利用余弦值，求出，进而得到，即可得到答案；（2）过点作于点，过点作于点，于点，由题意可知，利用三角函数分别求出，，即可得到答案．【小问1】解：如图，过点作于点，于点，四边形是矩形，，在中，，，，，，，，即托片底部点C 离底座的高度为，，不符合小明使用的舒适要求；90,37,12cm AB αβ︒︒===sin 370.6,cos370.8,tan 370.75︒≈︒≈︒≈60,90αβ=︒=︒AB 1cm 1.73≈4cm AB 14C CM AD ⊥M CN AB ⊥N 8cm BN =4cm AN =B BQ AD ⊥Q C CP D ⊥P CO BQ ⊥O 7cm OQ CP ==5cm =OB AB =C CM AD ⊥M CN AB ⊥N ∴AMCN CM AN ∴=Rt BNC △37β=︒10cm BC =cos BN BCβ∴=cos37100.88cm BN BC ∴=⋅︒≈⨯=12cm AB = 4cm AN AB BN ∴=-=4cm CM ∴=4cm 4cm 7cm < ∴【小问2】解：如图，过点作于点，过点作于点，于点，四边形是矩形，，点C 离底座的高度不小于时，才感觉舒适，点C 离底座的最低高度舒适要求为，，，，，，在中，，，，，在中，，，，即要伸缩到厘米时才能满足点C 离底座的最低高度舒适要求．23. 如图，在四边形中，于点F ，交BC 于点G ，交的延长线于点E ，且．B BQ AD ⊥QC CPD ⊥P CO BQ ⊥O ∴PQOC OQ CP ∴= 7cm ∴7cm 7cm OQ CP ∴==60α=︒ 30ABQ ∴∠=︒90β︒=Q 60CBO ∴∠=︒Rt BOC △10cm BC =60CBO ∠=︒1cos60105cm 2OB BC ∴=⋅︒=⨯=5712cm BQ OB OQ ∴=+=+=Rt AQB 60α=︒12cm BQ=14cm sin 60BQ AB ∴===≈︒AB 14ABCD 90,,︒∠=⊥∥ABC AD BC DE AC AB AE AC =（1）求证：；（2）如图2，连接AG ，若，请直接写出图2中的三角形，使写出的每个三角形的面积是面积的2倍．【答案】（1）见（2）【解析】【分析】本题考查了全等三角形判定与性质，以及共高三角形面积比等于底之比，熟练掌握基本知识是解题的关键；（1）用即可证明；（2）先证明，则，再证明，则，由与同底等高，得，再证明，则，最后与同底等高，得，所以．【小问1】证明：∵∴∴在和中，，∴；【小问2】的ABC AFE ≌30ACB ∠=︒BEG AEG ACG ACD ADG CDG△,△,△,△,△AAS ABC AFE ≌BA BE =2AEG BEG S S =△△AEG ACG △≌△2ACG BEG S S =△△ACG CDG 2GCD BEG S S =△△ADC AGC △△≌2ACD BEG S S =△△ACG CDG ACG GCD S S =△△2GCD BEG S S =△△DE AC⊥90AFE ∴∠=︒90ABC ∠=︒AFE ABC∴∠=∠ABC AFE △ABC AFE BAC FAE AC AE ∠=∠⎧⎪∠=∠⎨⎪=⎩ABC AFE ≌∵∴，∵，∴，∴∵，∴∵，∴，∴，∴，∵，∴，∴∵，,∴，∴∵∴与同底等高，∴,∴∵，∴，ABC AFE≌AB AF =AG AG =()Rt Rt HL ABG AFG ≌12∠=∠30ACB ∠=︒11260302∠=∠=⨯︒=︒ABC AFE ≌AE AC=30ACB E ∠=︒=∠1E ∠=∠GA GE =90ABC ∠=︒BA BE =2AEG BEGS S =△△AG AG =12∠=∠AE AC =AEG ACG △≌△2ACG BEGS S =△△AD BC∥ACG CDG ACG GCD S S =△△2GCD BEGS S =△△1230∠=∠=︒30DAC ∠=︒∴,∴，∴，∵，∴，∴，∵∴与同底等高，∴，∴，∴的面积为面积的2倍．24. 为拓展学生视野，某中学组织八年级师生开展研学活动，现有甲、乙两种客车，原计划租用甲种45座客车若干辆，但有15人没有座位；若租用同样数量的乙种60座客车，则多出三辆车，且其余客车恰好坐满．（1）求参加此次研学活动的师生共有多少人？（2）若同时租用两种客车，要使每位师生都有座位，甲种客车数量比乙种客车的5倍多1辆，则至少租用多少台乙种客车？【答案】（1）参加此次研学活动的师生共有600人（2）至少租用2台乙种客车【解析】【小问1】解：设参加此次研学活动的师生共有x 人，则：，解得：，答：加此次研学活动的师生共有600人．【小问2】设租用m 台乙种客车，由题意得：，230DAC ∠=∠=︒60ADG AGD ∠=∠=︒AD AG =AC AC =ADC AGC △△≌2ACD BEG S S =△△AD BC∥ACD DAG ACD GAD S S =△△2AGD BEG S S =△△AEG ACG ACD ADG CDG △,△,△,△,△BEG 1534560x x -=-600x =()455160600m m ++≥解得：，∵m 为整数，∴m 最小为2，∴至少租用2台乙种客车．答：至少租用2台乙种客车．25. 已知，、为两条弦，于点E ，连接，．（1）如图1，连接，求的度数；（2）如图2，连接，延长交于点N ，点F 为上一点，连接，在上方作等腰直角三角形，且，连接，求证：；（3）在（2）的条件下，连接，，当点G 落在线段上时，过点O 做，交于点L ，交于点T ，若，求半径的长．【答案】（1）（2）见（3）【解析】【分析】本题考查了圆与三角形的综合，涉及到全等三角形的判定与性质，等腰三角形的性质，平行线成比例，勾股定理，圆周角定理等，正确添加辅助线，熟练灵活运用知识点是解决本题的关键．（1）连接，证明即可；（2）过点G 作交于点R ，先证明，得，所以，得到，故．（3）过G 作交的延长线于点R ，连接，作于点K ，于点H ，先证明，∴，设，则，，证出，则，最后在中运用勾股定理求．【小问1】连接，3719m ≥AD BC O AD BC ⊥OE AE CE =OE AEO ∠AC EO AC AC EF EF EFG 90EGF ∠=︒NG NG BC ∥AB CD AB OL OE ⊥CDCE 2OE EG CL ==O 45︒,OA OC AEO CEO ≌△△GR GN ⊥EN GER GFN △≌△GR GN =45GNR GRN ∠=∠=︒GNR NEC ∠=∠GN BC GR GN ⊥NE ,OD OC OK CD ⊥OH CE ⊥ABE CDE ≌△△12EG CD =,2,4,3CL a EG a AB CD a DL a =====OD OC ==2,OK DK a KL a ===KOL OCT ∠=∠tan tan KOL OCT ∠=∠Rt OCHOC =,OA OC∵为半径，∴，∵，∴，∴，∵，∴，∴；【小问2】证明：过点G 作交于点R ，∴，∴，∴，∴，，,OA OC O OA OC =,EA EC OE OE ==AEO CEO ≌△△AEO CEO ∠=∠AD BC ⊥90AEC ∠=︒1452AEO CEO AEC ∠=∠=∠=︒GR GN ⊥EN 90RGN ∠=︒RGN EGF ∠=∠RGN RGF EGF RGF ∠-∠=∠-∠EGR FGN ∠=∠,AE CE AEN CEN =∠=∠∴，∴，∴，∴，又∵，∴，∴，∴，∴，∴．【小问3】过G 作交的延长线于点R ，连接，作于点K ，于点H ，由（2）得，得，∴，∵，∴，，∴，∴，∴，∴，设，，,EN AC AN CN ⊥=90ENC ∠=︒90ENC EGF ∠=︒=∠GEN GFN ∠=∠GE GF =GER GFN △≌△GR GN =45GNR GRN ∠=∠=︒GNR NEC ∠=∠GN BC GR GN ⊥NE ,OD OC OK CD ⊥OH CE ⊥GFN GER △≌△GN BC AN AG CN BG=AN CN =AG BG =90AEB ∠=︒1,,,2EG AB BAD BCD AE CE AEB CED =∠=∠=∠=∠ABE CDE ≌△△AB CD =12EG CD =,2,4,3CL a EG a AB CD a DL a =====9045EAC AEN ∠=︒-∠=︒∴，∴，∴，则，，在中，，∵，∴，∴，∵，，∴，∴，∵，在中，，∴26. 在平面直角坐标系中，抛物线分别交x 轴于A 、B 两点（A 在B 左边），交y 轴于点C ，连接，且．（1）如图1，求a 的值；（2）如图2，点Q 是第四象限内抛物线上的一点，过点Q 作轴于D ，连接，点E 在上，过E 点作轴于F ，点H 在上，纵坐标为，连接，若，点Q 的横坐标为t ，的长为d ，求d 与t 之间的函数关系式并直接写出自变量t 的取值范围；90DOC ∠=︒45DOK COK ∠=∠=︒45ODC OCD ∠=∠=︒OD OC ==2,OK DK a KL a ===Rt OKL △1tan 2LOK ∠=OL OE ⊥90EOL ∠=︒45OED OTE ∠=∠=︒45KOL LOC ∠+∠=︒45OCT LOC ∠+∠=︒KOL OCT ∠=∠tan tan KOL OCT ∠=∠6,12OE OH HC ===Rt OCH 222OC OH HC =+OC =()()()160y a x x a =+-≠AC 12tan 5OAC ∠=QD x ⊥AQ AQ EF x ⊥EF 2-HD 5tan tan 2DHF QAF ∠=∠DF（3）如图3，在（2）的条件下，延长交抛物线于点G ，连接延长至点M ，过点M 作x 轴的垂线，交抛物线于点N ，点P 为抛物线顶点，连接并延长交y 轴于点K ，连接并延长分别交、的延长线于点R 、T ，连接，若，求点K 的坐标．【答案】（1）（2）（3）【解析】【分析】（1）由，当时，得到，，在中，由三角函数得到，代入，即可求解，（2）设，表示出，，代入，结合，即可求解，（3）将化为标准式和顶点式，得到，，在中，表示出，代入，求出，进而得到，，，轴，作，，设，则，，，由，，解出，得到，，由，得到，结合，得到等腰直角，依次求出，，，，即可求解，本题考查了求二次函数解析式，三角函数，相似三角形的性质与判定，等腰直角三角形的性质与判定，解题的关键是：根据已知条件，列出等量关系式．【小问1】解：当时，，EF CG NP KM EG HD ED 5tan ,6EDQ RT ∠==25-()2126d t t =->()0,8K ()()()160y a x x a =+-≠0y =()1,0A -1OA =Rt OAC 120,5C ⎛⎫ ⎪⎝⎭()()16y a x x =+-()()2,165Q t t t ⎛⎫-+- ⎪⎝⎭DQ AD tan DQ DAQ AD ∠=5tan tan 2DHF QAF ∠=∠()()2165y x x =-+-549,210P ⎛⎫ ⎪⎝⎭13AF t =-Rt AEF EF 5tan 6DF EDQ EF ∠==7t =125,5E ⎛⎫- ⎪⎝⎭125,5G ⎛⎫ ⎪⎝⎭167,5Q ⎛⎫- ⎪⎝⎭EG y ∥NS OC ⊥PW NS ⊥2212,255N n n n ⎛⎫-++ ⎪⎝⎭52NW n =-NS n =22552PW n ⎛⎫=- ⎪⎝⎭PWN KSN ∽PW KS WN NS =2552KS n n ⎛⎫=- ⎪⎝⎭2225CS n n =-KC KS CS n CM =-==OK RE ∥45HRT SKN ∠=∠=︒2DF HF ==RHT RH RG KC OK 0y =()()()160y a x x a =+-≠∵，∴，解得：，，∴，，∴，在中，，∴，代入中，解得：，故答案为：，【小问2】解：由（1）得，设，则：，，∴，（），∴，∴，∴，即：，故答案为：，【小问3】解：，∴，∴，在中，，0a ≠()()160x x +-=11x =-26x =()1,0A -()6,0B 1OA =Rt OAC 1212tan 155OA OC OA C ⋅∠⨯===120,5C ⎛⎫ ⎪⎝⎭()()16y a x x =+-25a =-25-()()2165y x x =-+-()()2,165Q t t t ⎛⎫-+- ⎪⎝⎭()()()()220161655DQ t t t t ⎡⎤=--+-=+-⎢⎥⎣⎦()11AD t t =--=+()()()21625tan 615t t DQ DAQ t AD t +-∠===-+10t +≠()552tan tan 66225DHF QAF t t ∠=∠=⨯-=-tan 2DF DF DHF FH ∠==62DF t =-212d DF t ==-()2126d t t =->()()22221225491625555210y x x x x x ⎛⎫=-+-=-++=--+ ⎪⎝⎭549,210P ⎛⎫ ⎪⎝⎭()121213AF AD DF t t t =-=+--=-Rt AEF ()()2tan 1365EF AF DAQ t t =⋅∠=-⋅-∵∴，∵，∴，解得：，∴，，，∴轴，过点作于点，过点作于点，设，则，，，∵，∴，∴，即：，整理得：，5tan 6DF EDQ EF ∠==()()()265261365t t t -=--60t -≠()5226135t =-7t =125,5E ⎛⎫- ⎪⎝⎭125,5G ⎛⎫ ⎪⎝⎭167,5Q ⎛⎫- ⎪⎝⎭EG y ∥N NS OC ⊥S P PW NS ⊥W 2212,255N n n n ⎛⎫-++ ⎪⎝⎭52NW n =-NS n =2249212252105552PW n n n ⎛⎫⎛⎫=--++=- ⎪ ⎪⎝⎭⎝⎭PW KS ∥PWN KSN ∽PW KS WN NS =2255252n KS n n ⎛⎫- ⎪⎝⎭=-2552KS n n ⎛⎫=- ⎪⎝⎭∵，∴，∵，∴，∵，∴，∴，∴，∴，∴，∴，∴，故答案为：．2225M N CS MN y y n n ==-=-KC KS CS n CM =-==OK RE ∥45HRT SKN ∠=∠=︒2DF HF ==45RHT HRT ∠=∠=︒90T ∠=︒5RH ==1235255RG MG RH FH GF ==--=--=328555KC CM CG MG ==+=+=2812855OK KC OC =+=+=()0,8K ()0,8K。

2024年中考数学总复习教学计划（五篇）

2024年中考数学总复习教学计划本学期，我承担初三数学教学任务，为提升教学质量和学生的数学技能，特制定以下教学计划：一、教学目标：1、确保学生掌握数学基础知识和技能，培养他们的逻辑推理、运算、空间理解及解决实际问题的能力。

增强他们应用数学知识解决问题的能力。

2、培养学生的数学学习习惯，创造积极的学习环境，激发大多数学生的数学学习热情，提升整体数学素养，以期提高平均分。

3、关注并辅导学习困难的学生，对有潜力但成绩欠佳的学生给予特别关注，激发他们的学习积极性，促进成绩的快速提升。

二、教学措施：1、尽快熟悉学生，建立良好的师生关系，消除学生的抵触情绪，使他们尽快进入学习状态，营造积极的学习氛围。

2、精心备课，深入理解教材及考试大纲，明确教学目标，把握重难点，设计教学过程，注重各章节知识的联系和地位。

3、积极参与教学研讨，多听课评课，广泛学习，不断总结教学经验，提升教学能力。

4、做好常规教学，及时批改作业，适时复习，及时反馈，全面了解学生的学习状况，采取针对性的教学策略。

5、加强对学困生的辅导，课堂上增加提问机会，加强与学生的沟通，激发他们的学习潜力，增强学习信心。

三、其他方面：在完成教学任务的积极参与学校活动，提前规划，为下学期的毕业考试和升学做好充分的准备。

2024年中考数学总复习教学计划（二）一、基本情况概述本学期，本人担任九年级222班的数学教学工作，该班级共有学生____名。

回顾上学期，学生参加县局组织的统一考试，及格率为48.____%，平均分为55.____分，成绩表现不甚理想，存在较大的提升空间。

班级内部学习风气尚待加强，学生间的成绩差异较为显著。

二、教学指导思想本学期的数学教学工作，将紧密围绕党和国家的教育教学方针，严格遵循九年义务教育数学课程标准，致力于为学生提供最适合其个人发展的数学学习环境。

通过初三阶段的数学教学，旨在为学生奠定坚实的数学基础，包括基础知识与基本技能，同时进一步培养其运算能力、思维能力和空间想象能力，使学生能够运用所学知识解决实际问题，并在此过程中激发其数学创新意识，塑造良好的个性品质，初步形成唯物主义世界观。

2012年黑龙江省哈尔滨市中考数学试卷-答案

黑龙江省哈尔滨市2012年初中升学考试347=，故本选项错误；a a，故本选项正确；在△【解析】ABC【提示】根据锐角三角函数的定义得出【解析】圆心角⊥，OP AC，则O的半径为利用同弧所对的圆心角等于所对圆周角的【解析】平行四边形【解析】四边形∥AD BC∴∠=AGE∠=AED△在Rt ABE【提示】根据直角三角形斜边上的中线等于斜边的一半可得222(1)122x x x x x x x x x +++==+++31313cos30322222x ==⨯+=+=∴原式2=【解析】（1）如图①②，画一个即可；（2）如图③④，画一个即可.【解析】ABC∠+ABC ABD和△）12 a=-< 2bxa=-=-（2）根据题意知，喜欢C种套餐的学生有20090504020---=（名），补全图形如图所示；）全校有a ）2y x =+四边形ABCO 是平行四边形，如图，（2）如图，∠tan BAO=-+y xtan ODN∴∠3）如图，四边形BP=-4以OG为直径的圆经过点M，∠=BH BO BFH2OP=，∴=HO BO）BA AM ⊥MAN MAN =∠ANM PQ AB ⊥90ANM =︒，AQ MN =AN PQ ∴=，APM BPC ∠=∠AMB ∠+∠BC PQ PC ∴=，（角平分线的性质））2NP =，3PC =，∴AQ M N ==PAQ AMN ∠=∠tan ABC ∴∠，tan ABC ∠NE KC PEN PKC ENP KCP ∴∠=∠∠=∠∥，，又，PNE ∴△:2:3CK CF =，设2CK k =，则3CK k =(0)k ≠，2NE k ∴过N 作NT4，EF PM ⊥，EF NT NTC ∴∠=∠∥2，故CT PKC ∠+tan BDK ∴∠，tan BDK ∠37n n +==AB AC =DQ BQ ∴=。

2012年初中毕业与升学统一考试数学试卷(黑龙江哈尔滨市)

2012年黑龙江省哈尔滨市中考数学试卷及解析

2012年哈尔滨市道里区初中升学调研测试数学试卷(一)

数学考试后总结与反思

中国统一考试题库及答案

2012年初中毕业与升学统一考试数学试卷(贵州贵阳市)(详细解析)

中考真题电子版-数学哈尔滨-2012

2011年初中毕业升学考试(中考)数学试卷及答案

2006-2012【哈尔滨中考数学试题及答案】

盐城市二○一二年初中毕业与升学统一考试数学试卷

【初中数学】黑龙江省哈尔滨市2012年初中毕业学年调研测试数学试卷 通用

可数名词与不可数名词-讲义+练习题

2012年哈尔滨中考数学真题卷含答案解析

盐城市2012年初中毕业于升学统一考试数学试题与答案

2012年黑龙江省哈尔滨市中考数学试卷及解析

哈尔滨市中考考试说明

黑龙江省龙东地区2012年中考数学试题(word版,答案扫描版)

2024年黑龙江省哈尔滨市香坊区中考一模数学试题(解析版)

2024年中考数学总复习教学计划（五篇）

2012年黑龙江省哈尔滨市中考数学试卷-答案

【初中数学】黑龙江省哈尔滨市2012年初中毕业学年调研测试数学试卷通用