运筹学清华版习题答案(第五章)
清华大学运筹学教程胡运权主编课后习题答案
8 10
x1 , x2 0
目标函数最优值(下界)为:6.4
17
第18页/共66页
l.7 分别用单纯形法中的大M法和两阶 段法求解下列线性规划问题,并指出属哪—
类解。
max Z 3x1 x2 2x3
x1 x2 x3 6
(1)
st
2x1 2x2
x3 x3
0
2
x j 0(, j 1,,3)
所以最优解为X*=(1,3/2,0,0)T
第11页/共66页
0点
A1点 A2点
max Z 2x1 x2 3x1 5x2 15
(2) st.6x1 2x2 24 x1, x2 0
11
第12页/共66页
第13页/共66页
第14页/共66页
d
x
2
,
l.5 讨论c
,
上题(1)中,若目标函数变为max Z = d的值如何变化,使该问题可行域的每个
8
第9页/共66页
1.4 分别用图解法和单纯形法求解下述 线性规划问题,并对照指出单纯形表中的各 基可行解对应图解法中可行域的哪一顶点。
max Z 10x1 5x2
(1)
st.35xx11
4 x2 2 x2
9 8
x1, x2 0
9
第10页/共66页
cj
10
5 00
CB
xB
b
x1
x2
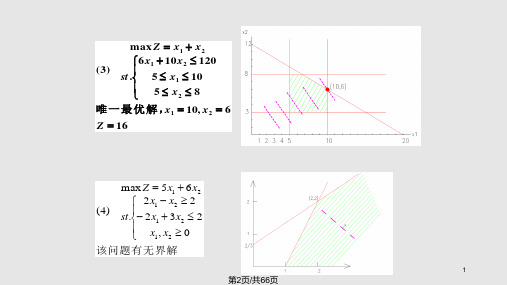
max Z x1 x2
(3)
st
6 .
x1 10x2 5 x1
120 10
5 x2 8
唯 一 最 优 解 ,x1 10, x2 6
Z 16
max Z 5x1 6x2 2x1 x2 2
题库 运筹学 清华版 1-5章

第一部分线性规划的基本概念一、填空题1.线性规划问题是求一个线性目标函数_在一组线性约束条件下的极值问题。
2.图解法适用于含有两个变量的线性规划问题。
3.线性规划问题的可行解是指满足所有约束条件的解。
4.在线性规划问题的基本解中,所有的非基变量等于零。
5.在线性规划问题中,基可行解的非零分量所对应的列向量线性无关6.若线性规划问题有最优解,则最优解一定可以在可行域的顶点(极点)达到。
7.线性规划问题有可行解,则必有基可行解。
8.如果线性规划问题存在目标函数为有限值的最优解,求解时只需在其基可行解_的集合中进行搜索即可得到最优解。
9.满足非负条件的基本解称为基本可行解。
10.在将线性规划问题的一般形式转化为标准形式时,引入的松驰数量在目标函数中的系数为零。
11.将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左_端加入松弛变量。
12.线性规划模型包括决策(可控)变量,约束条件,目标函数三个要素。
13.线性规划问题可分为目标函数求极大值和极小_值两类。
14.线性规划问题的标准形式中,约束条件取等式,目标函数求极大值,而所有变量必须非负。
15.线性规划问题的基可行解与可行域顶点的关系是顶点多于基可行解16.在用图解法求解线性规划问题时,如果取得极值的等值线与可行域的一段边界重合,则这段边界上的一切点都是最优解。
17.求解线性规划问题可能的结果有无解,有唯一最优解,有无穷多个最优解。
18.如果某个约束条件是“≤”情形,若化为标准形式,需要引入一松弛变量。
19.如果某个变量X j为自由变量,则应引进两个非负变量X j′,X j〞,同时令X j=X j′-X j。
20.表达线性规划的简式中目标函数为max(min)Z=∑c ij x ij。
21..(2.1 P5))线性规划一般表达式中,a ij表示该元素位置在i行j列。
二、单选题1.如果一个线性规划问题有n个变量,m个约束方程(m<n),系数矩阵的数为m,则基可行解的个数最为_C_。
清华大学《运筹学教程》胡运权主编课后习题答案

3 x1 x2 x5 3
st
4 x1 3 x2 x3 x6
x1
2 x2
x4
4
6
x j 0(, j 1,,4)
cj
CB
xB
b
-M x5 3
-M
x6
6
0
x4
4
cj zj
-4 x1 1
-M x6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
3
1
0
4
3 -1
1
20
7M-4 4M-1 -M
小于0 ,因此已经得到唯一最优解,最优解为:
X * 2 5 ,9 / 5,1,0T
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
6x2 x2 x3
15x3 5
15
x j 0(, j 1,,3)
39
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格,试求括
弧中未知数a∼l值。
项目
X1 X2 X3 X4 X5
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj-Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj-Zj
0 -7 (j) (k) (l)
6 4
x1 , x2 0
无穷多最优解
(蓝 色 线 段 上 的 点 都 是 最优 解 )
x1
6 5
,
x2
运筹学 第五章(清华三版)

构造割平面约束的一般方法如下: 构造割平面约束的一般方法如下: (1)在松弛问题的最优表中,设b列的第 个分量 k为 在松弛问题的最优表中, 列的第k个分量 在松弛问题的最优表中 列的第 个分量b 非整数,可将它分解为整数和非整数部分之和, 非整数,可将它分解为整数和非整数部分之和,即 bk =Nk + fk , Nk< bk 且为整数,0< fk <1。 且为整数, < 。 (2)然后,第k行中的每一个非基变量 xj的系数 akj也 然后, 然后 行中的每一个非基变量 分解为整数与非负数之和的形式, 分解为整数与非负数之和的形式,即 akj= Nkj + fkj ;Nkj ≤ akj ; 0≤ fk <1,则割平面方程为: 则割平面方程为: 则割平面方程为
−1
7
x3 − 2
7
x5 ≤ − 6
7
⑴
将割平面约束⑴变为等式约束后, ②将割平面约束⑴变为等式约束后,并入松弛问题 的最优表中,见下表。 的最优表中,见下表。
cj
CB
3 -1 0 0
3
-1
0
0
0
0
cj − zj
XB x1 x2 x4 x6
b
13/7 9/7 31/7 -6/7
x1
1 0 0 0 0
结论: 结论: 不能把松弛问题的最优解通过“四舍五入” ⑴ 不能把松弛问题的最优解通过“四舍五入” 或“截尾”(即凑整)处理后作为整数规划的 截尾” 即凑整) 最优解。不过,在变量取值很大时, 最优解。不过,在变量取值很大时,用上述方 法得到的解与最优解差别不大。 法得到的解与最优解差别不大。 不是可行域的顶点, ⑵ 点(4,1)不是可行域的顶点,所以直接用图解 不是可行域的顶点 法或单纯形法无法求出整数规划问题的最优 解.
清华_第三版_运筹学教程_课后答案~(_第一章_第五章部分)

清华第三版 运筹学 答案[键入文字] [键入文字] [键入文字]运筹学教程1. 某饲养场饲养动物出售,设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素.现有五种饲料可供选用,各种饲料每kg 营养成分含量及单价如表1所示. 表1要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
解:设总费用为Z.i=1,2,3,4,5代表5种饲料.i x 表示满足动物生长的营养需要时,第i 种饲料所需的数量.则有:⎪⎪⎩⎪⎪⎨⎧=≥≥++++≥++++≥++++++++=5,4,3,2,1,01008.022.05.0305.022.05.07008623..8.03.04.07.02.0min 54321543215432154321i x x x x x x x x x x x x x x x x t sx x x x x Z i2. 某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。
每班护士值班开始时间向病房报道,试决定:(1) 若护士上班后连续工作8h ,该医院最少需要多少名护士,以满足轮班需要; (2) 若除22:00上班的护士连续工作8h 外(取消第6班),其他班次护士由医院排定上1~4班的其中两个班,则该医院又需要多少名护士满足轮班需要.表2解:(1)设i x 第i 班开始上班的人数,i=1,2,3,4,5,6⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≥+≥+≥+≥+≥+≥++++++=且为整数6,5,4,3,2,1,0302050607060..min 655443322161654321i x x x x x x x x x x x x x t s x x x x x x Z i 解:(2)在题设情况下,可知第五班一定要30个人才能满足轮班需要。
则设设i x 第i 班开始上班的人数,i=1,2,3,4。
⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=≥=+++=≥+++=+++=≥+++=+++=≥+++=+++=≥+++++++=4,3,2,1,1002150216021702,160..30min i44434241444443342241143433323133443333223113242322212244233222211214131211114413312211114321j i y x y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y t s x x x x Z ij 变量,—是,,,第四班约束,,第三班约束,,第二班约束,第一班约束3. 要在长度为l 的一根圆钢上截取不同长度的零件毛坯,毛坯长度有n 种,分别为ja (j=1,2,…n )。
清华大学《运筹学教程》胡运权主编课后习题答案

-4 x1 1
-M x 6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
[3]
1
0
4
3 -1
1
20
7M-4 4M-1 -M
1
1/3 0
0 [5/3] -1
0
5/3 0
0 5M/3+1/3 -M
0 -M -M
i
x4
x5
x6
0
10
1
0
0 1 3/2
1
00
4
0
00
0 1/3 0 3
0 -4/3 1 6/5 1 -1/3 0 9/5 0 -7M/3+4/3 0
0
16/3
-7/6
(x2,x4,x6)
0
10
0
(x2,x5,x6)
0
3
0
(x3,x4,x6)
0
0
-5/2
(x3,x5,x6)
0
0
3/2
(x4,x5,x6)
0
0
0
x4
x5
x6
是否基
Z
可行解
0
0
0
否
-7
0
0
否
0
7/2
0
是
3
0
0
21/4
否
8
0
0
否
0
8
0
是
3
0
0
3
否
3
5
0
是
0
-2
0
15/4
否
0
2
9/4
清华大学《运筹学》教材相应的授课文档.第五章

= opt v k ( s k , u k ) + opt V k +1, n ( s k +1 , p k +1, n ) uk p k +1, n = opt {v k ( s k , u k ) + f k +1 ( s k +1 ) }
uk
* p k , n 表示 s k → s n的最优策略 , 则最优值函数
4.策略 策略:决策按顺序构成的序列,用p表示.
p k ,n ( sk ) : 第 k阶段起至第 n阶段止的策略 p k ,n ( s k ) = {u k ( sk ), u k +1 ( sk +1 )... , u n ( sn )} Pk ,n ( sk ) : 第 k阶段起至第 n阶段止的策略 p k ,n ( s k ) ∈ Pk ,n ( sk ) 当 k = 1时. p1,n ( s1 )为全过程策略 . p1,n ( s1 ) ∈ P ,n ( s1 ) 1
解:阶段n = 3, k = 1,2,3 s1 = A, s 2 = {B1 , B2 , B3}, s3 = {C1 , C2 }s4 = E u k = uk ( sk ) vk = vk ( sk , uk ) → 阶段运费 f k ( sk ) = min {vk ( sk , uk ) + f k +1 ( sk +1 )} k = 1,2,3 u ( k )∈Dk f 3+1 ( s3+1 ) = f 4 ( E ) = 0
4.2基本方程 设指标函数为 n
Vk ,n =
∑ v j ( s j , u j ) = v k ( s k , u k ) + V k + 1, n
《运筹学》 第五章习题及 答案
《运筹学》第五章习题1.思考题(1)试述动态规划的“最优化原理”及它同动态规划基本方程之间的关系。
(2)动态规划的阶段如何划分?(3)试述用动态规划求解最短路问题的方法和步骤。
(4)试解释状态、决策、策略、最优策略、状态转移方程、指标函数、最优值函数、边界函数等概念。
(5)试述建立动态规划模型的基本方法。
(6)试述动态规划方法的基本思想、动态规划的基本方程的结构及正确写出动态规划基本方程的关键步骤。
2.判断下列说法是否正确(1)动态规划分为线性动态规划和非线性动态规划。
(2)动态规划只是用来解决和时间有关的问题。
(3)对于一个动态规划问题,应用顺推法和逆推法可能会得到不同的最优解。
(4)在用动态规划的解题时,定义状态时应保证各个阶段中所做的决策的相互独立性。
(5)在动态规划模型中,问题的阶段等于问题的子问题的数目。
(6)动态规划计算中的“维数障碍”,主要是由于问题中阶段数的急剧增加而引起的。
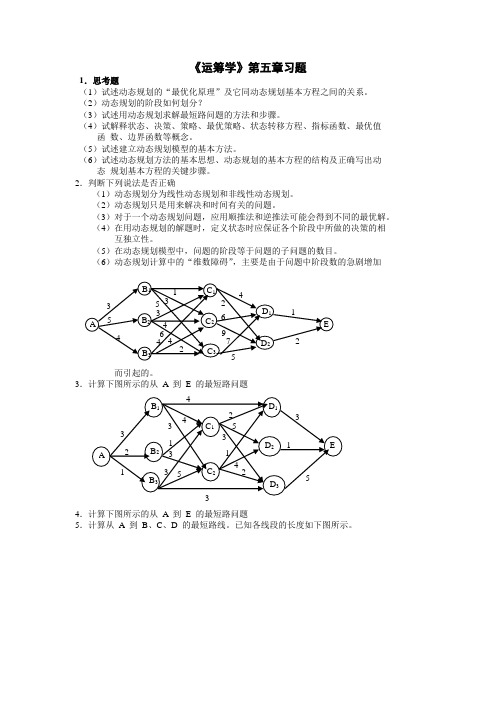
3.计算下图所示的从A 到E 的最短路问题4.计算下图所示的从A 到E 的最短路问题5.计算从A 到B、C、D 的最短路线。
已知各线段的长度如下图所示。
6.设某油田要向一炼油厂用管道供应油料,管道铺设途中要经过八个城镇,各城镇间的路程如下图所示,选择怎样的路线铺设,才使总路程最短?7.用动态规划求解下列各题(1).222211295max x x x x z -+-=;⎩⎨⎧≥≤+0,52121x x x x ;(2).33221max x x x z =⎩⎨⎧≥≤++0,,6321321x x x x x x ;8.某人外出旅游,需将3种物品装入背包,但背包重量有限制,总重量不超过10千克。
物品重量及其价值等数据见下表。
试问每种物品装多少件,使整个 背包的价值最大?913 千克。
物品重量及其价值的关系如表所示。
试问如何装这些物品,使整个背包 价值最大?10 量和相应单位价值如下表所示,应如何装载可使总价值最大?303011 底交货量,该厂的生产能力为每月600件,该厂仓库的存货能力为300件,又 每生产100件产品的费用为1000元。
运筹学第五章作业答案(1)教案资料

1
2
3
4
5
0
0
4
4
1
6
6
2
11
11
3
12
12
4
12
12
5
《运筹学》Ⅰ史慧萍
5
(阶段2)
x2
s2 0
0
0+0
1
0+4
2
0+6
3
0+11
4
0+12
5
0+12
2015/5/4
f2(s2) =P2(x2)+ f3(s2 -x2 )
1
2
3
4
5
5+0 5+4 10+0 5+6 10+4 11+0 5+11 10+6 11+4 11+0 5+12 10+11 11+6 11+4 11+0
《运筹学》Ⅰ史慧萍
f2(s2)
0 5 10 14 16 21
x2*(决)
0 1 2 2 1,2 2
6
(1)(设备数为4台): (阶段1)
s1
x1
f1(s1) =P1(x1)+ f2(4 -x1 )
f1(s1) =f1(4) x1*(决)
0
1
2
3
4
4
0+16 3+14 7+10 9+5 12+0
17
1,2
由计算表格的顺序反推:
1.由于x1*=1,根据s2=s1-x1*=4-1=3。查表知: x2*=2;由s3=s2-x2*=3-2=1, 故x3*=s3=1,即得到:甲工厂分配1台,乙工厂分配2台,丙工厂分配1台。 2.由于x1*=2,根据s2=s1-x1*=4-2=2。查表知: x2*=2;由s3=s2-x2*=2-2=0, 故x3*=s3=0,即得到:甲工厂分配2台,乙工厂分配2台,丙工厂分配0台。 以上两种分配方案的总盈利为17万元。
清华线性代数第五章课后习题及解答

第五章课后习题及解答3 -37穴1 =, $1.求下列矩阵的特征值和特征向量: (1)-3-31丿/\~37 A.所以, (■ 1I - A )X = 0的基础解系为:(6,1-一 37)T .因此,A 的属于'i 的所有特征向量为:匕(6,1 -、37)丁(匕=0).2I所以,(’2l-A )x=0的基础解系为:(6,1 . 37)T .因此,A 的属于■ 2的所有特征向量为:k 2(6,1 37)T (k 2 =0).'3 -1九-31-1 ⑵ 2 0 1 : 解: 打-A =-2 丸-1-12」-11h -2nn2亠=('-1)「-2)解:-2 3所以,特征值为:’1=1(单根),'2=2(二重根)J 2 1 -1、5 0 0、入 1 — A =-21 -1T0 1-11 -b1°0 °」所以,(、| —A )x =o 的基础解系为:(0,1,1)T .因此,A 的属于-1的所有特征向量为: 匕(0,1,1)丁你1 =0).'-11 -1、1 -1'花 1 — A =-2 2 -1 T 0 0 1r 11><00 0」所以,(,2l -A )x =:0的基础解系为:(1,1,0)T .因此,A 的属于-2的所有特征向量为:k 2(1,1,0)T (k 2 =0).所以,特征值为:1=2 (二重根)*0 0 0 "人I —A= -1 1—1 TIT 1 -b所以,(\l -A )X=0 的基础解系为:(1,1,0)T ,(-1,0,1)T .九-20 0 扎1—A=-1 丸-1 -1-11九一32 0 0' ⑶ 1 1 1 解:J -1 3」2)-210所以,(■1l -A )x =0的基础解系为:(1,0,0,0)T .因此,A 的属于 > 的所有特征向量为: k 1(1,0,0,0)T (k^-0)所以,特征值为:'1 - 1 (三重根)'-3 -5 2、「10 1、入1 —A=2 3-1 T ■" T 0 1 -1J1 0」e 0 0」T所以,(‘1l _A )x =0的基础解系为:(-1,1,1) •q 2 3 4^扎—1-2-3 -4 0 1 2 3解:XJ — A =0 &一1-2-3 0 0 1 2 0 0 九-1-2 1°0 0 bZ-1因此,A 的属于-i 的所有特征向量为:k i (1,1,0)T • k 2(-1,0,1)T (k i ,k 2为不全为零的任 意吊数)。
运筹学习题答案(第五章)

擅长位 中 中 前 前 置 锋 锋 锋 锋 出场阵容应满足以下条件:
前 锋
后 卫
后 卫
后 卫
(1) 只能有一名中锋上场; (2) 至少有—名后卫; (3) 如1号和4号均—上场,则6号不出场;
第五章习题解答
(4) 2号和8号至少有一个不出场。 问应当选择哪5名队员上场,才能使 出场队员平均身高最高,试建立数学模型。
解:设 x i 1表示第 i 个队员出场, max Z 1 i 1, 2 , , n 。
5
8
xi
i 1
8 xi 5 i 1 x1 x 2 1 x 6 x 7 x 8 1 x x 1 x x x 2 8 1 4 6 2 x i 是 0 1变量
第五章习题解答
解:设 x i 1表示第 i 项任务被选中, max Z 7 x 1 17 x 2 11 x 3 9 x 4 21 x 5 3 x 1 8 x 2 5 x 3 4 x 4 10 x 5 20 x x2 x3 x4 x5 3 1 x1 x 2 x x 1 4 3 x i 是 0 - 1变量 , i 1, 2 , 3 , 4 , 5 i 1, 2 , , 5。
j 1 n
i 1, 2 , , p
p
yi q
i 1
第五章习题解答
5.13 解下列系数矩阵的最小化问题:
(1) 10 7 5 13
3 7 3 6 5 5
运筹学(第五版) 习题答案

运筹学习题答案第一章(39页)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)max 12z x x =+ 51x +102x ≤501x +2x ≥12x ≤4 1x ,2x ≥0(2)min z=1x +1.52x1x +32x ≥3 1x +2x ≥2 1x ,2x ≥0(3)max z=21x +22x1x -2x ≥-1-0.51x +2x ≤21x ,2x ≥0(4)max z=1x +2x1x -2x ≥031x -2x ≤-31x ,2x ≥0解: (1)(图略)有唯一可行解,max z=14 (2)(图略)有唯一可行解,min z=9/4 (3)(图略)无界解 (4)(图略)无可行解1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)min z=-31x +42x -23x +54x 41x -2x +23x -4x =-21x +2x +33x -4x ≤14-21x +32x -3x +24x ≥21x ,2x ,3x ≥0,4x 无约束(2)max kkz s p =11nmk ik ik i k z a x ===∑∑11(1,...,)mikk xi n =-=-=∑ik x ≥0 (i=1…n; k=1,…,m)(1)解:设z=-z ',4x =5x -6x , 5x ,6x ≥0 标准型:Max z '=31x -42x +23x -5(5x -6x )+07x +08x -M 9x -M 10x s. t .-41x +2x -23x +5x -6x +10x =21x +2x +33x -5x +6x +7x =14-21x +32x -3x +25x -26x -8x +9x =21x ,2x ,3x ,5x ,6x ,7x ,8x ,9x ,10x ≥0(2)解:加入人工变量1x ,2x ,3x ,…n x ,得: Max s=(1/k p )1ni =∑1mk =∑ik αik x -M 1x -M 2x -…..-M n xs.t.11mi ik k x x =+=∑ (i=1,2,3…,n)ik x ≥0, i x ≥0, (i=1,2,3…n; k=1,2….,m)M 是任意正整数1.3在下面的线性规划问题中找出满足约束条件的所有基解。
运筹学5、7章作业题参考答案

运筹学第五章作业题参考答案5.1 解:设在A j 处建Xj 幢住宅. 则数学模型为 Max z =∑=ni jx1⎪⎩⎪⎨⎧且为整数01≥≤≤∑=j jj ni jj x a x Ddx5.2 解:设每种毛坯截取Xj 根 则数学模型为 Max z =∑=ni jx1⎪⎩⎪⎨⎧≥≤∑=且为整数01jj j ni x l x a 5.4 解:设X i =⎩⎨⎧名队员不上场第名队员上场第i 0i 1数学模型为:Max Z =( 1.92X 1+1.92X 2+…+1.78X 8)/5⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==≤+≤++≥++=+∑=5051211818264187621或i i i X X X X X X X X X X X X5.6 用割平面法解下列整数规划 (1) Max Z = X 1 + X 2 s.t⎪⎩⎪⎨⎧≥≤+≤+且为整数、0X 205462212121X X X X X 解:将其化为标准型为 Max Z = X 1 + X 2 s.t ⎪⎩⎪⎨⎧≥=++=++且为整数0,20546221421321X X X X X X X X从表中第二行产生割平面的约束条件: -1/3 X 3 - 1/3 X 43/2-≤ 引入松弛变量X 5为: -1/3 X 3 – 1/3 X 4 + X 5=-2/3∴X *=(0, 4)T 或 ( 2, 2)T , Z *=4(2) MinZ=51X +X 2⎪⎪⎩⎪⎪⎨⎧≥≥+≥+≥+且为整数0,8859321212121X X X X X X X X 解: 化为标准型为 max z ‘=-51X -X 2⎪⎪⎩⎪⎪⎨⎧≥-=+---=+---=+--0,,,,8859354321521421321X X X X X X X X X X X X X X因此,原问题的最优解为X=( 0, 9 ) T ,最优值Z * = 9 5.7用分支定界法解下列整数规划 (1) Max Z=2X 1+X 2⎪⎪⎩⎪⎪⎨⎧≥≤+≤+-≤+且为整数0,21260521212121X X X X X X X X解:用图解法求得该整数规划的松弛问题的最优解为 X 1=X 2=21/8 选择X 1=21/8进行分支B1: B2: Max Z =2X 1+X 2 Max Z =2X 1+X 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤+≤+-≤+0,2212605211212121X X X X X X X X X ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤+-≤+0,3212605211212121X X X X X X X X X 最优解为X 1=2 X 2=3 Z *=7; 最优解X 1=3 X 2= 3/2 Z *=15/2 > 7 选择X 2= 3/2进行分支B3 B4Max Z =2X 1+X 2 Max Z =2X 1+X 2⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤≥≤+≤+-≤+0,132126052121212121X X X X X X X X X X ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥≥≤+≤+-≤+0,223212605211212121X X X X X X X X X X 最优解为X 1=19/6 X 2=1 Z *=22/3 > 7; 无可行解 选择X 1=19/6 进行分支B5 B6 Max Z =2X 1+X 2⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≤≤≥≤+≤+-≤+0,31321260521121212121X X X X X X X X X X X ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧≥≥≤≥≤+≤+-≤+0,41321260521121212121X X X X X X X X X X X 最优解为X 1=3 X 2=1 Z *= 7; B6无可行解综上:原整数规划最优解为 X *= ( 2 , 3)或 ( 3 , 1) Z *=7 5.8 解下列0~1型 整数规划: (2) Max Z =2X 1+X 2- X 3⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥-+≤-+≤+≤++10,44225423,3,2132132132321或X X X X X X X X X X X X X X 解:最优解为X *=(1 , 0 , 0 )T Z *= 25.11(1) 解:引入一个虚拟人A 5,使之成为标准的指派问题,则系数矩阵为C = ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0000071011151314129651214101178241110将各行元素减去本行的最小元素得C →⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛0000003486974105734060298 = C ˊ由于只有4个独立零元素,小于系数矩阵阶数n=5,所以将第二行,第三行,第四行都减去1,第一列和第五列加上1得C ˊ→⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---00012375863014623160298→⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛1000102376963005623070299= C 〞C 〞中有5个独立零元素,则可确定指派问题的最优指派方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i =1 n
n ∑ ai xi ≤ l i =1 x 是整数 i
page 4 23 April 2012
School of Management
运筹学教程
第五章习题解答
5.3 有一批每根长度为 的圆钢,需要截取 种不 有一批每根长度为l的圆钢 需要截取n种不 的圆钢, 同长度的零件毛坯。长度为a 的毛坯必须有m 同长度的零件毛坯。长度为 j的毛坯必须有 j段(j=1, = , 2,…,n)。为了方便,每根圆钢只截取一种长度的 , , 。为了方便, 毛坯。应当怎样截取,才能使动用的圆钢数目最少, 毛坯。应当怎样截取,才能使动用的圆钢数目最少, 要求建立数学模型。 要求建立数学模型。
page 9 23 April 2012
School of Management
运筹学教程
第五章习题解答
5.6 用割平面法解下列整数规划: 用割平面法解下列整数规划:
max Z = x1 + x 2 2 x1 + x 2 ≤ 6 st . 4 x1 + 5 x 2 ≤ 20 x , x ≥ 0, 且为整数 1 2
page 10 23 April 2012
School of Management
运筹学教程
第五章习题解答
5.7 用分支定界法解下列整数规划: 用分支定界法解下列整数规划:
max Z = 2 x1 + x 2 x1 + x 2 ≤ 5 − x + x ≤ 0 (1) 2 . st 1 6 x1 + 2 x 2 ≤ 21 x1 , x 2 ≥ 0, 且为整数 解: x1 = 3, x 2 = 1, Z = 7 min Z = 5 x1 − x 2 + 2 x3 3 x1 + 10 x 2 ≤ 50 7 x − 2 x ≤ 28 ( 2) 2 . st 1 x1 , x 2 ≥ 0 x 2为整数 解: x1 = 0, x 2 = 5, x3 = 0, Z = − 5
分别表示三个产品的产量。 解:设x1,x2,x3分别表示三个产品的产量。 Y11,y12,y13,y14对应产品A的4个成本的 变量; 对应产品 的 个成本的0-1变量; 个成本的 变量 Y21,y22,y23对应产品 的3个成本的 变量; 对应产品B的 个成本的 变量; 个成本的0-1变量 Y31,y32对应产品 的3个成本的 变量; 对应产品B的 个成本的 变量; 个成本的0-1变量
运筹学教程
第五章习题解答
5.2 要在长度为 的一根圆钢上截取不同长度的零 要在长度为l的一根圆钢上截取不同长度的零 件毛坯,毛坯长度有n种 分别为a 件毛坯,毛坯长度有 种,分别为 j,(j=1,2,…,n)。 , , 。 问每种毛坯应当各截取多少根,才能使圆钢残料最少, 问每种毛坯应当各截取多少根,才能使圆钢残料最少, 试建立本问题的数学模型。 试建立本问题的数学模型。
page 7 23 April 2012
School of Management
运筹学教程
第五章习题解答
5.5 一个旅行者要在其背包里装一些最有用的旅 行物品。背包容积为a,携带物品总重量最多为b。现 行物品。 背包容积为 , 携带物品总重量最多为 。 有物品m 物品体积为 积为a 量为b 有物品 件 , 第 i 件 物品体 积为 i , 重 量为 i(i = 1, , 2,…,m)。为了比较物品的有用程度,假设第j件物 , , 。 为了比较物品的有用程度, 假设第 件物 品的价值为c = , , , 。 品的价值为 i(i=1,2,…,m)。若每件物品只能整件 携带,每件物品都能放人背包中, 携带 , 每件物品都能放人背包中 , 并且不考虑物品放 人背包后相互的间隙。问旅行者应当携带哪几件物品, 人背包后相互的间隙 。 问旅行者应当携带哪几件物品, 才能使携带物品的总价值最大, 才能使携带物品的总价值最大 , 要求建立本问题的数 学模型。 学模型。
page 12 23 April 2012
School of Management
运筹学教程
第五章习题解答
表5-11-12-13 11-12产品A 产品B 产品C 产品A 成本 产品B 成本 产品C 成本 产量( 产量( 产量( 产量(件)(元/件) 产量(件) (元/件) 产量(件) (元/件) 0~100 100 0~40 40 0~50 50 10 6 5 41~100 41 100 101~150 101 150 150以上 150以上 9 8 7 51~100 51 100 100以上 100以上 4 3 100以上 100以上 4
表5-10 队员 身高(m) 身高 擅长位置 1 1.92 2 1.90 3 1.88 4 1.86 5 1.85 6 1.83 7 1.80 8 1.78
中锋 中锋 前锋 前锋 前锋 后卫 后卫 后卫
出场阵容应满足以下条件: 出场阵容应满足以下条件: (1) 只能有一名中锋上场; 只能有一名中锋上场; (2) 至少有—名后卫; 至少有—名后卫; (3) 如1号和 号均—上场,则6号不出场; 号和4号均 号不出场; 号和 号均—上场, 号不出场
解:设 xi 表示在 Ai 处所建住宅的数量 , i = 1, 2, L , n 。 max Z = ∑ xi
i =1 n
n ∑ d i xi ≤ D , i =1 x 是整数 i
page 3 23 April 2012
xi ≤ a i
i = 1, 2, L , n
School of Management
(1)
解: x1 = 1, x 2 = 3, Z = 4
min Z = 5 x1 + x 2 3 x1 + x 2 ≥ 9 x + x ≥ 5 ( 2) 2 . st 1 x1 + 8 x 2 ≥ 8 x1 , x 2 ≥ 0, 且为整数 解: x1 = 4, x 2 = 1, Z = 5
page 14 23 April 2012
School of Management
运筹学教程
第五章习题解答
5.9 解下列 型整数规划: 解下列0-1型整数规划: 型整数规划
max Z = 2 x1 + x 2 − x3 min Z = 5 x1 + 7 x 2 + 10 x3 + 3 x 4 + x5 x1 + 3 x 2 + x3 ≤ 2 x1 − 3 x 2 + 5 x3 + x 4 − 4 x5 ≥ 2 4x + x ≤ 5 2 3 − 2 x + 6 x − 3 x − 2 x + 2 x ≥ 0 ( 2) (1) 1 2 3 4 5 st . x1 + 2 x 2 − x3 ≤ 2 st . x + 4x − x ≤ 4 − 2 x 2 + 2 x 3 − x 4 − x5 ≥ 1 2 3 1 x1 , x 2 , x3 , x 4 , x5 = 0或1 x1 , x 2 , x3 = 0或1 解:此题无解。 解: x1 = 1, x 2 = x3 = x 4 = 0, Z = 2
运筹学教程
第五章习题解答
5.1 某地准备投资 元建民用住宅。可以建住宅 某地准备投资D元建民用住宅 元建民用住宅。 的地点有n处:A1,A2,…,An。在Ai处每幢住宅的 的地点有 处 , 造价为d ;,最多可造 最多可造a 问应当在哪几处建住宅, 造价为 j;,最多可造 j幢。问应当在哪几处建住宅, 分别建几幢,才能使建造的住宅总数最多, 分别建几幢,才能使建造的住宅总数最多,试建立问 题的数学模型。 题的数学模型。
page 11 23 April 2012
School of Management
运筹学教程
第五章习题解答
5.8 某公司生产 ,B和C 3种产品,售价分别为 某公司生产A, 和 种产品 售价分别为12 种产品, 元和6元 生产每件A产品需要 技术服务、 产品需要1h技术服务 元、7元和 元。生产每件 产品需要 技术服务、10h 元和 直接劳动、 材料; 产品需要2h技术服务 直接劳动、3kg材料;生产每件 产品需要 技术服务、 材料 生产每件B产品需要 技术服务、 4h直接劳动、2kg材料;生产每件 产品需要 技术服 直接劳动、 材料; 产品需要1h技术服 直接劳动 材料 生产每件C产品需要 务、5h直接劳动、1k8材料。现在最多能提供100h技术 直接劳动、 材料。现在最多能提供 技术 直接劳动 材料 服务、 直接劳动、 材料。 服务、700h直接劳动、400kg材料。生产成本是生产量 直接劳动 材料 的非线性函数,如表5-11、表5-12、表5-13所示。要求 所示。 的非线性函数,如表 、 、 所示 建立一个总利润最大的生产计划的数学模型。提示: 建立一个总利润最大的生产计划的数学模型。提示: 对每种产品不同成本的产量范围各设一个0-1变量 变量。) 对每种产品不同成本的产量范围各设一个 变量。)
解:设 xi = 1表示第 i个队员出场, i = 1, 2, L , n 。 1 8 max Z = ∑ xi 5 i =1 8 ∑ xi = 5 i =1 x + x ≤ 1 x + x + x ≥ 1 1 2 6 7 8 x + x ≤ 1 x + x + x ≤ 2 8 1 4 6 2 xi 是 0 − 1变量
page 8 23 April 2012
School of Management
运筹学教程
第五章习题解答
解:设 xi = 1表示携带第 i件物品, i = 1, 2, L , m 。 max Z = ∑ ci xi
