第十八章-平行四边形-知识点总结

合集下载

第十八章平行四边形

平行四边形知识要求：1、掌握平行四边形、菱形、矩形、正方形的性质和判定；2、结合图形性质进行相关的角度和线段的计算。

3、结合几何图形证明。

知识重点：四边形性质的运用和判定是本章的重点。

知识难点：四边形性质的运用和判定是本章的难点。

考点：结合图形性质进行相关的角度和线段的计算及判定是考试的重点对象。

知识点：一、平行四边形1、定义：两组对边分别平行的四边形是平行四边形．符号：“”2、性质：对边相等、对角相等、对角线互相平分边：对边相等、平行角：对角相等、邻角互补对角线：平分周长：邻边之和*2面积：底*高平行四边形是中心对称图形，两条对角线的交点是对称中心例题1．已知平行四边形ABCD中，∠B=5∠A，则∠D= ．例题2如图，在□ABCD中，已知AD＝8cm， AB＝6cm， DE平分∠ADC交BC边于点E，则BE等于（）A．2cm B．4cm C．6cm D．8cm例题3如图，平行四边形ABCD的对角线AC、BD相交于点O，下列结论不正确的是（）A．DC∥AB B．OA=OC C．AD=BC D．DB平分∠ADCEBAFCD3、判定：边：两组对边分别平行的四边形是平行四边形两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形角：两组对角分别相等的四边形是平行四边形对角线：两条对角线互相平分的四边形是平行四边形例题4. 在四边形ABCD 中，对角线AC 、BD 相交于点O ，给出下列四组条件：① AB ∥CD ，A D ∥BC ；②AB ＝CD ，AD ＝BC ；③AO ＝CO ，BO ＝DO ；④AB ∥CD ，AD ＝BC ．其中，一定能判定四边形ABCD 是平行四边形的条件共有 ( ) A ．1组 B ．2组 C ．3组 D ．4组例题5如图，在等边三角形ABC 中，BC=6cm,射线AG ∥BC ，点E 从点A 出发沿射线AG 以1cm/s 的速度运动，点F 从点B 出发沿射线BC 以2cm/s 的速度运动.如果点E 、F 同时出发，设运动时间为t(s)当t= s 时，以A 、C 、E 、F 为顶点四边形是平行四边形.例题6.如图，在四边形ABCD 中，E 是BC 边的中点，连结DE 并延长，交AB 的延长线于F 点，AB BF =．添加一个条件，使四边形ABCD 是平行四边形．你认为下面四个条件中可选择的是（）A ．AD BC =B ．CD BF =C ．A C ∠=∠D ．F CDE ∠=∠ 例题7如图，EF ，是四边形ABCD 的对角线AC 上两点， AF CE DF BE DF BE ==，，∥．求证：（1）AFD CEB △≌△．（2）四边形ABCD 是平行四边形．4、三角形的中位线：三角形的中位线平行与第三边，且等于第三边的一半．（与中线区别）例题8如图，在△ABC 中，点D 、E 分别是AB 、AC 的中点，∠A ＝50°，∠ADE ＝60°，则∠C 的度数为 ( )A B DE F CA．50°B．60°C．70°D．80°例题9一个周长为12cm的三角形，三条中位线围成的三角形周长是cm．二、菱形1、定义：有一组邻边相等的平行四边形叫做菱形．2、性质：对边相等、对角相等、对角线互相垂直平分且平分对角边：四边相等、对边平行角：对角相等、邻角互补对角线：垂直平分、平分对角周长：边长*4面积：对角线乘积的一半(底*高)菱形是中心对称图形，两条对角线的交点是对称中心，也是轴对称图形。

初中数学：18.1.1 平行四边形的性质(人教版八年级数学下册第十八章平行四边形)

18．1平行四边形18．1.1平行四边形的性质第1课时平行四边形的边、角的特征1.理解平行四边形的定义及有关概念。

2.能根据定义探索并掌握平行四边形的对边相等、对角相等的性质。

3.了解平行四边形在实际生活中的应用，能根据平行四边形的性质进行简单的计算和证明。

重点：平行四边形的概念和性质。

难点：如何添加辅助线将平行四边形问题转化为三角形问题解决的思想方法.1.平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．平行四边形的定义既是平行四边形的性质，也是判断一个四边形是平行四边形的重要方法．2.平行四边形的性质：（1）平行四边形的对角相等，邻角互补；（2）平行四边形的对边平行且相等；（3）平行四边形的对角线互相平分.平行四边形的性质为以后证明线段平行或相等以及角相等提供了新的理论依据.3.推论：夹在两条平行线间的平行线段相等．探究点一：平行四边形的定义如图，在四边形ABCD中，∠B＝∠D，∠1＝∠2.求证：四边形ABCD是平行四边形．解析：根据三角形内角和定理求出∠DAC＝∠ACB，根据平行线的判定推出AD∥BC，AB∥CD，根据平行四边形的定义推出即可．证明：∵∠1＋∠B＋∠ACB＝180°，∠2＋∠D＋∠CAD＝180°，∠B＝∠D，∠1＝∠2，∴∠DAC＝∠ACB，∴AD∥BC.∵∠1＝∠2，∴AB∥CD，∴四边形ABCD是平行四边形．方法总结：平行四边形的定义既是平行四边形的性质，也是判断一个四边形是平行四边形的重要方法．探究点二：平行四边形的边、角特征【类型一】利用平行四边形的性质求边长如图，在△ABC中，AB＝AC＝5，点D，E，F分别是AC，BC，BA延长线上的点，四边形ADEF为平行四边形，DE＝2，则AD＝________．解析：∵四边形ADEF为平行四边形，∴DE＝AF＝2，AD＝EF，AD∥EF，∴∠ACB ＝∠FEB.∵AB＝AC，∴∠ACB＝∠B，∴∠FEB＝∠B，∴EF＝BF.∴AD＝BF，∵AB＝5，∴BF＝5＋2＝7，∴AD＝7.方法总结：本题考查了平行四边形对边平行且相等的性质及等腰三角形的性质，熟练掌握各性质是解题的关键．【类型二】利用平行四边形的性质求角如图，在平行四边形ABCD中，CE⊥AB于E，若∠A＝125°，则∠BCE的度数为A．35°B．55°C．25°D．30°解析：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠A＋∠B＝180°.∵∠A＝125°，∴∠B＝55°.∵CE⊥AB于E，∴∠BEC＝90°，∴∠BCE＝90°－55°＝35°.故选A.方法总结：平行四边形对角相等，邻角互补，并且已知一个角或已知两个邻角的关系，可求出其他角，所以利用该性质可以解决和角度有关的问题．【类型三】利用平行四边形的性质证明有关结论如图，点G 、E 、F 分别在平行四边形ABCD 的边AD 、DC 和BC 上，DG ＝DC ，CE ＝CF ，点P 是射线GC 上一点，连接FP ，EP .求证：FP ＝EP .解析：根据平行四边形的性质推出∠DGC ＝∠GCB ，根据等腰三角形性质求出∠DGC ＝∠DCG ，推出∠DCG ＝∠GCB ，根据“等角的补角相等”求出∠DCP ＝∠FCP ，根据“SAS”证出△PCF ≌△PCE 即可得出结论．证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠DGC ＝∠GCB .∵DG ＝DC ，∴∠DGC ＝∠DCG ，∴∠DCG ＝∠GCB .∵∠DCG ＋∠ECP ＝180°，∠GCB ＋∠FCP ＝180°，∴∠ECP ＝∠FCP .在△PCF 和△PCE ＝CE ，FCP ＝∠ECP ，＝CP ，∴△PCF ≌△PCE (SAS)，∴PF ＝PE .方法总结：平行四边形性质，等腰三角形的性质，全等三角形的性质和判定等常综合应用，利用平行四边形的性质可以解决一些相等的问题，在证明时应用较多．【类型四】判断直线的位置关系如图，在平行四边形ABCD 中，AB ＝2AD ，M 为AB 的中点，连接DM 、MC ，试问直线DM 和MC 有何位置关系？请证明．解析：由AB ＝2AD ，M 是AB 的中点的位置关系，可得出DM 、CM 分别是∠ADC 与∠BCD 的平分线．又由平行线的性质可得∠ADC ＋∠BCD ＝180°，进而可得出DM 与MC 的位置关系．解：DM 与MC 互相垂直．证明如下：∵M 是AB 的中点，∴AB ＝2AM .又∵AB ＝2AD ，∴AM ＝AD ，∴∠ADM ＝∠AMD .∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠AMD ＝∠MDC ，∴∠ADM ＝∠MDC ，则∠MDC ＝12∠ADC ，同理∠MCD ＝12∠BCD .∵AD ∥BC ，∴∠ADC ＋∠DCB ＝180°，∴∠MDC ＋∠MCD ＝12∠BCD ＋12∠ADC ＝90°.∵∠MDC ＋∠MCD ＋∠DMC ＝180°，∴∠DMC ＝90°，∴DM 与MC 互相垂直．方法总结：根据平行四边形的性质，将已知条件转化到同一个三角形中，即可判断两条直线的关系．探究点三：两平行线间的距离如图，已知l1∥l 2，点E ，F 在l 1上，点G ，H 在l 2上，试说明△EGO 与△FHO 面积相等．解析：结合平行线间的距离相等和三角形的面积公式即可证明．证明：∵l 1∥l 2，∴点E ，F 到l 2之间的距离都相等，设为h .∴S △EGH ＝12GH ·h ，S △FGH ＝12GH ·h ，∴S △EGH ＝S △FGH ，∴S △EGH －S △GOH ＝S △FGH －S △GOH ，∴△EGO 的面积等于△FHO 的面积．方法总结：根据两平行线间的距离可知，夹在两条平行线间的任何平行线段都相等，而后可推出两三角形同底等高，面积相等．第2课时平行四边形的对角线的特征1.探索并掌握平行四边形的性质：平行四边形的对角线互相平分.2.会运用平行四边形的性质进行推理和计算.重点：平行四边形的对角线互相平分.难点：平行四边形性质的灵活运用及几何计算题的解题表达.平行四边形的性质：（1）平行四边形的对角相等，邻角互补；（2）平行四边形的对边平行且相等；（3）平行四边形的对角线互相平分.平行四边形的性质为以后证明线段平行或相等以及角相等提供了新的理论依据.探究点一：平行四边形的对角线互相平分【类型一】利用平行四边形对角线互相平分求线段已知▱ABCD 的周长为60cm ，对角线AC 、BD 相交于点O ，△AOB 的周长比△DOA的周长长5cm ，求这个平行四边形各边的长．解析：平行四边形周长为60cm ，即相邻两边之和为30cm.△AOB 的周长比△DOA 的周长长5cm ，而AO 为共用，OB ＝OD ，因而由题可知AB 比AD 长5cm ，进一步解答即可．解：∵四边形ABCD 是平行四边形，∴OB ＝OD ，AB ＝CD ，AD ＝BC .∵△AOB 的周长比△DOA 的周长长5cm ，∴AB －AD ＝5cm ，又∵▱ABCD 的周长为60cm ，∴AB ＋AD ＝30cm ，则AB ＝CD ＝352cm ，AD ＝BC ＝252cm.方法总结：平行四边形被对角线分成四个小三角形，相邻两个三角形的周长之差等于邻边边长之差．【类型二】利用平行四边形对角线互相平分证明线段或角相等如图，▱ABCD 的对角线AC 、BD 相交于点O ，EF 过点O 与AB 、CD 分别相交于点E 、F .求证：OE ＝OF .解析：根据平行四边形的性质得出OD ＝OB ，DC ∥AB ，推出∠FDO ＝∠EBO ，证出△DFO ≌△BEO 即可．证明：∵四边形ABCD 是平行四边形，∴OD ＝OB ，DC ∥AB ，∴∠FDO ＝∠EBO .在△DFO 和△BEO ∠FDO ＝∠EBO ，OD ＝OB ，∠FOD ＝∠EOB ，∴△DFO ≌△BEO (ASA)，∴OE ＝OF .方法总结：利用平行四边形的性质解决线段的问题时，要注意运用平行四边形的对边相等，对角线互相平分的性质．【类型三】判断直线的位置关系如图，平行四边形ABCD 中，AC 、BD 交于O 点，点E 、F 分别是AO 、CO 的中点，试判断线段BE 、DF 的关系并证明你的结论．解析：根据平行四边形的性质“对角线互相平分”得出OA ＝OC ，OB ＝OD .利用中点的意义得出OE ＝OF ，从而利用△FOD ≌△EOB 可得出BE ＝DF ，BE ∥DF .解：BE ＝DF ，BE ∥DF .理由如下：∵四边形ABCD 是平行四边形，∴OA ＝OC ，OB ＝OD .∵E 、F 分别是OA 、OC 的中点，∴OE ＝OF ，又∵∠FOD ＝∠EOB ，∴△FOD ≌△EOB (SAS)，∴BE ＝DF ，∠ODF ＝∠OBE ，∴BE ∥DF .方法总结：在解决平行四边形的问题时，如果有对角线的条件时，则首选对角线互相平分的方法解决问题．探究点二：平行四边形的面积在▱ABCD 中，(1)如图①，O 为对角线BD 、AC 的交点．求证：S △ABO ＝S △CBO ；(2)如图②，设P 为对角线BD 上任一点(点P 与点B 、D 不重合)，S △ABP 与S △CBP 仍然相等吗？若相等，请证明；若不相等，请说明理由．解析：(1)根据“平行四边形的对角线互相平分”可得AO ＝CO ，再根据等底等高的三角形的面积相等解答；(2)根据平行四边形的性质可得点A 、C 到BD 的距离相等，再根据等底等高的三角形的面积相等解答．(1)证明：在▱ABCD 中，AO ＝CO .设点B 到AC 的距离为h ，则S △ABO ＝12AO ·h ，S △CBO ＝12CO ·h ，∴S △ABO ＝S △CBO ；(2)解：S △ABP ＝S △CBP .理由如下：在▱ABCD 中，点A 、C 到BD 的距离相等，设为h ，则S △ABP ＝12BP ·h ，S △CBP ＝12BP ·h ，∴S △ABP ＝S △CBP .方法总结：平行四边形的对角线将平行四边形分成四个面积相等的三角形．另外，等底等高的三角形的面积相等．本节学习总结：1.平行四边形的定义：两组对边分别平行的四边形叫做平行四边形．平行四边形的定义既是平行四边形的性质，也是判断一个四边形是平行四边形的重要方法．2.平行四边形的性质：（1）平行四边形的对角相等，邻角互补；（2）平行四边形的对边平行且相等；（3）平行四边形的对角线互相平分.平行四边形的性质为以后证明线段平行或相等以及角相等提供了新的理论依据.3.推论：夹在两条平行线间的平行线段相等．更多内容请见：资料下载汇总表（提示：按住ctrl+鼠标左键打开链接）。

第十八章四边形章节复习辅导讲义

第十八章、四边形章节复习辅导讲义一、四边形知识框架： 1.四边形的知识结构 2.平行四边形的知识结构二、四边形1. 定义：有不在同一直线上的四条首尾依次连接的线段构成的封闭图形。

2. 四边形的表示：四边形一般由依次的四个大写的字母表示，如四边形ABCD 等。

3. 四边形的分类：（1）按照四边形的凹凸性将四边形分为凸四边形和凹四边形。

注意：中学阶段学习的四边形都是凸四边形。

（2）按照四边形对边的平行性将四边形分为： ① 一般四边形：任何对边都不平行的四边形。

② 梯形：只有一组对边平行的四边形； A. 梯形分类： a ．一般的梯形b ．等腰梯形：一组对边平行，另一组对边相等的四边形。

c. 直角梯形：有一个内角为直角的梯形。

（3）平行四边形：两组对边分别平行的四边形。

① 平行四边形的分类： A. 一般的平行四边形 B. 矩形（长方形）：有一个较为直角的平行四边形。

C. 菱形：邻边相等的平行四边形。

D. 正方形：四条边都相等，四个内角也相等的四边形。

4. 四边形的内角和与外角和：（1）四边形的内角和为360度（2）四边形的外角和为360度。

5. 四边形的性质：依次连接四边形各边中点所得的四边形称为中点四边形。

不管原四边形的形状怎样改变，中点四边形的形状始终是平行四边形【基础练习】1. 顺次连接一个任意四边形四边的中点，得到一个_______四边形． 2．顺次连接对角线相等的四边形的各边中点，所得四边形是_________．3. 如图1，已知：在ABCD 中，AB=4cm ，AD=7cm ，∠ABC 的平分线交AD•于点E ，交CD 的延长线于点F ，则DF=______cm ．4. 如图，四边形ABCD 为正方形，△ADE 为等边三角形，AC 为正方形ABCD 的对角线，则∠EAC ＝___度．5. 四边形ABCD 的对角线AC BD ，的长分别为m n ，，可以证明当AC BD ⊥时（如图1），四边形ABCD 的面积12S mn =，那么当AC BD ，所夹的锐角为θ时（如图2），四边形ABCD 的面积S = ．（用含m n θ，，的式子表示）1250°1 2A BC DB F C6.在如图所示的四边形中，若去掉一个50的角得到一个五边形，则12+=∠∠ 度．7.如图，已知AC 平分BAD ∠，12∠=∠，3AB DC ==，则BC = ． 8.已知四边形ABCD 中，90A B C ∠=∠=∠=︒，若添加一个条件即可判定该四边形是正方形，那么这个条件可以是____________．三、平行四边形（一）平行四边形：1. 定义：两组对边分别平行的四边形。

人教版数学八年级下册第十八章平行四边形性质与判定专题复习辅导讲义

辅导讲义学员编号：年级：课时数：学员姓名：辅导科目：学科老师：授课类型T 平行四边形的概念、性质T 平行四边形的断定C中位线定理授课日期时段教学内容一、同步学问梳理学问点1：平行四边形的定义：两组对边分别平行的四边形是平行四边形．表示：平行四边形用符号“”来表示．如图，在四边形ABCD中，AB∥DC，AD∥BC，那么四边形ABCD是平行四边形．平行四边形ABCD，记作ABCD”，读作“平行四边形ABCD”．留意：平行四边形中对边是指无公共点的边，对角是指不相邻的角，邻边是指有公共端点的边，邻角是指有一条公共边的两个角．而三角形对边是指一个角的对边，对角是指一条边的对角．学问点2：平行四边形的性质：（1）边：平行四边形的对边平行且相等．（2）角：平行四边形的对角相等．邻角互补（3）对角线：平行四边形的对角线相互平分对称性：平行四边形是中心对称图形，两条对角线的交点是对称中心；二、同步题型分析题型1：平行四边形的边、角例1：已知，如图1，四边形ABCD为平行四边形，∠A＋∠C＝80°，平行四边形ABCD的周长为46 cm，且AB－BC＝3 cm，求平行四边形ABCD的各边长和各内角的度数．分析：由平行四边形的对角相等，邻角互补可求得各内角的度数；由平行四边形的对边相等，得AB＋BC＝23 cm，解方程组即可求出各边的长．解：由平行四边形的对角相等，∠A＋∠C＝80°，得∠A＝∠C＝40°又DC∥AB，∠D及∠A为同旁内角互补，∴∠D＝180°－∠A＝180°－40°＝140°．∴∠B＝140°．由平行四边形对边相等，得AB＝CD，AD＝BC．因周长为46 am，因此AB＋BC＝23 cm，而AB－BC＝3 cm，得AB＝13 cm，BC＝10 cm，∴CD＝13 am．AD＝10 cm．题后反思：留意充分利用性质解题．例2：如图2，在平行四边形ABCD中，E、F是直线BD上的两点，且DE＝BF，你认为AE＝CF吗？试说明理由．分析：本题主要考察平行四边形的性质．要证明AE＝CF，可以把两线段分别放在两个三角形里，然后证明两三角形全等．解：AE＝CF．理由：在平行四边形ABCD中，∵AB＝CD且AB∥CD．∴∠ABE＝∠CDF．∵DE＝BF，∴ DE＋BD＝BF＋BD，即BE＝DF：∴△ABE≌△CDF ∴ AE＝CF题后反思：利用平行四边形的性质解题时，一般要用到三角形全等学问，此题还可以证明其他三角形全等来证明两线段相等．题型2：平行四边形的周长例1：如图3，在平行四边形ABCD中，AC、BD相交于点O，作OE⊥BD于O，交CD于E，连接BE，若△BCE的周长为6，则平行四边形ABCD的周长为（ B ）图3A. 6B. 12C. 18D. 不确定分析：本题主要考察平行四边形的性质:对角线相互平分。

人教版八年级数学下册知识点第十八章《平行四边形》

第十八章平行四边形【思维导图】【平行四边形】(1)平行四边形的定义与表示定义：两组对边分别平行的四边形叫做平行四边形。

表示：平行四边形用“□”表示。

2)符号“□”必须与表示顶点的字母同时使用，不能单独使用。

的顺序依次排列。

点拨：1)在用“□”表示平行四边形时，应把表示顶点的字母按顺时针或逆时针边形。

平行四边形ABCD 记作“□ABCD”，读作“平行四边形ABCD”。

如图，在四边形ABCD 中，AB ∥DC ，AD ∥BC ，那么四边形ABCD 是平行四(2)平行四边形的基本元素如图，在□ABCD 中，邻边：AD 和AB ，AD 和DC ，DC 和BC ，BC 和AB对边：AB 和DC ，AD 和BC邻角：∠BAD 和∠ADC ，∠ADC 和∠DCB ，∠DCB 和∠ABC ，∠ABC 和∠BAD 对角：∠BAD 和∠BCD ，∠ABC 和∠ADC对角线：AC 和BD【平行四边形的性质】性质1：平行四边形的对边相等几何语言：如图1，∵四边形ABCD 是平行四边形，∴AB=CD ，AD=BC性质2：平行四边形的对角相等几何语言：如图1，∵四边形ABCD 是平行四边形，∴∠A=∠C ，∠B=∠D下面证明性质1和2证明：如图2，连接AC。

∵AD∥BC，AB∥CD∴∠1=∠2，∠3=∠4.又∵AC=CA，∴△ABC≌△CDA∴AD=BC，AB=CD，∠B=∠D∴∠1=∠2，∠3=∠4，∴∠1+∠4=∠2+∠3，即∠BAD=∠BCD性质3：平行四边形的对角线互相平分几何语言：如图3，∵四边形ABCD是平行四边形，∴OA=0C=1/2AC，OB=OD=1/2BD【典例】(中考)在□ABCD中，下列结论一定正确的是(）A.AC⊥BDB.∠A+∠B=1800C.AB=ADD.∠A≠∠C解析：平行四边形的对角线互相平分但不一定垂直，所以选项A错误；@简单初中生平行四边形的邻角互补，所以选项B正确；平行四边形的对边相等但邻边不一定相等，所以选项C错误；平行四边形的对角相等，所以∠A=∠C，所以选项D错误。

平行四边形知识归纳

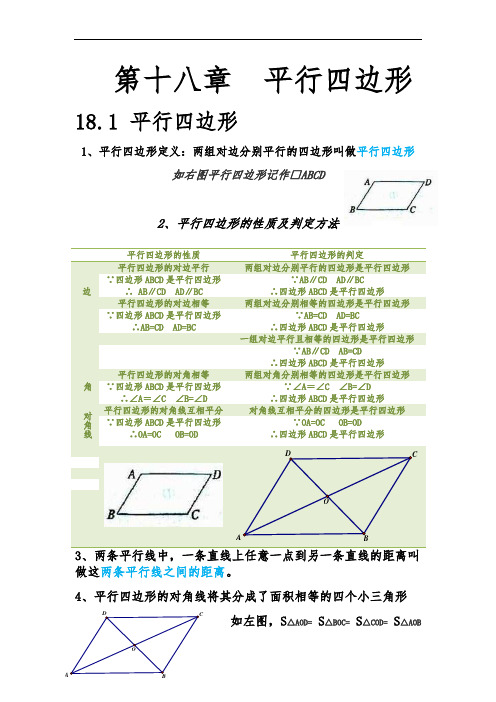
第十八章平行四边形18.1 平行四边形1、平行四边形定义：两组对边分别平行的四边形叫做平行四边形如右图平行四边形记作□ABCD平行四边形的性质平行四边形的判定2、平行四边形的性质及判定方法3、两条平行线中，一条直线上任意一点到另一条直线的距离叫做这两条平行线之间的距离。

4、平行四边形的对角线将其分成了面积相等的四个小三角形如左图，S △AOD= S △BOC= S △COD= S △AOB5、三角形的中位线连接三角形两边中点的线段叫做三角形的中位线。

三角形的中位线定理：三角形的中位线平行于三角形的第三边，并且等于第三边的一半。

数学符号语言：如右图，∵点D 、点E 分别为AB 、AC 的中点 ∴DE 为BC 的中位线 ∴DE ∥BC DE=1/2BC18.2特殊的平行四边形矩形1、矩形的定义：有一个角是直角的平行四边形叫做矩形。

矩形是一类特殊的平行四边形。

2、矩形的性质及判定注：矩形具有平行四边形的所有性质。

（即对边相等且平行）矩形的性质矩形的判定矩形的四个角都是直角有一个角是直角的平行四边形是矩形。

∵四边形ABCD 是矩形 ∴∠A=∠B=∠C=∠D=90 ∵四边形ABCD 是平行四边形, ∠A=90∴四边形ABCD 是矩形矩形的对角线相等且互相平分对角线相等的平行四边形是矩形∵四边形ABCD 是矩形∴AC=BD∴OA=OC=1/2AC OB=OD=1/2BD∵四边形ABCD 是平行四边形，AC=BD∴四边形ABCD 是矩形有三个角是直角的四边形是矩形3、如右图，可以观察出（1）S△AOD= S△BOC= S△COD= S△AOB（2）∵四边形ABCD是矩形∴AC=BD∴OA=OC=1/2AC OB=OD=1/2BD∴OA=OC=OB=OD（等量代换）（3）一共有四个等腰三角形（4）一共有八对全等三角形4、如果一个三角形是直角三角形，那么这个三角形斜边上的中线等于斜边的一半。

数学符号语言：∵在Rt△ACB中，CD为斜边AB上的中线，∠B=90∴CD=1/2AB菱形1、菱形的定义：有一组邻边相等的平行四边形叫做菱形。

平行四边形知识点及经典例题

第十八章平行四边形18.1.1 平行四边形的性质第一课时平行四边形的边、角特征知识点梳理1、有两组对边分别平行的四边形叫做平行四边形，平行四边形ABCD记作□ABCD。

2、平行四边形的对边相等，对角相等，邻角互补。

3、两条平行线中，一条直线上任意一点到另一条直线的距离，叫做这两条直线之间的距离。

知识点训练1．(3分)如图，两X对边平行的纸条，随意穿插叠放在一起，转动其中一X，重合的局部构成一个四边形，这个四边形是________．2．(3分)如图，在□ABCD中，EF∥BC，GH∥AB，EF，GH相交于点O，那么图中共有平行四边形( )A．6个B．7个C．8个D．9个3．(3分)在□ABCD中，AB＝6 cm，BC＝8 cm，那么□ABCD的周长为cm.4．(3分)用40 cm长的绳子围成一个平行四边形，使其相邻两边的长度比为3∶2，那么较长的边的长度为cm.5．(4分)在□ABCD中，假设∠A∶∠B＝1∶5，那么∠D＝；假设∠A＋∠C＝140°，那么∠D＝．6．(4分)(2014·XX)如图，在□ABCD中，DE平分∠ADC，AD＝6，BE＝2，那么□ABCD 的周长是．7．(4分)如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，假设∠EAD ＝53°，那么∠BCE的度数为( )A．53°B．37°C．47°D．123°8．(8分)(2013·XX)如下图，在平行四边形ABCD中，BE＝DF.求证：AE＝CF.9．(4分)如图，点E，F分别是□ABCD中AD，AB边上的任意一点，假设△EBC的面积为10 cm²，那么△DCF的面积为。

10．(4分)如图，梯形ABCD中，AD∥BC，记△ABO的面积为S1，△COD的面积为S2，那么S1，S2的大小关系是( )A．S1>S2 B．S1＝S2 C．S1＜S2 D．无法比拟11．在□ABCD中，∠A∶∠B∶∠C∶∠D的值可能是( )A．1∶2∶3∶4 B．1∶2∶2∶1C．2∶2∶1∶1 D．2∶1∶2∶112．如图，将平行四边形ABCD折叠，使顶点D恰落在AB边上的点M处，折痕为AN，那么对于结论：①MN∥BC；②MN＝AM，以下说法正确的选项是( )A．①②都对B．①②都错C．①对②错D．①错②13．如图，在□ABCD中，BE⊥CD，BF⊥AD，垂足分别为E，F，CE＝2，DF＝1，∠EBF ＝60°，那么□ABCD的周长为__．14．(2013·XX)如图，□ABCD与□DCFE的周长相等，且∠BAD＝60°，∠F＝110°，那么∠DAE的度数为。

人教版数学八年级下册第十八章-平行四边形-专题复习辅导讲义

辅导讲义是”；是平行四边形，可以记做“ABDC1题图2．如图所示，在ABCD所示，在ABCD125．在ABCD 中，∠B-∠A=30°，则∠A ，∠B ，∠C ，∠D 的度数是（）．A ．95°，85°，95°，85°B ．85°，95°，85°，95°C ．105°，75°，105°，75°D ．75°，105°，75°，105° 6．在ABCD 中，∠A ：∠B ：∠C ：∠D 的值可以是（）．A ．1：2：3：4B ．3：4：4：3C ．3：3：4：4D ．3：4：3：4 7．如图所示，如果ABCD 的对角线AC ，BD 相交于点O ，•那么图中的全等三角形有（）．A ．1对B ．2对C ．3对D ．4对8．如图所示，若平行四边形ABCD 的周长为22cm ，AC ，BD 相交于点O ，•△AOD 的周长比△AOB 的周长小3cm ，则AD=_______，AB=_______．答案：4cm 7cm知识点3 平行四边形的面积 9．如图所示，ABCD 的对角线AC 的长为10cm ，∠CAB=30°，AB 的长为6cm.求ABCD 的面积．答案：30cm 210．如图所示，在ABCD 中，AB=10cm ，AB 边上的高DH=6cm ，BC=6cm ，求BC 边上的高DF 的长．答案：10cm知识点4 平行四边形的判定11．1已知：如图，ABCD 中，E 、F 分别是AD 、BC 的中点，求证：BE=DF ．提示：证明DE ∥BF ，DE=BF12．1已知：如图，ABCD 中，E 、F 分别是AC 上两点，且BE ⊥AC 于E ，DF ⊥AC 于F ．求证：四边形BEDF 是平行四边形．提示：证明BE ∥DF ，BE=DF13．1已知：如图ABCD 的对角线AC 、BD 交于点O ，E 、F 是AC 上的两点，并且AE=CF ．求证：四边形BFDE 是平行四边形．提示：证明OB=OD, OE=OF知识点5 三角形的中位线14．1如图，A 、B 两点被池塘隔开，在AB 外选一点C ，连结AC 和BC ，并分别找出AC 和BC 的中点M 、N ，如果测得MN=20 m ，那么A 、B 两点3题图 4题图7题图 8题图3的距离是 m ，理由是．答案：40 三角形两边的中点连线平行于第三边且等于第三边的一半15．1△ABC 中，D 、E 分别为AB 、AC 的中点，若DE ＝4，AD ＝3，AE ＝2，则△ABC 的周长为______．答案：1816．1已知：如图（1），在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．提示：连结BD ，利用中位线定理得：EH BD ，GFBD知识点6 矩形的定义与性质 17．已知在四边形ABCD 中，AB CD ，请添加一个条件，使四边形ABCD 是矩形，•加上的条件是_______．答案：AC=BD (答案不唯一) 18．如图所示，M 是ABCD 的边AD 的中点，且MB=MC ．求证：ABCD 是矩形．提示：证明△ABM ≌△DCM ，得到∠A=∠D ，又因为∠A+∠D=180°19．如图所示，矩形ABCD 的两条对角线相交于点D ，∠AOD=120°，AB=4cm ，求矩形的对角线的长．答案：8cm知识点7 直角三角形斜边中线的性质20．已知直角三角形两直角边的长分别为6cm 和8cm ，则斜边上的中线长．答案：5cm21．如图所示，在△ABC 中，∠ACB=90°，点D ，E 分别为AC ，AB 的中点，点F•在BC 的延长线上，且∠CDF=∠A ．求证：四边形DECF 为平行四边形．提示：AE=CE,得到角相等，推出DF ∥CE ，又DE ∥BF ，即证 22．如图所示，在△ABC 中，∠C=90°，AC=BC ，AD=BD ，PE ⊥AC 于点E ，PF⊥BC 于点F ，求证：DE=DF ．提示：连结CD ，证明△ADE ≌△CDF 知识点8 矩形的判定 23．下列说法中：（1）四个角都相等的四边形是矩形．（2）两组对边分别相等并且有一个角是直角的四边形是矩形．（3）对角线相等并且有一个角是直角的四边形是矩形．B=AC，推出．如图所示，在菱形ABCD4如图，ABCD．对角线互相平分．若正方形的一条对角线长为，则它的边长是求∠AFD的度数．56提示：证明△ABE ≌△BCF知识点12 正方形的判定43．有下列命题，其中真命题有（）． ①四边都相等的四边形是正方形； ②四个内角都相等的四边形是正方形；③有三个角是直角，且有一组邻边相等的四边形是正方形； ④对角线与一边夹角为45°的四边形是正方形．A ．1个B ．2个C ．3个D ．4个 44．如图所示，在△ABC 中，∠ABC=90°，BD 平分∠ABC ，DE ⊥BC ，DF ⊥AB. 求证：四边形BEDF 是正方形．提示：由角平分线的性质可推出：DE=DF ，又三个角为90°的四边形是矩形，所以推出四边形BEDF 是正方形．一、专题精讲专题1 动点问题例1 1如图所示，在矩形ABCD 中，AB=4cm ，BC=8cm 、点P 从点D 出发向点A 运动，同时点Q 从点B 出发向点C 运动，点P 、Q 的速度都是1cm/s ．(1）在运动过程中，四边形AQCP 可能是菱形吗？如果可能，那么经过多少秒后，四边形AQCP 是菱形？(2）分别求出菱形AQCP 的周长、面积．分析：（1）设经过x 秒后，四边形AQCP 是菱形，根据菱形的四边相等列方程即可求得所需的时间．（2）根据第一问可求得菱形的边长，从而不难求得其周长及面积．解答：解：（1）经过x 秒后，四边形AQCP 是菱形 ∴DP=xcm，AP=CP=AD-DP=（8-x ）cm ， ∵DP 2+CD 2=PC 2，∴16+x 2=（8-x ）2，解得x=3 即经过3秒后四边形是菱形．（2）由第一问得菱形的边长为5∴菱形AQCP的周长=5×4=20（cm）菱形AQCP的面积=5×4=20（cm2）点评：此题主要考查菱形的性质及矩形的性质的理解及运用．ABC’D’是菱形，并请说8ABCFD ∴BC′=21AC ．而∠ACB=30°， ∴AB=21AC ∴AB=BC′．∴四边形ABC′D′是菱形．点评：本题即考查了全等的判定及菱形的判定，注意对这两个判定定理的准确掌握．考查了学生综合运用数学的能力．重合，点D 落到分析：（1）根据平行四边形的性质及折叠的性质我们可以得到∠B=∠D′，AB=AD′，∠1=∠3，从而利用ASA 判定△ABE≌△AD′F；（2）四边形AECF 是菱形，我们可以运用菱形的判定，有一组邻边相等的平行四边形是菱形来进行验证．∴△ABE≌△AD′F（ASA）．（2）解：四边形AECF是菱形．证明：由折叠可知：AE=EC，∠4=∠5．∵四边形ABCD是平行四边形，∴AD∥BC．∴∠5=∠6．∴∠4=∠6．∴AF=AE．∵AE=EC，∴AF=EC．又∵AF∥EC，∴四边形AECF是平行四边形．∵AF=AE，∴平行四边形AECF是菱形．点评：此题考查了全等三角形的判定及菱形的判定方法，做题时要求学生对常用的知识点牢固掌握．分析：要证明HG与HB是否相等，可以把线段放在两个三角形中证明这两个三角形全等，或放在一个三角形中证明这个三角形是等腰三角形，而图中没有这样的三角形，因此需要作辅助线，构造三角形．910∴Rt△AGH≌Rt△ABH（HL），∴HG=HB．证法2：连接GB，∵四边形ABCD，AEFG都是正方形，∴∠ABC=∠AGF=90°，由题意知AB=AG，∴∠AGB=∠ABG，∴∠HGB=∠HBG，∴HG=HB．点评：解答本题要充分利用正方形的特殊性质．注意在正方形中的特殊三角形的应用，搞清楚矩形、菱形、正方形中的三角形的三边关系，可有助于提高解题速度和准确率．二、专题过关1. 如图所示，△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠BCA的外角平分线于点F.(1)求证：EO=FO(2)当点O运动到何处时，四边形AECF是矩形？并证明你的结论.分析：（1）根据平行线性质和角平分线性质及，由平行线所夹的内错角相等易证．（2）根据矩形的判定方法，即一个角是直角的平行四边形是矩形可证解答：（1）证明：∵CE平分∠ACB，∴∠1=∠2，又∵MN∥BC，∴∠1=∠3，∴∠3=∠2，∴EO=CO，同理，FO=CO ，∴EO=FO．（2）解：当点O 运动到AC 的中点时，四边形AECF 是矩形．∵EO=FO，点O 是AC 的中点．∴四边形AECF 是平行四边形，∵C F 平分∠BCA 的外角，∴∠4=∠5，又∵∠1=∠2，∴∠2+∠4=21×180°=90°．即∠ECF=90度，∴四边形AECF 是矩形．点评：本题涉及矩形的判定定理，解答此类题的关键是要突破思维定势的障碍，运用发散思维，多方思考，探究问题在不同条件下的不同结论，挖掘它的内在联系，向“纵、横、深、广”拓展，从而寻找出添加的条件和所得的结论．12图3【解法指导】欲证两条线段之和等于第三条线段，可通过截长补1415 分析：过F 作AB 、CD 的平行线FG ，由于F 是AD 的中点，那么G 是BC 的中点，即Rt△BCE 斜边上的中点，由此可得BC=2EG=2FG ，即△GEF、△BEG 都是等腰三角形，因此求∠B 的度数，只需求得∠B EG 的度数即可；易知四边形ABGF 是平行四边形，得∠EFG=∠AEF，由此可求得∠FEG 的度数，即可得到∠AEG 的度数，根据邻补角的定义可得∠BEG 的值，由此得解．解答：解：过F 作FG∥AB∥CD，交BC 于G ；则四边形ABGF 是平行四边形，所以AF=BG ，即G 是BC 的中点；连接EG ，在Rt△BEC 中，EG 是斜边上的中线，则BG=GE=FG=21BC ； ∵AE∥FG，∴∠EFG=∠AEF=∠FEG=54°，∴∠AEG=∠AEF+∠FEG=108°，∴∠B=∠BEG=180°-108°=72°．故选D ．点评：此题主要考查了平行四边形的性质、直角三角形的性质以及等腰三角形的判定和性质，正确地构造出与所求相关的等腰三角形是解决问题的关键．17。

(完整版)第十八章_平行四边形_知识点总结

第十八章平行四边形知识点总结第十八章平行四边形知识点总结1．四边形的内角和与外角和定理：（ 1）四边形的内角和等于 360°；（ 2）四边形的外角和等于 360° .AD2．多边形的内角和与外角和定理：（ 1） n 边形的内角和等于 (n-2)180 °；（ 2）任意多边形的外角和等于360° .BCA 4D312 BC3．平行四边形的性质：（1）两组对边分别平行；DC（2）两组对边分别相等；因为 ABCD 是平行四边形（3）两组对角分别相等；（4）对角线互相均分；（5）邻角互补 .4. 平行四边形的判断：（1）两组对边分别平行OABD C（）两组对边分别相等2O（）两组对角分别相等 ABCD 是平行四边形 .3（）一组对边平行且相等AB4（）对角线互相均分55. 矩形的性质：DC（1）拥有平行四边形的所有通性 ;O因为 ABCD 是矩形（2）四个角都是直角 ; （3）对角线相等 .A BDCA B6. 矩形的判断：（1）平行四边形一个直角DC（2）三个角都是直角四边形 ABCD 是矩形 .O（3）对角线相等的平行四边形A BDCA B7．菱形的性质：D因为 ABCD是菱形（1）拥有平行四边形的所有通性；OC （2）四个边都相等；A（3）对角线垂直且均分对角 .B8．菱形的判断：D （1）平行四边形一组邻边等（2）四个边都相等四边形四边形ABCD是菱形 .AO C （3）对角线垂直的平行四边形9．正方形的性质：B因为 ABCD是正方形（1）拥有平行四边形的所有通性；（2）四个边都相等，四个角都是直角；（3）对角线相等垂直且平分对角 .D C D COA B（ 1）AB（ 2）（ 3）10．正方形的判断：（1）平行四边形一组邻边等一个直角（2）菱形一个直角四边形ABCD是正方形.（3）矩形一组邻边等D(3)C∵ABCD是矩形又∵ AD=AB∴四边形ABCD是正方形AB11．三角形中位线定理：三角形的中位线平行第三边，并且等于它的一半.AD E B C几种特别四边形的有关性质（1）矩形：①边：对边平行且相等；②角：四个角都是直角；③对角线：对角线互相均分且相等；④对称性：轴对称图形（对边中点连线所在直线， 2 条）．（2）菱形：①边：对边平行，且四条边都相等；②角：对角相等、邻角互补；③对角线：对角线互相垂直均分且每条对角线均分每组对角；④对称性：轴对称图形（对角线所在直线， 2 条）．（3）正方形：①边：四条边都相等；②角：四角相等；③对角线：对角线互相垂直均分且相等，对角线与边的夹角为45 ；几种特别四边形的判断方法（1）矩形的判断：满足以下条件之一的四边形是矩形①有一个角是直角的平行四边形；②对角线相等的平行四边形；③四个角都相等（2）菱形的判断：满足以下条件之一的四边形是矩形①有一组邻边相等的平行四边形；②对角线互相垂直的平行四边形；③四条边都相等．（3）正方形的判断：满足以下条件之一的四边形是正方形．① 有一组邻边相等且有一个直角的平行四边形② 有一组邻边相等的矩形；③ 对角线互相垂直的矩形．④ 有一个角是直角的菱形⑤ 对角线相等的菱形；几种特别四边形的面积问题① 设矩形ABCD的两邻边长分别为a,b ，则S 矩形 =ab ．② 设菱形ABCD的一边长为a ，高为h ，则S 菱形 =ah ；若菱形的两对角线的长分别为a,b ，则S 菱形 =1 ab ．2③ 设正方形ABCD的一边长为a ，则S 正方形= a 2 ；若正方形的对角线的长为a ，则S 正方形= 1 a 2 ．2④ 设梯形ABCD的上底为a ，下底为b ，高为 h ，则S梯形 = 1(a b)h ．2。

四边形知识点汇总

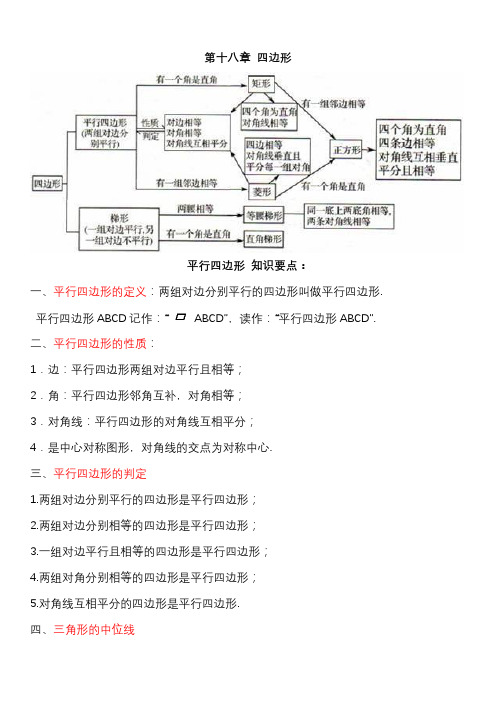
第十八章四边形平行四边形知识要点：一、平行四边形的定义：两组对边分别平行的四边形叫做平行四边形. 平行四边形ABCD记作：“ABCD”，读作：“平行四边形ABCD”.二、平行四边形的性质：1．边：平行四边形两组对边平行且相等；2．角：平行四边形邻角互补，对角相等；3．对角线：平行四边形的对角线互相平分；4．是中心对称图形，对角线的交点为对称中心.三、平行四边形的判定1.两组对边分别平行的四边形是平行四边形；2.两组对边分别相等的四边形是平行四边形；3.一组对边平行且相等的四边形是平行四边形；4.两组对角分别相等的四边形是平行四边形；5.对角线互相平分的四边形是平行四边形.四、三角形的中位线1．连接三角形两边中点的线段叫做三角形的中位线.2．定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半.说明（1）：三角形有三条中位线，每一条与第三边都有相应的数量关系，位置关系，（2）：三角形的三条中位线把原三角形分成可重合的4个小三角形，因而每个小三角形的周长为原三角形周长的一半，每个小三角形的面积为原三角形面积的1/4，（3）：三角形的中位线不同于三角形的中线五、平行线间的距离1.两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线间的距离. 注：距离是指垂线段的长度，是正值.2.平行线间的距离处处相等两条平行线间的任何两条平行线段都是相等的.3.平行四边形的面积：平行四边形的面积＝底×高；等底等高的平行四边形面积相等特殊的平行四边形（矩形）知识要点：一、矩形的定义：有一个角是直角的平行四边形叫做矩形.矩形定义的两个要素：①是平行四边形；②有一个角是直角.即矩形首先是一个平行四边形，然后增加一个角是直角这个特殊条件.二、矩形的性质(1)矩形是特殊的平行四边形，因而也是中心对称图形，过中心的任意直线可将矩形分成完全全等的两部分。

(2)矩形也是轴对称图形，有两条对称轴（分别通过对边中点的直线）.(3)矩形是特殊的平行四边形，矩形具有平行四边形的所有性质：从边看：矩形对边平行且相等；从角看：矩形四个角都是直角；从对角线看，矩形的对角线互相平分且相等。

2022年人教版八下数学第十八章《平行四边形》核心归纳《附答案

人教版八下数学第十八章单元核心考点归纳一、选择题1.在四边形ABCD中, AD=BC, 要使四边形ABCD是平行四边形, 那么还应满足( )A．∠A+∠C=180∘B．∠B+∠D=180∘C．∠A+∠B=180∘D．∠A+∠D=180∘2.在平行四边形ABCD中, AB=3, BC=4, 连接AC, BD, 当平行四边形ABCD的面积最大时,以下结论正确的有( )① AC=5；② ∠BAD+∠BCD=180∘；③ AC⊥BD；④ AC=BD．A．①②③B．①②④C．②③④D．①③④3.对于四边形ABCD, 给出以下6组条件：① ∠A=90∘, ∠B=∠C=∠D；② ∠A=∠B=90∘, ∠C=∠D；③ ∠A=∠B=∠C=∠D；④ ∠A=∠B=∠C=90∘；⑤ AC=BD；⑥ AB∥CD, AD∥BC．其中能得到“四边形ABCD是矩形〞的有( )A．1组B．2组C．3组D．4组4.在菱形ABCD中, 对角线AC, BD相交于点O, 以下结论：① AC⊥BD；② OA=OB；③∠ADB=∠CDB；④ △ABC是等边三角形, 其中一定成立的是( )．A．①②B．③④C．②③D．①③5.四边形ABCD的对角线AC, BD互相垂直, 那么以下条件能判定四边形ABCD为菱形的是( )A．BA=BC B．AC, BD互相平分C．AC=BD D．AB∥CD6.四边形ABCD中, AC=BD, AC⊥BD, E, F, G, H分别是AD, AB, BC, CD的中点, 那么四边形EFGH是( )A．平行四边形B．矩形C．菱形D．正方形二、填空题7.在平行四边形ABCD中, BM是∠ABC的平分线, 交边AD于点M, 且MD=2, 平行四边形ABCD的周长是16, 那么AM等于．8.平行四边形ABCD中, ∠A+∠C=200∘, 那么∠B的度数是．9.如图, 平行四边形ABCD的对角线AC与BD相交于点O, AB⊥AC．假设AB=4, AC=6,那么BD的长是．10.如图, 在四边形ABCD中, 对角线AC, BD相交于点E, ∠CBD=90∘, BC=4, BE=ED=3,AC=10, 那么四边形ABCD的面积为．11.在矩形ABCD中, AC, BD交于点O, ∠BOC=120∘, AB=5, 那么BD=, BC=．12.菱形的周长为40cm, 一条对角线长为16cm, 那么这个菱形的面积是．13.如图, 延长正方形ABCD的边BC至点E, 使CE=AC, 那么∠AFC=度．14.如图, 在正方形ABCD外侧, 作等边三角形ADE, AC, BE相交于点F, 那么∠BFC为度．15.如图, 正方形ABCD中, E是AD上一点, F是AB延长线上点, DE=BF．点G, H分别在边AB, CD上, 且GH=3√5, GH交EF于点M, 假设∠EMH=45∘, 那么EF的长为．16.如图, 平行四边形ABCD的对角线AC, BD相交于点O, 点E, F分别是线段AO, BO的中点,假设AC+BD=24cm, △OAB的周长是18cm, 那么EF=cm．17.矩形ABCD中, 对角线AC, BD交于点O, AE⊥BD于点E, 假设OE:ED=1:3, AE=√3, 那么BD的长是．18.正方形ABCD的边长为4, E为平面内任意一点, 连接DE, 过点D作DE的垂线, 在垂线上取DG=DE, 当点B, D, G在一条直线上时, 假设DG=√2, 那么CE的长为．三、解答题19.如图, 平行四边形ABCD中, BD是它的一条对角线, 过A, C两点作AE⊥BD, CF⊥BD, 垂足分别为E, F, 延长AE, CF分别交CD, AB于M, N．(1) 求证：四边形CMAN是平行四边形．(2) DE=4, FN=3, 求BN的长．20.如图, 在平行四边形ABCD中, E, F分别是AB, CD的中点, 连接AF, CE．(1) 求证：△BEC≌△DFA；(2) 连接AC, 当CA=CB时, 判断四边形AECF是什么特殊四边形, 并说明理由．21.如图, 在矩形ABCD中, 对角线BD的垂直平分线MN与AD相交于点M, 与BD相交于点O, 与BC相交于点N, 连接BM, DN．(1) 求证：四边形BMDN是菱形；(2) 假设AB=8, AD=16, 求MD的长．22.如图, 在△ABC中, AB=AC, AD⊥BC于点D, 点P是AD的中点, 延长BP交AC于点AC．N．求证：AN=1323.如图, 在△ABC中, 点D, E, F分别是AB, BC, CA的中点, AH是边BC上的高．(1) 求证：四边形ADEF是平行四边形；(2) 求证：∠DHF=∠DEF．答案一、选择题1. 【答案】C2. 【答案】B【解析】根据题意得, 当平行四边形ABCD的面积最大时, 四边形ABCD为矩形, ∴∠BAD=∠ABC=∠BCD=90∘, AC=BD．∴AC=√32+42=5．①正确, ②正确, ③不正确, ④正确．应选B．3. 【答案】D4. 【答案】D5. 【答案】B6. 【答案】D二、填空题7. 【答案】38. 【答案】80°9. 【答案】1010. 【答案】2411. 【答案】10；5√312. 【答案】96cm2【解析】∵周长是40cm,∴边长是10cm．如下列图：AB=10cm, AC=16cm．根据菱形的性质, AC⊥BD, AO=8cm,∴BO=6cm, BD=12cm．∴面积S=12×16×12=96〔cm2〕．13. 【答案】112.514. 【答案】6015. 【答案】3√1016. 【答案】3【解析】∵四边形ABCD是平行四边形,∴OA=12AC, OB=12BD,∵AC+BD=24cm,∴OA+OB=12cm,∵△OAB的周长是18cm, ∴AB=6cm,∵点E, F分别是线段AO, BO的中点,∴EF=12AB=3cm．17. 【答案】4或8√5518. 【答案】√10或√26三、解答题19. 【答案】(1) ∵AE⊥BD, CF⊥BD,∴AE∥CF．又四边形ABCD是平行四边形,∴CM∥AN.∴四边形CMAN是平行四边形．(2) ∵四边形CMAN是平行四边形,∴CM=AN.∵四边形ABCD是平行四边形,∴CD=AB.∴BN=DM.∵∠FBN=∠EDM, ∠BFN=∠DEM=90∘,∴△BFN≌△DEM.∴BF=DE.∵DE=4, FN=3,∴BF=4.∴BN=5．20. 【答案】(1) ∵四边形ABCD为平行四边形,∴AB=CD, ∠B=∠D, BC=AD．∵E, F分别是AB, CD的中点,∴BE=DF．∴△BEC≌△DFA(SAS)．(2) 四边形AECF是矩形．理由如下：∵AE=12AB, CF=12CD, AB=CD,∴AE=CF．∵AE∥CF,∴四边形AECF是平行四边形．当CA=CB时, CE⊥AB,∴∠AEC=90∘．∴四边形AECF是矩形．21. 【答案】(1) 证△MOD≌△NOB, OM=ON即可．(2) 设BM=DM=x, 那么AM=16−x,∴82+(16−x)2=x2,∴x=10,∴MD=10．22. 【答案】取CN的中点E, 取BN的中点F,证平行四边形ENFD,△APN≌△DPF即可．23. 【答案】(1) ∵点D, E, F分别是中点,∴DE∥AC, DE=12AC, EF∥AB, EF=12AB,∴四边形ADEF为平行四边形．(2) 连接DF．∵AH是边BC上的高,∴∠AHB=90∘, ∠AHC=90∘．∵点D, F是AB, CA的中点,∴DH=12AB, FH=12AC．∵DE=12AC, EF=12AB．∴DH=EF, FH=DE．∵DF=FD,∴△DHF≌△FED．∴∠DHF=∠FED．附第16章二次根式第一卷〔选择题〕评卷人得分一．选择题〔共10小题, 总分值20分, 每题2分〕1．〔2分〕〔2021秋•黄石期末〕以下运算正确的选项是〔〕A．+＝B．2×3＝6C．〔x2〕5＝x10D．x5•x6＝x30 2．〔2分〕〔2021秋•沈北新区校级期末〕a＜0, b≠0, 化简二次根式的结果是〔〕A．a B．﹣a C．a D．﹣a3．〔2分〕〔2021秋•乐亭县期末〕+2＝b+8, 那么的值是〔〕A．±3B．3C．5D．±54．〔2分〕〔2021秋•东莞市校级期中〕以下计算正确的选项是〔〕A．2a+3a＝6a B．〔﹣3a〕2＝6a2C．3﹣＝2D．〔x﹣y〕2＝x2﹣y25．〔2分〕〔2021•呼伦贝尔〕实数a在数轴上的对应点位置如下列图, 那么化简|a﹣1|﹣的结果是〔〕A．3﹣2a B．﹣1C．1D．2a﹣36．〔2分〕〔2021春•福州期末〕a＝2021×2021﹣2021×2021, b＝, c＝, 那么a, b, c的大小关系是〔〕A．a＜b＜c B．a＜c＜b C．b＜a＜c D．b＜c＜a7．〔2分〕〔2021•浙江自主招生〕假设x2+y2＝1, 那么的值为〔〕A．0B．1C．2D．38．〔2分〕〔2021春•兴县期末〕以下计算正确的选项是〔〕A．＝2B．+＝C．×＝D．÷＝29．〔2分〕〔2021春•同安区期中〕如图, 在矩形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片, 那么图中空白局部的面积为〔〕A．〔8﹣4〕cm2B．〔4﹣2〕cm2C．〔16﹣8〕cm2D．〔﹣12+8〕cm210．〔2分〕〔2021秋•永嘉县期中〕把四张形状大小完全相同的小长方形卡片〔如图①〕不重叠地放在一个底面为长方形〔长为cm, 宽为4cm〕的盒子底部〔如图②〕, 盒子底面未被卡片覆盖的局部用阴影表示．那么图②中两块阴影局部的周长和是〔〕A．4cm B．16cm C．2〔+4〕cm D．4〔﹣4〕cm第二卷〔非选择题〕评卷人得分二．填空题〔共9小题, 总分值18分, 每题2分〕11．〔2分〕〔2021•建湖县三模〕使二次根式有意义的x的取值范围是．12．〔2分〕〔2021秋•炎陵县期末〕计算：＝, ＝．13．〔2分〕〔2021秋•江北区校级期末〕, 且0＜x＜1, 那么＝．14．〔2分〕〔2021春•石城县期中〕假设x为整数, 且满足|x|＜π, 那么当也为整数时, x的值可以是．15．〔2分〕〔2021春•太湖县期末〕假设最简二次根式与是同类二次根式, 那么a+b ＝．16．〔2分〕〔2021春•灵宝市校级月考〕已化简的和是同类二次根式, 那么a+b ＝．17．〔2分〕〔2021秋•宜兴市期中〕假设m＝, 那么m5﹣2m4﹣2021m3＝．18．〔2分〕a为实数, 且与都是整数, 那么a的值是．19．〔2分〕计算〔﹣2〕2﹣2﹣1+〔1﹣〕0+＝．x＝+1, 那么＝．评卷人得分三．解答题〔共9小题, 总分值62分〕20．〔4分〕〔2021秋•南海区校级期末〕化简：﹣×﹣〔〕〔2﹣〕．21．〔8分〕〔2021秋•成都期末〕〔1〕计算：〔﹣2〕×﹣6；〔2〕解方程组：．22．〔6分〕〔2021秋•金川区校级期末〕：x＝+1, y＝﹣1, 求代数式x2+2xy+y2的值．23．〔6分〕〔2021秋•沿河县期末〕在进行二次根式化简时, 我们有时会碰上如, , 一样的式子, 其实我们还可以将其进一步化简：以上这种化简的步骤叫做分母有理化．还可以用以下方法化简：〔1〕请用不同的方法化简；〔2〕化简：．24．〔6分〕〔2021秋•梁平区期末〕张亮同学在作业本上做了这么一道题：“当a＝■时, 试求a+的值〞, 其中■是被墨水弄污的, 张亮同学所求得的答案为．〔1〕请你计算当a＝5时, 代数式a+的值；〔2〕是否存在数a, 使得a+的值为；〔3〕请直接判断张亮同学的答案是否正确．25．〔6分〕〔2021春•德城区校级月考〕x＝+, y＝﹣, 求：〔1〕+的值；〔2〕2x2+6xy+2y2的值．26．〔8分〕〔2021春•兴县期末〕阅读材料：小明在学习二次根式后, 发现一些含根号的式子可以写成另一个式子的平方, 如：3+2＝〔1+〕2, 善于思考的小明进行了以下探索：设a+b＝〔m+n〕2〔其中a、b、m、n均为整数〕, 那么有a+b＝m2+2n2+2mn．∴a＝m2+2n2, b＝2mn．这样小明就找到了一种把局部a+b的式子化为平方式的方法．请你仿照小明的方法探索并解决以下问题：〔1〕当a、b、m、n均为正整数时, 假设a+b＝〔m+n〕2, 用含m、n的式子分别表示a、b, 得a＝, b＝；〔2〕试着把7+4化成一个完全平方式．〔3〕假设a是216的立方根, b是16的平方根, 试计算：．27．〔9分〕〔2021春•商州区期中〕阅读理解材料：把分母中的根号化掉叫做分母有理化, 例如：①＝＝；②＝＝＝+1等运算都是分母有理化．根据上述材料,〔1〕化简：〔2〕计算：+++…+．28．〔9分〕〔2021春•邗江区校级月考〕阅读理解题：学习了二次根式后, 你会发现一些含有根号的式子可以写成另一个式子的平方, 如3+2＝〔1+〕2, 我们来进行以下的探索：设a+b＝〔m+n〕2〔其中a, b, m, n都是正整数〕, 那么有a+b＝m2+2n2+2mn, ∴a＝m+2n2, b＝2mn, 这样就得出了把类似a+b的式子化为平方式的方法．请仿照上述方法探索并解决以下问题：〔1〕当a, b, m, n都为正整数时, 假设a﹣b＝〔m﹣n〕2, 用含m, n的式子分别表示a, b, 得a＝, b＝；〔2〕利用上述方法, 找一组正整数a, b, m, n填空：﹣＝〔﹣〕2〔3〕a﹣4＝〔m﹣n〕2且a, m, n都为正整数, 求a的值．。

第十八章平行四边形及特殊的平行四边形知识点总结及经典习题

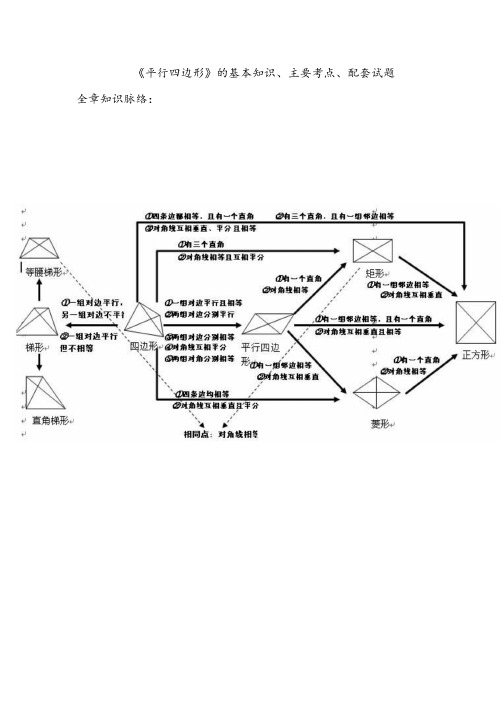
《平行四边形》的基本知识、主要考点、配套试题全章知识脉络：平行四边形◆考点 1．平行四边形的两组对边分别平行且相等推论：平行四边形一组邻边的和为周长的一半对边平行内错角相等（有“角平分线”会产生“等腰三角形”）1．□ABCD 的周长为 34cm，且 AB=7cm，则 BC= cm。

2．□ABCD 的周长为 26cm，相邻两边相差 3cm，则 AB= cm。

3、如果ABCD 的周长为 28cm，且 AB：BC=2∶5，那么 AB=cm，BC= cm，CD=_____cm，4、如图，□ABCD 中，CE 平分∠BCD，BG 平分∠ABC，BG 与 CE 交于点F。

(1)求证：AB=AG；(2)求证：AE=DG；(3)求证：CE⊥BG。

E GA DFB C推论：平行四边形◆考点 2．平行四边形的两组对角分别相等的邻角互补1 ．平行四边形的一个角为 50 度，则其余三个角分别为。

2．平行四边形相邻两个角相差 40 度，则相邻两角度数分别为。

3、□ABCD 中两邻角∠A：∠B=1：2，则∠C=_______度4、在□ABCD 中，若∠A-∠B=70°，则∠A=______，∠B=______，∠ C=______，∠D=______．◆考点 3．平行四边形的对角线互相平分推论 1：经过平行四边形对角线交点的直线具备双重平分作用：①该直线平分平行四边形的面积；②该直线在平行四边形内的部分被对角线平分。

1．如图，□ABCD 中，AC 、BD 交于点O ，△AOB 与△BOC 的周长相差2，AD且AB=5，则BC= 。

OBC2．如图△ABC 中，AB=3，AC=5，则 BC 边上的中线 AD 长度的取值范A围是。

BCD3．平行四边形的一条对角线长为 10，则它的两边可能长为（ A ．5 和 5B ．3 和 9C ．4 和 15D ．10 和 204．平行四边形的两条对角线长分别 6 和 10，则它的边长不可能是） A ．3B ．4C ．7D ．85．平行四边形的一条边长为 8，则它两条对角线可以是（ A ．6 和 12B ．6 和 10C ．6 和 8D ．6 和 66．如图，□ABCD 中，AC 、BD 交于点 O ，过点 O 作 OE ⊥AC 交 AD 于 E ，连接 CE ，若△CDE 的周长为 12，则□ABCD 的周长为）（）。

重庆市第八中学八年级数学下册第十八章《平行四边形》知识点总结(含答案)

一、选择题1．如图，E 是直线CD 上的一点，且12CE CD =．已知ABCD 的面积为252cm ，则ACE △的面积为（）A ．52B ．26C ．13D ．39C解析：C【分析】设平行四边形AB 边上的高为h ，分别表示出△ACE 的面积和平行四边形ABCD 的面积，从而求出结果．【详解】解：∵四边形ABCD 是平行四边形，12CE CD =，设平行四边形AB 边上的高为h ，∴△ACE 的面积为：12CE h ⋅，平行四边形ABCD 的面积为2CE h ⋅， ∴△ACE 的面积为平行四边形ABCD 的面积的14，又∵□ABCD 的面积为52cm 2，∴△ACE 的面积为13cm 2．故选C ．【点睛】本题考查平行四边形的性质，比较简单，解答本题的关键是根据图形的形状得出△ACE 的面积为平行四边形ABCD 的面积的14． 2．在ABCD 中AB BC ≠．F 是BC 上一点，AE 平分FAD ∠，且E 是CD 的中点，则下列结论：①AB BF =；②AF CF CD =+；③AF CF AD =+；④AE EF ⊥，其中正确的是（）A ．①②B ．②④C ．③④D ．①②④C解析：C【分析】首先延长AD ，交FE 的延长线于点M ，易证得△DEM ≌△CEF ，即可得EM ＝EF ，又由AE 平分∠FAD ，即可判定△AEM 是等腰三角形，由三线合一的知识，可得AE ⊥EF ，进而可对各选项进行判断．【详解】解：延长AD ，交FE 的延长线于点M ，∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠M ＝∠EFC ，∵E 是CD 的中点，∴DE ＝CE ，在△DEM 和△CEF 中，M EFC DEM CEF DE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DEM ≌△CEF （AAS ），∴EM ＝EF ，∵AE 平分∠FAD ，∴AM ＝AF ，AE ⊥EF ．即AF ＝AD +DM ＝CF +AD ；故③，④正确，②错误．∵AF 不一定是∠BAD 的角平分线，∴AB 不一定等于BF ，故①错误．故选：C ．【点睛】此题考查了平行四边形的性质、等腰三角形的判定与性质以及全等三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．3．如图，在平行四边形ABCD 中，90B ∠<︒，BC AB >．作AE BC ⊥于点E ，AF CD ⊥于点F ，记EAF ∠的度数为α，AE a =，AF b =．则以下选项错误的是（）A ．::a b CD BC =B ．D ∠的度数为αC ．若60α=︒，则四边形AECF 的面积为平行四边形ABCD 面积的一半D ．若60α=︒，则平行四边形ABCD )a b +C 解析：C【分析】由平行四边形的性质得出//AD BC ，AD BC =，AB CD =，B D ∠=∠，得出180D C ∠+∠=︒，求出180EAF C ∠+∠=︒，得出B D EAF α∠=∠=∠=；由平行四边形ABCD 的面积得出::a b CD BC =；若60α=︒，则60B D ∠=∠=︒，求出30BAE DAF ∠=∠=︒，由直角三角形的性质得出BE AE ==，DF ，得出2AB BE =，2AD DF ==，求出平行四边形ABCD 的周长2())AB AD a b =+=+；求出ABE ∆的面积212BE AE =⨯=，ADF ∆的面积2=，平行四边形ABCD 的面积BC AE a =⨯=⨯=，得出四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22)a b =+≠平行四边形ABCD 面积的一半；即可得出结论．【详解】解：四边形ABCD 是平行四边形，//AD BC ∴，AD BC =，AB CD =，B D ∠=∠，180D C ∴∠+∠=︒，AE BC ⊥于点E ，AF CD ⊥于点F ，360290180EAF C ∴∠+∠=︒-⨯︒=︒，B D EAF α∴∠=∠=∠=；平行四边形ABCD 的面积BC AE CD AF =⨯=⨯，AE a =，AF b =，BC a CD b ∴⨯=⨯，::a b CD BC ∴=；若60α=︒，则60B D ∠=∠=︒，30BAE DAF ∴∠=∠=︒，BE AE ∴==，DF =，2AB BE ∴==，2AD DF ==，∴平行四边形ABCD 的周长2())AB AD a b =+=+；ABE ∆的面积211332236BE AE a a a =⨯=⨯⨯=，ADF ∆的面积211332236DF AF b b b =⨯=⨯⨯=，平行四边形ABCD 的面积232333BC AE b a ab =⨯=⨯=， ∴四边形AECF 的面积=平行四边形ABCD 的面积ABE -∆的面积ADF -∆的面积22233()36ab a b =-+≠平行四边形ABCD 面积的一半；综上所述，选项A 、B 、D 不符合题意，选项C 符合题意；故选：C ．【点睛】本题考查了平行四边形的性质、直角三角形的性质、三角形面积等知识；熟练掌握平行四边形的性质和直角三角形的性质是解题的关键．4．如图，己知四边形ABCD 是平行四边形，下列说法正确．．的是（）A ．若AB AD =，则平行四边形ABCD 是矩形B ．若AB AD =，则平行四边形ABCD 是正方形C ．若AB BC ⊥，则平行四边形ABCD 是矩形D ．若AC BD ⊥，则平行四边形ABCD 是正方形C解析：C【分析】根据已知及各个特殊四边形的判定方法对各个选项进行分析从而得到最后答案．【详解】解：A 、若AB=AD ，则▱ABCD 是菱形，选项说法错误；B 、若AB=AD ，则▱ABCD 是菱形，选项说法错误；C 、若AB ⊥BC ，则▱ABCD 是矩形，选项说法正确；D 、若AC ⊥BD ，则▱ABCD 是菱形，选项说法错误；故选：C ．【点睛】此题考查了菱形，矩形，正方形的判定方法，对角线互相垂直平分且相等的四边形是正方形．5．如图，在正方形 ABCD 内有一个四边形AECF ，AE EF ⊥， CF EF ⊥且8AE CF ==，12EF =，则图中阴影分的面积为（）A ．100B ．104C ．152D ．304B解析：B【分析】由题意可证四边形AECF 是平行四边形，可得AO ＝CO ，EO ＝FO ＝12EF ＝6，由勾股定理可求AO ＝10，可得AC ＝20，由阴影分的面积＝S 正方形ABCD -S ▱AECF 可求解．【详解】解：连接AC ，∵AE ⊥EF ，CF ⊥EF ，∴AE ∥CF ，且AE ＝CF ，∴四边形AECF 是平行四边形，∴AO ＝CO ，EO ＝FO ＝12EF ＝6， ∴AO 22AE EO +10，∴AC ＝20， ∴阴影分的面积＝S 正方形ABCD -S ▱AECF ＝20202⨯-8×12＝104，故选：B ．【点睛】本题考查了正方形的性质以及勾股定理的应用．此题综合性较强，解题时要注意数形结合思想的应用．6．在菱形ABCD 中，∠ABC=60゜，AC=4，则BD=( )A ．3B ．23C ．33D ．43D解析：D【分析】根据菱形的性质可得到直角三角形，利用勾股定理计算即可；【详解】如图，AC 与BD 相较于点O ，∵四边形ABCD 是菱形，4AC =，∴AC BD ⊥，2AO =，又∵∠ABC=60゜，∴30ABO ∠=︒，∴24AB AO ==，∴224223BO =-=，∴243BD BO ==；故选D ．【点睛】本题主要考查了菱形的性质，结合勾股定理计算是解题的关键．7．如图，在Rt ABC 中，90C =∠，30A ∠=，D 是 AC 边的中点，DE AC ⊥于点D ，交AB 于点E ，若83AC =，则DE 的长是（）A ．8B ．6C ．4D ．2C解析：C【分析】根据直角三角形的性质得到AB=2BC ，利用勾股定理求出BC ，再根据三角形中位线定理求出DE ．【详解】解：∵在Rt △ABC 中，∠C=90°，∠A=30°，∴AB=2BC ，设BC=x ，则AB=2x ， ∴()222483x x =+，解得：x=8或-8（舍），∴BC=8，∵D 是 AC 边的中点，DE AC ⊥，∴DE=12BC=4，故选C ．【点睛】本题考查了含30°角的直角三角形的性质，三角形的中位线的性质，熟练掌握直角三角形的性质是解题的关键．8．如图，点E 为矩形ABCD 的边BC 上的点，DF AE ⊥于点F ，且DF AB =，下列结论不正确的是（）A ．DE 平分AEC ∠B ．ADE ∆为等腰三角形C ．AF AB =D ．AE BE EF =+C 解析：C【分析】根据矩形的性质及HL 定理证明Rt △DEF ≌Rt △DEC ，然后利用全等三角形的性质进行推理判断【详解】解：在矩形ABCD 中，∠C=90°，AB=CD∵DF AE ⊥于点F ，且DF AB =∴∠DFE=∠C=90°，DF=CD在Rt △DEF 和Rt △DEC 中DF DC DE DE =⎧⎨=⎩∴Rt △DEF ≌Rt △DEC∴∠FDE=∠CDE ，即DE 平分AEC ∠，故A 选项不符合题意；∵Rt △DEF ≌Rt △DEC∴∠FED=∠CED又∵矩形ABCD 中，AD ∥BC∴∠ADE=∠CED∴∠FED=∠ADE∴AD=AE，即ADE为等腰三角形，故B选项不符合题意∵Rt△DEF≌Rt△DEC∴EF=EC在矩形ABCD中，AD=BC，又∵AD=AE∴AE=AD=BC=BE+EC=BE+EF，故D选项不符合题意由于AB=CD=DF，但在Rt△ADF中，无法证得AF=DF，故无法证得AB=AF，故C选项符合题意故选：C．【点睛】本题考查矩形的性质及三角形全等的判定和性质，掌握相关性质定理正确推理论证是解题关键．9．如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，S菱形ABCD＝48，则OH的长为（）A．4 B．8 C13D．6A解析：A【分析】由菱形的性质得出OA＝OC＝6，OB＝OD，AC⊥BD，则AC＝12，由直角三角形斜边上的中线性质得出OH＝12AB，再由菱形的面积求出BD＝8，即可得出答案．【详解】解：∵四边形ABCD是菱形，∴OA＝OC＝6，OB＝OD，AC⊥BD，∴AC＝12，∵DH⊥AB，∴∠BHD＝90°，∴OH＝12BD，∵菱形ABCD的面积＝12×AC×BD＝12×12×BD＝48，∴BD＝8，∴OH＝12BD＝4；【点睛】本题考查了菱形的性质，直角三角形的性质，菱形的面积公式，关键是根据直角三角形斜边上的中线性质求得OH=12BD ． 10．如图在ABCD 中，对角线,AC BD 相交于点O ，AOD △与AOB 的周长相差3，8AB =，那么AD 为（）A ．5B ．8C ．11或5D ．11或14C解析：C【分析】根据平行四边形的性质可得BO=DO ，再根据AOD △与AOB 的周长相差3，可分情况得出结果．【详解】解：∵四边形ABCD 是平行四边形，∴BO=DO ，AO=AO ，∵AOD △与AOB 的周长相差3，∴AB-AD=3，或AD-AB=3，∵AB=8，∴AD 的长为5或11，故选C ．【点睛】本题考查平行四边形的性质，解题的关键是掌握平行四边形对角线互相平分．二、填空题11．如图，在平行四边形ABCD 中，10,AB BAD =∠的平分线与BC 的延长线交于点E ､与DC 交于点F ，且点F 为边DC 的中点，ADC ∠的平分线交AB 于点M ，交AE 于点N ，连接DE ．若6DM =，则DE 的长为_______．【分析】先判定△ADF ≌△ECF 即可得到AF=EF 依据平行线的性质以及角平分线的定义即可得出AF ⊥DM ；再根据等腰三角形的性质即可得到DN=MN=3最后依据勾股定理即可得到AN 与NE 的长进而解析：【分析】先判定△ADF≌△ECF，即可得到AF=EF，依据平行线的性质以及角平分线的定义，即可得出AF⊥DM；再根据等腰三角形的性质，即可得到DN=MN=3，最后依据勾股定理即可得到AN与NE的长，进而得出DE的长．【详解】解：∵点F为边DC的中点，∴DF=CF=12CD=12AB=5，∵AD∥BC，∴∠ADF=∠ECF，∵∠AFD=∠EFC，∴△ADF≌△ECF（ASA），∴AF=EF，∵CD∥AB，∴∠ADC+∠DAB=180°，又∵AF平分∠BAD，DM平分∠ADC，∴∠ADN+∠DAN=90°，∴AF⊥DM，∵AF平分∠BAD，∴∠BAF=∠DAF，又∵DC∥AB，∴∠BAF=∠DFA，∴∠DAF=∠DFA，∴AD=DF=5，同理可得，AM=AD=5，又∵AN平分∠BAD，∴DN=MN=3，∴Rt△ADN中，4=，∴AF=2AN=8，EF=8，∴NE=AE-AN=12，∴Rt△DEN中，=故答案为：【点睛】本题主要考查了平行四边形的性质以及勾股定理的运用，判定AF ⊥DM ，利用勾股定理进行计算是解决问题的关键．12．215，2，则该三角形最长边上的中线长为____．【分析】利用勾股定理逆定理判断出此三角形是直角三角形再根据直角三角形斜边上的中线等于斜边的一半解答【详解】∵∴此三角形是直角三角形斜边为5∴该三角形最长边上的中线长为：5=故答案为：【点睛】本题考查解析：52【分析】利用勾股定理逆定理判断出此三角形是直角三角形，再根据直角三角形斜边上的中线等于斜边的一半解答．【详解】 ∵221222255+==，∴此三角形是直角三角形，斜边为5，∴该三角形最长边上的中线长为：12⨯5=52．故答案为：52．【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理逆定理的应用，熟记性质并判断出此三角形是直角三角形是解题的关键．13．如图，在菱形ABCD 中，6AC =，5AB =，点E 是直线AB ，CD 之间任意一点，连接AE ，BE ，DE ，CE ，则EAB 和ECD 的面积之和是______．12【分析】连接BD根据菱形对角线的性质利用勾股定理计算BD的长根据两平行线的距离相等所以△EAB和△ECD的面积和等于菱形ABCD面积的一半再利用菱形面积等于对角线积的一半计算可得结论【详解】如图解析：12【分析】连接BD，根据菱形对角线的性质，利用勾股定理计算BD的长，根据两平行线的距离相等，所以△EAB和△ECD的面积和等于菱形ABCD面积的一半，再利用菱形面积等于对角线积的一半计算可得结论．【详解】如图，连接BD交AC于O，∵四边形ABCD是菱形，∴AC⊥BD，OA=12AC=12×6=3，∵AB＝5，由勾股定理得：224AB OA-=，∴BD=2OB=8，∵AB∥CD，∴△EAB和△ECD的高的和等于点C到直线AB的距离，∴△EAB 和△ECD 的面积和=12×ABCD S 菱形＝12×12×AC×BD=168=124⨯⨯．故答案为：12．【点睛】本题考查菱形的性质，三角形的面积，平行线的性质，熟知平行线的距离相等，得△EAB 和△ECD 的高的和等于点C 到直线AB 的距离是解题的关键．14．如图，在四边形ABCD 中，AC a =，BD b =，且AC BD ⊥顺次连接四边形ABCD 各边的中点，得到四边形1111D C B A ，再顺次连接四边形1111D C B A 各边中点，得到四边形2222A B C D …如此进行下去，得到四边形n n n n A B C D ，下列结论正确的有__________．①四边形2222A B C D 是矩形；②四边形4444A B C D 是菱形；③四边形5555A B C D 的周长是4a b +． ②③【分析】利用三角形的中位线的性质证明四边形是矩形四边形是菱形四边形是矩形四边形是菱形从而可得到规律序号n 是奇数时四边形是矩形当序号n 是偶数时四边形是菱形再探究n 是奇数时四边形的周长即可解决问题【解析：②③【分析】利用三角形的中位线的性质证明四边形1111D C B A 是矩形，四边形2222A B C D 是菱形，四边形3333A B C D 是矩形，四边形4444A B C D 是菱形，从而可得到规律，序号n 是奇数时四边形是矩形，当序号n 是偶数时四边形是菱形，再探究n 是奇数时四边形的周长即可解决问题．【详解】解： 1111,,,A B C D 分别是,,,AB BC CD DA 的中点，1111111111//,,//,,22A B AC A B AC C D AC C D AC ∴== 11//,A D BD 11111111//,,A B C D A B C D ∴=∴ 四边形1111D C B A 是平行四边形，,AC BD ⊥ 11//,A B AC 11//,A D BD1111,A B A D ∴⊥∴ 四边形1111D C B A 是矩形，1111,AC B D ∴=如图，2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点，∴ 2211221111,,22A B AC A D B D == 四边形2222A B C D 是平行四边形， 2222,A B A D ∴=∴ 四边形2222A B C D 是菱形，故①不符合题意，2222,A C B D ∴⊥同理可得：四边形3333A B C D 是矩形，四边形4444A B C D 是菱形，故②符合题意，······总结规律：四边形n n n n A B C D ，当序号n 是奇数时四边形是矩形，当序号n 是偶数时四边形是菱形，111111111111,,2222A B C D AC a A D B C BD b ====== ∴ 四边形1111D C B A 的周长为,a b +如图，四边形1111D C B A 是矩形，四边形2222A B C D 是菱形，2222,,,A B C D 分别是11111111,,,A B B C C D D A 的中点，222222112211,,,A C B D A C A D B D A B ∴⊥==由中位线的性质同理可得：33332233332211111111,,22242224A DBC BD a a D C A B A C b b ===⨯====⨯= 所以四边形3333A B C D 的周长为()1,2a b + 由规律可得：四边形5555A B C D 是矩形，同理可得：四边形5555A B C D 的周长是()11.224a b a b +⨯+=故③符合题意．故答案为②③．【点睛】本题考查三角形的中位线的性质，中点四边形，菱形的判定与性质，矩形的判定与性质，解题的关键是学会从特殊到一般，探究规律，利用规律解决问题．15．如图，在矩形ABCD 中，AB ＝3，BC ＝4，点M 为AD 的中点，点N 为AB 上一点，连接MN ，CN ，将△AMN 沿直线MN 折叠后，点A 恰好落在CN 上的点P 处，则CN 的长为_____．【分析】连接CM 由题意易证即得到PC=DC=3设AN=x 则PN=xBN=3-xCN=3+x 在中利用勾股定理即可求出x 即可得到CN 的长【详解】如图连接CM 由题意可知在和中∴∴PC=DC=3设AN=x 则解析：133【分析】连接CM ，由题意易证DMC PMC ≅，即得到PC=DC=3．设AN=x ，则PN= x ，BN=3-x ，CN=3+ x ．在Rt BCN △中利用勾股定理即可求出x ，即可得到CN 的长．【详解】如图，连接CM ，由题意可知122AM DM PM AD ====，在Rt DMC 和Rt PMC 中，PM PD MC MC =⎧⎨=⎩， ∴DMC PMC ≅，∴PC=DC=3．设AN=x ，则PN= x ，BN=3-x ，CN=3+ x ．在Rt BCN △中，222BC BN CN +=，即2224(3)(3)x x +-=+，解得：43x =，∴CN=3+413333CN +==．故答案为：133．【点睛】本题考查翻折的性质，矩形的性质，三角形全等的判定和性质以及勾股定理．作出常用的辅助线是解答本题的关键．16．如图，在ABC 中，已知AB =8，BC =6，AC =7，依次连接ABC 的三边中点，得到111A B C △，再依次连接111A B C △的三边中点，得到222A B C △，，按这样的规律下去，202020202020A B C △的周长为____．【分析】由再利用中位线的性质可得：再总结规律可得：从而运用规律可得答案【详解】解：探究规律：AB=8BC=6AC=7分别为的中点同理：总结规律：运用规律：当时故答案为：【点睛】本题考查的是图形周长的解析：2020212【分析】由21ABC C AB BC AC =++=，再利用中位线的性质可得：111121,22A B C ABC C C ==2221112121,22A B C A B C C C ==再总结规律可得：21,2n n n A B C n C =从而运用规律可得答案．【详解】解：探究规律：AB =8，BC =6，AC =7， 21ABC C AB BC AC ∴=++=，111,,A B C 分别为,,BC AC AB 的中点，111111111,,,222A B AB B C BC AC AC ∴=== 111121,22A B C ABC C C ∴== 同理：2221112112121,2222A B C A B C C C ==⨯= ······总结规律：21,2n n n A B C n C =运用规律：当2020n =时，202020202020202021.2A B C C= 故答案为：202021.2 【点睛】本题考查的是图形周长的规律探究，三角形中位线的性质，掌握探究规律的方法与三角形中位线的性质是解题的关键．17．如图，在Rt ABC ∆中，90,6,10ACB AC AB ∠===，过点A 作//,AM CB CE 平分ACB ∠交AM 于点,E Q 是线段CE 上的点，连接BQ ，过点B 作BP BQ ⊥交AM 于点P ，当PBQ ∆为等腰三角形时，AP =________________________．【分析】过点P 作PG ⊥CB 交CB 的延长线于点G 过点Q 作QF ⊥CB 运用AAS 定理证明△QBF ≌△BPG 根据平行线的性质和角平分线的定义求得△AEC 为等腰直角三角形利用勾股定理求得线段BC 的长然后结合全解析：10【分析】过点P 作PG ⊥CB ，交CB 的延长线于点G ，过点Q 作QF ⊥CB ，运用AAS 定理证明△QBF ≌△BPG ，根据平行线的性质和角平分线的定义求得△AEC 为等腰直角三角形，利用勾股定理求得线段BC 的长，然后结合全等三角形和矩形的性质求解．【详解】解：过点P 作PG ⊥CB ，交CB 的延长线于点G ，过点Q 作QF ⊥CB∵BP BQ⊥，PG⊥CB∴∠1+∠2=90°，∠2+∠3=90°∴∠1=∠3∵QF⊥CB，BP BQ⊥∴∠QFB=∠PGB=90°又∵PBQ∆为等腰三角形∴QB=PB在△QBF和△BPG中1=3QFB PGB QB PB∠∠⎧⎪∠=∠⎨⎪=⎩∴△QBF≌△BPG∴PG=BF，BG=QF∵∠ACB=90°，CE平分ACB∠∴∠ACE=∠ECB=45°又∵AM∥CB，∴∠AEC=∠ECB=45°∴∠AEC=∠ACE=45°∴△AEC为等腰直角三角形∵AM∥BC，∠ACB=90°∴∠CAM+∠ACB=180°，即∠CAM=90°∴∠CAM=∠ACB=∠PGB=90°∴四边形ACGP为矩形，∴PG=AC=6，AP=CG在Rt△ABC中，BC=228AB AC-=∴CF=BC-BF=BC-PG=8-6=2∵QF⊥BC，∠ECB=45°∴△CQF是等腰直角三角形，即CF=QF=2∴AP=CG=BC+BG=BC+QF=8+2=10【点睛】本题考查矩形的判定和性质、全等三角形的判定和性质以及勾股定理，掌握相关性质定理正确推理论证是解题关键18．已知：如图，把长方形纸片ABCD 沿EF 折叠，使D C 、分别落在D C ''、的位置，若65EFB ︒∠=，则AED '∠的度数为_________．【分析】由长方形纸片可得再求解由折叠的性质求解结合平角的定义可得答案【详解】解：长方形纸片由折叠可得：故答案为：【点睛】本题考查的是矩形与折叠平行线的性质简单题解题的关键是理解折叠的性质解析：50︒【分析】由长方形纸片ABCD ，65EFB ∠=︒可得//,AD BC 再求解,DEF ∠ 由折叠的性质求解,D EF '∠ 结合平角的定义可得答案．【详解】解：长方形纸片ABCD ，65EFB ∠=︒，//,AD BC ∴65DEF EFB ∴∠=∠=︒，由折叠可得：65D EF DEF '∠=∠=︒，180180656550.AED D EF DEF ''∴∠=︒-∠-∠=︒-︒-︒=︒故答案为：50.︒【点睛】本题考查的是矩形与折叠，平行线的性质，简单题，解题的关键是理解折叠的性质． 19．如图，在矩形ABCD 中，AD ＝2．将∠A 向内翻折，点A 落在BC 上，记为A '，折痕为DE ．若将∠B 沿EA '向内翻折，点B 恰好落在DE 上，记为B '，则AB ＝_______．【分析】利用矩形和折叠的性质证明∠ADE=∠ADE=∠ADC=30°∠C=∠ABD=90°推出△DBA ≌△DCA 那么DC=DB 设AB=DC=x 在Rt △ADE 中通过勾股定理可求出AB 的长度【详解】解： 3【分析】利用矩形和折叠的性质，证明∠ADE=∠A'DE=∠A'DC=30°，∠C=∠A'B'D=90°，推出△DB'A'≌△DCA'，那么DC=DB'，设AB=DC=x ，在Rt △ADE 中，通过勾股定理可求出AB 的长度．【详解】解：∵四边形ABCD 为矩形，∴∠ADC=∠C=∠B=90°，AB=DC ，由翻折知，△AED ≌△A'ED ，△A'BE ≌△A'B'E ，∠A'B'E=∠B=∠A'B'D=90°，∴∠AED=∠A'ED ，∠A'EB=∠A'EB'，BE=B'E ，∴∠AED=∠A'ED=∠A'EB=13×180°=60°， ∴∠ADE=90°-∠AED=30°，∠A'DE=90°-∠A'EB'=30°，∴∠ADE=∠A'DE=∠A'DC=30°，又∵∠C=∠A'B'D=90°，DA'=DA'，∴△DB'A'≌△DCA'（AAS ），∴DC=DB'，在Rt △AED 中，∠ADE=30°，AD=2，∴AE=23 =233，设AB=DC=x ，则BE=B'E=x-233 ∵AE 2+AD 2=DE 2，∴2222323233x x +=+-（）（）解得，x 1=−33 （负值舍去），x 2=3 ，故答案为：3．【点睛】本题考查了矩形的性质，轴对称的性质等，解题关键是通过轴对称的性质证明∠AED=∠A'ED=∠A'EB=60°．20．如图，将Rt △ABC 沿着点B 到A 的方向平移到△DEF 的位置，BC ＝8，FO ＝2，平移距离为4，则四边形AOFD 的面积为__．【分析】根据平移的性质判断AD ＝CF ＝BE ＝4AD ∥CF 再根据平行四边形的面积和三角形面积公式解答即可【详解】如图连接CF 由平移的性质知AD ＝CF ＝BE ＝4AD ∥CF ∴四边形ACFD 为平行四边形∴＝解析：28【分析】根据平移的性质，判断AD ＝CF ＝BE ＝4，AD ∥CF ，再根据平行四边形的面积和三角形面积公式解答即可．【详解】如图，连接CF ．由平移的性质知，AD ＝CF ＝BE ＝4，AD ∥CF ，∴四边形ACFD 为平行四边形．∴ACFD S ＝AD •BC ＝4×8＝32，∵FO ＝2，∴S △FOC ＝12OF •BE ＝1242⨯⨯＝4， ∴AOFD S 四边形＝ACFD FOC S S -＝32-4＝28．故答案为28．【点睛】本题考查图形的平移以及平行四边形的判定．根据题意得出AOFD S 四边形＝ACFD FOC SS -是解答本题的关键．三、解答题21．如图，在四边形ABCD 中，AB ∥CD ，∠ADC ＝90°，AD ＝12cm ，AB ＝18cm ，CD ＝23cm ，动点P 从点A 出发，以1cm/s 的速度向点B 运动，同时动点Q 从点C 出发，以2cm/s 的速度向点D 运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t 秒．（1）当t ＝3时，PB ＝ cm ．（2）当t 为何值时，直线PQ 把四边形ABCD 分成两个部分，且其中的一部分是平行四边形？（3）四边形PBQD 能否成为菱形？若能，求出t 的值；若不能，请说明理由．解析：（1）15；（2）t ＝6或233；（3）能，t ＝5. 【分析】（1）先求出AP ，即可求解；（2）分两种情况讨论，由平行四边形的性质可求解；（3）由菱形的性质可求DP ＝BP ，由勾股定理可求解．【详解】解：（1）当t ＝3时，则AP ＝3×1＝3cm ，∴PB ＝AB ﹣AP ＝18﹣3＝15cm ，故答案为：15．（2）若四边形PBCQ 是平行四边形，∴PB ＝CQ ，∴18﹣t ＝2t ，∴t ＝6，若四边形PQDA 是平行四边形，∴AP ＝DQ ，∴t ＝23﹣2t ，∴t ＝233，综上所述：t ＝6或233；（3）如图，若四边形PBQD 是菱形，∴BP ＝DP ，∵222AP AD DP +=，∴22144(18)AP AP +=-，∴AP ＝5，∴t ＝51＝5， ∴当t ＝5时，四边形PBQD 为菱形．【点睛】本题考查了平行四边形，菱形的判定，勾股定理，分类思想，熟练掌握菱形的判定定理，灵活运用分类思想是解题的关键.22．如图，已知点E 是ABCD 的边CD 延长线上的一点；连接AE ，BD ，且//AE BD ；过点E 作EF BC ⊥，交BC 的延长线于点F ，连接DF ；求证：DF DE =解析：见解析【分析】根据平行四边形的性质可得AB CD =，//AB CD ，然后结合题意利用两组对边分别平行的四边形是平行四边形可判定四边形ABDE 是平行四边形，然后利用平行四边形的性质和直角三角形斜边中线等于斜边一半证明求解．【详解】证明：∵四边形ABCD 是平行四边形，∴AB CD =，//AB CD ，又∵//AE BD∴四边形ABDE 是平行四边形；∴AB DE =，即CD DE =；又EF BC ⊥于点F ；∴∠EFC=90°∴在Rt CEF △中，点D 是斜边CE 的中点∴DF DE =．【点睛】本题考查平行四边形的性质和判定以及直角三角形斜边中线等于斜边的一半，掌握相关性质定理正确推理论证是解题关键．23．如图所示，沿AE 折叠长方形ABCD 使点D 恰好落在BC 边上的点F 处，已知8AB cm =，BC 10cm =．（1）求EC 的长（2）求AFE ∆的面积．解析：（1）3EC =cm ；（2）25cm 2【分析】（1）根据矩形的性质得DC=8cm ，AD=10cm ，再根据折叠的性质得到AF=AD=10cm ，DE=EF ，在Rt △ABF 中，利用勾股定理易得BF=6cm ，设DE=xcm ，则EF=xcm ，EC=(8-x)cm ，在Rt △CEF 中，利用勾股定理可求出x 的值，进一步得到EC 的长；（2）根据三角形面积公式计算即可求解．【详解】（1）∵AB=8cm ，BC=10cm ，∴DC=8cm ，AD=10cm ，又∵将△ADE 折叠使点D 恰好落在BC 边上的点F ，∴AF=AD=10cm ，DE=EF ，在Rt △ABF 中，AB=8cm ，AF=10cm ，∴BF=22221086AF AB (cm)， ∴FC=10-6=4(cm)，设DE=xcm ，则EF=xcm ，EC=(8-x)cm ，在Rt △CEF 中，EF 2=FC 2+EC 2，即x 2=42+(8-x)2，解得x=5，即DE 的长为5cm ， EC=8-x=8-5=3，即EC 的长为3cm ；（2）S △AEF =12EF×AF=12×5×10=25(cm 2)．故△AFE 的面积是25cm 2．【点睛】本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应线段相等．也考查了矩形的性质以及勾股定理．24．如图，菱形ABCD 中，60B ∠=︒，点E ，F 分别在BC 和CD 上，BE CF =，求证：AE AF =．解析：证明见解析．【分析】连接AC ，证ABE ACF ≌即可【详解】证明：连接AC ，∵四边形ABCD 是菱形，∴AB BC CD AD ===，AC 平分BCD ∠．∵60B ∠=︒，∴ABC 是等边三角形，∴AB AC =，60∠=∠=∠︒=B BCA ACF ．∴在ABE △与ACF 中，AB AC B ACF BE CF =⎧⎪∠=∠⎨⎪=⎩．∴ABE ACF ≌．∴AE AF =．【点睛】本题考查了菱形的性质，全等三角形的判定和性质，证明三角形全等是解此题的关键． 25．我们学习过利用尺规作图平分一个任意角，而“利用尺规作图三等分一个任意角”曾是数学史上一大难题，之后被数学家证明是不可能完成的．但人们可以通过折纸把一个角三等分，今天我们就通过折纸把一个直角三等分．操作如下：第一步：如图①，对折长方形纸片ABCD ，使AD 与BC 重合，沿EF 对折后，得到折痕EF ，把纸片展平；第二步：如图②，再一次折叠纸片，使点A 落在EF 上（标记为点O ），并使折痕经过点B ；第三步：如图③，再展开纸片，得到折痕BR ，同时连接BO RO 、．这时就可以得到BR BO 、把直角ABC 三等分．为了说明这一方法的正确性，需要对其进行证明．如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程．已知：如图④，线段EF 是长方形ABCD 对折后的折痕，BOR ∆是由BAR ∆沿BR 折叠后得到的三角形，求证：解析：点O 在折痕EF 上，BR BO 、把ABC ∠三等分，见解析【分析】如图④，线段EF 是长方形ABCD 对折后的折痕，BOR ∆是BAR ∆沿BR 折叠后得到的三角形，点O 在折痕EF 上；连接AO ，根据折叠的性质可得△AOB 为等边三角形，然后结合矩形的性质即可求证所求问题．【详解】解：已知：如图④，线段EF 是长方形ABCD 对折后的折痕，BOR ∆是BAR ∆沿BR 折叠后得到的三角形，点O 在折痕EF 上．求证：BR BO 、把ABC ∠三等分证明：连接AO线段EF 是长方形ABCD 对折后的折痕∴EF 垂直平分AB 又点O 在对称轴EF 上AO BO ∴=BOR ∆是BAR ∆沿BR 折叠后得到的三角形,12BO AB ∴=∠=∠AO BO AB ∴==ABO ∴∆是等边三角形60ABO ︒∴∠=又12ABO ∠+∠=∠1230︒∴∠=∠=又90ABC ︒∠=330ABC ABO ︒∴∠=∠-∠=123∴∠=∠=∠BR BO ∴、把ABC ∠三等分．【点睛】本题主要考查矩形的性质及等边三角形的性质和判定，还考查了学生的观察力和动手能力，动手操作一下，问题更容易解决．26．如图，在四边形ABCD 中，90B D ∠=∠=︒，60C ∠=°，5AB =．2AD =．（1）求CD 的长；（2）求四边形ABCD 的面积．解析：（1）32233 【分析】（1）作DM ⊥BC ，AN ⊥DM 垂足分别为M 、N ，易知四边形MNAB 是矩形，分别在Rt △ADN 中求出DN ，利用含60°的直角三角形求CD 即可；（2）由（1）可知，四边形ABCD 的面积就是△DCM 与梯形ADMB 的面积和．【详解】解：（1）如图作DM ⊥BC ，AN ⊥DM 垂足分别为M 、N ．∵∠B ＝∠NMB ＝∠MNA ＝90°，∴四边形MNAB 是矩形，∴MN ＝AB ＝5，AN ＝BM ，∠BAN ＝90°，∵∠C +∠B +∠ADC +∠BAD ＝360°，∠C ＝60°，∠B ＝∠ADC ＝90°，∴∠DAN ＝∠BAD ﹣∠BAN ＝30°，在RT △AND 中，∵AD ＝2，∠DAN ＝30°，∴DN ＝12AD ＝1，AN ＝2222213AD DN -=-=，在RT △DMC 中，∵DM ＝DN +MN ＝6，∠C ＝60°，∴∠CDM ＝30°，∴CD ＝2MC ，设MC ＝x ，则CD ＝2x ，∵CD 2＝DM 2+CM 2，∴4x 2＝x 2+62，∵x ＞0∴x ＝23，∴CD ＝43．（2）由（1）得，112366322DCM S CM DM =⨯⨯=⨯⨯=， 1111()3113222ADMB S AN DM AB =⨯⨯+=⨯⨯=梯形， 1123633322DCM ABCD ADMB S S S =+=+=四边形梯形．【点睛】本题考查了勾股定理和含有30°角的直角三角形的性质，通过作辅助线，构建特殊的直角三角形是解题关键．27．在Rt ABC 中，90ACB ︒∠=，以AC 为一边向外作等边三角形ACD ，点E 为AB 的中点，连接DE ．（1）证明：//DE CB ；（2）探索AC 与AB 满足怎样的数量关系时，四边形DCBE 是平行四边形，并说明理由．解析：（1）见解析；（2）AC ＝12AB 【分析】（1）首先连接CE ，根据直角三角形的性质可得CE ＝12AB ＝AE ，再根据等边三角形的性质可得AD ＝CD ，然后证明△ADE ≌△CDE ，进而得到∠ADE ＝∠CDE ＝30°，再有∠DCB ＝150°可证明DE ∥CB ；（2）当AC ＝12AB 或AB ＝2AC 时，四边形DCBE 是平行四边形．根据（1）中所求得出DC ∥BE ，进而得到四边形DCBE 是平行四边形．【详解】解：（1）证明：连结CE ．∵点E 为Rt △ACB 的斜边AB 的中点，∴CE ＝12AB ＝AE ． ∵△ACD 是等边三角形，∴AD ＝CD ．在△ADE 与△CDE 中，AD DC DE DE AE CE =⎧⎪=⎨⎪=⎩，∴△ADE ≌△CDE （SSS ），∴∠ADE ＝∠CDE ＝30°．∵∠DCB ＝150°，∴∠EDC +∠DCB ＝180°．∴DE ∥CB ．（2）当AC ＝12AB 或AB ＝2AC 时，四边形DCBE 是平行四边形，理由：∵AC ＝12AB ，∠ACB ＝90°， ∴∠B ＝30°，∵∠DCB ＝150°，∴∠DCB +∠B ＝180°，∴DC ∥BE ，又∵DE ∥BC ，∴四边形DCBE 是平行四边形．【点睛】此题主要考查了平行线的判定、全等三角形的判定与性质，以及平行四边形的判定，关键是掌握直角三角形的性质，以及等边三角形的性质．28．正方形ABCD 中，对角线AC 、BD 交于点O ，E 为BD 上一点，延长AE 到点N ，使AE EN =，连接CN 、CE ．（1）求证：CAN △为直角三角形．（2）若45AN =6，求BE 的长．解析：（1）见解析；（2）42BE =【分析】（1）由四边形ABCD 是正方形，易证得△ABE ≌△CBE ，继而证得AE=CE ，再由AE=CE ，AE=EN ，即可证得∠ACN=90°，则可判定△CAN 为直角三角形；（2）由56，易求得CN 的长，然后由三角形中位线的性质，求得OE 的长，继而求得答案．【详解】解：（1）证明：∵四边形ABCD 是正方形，∴∠ABD=∠CBD=45°，AB=CB ，在△ABE 和△CBE 中，AB CB ABE CBE BE BE ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ABE ≌△CBE （SAS ），∴AE=CE ；∵AE=CE ，AE=EN ，∴∠EAC=∠ECA ，CE=EN ，∴∠ECN=∠N ，∵∠EAC+∠ECA+∠ECN+∠N=180°，∴∠ACE+∠ECN=90°，即∠ACN=90°，∴△CAN 为直角三角形；（2）∵正方形的边长为6， ∴AC BD == ∵90,ACN AN ∠=︒=∴CN ==∵,OA OC AE EN ==，∴12OE CN ==∵12OB BD == ∴BE OB OE =+=【点睛】此题考查了正方形的性质、全等三角形的判定与性质、直角三角形的判定以及勾股定理等知识．注意利用勾股定理求得各线段的长是关键．。

人教版八年级下册数学第十八章平行四边形专题讲义(无答案)

1.平行四边形：两组对边分别平行的四边形是平行四边形．表示：平行四边形用符号“”来表示．如图，在四边形ABCD中，AB∥DC，AD∥BC，那么四边形ABCD是平行四边形．平行四边形ABCD记作“ ABCD”，读作“平行四边形ABCD”．注意：平行四边形中对边是指无公共点的边，对角是指不相邻的角，邻边是指有公共端点的边，邻角是指有一条公共边的两个角．而三角形对边是指一个角的对边，对角是指一条边的对角．2.平行四边形的性质：（1）边：平行四边形的对边平行且相等．（2）角：平行四边形的对角相等．邻角互补（3）对角线：平行四边形的对角线互相平分对称性：平行四边形是中心对称图形，两条对角线的交点是对称中心；【例题精讲】例1 ：如图，在平行四边形ABCD中，DB=DC、，CE BD于E，则．例2：如图，在□ABCD中，已知AD＝8㎝， AB＝6㎝，DE平分∠ADC交BC边于点E，则BE等于（）A.2cmB.4cmC.6cmD.8cm例3：如图，已知：平行四边形ABCD中，的平分线交边于，的平分线交于，交于．求证：．【课堂练习】（1）在ABCD 中，∠A= 50，则∠B= 度，∠C= 度，∠D= 度．（2）如果ABCD 中，∠A —∠B=24°，则∠A= 度，∠B= 度，∠C= 度，∠D= 度．（3）如果ABCD 的周长为28cm ，且AB ：BC=2∶5，那么AB= cm ，BC= cm ，CD= cm ，AD= cm ．2．如图4.3－9，在ABCD 中，AC 为对角线，BE ⊥AC ，DF ⊥AC ，E 、F 为垂足，求证：BE ＝DF ．3．在平行四边形中，周长等于48，① 已知一边长12，求各边的长 ② 已知AB=2BC ，求各边的长③ 已知对角线AC 、BD 交于点O ，△AOD 与△AOB 的周长的差是10，求各边的长4．如图，ABCD 中，AE ⊥BD ，∠EAD=60°，AE=2cm ，AC+BD=14cm ，则△OBC 的周长是_______cm ． 5．ABCD 一内角的平分线与边相交并把这条边分成cm 5，cm 7的两条线段，则ABCD 的周长是_____cm ．6．ABCD 的周长为36，AB=8cm ，BC=________；当∠B=60°时，AD 、BC 的距离AE=________，ABCD 的面积ABCD S =________。

第18章《平行四边形》知识点及考点典例

第十八章《平行四边形》知识点及考点典例一、平行四边形1、平行四边形的概念两组对边分别__________的四边形叫做平行四边形。

2、平行四边形的性质（1）平行四边形的邻角_______，对角_______。

（2）平行四边形的对边_______且________。

推论：夹在两条平行线间的平行线段_______。

（3）平行四边形的对角线_________。

（4）若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积。

3、平行四边形的判定（1）定义：两组对边分别________的四边形是平行四边形（2）定理1：两组对角分别_________的四边形是平行四边形（3）定理2：两组对边分别_________的四边形是平行四边形（4）定理3：对角线___________的四边形是平行四边形（5）定理4：一组对边_________的四边形是平行四边形二、矩形1、矩形的概念有一个角是_______的平行四边形叫做矩形。

2、矩形的性质（1）具有平行四边形的一切性质(边、角、对角线)；（2）矩形的四个角都是_______；（3）矩形的对角线_______；（4）矩形是______对称图形。

3、矩形的判定（1）定义：有一个角是________的平行四边形是矩形。

（2）定理1：有___________是直角的四边形是矩形。

（3）定理2：对角线相等的_______________是矩形。

4、矩形的面积S矩形=长×宽=ab三、菱形1、菱形的概念有一组___________的平行四边形叫做菱形2、菱形的性质（1）具有平行四边形的一切性质(边、角、对角线)；（2）菱形的________边相等（3）菱形的对角线________，并且每一条对角线平分一组对角（4）菱形是________对称图形3、菱形的判定（1）定义：有一组___________的平行四边形是菱形（2）定理1：___________都相等的四边形是菱形（3）定理2：对角线___________的平行四边形是菱形4、菱形的面积S菱形=底边长×高=两条对角线乘积的一半四、正方形1、正方形的概念有一组邻边相等并且有一个角是直角的______________叫做正方形。

第十八章平行四边形的常见题型总结(教案)

五、教学反思
在这次《平行四边形的常见题型总结》的教学过程中，我注意到了几个值得反思的地方。首先，我发现学生们在理解平行四边形的性质时，普遍能够快速掌握对边平行且相等这一特点，但对于对角线互相平分这一性质的理解还不够深入。在今后的教学中，我需要通过更多具体的实例和图形展示，帮助学生更好地理解这一性质。
（3）平行四边形与其他四边形的区别：学生容易混淆平行四边形与其他四边形的性质和判定方法。
突破方法：通过对比、总结，让学生明确平行四边形与其他四边形的区别，形成清晰的知识体系。
（4）实际应用问题：学生在解决实际应用问题时，难以将平行四边形的知识与实际问题相结合。
突破方法：引入实际生活中的案例，让学生学会将平行四边形知识应用于解决实际问题，提高数学应用能力。
第十八章平行四边形的常见题型总结（教案）
一、教学内容
第十八章平行四边形的常见题型总结：本章节以八年级数学教材为依据，围绕平行四边形的概念、性质及判定方法展开，主要包括以下内容：
1.平行四边形的定义及性质：对边平行且相等，对角线互相平分，对角线所分的角相等。
2.平行四边形的判定：两组对边分别平行的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对边分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形。
3.平行四边形的面积计算：底乘以高。
4.平行四边形与其他四边形（如矩形、菱形、梯形等）的关系与区别。
二、核心素养目标
本章节旨在培养学生以下核心素养：
1.培养学生的空间观念：通过探究平行四边形的性质与判定，使学生能够理解和运用空间几何图形的特征，发展其空间想象力。
2.提高学生的逻辑思维能力：在解决平行四边形相关问题时，引导学生运用逻辑推理，分析问题，培养其严密的逻辑思维。

第十八章-平行四边形-知识点总结