初中数学之阴影部分面积 (2)

合集下载

初中数学专题辅导：阴影面积求法9种方法(不规则图形)

阴影面积求法阴影部分的图形一般是不规则图形或没有可直接利用的公式，因此，同学们常感到困难。

本文指出：求解这类问题的关键是将阴影部分图形转化为可求解的规则图形的组合。

如何转化呢?这里给出常用的9种转化方法。

1.直接组合例1.如下图，圆A 、圆B 、圆C 、圆D 、圆E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）A.π B.1.5π C.2πD.2.5π（02年河南省中考）分析：由于每个扇形圆心角的具体角度未知，故无法直接进行计算。

因为五边形ABCDE 的内角和=540°=360°+180°，从而可知所求阴影部分的面积可以重新组合成一个圆和一个半圆的面积，即1.5个圆的面积：ππ5.1)1(5.12=⋅⨯，选（B ）。

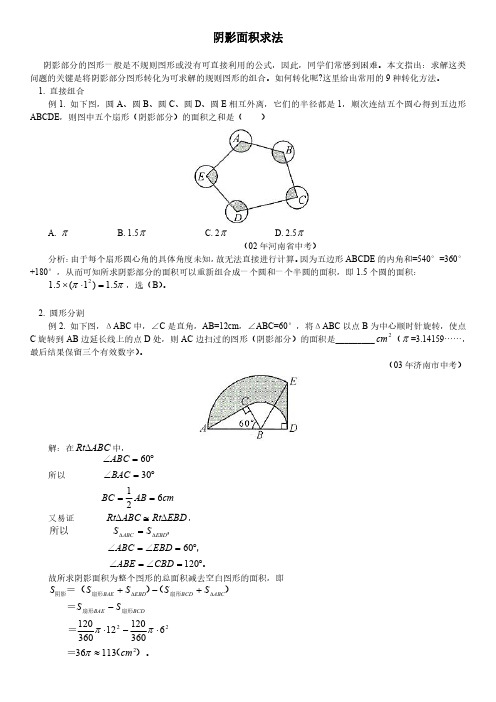
2.圆形分割例2.如下图，ΔABC 中，∠C 是直角，AB=12cm ，∠ABC=60°，将ΔABC 以点B 为中心顺时针旋转，使点C 旋转到AB 边延长线上的点D 处，则AC 边扫过的图形（阴影部分）的面积是_________2cm （π=3.14159……，最后结果保留三个有效数字）。

（03年济南市中考）解：在ABC Rt ∆中，所以cm AB BC BAC ABC 6213060==︒=∠︒=∠又易证EBD Rt ABC Rt ∆≅∆，。

，，所以︒=∠=∠︒=∠=∠=∆∆12060CBD ABE EBD ABC S S EBD ABC 故所求阴影面积为整个图形的总面积减去空白图形的面积，即）。

（＝＝＝）（）＝（扇形扇形扇形扇形阴影22211336636012012360120cm S S S S S S S BCDBAE ABC BCD EBD BAE ≈⋅-⋅-+-+∆∆πππ3.平移例3.如下图，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为________________。

2021年九年级数学初中几何圆、扇形、弓形的面积及阴影部分面积专项

初中几何圆、扇形、弓形的面积及阴影部分面积专项一、圆的面积计算公式：S=R 2，圆心角是1°的扇形面积等于圆面积的1360，圆心角是n 度的扇形面积等于圆的面积的360n ，扇形的弧长等于l=180n R ,⇒S 扇=12lR 。

二、运用公式法、割补法、拼凑法、等积变化法、平移法、旋转法、构造方程法等方法求组合图形的面积。

三、运用割补法、平移法、旋转法、等积变换法、容斥原理求阴影部分面积。

1、弓形面积弓形的面积可以转化为扇形的面积与三角形的面积之差，如下图所示，弓形AmB 的面积S弓形=S 扇性AOB -S △AOB弓形的面积可以转化为：扇形的面积与三角形的面积之和，如下图所示弓形AmB 的面积S 弓形= S 扇性AOB +S △AOB注：①当弓形所含的弧是劣弧时如甲图所示，弓形AmB 的面积S 弓形=S 扇性AOB -S △AOB②当弓形所含的弧是优弧时，如图乙所示，AnB 的面积S 弓形= S 扇性AOB +S △AOB③当弓形所含的弧是半圆时，弓形的面积S 弓形=12S 圆如图：半径OA=6cm,C 为OB 的中点，∠AOB=120°，求阴影部分面积S 。

（右：乙图）解：由图形可知，S 阴影ABC =S 扇性ABO -S △ACO ，而S 扇形ABO =21206360⋅=12，S △ACO =12×6×3×sin60°=932，所以S 阴影ABC =(93122-)cm 2。

2、割补法凡求与圆有关的不规则图形面积问题，一般都要把它转化为三角形、扇形、弓形的面积来求解，在进行复杂的图形的面积计算时，时常通过添加辅助线，把图形分割成若干个基本图形求解，这种求解的方法是经常用到的。

如图：⊙O 中的弦AC=2cm ，圆周角∠ABC=45°,求图中阴影部分的面积。

（部分与整体）解：做⊙O 的直径AB 1，则连结OC 、B 1C ，∠ACB=90°，∠B=∠B 1，AB 1=22，∵OA=2,∴S △AOC=1,S 扇形AOC =12,∴S 阴影=S 扇形AOC -S △AOC =12-1 例二：如图在两个半圆中大圆的弦MN 与小圆相切,D 为切点，且MN ∥AB ，MN=a ，ON ，CD 分别为两圆的半径，求阴影部分的面积。

初中数学阴影面积计算方法讲解

初中数学阴影面积计算方法讲解
阴影面积计算是初中数学中的重要内容之一。

阴影面积是指由两
个或多个平面图形组成的图形中被另一个平面图形遮盖部分的面积。

本文将为大家介绍阴影面积计算的方法。

一、明确题意，进行平面图形分析。

首先需要将整个图形分解成
几个简单的平面图形，例如直角三角形、长方形、正方形、圆形等等。

二、确定图形的基准面积。

基准面积是指被遮盖的部分所在的平
面图形的面积。

三、计算遮盖面积。

遮盖面积通常是由一个简单的图形组成，例
如梯形、矩形等等。

需要根据图形的特性，计算出它的面积。

四、计算阴影面积。

阴影面积就是基准面积减去遮盖面积。

例如，一个由三角形和长方形组成的图形，在给定面积的情况下，可以先计算长方形的面积，再减去三角形的面积，就可以得到阴影面积。

在计算阴影面积时，需要注意一些常见的错误。

例如，遮盖面积
和基准面积不要混淆，特别是在图形的边界处时更加容易犯错。

此外，计算过程中需要注意单位的转换，以及精度的控制。

总之，阴影面积计算是一项需要认真分析、耐心计算的工作。

只
有在认真思考每个步骤，并注意计算的准确性时，才能得到正确的答案。

阴影部分面积的多种求法

阴影部分面积的多种求法陕西延安市新区第一中学（716000）陈巧莲［摘要］求阴影部分面积，一方面考查了学生的基础知识、基本能力和基本方法，另一方面考查了学生观察分析能力、空间想象能力和运算能力.文章结合典型例题，提出求解阴影部分面积的方法：公式法、直接和差法、构造和差法、平移法、旋转法.［关键词］阴影部分；面积；求法［中图分类号］G 633.6［文献标识码］A［文章编号］1674-6058（2021）05-0027-02平面图形的面积计算问题是常见的数学题型，其中较难的是求平面图形阴影部分的面积，这类问题构思巧妙，属于综合类试题.其一方面考查了学生的基础知识、基本能力和基本方法，另一方面考查了学生的观察分析能力、空间想象能力和运算能力.一般所求阴影部分的图形为不规则图形，在解题时需进行分解组合，将不规则图形转化为规则图形.一、公式法某些阴影部分的图形是规则图形，求面积时可直接应用公式计算，如：S 三角形=12ah ，S 平行四边形=ah ，S 矩形=ab ，S 菱形=ah =12×对角线的乘积，S 正方形=a 2，S 扇形=n πr 2360，等等.［例1］如图1，在矩形ABCD 中，AB =3，AD =6，将AD 边绕点A 顺时针旋转，使点D 恰好落在BC 边上的点D '处，则阴影部分的面积为（）.图1A .9B.3πC .9πD .18分析：∵线段AD '由线段AD 旋转而成，AD =6，∴AD '=AD =6.∵AB =3，∠B =90°，∴∠AD 'B =30°.∵AD ∥BC ，∴∠DAD '=∠AD 'B =30°，∴S 阴影=30×π×62360=3π.故选B .评注：本题平面图形的阴影部分是一个扇形，欲求扇形面积，需求得扇形圆心角的度数和半径长，然后直接利用扇形面积公式求解.分析出阴影部分是什么样的图形是求解问题的关键.二、直接和差法某些阴影部分，虽然是不规则图形，但是可直接看出它是哪些图形的和或差，无须作辅助线，这样就可以分别求出各个图形的面积，然后再求和或作差.［例2］如图2，在Rt△ACB 中，∠C =90°，AC =BC =2，点D 是AB 的中点，DE 是以点A 为圆心，以AD 为半径的弧， DF 是以点B 为圆心，以BD 为半径的弧，则图中由 DE 、 DF 、EC 、FC 围成的阴影部分的面积为.图2分析：在Rt △ABC 中，∵∠C =90°，AC =BC =2，∴AB =22，∠A =∠B =45°，∵D 是AB 的中点，∴AD =DB =2，∴S 阴影=S △ABC -2S 扇形ADE =12×2×2-2×45×π×(2)2360=2-π2，故答案为2-π2.评注：此题可直接看出阴影部分面积等于三角形面积减去两个扇形的面积.当然，某些阴影部分图形面积可能是若干个图形面积的和，或和与差的组合.这里实际上将一个问题转化为三个小问题，从而达到解决问题的目的.三、构造和差法某些阴影部分，从已知图形中无法看出它是哪些图形的和或差，需要作辅助线才能看出来，此时应使用构造和差法，通过辅助线，补上一些规则图形，再减去其他规则图形，从而达到化不规则图形为规则图形的目的.［例3］如图3，在扇形OAB 中，C 是OA 的中点，CD ⊥OA ，CD 与AB 交于点D ，以O 为圆心，OC的长为半径作CE 交OB 于点E ，若OA =4，∠AOB =120°，则图中阴影部分的面积为.（结果保留π）图3图4分析：如图4，连接OD ，AD ，∵点C 为OA 的中点，∴OC =12OA =12OD ，∵CD ⊥OA ，∴∠CDO =30°，数学·解题研究∠DOC=60°，∴△ADO为等边三角形，∴CD=23，∴S扇形AOD=60×π×42360=83π，∴S阴影=S扇形AOB-S扇形COE-(S扇形AOD-S△COD)=120×π·42360-120×π·22360-()83π-12×2×23=163π-43π-83π+23=43π+23.故答案为43π+23.评注：需注意的是，在有弧线的图形中，通常会用扇形面积公式，此题还用到了等边三角形的判定、直角三角形的性质等，综合性比较强，不要把它看成只是求面积这样简单的问题，这样的题常作为压轴题，有一定的难度.四、平移法某些阴影部分的图形虽是不规则图形，但是通过将一部分图形平移，可以拼合成规则的图形，这是利用了图形平移后，图形的形状、大小都未变，只是位置变化的性质.一个图形平移后能否与另一个图形重合，主要看几个关键点按相同的方法平移后能否与对应点重合.［例4］如图5，抛物线的顶点为P（-2，2），与y轴交于点A（0，3）.若平移该抛物线，使其顶点P沿直线移动到点P'（2，-2），点A的对应点为A'，则图中抛物线上AP段、A'P'段、P P'、A A'围成的图形（阴影部分）面积为.图5图6分析：如图6，连接AP，A'P'，过点A作AD⊥PP'于点D，由题意可得出AP∥A'P'，AP=A'P'，∴四边形APP'A'是平行四边形，∵抛物线的顶点为P（-2，2），与y轴交于点A（0，3），平移该抛物线使其顶点P沿直线移动到点P'（2，-2），∴PO=22+22=22，PP'=22×2=42，∠AOP=45°，又∵AD⊥OP，是等腰直角三角形，∴AD=DO=sin45°·OA=×3=322，∴抛物线上AP段扫过的区域（阴影部分）的面积=平行四边形APP'A'的面积=42×322=12.故答案为12.评注：抛物线也是图形，平移后其形状与大小都不变，所以图中弓形AP与弓形A'P'的形状与大小是相同的；图形平移后形成平行四边形，注意平行四边形面积公式的使用.五、旋转法某些阴影部分的图形虽是不规则图形，但是将其中的一部分图形旋转后，可以拼接成规则图形，这是利用旋转后的图形其形状、大小不变，只是位置变化的性质.一个图形旋转后能否与另一个图形重合，主要看几个关键点按相同的旋转方法旋转后能否与对应点重合.［例5］如图7，AC是汽车挡风玻璃前的雨刷器，如果AO=45cm，CO=5cm，当AC绕点O顺时针旋转90°时，则雨刷器AC扫过的面积为cm2（结果保留π）.图7分析：∵OA=OA'，OC=OC'，AC=A'C'，∴△AOC≌△A'OC'，∴雨刷器AC扫过的面积=S扇形AOA'-S扇形COC'=452-524×π=500π（cm2），故答案为500π.评注：此题相当于将一个三角形旋转后，求边AC扫过的面积.通过上述试题我们发现，它实际上是两个扇形面积的差，这是中考的高频题型.求阴影部分图形的面积，本质就是将不规则图形转化为规则图形，转化的方法有直接和差法、构造和差法、平移法、旋转法、对称法、等积替代法、覆盖法等，然后结合已知数量，将几何问题转化为代数运算.这是始终不变的主线.［参考文献］［1］于秀坤.求阴影部分面积的思路和方法［J］.中学生数理化（初中版·中考版），2020（8）:2-3.［2］王金伟.求阴影部分面积的方法技巧［J］.数理天地（初中版），2019（10）:12-13.［3］罗峻，段利芳.十招走出圆中面积阴影［J］.数理化学习（初中版），2019（7）:29-33.［4］王文智.利用对称性求解与扇形相关的阴影面积［J］.理科考试研究，2019（10）:27-28.（责任编辑陈昕）数学·解题研究。

与圆有关的计算——求阴影部分面积

㊀㊀㊀解题技巧与方法１２５㊀数学学习与研究㊀２０２３０４与圆有关的计算与圆有关的计算㊀㊀㊀求阴影部分面积Һ王㊀玮㊀（十堰市东风第五中学，湖北㊀十堰㊀４４２０００）㊀㊀ʌ摘要ɔ面积问题是初中数学中的常见题型，与圆有关的求阴影部分面积问题是这类问题中的一个难点，通常不规则的阴影图形的面积是由三角形㊁四边形㊁扇形㊁圆和弓形等基本图形组合而成的，学生在解决问题时需要观察图形特点，会分割或组合图形．ʌ关键词ɔ计算；阴影部分面积在近几年的中考试题中，求阴影部分的面积是一个热点．观察㊁分析图形可知，阴影部分通常是由三角形㊁四边形㊁扇形和圆等常见的几何图形组成的．学生在解决问题时首先要明确需要计算面积的阴影部分是由哪些图形分解或组合而成的，才能找到解题的途径．下面将求阴影部分面积的常见方法总结如下．类型一：直接公式法例１㊀如图１，矩形ＡＢＣＤ的边长ＡＢ＝１，ＢＣ＝２．把ＢＣ绕Ｂ逆时针旋转，使Ｃ恰好落在ＡＤ上的点Ｅ处，线段ＢＣ扫过部分为扇形ＢＣＥ，则扇形ＢＣＥ的面积是．图１ʌ分析ɔ根据矩形的性质得出ＡＤʊＢＣ，øＡ＝９０ʎ，易得øＥＢＣ＝øＡＥＢ＝３０ʎ，再根据扇形的面积公式求出即可．例２㊀如图２，在等腰直角三角形ＡＢＣ中，øＡ＝９０ʎ，ＢＣ＝４．分别以点Ｂ㊁点Ｃ为圆心，线段ＢＣ长的一半为半径作圆弧，交ＡＢ，ＢＣ，ＡＣ于点Ｄ，Ｅ，Ｆ，则图中阴影部分的面积为．ʌ分析ɔ阴影部分的面积Ｓ＝ＳәＡＢＣ－Ｓ扇形ＢＤＥ－Ｓ扇形ＣＥＦ．图２例３㊀如图３，在▱ＡＢＣＤ中，Ｅ为ＢＣ的中点，以Ｅ为圆心，ＢＥ长为半径画弧交对角线ＡＣ于点Ｆ，若øＢＡＣ＝６０ʎ，øＡＢＣ＝１００ʎ，ＢＣ＝４，则扇形ＥＢＦ的面积为．图３ʌ分析ɔ先根据三角形内角和定理求出øＡＣＢ，再根据三角形外角的性质求出øＢＥＦ，最后根据扇形面积公式直接计算即可．例４㊀如图４，ＡＢ是☉Ｏ的直径，ＣＤ是弦，øＢＣＤ＝３０ʎ，ＯＡ＝２，则阴影部分的面积是．图４ʌ分析ɔ先根据圆周角定理得到øＢＯＤ＝６０ʎ，然后根据扇形的面积公式计算阴影部分的面积即可．类型二：直接和差法阴影部分面积可由扇形㊁三角形㊁特殊四边形的面积相加减得到．㊀图５例５㊀如图５，在扇形ＯＡＢ中，已知øＡＯＢ＝９０ʎ，ＯＡ＝２，过ＡＢ(的中点Ｃ作ＣＤʅＯＡ，ＣＥʅＯＢ，垂足分别为Ｄ，Ｅ，则图中阴影部分的面积为．ʌ分析ɔ先根据矩形的判定定理得到四边形ＣＤＯＥ是矩形，再连接ＯＣ，根据全等三角形的性质得到ＯＤ＝ＯＥ，得到矩形ＣＤＯＥ是正方形，最后根据扇形和正方形的面积公式即可得到结论．图６例６㊀如图６，在菱形ＡＢＣＤ中，对角线ＡＣ，ＢＤ交于点Ｏ，øＡＢＣ＝６０ʎ，ＡＢ＝２，分别以点Ａ㊁点Ｃ为圆心，以ＡＯ的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．ʌ分析ɔ先根据菱形的性质得到ＡＣʅＢＤ，øＡＢＯ＝１２øＡＢＣ＝３０ʎ，øＢＡＤ＝øＢＣＤ＝１２０ʎ，再根据直角三角形的性质求出ＡＣ，ＢＤ的长，最后根据扇形面积公式㊁菱形面积公式计算即可．图７例７㊀如图７，在边长为２３的正方形ＯＡＢＣ中，Ｄ为边ＢＣ上一点，且ＣＤ＝２，以Ｏ为圆心㊁ＯＤ为半径作圆弧，分别与ＯＡ，ＯＣ的延长线交于点Ｅ，Ｆ，则阴影部分的面积为．㊀㊀解题技巧与方法㊀㊀１２６数学学习与研究㊀２０２３０４ʌ分析ɔ设ＡＢ交ＥＦ(于Ｍ，阴影部分的面积Ｓ＝Ｓ正方形ＯＡＢＣ－ＳәＯＡＭ－Ｓ扇形ＯＤＭ－ＳәＯＣＤ．例８㊀如图８，已知四边形ＡＢＣＤ和四边形ＢＥＦＭ均为正方形，以Ｂ为圆心㊁ＢＥ为半径作弧ＥＭ．若大正方形的边长为８，则图中阴影部分的面积为．（结果保留π）图８ʌ分析ɔ根据正方形的性质得出øＡＢＣ＝øＤＣＭ＝９０ʎ，ＢＥ＝ＢＭ＝８，ＡＢ＝ＢＣ＝ＣＤ＝ＡＤ，设ＡＢ＝ＢＣ＝ＣＤ＝ＡＤ＝ａ，则阴影部分的面积Ｓ＝Ｓ扇形ＢＭＥ＋Ｓ正方形ＡＢＣＤ＋ＳәＤＭＣ－ＳәＡＤＥ，代入求出即可．类型三：构造和差法阴影部分面积需要通过添加辅助线构造扇形㊁三角形或特殊四边形，然后相加减．图９例９㊀如图９，ＡＢ是☉Ｏ的直径，ＣＤ为☉Ｏ的弦，ＡＢʅＣＤ于点Ｅ，若ＣＤ＝６３，ＡＥ＝９，求阴影部分的面积．ʌ分析ɔ根据垂径定理得出ＣＥ＝ＤＥ＝１２ＣＤ＝３３，再利用勾股定理求得半径，根据锐角三角函数关系得出øＥＯＤ＝６０ʎ，进而结合扇形面积公式即可求出答案．例１０㊀如图１０，正方形ＡＢＣＤ内接于☉Ｏ，ＰＡ，ＰＤ分别与☉Ｏ相切于点Ａ和点Ｄ，ＰＤ的延长线与ＢＣ的延长线交于点Ｅ．已知ＡＢ＝２，则图中阴影部分的面积为．图１０ʌ分析ɔ如图１０所示，连接ＡＣ，ＯＤ，根据已知条件得到ＡＣ是☉Ｏ的直径，øＡＯＤ＝９０ʎ，根据切线的性质得到øＰＡＯ＝øＰＤＯ＝９０ʎ，易得әＣＤＥ是等腰直角三角形，再根据等腰直角三角形的性质得到ＰＥ＝３２，最后根据梯形和圆的面积公式即可求出阴影部分的面积．图１１例１１㊀如图１１，等边三角形ＡＢＣ的边长为２，以Ａ为圆心，１为半径作圆弧分别交ＡＢ，ＡＣ边于Ｄ，Ｅ，再以点Ｃ为圆心，ＣＤ长为半径作圆交ＢＣ边于Ｆ，连接Ｅ，Ｆ，那么图中阴影部分的面积为．ʌ分析ɔ如图１１，过Ａ作ＡＭʅＢＣ于Ｍ，ＥＮʅＢＣ于Ｎ，根据等边三角形的性质得到ＡＭ＝３２ＢＣ＝３２ˑ２＝３，求得ＥＮ＝１２ＡＭ＝３２，再根据三角形的面积和扇形的面积公式计算即可．例１２㊀如图１２，在ＲｔәＡＢＣ中，øＢＡＣ＝３０ʎ，以直角边ＡＢ为直径作半圆交ＡＣ于点Ｄ，以ＡＤ为边作等边三角形ＡＤＥ，延长ＥＤ交ＢＣ于点Ｆ，ＢＣ＝２３，则图中阴影部分的面积为．（结果不取近似值）图１２ʌ分析ɔ如图１２，根据题意结合等边三角形的性质分别得出ＡＢ，ＡＣ，ＡＤ，ＤＣ的长，进而利用Ｓ阴影＝ＳәＡＢＣ－ＳәＡＯＤ－Ｓ扇形ＯＤＢ－ＳәＤＣＦ求出答案．图１３例１３㊀如图１３，在菱形ＡＢＣＤ中，øＤ＝６０ʎ，ＡＢ＝２，以Ｂ为圆心㊁ＢＣ长为半径画ＡＣ(，点Ｐ为菱形内一点，连接ＰＡ，ＰＢ，ＰＣ．当әＢＰＣ为等腰直角三角形时，图中阴影部分的面积为．ʌ分析ɔ如图１３，连接ＡＣ，延长ＡＰ交ＢＣ于Ｅ，根据菱形的性质得出әＡＢＣ是等边三角形，进而通过三角形全等证得ＡＥʅＢＣ，从而求得ＡＥ，ＰＥ，则Ｓ阴影＝Ｓ扇形ＢＡＣ－ＳәＰＡＢ－ＳәＰＢＣ．例１４㊀如图１４，在әＡＢＣ中，Ｏ为ＢＣ边上的一点，以Ｏ为圆心的半圆分别与ＡＢ，ＡＣ相切于点Ｍ，Ｎ．已知øＢＡＣ＝１２０ʎ，ＡＢ＋ＡＣ＝１６，ＭＮ(的长为π，则图中阴影部分的面积为．图１４ʌ分析ɔ如图１４，连接ＯＭ，ＯＮ，根据半圆分别与ＡＢ，ＡＣ相切于点Ｍ，Ｎ，可得ＯＭʅＡＢ，ＯＮʅＡＣ，由øＢＡＣ＝１２０ʎ，可得øＭＯＮ＝６０ʎ，进而得出øＭＯＢ＋øＮＯＣ＝１２０ʎ，再根据ＭＮ(的长为π，可得ＯＭ＝ＯＮ＝ｒ＝３，连接ＯＡ，根据ＲｔәＡＯＮ中，øＡＯＮ＝３０ʎ，ＯＮ＝３，可得ＡＭ＝ＡＮ＝３，进而可求得图中阴影部分的面积．类型四：等积转化法利用等积转化法将阴影部分面积转化为求扇形㊁三角形㊁特殊四边形的面积或它们面积的和差．㊀㊀㊀解题技巧与方法１２７㊀数学学习与研究㊀２０２３０４例１５㊀如图１５，将半径为２㊁圆心角为９０ʎ的扇形ＢＡＣ绕点Ａ逆时针旋转６０ʎ，点Ｂ，Ｃ的对应点分别为Ｄ，Ｅ，点Ｄ在ＡＣ(上，则阴影部分的面积为．图１５ʌ分析ɔ如图１５，连接ＢＤ，直接利用旋转的性质结合扇形面积求法及等边三角形的判定与性质得出Ｓ阴影＝Ｓ扇形ＢＡＣ－Ｓ弓形ＡＤ＝Ｓ扇形ＢＤＣ＋ＳәＡＤＢ，进而得出答案．例１６㊀如图１６，在әＡＢＣ中，ＣＡ＝ＣＢ，øＡＣＢ＝９０ʎ，ＡＢ＝２，点Ｄ为ＡＢ的中点，以点Ｄ为圆心作圆心角为９０ʎ的扇形ＤＥＦ，点Ｃ在弧ＥＦ上，则图中阴影部分的面积为．图１６ʌ分析ɔ如图１６，连接ＣＤ，证明әＤＣＨɸәＤＢＧ，则Ｓ四边形ＤＧＣＨ＝ＳәＢＤＣ，求得扇形ＦＤＥ的面积，则阴影部分的面积即可求得．例１７㊀如图１７，ＡＢ是半圆Ｏ的直径，线段ＤＣ是半圆Ｏ的弦，连接ＡＣ，ＯＤ，若ＯＤʅＡＣ于点Ｅ，øＣＡＢ＝３０ʎ，ＣＤ＝３，则阴影部分的面积为．图１７ʌ分析ɔ如图１７，连接ＯＣ，先证得әＣＯＤ是等边三角形，然后证得ＲｔәＡＯＥɸＲｔәＣＯＥ，即可得出Ｓ阴影＝Ｓ扇形ＯＣＤ．㊀图１８例１８㊀如图１８，在边长为４的正方形ＡＢＣＤ中，以ＡＢ为直径的半圆交对角线ＡＣ于点Ｅ，以Ｃ为圆心㊁ＢＣ长为半径画弧交ＡＣ于点Ｆ，则图中阴影部分的面积是．ʌ分析ɔ如图１８，连接ＢＥ，易证Ｓ弓形ＡＥ＝Ｓ弓形ＢＥ，ʑ图中阴影部分的面积＝Ｓ半圆－１２（Ｓ半圆－ＳәＡＢＥ）－（ＳәＡＢＣ－Ｓ扇形ＣＢＦ）．类型五：容斥原理法当阴影部分是由几个图形叠加形成时，求阴影部分面积需先找出叠加前的几个图形，然后厘清图形之间的重叠关系．计算方法：叠加前的几个图形面积之和－（多加部分面积＋空白部分面积）．例１９㊀如图１９，直径ＡＢ＝６的半圆，绕Ｂ点顺时针旋转３０ʎ，此时点Ａ到了点Ａᶄ处，则图中阴影部分的面积为．图１９ʌ分析ɔȵ半圆绕Ｂ点顺时针旋转３０ʎ，ʑＳ阴影＝Ｓ半圆＋Ｓ扇形ＢＡＡᶄ－Ｓ半圆＝Ｓ扇形ＢＡＡᶄ．例２０㊀如图２０，点Ｏ在坐标原点上，ＯＡ边在ｘ轴上，ＯＡ＝８，ＡＣ＝４，把әＯＡＣ绕点Ａ按顺时针方向转到әＯᶄＡＣᶄ的位置，使得点Ｏᶄ的坐标是（４，４３），则在这次旋转过程中线段ＯＣ扫过部分（阴影部分）的面积为．图２０ʌ分析ɔ如图２０，过Ｏᶄ作ＯᶄＭʅＯＡ于Ｍ，解直角三角形求出旋转角的度数，根据图形得出阴影部分的面积Ｓ＝Ｓ扇形ＡＯＯᶄ＋ＳәＯᶄＡＣᶄ－ＳәＯＡＣ－Ｓ扇形ＡＣＣᶄ＝Ｓ扇形ＡＯＯᶄ－Ｓ扇形ＡＣＣᶄ，分别求出即可．㊀图２１例２１㊀如图２１，在矩形ＡＢＣＤ中，ＡＢ＝６，ＢＣ＝４，以Ａ为圆心㊁ＡＤ长为半径画弧交ＡＢ于点Ｅ，以Ｃ为圆心㊁ＣＤ长为半径画弧交ＣＢ的延长线于点Ｆ，求图中阴影部分的面积．ʌ分析ɔ图中阴影部分的面积＝Ｓ扇形ＣＦＤ－（Ｓ矩形ＡＢＣＤ－Ｓ扇形ＡＤＥ）．㊀图２２例２２㊀如图２２，在扇形ＯＡＢ中，øＡＯＢ＝１２０ʎ，连接ＡＢ，以ＯＡ为直径作半圆Ｃ交ＡＢ于点Ｄ，若ＯＡ＝４，则图中阴影部分的面积为．ʌ分析ɔ如图２２，连接ＯＤ，ＣＤ，根据圆周角定理得到ＯＤʅＡＢ，根据等腰三角形的性质得到ＡＤ＝ＤＢ，øＯＡＤ＝３０ʎ，再根据扇形面积公式㊁三角形的面积公式计算即可．阴影部分的面积Ｓ＝Ｓ扇形ＯＡＢ－ＳәＡＯＢ－（Ｓ扇形ＣＡＤ－ＳәＡＣＤ）．ʌ参考文献ɔ［１］中华人民共和国教育部．义务教育数学课程标准（２０２２年版）［Ｍ］．北京：北京师范大学出版社，２０２２．［２］章士藻．中学数学教育学［Ｍ］．北京：高等教育出版社，２００７．［３］曹一鸣，冯启磊，陈鹏举，等．基于学生核心素养的数学学科能力研究［Ｍ］．北京：北京师范大学出版社，２０１７．。

几种关于阴影部分面积的求法

(2)P(-1,- 4 ) 3
• 如图5，在四边形ABCD中，AB=2，
CD=1，
，
• 求四边形ABCD所在阴影部分的面积。
1
1
33
S 阴影 S A B E S C D E 2 A B B E 2 C D D E 2
如图，半圆A和半圆B均与y轴相切于点O，其直径CD、EF均和x轴垂直，以O为顶点的两条抛物线分别经过C、E和D•、 F，则图中阴影部分的面积是_________（2005年河南省中考题）
2. 反思一下你所获成功的经验, 与同学交流!
几
种
面
积
1、直接法
问
• 1、利用和差
题
• 2 利用平移
求解的
2、转化法
• 3 利用整体 • 4 利用对称
方
• 5 利用等积
法数学思想：转化思想
1、如图,平行于y轴的直线l被抛物线y=x2+1, y=x2-1所截,当直线l向右平移3个单位时, 直线l被两条抛物线所截得的线段扫过的图形面积为（2005.德阳）
2.如图，正方形ABCD 的边长为4，MN∥BC，分别交 AB、CD于点M、N ，在MN上任取两点P、Q，则图中阴影部分的面积是。（2008 泰安）
3、（06云南）如图，矩形ABCD中，BC=4，DC=2，
以AD为直径的半圆O与BC相切与点E，则图中阴影
部分的面积是
（结果保留π ）
AOΒιβλιοθήκη DBEC
4
积是（） C
C
a2 1 a2
2
D a2 1 a2
2
• 利用中心对称的性质，将不规则的阴影部分转化为特殊的图形，进行求解。

初中数学论文“阴影面积型中考试题解法例析

初中数学论文“阴影面积型中考试题解法例析近几年来，全国各地的中考卷中频频出现“阴影面积问题”的试题，逐渐成为中考命题的一个热点问题，这类试题题型较多，解题方法也颇为讲究，现选取部分中考试题，谈谈“阴影面积问题”的求解方法，供参考探讨。

一、拼凑法拼凑法是指各个阴影部分面积无法求或很难求时，可把分散的图形集中拼成大块图形来求，它其实是整体思想的一个渗透.例1、(钦州)某花园内有一块五边形的空地如图1所示，为了美化环境，现计划在五边形各顶点为圆心，2m长为半径的扇形区域（阴影部分）种上花草，那么种上花草的扇形区域总面积是()（A）6m2（B）5m2（C）4m2（D）3m2图1图2析解：观察图形，通过拼凑可知，阴影部分面积为5个扇形的面积和，而5个扇形的圆心角度数之和为五边形的内角和540°，可求阴影部分面积为6π，故选A.练习:（巴中）如图2所示，以六边形的每个顶点为圆心，1为半径画圆，则图中阴影部分的面积为参考答案：2π二、转化法此法就是将原图形中局部或整体进行适当的变换，实现将不规则图形的面积转化为一个或几个规则图形的面积的代数和的一种有效方法，也是不规则图形的面积计算中涉及最为广泛、灵活的一种方法，在转化过程中常常会用到图形的平移、旋转、对称变换、割补、等积代换等方法。

10平移法：例2、(泸州)在反比例函数y(某0)的图象上，有一系列点某A1，A2，A3，，...An，An+1，若A1的横坐标为2，且以后每点的横坐标与它前一个点的横坐标的差都为2,现分别过点A1，A2，A3，，...An，An+1作某轴与y轴的垂线段，构成若干个矩形如图2（1）所示，将图中阴影部分的面积从左到右依次记为S1，S2，S3，，...Sn，则S1=_______，S1+S2+S3+...+Sn______.(用n的代数式表示)析解：此题可以通过平移转化为一个规则图形，第一问中，只要直接计算矩形的面积即可，由题意可得，矩形的宽为2，长为A1的纵坐标减A2的纵坐标，易求长为5-2.5=2.5，所以S1=2某2.5=5.第二问中，只要把S2、S2…Sn平移到如图2（2）的位置，这样阴影部分面积就转化成矩形A1Q1QnA的面积，很显然这个矩形的宽为2，只要求出长就可以了，我们可以先求得A1的纵坐标为5，再求出55nAn+1的纵坐标为，相减即得矩形A1Q1QnA的长为；所以n1n15n10n=某2=.S1+S+S+.+..SS23n矩形n1n1图2（1）图2（2）k旋转法：例3、(深圳)如图3，点P（3a，a）是反比例函y＝（k＞0）与某⊙O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（）35A．y＝B．y＝某某C．y＝10某D．y＝12某析解：此题可以通过旋转转化为规则图形求解，将小的阴影部分绕着点O旋转1180°可得到圆的面积，由题意得：41πr210π，解得r2=40因为P(3a,a)，所以(3a)2a2r2，即：10a240，4因为a0所以a2，所以P(6,2)，所以k=12，故选D.对称变换法：例4、(临沂)正方形ABCD的边长为a，点E、F分别是对角线BD上的两点，过点E、F分别作AD、AB的平行线，如图所示，则图中阴影部分的面积之和等于_________.析解：此题可以通过对称变换转化为规则图形求解，观察图形，利用对称性，把阴影部的面积转化为S△ABD 的面积，故答案1为a22割补法：例5、(河北省)把三张大小相同的正方形卡片A，B，C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图5(1)摆放时，阴影部分的面积为S1；若按图5(2)摆放时，阴影部分的面积为S2，则S1S2（填“＞”、“＜”或“=”）．CAB图5(1)A图5(2)图5(3)CCBABA图5(4)CB析解：此题可以通过割补转化为规则图形求解，由题意可设图5(1)中的大正方形的边长为a,小正方形的边长为b,通过割补可得如图5(3)的阴影部分，此图形为边长(ab)的正方形，同理可得图5(2)的阴影部分也是边长为(ab)的正方形（如图5(4)），所以可得S1=S2等积代换法：例6、（南宁）正方形ABCD、正方形BEFG和正方形RKPF的位置如图6（1）所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为()（Ａ）10（Ｂ）12（Ｃ）14（Ｄ）16析解：此题可以通过等积代换转化为一个规则图形，如图6（2），连结BD、EG、KF，可证FK‖EG‖BD,由平行线的性质可知，S△DGBS△EDB,进而可求S△DGMS△EBM,同理可证S△GFNS△EKN,由此就将阴影部分面积根据等积代换转化为如图6（3）的正方形GBEF的面积，求得S=16.故选D.三、叠合法叠合法是指当一种图形被其他图形完全覆盖、且要求的阴影部分又正好是覆盖与被覆盖图形的重叠部分时，所采用的一种简捷有效的计算方法，这种方法往往需要观察图形的结构特征，理顺图形间的大小关系，分清覆盖和被覆盖图形的面积关系，通常方法：S重叠部分=S覆盖图形-S被覆盖图形.例7、（衡阳）如图7，在Rt△ABC中，∠C90°，AC4，BC2，分别以AC.BC为直径画半圆，则图中阴影部分的面积为．（结果保留）析解：观察图形，可得：S阴影S大半圆S小半圆S△ABC，所以S阴影练习、（自贡）边长为1的正方形ABCD绕点A逆时针旋转A30°得到正方形AB′C′D′，两图叠成一个“蝶形风筝”（如图7图所示阴影部分），则这个风筝的面积是（）。

初中数学求阴影部分面积试题专项训练

初中数学求阴影部分面积试题专项训练在中考中，频频出现求阴影部分图形的面积的题目，而其阴影部分图形大多又是不规则的，部分同学乍遇这类题目则显得不知所措.下面将分类例谈这类问题的解法：一.直接法：当已知图形为我们熟知的基本图形时，先求出涉及适合该图形的面积计算公式中某些线段、角的大小，然后直接代入公式进行计算。

例1.如图1，矩形ABCD中，AB=1，AD=3，以BC 的中点E为圆心的MPN与AD相切于P，则图中的阴影部分的面积为（）A 23π B34π C3π D3π图1 图2二.和差法：即是把阴影部分的面积转化为若干个图形面积的和、差来计算。

例2，如图2，正方形ABCD的边长为a，以A为圆心，AB为半径画BD，又分别以BC和CD为直径画半圆，则图中的阴影部分的面积为_______.三.割补法：即是把阴影部分的图形通过割补，拼成规则图形，然后再求面积。

例3，如图3(1)，在以AB为直径的半圆上，过点B做半圆的切线BC，已知AB=BC=a，连结AC，交半圆于D，则阴影部分图形的面积是______.第 1 页共9 页图3练习：1、如图1，将半径为2cm的⊙O分割成十个区域，其中弦AB、CD 关于点O对称，EF、GH关于点O对称，连接PM，则图中阴影部分的面积是_____cm2（结果用π表示）．2、如图2，在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为2，则图中阴影部分的面积为_______．3、如图3，在Rt△ABC中，已知∠BCA=90°，∠BAC=30°，AB=6cm，把△ABC以点B为中心旋转，使点C旋转到AB边的延长线上的点C′处，那么AC边扫过的图形（图中阴影部分）的面积是_______cm2（不取近似值）．四.整体法：例4.如图4,,,,,A B C D E相互外离,它们的半径都是1,顺次连结五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是( ) A.π B.1.5π C.2π D.2.5π图4五.等积变形法（思想：）把所求阴影部分的图形适当进行等积变形，即是找出与它面积相等的特殊图形，从而求出阴影部分图形的面积。

初三数学圆阴影部分面积10种解题方法

初三数学圆阴影部分面积10种解题方法01和差法对于不规则图形实施分割、叠合后，把所求的图形面积用规则图形面积的和、差表示，再求面积．贵港中考如图1，在扇形OAB中，C是OA的中点，CD⊥OA，CD与弧AB交于点D，以O为圆心，OC的长为半径作弧CE交OB于点E，若OA= 4，∠AOB=120°，则图中阴影部分的面积为( 结果保留π) ．图1解析: 图形中的阴影部分是不规则图形，较难直接计算．注意到阴影部分是环形BECA的一部分，因此阴影部分面积等于环形BECA的面积减去图形DCA的面积，又图形DCA的面积等于扇形DOA 的面积减去△ODC的面积．图2如图2，连接OD交弧CE于M．因为OA=4，C是OA的中点，CD⊥OA，所以OD=4，OC=2，DC=2√3，所以∠ODC=30°，∠DOC=60°02割补法对图形合理分割，把不规则图形补、拼成规则图形会，再求面积.吉林中考如图3，将半径为3的圆形纸片，按下列顺序折叠，若弧AB和弧BC都经过圆心O，则阴影部分的面积是( 结果保留π) ．图3解析: 观察图形可以发现: 下方树叶形阴影部分的面积分成左右两块后，可以补到上方两个空白的新月形的位置．是否能够完全重合，通过计算验证即可．图4如图4，过点O作OD⊥AB于D，连接OA、OC、OB．由折叠性质知OD=1/2r=1/2AO，03等积变形法运用平行线性质或其他几何图形性质把不规则图形面积转化为与它等面积的规则图形来进行计算.天水中考如图5，以AD为直径的半圆O经过Ｒt△ABC斜边AB的两个端点，交直角边AC于点E，B、E 是半圆弧的三等分点，弧BE的长为2π/3，则阴影部分的面积为图5解析: 阴影部分是Ｒt△ABC的一部分，运用平行线的性质可将图形ABE面积转化成扇形BOE面积．连接BD、BE、BO、OE，如图6．图6因为点E、B是半圆弧的三等分点，所以∠DOB=∠BOE=∠EOA=60°，所以∠BAD=∠EBA=∠BAE=30°，所以BE∥AD．04平移法一些图形看似不规则，将某一个图形进行平移变换后，利用平移的性质，把不规则的图形的面积转化为规则图形的面积来计算．2019年黄石中考模拟如图7，从大半圆中剪去一个小半圆( 小半圆的直径在大半圆的直径MN上)，点O为大半圆的圆心，AB是大半圆的弦，且与小半圆相切，AB∥MN，已知AB=12cm，则阴影部分的面积是．图7解析: 因为AB∥MN，由平行线间的距离处处相等，可以平移小半圆，使小半圆的圆心与大半圆的圆心重合，这样不规则的阴影图形就变成一个环形.图8如图8．过点O作OC⊥AB，垂足为C，连接OB，设大半圆的半径为Ｒ，小半圆的半径为r.05旋转法一些图形看似不规则，把某个图形进行旋转变换后，利用旋转的性质，把不规则图形的面积转化为规则图形的面积，再进行计算．安顺中考如图9，矩形ABCD中，BC=2，DC=4，以AB 为直径的⊙O与DC相切于点E，则阴影部分的面积为图9解析: 若直接利用弓形面积公式求解相当繁琐，根据已知条件及圆的旋转不变性，利用图形的旋转可实现解题．图10如图10，连接OE 交BD于M．因为CD 是⊙O 的切线，所以OE⊥CD，又AB∥CD，则OE⊥AB，而OE=OB，易知△OBM ≌△EDM，把△OBM绕点M旋转180°就会转到△EDM，阴影部分就转化为扇形BOE，恰好是半径为2的圆的四分之一，06对称法一些图形看似不规则，利用轴对称和中心对称的性质，把不规则图形进行轴对称和中心对称变换，转化为规则图形的面积，再进行计算．赤峰中考如图11，反比例函数y=k/x( k＞0) 的图象与以原点(0,0)为圆心的圆交A、B两点，且A( 1,√3) ，图中阴影部分的面积等于 (结果保留π) ．图11解析: 根据反比例函数图象及圆的对称性———既是轴对称图形，又是中心对称图形，可知图中两个阴影面积的和等于扇形AOB的面积．过点A作AD⊥x轴于D，如图12．图12因为A( 1，√3) ，所以∠AOD=60°，OA=2，又因为点A、B关于直线y=x对称，所以∠AOB=2×( 60°－45°)=30°．07整体法当已知条件不能或不足以直接求解时，可整体思考，化单一、分散为整体，把所求的未知量整体转换为已知量，再将问题整体化求解．安徽中考如图13，半径均为1的⊙A、⊙B、⊙C、⊙D、⊙E两两外离，A、B、C、D、E分别为五边形的五个顶点，则图中阴影部分的面积是图13解析: 由已知条件，分别求阴影部分的圆心角不易求得，但将五个扇形的圆心角合为一整体，它们的圆心角的和也是五边形的外角之和360°，所以阴影部分面积是一个整圆的面积，所以S阴影=π．08方程法有些图形的局部可以看成某个规则图形，或某些图形具有等面积的性质，这时可以把它们的关系用方程( 组) 来表示，再解方程( 组) ，求出图形的面积．2019年武汉模拟如图14，在边长为2的正方形ABCD 中，分别以2为半径，A、B、C、D 为圆心作弧，则阴影部分的面积是 ( 结果保留π) ．图14解析: 仔细观察图形，有两种相同特征的图形在正方形内部，一起围成所求的阴影部分．设弧AC与弧BD交于点G，连接BE、EC，如图15．图15设形如AED 图形的面积为x，形如DEG 图形的面积为y，那么S阴影= S正-4 ( x+y) ，只需求出(x+y)的结果即可．09推算法某些题目运用已知条件，和图形的性质或定理进行推理，可把阴影部分面积用某个式子表示，从而求得不规则图形的面积．南宁中考如图16，Ｒt△ABC 中，AC=8，BC=6，∠C=90°，分别以AB、BC、AC 为直径作三个半圆，那么阴影部分的面积为平方单位．图16解析: 设左边阴影部分面积为S1，右边阴影部分面积为S2，整个图形的面积可以表示成: 以AC 为直径的半圆+ 以BC为直径的半圆+△ABC．也可以表示成: S1+S2+以AB为直径的半圆。

初中数学阴影面积计算方法讲解

初中数学阴影面积计算方法讲解阴影面积是指在光照、光线等因素影响下，物体表面未被直接照射到的面积部分。

在初中数学中，我们可以通过一些基本的几何知识和方法计算阴影面积。

下面就介绍一下初中数学中常见的几种阴影面积计算方法。

一、计算矩形阴影面积：```A，—BC，—D```在光线OA和OC照射下，阴影面积为ADCB区域。

矩形的阴影面积计算方法为：阴影面积=矩形面积-三角形面积其中，矩形面积为AB * BC，三角形面积可通过以下公式计算：三角形面积 = 1/2 * BC * heightheight为光线OC到AB的距离，可以通过相似三角形的比例关系计算得到：height = (OC / OA) * BC将得到的height代入三角形面积公式，即可计算出阴影面积。

二、计算三角形阴影面积：```A\C，—B```在光线OA和OC照射下，阴影面积为ACB区域。

三角形的阴影面积计算方法为：阴影面积=三角形面积-三个小三角形面积之和其中，三角形面积可以通过以下公式计算：三角形面积=1/2*AC*BC 小三角形面积为：1/2 * AC * height_ACO + 1/2 * BC *height_BCO + 1/2 * AB * height_ABOheight_ACO、height_BCO和height_ABO分别为光线OC到AC、BC、AB的距离，可以通过相似三角形的比例关系计算得到。

将得到的三角形面积和小三角形面积相减，即可计算出阴影面积。

三、计算圆形阴影面积：```O/\/\A，—C\/\/在光线OA和OC照射下，阴影面积为ACO区域。

圆形的阴影面积计算方法为：阴影面积=圆形面积-扇形面积其中，圆形面积为π*r*r，扇形面积可通过以下公式计算：扇形面积=1/2*扇形的弧长*r扇形的弧长可以通过扇形角的度数和圆的周长计算得到：扇形的弧长=(扇形角的度数/360)*2*π*r将得到的扇形的弧长代入扇形面积公式，即可计算出阴影面积。

求阴影部分面积“六法”

因ｓ彤÷ｓＥｆ６９ｍ）此，＝ｔ帮ｆ（＝ ÷× ｃ．
四、积变彩法把所求阴影部分的图形适当进行等积变形，等即是找出与它面积相等的特殊图形．而求出阴影部分图形的面积．从例４如图４，、半圆周上的三等份点，ＣＤ是圆的半径为Ｒ，阴影求
６ｍ．图中的阴影部分的面积为ｃ则．解：别作ＪＧＡＪＧ垂足分别为、设ＡＤ、Ｈ交于分＿Ｈ，Ｎ尸，＿ Ⅳ，Ｇ点Ｐ，则有ＡＡＭ￣ＡＡＮ，以，△ Ｓ＾Ⅳ Ｐ－Ｑ所Ｓ＾ △０．
１１１，
Ｂ．７ｒ
４
）．
Ａ．仃
一
ｃ．
斗
仃
Ｄ．
ｊ
，
．．
．
．
．一
３
解：题设有：ＮＰ＝ＢｌＥ＝１Ｂ＝依Ｅ＝ＥＡ＝，Ｃｃ
栅
／ＮＥ＝０．Ｃ３。
Ⅳ中，ｏＡＮｃｃｓＥ＝
＝
，而，从
蹿方浩接
维普资讯
所以．ＬＭＥＮ＝１０－ｘ０２＇８￣２３＇０。＝１．
毗
＝．詈故
Ｅ
茎
ｃＡ
Ａ
Ｂ
Ｄ
图１、差法把阴影部分的面积转化为若干个图形面积的和、和差来计算．例２如图２正方ＡＢＤ的边长为ａ￣Ａ为圆心，Ｂ为半径画，Ｃ，ＸＡ
维普资讯

中考专题-圆中阴影部分面积求解解析(教案)

（4）数学运算的熟练程度：在求解阴影部分面积时，学生需题失败。
难点举例：在计算过程中，注意分数、小数的运算，以及平方、开方等运算的准确性。
（5）数据分析能力的运用：在解决不同类型的题目时，学生需要分析数据，找出解题规律，提高解题效率。
难点举例：分析不同类型题目的共同点和差异，总结解题方法，形成自己的解题策略。
在学生小组讨论环节，我发现学生们在讨论过程中能够积极思考，提出自己的观点。但与此同时，也有一部分学生在讨论中过于依赖他人，缺乏独立思考。为了解决这个问题，我将在今后的教学中注重培养学生的独立思考能力，鼓励他们在讨论中敢于发表自己的见解。
最后，我注意到在总结回顾环节，部分学生对所学知识点的掌握程度并不理想。这说明我在教学过程中可能没有充分关注到学生的个体差异，导致他们在学习过程中跟不上整体进度。因此，我将在今后的教学中更加关注每个学生的学习情况，因材施教，确保每个学生都能掌握所学知识。
五、教学反思
在今天的教学中，我发现学生们在圆中阴影部分面积求解方面存在一些问题。首先，他们在构建空间观念上还有一定的困难，尤其是在处理复杂的几何图形时，难以准确把握图形之间的关系。在接下来的教学中，我需要加强这方面的训练，多提供一些直观的教具或图形，帮助学生建立更清晰的空间观念。
其次，学生在逻辑推理能力方面也表现出一定的不足。在解决实际问题时，他们往往不能迅速找到解题的关键步骤，导致解题思路不清晰。针对这一问题，我打算在讲授过程中，更多地运用案例分析，引导学生逐步分析问题，培养他们的逻辑推理能力。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如绘制圆形和扇形，并进行面积求解。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）

【初中数学】阴影部分面积计算超好用方法总结,学会不丢分

【初中数学】阴影部分面积计算超好用方法总结，学会不丢分
阴影部分面积计算是全国中考的高频考点，常在选择题和填空题中考查，要想中考不丢分，这些方法你一定不能错过哦！
求阴影部分面积的常用方法有以下三种：
一、公式法
所求面积的图形是规则图形：
二、和差法
所求图形面积是不规则图形，可通过添加辅助线转化为规则图形的和或差：（1）直接和差法
（2）构造和差法
三、等积变换法
直接求面积无法计算或者较复杂，通过对图形的平移、选择、割补等，为利用公式法或和差法求解创造条件：
（1）全等法
（2）对称法
（3）平移法（4）旋转法练习题。

中考数学复习：专题9-15 例谈求阴影部分面积的几种常见方法

例谈求阴影部分面积的几种常见方法【专题综述】在初中数学中，求阴影部分的面积问题是一个重要内容，在近年来的各地中考试题中屡见不鲜．这类试题大多数都是求不规则图形的面积，具有一定的难度，因此，正确把握求阴影部分面积问题的解题方法，显得尤为重要．本文举例介绍解决这类问题的常见方法．【方法解读】一、直接求解法例1 如图1，有一矩形纸片ABCD，AB＝10，AD＝6，将纸片折叠，使AD边落在AB边上，AD变到AD1位置，折痕为AE．再将△AED1以D1E为折痕，向右折叠，AE变到A1E位置，且A1E交BC于点F．求图中阴影部分的面积．分析因为阴影部分是一个规则的几何图形Rt△CEF，故根据已知条件可以直接计算阴影部分面积．解如图1，根据对称性可得AD＝AD1＝A1D1＝6．由已知条件易知：EC＝D1B＝4，BC＝6；Rt△FBA1∽Rt△FCE．设FC为x，则FB＝6－x．二、间接求解法例2 如图2，⊙O1与⊙O2外切于点C，且两圆分别和直线l相切于A、B两点，若⊙O1半径为3cm；⊙O2半径为1cm，求阴影部分面积．分析这是求一个不规则图形的面积，没有现成的面积公式，因此应采用间接的方法，设法转化为规则图形的面积的和或差去计算．三、整体合并法例3 如图3，⊙A、⊙B、⊙C两两不相交，且半径都是0.5cm，求三个阴影部分面积之和．分析所求的阴影部分面积是三个扇形面积之和，因为三个扇形圆心角度数不知道，所以无法单独求解，但仔细观察发现，三个扇形的圆心角分别是△ABC的三个内角，其和为180°，而扇形半径都相等，所以三个扇形能合并成一个半圆．于是问题获解．解如图3，因为三个圆的半径相等，三个扇形圆心角之和是180°，所以其面积就是半圆面积．四、等积变换法例4 如图4，A是半径为R的⊙O外一点，弦BC为3R，OA∥BC，求阴影部分面积．分析本题的阴影部分是不规则的图形，求其面积较困难，但灵活运用等积变换，就可以把它的面积转化为扇形OBC的面积，从而获解．解连接OC，OB，五、分割法例5 如图5，在Rt△ABC中，∠C＝90°，AC＝4，BC＝2，分别以AC、BC为直径画半圆，求阴影部分面积．分析阴影部分图形不规则，不能直接求面积，可以把它分割成几个部分求面积的和．解如图5，连接CD．∵AC、BC是直径，∴∠ADC＝∠BDC＝90°，∴A、D、B三点共线．设阴影部分面积被分割为S1、S2、S3、S4四部分．则六、转化法例6如图(1)，大半圆O与小半圆O1相切于点C，大半圆的弦AB与小半圆相切于点F，且AB∥CD，AB ＝4cm，求阴影部分面积．分析如果想直接求阴影部分面积，无法求解，因为它不是规则图形．但要采取转化思想，把小半圆平移到与大半圆的圆心重合的位置，作OE⊥AB于点E．连接OB，可知BE＝2cm，阴影部分面积等于大半圆面积减去小半圆的面积．解如图(2)，将小半圆O1移至与大半圆圆心重合，作O E⊥AB于点E，则BE＝12AB＝2cm．设大圆半径为R，小圆半径为x，在Rt△OEB中，有七、割补法例7 如图7，点P(3a，a)是反比例函数y＝12x与⊙O在第一象限内的一个交点，求阴影部分的面积．分析阴影部分分两部分，难于逐一求解，但考虑反比例函数的对称性，结合割补原理，问题变得特别简单．解如图7，把右上角的S1部分分割下来，移到左下方补在S3处，与S2就组成了一个扇形OAB．易知：∵P(3a，a)在反比例函数y＝12x的图象上，∴3a＝12a．解得：a1＝2，a2＝－2（舍去）．∴P坐标为(6，2)．连接OP，作PC⊥x轴于点C，得：八、方程建模法例8如图8，正方形边长为a，以每边为直径在正方形内画四个半圆，求阴影部分的面积．分析本题直接求阴影部分面积较复杂，但观察图形特点引入方程的思想，问题变得非常简单．解正方形由四个阴影花瓣和四个空白图形组成，如图8，设一个阴影花瓣面积为x，一个空白图形面积为y．根据题意得：因此阴影部分面积为．222aaπ-．【强化训练】1．（2017内蒙古包头市）如图，在△ABC中，AB=AC，∠ABC=45°，以AB为直径的⊙O交BC于点D，若BC=42，则图中阴影部分的面积为（）A．π+1B．π+2C．2π+2D．4π+12．（2017四川省凉山州）如图，一个半径为1的⊙O1经过一个半径为2的⊙O的圆心，则图中阴影部分的面积为（）A．1B．12C．2D．223．（2017四川省资阳市）如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，将Rt△ABC绕点A逆时针旋转30°后得到△ADE，则图中阴影部分的面积为（）A．1312πB．34πC．43πD．2512π4．（2017衢州）运用图形变化的方法研究下列问题：如图，AB是⊙O的直径，CD、EF是⊙O的弦，且AB∥CD∥EF，AB=10，CD=6，EF=8．则图中阴影部分的面积是（）A．252πB．10πC．24+4πD．24+5π5. （2017云南省）如图，边长为4的正方形ABCD外切于⊙O，切点分别为E、F、G、H．则图中阴影部分的面积为．6．（2017吉林省）如图，分别以正五边形ABCDE的顶点A，D为圆心，以AB长为半径画BE，CE．若AB=1，则阴影部分图形的周长为（结果保留π）．7. （2017四川省达州市）如图，矩形ABCD中，E是BC上一点，连接AE，将矩形沿AE翻折，使点B落在CD边F处，连接AF，在AF上取点O，以O为圆心，OF长为半径作⊙O与AD相切于点P．若AB=6，BC=33，则下列结论：①F是CD的中点；②⊙O的半径是2；③AE=92CE；④32S阴影．其中正确结论的序号是．8. （2017湖北省恩施州）如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=23，则图中阴影部分的面积为．（结果不取近似值）9. （2017内蒙古赤峰市）如图，点A是直线AM与⊙O的交点，点B在⊙O上，BD⊥AM垂足为D，BD 与⊙O交于点C，OC平分∠AOB，∠B=60°．（1）求证：A M是⊙O的切线；（2）若DC=2，求图中阴影部分的面积（结果保留π和根号）．10．（2017新疆）如图，AC为⊙O的直径，B为⊙O上一点，∠ACB=30°，延长CB至点D，使得CB=BD，过点D作DE⊥AC，垂足E在CA的延长线上，连接BE．（1）求证：B E是⊙O的切线；（2）当BE=3时，求图中阴影部分的面积．。

初中数学之求阴影面积方法总结

初中数学之求阴影面积方法总结一、简单图形的阴影面积求解方法：1.长方形或正方形的阴影面积求解：对于长方形或正方形的阴影面积，只需计算图形的面积，然后与整个长方形或正方形的面积相减即可。

具体的计算公式为：阴影面积=整个长方形或正方形的面积-图形的面积。

2.圆形的阴影面积求解：对于圆形的阴影面积，需要先计算整个圆形的面积，然后找出圆形内的阴影部分，最后两者相减即可。

计算整个圆形面积的公式为：整个圆形的面积=π*半径²。

3.三角形的阴影面积求解：对于三角形的阴影面积，需要先计算整个三角形的面积，然后找出三角形内的阴影部分，最后两者相减即可。

计算三角形面积的公式为：三角形的面积=底边长度*高/2二、复杂图形的阴影面积求解方法：1.矩形与半圆阴影面积求解：当图形由矩形和半圆组成时，需要分别计算矩形和半圆的面积，然后相加即可。

具体步骤为：计算矩形面积，矩形面积=长*宽；计算半圆面积，半圆面积=π*半径²/2；最后将两部分面积相加得到阴影面积。

2.矩形与等腰梯形阴影面积求解：当图形由矩形和等腰梯形组成时，同样需要分别计算矩形和等腰梯形的面积，然后相加即可。

具体步骤为：计算矩形面积，矩形面积=长*宽；计算等腰梯形面积，等腰梯形面积=(上底+下底)*高/2；最后将两部分面积相加得到阴影面积。

三、图形的分割和组合：1.图形的分割：对于复杂的图形，可以通过将图形分割成简单的图形来计算阴影面积。

具体方法包括将图形分割成矩形、三角形、半圆等简单的图形，然后依次计算每个简单图形的面积，最后将各个部分的面积相加得到阴影面积。

2.图形的组合：当图形由多个简单图形组合而成时，可以分别计算每个简单图形的面积，然后将各个部分的面积相加得到阴影面积。

需要注意的是，图形的组合可能会产生重叠的部分，要注意将其去除或计算重叠部分的面积然后进行调整。

综上所述，求阴影面积主要涉及到计算图形的面积以及图形的分割和组合。

通过对不同图形的特点和求解方法的了解，我们可以灵活运用数学知识来计算阴影面积。

常考压轴04 阴影面积问题-2020年中考数学特训营

【十大常考压轴题特训】解题策略指导04——阴影面积问题求阴影面积问题是一种非常常见的题型，所以也是常考题型，频频出现在很多城市的中考数学试卷中，它的难度不算太大，但也不小，应该属于中等偏上的难度，一般这种题多位于填空题的最后一两题的位置，所以得分率非常低，我们也把它划到压轴题的范畴内．初中数学中的求阴影面积问题多与圆有关，当然也有少部分与圆没有关系，有的与三角函数和勾股定理相关．所以我们把它基本上可以分成两大类，第一类是与圆相关的，它主要考查的是扇形的面积公式；第二类与圆无关的，它主要考查的是勾股定理、三角函数、解直角三角形、相似等知识。

解决这类问题常用策略有以下几个．★策略一﹕转化——将不规则图形转化成规则图形★求阴影部分面积，这种问题绝大多数遇到的都是不规则图形，也就是说我们没有现成的公式去计算它们的面积，所以我们只能将其转化成规则图形，转化方面有下面常用的两种．例如，问题2．（2019年四川省宜宾市）、问题4．（2019江苏省扬州市）、问题8．（2019湖北省十堰市）等．★策略二﹕割补★割补法求阴影部分面积，这个方法我们从小学就知道，这也是我们解决这种问题（2019（2019河南省中考）、问题7．的主要策略，不用多说．例如本专题中的问题6．浙江省丽水市）、问题10．(2019 山东省临沂市)等．★策略三﹕大—小★所求阴影部分的面积有时割补法不太方便做，或者能割补，但计算量会特别大，这时我们可以利用第二种策略大—小，这种方法快捷方便，计算量较小，非常好用，例如本专题中的问题1．（2019年内蒙古鄂尔多斯市）、问题3．（2019山西省中考）、问题9．（2019重庆市中考A卷）、问题5．（2019江苏省苏州市）、问题8等都可以利用这种方法．★策略四﹕建系★在直接利用以上方法都不方便或者很难求出的面积时(只能是与圆无关的问题，多为与等边三角形、正方形有关的问题)，我们可以利用建立坐标系，采用代数法求解．【十大常考压轴题特训】特训04——阴影面积问题题量﹕20题；分值﹕每小题5分，共计100分；推荐时间﹕45分钟问题1．（2019年内蒙古鄂尔多斯市）如图，ABC∆中，AB AC=，以AB为直径的⊙O分别与BC，AC交于点D，E，连接DE，过点D作DF AC⊥于点F．若6∠=︒，则阴影部分的面积是AB=，15CDF．问题2．（2019年四川省宜宾市）如图，∠EOF的顶点O是边长为2的等边△ABC的重心，∠EOF的两边与△ABC的边交于E，F，∠EOF＝120°，则∠EOF与△ABC的边所围成阴影部分的面积是（）A ．32B ．235C ．33D ．34问题3．（2019山西省中考）如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝32，BC ＝2，以AB 的中点为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为（）A.2435π-B.2435π+C.π-32D.234π-问题4．（2019江苏省扬州市）如图，将四边形ABCD 绕顶点A 顺时针旋转45°至四边形AB ′C ′D ′的位置，若AB ＝16cm ，则图中阴影部分的面积为 cm 2．问题5．（2019江苏省苏州市）如图，一块含有45︒角的直角三角板，外框的一条直角边长为10cm ，三角板的外框线2cm ，则图中阴影部分的面积为_______cm （结果保留根号）问题6．（2019河南省中考）如图，在扇形AOB中，∠AOB＝120°，半径OC交弦AB于点D，且OC⊥O A．若OA ＝2，则阴影部分的面积为．问题7．（2019浙江省丽水市）图2，图3是某公共汽车双开门的俯视示意图，ME、EF、FN是门轴的滑动轨道，∠E ＝∠F＝90°，两门AB、CD的门轴A、B、C、D都在滑动轨道上，两门关闭时（图2），A、D分别在E、F处，门缝忽略不计（即B、C重合）；两门同时开启，A、D分别沿E→M，F →N的方向匀速滑动，带动B、C滑动：B到达E时，C恰好到达F，此时两门完全开启，已知AB＝50cm，CD＝40cm．（1）如图3，当∠ABE＝30°时，BC＝cm．（2）在（1）的基础上，当A向M方向继续滑动15cm时，四边形ABCD的面积为2256 cm2．问题8．（2019湖北省十堰市）如图，AB为半圆的直径，且AB＝6，将半圆绕点A顺时针旋转60°，点B旋转到点C 的位置，则图中阴影部分的面积为．问题9．（2019重庆市中考A卷）如图，在菱形ABCD中，对角线AC，BD交于点O，∠ABC＝60°，AB＝2，分别以点A、点C为圆心，以AO的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．（结果保留π）问题10．(2019山东省临沂市)如图，⊙O中，⌒AB＝⌒AC，∠ACB＝75°，BC＝2，则阴影部分的面积是（）A．2＋23πB．2＋3＋23πC．4＋23πD．2＋43π问题11. (2019山西省)如图，在Rt△ABC中，∠ABC＝90°，AB＝32，BC＝2，以AB的中点为圆心，OA 的长为半径作半圆交AC于点D，则图中阴影部分的面积为（）A .2435π-B .2435π+C .π-32D .234π-问题12. (2019 四川省广安市)如图，在Rt △ABC 中，∠ACB ＝90°，∠A ＝30°，BC ＝4，以BC 为直径的半圆O 交斜边AB 于点D ，则图中阴影部分的面积为（）A ． 43π－ 3B ．23π－32C ．13π－32D ．13π－3 问题13. (2019 福建省龙岩市)如图，边长为2的正方形ABCD 中心与半径为2的⊙O 的圆心重合，E 、F 分别是AD 、BA 的延长与⊙O 的交点，则图中阴影部分的面积是．（结果保留π）问题14．(2019 甘肃省天水市)如图，在平面直角坐标系中，已知⊙D 经过原点O ，与x 轴、y 轴分别交于A 、B 两点，点B 坐标为（0，23），OC 与⊙D 交于点C ，∠OCA ＝30°，则圆中阴影部分的面积为．问题15. (2019湖北省荆门市)如图，等边三角形ABC的边长为2，以A为圆心，1为半径作圆分别交AB，AC边于D，E，再以点C为圆心，CD长为半径作圆交BC边于F，连接E，F，那么图中阴影部分的面积为．问题16. (2019湖北省十堰市)如图，AB为半圆的直径，且AB＝6，将半圆绕点A顺时针旋转60°，点B旋转到点C 的位置，则图中阴影部分的面积为．问题17. (2019山东省泰安市)如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点A、点C，交OB于点D，若OA＝3，则阴影都分的面积为．问题18. (2019山东省烟台市)如图，分别以边长为2的等边三角形ABC的三个顶点为圆心，以边长为半径作狐，三段弧所围成的图形是一个曲边三角形，已如⊙O是△ABC的内切圆，则阴影部分面积为__________OAB C问题19. (2019山东省淄博市)如图，在Rt ABC∆中，90B∠=︒，BAC∠的平分线AD交BC于点D，点E在AC上，以AE 为直径的⊙O经过点D．若点F是劣弧AD的中点，且3CE=，阴影部分的面积是．问题20. (2019重庆市綦江县)如图，四边形ABCD是矩形，AB＝4，AD＝22，以点A为圆心，AB长为半径画弧，交CD 于点E，交AD的延长线于点F，则图中阴影部分的面积是．【十大常考压轴题特训】特训04——阴影面积问题题量﹕20题；分值﹕每小题5分，共计100分；推荐时间﹕45分钟问题1．（2019年内蒙古鄂尔多斯市）如图，ABC ∆中，AB AC =，以AB 为直径的⊙O 分别与BC ，AC 交于点D ，E ，连接DE ，过点D 作DF AC ⊥于点F ．若6AB =，15CDF ∠=︒，则阴影部分的面积是．【分析】根据S 阴影部分＝S 扇形OAE －S △OAE 即可求解．【解答】解：连接OE ，∵∠CDF ＝15 °，∠C ＝75 °，∴∠OAE ＝∠OEA ＝30 °，∴∠AOE ＝120 °S △OAE ＝12AE · OE · sin ∠OEA ＝12×2 · OE · cos ∠OEA · OE · sin ∠OEA ＝934， S 阴影部分＝S 扇形OAE －S △OAE ＝120360π ×32 － 934 ＝3 π － 934．故答案3 π － 934 ．【点评】本题考查扇形的面积公式，等腰三角形的性质，三角形的面积等知识，解题的关键是学会用分割法求阴影部分的面积．问题2．（2019年四川省宜宾市）如图，∠EOF 的顶点O 是边长为2的等边△ABC 的重心，∠EOF 的两边与△ABC 的边交于E ，F ，∠EOF ＝120°，则∠EOF 与△ABC 的边所围成阴影部分的面积是（）A ．32B ．235C ．33D ．34【分析】连接OB 、OC ，过点O 作ON ⊥BC ，垂足为N ，由点O 是等边三角形ABC 的内心可以得到∠OBC ＝∠OCB ＝30°，结合条件BC ＝2即可求出△OBC 的面积，由∠EOF ＝∠BOC ，从而得到∠EOB ＝∠FOC ，进而可以证到△EOB ≌△FOC ，因而阴影部分面积等于△OBC 的面积．【解答】连接OB 、OC ，过点O 作ON ⊥BC ，垂足为N ，∵△ABC 为等边三角形，∴∠ABC ＝∠ACB ＝60°，∵点O 为△ABC 的内心∴∠OBC ＝∠OBA ＝12∠ABC ，∠OCB ＝12∠AC B ． ∴∠OBA ＝∠OBC ＝∠OCB ＝30°．∴OB ＝O C ．∠BOC ＝120°，∵ON ⊥BC ，BC ＝2， ∴BN ＝NC ＝1，∴ON ＝tan ∠OBC •BN ＝33×1＝33， ∴S △OBC ＝12BC •ON ＝33．∵∠EOF ＝∠AOB ＝120°，∴∠EOF ﹣∠BOF ＝∠AOB ﹣∠BOF ，即∠EOB ＝∠FO C ．在△EOB 和△FOC 中，⎩⎪⎨⎪⎧∠OBE ＝∠OCF ＝30°OB ＝OC ∠EOB ＝∠FOC， ∴△EOB ≌△FOC （ASA ）．∴S 阴影＝S △OBC ＝33故选：C ．【点评】此题考查了等边三角形的性质、等腰三角形的性质、三角函数的定义、全等三角形的判定与性质、三角形的内心、三角形的内角和定理，有一定的综合性，作出辅助线构建全等三角形是解题的关键．问题3．（2019山西省中考）如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝32，BC ＝2，以AB 的中点为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为（）A.2435π- B.2435π+C.π-32D.234π-【分析】阴影部分的面积可以用S 阴影＝S △ABC －S △AOD －S 扇形BOD 来计算．【解答】作DE ⊥AB 于点E ，连接OD ，在Rt △ABC 中：tan ∠CAB ＝BCAB ＝ 223 ＝ 33 ,∴∠CAB ＝30°，∠BOD ＝2∠CAB ＝60°.在Rt △ODE 中：OE ＝12OD ＝32，DE ＝3OE ＝32.S 阴影＝S △ABC －S △AOD －S 扇形BOD ＝12AB ·BC －12OD ·DE －60360π·OB 2＝12 × 23×2 － 12×3×32 － 60360×π×(3)2＝534－π2，故选A【点评】本题主要考查了扇形面积公式、三角函数、解直角三角形、圆周角与圆心角的关系等知识．难度中等．问题4．（2019江苏省扬州市）如图，将四边形ABCD 绕顶点A 顺时针旋转45°至四边形AB ′C ′D ′的位置，若AB ＝16cm ，则图中阴影部分的面积为 cm 2．【分析】由旋转的性质得：∠BAB '＝45°，四边形AB 'C 'D '≌四边形ABCD ，图中阴影部分的面积＝四边形ABCD 的面积＋扇形ABB '的面积﹣四边形AB 'C 'D '的面积＝扇形ABB '的面积，代入扇形面积公式计算即可．【解答】由旋转的性质得：∠BAB '＝45°，四边形AB 'C 'D '≌四边形ABCD ，则图中阴影部分的面积＝四边形ABCD 的面积＋扇形ABB '的面积﹣四边形AB 'C 'D '的面积＝扇形ABB '的面积＝45π×162360＝32π；故答案为：32π．【点评】本题考查了旋转的性质、扇形面积公式；熟练掌握旋转的性质，得出阴影部分的面积＝扇形ABB '的面积是解题的关键．问题5．（2019江苏省苏州市）如图，一块含有45 角的直角三角板，外框的一条直角边长为10cm ，三角板的外框线2cm ，则图中阴影部分的面积为_______cm （结果保留根号）【分析】C D【解答】如右图：过顶点A 作AB ⊥大直角三角形底边由题意：CE ＝2，AC ＝2 AB ＝5 2∴CD ＝AB －AC －BD ＝52－（2＋2）＝42－2 ∴12 ×10×10－12×(42－2)2＝14＋16 2 【点评】本题主要考查了等腰直角三角形的性质、勾股定理、平行线之间的距离处处相等等知识，当然本题也可以利用相似求解．问题6．（2019河南省中考）如图，在扇形AOB 中，∠AOB ＝120°，半径OC 交弦AB 于点D ，且OC ⊥O A ．若OA ＝2，则阴影部分的面积为．【分析】根据题意，作出合适的辅助线，然后根据图形可知阴影部分的面积是△AOD 的面积与扇形OBC 的面积之和再减去△BDO 的面积，本题得以解决．【解答】作OE ⊥AB 于点F ，∵在扇形AOB 中，∠AOB ＝120°，半径OC 交弦AB 于点D ，且OC ⊥O A ．OA ＝23， ∴∠AOD ＝90°，∠BOC ＝90°，OA ＝OB ， ∴∠OAB ＝∠OBA ＝30°，∴OD ＝OA •tan 30°＝23×33＝2，AD ＝4，AB ＝2AF ＝2×23×32＝6，OF ＝3， ∴BD ＝2，∴阴影部分的面积是：S △AOD ＋S 扇形OBC ﹣S △BDO ＝23×22＋30×π×(23)2360－2×32＝3＋π，故答案为：3＋π．【点评】本题考查扇形面积的计算，解答本题的关键是明确题意，利用数形结合的思想解答．问题7．（2019浙江省丽水市）图2，图3是某公共汽车双开门的俯视示意图，ME 、EF 、FN 是门轴的滑动轨道，∠E ＝∠F ＝90°，两门AB 、CD 的门轴A 、B 、C 、D 都在滑动轨道上，两门关闭时（图2），A 、D 分别在E 、F 处，门缝忽略不计（即B 、C 重合）；两门同时开启，A 、D 分别沿E →M ，F →N 的方向匀速滑动，带动B 、C 滑动：B 到达E 时，C 恰好到达F ，此时两门完全开启，已知AB ＝50cm ，CD ＝40cm ．（1）如图3，当∠ABE ＝30°时，BC ＝ cm ．（2）在（1）的基础上，当A 向M 方向继续滑动15cm 时，四边形ABCD 的面积为 2256 cm 2．【分析】（1）先由已知可得B 、C 两点的路程之比为5：4，再结合B 运动的路程即可求出C 运动的路程，相加即可求出BC 的长；（2）当A 向M 方向继续滑动15cm 时，AA '＝15cm ，由勾股定理和题目条件得出△A 'EB '、△D 'FC '和梯形A 'EFD '边长，即可利用割补法求出四边形四边形ABCD 的面积．【解答】∵A 、D 分别在E 、F 处，门缝忽略不计（即B 、C 重合）且AB ＝50cm ，CD ＝40cm ． ∴EF ＝50＋40＝90cm∵B 到达E 时，C 恰好到达F ，此时两门完全开启， ∴B 、C 两点的路程之比为5：4（1）当∠ABE ＝30°时，在Rt △ABE 中，BE ＝32AB ＝253cm ， ∴B 运动的路程为（50﹣253）cm ∵B 、C 两点的路程之比为5：4∴此时点C 运动的路程为（50﹣253）×45＝（40﹣203）cm∴BC ＝（50﹣253）＋（40﹣203）＝（90﹣453）cm 故答案为：90﹣453；（2）当A 向M 方向继续滑动15cm 时，设此时点A 运动到了点A '处，点B 、C 、D 分别运动到了点B '、C '、D '处，连接A 'D '，如图：则此时AA '＝15cm ∴A 'E ＝15＋25＝40cm 由勾股定理得：EB '＝30cm ， ∴B 运动的路程为50﹣30＝20cm ∴C 运动的路程为16cm ∴C 'F ＝40﹣16＝24cm 由勾股定理得：D 'F ＝32cm ，∴四边形A 'B 'C 'D '的面积＝梯形A 'EFD '的面积﹣△A 'EB '的面积﹣△D 'FC '的面积＝12 ×90× (40＋32)﹣12 ×30×40﹣12×24×32＝2256cm 2．∴四边形ABCD 的面积为2256cm 2．故答案为：2256．【点评】本题考查解直角三角形，解题的关键是熟练运用锐角三角函数的定义，本题属于中等题型．问题8．（2019湖北省十堰市）如图，AB 为半圆的直径，且AB ＝6，将半圆绕点A 顺时针旋转60°，点B 旋转到点C 的位置，则图中阴影部分的面积为．【分析】根据图形可知，阴影部分的面积是半圆的面积与扇形ABC 的面积之和减去半圆的面积．【解答】由图可得，图中阴影部分的面积为：60π×62360 ＋ π×(6÷2)22 －π×(6÷2)22＝6π，故答案为：6π．【点评】本题考查扇形面积的计算、旋转的性质，解答本题的关键是明确题意，利用数形结合的思想解答．问题9．（2019重庆市中考A 卷）如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，∠ABC ＝60°，AB ＝2，分别以点A 、点C 为圆心，以AO 的长为半径画弧分别与菱形的边相交，则图中阴影部分的面积为．（结果保留π）【分析】根据菱形的性质得到AC ⊥BD ，∠ABO ＝12∠ABC ＝30°，∠BAD ＝∠BCD ＝120°，根据直角三角形的性质求出AC 、BD ，根据扇形面积公式、菱形面积公式计算即可．【解答】∵四边形ABCD 是菱形，∴AC ⊥BD ，∠ABO ＝12∠ABC ＝30°，∠BAD ＝∠BCD ＝120°，∴AO ＝12AB ＝1，由勾股定理得，OB ＝AB 2－OA 2＝3, ∴AC ＝2，BD ＝23，∴阴影部分的面积＝12×2×23﹣120π×12360×2＝23﹣23π，故答案为：23﹣23π．【点评】本题考查的是扇形面积计算、菱形的性质，掌握扇形面积公式是解题的关键．问题10．(2019 山东省临沂市)如图，⊙O 中， ⌒AB ＝⌒AC ，∠ACB ＝75°，BC ＝2，则阴影部分的面积是（）A ．2＋23πB ．2＋3＋23πC ．4＋23πD ．2＋43π【分析】分析连接OB 、OC ，先利用同弧所对的圆周角等于所对的圆心角的一半，求出扇形的圆心角为60度，即可求出半径的长2，利用三角形和扇形的面积公式即可求解【解答】∵⌒AB ＝⌒AC ，∴AB ＝AC ， ∵∠ACB ＝75°， ∴∠ABC ＝∠ACB ＝75°， ∴∠BAC ＝30°， ∴∠BOC ＝60°， ∵OB ＝OC ，∴△BOC 是等边三角形， ∴OA ＝OB ＝OC ＝BC ＝2，作AD ⊥BC ， ∵AB ＝AC ， ∴BD ＝CD ， ∴AD 经过圆心O ，∴OD ＝32OB ＝3，∴AD ＝2＋3，∴S △ABC ＝12BC •AD ＝2＋3，S △BOC ＝12BC •OD ＝3，∴S 阴影＝S △ABC ＋S 扇形BOC ﹣S △BOC ＝2＋3＋60π×22360－3＝2＋23，故选：A ．【点评】本题主要考查了扇形的面积公式，圆周角定理，垂径定理等，明确S阴影＝S △ABC ＋S扇形BOC ﹣S △BOC 是解题的关键．问题11. (2019 山西省)如图，在Rt △ABC 中，∠ABC ＝90°，AB ＝32，BC ＝2，以AB 的中点为圆心，OA 的长为半径作半圆交AC 于点D ，则图中阴影部分的面积为（）A .2435π- B .2435π+C .π-32D .234π-【分析】所求阴影部分的面积表示为S 阴影＝S △ABC －S △AOD －S 扇形BOD ,这样方便求出各个图形的面积．问题即可得到解决．【解答】作DE ⊥AB 于点E ，连接OD ，在Rt △ABC 中：tan ∠CAB ＝BCAB ＝223＝33， ∴∠CAB ＝30°，∠BOD ＝2∠CAB ＝60°.在Rt△ODE中：OE＝12OD＝32，DE＝3OE＝32S阴影＝S△ABC－S△AOD－S扇形BOD＝12·AB·BC－12·OD·OE－60360·π·OB2＝12×23×2－12× 3 ×32－60360×π× (3)2＝532－π2故选A【点评】本题主要考查了扇形的面积计算公式，勾股定理，解答本题的关键是将所求阴影部分的面积表示成一些规则图形的面积和差．问题12. (2019四川省广安市)如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝4，以BC为直径的半圆O交斜边AB于点D，则图中阴影部分的面积为（）A．43π－ 3 B．23π－32C．13π－32D．13π－3【分析】根据三角形的内角和得到∠B＝60°，根据圆周角定理得到∠COD＝120°，∠CDB＝90°，根据扇形和三角形的面积公式即可得到结论．【解答】∵在Rt△ABC中，∠ACB＝90°，∠A＝30°，∴∠B＝60°，∴∠COD＝120°，∵BC＝4，BC为半圆O的直径，∴∠CDB＝90°，∴OC＝OD＝2，∴CD＝32BC＝23，图中阴影部分的面积＝S扇形COD﹣S△COD＝120π×22360－12×23×1＝4π3－3，故选：A．【点评】本题考查扇形面积公式、直角三角形的性质、解题的关键是学会分割法求面积，属于中考常考题型．问题13. (2019福建省龙岩市)如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是．（结果保留π）【分析】延长DC，CB交⊙O于M，N，根据圆和正方形的面积公式即可得到结论．【解答】延长DC，CB交⊙O于M，N，则图中阴影部分的面积＝14×（S圆O－S正方形ABCD）＝14×（4π－4）＝π－1，故答案为：π－1．【点评】本题考查了扇形面积的计算，正方形的性质，正确的识别图形是解题的关键．问题14．(2019甘肃省天水市)如图，在平面直角坐标系中，已知⊙D经过原点O，与x轴、y轴分别交于A、B两点，点B坐标为（0，23），OC与⊙D交于点C，∠OCA＝30°，则圆中阴影部分的面积为．【分析】连接AB，根据∠AOB＝90°可知AB是直径，再由圆周角定理求出∠OBA＝∠C＝30°，由锐角三角函数的定义得出OA及AB的长，根据S阴影＝S半圆﹣S△ABO即可得出结论．【解答】连接AB，∵∠AOB＝90°，∴AB是直径，根据同弧对的圆周角相等得∠OBA＝∠C＝30°，∵OB＝23，∴OA＝OB tan∠ABO＝OB tan30°＝23×33＝2，AB＝AO÷sin30°＝4，即圆的半径为2，∴S阴影＝S半圆﹣S△ABO＝π×222﹣12×2×23＝2π﹣23．故答案为：2π－23．【点评】本题考查的是扇形面积的计算，根据题意作出辅助线，构造出直角三角形是解答此题的关键．问题15. (2019湖北省荆门市)如图，等边三角形ABC的边长为2，以A为圆心，1为半径作圆分别交AB，AC边于D，E，再以点C为圆心，CD长为半径作圆交BC边于F，连接E，F，那么图中阴影部分的面积为．【分析】分析过A作AM⊥BC于M，EN⊥BC于N，根据等边三角形的性质得到AM＝32BC＝3 2×2＝3,求得EN＝12AM＝32，根据三角形的面积和扇形的面积公式即可得到结论．【解答】过A作AM⊥BC于M，EN⊥BC于N，∵等边三角形ABC的边长为2，∠BAC＝∠B＝∠ACB＝60°，∴AM＝32BC＝32×2＝3，∵AD＝AE＝1，∴AD＝BD，AE＝CE，∴EN＝12AM＝32，∴图中阴影部分的面积＝S△ABC－S扇形ADE－S△CEF－（S△BCD－S扇形DCF）＝12×2×3－60π×1360－1 2×3×32﹣（12×12× 2 × 3 –30π×3360）＝π12＋32－34，故答案为：π12＋32－34．【点评】本题考查了扇形的面积的计算，等边三角形的性质，正确的作出辅助线是解题的关键．问题16. (2019湖北省十堰市)如图，AB为半圆的直径，且AB＝6，将半圆绕点A顺时针旋转60°，点B旋转到点C 的位置，则图中阴影部分的面积为．【分析】阴影部分的面积是半圆的面积与扇形ABC的面积之和减去半圆的面积；【解答】根据图形可知，阴影部分的面积是半圆的面积与扇形ABC的面积之和减去半圆的面积．解答解：由图可得，图中阴影部分的面积为：60π×62360＋π×(6÷2)22－π×(6÷2)22＝6π，故答案为：6π．【点评】本题考查扇形面积的计算、旋转的性质，解答本题的关键是明确题意，利用数形结合的思想解答．问题17. (2019山东省泰安市)如图，∠AOB＝90°，∠B＝30°，以点O为圆心，OA为半径作弧交AB于点A、点C，交OB于点D，若OA＝3，则阴影都分的面积为．【分析】连接OC，作CH⊥OB于H，根据直角三角形的性质求出AB，根据勾股定理求出BD，证明△AOC为等边三角形，得到∠AOC＝60°，∠COB＝30°，根据扇形面积公式、三角形面积公式计算即可．【解答】连接OC ，作CH ⊥OB 于H ，∵∠AOB ＝90°，∠B ＝30°， ∴∠OAB ＝60°，AB ＝2OA ＝6，由勾股定理得，OB ＝AB 2－OA 2＝ 33， ∵OA ＝OC ，∠OAB ＝60°， ∴△AOC 为等边三角形， ∴∠AOC ＝60°， ∴∠COB ＝30°，∴CO ＝CB ，CH ＝12OC ＝32，∴阴影都分的面积＝60π×32360 － 12 ×3×3×32＋12×33×32－ 30π×32360＝34π，故答案为：34π．【点评】本题考查的是扇形面积计算、等边三角形的判定和性质，掌握扇形面积公式、三角形的面积公式是解题的关键．问题18. (2019 山东省烟台市)如图，分别以边长为2的等边三角形ABC 的三个顶点为圆心，以边长为半径作狐，三段弧所围成的图形是一个曲边三角形，已如⊙O 是△ABC 的内切圆，则阴影部分面积为__________ABC【分析】本题中所求阴影部分的面积可表示为三倍弓形AB 的面积＋△ABC 的面积－ ⊙O 面积，问题可得到解决．【解答】令⊙O得半径为r，过点O作OD⊥AB于D,连接OB，则OB＝2r，BD＝3r＝12AB＝1，∴r＝33．由题意，可知扇形ABC的面积＝60π×22360＝23π，△ABC的面积＝12AB2·sin60°＝3．⊙O面积＝πr2＝13π．∴阴影部分面积＝3×扇形ABC的面积﹣2×△ABC的面积﹣⊙O面积＝3×23π﹣2 3 ﹣13π＝53π﹣23．【点评】本题考查了与扇形有关的阴影部分面积的计算．问题19. (2019山东省淄博市)如图，在Rt ABC∆中，90B∠=︒，BAC∠的平分线AD交BC于点D，点E在AC上，以AE 为直径的⊙O经过点D．若点F是劣弧AD的中点，且3CE=，阴影部分的面积是．【分析】证明△OFD、△OF A是等边三角形，S阴影＝S扇形DFO，即可求解．【解答】（1）①连接OD，OAB CD∵AD是∠BAC的平分线，∴∠DAB＝∠DAO，∵OD＝OA，∴∠DAO＝∠ODA，∴∠DAO＝∠ADO，∴DO//AB，而∠B＝90°，∴∠ODB＝90°，∴BC是⊙O的切线；②连接DE，∵BC是⊙O的切线，∴∠CDE＝∠DAC，∠C＝∠C，∴△CDE∽△CAD，∴CD2＝CE·CA；（2）连接DE、OE，设圆的半径为R，∵点F是劣弧AD的中点，是OF是DA中垂线，∴DF＝AF，∴∠FDA＝∠FAD，∵DO//AB，∴∠PDA＝∠DAF，∴∠ADO＝∠DAO＝∠FDA＝∠F AD，∴AF＝DF＝OA＝OD，∴△OFD、△OF A是等边三角形，∴∠C＝30°，∴OD＝12OC＝(OE＋EC)，而OE＝OD，∴CE＝OE＝R＝3，S阴影＝S扇形DFO＝60360×π× 32＝3π2．【点评】此题属于圆的综合题，涉及了平行四边形的性质、等边三角形的判定与性质、三角函数值的知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．问题20. (2019重庆市綦江县)如图，四边形ABCD是矩形，AB＝4，AD＝22，以点A为圆心，AB长为半径画弧，交CD 于点E，交AD的延长线于点F，则图中阴影部分的面积是．【分析】根据题意可以求得∠BAE和∠DAE的度数，然后根据图形可知阴影部分的面积就是矩形的面积与矩形中间空白部分的面积之差再加上扇形EAF与△ADE的面积之差的和，本题得以解决．【解答】连接AE，∵∠ADE＝90°，AE＝AB＝4，AD＝22，∴sin∠AED＝ADAE＝224＝22，∴∠AED＝45°，∴∠EAD＝45°，∠EAB＝45°，∴AD＝DE＝22，∴阴影部分的面积是：（4×2 2 –45π×42360－2 2 ×222）＋（45π×42360－2 2 ×222）＝82﹣8，故答案为：82－8．【点评】本题考查扇形面积的计算、矩形的性质，解答本题的关键是明确题意，利用数形结合的思想解答．。

阴影部分面积的计算

浅析阴影面积计算方法湖北省安陆市王义贞镇初级中学周永爱徐金菊【摘要】不规则图形面积的求法便于培养和考查同学们对图形的观察、分解、组合能力,及综合运用知识的能力．而不规则图形面积的求法是学生学习的难点，将不规则图形化为规则图形是解决问题的关键.下面介绍几种方法,供参考.【关键词】阴影面积、和差求解、等积变换、割补法、方程求解.阴影部分面积的计算是初中数学中的重要知识点，同时也是中考中的考点之一，如何化不规则图形为规则图形是学生学习的难点.下面列举常见的几种分析思路，以供参考：一、和差求解在图形较复杂情况下，可以把阴影部分面积转化为几个规则图形面积的和差进行计算.例、在△ABC中，∠B=90°，AC=4，BC=2，分别以AB，BC 为直径画半圆，则图中阴影部分的面积为分析：连结BD。

由于AB、BC是直径，所以△ABD和△BCD是两直角三角形，不难看出：S阴影=S半圆ADB+S半圆BCD-S△ABC=2π-4 .二、等积变换先把所求阴影面积中部分图形进行等积变换，转化为几个规则图形，再运用和差求解.例、△ABC是直角边为ａ的等腰直角三角形，直角边AB是半圆Q的直径，半圆P过点C 且与圆Q外切，则图中阴影部分的面积是 .分析：根据圆的性质，相等的圆周角所弦相等，弧相等，所以弓形面积也相等，因为△ABC是等腰直角三角形，所以通过弓形等积位置变换，可化为:S阴影=S△ABC-S△CMN-S△ABG，即为（365a2）三、割补法把阴影部分的图形通过分割，运用平移，旋转，轴对称等全等变换方法化归为规则图形进行求解.1、平移例、如图，平行于Y 轴的直线L 被抛物线ｙ=21ｘ2+1和ｙ=21ｘ2-1所截，当直线L 向右平移4个单位长度时，直线L 被两条抛物线所截得的直线扫过的面积是平方单位. 分析：由于二次项系数相同，抛物线的开口大小相同，可过直线与抛物线ｙ=21ｘ2-1的交点作截线截得下面部分图形沿ｙ轴向上平移2个单位构建平行四边形，其阴影面积为（ 8 ）平方单位2、旋转例、如图，在△ABC 中，∠C=90ｏ，AB=12，∠ABC=60ｏ，将△ABC 以点B 为旋转中心顺时针旋转，使点C 落在AB 的延长线上的D 处，求AC 边扫过的阴影面积.分析：根据旋转对称的性质，△ABC 和△EBD 全等，且两三角形中的阴影面积也相等，故: S 阴影=S 扇形ABE -S 扇形MBN ，即面积为（ 36π ）.3、轴对称例、如图，已知正六边形ABCDEF 的半径为R ，试求出阴影部分面积.分析：因为正六边形既是中心对称图形又是轴对称图形，因此以BE 所在直线为对称轴对折，不难发现阴影面积正好等于正六边形面积的一半，即（433R 2）.四、方程求解例、如图，正方形的边长为a ，以四边为直径分别画半圆，求图中阴影部分面积.分析：设阴影中每一小块的面积为x ，另外非阴影部分每一小块面积为ｙ，可得方程组：4(ｘ+ ｙ)= a 22ｘ+ｙ=21π（21a ）2, 解得： 4ｘ= 21πa 2- a 2即阴影面积为21πa 2- a 2综上所述，有关阴影部分面积的计算，先看能否直接运用和、差求解，后考虑转化思想方法，最后考虑是否可以用方程思想来求解.【参考文献】［1］《中学生数理化(教与学.教研版)》2006年09期［2］《中学生数理化(初中版.中考版)》2007年04期.。

人教版九年级数学上册专题十一+不规则图形面积计算的技巧同步测试

不规则图形面积计算的技巧教材P115习题24.4第4题)图1如图1，正方形的边长为a ，以各边为直径在正方形内画半圆，求图中阴影部分的面积．解：方法一：由图形可以看出，4个相同阴影部分的面积＝4个半圆的面积－正方形的面积＝12πa 2－a 2. 方法二：阴影部分和空白部分都由四部分组成，且形状大小一样，因此可以根据图形中隐含的数量关系来构造方程求解．设每一部分的阴影部分面积为x ，每一部分的空白部分面积为y ，根据图形得⎩⎪⎨⎪⎧2x ＋y ＝12π⎝⎛⎭⎫a 22，4x ＋4y ＝a 2，解得⎩⎨⎧x ＝18πa 2－a 24，y ＝a 22－18πa 2，所以阴影部分面积＝4x ＝4⎝⎛⎭⎫18πa 2－a 24＝12πa 2－a 2.【思想方法】将阴影部分的面积转化为规则图形的面积的和差．图2如图2，正方形的边长为2，以各边为直径在正方形内画半圆，则图中阴影部分的面积为__1.7__．(结果保留两个有效数字，参考数据：π≈3.14)【解析】空白部分的面积等于四个半圆的面积减去正方形的面积，再利用阴影部分的面积等于正方形的面积减去空白部分的面积计算．空白部分的面积＝12π⎝⎛⎭⎫222×4－2×2＝2π－4，阴影部分的面积＝2×2－(2π－4)＝4－2π＋4＝8－2π≈8－2×3.14＝8－6.28＝1.72≈1.7.如图3，以等腰直角△ABC 两锐角顶点A ，B 为圆心作等圆，⊙A 与⊙B 恰好外切，若AC ＝2，那么图中两个扇形(即阴影部分)的面积之和为( B )A.14πB.12πC.22π D.2π图3【解析】∵⊙A与⊙B恰好外切，∴⊙A与⊙B是等圆，∵AC＝2，△ABC是等腰直角三角形，∴AB＝22，∴⊙A，⊙B的半径均为 2.∴两个扇形(即阴影部分)的面积之和＝∠AπR2360＋∠BπR2360＝（∠A＋∠B）πR2360＝14πR2＝π2.第2课时圆锥的侧面积和全面积 [见B 本P50]1．已知圆柱的底面半径为3 cm ，母线长为5 cm ，则圆柱的侧面积是( B )A ．30 cm 2B ．30π cm 2C ．15 cm 2D ．15π cm 22．用半径为3 cm ，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为( D )A ．2π cmB ．1.5 cmC ．π cmD ．1 cm【解析】设此圆锥的底面半径为r ，根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得，2πr ＝120π×3180，解得r ＝1 cm. 3．在学校组织的实践活动中，小新同学用纸板制作了一个圆锥模型，它的底面半径为1，高为22，则这个圆锥的侧面积是( B )A ．AπB ．3πC ．22πD ．2π【解析】 ∵底面半径为1，高为22， ∴母线长＝2（2）2＋12＝3.底面圆的周长为：2π×1＝2π，∴圆锥的侧面积为：S 侧＝12×2π×3＝3π. 4．如图24－4－12，扇形OAB 是圆锥的侧面展开图，若小正方形方格的边长为1 cm ，则这个圆锥的底面半径为( C )图24－4－12 A ．2 2 cm B. 2 cm C.22 cm D.12cm 【解析】由图形可知扇形的圆心角为90°，半径为2 2 cm ，根据圆锥的底面圆的周长等于圆锥的侧面展开扇形的弧长可以得2πr ＝90180×22π，解得r ＝22(cm)． 5．如果圆锥的母线长为5 cm ，底面半径为3 cm ，那么圆锥的表面积为( C )A ．39π cm 2B ．30π cm 2C ．24π cm 2D ．15π cm 2【解析】 S 表＝S 侧＋S 底＝π×3×5＋π×32＝24π.故选C.6．一个圆锥的侧面积是36π cm 2，母线长是12 cm ，则这个圆锥的底面直径是__6__ cm.7．已知圆锥的底面周长是10π，其侧面展开后所得扇形的圆心角为90°，则该圆锥的母线长是__20__．8．底面半径为1，高为3的圆锥的侧面积等于__2π__．【解析】 ∵圆锥的高为3，底面的半径是1， ∴由勾股定理知：母线长＝（3）2＋1＝2， ∴圆锥的侧面积＝12底面周长×母线长＝12×2π×2＝2π. 9．如图24－4－13，如果从半径为5 cm 的圆形纸片上剪去15圆周的一个扇形，将留下的扇形围成一个圆锥(接缝处不重叠)，那么这个圆锥的高是__3__cm.图24－4－13【解析】 ∵从半径为5 cm 的圆形纸片上剪去15圆周的一个扇形， ∴留下的扇形的弧长＝4（2π×5）5＝8π，根据底面圆的周长等于扇形弧长，∴圆锥的底面半径r ＝8π2π＝4 cm ， ∴圆锥的高为52－42＝3 cm.故答案为3.10．已知一个扇形的半径为60厘米，圆心角为150°.用它围成一个圆锥的侧面，那么圆锥的底面半径为__25__厘米．【解析】扇形的弧长是：150π×60180＝50π cm ，设底面半径是r cm ，则2πr ＝50π，解得：r ＝25.故答案是25.11．已知圆锥的高为4，底面半径为2，求：(1)圆锥的全面积；(2)圆锥侧面展开图的圆心角．解： (1)∵圆锥的高为4，底面半径为2，∴圆锥的母线长为25，底面周长是2×2π＝4π，则侧面积是12×4π×25＝45π，底面积是π×22＝4π，则全面积是45π，＋4π＝(4＋45)π.(2)∵圆锥底面半径是2，∴圆锥的底面周长为4π，设圆锥的侧面展开的扇形圆心角为n °，n π×25，180＝4π，解得n ＝725，圆锥侧面展开图的圆心角为72(5)°.12．如图24－4－14，Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝22，若把Rt △ABC 绕边AB 所在直线旋转一周，则所得的几何体的表面积为( D )图24－4－14A ．4πB ．42πC ．8π D. 82π【解析】如图，过C 作CO ⊥AB ，则 Rt △ABC 绕边AB 所在直线旋转一周所得的几何体的表面积为2×π×OC ·AC ＝2×π×2×22＝82π.13．一个几何体由圆锥和圆柱组成，其尺寸如图24－4－15所示，则该几何体的全面积(即表面积)为__68π__(结果保留π)．图24－4－15【解析】圆锥的母线长是32＋42＝5，圆锥的侧面积是12×8π×5＝20π，圆柱的侧面积是8π×4＝32π，几何体的下底面面积是π×42＝16π，则该几何体的全面积(即表面积)为20π＋32π＋16π＝68π.14．如果圆锥的底面周长是20π，侧面展开后所得的扇形的圆心角为120°，则圆锥的母线长是__30__．15．已知在△ABC 中，AB ＝6，AC ＝8，∠A ＝90°，把Rt △ABC 绕直线AC 旋转一周得到一个圆锥，其表面积为S 1，把Rt △ABC 绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，求S 1∶S 2.【解析】以直角三角形的直角边为轴旋转一周得到的几何体是圆锥．圆锥的表面积S 表＝S 侧＋S 底．解：在Rt △ABC 中，∠A ＝90°，AB ＝6，AC ＝8，∴BC ＝AB 2＋AC 2＝62＋82＝10.(1)绕直线AC 旋转一周所得圆锥的表面积：S 1＝π·AB ·BC ＋π·AB 2＝π×6×10＋π×62＝60π＋36π＝96π；(2)绕直线AB 旋转一周所得圆锥的表面积：S 2＝π·AC ·BC ＋π·AC 2＝π×8×10＋π×82＝80π＋64π＝144π.∴S 1S 2＝96π144π＝23. 16．如图24－4－16，已知在⊙O 中，AB ＝4，AC 是⊙O 的直径，AC ⊥BD 于F ，∠A ＝30°.(1)求图中阴影部分的面积；(2)若用阴影扇形OBD 围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．(3)试判断⊙O 中其余部分能否给(2)中的圆锥做两个底面．图24－4－16解： (1)∵AC ⊥BD 于F ，∠A ＝30°，∴∠BOC ＝60°，∠OBF ＝30°，∵在Rt △ABF 中，AB ＝4，∴BF ＝2，∴OB ＝4，∴S 阴影＝S 扇形BOD ＝120·π·42360＝163π； (2)设底面半径为r ，∵半径OB ＝4，2πr ＝120·2π·4360∴r ＝43； (3)∵⊙O 其余部分面积为323 π，而圆锥底面面积为169π. ∴⊙O 中其余部分能给(2)中的圆锥做两个底面．17．在一次数学探究性学习活动中，某学习小组要制作一个圆锥体模型，操作规则是：在一块边长为16 cm 的正方形纸片上剪出一个扇形和一个圆，使得扇形围成圆锥的侧面时，圆恰好是该圆锥的底面．他们首先设计了如图24－4－17所示的方案一，发现这种方案不可行，于是他们调整了扇形和圆的半径，设计了如图24－4－17所示的方案二．(两个方案的图中，圆与正方形相邻两边及扇形的弧均相切)(1)请说明方案一不可行的理由；(2)判断方案二是否可行，若可行，请确定圆锥的母线长及其底面圆的半径；若不可行，请说明理由．图24－4－17解：(1)理由如下：∵扇形的弧长＝2π×164＝8π，圆锥的底面周长＝2πr ，∴圆的半径为4 cm. 由于所给正方形纸片的对角线长为16 2 cm ，而制作这样的圆锥实际需要正方形纸片的对角线长为16＋4＋42＝20＋42＞162，∴方案一不可行．(2)方案二可行．理由如下：设圆锥底面圆的半径为r cm ，圆锥的母线长为R cm ，则(1＋2)r ＋R ＝162，①2πr ＝2πR 4.② 由①②，可得R ＝6425＋2＝3202－12823， r ＝1625＋2＝802－3223，故所求的圆锥的母线长为3202－12823cm ，底面圆的半径为802－3223cm.。

初中数学复习(圆的阴影部分的面积)

初中数学复习（圆）1、已知：如图，AB为半圆⊙O的直径，C、D为半圆⊙O的三等分点，若AB=12，求阴影部分的面积。

2、如图，已知：∠AOB=90°，AC∥OB，AO=3，分别以O点，A点为圆心，AO、AB为半径画弧，交OB、AC于B、C，求阴影部分的周长和面积。

3、如图，已知半径分别为1和3的⊙O1和⊙O2外切于P，AB切二圆于A、B两点，求图中阴影部分的面积。

4、如图，已知：⊙O1与⊙O2相交于B、D，AB为⊙O1直径，BC=AD，若AB=12,DE=30，求圆中阴影部分的面积。

6、一个扇形的半径等于一个圆的半径的2倍，如果这个扇形的面积与圆的面积相等，则这个扇形的圆心角等于( ) A.180° B.90° C.45° D.22.5°π，则大圆的面积为，小圆的面积为7、两圆的半径之比为3∶5，面积相差32；正三角形的内切圆与外接圆的面积之比为。

8、圆心角为40°，半径为6的扇形的面积为；半径为3，弧长为4的扇形的面积为；弧长为2π，面积为4π的扇形的半径为，圆心角为；圆心角为60°，弧长为6π的扇形的半径为，面积为。

9、如图，四个等圆两两外切，半径均为2cm ，且∠O 2O 1O 4=90°，求图中的阴影部分的面积为S 。

10、已知扇形的圆心角为60°，面积为6π，求这个扇形的周长。

11、如图，在菱形ABCD 中，AC 与BD 相交于点O ，AC=4，34BD=，以B 为圆心，BO 为半径画弧交AB 于E ，交BC 于F ，以D 为圆心，DO 为半径画弧交AD 于G ，交DC 于H ，求阴影部分的面积S 。

12、如图，PA 、PB 是⊙O 的切线，A 、B 是切点，∠P=60°，AB=12，求阴影部分的面积。

13如图，已知△ABC 中，∠C=90°，AC=8，BC=6，M 为AB 的中点，分别以A 、B 为圆心，AM 为半径画弧交AC 于D ，交BC 于E ，求阴影部分的面积。