初三数学中考几何面积问题
九年级面积问题知识点

九年级面积问题知识点在九年级学习数学时,面积问题是一个非常重要的知识点。
面积是描述平面图形内部的覆盖面积大小的概念,通过学习面积问题,我们可以更好地理解图形的属性和关系,进一步提升解决实际问题的能力。
本文将介绍九年级面积问题的几个重要知识点,并提供例题进行讲解和练习。
一、长方形的面积计算长方形是最基本的平面图形之一,我们先来学习如何计算长方形的面积。
长方形的面积等于它的长度乘以它的宽度。
假设一个长方形的长度为L,宽度为W,则它的面积S可以通过以下公式计算得出:S = L × W例如,如果一个长方形的长度是5厘米,宽度是3厘米,那么它的面积为:S = 5 × 3 = 15平方厘米通过这个例子,我们可以看出计算长方形面积的方法是相对简单和直接的。
二、正方形的面积计算正方形是一种特殊的长方形,它的四条边相等。
正方形的面积计算同样也非常简单,因为它的长度和宽度相等。
我们可以使用以下公式计算正方形的面积:S = 边长 ×边长例如,如果一个正方形的边长是6厘米,那么它的面积为:S = 6 × 6 = 36平方厘米正方形的面积计算方法和长方形类似,只不过边长相等。
三、三角形的面积计算接下来我们来学习如何计算三角形的面积。
三角形是由三条边围成的平面图形,它的面积计算方法稍微复杂一些。
我们可以使用以下公式计算三角形的面积:S = 1/2 ×底边长 ×高其中,三角形的底边长是指与高垂直的一条边的长度,高是指从底边向垂直方向作垂线的长度。
例如,如果一个三角形的底边长是5厘米,高是4厘米,那么它的面积为:S = 1/2 × 5 × 4 = 10平方厘米通过这个例子我们可以看到,计算三角形的面积需要明确底边长和高的长度。
四、圆的面积计算圆是一个非常特殊的图形,它的面积计算方式与之前所学的长方形、正方形和三角形不同。
圆的面积计算需要使用圆的半径,而不是直接使用线段的长度。
中考复习题面积问题(解析版)

专题04 面积问题求解平面直角坐标系中由动点生成的图形的面积问题,是初中数学一种重要的题型,它主要结合函数图形的相关知识点,在平面直角坐标中的框架中构建图形求面积,求图形面积常常转化为三角形、特殊的四边形,求面积常用的方法有以下几种:方法1:直接法,求出三角形底边和底边上的高,进而求出其面积;方法2:补形法,将三角形面积转化为若干个特殊的四边形和三角形的和或差;方法3:分割法,选择一种恰当的直线,将三角形分割成两个便于计算的面积的三角形。
一、填空题1.在平面直角坐标系中,,,若的面积为,且点在坐标轴上,则符合条件的点的坐标为__________.【答案】或或或【解析】解:①如图所示,若点C在x轴上,且在点A的左侧时,∵∴OB=3∴S△ABC=AC·OB=6 解得:AC=4∵,∴此时点C的坐标为:;②如图所示,若点C在x轴上,且在点A的右侧时,同理可得:AC=4 ∴此时点C的坐标为:;图①图②③如图所示,若点C在y轴上,且在点B的下方时,∵∴AO=2 ∴S△ABC=BC·AO=6 解得:BC=6∵∴此时点C的坐标为:;④如图所示,若点C在y轴上,且在点B的上方时,同理可得:BC=6 ∴此时点C的坐标为:. 故答案为:或或或.图③图④【点拨】此题考查的是平面直角坐标系中已知面积求点的坐标,根据C点的位置分类讨论是解决此题的关键.2.在平面直角坐标系中,的位置如图所示,则的面积是________.【答案】9.【解析】如图,.【点拨】利用网格特点,将所求的的面积转化为规则图形面积的差即可.本题考查了坐标系中三角形面积的计算,属于常考题型,掌握求解的方法是关键.二、解答题3.如图,在平面直角坐标系中,、.求的面积.【答案】【解析】如图,过点A、B分别作x轴的垂线交x轴于点C、D.根据面积公式求得S△BOD、S梯形ACDB、S△AOC的值,然后由图形可以求得S△AOB= S△AOC +S梯形ACDB- S△BOD.解:过点A、B分别作x轴的垂线交x轴于点C、D.∵A(3,4),B(5,1),∴OC=3,AC=4,OD=5,BD=1.∴S△AOC=×OC•AC=×3×4=6,S△BOD=OD•BD=×5×1=,S梯形ACDB=( BD+AC)•CD=×(1+4)×2=5,∴S△AOB= S△AOC +S梯形ACDB- S△BOD =6+5-=.【点拨】本题考查了三角形的面积、坐标与图形性质.通常采用“割补法”解答此类题目.4.在平面直角坐标系中描出点A(﹣2,0)、B(3,1)、C(2,3),将各点用线段依次连接起来,并解答如下问题:(1)在平面直角坐标系中画出△ A′B′C′,使它与△ ABC 关于x 轴对称,并直接写出△ A′B′C′三个顶点的坐标;(2)求△ABC的面积.【答案】(1)作图见解析;A'(-2,0)、B'(3,-1)C'(2,-3);(2)5.5【解析】(1)在坐标系内画出△ABC,再作出各点关于x轴的对称点,顺次连接各点即可;(2)利用矩形的面积减去三个顶点上三角形的面积即可.【详解】(1)如图所示,由图可知A'(-2,0)、B'(3,-1)C'(2,-3);2)由图可知,S△ABC=5×3-×5×1-×3×4-×2×1,=15--6-1=5.5.【点拨】本题考查的是作图-轴对称变换,熟知关于x轴对称的点的坐标特点是解答此题的关键.5.如图所示,在平面直角坐标系中,已知A(0,1)B(2,0)C(4,3),(1)在平面直角坐标系中画出△ABC,并求△ABC的面积(2)已知P为x轴上一点,若△ABP的面积为4,求点P的坐标。
初中面积问题方法总结

初中面积问题方法总结
初中面积问题通常涉及到平面几何中的基本图形,如三角形、四边形、圆等。
解决这类问题的方法主要包括以下几种:
1.公式法:对于常见的图形,如三角形、矩形、正方形、圆等,都有相应的面积计算公式。
熟练掌握这些公式,并能灵活应用,是解决面积问题的基本方法。
2. 分割法:对于复杂的图形,可以将其分割成几个简单的图形,然后分别计算这些图形的面积,最后求和。
这种方法需要准确判断图形的构成和分割方式。
3.补全法:有些图形可以通过补全成一个更简单的图形来方便计算面积。
例如,通过补全一个三角形为一个矩形或正方形,可以更容易地找到三角形的面积。
4.相似图形法:如果两个图形相似,那么它们的面积之比等于它们对应边长的平方之比。
利用这个性质,可以通过已知图形的面积来求解未知图形的面积。
5.坐标法:在平面直角坐标系中,可以通过计算图形各顶点的坐标,然后利用坐标来计算面积。
这种方法通常用于求解不规则图形的面积。
6.面积比法:在一些情况下,可以通过比较图形的面积来求解问题。
例如,在比例尺问题中,可以通过比较实际面积和图上面积的比例来求解。
7.代数法:对于一些涉及变量和方程的面积问题,可以通过代数方法来求解。
这通常涉及到建立方程或不等式,并解出未知数的值。
解决初中面积问题时,首先要仔细分析问题的条件,选择合适的方法。
同时,还需要注意计算过程中的准确性和规范性,避免因为计
算错误而导致结果不正确。
九年级面积问题知识点归纳总结

九年级面积问题知识点归纳总结面积是数学中一个重要的概念,它在日常生活中的应用广泛。
九年级学生需要掌握与面积有关的几何图形的计算方法,理解面积的性质和应用。
本文将对九年级面积问题的知识点进行归纳总结。
一、矩形的面积计算方法矩形是最基础的几何图形之一,其面积可以通过长度和宽度相乘得到。
设矩形的长度为l,宽度为w,则矩形的面积S为S = l * w。
二、平行四边形的面积计算方法平行四边形是另一个常见的几何图形,它的面积可以通过底边和高的乘积得到。
设平行四边形的底边为b,高为h,则平行四边形的面积S为S = b * h。
三、三角形的面积计算方法三角形也是常见的几何图形,它的面积计算稍微复杂一些。
九年级学生需要掌握两种计算三角形面积的方法:通过底边和高的乘积,以及通过三边的长度计算。
1. 通过底边和高的乘积:设三角形的底边为b,高为h,则三角形的面积S为S = 0.5 * b * h。
2. 通过三边的长度计算:设三角形的三边分别为a、b、c,则可以使用海伦公式计算三角形的面积。
海伦公式为S = √[s(s-a)(s-b)(s-c)],其中s = (a + b + c) / 2。
利用海伦公式,可以根据三边的长度计算出三角形的面积。
四、圆的面积计算方法圆是一个特殊的几何图形,九年级学生需要掌握圆的面积计算方法。
圆的面积可以通过半径的平方乘以圆周率π来计算。
设圆的半径为r,则圆的面积S为S = π * r^2。
五、复合图形的面积计算方法复合图形是由两个或多个基本图形组成的图形。
计算复合图形的面积需要将其分解为基本图形的面积之和。
九年级学生需要学会计算常见的复合图形,如矩形与三角形的组合、矩形与圆的组合等。
六、面积性质和应用九年级学生还需要了解面积的性质和应用。
以下是一些常见的性质和应用:1. 对于相似的图形,其面积与边长的比例为平方关系。
即如果两个图形的边长之比为a:b,那么它们的面积之比为a^2:b^2。
2. 面积可以应用于解决实际问题,如计算土地面积、涂料要求以及物体的表面积等。
最新九年级中考数学复习:几何探究压轴题(面积问题)

(2)如图2,在等腰三角形ABC中,∠C=120°,点O为AB的中点,点M为AC上一点,将射线OM绕点O顺时针旋转60°交BC于点N,则OM与ON的数量关系是否改变,请说明理由;
9.在△ABC中,CA=CB,∠ACB=a,将△CAD绕点C按逆时针方向旋转角a得到△CBE,点A,D的对应点分别为点B,E.
(1)如图1,若A,D,E三点在同一直线上,则∠CDE=(用含a的代数式表示);
(2)如图2,若A,D,E三点在同一直线上,a=60°,过点C作CF⊥AE于点F,然后探究线段CF,AE,BE之间的数量关系,并证明你的结论;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=3,AB=7,请直接写出△PMN面积的最大值.
18.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D、E分别在边AB、AC上,AD=AE,连接BE,点M、N、P分别为DE、BE、BC的中点.
(1)观察猜想:图1中,线段NM、NP的数量关系是,∠MNP的大小为;
(2)在三角板旋转的过程中,边 与AB所在直线交于点D,过点D作DE∥ 交 边于点E,连接BE.
①当 时,设AD= ,BE= ,求 与 之间的函数解析式及自变量 的取值范围;
②当 时,求AD的长.
13.在中 中. , ,点E在射线CB上运动.连接AE,将线段AE绕点E顺时针旋转90°得到EF,连接CF.
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.
2.如图,矩形 中, 为等边三角形.点E,F分别为 边上的动点,且 ,P为 上一动点,连接 ,将线段 绕点B顺时针旋转 至 ,连接 .
中考数学复习之因动点产生的面积问题解题策略

因动点产生的面积问题解题策略一.解题策略解读:面积的存在性问题常见的题型和解题策略有两类:图1 图2 图3 计算面积常用到的策略还有:图4 图5 图6例1.已知抛物线y=mx2+(1-2m)x+1-3m与x轴交于不同的两点A、 B.(1) 求m的取值范围;(2) 证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3) 当<m≤8时,由(2)求出的点P和点A、 B构成的△ABP的面积是否有最值,若有,求出最值及相应的m的值;若没有,请说明理由.思路:1. 已知的抛物线的解析式可以因式分解的,抛物线过x轴上的定点(-1, 0).2. 第(2)题分两步,先对m赋予两个不同的值,联立求方程组的解,再验证这个点是确定的.3. 第(3)题中△ABP的高为定值,点A为定点,求△ABP的最大面积,其实就是求点B的横坐标的最大值.例2.问题提出(1) 如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2) 如图2,在矩形ABCD中,AB=4, AD=6, AE=4, AF=2.是否在边BC、CD上分别存在点G、 H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3) 如图3,有一块矩形板材ABCD, AB=3米, AD=6米,现想从此板材中截出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,米,∠EHG=45°.经研究,只有当点E、 F、 G分别在边AD、 AB、 BC上时,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.图1 图2 图3思路:1. 第(2)题的模型是“打台球”两次碰壁问题,依据光的反射原理.2. 第(3)题需先设AF的长并求解,再验证点H在矩形内部,然后计算面积.例3.如图1,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8, OE=17.抛物线y=x2-3x+m与y轴交于点A,抛物线的对称轴与x轴交于点B,与CD交于点K.(1) 将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①求点F的坐标;②请直接写出抛物线的函数表达式;(2) 将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连结OG,折痕与OG交于点H,点M是线段EH上的一个动点(不与点H重合),连结MG, MO,过点G作GP⊥OM于点P,交EH于点N,连结ON.点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1·S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化的范围;若不变,请直接写出这个值.温馨提示: 考生可以根据题意,在备用图中补充图形,以便作答.图1 备用图思路:1. 第(1)题中点F的位置是由A、 B两点确定的,A、 B两点的坐标都隐含在抛物线的解析式中.2. 第(2)题思路在画示意图过程中,点G是关键点.以E为圆心,EO为半径画弧,交CD于点G.例 4.如图,已知平行四边形ABCD的三个顶点A(n, 0)、 B(m, 0)、 D(0,2n)(m>n>0),作平行四边形ABCD关于直线AD的对称图形AB1C1 D.(1) 若m=3,试求四边形CC1B1B面积S的最大值;(2) 若点B1恰好落在y轴上,试求的值.思路:1. 第(1)题先说理再计算,说理四边形CC1B1B是矩形.2. 第(2)题根据AB1=AB列关于m、 n的方程,整理就可以得到m与n的关系.例5.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3, 0)和点B(2, 3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=.(1) 求这条抛物线的表达式及对称轴;(2) 连结AB、 BC,求∠ABC的正切值;(3) 若点D在x轴下方抛物线的对称轴上,当S△ABC =S△ADC时,求点D的坐标.解析:1. 直觉告诉我们,△ABC是直角三角形.2. 第(3)题的意思可以表达为: B、 D在直线AC的两侧,到直线AC的距离相等.于是我们容易想到,平行线间的距离处处相等.例6.如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、D分别不与点A、 B重合),点E、 F在AB上,EC⊥CD, FD⊥CD.(1) 求证:EO=FO;(2) 连结OC,如果△ECO中有一个内角等于45°,求线段EF的长;(3) 当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE的面积为S,周长为l,问:S与l是否分别随着x变化而变化?试用所学过的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.思路:1. 用垂径定理和平行线等分线段定理证明点O是EF的中点.2. 第(2)题的△ECO中,∠ECO是定值,45°的角分两种情况.3. 第(3)题用x表示OE的长,在△ECO中,∠ECO是定值.例7.直线y=2x+m与抛物线y=ax2+ax+b都过点M(1, 0),且a<b.(1) 求抛物线顶点Q的坐标(用含a的式子表示);(2) 试说明抛物线与直线有两个交点;(3) 设抛物线与直线的另一个交点为N.①若-1≤a≤-时,求MN的取值范围;②求△QMN的面积最小值.思路:1. 将M(1, 0)分别代入直线和抛物线的解析式,可以确定m的值,用a表示b.2. 联立直线与抛物线的解析式,消去y,得到关于a的一元二次方程,判断Δ>0.3. 第(3)题①,分别求a=-1和a=-时直线与抛物线的交点M、 N的坐标,再求MN的长,两个MN的长,就是MN的取值范围的两端值.例8.已知Rt△EFP和矩形ABCD如图1摆放(点P与点B重合),点F、 B(P)、 C 在同一直线上,AB=EF=6cm, BC=FP=8cm, ∠EFP=90°.如图2, △EFP从图1位置出发,沿BC方向匀速运动,速度为1cm/s, EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连结AF、 PQ.当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6).解答下列问题:(1) 当t为何值时,PQ∥BD?(2) 设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3) 在运动过程中,是否存在某一时刻t,使S五边形AFPQM ∶S矩形ABCD=9∶8?若存在,求出t的值;若不存在,请说明理由;(4) 在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.图1 图2思路:1. 把线段BP、 PC、 CQ、 DQ的长用t表示出来.再把线段BG、 DM的长用t表示出来.2. 用割补法求五边形AFPQM的面积,等于直角梯形减去两个直角三角形的面积.3. 第(3)题用第(2)题的结果,直接解方程就可以了.4. 第(4)题是根据MP2=MG2列方程,需要构造以MP为斜边的直角三角形.例9.如图1,在平面直角坐标系中,过原点O及点A(8, 0)、 C(0, 6)作矩形OABC,连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从点A出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.(1) 如图1,当t=3时,求DF的长;(2) 如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3) 连结AD,当AD将△DEF分成的两部分的面积比为1∶2时,求相应的t的值.图1 图2思路;1. 作DM⊥AB于M, DN⊥OA于N,那么△NDF与△MDE的相似比为3∶4.2. 面积比为1∶2要分两种情况讨论.把面积比转化为两个同高三角形底边的比.3. 过点E作OA的平行线,构造“8字型”相似,这样就把底边的比利用起来了.例10.如图1,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,与y轴交于点C, OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1) 求b、 c的值;(2) 如图1,连结BE,线段OC上点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3) 如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.图1 图2思路:1. 由已知抛物线的解析式可得C(0, c),再用c表示B、 D两点的坐标,然后将B、 D代入抛物线的解析式列关于b、 c的方程组.2. 第(2)题: 通过点C、 F分别与点D、 F'关于直线l对称,得到点F'是BE的中点,从而求得点F的坐标.3. 第(3)题: 设点P的横坐标为m,用m表示点M、 N的坐标,进而用m表示线段PM、 PN、 PA的长,根据两个三角形的面积相等,求出PN边上的高QH.最后讨论NQ与QH的关系.例11.如图,在平面直角坐标系中,直线y=12x+2与x 轴交于点A,与y 轴交于点C.抛物线y=-x 2+bx+c 经过A 、 C 两点,与x 轴的另一个交点为点B.(1) 求抛物线的函数表达式;(2) 点D 为直线AC 上方抛物线上一动点.① 连结BC 、 CD.设直线BD 交线段AC 于点E, △CDE 的面积为S 1, △BCE 的面积为S 2,求 12S S 的最大值; ② 过点D 作DF ⊥AC,垂足为F,连结CD.是否存在点D,使得△CDF 中的某个角恰好等于∠BAC 的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.图1 备用图思路: 1. △CDE 与△BCE 是同高三角形,面积比等于底边的比.构造“8字型”,把底边的比转化为竖直线段的比.2. 第(3)题的第一种情况∠DCF=2∠BAC,过点C 作x 轴的平行线,通过内错角相等,再作轴对称的角,很容易找到点D 的位置.3. 第(3)题的第二种情况∠CDF=2∠BAC,先要探求2∠BAC的大小(正切值),如果这一步探究不出来,基本上进行不下去.例12.已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如题图1,连接BC.(1)填空:∠OBC= ;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN 的面积为y,求当x为何值时y取得最大值?最大值为多少?思路:(1)由旋转的性质可以证明△OBC是等边三角形,从而可得∠OBC的度数;(2)求出△AOC的面积,利用三角形的面积公式计算即可;(3)分三种情形讨论求解即可解决问题:①当0<x≤83时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E,利用面积公式表示出△OMN的面积(y值);②当8 3<x≤4时,M在BC上运动,N在OB上运动.作MH⊥OB于H,利用∠CBO=60°表示出MH,再利用面积公式表示出△OMN的面积(y值);③当4<x≤4.8时,M、N都在BC上运动,作OG⊥BC于G,易求OG,再利用面积公式表示出△OMN的面积(y值),最后分别求出三种情况下面积最大值,从而求出整个运动过程中y的最大值.例13. 在平面直角坐标系中,抛物线2y ax bx c=++交x轴于A、B两点,交y轴于点C(0,43-),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=34.(1)求抛物线的解析式;(2)动点P从点B出发,沿x轴正方向以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动为t秒.①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由;②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.思路:本题是代数几何综合题,以平面直角坐标系为背景,考查了求二次函数解析式,二次函数的性质,,方程组的解法,几何图形面积的表示,相似三角形的判定与性质,分类讨论思想,三角形的面积的最值问题,综合性强,难度大,解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力,还得富有耐心.(1)利用A、B、C三点的坐标确定二次函数的解析式.(2)利用题目的已知条件表示出相关线段的长,①中利用三角函数值探索出∠PAQ=∠ACD,再根据题目中的要求使得△ADC与△PQA相似,进行分类讨论得到对应线段成比例,列出关于t的方程求解即可;②直接利用三角形的面积公式列出△APQ与△CAQ 的面积之和与时间t之间的函数关系式,再将所得的二次函数的解析式配方确定最值即可得到答案.。
几何图形中求线段,线段和,面积等最值问题(4题型)—2024年中考数学压轴题(全国通用)(解析版)

几何图形中求线段,线段和,面积等最值问题(压轴通关)目录【中考预测】预测考向,总结常考点及应对的策略 【误区点拨】点拨常见的易错点【抢分通关】精选名校模拟题,讲解通关策略(含新考法、新情境等)几何图形中求线段、线段和、面积最值题是全国中考的热点内容,更是全国中考的必考内容。
每年都有一些考生因为知识残缺、基础不牢、技能不熟、答欠规范等原因导致失分。
1.从考点频率看,几何图形中的性质综合问题,是高频考点、也是必考点。
2.从题型角度看,以解答题的最后一题或最后二题为主,分值12分左右,着实不少!题型一 线段最值问题【例1】(2024·四川成都·一模)如图1,在四边形ABFE 中,90F ∠=︒,点C 为线段EF 上一点,使得AC BC ⊥,24AC BC ==,此时BF CF =,连接BE ,BE AE ⊥,且AE BE =.(1)求CE 的长度;(2)如图2,点D 为线段AC 上一动点(点D 不与A ,C 重合),连接BD ,以BD 为斜边向右侧作等腰直角三角形BGD .①当DG AB ∥时,试求AD 的长度;②如图3,点H 为AB 的中点,连接H G ,试问H G 是否存在最小值,如果存在,请求出最小值;如果不存在,请说明理由.【答案】(2)①103;②2【分析】(1)取AB 的中点H ,连接,EH HC ,证明FEB CAB ∠=∠,得出1tan tan 2FB FEB CAB EF ∠==∠=则12BF EF =,进而根据CE EF CF =−(2)①如图所示,过点D 作DM EF ⊥于点M ,过点D 作DN AB ⊥于点N ,证明DBC GBF ∽得出DC ,即可得出DM GF =,证明DMG GFB ≌,进而证明G 在EF 上,根据已知条件证明D 在EB上,然后解直角三角形,即可求解;②如图所示,过点H 作HP EF ⊥于点P ,连接EH ,由①可得G 在EF 上运动,当HG EF ⊥时,H G 取得最小值,即,G P 重合时,HP 的长即为HG 的最小值,由①可得103AT =,求得sin ETA ∠=45HEF ETA α∠=+︒=∠,即可求解.【详解】(1)解:如图所示,取AB 的中点H ,连接,EH HC ,∵BF CF =,90F ∠=︒,∴45BCF ∠=︒,BC , 又∵AC BC ⊥ ∴45ECA ∠=︒ ∵AE BE =,BE AE ⊥ ∴45EBA ∠=︒ ∴45ECA ABE ∠=∠=︒ ∴FEB CAB ∠=∠ ∵24AC BC ==, ∴2BC =∴BF CF = ∴1tan 2CB CAB AC ∠== ∴1tan tan 2FB FEB CAB EF ∠==∠= ∴12BF EF =∴EF =∴CE EF CF =−(2)①如图所示,过点D 作DM EF ⊥于点M ,过点D 作DN AB ⊥于点N ,由(1)可得45ACE ABE ∠=∠=︒ ∴CDM V 是等腰直角三角形,∴CD ,∵,CBF DBG 都是等腰直角三角形,∴CB DBBF BG==∴BD BGBC BF= 又∵DBG CBF ∠=∠ ∴DBC GBF ∠=∠ ∴DBC GBF ∽∴DC DBGF GB==∴DC ∴DM GF = 在,DMG GFB 中,DM GF DMG F DG BG =⎧⎪∠=∠⎨⎪=⎩∴DMG GFB ≌ ∴MGD FBG ∠=∠ ∵90FBG FGB ∠+∠=︒∴90MGD FGB ∠+∠=︒ 又∵90DGB ∠=︒ ∴180MGF ∠=︒ ∴G 在EF 上,∵DG AB ∥,90DGB ∠=︒ ∴90GBA ∠=︒∵45,45ABE DBG ABD ∠=︒∠=︒=∠ ∴D 在EB 上, ∵1tan 2CAB ∠=,∴12DN AN =,则AD ∵,45DN AB ABE ⊥∠=︒ ∴DN DB = ∴3AB DN =, ∵4AC =,2CB =∴AB ==∴13DN AB ==∴103AD ==, ②如图所示,过点H 作HP EF ⊥于点P ,连接EH ,由①可得G 在EF 上运动,∴当HG EF ⊥时,HG 取得最小值,即,G P 重合时,HP 的长即为H G 的最小值, 设,AC EB 交于点T ,即与①中点D 重合,由①可得103AT =∵AB =∴AE 12EH AB ==∴sin 3AE ETA AT ∠=== 设FEB CAB α∠=∠= 则45HEF ETA α∠=+︒=∠,在Rt PEH △中,sin sin 102PH HEF EH ETA EH =∠⨯=∠⨯= 【点睛】证明G 点在EF 上是解题的关键.【例2】(2024·天津红桥·一模)在平面直角坐标系中,点()0,0O ,()2,0A , (2,B ),C ,D 分别为OA ,OB 的中点.以点O 为中心,逆时针旋转OCD ,得OC D '',点C ,D 的对应点分别为点C ',D ¢.(1)填空∶如图①,当点D ¢落在y 轴上时,点D ¢的坐标为_____,点C '的坐标为______; (2)如图②,当点C '落在OB 上时, 求点D ¢的坐标和 BD '的长; (3)若M 为C D ''的中点,求BM 的最大值和最小值(直接写出结果即可). 逆时针旋转OCD ,得OC D '',知为中心,逆时针旋转OCD,得OC D'',可得(2,23B为中心,逆时针旋转OCD,得OC D'',()A,2,0()A2,0,(2,23 B是AOB的中位线,为中心,逆时针旋转OCD,得OC D'','==,D CD3M是C'(2,23B1.(2024·山东济宁·模拟预测)已知,四边形ABCD 是正方形,DEF 绕点D 旋转(DE AB <),90EDF ∠=︒,DE DF =,连接AE CF ,.(1)如图1,求证:ADE CDF ≅; (2)直线AE 与CF 相交于点G .①如图2,BM AG ⊥于点M ,⊥BN CF 于点N ,求证:四边形BMGN 是正方形;②如图3,连接BG ,若6AB =,3DE =,直接写出在DEF 旋转的过程中,线段BG 长度的最小值为 . 再证明AMB CNB ≅可得MB ,证明BGM 是等腰直角三角形,然后求出【详解】(1)证明:四边形ABCD 是正方形,AD DC ∴=,90ADC ∠=︒,DE DF =,90EDF ∠=︒,ADC EDF ∴∠=∠,ADE CDF \Ð=Ð,在ADE V 和CDF 中,DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩, SAS ADE CDF ∴()≌. (2)解:①证明:如图2中,设AG 与CD 相交于点P ,90ADP ∠=︒, 90DAP DPA ∴∠+∠=︒,ADE CDF ≅,DAE DCF ∴∠=∠,DPA GPC ∠∠=,90DAE DPA GPC GCP ∠∠∠∠∴+=+=︒, 90PGN ∠∴=︒,BM AG ⊥,BN GN ⊥,∴四边形BMGN 是矩形,90MBN ∴∠=︒,四边形ABCD 是正方形,AB BC ∴=,90ABC MBN∠∠==︒,ABM CBN ∴∠=∠,又90AMB BNC ∠∠==︒,AMB CNB ∴≅,MB NB ∴=,∴矩形BMGN 是正方形;∵DAH BAM ABM ∠+∠=∠∴DAH ABM ∠=∠,又∵AD BA =,DHA ∠∴AMB DHA ≌△△, BM AH ∴=,2AH AD =DH ∴最大时,可知,BGM 是等腰直角三角形,23⨯=(1)若AC AB AD BC >⊥,,当点E 在线段AC 上时,AD BE ,交于点F ,点F 为BE 中点.①如图1,若37BF BD AD ===,,求AE 的长度;②如图2,点G 为线段AF 上一点,连接GE 并延长交BC 的延长线于点H .若点E 为GH 中点,602BAC DAC EBC ∠=︒∠=∠,,求证:12AG DF AB +=. (2)如图3,若360AC AB BAC ︒==∠=,.当点E 在线段AC 的延长线上时,连接DE ,将DCE △沿DC 所在直线翻折至ABC 所在平面内得到DCM △,连接AM ,当AM 取得最小值时,ABC 内存在点K ,使得ABK CAK ∠=∠,当KE 取得最小值时,请直接写出2AK 的值.的长,证明(AAS)FDB FGE ≌AD BC EG AD ⊥⊥,, 90BDF ∴∠=︒,EGF ∠=BDF EGF ∴∠=∠,在Rt BDF △中,90BDF ∠=点(AAS)FDB FGE ∴≌3BD GE ∴==DFAD=,7∴=AG ADRt AGE中,2⊥,AD BC90∴∠=︒,ADC点E为GH的中点,∴=,GE HE在AGE和KHE△中,=AE KE∴≌(SAS) AGE KHE∴∠=∠34∠=DAC∴设EBC∠点和KEF中,(SAS)AFB KEF ∴≌89AB FK ∴=∠=∠,BAC ∠=Rt FDM 中,1由题意可知:160∠=︒,AC 30CAM ∴∠=︒,1322CM AC ∴==, ABK ∠=ABK ∴∠+∠EKQ EOA ∴∽,KE KQ QE(1)如图①,在ABC 中,点M ,N 分别是AB ,AC 的中点,若BC =MN 的长为__________. 问题探究:(2)如图②,在正方形ABCD 中,6AD =,点E 为AD 上的靠近点A 的三等分点,点F 为AB 上的动点,将AEF △折叠,点A 的对应点为点G ,求CG 的最小值. 问题解决:(3)如图③,某地要规划一个五边形艺术中心ABCDE ,已知120ABC ∠=︒,60BCD ∠=︒,40m AB AE ==,80m BC CD ==,点C 处为参观入口,DE 的中点P 处规划为“优秀”作品展台,求点C 与点P 之间的最小距离.是ABC 的中位线,由中位线的性质,即可求解,Rt EDC 中,根据勾股定理,求出∵点E为AD上的靠近点∴11633AE AD==⨯=在Rt EDC中,EC 根据折叠的性质,【问题提出】(1)如图1,点D 为ABC 的边BC 上一点,连接2,,3BD AD BDA BAC AB ∠=∠=,若ABD △的面积为4,则ACD 的面积为______; 【问题探究】(2)如图2,在矩形ABCD 中,6,5AB BC ==,在射线BC 和射线CD 上分别取点E F 、,使得65BE CF =,连接AE BF 、相交于点P ,连接CP ,求CP 的最小值; 【问题解决】(3)如图3,菱形ABCD 是某社区的一块空地,经测量,120AB =米,60ABC ∠=︒.社区管委会计划对该空地进行重新规划利用,在射线AD 上取一点E ,沿BE CE 、修两条小路,并在小路BE 上取点H ,将CH 段铺设成某种具有较高观赏价值的休闲通道(通道宽度忽略不计),根据设计要求,BHC BCE ∠=∠,为了节省铺设成本,要求休闲通道CH 的长度尽可能小,问CH 的长度是否存在最小值?若存在,求出CH 长度的最小值;若不存在,请说明理由.994CBAABDSS ==,即可得到ACD 的面积;为直径的O 上交O 于点P )证明,CBH EBC ∽得到,再证明,ABH EBA ∽得到在O 的劣弧与O 相交于点ABDCBAS S=994CBAABDSS ==,∴ACD 的面积为9CBAABDS S−=故答案为:为直径的O 上运动,交O 于点P,作ABH 的外接圆O ,连接∴,CBH EBC ∽ BC BH∴,ABH EBA ∽ 120AHB EAB ∠=∠=在O 的劣弧120=︒在AOB 中,则1602BM AM AB ===米, 与O 相交于点题型二 线段和的最小值问题【例1】(2024·四川达州·模拟预测)【问题发现】(1)如图1,在OAB 中,3OB =,若将OAB 绕点O 逆时针旋转120︒得OA B '',连接BB ',则BB '=________. 【问题探究】(2)如图2,已知ABC 是边长为BC 为边向外作等边BCD △,P 为ABC 内一点,连接AP BP CP ,,,将BPC △绕点C 逆时针旋转60︒,得DQC △,求PA PB PC ++的最小值; 【实际应用】(3)如图3,在长方形ABCD 中,边1020AB AD ==,,P 是BC 边上一动点,Q 为ADP △内的任意一点,是否存在一点P 和一点Q ,使得AQ DQ PQ ++有最小值?若存在,请求出此时PQ 的长,若不存在,请说明理由.将AQD 绕点BC ⊥在OAB 中,3OB =,将OAB 绕点120BOB '∴∠=︒,3OB OB '==,OBB OB B ''∴∠=∠,OBB '∠+OC BB ⊥OCB '∴∠将∴++=+PA PB PC PA∴当点D、Q、P、A⊥连接AD,作DE AC∠=,ABC边长为DCBDCE BCA∴∠=∠=60)如图所示,将AQD绕点,90EA︒=【例2】(2024·贵州毕节·一模)在学习了《图形的平移与旋转》后,数学兴趣小组用一个等边三角形继续进行探究.已知ABC 是边长为2的等边三角形.(1)【动手操作】如图1,若D 为线段BC 上靠近点B 的三等分点,将线段AD 绕点A 逆时针旋转60︒得到线段AE ,连接CE ,则CE 的长为________;(2)【探究应用】如图2,D 为ABC 内一点,将线段AD 绕点A 逆时针旋转60︒得到线段AE ,连接CE ,若,,B D E本题主要考查了等边三角形的性质与判定,矩形的性质与判定,旋转的性质,勾股定理,含度角的直角三角形的性质,解题的关键在于利用旋转构造等边三角形,从而把三条不在一条直线的线段之和的问题,转换成几点共线求线段的最值问题是解题的关键.三点共线,求证:EB 平分AEC ∠;(3)【拓展提升】如图3,若D 是线段BC 上的动点,将线段AD 绕点D 顺时针旋转60︒得到线段DE ,连接CE .请求出点D 在运动过程中,DEC 的周长的最小值. 证明BAD CAE ≌,的三等分点和ABC 是边长为ADB AEC =∠60BEC ∠=︒EB(3)由ABD ACE ≌△△,得CE BD =,可得DEC 的周长BC DE =+,而DE AD =,知AD 的最小时,DEC的周长最小,此时AD BC ⊥,即可求得答案.∵ABC 是等边三角形,AB AC =,∴SAS ABD ACE ≌()BD CE =;的三等分点,且ABC 是边长为∵ABC 是等边三角形,AB AC =,∴SAS ABD ACE≌(),120ADB AEC ∠=∠=上时,DEC 的周长存在最小值,如图:∵ABD ACE ≌△△, ∴CE BD =,∴DEC 的周长DE CE =++∴当点D 在线段BC 上时,DEC 的周长∵DEC 为等边三角形,DE AD =,的最小时,DEC 的周长最小,此时∴DEC 的周长的最小值为【点睛】本题考查几何变换综合应用,旋转性质、涉及等边三角形的性质,全等三角形的判定和性质,垂1.(2024·陕西·二模)在平面直角坐标系中,A 为y 轴正半轴上一点,B 为x 轴正半轴上一点,且4OA OB ==,连接AB .(1)如图1,C 为线段AB 上一点,连接OC ,将OC 绕点O 逆时针旋转90︒得到OD ,连接AD ,求AC AD +的值.(2)如图2,当点C 在x 轴上,点D 位于第二象限时,90ADC ∠=︒,且AD CD =,E 为AB 的中点,连接DE ,试探究线段AD DE +是否存在最小值?若存在,求出AD DE +的最小值;若不存在,请说明理由.≌,可得出点,证明AND CMDAOC的平分线对称,由∴AND CMD≌,DN DM=,P大值和最小值分别是______和______;(2)如图2,在矩形ABCD中,4AB=,6AD=,点P在AD上,点Q在BC上,且AP CQ=,连接CP、QD,求PC QD+最小时AP的长;(3)如图3,在ABCDY中,10AB=,20AD=,点D到AB的距离为动点E、F在AD边上运动,始终保持3EF=,在BC边上有一个直径为BM的半圆O,连接AM与半圆O交于点N,连接CE、FN,求CE EF FN++的最小值.()SASABP CDQ≌=的O 外有一点在O 上, 如图,当点P 在AO 的延长线上时,此时PA 的最大值为:PO OA +故答案为:11;3;(2)延长BA 至点B ',使AB ∵在矩形ABCD 中,4AB =,∴DAB BAP CBA DCQ '∠=∠=∠=∠在ABP 和CDQ 中,AB CD =∴()SAS ABP CDQ ≌Rt B BC '中,AB P BB ''=∠ (3)如图,过点F 作FG EC ∥,交BC OG ',NO ,∵在ABCD Y 中,10AB =,20AD =,点∴AD BC ∥,即EF CG ∥,BC AD =EFGC【点睛】本题考查圆的基本性质,全等三角形的判定和性质,相似三角形的判定和性质,矩形的性质,平行四边形的判定和性质,对称的性质,勾股定理,三角形三边关系定理,两点之间线段最短等知识点.灵活运用所学知识、弄清题意并作出适当辅助线是解题的关键.3.(2024·陕西西安·三模)【问题提出】(1)如图①,AB 为半圆O 的直径,点P 为半圆O 的AB 上一点,BC 切半圆O 于点B ,若10AB =,12BC =,则CP 的最小值为 ; 【问题探究】(2)如图②,在矩形ABCD 中,3AB =,5BC =,点P 为矩形ABCD 内一点,连接PB 、PC ,若矩形ABCD 的面积是PBC 面积的3倍,求PB PC +的最小值; 【问题解决】(3)如图③,平面图形ABCDEF 为某校园内的一片空地,经测量,AB BC ==米,=60B ∠︒,150BAF BCD ∠=∠=︒,DE DC ⊥,20CD =米,劣弧E F 所对的圆心角为90︒,E F 所在圆的圆心在AF 的延长线上,10AF =米.某天活动课上,九(1)班的同学准备在这块空地上玩游戏,每位同学在游戏开始前,在BC 上选取一点P ,在弧E F 上选取一点Q ,并在点P 和点Q 处各插上一面小旗,从点A 出发,先到点P 处拔下小旗,再到点Q 处拔下小旗,用时最短者获胜.已知晓雯和晓静的跑步速度相同,要使用时最短,则所跑的总路程()AP PQ +应最短,问AP PQ +是否存在最小值?若存在,请你求出AP PQ +的最小值;若不存在,请说明理由.交O于点P⊥PH BC交O于点P点P为半圆O的AB上一点,∴当点P与点P不重合时,1当点P与点P重合时,BC切半圆∴∠=ABC=OB OP矩形ABCD 的面积是PBC 面积的13553PBCS∴=⨯⨯=CF PH =又5BC =,60ABC ∠=︒,AB BC ==ABC ∴是等边三角形, 60BAC BCA ∴∠=∠=︒,150BAF BCD ∠=∠=︒,DE AA M '∴和CMN ∴∠=点'A Q OQ+∴的最小值为A Q'ABC为等边三角形,点∴点为BC△,E G分别作,,⊥⊥与EF交于点F,连接CF.EF AD FG AB FG特例感知(1)以下结论中正确的序号有______;ED CF BG为边围成的三角形不是直①四边形AGFE是矩形;②矩形ABCD与四边形AGFE位似;③以,,角三角形;类比发现(2)如图2,将图1中的四边形AGFE绕着点A旋转,连接BG,观察CF与BG之间的数量关系和位置关系,并证明你的发现;拓展应用(3)连接CE ,当CE 的长度最大时, ①求BG 的长度;②连接,,AC AF CF ,若在ACF △内存在一点P ,使CP AP ++的值最小,求CP AP ++的最小值.先证明APF AKL ∽,得到∴HF DE =,CH BG =,∴CHF 是直角三角形,∵四边形ABCD 是矩形,∴43AB CD ==,AD =∴228AC AB BC =+=,则由(2)知,90CEF ∠=︒,∵2247CF CE EF =+=,根据旋转,可得30PAF KAL ∠=∠=,根据两边对应成比例且夹角相等可得APF AKL ∽, ∴3KL PF =,过P 作PS AK ⊥于S ,则12PS AP =题型三 面积的最小值问题【例1】(新考法,拓视野)(2024·陕西西安·一模)【问题提出】(1)如图1,已知在边长为5的等边ABC 中,点D 在边BC 上,3BD =,连接AD ,则ACD 的面积为 ; 【问题探究】(2)如图2,已知在边长为6的正方形ABCD 中,点E 在边BC 上,点F 在边CD 上,且45EAF ∠=︒,若5EF =,求AEF △的面积; 【问题解决】(3)如图3是某座城市廷康大道的一部分,因自来水抢修在4AB =米,AD =ABCD 区域内开挖一个AEF △的工作面,其中B 、F 分别在BC CD 、边上(不与B 、C 、D 重合),且60EAF ∠=︒,为了减少对该路段的拥堵影响,要求AEF △面积最小,那么是否存在一个面积最小的AEF △?若存在,请求出AEF △面积的最小值;若不存在,请说明理由.,证明()SAS ABG ADF ≌,再证明()SAS AEF AEG ≌,得到ABG ,则)()33AEF AEG SS==最小值最小值∵ABC 是边长为 ∴()SAS ABG ADF ≌∴()SAS AEF AEG ≌,得到ABG , )()33AEF AEG SS==最小值最小值【例2】(2024·陕西西安·二模)图形旋转是解决几何问题的一种重要方法.如图1,正方形ABCD 中,E F 、分别在边AB BC 、上,且45EDF ∠=︒,连接EF ,试探究AE CF EF 、、之间的数量关系.解决这个问题可将ADE V 绕点D 逆时针旋转90︒到CDH △的位置(易得出点H 在BC 的延长线上),进一步证明DEF 与DHF △全等,即可解决问题.(1)如图1,正方形ABCD 中,45,3,2EDF AE CF ∠=︒==,则EF =______;(2)如图2,正方形ABCD 中,若30EDF ∠=︒,过点E 作EM BC ∥交DF 于M 点,请计算AE CF +与EM 的比值,写出解答过程;(3)如图3,若60EDF ∠=︒,正方形ABCD 的边长8AB =,试探究DEF 面积的最小值. 进一步证明DEF,,,D F H G 四点共圆;进而可得30FHG ∠=,根据1tan 30AE CF CH CF FH EM GH GH ++====︒(3)过点E 作EK CD ⊥于K ,交DF 于M ,作FT EK ⊥于T ,得出 4DEFS EM =,进而根据(2)的方法得出EM GH =,根据FC AE CH ==时,面积最小,得出32OF =− 【详解】(1)解:∵将ADE V 绕点D 逆时针旋转90︒, ∴90DCH A DCB ∠=∠=︒=∠,DH DE HDC EDA =∠=∠, ∴点H 在BC 的延长线上, ∵四边形ABCD 是正方形 ∴90ADC ∠=︒, ∵45EDF ∠=︒,∴45HDF CDH FDC ADE FDC EDF ∠=∠+∠=∠+∠=︒=∠ 又∵DF DF =,∴DEF ()SAS DHF ≌,∴235EF FH FC CH FC AE ==+=+=+=, 故答案为:5.(2)解:将ADE V ,DEM △绕点D 逆时针旋转90︒,得,DCH DHG∴,AED CHD DEM DHG ∠=∠∠=∠, ∵EM BC ∥,则EM AB ⊥, ∴90AEM ∠=︒,∴90CHG CHD DHG AED DEM AEM ∠=∠+∠=∠+∠=∠=︒, ∵30EDF ∠=︒,EM BC ∥则EM AD ∥, ∴ADE CDH ∠=∠,30GDH MDE ∠=∠=︒, ∵EM BC ∥, ∴EMF DFC ∠=∠,∴180EMD EMF EMD DFC ∠+∠=∠+∠=︒, 即180DFC DGH ∠+∠=︒, ∴,,,D F H G 四点共圆; ∴30GFH GDH ∠=∠=︒, 又30FHG ∠=︒∴1tan 30AE CF CH CF FH EM GH GH ++====︒(3)如图,过点E 作EK CD ⊥于K ,交DF 于M ,作FT EK ⊥于T ,90FTK TKC BCD ∠=∠=∠=︒∴四边形CFTK 是矩形, FT CK ∴=8DK CK DK FT ∴+=+= 111()4222DEFEMDEMFSSSEM DK EM FT EM DK FH EM ∴=+=⋅+⋅=+=同(2)将ADE V ,DEM △绕点D 逆时针旋转90︒,得,DCH DHG , 可得60GFH EDM ∠=∠=︒,EM GH = 取得最小值时,DEF 的面积最小,∵2220−=≥,∴FH x y =+≥ 当且仅当x y =时取得等于号, 此时FC AE CH ==, 设,,,D F H G 的圆心为O , ∵DC FH ⊥,FC CH =, ∴DC 经过点O ,∴OF OD =,sin 602OC OF =︒= ∵8OD OC +=8OF +=解得:32OF =−∴232FH FC OF ===−∴48GH =,∴()44448192DEFSEM GH ====,即DEF 面积的最小为192.【点睛】本题考查了旋转的性质,正方形的性质、全等三角形的判定与性质、四点共圆等知识,解直角三角形,熟练掌握旋转的性质是解题的关键.1.(2023·陕西西安·一模)问题发现(1)在ABC 中,2AB =,60C ∠=︒,则ABC 面积的最大值为 ;(2)如图1,在四边形ABCD 中,6AB AD ==,90BCD BAD ∠=∠=︒,8AC =,求BC CD +的值. 问题解决(3)有一个直径为60cm 的圆形配件O ,如图2所示.现需在该配件上切割出一个四边形孔洞OABC ,要求60O B ∠=∠=︒,OA OC =OABC 的面积尽可能小.试问,是否存在符合要求的面积最小的四边形OABC ?若存在,请求出四边形OABC 面积的最小值及此时OA 的长;若不存在,请说明理由.为弦的确定的圆上,作ABC 的外接圆,可得当点时,ABC 的面积最大,求出,再根据三角形的面积公式计算即可;将ABC 绕点A 逆时针旋转、D 、E 在同一条直线上,求出BCES,可得要使四边形面积最小,就要使BCE 的面积最大,然后由(时,BCE 的面积最)的方法求出BCE 面积的最大值,可得四边形,根据OA 如图,作ABC 的外接圆,∴当点C 在C '的位置,即时,ABC 的面积最大,∴C A C B ''=,BD =∴ABC '△是等边三角形,∴ABC 面积的最大值为)如图,将ABC 绕点∴B ADE ∠=∠,BAC ∠∵6AB AD ==,BCD ∠∴180B ADC ∠+∠=︒,∵60AOC ∠=︒,OA OC =∴将AOB 绕O 点顺时针旋转至COE ,连接∴60BOE ∠=︒,OE OB =∴BOE △是等边三角形,AOBBCOSS+COEBCOSS+ BOE BCES S− BCESBCES,的面积最小,就要使BCE 的面积最大,作BCE 的外接圆I ,点F 是I 上一点,CF 交由(1)可知,当CF 是直径,且CF BE ⊥时,BCE 的面积最大,∴BCE 面积的最大值为150BCES=(1)如图①,已知ABC 是面积为AD 是BAC ∠的平分线,则AB 的长为______. 问题探究:(2)如图②,在ABC 中,90C ∠=︒,AC BC =,4AB =,点D 为AB 的中点,点E ,F 分别在边AC ,BC 上,且90EDF ∠=︒.证明:DE DF =.问题解决:(3)如图③,李叔叔准备在一块空地上修建一个矩形花园ABCD ,然后将其分割种植三种不同的花卉.按照他的分割方案,点P ,Q 分别在AD ,BC 上,连接PQ 、PB 、PC ,60BPC ∠=︒,E 、F 分别在PB 、PC 上,连接QE 、QF ,QE QF =,120EQF ∠=︒,其中四边形PEQF 种植玫瑰,ABP 和PCD 种植郁金香,剩下的区域种植康乃馨,根据实际需要,要求种植玫瑰的四边形PEQF 的面积为2,为了节约成本,矩形花园ABCD 的面积是否存在最小值?若存在,请求出矩形ABCD 的最小面积,若不存在,请说明理由.)设ABC 的边长为EQG ,根据四边形则当PQ BC ⊥时,矩形ABCD 的面积最小,根据2ABCD PEQF S S =四边形四边形,即可求解.【详解】解:(1)∵ABC 是面积为AD 是BAC ∠的平分线, ∴12BD CD AB ==设ABC 的边长为a∴AD ==∴2112224ABCS BC AD a =´=´´=∴24a =解得:4a =, 故答案为:4.(2)如图所示,连接CD ,∵在ABC 中,90C ∠=︒,AC BC =,4AB =,点D 为AB 的中点, ∴CD AD =,90ADC ∠=︒,45A DCF ∠=∠=︒ 又∵90EDF ∠=︒∴ADE ADC CDE EDF EDC CDF ∠=∠−∠=∠−∠=∠ 在,ADE CDF △△中,45A DCF ADE CDF AD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴ADE CDF V V ≌ ∴DE DF =; (3)如图所示,∵60BPC ∠=︒,120EQF ∠=︒, ∴36060120180PFQ PEQ ∠+∠=︒−︒−︒=︒ 将QFP △绕点Q 逆时针旋转120︒,得到EQG , ∴,,P E G 三点共线,∴四边形PEQF 的面积等于PQG , 又∵120,PQG PQ GQ ∠=︒=,∴30QPG QGP ∠=∠=︒过点Q 作QN PG ⊥于点N ,则12QN PQ =设PQ b =,则1,22NQ b PN ==∴2PG PN ==∴2111222PQGSPG NQ b =⨯=⨯=∵四边形PEQF 的面积为 ∴16b =,即16PQ =,如图所示,作QM PM ⊥于点M ,∵30EPQ FPQ ∠=∠=︒,QM PM ⊥,QN PG ⊥,则QN QM =, 在,ENQ FMQ 中,QN QM EQ FQ =⎧⎨=⎩∴()HL ENQ FMQ ≌, 同理可得PNQ PMQ ≌ 则2PNQPEQF S S=四边形∴PEQF PNQM S S =四边形四边形,作点Q 关于PE 的对称点T ,连接PT ,则PTQ 是等边三角形,则PTQS=如图所示,依题意,当PQ BC ⊥时,矩形ABCD 的面积最小,此时,E F 与,N M 重合,,∴22ABCD PEQF S S ==⨯四边形四边形∴矩形ABCD 的最小面积为2【点睛】本题考查了全等三角形的性质与判定,等边三角形的性质与判定,等腰三角形的性质与判定,勾股定理,旋转的性质,综合运用以上知识是解题的关键.3.(2024·陕西榆林·二模)(1)如图1,AB CD ∥,1,2AB CD ==,AD ,BC 交于点E ,若4=AD ,则AE = ;(2)如图2,矩形ABCD 内接于O , 2,AB BC ==点 P 在AD 上运动,求 PBC 的面积的最大值; (3)为了提高居民的生活品质,市政部门计划把一块边长为 120米的正方形荒地 ABCD (如图3)改造成一个户外休闲区,计划在边AD ,BC 上分别取点P ,Q ,修建一条笔直的通道PQ ,要求 2CQ AP =,过点 B 作 BE PQ ⊥于点E ,在点E 处修建一个应急处理中心,再修建三条笔直的道路BE CE DE ,,,并计划在 CDE 内种植花卉, DEP 内修建老年活动区, BCE 内修建休息区,在四边形ABEP 内修建儿童游乐园.问种植花卉的 CDE 的面积是否存在最小值? 若存在,求出最小值;若不存在,请说明理由.得ABE DCE ∽,得对应成比例的线段,于是得到结论;时,PBC 的面积有最大值,解直角三角形求出PBC 的高即可得到结论;于点M ,作BME 的外接圆O ,过点OF DC ⊥₂E CD ₂的面积最小. ()∥AB CD DCE ,是O的直径.₂的面积最大.P BC上任意另取一点P₁PBC的面积最大.Rt OBE中,.S=PBC。
初三数学专题一~面积问题
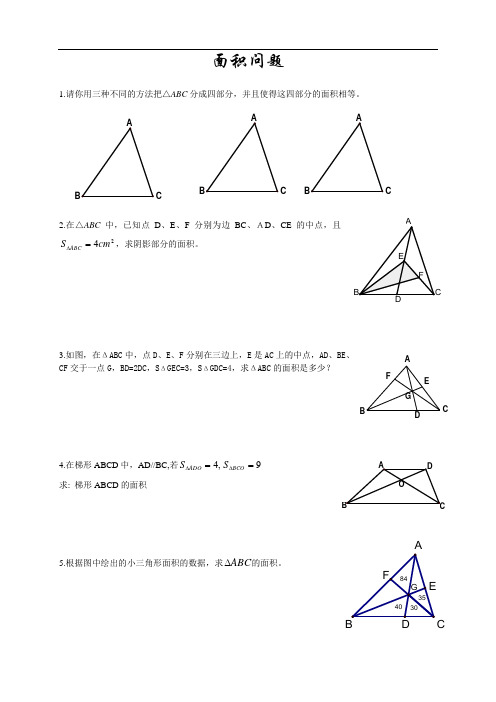
面积问题1.请你用三种不同的方法把△ABC 分成四部分,并且使得这四部分的面积相等。
2.在△ABC 中,已知点D 、E 、F 分别为边BC 、AD 、CE 的中点,且24cm S ABC =∆,求阴影部分的面积。
3.如图,在ΔABC 中,点D 、E 、F 分别在三边上,E 是AC 上的中点,AD 、BE 、CF 交于一点G ,BD=2DC ,S ΔGEC=3,S ΔGDC=4,求ΔABC 的面积是多少?4.在梯形ABCD 中,AD//BC,若9,4==∆∆BCO AD O S S 求: 梯形ABCD 的面积5.根据图中绘出的小三角形面积的数据,求ABC ∆的面积。
A B C DEFGCCCCA6.(1)等腰三角形ABC 中,AB=AC=5,BC=8,则腰AB 上的高为__________ (2)在直角三角形ABC 中,,90︒=∠C AC=12,BC=5,求斜边AB 的高_________(3)直角ABC ∆三边长分别是1,+x x 和5,则ABC ∆的周长为 ,ABC ∆的面积为 。
7.已知等边三角形ABC 和点P ,设点P 到ABC ∆三边AB 、AC 、BC 的距离分别为321h h h 、、,ABC ∆的高为h ,如图,“若点P 在三角形的边BC 上,此时03=h ,可得出结论是h h h h =++321”请解决下列问题:当点P 在ABC ∆内,点P 在ABC ∆外,这两种情况时,上述结论是否还成立?若成立,请给予证明;若不成立,321h h h 、、和h 之间又有什么关系?给出你的猜想。
8.如图所示,E 是矩形ABCD 边AD 上一点,且BE=ED ,P 是对角线BD 上任一点,PF•⊥BE ,PG ⊥AD ,垂足分别为F ,G .试探索线段PF ,PG ,AB 之间的数量关系,并证明之.9.已知Rt △ABC 中,∠C =90°,若a +b =14cm ,c =10cm ,则Rt △ABC 的面积是( )A. 24cm 2B. 36cm 2C. 48cm 2D. 60cm 210. 如图,在四边形ABCD 中,AB =1,BC =5,CD =4,AD =22,且AB ⊥AD 。
初三数学求面积练习题

初三数学求面积练习题题1:矩形的面积计算已知矩形的长为6cm,宽为4cm,求其面积。
解答:给定矩形的长为6cm,宽为4cm,可以使用公式计算其面积。
矩形的面积公式为“长度 ×宽度”。
将已知值代入公式计算,可得:面积 = 6cm × 4cm = 24cm²。
因此,该矩形的面积为24平方厘米。
题2:正方形的面积计算已知正方形的边长为5cm,求其面积。
解答:给定正方形的边长为5cm,可以利用正方形面积的公式计算。
正方形的面积公式为“边长 ×边长”。
将已知值代入公式计算,可得:面积 = 5cm × 5cm = 25cm²。
因此,该正方形的面积为25平方厘米。
题3:三角形的面积计算已知三角形的底边长为8cm,高为6cm,求其面积。
解答:给定三角形的底边长为8cm,高为6cm,可以使用三角形面积的公式计算。
三角形的面积公式为“底边长 ×高÷ 2”。
将已知值代入公式计算,可得:面积 = 8cm × 6cm ÷ 2 = 24cm²。
因此,该三角形的面积为24平方厘米。
题4:梯形的面积计算已知梯形的上底长为10cm,下底长为6cm,高为4cm,求其面积。
解答:给定梯形的上底长为10cm,下底长为6cm,高为4cm,可以使用梯形面积的公式计算。
梯形的面积公式为“(上底长 + 下底长) ×高÷ 2”。
将已知值代入公式计算,可得:面积 = (10cm + 6cm) × 4cm ÷ 2 = 32cm²。
因此,该梯形的面积为32平方厘米。
题5:圆的面积计算已知圆的半径为5cm,求其面积。
解答:给定圆的半径为5cm,可以使用圆面积的公式计算。
圆的面积公式为“π × 半径²”。
由于π是一个无理数,通常取近似值3.14。
将已知值代入公式计算,可得:面积 = 3.14 × 5cm × 5cm = 78.5cm²。
中考数学几何图形与面积计算专题

中考数学几何图形与面积计算专题在中考数学中,几何图形与面积计算是一个重要的考点,它不仅要求我们掌握基本的几何图形性质,还需要熟练运用各种面积计算公式来解决问题。
这一专题对于培养我们的空间想象力、逻辑思维能力和数学运算能力都具有重要意义。
首先,让我们来回顾一下常见的几何图形及其面积公式。
三角形是最基本的几何图形之一。
对于一个底为 b,高为 h 的三角形,其面积 S = 1/2 × b × h。
如果已知三角形的两边 a、b 及其夹角 C,那么面积可以通过 S = 1/2 × a × b × sinC 来计算。
矩形的面积计算则相对简单,长为 a,宽为 b 的矩形面积 S = a × b。
平行四边形的面积等于底乘以高,即 S = a × h,其中 a 是底边长,h 是这条底边对应的高。
梯形的面积公式为 S = 1/2 ×(上底+下底)×高。
圆形的面积 S =πr²,其中 r 是圆的半径。
接下来,我们通过一些具体的例子来看看如何运用这些公式解决问题。
例 1:如图,在直角三角形 ABC 中,∠C = 90°,AC = 6,BC =8,求三角形 ABC 的面积。
解:因为∠C = 90°,所以这是一个直角三角形,根据直角三角形的面积公式,S = 1/2 × AC × BC = 1/2 × 6 × 8 = 24 。
例 2:已知平行四边形 ABCD 的底边长为 10,高为 6,求其面积。
解:平行四边形的面积 S =底 ×高= 10 × 6 = 60 。
在解决几何图形面积计算问题时,常常会遇到一些复杂的图形,这时需要我们通过合理的分割或组合,将其转化为我们熟悉的基本图形。
例如,对于一个不规则的多边形,我们可以通过连接对角线,将其分割成若干个三角形,然后分别计算这些三角形的面积,最后相加得到多边形的面积。
初中数学几何模型(九)面积模型
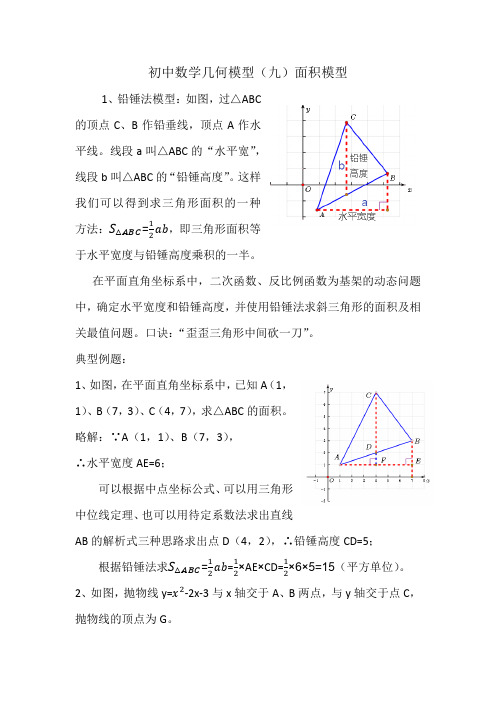
初中数学几何模型(九)面积模型1、铅锤法模型:如图,过△ABC的顶点C、B作铅垂线,顶点A作水平线。
线段a叫△ABC的“水平宽”,线段b叫△ABC的“铅锤高度”。
这样我们可以得到求三角形面积的一种方法:S△ABC=12ab,即三角形面积等于水平宽度与铅锤高度乘积的一半。
在平面直角坐标系中,二次函数、反比例函数为基架的动态问题中,确定水平宽度和铅锤高度,并使用铅锤法求斜三角形的面积及相关最值问题。
口诀:“歪歪三角形中间砍一刀”。
典型例题:1、如图,在平面直角坐标系中,已知A(1,1)、B(7,3)、C(4,7),求△ABC的面积。
略解:∵A(1,1)、B(7,3),∴水平宽度AE=6;可以根据中点坐标公式、可以用三角形中位线定理、也可以用待定系数法求出直线AB的解析式三种思路求出点D(4,2),∴铅锤高度CD=5;根据铅锤法求S△ABC=12ab=12×AE×CD=12×6×5=15(平方单位)。
2、如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C,抛物线的顶点为G。
(1)求△ABC和△BCG的面积;(2)若点D在直线BC下方抛物线上运动,求△BCD面积的最大值。
(3)若点D在直线BC下方抛物线上运动,求四边形ACDB面积的最大值。
2、等积模型:用不同方法表示同一个图形的面积,结果相等。
(1)当所表示的图形是“规则”图形时,不同的方法指的是:①直接用面积公式表示;②用其他图形面积的和或差表示。
(2)当所表示的图形是“不规则”的图形时,不同方法指的是:用割补法来表示。
典型例题:1、在Rt△ABC中,∠C=90°,CD是斜边上的高,用直角三角形的三边表示斜边上的高CD。
解:∵S △ABC =12ch ,S △ABC =12ab ,∴12ch =12ab ,∴h=ab c。
结论:直角三角形斜边上的高等于两直角边的乘积除以斜边。
2、(1)如图①,已知△ABC 中,AB=AC ,点P 是BC 上的一点,PN ⊥AC 于点N ,PM ⊥AB 于点M ,CG ⊥AB 于点G ,求证:CG=PM+PN 。
面积问题中考压轴题

2014年中考解决方案面积类问题学生姓名:上课时间:SSS DCBAtO 1234213tO1234213tO12342133124321OtS一:选择题中的面积问题(一) 分类讨论问题1.如图,Rt △ABC 中,AC=BC =2,正方形CDEF 的顶点D 、F 分别在AC 、BC 边上, C 、D 两点不重合,设CD 的长度为x ,△ABC 与正方形CDE F 重叠部分的面积为y ,则下列图象中能表示y 与x 之间的函数关系的是( )A B C D 2. 如图,在边长为4的正方形ABCD 中,动点P 从A 点出发,以每秒1个单位长度的速度沿AB 向B 点运动,同时动点Q 从B 点出发,以每秒2个单位长度的速度沿BC →CD 方向运动,当P 运动到B 点时,P ,Q 两点同时停止运动.设P 点运动的时间为t ,△APQ 的面积为S ,则S 与t 的函数关系的图象是3. 如图,在直角坐标系xoy 中,已知()01A ,,()0B3,,以线段AB 为边向上作菱形ABCD ,且点D在y 轴上.若菱形ABCD 以每秒2个单位长度的速度沿射线AB 滑行,直至顶点D 落在x 轴上时停止.设菱形落在x 轴下方部分的面积为S ,则表示S 与滑行时间t 的函数关系的图象为y O 12x 1241x 21O y y O 12x 12yO 12x 12y xOABCD第8题图(2)第8题图(1)DCBA Oxy5.如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,点P 以每秒一个单位的速度沿着B —C —A 运动,⊙P 始终与AB 相切,设点P 运动的时间为t ,⊙P 的面积为y ,则y 与t 之间的函数关系图像大致是(二) 特殊值,排除法6.如图,在矩形ABCD 中,AB=2,BC=4.将矩形ABCD 绕点C 沿顺时针方向旋转90°后,得到矩形FGCE (点A 、B 、D 的对应点分别为点F 、G 、E ).动点P 从点B 开始沿BC-CE 运动到点E 后停止,动点Q 从点E 开始沿EF -FG 运动到点G 后停止,这两点的运动速度均为每秒1个单位.若点P 和点Q 同时开始运动,运动时间为x (秒),△APQ 的面积为y ,则能够正确反映y 与x 之 间的函数关系的图象大致是7. 如图,点P 是以O 为圆心,AB 为直径的半圆上的动点,AB=2,设弦AP 的长为x ,△APO 的面积为PCB A第8题图t° ° °° ° ° ° .t O y O yO y t O yty ,则下列图象中,能表示y 与x 的函数关系的图象大致是8. 如图(1),E 为矩形ABCD 边AD 上一点,点P 从点B 沿折线DC ED BE --运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止,它们运动的速度都是s cm /1.如果点P 、Q 同时开始运动,设运动时间为)(s t ,BPQ ∆的面积为)(2cm y ,已知y 与t 的函数关系的图象如图(2)所示,那么下列结论正确的是( ) A. 8AE =B. 100≤≤t 当时,254t y = C. 4sin 5EBC ∠=D. 当s t 12=时,BPQ ∆是等腰三角形(三) 其它类9.如图,在平面直角坐标系xOy 中,(2,0)A ,(0,2)B ,⊙C 的圆 心为点(1,0)C -,半径为1.若D 是⊙C 上的一个动点,线段 DA 与y 轴交于点E ,则△ABE 面积的最大值是 A .2 B . 83C .222+D .222-图(2)y/cm 21440Q 图(1)PDCBA10. 如图,任意四边形ABCD 中,AC 和BD 相交于点O ,把△AOB 、△AOD 、△COD 、△BOC 的面积分别记作S 1 、S 2 、S 3 、S 4,则下列各式成立的是A .S 1 + S 3 = S 2+S 4B .S 3-S 2 = S 4-S 1C .S 1·S 4= S 2·S 3D .S 1·S 3 = S 2·S 411.如图,在矩形ABCD 中,3=AB ,BC=1. 现将矩形ABCD绕点C 顺时针旋转90°得到矩形A B CD ''',则AD 边扫过的 面积(阴影部分)为 A . 21π B. 31π C.41π D. 51π二:填空题中的面积问题(一)同底等高问题12.如图,直角三角形纸片ABC 中,∠ACB =90°,AC=8,BC =6.折叠该纸片使点B 与点C 重合,折痕与AB 、BC 的交点分别 为D 、E . (1) DE 的长为 ;(2) 将折叠后的图形沿直线AE 剪开,原纸片被剪成三块,其中最小一块的面积等于 .13.如图,在正方形ABCD 中,AB =1,E 、F 分别是BC 、CD 边上点,(1)若CE =12CB ,CF =12CD ,则图中阴影部分的面积是 ;(2)若CE =1n CB ,CF =1n CD ,则图中阴影部分的面积是 (用含n 的式子表示,n 是正整数).BA S 1S 2 O S 4S 3DC A14.已知如图,△ABC 和△DCE 都是等边三角形,若△ABC 的边长为1,则△BAE 的面积是 .四边形ABCD 和四边形BEFG 都是正方形,若正方形ABCD 的边长为4,则△FAC 的面积是 . ……如果两个正多边形ABCDE …和BPKGY …是正n (n ≥3)边形,正多边形ABCDE …的边长是2a ,则△KCA 的面积是 .(结果用含有a 、n 的代数式表示)15.如图,对面积为1的△ABC 逐次进行以下操作: 第一次操作,分别延长AB 、BC 、CA 至A 1、B 1、C 1, 使得A 1B =2AB ,B 1C =2BC ,C 1A =2CA ,顺次连接A 1、 B 1、C 1,得到△A 1B 1C 1,记其面积为S 1;第二次操作, 分别延长A 1B 1,B 1C 1,C 1A 1至A 2,B 2,C 2,使得 A 2B 1=2A 1B 1,B 2C 1=2B 1C 1,C 2A 1=2C 1A 1,顺次连接 A 2,B 2,C 2,得到△A 2B 2C 2,记其面积为S 2……, 按此规律继续下去,可得到△A 5B 5C 5,则其面积为 S 5=_________. 第n 次操作得到△A n B n C n , 则△A n B n C n 的面积S n = .16. 如图,已知△ABC 的面积S △ABC =1.在图(1)中,若21111===CACC BCBB ABAA , 则41S 111C B A △=;在图(2)中,若31222===CA CC BC BB AB AA , 则31S 222C B A △=; 在图(3)中,若41333===CA CC BC BB AB AA , 则167S 333C B A △=; 按此规律,若44415AA BB CC AB BC CA ===, 则444A B C S =P H GA E D C E FA D AB E DC G B F若91888===CA CC BC BB AB AA , 则=888C B A △S .(二)相似与同底等高17如图,n +1个边长为2的等边三角形有一条边在同一直线上,设211B D C ∆的面积为1S ,322B D C ∆的面积为2S ,…,1n n n B D C +∆的面积为n S ,则2S = ;n S =____ (用含n 的式子表示).D 4D 3D 2D 1C 5C 4C 3C 2C 1B 54B 3B B 1A……18如图,n +1个上底、两腰长皆为1,下底长为2的等腰梯形的下底均在同一直线上,设四边形P 1M 1N 1N 2面积为S 1,四边形P 2M 2N 2N 3的面积为S 2,……,四边形P n M n N n N n+1的面积记为S n ,通过逐一计算S 1,S 2,…,可得S n = .19已知:如图,在Rt ABC ∆中,点1D 是斜边AB 的中点,过点1D 作11D E AC ⊥于点1E ,连接1BE 交1CD 于点2D ;过点2D 作22D E AC ⊥于点2E ,连接2BE ,交1CD 于点3D ;过点3D 作33D E AC ⊥于点3E ,如此继续,可以依次得到点4D 、5D 、…n D ,分别记11BD E ∆、22BD E ∆、33BD E ∆、…n n BD E ∆的面积 为1S 、2S 、3S …n S .设ABC ∆的面积是1,则1______S =,(第18题)N 1N 2N 3N 4N 5M 1M 2M 3M 4…D 4D 1D 2D 3AB321______nS=(用含n的代数式表示).(三)割补20.如图,P为边长为2的正三角形中任意一点,连接PA、PB、P C,过P点分别做三边的垂线,垂足分别为D、E、F,则PD+PE+PF= ;阴影部分的面积为__________.21如图1,将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1;取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分;取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分;如此下去…,则正六角星形A4F4B4D4C4E4的面积为_________________.22 如图,Rt ABC△中,90ACB∠=,30CAB∠=,2BC=,O H,分别为边AB AC,的中点,将ABC△绕点B顺时针旋转120到11A BC△的位置,则整个旋转过程中线段OH所扫过图1A1B CAF EB CAF EB CDAF EB1C1F1D1E1A1B1C1F1D1图3AHBOC1O1H1A1C部分的面积(即阴影部分面积)为 .24.如图,在Rt ABC △中,90ACB ∠=︒,60A ∠=︒.将ABC △绕直角顶点C 按顺时针方向旋转,得''A B C △,斜边''A B 分别与BC 、AB 相交于点D 、E ,直角边'A C 与AB 交于点F .若2CD AC ==,则ABC △至少旋转度才能得到''A B C △,此时ABC △与''A B C △的重叠部分(即四边形CDEF )的面积为 .三:22题中的面积问题(一) 同底等高相似类FE DB'A'B C25. 已知△ABC 的面积为a ,O 、D 分别是边AC 、BC 的中点.(1)画图:在图1中将点D 绕点O 旋转180︒得到点E , 连接AE 、CE . 填空:四边形ADCE 的面积为 ;(2)在(1)的条件下,若F 1是AB 的中点,F 2是AF 1的中点, F 3是AF 2的中点,…, F n 是AF n -1的中点 (n 为大于1的整数), 则△F 2CE 的面积为 ; △F n CE 的面积为 . 解: (1)画图:图1填空:四边形ADCE 的面积为 .(2)△F 2CE 的面积为 ; △F n CE 的面积为 .26.问题背景(1)如图1,△ABC 中,DE ∥BC 分别交AB ,AC 于D ,E 两点, 过点E 作EF ∥AB 交BC 于点F .请按图示数据填空: 四边形DBFE 的面积S = , △EFC 的面积1S = , △ADE 的面积2S = .探究发现(2)在(1)中,若BF a =,FC b =,DE 与BC 间的距离为h .请证明2124S S S =. 拓展迁移(3)如图2,□DE FG 的四个顶点在△ABC 的三边上,若 △ADG 、△DBE 、△GFC 的面积分别为2、5、3,试利用..(2.) 中的结论....求△ABC 的面积. 图1(二) 利用全等28.阅读材料并解答问题如图①,以Rt △ABC 的直角边AB 、AC 为边分别向外作正方形ABDE 和正方形ACFG ,连结EG ,可以得出结论△ABC 的面积与△AEG 的面积相等.(1)在图①中的△ABC 的直角边AB 上任取一点H ,连结CH ,以BH 、HC 为边分别向外作正方形HBDE 和正方形HCFG ,连结EG ,得到图②,则△HBC 的面积与△HEG 的面积的大小关系为 .(2)如图③,若图形总面积是a ,其中五个正方形的面积和是b ,则图中阴影部分的面积是 . (3)如图④,点A 、B 、C 、D 、E 都在同一直线上,四边形X 、Y 、Z 都是正方形,若图形总面积是m ,正方形Y 的面积是n ,则图中阴影部分的面积是 .F CDABEGGEDCA HZX Y EDABC图① 图② 图③ 图④BCDGF E 图2A30.如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中90,C ∠=︒ 30B E ∠=∠=︒. (1)操作发现如图2,固定△ABC ,使△DEC 绕点C 顺时针旋转.当点D 恰好落在AB 边上时,填空:图1 图2 ① 线段DE 与AC 的位置关系是 ;② 设△BDC 的面积为1S ,△AEC 的面积为2S ,则1S 与2S 的数量关系是 ,证明你的结论; (2)猜想论证当△DEC 绕点C 旋转到图3所示的位置时,小明猜想(1)中1S 与2S 的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中BC ,CE 边上的高,请你证明小明的猜想.(三) 割补类31.阅读下面材料:小明遇到这样一个问题:如图1,在边长为)2( a a 的正方形ABCD 各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ 的面积。
初中数学重点梳理:面积问题的解决方法
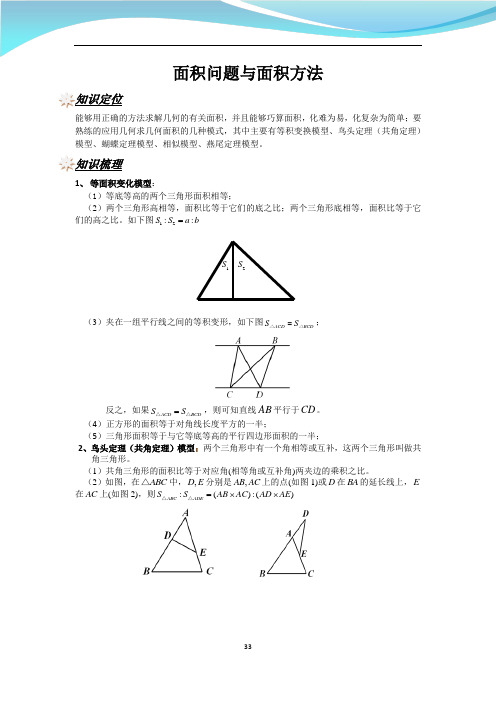
面积问题与面积方法知识定位能够用正确的方法求解几何的有关面积,并且能够巧算面积,化难为易,化复杂为简单;要熟练的应用几何求几何面积的几种模式,其中主要有等积变换模型、鸟头定理(共角定理)模型、蝴蝶定理模型、相似模型、燕尾定理模型。
知识梳理1、 等面积变化模型:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如下图12::S S a b =(3)夹在一组平行线之间的等积变形,如下图ACD BCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD 。
(4)正方形的面积等于对角线长度平方的一半;(5)三角形面积等于与它等底等高的平行四边形面积的一半;2、鸟头定理(共角定理)模型:两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
(1)共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
(2)如图,在ABC △中,,D E 分别是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△1S 2S3、蝴蝶定理模型:任意四边形中的比例关系。
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
① 1243::S S S S =1324S S S S ⨯=⨯ ② ()()1243::AO OC S S S S =++ 4、相似模型:相似三角形:相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:(1)相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; (2)相似三角形的面积比等于它们相似比的平方。
中考数学专题复习 专题28 求几何图形面积及面积法解题的问题(学生版)

中考专题28 求几何图形面积及面积法解题的问题一、几何图形面积公式1.三角形的面积:设三角形底边长为a ,底边对应的高为h ,则面积S=ah/22.平行四边形的面积:设平行四边形的底边长为a ,高为h ,则面积S=ah3.矩形的面积:设矩形的长为a ,宽为b ,则面积S=ab4.正方形的面积:设正方形边长为a ,对角线长为b ,则面积S=222b a = 5.菱形的面积:设菱形的底边长为a ,高为h ,则面积S=ah若菱形的两条对角线长分别为m 、n ,则面积S=mn/2也就是说菱形的面积等于两条对角线乘积的一半。
6.梯形的面积:设梯形的上底长为a,下底长为b ,高为h ,则面积S=(a+b)h/27.圆的面积:设圆的半径为r,则面积S=πr 28.扇形面积计算公式9.圆柱侧面积和表面积公式(1)圆柱的侧面积公式S 侧=2πrh(2)圆柱的表面积公式:S 表=2S 底+S 侧=2πr 2+2πrh2360r n s π⋅=lr s 21=或10.圆锥侧面积公式从右图中可以看出,圆锥的母线L 即为扇形的半径,而圆锥底面的周长是扇形的弧长2πr ,这样,圆锥侧面积计算公式:S 圆锥侧=S 扇形=πrL注意:有时中考专题题还经常考查圆的周长、扇形的弧长的公式的应用。
(1)圆的周长计算公式为:C=2πr(2)扇形弧长的计算公式为:(3)其他几何图形周长容易计算,不直接给出。
二、用面积法解题的理论知识1.面积方法:运用面积关系来证明或计算平面几何题的方法,称为面积方法,它是几何中的一种常用方法。
2.面积法解题的特点:把已知量和未知量用面积公式联系起来,通过运算达到求证的结果。
所以用面积法来解几何题,几何元素之间关系变成数量之间的关系,只需要计算,有时可以不添置补助线,即使需要添置辅助线,也很容易考虑到。
三、面积方法问题主要涉及以下两部分内容1.证明面积相等的理论依据(1)三角形的中线把三角形分成两个面积相等的部分。
2023年中考数学复习第一部分考点梳理第三章函数第5节第2课时几何图形面积问题

域Ⅱ的面积不超过矩形ABCD面积的 ,设OP=x
m.
(1)当x= 时,求区域Ⅱ的面积.
基础过关
基础过关
能力提升
-6-
第2课时 几何图形面积问题
(2)计划在区域Ⅰ,Ⅱ分别铺设甲、乙两款不同的深色瓷砖,区
域Ⅲ铺设丙款白色瓷砖,在相同光照条件下,当场地内白色区
域的面积越大,室内光线亮度越好.当x为多少时,室内光线亮
饲养室面积最大为 75 m2.
基础过关
基础过关
能力提升
-5-
第2课时 几ห้องสมุดไป่ตู้图形面积问题
4.如图,某校准备给长12 m、宽8 m的矩形ABCD室内场地进
行地面装饰,现将其划分为区域I(菱形PQFG),区域Ⅱ(4个全等
的直角三角形),剩余空白部分记为区域Ⅲ,点O为矩形和菱形
的对称中心,OP∥AB,OQ=2OP,AE= PM.为了美观,要求区
第2课时
几何图形面积问题
第2课时 几何图形面积问题
1.如图,在长为20 m、宽为14 m的矩形花圃里建有等宽的十
字形小径.若小径的宽不超过1 m,则花圃中的阴影部分的面积
有( A )
A.最小值247 m2
B.最小值266 m2
C.最大值247 m2
D.最大值266 m2
基础过关
基础过关
能力提升
-2-
∵AF=x,∴CH=x-4,
设AQ=z,则PH=BQ=6-z.
−
−
∵PH∥EG,∴ = , 即
=
,∴
−
∴y=
·
=-
模型43 几何中等分面积问题(解析版)-中考数学解题大招复习讲义
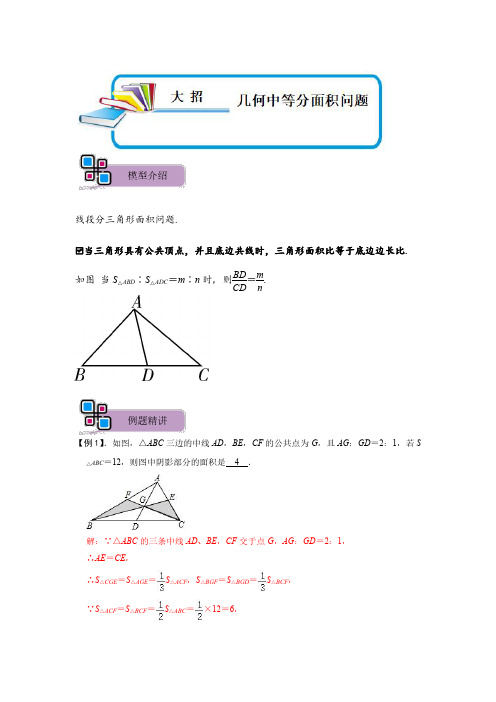
模型介绍线段分三角形面积问题.☑当三角形具有公共顶点,并且底边共线时,三角形面积比等于底边边长比.如图当S △ABD ∶S △ADC =m ∶n 时,则BD CD =m n .例题精讲【例1】.如图,△ABC 三边的中线AD ,BE ,CF 的公共点为G ,且AG :GD =2:1,若S △ABC =12,则图中阴影部分的面积是4.解:∵△ABC 的三条中线AD 、BE ,CF 交于点G ,AG :GD =2:1,∴AE =CE ,∴S △CGE =S △AGE =S △ACF ,S △BGF =S △BGD =S △BCF ,∵S △ACF =S △BCF =S △ABC =×12=6,∴S△CGE=S△ACF=×6=2,S△BGF=S△BCF=×6=2,∴S阴影=S△CGE+S△BGF=4.故答案为:4.变式训练【变式1-1】.如图,在△ABC中,点D、E、F分别是BC、AD、CE的中点,且S△ABC=8cm2,则S△BEF的面积是()A.4cm2B.3cm2C.2cm2D.1cm2解:∵D是BC的中点,∴S△ABD=S△ACD=S△ABC,∵E是AD的中点,∴S△ABE=S△BDE=S△ABD,S△AEC=S△CDE=S△ADC,∵F是EC的中点,∴S△BEF=S△BCF=S△BCE,∵S△ABC=8cm2,∴S△BCE=4cm2,∴S△BCF=2cm2,故选:C.【变式1-2】.如图,在直角坐标系中,平行四边形OABC的顶点坐标B(17,6),C(5,6),直线y=x+b恰好将平行四边形OABC的面积分成相等的两部分,那么b=﹣.解:连接AC、BO,交于D.∵平行四边形OCBA,∴BC∥OA,DB=OD,DC=DA,∴∠MCD=∠DAN,∠CMD=∠DNA,∴△CMD≌△AND,同理△BMD≌△OND,∴过D的任意直线都能把平行四边形的面积分成面积相等的两部分.过D作DF⊥x轴于F,过B作BE⊥x轴于E.∵平行四边形OCBA,B(17,6),C(5,6),∴DO=BD,DF∥BE,∴OF=EF,∴DF=3,OF=×17=8.5,∴D(8.5,3),代入y=x+b得:3=×8.5+b,∴b=﹣,故答案为:﹣.【例2】.如图,在平面直角坐标系xOy中,长方形OABC的顶点B的坐标为(6,4),直线y=﹣x+b恰好将长方形OABC分成面积相等的两部分,那么b=5.解:∵直线y=﹣x+b恰好将长方形OABC分成面积相等的两部分∴直线y=﹣x+b要经过矩形的中心∵矩形的中心为(3,2)∴把点(3,2)代入y=﹣x+b,解得:b=5.变式训练【变式2-1】.如图,在菱形ABCD中,AB=6,∠B=60°,点E在边AD上,且AE=2.若直线l经过点E,将该菱形的面积平分,并与菱形的另一边交于点F,则线段EF的长为2.解:如图,过点A和点E作AG⊥BC,EH⊥BC于点G和H,得矩形AGHE,∴GH=AE=2,∵在菱形ABCD中,AB=6,∠B=60°,∴BG=3,AG=3=EH,∴HC=BC﹣BG﹣GH=6﹣3﹣2=1,∵EF平分菱形面积,EF经过菱形对角线交点,∴FC=AE=2,∴FH=FC﹣HC=2﹣1=1,在Rt△EFH中,根据勾股定理,得EF===2.故答案为:2.【变式2-2】.如图,△ABC的面积为1,D、E分别为AB、AC的中点,F、G是BC边上的三等分点.那么△DEF的面积是多少?△DOE的面积是多少?解:①如图,过点A作AQ⊥BC于Q,过点D作DM⊥BC于M,∵D是AB的中点,DM∥AQ,∴M是BQ的中点,∴DM=AQ,∴三角形ABC的面积是=BC×AQ=1,∴BC×AQ=2,∵D、E分别为AB、AC的中点,∴DE=BC,∴三角形DEF的面积为=DE×DM=××BC××AQ=;②∵DE=,FG=,∴=,∴三角形DOE面积=三角形DEF面积×=.【变式2-3】.如图,在平面直角坐标系xOy中,多边形OABCDE的顶点坐标分别是O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).若直线l经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,求直线l 的函数表达式.解:如图,延长BC交x轴于点F,连接OB,AF,DF,CE,DF和CE相交于点N,∵O(0,0),A(0,6),B(4,6),C(4,4),D(6,4),E(6,0).∴四边形OABF为矩形,四边形CDEF为矩形,∴点M(2,3)是矩形OABF对角线的交点,即点M为矩形ABFO的中心,∴直线l把矩形ABFO分成面积相等的两部分又∵点N(5,2)是矩形CDEF的中心,∴过点N(5,2)的直线把矩形CDEF分成面积相等的两部分.∴直线MN即为所求的直线L,设直线l的解析式为y=kx+b,则2k+b=3,5k+b=2,解得k=,b=,因此所求直线l的函数表达式是:y=﹣x+.1.如图,长方形ABCD的面积为36cm2,E,F,G分别为AB,BC,CD的中点,H为AD上任一点,则图中阴影部分的面积为()A.18cm2B.16cm2C.20cm2D.24cm2解:设长方形ABCD中,AD=a,AB=b,则AE=b=GC,BF=a,∴S阴=S长方形ABCD﹣S△AEH﹣S△HFC﹣S△HCG,=36﹣AE•AH﹣FC•AB﹣HD•CG,=36﹣AD•AE﹣FC•AB,=36﹣ab,=18cm2.故选:A.2.已知梯形ABCD的四个顶点的坐标分别为A(﹣1,0),B(5,0),C(2,2),D(0,2),直线y=kx+2将梯形分成面积相等的两部分,则k的值为()A.B.C.D.解:∵梯形ABCD的四个顶点的坐标分别为A(﹣1,0),B(5,0),C(2,2),D(0,2),∴梯形的面积为:=8,∵直线y=kx+2将梯形分成面积相等的两部分,∴直线y=kx+2与AD、AB围成的三角形的面积为4,设直线与x轴交于点(x,0),∴(x+1)×2=4,∴x=3,∴直线y=kx+2与x轴的交点为(3,0)∴0=3k+2解得k=﹣故选:A.3.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD 于点G,交BE于点H.①△ABE的面积=△BCE的面积;②AF=FB;③∠FAG=2∠ACF.以上说法正确的是()A.①③B.①②C.②③D.①②③解:∵E是AC的中点,∴AE=EC,∴△ABE的面积=△BCE的面积,故①符合题意;若AF=FB,则F是AB的中点,∵CF是∠ACB的平分线,∴BC=AC与BC>AC矛盾,故②不符合题意;∵∠BAC=90°,∴∠FAG+∠CAD=90°,∵AD⊥BC,∴∠CAD+∠ACB=90°,∴∠FAG=∠ACD,∵CF平分∠ACB,∴∠ACD=2∠ADF,∴∠FAG=2∠ACF,故③符合题意;故选:A.4.如图,在△ABC中,已知点D、E、F分别为BC、AD、CE的中点,若阴影部分的面积为4,则△ABC的面积为16.解:∵点E是AD的中点,=S△ABD,S△ACE=S△ADC,∴S△ABE+S△ACE=S△ABC,∴S△ABE=S△ABC,∴S△BCE∵点F是CE的中点,=S△BCE,∴S△BEF=4S△BEF=4×4=16.∴S△ABC故答案为:16.5.如图,已知在平面直角坐标系中,平行四边形ABCD顶点A(0,0),C(10,4),直线y=ax﹣2a﹣1将平行四边形ABCD分成面积相等的两部分,求a的值.解:连接AC、BD,AC与BD相交于点M,过点M作ME⊥x轴于点E,过点C作CF ⊥x轴于点F,∵C(10,4),∴AF=10,CF=4,…(2分)∵四边形ABCD为平行四边形,∴AM=CM,即=,∵ME⊥x轴,CF⊥x轴,∴∠MEA=∠CFA=90°,∴ME∥CF,∴∠AME=∠ACF,∠AEM=∠AFC,∴△AME∽△ACF,∴==,即E为AF的中点,∴ME为△AFC的中位线,…(4分)∴AE=AF=5,ME=CF=2,∴M(5,2),…(6分)∵直线y=ax﹣2a﹣1将平行四边形ABCD分成面积相等的两部分,∴直线y=ax﹣2a﹣1经过点M,…(8分)将M(5,2)代入y=ax﹣2a﹣1得:a=1.…(9分)6.如图,在平面直角坐标系中,四边形ABCO是正方形,点B的坐标为(4,4),直线y =mx﹣2恰好把正方形ABCO的面积分成相等的两部分,则m=2.解:∵直线y=mx﹣2恰好把正方形ABCO的面积分成相等的两部分∴直线必经过正方形的中心∵点B的坐标为(4,4)∴中心为(2,2),代入直线中得:2=2m﹣2,m=27.已知平面上四点A(0,0),B(10,0),C(14,6),D(4,6),若直线y=mx﹣3m﹣1将四边形ABCD分成面积相等的两部分,则m的值为1.解:∵点A(0,0),B(10,0),C(14,6),D(4,6),∴四边形ABCD为平行四边形,∵直线y=mx﹣3m﹣1四边形ABCD分成面积相等的两部分,∴直线y=mx﹣3m﹣1过矩形的对角线的交点,而平行四边形的对角线的交点坐标为(7,3),∴7m﹣3m﹣1=3,∴m=1.故答案为:1.8.在△ABC中,BC=5,AC=12,AB=13,在AB、AC上分别取点D、E,使线段DE将△ABC分成面积相等的两部分,则这样线段的最小值是2.解:∵BC2+AC2=AB2,∴△ABC为直角三角形,过D作DF⊥AC于F,设DF=x,则=,∴AF=x,=x•AE=S△ABC=15,∵S△ADE∴AE=,EF=﹣x,∴DE2=DF2+EF2=x2+(﹣x)2=x2+﹣144=(x﹣)2+12≥12,故可得DE2最小值是12,∴DE最小值为2.故答案为:2.9.如图,在直角坐标系中,矩形OABC的顶点B的坐标为(15,6),直线恰好将矩形OABC分成面积相等的两部分,那么b=.解:由B的坐标(15,6),得到矩形中心的坐标为(7.5,3),直线y=x+b恰好将矩形OABC分成面积相等的两部分,将(7.5,3)代入直线y=x+b得:3=×7.5+b,解得:b=.故答案为:.10.如图,△ABC中,AD是中线,延长AD到E,使DE=AD,DF是△DCE的中线.已知△ABC的面积为2,求:△CDF的面积.解:∵AD是△ABC的中线,=S△ABC=×2=1,∴S△ACD∵CD是△ACE的中线,=S△ACD=1,∴S△CDE=S△CDE=×1=.∵DF是△CDE的中线,∴S△CDF∴△CDF的面积为.11.正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).(1)直线y=x经过点C,且与x轴交于点E,求四边形AECD的面积;(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;(3)若直线l1经过点F(﹣,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移个单位交轴x于点M,交直线l1于点N,求△NMF的面积.解:(1)在y=x中,令y=4,即x=4,解得:x=5,则B的坐标是(5,0);令y=0,即x=0,解得:x=2,则E的坐标是(2,0).则OB=5,OE=2,BE=OB﹣OA=5﹣2=3,∴AE=AB﹣BE=4﹣3=1,S四边形AECD=(AE+CD)•AD=(4+1)×4=10;(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).设直线的解析式是y=kx+b,则,解得:.则直线l的解析式是:y=2x﹣4;(3)∵直线l1经过点F(﹣,0)且与直线y=3x平行,设直线l1的解析式是y1=kx+b,则:k=3,代入得:0=3×(﹣)+b,解得:b=,∴y1=3x+,已知将(2)中直线l沿着y轴向上平移个单位,则所得的直线的解析式是y=2x﹣4+,即:y=2x﹣3,当y=0时,x=,∴M(,0),解方程组得:,即:N(﹣7,﹣19),S△NMF=×[﹣(﹣)]×|﹣19|=.答:△NMF的面积是.12.如图,直线y=2x+4与x轴、y轴分别交于A、B两点,把△OAB绕点O顺时针旋转90°得到△OCD.(1)求经过A、B、D三点的抛物线的解析式;(2)在所求的抛物线上是否存在一点P,使直线CP把△OCD分成面积相等的两部分?如果存在,求出点P的坐标;如果不存在,请说明理由.解:(1)在y=2x+4中,分别令y=0和x=0来得到:A(﹣2,0)、B(0,4)、D点是因为旋转,OD=OB,所以,D点(4,0);C点也是因为旋转,OA=OC,所以,C点(0,2);设经过A、B、D的抛物线解析式为y=ax2+bx+c,则有:4a﹣2b+c=0①,c=4②,16a+4b+c=0③(3分)解①②③得:,b=1,c=4,∴抛物线的解析式为:.(4分)(2)若存在点P满足条件,则直线CP必经过OD的中点E(2,0);(5分)易知经过C、E的直线为y=﹣x+2,(6分)于是可设点P的坐标为P(m,﹣m+2);将P(m,﹣m+2)代入得:,(7分)整理,得:m2﹣4m﹣4=0,解得:,;所以满足条件的点P有两个:P1(2+2,﹣2),.(9分)13.已知菱形OABC在坐标系中的位置如图所示,O是坐标原点,点C(1,2),点A在x 轴上.点M(0,2).(1)点P是直线OB上的动点,求PM+PC最小值.(2)将直线y=﹣x﹣1向上平移,得到直线y=kx+b.①当直线y=kx+b与线段OC有公共点时,结合图象,直接写出b的取值范围.②当直线y=kx+b将四边形OABC分成面积相等的两部分时,求k,b.解:(1)由已知,OA=OC=,连接AC、AM,如图1所示.∵四边形OABC是菱形,∴PC=PA,∴PC+PM=PM+PA≤AM,即PC+PM≤==3.(2)∵y=kx+b为y=﹣x﹣1平移得来的,∴k=﹣1.①依照题意画出图形,如图2所示.结合函数图象可知,当点O在直线y=﹣x+b上时,b最小,此时b=0;当点C在直线y=﹣x+b上时,b值最大,∵点C(1,2),∴2=﹣1+b,解得:b=3.故0≤b≤3.②连接AC、OB,设AC与OB的交点为D,当直线y=﹣x+b过点D时,直线y=﹣x+b 将四边形OABC分成面积相等的两部分,如图3所示.∵OA=OC=,∴点A(,0).∵四边形OABC为菱形,C(1,2),A(,0),∴点D(,1).∵直线y=﹣x+b过点D,∴1=﹣+b,解得:b=.∴当直线y=kx+b将四边形OABC分成面积相等的两部分时,k=﹣1,b=.14.已知,y=ax2+bx﹣3过(2,﹣3),与x轴交于A(﹣1,0),B(x2,0),交y轴于C.(1)求抛物线的解析式;(2)过点C作CD∥x轴,交抛物线于D,是否存在直线y=kx+1将四边形ACDB分成面积相等的两部分,若存在,请求k的值;若不存在,请说明理由;(3)若直线y=m(﹣3<m<0)与线段AC、BC分别交于D、E两点,则在x轴上是否存在点P,使得△DPE为等腰直角三角形,若存在,请求P点的坐标;若不存在,请说明理由.解:(1)∵y=ax2+bx﹣3过(2,﹣3),A(﹣1,0),∴,解得a=1,b=﹣2,所以抛物线的解析式为:y=x2﹣2x﹣3;(2)设直线y=kx+1与x轴交于点E,于CD交于点F,A(﹣1,0),B(3,0),E(),F();S四边形ACFE=(CF+AE)•OC=(1);S四边形EFDB=(DF+BE)•OC=(5);即(1)=(5),k=.(3)存在点P.直线y=m与y轴交点为F(0,m),①当DE为腰时,分别过D、E作DP1⊥x轴于P1,作EP2⊥x轴于P2;如图,则△DP1E和△DEP2均为等腰直角三角形,又DP1=DE=EP2=OF=﹣m,又AB=x B﹣x A=3+1=4,又△ECD∽△BCA,即,即m=;P1(,0),P2(,0);②当DE为底时,过P3作GP3⊥DE于G,如图,又DG=GE=GP3=OF=﹣m,由△ECD∽△BCA,,即m=;P3(,0)综上所述,P1(,0),P2(,0),P3(,0).15.如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,矩形DEFG的顶点G与△ABC 的顶点C重合,边GD、GF分别与AC,BC重合.GD=12,GF=16,矩形DEFG沿射线CB的方向以每秒4个单位长的速度匀速运动,点Q从点B出发沿BA方向以每秒5个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC﹣CA于点H,矩形DEFG、点Q同时出发,当点Q到达点A时停止运动,矩形DEFG也随之停止运动.设矩形DEFG、点Q运动的时间是t秒(t>0).(1)求线段DF的长;(2)求运动过程中,矩形DEFG与Rt△ABC重叠部分的面积s与t的函数关系式(写出自变量的取值范围);(3)射线QK能否把矩形DEFG分成面积相等的两部分?若能,求出t值;若不能,说明理由;(4)连接DH,当DH∥AB时,请直接写出t值.解:(1)如图1:连接DF,在Rt△CDF中,CD=12,CF=16,根据勾股定理:DF==20;(2)∵在Rt△ABC中,∠C=90°,AB=50,AC=30,∴BC==40,根据题意得:当t==10时,停止运动;如图2:当点E在AB上时,∵∠C=90°,∠EFG=90°,∴EF∥AC,∴△BEF∽△BAC,∴EF:AC=BF:BC,∴12:30=BF:40,∴BF=16,∴CG=BC﹣BF﹣GF=40﹣16﹣16=8,此时,t=8÷4=2;如图3:当F与B重合时,CG=BC﹣BG=40﹣16=24,此时,t=24÷4=6,∵tan∠ABC==,tan∠GBD==,∴此时,点D在直线AB上;①当0<t≤2时,s=S矩形DEFG=12×16=192,②如图4:当2<t≤6时,设矩形DEFG的边EF交BC于点M,边DE交AB于点N ∵BF=24﹣4t tan B=∴MF=(24﹣4t)=18﹣3t,∴EM=EF﹣FM=12﹣(18﹣33t﹣6,∴NE=EM=4t﹣8,﹣S△EMN=192﹣EM•EN=192﹣6(t﹣2)2,∴s=S矩形DEFG③如图5:当6<t≤10时,设DG与AB交于点M,BG=40﹣4t,则MG=BG=30﹣3t,=BG•MG=×(40﹣4t)(30﹣3t)=6(10﹣t)2;则s=S△BMG(3)能,如图6:当QK经过矩形DEFG的对称中心O时,就可以把矩形DEFG分成面积相等的两部分;∵在Rt△GDF与Rt△CAB中,tan∠GDF===,tan∠B==,∴∠GFD=∠B,∴DF∥AB,∴,∵DF=20,∴OF=10,∵BF=24﹣4t,HF==,QB=5t,∴BH=BF+FH=24﹣4t+,∴,解得:t=;(4)如图7:过点D作MN⊥AB于N,交BC于M,∵∠GMD+∠B=90°,∠GMD+∠GDM=90°,∴∠GDM=∠B,∴GM=GD•tan∠GDM=×12=9,∴DM==15,∵BG=40﹣4t,∴BM=BG+GM=40﹣4t+9=49﹣4t,∴MN=BM•cos∠B=(49﹣4t),∴DN=MN﹣DM=(49﹣4t)﹣15,∵QH=QB=×5t=t,∵DH∥AB,∴QH=DN,则t=(49﹣4t)﹣15,解得t=.故t值为.16.已知m,n是方程x2﹣6x+5=0的两个实数根,且m<n.如图,若抛物线l:y=﹣x2+bx+c 的图象经过点A(m,0),B(0,n).(1)求抛物线的解析式;(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,求C,D的坐标和△BCD的面积;(3)已知P是线段OC上一点,过点P作PH⊥x轴,交抛物线于点H,若直线BC把△PCH分成面积相等的两部分,求P点的坐标.解:(1)由方程x2﹣6x+5=0得x1=1,x2=5,∵m<n,∴m=1,n=5,∴A(1,0),B(0,5).把A(1,0),B(0,5)代入y=﹣x2+bx+c得:,解得,∴抛物线的解析式y=﹣x2﹣4x+5;(2)C(﹣5,0),D(﹣2,9),过D作DE⊥x轴于E,∵易得E(﹣2,0).=S△CDE+S梯形OBDE﹣S OBC=;∴S△BCD(3)设P(a,0),则H(a,﹣a2﹣4a+5),由于直线BC把△PCH分成面积相等的两部分,须且只须BC等分线段PH,亦即PH的中点在直线BC上.∵易得直线BC的解析式为y=x+5,∴,解得a1=﹣1,a2=﹣5(不合题意,舍去),∴P点坐标为(﹣1,0).17.【数学经验】三角形的中线能将三角形分成面积相等的两部分.【经验发展】面积比和线段比的联系:如果两个三角形的高相同,则它们的面积比等于对应底边的比.如图1,△ABC的边AB上有一点M,请证明:=.【结论应用】如图2,△CDE的面积为1,=,=,求△ABC的面积.【拓展延伸】如图3,△ABC的边AB上有一点M,D为CM上任意一点,请利用上述结论,证明:=.【迁移应用】如图4,△ABC中,M是AB的三等分点(AM=AB),N是BC的中点,若△ABC的面积是1,请直接写出四边形BMDN的面积.解:【经验发展】如图1,过C作CH⊥AB于H,=AM×CH,S△BCM=BM×CH,∵S△ACM∴==,即=.【结论应用】如图2,连接AE,∵=,=S△ACE,∴S△CDE又∵=,=S△ABC,∴S△ACE=×S△ABC=S△ABC,∴S△CDE又∵△CDE的面积为1,∴△ABC的面积12.【拓展延伸】如图3,∵M是AB上任意一点,∴=,∵D是CM上任意一点,=×S△ACM,S△BCD=×S△BCM,∴S△ACD∴==,即=.【迁移应用】如图4,连接BD,∵M是AB的三等分点(AM=AB),∴=,∵N是BC的中点,∴==1,=a,则S△BDM=2a,S△ACD=3a,S△CDN=S△BDN=S△BCD=3a,设S△ADM=5a,S△ABC=12a,∴S四边形BMDN=S△ABC=×1=.∴S四边形BMDN故答案为:.18.已知抛物线y=﹣x2+bx+c的图象经过点A(m,0)、B(0,n),其中m、n是方程x2﹣6x+5=0的两个实数根,且m<n.(1)求抛物线的解析式;(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,求C、D点的坐标和△BCD的面积;(3)P是线段OC上一点,过点P作PH⊥x轴,交抛物线于点H,若直线BC把△PCH 分成面积相等的两部分,求P点的坐标.解:(1)解方程x2﹣6x+5=0,得x1=5,x2=1,由m<n,知m=1,n=5,∴A(1,0),B(0,5),∴即;所求抛物线的解析式为y=﹣x2﹣4x+5.(2)由﹣x2﹣4x+5=0,得x1=﹣5,x2=1,故C的坐标为(﹣5,0),由顶点坐标公式,得D(﹣2,9);过D作DE⊥x轴于E,得E(﹣2,0),=S△CDE+S梯形OBDE﹣S△OBC==15.∴S△BCD=S△CFD﹣S△CFB也可求得)(注:延长DB交x轴于F,由S△BCD(3)设P(a,0),则H(a,﹣a2﹣4a+5);直线BC把△PCH分成面积相等的两部分,须且只需BC等分线段PH,亦即PH的中点,()在直线BC上,易得直线BC方程为:y=x+5;∴.解之得a1=﹣1,a2=﹣5(舍去),故所求P点坐标为(﹣1,0).19.【背景知识】研究平面直角坐标系,我们可以发现一条重要的规律:若平面直角坐标系上有两个不同的点A(x A,y A)、B(x B,y B),则线段AB的中点坐标可以表示为(,).【简单应用】如图1,直线AB与y轴交于点A(0,3),与x轴交于点B(4,0),过原点O的直线L将△ABO分成面积相等的两部分,请求出直线L的解析式;【探究升级】小明发现“若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点”=S△BCD.试说明AO=如图2,在四边形ABCD中,对角线AC、BD相交于点O,S△ABDCO;【综合运用】如图3,在平面直角坐标系中A(1,4),B(3,﹣2),C(2m,﹣m+5),若OC恰好平分四边形OACB的面积,求点C的坐标.解:【简单应用】:∵直线L将△ABO分成面积相等的两部分,∴直线L必过线段AB的中点,设线段AB的中点为E,∵A(0,3),B(4,0),∴E(,),∴E(2,),∵直线L过原点,∴设直线L的解析式为y=kx,∴2k=,∴k=,∴直线L的解析式为y=x;【探究升级】:如图2,过点A作AF⊥BD于F,过点C作CG⊥BD于G,=BD•AF,S△CBD=BD•CG,∴S△ABD=S△BCD,∵S△ABD∴BD•AF=BD•CG,∴AF=CG,在△AOF和△COG中,,∴△AOF≌△COG(AAS),∴OA=OC;【综合运用】:如图3,由【探究升级】知,若四边形一条对角线平分四边形的面积,则这条对角线必经过另一条对角线的中点,∵OC恰好平分四边形OACB的面积,∴OC过四边形OACB的对角线AB的中点,连接AB,设线段AB的中点为H,∵A(1,4),B(3,﹣2),∴H(2,1),设直线OC的解析式为y=k'x,∴2k'=1,∴k'=,∴直线OC的解析式为y=x,∵点C(2m,﹣m+5)在直线OC上,∴﹣m+5=×2m,∴m=,∴C(5,).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.过平行四边形ABCD的顶点A引直线,和BC、DC或其延长线分别交 于E、F,求证:S△ABF=S△ADE
A
D
BEC源自F7.从△ABC的各顶点作三条平行线AD、BE、CF,各与对边或延长线 交于D、E、F,求证:S△DEF=2S△ABC。
F E
A
B
D
C
8. 在平行四边形ABCD的两边AD、CD上各取一点F、E,使AE=CF ,连AE、CF交于P,求证:BP平分∠APC。
5.如图,△ABC中,点D、E、F 分别在三边上,E是AC的中点,AD、
BE、CF交于一点 , BD 2DC , SGEC 3, SGDC 4
,求△ ABC的面积及BF:AF的比值.
A
F
GE
B
DC
6.如图5,E、F分别是 ABCD的边AB、CD上的点,AF与DE相交于点
P,BF与CE相交于点点Q,若SAPD 10cm2 , SBQC 20cm2
.
3.如图2,O为平行四边形ABCD的对角线交点,E为AB的中点,DE交 AC于点F,若平行四边形ABCD的面积为12,则△DOE的面积为( )
A、1 B、1.5 C、2 D、2.25
4.如图3,已知△ABC中,D、E分别为AB、AC的中点,M为DE的中 点,连结CM并延长交AD于点N,则△ANM的面积与△AME的面 积之比为 .
C
G
F
A
E
B
2. 已 知 △ ABC 中 , AB = AC , P 为 底 边 BC 上 任 一 点 , PE ⊥ AB , PF⊥AC,BH⊥AC,求证:PE+PF=BH
A
H F
E
BP
C
3. Rt△ABC中,∠ACB=90°,a、b为两直角边,斜边AB上的高为h
,求证: 1 a2
1 b2
1 h2
,则阴影部分的面积为
cm2 .
7.在△ABC中,D是AB的中点,E在AC上,且CE:AC=1:3 ,CD和 BE交于G,求△ABC和四边形ADGE的面积比。
A
D GE
B
C
8.如图,E,F分别是长方形ABCD的边AB,BC的中点,连接AF,CE
,AF与CE交于点G,则 S AGCD =( )
D S ABCD
D
E
C
F
P
A
B
1.如图,梯形ABCD被对角线分为4个小三角形,已知△AOB和△BOC 的面积分别为 25cm2,35cm2,求梯形的面积。
A
B
25 O 35
D
C
2.如图1所示,在△ABC中,DE∥AB∥FG,且CD:DF:AF=1:2:3. 若
△CDE的面积为2,则△CFG的面积=
, 梯 形 ABGF 的
面积=
C
b A
a
h
D
B
在 △ ABC 中 , 点 D,E 分 别 在 边 AB,AC 上 , 若 DE∥BC , 求 证 : AD:DB=AE:EC(用面积法证)
4.已知△ABC中,AD是∠BAC的角平分线,求证:AB:AC=BD:DC
5.如图,已知以△ABC的两边AB、AC为边向外作正方形ABDE、ACFG, 联结EC、BG交于点O,再联结AO,证明:OA平分∠EOG。
