初中数学《几何最值问题》典型例题(20200906080531)

合集下载

(完整版)初中数学《几何最值问题》典型例题

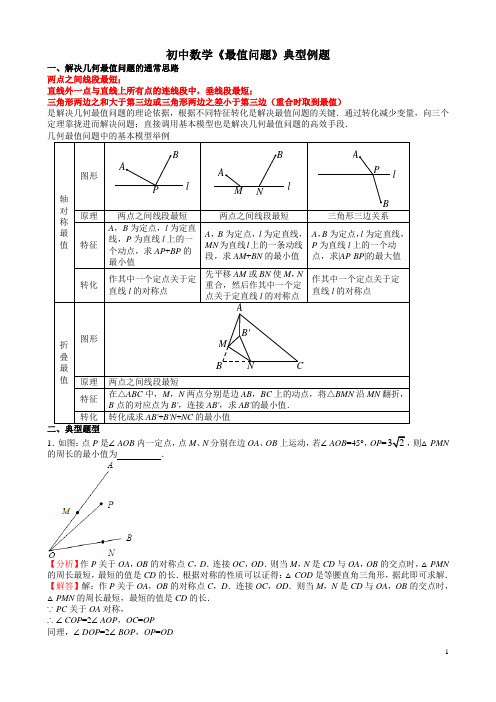
初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．轴对称最值图形lPBANM lBAAPBl 原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'，连接AB'，求AB'的最小值．转化转化成求AB'+B'N+NC的最小值1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=32，则△PMN 的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN 的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=2OC=2×32=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形P ABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出P A+NB的长度就行了．问题就是P A+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时P A+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b=+⎧⎨-=+⎩，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A 、B 两点在直线的两侧，点A 到直线的距离AM =4，点B 到直线的距离BN =1，且MN =4，P 为直线上的动点，|P A ﹣PB |的最大值为．D PB′N MA【分析】作点B 于直线l 的对称点B ′，则PB =PB ′因而|P A ﹣PB |=|P A ﹣PB ′|，则当A ，B ′、P 在一条直线上时，|P A ﹣PB |的值最大．根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值，进而求得|P A ﹣PB |的最大值．【解答】解：作点B 于直线l 的对称点B ′，连AB ′并延长交直线l 于P ． ∴B ′N =BN =1，过D 点作B ′D ⊥AM ，利用勾股定理求出AB ′=5 ∴|P A ﹣PB |的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD 中，AB =3，AD =5．如图所示，折叠纸片，使点A 落在BC 边上的A ′处，折痕为PQ ，当点A ′在BC 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P 、Q 分别在AB 、AD 边上移动，则点A ′在BC 边上可移动的最大距离为．【分析】本题关键在于找到两个极端，即BA ′取最大或最小值时，点P 或Q 的位置．经实验不难发现，分别求出点P 与B 重合时，BA ′取最大值3和当点Q 与D 重合时，BA ′的最小值1．所以可求点A ′在BC 边上移动的最大距离为2．【解答】解：当点P 与B 重合时，BA ′取最大值是3，当点Q 与D 重合时（如图），由勾股定理得A ′C =4，此时BA ′取最小值为1．则点A ′在BC 边上移动的最大距离为3﹣1=2．故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD ，AD ⊥AB ，AB =8，AD =CD =4，点E 、F 分别在线段AB 、AD 上，将△AEF 沿EF 翻折，点A 的落点记为P ．当P 落在直角梯形ABCD 内部时，PD 的最小值等于．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PF AE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458 ．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE=AE=12AB=1，∵BC=1，四边形ABCD是矩形，∴AD，∴DE2，根据三角形的三边关系，OD＜OE+DE，∴当OD过点E是最大，最大值为2+1．故答案为：2+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE，那么DE长的最小值是．【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=22x，CD′=22（4﹣x），根据勾股定理然后用配方法即可求解．【解答】解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=22x，CD′=22（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=12x2+12（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK 的最小值为．【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为2×33∴PK+QK3故答案为：3．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′+CC′+DD′的取值范围是．【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，继而可得12AP•（BB′+CC′+DD′）=1，又由1≤AP≤2，即可求得答案．【解答】解：连接AC，DP．∵四边形ABCD是正方形，正方形ABCD的边长为1，∴AB=CD，S正方形ABCD=1，∵S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，∴S△ADP+S△ABP+S△ACP=1，∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•（BB′+CC′+DD′）=1，则BB′+CC′+DD′=2 AP，∵1≤AP≤2，∴当P当P与C重合时，有最小值2．∴2≤BB′+CC′+DD′≤2．故答案为：2≤BB′+CC′+DD′≤2．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADP+S△ABP+S△ACP=1，继而得到BB′+CC′+DD′=2 AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A 和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。

初中数学几何模型与最值问题09专题-一元二次方程在实际应用中的最值问题(含答案)

初中数学几何模型与最值问题专题9 一元二次方程在实际应用中的最值问题【应用呈现】1、近年来，某县为发展教育事业，加大了对教育经费的投入，2009年投入6000万元，2011年投入8640万元．（1）求2009年至2011年该县投入教育经费的年平均增长率；（2）该县预计2012年投入教育经费不低于9500万元，若继续保持前两年的平均增长率，该目标能否实现？请通过计算说明理由．2、如图，要建造一个四边形花圃ABCD ，要求AD 边靠墙，CD ⊥AD ，AD ∥BC ，AB ∶CD ＝5∶4，且三边的总长为20 m ．设AB 的长为5x m . (1)请求AD 的长；(用含字母x 的式子表示)(2)若该花圃的面积为50 m 2，且周长不大于30 m ，求AB 的长．【方法总结】一、一元二次方程判别式求解1、已知x 、y 为实数，且满足x y m ++=5，xy ym mx ++=3，求实数m 最大值与最小值。

2、已知m ，n 是关于x 的一元二次方程x 2﹣2tx +t 2﹣2t +4=0的两实数根，则（m +2）（n +2）的最小值是（） A ．7 B ．11 C ．12 D ．16二、配方法求最值1、设a 、b 为实数，那么a ab b a b 222++--的最小值为_______。

2、将形状、大小完全相同的两个等腰三角形如图所示放置，点D 在AB 边上，△DEF 绕点D 旋转，腰DF 和底边DE 分别交△CAB 的两腰CA ，CB 于M ，N 两点，若CA =5，AB =6，AB =1：3，则MD +的最小值为．三、 “夹逼法”求最值1、不等边三角形∆ABC 的两边上的高分别为4和12且第三边上的高为整数，那么此高的最大值可能为________。

1、国家实施“精准扶贫”政策以来，很多贫困人口走向了致富的道路．某地区2017年底有贫困人口1万人，通过各方面的共同努力，2019年底该地区贫困人口减少到0.25万人，求该地区2017年底至2019年底贫困人口年平均下降的百分率．2、某商场销售一批名牌衬衫，平均每天能售出20件，每件盈利50元．经调查发现：这种衬衫的售价每降低1元，平均每天能多售出2件，设每件衬衫降价x元．（1）降价后，每件衬衫的利润为元，平均每天的销量为件；（用含x的式子表示）（2）为了扩大销售，尽快滅少库存，商场决定采取降价措施，但需要平均每天盈利1600元，那么每件衬衫应降价多少元？3、2020年，我国脱贫攻坚在力度、广度、深度和精准度上都达到了新的水平，重庆市深度贫困地区脱贫进程明显加快，作风治理和能力建设初见成效，精准扶贫、精准脱贫取得突破性进展．为助力我市脱贫攻坚，某村村委会在网上直播销售该村优质农产品礼包，该村在今年1月份销售256包，2、3月该礼包十分畅销，销售量持续走高，在售价不变的基础上，3月份的销售量达到400包．（1）若设2、3这两个月销售量的月平均增长率为a%，求a的值；（2）若农产品礼包每包进价25元，原售价为每包40元，该村在今年4月进行降价促销，经调查发现，若该农产品礼包每包降价1元，销售量可增加5袋，当农产品礼包每包降价多少元时，这种农产品在4月份可获利4620元？4、某商场第一年销售某品牌手机5000部，如果每年的销售量比上年增长相同的百分率x，且第三年比第二年多销售了1200部，求x的值．5、某通讯公司规定：一名客户如果一个月的通话时间不超过A分钟，那么这个月这名客户只要交10元通话费；如果超过A分钟，那么这个月除了仍要交10元通话费外，超过部分还要按每分钟元交费．（Ⅰ）某名客户7月份通话90分钟，超过了规定的A分钟，则超过部分应交通话费元（用含A的代数式表示）；（Ⅱ）下表表示某名客户8月份、9月份的通话情况和交费情况：月份通话时间/分钟通话费总数/元8月份80 259月份45 10根据上表的数据，求A的值．6、在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角，墙DF足够长，墙DE长为9米，现用20米长的篱笆围成一个矩形花园ABCD，点C在墙DF上，点A在墙DE上，（篱笆只围AB，BC两边）．（Ⅰ）根据题意填表；BC（m） 1 3 5 7矩形ABCD面积（m2）（Ⅱ）能够围成面积为100m2的矩形花园吗？如能说明围法，如不能，说明理由．专题9 一元二次方程在实际应用中的最值问题答案【应用呈现】2、近年来，某县为发展教育事业，加大了对教育经费的投入，2009年投入6000万元，2011年投入8640万元．（1）求2009年至2011年该县投入教育经费的年平均增长率；（2）该县预计2012年投入教育经费不低于9500万元，若继续保持前两年的平均增长率，该目标能否实现？请通过计算说明理由．【解析】（1）设每年平均增长的百分率为x ． 60002)1(x +=8640，2)1(x +=1.44，∵1+x ＞0， ∴1+x =1.2， x =20%．答：每年平均增长的百分率为20%；（2）2012年该县教育经费为8640×（1+20%）=10368（万元）＞9500万元．故能实现目标．2、如图，要建造一个四边形花圃ABCD ，要求AD 边靠墙，CD ⊥AD ，AD ∥BC ，AB ∶CD ＝5∶4，且三边的总长为20 m ．设AB 的长为5x m . (1)请求AD 的长；(用含字母x 的式子表示)(2)若该花圃的面积为50 m 2，且周长不大于30 m ，求AB 的长．【解析】(1)作BH ⊥AD 于点H ，则AH ＝3x ，由BC ＝DH ＝20－9x 得AD ＝20－6x (2)由2(20－9x )＋3x ＋9x ≤30得x ≥53，由12[(20－9x )＋(20－6x )]×4x ＝50得3x 2－8x ＋5＝0，∴x 1＝53，x 2＝1(舍去)，∴5x ＝253.答：AB 的长为253米【方法总结】一、一元二次方程判别式求解1、已知x 、y 为实数，且满足x y m ++=5，xy ym mx ++=3，求实数m 最大值与最小值。

(完整word版)初中几何最值问题

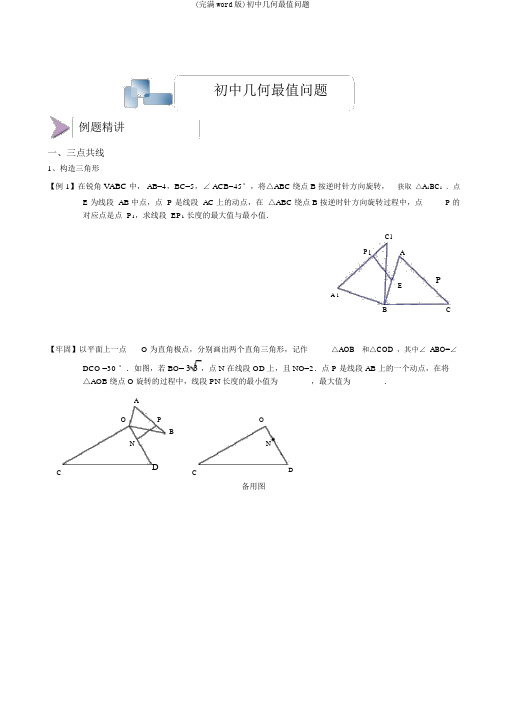
初中几何最值问题例题精讲一、三点共线1、构造三角形【例 1】在锐角VABC中， AB=4，BC=5，∠ ACB=45°，将△ABC 绕点 B 按逆时针方向旋转，获取△A1BC1．点E 为线段 AB 中点，点 P 是线段 AC 上的动点，在△ABC 绕点 B 按逆时针方向旋转过程中，点P 的对应点是点 P1，求线段 EP1长度的最大值与最小值．C1P1 AEPA 1B C 【牢固】以平面上一点O 为直角极点，分别画出两个直角三角形，记作△AOB和△COD，其中∠ ABO=∠DCO =30 °．如图，若 BO= 3 3，点 N 在线段 OD 上，且 NO=2．点 P 是线段 AB 上的一个动点，在将△AOB 绕点 O 旋转的过程中，线段 PN 长度的最小值为 _______，最大值为 _______．AO P OBN NC DC D备用图【例 2】如图，MON 90°，矩形ABCD 的极点 A． B 分别在边OM ， ON 上，当 B 在边 ON 上运动时， A 随之在边 OM 上运动，矩形ABCD 的形状保持不变，其中AB=2， BC=1，运动过程中，点 D 到点O 的最大距离为 __________【牢固】已知：△AOB 中， AB OB 2 ，△COD 中，CD OC 3 ,∠ABO ∠DCO .连接AD 、BC ，点 M 、N、 P 分别为OA、OD、BC的中点.若 A 、O、C三点在同素来线上，且∠ ABO 2 ，固定△AOB ，将△ COD 绕点 O 旋转，则PM的最大值为____________B AMOP NDC【牢固】在平面直角坐标系xOy 中，点 A 、 B 分别在x轴、y轴的正半轴上，点M为线段AB的中点．点D 、E 分别在x轴、y轴的负半轴上，且DE AB 10 ．以 DE 为边在第三象限内作正方形DGFE ，央求出线段MG 长度的最大值，并直接写出此时直线MG 所对应的函数的剖析式．yBMD O A xGEF【例 3 】如图，已知 A( 1, y ) ，B(2, y 2 ) 为反比率函数1P(x,0) 在x正半轴上运y图像上的两点，动点2 1 x动，当线段AP与线段BP之差达到最大时，点P的坐标是 _________yABO P x2、轴对称【例 1】求x 3 2 2 1 的最小值4x【例 2】ABE ,CD CD 是半径为5的MN 于点F，P为e O 的两条弦，EF 上任意一点，则AB 8 ，PA+PCCD 6 ，的最小值为MN 为直径，_________AB MN 于点ACM NE O P FDB【牢固】设半径为 1 的半圆的圆心为O ，直径为AB , C、 D 是半圆上两点，若弧AC 的度数为96 °，弧 BD的度数为36°，动点P在直径AB上，则CP+PD的最小值是 _______【牢固】设正三角形 ABC 的边长是2， M 是 AB 边上的中点， P 是边 BC 上任意一点，则PA+PM 的最大值为 _______,最小值为 ________【例 3】如图，已知等边△ABC 的边长为1， D、E、 F 分别是 AB、 BC、 AC 边上的点（均不与点A、 B、 C 重合），记△ DEF的周长为p .若D、E、F分别是AB、BC、AC边上任意点，则p的取值范围是.ADFB EC【例 4】如图 1，在平面直角坐标系中，抛物线y＝— x2＋ 2x＋ 3 与 x 轴交于 A．B 两点，与y 轴交于点C，点D 是抛物线的极点．（1）求直线 AC 的剖析式及 B． D 两点的坐标；（ 2）请在直线AC 上找一点M，使△BDM 的周长最小，求出点M 的坐标．图 1【例 5】如图，直线y 3 分别交 x 轴、 y 轴于 C、A 两点，将射线 AM 绕点 A 顺时针旋转 45°获取射x 23线A N， D 为 AM 上的动点， B 为 AN 上的动点，点 C 在∠ MAN 的内部．（1）当 AM∥ x 轴，且四边形 ABCD 为梯形时，求△ BCD 的面积；（2）求△BCD 周长的最小值；（ 3）当△BCD 的周长获取最小值，且BD 5 2时，求△ BCD 的面积．3yA yAyA2 2 2D1 M 1 1O 123C 4x O 123C 4x O 12 3 C 4x BN备用图备用图【例 6】在直角坐标系中， A 1, 2 ， B 4, 1 ， C m,0 ， D n, n 为四边形的 4 个极点，当四边形ABCD 的周长最短时，m_________nyODC xBA【牢固】如图1，抛物线 y＝ ax2＋ bx＋ c（ a≠0）的极点为 C（ 1， 4），交 x 轴于 A、 B 两点，交 y 轴于点 D，其中点 B 的坐标为（ 3， 0）。

几何图形中的最值问题

几何图形中的最值问题引言：最值问题可以分为最大值和最小值。

在初中包含三个方面的问题：1. 函数:①二次函数有最大值和最小值；②一次函数中有取值范围时有最大值和最小值。

2. 不等式：①如x w 7最大值是7;②如x> 5，最小值是5.3.几何图形：①两点之间线段线段最短。

②直线外一点向直线上任一点连线中垂线段最短，③在三角形中，两边之和大于第三边，两边之差小于第三边。

一、最小值问题B镇*A镇♦' -------------------------- '燃气管例1.如图4，已知正方形的边长是8, M在DC上，且DM=2 N为线段AC 上的一动点，求DN+MN勺最小值。

解：作点D关于AC的对称点D，则点D与点B重合，连BM交AC于N,连DN 贝U DN+MN t短，且DN+MN=BM•/ CD=BC=8,DM=2, /• MC=6,在Rt △ BCM中,BM= 82 62=10，••• DN+MN勺最小值是10。

例2，已知，MN是O O直径上，MN=2点A在O O上，/ AMN=3&B是弧AN的中点，P是MN上的一动点，贝U PA+PB的最小值是__________ 解：作A点关于MN的对称点A,连AB,交MN于P,贝U PA+PB最短。

连OB oA,•••/ AMN=30B是弧AN的中点,•••/ BOA=30°,根据对称性可知:丄 NOA=60°,:丄 MOA=900, DDMBNAMOA在 Rt △ A ’BO 中，OA=OB=1,••• A B =、2 即 PA+PB= 2作点A 关于杯上沿 MN 的对称点B ,连接BC 交MN 于点P ,连接BM 过点C 作AB 的垂线交剖开线 MA 于点Do由轴对称的性质和三角形三边关系知例3.如图6，已知两点 D(1,-3),E(-1,-4), 试在直线y=x 上确定一点 P,使点P 到DE 两点的距离之和最小，并求出最小值。

(完整)初中数学《几何最值问题》典型例题

初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．几何最值问题中的基本模型举例轴对称最值图形lPBANM lBAAPBl原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'，连接AB'，求AB'的最小值．转化转化成求AB'+B'N+NC的最小值二、典型题型1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=32，则△PMN 的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN 的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=2OC=2×32=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形P ABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出P A+NB的长度就行了．问题就是P A+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时P A+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b=+⎧⎨-=+⎩，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A 、B 两点在直线的两侧，点A 到直线的距离AM =4，点B 到直线的距离BN =1，且MN =4，P 为直线上的动点，|P A ﹣PB |的最大值为．D PB′N BMA【分析】作点B 于直线l 的对称点B ′，则PB =PB ′因而|P A ﹣PB |=|P A ﹣PB ′|，则当A ，B ′、P 在一条直线上时，|P A ﹣PB |的值最大．根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值，进而求得|P A ﹣PB |的最大值．【解答】解：作点B 于直线l 的对称点B ′，连AB ′并延长交直线l 于P ． ∴B ′N =BN =1，过D 点作B ′D ⊥AM ，利用勾股定理求出AB ′=5 ∴|P A ﹣PB |的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD 中，AB =3，AD =5．如图所示，折叠纸片，使点A 落在BC 边上的A ′处，折痕为PQ ，当点A ′在BC 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P 、Q 分别在AB 、AD 边上移动，则点A ′在BC 边上可移动的最大距离为．【分析】本题关键在于找到两个极端，即BA ′取最大或最小值时，点P 或Q 的位置．经实验不难发现，分别求出点P 与B 重合时，BA ′取最大值3和当点Q 与D 重合时，BA ′的最小值1．所以可求点A ′在BC 边上移动的最大距离为2．【解答】解：当点P 与B 重合时，BA ′取最大值是3，当点Q 与D 重合时（如图），由勾股定理得A ′C =4，此时BA ′取最小值为1．则点A ′在BC 边上移动的最大距离为3﹣1=2．故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD ，AD ⊥AB ，AB =8，AD =CD =4，点E 、F 分别在线段AB 、AD 上，将△AEF 沿EF 翻折，点A 的落点记为P ．当P 落在直角梯形ABCD 内部时，PD 的最小值等于．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PF AE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458 ．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE=AE=12AB=1，∵BC=1，四边形ABCD是矩形，∴AD，∴DE2，根据三角形的三边关系，OD＜OE+DE，∴当OD过点E是最大，最大值为2+1．故答案为：2+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE，那么DE长的最小值是．【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=22x，CD′=22（4﹣x），根据勾股定理然后用配方法即可求解．【解答】解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=22x，CD′=22（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=12x2+12（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK 的最小值为．【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为2×33∴PK+QK3故答案为：3．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′+CC′+DD′的取值范围是．【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，继而可得12AP•（BB′+CC′+DD′）=1，又由1≤AP≤2，即可求得答案．【解答】解：连接AC，DP．∵四边形ABCD是正方形，正方形ABCD的边长为1，∴AB=CD，S正方形ABCD=1，∵S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，∴S△ADP+S△ABP+S△ACP=1，∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•（BB′+CC′+DD′）=1，则BB′+CC′+DD′=2 AP，∵1≤AP≤2，∴当P与B重合时，有最大值2；当P与C重合时，有最小值2．∴2≤BB′+CC′+DD′≤2．故答案为：2≤BB′+CC′+DD′≤2．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADP+S△ABP+S△ACP=1，继而得到BB′+CC′+DD′=2 AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A 和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。

2024年中考数学重难点《几何最值问题》题型及答案解析

重难点几何最值问题中考数学中《几何最值问题》部分主要考向分为五类：一、将军饮马类最值二、动点辅助圆类最值三、四点共圆类最值四、瓜豆原理类最值五、胡不归类最值几何最值问题虽然在中考数学中经常考察的是将军饮马类和辅助圆类，剩余几种虽然不经常考察，但是考到的时候难度都比较大，所以也需要理解并掌握不同类型的几何最值问题的处理办法，这样到考到的时候才能有捷径应对。

考向一：将军饮马类最值一动”“两定异侧普通一动”“两定同侧普通动”两定“一动”两定“两两动”“两定同侧两动”“两定异侧满分技巧将军饮马：。

1．（2023•绥化）如图，△ABC是边长为6的等边三角形，点E为高BD上的动点．连接CE，将CE绕点C 顺时针旋转60°得到CF．连接AF，EF，DF，则△CDF周长的最小值是3+3．【分析】分析已知，可证明△BCE≌△ACF，得∠CAF＝∠CBE＝30°，可知点F在△ABC外，使∠CAF ＝30°的射线AF上，根据将军饮马型，求得DF+CF的最小值便可求得本题结果．【解答】解：∵△ABC是等边三角形，∴AC＝BC＝6，∠ABC＝∠BCA＝60°，∵∠ECF＝60°，∴∠BCE＝60°﹣∠ECA＝∠ACF，∵CE＝CF，∴△BCE≌△ACF（SAS），∴∠CAF＝∠CBE，∵△ABC是等边三角形，BD是高，∴∠CBE＝∠ABC＝30°，CD＝AC＝3，过C点作CG⊥AF，交AF的延长线于点G，延长CG到H，使得GH＝CG，连接AH，DH，DH与AG 交于点I，连接CI，FH，则∠ACG＝60°，CG＝GH＝AC＝3，∴CH＝AC＝6，∴△ACH为等边三角形，∴DH＝CD•tan60°＝，AG垂直平分CH，∴CI＝HI，CF＝FH，∴CI+DI＝HI+DI＝DH＝3，CF+DF＝HF+DF≥DH，∴当F与I重合时，即D、F、H三点共线时，CF+DF的值最小为：CF+DF＝DH＝3，∴△CDF的周长的最小值为3+3．故答案为：3+3．2．（2023•德州）如图，在四边形ABCD中，∠A＝90°，AD∥BC，AB＝3，BC＝4，点E在AB上，且AE＝1．F，G为边AD上的两个动点，且FG＝1．当四边形CGFE的周长最小时，CG的长为．【分析】先确定FG和EC的长为确定的值，得到四边形CGFE的周长最小时，即为CG+EF最小时，平移CG到C'F，作点E关于AD对称点E'，连接E'C'交AD于点G'，得到CG+EF最小时，点G与G'重合，再利用平行线分线段成比例求出C'G'长即可．【解答】解：∵∠A＝90°，AD∥BC，∴∠B＝90°，∵AB＝3，BC＝4，AE＝1，∴BE＝AB﹣AE＝3﹣1＝2，在Rt△EBC中，由勾股定理，得EC＝＝＝，∵FG＝1，∴四边形CGFE的周长＝CG+FG+EF+EC＝CG+EF+1+，∴四边形CGFE的周长最小时，只要CG+EF最小即可．过点F作FC'∥GC交BC于点C'，延长BA到E'，使AE'＝AE＝1，连接E'F，E'C'，E'C'交AD于点G'，可得AD垂直平分E'E，∴E'F＝EF，∵AD∥BC，∴C'F＝CG，CC'＝FG＝1，∴CG+EF＝C'F+E'F≥E'C'，即CG+EF最小时，CG＝C'G'，∵E'B＝AB+AE'＝3+1＝4，BC'＝BC﹣CC'＝4﹣1＝3，由勾股定理，得E'C'＝＝＝5，∵AG'∥BC'，∴＝，即＝，解得C'G'＝，即四边形CGFE的周长最小时，CG的长为．故答案为：．考向二：动点辅助圆类最值满分技巧动点运动轨迹为辅助圆的三种类型：一．定义法——若一动点到定点的距离恒等于固定长，则该点的运动轨迹为以定点为圆心，定长为半径的圆（或圆弧）二.定边对直角模型原理：直径所对的圆周角是直角思路构造：若一条定边所对的“动角”始终为直角，则直角顶点运动轨迹是以该定边为直径的圆（或圆弧）三．定边对定角模型原理：在同圆或等圆中，同弧所对的圆周角相等思路构造：若一条定边所对的“动角”始终为定角，则该定角顶点运动轨迹是以该定角为圆周角，该定边为弦的圆（或圆弧）1．（2023•徐州）如图，在Rt△ABC中，∠C＝90°，CA＝CB＝3，点D在边BC上．将△ACD沿AD折叠，使点C落在点C′处，连接BC′，则BC′的最小值为．【分析】由折叠性质可知AC＝AC'＝3，然后根据三角形的三边不等关系可进行求解．【解答】解：∵∠C＝90°，CA＝CB＝3，∴，由折叠的性质可知AC＝AC'＝3，∵BC'≥AB﹣AC'，∴当A、C′、B三点在同一条直线时，BC'取最小值，最小值即为，故答案为．2．（2023•黑龙江）如图，在Rt△ACB中，∠BAC＝30°，CB＝2，点E是斜边AB的中点，把Rt△ABC绕点A顺时针旋转，得Rt△AFD，点C，点B旋转后的对应点分别是点D，点F，连接CF，EF，CE，在旋转的过程中，△CEF面积的最大值是4+．【分析】线段CE为定值，点F到CE距离最大时，△CEF的面积最大，画出图形，即可求出答案．【解答】解：∵线段CE为定值，∴点F到CE的距离最大时，△CEF的面积有最大值．在Rt△ACB中，∠BAC＝30°，E是AB的中点，∴AB＝2BC＝4，CE＝AE＝AB＝2，AC＝AB•cos30°＝2，∴∠ECA＝∠BAC＝30°，过点A作AG⊥CE交CE的延长线于点G，∴AG＝AC＝，∵点F在以A为圆心，AB长为半径的圆上，∴AF＝AB＝4，∴点F到CE的距离最大值为4+，∴，故答案为：．3．（2023•大庆模拟）如图，AB是⊙O的直径，AB＝4，C为的三等分点（更靠近A点），点P是⊙O上个动点，取弦AP的中点D，则线段CD的最大值为（）A．2B．C．D．【分析】如图，连接OD，OC，首先证明点D的运动轨迹为以AO为直径的⊙K，连接CK，当点D在CK的延长线上时，CD的值最大，利用勾股定理求出CK即可解决问题．【解答】解：如图，连接OD，OC，∵AD＝DP，∴OD⊥P A，∴∠ADO＝90°，∴点D的运动轨迹为以AO为直径的⊙K，连接CK，AC，当点D在CK的延长线上时，CD的值最大，∵C为的三等分点，∴∠AOC＝60°，∴△AOC是等边三角形，∴CK⊥OA，在Rt△OCK中，∵∠COA＝60°，OC＝2，OK＝1，∴CK＝＝，∵DK＝OA＝1，∴CD＝+1，∴CD的最大值为+1，故选：D．考向三：四点共圆类最值满分技巧对角互补的四边形必有四点共圆，即辅助圆产生模型原理：圆内接四边形对角互补∴FD＝，在四边形ACBF中，∠ACB＝∠AFB＝90°，∴A、C、B、F四点共圆，∴∠ACF＝∠ABF＝45°，∠CAB＝∠CFB，∵∠PCD＝45°∴∠ACP＝∠FCD，又∵△ABE∽△FBD，∴∠BAE＝∠BFD，∴∠CAP＝∠CFD，∴△CAP∽△CFD，∴，在四边形ACBF中，由对角互补模型得AC+CB＝，∴CF＝∴，∴AP＝1，∴PE＝2，故答案为：2考向四：瓜豆原理类最值满分技巧瓜豆原理的特征和结论：∴AB＝CD＝6，∠B＝∠BCD＝90°，∵∠BET＝∠FEG＝45°，∴∠BEF＝∠TEG，∵EB＝ET，EF＝EG，∴△EBF≌△ETG（SAS），∴∠B＝∠ETG＝90°，∴点G在射线TG上运动，∴当CG⊥TG时，CG的值最小，∵BC＝，BE＝，CD＝6，∴CE＝CD＝6，∴∠CED＝∠BET＝45°，∴∠TEJ＝90°＝∠ETG＝∠JGT＝90°，∴四边形ETGJ是矩形，∴DE∥GT，GJ＝TE＝BE＝，∴CJ⊥DE，∴JE＝JD，∴CJ＝DE＝3，∴CG＝CJ+GJ＝+3，∴CG的最小值为+3，故答案为：+3．2．（2023•宿城区二模）如图，矩形ABCD中，AD＝6，DC＝8，点E为对角线AC上一动点，BE⊥BF，，BG⊥EF于点G，连接CG，当CG最小时，CE的长为．【分析】过点B作BP⊥AC于点P，连接PG，则可得△ABE∽△PBG，进而可知∠BPG为定值，因此CG⊥PG时，CG最小，通过设元利用三角函数和相似比可表示出PG、CP，即可求出结果．【解答】解：如图，过点B作BP⊥AC于点P，连接PG，∵，∠ABC＝∠EBF，∴△ABC∽△EBF，∴∠CAB＝∠FEB，∵∠APB＝∠EGB＝90°，∴△ABP∽△EBG，∴＝，∠ABP＝∠EBG，∴∠ABE＝∠PBG，∴△ABE∽△PBG，∴∠BPG＝∠BAE，即在点E的运动过程中，∠BPG的大小不变且等于∠BAC，∴当CG⊥PG时，CG最小，设此时AE＝x，∵，∴PG＝，∵CG⊥PG，∴∠PCG＝∠BPG＝∠BAC，∴，代入PG＝，解得CP＝x，∵CP＝BC•sin∠CBP＝BC•sin∠BAC＝，∴x＝，∴AE＝∴CE＝，故答案为：．考向五：胡不归类最值满分技巧胡不归模型解决步骤：模型具体化：如图，已知两定点A、B，在定直线BC上找一点P，使从B走道P，再从P走到A的总时间最小解决步骤：由系数k·PB确定分割线为PBPA在分割线一侧，在分割线PB另一侧依定点B构α角，使sinα=k，α角另一边为BD过点P作PQ⊥BD，转化kPB=PQ过定点A作AH⊥BD，转化（PA+k·PB）min=AH，再依“勾股法”求AH的长即可。

初三数学几何中的最值问题

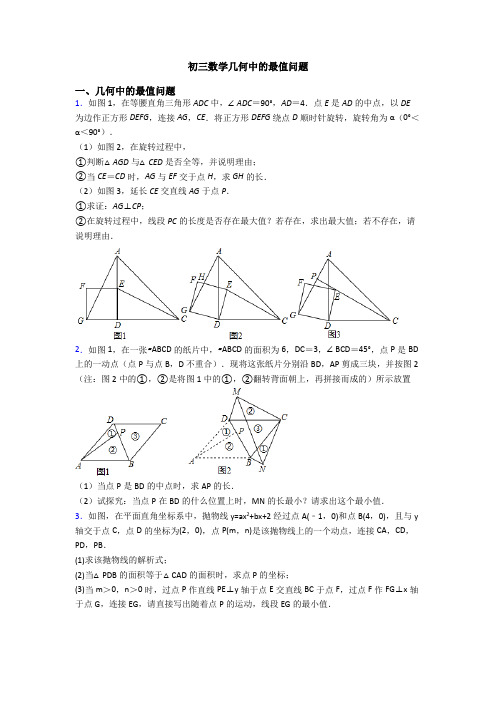
初三数学几何中的最值问题一、几何中的最值问题1．如图1，在等腰直角三角形ADC中，∠ADC＝90°，AD＝4．点E是AD的中点，以DE 为边作正方形DEFG，连接AG，CE．将正方形DEFG绕点D顺时针旋转，旋转角为α（0°＜α＜90°）．（1）如图2，在旋转过程中，①判断△AGD与△CED是否全等，并说明理由；②当CE＝CD时，AG与EF交于点H，求GH的长．（2）如图3，延长CE交直线AG于点P．①求证：AG⊥CP；②在旋转过程中，线段PC的长度是否存在最大值？若存在，求出最大值；若不存在，请说明理由．2．如图1，在一张▱ABCD的纸片中，▱ABCD的面积为6，DC＝3，∠BCD＝45°，点P是BD 上的一动点（点P与点B，D不重合）．现将这张纸片分别沿BD，AP剪成三块，并按图2（注：图2中的①，②是将图1中的①，②翻转背面朝上，再拼接而成的）所示放置（1）当点P是BD的中点时，求AP的长．（2）试探究：当点P在BD的什么位置上时，MN的长最小？请求出这个最小值．3．如图，在平面直角坐标系中，抛物线y=ax2+bx+2经过点A(﹣1，0)和点B(4，0)，且与y 轴交于点C，点D的坐标为(2，0)，点P(m，n)是该抛物线上的一个动点，连接CA，CD，PD，PB．(1)求该抛物线的解析式；(2)当△PDB的面积等于△CAD的面积时，求点P的坐标；(3)当m＞0，n＞0时，过点P作直线PE⊥y轴于点E交直线BC于点F，过点F作FG⊥x轴于点G，连接EG，请直接写出随着点P的运动，线段EG的最小值．4．定义：有一组对边相等目这一组对边所在直线互相垂直的凸四边形叫做“等垂四边形”．（1）如图①，四边形ABCD 与四边形AEEG 都是正方形，135AEB 180<∠<︒︒，求证：四边形BEGD 是“等垂四边形”；（2）如图②，四边形ABCD 是“等垂四边形”，AD BC ≠，连接BD ，点E ，F ，G 分别是AD ，BC ，BD 的中点，连接EG ，FG ，EF ．试判定EFG 的形状，并证明；（3）如图③，四边形ABCD 是“等垂四边形”，4=AD ，6BC =，试求边AB 长的最小值．5．问题探究（1）如图1．在ABC 中，8BC =，D 为BC 上一点，6AD =．则ABC 面积的最大值是_______．（2）如图2，在ABC 中，60BAC ∠=︒，AG 为BC 边上的高，O 为ABC 的外接圆，若3AG =，试判断BC 是否存在最小值？若存在，请求出最小值：若不存在，请说明理由．问题解决：如图3，王老先生有一块矩形地ABCD ，6212AB =+，626BC =+，现在他想利用这块地建一个四边形鱼塘AMFN ，且满足点E 在CD 上，AD DE =，点F 在BC 上，且6CF =，点M 在AE 上，点N 在AB 上，90MFN ∠=︒，这个四边形AMFN 的面积是否存在最大值？若存在，求出面积的最大值；若不存在，请说明理由．6．如图，在矩形纸片ABCD 中，AB=3cm ，AD=5cm ，折叠纸片使B 点落在边AD 上的点E 处，折痕为PQ ．过点E 作EF ∥AB 交PQ 于点F,连接BF（1）若AP ： BP=1：2，则AE 的长为．（2）求证：四边形BFEP 为菱形；（3）当点E 在AD 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P ，Q 分别在边AB 、BC 上移动，求出点E 在边AD 上移动的最大距离．7．在图1至图3中，O 的直径30BC =，AC 切O 于点C ，40AC =，连接AB 交O 于点D ，连接CD ，P 是线段CD 上一点，连接PB ．（1）如图1，当点P ，O 的距离最小时，求PD 的长；（2）如图2，若射线AP 过圆心O ，交O 于点E ，F ，求tan F 的值；（3）如图3，作DH PB ⊥于点H ，连接CH ，直接写出．．．．CH 的最小值．8．如图，在平面直角坐标系中，一次函数y ＝12x +2的图象与y 轴交于A 点，与x 轴交于B 点，⊙P 5P 在x 轴上运动．（1）如图1，当圆心P 的坐标为（1，0）时，求证：⊙P 与直线AB 相切；（2）在（1）的条件下，点C 为⊙P 上在第一象限内的一点，过点C 作⊙P 的切线交直线AB 于点D ，且∠ADC ＝120°，求D 点的坐标；（3）如图2，若⊙P 向左运动，圆心P 与点B 重合，且⊙P 与线段AB 交于E 点，与线段BO 相交于F 点，G 点为弧EF 上一点，直接写出12AG +OG 的最小值． 9．在ABC ∆中，90,2ACB BC AC ︒∠===，将ABC ∆绕点A 顺时针方向旋转α角0180()α︒<<︒至''AB C ∆的位置．（1）如图1，当旋转角为60︒时，连接'C C 与AB 交于点M ，则'C C = ．（2）如图2，在（1）条件下，连接'BB ，延长'CC 交'BB 于点D ，求CD 的长．（3）如图3，在旋转的过程中，连线'','CC BB CC 、所在直线交'BB 于点D ，那么CD 的长有没有最大值?如果有，求出CD 的最大值：如果没有，请说明理由．10．在△ABC 中，AB=AC ，∠BAC =120°，以CA 为边在∠ACB 的另一侧作∠ACM =∠ACB ，点D 为射线BC 上任意一点，在射线CM 上截取CE=BD ，连接AD 、DE 、AE ．（1）如图1，当点D 落在线段BC 的延长线上时，求∠ADE 的度数；（2）如图2，当点D 落在线段BC （不含边界）上时，AC 与DE 交于点F ，试问∠ADE 的度数是否发生变化？如果不变化，请给出理由；如果变化了，请求出∠ADE 的度数；（3）在（2）的条件下，若AB =6，求CF 的最大值．11．如图，在矩形ABCD 中，AB=2，E 为BC 上一点，且BE=1，∠AED=90°，将AED 绕点E 顺时针旋转得到A ED ''△，A′E 交AD 于P ， D′E 交CD 于Q ，连接PQ ，当点Q 与点C 重合时，AED 停止转动．（1）求线段AD 的长；（2）当点P 与点A 不重合时，试判断PQ 与A D ''的位置关系，并说明理由；（3）求出从开始到停止，线段PQ 的中点M 所经过的路径长．12．如图，在▱ABCD 中，AB 32=，BC 5=，B 45∠=，点E 为CD 上一动点，经过A 、C 、E 三点的O 交BC 于点F ．（操作与发现）()1当E 运动到AE CD ⊥处，利用直尺与规作出点E 与点F ；(保留作图痕迹) ()2在()1的条件下，证明：AF AB AE AD =．（探索与证明）()3点E 运动到任何一个位置时，求证：AF AB AE AD=；（延伸与应用）()4点E 在运动的过程中求EF 的最小值．13．在Rt △ABC 中，∠ACB ＝90°，tan ∠BAC ＝12．点D 在边AC 上（不与A ，C 重合），连结BD ，F 为BD 中点．（1）若过点D 作DE ⊥AB 于E ，连结CF 、EF 、CE ，如图1．设CF ＝kEF ，则k ＝；（2）若将图1中的△ADE 绕点A 旋转，使得D 、E 、B 三点共线，点F 仍为BD 中点，如图2．求证：BE-DE ＝2CF ；（3）若BC ＝6，点D 在边AC 的三等分点处，将线段AD 绕点A 旋转，点F 始终为BD 中点，求线段CF 长度的取值范围．14．（阅读材料）某兴趣小组的同学将一个矩形ABED 和一个等腰直角三角形DEC 拼成如图1的一个四边形ABCD ，已知1,2AD DC ==（1）①直接写出BC 的长为②如图2，若P 为AB 边上任意一点，以PD PC 、为边作PCQD ，请问对角线PQ 的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．爱动脑筋的小明得到如下思路：过点Q 作//QH AB ，交BC 的延长线于点H ，因为APQ DPQ PQH PQC ∠-∠=∠-∠，即APD HQC ∠=∠，则PAD QHC ∆≅∆，得AD CH =，所以BH BC CH BC AD =+=+，即PQ 存在最小值为（方法应用）（2）①若P 为AB 边上任意一点，延长PD 到F ，使2PF PD =，再以PF PC 、为边作PCQF ，请在图3中画图研究，求出对角线PQ 的长的最小值？②若P 为AB 边上任意一占，延长PD 到F ，使 PF nPD =（n 为常数），再以PF PC 、为边作PCQF ，则对角线PQ 的长的最小值=（延伸拓展）（3）如图4，若P 为直线DC 上任意一点，延长PA 到F ，使PF nPA =（n 为常数），以PF PB 、为边作PBQF ，请探究对角线PQ 的长是否也存在最小值？如果存在，直接写出最小值；如果不存在，请说明理由．15．如图1所示，菱形ABCD的顶点A，B在x轴上，点A在点B的左侧，点D在y轴的正半轴上，其中点9,02B⎛⎫⎪⎝⎭、()0,6D．（1）求C点的坐标；（2）如图2，E是AD上一点，且AE＝114，P是AC上一动点，求PD PE+的最小值；（3）如图3，动点Q从点B出发，以每秒54个单位长度的速度，沿折线B C D→→在菱形的两边上匀速运动，设运动时间为t秒．若点Q到BD的距离是52，则t＝．16．如图，△ABC的两条中线BD、CE交于点F．（1）DFBF= _______；（2）若BE2= EF▪EC，且BEDF=32，6，求DE的长；17．将一个直角三角形纸片ABO，放置在平面直角坐标系中，点(3)A，，点()0, 3B，点(0,0)O(I)过边OB上的动点D (点D不与点B，O重合)作DE OB⊥交AB于点E，沿着DE折叠该纸片，点B落在射线BO上的点F处．①如图，当D为OB中点时，求E点的坐标；②连接AF，当AEF∆为直角三角形时，求E点坐标：(Ⅱ)P是AB边上的动点(点P不与点B重合)，将AOP∆沿OP所在的直线折叠，得到'A OP∆，连接'BA，当'BA取得最小值时，求P点坐标(直接写出结果即可)．18．已知在四边形ABCD中，AD∥BC，AB⊥BC，AD＝2，AB＝4，BC＝6．（1）如图1，P为AB边上一点，以PD，PC为边作平行四边形PCQD，过点Q作QH⊥BC，交BC的延长线于H．求证：△ADP≌△HCQ；（2）若P为AB边上任意一点，延长PD到E，使DE＝PD，再以PE，PC为边作平行四边形PCQE．请问对角线PQ的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．（3）如图2，若P为DC边上任意一点，延长PA到E，使AE＝nPA（n为常数），以PE，PB为边作平行四边形PBQE．请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．19．如图，一次函数y＝12x+1的图象与二次函数y＝12x2+bx+c的图象交于A，B两点，点A在x轴上．点B的横坐标为4．（1）b＝，c＝；（2）设二次函数的图象与y轴交于C点，与x轴的另一个交点为D．连接AC，CD，求∠ACD的正弦值；（3）若M点在x轴下方二次函数图象上，①过M点作y轴平行线交直线AB于点E，以M点为圆心，ME的长为半径画圆，求圆M 在直线AB上截得的弦长的最大值；②若∠ABM＝∠ACO，则点M的坐标为．20．如图，△ABC中，O是△ABC内一点，AO平分∠BAC，连OB，OC．（1）如图1，若∠ACB＝2∠ABC，BO平分∠ABC，AC＝5，OC＝3，则AB＝；（2）如图2，若∠CBO+∠ACO＝∠BAC＝60°，求证：BO平分∠ABC；（3）如图3，在（2）的条件下，若BC＝23，将点B绕点O逆时针旋转60°得点D，直接写出CD的最小值为．21．如图，以G(0，1)为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D两点，点E为⊙O上一动点，CF⊥AE于F，当点E在⊙O的运动过程中，线段FG的长度的最小值为________．22．如图，△ABC中，AC＝BC，CD是△ABC的高，AB＝8，CD＝3，以点C为圆心，半径为2作⊙C，点E是⊙C上一动点，连接AE，点F是AE的中点，求线段DF的最小值23．n（n n矩形．下面，我们通过折叠的方式折出一个2矩形，如图a 所示．操作1：将正方形ABEF 沿过点A 的直线折叠，使折叠后的点B 落在对角线AE 上的点G 处，折痕为AH ．操作2：将FE 沿过点G 的直线折叠，使点F 、点E 分别落在边AF 、BE 上，折痕为CD ．则四边形ABCD 2矩形．（1）证明：四边形ABCD 2（2）点M 是边AB 上一动点．①如图b ，O 是对角线AC 的中点，若点N 在边BC 上，OM ON ⊥，连接MN ．求tan OMN ∠的值；②若AM AD =，点N 在BC 边上，当DMN 周长最小时，求CN NB 的值． ③连接CM ，作BR CM ⊥，垂足为R ．若2AB =DR 的最小值为． 24．如图，点A 在抛物线y ＝﹣x 2+6x 上，且横坐标为1，点B 与点A 关于抛物线的对称轴对称，直线AB 与y 轴交于点C ，点D 为抛物线的顶点，点E 的坐标为（2，2）．（1）求线段AB 的长；（2）点P 为线段AB 上方抛物线上的任一点，过P 作AB 的垂线交AB 于点H ，点F 为y 轴上一点，当△PBE 的面积最大时，求PH +HF +32FO 的最小值；（3）在（2）中，当PH +HF 3取得最小值时，将△CFH 绕点C 顺时针旋转60°后得到CF H ''，过点F '作CF '的垂线与直线AB 交于点Q ，点R 为y 轴上一动点，M 为平面直角坐标系中的一动点，是否存在使以点D ，Q ，R ，M 为顶点的四边形为矩形？若存在请直接写出点R 的坐标，若不存在，请说明理由．25．如图1，在ABC 中，90ACB ∠=︒，2AC =，23BC =，以点B 为圆心，3为半径作圆．点P 为B 上的动点，连接PC ，作P C PC '⊥，使点P '落在直线BC 的上方，且满足:1:3C PC P ='，连接BP ，'AP ．（1）求BAC ∠的度数，并证明AP C BPC '△△∽；（2）如图2，若点P 在AB 上时，连接BP '，求BP '的长；（3）点P 在运动过程中，BP '是否有最大值或最小值？若有，请求出当BP '取得最大值或最小值时，PBC ∠的度数；若没有，请说明理由．【参考答案】***试卷处理标记，请不要删除一、几何中的最值问题1．（1）①全等，理由见解析； ②GH 815=（2）①见解析；②PC 的最大值为3【分析】（1）①结论：△AGD ≌△CED ．根据SAS 证明即可．②如图2中，过点A 作AT ⊥GD 于T ．解直角三角形求出AT ，GT ，再利用相似三角形的性质求解即可．（2）①如图3中，设AD 交PC 于O ．利用全等三角形的性质，解决问题即可．②因为∠CPA ＝90°，AC 是定值，推出当∠ACP 最小时，PC 的值最大，推出当DE ⊥PC 时，∠ACP的值最小，此时PC 的值最大，此时点F 与P 重合（如图4中）．【详解】（1）①如图2中，结论：△AGD ≌△CED ．理由：∵四边形EFGD 是正方形，∴DG ＝DE ，∠GDE ＝90°，∵DA ＝DC ，∠ADC ＝90°，∴∠GDE ＝∠ADC ，∴∠ADG ＝∠CDE ，∴△AGD ≌△CED （SAS ）．②如图2中，过点A 作AT ⊥GD 于T ．∵△AGD ≌△CED ，CD ＝CE ，∴AD ＝AG ＝4，∵AT ⊥GD ，∴TG ＝TD ＝1，∴AT 2215AG TG =-∵EF ∥DG ，∴∠GHF ＝∠AGT ，∵∠F ＝∠ATG ＝90°，∴△GFH ∽△ATG ， ∴GH FG AG AT =， ∴415GH =， ∴GH 815=．（2）①如图3中，设AD 交PC 于O ．∵△AGD≌△CED，∴∠DAG＝∠DCE，∵∠DCE+∠COD＝90°，∠COD＝∠AOP，∴∠AOP+∠DAG＝90°，∴∠APO＝90°，∴CP⊥AG．②∵∠CPA＝90°，AC是定值，∴当∠ACP最小时，PC的值最大，∴当DE⊥PC时，∠ACP的值最小，此时PC的值最大，此时点F与P重合（如图4中），∵∠CED＝90°，CD＝4，DE＝2，∴EC222242CD DE=-=-=3∵EF＝DE＝2，∴CP＝CE+EF＝3，∴PC的最大值为3【点睛】本题属于四边形综合题，考查了正方形的性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找全等三角形解决问题，学会寻找特殊位置解决最值问题，属于中考压轴题．2．（1）292；（2）当AP⊥BD时，MN的长最小，105【分析】（1）连接AC交BD于P，根据平行四边形的性质得到PD＝PB，即点P是BD的中点，过D作DH⊥AB于H，PE⊥AB于E，根据三角形的中位线的性质得到PE＝12DH，BE＝12BH，根据已知条件得到DH＝2，解直角三角形即可得到结论；（2）由题意得，CM＝CN＝AP，∠MCD＝∠PAB，∠NCB＝∠PAD，于是得到∠MCN＝90°，当AP⊥BD时，MN的长最小，过D作DH⊥AB于H，根据勾股定理得到BD＝22DH BH+＝5，根据三角形的面积公式得到AP＝655，根据勾股定理即可得到结论．【详解】解：（1）连接AC交BD于P，∵四边形ABCD是平行四边形，∴PD＝PB，即点P是BD的中点，过D作DH⊥AB于H，PE⊥AB于E，∴PE∥DH，∴PE＝12DH，BE＝12BH，∵▱ABCD的面积为6，DC＝3，∴DH＝2，∴PE＝1，∵∠BCD＝45°，∴∠DAB＝45°，∴AH＝DH＝2，∴BH＝1，∴HE＝BE＝12，∴AE＝52，∴AP＝22AE PE+＝292；（2）由题意得，CM＝CN＝AP，∠MCD＝∠PAB，∠NCB＝∠PAD，∴∠MCD+∠NCB＝45°，∴∠MCN＝90°，当AP⊥BD时，MN的长最小，过D作DH⊥AB于H，由（1）求得DH＝2，BH＝1∴BD ＝22DH BH +＝5 ，∵AP ⊥BD ， ∴S △ABD ＝12AB•DH ＝12BD•AP ， ∴AP ＝655， ∴CM ＝CN ＝AP ＝655， ∴MN ＝22CM CN +＝6105， ∴MN 长的最小值是6105．【点睛】本题考查了平行四边形的性质，勾股定理，三角形面积的计算，三角形准确性的性质，正确的作出辅助线是解题的关键．3．（1）213222y x x =-++；（2）点P 的坐标是（1，3）、（2，3）、（5，-3）或（-2，-3）；（3）线段EG 的最小值为455.. 【分析】（1）根据抛物线y=ax 2+bx+2经过点A （-1，0）和点B （4，0），应用待定系数法，求出该抛物线的解析式即可；（2）首先根据三角形的面积的求法，求出△CAD 的面积，即可求出△PDB 的面积，然后求出BD=2，即可求出|n|=3，据此判断出n=3或-3，再把它代入抛物线的解析式，求出x 的值是多少，即可判断出点P 的坐标；（3）首先应用待定系数法，求出BC 所在的直线的解析式，然后根据点P 的坐标是（m ，n ），求出点F 的坐标，再根据二次函数最值的求法，求出EG 2的最小值，即可求出线段EG 的最小值．【详解】解：（1）把A （-1，0），B （4，0）两点的坐标代入y=ax 2+bx+2中，可得2016420a b a b -+=⎧⎨++=⎩，解得：1232a b ⎧=-⎪⎪⎨⎪=⎪⎩， ∴抛物线的解析式为：213222y x x =-++；（2））∵抛物线的解析式为213222y x x =-++，当x=0时，y=2，∴点C 的坐标是（0，2），∵点A （-1，0）、点D （2，0），∴AD=2-（-1）=3， ∴S △CAD =13232⨯⨯=， ∴S △PDB =3， ∵点B （4，0）、点D （2，0），∴BD=2，∴|n|=3×2÷2=3，∴n=3或-3，①当n=3时，2132322m m -++=，解得：m=1或m=2，∴点P 的坐标是（1，3）或（2，3）；②当n=-3时，2132322m m -++=- 解得m=5或m=-2，∴点P 的坐标是（5，-3）或（-2，-3）；综上，可得点P 的坐标是（1，3）、（2，3）、（5，-3）或（-2，-3）；（3）如图，设BC 所在的直线的解析式是：y=mx+n ，∵点C 的坐标是（0，2），点B 的坐标是（4，0），∴240n m n =⎧⎨+=⎩，解得：122m n ⎧=-⎪⎨⎪=⎩，∴BC 所在的直线的解析式是：122y x =-+， ∵点P 的坐标是（m ，n ），∴点F 的坐标是（4-2n ，n ），∴()22242EG n n =-+ 251616n n =-+2816555n ⎛⎫=-+ ⎪⎝⎭， ∴当85n =时，线段EG= ∴线段EG的最小值为5. 【点睛】本题是对二次函数知识的综合考查，熟练掌握二次函数的图像和性质是解决本题的关键，难度较大，属于中考的常考题型.4．（1）见解析；（2）EFG 是等腰直角三角形．理由见解析；（3【分析】（1）延长,BE DG 交于点H ，根据四边形ABCD 与四边形AEFG 都为正方形，易证()ABE ADG SAS ≌△△，则有BE DG =，ABE ADG ∠=∠，可证BHD 90∠=︒，根据BE DG =，可证四边形BEGD 是等垂四边形．（2）延长,BA CD 交于点H ，根据四边形ABCD 是等垂四边形，AD BC ≠，有AB CD ⊥，AB CD =，HBC HCB 90∠+∠=︒，根据点E,F,G 分别是AD,BC,BD 的中点可得1EG AB 2=，1GF CD 2=，//EG AB ，//GF DC ，则可证EGF 90，即有EFG 是等腰直角三角形；（3）延长,BA CD 交于点H 分别取,AD BC 的中点,E F ，连接,,HE EF HF ，根据11EF HF HE BC AD 32122-=-=-=，EFG 是等腰直角三角形，可得12GE GF AB ，22EF AB ，即可得出AB ．【详解】（1）如图，延长,BE DG 交于点H ，∵四边形ABCD 与四边形AEFG 都为正方形∴AB AD =，AE AG =，90BAD EAG ∠=∠=︒．∴BAE DAG ∠=∠．∴()ABE ADG SAS ≌△△．∴BE DG =，ABE ADG ∠=∠．∵ABD ADB 90∠+=︒∴90ABE EBD ADB DBE ADB ADG ∠+∠+∠=∠+∠+∠=︒即EBD BDG 90∠+∠=︒，∴BHD 90∠=︒．∴BE DG ⊥．又∵BE DG =，∴四边形BEGD 是等垂四边形．（2）EFG 是等腰直角三角形．理由如下：如图，延长,BA CD 交于点H ，∵四边形ABCD 是等垂四边形，AD BC ≠，∴AB CD ⊥，AB CD =∴HBC HCB 90∠+∠=︒∵点E,F,G 分别是AD,BC,BD 的中点 ∴1EG AB 2=，1GF CD 2=，//EG AB ，//GF DC ， ∴BFG C ∠=∠，EGD HBD ∠=∠，EG GF =． ∴EGF EGD FGD ABD DBC GFB ABD DBC C HBC HCB 90， ∴EFG 是等腰直角三角形；（3）如图，延长,BA CD 交于点H 分别取,AD BC 的中点,E F ，连接,,HE EF HF ，则11EF HF HE BC AD 32122-=-=-=，由（2）可知EFG 是等腰直角三角形， ∴12GEGF AB ∴2222112222EFGE GF AB AB AB ∴AB 2EF 2=．∴AB 2．【点睛】本题是新定义类探究题，主要考查了等腰直角三角形的性质、正方形的性质和勾股定理，解决本题需利用新定义，逐一讨论，解题中利用条件，构造直角三角形是解题的关键． 5．问题探究：（1）24；（2）存在，BC 的最小值为23144【分析】（1）根据三角形的面积公式即可得到结论；（2）如图2中，连接OA ，OB ，OC ，作OE BC ⊥于E ．设2OB OC x ==．求出x 的最小值即可解决问题；（3）如图3中，连接AF ，延长BC 交AE 的延长线于G ，将EFM △顺时针旋转得到FBH ，作FNH △的外接圆O ．由（2）可知，当FNH △的外接圆的圆心O 在线段BF 上时，FNH △的面积最小，此时四边形ANFM 的面积最大．【详解】解：（1）当AD BC ⊥时，ABC 面积的最大，则ABC 面积的最大值是11862422BC AD ⋅=⨯⨯=，故答案为：24；（2）如图中，连接OA ，OB ，OC ，作OE BC ⊥于E ．设2OA OC x ==，∵2120COB CAB ∠=∠=︒，OC OB =，OE CB ⊥，∴CE EB =，60COE BOE ∠=∠=︒， ∴12OE OB x ==，3BE x =． ∵OC OE AG +，∴33x ，∴1x ，∴x 的最小值为1，∵23BC x =，∴BC 的最小值为23；（3）如图中，连接AF ，EF ，延长BC 交AE 的延长线于G ，∵90D ∠=︒，626AD DE ==+，∴45DAE AED ∠=∠=︒，∵6212CD AB ==，∴6CE CF ==，∴45CEF CFE ∠=∠=︒，∴90AEF ∠=︒，∴62EF BF ==，将EFM △顺时针旋转得到FBH ，作FHB △的外接O 交BC 于N ，连接ON ，∵90AEF ABF ∠=∠=︒，AF AF =，EF BF =，∴Rt Rt ()AEF ABF HL △≌△，∴AEF ABF S S =△△，∵45EFG ∠=︒，∵90FEG ∠=︒，45EFG ∠=︒， ∴EF EG == ∴12FG ==，由（2）可知，当FHN △的外接圆的圆心O 在线段BF 上时，FNH △的面积最小，此时四边形ANFE 的面积最大，设OF ON r ==，则2OB BN r ==，∴r +=∴r ⋅=-， ∴12(2NH ==-，∴四边形ANFM 的面积的最大值112(1212(222=⨯⨯+⨯⨯⨯ 144=．【点睛】本题属于圆综合题，考查了三角形的外接圆，解直角三角形，最值问题等知识，解题的关键是学会用转化的思想思考问题．6．，(2)证明见解析；(3)2cm ；【分析】(1) 先根据AB=3cm ，AP ： BP=1：2，计算出AP 、BP 的长度，再根据勾股定理即可求得AE 的长度；(2)根据折叠的性质得到点B 与点E 关于PQ 对称，进而得到PB=PE ，BF=EF ，∠BPF=∠EPF ，根据平行的性质再证明BP=BF=EF=EP 即可得到答案；(3) 找到E 点离A 最近和最远的两种情况，运用矩形的性质以及勾股定理即可求出点E 在边AD 上移动的最大距离；【详解】解：(1)∵AB=3cm ，若AP ： BP=1：2，则AP=113AB cm = ，BP=223AB cm =，根据折叠的性质得到：PE=PB=2cm ，又∵四边形ABCD 是矩形，∴∠A=90°， ∴222AP AE PE += ,即：22212AE +=，∴23AE=，AE=，即：3故AE的长为：3cm；(2)∵折叠纸片使B点落在边AD上的E处，折痕为PQ，∴点B与点E关于PQ对称．∴PB=PE，BF=EF，∠BPF=∠EPF．又∵EF∥AB，∴∠BPF=∠EFP（两直线平行，内错角相等），∴∠EPF=∠EFP（等量替换），∴EP=EF，∴BP=BF=EF=EP（四边相等的四边形是菱形），∴四边形BFEP为菱形；(3)当点Q与点C重合时，如图2所示，此时点E离点A最近，∵四边形ABCD是矩形，BC=AD=5cm，CD=AB=3cm，∠A=∠D=90°．∵点B与点E关于PQ对称，∴CE=BC=5cm，在Rt△CDE中，224=-=DE CE CD∴AE=AD-DE=5-4=1cm，此时AE=1cm；当P点与A点重合时，如图3所示，点E离点A最远．此时四边形ABQE为正方形，AE=AB=3cm．点E在边AD上移动的最大距离为2cm．【点睛】本题主要考查了矩形的性质、菱形的判定方法、勾股定理等知识，解题的关键是依题意画出正确的图形，运用折叠的对称性解决问题．7．（1）12；（2）73388-；（3）CH 的最小值为3739- 【分析】（1）连接OP ，根据切线的性质和圆周角定理的推论可得AC BC ⊥,∠BDC=90°，利用勾股定理求出AB ，然后根据三角形的面积公式即可求出CD ，根据垂线段最短可得当OP CD ⊥时，点P ，O 的距离最小，从而求出PD 的长；（2）连接CE ，则90ECF ∠=︒，利用勾股定理即可求出AE ，然后根据相似三角形的判定定理证出Δ~ΔACE AFC ，列出比例式，根据正切的定义即可求出结论；（3）以BD 为直径作G ，则G 为BD 的中点，利用勾股定理和圆的基本性质求出半径DG ，根据直径所对的圆周角是直角可得点H 一定在G 上，当点C ，H ，G 在一条直线上时，CH 最小，利用勾股定理求出CG ，即可求出结论．【详解】解：（1）如图1，连接OP ，AC 切O 于点C ，BC 为直径AC BC ∴⊥,∠BDC=90°30BC =，40AC =，50AB ∴=．由Δ1122ADC S AB CD AC BC =⋅=⋅, 即1150403022CD ⨯⨯=⨯⨯, 解得24CD =，当OP CD ⊥时，点P ，O 的距离最小，此时1122PD CD ==．（2）如图2，连接CE ，则90ECF ∠=︒．由（1）知，90ACB ∠=︒，由222AO AC OC =+，得()222154015AE +=+，解得57315AE =． 90ACB ECF ∠=∠=︒，ACE BCF AFC ∴∠=∠=∠．又CAE FAC ∠=∠，Δ~ΔACE AFC ∴， CE AE FC AC ∴=． 57315733tan 404088CE AE F CF AC ∴===-=-．（3）CH 的最小值为3739-．如图3，以BD 为直径作G ，则G 为BD 的中点，BD=2218-=BC CD ∴192==DG BD ， DH PB ⊥，∴点H 总在G 上，9GH =， ∴当点C ，H ，G 在一条直线上时，CH 最小，此时，2222249373CG CD DG =+=+=，3739CH =-，即CH 的最小值为3739-．【点睛】此题考查的是圆的综合大题、相似三角形的判定及性质、锐角三角函数和勾股定理，掌握切线的性质、圆周角定理及推论、相似三角形的判定及性质、锐角三角函数和勾股定理是解决此题的关键．8．（1）见解析；（2）D（233，33+2）；（3）372．【分析】（1）连接PA，先求出点A和点B的坐标，从而求出OA、OB、OP和AP的长，即可确定点A在圆上，根据相似三角形的判定定理证出△AOB∽△POA，根据相似三角形的性质和等量代换证出PA⊥AB，即可证出结论；（2）连接PA，PD，根据切线长定理可求出∠ADP＝∠PDC＝12∠ADC＝60°，利用锐角三角函数求出AD，设D（m，12m+2），根据平面直角坐标系中任意两点之间的距离公式求出m的值即可；（3）在BA上取一点J，使得BJ＝52，连接BG，OJ，JG，根据相似三角形的判定定理证出△BJG∽△BGA，列出比例式可得GJ＝12AG，从而得出12AG+OG＝GJ+OG，设J点的坐标为（n，12n+2），根据平面直角坐标系中任意两点之间的距离公式求出n，从而求出OJ的长，然后根据两点之间线段最短可得GJ+OG≥OJ，即可求出结论．【详解】（1）证明：如图1中，连接PA．∵一次函数y＝12x+2的图象与y轴交于A点，与x轴交于B点，∴A（0，2），B（﹣4，0），∴OA＝2，OB＝4，∵P（1，0），∴OP＝1，∴OA2＝OB•OP，225+=OA OP∴OAOP ＝OBOA，点A在圆上∵∠AOB＝∠AOP＝90°，∴△AOB∽△POA，∴∠OAP＝∠ABO，∵∠OAP+∠APO＝90°，∴∠ABO+∠APO＝90°，∴∠BAP＝90°，∴PA⊥AB，∴AB是⊙P的切线．（2）如图1﹣1中，连接PA，PD．∵DA，DC是⊙P的切线，∠ADC＝120°，∴∠ADP＝∠PDC＝12∠ADC＝60°，∴∠APD＝30°，∵∠PAD＝90°∴AD＝PA•tan30°＝153，设D（m，12m+2），∵A（0，2），∴m2+（12m+2﹣2）2＝159，解得m＝23∵点D在第一象限，∴m＝233，∴D233）．（3）在BA上取一点J，使得BJ5，连接BG，OJ，JG．∵OA＝2，OB＝4，∠AOB＝90°，∴AB22OA OB+2224+5∵BG5BJ5，∴BG2＝BJ•BA，∴BGBJ＝BABG，∵∠JBG＝∠ABG，∴△BJG∽△BGA，∴JGAG＝BGAB＝12，∴GJ＝12AG，∴12AG+OG＝GJ+OG，∵BJ5，设J点的坐标为（n，12n+2），点B的坐标为（-4,0）∴（n+4）2+（12n+2）2＝54，解得：n=-3或-5（点J在点B右侧，故舍去）∴J（﹣3，12），∴OJ22132⎛⎫+ ⎪⎝⎭37∵GJ+OG≥OJ，∴12AG+OG37，∴12AG+OG37故答案为372．【点睛】此题考查的是一次函数与圆的综合大题，掌握相似三角形的判定及性质、切线的判定及性质、切线长定理、勾股定理、锐角三角函数和两点之间线段最短是解决此题的关键． 9．（1）2；（2）13CD =+；（3）CD 的值最大，此时22CD =.【分析】(1)由旋转60°可知，△ACC’为等边三角形，进而'C C =AC=2即可求解.(2)过点B 作BH ⊥CD 于H ，求得△CBH 三边之比为1:3:2，进而求出CH 和BH 的长，再求得△DBH 为等腰直角三角形，最后得到CD=DH+CH 即可求解.(3)证明''∆∆B AB C AC ，再取AB 的中点H ，以H 为圆心，HB 为半径作H ，连接CH ，得出D 点的运动轨迹为以H 为圆心，HA 为半径的圆，当CD 是该圆的直径时CD 最大，即可求解.【详解】解：(1) ∵旋转前后对应的边相等，∴AC=AC’又∵旋转60°，∴△ACC’为等边三角形∴'2==C C AC .故答案为2.(2)如图2中，作BH CD ⊥于H ，如下图所示：','60AB AB BAB ︒=∠='ABB ∴∆是等边三角形，60︒∴∠=∠=DBM ACM ，DMB AMC ，45BDC BAC ︒∴∠=∠=，且△DBH 为等腰直角三角形，'30BCH BCA ACC ︒∠=∠-∠=11,32BH DH BC CH ∴==== 13CD CH DF ∴=+=故答案为：13+.()3CD 的长有最大值为22，理由如下，如下图3中，’'45B AC BAC ︒∠=∠=''B AB C AC ∴∠=∠','AB AB AC AC ==''AB AB AC AC∴= ''B AB C AC ∴∆∆DBM ACM DMB AMC ∴∠=∠45BDM MAC ︒∴∠=∠=取AB 的中点H ，以H 为圆心，HB 为半径作H ，连接CH ．,90CA CB ACB ︒=∠=,CH AB CH BH AH ∴⊥==，90BHC ︒∠=∴12BDC BHC ∴点D 的运动轨迹是以H 为圆心，HA 为半径的圆，当CD 是该圆的直径时CD 最大, 故CD AB =时，CD 的值最大，此时22CD =故答案为2.【点睛】本题综合考察了旋转图形的性质、含30°角的直角三角形三边之比、相似三角形的性质和判定、圆的相关知识等，熟练掌握线段绕其端点旋转60°会得到等边三角形这个特点进而求解本题.10．（1）∠ADE=30°；（2）∠ADE=30°，理由见解析；（3）92 【分析】（1）利用SAS 定理证明△ABD ≌△ACE ，根据全等三角形的性质得到AD =AE ，∠CAE=∠BAD，根据等腰三角形的性质、三角形内角和定理计算即可证明；（2）同（1）的证明方法相同；（3）证明△ADF∽△ACD，根据相似三角形的性质得到26ADAF=，求出AD的最小值，得到AF的最小值，求出CF的最大值．【详解】解：（1）∠ADE=30°．理由如下：∵AB=AC，∠BAC=120°，∴∠ABC=∠ACB=30°，∵∠ACM=∠ACB，∴∠ACM=∠ABC，在△ABD和△ACE中，∵AB ACABC ACE BD CE=⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ACE，∴AD=AE，∠CAE=∠BAD，∴∠DAE=∠BAC=120°，∴∠ADE=30°；（2）（1）中的结论成立，证明：∵∠BAC=120°，AB=AC，∴∠B=∠ACB=30°．∵∠ACM=∠ACB，∴∠B=∠ACM=30°．在△ABD和△ACE中，∵AB ACABC ACE BD CE=⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ACE，∴AD=AE，∠BAD=∠CAE，∴∠CAE+∠DAC=∠BAD+∠DAC=∠BAC=120°．即∠DAE=120°，∵AD=AE，∴∠ADE=∠AED=30°；（3）∵AB=AC，AB=6，∴AC=6，∵∠ADE=∠ACB=30°且∠DAF=∠CAD，∴△ADF∽△ACD，∴AD AFAC AD =， ∴AD 2=AF•AC ， ∴AD 2=6AF ，∴AF=26AD ，∴当AD 最短时，AF 最短、CF 最长，易得当AD ⊥BC 时，AF 最短、CF 最长，此时AD=12AB=3， ∴AF 最短=26AD =96=32，∴CF 最长=AC －AF 最短=6－32=92．【点睛】本题属于三角形综合题，考查了等腰三角形的性质，全等三角形的判定和性质以及相似三角形的判定与性质等知识，解题的关键是正确寻找全等三角形、相似三角形解决问题，属于中考常考题型．11．（1）5；（2）PQ ∥A D ''，理由见解析；（3 【分析】（1）求出AE △ABE ∽△DEA ，由AD AEAE BE=可求出AD 的长；（2）过点E 作EF ⊥AD 于点F ，证明△PEF ∽△QEC ，再证△EPQ ∽△A'ED'，可得出∠EPQ ＝∠EA'D'，则结论得证；（3）由（2）知PQ ∥A′D′，取A′D′的中点N ，可得出∠PEM 为定值，则点M 的运动路径为线段，即从AD 的中点到DE 的中点，由中位线定理可得出答案．【详解】解：（1）∵AB ＝2，BE ＝1，∠B ＝90°， ∴AE∵∠AED ＝90°， ∴∠EAD+∠ADE ＝90°，∵矩形ABCD 中，∠ABC ＝∠BAD ＝90°， ∴∠BAE+∠EAD ＝90°， ∴∠BAE ＝∠ADE ， ∴△ABE ∽△DEA ， ∴AD AEAE BE=，∴=，∴AD ＝5；（2）PQ ∥A′D′，理由如下： ∵5,5AD AE ==，∠AED ＝90°∴22DE DA AE =-＝225(5)-＝25，∵AD ＝BC ＝5，∴EC ＝BC ﹣BE ＝5﹣1＝4，过点E 作EF ⊥AD 于点F ，则∠FEC ＝90°， ∵∠A'ED'＝∠AED ＝90°， ∴∠PEF ＝∠CEQ ， ∵∠C ＝∠PFE ＝90°， ∴△PEF ∽△QEC ， ∴2142EP EF EQ EC ===， ∵51225EA EA ED ED ''===， ∴EP EA EQ ED ''=， ∴PQ ∥A′D′；（3）连接EM ，作MN ⊥AE 于N ，由（2）知PQ ∥A′D′， ∴∠EPQ ＝∠A′＝∠EAP ，又∵△PEQ 为直角三角形，M 为PQ 中点， ∴PM ＝ME ， ∴∠EPQ ＝∠PEM ，∵∠EPF ＝∠EAP+∠AEA′，∠NEM ＝∠PEM+∠AEA′ ∴∠EPF ＝∠NEM ，又∵∠PFE ＝∠ENM ﹣90°， ∴△PEF ∽△EMN ， ∴NM EM EF PE =＝PQ2PE为定值，又∵EF ＝AB ＝2，∴MN 为定值，即M 的轨迹为平行于AE 的线段， ∵M 初始位置为AD 中点，停止位置为DE 中点， ∴M 的轨迹为△ADE 的中位线， ∴线段PQ 的中点M 所经过的路径长＝1AE 2＝52．【点睛】本题考查了矩形的性质，相似三角形的判定与性质，勾股定理，平行线的判定，中位线定理等知识，熟练掌握相似三角形的判定与性质是解题的关键．12．()1作图见解析；()2证明见解析；()3证明见解析；()4 EF 最小值为262. 【分析】()1当AE CD ⊥，此时AC 是O 的直径，作出AC 的中点O 后，以OA 为半径作出O即可作出点E 、F ；()2易知AC 为直径，则AF BC ⊥，ABCD S BC AF CD AE =⋅=⋅四边形，从而得证；()3如图，作AM BC ⊥，AN CD ⊥，若E 在DN 之间，由()2可知，AMABANAD=，然后再证明AMF ∽ANE ，从而可知AM AF ABAN AE AD==，若E 在CN 之间时，同理可证；()4由于A 、F 、C 、E 四点共圆，所以180FAE BCD ∠+∠=，由于四边形ABCD 为平行四边形，45B ∠=，从而可证FOE 为等腰直角三角形，所以2FE R =，由于2AN AC R ≤≤，所以E 与N 重合时，FE 最小．【详解】()1如图1所示，()2如图，易知AC 为直径，则AF BC ⊥，则ABCD S BC AF CD AE =⋅=⋅四边形，AF CD ABAE BC AD∴==， ()3如图，作AM BC ⊥，AN CD ⊥，若E 在DN 之间由()2可知，AM ABAN AD= A 、F 、C 、E 四点共圆，AFC AEC 180∠∠∴+=，AFC AFM 180∠∠+=， AEN AFM ∠∠∴=， AMF ANE ∠∠=， AMF ∴∽ANE AM AF AB AN AE AD∴==，若E 在CN 之间时，同理可证()4A 、F 、C 、E 四点共圆，FAE BCD 180∠∠∴+=，四边形ABCD 为平行四边形，B 45∠=，BCD 135∠∴=， FAE 45∠∴=， FOE 90∠∴=，FOE ∴为等腰直角三角形， FE 2R ∴=，AN AC 2R ≤≤，E ∴与N 重合时，FE 最小，此时2FE =，在ABC 中，AM BM 3==，则CM 2=∴由勾股定理可知：AC 13=此时EF 最小值为262. 【点睛】。

初中数学几何最值问题

○ 转化为两定点之问的折线段，利用两点之间
○ 线段最短确定在点共线的情形下取得最值．
2 模型思想
2．1 建立方程模型
例4 已知△ XYZ是直角边长为1的等腰直角三角形( ∠Z=90 。)，它的三个顶点分别在等腰Rt△ ABC(∠ C=90。)的三边上．
求△ ABC直角边长的最大可能值．
感谢观看
添加副标题
汇报人姓名
几何最值问题
添加副标题
汇报人姓名
1
几何变换
1．1 利用平移变换
例1 ：已知点P在锐角△ABC的边上运动．试确定点P的位置，使P A+PB+PC最小，并证明你的结论．
解：当点P在锐角△ ABC最短边上的高的垂足位置时， P A+型线段组

2020年九年级数学中考经典几何题讲义系列：几何最值问题

中考经典几何题系列：几何最值问题【知识点】几何中最值问题包括： ①“面积最值” ②“线段（和、差）最值”.（1）求面积的最值方法：需要将面积表达成函数，借助函数性质结合取值范围求解；（2）求线段及线段和、差的最值方法：需要借助“垂线段最短”、“两点之间线段最短”及“三角形三边关系”等相关定理转化处理.一般处理方法：常用定理：两点之间，线段最短（已知两个定点时）垂线段最短（已知一个定点、一条定直线时）三角形三边关系下面对三类线段和的最值问题进行分析、讨论。

（1）两点一线的最值问题: （两个定点 + 一个动点）问题特征：已知两个定点位于一条直线的同一侧，在直线上求一动点的位置，使动点与定点线PA +PB 最小，需转化，使点在线异侧 Bl段和最短。

核心思路：这类最值问题所求的线段和中只有一个动点，解决这类题目的方法是找出任一定点关于直线的对称点，连结这个对称点与另一定点，交直线于一点，交点即为动点满足最值的位置。

方法：1.定点过动点所在直线做对称。

2.连结对称点与另一个定点，则直线段长度就是我们所求。

变异类型：实际考题中，经常利用本身就具有对称性质的图形，比如等腰三角形，等边三角形、正方形、圆、二次函数、直角梯形等图形，即其中一个定点的对称点就在这个图形上。

1.如图，直线l和l的同侧两点A、B，在直线l上求作一点P，使PA+PB最小。

（2）一点两线的最值问题: （两个动点+一个定点）问题特征：已知一个定点位于平面内两相交直线之间，分别在两直线上确定两个动点使线段和最短。

核心思路：这类问题实际上是两点两线段最值问题的变式，通过做这一定点关于两条线的对称点，实现“搬点移线”，把线段“移”到同一直线上来解决。

变异类型：1.如图，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△PAB的周长最小。

2.如图，点A 是∠MON 外的一点，在射线OM 上作点P ，使PA 与点P 到射线ON 的距离之和最小。

初中数学几何最值问题

初中数学几何最值问题公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]初中数学几何最值问题在平面几何的动态问题中，当某几何元素在给定条件变动时，求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题，称为几何最值问题.近年来，各地中考题常通过几何最值问题考查学生的实践操作能力、空间想象能力、分析问题和解决问题的能力.本文针对不同类型的几何最值问题作一总结与分析，希望对大家有所帮助.最值问题的解决方法通常有如下6大类:1.三角形的三边关系例1.如图，在矩形纸片ABCD中，AB=2，AD=3，点E是AB的中点，点F是AD边上的一个动点，将△AEF沿EF所在直线翻折，得到△A′EF，则A′C的长的最小值是．2.两点间线段最短例2 如图2，圆柱底面半径为2cm,高为9 cm，点,A B分别是回柱两底面圆周上的点，且,A B在同一母线上，用一棉线从A顺着圆柱侧面绕3圈到B，求棉线长度最短为 .` 3.垂线段最短例3 如图，在Rt△ABC中，∠B=90°，AB=6，BC=8，点D在BC 上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是____________•4.利用轴对称例4.如上右图，矩形ABOC的顶点A的坐标为（﹣4，5），D是OB的中点，E是OC上的一点，当△ADE的周长最小时，点E的坐标是（）A．（0，）B．（0，）C．（0，2）D．（0，）例5 如图5，正方形ABCD，4AB=，E是BC的中点，点P是对角线AC上一动点，则PE PB+的最小值为 .5.利用二次函数例6在边长为2的等边三角形ABC中，P是BC边上任意一点，过点P分别作 PM⊥A B，PN⊥AC，M、N分别为垂足．（1）求证：不论点P在BC边的何处时都有PM+PN的长恰好等于三角形ABC一边上的高；（2）当BP的长为何值时，四边形AMPN的面积最大，并求出最大值．6利用圆中直径是最长的弦例7.如图，AB是⊙O的弦，AB=6，点C是⊙O上的一个动点，且∠ACB=45°．若点M，N分别是AB，BC的中点，则MN长的最大值是．同步练习1.如图，将矩形MNPQ放置在矩形ABCD中，使点M，N分别在AB，AD 边上滑动，若MN=6，PN=4，在滑动过程中，点A与点P的距离AP的最大值为___________.2.李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长。

几何最值问题(习题及答案)

几何最值问题（习题）例题示范例 1：如图，折叠矩形纸片ABCD，使点B 落在边AD 上，折痕EF 的两端分别在A B，BC 上（含端点）．若A B=6cm，BC=10cm，则AB' 的取值范围是．B F CEA B' D【思路分析】1.明确目标，分析定点、动点要求AB' 的取值范围，即求AB' 的最大值与最小值，定点是A，动点是B' ；2.分析动点的形成因素，寻找不变特征动点B' 是由点B 折叠得到的，所以B'E =BE，B'F =BF，因为AE+BE=6，CF+BF=10，所以AE +B'E =6，C F +B'F =10（不变特征）．先求AB' 的最大值：把AE，B'E ，AB' 放在一个三角形中，根据三角形三边关系：两边之和大于第三边，可得：AB' < AE +B'E ，即AB' < 6 ，如果AB' 有最大值，则三角形三个顶点应该共线，即点E 与点A 重合，此时AB'=6 ，由此可得，AB' ≤6，即AB' 的最大值是 6．再求AB' 的最小值：转化为求B'D 的最大值，考虑把B'D 放入 Rt△B'DC 中，只需B'C 最大即可，把CF，B'F ，B'C 放在一个三角形中，根据三角形三边关系，类比上面求解AB' 最大值的方法得到B'C 的最大值为 10，由此得到B'D 的最大值是 8，即AB' 的最小值是 2．综上，AB' 的取值范围是：2cm≤AB' ≤6cm．3.作出图形，验证是否符合题意．B FC B C(F)EA(E)B' D A B' D图1图2巩固练习1.如图，在△ABC 中，∠BAC=120°，AB=AC=4，点M，N 分别在边A B，AC 上，将△AMN 沿M N 翻折，点A的对应点为A' ，连接BA' ，则B A' 长度的最小值为．AM NA'B C2.如图，在三角形纸片ABC 中，已知∠ABC=90°，AC=5，BC=4．过点A 作直线l 平行于BC，折叠三角形纸片ABC，使直角顶点B 落在直线l上的点P处，折痕为M N．当点P在直线l上移动时，折痕的端点M，N 也随之移动，若限定端点M，N 分别在AB，BC 边上（包括端点）移动，则线段A P 长度的最大值与最小值之差为．A P lB N C3.在锐角△ABC 中，AB=4，BC=5，将△ABC 绕点B按逆时针方向旋转，得到△A1BC1．若E为线段A B 的中点，则在△ABC绕点B 按逆时针方向旋转的过程中，线段EC1 长度的最大值是，最小值是．C1B C4.如图，在△ABC 中，AB=5，AC=12，BC=13，P 为BC 边上任一点，PE⊥AB 于点E，PF⊥AC 于点F，M 为E F 中点，则线段P M 长度的最小值为．AB P C5.正方形ABCD 的边长为a，P 是BC 边上任意一点（可与B，C 重合），B，C，D 三点到射线A P 的距离分别是h1，h2，h3，设h1+h2+h3=y，则y的最大值是，最小值是D CA B6.如图，已知AB=10，P 是线段AB 上任意一点，在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD，则线段CD 长度的最小值为．CA P B7.如图，在R t△ABC 中，∠ACB=90°，AC=6，BC=4，在△ABC 内部以A C 为斜边任意作R t△ACD，连接B D，则线段B D 长度的最小值为．BC A8.如图，正方形ABCD 的边长是2，以正方形ABCD 的边AB 为边，在正方形内作等边三角形A BE，P 为对角线A C 上的一动点，则P D+PE 的最小值为．A DB C9.如图，在菱形ABCD 中，AB=2，∠A=120°，若P，Q，K 分别为线段BC，CD，BD 上的任一点，则PK+QK 的最小值为A DB P C思考小结1．几何最值问题的处理思路①分析定点、动点，寻找不变特征；②若属于常见模型、结构，调用模型、结构解决问题；若不属于常见模型，要结合所求目标，根据不变特征转化为基本定理或表达为函数解决问题．2．转化原则：尽量减少变量，向定点、定线段、定图形靠拢，或使用同一变量表达所求目标．3．基本定理：两点之间，线段最短（已知两个定点）垂线段最短（已知一个定点、一条定直线）三角形三边关系（已知两边长固定或其和、差固定）4．常用模型、结构示例：①轴对称最值模型AllB求P A+PB 的最小值，求|PA-PB|的最大值，对称至异侧对称至同侧B' BlM N固定长度线段MN 在直线l 上滑动，求AM+MN+BN 的最小值，需平移BN（或AM），转化为AM +MB'解决．②折叠求最值结构AM NA'B C求BA′的最小值，转化为求BA′+A′N+NC 的最小值（利用A′N+NC 为定值）．【参考答案】1．4 42． 1 3．7，34．30 135．2a，2a 6．57．28．29．。

(word完整版)初中数学《最值问题》典型例题

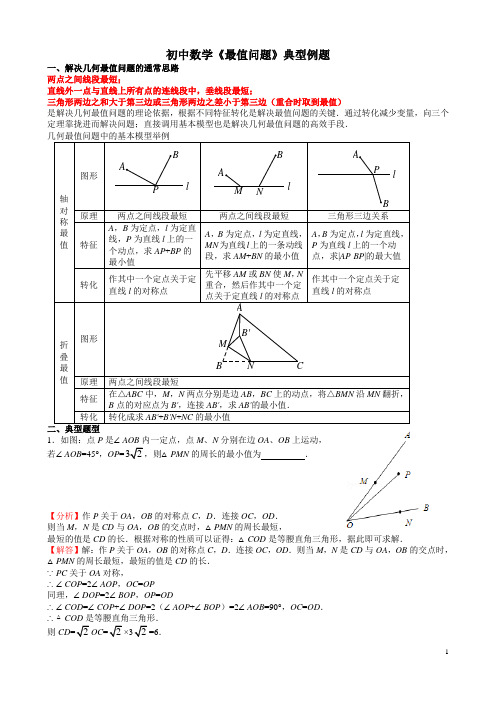
初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．轴对称最值图形lPBANM lBAAPBl原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'，连接AB'，求AB'的最小值．转化转化成求AB'+B'N+NC的最小值1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=32，则△PMN的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=2OC=2×32=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形P ABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出P A+NB的长度就行了．问题就是P A+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时P A+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b=+⎧⎨-=+⎩，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A、B两点在直线的两侧，点A到直线的距离AM=4，点B到直线的距离BN=1，且MN=4，P为直线上的动点，|P A﹣PB|的最大值为．DPB′NMA【分析】作点B于直线l的对称点B′，则PB=PB′因而|P A﹣PB|=|P A﹣PB′|，则当A，B′、P在一条直线上时，|P A﹣PB|的值最大．根据平行线分线段定理即可求得PN和PM的值然后根据勾股定理求得P A、PB′的值，进而求得|P A﹣PB|的最大值．【解答】解：作点B于直线l的对称点B′，连AB′并延长交直线l于P．∴B′N=BN=1，过D点作B′D⊥AM，利用勾股定理求出AB′=5∴|P A﹣PB|的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD中，AB=3，AD=5．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为．【分析】本题关键在于找到两个极端，即BA′取最大或最小值时，点P或Q的位置．经实验不难发现，分别求出点P与B重合时，BA′取最大值3和当点Q与D重合时，BA′的最小值1．所以可求点A′在BC边上移动的最大距离为2．【解答】解：当点P与B重合时，BA′取最大值是3，当点Q与D重合时（如图），由勾股定理得A′C=4，此时BA′取最小值为1．则点A′在BC边上移动的最大距离为3﹣1=2．故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD，AD⊥AB，AB=8，AD=CD=4，点E、F分别在线段AB、AD上，将△AEF 沿EF翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，PD的最小值等于．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PF AE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458 ．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE=AE=12AB=1，∵BC=1，四边形ABCD是矩形，∴AD，∴DE2，根据三角形的三边关系，OD＜OE+DE，∴当OD过点E是最大，最大值为2+1．故答案为：2+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE，那么DE长的最小值是．【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=22x，CD′=22（4﹣x），根据勾股定理然后用配方法即可求解．【解答】解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=22x，CD′=22（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=12x2+12（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK 的最小值为．【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为2×33∴PK+QK3故答案为：3．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′+CC′+DD′的取值范围是．【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，继而可得12AP•（BB′+CC′+DD′）=1，又由1≤AP≤2，即可求得答案．【解答】解：连接AC，DP．∵四边形ABCD是正方形，正方形ABCD的边长为1，∴AB=CD，S正方形ABCD=1，∵S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，∴S△ADP+S△ABP+S△ACP=1，∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•（BB′+CC′+DD′）=1，则BB′+CC′+DD′=2 AP，∵1≤AP≤2，∴当P2；当P与C重合时，有最小值2．∴2≤BB′+CC′+DD′≤2．故答案为：2≤BB′+CC′+DD′≤2．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADP+S△ABP+S△ACP=1，继而得到BB′+CC′+DD′=2 AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A 和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。

(完整word版)初中数学《几何最值问题》典型例题

几何最值问题(习题及答案)

2 4. 12
5
5. 3 3
6.
（1
；
（2）点 P 的坐标为(0，2)；
（3）-5＜x＜0 或 x＞3．
7. （1） y 1 x2 1 x 1，对称轴为直线 x=1； 84
（2）存在，点 P 的坐标为(1， 1 )． 2
8. D
4
B．3
C．4
D．5
C
C
MD D
E
A
B
F
OE
B
第 1 题图
第 2 题图
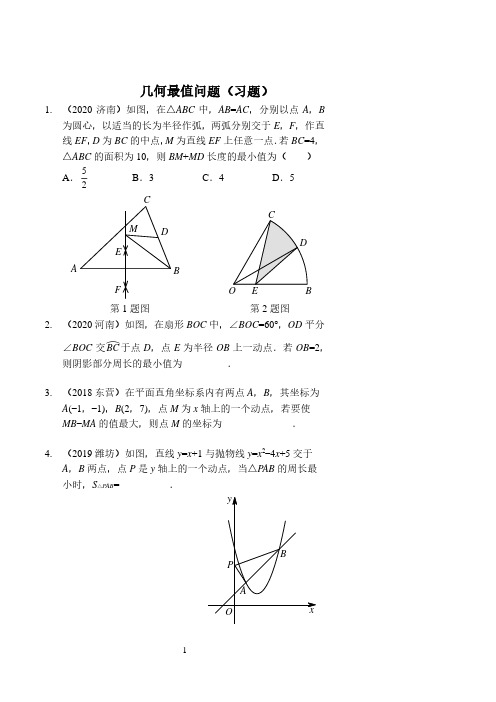
2. （2020 河南）如图，在扇形 BOC 中，∠BOC=60°，OD 平分
︵ ∠BOC 交 BC 于点 D，点 E 为半径 OB 上一动点．若 OB=2，
则阴影部分周长的最小值为_________．
3. （2018 东营）在平面直角坐标系内有两点 A，B，其坐标为 A(-1，-1)，B(2，7)，点 M 为 x 轴上的一个动点，若要使 MB-MA 的值最大，则点 M 的坐标为______________．
几何最值问题（习题）
1. （2020 济南）如图，在△ABC 中，AB=AC，分别以点 A，B
为圆心，以适当的长为半径作弧，两弧分别交于 E，F，作直
线 EF，D 为 BC 的中点，M 为直线 EF 上任意一点．若 BC=4，
△ABC 的面积为 10，则 BM+MD 长度的最小值为（）
A． 5 2
y
O
AC
B
x
y
O
AC
B
x
备用图
8. （2019 泰安）如图，矩形 ABCD 中，AB=4，AD=2，E 为 AB 的中点，F 为 EC 上一动点，P 为 DF 中点，连接 PB，则 PB 的最小值是（）