【2020】最新小升初数学几何图形阴影部分面积题型大全(详细答案解析)
小升初求阴影部分面积专题训练——经典例题(含答案)

小升初求阴影部分面积专题训练1.求如图阴影部分的面积.(单位:厘米)2.如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
小升初数学几何求阴影部分面积题带解析
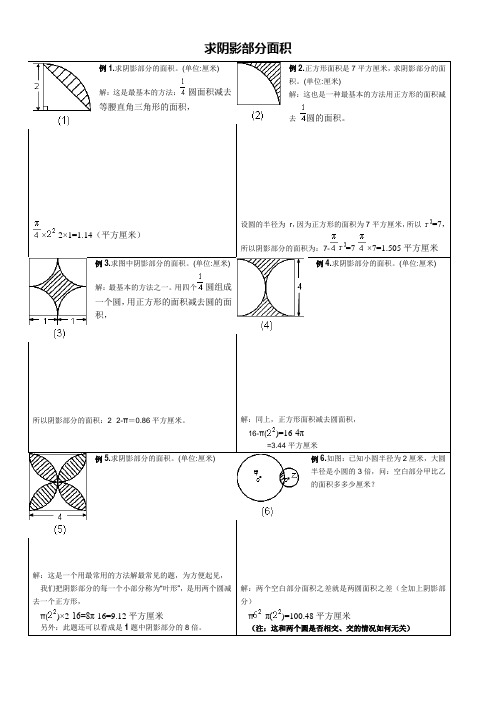
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积。
30道小升初数学几何问题(附答案)
图1
图2
【解析】我们可以让静止的瓷砖动起来,把对角线上的黑瓷砖,通过平移这种动态的
处理,移到两条边上(如图 2).在这一转化过程中瓷砖的位置发生了变化,但数量没
有变,此时白色瓷砖组成一个正方形.大正方形的边长上能放 (1011) 2 51(块),白
色 瓷 砖 组 成 的 正 方 形 的 边 长 上 能 放 : 511 50 ( 块 ) , 所 以 白 色 瓷 砖 共 用 了 :
60 的扇形面积 60 π 32 3 π 4.5(cm2 ) .
360
2
2.【割补法求面积】求下列各图中阴影部分的面积(图中长度单位为 cm ,圆周率按 3 计 算):
3
⑴
4
⑵
1
2
1
⑶
1
⑷
【解析】⑴ 4.5 ⑵ 4 ⑶1 ⑷ 2
3.【差不变】三角形 ABC 是直角三角形,阴影 I 的面积比阴影 II 的面积小 25cm2 , AB 8cm ,求 BC 的长度.
5
【解析】根据题意可知,挖去的 6 个边长 1 厘米的正方体相互之间是独立的,所以挖 去之后,原正方体的表面积相当于增加了六个小正方体的侧面积,所以现在它的表面 积为: 4 4 6 11 4 6 120 平方厘米. 16.【共高模型】如图,把四边形 ABCD 的各边都延长 2 倍,得到一个新四边形 EFGH 如果 ABCD 的面积是 5 平方厘米,则 EFGH 的面积是多少平方厘米?
【解析】该图形的上、左、前三个方向的表面分别由 9、7、7 块正方形组成.
该图形的表面积等于 (9 7 7) 2 46 个小正方形的面积,所以该图形表面积 为 46 平方厘米.
21.【取特殊点】长方形 ABCD 的面积为 36, E 、 F 、 G 为各边中点, H 为 AD 边上任 意一点,问阴影部分面积是多少?
(完整版)小学求阴影部分面积专题—含答案

(5)【史上最全小学求阴影部分面积专题一含答案】 小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区 分。
面积求解大致分为以下几类:1、 从整体图形中减去局部;2、 割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本 的平面图形的面积求阴影部分的面积。
(4)例1•求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)(2)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为 2厘米,大圆半径是小圆的 问:空白部分甲比乙的面积多多少即3倍, 厘22㈣厘米)3-10-(M)3(13)—了 —⑴)例8.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米) 例13.求阴影部分的面积。
(单位:厘米) 例10.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位 例14.求阴影部分的面积。
(单位:厘米)例7.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米) 3(12)2十“7I* --- 5 —积45(15)扇形,求阴影部分的周长。
BAE C(18)分的面积(佟)(20)(22?(21)例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形 ABCD 的面积是36平方厘米,求阴影部 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的 例21.图中四个圆的半径都是 1厘米,求阴影部分的面积。
例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例16.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是 12平方厘米,求阴影部分的面 例22.如图,正方形边长为 8厘米,求阴影部分的面积。
小学及小升初复习阴影部分求面积及周长用—含完整答案

【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)ﻫ例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
ﻫ例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
ﻫ例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
【2020】最新小升初数学几何图形阴影部分面积题型大全(详细答案解析)
解:根据沙漏模型,可知
AF:FD =AB:DE=4:(10-4)=2:3 ,
AF+FD=,4 所以 AF=4× 2 =1.6cm, 23
S
ABF
=
1 2
AF
AB = 1 1.6 4 =3.2 cm 2 2
19、如图,在边长为 6cm 的正方形内有一个三角形 BEF ,线段 AE=3cm ,DF=2cm , 求三角形 BEF 的面积。
30.如图,已知 AB=8 厘米, AD=12 厘米,三角形 ABE 和三角形 ADF 的面积各 占长方形 ABCD 的三分之一。 求三角形 AEF 的面积。
解: S梯形 ABCF= 2 SABCD = 2 8 12 =64 平方厘米。
3
3
CF 2S梯形 ABCF BC-AB =2× 64÷ 12-8= 8 厘米,同 3
1 4
S圆
,
S阴
=S
①
S②
= S BCD S③ = S BCD
SEFDC
1 S圆
=1
BC
CD
4
2
EF 2 1 2 4
= 1 8 4 42 1 3.14 42 =16-(16-12.56)=12.56 cm2
解: DE=AD-AE=6-3=3厘米, FC=CD-DF=6-2=4c,m
S BEF SABCD S ABE S DEF S BCF
= AB AD
1 (AB AE
BC FC DE DF)
2
=62 1 (6 3 6 4 3 2) =12cm2 。 2
20、已知梯形 ABCD 的面积是 27.5 平方厘米,求三角形 ACD 的面积。 解: AB=2S梯形 ÷ (AD+BC)=2× 27.5 ÷ (7+4)=5cm,
小升初图形阴影部分面积教案(包含答案)

小升初图形阴影部分面积(专题)课堂引导:问题: 大家的小学生活马上就要结束了,在小学中我们学习过哪些几何图形呢知识点回顾:正方形的面积=长方形的面积=梯形的面积=三角形的面积=圆的面积=大家想一想,我们还有哪些面积公式没有想到扇形的面积=平行四边形的面积=互动环节:我画大家猜,怎样计算下列阴影部分的面积目的:引导学生初步掌握阴影部分面积的计算方法。
涂色面积=长方形面积+三角形面积涂色部分面积=长方形面积+半圆面积×2涂色部分面积=长方形面积+圆形面积涂色面积=正方形面积+半圆面积涂色面积=外圆面积—内圆面积涂色面积=正方形面积—圆形面积涂色面积=半圆面积—三角形面积涂色面积=外半圆面积—内半圆面积问题:一、序号为1、2、3、6的图形,它们的阴影部分面积是怎样计算大家有没有发现什么规律!引导学生回答出来:涂色部分面积是几个简单图形面积的差二、那么序号为4、5、7的图形,它们的阴影部分的面积又是怎样计算根据题意引导学生回答:涂色部分面积是几个简单图形面积的和经典题型【例题1】:图中两个正方形的边长分别是6厘米和4厘米,求阴影部分的面积。
【试一试】:1、边长分别为3厘米与5厘米的两个正方形拼在一起(如图)。
求阴影部分的面积。
2、求图形阴影部分面积(单位:厘米)【例题2】:求组合图形的面积。
(单位:厘米)【分析与解答】:上图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.4÷2=2(米)4×4+2×2×3.14÷2=22.28(平方厘米)【试一试】:长方形长6厘米,宽4厘米,求阴影部分的面积。
【分析与解答】:上图中,若求阴影部分的面积,只需先求出长方形面积再减去里面圆的面积即可.4÷2=2(米)6×4-2×2×3.14=11.44(平方厘米)【例题】3、计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.4、求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.【试一试】:求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.【例题】5.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.【试一试】:求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.【例题】6、求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.【试一试】:如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.【例题】7、求阴影部分面积(单位:厘米)8、求阴影部分面积(单位:厘米)【试一试】:求阴影部分的面积。
小学求阴影部分面积专题—含答案
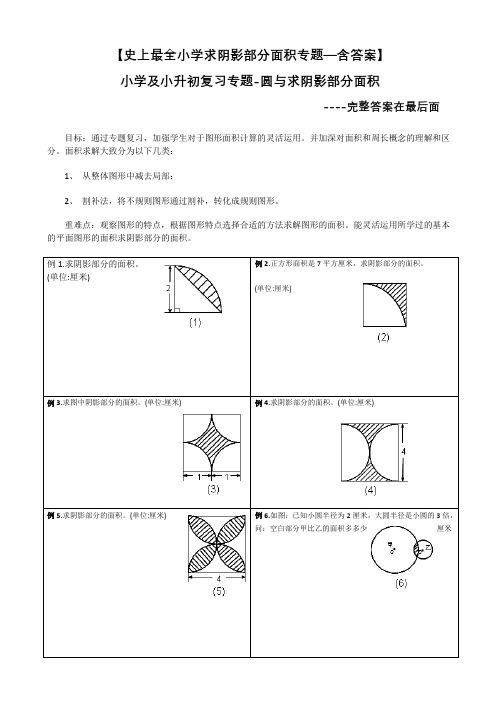
【史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题-圆与求阴影部分面积----完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例1.求阴影部分的面积。
(单位:厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例16.求阴影部分的面积。
(单位:厘米)例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米) 例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22.如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
完整版)小学求阴影部分面积专题—含答案

完整版)小学求阴影部分面积专题—含答案本文是一个小学及小升初复专题,主要介绍了圆与求阴影部分面积的相关知识。
文章提到了面积求解的两种方法,并强调了观察图形特点的重要性。
接下来列举了多个例子,要求读者求解阴影部分的面积。
最后一个例子是四个扇形的半径相等,需要求阴影部分的面积。
为了更好地理解文章,下面将对每个例子进行简单的解释和改写。
例1:给定一个图形,要求求出阴影部分的面积。
这个例子没有具体的图形,需要根据题目所给的数据进行计算。
例2:一个正方形的面积是7平方厘米,求阴影部分的面积。
这个例子需要注意正方形的面积和阴影部分的关系。
例3:给定一个图形,要求求出阴影部分的面积。
这个例子需要观察图形的特点,选择合适的方法求解面积。
例4:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例5:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例6:已知小圆半径为2厘米,大圆半径是小圆的3倍,问空白部分甲比乙的面积多多少。
这个例子需要根据圆的面积公式求解。
例7:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例8:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例9:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例10:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例11:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例12:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例13:给定一个图形,要求求出阴影部分的面积。
同样需要观察图形的特点,选择合适的方法求解面积。
例14:给定一个图形,要求求出阴影部分的面积。
小升初数学 阴影部分算面积
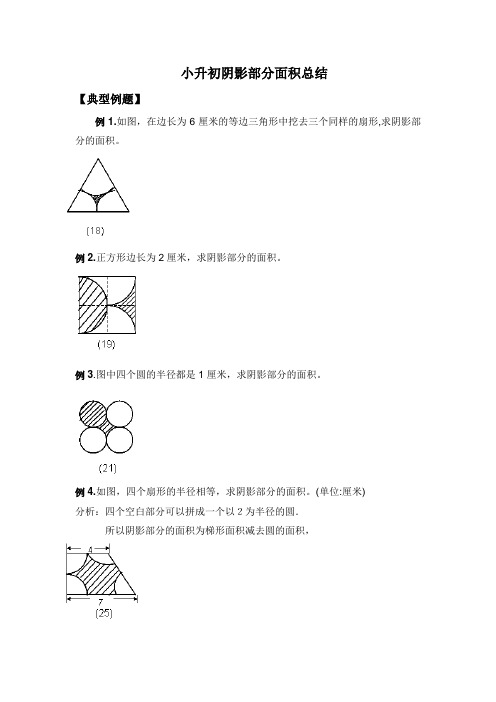
小升初阴影部分面积总结【典型例题】例1.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的面积。
例2.正方形边长为2厘米,求阴影部分的面积。
例3.图中四个圆的半径都是1厘米,求阴影部分的面积。
例4.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米)分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,例22.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
例23.求阴影部分的面积。
(单位:厘米)例24.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)【练习】1、求阴影部分的面积。
(单位:厘米)〖综合练习〗 一、填空题。
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
2. 下图中,∠1=( )度,∠2=( )度。
3. 一个三角形中,最小的角是46°,按角分类,这个三角形是( )三角形。
4. 下图是三个半径相等的圆组成的图形,它有( )条对称轴。
5. 用百分数表示以下阴影部分是整个图形面积的百分之几。
6. 把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少( )平方分米。
13027. “”和“”的周长之比是(),面积之比是()。
8.下图是由棱长1厘米的小正方体木块搭成的,这个几何体的表面积是()平方厘米。
至少还需要()块这样的小正方体才能搭成一个大正方体。
9. 画一个周长25.12厘米的圆,圆规两脚间的距离是()厘米,画成的圆的面积是()。
10. 下面的小方格边长为1厘米,估一估图①中“福娃”的面积,算一算图②中阴影部分的面积。
11. 一个梯形,上底长a厘米,下底长b厘米,高h厘米。
小升初数学 阴影部分算面积
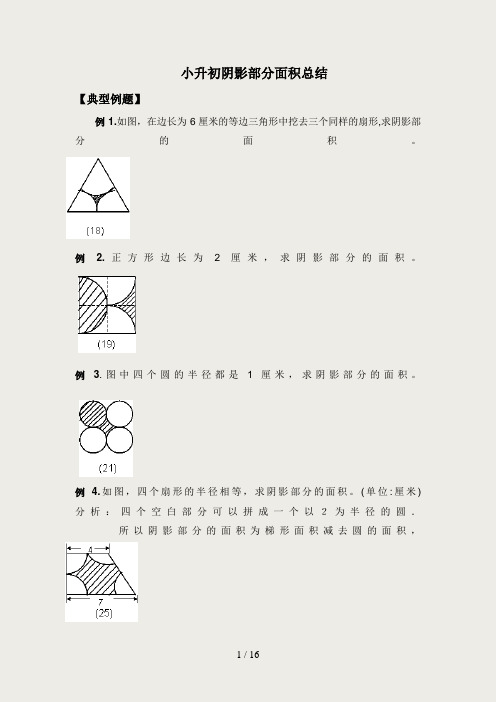
小升初阴影部分面积总结【典型例题】例1.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的面积。
例 2.正方形边长为2厘米,求阴影部分的面积。
例3.图中四个圆的半径都是1厘米,求阴影部分的面积。
例 4.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米) 分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,例22.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
例23.求阴影部分的面积。
(单位:厘米)例24.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
例 2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)【练习】1、求阴影部分的面积。
(单位:厘米)〖综合练习〗一、填空题。
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线()的线段。
2. 下图中,∠1=()度,∠2=()度。
13023. 一个三角形中,最小的角是46°,按角分类,这个三角形是()三角形。
4. 下图是三个半径相等的圆组成的图形,它有()条对称轴。
5. 用百分数表示以下阴影部分是整个图形面积的百分之几。
6. 把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少()平方分米。
7. “”和“”的周长之比是(),面积之比是()。
8.下图是由棱长1厘米的小正方体木块搭成的,这个几何体的表面积是()平方厘米。
至少还需要()块这样的小正方体才能搭成一个大正方体。
9. 画一个周长25.12厘米的圆,圆规两脚间的距离是()厘米,画成的圆的面积是()。
10. 下面的小方格边长为1厘米,估一估图①中“福娃”的面积,算一算图②中阴影部分的面积。
11. 一个梯形,上底长a厘米,下底长b厘米,高h厘米。
小升初数学 阴影部分算面积

小升初阴影部分面积总结【典型例题】例1.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的面积。
例2.正方形边长为2厘米,求阴影部分的面积。
例3.图中四个圆的半径都是1厘米,求阴影部分的面积。
例4.如图,四个扇形的半径相等,求阴影部分的面积。
(单位:厘米)分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,例22.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积。
例23.求阴影部分的面积。
(单位:厘米)例24.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米。
求BC的长度。
例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)【练习】1、求阴影部分的面积。
(单位:厘米)〖综合练习〗 一、填空题。
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
2. 下图中,∠1=( )度,∠2=( )度。
3. 一个三角形中,最小的角是46°,按角分类,这个三角形是( )三角形。
4. 下图是三个半径相等的圆组成的图形,它有( )条对称轴。
5. 用百分数表示以下阴影部分是整个图形面积的百分之几。
6. 把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体,原来的圆柱体表面积减少( )平方分米。
13027. “”和“”的周长之比是(),面积之比是()。
8.下图是由棱长1厘米的小正方体木块搭成的,这个几何体的表面积是()平方厘米。
至少还需要()块这样的小正方体才能搭成一个大正方体。
9. 画一个周长25.12厘米的圆,圆规两脚间的距离是()厘米,画成的圆的面积是()。
10. 下面的小方格边长为1厘米,估一估图①中“福娃”的面积,算一算图②中阴影部分的面积。
11. 一个梯形,上底长a厘米,下底长b厘米,高h厘米。
(完整版)小学求阴影部分面积专题—含答案

史上最全小学求阴影部分面积专题—含答案】小学及小升初复习专题- 圆与求阴影部分面积- 完整答案在最后面目标:通过专题复习,加强学生对于图形面积计算的灵活运用。
并加深对面积和周长概念的理解和区分。
面积求解大致分为以下几类:1、从整体图形中减去局部;2、割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例 1. 求阴影部分的面积。
(单位:厘米)例 2. 正方形面积是7 平方厘米,求阴影部分的面积。
(单位:厘米)例 3. 求图中阴影部分的面积。
(单位:厘米)例 4.求阴影部分的面积。
(单位:厘米)例 5.求阴影部分的面积。
(单位:厘米)例 6. 如图:已知小圆半径为 2 厘米,大圆半径是小圆的问:空白部分甲比乙的面积多多少3 倍,厘厘米)例 8.求阴影部分的面积。
(单位:厘米 )例 11.求阴影部分的面积。
(单位 :厘米)例 13.求阴影部分的面积。
(单位 :厘米) 例 10.求阴影部分的面积。
(单位 :厘米 )例 12. 求阴影部分的面积。
(单位 例 14.求阴影部分的面积。
(单位 :厘米 )例 7.求阴影部分的面积。
(单位:厘米 )例 9.求阴影部分的面积。
(单位:厘米 )积扇形 ,求阴影部分的周长。
分的面积例 19. 正方形边长为 2 厘米,求阴影部分的面积。
例 20.如图,正方形 ABCD 的面积是 36 平方厘米,求阴影部 例 18.如图,在边长为 6 厘米的等边三角形中挖去三个同样的 例 21 .图中四个圆的半径都是 1 厘米,求阴影部分的面积。
例 17.图中圆的半径为 5 厘米,求阴影部分的面积。
(单位:厘米)例 16.求阴影部分的面积。
(单位 :厘米 )例 15. 已知直角三角形面积是 12 平方厘米,求阴影部分的面 例 22. 如图,正方形边长为 8 厘米,求阴影部分的面积。
六年级求阴影部分面积典型题和答案,一定要掌握!

六年级求阴影部分面积典型题和答案,一定要掌握!求平面图形中阴影部分的面积,是每年小升初考试中得几何热点,思维能力要求高,学生失分率高。
由于阴影部分的图形常常不是以基本几何图形的形状出现,没法直接利用课本中的基本公式来计算,所以比较麻烦,有的甚至无法求解。
家长辅导孩子处理这类型的几何题,除了要让孩子熟练地掌握平面图形的概念和面积公式之外,关键还在于懂得如何“巧用方法、妙在变形”。
以下是小学阶段常见的求阴影面积的方法,家长可以让孩子边做边总结方法,逐一攻关。
求阴影部分的面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
小升初求阴影部分的面积讲义+习题解答

求阴影面积专题讲解一、知识点梳理1、几种主要的平面几何图形的周长和面积公式:2、等积变换:(1)等底等高的两个三角形面积相等;(2)两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;(3)夹在一组平行线之间的等底的三角形面积相等;(4)等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);(5)三角形面积等于与它等底等高的平行四边形面积的一半;(6)两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比。
在小学的学习中几何是一个很重要的部分,每一个几何图形都非常美妙,几何图形的美妙不仅来源于它的外形,更重要的是在几何模型上出现的那些美妙的规律,下面我们就一起来看看几个美妙的几何模型:1、鸟头定理:在ABC ∆中,点E 是AB 上的n 等分点,AE AB n =÷;点F 是AC 上的m 等分点,AF AC m =÷,那么ABC AEF ABCSS S n m n m=÷÷=⨯V V V 。
例1、如图,在三角形ABC 中,D 为BC 的中点,E 、F 是AC 的三等分点。
已知三角形ABF 的面积是108平方厘米,求三角形CDE 的面积。
【分析】 13ABF ABC S S =V V ,111236CDE ABC ABC S S S =⨯⨯=V V V ,所以11082542CDE ABF S S ==÷=V V (平方厘米)。
2、任意四边形中的比例关系(“蝴蝶定理”):(1)1243::S S S S = 或者 1324S S S S ⨯=⨯ (2)()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.例2、三个正方形如图排列,中间正方形的边长是3厘米,求阴影部分的面积。
2020年新人教版小升初复习专题求阴影部分面积(含答案)

2020年小升初复习专题-求阴影部分面积(含答案)目标:巩固小学几何图形计算公式,并通过专题复习,加强学生对于图形面积计算的灵活运用。
1、几何图形计算公式:1)正方形: 周长=边长×4 C=4a 面积=边长×边长S=a×a2)正方体:表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3)长方形:周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4)长方体:表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高V=abh5)三角形:面积=底×高÷2 s=ah÷26)平行四边形:面积=底×高s=ah7)梯形:面积=(上底+下底)×高÷2 s=(a+b)×h÷28)圆形: 周长=直径×Π=2×Π×半径C=Πd=2Πr 面积=半径×半径×Π9)圆柱体:侧面积=底面周长×高表面积=侧面积+底面积×2 体积=底面积×高10)圆锥体:体积=底面积×高÷32、面积求解大致分为以下几类:➢从整体图形中减去局部;➢割补法,将不规则图形通过割补,转化成规则图形。
重难点:观察图形的特点,根据图形特点选择合适的方法求解图形的面积。
能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。
例 1.求阴影部分的面积。
(单位:厘米) 例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3.求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米) 例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米,1S =S =DE AB)AD 2⨯+⨯阴梯形(=137)42⨯+⨯(=20(平方厘米)2、求阴影部分的面积。
解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是圆的半径,S =S 阴梯形=124)22⨯+⨯(=6(2cm )3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
解:S =AD AO ⨯ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。
由图形可知AED ∆是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。
解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
解:S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm , 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。
7、如图,正方形的面积 是10平方厘米,求圆的面积。
解:正方形的边长=圆的半径,设为r ,2r =10,2S =r π圆=3.14×10=31.42cm 。
8、如图,已知梯形的两个底分别为4厘米和7厘米,梯形的面积是多少平方厘米?解:由图,易知ABE ∆、DCE ∆是等腰直角三角形,所以AB=BE=4cm ,DC=CE=7cm ,BC=BE+CE=4+7=11cm ,1S =AB CD)BC 2⨯+⨯梯形(=147)112⨯+⨯(=60.52cm 。
9、如图,ABCD 是一个长方形,AB=10厘米,AD=4厘米,E 、F 分别是BC 、AD 的中点,G 是线段CD 上任意一点,求阴影部分的面积。
解:过G 点作GH AB ⊥,可知DAHG 、GHBC 都是长方形,根据狗牙模型,易知DAHG 1S =S 4∆GFA ,GHBC 1S =S 4∆GEC ,所以S =S +S ∆∆GFA GEC 阴=GHBC DAHG 11S +S 44=()GHBC DAHG 1S +S 4⨯=ABCD 1S 4⨯=11044⨯⨯=102cm 。
10、如图,阴影部分的面积是空白部分的2倍,求阴影部分三角形的底。
(单位:厘米)解:阴影部分的面积是空白部分的2倍,这2个三角形是等高三角形,阴影三角形的底是空白三角形的2倍,即2×4=8cm 。
11、如图,梯形的面积是60平方厘米,求阴影部分的面积。
解:S 梯形=60平方厘米,所以梯形的高=2×S 梯形÷上下底之和=2×60÷(9+11)=6cm。
11S =S -S 42⨯阴大圆小圆=()2211AB AB -422ππ⎛⎫⨯⨯⨯⨯ ⎪⎝⎭=221163.146- 3.14422⎛⎫⨯⨯⨯⨯ ⎪⎝⎭ =14.132cm 。
12、求阴影部分的面积。
解:由图可知,ABCD EFGC BFG 1S =S S S 2∆+-阴=221185(85)522⨯+-⨯+⨯ =24.52cm 。
13、已知平行四边形的面积是20平方厘米,E 是底边上的中点,求阴影部分的面积。
解:连接AC ,可知ABCD 1S =S 2∆ABC ,ABC ∆与 ABE ∆等高,BE=12BC ,所以ABC 1S =S 2∆∆ABE =ABCD 1S 4=1204⨯=52cm 。
14、如图,已知半圆的面积是31.4平方厘米,求长方形的面积。
解:S 半圆=31.4,圆的半径2r =2S π÷半圆=2×31.4÷3.14=20,。
长方形的宽为r ,长为2r ,所以长方形的面积=r ×2r=22r =2×20=402cm 。
15、求下图中阴影部分的面积和周长。
(单位:厘米) 解:S =S -S 阴正方形半圆=22122-22π⎛⎫⨯⨯ ⎪⎝⎭=2.43(2dm )3C =C +C 4阴正方形半圆=132+22π⨯⨯⨯=9.14(dm)16、如图,求阴影部分①比阴影部分②的面积少多少?(单位:厘米)解:如图,设空白部分三角形的面积为③,②①②③③①S S S S ++-=-=S S ∆-扇形=o2o13046- 3.1462360⨯⨯⨯⨯=12-9.42=2.582cm 。
17、求阴影部分的面积。
解:空白三角形是一个等腰直角三角形,且腰等于圆的半径,为3cm 。
S =S -S ∆阴半圆=9.632cm 。
18、如图所示,正方形ABCD 的边AB=4厘米,EC=10厘米,求阴影部分的面积。
解:根据沙漏模型,可知AF:FD =AB:DE=4:(10-4)=2:3,AF+FD=4,所以AF=4×223+=1.6cm ,ABF S ∆=1AF AB 2⨯⨯=11.642⨯⨯=3.22cm19、如图,在边长为6cm 的正方形内有一个三角形BEF ,线段AE=3cm ,DF=2cm ,求三角形BEF 的面积。
解:DE=AD-AE=6-3=3厘米,FC=CD-DF=6-2=4cm ,BEF ABCD ABE DEF BCF S S S S S ∆∆∆∆=---=1AB AD (AB AE BC FC DE DF)2⋅-⋅+⋅+⋅=216(636432)2-⨯⨯+⨯+⨯=122cm 。
20、已知梯形ABCD 的面积是27.5平方厘米,求三角形ACD 的面积。
解:AB=2S 梯形÷(AD+BC)=2×27.5÷(7+4)=5cm ,ACD S ∆=1AD AB 2⋅=1752⨯⨯=17.52cm 。
21、如图,已知一个四边形的两条边的长度和三个角的度数,这个四边形的面积是多少?(单位:厘米)解:延长BC 、AD 交于点E ,可知∆ABE 、∆DEC 都是等腰直角三角形,ABCD ABE DEC S S S ∆∆=-=11AB BE DE DC 22⋅-⋅ =22119322⨯-⨯=362cm 。
22、求下图阴影部分的面积。
解:如图,阴影的上半部分是一个半圆,下半部分是长方形与2个四分之一圆的差,这3个圆的半径都相等=8÷2=4厘米。
1S S +S -2S 4⎛⎫=⨯ ⎪⎝⎭阴圆半圆长方形=S 长方形=4×8=322cm 。
此题也可以把上面的半圆切成2个四分之一圆,补到下面的四分之一圆的空白处,可直接求出面积。
23、求图中阴影部分的面积。
(单位:厘米)解:阴影部分是一个圆环。
S S =S -S =阴圆环大圆小圆 =22R r ππ-=()22R r π-=()223.1454⨯-=28.262cm 。
24、求下图中阴影部分的面积。
(单位:厘米) 解:S S -S ∆=ABCD ABE 阴=S -S ∆ABFG ABE =EFGA S 梯形 =(EF+GA)×GF ÷2=(9+20)×10÷2=1452cm 。
25、求阴影部分的面积。
(单位:厘米)解:把左上方的弓形阴影部分割补到右下方,实际上阴影部分就是一个梯形。
梯形的上底和高都是4厘米。
S S =阴梯形=(4+7)×4÷2=222cm 。
26、求下图阴影部分的面积。
(单位:厘米)解:ECG ABG S S S S ∆∆=+-阴梯形ABCE=(CE+AB)·BC ÷2+CE ·CG ÷2-AB ·(BC+CG)÷2=(2+4)×4÷2+2×2÷2-4×(4+2)÷2 =12+2-12=22cm 。
27、求下图阴影部分的面积。
(单位:厘米) 解:半圆的半径=梯形的高=4÷2=2厘米,S S -S =阴半圆梯形=(4+6)×2÷2-3.14×22÷2=10-6.28=3.722cm 。
28、四边形BCED 是一个梯形,三角形ABC 是一个直角三角形,AB=AD ,AC=AE ,求阴影部分的面积。
(单位:厘米)解:ABC S ∆=AB ·AC ÷2=BC ×高÷2,所以,高=3×4÷5=2.4厘米。
ADB AEC S S ∆∆+=(AD AE)2+⨯÷高=(3+4)×2.4÷2=8.42cm 。
29、求阴影部分的面积。
(单位:分米)解:把上面半圆的2个弓形割补到下半圆,可知阴影部分的面积=梯形的面积-三角形的面积,梯形的高=圆的半径=4dm ,梯形的上底=圆的直径=4×2=8dm ,梯形的下底=3个圆的半径=3×4=12dm ,S S -S ∆=阴梯形=(8+12)×4÷2-8×4÷2=242dm30.如图,已知AB=8厘米,AD=12厘米,三角形ABE 和三角形ADF 的面积各占长方形ABCD 的三分之一。
求三角形AEF 的面积。
解:ABCD2S =S 3梯形ABCF =28123⨯⨯=64平方厘米。
CF 2S BC-AB =÷梯形ABCF =2×64÷12-8=83厘米,同理可求出EC=4厘米,所以S ∆AEF =ABCD 1S S 3∆-ECF =8×12×13-83×4÷2=8032cm 。
31.如图,直角三角形ABC 三条边分别是3cm ,4cm ,5cm ,分别以三边为直径画半圆,求阴影部分的面积。
